Goals and plans in decision making

Abstract

We propose a constructed-choice model for general decision making. The model departs from utility theory and prospect theory in its treatment of multiple goals and it suggests several different ways in which context can affect choice.

It is particularly instructive to apply this model to protective decisions, which are often puzzling. Among other anomalies, people insure against non-catastrophic events, underinsure against catastrophic risks, and allow extraneous factors to influence insurance purchases and other protective decisions. Neither expected-utility theory nor prospect theory can explain these anomalies satisfactorily. To apply this model to the above anomalies, we consider many different insurance-related goals, organized in a taxonomy, and we consider the effects of context on goals, resources, plans and decision rules.

The paper concludes by suggesting some prescriptions for improving individual decision making with respect to protective measures.

1 Introduction

A concept of goal (or aim, motive, purpose, etc.) has been long been taken for granted in many accounts of human behavior. Behavior is attributed to aims or goals in everyday discourse (“he wore his best suit in order to make a good first impression”), in literature (epics, novels, etc.), and in scientific discourse, for example, in the widely differing accounts in Aristotle's Ethics (circa 350 B.C.E.), William James's Principles of Psychology (1890/1950), and Kurt Lewin's Dynamic Theory of Personality (1935). Despite the obviousness and wide use of goal concepts, the dominant tradition in economics and the decision sciences has emphasized utility or value as a basis for choice. Particular goals are viewed as ways of increasing utility (or happiness). Utility can be thought of as a sort of common currency that integrates multiple goals or multiple quantitative attributes of outcomes. From this standpoint, tradeoffs among goals are attempts to maximize utility.

The view that all goals contribute to a single common currency was clearly enunciated by Plato, in The Symposium. He used the metaphor of weighing different pleasures and pains in a balance.

“And do you, like a skillful weigher, put into the balance the pleasures and the pains, and their nearness and distance, and weigh them, and then say which outweighs the other....”

(Jowett translation)

This view is central to Plato's thought, underlying his theories of education and government. Studies in mathematics, science, and metaphysics are needed to educate the “skillful weigher”, who must integrate across different goals and across near and distant times.Similar views dominated utilitarian thought in the 17th to 19th centuries, and included integration of value across individuals in a society as well as different goals and times. (e.g., Bentham, 1789).

Aristotle's Ethics, by contrast, partially disagreed, emphasizing multiple goods, and stating that the way in which different goals fit together should vary with the occasion. Aristotle can perhaps be read as advocating situation-dependent integration of multiple goals, an idea that we pursue and elaborate in this paper.

Despite this hint from Aristotle, Plato's concept of a single common currency that serves to integrate value across myriad goals has largely held sway both in general psychology and in decision science. Freud's concept of libido (1920), Beebe-Center's hedonic tone (1932), Hull's concept of generalized drive (1951), work on reward systems in the brain (Olds & Milner, 1954; Wise, 2004), and Diener's and Seligman's concepts of general happiness (e.g., Diener & Seligman, 2002) all suggest some general quality that is linked to many different goals. An exception is Keeney (1992), who advocates that decision analysis focus on separate goals and values as a starting point, rather than on goal tradeoffs as represented by overall utility.

In decision science, the concept of maximization is linked closely to a mapping onto a single dimension of utility. A bounded set of real numbers has a limiting maximum; but there is no natural total ordering of sets of vectors in two or more dimensions, and therefore no natural concept of maximization. In fact, total ordering is fundamental to most foundational theories in decision science (Savage, 1954; Krantz, Luce, Suppes & Tversky, 1971; Kahneman & Tversky, 1979; Tversky & Kahneman, 1992).

The idea that all human goods can be weighed in the same balance is a fascinating scientific hypothesis that has been worth pursuing, to determine the extent of its applicability and the ways in which it fails. Translating many goods into a one-dimensional currency fits well with human thought processes, especially analog mental models (Attneave, 1974; Egan & Grimes-Farrow, 1982). Unidimensionality opens the way to the application of powerful mathematical methods for computing or for approximating maxima (Gregory & Lin, 1992; Nocedal & Wright, 2006).

1.1 An alternative general theory

In this paper, we pursue a more Aristotelian theory of decision making, where preferences are constructed based on the decision context (Slovic, 1995), and a decision maker focuses on goals, rather than on maximizing happiness or utility. We attempt to show that this alternative approach leads to new explanations of how people make choices and raises novel questions with respect to descriptive theories of behavior and prescriptive guidelines for aiding the decision maker and improving choices.

As our title implies, the theory we present is about goals and plans. Many plans — going out to a movie, embarking on a shopping trip, purchasing insurance, or the invasion of Iraq by the United States — are or were selected with a view to achieving several different goals at once. A shopping trip is paradigmatic, because it often involves several discrete stops, each with one or more goals; but an evening at a movie may simultaneously satisfy the goals of companionship, emotional and visual stimulation, and keeping up with current culture. Insurance plans are often aimed both at financial goals and at emotional goals (“peace of mind”). We will discuss multiple goals of insurance and other protective plans in detail below.

In accord with Miller, Galanter & Pribram (1960), we regard the plan as a fundamental structural unit in decision theory. We do not consider each tiny muscle movement or each phoneme in an utterance to be a choice. Rather, decision theory offers explanations only at the behavioral level where someone (consciously or unconsciously) considers what goals will be accomplished by various possible plans, or what plan can be designed that will be likely to achieve several important goals.

Past research on plans can be unearthed from various areas of cognitive science. The area of motor control is particularly rich in evidence for (unconscious) higher-level programs governing sequences of skilled movements (Rosenbaum & Krist, 1996). Interest in movement planning is very explicit in robotics (Patnaik & Karibasappa, 2005). Planning has sporadically been considered in other theories of human and/or artificial intelligence.

One of the major virtues of considering goals and plans together is that individual decision making is brought into close analogy with organizational decision making. In the latter, goals and plans are shared among the individuals or groups that select and implement plans. For a new railroad bridge, or for an advertising campaign, the goals, the plans, and their perceived relationship are made explicit and often recorded. For an individual decision, goals, plans, and their perceived relationship are hidden within that person's conscious and unconscious cognitions and emotions, but one can try nonetheless to gather data that provide some information about these processes.

This stance also requires us to distinguish between goals and resources. Plans draw on resources to achieve goals. Some resources, such as money or favors owed, can be accumulated; sometimes, accumulation of a resource may itself become a goal. We nonetheless continue to distinguish, for example, between money considered as a resource and the same money considered as a goal.

1.2 Protective decisions and insurance

A main concern of our paper is protective decision making. In much of it, the focus is even narrower: we consider insurance decisions at length. The theory we offer is much more broadly applicable. However, we have found the narrower focus to be useful for theory development. There are many apparent anomalies in insurance decisions by individuals and households. Classical utility theory is supposed to account for decision making under risk, and especially for insurance purchase. It was not obvious to us initially that a goal/plan approach would do better than utility theory, or its popular alternative, prospect theory. Applying a multiple-goal theory in this domain has been both challenging and enlightening, compared to the more obvious examples such as shopping trips and movie excursions.

In discussing insurance choices, we start from the idea that insurance is designed principally as a device to share financial risk, for situations where many are at risk, but relatively few actually suffer a financial loss. In many cases, it is easy to share financial risk, but difficult, if not impossible, to share other risks. Having one's home burn down, for example, is extremely stressful, even if nobody is hurt. The stress may persist for a considerable period of time. Stress-induced suffering cannot readily be shared by others not directly affected by the fire, although social practices exist that can ease it. What can most easily be shared is the financial risk. Each household at risk pays a relatively small amount, the insurance premium, to participate in this risk sharing. When a participant's home does burn down, the insurer pays the contracted amount to cover some of the cost of rebuilding or purchasing a replacement home. Instead of a few cases where victims suffer catastrophic financial loss, everyone at risk bears a much smaller financial payment.

Insurance premiums must be large enough in aggregate to cover not only the total insured financial losses, but also the costs to the insurer of the risk-sharing effort.¹ Thus, premiums (unless subsidized) usually exceed average losses. In common-sense terms, and in standard economic theory, people are willing to pay more than the expected loss because they are risk-averse. Paying the premium does not lower overall utility or happiness level significantly, but suffering a large financial loss would result in a very large drop in utility or happiness. This ratio of utility changes is much greater than the inverse probability of incurring the loss, thus suggesting that individuals purchase insurance so as to maximize their expected utility.²

From a financial standpoint, anomalies arise when consumer choices with respect to insurance sometimes appear to be suboptimal given reasonable degrees of risk aversion. For example, it is common for people to pay added premiums that seem excessive to obtain automobile collision insurance with a low rather than high deductible that requires them to pay for the initial portion of the loss. To make matters worse, some decide not to file a claim following a small accident whose cost could largely be reimbursed via this low deductible³: they fear that a claim would lead to increased premiums in the next and succeeding years and/or they prefer to avoid incurring the transaction costs involved in settling the claim with their insurer. A higher deductible would have saved these individuals money before the accident and avoided the costs associated with deciding whether or not to file a claim.

A rather different example emerged after the passage of the National Flood Insurance Program (NFIP) in 1968. Insurance coverage against water damage from flooding was offered both to homeowners and to commercial enterprises in high hazard areas at subsidized low rates. Yet there was limited interest in purchasing this coverage despite the subsidy and despite the potential for catastrophic losses (Kunreuther, 1978).

As a third example, many people are prepared to pay considerably more to insure possessions that they find very attractive than to insure possessions toward which they feel neutral or negative (Hsee and Kunreuther, 2000). If such a possession is needed, then it must be replaced after loss or damage. The replacement cost remains the same, independent of one's positive or negative feelings toward the object. Since the insurance offers exactly the claims payment, it is hard to justify financially paying more for insuring the attractive than the less attractive object.

The remainder of the paper is organized in the following manner. We next (Section 2) discuss the types of insurance anomaly illustrated by the preceding three examples, and suggest psychological processes related to goals that might account for each type. Section 3 presents the elements of a quantitative theory of constructed choice, based on goals, plans, and decision weights, and contrasts this theory with the standard theory of expected utility maximization. Section 4 presents a taxonomy of insurance-related goals. Section 5 draws on this taxonomy to explain the insurance anomalies in terms of our constructed-choice theory. This section also probes the failings of utility theory and prospect theory with respect to characterizing insurance decisions. The paper concludes (Section 6) with a set of prescriptive implications concerning protective activities, based on our theory of decision making.

2 Types of anomaly

In each example presented above, people make choices that seem anomalous, in the sense that they cannot be explained on the basis of financial calculations with reasonable risk aversion. One broad class of anomalous behavior is insuring against a non-catastrophic loss. A second type is underinsuring against a truly catastrophic loss. The third category is considering factors that have little or nothing to do with magnitudes or probabilities of financial loss when making insurance-purchase decisions.

Insuring against non-catastrophic losses.  Many insurance contracts have a deductible whereby only losses in excess of that amount will be reimbursed. Thus, with a $200 deductible, a $900 loss results in a reimbursement of $700, a $300 loss yields only $100, and a $100 loss will not be reimbursed at all. Usually, the additional premium for a low deductible is set high enough so that the insurer has a positive expected value. On the average, therefore, individuals lose money by purchasing insurance with low rather than high deductibles. Nonetheless, low deductibles are popular, and a common strategy is to purchase the lowest possible deductible (Kunreuther & Pauly, 2006). A number of years ago the Insurance Commissioner of Pennsylvania, Herbert Denenberg, mandated at least a $100 deductible (rather than a $50 deductible) for automobile collision policies. Although the plan purportedly saved consumers millions of dollars it was opposed by the public and had to be rescinded (Cummins, et al., 1974).

Apart from seeking low deductibles, people insure against other non-catastrophic losses. A good example is insuring mailed packages with only modest monetary value. For people with considerable financial means, loss of personal property (e.g., jewelry, expensive stereo equipment) is often non-catastrophic, yet many purchase floater insurance to cover such items. If one insures against many non-catastrophic losses, one is nearly certain to come out behind financially, as compared with a strategy of not insuring against any of those losses. This follows from the law of large numbers, together with fact that the insurance contracts have negative expected value. As a purely financial norm, people ought to self-insure against all manageable losses; we discuss below why some do not.

Underinsuring against truly catastrophic losses.  Many people fail to purchase protection against low-probability high-impact events unless they are required to do so. Examples are the financial catastrophes that can arise from a destructive earthquake or flood, from a prolonged major illness, or from a large adverse civil judgment. For such events, the pool of individuals at risk is often large. Therefore, although the probability facing an individual is low for each of these events, some people will inevitably be victims. For those who are affected, the financial protection from insurance can make the difference between recovery of one's life pattern versus very deep and continuing difficulties. If the risk pool of individuals facing a potentially catastrophic event is large, the financial risk can be spread widely. The cost of insurance for each person can be relatively low compared to the loss should such an untoward event occur. We will discuss below some of the reasons why individuals fail to budget moderate amounts to protect themselves against such financial catastrophe through insurance and why this behavior seems imprudent.

Sensitivity to “extraneous” factors.  We group together here behavioral phenomena in which insurance purchase is influenced by factors that are irrelevant or extraneous, in the sense that they affect neither the financial costs and benefits of the insurance nor the probability of an adverse event covered by it. Factors that are often extraneous, in this sense, include: (i) the positive or negative affect attached to an object or event; (ii) recent experience of events such as flooding; (iii) what friends and relatives have decided to do; and (iv) minor transaction costs.

2.1 Psychological explanations for anomalies

To illustrate our general approach, we introduce two types of explanation at this point⁴: extra-financial goals and context effects. First, individuals consider multiple goals, not just financial ones in making insurance decisions. As a result, people sometimes purchase insurance that appears to be unattractive from a financial point of view but achieves other goals. Second, the particular context may increase or decrease the salience of some goals. A person who puts heavy weight on salient goals may decide to purchase insurance that is overpriced or not really needed, or, on the other hand, may neglect to adopt protective measures that are attractive financially.

Consider the example of flight insurance, which typically costs $5 to $10 per $100,000 of coverage. A general accidental death insurance policy that offers $500,000 for death in any common-carrier accident (including commercial airplane flights), plus many other benefits (injury, automobile accident, etc.) can be obtained for about $12 per month for one person. Thus, coverage for $500,000 for a single airplane flight is much cheaper if one gets the general insurance policy for a full month, rather than insurance for a specific flight. However, purchasing flight insurance at the airport may, for some people, provide “peace of mind” and for the purpose of such anxiety reduction may be preferred to drinking alcohol at an airport bar. A person might also purchase such coverage to demonstrate that she cares for her loved ones. These extra-financial goals might make flight insurance worth the cost. Note, however, that flight insurance usually is purchased because these extra-financial goals are especially salient in the airport context. Such coverage would probably be much less popular if policies were sold at grocery stores.

The presence of multiple goals and the influence of context are important for prescriptive analyses and decision aids as well as for understanding decision anomalies. When important and stable extra-financial goals motivate insurance purchase, one might regard the decision as anomalous from a financial perspective, but quite rational from a broader perspective of multiple goals. Such extra-financial goals need to be taken into account in formulating prescriptive aids to decision making. On the other hand, goals that arise in a particular context might be quite unstable. Someone who purchases flight insurance might regret doing so after thinking (in a more neutral context) about cheaper general accident coverage. In this case, the anomalous purchase might be viewed as a poor decision. From a prescriptive point of view one might want to develop decision aids or instructional materials that help people avoid decisions that they will regret in most contexts.

3 Goal-based models of choice

In this section we contrast a standard framework for choice theory, based on subjective expected (multi-attribute) utility, with a framework based on goals and plans, inspired by the theory of constructed choice.

People often construct or select plans designed to achieve multiple goals. Protective plans are no exception in this regard. For example, a plan to purchase fire and theft insurance (on a home, say, or on the contents of a rented apartment) may be designed to satisfy as many as seven goals simultaneously: (i) reducing the chances of a catastrophic loss, (ii) reducing anxiety about risks of fire and theft, (iii) avoiding regret and/or providing consolation in case a loss occurs, (iv) satisfying requirements stated by a bank or by a landlord, (v) presenting the appearance of prudence to others who will learn about the insurance purchase, (vi) maintaining ones relationship with an insurance agent, and (vii) avoiding highly burdensome insurance premium payments. The importance of these goals obviously varies with the decision maker, but may also be affected temporarily by contextual variables. When reflecting on paying monthly bills, an insurance purchaser may think chiefly about the goals of satisfying the requirements of the bank that holds the mortgage loan (goal iv above), and minimizing the cost of insurance (goal vii). When that same person reflects on her valuable works of art, she may think chiefly about reducing anxiety (goal ii) and avoiding regret (goal iv).

There is a subtle and important question about how such multiple goals should be represented in theories of human decision making and in prescriptive principles aimed at better decisions. If goals are viewed as stable, then the tradeoffs among different goals may well be represented at least approximately by a multi-attribute utility function. In this framework one may include non-financial goals in the utility function. If, on the other hand, context strongly influences what goals are considered and how they are weighted, as illustrated by the flight-insurance and fire-insurance examples mentioned above, then a theory of constructed choice may be more appropriate than a utility model.

The idea that preferences are constructed, rather than revealed, emerged from many lines of research in the late 1980s and early 1990s (e.g., Tversky, Sattath & Slovic, 1988, Tversky, Slovic & Kahneman, 1990, Chapman & Johnson, 1995) and was well characterized by Slovic (1995). This idea is more or less taken for granted in current psychological work on decision making (e.g., Sedikides, Ariely & Olsen, 1999; Zhang & Markman, 2001). In order to apply the idea systematically to protective decision making with multiple goals, and in order to consider its prescriptive implications, we outline and discuss a theory of context-dependent choice parallel to the theory of expected utility.

The remainder of Section 3 is structured as follows. We first present matrix structures (Tables 1 and 2) that partially represent utility and multiple-goal theories. These two matrices have similar rows (representing alternative possible strategies or plans) but interchange the roles played by columns and matrix cells. In utility theory (Table 1), the matrix columns represent uncertain events and the cell entries represent outcomes (possibly involving multiple goals). In multiple-goal theory (Table 2), columns represent goals, while cell entries represent uncertainties or distances from achieving goals. Second, we illustrate some similarities and differences between these two matrix structures, using a simplified example of a decision about whether to purchase flood insurance (Tables 3 and 4). Third, we discuss some relationships of the partially formalized multiple-goal theory to constructed choice. Fourth, we discuss possible decision rules for plan selection in multiple-goal theory, and indicate how the problem of quantitative measurement of goal values and decision weights might be solved in the context of this theory. Finally, we summarize the main advantages of the multiple-goal/constructed-choice theory.

Table 1: General strategy/event structure for decision making under uncertainty. Matrix entries are multiattribute outcomes for strategy/event combinations

Events have subjective probabilities p_j = prob(E_j)

Outcomes have subjective values u _ij= value(o _ij)

u _ij may be integrated across multiple attributes of o _ij.

Multi-attribute utility is integrated across uncertain events:

Table 2: General plan/goal structure for decision making. Matrix entries are decision weights for different goals, conditional on events

Goals have subjective values: v_j = v(G_j).

Plans have decision weights for each goal:

w_ij=w(G_j|plan i)

Plan i is evaluated in terms of the v_j and w_ij.

Table 3: Strategy/event matrix for purchase of flood insurance

Table 4: Plan/goal matrix for purchase of flood insurance

3.1 Matrix structures for utility and multiple-goal theories

In traditional decision theory, a choice among several alternative plans, each with multiple goals, is usually cast in the framework of multi-attribute utility theory (Debreu, 1960; Krantz, Luce, Suppes & Tversky, 1971; Keeney & Raiffa, 1976). To incorporate uncertainty, a decision problem is often represented as a matrix (Savage, 1954): the rows represent possible actions or strategies for the decision maker, the columns represent possible events that could occur, and the entry in any cell of the matrix (any given strategy-event combination) is a multi-attribute outcome, composed of all goals that will be achieved if that particular strategy is selected by the decision maker and that particular event happens to occur.

Table 1 depicts aspects of this model in an abstract matrix form and also indicates how the model is used for measurement and decision making. The outcome of the ith strategy, given that the jth event occurs, is denoted o _ij (cell entries). This simple notation does not explicitly show the multiple attributes or multiple goals that comprised a single outcome o _ij. In the model, each such outcome is assigned a multi-attribute utility u _ij (Keeney and Raiffa 1976). Also each uncertain event is assigned a subjective probability p _j. Each strategy i thus has an expected utility given by:

The central feature of the model is that people do or should select the strategy that maximizes U. As shown by Savage (1954), this expected-utility equation serves as the basis for measurement of outcome utilities u _ij and subjective probabilities p _j. We refer to this model as subjective expected multi-attribute utility (SEMAUT).

We contrast the matrix shown above with Table 2, which depicts aspects of the plan/goal model in a similar abstract form. Here, the ith plan yields a decision weight w _ij (cell entries) for the jth goal, G _j. This notation does not, however, explicitly show the contingencies leading to each goal. Each G _j is assigned a value v _j.

These two structures will be discussed more thoroughly below, following an example related to the purchase of flood-insurance (depicted in Tables 3 and 4). Here, we note a few important differences between the strategy/event and plan/goal structure at a more abstract level.

First, the SEMAUT matrix highlights a partition of uncertain events, leaving multiple goals embedded in the matrix cells (o _ij), while the plan/goal matrix highlights multiple goals, leaving uncertainty embedded in the matrix cells (w _ij). This difference is heuristic, rather than mathematical. Each of these representations may have advantages for some decision settings.

Second, while the rows are analogous, the terminology used is different: the SEMAUT rows are labeled strategies, while the plan/goal rows are labeled plans. For immediate purposes, one can treat these labels as synonymous. We provide reasons for our terminology later.

Finally, the SEMAUT model has a clear-cut decision rule: select the strategy i for which U(strategy i) is maximized. The values of U(strategy i) in turn depend on the u _ij and the p _j, with a clearly stated additive/multiplicative formula (expected utility). In the plan/goal formulation, we merely say that that each plan is evaluated in terms of the v _j and w _ij, without committing to any formula for such evaluation. While in fact, an additive/multiplicative formula might be useful here also, e.g.,

Anecdotal evidence, at least, suggests that many different decision rules may, in fact, be used. A focus on adoption of a decision rule is an important aspect of constructed choice theory. Below we discuss some possible decision rules (and their relationship to measurement of v _j and w _ij). Note that even if an additive/multiplicative formula is used to evaluate each plan, the resulting plan/goal model might be quite different from SEMAUT because the values of the goals, indeed, the goals themselves, might be strongly context-dependent.

The SEMAUT framework can require rather complex utility measurements (u _ij) for the conjunctions of different goals that are bundled together within one outcome o _ij. Multi-attribute utility may be especially hard to measure for the mixture of goals that are involved in protective decision making. The plan/goal structure, by contrast, demands a separate (context-dependent) value v _j for each goal. We illustrate this difference in Tables 3 and 4, in which the matrices of Tables 1 and 2 are instantiated for a simplified version of a decision concerning flood insurance.

3.2 Example: To purchase flood insurance, or not

Tables 3 and 4 have only two rows. We achieve this simplification by assuming that only one insurance policy is available, thus the only two strategies are to purchase insurance or not. In Table 3, each of the two rows is wide enough to encompass several different outcome components (financial cost, hassles, various feelings) listed as subheadings. The columns distinguish four events: E ₁, no flood; E ₂, a flood in which one manages to avoid major property damage; E ₃, a flood that leads to major property damage; and E₄, a destructive flood that causes catastrophic property damage. We treat E ₁ through E ₄ as mutually exclusive and exhaustive. For concreteness assume that these four events have respective annual probabilities 85%, 9%, 4%, and 2%. Such probabilities could be the output of an elaborate scientific model, or might represent the decision maker's best (subjective) judgment. The utility assigned to a specific outcome depends on the levels of the components, i.e., the level of financial cost, hassles, anxiety, etc.

By contrast, the rows in Table 4 are narrow, since they need contain only decision weights — in this case, just probabilities — but there are many columns, representing multiple goals.

To use Table 3 as a decision aid, one needs to evaluate subjectively some rather complicated conjunctions of consequences. For example, if one does not purchase insurance and a damaging flood occurs, what is the (dis)utility of the resulting combination of large financial loss, acute anxiety at the time of the flood, chronic anxiety prior to the flood, major hassles, and major regret? It might be difficult for a person to imagine this full scenario and how unhappy he or she would be, and therefore difficult to measure the utility of this complex outcome.

In Table 4, the flood-insurance decision is represented by a two-row matrix with eight columns, many of them corresponding to different aspiration levels⁵ for avoidance of financial loss or avoidance of negative emotions. Each of these eight goals is assumed to have its own value v _j . Avoiding a catastrophic financial loss is one goal — the minimal financial goal, since a major loss might still occur. Avoiding any major loss is a higher aspiration, and avoiding any loss, even a small one, is the highest aspiration. The values assigned to such an ordered set of goals are increments in value, as in cumulative prospect theory; thus, someone who avoided any loss would attain all three aspirations and would get all three v _j values. In Table 4, most of the outcome components shown in Table 3 have been transformed into goals, especially, losses or emotions to be avoided. Not all eight goals may be active or important for a given decision maker. Goals relating to avoidance of hassles could also be included (they are outcome components in Table 3), but we omit them here because the hassles, minor or otherwise, are unavoidable if a flood occurs, whether or not one purchases insurance. Thus, they are irrelevant to the decision. In using Table 4, the value v _j for each active goal would be estimated separately.

The rows are narrow in Table 4, because in this example, the conditions under which a given plan achieves each goal can mostly be stated as numeric probabilities, by cumulating the event probabilities from Table 3 appropriately. For example, the decision maker will avoid catastrophic financial loss and vast regret, under the no-insurance plan, provided that there is no destructive flood, an event with probability .85 + .09 + .04 = .98. Note that this cumulation of events relative to a particular goal is akin to the formalism of cumulative prospect theory (Tversky & Kahneman, 1992), and indeed, the model we present here is motivated by that theory.

3.3 Goals, plans, and constructed choice

With additive utilities, the change from Table 3 to Table 4 could be viewed as just the rearrangement of displayed information. For example, in Table 3, under strategy 1, the additive utility of “feel justified” could be separated out and multiplied by .09 + .04 + .02 = .15, corresponding to the flood events E ₂, E ₃, E ₄; while in Table 4, under plan 1, the value of attaining the goal “feel justified” would again be multiplied by the weight factor .15. In other words, we are just taking the components of multi-attribute utility from Table 3 and turning them into goal values for the columns of Table 4, and we are cumulating the event probabilities from the columns of Table 3 and inserting them appropriately as matrix entries in Table 4.

There are several reasons why the change from a strategy/event matrix to a plan/goal matrix is deeper than just a rearrangement. All of them relate to the theory of constructed choice.

Our first point is seen most easily by contrasting Tables 3 and 4 as guides to a decision about flood insurance. The SEMAUT structure incorporates feelings, but at the price of asking difficult questions about the utility of multi-attribute outcomes compounded from heterogeneous elements — financial outcomes combined with an assortment of different feelings that may arise. To elicit such utilities involves probing artificial decision situations that are likely to puzzle respondents far more than the original question about whether or not to purchase flood insurance. Preferences are constructed, not revealed, and heterogeneous goals make their construction difficult.

When we put goals first, as in Tables 2 and 4, we drop such artificial compounds. The goals whose values are elicited are simple rather than compound. There does remain the question of how the goal values v _j will be used to select a plan. The plan/goal approach moves the complications away from multi-attribute utility elicitation into the problem of evaluating plans using specific decision rules. Of course, there do exist natural compound goals that can be reported as a single column in Table 4. An example of a natural compound protective goal would be insuring against both water damage and wind damage, in a coastal zone subject to hurricanes.⁶ The plan/goal formalism can include natural compound goals as single columns, but it does not force one to create extraneous compounds. Difficult tradeoffs among heterogeneous goals are still present in the plan/goal setup, but they are taken into consideration at the level of decision rules for selecting among competing plans, not at the level of utility measurement.

Second, the goals considered by the decision maker are context dependent, as are their subjective values v(G), which function as contingent weights, in the sense of Tversky, Sattath and Slovic (1988). Context elements, including some of the plans available as options, can suggest goals that might not otherwise be considered. This is almost standard when one goes to a new restaurant, reputed to be excellent: the menu offers plans, or components that can be put together into plans; seeing what is available often leads the diner to adopt a goal that is entirely novel (e.g., ostrich livers in garlic butter) or to change the value v _j for an existing goal (e.g., a low- calorie diet). The same can be true for protective goals: one can adopt a new goal or revise the valuation of an existing goal in light of a protective device offered for sale in a catalog (e.g., a new type of car alarm) or in light of a change in the provision of an insurance contract. (e.g. raising the coverage limit could increase the weight given to peace of mind).

An innovative plan may be selected because it seems more likely that an important goal can be achieved, i.e., the decision weight w for that goal is high, for the plan in question. Here, however, we are making a different point: it is not merely that the decision weight w is high, rather, it is the value v for the goal that is changed when the particular plan (or any other context element) makes that goal salient. In the extreme, the goal might be one that was entirely unknown to the decision maker before the context made it salient. We discuss this further below in relation to Tversky-type intransitivities.

Third, the uncertain events on which outcomes depend are relegated to the cells of the matrix. In Tables 2 and 4 we show probabilities or decision weights in the cells. The thinking underlying the determination of decision weights is hidden in the matrix representation, but it has to be made explicit when one uses this model. For example, the weights in Table 4 are cumulative sums of probabilities for an ordered series of events. In other settings, decision weights may arise from subjective support, i.e., the weighing of evidence (Tversky & Koehler, 1994). Decision weights may also be affected by poor timing in the delivery of an outcome (e.g., untoward delay) or by incompleteness. This is illustrated by the entry mostly in Table 4 when referring to the impact of purchasing flood insurance on avoiding acute anxiety. One may not entirely escape acute anxiety over an impending flood by purchasing insurance, but greatly reduce it.

Fourth, Table 2 allows, but does not commit to a sum-of-products decision rule. In the next subsection we discuss three classes of rules that we think play important roles in some types of decisions, all of them different from a sum-of-products rule. Suppose a sum-of-products rule is used, and is formally identical to that used in calculating SEMAUT because the u_ij are additive multi-attribute utilities and the w_ij are sums of atomic probabilities. The plan/goal framework is still not equivalent to SEMAUT because the v_j can change with context. Among other things, such context-dependence allows intransitivity of pairwise choice.

Our final point relates to the substitution of plan for strategy. In many cases, nothing is gained or lost by this change: in non-technical contexts, the two words are more or less synonyms. However, strategy already has a technical meaning in game theory, where it refers to a choice element for a game represented in normal (rather than extensive) form. That is, a strategy specifies exactly what the player will do in every circumstance that arises in the course of playing a game. This technical meaning is one that we emphatically do not wish to convey: we view plans as hierarchically organized, containing new decision nodes within them. For example, a plan to buy insurance would not normally include a specification of how to travel from one's home or workplace to an insurance agent's office. If the latter trip becomes necessary, a new decision process is set in motion to decide how to get there. Similarly, chess players (including grandmasters) select plans, with room for improvisation; they cannot select strategies, because the number of branches in the chess tree is much too large to allow even one game-theoretic strategy to be specified fully.

Our use of plan is partly drawn from Miller, Galanter and Pribram (1960), and from the similar uses of this term in the psychology of motor performance and problem solving. Like Miller, Galanter and Pribram, we are concerned with behavior structure, and particularly with the problem of specificity level in the field of decision making. What is actually decided (consciously or unconsciously) and what is simply done pursuant to a plan already adopted (with minor parametric adjustments guided by external circumstances)? We confront this problem by making explicit the assumption that decision making is plan selection. Executing a plan usually requires many actions, but may not require any new decisions. Sometimes, a plan leaves open a choice of subplans at some critical juncture, and in that case, there is an additional decision that has to be made.

The distinction between plan selection and plan execution is related to that between categorical and continuous perception. We perceive objects on continua (size, distance, weight, friendliness, etc.) in order to adjust existing plans to reality, but we categorize objects in order to decide what new plan (or new subordinate plan) should be chosen. For example, one may be concerned about fire hazard from old papers in a storage room, and may select a plan that involves spending an afternoon clearing them out. One has categorized the papers as sufficiently at risk to adopt a goal of eliminating this specific hazard and one selects a plan that can achieve it. When it comes to executing the plan, details will vary depending on a more continuous perceptual response. If one is unexpectedly done after one hour's work, one begins to modify the plan so as to make good use of the time gained by finishing early. Similarly, a plan to seek insurance may be triggered by categorization of a financial risk as too great to ignore, but the execution of the search plan will be a function of the details of information sources about insurance plans.

3.4 Measurement issues and decision rules

Two crucial questions about the plan/goal framework in Table 2 have not yet been addressed adequately:

1. (i) measurement: How can values v_j and decision weights w _ij be measured in practice?

2. (ii) decision rule: How are these measured values combined when selecting among plans?

These questions are closely related. In one approach to measurement (discussed below), numeric values are inferred from observed choices, and this must be based on a quantitative decision rule relating observed choices to underlying v _j and w _ij.

These questions can be addressed from either a descriptive, normative or prescriptive standpoint. In the descriptive mode, one asks what plan-selection rule a decision maker actually uses in a given setting, and relates numeric values of v _j and w _ij to that decision rule. In the normative mode, one asks what decision rule(s) can be considered rational in a given setting. In the prescriptive mode one asks how one can improve the choice process for a particular problem/context given an understanding of how actual behavior (descriptive) differs from what is considered to be rational. One might aid a decision-maker by using methods to "elicit" numeric values of v _j and w _ij. These numeric values can then be used in conjunction with a normative decision rule to recommend which plan should be selected.

There remains a widespread view that SEMAUT represents rational decision making, while constructed choice represents actual choice behavior with its deviations from rationality. Based on this view, questions about decision rules in the plan/goal framework can only be descriptive. We believe, on the contrary, that the claim to rationality of SEMAUT is flawed, because the supposed preferences sometimes do not exist, but can only be constructed. SEMAUT may be an excellent deliberative preference-construction tool, for some situations, but it is no more than that. In our view, therefore, questions about decision rules and measurement have both descriptive and prescriptive aspects. Prescriptions should be based on normative principles consistent with the view that choices are constructed, rather than based on definite preferences. There still is much thinking to be done in order to attain “reflective equilibrium” between formal principles of rationality and human intuitions about good decisions; the latter are essential, albeit sometimes deeply flawed. Goodman (1955) discussed the equilibrium between inductive intuitions and inductive logic. Rawls (1972) discussed a similar equilibrium between intuitions and theories of justice. A similar equilibrium must be sought with respect to decision making, and should, in our view, consider a variety of “rational” rules for plan selection.

Measurement. For quantitative models of decision making, there are two different approaches to measurement of desired quantities: values or utilities (v _j or u _ij) and decision weights or subjective probabilities (w _ij or p _j). We refer to these two approaches as behavioral and psychophysical.

The behavioral approach mirrors the concept of revealed preference in economics: estimates of the desired quantities are inferred from an individual's choices. This approach has dominated theoretical research on measurement in relation to SEMAUT. For details and discussion, see Chapters 5 and 8 in Krantz, Luce, Suppes and Tversky (1971). It has sometimes been used, with limited success, to estimate utilities and subjective probabilities from laboratory or field observations. Tversky (1967) provided a paradigmatic example using tradeoffs between cigarettes and candy in risky and riskless situations. A broad class of later examples related to marketing research is found in the use of conjoint analysis (Green & Srinivasan, 1978; Gustafsson, Huber & Hermann, 2001).

In the psychophysical approach the desired quantities are obtained from an individual's numerical judgments or comparisons of intervals. These measurement theories are discussed in Chapter 4 of Krantz, Luce, Suppes & Tversky (1971). We mention a few of the many examples of the use of psychophysical methods, mainly tied to the SEMAUT framework: Galanter (1962), Anderson and Shanteau (1970), Seaver, von Winterfeldt and Edwards (1978), Breault (1983), and Edwards and von Winterfeldt (1987).

The behavioral approach requires commitment to a decision rule, a law linking observed choices to underlying measured values. For SEMAUT, the decision rule is maximization of expected utility. The conditions under which p _j and u _ij can be consistently measured from observed choices are given in various axiomatizations, e.g., Savage (1954), Krantz, Luce, Suppes & Tversky (1971), or Koebberling & Wakker (2004). Methods of measurement are implicit in the various constructive proofs of representation and uniqueness theorems for the expected-utility representation (Krantz, 1991).

A behavioral approach within the plan/goal framework would likewise depend on commitment to a decision rule, a specific linkage between the v _j and w _ij and the choice of a plan. Our discussion of question (ii) below suggests that several different decision rules may be used in different contexts. It therefore seems premature (at least) to axiomatize behavioral measurement procedures based on a particular decision rule. Estimating v _j and w _ij based on psychophysical judgment, or, in the case of w _ij, based on the relationship between decision weights and probabilities previously established in the literature on prospect theory, is less problematic because it does not assume a decision rule. In fact, such numerical estimates could be used to test which individuals use a particular decision rule in a given context.

Decision rules. We now turn to question (ii), types of plan-selection rule that might be considered within the plan/goal framework. We have already mentioned sum-of- products maximization, similar to SEMAUT and a generalization of cumulative prospect theory. Almost any descriptive choice model that differs from SEMAUT can be considered a candidate plan-selection rule. We discuss four here: Tversky's additive difference model, majority voting by goals, contingent weighting models, and conjunctive- choice models with thresholds.

The additive difference and majority-vote models apply only to pairwise choices. We illustrate their application to pairwise choice among insurance plans, showing that they can generate opposite intransitive cycles. Consider someone who is choosing among three plans, A, B, C, with three goals in mind: avoiding catastrophic loss; avoiding regret should a modest loss occur; and avoiding large premium payments. The three plans are shown as rows and the three goals are the columns in Table 5. The cell entries (decision weights) in this case are just verbal descriptions of how well a given plan satisfies a particular goal. Plan A guarantees protection against catastrophic loss through a high coverage limit but is expensive. Plan B is the least costly of the three plans. Plan C has lower coverage limits so that the insured will have to cover a significant portion of the losses if a catastrophe occurs; however, it has a lower deductible than the other two plans, so modest losses will not lead to regret as little will be paid out of pocket.

Table 5: Goal conflict for three insurance plans

Table 5 is structured so that for each pair of plans, there is a large, presumably salient difference with respect to one of the goals, but smaller and opposite differences with respect to the other two goals. For example, Plan B is much cheaper than A, but B has a coverage limit somewhat lower than A (less guarantee against catastrophic loss) and B has a deductible somewhat higher than A, so there is more chance of a modest loss that will lead to regret. Similarly, Plan C has a much lower deductible than B but is somewhat worse than B for the other two goals, and Plan A has a much higher coverage limit than C but is not as attractive with respect to the remaining goals.

The first thing to note is that someone might decide between any two plans by counting the number of goals that are better satisfied by each of them. This is the majority-vote rule for pairwise choice, applied here to individual rather than social choice, with the individual's goals as “voters.” This method may seem perfectly reasonable for any one pairwise choice, but in Table 5, it leads to the classic Condorcet/Arrow intransitivity, as depicted in Figure 1 (a). The figure shows that A˃B, B˃C, and C˃A, each by a "vote" of two goals to one.

Figure 1: Two bases for intransitivity

Alternatively, one might decide between two plans by evaluating the differences in the decision weights for each goal using a function that expands large differences relative to small ones, and then integrating across the goals by adding up the signed differences. This is a special case of the additive-difference theory of Tversky (1969). If the difference between excellent and OK is taken as one unit and that between OK and poor is also one unit, and if one cubes the differences (preserving sign), then the A, B difference reverses: B˃A, because the cost difference is worth 2³= 8 units, while the regret and coverage differences are each only -1. In fact, the whole intransitive cycle is reversed, as shown in Figure 1 (b).

There is strong evidence that, in multi-attribute situations, people tend to make within-attribute comparisons early and often (Russo & Dosher, 1983; Payne, Bettman & Johnson, 1993). This supports the idea that differences with respect to particular goals are evaluated first, and then integrated in making a choice. Russo and Dosher, in fact, showed that some subjects do choose the alternative that has the majority of confirming dimensions: a vote-count decision rule. One might guess that vote counts would often be used to integrate multiple differences when decision making is deliberative and tradeoffs among different goals are difficult, whereas something like the Tversky mechanism would often be used where time is short and the decision maker looks for the most salient difference between two plans.

While there have been many models for pairwise choice, fewer apply to larger sets of alternative plans. Contingent weighting models (Tversky, Sattath and Slovic, 1988) are an important class that apply to multi-alternative choice. They also relate well to context-dependent constructed choice. One could account for the Tversky-type intransitivity (Figure 1b) by contingent weighting by assuming that large differences with respect to a particular goal lead to a high weight on that attribute. In the context of the plans/goals model, a high attribute weight increases the v_j for that goal.

Finally, a threshold model is one that requires that one or more goals be satisfied to some minimum degree — the threshold is set with respect to the decision weight.⁷ An insurance purchaser who considered plans such as those depicted by Table 5 might first set a threshold of “pretty likely” for the goal “avoid catastrophic loss.” This decision-weight threshold for one goal would exclude plan C because of its low coverage limit. By eliminating C, the conflict between A and B might be resolved in favor of A (two goals to one) or in favor of B (minimize up-front cost being given a very high weight). If, instead, the decision weight threshold for “avoid catastrophic loss” were set at “nearly certain” only plan A could be chosen. A decision-weight threshold could also be set for each of two goals, e.g., “pretty likely” to avoid catastrophic loss and also to avoid regret. This would eliminate plans B and C, leaving A as the only choice. A decision-weight threshold of “nearly certain” for both those goals would create severe conflict, since none of the plans available satisfy these criteria.

In summary, behavioral measurement of v _j and w _ij, within the plan/goal framework, would depend on a particular plan-selection rule, which would have to be used both during the measurement process and in application to subsequent decision problems. Design of behavioral measurement would depend on the particular decision rule and would be facilitated by axiomatization of measurement relative to that rule. The plan/goal framework forces the decision analyst to think about what plan-selection rules are actually used for a particular problem, and about their appropriateness for prescriptive analysis. A psychophysical approach to measurement of v and w parameters would facilitate investigation of various plan-selection rules.

3.5 Advantages of the plan/goal framework

The overriding difference between the plan/goal and the SEMAUT framework lies in what questions are asked and answered most naturally. The plan/goal framework leads one to raise many different questions that are not usually considered under SEMAUT.

A strategy/event structure, as in SEMAUT, focuses on the uncertain events that determine what outcomes will occur, given the choice of a particular strategy. Consideration of the decision- maker's goals is secondary. In fact, consideration of multiple goals is inhibited, because it requires evaluating complex multi- attribute outcomes for each cell of the strategy/event matrix. A plan/goal layout focuses on active goals and asks how likely or to what extent each plan can achieve that goal. The approach is thus similar to the one taken by Keeney (1992) on the importance of values and goals as the driving force in decision making.

Since it is easy to think about each goal, the plan/goal schema is easy to apply. In analyzing a choice among plans, one tries to encompass all the goals under consideration, to ask which ones actually are considered and whether any important goals are not yet included. One also can ask probing questions about each goal. Is it a product of the particular context? Would the decision maker pursue the goal if the context made it less salient? Is a particular goal underweighted because of the context?

The plan/goal representation appears to capture the insurance decision making process, as illustrated by the following example (already mentioned in Section 1).

People often purchase flood insurance after suffering damage in a flood, but then many cancel their policies when several consecutive years pass with no flood (Kunreuther, Sanderson & Vetschera, 1985). A simple explanation, using Table 4, is that avoiding anxiety and feeling justified are both important goals. Following flood damage, anxiety is high, and reducing it is a salient goal; it is also easy to justify buying the insurance, since a flood has just occurred. Thus, plan 1 is selected, based strongly on feel justified and avoid anxiety. After several years, many people may find that the prospect of a flood no longer troubles their "peace of mind" so anxiety avoidance now has low value (v). Meanwhile, insured individuals do not feel justified in continuing to pay premiums and not collecting on their policy; the unfulfilled feel justified goal becomes more salient. The differential weighting of these two goals can lead to not purchasing insurance. Note that this theory predicts that a decision maker who puts heavy weight on the goals of avoid catastrophic loss and avoid vast regret will likely continue to purchase flood insurance year after year if the cost is modest. A decision advisor, confronting someone who wants to cancel insurance, might well ask the individual about the role played by feeling that insurance is unjustified, about the importance of having a good justification for purchasing insurance, and about whether protection against catastrophic losses might justify paying the premium.

As noted above, the plan/goal framework also raises the useful question of what plan-selection rules are used and should be used. It thus implicitly raises questions about the effects of uncertainty (w _ij) on any given goal and the effects of time delay on the importance of each goal. One can also ask whether a goal is valued for itself (v _j) or valued as a resource in pursuit of other goals. The discussion (above) of plan selection versus plan execution also leads one to ask whether choosing a particular action was based on a decision process (conscious or not) or on a previously selected plan.

4 Taxonomy of insurance-related goals

In this and the next section, we apply the general framework of Section 3 to consumer insurance decisions. Our general framework assumes that choice involves the selection of a plan among several alternative options, that most plans are designed to achieve multiple goals, and that the set of goals to which a plan is directed may or may not be fully integrated into a single coherent mental representation with a clear evaluative component. Choice context (which includes the particular set of plans made explicitly available) affects which goals are considered, what value is placed on each goal, and how each plan is evaluated. Evaluation of a plan may take into account uncertainty about achieving various goals, the time at which different goals are likely to be achieved, who is likely to benefit or lose in each case, and what resources are likely to be needed. This section focuses on the goals underlying insurance decisions, while Section 5 considers how these goals and the process of constructed choice account for anomalies in consumer insurance decisions.

We discuss five main goal categories: sharing financial risk, getting a return from an investment, emotion-related goals, satisfying legal or other official requirements, and satisfying social and/or cognitive norms.

1. (1) Financial protection by risk sharing.

   Individuals can purchase insurance at relatively low cost and be financially protected against a catastrophic loss if the negative event in question has low probability, there are many at risk, and occurrences of the event are statistically independent.

   Some people may also hope for financial protection against negative events that have relatively high probabilities and relatively small financial impacts. An example would be floater insurance that covers property that is easily movable. In this case, one does expect to make insurance claims and be reimbursed, perhaps many times during a period of years. Such a goal might be predicated on the belief — usually, but not always erroneous — that total premium payments, over a period of years, will be less than aggregate claims from the series of negative events. One believes, in effect, that the insurer will lose money in the long run. One might also hold this goal without such a belief, by simply neglecting probability considerations and focusing on the consequences if the event occurs. Failing to think about probability and believing that an insurer will lose in the long run, are cognitive errors. There is nothing paradoxical or uncommon about maintaining a goal on the basis of a wrong belief and/or an error in reasoning.

2. (2) Benefits of investment.

   Life insurance and annuity contracts sometimes combine financial protection for beneficiaries in the event of the death of the insured person with various investment benefits, such as capital accumulation and/or regularly received payments. These contracts are attractive because people do have such investment goals. Health insurance policies usually do not accumulate cash value or pay dividends, but often provide other financial benefits, such as free or low-cost annual checkups and discounts on prescription drugs.

   The ability to be reimbursed, irregularly but frequently, for small losses may be perceived as a dividend stream coming from insurance contracts with low deductibles. The goal of getting fairly regular returns can be distinguished from the goal of protection against small losses, discussed above. For the investment goal, one does not expect a net positive cash flow from the insurance; one merely expects some kind of cash-back return. In this sense, many individuals view one of the goals in purchasing an insurance policy as getting a financial return on their investment. Those who do not collect on their policies for several years period feel that their premiums have been wasted. It is hard to convince them that the best return on an insurance policy is no return at all.

   Consider the case of flood insurance. As pointed out above, many individuals who are not required to have insurance cancel their coverage if they have not made a claim over the past several years (Kunreuther, Sanderson & Vetschera, 1985). Such behavior would be understandable for people who revise the probability of a loss downward in the light of experience. Most people respond that the probability and the consequences of a similar event remain about the same as before and they are generally correct in this view.

   Furthermore flood insurance in the United States has been highly subsidized on existing homes by the federal government so that the purchase of coverage has positive expected value in addition to protecting against other catastrophic events. We hypothesize that it is unpopular because it fails to provide cash-back returns.

3. (3) Emotion-related goals.

   There is a growing literature on how affect and emotional goals impact on individuals decisions under risk (Loewenstein et al 2001; Finucane et al 2001). Three goals in this category with respect to insurance are reduction of anxiety (i.e. peace of mind), avoidance of anticipated regret and consolation. Because emotions, even anticipations of anxiety or regret, have considerable immediate presence, insurance expenditures to satisfy these goals now may lead to a shortage of funds to pursue goals more distant in time.⁸

   We noted above that for low-probability, high-impact events, one benefit from purchasing insurance is being protected against the risk of a large financial loss. In addition individuals may buy coverage to reduce their anxiety about experiencing such a financial loss. It is important to separate these two goals, financial protection against the loss and reduction of anxiety about the loss, because people vary as to the importance of each goal, situations vary in the degree to which they make financial losses vivid and to which they provoke or relieve anxiety, and the relative importance of these goals may change over time. One may also anticipate anxiety, and take measures to avoid it. For example, some people claim that they refuse to fly, not because they fear a crash, but because they anticipate and dislike being anxious about a crash. However, if one cannot avoid anxiety about a loss, one may still find opportunities to reduce the anxiety by taking protective measures, including insurance, where appropriate.

   Regret (Loomes & Sugden, 1982) is quite different from anxiety, in that it is primarily experienced after a loss occurs rather than before. Consider the example of mailing a package worth $50. Insurance may be readily available. If one does not purchase it, then if the package is lost or badly damaged, one is quite likely to wish that one had purchased the coverage. Sometimes, the emotion of regret accompanying such a wish is quite unpleasant. If, at the time of mailing, one anticipates unpleasant regret if an uninsured loss occurs, then one may decide to purchase insurance as a way of avoiding the possibility of such regret.

   Individuals may also purchase insurance as a form of consolation should they suffer a loss. In particular, if one has special affection for an item, such as a piece of art, then the knowledge that one can make a claim should the item by destroyed or stolen has special meaning to the person. Hsee and Kunreuther (2000) attribute the need for consolation as the reason why individuals are willing to pay higher premiums for the same amount of coverage for objects they love than for those where they don't have special feeling.

   Usually, a strong positive attachment to an object either has no effect on the probability of damage, theft, etc., or may even reduce this probability, if extra care is taken. Indeed, in a recent study of willingness to purchase warranties (Piao & Kunreuther, 2006), subjects believed that loving an object made it seem less likely that the object would need repair than if one was neutral or disappointed with the object. This was true whether or not statistical information about repair frequencies was given. This same study also showed that love did not, on average, produce a significant change in the anticipated cost of repair. If anything, anticipated cost decreases for objects that one loves. People should thus be less willing to purchase warranties for loved objects than for ones for which they have no special affection, but, in fact, are more willing to do so.

4. (4) Satisfying requirements.

   Insurance coverage is often mandatory. Automobile liability insurance is required by most states, homeowners insurance is normally required by mortgage lenders, flood insurance must be purchased as a condition for a federally insured mortgage in special flood hazard areas, and malpractice insurance is needed for several different professions.

   In these cases, purchase of insurance may be viewed as a subgoal for meeting endgoals such as owning a car or a home or practicing one's profession.

5. (5) Satisfying social and/or cognitive norms.

   Many insurance decisions are based on what other people are doing, or on what respected others think is an appropriate action to take. For example, a new parent may purchase life insurance mainly because his or her own parent, partner, or financial advisor thinks that it is important to provide protection for the spouse and child, and the amount purchased might follow some standard guideline (e.g., three times annual income). Once again, multiple goals may come into play: the new parent may be trying to achieve goal (1), financial protection of the family against a low-probability high- impact event, but also may be trying to do what others expect or wish.

   There is also empirical evidence that purchase of insurance, like adoption of new products, is based on knowledge of what friends and neighbors have done (Kunreuther, et al., 1978). There is a vast literature on social influence, some of it especially relevant to protective decision making (e.g., Riad, Norris & Ruback, 1999). For present purposes, however, we mainly want to distinguish between "non-extraneous" social influence — those actions and opinions of other people that provide useful information to a decision maker about the probability of a catastrophic event, about the likely consequences of such an event, or about the nature of insurance plans that could be advantageous — versus social influence that seems extraneous, in the sense used here.

   A clear-cut demonstration of extraneous social influence would show an associated change in the likelihood of selecting a particular plan involving insurance that is unaccompanied by changes in beliefs about the probabilities or consequences of a loss event. An illustration of this behavior came from a pretest interview of an earthquake questionnaire when a homeowner hearing that his neighbor had purchased earthquake insurance indicated that he would want to buy such coverage himself without changing his beliefs about the risk he was facing or knowing about the actual cost of coverage (Kunreuther, 1978).

   Numerous other examples can be cited. In our discussion of flood insurance using a plan/goal matrix (Table 4), we introduced feel justified as a possibly important goal. Someone who purchases flood insurance soon after suffering damage from such a disaster may do so in part because it is easy to justify the expenditure by pointing to the flood that just occurred. Cancellation of insurance coverage after some years of coverage may occur by using the social norm that it is hard to justify an expenditure that has not paid off.

   In fact, people are concerned with justifying their decisions to themselves and others (Shafir, Simonson & Tversky 1993). In the process, people often use arguments that have little to do with the tradeoffs between the cost of insurance and the expected loss that forms the bases of economic analyses of insurance or warranty transactions (Hogarth & Kunreuther 1995).

5 Explaining insurance decisions and anomalies

In this section we examine whether SEMAUT, Cumulative Prospect Theory (CPT), and the present model of constructed choice can explain what appear to be anomalies or suboptimal insurance decisions. It will be obvious that one of our reasons for preferring the constructed-choice model to SEMAUT has to do with the context-sensitivity of insurance decisions. We argue, however, that quite apart from this criticism, neither SEMAUT nor CPT comes close to describing the realities of insurance.

5.1 The expected-utility account and its limitations

We begin by considering the simple classical account of insurance decisions, based on a concave utility function for total assets. Since insurance contracts normally have negative expected value, it is natural to account for the fact that people do purchase insurance by hypothesizing a risk-averse (concave) utility function U(A), relating utility U to total assets A. Such a concave function accords with the more qualitative concept of catastrophic loss. Compare the reduction in assets by a loss L or by a loss one tenth as large, L/10. For a concave curve, the decrease in utility for loss L is more than 10 times larger than the decrease for loss L/10. Thus, the decision maker prefers to make a premium payment Q = L/10 rather than to accept a 10% chance of the loss L. More generally, the decision maker prefers to pay premium Q rather than to accept a probability p of loss L if and only if

(1)

We next give a concrete example, both to illustrate the reasoning given above and as an introduction to the limitations of this idea. Suppose that a decision maker has an exponential utility function for total assets, specifically:

(2)

This utility function approaches an asymptote of 1 for very large A; the parameter A ₀ is the asset level for which utility difference from zero asset level is about 63.2% of the difference between zero assets and the saturated maximum utility level.

Note that 1/A ₀ is usually thought of as the Arrow-Pratt measure of absolute risk aversion, i.e., it is the curvature ‒U ^″/U ^′ of the utility function. The exponential function is often used because it has the simple property that absolute risk aversion is independent of asset level A. Here, however, we find it more useful to interpret A ₀ as a gauge of the magnitude of a loss L. To do this, we view zero assets as a natural reference point. An increment or decrement in assets of A ₀, which spans over 60% of the utility range between zero assets and the utility asymptote can safely be classified as a large gain or loss. The usual (Arrow-Pratt) interpretation of A ₀ is local: its inverse is the curvature of the utility function. By treating zero asset level as a natural reference point, we are able to give it this more global interpretation.

An example: the "loading" factor of an insurance contract. Consider a household with total assets of $300,000, including a home worth $200,000, and suppose that for this household, A ₀ happens to be $100,000. Suppose that the probability of a severe fire or natural disaster that would destroy its home is about 1/400 per year. By the preceding criterion, the loss of $200,000 would be viewed as a large loss for this household. Its expected annual loss, however, is $200,000/400 = $500. The household might be able to purchase insurance that would fully reimburse a $200,000 loss for about $1000 annual premium: this would allow the insurer to pay claims, cover administrative costs, and make a profit. Because of the sharp curvature of the exponential utility curve, the household should be happy to pay $1000 annually for this coverage; in fact, with this utility function, the maximum value of Q that satisfies inequality (1) is about $1585.

This account of insurance seems plausible in the given example. However, it does not fare well when it comes to smaller losses. First, at the opposite extreme, it predicts unwillingness to pay much more than an actuarially fair price to eliminate deductibles.

Suppose that the household under discussion has a 1/20 chance per year of fire or damage producing a loss of $1000 or less. Its utility is nearly linear with money over a range of $1000, and so the household should be willing to pay only a few cents more than the expected loss to eliminate a $1000 deductible. In fact, the premium increases substantially to eliminate a $1000 deductible, and many people are willing to pay it.

Even if one is willing to treat behavior vis-à-vis deductibles as an anomaly that the theory simply does not address, there remains the problem of insuring against intermediate losses. Consider the household in the above example with a home worth only $100,000 that could be destroyed by fire or natural disaster. The expected annual loss is cut in half, to $250, but because of the concavity of U, willingness to pay for insurance drops by more than a factor of 3 to less than $430. If the household can insure a $200,000 home for $1000, the premium for a $100,000 home will be at least $500; and so the theory predicts that it would prefer to self-insure for $100,000!

This is not a minor anomaly. Many types of insurance contracts have loading factors of 2.0 or more: the insurer charges at least twice the expected loss, in order to cover claims with a safety factor, cover administrative costs and make a profit. Homeowners insurance, even with a large deductible, generally has a loading factor of more than 2. For example, Sydnor, 2006 reports a loading factor of 2.6 in one western state for policies with $1000 deductible, and much larger loading factors for decrements in the deductible. The first example shows that for a loss of 2 A ₀, with probability 1/400, the maximum acceptable loading factor for the household in question is $1585/$500 = 3.17, a quite reasonable figure. But if the loss in question is only A ₀ = $100,000, the maximum acceptable loading factor is $430/$250 = 1.72, a value that might be difficult or impossible to find in the market for homeowner's insurance.

Maximum acceptable loading factor for a discrete loss L. One can solve inequality (1) and equation (2) for the maximum premium, Q, that a household is willing to pay, as a function of the loss L and the probability p, and ask when the ratio Q/pL will be at least 2. Figure 2 shows a contour plot of the maximum acceptable loading factor, Q/pL. Here L, the horizontal axis, is scaled in units of A ₀. In the above example, 1 unit is $100,000. The vertical axis is just probability, confined to the domain of reasonably low-probability events. What the figure shows dramatically is that acceptance of loading factors of 2 or more requires losses that are at least 1.4A ₀ (increasing to 1.6 for higher loss probabilities). All the maximum acceptable loading factors exceed 1; thus, as we already knew, exponential utility leads everywhere to insurance seeking; but under this theory, realistic prices will be paid only for insuring losses that are large, on the scale of the 63.2% saturation constant. Since even wealthy people routinely insure possessions worth a few tens of thousands of dollars, accepting loading factors of 2 or more, the theory is contradicted widely by actual consumer insurance behavior.

Figure 2: Maximal acceptable loading factor for insurance (exponential utility)

Since Figure 2 is scaled by A ₀, it is hard to argue that the conclusions would be changed by any plausible degree of risk aversion. To explain why a millionaire would insure a $50,000 possession with an insurance loading factor around 2, one would have to assume that $50,000˃1.4A ₀, or A ₀ <$35,000. But for the millionaire, a loss leading to total assets of only $35,000 would be a financial disaster.

Similar calculations could be made for more realistic scenarios, in which there is a continuous probability distribution of losses rather than a discrete probability for a single known loss, and with alternative concave utility functions. Calculations with hyperbolic and power utility functions (for which the zero asset level is a very clear reference point) suggest that results similar to those in Figure 2 are fairly general.

Note that Figure 2 makes it easy to see why the exponential utility fails to account for decisions to have low or zero deductibles. In the extreme case, for a loading factor of 2 to be acceptable for eliminating a $100 deductible, so that one has full coverage, the individual must satisfy the equation $100 ≈ 1.4 A ₀, thus, A ₀ ≈ $70. This means that the decision maker in question would prefer a sure $70 over a 60% chance to win billions of dollars⁹

In light of the fact that people do insure against small and intermediate losses, and in light of the discussion of insurance-related goals in Section 4, one may wish to modify the preceding simple theory by using the full strength of SEMAUT to incorporate multiple goals for insurance decisions, while retaining the core idea of a concave utility function for total assets. In Section 3, we suggested one reason why this might be difficult, or might lead to an unsatisfactory theory. Permanent goals with stable tradeoffs might indeed lend themselves to such a theory. Goals that are context dependent and hence influenced by what appears salient and/or goals that are suggested by the very alternative plans among which the decision maker must choose can not be incorporated in a SEMAUT model.

In addition to the above argument based on context-dependence, there is another reason why SEMAUT cannot explain behavior. This is the phenomenon of reference dependence, which provides a segue to discussing Prospect Theory. Many financial goals are perceived as deviations from the status quo, rather than as changes in total assets. The exponential utility function partially deals with this perception, since its prescribed choices among lotteries are independent of wealth and can thus be interpreted in terms of increments and decrements from the current asset level. However, even with an exponential utility curve, expected utility theory does not account for the difference between loss framing and gain framing for the same increments and decrements. For example, many owners of relatively new automobiles would be happy to pay a $40 additional premium per year to have a small deductible, say $100, on their collision insurance, rather than a $500 deductible on an otherwise identical insurance contract. Yet the same owners would balk at paying $40 for a lottery ticket that wins $400 just in case their automobile happens to suffer appreciable collision damage during the coming 12 months. One would view such a lottery ticket as unlikely to win; moreover, the prize is not very large, even if one does win. So $40 seems much too high a price. From the standpoint of utility theory, however, the lottery ticket is at least as valuable as the lower deductible on the insurance contract. The lottery ticket nets $400 if there is appreciable collision damage. The insurance contract nets the full $400 only if the damage exceeds $500.

5.2 Prospect theory and its limitations

Characteristic features of prospect theory. Prospect theory (Kahneman & Tversky, 1979) was developed as a descriptive account of risky choice. One important type of context effect — the effect of reference point — is accepted as an empirical fact and used as a starting point for the theory. Current assets serve as a reference point, relative to which losses are differentiated sharply from gains, and are valued quite differently. The theory replaces the concave utility function for total assets with a value function that has one branch for changes perceived as gains and another for perceived losses. Investigations of lotteries with known probabilities and gains or losses as outcomes led to a specification of the general form of the value function — concave for gains, but convex for losses — and to a general form for decision weights as a function of specified probability. Decision weights are applied as multipliers to the values that arise from gains and losses. For present purposes, the most important feature of the decision weight is that low probabilities, the ones most relevant in insurance contexts, are overweighted.

Cumulative prospect theory (CPT) was developed by Tversky and Kahneman (1992) for multi-outcome lotteries. It deals with the phenomenon of rank-dependence of the decision weights that are applied to particular gains or losses. This has become the standard form for the theory. For our simplified examples, where the insurance decision compares a sure loss of Q (i.e., the premium paid) with a chance p to lose L (otherwise nothing), the distinction is unimportant, but we continue to use the acronym CPT.

As a sidelight on CPT, one interpretation of rank dependence might be that multiple gains or losses are construed by the decision maker as defining a set of goals. For example, consider a lottery in which one wins $1000 with probability 1%, $50 with probability 9%, and otherwise (90%) nothing is won or lost. The CPT value for this lottery can be written in the following form, where V(x) is the value for gain x and W(p) is the decision-weight for probability p.

(3)

One can interpret this in terms of two goals: getting at least $50, and getting $1000 rather than $50. The first term multiplies the value of the first goal [V(50) - V(0)] by a decision weight based on the cumulative probability (9% + 1%) of achieving it, the second term similarly multiplies the incremental value of the second goal (given that the first has been achieved) by the decision weight for 1%. This makes sense when goals are ordered, as they often are (e.g., getting at least a cost-of-living salary increase, then perhaps getting a large increase; at least not losing a chess game, then perhaps winning the game). It is this form of the equation that suggested the general sum-of-products decision rule for combining goal values with decision weights in Table 2, i.e., ∑ v_j w_ij, and thus led to the more general discussion of possible decision rules in a plan/goal framework.

CPT and insurance. Explanations of insurance decisions based on CPT differ in a fundamental way from ones based on expected utility. The CPT value function is convex, not concave, in the loss domain — the opposite of what might be thought appropriate for explanation of insurance purchases with negative expected value for the purchaser.

This shape is strongly supported by robust and oft-replicated laboratory findings that decision makers are risk-seeking, not risk-averse, in the domain of losses. The question arises as to how to reconcile two basic facts: people are risk-seeking with respect to losses, yet willing to insure against losses.

The usual CPT explanation of insurance purchase is based entirely on decision weights, rather than gains and losses: people exhibit high decision weights to low-probability events. This means that they are willing to pay more than the expected loss for insurance.

This explanation has some intuitive psychological plausibility: people worry (sometimes excessively, sometimes not) about low-probability high-negative-impact events, and give them high weights in decision making. Within the standard parameterization of CPT (Tversky & Kahneman, 1992), however, this explanation is not viable quantitatively, as we show next. Corresponding to Inequality 1, the CPT condition for paying premium Q to insure against loss L with probability p is simply this:

(4)

Define the maximum acceptable loading factor as ⋋ = Q/pL, where Q is the maximum willingness to pay for the insurance. Combining this with Inequality (4) gives

V(-⋋ p L) = W(p) V(-L). In the standard parameterization of CPT, however, V is a power function (using absolute values) with exponent ∝. This means that the factor L ^∝ drops out of both sides of the above equation, giving a simple formula for ⋋ as a function of p:

(5)

Therefore the maximum acceptable loading factor is a function of loss probability and is independent of L. In Figure 2, depicting the exponential utility, the loading-factor contours are fairly vertical, i.e., they depend mostly on L and only weakly on p, especially for low or intermediate losses relative to the saturation asset level, and for p˃1/100 . By contrast, in CPT the corresponding contours would be perfectly horizontal, depending only on p and not at all on L. Consequently, rather than plotting loading-factor contours in (L, p) coordinates, we simply plot maximum loading factor as a function of p.

The solid (lower) curve in Figure 3 shows the plot of equation (5), using the standard CPT parameterization of W(p) for losses. The maximum acceptable loading factor is already below 2 for p˃ 2.6%, and falls below 1 for p˃ 25%. People with maximum loading factor below 1 will not purchase insurance even when the transaction has a positive expected value.

Figure 3: Loading factors in Cumulative Prospect Theory (standard parameterization).

The loading factors below 1 are perhaps not fatal for CPT: negative events with probability over 25% are unlikely to have high impact (or we would all be in sorry shape), and it may be both difficult and undesirable to insure against them. However, loss probabilities in the range between 3% and 10% are staples of insurance sales, mostly at loading factors above 2. Thus, CPT, in its usual form, simply cannot account for the market for insurance.

Figure 3 carries the calculation of loading factor down to a loss probability of 1/100; but in fact, another problem for CPT is that the probability weighting function derived from laboratory experiments cannot be extrapolated to very low probabilities, because at some point many people in effect round a low probability down to 0, saying “this means it won't happen to me.” Thus, CPT does not really deal with insurance against events with very low probability but very high negative impact.

An alternative interpretation. Sydnor (2006) examined loading factors for deductibles in homeowner's insurance. He reached a similar conclusion: neither expected utility (where he focuses chiefly on the power, rather than the exponential form for the function U) nor CPT in its standard form can account for people's purchase of low deductibles. However, Sydnor suggested an important variant of CPT, according to which payments made for purchase (including premiums for purchase of insurance) are treated as negative gains, rather than as losses. This is the “NLIB” (no loss in buying) interpretation (Novemsky & Kahneman, 2005). This assumption changes inequality (4): V(–Q) is replaced by –V(Q), i.e., losing Q is replaced by losing the value that corresponds to a gain of Q. The inequality becomes:

(4‵)

In the standard parameterization of CPT, the ratio –V(Q)/V(–Q) is 1/2.25, the inverse of the loss-aversion coefficient. The NLIB assumption therefore leads to the loading-factor equation

(5‵)

This is shown as the dashed curve in Figure 3. Since ∝ = 0.88 in the standard parameterization, the dashed curve is about 2.5 times higher than the solid curve. The loading factors given by this curve do not reject prospect theory out of hand as an account of insurance purchase. This is consistent with Sydnor's conclusion for deductibles on homeowner's insurance policies.

In short, Sydnor interprets willingness to purchase insurance as principally an effect of framing: though people are risk-seeking in the domain of losses, reframing a sure loss as payment of an insurance premium eliminates the loss- aversion factor for the premium, and then the overweighting of low probability for potential losses covered by the policy makes the insurance policy attractive. As Figure 3 shows, Sydnor's theory makes strong quantitative predictions about willingness to pay for insurance: the maximum loading factor should be independent of loss magnitude, and people should purchase insurance at loading factors of around 2.0 even for loss probabilities between 1/2 and 1. These predictions, which seem unlikely to be confirmed, could be tested more extensively in laboratory and field studies of acceptable insurance contracts.

Overweighting, underweighting and neglecting probabilities. There is a more fundamental difficulty with the CPT account of insurance purchase and Sydnor's variation of the theory. People considering insurance contracts rarely, if ever, have available explicit loss probabilities. Often, loss probability does not seem to play a role in their decisions (Camerer & Kunreuther, 1989; Hogarth & Kunreuther, 1995; Huber, Wider & Huber, 1997). When loss probability is in fact considered, it is derived from experience, not from actuarial tables. However, Hertwig et al. (2004) showed that when the probabilities are based on experience, rather than on statistical summaries, people underweight low probabilities in making risky decisions except when there has been a very recent occurrence of the event class in question. Such underweighting could, of course, be one important factor in phenomena such as the cancellation of flood insurance policies that was noted above; it may not be easy to separate underweighting of the probability from the difficulty in justifying a decision to renew an insurance policy and from fading anxiety. In any case, the overweighting postulated in CPT may not be relevant to most insurance decisions.

It also seems implausible that people's willingness to pay for insurance is linked tightly to probability of loss and not at all to magnitude of loss. On the one hand, people often neglect probability in their thinking about insurance; on the other hand, people undoubtedly pay some attention to the affordability of losses. Insurance protection against very small losses, e.g., breakage of glassware in one's kitchen, would be viewed as absurd. The power-function formulation of the CPT value function leads to willingness to pay that is scale free, as shown in Equation 5 and 5^′ above. This is one of the great conveniences in applying CPT — it does not matter whether the monetary amounts are dollars, Euros, or yen. But from the standpoint of insurance, it is a weakness. Losing 100 yen is much less serious than losing 100 dollars, and it is implausible that the loading factor for insurance will be exactly the same. In the domain of insurance, utility theory makes more sense psychologically, since it postulates that magnitude of loss does matter considerably. It would, of course, be possible to replace the CPT value function by a family of functions that do reflect the underlying scale of gains and losses. The family of functions could be constructed to be linear over some range of sufficiently small losses and gains, to be concave for gains and convex for intermediate losses, and finally, to have another concave region corresponding to catastrophic losses for a given decision maker. Even such a function, however, would fail to account for insurance decisions that are based on multiple goals. In our view, a satisfactory understanding of insurance behavior needs to take into account the behavioral evidence that a number of different goals are sometimes considered in connection with insurance and other protective decisions. It is to this multiple-goal perspective that we now turn.

5.3 Explanations based on constructed choice

In the introduction we noted three classes of anomaly: (1) insuring against non-catastrophic losses, (2) underinsuring against truly catastrophic losses, and (3) exhibiting sensitivity to “extraneous” factors. In exemplifying these anomalies, we have already indicated several ways in which the theory partially explains behavior.

Our classification of anomalies assumes that the main goal for insurance purchase is protection against catastrophic financial loss. Failure to pursue this goal, when it is readily attainable, as well as pursuit of other goals are viewed as anomalous. It is natural to explain these anomalies in terms of the alternative goals that people do in fact pursue, such as avoiding regret, reducing anxiety, getting a return on investment, or satisfying social norms, as suggested in our taxonomy in Section 4.

According to the plan/goal account, choices depend not only on goals, but on the decision rules used in plan selection. For example, the discussion of possible intransitivity with multiple goals (Figure 1) indicated how particular decision rules might increase the tendency to choose a low deductible and/or decrease the tendency to insure fully against a catastrophic loss.

5.3.1 A process-oriented schema for constructed choice

In the remainder of this section, we focus on some of the main cognitive processes involved in choice according to the plan/goal theory. To this end, Figure 4 offers a process-oriented schema for context-dependent constructed choice. The four dark arrows indicate some of the psychological functions essential to plan construction and plan selection, while the five dotted arrows indicate mechanisms of human perception or memory through which context influences plans, goals, resources and decision rules.

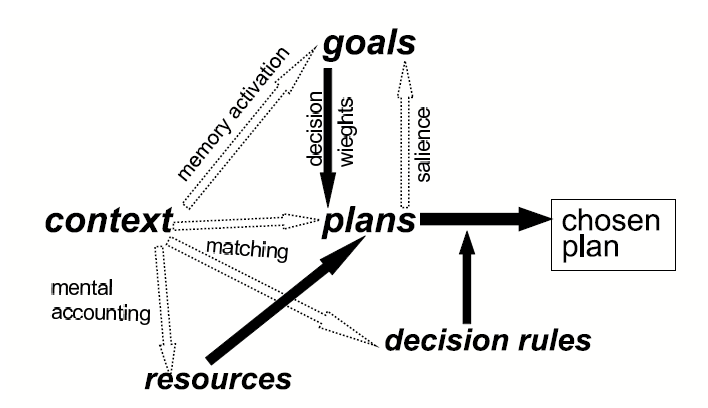
Figure 4: A schema for constructed choice. (Dashed arrows show context effects.

Central to the schema, as discussed in Section 3, are goals and plans. The heavy downward arrow from goals to plans indicates the main way in which goals bear on plans: via decision weights w _ij. Psychologically, this arrow corresponds to the decision maker's beliefs about the likelihood of attaining goal j, or the degree of approximation to goal j, if plan i is selected.

There is also an upward, dashed arrow from plans back to goals. This represents a feedback process, whereby a plan that is considered suggests additional goals that could be achieved through that plan, or, more generally, alters the importance values v _j for the various goals. This feature was discussed at length with respect to Table 2. As examples in which a goal is suggested or emphasized by a plan, a person may consider installing a protective device after seeing one offered for sale in a catalog, or may opt for an innovative provision available as an option in an insurance contract. We emphasize that this is not merely a question of a plan being attractive because it gives a high decision weight w to an existing important goal. Rather, it is the value v of the goal that is changed when it is made salient by the plan. In the extreme, the goal may have been unknown, in effect, v = 0, prior to the decision maker's considering a particular plan.

The upward feedback arrow is one of five dashed arrows, each suggesting a different route by which context can affect constructed choice. We regard this feedback as a context effect because the plans initially presented for consideration constitute an important part of the choice context. In a fluid situation, where novel plans can be sought and constructed, the two arrows reciprocally linking goals and plans could be activated repeatedly.

The dashed arrow directly from context to goals represents another type of contextual influence. This arrow is labeled memory activation (Cantor & Engle, 1993), because the context serves as a memory cue to activate concepts and thoughts related to particular goals. For example, if one recently regretted one's failure to purchase insurance, then thoughts about the possibility of a similar loss will remind one of that recent regret, and might thus strongly activate the goal of avoiding regret. Similarly, if one experienced anxiety because of lack of insurance, a contextual reminder of that anxiety might strongly activate the goal of avoiding future anxiety. More generally, most effects of context on emotion-related goals are tied to this arrow.

Context can also affect what plans are available and what decision rule is used to select a plan. These two dashed arrows in Figure 4 are labeled with another process in human memory: matching (Seifert, et al., 2002). Generally speaking, matching is linked to recognition: a present stimulus matches something stored in memory. Here, the matching process establishes a correspondence, or partial analogy, between the current choice context and some familiar situation. Finding such an analogy often leads the decision maker to recall the plan selected previously, and to select a partially analogous plan. Context thus adds to the set of plans under consideration. For example, if one has decided in one situation to self-insure (or not) against small losses, one may in a different but partly analogous situation seek an insurance plan with a high (or a low) deductible.

Alternatively or additionally, if there is severe conflict concerning the available plans, the decision maker may recall the method used previously to resolve the analogous conflict. Thus, context can make an additional decision rule available. This is most obvious in cases where analogy is used to support a complex decision rule, such as estimation and maximization of subjective expected utility, but context can also suggest simpler decision heuristics. For example, if one has previously simplified a decision problem by eliminating some of the available plans (e.g., by setting a threshold decision weight for an important goal), one may be led to attempt a similar simplification in the current choice situation.

The final dashed arrow in Figure 4 goes from context to resources. One psychological process that can mediate this influence is mental accounting (Kahneman & Tversky, 1984; Thaler, 1999); we use it to label this arrow. Changing the arrangement of mental accounts may either increase or decrease the resources available to solve a decision problem, and may thus suggest new plans or eliminate plans that draw on untapped resources. Here is an illustrative anecdote. A couple planning a temporary partial move to a not-too-distant city was considering how to manage their two owned vehicles through the duration of this move. Each plan considered had severe disadvantages. In the context of a recent car rental, however, it occurred to them that in addition to their existing vehicles, money could be used as a resource to solve transportation problems. They could simply lease an additional vehicle in the new city. Although this solution involved additional expense, it seemed superior to previously considered plans. As long as their mental accounting only concerned the management of existing vehicles, the better solution was unavailable; their insight was that money could be added to the resources already in play.

Insurance decisions are often influenced by considerations related to resources. A person might choose not to pay a $150 annual premium for general accident insurance (paying $500,000 for loss of life in any accident involving a common carrier), but might pay $25 for $500,000 insurance on a single flight. The $150 annual premium could be reframed temporally (less than $3/week), or it could be framed as an expenditure within an insurance budget (find the needed $150 by increasing the deductible on homeowners and/or automobile collision insurance), or yet alternatively, it could be framed as an expenditure within a general household budget (save $150 by bring lunch from home every day for two months). Context (including advertising) determines how such an expenditure is framed.

Without going into great detail, we remark that under the plan/goal theory, mental accounting is not always “irrational.” A decision rule that treats each of several goals as extremely important might well lead to selection of a plan that sets aside or otherwise designates resources devoted to each goal. As noted in Section 3, such decision rules cannot be considered irrational. Indeed, group decisions (by governments and other organizations) use explicit budgets as a resolution of goal conflict. For individual decisions, similarly, resolution of large intra- individual goal conflict may only be feasible through such accounting, whether done mentally or through written budgets, dedicated savings, etc. Yet excessive rigidity in accounting may indeed be irrational: this is shown most clearly when small shifts in context lead to redrawing the boundaries of such accounts.

Figure 4 provides a rich set of possible mechanisms that should be considered in a general theory of decision making and in particular as they relate to insurance anomalies. The first two classes of anomaly, insuring against non-catastrophic losses and underinsuring against truly catastrophic losses, relate directly to the multiple goals involved in selecting an insurance plan. Since goals can be made salient by plans, and salient goals may dominate the decision rule that is used to choose a plan, it is easy to see how marketing of insurance plans affects choices, and how the default settings for parameters within insurance plans also affect choices. Flight insurance is sold at airports, package insurance at post offices, credit-balance life and disability insurance is offered to credit-card applicants and bill-payers, dormitory theft insurance is offered to parents of college students, etc. In all these cases, the available insurance plans make salient one or more goals that might get little or no weight in a different context. Insurance plans also define temporal frames for planning (e.g., month, year, or lifetime), and thereby affect mental accounting and alter the perceived resources available.

The mechanisms shown in Figure 4 also help explicate some of the effects of "extraneous" factors on insurance decisions. Positive or negative affect attached to an object or event activates emotion-related goals. Thus, thinking about the possible loss of a loved object activates a goal of avoiding regret, and insurance may be perceived as reducing regret, even though the financial benefit of the insurance is no greater than in the case of an unloved (but needed) object. We have already discussed how recent experience of events, such as flooding, can also activate emotion-related goals.

What friends and relatives advise or themselves decide to do is often extraneous, i.e., it does not change the set of plans available or expectations about probability or magnitude of loss. Adherence to quasi-legal or legal norms and to social norms is itself an important goal, however, and may strongly influence the selection of a plan. Sometimes the decision rule itself may be no more complicated than adherence to a clear norm. One may purchase insurance (or not) simply because that is the expectation of one's boss or one's spouse. One may start wearing a seat belt because it is the law to do so. There are also important cases of formally mandated protection: examples include homeowners insurance, automobile liability insurance, and professional malpractice insurance, as well as fire-safety inspections, required fire drills, and seatbelt requirements. Large employers in the United States provide group health and life insurance. We also note the important role of defaults (which in many cases can be viewed as social norms) in affecting the details of chosen insurance plans. Being able to justify decisions is itself an important social norm; protective actions that other people select themselves define a norm, and in addition, doing the same is unlikely to be challenged or will be easy to justify.

5.4 Novel prescriptive questions in constructed choice

The goal/plan approach to decision making raises prescriptive questions of a sort not addressed in previous work on constructed choice. Consider the original loss/gain framing demonstration of Kahneman and Tversky (1979). The intent was purely descriptive: gain framing produces risk aversion, while loss framing, for logically equivalent outcomes, leads to selection of the risky plan. There is no guidance about which frame, if either, should be used. Advice about the right choice would presumably be given on an entirely different basis, maximization of expected utility. In the constructed choice framework, however, the “true” preferences that lead to maximization are mythical: all choices are context-dependent. In the absence of other prescriptive guidance, one is forced to consider whether a given problem should be framed in terms of a loss or gain.

In what follows, we discuss in greater detail the two features of our theory that are especially important for understanding insurance anomalies. That plans available in the decision context can suggest new goals leads to insights about insuring against non-catastrophic losses and about sensitivity to extraneous factors. We mention several additional examples. The idea of decision mechanisms involving decision-weight thresholds for important goals helps us to understand failures to insure against truly catastrophic losses.

5.4.1 Goals suggested by plans

The very idea of risk sharing through insurance was once a novel family of plans. Prior to its invention, some severe financial risks (especially in shipping and trading over long distances) would have seemed unavoidable. The advent of insurance plans would have led many to adopt the goal of reducing financial risk, just as the availability of seat belts, and later of air bags led many to install them. The availability of these innovations led to people adopting the goal of reducing their risk of death from automobile accidents. At a later time, both became mandatory. Indeed, the fact that people adopt new goals in response to novel plans is probably one of the principal forces underlying technological and social change.

In the realm of health insurance deductibles, a rather important goal comes into play: one might wish to avoid being placed in a future position where one can reduce out-of-pocket costs by accepting increased health risks for oneself or one's family, e.g., by declining preventive care or other advisable but optional treatments. Avoiding such difficult tradeoffs is made salient by the availability of health-insurance plans that pay for routine and preventive care. If the available health plans included only hospitalization and major medical expenses, then people would continually make health-care/money tradeoffs. They might very well wish they didn't have to do so; but if people were accustomed to making these tradeoffs, many would be reluctant to pay large up-front premiums to gain coverage for routine and preventive care. This also illustrates how plans affect temporal framing: full-coverage plans place health-care decisions in a fairly long-term frame, envisaging repeated use of the health-care system, and thus make more salient the goal of avoiding repeated difficult tradeoffs.

Though one can give many additional positive examples of important goals that are adopted in response to novel plans, it is also clear that marketers can take advantage of human goal malleability to generate plans that are deceptively attractive to consumers and highly profitable for the marketers. One broad area where this can occur is in setting default values for plans.

A dramatic example of the effect of defaults was uncovered with the introduction of no-fault automobile insurance in New Jersey and Pennsylvania. Both states introduced the option of a reduced right to sue accompanied by lower insurance rates. In New Jersey individuals had to acquire the right to sue and in Pennsylvania the default was the full right to sue. When offered the choice, only about 20 percent of New Jersey drivers chose to acquire the full right to sue while approximately 75% of Pennsylvania drivers retained this right. In other words residents in both states maintained the default option. This finding was confirmed in a laboratory experiment where subjects were given a similar choice, but were randomly assigned to one of three groups: current automobile insurance with full right to sue, with limited right to sue, or with no information about current right to sue. (Johnson, Hershey, Meszaros and Kunreuther, 1993)

The over acceptance of default values has become a well-known and much studied phenomenon, and probably is caused by several different underlying mechanisms. Among these, we believe, is the influence of the default on people's actual goals. Many more New Jersey than Pennsylvania motorists may have thought that they would actually like to sue, since that option was endorsed as a norm by the default plan they encountered. More generally, defaults may be viewed by consumers as goal-setting norms, when in fact, they are often the most profitable option for a vendor and thus possibly the least favorable for the consumer.

Insurance plans that bring in high profits to insurers, in part by suggesting goals that might otherwise not be adopted, include low deductibles, so-called disappearing deductibles, rebate plans, credit-card insurance, flight insurance, and insurance on packages sent through the mail.

Low deductibles were discussed above. Disappearing deductibles are plans for which the deductible applies in the case of small and moderate losses, but not for large losses. This may suggest the goal of avoiding an out-of-pocket payout in a situation where one is already dealing with the hassles of a major loss. This sounds attractive; but, in fact, loading factors are high: the probability of a major loss is low, the additional amount reimbursed by the insurer with a major loss is not very high (only the deductible), and so the average return to the insurance purchasers is much less than the additional premium paid.

Rebate plans return a portion of the insurance premium, provided that no claim has been made in a specified period of time. These plans may lead consumers to adopt the goal of getting an “investment return” on their insurance premiums. A number of years ago, an insurance company introduced a disability insurance plan for which policyholders received at age 65 a full rebate of all the premiums paid to that date, provided that no claim had been made. This promised an attractive return, but it created an economic incentive for those approaching the age of 65 to avoid making a claim, if they had never made one up to that point. People who were likely to need disability payments found themselves not wanting to use their policies. This reverse moral hazard led regulators to request that the company withdraw this plan from the market, since it undermined the main goal of insurance: those who suffer an insured loss should be able to collect the amounts for which they are covered.

Credit-card insurance and flight insurance are egregious examples of plans that suggest goals in a particular context and exhibit very high loading factors. In each case, the suggested goals can be achieved much less expensively. Flight insurance was discussed in our introduction. The cost of this insurance is 4 to 8 times higher than for the same level of coverage with general accident insurance, and the latter covers many additional risks for a much longer period of time. Credit-card insurance is essentially life-and-disability insurance, covering only the amount of one's credit card debt. Its selling point is that the current credit-card balance would be paid off in case of death or disability. For people whose credit-card balances are burdensome, this would have been an attractive goal. Unlike the usual life and disability policies, the premiums for such insurance plans do not take age into account. For a person at low risk, or one who is already adequately protected by life insurance and disability insurance, adopting the goal of paying off a credit-card balance in this way seems unwise: the risk is not catastrophic, and with premiums in the neighborhood of $2 per $100 coverage, the loading factor is high. We do not know who actually purchases this insurance. If it is mostly people at high risk, then the average loading factor may be reasonable.

As a final example, consider insurance on packages sent through the mail. Within the U.S., current rates are slightly over $1 per $100 of insured value (more for insured value less than $200, and up to a maximum of only $500). While we do not know the probability of loss or damage, experience suggests that it is far less than 1%. The loading factor is high, and the losses involved are seldom catastrophic. However, people generally do what they can to protect objects sent through the mail; for example, they may take care in preparing the package. An insurance plan may be viewed as offering an additional opportunity to take care.

5.4.2 Thresholds for decision weights

Above, we discussed plan selection mechanisms involving thresholds for the decision weights pertaining to a set of important goals. We suspect that this is one of the most frequently used mechanisms. It is observable when group decisions are made in public: several goals are discussed, and the plan finally adopted is one that offers a good chance to achieve each of them. A plan for a new bridge is selected because the decision makers believe that the construction cost will be within the budget limit, that the bridge will handle the expected volume of traffic, that it will be safe, and that it will have a long lifetime with acceptable maintenance costs. Other goals (e.g., aesthetic quality) may also be considered and traded off against additional costs, but the four goals just listed are essential, and the likelihood of achieving each must be high. One may ask, how high? Certainty is not achievable for any of the goals. Most likely the threshold for acceptance will be set very high for safety and lower for the other goals.

When it comes to protective decisions, low probabilities of negative events may fall within acceptance thresholds. Table 4 provides a simple example. Someone may regard the avoidance of a catastrophic loss as an essential goal, yet the probability of 0.98 of achieving that goal may be high enough to satisfy this person's acceptance threshold — in which case plan 2, no insurance, may be selected.

In fact, failures to purchase flood or earthquake insurance are very common. Individuals know that floods and earthquakes occur, but they “do not think it will happen to them.” This can be viewed as underweighting low probabilities, consistent with Hertwig, et al. (2004). We take the slightly different view that the mechanism is one of acceptance thresholds for plan selection. Support for a threshold view of decision making comes from an insurance experiment by McClelland, Schulze and Coursey (1993). For the case where there was a .01 chance of losing $10 they found a bimodal distribution of willingness to pay for insurance: over 25 percent would not pay even a penny while approximately 20 percent were willing to pay premiums that were four or more times the expected loss. This suggests a decision weight for the outcome no loss that exceeded the acceptance threshold for those who would not even pay a penny, but was below this threshold for many others who decided to purchase insurance at premiums that implied extraordinarily high loading factors.

Theories that postulate over- or underweighting of low probabilities must commit to one or the other, for any given probability level. Our view, by contrast, is that the threshold level in a decision rule depends on the importance of the particular goal, on the importance of other competing goals, and quite possibly on other factors, especially on social norms concerning acceptable levels of risk. Thus, a given risk of failure to achieve the goal may appear to be underestimated (as in the example above, where a 2/100 chance of severe flood is neglected) or the same probability, based on the same evidence, may appear to be overestimated (e.g., where a social norm demands near certainty for a particular goal).

In the case of natural hazards, these acceptance thresholds may well be too low prior to the occurrence of a disaster, since the events can be catastrophic for uninsured victims. These cases are complex; however, because for some hazards, private insurers are reluctant to enter the market or charge very high premiums due to high spatial correlation of losses from disaster. Two things are needed in such cases. One is a clear reinsurance mechanism, government and/or private, to spread risk more widely and thereby lower premiums. The other is a norm that leads people to purchase the insurance at these reduced premiums. This could take the form of a social norm within a group or the form of a requirement to insure as banks currently do with respect to homeowners insurance as a condition for a mortgage. Mandates, sanctions, and social norms all play a role in getting people to protect themselves adequately.

6 Prescriptive implications

In standard economic analysis, consumer tastes go unchallenged. It is not irrational to pay $500 for an extraordinary bottle of wine that cannot be purchased for less. Paying $80 for a feeling of “peace of mind” likewise should go unchallenged. In a constructed choice framework, however, these are not literal tastes, comparable to liking raspberries or disliking prunes; they are constructed choices. It is the construction process that can be examined critically.

Construction of choice is influenced by education and culture. Probability offers a powerful example. Four hundred years ago, people undoubtedly had some strong probabilistic intuitions, but these were not systematized, and the word probable had a meaning quite different from most of its modern senses.¹⁰ Today, people sometimes use numerical probabilities in their reasoning and decision making, and those educated in probability or statistics do so much more than others (Nisbett, Krantz, Jepson & Kunda, 1983). Another example derives from the statistical associations among women's education, contraceptive use, and fertility rate. It may be hard to infer causality unambiguously, but there seems little doubt that in this domain, some combination of education and cultural change has powerful effects on reproductive decision-making.

From this viewpoint, consumer education could lead to changes in protective decision making that are financially advantageous to most people and also leave people more confident and more satisfied with their decisions. Suppose, for example, that “peace of mind” is obtained by paying $80 to reduce the deductible on homeowner's insurance from $500 to $250, and that the purchaser also believes (rather accurately) that she, and others in comparable situations average only about 1 claim every 25 years that exceeds $250. If she thinks about a commitment to 10 years of insurance-with-peace-of-mind, this will cost $800 extra over that time frame. The chance that she will collect the extra $250 at least 3 times in the 10 years (thus breaking about even) is about 1 in 100,000.

Alternatively, she can think about the commitment in terms of cost per week: less than $2 for peace of mind. Her choice may very well change, depending on whether she thinks about the cost for peace of mind in a weekly, annual, or ten-year time frame. In the weekly frame, $2 seems trivial and $250 looms large (despite its low probability). In the ten-year frame, $800 looms large and the prospect of a $250 loss will then not have much effect on peace of mind.

Educating the consumer to consider temporal framing ranging from weeks to decades and to translate costs and probabilities across such time frames will probably lead to decisions that are more financially advantageous for most consumers.

The constructed-choice framework in fact raises a host of difficult prescriptive questions. We provide a sampler here but note that most of the answers are beyond the scope of this paper and should be addressed by future research.

• • What is the “right” temporal framing?

• • Assuming that long-term temporal framing is usually advantageous, compared to short-term horizons, what education programs are needed to overcome myopia?

• • What about framing outcomes as gains versus losses?

• • What is the best way to keep mental accounts, i.e., what resources should be committed to important goals and what should remain fungible?

• • What decision-weight thresholds should be set on various goals?

• • Are there intrinsically maladaptive configurations of goals? When should one use social norms as a guide?

• • When should one pursue emotion-related goals, versus attempting to manipulate and control one's own emotions?

Rather than tackling these questions, we limit our prescriptive remarks to three short subsections. The first concerns financial benchmarks for insurance, the second discusses emotion-related goals, and the third offers a few specific ideas about consumer education.

6.1 Financial benchmarks

Financial benchmarks are useful starting points for critical analysis of constructed choices. For example, the preceding example, in which someone pays $80 per year extra to decrease a homeowner's deductible from $500 to $250 should raise a warning flag, because we think that in the world of insurance contracts, higher deductibles are almost always better. More generally, violation of any of the benchmarks we propose here deserves careful analysis.

The three simple benchmarks we suggest provide advice that runs counter to popular choice. The reason is simple: insurance plans that satisfy prevalent non-financial goals and also have high loading factors are both profitable and easily marketable, therefore are frequently offered and chosen. Less popular plans, when available, sometimes offer excellent protection from financial risk at reasonable cost.

1. 1. Consider the maximum loss and its probability.

   What is the maximum loss one could suffer from a particular type of negative event, how likely is such a loss, and how much would it cost to insure fully against it? A person earning $60,000 per year probably does not need $1 million life insurance; a $300,000 policy would give that person's beneficiaries five years to adjust to the loss of income. The probability of death in the next year, from all causes, is never negligible, and death can be financially catastrophic for the survivors, so insurance equivalent to a few years annual income should be purchased, if one can find the money for the premium. Similarly, homeowner's insurance should, if at all possible, cover the full replacement value of one's house at least in case of fire, since the probability of total destruction by fire is not negligible.

2. 2. Look for the highest deductible.

   To opt for a high deductible means that one is self-insuring against losses smaller than that amount. One is thereby saving money on insurance. Of course, the deductible must be set low enough so that one can handle the loss if it occurs. Again, a person earning $60,000 per year may not be able to manage a $10,000 loss; however, a $2000 loss, although very painful, might be manageable.

   To illustrate the operation of these two benchmarks, consider the following three homeowner's insurance policies:

   

   Assuming that the individual can manage a loss of $1000, policy A is superior to B: $150 is much more than the expected financial gain from reducing the deductible by $500. Assuming that the home would cost $150,000 to replace, policy C achieves much more important goals than B. Someone who purchased B and whose home was destroyed by fire would be $50,000 short of the funds needed to rebuild. The comparison of A with C is a bit less clear. If the loading factor for the extra coverage is about 2.0, then the extra $150 premium implies a probability of $75/$50000 = .0015 per year for a total loss by fire. If more than 1 in 1000 homes of this type in this region are lost to fire each year, then $150 extra would be well spent on maintaining the needed coverage.

3. 3. Avoid policies with rebates or other return of premium.

   Consider the following two policies for disability insurance:

   

   Policy A dominates policy B financially: it costs $600 less, and B only provides the rebate in case the individual makes no claim during the given period. In fact, by purchasing policy A rather than B, the decision maker can earn interest on the $600 that he or she has saved. Yet, when the choice between these two policies was given to a set of subjects in an experiment, a majority chose B over A. (Johnson, Hershey, Meszaros and Kunreuther, 1993) Presumably many of these subjects adopted a goal of maximizing the chance that they would get a return on their insurance investment.

   As noted in Section 1, there is another reason for avoiding Policy B: the insured person may decide not to make a justified claim in order to obtain the rebate. This is a form of reverse moral hazard for insurance. It defeats the main goal of the insurance.

6.2 Emotion-related goals

Emotion-related goals may lead to purchasing financially unattractive insurance policies. Hsee and Kunreuther (2000) tested the following scenario:

You are shipping two vases you purchased for $200 each to your home. Suppose that the two vases will be packed in the same box so that if one vase is damaged, the other is also damaged, and if one is not damaged, the other is also not damaged. Of the two vases, you love one much more than the other. You feel that the vase you love is worth $800 to you and the other one is worth only $200 to you. Suppose you have the opportunity to purchase shipping insurance and that you have enough money to insure only one vase. Which one of the two polices will you purchase?

Policy A: The insurance premium for the vase you love is $12.

Policy B: The insurance premium for the vase you don't love as much is $10.

The decision maker should choose Policy B, because it costs only $10, yet offers exactly the same financial benefit as Policy A. When subjects were asked to make the choices between the two policies 63.5% of the respondents chose Policy A. Presumably policy A evoked a goal of being consoled somewhat for the loss of the vase that was loved, or the goal of showing how much one cares about the loved vase.

Of course, this is a contrived situation, in which there is no real benefit, emotional or otherwise, to paying $2 extra for the insurance. The more general point is that attachment to objects, and other s emotional goals, should raise a flag for consideration as to how important the goals are and what one is really getting from the insurance, in the same way that violation of the financial benchmarks raises a flag.

There are certainly situations where an individual should be willing to violate financial benchmarks to satisfy important emotional goals. Consider the following example. A couple is renting a car for a vacation trip and is asked by the rental company whether they want to pay $2 extra per day to avoid paying up to $1000 if they should have an accident. The couple can manage the payment of $1000 if necessary, and the chance of an accident happening on any one day is much less than 1/500, so paying the $2 has negative expected value. According to the second financial benchmark, they should take the $1000 deductible and save $2 per day. Suppose, however, that the person arranging for the contract is unable to convince her spouse of the benefits of following this rule he will worry much less if they pay the $2 per day for full coverage. She will probably conclude that $2 per day is a small price to maintain peace of mind for her husband and harmony on the vacation.

6.3 Consumer education

What should be the goals and methods of a program of consumer education for insurance? Based on the model of constructed choice that we have developed in this paper, the most appropriate instructional strategy would focus on the goals that underlie consumers' choices and would highlight features of desirable insurance plans that can achieve those goals that matter most to each person.

6.3.1 Extend the frame

It seems useful to consider competing plans in multiple frames. The most obvious framing is temporal: a small deductible that generates peace of mind at what seems like a low price for one year looks much worse, as noted above, when the expense is added up over ten years. Probability of loss is also easier to understand in a longer time frame: a probability of 4% per year translates into about a 1 in 3 chance of having one or more losses in 10 years, i.e., a 2/3 chance of no loss at all. Extended temporal framing also has the effect of putting the loss in a long-run perspective. Paying $1000 out of pocket is very painful for most people, but may seem more manageable if it happens only once in 10 or 20 years.

Apart from temporal framing, it may make sense to broaden the frame of any single insurance decision to include other protective needs. A financially unfavorable choice in one domain, multiplied by 3 or 4 different domains, can seem obviously wrong.

The goal of obtaining a return on one's investment may be more resistant to broadening the frame temporally, since the return is also multiplied by the extended time period. Thus, insurance needs to be framed alongside other investments. Paying $600 extra for a rebate policy, which may or may not bring a return of $600, seems obviously inferior to investing the $600 in a certificate of deposit or in mutual funds. Such reframing is of course only meaningful for those who perceive other investment opportunities as accessible.

6.3.2 Provide economic incentives

Our suggestion here is predicated on the constructive involvement of insurers and agents in consumer education. The most obvious economic incentive that could be provided to an individual is a rebate check: imagine that the person is contacted by his insurance agent, after having purchased a policy with a low deductible, and urged to increase it to a higher one. The agent could indicate to him that he would save $100 by converting his policy from a $500 deductible to $1000, and would be mailed a check for $100 if he decided to do so.

6.3.3 Address emotional concerns

Individuals are likely to buy insurance in order to meet emotion-related goals, such as achieving peace of mind, avoiding regret, or gaining consolation in case of a loss. Consumer education could point out paths by which they can still meet some of these goals through insurance plans that are more attractive financially. In the example given above under emotion-related goals, it may not be difficult to convince a person who was willing to pay $12 for an insurance policy on a vase he loved that he would still be able to gain consolation by only paying $10 to insure the vase he didn't love, since the claim would be based on both vases being destroyed simultaneously. The fact that the person didn't purchase a policy on the vase he loved would be irrelevant for obtaining compensation and hence consolation.

It may also be necessary to challenge emotion-related goals. Wanting to avoid regret is understandable; but once the individual sees clearly that this is what he is doing, he may think it is not worth the extra money.

6.3.4 Examples of instructional material

Understanding and use of probabilistic concepts is a modern development in human reasoning, and is attained only through some combination of formal instruction, casual learning, and apprenticeship experiences. Nisbett, Krantz, Jepson and Kunda (1983) introduced the concept of statistical heuristics: short-cut guides to reasoning that incorporate some probabilistic concepts and lead to their use in everyday reasoning. Fong, Krantz and Nisbett (1986) showed substantial temporary improvements in everyday probabilistic reasoning from suitably designed instructional modules. Protective decision making could similarly benefit from instruction. In fact, individuals can be aided in their understanding of the functions of insurance by instructional material (Piao, Kunreuther & Krantz, 2006).

More specifically, one way to convince people of the importance of financial benchmark 1 is to provide graphic examples of the importance of having protection against a catastrophic loss rather than a small loss. A homeowner would be more likely to purchase a policy with coverage of $150,000 and a $1000 deductible rather than $100,000 policy with a $500 deductible if she was presented with a clear explanation of the types of tradeoffs that would have to be made in choosing between the two policies and the impact on her resources if a fire destroyed her $150,000 house and she only had $100,000 worth of insurance.

6.3.5 The importance of social settings

There are vast advantages to conducting consumer education in groups, rather than in the normal one-on-one relationship between seller (insurance agent) and prospective buyer (policyholder). Social facilitation increases engagement in learning. People learn even more by teaching one another. Misunderstandings are given voice and can more easily be corrected. Finally, the group conclusions are more readily adopted as social norms.

6.3.6 Regulation, education, and paternalism

In the preceding, we have emphasized consumer education partly in the spirit of libertarian paternalism (Sunstein and Thaler 2003) and partly in the pragmatic belief that the issues involved are too diverse and changeable to permit effective regulation. Insurance is already highly regulated, and the regulations do prevent some attractive but financially disadvantageous products from entering the consumer market, but the prevalence of low deductibles shows how difficult it is to regulate products that people strongly desire. Unlike nicotine, however, low deductibles are not physiologically addictive, and education may lead to the construction of quite different choices.

Insurance providers are perhaps in the best position to provide good instruction, and many independent insurance agents pride themselves on doing so. Mandating and monitoring consumer education by insurance providers may be a valuable regulatory function.