INTRODUCTION
Vector-borne diseases are influenced by environmental conditions in all countries not just some. Between 1999 and 2011, more than 30 000 humans in the USA were infected with West Nile virus (WNV) and 400 of these cases resulted in death [1]. California and Colorado recorded some of the highest cases of WNV in the USA between 2003 and 2007 [1]. During this time period, these two states accounted for about 28·2% of all WNV cases and 20% of all fatalities [1]. In fact, these states have consistently ranked either first or second in terms of WNV infections during the time period under study [1]. The transmission cycle of WNV involves three organisms: a vector (mosquitoes), host (birds) and infectious agent (virus). Humans and animals are considered to be accidental or dead-end hosts and develop very low levels of viraemia which is not sufficient to infect mosquitoes [Reference Hayes2]. The geographical distribution of the disease is determined by certain socioeconomic, climatic, anthropogenic and environmental factors [Reference Kiszewski3]. It is reasonable to argue that the presence of the Culex genus is necessary for WNV infection, but not sufficient for an outbreak or spread of the disease. The amplification of the disease is determined by the manner in which these factors impact the transmission cycle. It is intriguing why the incidence of WNV is higher in these states. These states are quite diverse in terms of geographical, climatic, demographic, socioeconomic and environmental factors so they merit a separate investigation as to the determinants of WNV incidence.
A number of WNV studies conducted in California [Reference Reisen4, Reference Harrigan5] focused on the role of economic conditions (per capita income and mortgage delinquencies) in the transmission of WNV. These studies, however, were limited to only two counties in California, i.e. Orange and Kern counties. Moreover, recent studies [Reference Patnaik, Juliusson and Vogt6–Reference Carney9] which examined the role of environmental factors such as dead birds and mosquitoes in WNV transmission in Colorado and California were restricted to a few counties. A critical review of the literature reveals that these studies did not adequately address some or all of estimation issues such as spatial autocorrelation, endogeneity, and the panel nature of the data. Albeit some studies [Reference Messina10, Reference Linard11] have used negative binomial models to address some of these problems, they failed to adequately address the panel structure of the data and endogeneity issues. The failure of prior studies to recognize the possibility that WNV counts in one county could be dependent on WNV counts in adjacent counties could be costly. Insofar as this is true, omitting such information may lead to biased estimates of the impact of county-level factors on WNV prevalence.
The spatial statistics literature has not evolved enough in terms of its application to panel-count data models. The motivation for this study is to fill such a void. Two competing methodologies available in the literature that can be employed to correct spatial autocorrelation in nonlinear models such as generalized linear models (GLM) are the spatial lag method [Reference Lambert, Brown and Florax12] and the spatial filtering technique [Reference Patuelli13]. The spatial lag approach is a parametric method that incorporates the structure of spatial autocorrelation into the model to rectify the problem and is motivated by the spatial lag specification for linear models. It includes a spatially lagged dependent variable as an additional covariate in the nonlinear model to correct the problem. The spatial filtering approach is a non-parametric method used to correct for spatial autocorrelation. It does not assume any prior structure of the nature of spatial autocorrelation, but incorporates selected eigenvectors into the model to filter out spatial autocorrelation. It is the approach pursued in this paper. This study, to the best of our knowledge, is one of the first empirical WNV research studies in California and Colorado to employ a spatial filtering technique.
Home foreclosures were considered a potential risk factor in the transmission of human WNV during the housing crisis that began in 2004 and culminated in the financial crisis of 2007 [Reference Reisen4, Reference Harrigan5]. The Federal Reserve [14] stated that the hardest hit states were California, Arizona, Nevada, Colorado, Florida and some New England states. The argument was that the economic downturn and accompanying housing market crisis adversely affected the economy of the USA in general, and particularly the states of California and Colorado. The combined effect was a growing number of neglected swimming pools, particularly across Southern California. This was attributed to the high number of home foreclosures because home owners could not afford their mortgages. Most of these neglected swimming pools on foreclosed homes collected small pockets of water and served as breeding grounds for mosquitoes [Reference Reisen4, Reference Harrigan5]. According to Reisen et al. [Reference Reisen4], WNV cases escalated by 276% in Kern county in the summer of 2007. From the foregoing discussion, it is reasonable to hypothesize a positive relationship between home foreclosures and the transmission of WNV.
The general consensus is that the presence of the Culex mosquito vector is necessary for the outbreak of WNV [Reference Linard11]. In western USA, C. tarsalis and C. quinquefasciatus species are found in abundance [Reference DeGroote15]. C. tarsalis is found in both Colorado and California, but C. quinquefasciatus is mostly restricted to California. C. tarsalis is the predominant vector in rural settings [Reference Epstein and Delfilippo16], although its presence has been reported in urban areas of California [Reference Reisen4]. Their habitat includes areas characterized by standing water such as irrigated fields, poor drainage, sewage treatment lagoons/pools, urban catch basins, and containers found on the compounds of many low-cost houses [Reference Savage and Miller17, Reference Huhn18]. The presence of C. pipiens has also been reported in Southern California [Reference Kwan7]. They are mostly found in urban areas and lay their eggs in stagnant water [Reference Huhn18]. Mosquitoes become infected by feeding on a bird with the virus in its bloodstream. Mosquitoes then spread the virus to new hosts by biting another bird or person. The biological evidence from the foregoing discussion suggests that the number of mosquito pools is positively related to human WNV.
The primary objective of this research is to investigate the significance of environmental (mosquito pools and home foreclosures) factors in human WNV transmission in California and Colorado. This study contributes to the literature in a number of ways. First, it employs a spatial filtering random-effects negative binomial model to study the importance of home foreclosures in the transmission of WNV; many studies have focused on the significance of climatic, geographical factors and other environmental factors. Second, it addresses the issue of spatial autocorrelation in the dependent variable within a panel-count data model context. The presence of spatial autocorrelation in the dependent variable will cause estimates of the variance to be biased if not corrected. Third, it applies an instrumental variable technique to the spatial filtering random-effects negative binomial models to correct for endogeneity in income and home foreclosures.
MATERIALS AND METHODS
Data sources
Data used in this study were collected from several sources. Data on temperature ( temp ), precipitation ( precip ) and the drought index ( pdsi ) were collated from NOAA [19]. County-level climatic data was not readily available so information from weather stations in each county was used to calculate annual climate data. An arithmetic average was used to calculate the climatic variables in counties with several weather stations. Information on human WNV ( hv ) and the number of mosquito pools ( mosquito ) were acquired from the CDC [1]. Data on income ( income ) and population density ( popdense ) were taken from the US Census Bureau [20]. Data on home foreclosures ( forclose ) were acquired from Data Quick News [21] and the Colorado Department of Local Affairs [22]. A detailed description of the variables used this study is provided in Tables 1 and 2.
Table 1. Factors used to assess risk of human WNV in California
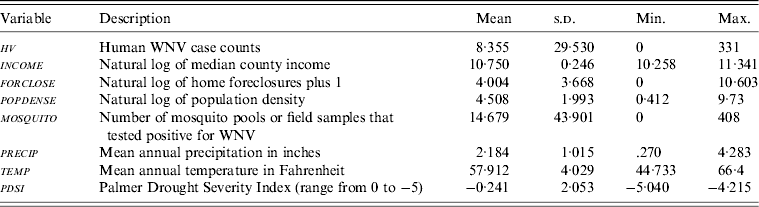
s.d., standard deviation; Min., minimum; Max., maximum.
Table 2. Factors used to assess risk of human WNV in Colorado
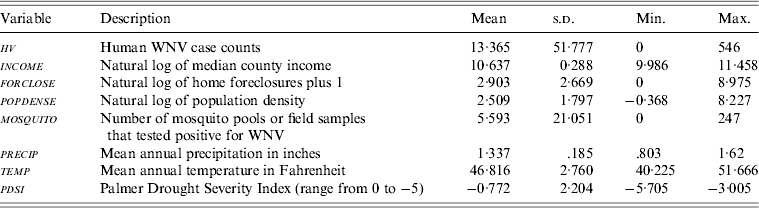
s.d., Standard deviation; Min., minimum; Max., maximum
Empirical model specification
The following random effects negative binomial model (RENB) is specified to investigate the determinants of human WNV:
where i (1, …, N) indexes counties, t (1, …, T) indexes time, and u i is the random-effects term. The choice of controls is driven by a mix of theory and empirical findings. The vector Z′ comprises control variables such as annual precipitation ( precip ), annual temperature ( temp ), annual drought ( pdsi ), income ( income ), population density ( popdense ) and time dummies for 2004–2007 ( d2004, d2005, d2006 and d2007).
In order to further verify and clarify the role of home foreclosures on WNV transmission, the variable forclose is included in the model. The variable mosquito is included to control for vector abundance. It should be mentioned that the environmental factors identified in this research are partly caused by economic conditions. In that regard, economic conditions could exacerbate the transmission of WNV.
Endogeneity
The model specified in equation (1) is appropriate only if all the explanatory variables are exogenous. This is potentially a problem due to the possibility of a simultaneity bias between human WNV on the one hand and income and home foreclosures on the other. In other words, human WNV, income and home foreclosures may be jointly determined. To correct for this endogeneity problem, an instrumental variable method is applied to the RENB. To implement this method the contaminated variables (income and home foreclosures) are regressed on an array of instruments and the predicted values inchat and forhat are used to replace income and home foreclosures in equations (1) and (2).
Spatial filtering technique
This technique is based on the spatial eigenvector mapping method. The rationale behind this method is that the configuration of spatial data points on a map, are reflected in covariates that capture spatial effects at different spatial scales. This is a non-parametric method for correcting spatial autocorrelation [Reference Patuelli13]. Spatial filtering techniques have been developed and implemented by several authors [Reference Griffith23–Reference Tiefelsdorf and Griffith26]. The spatial filtering technique employed in this paper is according to Griffith [Reference Griffith27]. It is based on the eigenvector decomposition of a modified spatial weights matrix. The eigenvectors of this matrix are judiciously selected based on a stepwise selection method to filter out spatial autocorrelation from the model residuals. The selected eigenvectors are then used as components of the spatial filter and included as covariates in the GLM regression. This transformed spatial weights matrix reflects the latent spatial autocorrelation inherent in the dependent variable. The spatial filtering RENB model is specified as follows:
where sfilter i is an array of selected eigenvectors (spatial filter components), denoted by vec , of the transformed spatial weights matrix. The spatial filter can be perceived as a proxy for omitted or missing variables from the regression [Reference Patuelli13]. Getis & Griffith [Reference Getis and Griffith25] contend that all the n eigenvectors extracted represent all the possible orthogonal map patterns. In other words, they represent a kaleidoscope of all possible map patterns. Specifically the first two principal eigenvectors extracted are often associated with North–South and East–West patterns, respectively. Eigenvectors with intermediate values of Moran's I typically exhibit regional patterns, while eigenvectors with extremely low values of Moran's I are associated with local map patterns.
ESTIMATION AND RESULTS
Statement of hypotheses
The following hypotheses regarding the environmental variables are tested.
Hypothesis 1: βFORCLOSE >0
This hypothesis states that home foreclosures will have a positive effect on the prevalence of WNV. Under this hypothesis the regression coefficient on forclose is expected to be positive.
Hypothesis 2: βMOSQUITO >0
This hypothesis states that the number of mosquito pools will have a positive effect on the prevalence of WNV. Under this hypothesis the regression coefficient on mosquito is expected to be positive.
Moran's I [Reference Moran28] was employed to verify the presence of spatial autocorrelation in hv in both states. It is a coefficient to measure the strength of spatial autocorrelation in regional data and the results are given in Table 3. The calculation of Moran's I is based on Pearson's correlation coefficient formula and was derived using neighbouring values of hv . The Z value is 8·552 for California, while that for Colorado is 14·848. Both are positive and significant indicating the presence of positive spatial autocorrelation.
Table 3. Global spatial autocorrelation test on human WNV counts

Estimation of the parameters of the RENB model was undertaken by the technique of maximum likelihood and estimations were performed in Stata v. 9.2 (StataCorp, USA). Pearson's correlation was employed to ascertain the degree of multi-collinearity among the potential risk factors identified in this study. In conformity with the literature, only those risk factors whose correlations were not in excess of 0·8 were included [Reference Linard11]. The econometric analysis estimates four different regressions models using hv as the dependent variable. The baseline model (model 1) excludes climatic and economic variables. In model 2, precip and income are included. In model 3, only the climatic variable temp is included. Finally in model 4, only the pdsi climatic variable is included. The results of models 2–4 are used as a robustness check of the stated hypotheses.
The results of the instrumental variable spatial filtering RENB for California are presented in Table 4. The estimated coefficients on forhat are positive and statistically significant at the 5% level in all models, with values ranging from 0·382 to 0·413. The expected positive relationship suggests that WNV prevalence is higher in counties with a higher number of foreclosed homes. The coefficients on mosquito are highly significant at either the 1%, 5% or 10% level in all models with values ranging from 0·005 to 0·11. This result provides evidence that WNV prevalence is higher in counties with a higher number of mosquito pools. Only the eigenvectors vec4 , vec15 and vec16 are significant at either the 1%, 5% or 10% level. The results of the instrumental variable spatial filtering RENB for Colorado are presented in Table 5. The coefficients on forhat are consistently positive and statistically significant at the 1% level, with values ranging from 2·631 to 2·926. This provides evidence that home foreclosures contributed significantly to the high prevalence of human WNV in Colorado. The coefficients on mosquito are positive and statistically significant at the 5% and 10% levels with values ranging from 0·006 to 0·009 in models 1, 3 and 4. These results provide evidence that human WNV is higher in counties with a higher number of mosquito pools. All the components of sfilter are significant at either the 1% or 10% levels. Based on Akaike's Information Criterion (AIC), models 1 and 2 are the most parsimonious for California and Colorado, respectively.
Table 4. Instrumental variable spatial filtering random-effects negative binomial regression for California
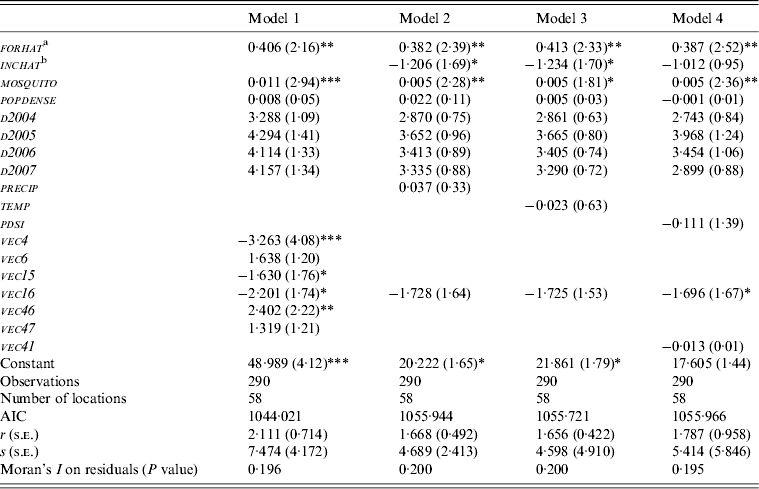
s.e., Standard error; AIC, Akaike's Infornation Criterion.
Z statistics in parentheses.
*Significant at 10%, ** significant at 5%, *** significant at 1%.
a, b Represent instrumentalized versions of forclose and income , respectively. Instruments are bird, mosquito, net migration, precip, temp, PDSI poverty, unemployment rate, education, airport, equine, elevation, urbanization, popdense, roads, log of area and D2004–D2007.
Table 5. Instrumental variable spatial filtering random-effects negative binomial regression for Colorado
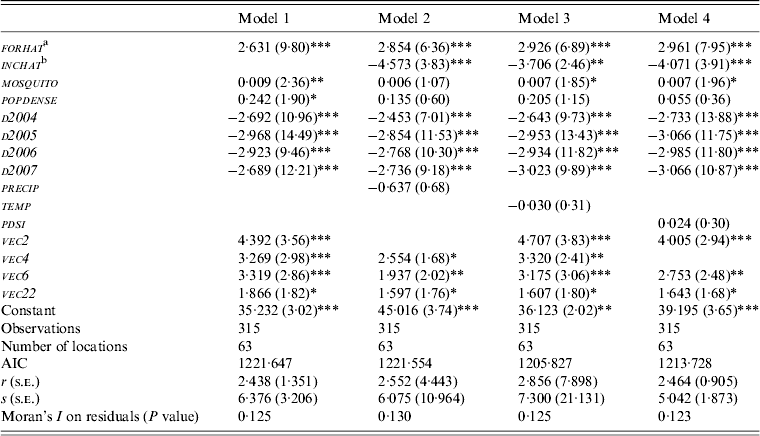
s.e., Standard error; AIC, Akaike's Infornation Criterion.
Z statistics in parentheses.
*Significant at 10%, ** significant at 5% *** significant at 1%.
a, b Represent instrumentalized versions of forclose and income , respectively. Instruments are bird, mosquito, net migration precip, temp, PDSI poverty, unemployment rate, education, airport, equine, elevation, urbanization, popdense, roads, log of area and D2004–D2007.
DISCUSSION AND CONCLUSIONS
This study set out to investigate the environmental determinants of human WNV in the states of California and Colorado from 2003 to 2007. The presence of spatial autocorrelation is not surprising at all because the geographical distribution of WNV is determined by climatic, environmental and anthropogenic factors [Reference Kiszewski3, Reference Sattler29]. These are factors that do not adhere to county boundaries so events in one location are dependent on events in another location. In particular, the prevalence of WNV in one county may spill over into an adjoining county. This study consequently employs a spatial filtering random-effects negative binomial model to test a series of hypotheses relating to mosquito pools and home foreclosures. We find that a high number of home foreclosures lead to a greater number of unmaintained properties that could serve as breeding grounds for the mosquito vector thus leading to a greater number of WNV cases. This finding is consistent with previous results [Reference Reisen4, Reference Harrigan5] that delinquent mortgages and neglected swimming pools contributed to the outbreak of WNV in Kern and Orange counties, respectively. This finding is quite novel because the impact of home foreclosures on the transmission of human WNV has hitherto not been explicitly investigated. Mosquitoes serve as the primary vector for WNV. A large number of mosquito pools means an increased vector population, hence a high prevalence of WNV and an increased risk of West Nile infection in humans. This is consistent with the findings of Patnaik et al. [Reference Patnaik, Juliusson and Vogt6] that mosquito pools were significant in predicting WNV prevalence in Colorado. These results are robust to a variety of model specifications. In terms of policy implications, interventions such as the control of the mosquito vector and increased attention to the maintenance of foreclosed homes are implied by our findings. The results of this study also suggest that counties that exhibit characteristics such as a high number of mosquito pools and a high number of home foreclosures should be allocated more resources for WNV surveillance and abatement.
There are two possible limitations of this study. First, this study was conducted at the county-level. Using data at a finer spatial scale, such as census tract or block level, may produce different results. Second, since data on home foreclosures reveal that they peaked in 2010, it would be worthwhile extending the data to 2012 to further verify the home foreclosure hypothesis examined in this study. Despite these limitations, the findings of this study are informative and a significant contribution to current knowledge on WNV transmission.
DECLARATION OF INTEREST
None.








