Pathwise large deviations for the rough Bergomi model: Corrigendum

Abstract

This note corrects an error in the definition of the rate function in Jacquier, Pakkanen, and Stone (2018) and slightly simplifies some proofs.

1. Corrected rate function

Note that the correct rate function also appears in the PhD thesis [3] (see Proposition 1.4.18), but with a different proof. We first give a slightly simplified proof of [1, Theorem 3.1]. Any unexplained notation is as in [1].

Let $Y:= \int_0^\cdot \varphi(u,\cdot)\,\mathrm{d} W_u$ be the Gaussian process from that theorem, and $K_Y:\mathcal{C}^* \to \mathcal{C}$ its covariance operator (definition in [2, p. 5]). As noted in [1], $\mathcal{I}^\varphi$ is injective by Titchmarsh’s convolution theorem. By the factorization theorem [2, Theorem 4.1] and the discussion in [2, pp. 32–33], it suffices to verify the factorization identity $\mathcal{I}^\varphi(\mathcal{I}^\varphi)^*=K_Y$ to conclude that the reproducing kernel Hilbert space (RKHS) is the image $\mathcal{I}^\varphi\big(L^2([0,1])\big)$ . By Fubini’s theorem, we have $(\mathcal{I}^\varphi)^* \mu = \int_\cdot^1 \varphi(\cdot,t)\mu(\mathrm{d} t)$ for any measure $\mu \in \mathcal{C}^*$ . We then compute, for $\mu,\nu \in \mathcal{C}^*$ ,

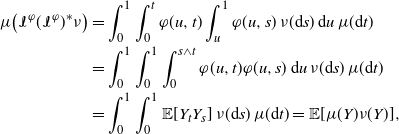\begin{align*} \mu\big(\mathcal{I}^\varphi(\mathcal{I}^\varphi)^* \nu\big) &= \int_0^1 \int_0^t \varphi(u,t) \int_u^1 \varphi(u,s)\, \nu(\mathrm{d} s)\, \mathrm{d} u\, \mu(\mathrm{d} t) \\[2pt] &= \int_0^1 \int_0^1 \int_0^{s \wedge t} \varphi(u,t) \varphi(u,s)\, \mathrm{d} u\, \nu(\mathrm{d} s)\, \mu(\mathrm{d} t) \\[2pt] &= \int_0^1 \int_0^1 \mathbb{E}[Y_t Y_s]\, \nu(\mathrm{d} s)\, \mu(\mathrm{d} t) = \mathbb{E}[ \mu(Y) \nu (Y)],\end{align*}

which proves the theorem.

The second definition in [1, (2.3)] should be replaced by the following one.

Definition 1. For $\Phi:\mathbb{R}^+ \times \mathbb{R}^+ \to \mathbb{R}^{2\times2},$ define $\mathcal{I}^{\Phi}:L^2([0,1],\mathbb{R}^2) \to L^2([0,1],\mathbb{R}^2)$ by

\begin{equation*} \mathcal{I}^{\Phi} f := \int_0^\cdot \Phi(u,\cdot)f(u) \, \mathrm{d} u. \end{equation*}

The following theorem replaces [1, Theorem 3.2].

Theorem 1. Let $\varphi_1,\varphi_2$ satisfy [1, Assumption 3.1], and define $Y_i:= \int_0^\cdot \varphi_i(u,\cdot) \, \mathrm{d} W_u^i$ , $i=1,2$ , where $W^1$ and $W^2$ are standard Brownian motions with correlation parameter $\rho \in(-1,1)$ . Then, the RKHS of $(Y_1,Y_2)$ is $\mathcal{H}^\Phi := \{ \mathcal{I}^\Phi f : f \in L^2([0,1],\mathbb{R}^2) \}$ , with inner product $\langle \mathcal{I}^\Phi f, \mathcal{I}^\Phi g \rangle = \langle f,g \rangle$ , where

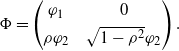\begin{equation*} \Phi = \begin{pmatrix} \varphi_1 &\quad 0 \\[3pt] \rho \varphi_2 &\quad \sqrt{1-\rho^2}\varphi_2 \end{pmatrix}. \end{equation*}

Proof. Analogous to the proof above. Injectiveness of $\mathcal{I}^\Phi$ follows from the Titchmarsh convolution theorem. We have $(\mathcal{I}^\Phi)^*\mu = \int_\cdot^1 \Phi^{\top}(\cdot,t) \mu(\mathrm{d} t)$ for any measure $\mu\in(\mathcal{C}^2)^*$ . The factorization identity $\mathcal{I}^\Phi(\mathcal{I}^\Phi)^*=K_{Y_1,Y_2}$ is verified as above.

Theorem 1 implies the following corollary, which replaces [1, Corollary 3.2].

Corollary 1. The RKHS of the measure induced on $\mathcal{C}^2$ by the process (Z,B) is $\mathcal{H}^{\Psi}$ , where

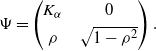\begin{equation*} \Psi = \begin{pmatrix} K_\alpha &\quad 0 \\[3pt] \rho &\quad \sqrt{1-\rho^2} \end{pmatrix}. \end{equation*}

Consequently, $\| \cdot \|_{\mathcal{H}^{\Psi}}$ should replace $\| \cdot \|_{\mathcal{H}_\rho^{K_\alpha}}$ in line 4 of p. 1083 and in the proof of [1, Theorem 2.1] on p. 1088. The special case $\rho=0$ requires no separate treatment, and the result agrees with [1, Section 5].

2. Minor corrections

1. 1. On p. 1079, last line of the introduction: replace $\int_0^1$ by $\int_0^\cdot$ .

2. 2. On p. 1084, definition of topological dual: add ‘continuous’ before ‘linear functionals’.

3. 3. On p. 1085, second displayed formula: after the second $=$ , replace f by $\Gamma(f^*)$ .

4. 4. In the statement of Theorem 3.4, $\varepsilon \mu$ should be replaced by $\mu(\varepsilon^{-1/2}\,\cdot)$ . The speed $\varepsilon^{-\beta}$ resulting from the application of the theorem on p. 1088 is correct, though.

5. 5. First line of p. 1089: Replace $v_0^{1+\beta}$ by $v_0 \varepsilon^{1+\beta}$ . To make the estimate work for $t=0$ , confine $\varepsilon$ to the finite interval [0,1] instead of $\mathbb{R}^+$ in line ${-4}$ of p. 1088.