Fast electron transport patterns in intense laser-irradiated solids diagnosed by modeling measured multi-MeV proton beams

Abstract

The measured spatial-intensity distribution of the beam of protons accelerated from the rear side of a solid target irradiated by an intense (>10¹⁹ Wcm⁻²) laser pulse provides a diagnostic of the two-dimensional fast electron density profile at the target rear surface and thus the fast electron beam transport pattern within the target. An analytical model is developed, accounting for rear-surface fast electron sheath dynamics, ionization and projection of the resulting beam of protons. The sensitivity of the spatial-intensity distribution of the proton beam to the fast electron density distribution is investigated. An annular fast electron beam transport pattern with filamentary structure is inferred for the case of a thick diamond target irradiated at a peak laser intensity of 6 × 10¹⁹ Wcm⁻².

INTRODUCTION

The demonstration, over a decade ago, of multi-MeV/nucleon ion acceleration from foil targets irradiated by intense laser pulses (Snavely et al., 2000; Clark et al., 2000; Maksimchuk et al., 2000) has stimulated intense research into laser-driven ion acceleration. Controling the ion source and beam properties are key to the development of potential applications, such as proton oncology (Borghesi et al., 2006) and the proton-driven fast ignition approach to inertial confinement fusion (ICF) (Roth et al., 2001). At typical laser intensities >10¹⁹ Wcm⁻² and micron-scale thickness targets the dominant acceleration mechanism is target normal sheath acceleration (TNSA) (Wilks et al., 2001).

The interaction of an intense laser pulse with the front surface of a solid target creates a plasma and couples a significant fraction (typically tens of percent) of the laser energy into the generation of a mega-Ampére current of relativistic electrons, which are injected into the target. The transport of this fast electron beam is subject to a range of transverse and longitudinal instabilities (such as the Weibel et al., 1959), two-stream (Hao et al., 2009), and resistive filamentation instabilities (Gremillet et al., 2002)), and to self-generated magnetic fields (Bell & Kingham, 2003). Upon reaching the target rear side, a small population of the highest energy electrons escape, but the remainder form a sheath layer with a large electric field, which evolves spatially and temporally. The field strength, on the order of TV/m, is large enough to ionize atoms on the target rear surface and accelerate them to multi-MeV/nucleon energies. Since the ions originate due to the action of the sheath field, the properties of the ion beam are a direct consequence of this field evolution, which in turn is directly affected by the fast electron propagation inside the target. Measurement of the ion beam properties can thus provide a diagnostic of fast electron beam transport within the solid.

In this article, we present example measurements of the spatial-intensity distribution of the beam of multi-MeV protons accelerated from the rear surface of three different target materials irradiated by an intense laser pulse. We report on a model developed to infer the initial two-dimensional (2D) fast electron density distribution at the target rear surface, and hence the fast electron transport pattern within the target, from the measured 2D proton beam dose distribution. The model is applied to determine the fast electron transport pattern in diamond, which produces an unusual proton beam profile—cusp-like intensity structures at the center of an otherwise smooth beam.

EXPERIMENTAL SETUP AND RESULTS

The proton beam measurements used in this study were obtained during an experiment using the Vulcan laser at the Rutherford Appleton Laboratory, UK. Laser pulses with wavelength equal to 1.053 µm, an on-target energy of 60 J and duration, τ_L = 1 ps (full width at half maximum, FWHM) were focused to a focal spot of 6 μm diameter (FWHM). The resulting peak intensity was calculated to be 6 × 10¹⁹ Wcm⁻². The core diagnostic set-up is shown schematically in Figure 1. Three different target samples were used, silicon, single-crystalline diamond, and vitreous carbon, each 3 mm × 3 mm and 300 µm-thick, with highly polished surfaces. The spatial-intensity profile of sheath-accelerated proton beams was measured using passive stacks of 5 cm × 5 cm dosimetry film (RCF), positioned 6 cm from the rear of the target.

Fig. 1. (Color online) Schematic of the diagnostic approach. A high power laser pulse is focused (to a peak intensity equal to 6 × 10¹⁹ Wcm⁻²) onto the front surface of the solid target. Fast electrons are generated in the focal region and propagate through the target, creating a sheath layer, with a multi-TV/m field at the target rear surface. The spatial-intensity dose distribution of the resulting beam of accelerated protons is measured using a stack of dosimetry radiochromic film (RCF).

As discussed above, the accelerated protons are produced as a result of an electrostatic sheath field established at the target rear surface by the fast electrons originating in the laser focal region. Due to the rapid nature of the proton acceleration, any large spatial modulations in the sheath field strength, resulting from modulations or instabilities in the fast electron beam transport pattern, are mapped into the expanding proton beam intensity distribution (Fuchs et al., 2003). Measurement of the spatial-intensity dose distribution of the sheath-accelerated protons thus enables the electric sheath properties and fast electron propagation dynamics to be inferred.

Figure 2 shows example measured proton spatial-intensity dose profiles for (2a) 300 µm silicon, (2b) 300 µm diamond, and (2c) 300 µm vitreous carbon, all for peak laser intensity equal to 6 × 10¹⁹ Wcm⁻². The results shown are for 5 MeV protons, but similar features are observed at all energies (i.e., throughout the RCF stack). The proton beam profiles are quite different for the three different target materials. The results emphasize the acute sensitivity of sheath-accelerated protons to different fast electron transport properties within the three materials.

Fig. 2. (Color online) Representative measurements of the spatial-intensity dose distribution of protons (at an example energy of 5 MeV) for (a) 300 µm silicon (lower half of the proton beam), (b) 300 µm diamond, and (c) 300 µm vitreous carbon. A small portion of the proton beam on the bottom-right in each image is blocked. (d) Percentage variation in the proton dose as a function of radius from the centre of the beam. Details of the methodology are given in the text.

As shown in Figure 2a, the measured proton beam profile for silicon is circular and highly uniform, reflecting smooth fast electron transport. The corresponding measurement for vitreous (disordered, or glassy-like) carbon shows a highly structured beam intensity profile, with cusp-like features extending all the way out to the beam profile edge (Fig. 2c). As discussed in McKenna et al. (2011), this structure arises due to filamentation of the fast electron beam during propagation through the target, giving rise to multiple hot-spots in the fast electron density distribution, and thus multiple regions of high proton emission within the sheath. The proton front from these sources overlap downstream in the detector plane giving rise to the measured cusp-like features across the beam. Interestingly, the measurements with diamond, as shown in Figure 2b, for the same laser drive parameters, including peak intensity of 6 × 10¹⁹ Wcm⁻², produces an unusual proton beam distribution with a fairly circular profile and uniform distribution at large radii, but with strong cusp-like structure at the center. Repeat laser shots were taken on each of the target materials and the results are fully reproduced.

To quantify the degree of structure or variation across each proton beam, we calculate the coefficient of variation of the dose (converted from optical density) across each RCF image. The coefficient of variation C _p quantifies the percentage statistical variation (standard deviation σ_p) in the proton beam dose relative to the mean m _p of the sampled region, as follows:

(1)$$C_p=\displaystyle{{{\rm \sigma} _p } \over {m_p }} \times 100. $$

We calculate C _p for multiple angles N _θ = 90, in the lower left quadrant of each proton beam profile, in sampling regions of 30 × 30 pixel dimension. The mean across the N _θ angular selections is calculated, giving the mean coefficient of variation, C _{M p}, at a given radius, r, as:

(2)$$C_{M_p } \lpar r\rpar =\displaystyle{{\sum\nolimits_{k=1}^{N_{\rm \theta} } \, C_p \lpar k\comma \; r\rpar } \over {N_{\rm \theta} }}\comma \;$$

where k = 1,2,…,N _θ. This calculation is then performed as a function of radius from the beam center, to quantify the proton beam dose variation radially across the beam profile. Higher values of C _{M p}(r) correspond to regions of strong dose variation or structure.

This analysis is performed on the measured proton beams for each target type, for the three examples shown in Figure 2a–2c, and the results are shown in Figure 2d. The error bars correspond to statistical variations across multiple angular samples, with large error bars indicative of angular inhomogeneity in the proton beam dose profile and small error bars corresponding to regions of high angular homogeneity. The resulting structure-radius profiles reflect what is visually observed in each 2D proton dose profile measurement. A low dose variance value is obtained for silicon and a high value for vitreous carbon for all radii. In the case of diamond, the structure or degree of dose variation at the center of the beam is similar to the vitreous carbon, but with increasing radius the variation decreases to a value more similar to silicon.

As discussed above, the different proton beam dose variation profiles result from differences in the fast electron transport patterns within the target. As it propagates, the fast electron beam is subject to a number of different transport instabilities and the effects of self-generated fields. In a recent relevant investigation reported in McKenna et al. (2011), it was shown that the fast electron beam transport pattern, and thus the resulting proton beam spatial-intensity dose profile, is strongly affected by the target electrical resistivity at relatively low temperatures. In that study, performed at a higher peak laser intensity (2 × 10²⁰ Wcm⁻²) smooth proton beams were obtained for diamond targets (across the full proton beam area) and structured beams were measured with vitreous carbon. The difference between the two results was explained by the higher resistivity of vitreous carbon at relatively low temperatures of 1–50 eV, giving rise to higher resistive instability growth rates. The differences in resistivity of the two carbon targets arises due to the different degree of ordering of the carbon ions (i.e., the lattice structure). The distinctly different proton beam profile measured with diamond for the lower peak laser intensity in the present work points to a different fast electron beam transport pattern within the target.

Given that lattice structure has been identified as playing an important role in defining fast electron transport patterns, it is interesting to compare the proton beam profiles for diamond and silicon, which both have the same diamond-cubic lattice structure. While investigation of the differences in the underlying fast electron transport physics in the three target materials is beyond the scope of this paper, as a starting point we develop a model to infer the electron transport pattern from the measured proton beam profile. Specifically, we focus on the interesting case of diamond, giving rise to the smooth proton beam with structure limited to the beam center. This will provide a basis for further investigation of the underlying transport physics.

MODEL

The analytical model developed to explore the 2D mapping of the fast electron density distribution into the spatial-intensity distribution of the beam of accelerated protons builds on previous work reported by Quinn et al. (2011) and Yuan et al. (2010). By performing a systematic investigation of various initial fast electron density and hence electric field profiles, their subsequent evolution in space and time, and the final mapping into the 2D proton profile at the detector, we find that the proton beam spatial-intensity distribution measured for the diamond targets is explained by an annular fast electron beam with a filamented electric sheath field distribution.

The electric field profile and final proton spatial-intensity distribution are calculated as follows. First, an initial diameter, d ₀, equal to ~300 µm is assumed for the fast electron beam arriving at the target rear surface — this corresponds to ballistic transport of the fast electrons through the L = 300 µm-thick target, with an effective half-angle of divergence θ_1/2 equal to 26°. Fast electron transport is typically not ballistic due to the effects of self-generated fields, but an “effective” transport angle, which averages over differences in local beam divergence within the target is found to provide a good approximation of the beam transport—see for example: Coury et al., (2013). A 2D spatial grid of cell dimensions 1000 × 1000 is defined, with 1 µm cell resolution, to represent the rear target surface. The 2D sheath grid is populated with n _s = 30 “sub-sheaths” to represent individual filaments, each assigned a random relative field strength of R _i, where 0 < R _i < 1.

As reported in McKenna et al. (2011), the cusp-like features across the full proton beam for the case of vitreous carbon results from a random distribution of these filaments across the sheath surface, as expected from the stochastic nature of fast electron beam filamentation within the target. However, for the interesting case of the diamond measurement shown in Figure 2b, we find that we can reproduce the measured proton beam spatial-intensity profile only when the filaments are arranged in an annular pattern and furthermore when there is some degree of asymmetry in the distribution.

The filaments are positioned in a ring of diameter d ₀ centered on x = y = 0. The spatial profile of each filament is described using a Gaussian function f _i(x,y,t) of half width W _i(t), where i = 1,2,…,n _s. The transverse expansion velocity v _⊥ across the 2D grid is initially set to c in agreement with previous studies of sheath expansion for similar laser conditions (for example, Brambrink et al. (2006); McKenna et al. (2007). The value of v _⊥ decreases exponentially with time, with 1/e = 1.6 ps, consistent with optical probe reflectometry measurements of sheath expansion (Antici et al. 2007). The sheath field spatial distribution is calculated in 100 fs temporal steps as it expands over the predefined 2D grid for a total duration of 2 ps. The magnitude of the field, E ₀.G(t) increases with the rising Gaussian temporal profile, G(t), of the laser pulse to a maximum value E ₀ at t _p ≈ τ_L. Thereafter, the field strength follows an exponential decrease with 1/e = 1.6 ps. The annular group of filaments evolve as individual sub-sheaths and spread radially along the target rear surface with velocity v _⊥(t), coalescing to form a total electric sheath field F(x,y,t):

(3)$$F\lpar x\comma \; y\comma \; t\rpar =\sum\limits_{i=1}^{n_s } \, f_i \lpar x\comma \; y\comma \; t\rpar . $$

The spatial and temporal evolution of the sheath field magnitude, E(x,y,t) is calculated using:

(4)$$E\lpar x\comma \; y\comma \; t\rpar =E_0 .G\lpar t\rpar .F\lpar x\comma \; y\comma \; t\rpar .$$

To produce protons for acceleration by this field, a uniform layer of hydrogen is defined on the target rear surface and the electric sheath field E(x,y,t) ionizes the hydrogen, via field ionization. The resulting protons are accelerated in each time step by the evolving electric sheath field. The expanding ion front is calculated from the local electric sheath field profile, and the protons are accelerated in the direction normal to this ion front. Finally, the protons are translated from the target grid to detector grid using polar coordinates to extrapolate the local gradients from the ion front surface into the angular mapping of the protons. The detector plane is defined as a 6 cm × 6 cm spatial grid positioned 6 cm from the target rear surface (i.e. equal to the distance between the target and RCF stack in the experiment).

Two example results from the modeling are shown in Figure 3. The case of an annular ring without filamentary structure (Fig. 3a) results in a cylindrically symmetric proton beam spatial-intensity profile, with a ring-like feature within it. The second case, shown in Figure 3d, involves a ring of filaments. The proton beam resulting from this profile is shown in Figure 3f, and has similar features to the measured proton beam for diamond, in Figure 2b. Specifically, the protons accelerated by the fast electron hot-spots in the ring superimpose to produce cusp-like structures at the center of the beam, whereas the beam intensity profile is relatively smooth at large radii, and the overall beam is quite circular. The edges of the initial annular distribution, which have the largest field gradients, are maintained throughout the temporal evolution. Since the protons are accelerated normal to the local gradients at the sheath surface, these large spatial field gradients produce large divergence angles in the proton beam, which creates the relatively high degree of circularity in the final beam profile.

Fig. 3. (Color online) Results from model calculations mapping 2D sheath field dynamics into the beam of accelerated protons. Two cases are shown. The top one, (a–c), corresponds to an annular fast electron distribution without filamentary structure: (a) log₁₀ sheath field (Vm⁻¹) after 300 fs; (b) the proton acceleration front; and (c) the time-integrated proton beam spatial-intensity profile in the detector plane (in units of log₁₀ proton number). The bottom case, (d–f), is the same, but with filamentary structure in the annular fast electron distribution, as shown in (d).

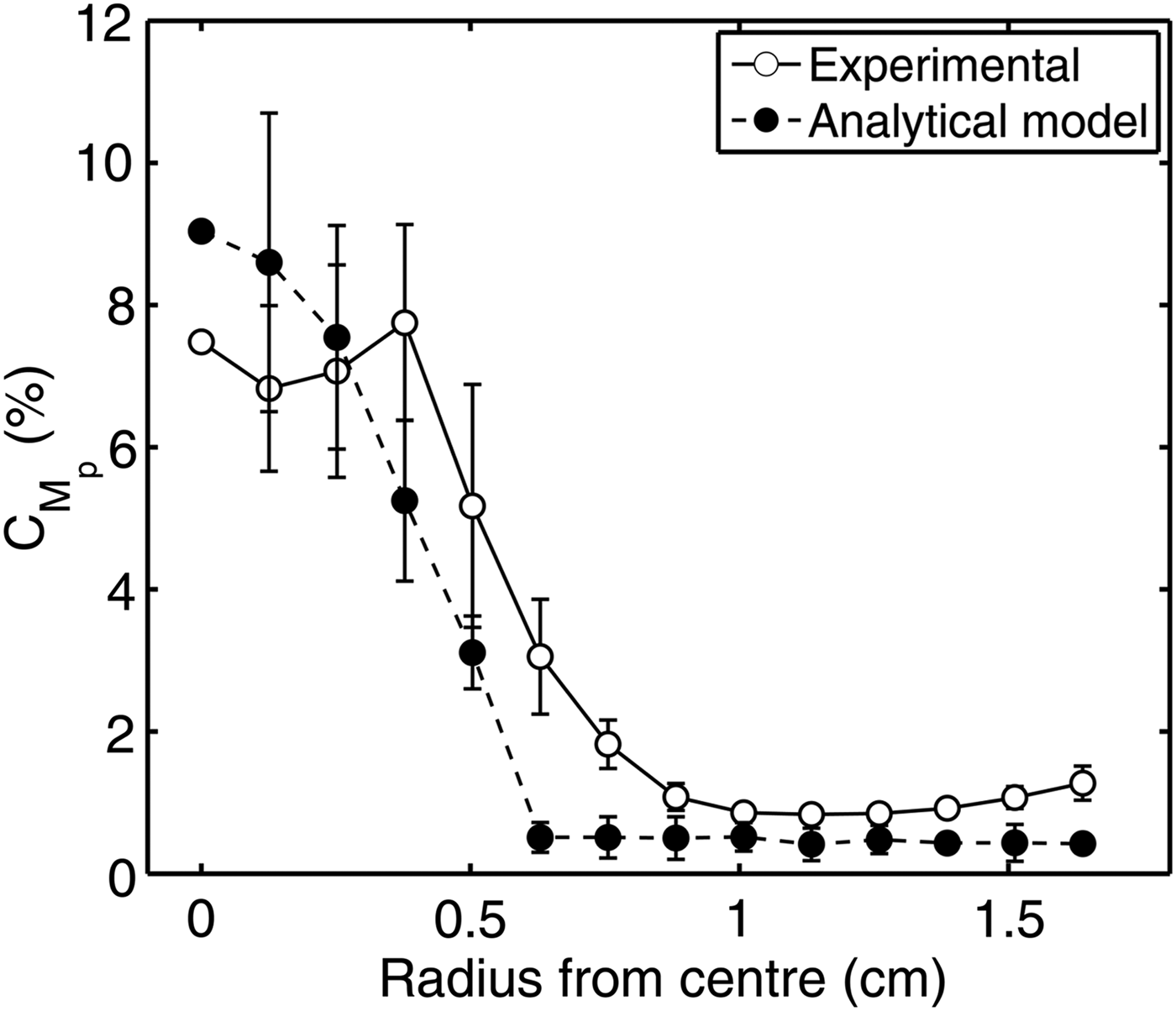
To compare the model calculations of proton beam uniformity with the experimentally measured proton distributions, we performed the previously described radial statistical analysis on the model result in Figure 3f. The results are shown in Figure 4, alongside the corresponding experimental profile. Good quantitative agreement is found. Whilst there is some differences in the statistical variation between the experimental and model proton beams at certain radii, particularly between 0 cm and 0.5 cm, the overall features of the experimental result are well reproduced.

Fig. 4. Percentage variance in the proton beam intensity as a function of radius. Good overall agreement is obtained between the model calculations (Fig. 3f) and experiment (Fig. 2b).

SUMMARY

In summary, a model has been developed to investigate the mapping of the initial 2D fast electron density distribution at the target rear surface into the spatial-intensity distribution of the beam of accelerated protons. This model takes account of the fast electron sheath field evolution, field ionization and expansion, and projection of the resulting proton front to the detector plane. Building on recent fast electron investigations performed by our group (McKenna et al., 2011) measurements of proton beam spatial-intensity distributions for three example targets are presented.

The case of diamond, irradiated at a peak intensity equal to 6 × 10¹⁹ Wcm⁻², is selected due to the unusual feature of structure occurring only at the center of an otherwise smooth proton beam profile, and the analytical model is applied to infer the initial fast electron density distribution at the target rear surface. The measured beam profile is reproduced using an annular fast electron density distribution with a filamentary structure. The physics of the fast electron beam transport within the target which gives rise to this unusual pattern will be the subject of future work.

Finally we note that the modeling developed in the course of this investigation can be applied to determine the optimum fast electron density distribution to produce a desired proton beam spatial-intensity distribution. Potential applications of laser-driven ion sources, such as hadron therapy and ion-fast ignition, are likely to benefit from an ability to tune the proton beam profile.