1 Introduction
We are living in an uncertain world, where people make probability predictions almost all the time. For example, people might wonder whether it will rain tomorrow, whether housing prices will increase continuously, whether an earthquake will happen in a specific area, and so on. When facing uncertain events, people need to predict their likelihood. This probability becomes an instructional tool and helps determine what decision will be made. To cope with uncertainty and brace for the unknown, people must maintain a good balance between a high level of specific readiness for the events that are most likely to occur and a general ability to respond appropriately when the unexpected happens. When discussing probability, people use two kinds of probabilistic statements to transmit or communicate the degree of uncertainty. One is the verbal probability, such as “rain is likely tonight.” The other is the numerical probability, such as “the probability of rain tonight is 60%.”
The uncertain world around us consists of both animate (i.e., living) and inanimate (i.e., non-living) things (Reference Barry and CahillBarry & Cahill, 2007), yet our knowledge of animacy is completely different from that of inanimacy. For example, scientific fields are commonly divided into the following two branches: natural sciences, which study natural phenomena, and social sciences, which study human behavior and societies. Natural sciences are typically further divided into life and physical sciences. Previous studies have shown that people’s understanding of living and non-living things are quite distinct and that the animate-inanimate distinction begins to develop in infancy (Reference Gelman, Spelke, Flavell and RossGelman & Spelke, 1981; Reference LegersteeLegerstee, 1992; Reference Rakison and Poulin-DuboisRakison & Poulin-Dubois, 2001). Conceptual distinctions ought to be reflected in language (Reference Fox, Ülkümen, Brun, Keren, Kirkebøen and MontgomeryFox & Ülkümen, 2011; Reference HutchinsHutchins, 1996). Reference TeigenTeigen (1988) also argued that different forms of uncertainty may have markers in natural language. Therefore, the selection of probability expressions that describe our beliefs about event probabilities might be determined by whether the relevant cognitive concept is animate or inanimate.
1.1 Probability expressions and the (in)animate
Numerical probability may be the more appropriate way to express inanimate uncertainty than animate uncertainty. This association may result from history, going back to the development of probability theory in the seventeenth century. Probability theory was initially inspired by games of chance, as it attempted to apply mathematical thinking to uncertain random phenomena. The numerical probability of the occurrence of future events can be calculated based on algebraic rules and formulas. The numerical probability calculus originally depended on specific requirements, including “objectiveness” and “randomness” (Reference HoppeHoppe, 2007; Reference MisesMises, 1957). The “objectiveness” requirement holds that the probabilities should be objective empirical properties and magnitudes rather than subjective beliefs or degrees of confidence (Reference HoppeHoppe, 2007). The “randomness” requirement holds that the sequence of events is completely lawless, such that the probabilities are not easily affected by any place selection, or as Ludwig von Mises said, “nothing is known about any particular event except its membership in a known class.” By contrast, animate things (especially human beings) do not behave objectively, as in they are not like a “fair coin”. They act independently, possess feelings and intentions, and have their own preferences, which may drive them to make irrational decisions. For another thing, “randomness” entails that we know nothing about any particular event except its membership in a known class. This is true for inanimate things such as a throw of dice in which the “three” outcome is one of six possible outcomes. However, this assumption is less tenable in the case of human action, given some of the factors that will determine people’s outcomes (Reference HoppeHoppe, 2007).
In contrast, verbal probability may be the appropriate way to express animate uncertainty. Verbal probability is surely older, historically, than numerical probability. It is more flexible and less precise in meaning (Reference Budescu, Weinberg and WallstenBudescu et al., 1988), and it allows people to incorporate infrequent connotations (Reference Weber and HiltonWeber & Hilton, 1990). Every verbal probability can be represented as a “membership function” on the [0, 1] numerical probability interval, with the location and shape varying with individuals and contexts (Reference Wallsten, Budescu, Rapoport, Zwick and ForsythWallsten et al., 1986). For example, in one situation, “likely” may be represented as a membership function on the numerical probability range from 50% to 90%, with 60% as the best point of equivalence because it represents the maximum value of the function. Yet, in another situation, the numerical range and the best point of equivalence (the maximum value of the function) could be quite different. The movement of non-living things is predictable given our knowledge of the physical forces acting upon them (Reference Glick, Glick and Clarke-StewartGlick, 1978; Reference Hoffman, Flavell and RossHoffman, 1981), whereas people and animals can move independently and their actions often vary in time and are unexpected. Thus, it seems likely that verbal probability is more adept at expressing the animate uncertainty, given that it provides individuals with the opportunity for any potential changes.
Based on the previous analysis, we expect that numerical probabilities are more compatible with the uncertainty rooted in inanimate things, whereas verbal probabilities are more compatible with the uncertainty rooted in animate things.
1.2 Overview of present research
Four studies were designed to examine whether verbal probability is more closely associated with animate uncertainty whereas numerical probability is more closely associated with inanimate uncertainty. Studies 1–3, using a forced-choice paradigm, tested the bidirectional relationship between verbal/numerical probability and animate/inanimate uncertainty in scenarios in which probability could be constructed based on equally likely outcomes information (Study 1), on relative frequency information (Study 2) or on personal beliefs (Study 3). We found that: 1) people preferred verbal probability expression when required to predict the likelihood of events happening to something animate but preferred numerical probability expression when required to predict the likelihood of events happening to something inanimate; 2) people thought that the events of which the likelihood was expressed in verbal probability was more likely related to animate things, but thought that the events of which the likelihood was expressed in numerical probability was more likely related to inanimate things. Study 4 provided further evidence for our findings using a free response paradigm in which the subjects freely predicted the likelihood of events or gave reasons for statements containing probabilities.
2 Study 1
Three theories describe how numerical probabilities are assigned to events: logical theory, which assigns probability based on logically equivalent propositions (such as equally likely outcomes), frequency theory, which relies on the relative frequency of particular events, and personal theory, which is based on beliefs (Reference BaronBaron, 2008). We began our tests with a scenario in which the verbal/numerical probability was based on logical theory.
2.1 Method
Two hundred and twenty-three Chinese students from Beijing Forestry University and Beijing Normal University (102 female) were recruited. Each subject filled in a questionnaire consisting of four situational questions (within-subjects design). We tested the associations between verbal/numerical probability and animate/inanimate things in two ways. One was designed to test whether preferred probability expression (verbal or numerical) varied as a function of animacy (animate or inanimate thing). The other was designed to test whether inferred animacy (by an animate or inanimate thing) varied as a function of the probability expression (verbal or numerical).
At the beginning of the questionnaire, the definitions of verbal and numerical probability as well as examples of each were presented. Following the definitions were four questions based on a scenario in which an object was placed inside a hollow ball which had five holes on its surface (Figure 1). To test whether the preferred probability expression (verbal or numerical) varied as a function of animacy (animate or inanimate), we prepared two questions (Mouse-trigger Problem, Marble-trigger Problem). The subjects were asked to imagine that something, either a mouse or a marble, was placed inside a hollow ball and then to indicate which form of probability (verbal or numerical) would be their preferred form for predicting the likelihood of the mouse or the marble coming out of Hole 1 after the ball had rolled around for a while. To test whether inferred animacy (animate or inanimate) varied as a function of probability expression (verbal or numerical), we prepared two additional questions (Numerical-trigger Problem, Verbal-trigger Problem). The subjects were asked to imagine that an unidentified (either mouse or marble) object was placed inside a hollow ball and were either told that the object had a 1 in 5 likelihood or that it had a small chance of coming out of Hole 1 after the ball rolled around for a while. The task of subjects was to guess which object (a mouse or a marble) they would expect would be the one to come out of Hole 1. The order between “Mouse-trigger Problem” and “Marble-trigger Problem”, or between “Numerical-trigger Problem” and “Verbal-trigger Problem” was counterbalanced between subjects. (See Appendix A for details of stimuli)

Figure 1: The hollow ball picture used in the questionnaire.
2.2 Results and discussion
The results are summarized in Tables 1a and 1b. In Table 1a, the percentages represent the relative numbers of subjects who preferred one type of probability expression (verbal or numerical) in one condition (a mouse or a marble). Whether they were predicting the likelihood of an animate or an inanimate thing had a significant effect on their preference for verbal or numerical probability expression (McNemar’s test, p = .022). More subjects preferred to use numerical probability when predicting how likely a marble would be to come out (71.3%) than when predicting how likely a mouse would be to come out (61.9%). In addition, more subjects preferred verbal probability when predicting a mouse (38.1%) than when predicting a marble (28.7%). In Table 1b, the percentages represent the relative numbers of subjects who chose one possible object (a mouse or a marble) in one condition (verbal or numerical probability). Receiving verbal or numerical probability information influenced the subjects’ expectation of which object (animate or inanimate) would come out (McNemar’s test, p < .001). As illustrated in Table 1b, when the prediction was made using a verbal probability, more subjects believed it was a mouse (57.4%) than believed it was a marble (42.6%) that would come out of the ball; when the prediction was made using a numerical probability, more subjects believed it was a marble (88.8%) than a mouse (11.2%).
Table 1a: Number (percentage) distribution of preferred probability expression (verbal or numerical) as a function of animacy (animate or inanimate).

Table 1b: Number (percentage) distribution of inferred animacy (animate or inanimate) as a function of probability expression (verbal or numerical).

These results provided evidence that people associate the uncertainty of animate things more closely with verbal probabilities and associate the uncertainty of inanimate things more closely with numerical probabilities when they predicted the likelihood of uncertain events in the context of equally likely outcomes.
3 Study 2
Study 1 provided initial support for the hypothesis that people associate verbal probability with the likelihood of an animate thing and associate numerical probability with the likelihood of an inanimate thing. The goal of Study 2 was to examine the robustness of the findings by testing whether the associations revealed in Study 1 would extend to scenarios in which the probability was derived from frequency theory. So in Study 2, the relative frequency of the outcome was provided as the basis for the assessment of probability.
3.1 Method
A hundred and three undergraduate Chinese students from Beijing Normal University (49 female) participated in Study 2 for a gift worth about ¥3. Each subject was randomly assigned to respond in only one of two scenarios, each scenario containing two questions (within subjects design). Each scenario consisted of two questions. Scenario 1 was designed to test whether the preferred probability expression (verbal or numerical) varied as a function of animacy (animate or inanimate), whereas Scenario 2 was designed to test whether inferred animacy (animate or inanimate) varied as a function of the probability expression (verbal or numerical).
Scenario 1:
A lie detection expert or a lie detector machine is about to detect whether a suspect is lying. The lie detection expert or the lie detector machine has recently tested 9 suspects, 7 of which were correct and 2 of which were wrong. If you were asked to predict the likelihood that the lie detection expert or the lie detector machine will make a correct judgment in the current case, which probability expression would you be more likely to use, verbal (e.g., very likely) or numerical (e.g., a likelihood of 70%~80%)?
Scenario 2:
Lies can be detected by a lie detection expert (who has recently tested 9 suspects, 7 of which were correct and 2 of which were wrong) or by a lie detector machine (which has also recently tested 9 suspects, 7 of which were correct and 2 of which were wrong). During a lie detection case, if you were informed of a likelihood prediction regarding correct detection in a verbal probability (e.g., “The current lie detection is very likely to be correct”) or a numerical probability (e.g., “The current lie detection has a 70-80% likelihood of being correct”), which option do you think was more likely to have conducted this lie detection, a lie detection expert or a lie detector machine?
To avoid order effects, the order of the two questions and the two options in each scenario was counterbalanced. (See Appendix B for details of stimuli.)
3.2 Results and discussion
The results of Study 2, summarized in Table 2a and Table 2b, replicated those of Study 1. As the results in Table 2a indicated, predicting the likelihood of an animate being (a lie detection expert) or an inanimate thing (a lie detector machine) had a significant influence on the preference for verbal or numerical probability in the scenario where relative frequency information was available (McNemar’s test, p = .029). More subjects preferred to use verbal probability when predicting how likely a lie detection expert would be to make a correct judgment (45.1%) than when predicting how likely a lie detector machine would be (21.6%). Similarly, more subjects preferred numerical probability when predicting a lie detector machine (78.4%) than when predicting a lie detection expert (54.9%). As illustrated in Table 2b, receiving verbal or numerical probability information influenced the subjects’ guesses about whether the animate or the inanimate thing carried out the lie detection (McNemar’s test, p < .001). In particular, when the likelihood of making a correct judgment was described by a verbal probability, more subjects believed a lie detection expert (84.6%) carried out the detection than a lie detector machine (15.4%); when the likelihood was described by numerical probability, more subjects thought it was a lie detector machine (75.0%) accomplishing the detection than a lie detection expert (25.0%).
Table 2a: Number (percentage) distribution of preferred probability expression (verbal or numerical) as a function of animacy (animate or inanimate).
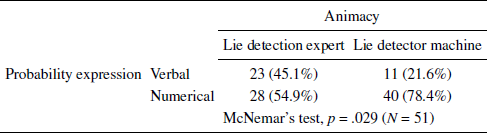
Table 2b: Number (percentage) distribution of inferred animacy (animate or inanimate) as a function of probability expression (verbal or numerical)

In sum, the bidirectional associations between verbal/numerical probability and animate/inanimate things were robust enough to be detected in a scenario in which probability was primarily based on relative frequency information.
4 Study 3
Studies 1 and 2 confirmed that an association between verbal probability and animate beings and between numerical probability and inanimate things could be identified in scenarios in which either equally likely outcomes or frequency information was available for assigning numerical probabilities to events. Study 3 was designed to test whether these hypothetical associations could also extend to situations in which neither equally likely outcomes nor frequencies could be relied on but rather in which probabilities were estimated based on people’s own beliefs or knowledge. In this case, the probability is relatively difficult to construct and the uncertainty is vague compared to the two previous studies.
4.1 Method
Ninety five Chinese students from Central University of Finance and Economics participated in Study 3 for a gift worth about ¥2.2. (The data from 3 subjects were removed because they misunderstood the questions.) The basic procedure was identical to Study 2 except that the scenario was changed into one to which personal theory would be applied. The scenario used in Study 3 was a classical Prison Dilemma game with a payoff matrix. The scenario read as follows:
You are going to play a game with an opponent. You have two options in the game, Move 1 or Move 2. If you choose Move 1 and your opponent chooses Move 2, you receive ¥25 and your opponent receives ¥85. If you choose Move 2 and your opponent chooses Move 1, you receive ¥85 and your opponent receives ¥25. If both you and your opponent choose Move 1, each of you receives ¥75. If both you and your opponent choose Move 2, each of you receives ¥30.
To test whether the preferred probability expression (verbal or numerical) would vary as a function of animacy (animate or inanimate), 48 subjects were asked to imagine their opponent was a stranger or an intelligent computer and then to indicate which form of probability (verbal: e.g., “possible”, or numerical: e.g., “a likelihood of 30%–40%”) would be their preferred form when predicting the likelihood of their opponent choosing Move 2. To test whether inferred animacy (animate or inanimate) varied as a function of probability expression (verbal or numerical), 44 subjects were asked to imagine that they were informed of a message predicting their opponents’ likelihood of choosing Move 2 using verbal probability (e.g., “possible”) or numerical probability (e.g., “a likelihood of 30%–40%”). The task of these subjects was to guess whether their opponents were more likely to be a stranger or an intelligent computer. To avoid order effects, the order of the two questions and the two options for each subject was counterbalanced as in Study 2. (See Appendix C for details of stimuli.)
4.2 Results and discussion
The results were consistent with the previous two studies, indicating that people’s preferred probability expression (verbal or numerical) varied as a function of animacy (animate or inanimate) and people’s inferred animacy (animate or inanimate) varied as a function of their probability expression (verbal or numerical) even in a scenario where neither equally likely outcomes nor equal frequencies, but rather personal beliefs and knowledge, were available for assigning numerical probabilities to events.
As indicated in Table 3a, predicting either the likelihood of an animate being (stranger) or an inanimate thing (intelligent computer) had a significant influence on the preference for verbal or numerical probability (McNemar’s test, p < .001). More subjects preferred to use verbal probability when predicting the action of a stranger (58.3%) than when predicting that of an intelligent computer (16.7%), whereas more subjects preferred numerical probability when predicting the action of an intelligent computer (83.3%) than when predicting that of a stranger (41.7%). The results in Table 3b indicate whether receiving verbal or numerical probability information would influence the subjects’ prediction of whether the animate being or the inanimate thing would make the choice (McNemar’s test, p = .014). When the probability information was expressed as verbal probability, more subjects anticipated that their opponent would be a stranger (72.7%) than an intelligent computer (27.3%); when the probability information was expressed by numerical probability, more subjects anticipated that their opponent would be an intelligent computer (63.6%) than a stranger (36.4%).
Table 3a: Number (percentage) distribution of preferred probability expression (verbal or numerical) as a function of animacy (animate or inanimate).

Table 3b: Number (percentage) distribution of inferred animacy (animate or inanimate) as a function of probability expression (verbal or numerical).

The results of the above three studies seem to demonstrate that verbal probability is more closely associated with the uncertainty of animate things, whereas numerical probability is more closely associated with the uncertainty of inanimate things regardless of which theory or information was used as a basis for constructing the probability.
5 Study 4
The above three studies employed forced-choice procedures in which the subjects consciously compared and chose between verbal probability and numerical probability or between animate and inanimate things. This process was fairly different from what people experience in daily communication situations. Thus, in Study 4, we used two free response procedures in order not to prejudice the subjects. To test whether the preferred probability expression (verbal or numerical) varied as a function of animacy (animate or inanimate), subjects were asked to freely write, not to choose between offered options as in Studies 1–3, their prediction of the likelihood of events happening to an animate being or an inanimate thing. In addition, we employed a sentence-completion technique with statements ending with “because…” (Reference Teigen and BrunTeigen & Brun, 1995, Reference Teigen and Brun1999) to test whether inferred animacy (animate or inanimate) varied as a function of probability expression (verbal or numerical). In this exercise, the subjects were asked to give reasons (human-related reasons or non-human-related reasons) for statements containing verbal or numerical probabilities. If our assumption was true, we would expect that (1) the subjects would be more likely to write verbal probability when predicting the likelihood of events happening to animate beings but to write numerical probability when predicting the likelihood of events happening to inanimate things and that (2) the subjects would be more likely to give human-related reasons under the verbal probability condition but to give non-human-related reasons under the numerical probability condition.
According to Reference Budescu and WallstenBudescu and Wallsten (1995), the three scenarios for assigning numerical probabilities to events used in Studies 1–3 can be simply represented on a continuum from precise to vague. That is, both equally likely outcomes and frequency information (Studies 1–2) can be viewed as external sources which make the experienced uncertainty relatively precise (easy to be represented by numerical probability); whereas personal beliefs and knowledge (Study 3) can be viewed as internal sources which make the experienced uncertainty relatively vague (difficult to be represented by numerical probability). To simplify the experimental manipulation, in Study 4 we adopted a precise/vague classification to test the preferred probability expression under different animacy conditions (animate or inanimate).
5.1 Method
One hundred and sixty-eight college students from Beijing Forestry University and China Agricultural University (78 female) participated in Study 4 for a gift worth about ¥2. Each subject filled in a questionnaire consisting of two sets of questions.
In one set, the subjects were given two scenarios (see Appendix D) which were similar to those in Studies 1–3. The scenarios were designed to test whether the preferred probability expression (verbal or numerical) varied as a function of animacy (animate or inanimate) under both precise and vague uncertainty conditions. Each scenario had two versions, A and B, both describing the same event but with different animacy manipulations (animate or inanimate). In the precise uncertainty condition, frequency information was provided to facilitate constructing numerical probability. Subjects were told that a general practitioner (Version A) or a medical instrument (Version B) would examine a patient to see whether a certain disease was present and that the general practitioner or the medical instrument had recently examined seven suspected cases, of which five were diagnosed correctly. The task of subjects was to predict and write down the likelihood of the general practitioner or the medical instrument making a correct diagnosis in the current case. In the vague uncertainty condition, subjects mainly relied on their own knowledge to construct probabilities. They were told that an intelligent computer (Version A) or a Chinese chess player (Version B) that had never lost was about to play another Chinese chess game. The task of subjects was also to predict and write down the likelihood that the intelligent computer or the Chinese chess player would win the current game.
In the other set of questions, which were designed to test whether inferred animacy (animate or inanimate) varied as a function of probability expression (verbal or numerical), the subjects were given three incomplete sentences involving stockbrokers, transport problems or building construction (see Appendix E) containing verbal or numerical probability expressions. The three incomplete sentences also had two versions, A and B, both of which described the same three events but with different probability formats (verbal or numerical). The following incomplete sentences are examples of the ones we used. In Version A, the sentence said “A stockbroker recommends a stock for you and it is very likely to gain profits in the coming year, because…” In Version B, the incomplete sentence was changed to “A stockbroker recommends a stock for you and it has a probability of 80% of gaining profits in the coming year, because…” The task of subjects was to complete the sentences in a way that made sense. For both sets of questions, each subject was randomly assigned to Version A or Version B (between subjects design).
The probability predictions were categorized by two independent raters who were unfamiliar with this research as: (a) verbal probability, e.g. “very likely”, or “very probably”; (b) numerical probability, e.g. “70%–80%”, or “5/7”; (c) other, e.g. mixed or combined probabilities (verbal and numerical), or non probability expressions (“rich experience” or “high technology”). The inter-rater agreement was 86.3% for the precise uncertainty condition and 90.5% for the vague uncertainty condition, respectively. Discrepancies (mostly about the nature of “other”) were resolved by discussion.
The reasons in the sentence completions were coded by the same two independent raters as (a) human-related, e.g. “the stockbroker is experienced in buying and selling stocks”; (b) non-human-related, e.g. “the stock market has been rising recently”; (c) other, i.e., reasons unclassifiable as clearly non-human-related or human-related, such as “the stock is affected by various factors.” The inter-rater agreement range was 95.2%, 66.1%, and 81.5%, respectively, for the three incomplete sentences. Discrepancies (also mostly about the nature of “other” reasons) were resolved by discussion.
5.2 Results and discussion
The results from the questions used to test the effects of animacy on preferred probability expression are summarized in Table 4a. In the precise uncertainty condition in which frequency information was available, predicting the likelihood of the animate being (a general practitioner) or the inanimate thing (a medical instrument) had a significant influence on the preference for verbal or numerical probability even in a free response procedure, χ2 (1) = 3.989, p = .046. In keeping with our expectations, when predicting the performance of the general practitioner, more subjects used verbal probability (56.1%) than numerical probability (39.0%). In contrast, when predicting the performance of the medical instrument, more subjects used numerical probability (52.3%) than verbal probability (39.5%). In the vague uncertainty condition in which only personal beliefs or knowledge could be relied on, the subjects’ preference for using verbal probability decreased from 68.6% (when predicting the performance of the Chinese chess player) to 62.2% (when predicting the performance of the intelligent computer), but the effect of animacy failed to reach statistical significance, χ2 (1) = .609, p = .435.
Table 4a: Number (percentage) distribution of written probability expression (verbal or numerical) as a function of animacy (animate or inanimate) under precise and vague uncertainty conditions

The results from the questions designed to test the effects of probability expression on inferred animacy are summarized in Table 4b. They show that predicting an event using a verbal or a numerical probability expression had a significant influence on the subjects’ attribution to human or non-human reasons (all χ2>5.3, all p <.05). Specifically, more subjects completed the sentences with human-related reasons when an event was predicted using verbal probability than when it was presented using numerical probability (61.0% vs. 44.2%, 43.0% vs. 24.4%, 35.4% vs. 12.8%). Similarly, more subjects completed the sentences with non-human-related reasons when an event was predicted using numerical probability than when it was presented using verbal probability.
Table 4b: Number (percentage) distribution of subjects giving human-related or non-human-related reasons when completing sentences containing verbal or numerical probability

In summary, Study 4, although it employed free responses, provided further evidence for the bidirectional “verbal-animate” and “numerical-inanimate” associations. Specifically, in one direction, when the probability expression was manipulated, its effect on people’s attribution was significant in all incomplete sentences, showing the “verbal-to-animate” and “numerical-to-inanimate” links. In the other direction, when the animacy was manipulated, its effect on people’s preference for the probability expression showed significance in the precise uncertainty condition, revealing the “animate-to-verbal” and “inanimate-to-numerical” links. But, in the vague uncertainty condition, although subjects showed a decrease in preference for verbal probability when predicting the inanimate compared to predicting the animate, the results failed to reach a significant level. One potential explanation was that the subjects felt that writing an actual numerical probability was difficult when the underlying uncertainty was fairly vague (only 29.2% of subjects wrote numerical probabilities overall), even though they might have preferred to use numerical probability when predicting about an inanimate thing (as indicated by Study 3). In short, our assumption was largely confirmed in cases in which free response procedures were used, though we found one statistical exception, as noted above.
6 General discussion
Converging evidence supporting verbal-animate/numerical-inanimate associations was investigated in four studies. In these experimental studies, different scenarios or approaches were employed to explore the generality of our findings. Reference Budescu and WallstenBudescu and Wallsten (1995) suggested that experienced uncertainty regarding the occurrence of an event can range on a continuum from precise to vague and that this experience-based continuum has a strong effect on the preference for modes of communicating probabilities (Reference Olson and BudescuOlson & Budescu, 1997). Therefore, we examined the associations across different scenarios in which the probabilities were constructed based on information about equally likely outcomes (Study 1), relative frequencies (Study 2) or personal beliefs (Study 3). Although the underlying uncertainty in these scenarios ranged from precise (Studies 1–2) to vague (Study 3), consistent results were obtained, confirming that people associated numerical probabilities more closely with inanimate uncertainty and verbal probabilities more closely with animate uncertainty.
Previous research has shown that the mode of response (e.g., choice or estimation) can often affect personal probabilistic reasoning (Reference WedellWedell, 2011; Reference Wedell and MoroWedell & Moro, 2008). Because only forced-choice procedures were used in Studies 1–3, we further examined our findings by using free-response measures in Study 4. Again, the findings were generally consistent except when people were asked to write probability predictions for scenarios in which the underlying uncertainty was very vague. This exception may be explained by previous observations that people prefer to use verbal probabilities when conveying information than when they receive uncertainty information (Reference Olson and BudescuOlson & Budescu, 1997). Thus, the “animate-to-verbal” and “inanimate-to-numerical” associations can be overwhelmed by a preference to convey vague uncertainty in terms of verbal probability. Another possible explanation is that (as one reviewer mentioned), in contrast to other scenarios, the numbers were not mentioned in the vague scenario text. This issue should be tested in future studies.
There are several possible explanations for why people prefer to associate verbal probabilities, as opposed to numerical probabilities, with animate things. In the Introduction, we speculated that these associations are due to the limitations of numerical probabilities and the vagueness of verbal probabilities. This might explain the popular use of verbal probabilities in daily life (Reference Budescu, Weinberg and WallstenBudescu et al., 1988; Reference Reagan, Mosteller and YoutzReagan et al., 1989; Reference Wallsten, Budescu, Rapoport, Zwick and ForsythWallsten et al., 1986) and the rather limited role of numerical probabilities in conveying scientific information to the public (with the exception of fields such as genetic testing and weather forecasting in which numerical probabilities are commonly used).
Considering that living things continuously undergo changes (Reference McCrackenMcCracken, 1952), another possible explanation is that verbal probabilities may be more suitable for expressing changeable uncertainty. Previous studies examining the animate-inanimate distinction have found that people often focus on animate things’ psychological properties, which are indeterminate and varying, but they focus on inanimate things’ physical properties, which are more fixed (Reference Gelman, Spelke, Flavell and RossGelman & Spelke, 1981). Thus, the uncertainty of animate things is considered more changeable than that of inanimate things. Previous studies examining probability expressions have shown that verbal phrases are less precise than numerical probabilities and that interpretations of verbal probabilities are influenced by many factors, such as outcome severity (Reference Harris and CornerHarris & Corner, 2011; Reference Weber and HiltonWeber & Hilton, 1990), perceived base rate (Reference Weber and HiltonWeber & Hilton, 1990) and whose future (i.e., self or other) is being predicted (Reference Smits and HoorensSmits & Hoorens, 2005). These factors suggest that verbal probabilities can provide the opportunity for potential changes. Therefore, it is not surprising that there is a good match between the changeable uncertainty of animate things and verbal probabilities’ ability to accommodate change, which may explain the close association between living things and verbal phrases. In contrast, non-living things and numerical probabilities may be closely associated because both lack the ability to change. Of course, an alternative possibility is evident from previous studies claiming that people dealing with incomplete knowledge prefer to use verbal phrases because verbal phrases offer the chance to be vague (Reference Erev and CohenErev & Cohen, 1990; Reference Xu, Ye and LiXu, Ye, & Li, 2009). Given that living things are more complex and unpredictable than non-living things, it is possible that people feel more uncertain about animate things and, therefore, prefer to use verbal probabilities to express this uncertainty. In contrast, people may feel more certain about inanimate things and therefore assign precise numerical probabilities to them. Thus, vagueness may also be able to explain the close associations between verbal probabilities and animacy as well as the association between numerical probabilities and inanimacy. This mechanism needs to be clarified in future studies.
Previous studies have suggested that a verbal probability (such as “possible”) is not just another way of expressing a quantitative probability; rather, it is a carrier that conveys important semantic information, including revealing features of directionality, internal/external attribution and self-serving interpretation (Reference Kahneman and TverskyKahneman & Tversky, 1982; Reference Smits and HoorensSmits & Hoorens, 2005; Reference Teigen and BrunTeigen & Brun, 1999, Reference Teigen and Brun2000). The present research contributes to this literature by detecting an additional semantic feature of verbal probability: “animacy”. According to the current results, people prefer to use verbal probabilities for animate (i.e., living things) uncertainty, whereas they prefer to use numerical probabilities to describe inanimate (i.e., non-living things) uncertainty. To the best of our knowledge, this animacy feature of verbal probability is reported for the first time in the field of uncertainty communication in this paper. We are living in a world of rapid change in which most uncertainty changes are caused (or necessitated) by living social beings. Accordingly, verbal probability must play an important role in describing the uncertain world regardless of whether the so-called animacy feature is laboratory-supported. Therefore, although animacy is a late addition to the group of verbal probability features, it is not a simple accumulation of terminology; rather, it is very important for enabling researchers to understanding how people cope with the living world. Future research should investigate this feature more fully to clarify its effect on decision making under risk and uncertainty.
Our findings may provide supportive evidence for the human-nonhuman perception boundary. Reference Kwan and FiskeKwan and Fiske (2008) suggested that the perceived boundary between human and nonhuman agents is malleable and that certain factors, such as the speed of movement, can lead to more or less anthropomorphism, in which human personality characteristics are attributed to nonhuman agents (Reference Morewedge, Preston and WegnerMorewedge et al., 2007). According to present results, verbal and numerical probabilities appear to be factors that influence the degree to which an object is perceived to be human or nonhuman. In particular, given the “animate-verbal” and “inanimate-numerical” associations, expecting that verbal probability can lead to more anthropomorphism, compared to numerical probability, is reasonable.
Two limitations should be noted. First, in Studies 2 and 4, when we constructed the scenarios consisting of frequency information, relatively small samples were chosen. Therefore, the probabilities involved may not be very precise. This limitation should be addressed in future studies. Second, this study only refers to Chinese verbal probability and the preference mode of Chinese speakers. Previous studies have indicated that English speakers generate a greater variety of English verbal probabilities, which had more precise numerical probability values compared to Chinese verbal probabilities. These studies also indicated that English speakers tended to think more probabilistically with regard to uncertainty than Chinese speakers (Reference Lau and RanyardLau & Ranyard, 1999; Reference Phillips, Wright, Jungermann and de ZweeuwPhillips & Wright, 1977; Reference Xu and LiXu & Li, 2007). Therefore, the findings of this study need to be extended to other languages.
Researchers and practitioners of decision analysis are often faced with the need to choose a single mode for communicating probabilistic information. Consistent with previous studies (Reference Olson and BudescuOlson & Budescu, 1997; Reference Wallsten, Budescu, Zwick and KempWallsten et al., 1993), our results show that neither the verbal nor the numerical mode of communication is universally preferred, and it may be that each probability expression is more appropriate for a specific set of target events. Specifically, people prefer to use verbal probabilities to predict animate things, whereas they prefer to use numerical probabilities to predict inanimate things. Because choosing an appropriate probability mode that people prefer may increase the acceptability of uncertainty information, these research findings may offer useful guidance about how to communicate risk information. In medical fields, health professionals are often required to inform patients and their families about the chances of developing certain diseases, particularly when the diagnoses are not mutually exclusive. Practitioners can reasonably infer that, if the examination results are derived from medical instruments (i.e., inanimate), numerical probability predictions (mostly referring to frequency data) may be the proper expression for communicating the likelihood of making a correct diagnosis. However, if the examination results mainly refer to the experiences of the doctors, then verbal probability predictions may sound more natural to the patients. This observation would be similar across other fields. For example, numerical probabilities may be more ideal for weather forecasting, whereas verbal probabilities may be better suited for some gambling which involves living things, such as betting on ballgames, boxing, horse-racing, greyhound-racing, etc. In addition, these results can be applied to conveying safety evaluation information (such as information about nuclear power plants, high-speed railways or genetically modified food) to the public. Providing verbal phrases may encourage people to think of more human-relevant factors, whereas providing numerical probabilities may encourage them to consider more human-irrelevant factors. It is important to note that the present research only confirmed associations, and future research should focus on whether these associations affect communication and the ability to make decisions under risk and uncertainty in real life.
Appendix A
Mouse-trigger Problem:
Imagine that a mouse is placed inside a hollow ball (see the picture), and after the ball has rolled around for a while, you have to estimate the likelihood that the mouse will come out of Hole 1. Please take some time to think about this likelihood. Which form of probability expression do you initially think of using?

□ Verbal probability □ Numerical probability
Marble-trigger Problem:
Imagine that a marble is placed inside a hollow ball (see the picture), and after the ball rolls around for a while, you have to estimate the likelihood that the marble will come out of Hole 1. Please take some time to think about this likelihood. Which form of probability expression do you initially think of using?
□ Verbal probability □ Numerical probability
Numerical-trigger Problem:
Imagine that an unidentified object is placed inside a hollow ball (see the picture), and you are told that the object has a 1 in 5 likelihood of coming out of Hole 1 after the ball rolls around for a while. Which object do you expect will come out of Hole 1?
□ A mouse □ A marble
Verbal-trigger Problem:
Imagine that an unidentified object is placed inside a hollow ball (see the picture), and you are told that the object has a small chance of coming out of Hole 1 after the ball rolls around for a while. Which object do you expect will come out of Hole 1?
□ A mouse □ A marble
Appendix B
Scenario 1
I. A lie detection expert is about to detect whether a suspect is lying. He has recently tested 9 suspects, 7 of which were correct and 2 of which were wrong. If you were asked to predict the likelihood that the lie detection expert will make a correct judgment in the current case, which probability expression would you be more likely to use?
1) Verbal (e.g., very likely) 2) Numerical (e.g., a likelihood of 70-80%)
II. A lie detector machine is about to detect whether a suspect is lying. It has recently tested 9 suspects, 7 of which were correct and 2 of which were wrong. If you were asked to predict the likelihood that the lie detector machine will make a correct judgment in the current case, which probability expression would you be more likely to use?
1) Verbal (e.g., very likely) 2) Numerical (e.g., a likelihood of 70-80%)
Scenario 2:
Lies can be detected by a lie detection expert (who has recently tested 9 suspects, 7 of which were correct and 2 of which were wrong) or by a lie detector machine (which has also recently tested 9 suspects, 7 of which were correct and 2 of which were wrong).
I. During a lie detection case, if you were informed of a likelihood prediction regarding correct detection in a verbal probability (e.g., “The current lie detection is very likely to be correct”), which option do you think was more likely to have conducted this lie detection?
1) A lie detection expert 2) A lie detector machine
II. During a lie detection case, if you were informed of a likelihood prediction regarding correct detection in a numerical probability (e.g., “The current lie detection has a 70-80% likelihood of being correct”), which option do you think was more likely to have conducted this lie detection?
1) A lie detection expert 2) A lie detector machine
Appendix C
You are going to play a game with an opponent. You have two options in the game, Move 1 or Move 2. If you choose Move 1 and your opponent chooses Move 2, you receive ¥25 and your opponent receives ¥85. If you choose Move 2 and your opponent chooses Move 1, you receive ¥85 and your opponent receives ¥25. If both you and your opponent choose Move 1, each of you receives ¥75. If both you and your opponent choose Move 2, each of you receives ¥30.

(To test the effect of animacy on the preferred probability expression)
I. Imagine that your opponent was a stranger. Please estimate the likelihood that the stranger will choose Move 2. Which form of probability expression would you prefer to use?
1) Verbal (e.g., “possible”) 2) Numerical (e.g., “a likelihood of 30-40%”)
II. Imagine that your opponent was an intelligent computer. Please estimate the likelihood that the computer will choose Move 2. Which form of probability expression would you prefer to use?
1) Verbal (e.g., “possible”) 2) Numerical (e.g., “a likelihood of 30-40%”)
(To test the effect of probability expression on inferred animacy)
I. Imagine that you received a message predicting your opponent’s likelihood of choosing Move 2, and this message was expressed as a verbal probability (e.g., “possible”). Which one would you think was your opponent?
1) A stranger 2) An intelligent computer
II. Imagine that you received a message predicting your opponent’s likelihood of choosing Move 2, and this message was expressed as a numerical probability (e.g., “a likelihood of 30-40%”). Which one would you think was your opponent?
1) A stranger 2) An intelligent computer
Appendix D
Two scenarios (in precise and vague conditions) were employed in Study 4 to test the effect of animacy (animate or inanimate) on the preferred probability expression (verbal or numerical).
Precise condition
Version A:
Imagine that a general practitioner will examine a patient to see whether he has caught a certain disease. The general practitioner has recently examined seven suspected cases, of which five were diagnosed correctly. If you were asked to predict the likelihood of the general practitioner making a correct diagnosis in the current case, what would you say?
Version B:
Imagine that a medical instrument will be used to examine a patient to see whether he has caught a certain disease. The medical instrument has recently been used to examine seven suspected cases, of which five were diagnosed correctly. If you were asked to predict the likelihood of the medical instrument making a correct diagnosis in the current case, what would you say?
Vague condition
Version A:
Imagine that an intelligent computer which has never lost is about to play another Chinese chess game. If you were asked to predict the likelihood of the intelligent computer winning in the current game, what would you say?
Version B:
Imagine that a Chinese chess player who has never lost is about to play another Chinese chess game. If you were asked to predict the likelihood of the Chinese chess player winning in the current game, what would you say?
Appendix E
Three incomplete sentences were employed in Study 4 to test the effect of probability expression (verbal or numerical) on the inferred animacy (animate or inanimate).
Sentence 1
Version A:
A stockbroker recommends a stock for you. It is very likely to make a profit in the coming year, because ________.
Version B:
A stockbroker recommends a stock for you. It has a probability of 80% of making a profit in the coming year, because________.
Sentence 2
Version A:
A team of builders has a probability of 45%-65% of completing a new building project in time, because _________.
Version B:
A team of builders will find it quite possible to complete a new building project in time, because _________.
Sentence 3
Version A:
A transport fleet will very probably reach the destination in time, because ________.
Version B:
A transport fleet has a probability of 85% of reaching the destination in time, because ________.











