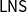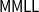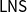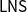1. Introduction
Proof systems are frameworks for formalizing reasoning, where inference rules dictate how theorems can be derived from the given hypotheses. Since proofs themselves are mathematical objects of study, proof systems can also be used as (meta-level) tools for analyzing the structural properties of proofs. One of the most important of such properties is analyticity.
Analytic calculi consist solely of rules that decompose the formulas to be proved in a step-wise manner. As a result, proofs from an analytic calculus satisfy the subformula property: every formula that appears (anywhere) in the proof must be a subformula of the formulas to be proved. This is a powerful restriction on the shape of proofs, and it can be exploited to prove important meta-logical properties of logical systems such as consistency, decidability, and interpolation.
The best-known formalism for proposing analytic proof systems is Gentzen’s sequent calculus (Gentzen Reference Gentzen1969), which manipulates consequence relations between contexts of formulas, represented by
![]() $\Gamma\vdash \Delta$
. In sequent calculus systems, analyticity is often guaranteed by proving a property called cut admissibility: if
$\Gamma\vdash \Delta$
. In sequent calculus systems, analyticity is often guaranteed by proving a property called cut admissibility: if
![]() $\Gamma_1\vdash \Delta_1,H$
is provable and
$\Gamma_1\vdash \Delta_1,H$
is provable and
![]() $H, \Gamma_2\vdash \Delta_2$
is provable, then so is
$H, \Gamma_2\vdash \Delta_2$
is provable, then so is
![]() $\Gamma_1,\Gamma_2\vdash \Delta_1,\Delta_2$
. In other words, one needs to prove that the cut rule below can be eliminated.
$\Gamma_1,\Gamma_2\vdash \Delta_1,\Delta_2$
. In other words, one needs to prove that the cut rule below can be eliminated.

Note the inherent duality: the cut formula H is both a conclusion of a statement and a hypothesis of another. In analytic systems, this duality is often an invariant, being preserved throughout the cut-elimination process. Developing general methods for detecting such invariants enables the use of meta-level frameworks to uniformly reasoning about object-level properties.
Unfortunately, sequent systems are not expressive enough for constructing analytic calculi for many logics of interest. The critical examples are modal logics: sequents appear to be too coarse for capturing the subtle behavior of modalities. As a result, many new formalisms extending sequent systems have been proposed over the last 30 years, including hypersequent calculi (Avron Reference Avron1996), nested calculi (Brünnler Reference Brünnler2009; Bull Reference Bull1992; Kashima Reference Kashima1994; Poggiolesi Reference Poggiolesi2009) and labeled calculi (Simpson Reference Simpson1994; Viganò Reference Viganò2000).
In this work, we study cut admissibility under the linear nested system formalism (
![]() $\mathsf{LNS}$
for short, Lellmann Reference Lellmann2015), where a single sequent is replaced by a list of sequents, and the inference rules govern the transfer of formulas between the different sequents.
$\mathsf{LNS}$
for short, Lellmann Reference Lellmann2015), where a single sequent is replaced by a list of sequents, and the inference rules govern the transfer of formulas between the different sequents.
![]() $\mathsf{LNS}$
form a particular subclass of nested systems, where the tree structure is restricted to a line.
$\mathsf{LNS}$
form a particular subclass of nested systems, where the tree structure is restricted to a line.
While such a more expressive formalism enables calculi for a broader class of logics, the greater bureaucracy makes it harder to prove logical properties, such as analyticity itself (Bruscoli and Guglielmi Reference Bruscoli and Guglielmi2006). We hence lift to
![]() $\mathsf{LNS}$
the method developed by Miller and Pimentel (Reference Miller and Pimentel2013) and revisited by Felty et al. (Reference Felty, Olarte and Xavier2021). The idea is to use a meta-level framework in order to specify and reason about, in a uniform way, different logical (object-level) proof systems. Such a framework should be powerful enough so as to be able to handle a great amount of systems. In Miller and Pimentel (Reference Miller and Pimentel2013), the meta-logical framework was linear logic (
$\mathsf{LNS}$
the method developed by Miller and Pimentel (Reference Miller and Pimentel2013) and revisited by Felty et al. (Reference Felty, Olarte and Xavier2021). The idea is to use a meta-level framework in order to specify and reason about, in a uniform way, different logical (object-level) proof systems. Such a framework should be powerful enough so as to be able to handle a great amount of systems. In Miller and Pimentel (Reference Miller and Pimentel2013), the meta-logical framework was linear logic (
![]() $\mathsf{LL}$
Girard Reference Girard1987). The advantage of having
$\mathsf{LL}$
Girard Reference Girard1987). The advantage of having
![]() $\mathsf{LL}$
as a framework is that it is a relatively simple, resource aware system, where steps of computation can be naturally specified. The problem is that simplicity often comes with a price, and
$\mathsf{LL}$
as a framework is that it is a relatively simple, resource aware system, where steps of computation can be naturally specified. The problem is that simplicity often comes with a price, and
![]() $\mathsf{LL}$
is not suitable for reasoning about modalities other than its own. In the present work, we adopt
$\mathsf{LL}$
is not suitable for reasoning about modalities other than its own. In the present work, we adopt
![]() $\mathsf{MMLL}$
, a multimodal extension of
$\mathsf{MMLL}$
, a multimodal extension of
![]() $\mathsf{LL}$
, as the meta-level framework. Object-level logical systems (OL for short) are specified as
$\mathsf{LL}$
, as the meta-level framework. Object-level logical systems (OL for short) are specified as
![]() $\mathsf{MMLL}$
theories, where OL rules are specified as
$\mathsf{MMLL}$
theories, where OL rules are specified as
![]() $\mathsf{MMLL}$
clauses. Such clauses have a very special shape: they are bipoles, formulas that can be totally decomposed in one focused step (Andreoli Reference Andreoli1992). In this way, the focusing proof strategy enforces a one-to-one correspondence between a OL-rule application and the decomposition of the respective
$\mathsf{MMLL}$
clauses. Such clauses have a very special shape: they are bipoles, formulas that can be totally decomposed in one focused step (Andreoli Reference Andreoli1992). In this way, the focusing proof strategy enforces a one-to-one correspondence between a OL-rule application and the decomposition of the respective
![]() $\mathsf{MMLL}$
formula in its focused system
$\mathsf{MMLL}$
formula in its focused system
![]() $\mathsf{LNS}_\mathsf{FMLL}$
. This is called adequacy, and it completely ties OL-{formulas, rules, derivations} to
$\mathsf{LNS}_\mathsf{FMLL}$
. This is called adequacy, and it completely ties OL-{formulas, rules, derivations} to
![]() $\mathsf{MMLL}-$
{formulas, bipoles, focused derivations}. We thus smoothly generalize the cut-admissibility criterion given in Miller and Pimentel (Reference Miller and Pimentel2013) to the linear nested setting, capturing at the meta-level the duality invariant mentioned above for the specified logical systems. In this work, we will apply this method for reasoning about classical/substructural normal multimodal logical systems, as well as the multiconclusion system for intuitionistic logic.
$\mathsf{MMLL}-$
{formulas, bipoles, focused derivations}. We thus smoothly generalize the cut-admissibility criterion given in Miller and Pimentel (Reference Miller and Pimentel2013) to the linear nested setting, capturing at the meta-level the duality invariant mentioned above for the specified logical systems. In this work, we will apply this method for reasoning about classical/substructural normal multimodal logical systems, as well as the multiconclusion system for intuitionistic logic.
This paper extends our previous work (Olarte et al. Reference Olarte, Pimentel and Xavier2020) in the following ways. (1) The meta-level frameworks adopted here and in Olarte et al. (Reference Olarte, Pimentel and Xavier2020) are based on
![]() $\mathsf{LL}$
with multimodalities (called subexponentials). Different from op. cit.,
$\mathsf{LL}$
with multimodalities (called subexponentials). Different from op. cit.,
![]() $\mathsf{MMLL}$
considers both unbounded (classical) and bounded (linear) subexponentials, depending if they assume or not the axioms of weakening and contraction. Hence, in this paper, we can also reason about (multimodal) substructural systems; (2) In Olarte et al. (Reference Olarte, Pimentel and Xavier2020), both the object- and meta-level logical systems had the sequent system presentation. In this work, all systems are represented as
$\mathsf{MMLL}$
considers both unbounded (classical) and bounded (linear) subexponentials, depending if they assume or not the axioms of weakening and contraction. Hence, in this paper, we can also reason about (multimodal) substructural systems; (2) In Olarte et al. (Reference Olarte, Pimentel and Xavier2020), both the object- and meta-level logical systems had the sequent system presentation. In this work, all systems are represented as
![]() $\mathsf{LNS}$
, so we can reason about a broader class of OL (including multi-modal ones); (3) In the focused system proposed here (
$\mathsf{LNS}$
, so we can reason about a broader class of OL (including multi-modal ones); (3) In the focused system proposed here (
![]() $\mathsf{LNS}_\mathsf{FMLL}$
), the modal rules are completely deterministic, improving the proof search procedure; (4) The proof of cut admissibility of the meta-logic is done directly in
$\mathsf{LNS}_\mathsf{FMLL}$
), the modal rules are completely deterministic, improving the proof search procedure; (4) The proof of cut admissibility of the meta-logic is done directly in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
, without the need of translating this system to the unfocused version and proving the completeness of focusing; (5) We provide a companion repository available at Xavier and Olarte (Reference Xavier and Olarte2021) with the Coq formalization of the cut-admissibility theorem for
$\mathsf{LNS}_\mathsf{FMLL}$
, without the need of translating this system to the unfocused version and proving the completeness of focusing; (5) We provide a companion repository available at Xavier and Olarte (Reference Xavier and Olarte2021) with the Coq formalization of the cut-admissibility theorem for
![]() $\mathsf{LNS}_\mathsf{FMLL}$
, as well as adequacy and the application of the cut-coherent criterion for some specified OL.
$\mathsf{LNS}_\mathsf{FMLL}$
, as well as adequacy and the application of the cut-coherent criterion for some specified OL.
Organization and contributions. We start Section 2 by recalling linear nested systems, and presenting
![]() $\mathsf{LNS}$
systems for propositional classical and intuitionistic logics, as well as for modal logics that are extensions of the basic modal logic
$\mathsf{LNS}$
systems for propositional classical and intuitionistic logics, as well as for modal logics that are extensions of the basic modal logic
![]() $\mathsf{K}$
with axioms from the set
$\mathsf{K}$
with axioms from the set
![]() $\{\mathsf{T},\mathsf{4},\mathsf{D}\}$
. In Section 3, we show how to lift the
$\{\mathsf{T},\mathsf{4},\mathsf{D}\}$
. In Section 3, we show how to lift the
![]() $\mathsf{LNS}$
formalism to
$\mathsf{LNS}$
formalism to
![]() $\mathsf{LL}$
with subexponentials, considering not only the structural axioms for contraction and weakening, but also the subexponential version of modal axioms (system
$\mathsf{LL}$
with subexponentials, considering not only the structural axioms for contraction and weakening, but also the subexponential version of modal axioms (system
![]() $\mathsf{MMLL}$
). Section 3.1 presents
$\mathsf{MMLL}$
). Section 3.1 presents
![]() $\mathsf{LNS}_\mathsf{FMLL}$
, a focused linear nested system for
$\mathsf{LNS}_\mathsf{FMLL}$
, a focused linear nested system for
![]() $\mathsf{MMLL}$
, which will be the adopted logical framework for specifying and characterizing OL cut-admissibility. In Section 3.2, we prove that
$\mathsf{MMLL}$
, which will be the adopted logical framework for specifying and characterizing OL cut-admissibility. In Section 3.2, we prove that
![]() $\mathsf{LNS}_\mathsf{FMLL}$
is itself analytic, with the proof formalized in Coq. As far as we know, this is the first formalization of cut admissibility of a
$\mathsf{LNS}_\mathsf{FMLL}$
is itself analytic, with the proof formalized in Coq. As far as we know, this is the first formalization of cut admissibility of a
![]() $\mathsf{LNS}$
-focused system. Section 4 shows how object logics can be specified as
$\mathsf{LNS}$
-focused system. Section 4 shows how object logics can be specified as
![]() $\mathsf{MMLL}$
theories. The encoding is natural and direct, and the proof of adequacy is immediate due to the focusing discipline. Different from Olarte et al. (Reference Olarte, Pimentel and Xavier2020), such encoding is general enough to consider multimodal substructural logics. Finally, the criteria for establishing OL cut admissibility are presented in Section 5. We show that such criteria can be easily checked. Section 6 concludes the paper.
$\mathsf{MMLL}$
theories. The encoding is natural and direct, and the proof of adequacy is immediate due to the focusing discipline. Different from Olarte et al. (Reference Olarte, Pimentel and Xavier2020), such encoding is general enough to consider multimodal substructural logics. Finally, the criteria for establishing OL cut admissibility are presented in Section 5. We show that such criteria can be easily checked. Section 6 concludes the paper.
2. Linear Nested Systems
In this section, we present a brief introduction to linear nested systems. For further details, please refer to Lellmann (Reference Lellmann2015), Lellmann and Pimentel (Reference Lellmann and Pimentel2019).
One of the main problems of using sequent systems as a framework is that sequents are often not adequate for expressing modal behaviors. Indeed, the usual introduction rule for the box modality in the modal logic
![]() $\mathsf{K}$
$\mathsf{K}$

is somehow unsatisfactory: it modifies the context (by adding boxes to the hypothesis), and the distinction between left and right rules for the modal connective box is lost. In order to propose a better formulation, we need a tighter control of formulas in the context, something that sequents do not provide. Hence, the need for extending the notion of sequent systems.
Definition 1. Let
![]() $\mathcal{L}$
be a formal language consisting of well-formed formulas. A sequent is an expression of the form
$\mathcal{L}$
be a formal language consisting of well-formed formulas. A sequent is an expression of the form
![]() $\Gamma\vdash \Delta$
where
$\Gamma\vdash \Delta$
where
![]() $\Gamma$
(the antecedent) and
$\Gamma$
(the antecedent) and
![]() $\Delta$
(the succedent) are finite multisets of formulas in
$\Delta$
(the succedent) are finite multisets of formulas in
![]() $\mathcal{L}$
, and
$\mathcal{L}$
, and
![]() $\vdash$
is the consequence symbol.
$\vdash$
is the consequence symbol.
The set
![]() $\mathsf{LNS}$
of linear nested sequents is given recursively by
$\mathsf{LNS}$
of linear nested sequents is given recursively by
-
(i) if
 $\Gamma\vdash \Delta$
is a sequent then
$\Gamma\vdash \Delta$
is a sequent then
 $\Gamma\vdash \Delta\in\mathsf{LNS}$
$\Gamma\vdash \Delta\in\mathsf{LNS}$
-
(ii) if
 $\Gamma\vdash \Delta$
is a sequent and
$\Gamma\vdash \Delta$
is a sequent and
 $\mathcal{G}\in\mathsf{LNS}$
then
$\mathcal{G}\in\mathsf{LNS}$
then
 $\mathcal{G}\mathbin{\!/\mkern-5mu/^{\Gamma}\!}\vdash\Delta\in\mathsf{LNS}$
.
$\mathcal{G}\mathbin{\!/\mkern-5mu/^{\Gamma}\!}\vdash\Delta\in\mathsf{LNS}$
.
We call each sequent in a linear nested sequent a component and slightly abuse notation, abbreviating “linear nested sequent” to
![]() $\mathsf{LNS}$
. We shall denote by
$\mathsf{LNS}$
. We shall denote by
![]() $\mathsf{LNS}_{\mathcal{L}}$
a linear nested sequent system for the logic
$\mathsf{LNS}_{\mathcal{L}}$
a linear nested sequent system for the logic
![]() $\mathcal{L}$
. In words, a linear nested sequent is simply a finite list of sequents. This data structure matches exactly that of a history in a backwards proof search in an ordinary sequent calculus (Lellmann Reference Lellmann2015). The local behavior of modalities in the rule
$\mathcal{L}$
. In words, a linear nested sequent is simply a finite list of sequents. This data structure matches exactly that of a history in a backwards proof search in an ordinary sequent calculus (Lellmann Reference Lellmann2015). The local behavior of modalities in the rule
![]() $\mathsf{k}$
is obtained as follows:
$\mathsf{k}$
is obtained as follows:

Reading bottom up, while in
![]() $\Box_R$
a new nesting/component is created and F is moved in it, in
$\Box_R$
a new nesting/component is created and F is moved in it, in
![]() $\Box_L$
exactly one boxed formula is moved into an existing nesting, losing its modality.
$\Box_L$
exactly one boxed formula is moved into an existing nesting, losing its modality.
We will explore the local/linear structure of
![]() $\mathsf{LNS}$
in two ways. First, components have a tight connection to worlds in Kripke-like semantics, so that
$\mathsf{LNS}$
in two ways. First, components have a tight connection to worlds in Kripke-like semantics, so that
![]() $\mathsf{LNS}$
is an adequate framework for describing alethic modalities in logical systems driven by this kind of semantics. Second, since information is fragmented into components, rules act locally on formulas and are usually context independent. Hence, the movement of formulas on derivations can be better predicted and controlled. This implies that both: we will be able to adequately specify a representative class of logical systems (see Section 4); and the techniques developed in Miller and Pimentel (Reference Miller and Pimentel2013) will remain valid in the proposed framework.
$\mathsf{LNS}$
is an adequate framework for describing alethic modalities in logical systems driven by this kind of semantics. Second, since information is fragmented into components, rules act locally on formulas and are usually context independent. Hence, the movement of formulas on derivations can be better predicted and controlled. This implies that both: we will be able to adequately specify a representative class of logical systems (see Section 4); and the techniques developed in Miller and Pimentel (Reference Miller and Pimentel2013) will remain valid in the proposed framework.
A further advantage of this framework is that it is often possible to restrict the list of sequents in a
![]() $\mathsf{LNS}$
to the last two components, that we call active.
$\mathsf{LNS}$
to the last two components, that we call active.
Definition 2. (End-active). An application of a linear nested sequent rule is end-active if the rightmost components of the premises are active and the only active components (in premises and conclusion) are the two rightmost ones. The end-active variant of a
![]() $\mathsf{LNS}$
calculus is the calculus with the rules restricted to end-active applications. All the logical systems studied in Lellmann (Reference Lellmann2015), Lellmann et al. (Reference Lellmann, Olarte and Pimentel2017), Lellmann and Pimentel (Reference Lellmann and Pimentel2019) can be restricted to the end-active version. This means that, for example, when restricted to classical logic, new components are never created (this reflects the fact that the Kripke structure for classical logic is flat). Hence, the
$\mathsf{LNS}$
calculus is the calculus with the rules restricted to end-active applications. All the logical systems studied in Lellmann (Reference Lellmann2015), Lellmann et al. (Reference Lellmann, Olarte and Pimentel2017), Lellmann and Pimentel (Reference Lellmann and Pimentel2019) can be restricted to the end-active version. This means that, for example, when restricted to classical logic, new components are never created (this reflects the fact that the Kripke structure for classical logic is flat). Hence, the
![]() $\mathsf{LNS}$
collapses to the usual sequent system
$\mathsf{LNS}$
collapses to the usual sequent system
![]() $\mathsf{LK}$
(Gentzen Reference Gentzen1969). Figure 1 presents the (end-active)
$\mathsf{LK}$
(Gentzen Reference Gentzen1969). Figure 1 presents the (end-active)
![]() $\mathsf{LNS}$
rules for classical propositional logic where the history “
$\mathsf{LNS}$
rules for classical propositional logic where the history “
![]() $\mathcal{G}/\!\!/\, $
” is always empty. Figure 2 presents the structural rules of weakening and contraction.
$\mathcal{G}/\!\!/\, $
” is always empty. Figure 2 presents the structural rules of weakening and contraction.

Figure 1. System
![]() $\mathsf{LNS}_{\mathsf{G}}$
for classical logic.
$\mathsf{LNS}_{\mathsf{G}}$
for classical logic.

Figure 2. The structural rules of contraction and weakening.
A more interesting case is the linear-nested system for propositional intuitionistic logic.
![]() $\mathsf{LNS}_{\mathsf{I}}$
(Lellmann Reference Lellmann2015) is the system sharing with
$\mathsf{LNS}_{\mathsf{I}}$
(Lellmann Reference Lellmann2015) is the system sharing with
![]() $\mathsf{LNS}_{\mathsf{G}}$
the axioms, structural rules, and rules for conjunction and disjunction, but adding the rules for intuitionistic implication
$\mathsf{LNS}_{\mathsf{G}}$
the axioms, structural rules, and rules for conjunction and disjunction, but adding the rules for intuitionistic implication
![]() $\supset$
shown in Figure 3. Observe that, bottom-up, the rule for implication right creates a new component, adds the sequent
$\supset$
shown in Figure 3. Observe that, bottom-up, the rule for implication right creates a new component, adds the sequent
![]() $ F\vdash G$
there, and erases the back history. The lift rule, on the other hand, moves left formulas into the next component. The consecutive application of these rules mimics, possibly in many steps, the behavior of the sequent right rule for implication in the multiconclusion intuitionistic sequent system
$ F\vdash G$
there, and erases the back history. The lift rule, on the other hand, moves left formulas into the next component. The consecutive application of these rules mimics, possibly in many steps, the behavior of the sequent right rule for implication in the multiconclusion intuitionistic sequent system
![]() $\mathsf{mLJ}$
(Maehara Reference Maehara1954)
$\mathsf{mLJ}$
(Maehara Reference Maehara1954)

Figure 3. Rules for intuitionistic implication in the system
![]() $\mathsf{LNS}_{\mathsf{I}}$
.
$\mathsf{LNS}_{\mathsf{I}}$
.

where the double line indicates multiple applications of the
![]() $\mathtt{lift}$
rule.
$\mathtt{lift}$
rule.
This also interprets, proof theoretically, the definition of satisfaction for intuitionistic logic (see Pimentel Reference Pimentel2018). Observe that, once all formulas in the left context are lifted, the only possible action is the application of rules in the last (right-most) component. Hence, the right context
![]() $\Delta$
is forgotten. This shows an interesting dynamic in end-active systems: apply first rules that do not involve moving-between or creating-new components; then apply a rule that creates a new component, followed by the lift rules as much as possible; finally, come back to the beginning of the cycle, with local rules applied to the (active) last component.
$\Delta$
is forgotten. This shows an interesting dynamic in end-active systems: apply first rules that do not involve moving-between or creating-new components; then apply a rule that creates a new component, followed by the lift rules as much as possible; finally, come back to the beginning of the cycle, with local rules applied to the (active) last component.
The possibility of having such a notion of “proof normalization” was studied in Pimentel et al. (Reference Pimentel, Ramanayake and Lellmann2019) in the nested systems framework. In that work, it was shown that end-active nested systems with very specific rules’ shape can be sequentialized. This implies that such nested systems correspond to well-known sequent systems. In this work, we will use this result in a very pragmatic way. Namely, since some sequent systems are not adequate for specification and reasoning, we will consider the corresponding (end-active)
![]() $\mathsf{LNS}$
that: have the same logical properties as the original systems; can be easily specified in our framework; and entails easy-to-check meta-level conditions for cut admissibility.n the present work, besides reasoning about intuitionistic and classical logics, we shall also reason about linear nested systems for some notable extensions of the normal modal logic
$\mathsf{LNS}$
that: have the same logical properties as the original systems; can be easily specified in our framework; and entails easy-to-check meta-level conditions for cut admissibility.n the present work, besides reasoning about intuitionistic and classical logics, we shall also reason about linear nested systems for some notable extensions of the normal modal logic
![]() $\mathsf{K}$
. Figure 4 presents some modal axioms and the respective linear nested rules.
Footnote 1
The calculus
$\mathsf{K}$
. Figure 4 presents some modal axioms and the respective linear nested rules.
Footnote 1
The calculus
![]() $\mathsf{LNS}_\mathsf{K}$
contains the rules of
$\mathsf{LNS}_\mathsf{K}$
contains the rules of
![]() $\mathsf{LNS}_\mathsf{G}$
together with the rules
$\mathsf{LNS}_\mathsf{G}$
together with the rules
![]() $\Box_R$
and
$\Box_R$
and
![]() $\Box_L$
. Let
$\Box_L$
. Let
![]() $\mathcal{A}=\{\mathsf{T},\mathsf{4},\mathsf{D}\}$
. Extensions of the logic
$\mathcal{A}=\{\mathsf{T},\mathsf{4},\mathsf{D}\}$
. Extensions of the logic
![]() $\mathsf{K}$
are represented by
$\mathsf{K}$
are represented by
![]() $\mathsf{K}\ell$
, where
$\mathsf{K}\ell$
, where
![]() $\ell\subseteq\mathcal{A}$
. As usual, we write
$\ell\subseteq\mathcal{A}$
. As usual, we write
![]() $\mathsf{S4}=\mathsf{K}\mathsf{T}\mathsf{4}$
.
$\mathsf{S4}=\mathsf{K}\mathsf{T}\mathsf{4}$
.

Figure 4. Some modal axioms and their linear-nested sequent rules.
Modalities can be combined, giving rise to multimodal logics.
Definition 3. Simply dependent multimodal logics (Demri Reference Demri2000) are characterized by a triple
![]() $(N,\preccurlyeq,f)$
, where N is a denumerable set,
$(N,\preccurlyeq,f)$
, where N is a denumerable set,
![]() $(N,\preccurlyeq)$
is a partial order, and f is a mapping from N to the set L of extensions of modal logic
$(N,\preccurlyeq)$
is a partial order, and f is a mapping from N to the set L of extensions of modal logic
![]() $\mathsf{K}$
with axioms from the set
$\mathsf{K}$
with axioms from the set
![]() $\mathcal{A}$
. The order
$\mathcal{A}$
. The order
![]() $\preccurlyeq$
is upwardly closed with respect to f, that is, if
$\preccurlyeq$
is upwardly closed with respect to f, that is, if
![]() $i\preccurlyeq j$
then
$i\preccurlyeq j$
then
![]() $f(i)\subseteq f(j)$
. The logic described by
$f(i)\subseteq f(j)$
. The logic described by
![]() $(N,\preccurlyeq,f)$
has modalities
$(N,\preccurlyeq,f)$
has modalities
![]() ${\Box^{i}}$
for every
${\Box^{i}}$
for every
![]() $i \in N$
, with axioms for the modality i given by the logic f(i) and interaction axioms
$i \in N$
, with axioms for the modality i given by the logic f(i) and interaction axioms
![]() ${\Box^{j}} F \to {\Box^{i}} F$
for every
${\Box^{j}} F \to {\Box^{i}} F$
for every
![]() $i,j \in N$
with
$i,j \in N$
with
![]() $i \preccurlyeq j$
. The linear nested system
$i \preccurlyeq j$
. The linear nested system
![]() $\mathsf{LNS}_{(N,\preccurlyeq,f)}$
for the simply dependent multimodal logic given by the description
$\mathsf{LNS}_{(N,\preccurlyeq,f)}$
for the simply dependent multimodal logic given by the description
![]() $(N,\preccurlyeq,f)$
is given in Lellmann and Pimentel (Reference Lellmann and Pimentel2019), Figure 6.
$(N,\preccurlyeq,f)$
is given in Lellmann and Pimentel (Reference Lellmann and Pimentel2019), Figure 6.
3. LL and its Variants
Classical LL (Girard Reference Girard1987) is a resource conscious logic, in the sense that formulas are consumed when used during proofs, unless marked with the exponential
![]() $?$
(whose dual is
$?$
(whose dual is
![]() $\mathop{!}$
). Formulas marked with
$\mathop{!}$
). Formulas marked with
![]() $?$
behave classically, i.e., they can be contracted and weakened during proofs.
$?$
behave classically, i.e., they can be contracted and weakened during proofs.
![]() $\mathsf{LL}$
connectives include the additive conjunction
$\mathsf{LL}$
connectives include the additive conjunction
![]() $\mathbin{\&}$
and disjunction
$\mathbin{\&}$
and disjunction
![]() $\oplus$
and their multiplicative versions
$\oplus$
and their multiplicative versions
![]() $\otimes$
and
$\otimes$
and ![]() , together with their units and the first-order quantifiers:
, together with their units and the first-order quantifiers:

Note that
![]() $(\!\cdot\!)^\perp$
(negation) has atomic scope. For an arbitrary formula F,
$(\!\cdot\!)^\perp$
(negation) has atomic scope. For an arbitrary formula F,
![]() $F^\perp$
denotes the result of moving negation inward until it has atomic scope. We shall refer to atomic (A) and negated atomic (
$F^\perp$
denotes the result of moving negation inward until it has atomic scope. We shall refer to atomic (A) and negated atomic (
![]() $A^\bot$
) formulas as literals. The connectives in the first line denote the de Morgan dual of the connectives in the second line. Hence, for atoms A,B, the expression
$A^\bot$
) formulas as literals. The connectives in the first line denote the de Morgan dual of the connectives in the second line. Hence, for atoms A,B, the expression
![]() $(\bot \mathbin{\&} (A \otimes (! B)))^\perp$
denotes
$(\bot \mathbin{\&} (A \otimes (! B)))^\perp$
denotes ![]() . The linear implication
. The linear implication
![]() $F \mathbin{-\circ} G$
is a short hand for
$F \mathbin{-\circ} G$
is a short hand for ![]() . The equivalence
. The equivalence
![]() $F \equiv G$
is defined as
$F \equiv G$
is defined as
![]() $(F \mathbin{-\circ} G) \mathbin{\&} (G \mathbin{-\circ} F)$
.
$(F \mathbin{-\circ} G) \mathbin{\&} (G \mathbin{-\circ} F)$
.
The rules for the exponentials in
![]() $\mathsf{LL}$
are promotion, dereliction, weakening, and contraction, presented below in the one-sided sequent presentation
$\mathsf{LL}$
are promotion, dereliction, weakening, and contraction, presented below in the one-sided sequent presentation

Note that, in the promotion rule, the banged formula
![]() $\mathop{!} F$
can be introduced only if all the formulas in the context are marked with the exponential
$\mathop{!} F$
can be introduced only if all the formulas in the context are marked with the exponential
![]() $?$
. That is, promotion is not context-independent, just like the rule
$?$
. That is, promotion is not context-independent, just like the rule
![]() $\mathsf{k}$
in the previous section.
$\mathsf{k}$
in the previous section.
In the quest for locality, Guerrini et al. (Reference Guerrini, Martini and Masini1998) proposed 2-sequents systems for
![]() $\mathsf{LL}$
variants, with separate rules for the exponentials. In Lellmann et al. (Reference Lellmann, Olarte and Pimentel2017), this work was revisited, establishing a lighter notation and extending the discussion to multimodalities.
$\mathsf{LL}$
variants, with separate rules for the exponentials. In Lellmann et al. (Reference Lellmann, Olarte and Pimentel2017), this work was revisited, establishing a lighter notation and extending the discussion to multimodalities.
![]() $\mathsf{LNS}_\mathsf{LL}$
(Lellmann et al. Reference Lellmann, Olarte and Pimentel2017) is an end-active, linear nested system for linear logic. In this system, the promotion rule is split into the following local rules:
$\mathsf{LNS}_\mathsf{LL}$
(Lellmann et al. Reference Lellmann, Olarte and Pimentel2017) is an end-active, linear nested system for linear logic. In this system, the promotion rule is split into the following local rules:

Observe that no checking must be done in the context in order to apply the
![]() $?$
rule: the only checking is in the
$?$
rule: the only checking is in the
![]() $\mathop{!}$
rule, where
$\mathop{!}$
rule, where
![]() $\mathcal{ E}$
should be the empty sequent or an empty list of components. Note the similarities between the
$\mathcal{ E}$
should be the empty sequent or an empty list of components. Note the similarities between the
![]() $\mathsf{LNS}$
rules
$\mathsf{LNS}$
rules
![]() $!$
and
$!$
and
![]() $\Box_R$
, as well as
$\Box_R$
, as well as
![]() $?$
and
$?$
and
![]() $\mathsf{4}$
are shown in Figure 4. Indeed, in Lellmann et al. (Reference Lellmann, Olarte and Pimentel2017) such similarities were exploited in order to propose extensions of
$\mathsf{4}$
are shown in Figure 4. Indeed, in Lellmann et al. (Reference Lellmann, Olarte and Pimentel2017) such similarities were exploited in order to propose extensions of
![]() $\mathsf{LNS}_\mathsf{LL}$
with multimodalities, called subexponentials, allowing for different modal behaviors.
$\mathsf{LNS}_\mathsf{LL}$
with multimodalities, called subexponentials, allowing for different modal behaviors.
Since the proof of adequacy of the proposed encodings in Section. 4 is greatly alleviated if a focusing discipline is used, we introduce next
![]() $\mathsf{LNS}_\mathsf{FMLL}$
, a novel focused version of the
$\mathsf{LNS}_\mathsf{FMLL}$
, a novel focused version of the
![]() $\mathsf{LNS}$
for linear logic with subexponentials. As we shall see, the modal/subexponential phase of the system
$\mathsf{LNS}$
for linear logic with subexponentials. As we shall see, the modal/subexponential phase of the system
![]() $\mathsf{LNS}_\mathsf{FMLL}$
has a better control of the flow of formulas than the system in Olarte et al. (Reference Olarte, Pimentel and Xavier2020).
$\mathsf{LNS}_\mathsf{FMLL}$
has a better control of the flow of formulas than the system in Olarte et al. (Reference Olarte, Pimentel and Xavier2020).
3.1. Multimodalities in linear logic and the focused system
 $\mathsf{LNS}_\mathsf{FMLL}$
$\mathsf{LNS}_\mathsf{FMLL}$
Similar to modal connectives, exponentials in
![]() $\mathsf{LL}$
are not canonical (Danos et al. Reference Danos, Joinet and Schellinx1993), in the sense that, even having the same scheme for introduction rules, marking the exponentials with different labels does not preserve equivalence: if
$\mathsf{LL}$
are not canonical (Danos et al. Reference Danos, Joinet and Schellinx1993), in the sense that, even having the same scheme for introduction rules, marking the exponentials with different labels does not preserve equivalence: if
![]() $i\not= j$
then
$i\not= j$
then ![]() .
.
Let
![]() $\mathcal{I}$
be a set of labels, organized in a preorder
$\mathcal{I}$
be a set of labels, organized in a preorder
![]() $\preceq$
. We will call
$\preceq$
. We will call ![]() , subexponentials, which can be seen as substructural multimodalities.
, subexponentials, which can be seen as substructural multimodalities.
There are, however, two main differences between multimodalities in normal modal logics and subexponentials in linear logic:
(i). Substructural behavior . Subexponentials carry the possibility of being unbounded (or classical) if weakening and contraction are allowed or bounded otherwise (thus having a linear behavior);
(ii).
Nature of modalities
. Normal modal logics start from the weakest version, assuming only the axiom
![]() $\mathsf{K}$
. Then, extensions are considered, by adding other axioms. Exponentials in linear logic, on the other side “take for granted” the behaviors expressed by axioms
$\mathsf{K}$
. Then, extensions are considered, by adding other axioms. Exponentials in linear logic, on the other side “take for granted” the behaviors expressed by axioms
![]() $\mathsf{K}$
,
$\mathsf{K}$
,
![]() $\mathsf{T}$
, and
$\mathsf{T}$
, and
![]() $\mathsf{4}$
(Martini and Masini Reference Martini and Masini1994) – and this is inherited by subexponentials.
$\mathsf{4}$
(Martini and Masini Reference Martini and Masini1994) – and this is inherited by subexponentials.
We observe that (i) opened a venue for proposing different multimodal substructural logical systems, that encountered a number of different applications e.g. in the specification and verification of concurrent systems (Nigam et al. Reference Nigam, Olarte and Pimentel2017), biological systems (Olarte et al. Reference Olarte, Chiarugi, Falaschi and Hermith2016), bigraphs (Chaudhuri and Reis Reference Chaudhuri and Reis2015), applications in linguistics (Kanovich et al. Reference Kanovich, Kuznetsov, Nigam and Scedrov2019), and the specification of systems with multiple contexts, which may be represented by sets or multisets of formulas (Nigam et al. Reference Nigam, Pimentel and Reis2016). Regarding (ii), Guerrini et al. (Reference Guerrini, Martini and Masini1998) unified the modal and
![]() $\mathsf{LL}$
approaches, with the exponentials assuming only the linear version of
$\mathsf{LL}$
approaches, with the exponentials assuming only the linear version of
![]() $\mathsf{K}$
, with the possibility of adding modal extensions to it.
$\mathsf{K}$
, with the possibility of adding modal extensions to it.
In Lellmann et al. (Reference Lellmann, Olarte and Pimentel2017), we brought this discussion to the multimodal case, extending the concept of simply dependent multimodal logics to the substructural setting, where subexponentials consider not only the structural axioms for contraction and weakening:
but also the subexponential version of axioms
![]() $\{\mathsf{K},\mathsf{4},\mathsf{D},\mathsf{T}\}$
:
$\{\mathsf{K},\mathsf{4},\mathsf{D},\mathsf{T}\}$
:
This means that ![]() can behave classically (
can behave classically (
![]() $\mathsf{U}$
) or not, but also with exponential behaviors different from those in
$\mathsf{U}$
) or not, but also with exponential behaviors different from those in
![]() $\mathsf{LL}$
. Hence, by assigning different modal axioms one obtains, in a modular way, a class of different substructural modal logics. For instance, subexponentials assuming
$\mathsf{LL}$
. Hence, by assigning different modal axioms one obtains, in a modular way, a class of different substructural modal logics. For instance, subexponentials assuming
![]() $\mathsf{T}$
allow for dereliction, those assuming
$\mathsf{T}$
allow for dereliction, those assuming
![]() $\mathsf{4}$
are persistent, and those assuming only
$\mathsf{4}$
are persistent, and those assuming only
![]() $\mathsf{K}$
are functorial (Girard Reference Girard1998). In particular, substructural
$\mathsf{K}$
are functorial (Girard Reference Girard1998). In particular, substructural
![]() $\mathsf{K}\mathsf{D}$
can be seen as a fragment of elementary linear logic
$\mathsf{K}\mathsf{D}$
can be seen as a fragment of elementary linear logic
![]() $\mathsf{ELL}$
(Guerrini et al. Reference Guerrini, Martini and Masini1998).
$\mathsf{ELL}$
(Guerrini et al. Reference Guerrini, Martini and Masini1998).
The main goal of the present work is to show how this new class of subexponentials can be applied to the problem of characterizing cut admissibility of object-level logical systems. This line of work of using
![]() $\mathsf{LNS}$
systems at the meta-level started in Olarte et al. (Reference Olarte, Pimentel and Xavier2020), where we have considered a finite class of unbounded subexponentials for specifying classical modal logics. In this work, we extend the meta-logic to support an infinite set of subexponentials, which can be bounded or unbounded, for specifying classical and linear
$\mathsf{LNS}$
systems at the meta-level started in Olarte et al. (Reference Olarte, Pimentel and Xavier2020), where we have considered a finite class of unbounded subexponentials for specifying classical modal logics. In this work, we extend the meta-logic to support an infinite set of subexponentials, which can be bounded or unbounded, for specifying classical and linear
![]() $\mathsf{LNS}$
systems for multimodal logics.
$\mathsf{LNS}$
systems for multimodal logics.
Before presenting the formal definition, let us start with some intuitions. First of all, observe that systems at meta- and object levels are presented in the linear nested formulation. This allows not only broadening the range of specified systems, but also a more granular control of modalities. However, this comes with a price: the meta-level role of exponentials becomes highly overloaded. Indeed, they should not only handle the internal structural properties of formulas, but also the external structural properties of modalities. For example, how a classical, nonpersistent OL box modality
![]() $\Box$
should be encoded at the meta-level? The natural answer would be: via an unbounded, non persistent subexponential
$\Box$
should be encoded at the meta-level? The natural answer would be: via an unbounded, non persistent subexponential ![]() . Note that the object rule
. Note that the object rule
![]() $\Box_L$
suppresses the modality of the boxed formula when moving between components (reading the rule in Figure 4 bottom-up). If the subexponential modality
$\Box_L$
suppresses the modality of the boxed formula when moving between components (reading the rule in Figure 4 bottom-up). If the subexponential modality ![]() is also removed at the meta-level (when moving to the next component), this would impose a linear nature on formulas. On the other hand, keeping the subexponential while moving between components implies that the box will be persistent (a mismatch with respect to the OL behavior).
is also removed at the meta-level (when moving to the next component), this would impose a linear nature on formulas. On the other hand, keeping the subexponential while moving between components implies that the box will be persistent (a mismatch with respect to the OL behavior).
We solve this problem by introducing the unbounded, confined subexponentials ![]() , matching the exact same behavior of the
, matching the exact same behavior of the
![]() $\mathsf{LL}$
exponentials in sequent systems. That is, promotion is restricted to a component, and it can be applied only when the linear context is empty (see rule
$\mathsf{LL}$
exponentials in sequent systems. That is, promotion is restricted to a component, and it can be applied only when the linear context is empty (see rule ![]() in Figure 5). Although it seems that we are sacrificing locality for the sake of modularity and uniformity, this is not the case: banged formulas with label
in Figure 5). Although it seems that we are sacrificing locality for the sake of modularity and uniformity, this is not the case: banged formulas with label
![]() $\texttt{c}$
will never appear in the encodings – the confined classical behavior is encoded using the question-mark exponential. Hence, the nonlocal promotion rule
$\texttt{c}$
will never appear in the encodings – the confined classical behavior is encoded using the question-mark exponential. Hence, the nonlocal promotion rule ![]() will never be applied. It is part of the systems, however, for completeness of the cut-elimination procedure (see Section 3.2).
will never be applied. It is part of the systems, however, for completeness of the cut-elimination procedure (see Section 3.2).

Figure 5. End-active focused system
![]() $\mathsf{LNS}_\mathsf{FMLL}$
.
$\mathsf{LNS}_\mathsf{FMLL}$
.
![]() $\Theta^u$
(resp.
$\Theta^u$
(resp.
![]() $\Theta^l$
) contains only unbounded (resp. linear) subexponentials. In
$\Theta^l$
) contains only unbounded (resp. linear) subexponentials. In
![]() $\mathsf{l_{s}}$
and
$\mathsf{l_{s}}$
and
![]() $\mathsf{I_l}$
, A is atomic. In
$\mathsf{I_l}$
, A is atomic. In
![]() $\forall$
, y is fresh. In
$\forall$
, y is fresh. In
![]() $\mathsf{store}$
, S is a literal or a positive formula. In
$\mathsf{store}$
, S is a literal or a positive formula. In
![]() $\mathsf{\mathsf{R_n}}$
, N is a negative formula. In
$\mathsf{\mathsf{R_n}}$
, N is a negative formula. In
![]() $\mathsf{D_l}$
, P is positive, and in
$\mathsf{D_l}$
, P is positive, and in
![]() $\mathsf{D^u_s}, \mathsf{D^l_s}$
,
$\mathsf{D^u_s}, \mathsf{D^l_s}$
,
![]() $P_a$
is not atomic. In
$P_a$
is not atomic. In
![]() $\mathsf{D^u_s}, \mathsf{D^l_s}$
and
$\mathsf{D^u_s}, \mathsf{D^l_s}$
and
![]() $\mathsf{l_{s}}$
,
$\mathsf{l_{s}}$
,
![]() $\mathsf{T} \in \mathcal{U}(i)$
. In all question-marked rules
$\mathsf{T} \in \mathcal{U}(i)$
. In all question-marked rules
![]() $i\preceq j$
. Moreover,
$i\preceq j$
. Moreover,
![]() $i\neq \texttt{c}$
in
$i\neq \texttt{c}$
in ![]() ;
;
![]() $\mathsf{D}\in \mathcal{U}(i)$
in
$\mathsf{D}\in \mathcal{U}(i)$
in
![]() $\mathsf{D_d}$
;
$\mathsf{D_d}$
;
![]() $\mathsf{4} \in \mathcal{U}(j)$
in
$\mathsf{4} \in \mathcal{U}(j)$
in
![]() $?^i_\mathsf{4}$
;
$?^i_\mathsf{4}$
;
![]() $\{\mathsf{4},\mathsf{C},\mathsf{W}\} \cap \mathcal{U}(j) = \emptyset$
in
$\{\mathsf{4},\mathsf{C},\mathsf{W}\} \cap \mathcal{U}(j) = \emptyset$
in
![]() $?^i_\mathsf{kl}$
;
$?^i_\mathsf{kl}$
;
![]() $\mathsf{4} \not\in \mathcal{U}(i)$
and
$\mathsf{4} \not\in \mathcal{U}(i)$
and
![]() $\mathsf{U} \subseteq \mathcal{U}(i)$
in
$\mathsf{U} \subseteq \mathcal{U}(i)$
in
![]() $?^i_\mathsf{ku}$
and in
$?^i_\mathsf{ku}$
and in
![]() $\mathsf{D^u_s}$
.
$\mathsf{D^u_s}$
.
Definition 4. (
![]() $\mathsf{MMLL}$
) Multimodal linear logic (
$\mathsf{MMLL}$
) Multimodal linear logic (
![]() $\mathsf{MMLL}$
) shares with linear logic all connectives except the exponentials:
$\mathsf{MMLL}$
) shares with linear logic all connectives except the exponentials:
![]() $\mathsf{MMLL}$
contains labeled subexponentials
$\mathsf{MMLL}$
contains labeled subexponentials ![]() , specified by the subexponential signature given by
, specified by the subexponential signature given by
![]() $\Sigma = \langle\mathcal{I}, \preceq,\mathcal{U}(i)\rangle$
, where
$\Sigma = \langle\mathcal{I}, \preceq,\mathcal{U}(i)\rangle$
, where
-
–
 $\mathcal{I}$
is a set of labels;
$\mathcal{I}$
is a set of labels; -
–
 $\mathcal{U}(i)$
represents the set of axioms within
$\mathcal{U}(i)$
represents the set of axioms within
 $\{\mathsf{C},\mathsf{W}, \mathsf{K},\mathsf{4},\mathsf{D},\mathsf{T}\}$
that the subexponential
$\{\mathsf{C},\mathsf{W}, \mathsf{K},\mathsf{4},\mathsf{D},\mathsf{T}\}$
that the subexponential
 $i\in\mathcal{I}$
assumes, with
$i\in\mathcal{I}$
assumes, with
 $\mathsf{K}\in\mathcal{U}(i)$
for all
$\mathsf{K}\in\mathcal{U}(i)$
for all
 $i\in \mathcal{I}$
;
$i\in \mathcal{I}$
; -
–
 $\preceq$
is a preorder among the elements of
$\preceq$
is a preorder among the elements of
 $\mathcal{I}$
that is upwardly closed with respect to
$\mathcal{I}$
that is upwardly closed with respect to
 $\mathcal{U}(i)$
, i.e., if an axiom
$\mathcal{U}(i)$
, i.e., if an axiom
 $\mathsf{A} \in \mathcal{U}(i)$
and
$\mathsf{A} \in \mathcal{U}(i)$
and
 $i \preceq j$
, then
$i \preceq j$
, then
 $\mathsf{A} \in \mathcal{U}(j)$
.
$\mathsf{A} \in \mathcal{U}(j)$
.
We assume
![]() $\texttt{c} \in \mathcal{I}$
to be a distinguished element s.t.
$\texttt{c} \in \mathcal{I}$
to be a distinguished element s.t.
![]() $\mathcal{U}(\texttt{c})=\{\mathsf{C},\mathsf{W},\mathsf{K},\mathsf{T}\}$
and
$\mathcal{U}(\texttt{c})=\{\mathsf{C},\mathsf{W},\mathsf{K},\mathsf{T}\}$
and
![]() $\texttt{c}$
is only
$\texttt{c}$
is only
![]() $\preceq$
-related with itself. Finally, for every subexponential
$\preceq$
-related with itself. Finally, for every subexponential
![]() $i\in \mathcal{I}$
, we assume a subexponential
$i\in \mathcal{I}$
, we assume a subexponential
![]() $i+\in \mathcal{I}$
s.t.
$i+\in \mathcal{I}$
s.t.
![]() $\mathcal{U}(i+\!)= \mathcal{U}(i)\cup \{\mathsf{T}\}$
,
$\mathcal{U}(i+\!)= \mathcal{U}(i)\cup \{\mathsf{T}\}$
,
![]() $i \preceq i+$
, and if
$i \preceq i+$
, and if
![]() $i\preceq j$
then
$i\preceq j$
then
![]() $i+\preceq j+$
.
$i+\preceq j+$
.
As usual, the upwardly condition is needed for cut elimination (Danos et al. Reference Danos, Joinet and Schellinx1993). Since we are considering extensions of normal modal logics, all the subexponentials are assumed to have the axiom
![]() $\mathsf{K}$
. Finally, the subexponential
$\mathsf{K}$
. Finally, the subexponential
![]() $i+$
, that adds
$i+$
, that adds
![]() $\mathsf{T}$
to
$\mathsf{T}$
to
![]() $\mathcal{U}(i)$
, will be used to give a more deterministic rule for exponentials containing the axiom
$\mathcal{U}(i)$
, will be used to give a more deterministic rule for exponentials containing the axiom
![]() $\mathsf{4}$
(more on this below).
$\mathsf{4}$
(more on this below).
The focused proof system for
![]() $\mathsf{MMLL}$
is presented in Figure 5 and explained in the following. Focusing (Andreoli Reference Andreoli1992) is a discipline on proofs aiming at reducing nondeterminism during proof search. Focusing in
$\mathsf{MMLL}$
is presented in Figure 5 and explained in the following. Focusing (Andreoli Reference Andreoli1992) is a discipline on proofs aiming at reducing nondeterminism during proof search. Focusing in
![]() $\mathsf{LL}$
-based systems is grounded on two kinds of separations: (a) classical/linear behavior of formulas and (b) invertible/non invertible introduction rules.
$\mathsf{LL}$
-based systems is grounded on two kinds of separations: (a) classical/linear behavior of formulas and (b) invertible/non invertible introduction rules.
For (a), observe that it is possible to incorporate the structural rules of contraction and weakening for formulas of the shape
![]() $? F$
into the
$? F$
into the
![]() $\mathsf{LL}$
introduction rules. This is reflected into the syntax in the so called dyadic sequents where the context is split into two, a classical (set of formulas
$\mathsf{LL}$
introduction rules. This is reflected into the syntax in the so called dyadic sequents where the context is split into two, a classical (set of formulas
![]() $\Theta$
) and a linear (multiset of formulas
$\Theta$
) and a linear (multiset of formulas
![]() $\Gamma$
). The dyadic sequent
$\Gamma$
). The dyadic sequent
![]() $\vdash \Theta;\ \Gamma$
is then interpreted as the linear logic sequent
$\vdash \Theta;\ \Gamma$
is then interpreted as the linear logic sequent
![]() $\vdash ? \Theta, \Gamma$
where
$\vdash ? \Theta, \Gamma$
where
![]() $? \Theta = \{? F \mid F \in\Theta\}$
. This idea can be generalized to the case of the subexponentials. The subexponential context is a multiset of the form
$? \Theta = \{? F \mid F \in\Theta\}$
. This idea can be generalized to the case of the subexponentials. The subexponential context is a multiset of the form
![]() $\Theta=\{i:F \mid i\in\mathcal{I}\}$
, and the dyadic sequent
$\Theta=\{i:F \mid i\in\mathcal{I}\}$
, and the dyadic sequent
![]() $\vdash \Theta;\ \Gamma$
is interpreted as the (subexponential) linear logic sequent
$\vdash \Theta;\ \Gamma$
is interpreted as the (subexponential) linear logic sequent
![]() $\vdash \{?^i F \mid i:F \in \Theta\}, \Gamma$
. That is,
$\vdash \{?^i F \mid i:F \in \Theta\}, \Gamma$
. That is,
![]() $i:F\in\Theta$
represents that F is stored in the (subexponential) context in
$i:F\in\Theta$
represents that F is stored in the (subexponential) context in
![]() $\Theta$
labeled by i. We extend the indexed notation to contexts as follows: given a linear context
$\Theta$
labeled by i. We extend the indexed notation to contexts as follows: given a linear context
![]() $\Gamma=\{F_1,\ldots,F_n\}$
, we will write
$\Gamma=\{F_1,\ldots,F_n\}$
, we will write
![]() $i:\Gamma$
for the subexponential context
$i:\Gamma$
for the subexponential context
![]() $\{i:F_1,\ldots,i:F_n\}$
. Finally, we shall use the superindex
$\{i:F_1,\ldots,i:F_n\}$
. Finally, we shall use the superindex
![]() $\Theta^u$
(resp.
$\Theta^u$
(resp.
![]() $\Theta^l$
) to denote a context where all the subexponentials are unbounded (resp. linear). When we simply write
$\Theta^l$
) to denote a context where all the subexponentials are unbounded (resp. linear). When we simply write
![]() $\Theta$
, the context may contain both, linear and unbounded subexponentials.
$\Theta$
, the context may contain both, linear and unbounded subexponentials.
For (b), it turns out that proofs can be organized in two alternating phases: negative containing only invertible rules, and positive containing only noninvertible rules. The connectives ![]() have invertible introduction rules and are thus classified as negative. The remaining connectives
have invertible introduction rules and are thus classified as negative. The remaining connectives ![]() are positive. Formulas inherit their polarity from their main connective, e.g.,
are positive. Formulas inherit their polarity from their main connective, e.g.,
![]() $F \otimes G$
is positive and
$F \otimes G$
is positive and ![]() is negative. Although the bias assigned to atoms does not interfere with provability (Andreoli Reference Andreoli1992; Miller and Saurin Reference Miller and Saurin2007), here we follow Andreoli’s convention of classifying atomic formulas as negative, thus negated atoms as positive.
is negative. Although the bias assigned to atoms does not interfere with provability (Andreoli Reference Andreoli1992; Miller and Saurin Reference Miller and Saurin2007), here we follow Andreoli’s convention of classifying atomic formulas as negative, thus negated atoms as positive.
The inference rules of the focused system
![]() $\mathsf{LNS}_\mathsf{FMLL}$
in Figure 5 involve two kinds of sequents
$\mathsf{LNS}_\mathsf{FMLL}$
in Figure 5 involve two kinds of sequents
where L is a (possibly empty) list of formulas. The formula occurrence F in a
![]() $\Downarrow$
-sequent is called the focus of that sequent. Moreover, linear nested sequents in
$\Downarrow$
-sequent is called the focus of that sequent. Moreover, linear nested sequents in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
have the shape
$\mathsf{LNS}_\mathsf{FMLL}$
have the shape
where
![]() $\mathcal{ G}$
is either an unfocused sequent or it is empty (in this case //i is not present). The superscript in “//i” indicates that the component was created by a subexponential labeled with i.
$\mathcal{ G}$
is either an unfocused sequent or it is empty (in this case //i is not present). The superscript in “//i” indicates that the component was created by a subexponential labeled with i.
![]() $\textit{Seq}$
, above, is a focused or unfocused
$\textit{Seq}$
, above, is a focused or unfocused
![]() $\mathsf{LNS}_\mathsf{FMLL}$
sequent.
$\mathsf{LNS}_\mathsf{FMLL}$
sequent.
The different
![]() $\mathsf{LNS}$
above reflect not only the negative/positive proof phases but also the behavior of the promotion rule:
$\mathsf{LNS}$
above reflect not only the negative/positive proof phases but also the behavior of the promotion rule:
-
–
 $\vdash \Theta;\ \Gamma \Uparrow L$
belongs to the negative phase. During this phase, all negative formulas in the list L are introduced and all positive formulas and literals are moved to the linear context
$\vdash \Theta;\ \Gamma \Uparrow L$
belongs to the negative phase. During this phase, all negative formulas in the list L are introduced and all positive formulas and literals are moved to the linear context
 $\Gamma$
;
$\Gamma$
; -
–
 $\vdash \Theta;\ \Gamma\Downarrow \, F$
belongs to the positive phase, where all positive connectives at the root of F are introduced; and
$\vdash \Theta;\ \Gamma\Downarrow \, F$
belongs to the positive phase, where all positive connectives at the root of F are introduced; and -
–
 belongs to the exponential/modal phase. During this phase, only applications of the rules for
belongs to the exponential/modal phase. During this phase, only applications of the rules for
 $?^{i}$
are allowed, ending with an application of
$?^{i}$
are allowed, ending with an application of
 $\mathsf{R_{\mathsf{r}}}$
(release rule). The dynamics of the different phases is detailed below.
$\mathsf{R_{\mathsf{r}}}$
(release rule). The dynamics of the different phases is detailed below.
Negative Phase. Negative rules can be applied eagerly, in any order. This process includes storing formulas. Note that the rule
![]() $\mathsf{store}$
moves, to the linear zone
$\mathsf{store}$
moves, to the linear zone
![]() $\Gamma$
, the literal or positive formula S since it cannot be decomposed during the negative phase;
$\Gamma$
, the literal or positive formula S since it cannot be decomposed during the negative phase;
![]() $\mathsf{store}_\mathsf{s}$
stores formulas marked with
$\mathsf{store}_\mathsf{s}$
stores formulas marked with ![]() into the correspondent subexponential context.
into the correspondent subexponential context.
The negative phase ends when the list L in unfocused sequents is empty. A decision rule is then applied. There are four possibilities.
-
 $\mathsf{D_l}$
,
$\mathsf{D_l}$
,
 $\mathsf{D_{s}^{u}}$
,
$\mathsf{D_{s}^{u}}$
,
 $\mathsf{D_s^l}$
: a positive phase starts by focusing on a non-atomic formula F such that
$\mathsf{D_s^l}$
: a positive phase starts by focusing on a non-atomic formula F such that-
–
 $\mathsf{D_l}$
: F is taken from the linear context (and thus erased from it);
$\mathsf{D_l}$
: F is taken from the linear context (and thus erased from it); -
–
 $\mathsf{D_{s}^{u}}$
: a copy of F is taken from the subexponential context i, thus making an implicit contraction (
$\mathsf{D_{s}^{u}}$
: a copy of F is taken from the subexponential context i, thus making an implicit contraction (
 $\mathsf{U} \subseteq\mathcal{U}(i)$
) and a dereliction (
$\mathsf{U} \subseteq\mathcal{U}(i)$
) and a dereliction (
 $\mathsf{T}\in\mathcal{U}(i)$
);
$\mathsf{T}\in\mathcal{U}(i)$
); -
–
 $\mathsf{D_s^l}$
: analogous to
$\mathsf{D_s^l}$
: analogous to
 $\mathsf{D_{s}^{u}}$
, with the difference that
$\mathsf{D_{s}^{u}}$
, with the difference that
 $\mathsf{U} \cap \mathcal{U}(i) = \emptyset$
and the formula is not contracted.
$\mathsf{U} \cap \mathcal{U}(i) = \emptyset$
and the formula is not contracted.
-
-
 $\mathsf{D_d}$
: starts an exponential phase.
$\mathsf{D_d}$
: starts an exponential phase.
Positive Phase. Once we focus on a formula, the proof follows by applying positive rules, where the focus persists on the decomposed subformulas until either: the proof ends with an instance of an axiom; a negative formula is reached, and the positive phase ends with the application of
![]() $\mathsf{R_n}$
; or a banged formula is derived, which either moves the proof to the negative case (if the subexponential is
$\mathsf{R_n}$
; or a banged formula is derived, which either moves the proof to the negative case (if the subexponential is ![]() ) or triggers an exponential phase execution (otherwise). In the latter, only the rules for
) or triggers an exponential phase execution (otherwise). In the latter, only the rules for ![]() , moving formulas between components, are allowed. When this moving is over, the exponential phase ends with an application of the rule
, moving formulas between components, are allowed. When this moving is over, the exponential phase ends with an application of the rule
![]() $\mathsf{R_{\mathsf{r}}}$
, starting again a negative phase.
$\mathsf{R_{\mathsf{r}}}$
, starting again a negative phase.
There are two initial rules. In
![]() $\mathsf{I_l}$
, the atom A is in the linear zone and the subexponential context must be unbounded (being implicitly weakened); in
$\mathsf{I_l}$
, the atom A is in the linear zone and the subexponential context must be unbounded (being implicitly weakened); in
![]() $\mathsf{I_s}$
, the atom is placed in a subexponential context i with
$\mathsf{I_s}$
, the atom is placed in a subexponential context i with
![]() $\mathsf{T} \in \mathcal{U}(i)$
. The need of the axiom
$\mathsf{T} \in \mathcal{U}(i)$
. The need of the axiom
![]() $\mathsf{T}$
comes from the fact that it embodies the capacity of using the formula in the same component, corresponding to dereliction in linear logic.
$\mathsf{T}$
comes from the fact that it embodies the capacity of using the formula in the same component, corresponding to dereliction in linear logic.
Exponential Phase. The exponential phase starts with the application of a ![]() rule, with
rule, with
![]() $i\not= \texttt{c}$
, or the rule
$i\not= \texttt{c}$
, or the rule
![]() $\mathsf{D}_\mathsf{d}$
. The distinguished subexponential
$\mathsf{D}_\mathsf{d}$
. The distinguished subexponential ![]() behaves as the
behaves as the
![]() $\mathsf{LL}$
bang exponential. Hence, its introduction rule simply ends the positive phase and assumes that the subexponential context is unbounded. For any other subexponential in
$\mathsf{LL}$
bang exponential. Hence, its introduction rule simply ends the positive phase and assumes that the subexponential context is unbounded. For any other subexponential in
![]() $\mathsf{MMLL}$
, the rule
$\mathsf{MMLL}$
, the rule ![]() creates a new component, moving the active formula to it. Once the new component is created, the
creates a new component, moving the active formula to it. Once the new component is created, the ![]() rules dictate the movement of formulas between components, as described in the following.
rules dictate the movement of formulas between components, as described in the following.
Usually, nested-based systems for modal/linear logics present one core box left/question mark rule, and other modal rules with different behaviors are added on the top of it, depending on the modal axioms of the underlying modality/subexponential. In Olarte et al. (Reference Olarte, Pimentel and Xavier2020), we have adopted such approach, lifting to the meta-level the OL modal rules. Although resulting into adequate specifications, in the sense of successfully capturing the object-level behavior, this approach is not satisfactory for the meta-level focused system, since it adds a great deal of nondeterminism during proof search.
In this work, we propose more efficient modal rules from the proof theoretical point of view using all the subexponential features present in
![]() $\mathsf{MMLL}$
. First of all, when
$\mathsf{MMLL}$
. First of all, when
![]() $\mathsf{4} \in \mathcal{U}(j)$
, the rules
$\mathsf{4} \in \mathcal{U}(j)$
, the rules ![]() and
and ![]() cannot be applied. Dually, if
cannot be applied. Dually, if
![]() $\mathsf{4} \not\in \mathcal{U}(j)$
, then the rule
$\mathsf{4} \not\in \mathcal{U}(j)$
, then the rule ![]() is not enabled and the use of
is not enabled and the use of ![]() is only possible if
is only possible if
![]() $\mathsf{U} \not\subset \mathcal{U}(j)$
(resp.
$\mathsf{U} \not\subset \mathcal{U}(j)$
(resp.
![]() $\mathsf{U} \subseteq \mathcal{U}(j)$
). Second, the proposed rules have a better control of contraction, thus avoiding the need of guessing the number of times a formula must be copied to the next component. Note that the rule
$\mathsf{U} \subseteq \mathcal{U}(j)$
). Second, the proposed rules have a better control of contraction, thus avoiding the need of guessing the number of times a formula must be copied to the next component. Note that the rule ![]() moves the formula F stored in the context j to the context
moves the formula F stored in the context j to the context
![]() $j+$
. This has two immediate effects: the formula F can be copied to yet another component (once it is created) reflecting the behavior of the modal rule
$j+$
. This has two immediate effects: the formula F can be copied to yet another component (once it is created) reflecting the behavior of the modal rule
![]() $\mathsf{4}$
(persistence); moreover, since
$\mathsf{4}$
(persistence); moreover, since
![]() $\mathsf{T} \in \mathcal{U}(j+)$
, the formula F can be also used in the last component by applying the decision rule. Finally, when
$\mathsf{T} \in \mathcal{U}(j+)$
, the formula F can be also used in the last component by applying the decision rule. Finally, when
![]() $\mathsf{U} \subseteq \mathcal{U}(j)$
,
$\mathsf{U} \subseteq \mathcal{U}(j)$
,
![]() $j+$
is also unbounded and decision/dereliction on the same formula can be performed several times. In other words, the rule
$j+$
is also unbounded and decision/dereliction on the same formula can be performed several times. In other words, the rule
![]() $?^i_\mathsf{4}$
embeds both the behavior of
$?^i_\mathsf{4}$
embeds both the behavior of
![]() $\mathsf{K}$
(moving formulas between components) and also
$\mathsf{K}$
(moving formulas between components) and also
![]() $\mathsf{4}$
(by keeping the modality of the formula). On the other hand, the behavior of
$\mathsf{4}$
(by keeping the modality of the formula). On the other hand, the behavior of
![]() $\mathsf{K}$
, without
$\mathsf{K}$
, without
![]() $\mathsf{4}$
, is specified by the rules
$\mathsf{4}$
, is specified by the rules ![]() and
and ![]() . In the first case, j is linear and then F is not contracted. In the second case, F is placed in the context
. In the first case, j is linear and then F is not contracted. In the second case, F is placed in the context
![]() $\texttt{c}$
. Since
$\texttt{c}$
. Since
![]() $\mathsf{T}\in \mathcal{U}(\texttt{c})$
, F can be used as many times as needed in the last component (by using the decision rule during the positive phase). Also, since
$\mathsf{T}\in \mathcal{U}(\texttt{c})$
, F can be used as many times as needed in the last component (by using the decision rule during the positive phase). Also, since
![]() $\texttt{c}$
is not related to any subexponential, the formula F cannot be moved to other components and thus confined to the last component.
$\texttt{c}$
is not related to any subexponential, the formula F cannot be moved to other components and thus confined to the last component.
All this is illustrated in the next example.
Example 3.1. Let
![]() $4,4+,k,k+$
be subexponentials s.t.
$4,4+,k,k+$
be subexponentials s.t.
![]() $\mathcal{U}(4)=\{\mathsf{K},\mathsf{4}\}$
,
$\mathcal{U}(4)=\{\mathsf{K},\mathsf{4}\}$
,
![]() $\mathcal{U}(4+)=\{\mathsf{K},\mathsf{4},\mathsf{T}\}$
,
$\mathcal{U}(4+)=\{\mathsf{K},\mathsf{4},\mathsf{T}\}$
,
![]() $\mathcal{U}(k)=\{\mathsf{K},\mathsf{C},\mathsf{W}\}$
and
$\mathcal{U}(k)=\{\mathsf{K},\mathsf{C},\mathsf{W}\}$
and
![]() $\mathcal{U}(k+)=\{\mathsf{K},\mathsf{C},\mathsf{W},\mathsf{T}\}$
. The following derivations show, respectively, that the axioms
$\mathcal{U}(k+)=\{\mathsf{K},\mathsf{C},\mathsf{W},\mathsf{T}\}$
. The following derivations show, respectively, that the axioms
![]() $\mathsf{K}$
and
$\mathsf{K}$
and
![]() $\mathsf{4}$
are provable:
$\mathsf{4}$
are provable:

The first derivation involves three components (two of them created using the ![]() rule). The information
rule). The information
![]() $A^\perp$
is passed from the 1st to the 2nd and 3rd components through the subexponential
$A^\perp$
is passed from the 1st to the 2nd and 3rd components through the subexponential
![]() $4+$
via rule
$4+$
via rule ![]() . Since this subexponential is linear, the context
. Since this subexponential is linear, the context
![]() $4+$
disappear after the application of
$4+$
disappear after the application of
![]() $\mathsf{D^l_s}$
. The second derivation illustrates the application of the rule
$\mathsf{D^l_s}$
. The second derivation illustrates the application of the rule ![]() in the unbounded subexp. k. Note that the formula
in the unbounded subexp. k. Note that the formula
![]() $A \otimes B^\perp$
is copied to the context
$A \otimes B^\perp$
is copied to the context
![]() $\texttt{c}$
. All the other axioms in Figure 4 can be proved similarly, using a subexponential featuring the needed modal behaviors.
$\texttt{c}$
. All the other axioms in Figure 4 can be proved similarly, using a subexponential featuring the needed modal behaviors.
Finally, it should be noted that the proposed focused system is complete w.r.t. the unfocused version. For the plain linear logic rules, completeness is guaranteed by Andreoli’s result in Andreoli (Reference Andreoli1992). For the modal rules, it is straightforward to simulate the
![]() $\mathsf{LNS}$
rules from the focused ones, following the same lines as the process of obtaining sequent rules from the
$\mathsf{LNS}$
rules from the focused ones, following the same lines as the process of obtaining sequent rules from the
![]() $\mathsf{LNS}$
ones (see the example for implication right rule for
$\mathsf{LNS}$
ones (see the example for implication right rule for
![]() $\mathsf{mLJ}$
in Section 2).
$\mathsf{mLJ}$
in Section 2).
3.2 Cut Admissibility for
 $\mathsf{LNS}_\mathsf{FMLL}$
$\mathsf{LNS}_\mathsf{FMLL}$
In this section, we present a cut-admissibility result for the system
![]() $\mathsf{LNS}_\mathsf{FMLL}$
. It should be noted that this is, for the best of our knowledge, the first formally verified proof of cut admissibility for focused
$\mathsf{LNS}_\mathsf{FMLL}$
. It should be noted that this is, for the best of our knowledge, the first formally verified proof of cut admissibility for focused
![]() $\mathsf{LNS}$
.
Footnote 2
This is not a simple enhancement w.r.t. other formalizations: usually cut-admissibility of focused systems is done in two steps, first translating it into the unfocused version, then proving the completeness of focusing. Here, we prove the cut admissibility of
$\mathsf{LNS}$
.
Footnote 2
This is not a simple enhancement w.r.t. other formalizations: usually cut-admissibility of focused systems is done in two steps, first translating it into the unfocused version, then proving the completeness of focusing. Here, we prove the cut admissibility of
![]() $\mathsf{LNS}_\mathsf{FMLL}$
directly, observing that the multimodal flavor of the system makes the task even less trivial.
$\mathsf{LNS}_\mathsf{FMLL}$
directly, observing that the multimodal flavor of the system makes the task even less trivial.
We proceed by double induction on the complexity of the cut formula and the sum of the premises’ heights of the cut rule. Since we are proving the theorem directly on a focused system, we require to eliminate, simultaneously, different rules dealing with the different phases of the proof (see e.g., Liang and Miller Reference Liang and Miller2009). The cut rules are in Figure 6.

Figure 6. Cut-rules for the system
![]() $\mathsf{LNS}_\mathsf{FMLL}$
.
$\mathsf{LNS}_\mathsf{FMLL}$
.
![]() $\Lambda$
is unbounded and
$\Lambda$
is unbounded and
![]() $\Theta=(\Theta_1,\Theta_2)$
is linear.
$\Theta=(\Theta_1,\Theta_2)$
is linear.
In the following, we show the most interesting proof reductions needed to establish the main result (Theorem 3.5). In the repository (Xavier and Olarte Reference Xavier and Olarte2021), the reader can find the formalization in Coq of all the results of this section, together with a companion PDF with extra details about the proof.
Auxiliary results. We start with a series of auxiliary results for the system
![]() $\mathsf{LNS}_\mathsf{FMLL}$
. They are not only needed for the proof of the main theorem, but they will also help on understanding better the dynamics of the system.
$\mathsf{LNS}_\mathsf{FMLL}$
. They are not only needed for the proof of the main theorem, but they will also help on understanding better the dynamics of the system.
Notation 5. We use
![]() $\vdash \Theta;\ \Gamma \Updownarrow X$
to represent a sequent that can belong to the negative phase – and X is a list of formulas, or to the positive phase – and X is a formula. We use
$\vdash \Theta;\ \Gamma \Updownarrow X$
to represent a sequent that can belong to the negative phase – and X is a list of formulas, or to the positive phase – and X is a formula. We use
![]() $\vdash_n \mathcal{S}$
to indicate that the linear nested sequent
$\vdash_n \mathcal{S}$
to indicate that the linear nested sequent
![]() $\mathcal{S}$
has a derivation of height at most n. If
$\mathcal{S}$
has a derivation of height at most n. If
![]() $\Theta=\{i_1:F_1,...,i_n:F_n\}$
is a subexponential context, then
$\Theta=\{i_1:F_1,...,i_n:F_n\}$
is a subexponential context, then
![]() $\Theta+$
denotes the subexponential context
$\Theta+$
denotes the subexponential context
![]() $\{i_1+:F_1,...,i_n+:F_n\}$
and
$\{i_1+:F_1,...,i_n+:F_n\}$
and
![]() $\mathcal{F}(\Theta)$
denotes the list of formulas
$\mathcal{F}(\Theta)$
denotes the list of formulas
![]() $F_1,\ldots,F_n$
. For easing the notation, we will write
$F_1,\ldots,F_n$
. For easing the notation, we will write
![]() $i:\Theta$
instead of
$i:\Theta$
instead of
![]() $i:\mathcal{F}(\Theta)=\{i:F_1,\ldots,i:F_n\}$
. Finally,
$i:\mathcal{F}(\Theta)=\{i:F_1,\ldots,i:F_n\}$
. Finally,
![]() $\Theta = (\Theta_1,\ldots,\Theta_n)$
denotes that
$\Theta = (\Theta_1,\ldots,\Theta_n)$
denotes that
![]() $\Theta_1,\ldots,\Theta_n$
is a partition of
$\Theta_1,\ldots,\Theta_n$
is a partition of
![]() $\Theta$
. In this section,
$\Theta$
. In this section,
![]() $\Omega$
will be used to denote a context assuming axiom
$\Omega$
will be used to denote a context assuming axiom
![]() $\mathsf{4}$
(called
$\mathsf{4}$
(called
![]() $\mathsf{4}$
-context), and
$\mathsf{4}$
-context), and
![]() $\Psi$
a context without
$\Psi$
a context without
![]() $\mathsf{4}$
. Recall that the axiom
$\mathsf{4}$
. Recall that the axiom
![]() $\mathsf{T}$
allows for dereliction. The following result shows some particular behaviors of
$\mathsf{T}$
allows for dereliction. The following result shows some particular behaviors of
![]() $\mathsf{T}$
-contexts.
$\mathsf{T}$
-contexts.
Theorem 3.1. (The axiom
![]() $\mathsf{T}$
) The following propositions hold:
$\mathsf{T}$
) The following propositions hold:
-
( T 1) If
 $\{\mathsf{T},\mathsf{C},\mathsf{W}\}\subseteq\mathcal{U}(i)$
and
$\{\mathsf{T},\mathsf{C},\mathsf{W}\}\subseteq\mathcal{U}(i)$
and
 $\vdash_n \Theta,i:F,\texttt{c}:F;\ \Gamma \Updownarrow X$
, then
$\vdash_n \Theta,i:F,\texttt{c}:F;\ \Gamma \Updownarrow X$
, then
 $\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
.
$\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
. -
( T 2) If
 $\{\mathsf{T},\mathsf{C},\mathsf{W}\}\subseteq\mathcal{U}(i)$
and
$\{\mathsf{T},\mathsf{C},\mathsf{W}\}\subseteq\mathcal{U}(i)$
and
 $\vdash_n \Theta,i:F;\ \Gamma,F \Updownarrow X$
, then
$\vdash_n \Theta,i:F;\ \Gamma,F \Updownarrow X$
, then
 $\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
.
$\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
. -
( T 2) If
 $\mathsf{T}\in\mathcal{U}(i)$
and
$\mathsf{T}\in\mathcal{U}(i)$
and
 $\vdash_n \Theta;\ \Gamma,F \Updownarrow X$
, then
$\vdash_n \Theta;\ \Gamma,F \Updownarrow X$
, then
 $\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
.
$\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
. -
(
 $\mathcal{L}A_1$
) If
$\mathcal{L}A_1$
) If
 $\{\mathsf{T},\mathsf{C},\mathsf{W}\}\subseteq\mathcal{U}(i)$
and
$\{\mathsf{T},\mathsf{C},\mathsf{W}\}\subseteq\mathcal{U}(i)$
and
 $\vdash \Theta,i:F;\Gamma \Uparrow L,F$
then
$\vdash \Theta,i:F;\Gamma \Uparrow L,F$
then
 $\vdash \Theta,i:F;\Gamma \Uparrow L$
.
$\vdash \Theta,i:F;\Gamma \Uparrow L$
. -
(
 $\mathcal{L}A_2$
) If
$\mathcal{L}A_2$
) If
 $\mathsf{T}\in\mathcal{U}(i)$
and
$\mathsf{T}\in\mathcal{U}(i)$
and
 $\vdash \Theta;\ \Gamma \Uparrow L,F$
then
$\vdash \Theta;\ \Gamma \Uparrow L,F$
then
 $\vdash \Theta,i:F;\Gamma \Uparrow L$
.
$\vdash \Theta,i:F;\Gamma \Uparrow L$
.
All these results can be easily generalized to contexts featuring the corresponding axioms. For example, in the case of the absorption lemma (
![]() $\mathcal{L}A_2$
), if
$\mathcal{L}A_2$
), if
![]() $\vdash \Theta;\Delta \Uparrow L,\Gamma$
, then
$\vdash \Theta;\Delta \Uparrow L,\Gamma$
, then
![]() $\vdash \Theta,i:\Gamma;\Delta \Uparrow L$
. Moreover, (T1) states that if a formula is stored in a context i where
$\vdash \Theta,i:\Gamma;\Delta \Uparrow L$
. Moreover, (T1) states that if a formula is stored in a context i where
![]() $\mathsf{T}$
holds, then it is “redundant” to place that formula also in the local context
$\mathsf{T}$
holds, then it is “redundant” to place that formula also in the local context
![]() $\texttt{c}$
. The other results allow us for moving formulas in the different zones of a sequent where
$\texttt{c}$
. The other results allow us for moving formulas in the different zones of a sequent where
![]() $\mathsf{T}$
holds.
$\mathsf{T}$
holds.
The next theorem highlights the difference between multisets and lists in contexts. Namely, while permuting a list preserves provability, it may not preserve the height of a derivation. On the other hand, weakening and contraction are height-preserving admissible for unbounded contexts.
Theorem 3.2. (Structural Rules). The following propositions hold.
-
(
 $\equiv_P$
) If
$\equiv_P$
) If
 $L_1$
is a permutation of
$L_1$
is a permutation of
 $L_2$
and
$L_2$
and
 $\vdash \Theta;\ \Gamma \Uparrow L_1$
then
$\vdash \Theta;\ \Gamma \Uparrow L_1$
then
 $\vdash \Theta;\ \Gamma \Uparrow L_2$
$\vdash \Theta;\ \Gamma \Uparrow L_2$
-
(
 $\mathsf{W}$
) If
$\mathsf{W}$
) If
 $\mathsf{U}\subseteq\mathcal{U}(i)$
and
$\mathsf{U}\subseteq\mathcal{U}(i)$
and
 $\vdash_n \Theta;\ \Gamma \Updownarrow X$
then
$\vdash_n \Theta;\ \Gamma \Updownarrow X$
then
 $\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
.
$\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
. -
(
 $\mathsf{C}$
) If
$\mathsf{C}$
) If
 $\mathsf{U}\subseteq\mathcal{U}(i)$
and
$\mathsf{U}\subseteq\mathcal{U}(i)$
and
 $\vdash_n \Theta,i:F,i:F;\ \Gamma \Updownarrow X$
then
$\vdash_n \Theta,i:F,i:F;\ \Gamma \Updownarrow X$
then
 $\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
.
$\vdash_n \Theta,i:F;\ \Gamma \Updownarrow X$
.
As usual in focused systems, the shape of phases can be totally characterized. In the subexponential phase, since the only action allowed is moving formulas between components until the release rule (
![]() $\mathsf{R_{\mathsf{r}}}$
) is applied, every derivation has the shape
$\mathsf{R_{\mathsf{r}}}$
) is applied, every derivation has the shape

where
![]() $\Xi$
contains all the unbounded subexponentials not related to i,
$\Xi$
contains all the unbounded subexponentials not related to i,
![]() $\Psi = (\Psi_1^u, \Psi_2^l)$
and
$\Psi = (\Psi_1^u, \Psi_2^l)$
and
![]() $i \preceq j$
for all
$i \preceq j$
for all
![]() $j:F$
in
$j:F$
in
![]() $\Omega\cup\Psi_1$
. Observe that
$\Omega\cup\Psi_1$
. Observe that
![]() $\Xi$
is weakened when the release rule is applied. The formulas in
$\Xi$
is weakened when the release rule is applied. The formulas in
![]() $\Omega$
gain the axiom
$\Omega$
gain the axiom
![]() $\mathsf{T}$
, the unbounded formulas in
$\mathsf{T}$
, the unbounded formulas in
![]() $\Psi$
are stored in
$\Psi$
are stored in
![]() $\texttt{c}$
and the linear ones are placed in the linear context (
$\texttt{c}$
and the linear ones are placed in the linear context (
![]() $\mathcal{F}(\Psi_2)$
). On the left, the subexponential phase is triggered by the promotion rule and
$\mathcal{F}(\Psi_2)$
). On the left, the subexponential phase is triggered by the promotion rule and
![]() $L=P$
. On the right, the rule
$L=P$
. On the right, the rule
![]() $\mathsf{D_d}$
is applied and L is empty.
$\mathsf{D_d}$
is applied and L is empty.
Theorem 3.3. (Subexp. phase). Assume that
![]() $\Xi$
is unbounded,
$\Xi$
is unbounded,
![]() $\Psi = (\Psi_1^u,\Psi_2^l)$
,
$\Psi = (\Psi_1^u,\Psi_2^l)$
,
![]() $\Omega = (\Omega_1^u,\Omega_2^l)$
, and if
$\Omega = (\Omega_1^u,\Omega_2^l)$
, and if
![]() $j:F \in \Omega \cup \Psi_1$
then
$j:F \in \Omega \cup \Psi_1$
then
![]() $i \preceq j$
. Then
$i \preceq j$
. Then
(
S
) ![]()
where
![]() $n=|\Omega,\Psi|$
.
$n=|\Omega,\Psi|$
.
This result can be further specialized depending whether the index i in the subexponential phase (
![]() $\cdot\mathbin{\!/\mkern-5mu/^{i}\!}\cdot$
) is unbounded or
$\cdot\mathbin{\!/\mkern-5mu/^{i}\!}\cdot$
) is unbounded or
![]() $\mathsf{4}\in \mathcal{U}(i)$
. Remember the upwardly closeness condition: if
$\mathsf{4}\in \mathcal{U}(i)$
. Remember the upwardly closeness condition: if
![]() $i\preceq j$
and some axiom
$i\preceq j$
and some axiom
![]() $\mathsf{A}\in \mathcal{U}(i)$
then,
$\mathsf{A}\in \mathcal{U}(i)$
then,
![]() $\mathsf{A}\in \mathcal{U}(j)$
. Hence, if i is unbounded, there is no linear subexponentials in
$\mathsf{A}\in \mathcal{U}(j)$
. Hence, if i is unbounded, there is no linear subexponentials in
![]() $\Omega,\Psi,\Xi$
and, thus,
$\Omega,\Psi,\Xi$
and, thus,
![]() $\Psi_2$
and
$\Psi_2$
and
![]() $\Omega_2$
are necessarily empty in
$\Omega_2$
are necessarily empty in
![]() $\textbf{(S)}$
. Moreover, if
$\textbf{(S)}$
. Moreover, if
![]() $\mathsf{4} \in \mathcal{U}(i)$
,
$\mathsf{4} \in \mathcal{U}(i)$
,
![]() $\Psi$
(containing the indices without
$\Psi$
(containing the indices without
![]() $\mathsf{4}$
) must be necessarily unbounded and weakened in the application of
$\mathsf{4}$
) must be necessarily unbounded and weakened in the application of
![]() $\mathsf{R_{\mathsf{r}}}$
. More precisely:
$\mathsf{R_{\mathsf{r}}}$
. More precisely:
-
(
 $\textbf{S}\mathsf{U}$
)
$\textbf{S}\mathsf{U}$
)
 $\vdash_{m}\Omega_{1+}, \texttt{c}:\Psi_1 ; \cdot\Uparrow L\quad\mbox{iff}\quad\vdash_{m+k+1}\Omega_1,\Psi_1,\Xi; \cdot\Uparrow \cdot \mathbin{\!/\mkern-5mu/^{i}\!} \cdot ; \cdot\Uparrow L$
$\vdash_{m}\Omega_{1+}, \texttt{c}:\Psi_1 ; \cdot\Uparrow L\quad\mbox{iff}\quad\vdash_{m+k+1}\Omega_1,\Psi_1,\Xi; \cdot\Uparrow \cdot \mathbin{\!/\mkern-5mu/^{i}\!} \cdot ; \cdot\Uparrow L$
-
(
 $\textbf{S}\mathsf{4}$
)
$\textbf{S}\mathsf{4}$
)
 $\vdash_{m}\Omega+; \cdot\Uparrow L \quad\mbox{iff}\quad\vdash_{m+r+1}\Omega,\Xi ; \cdot\Uparrow \cdot \mathbin{\!/\mkern-5mu/^{i}\!} \cdot ; \cdot\Uparrow L$
$\vdash_{m}\Omega+; \cdot\Uparrow L \quad\mbox{iff}\quad\vdash_{m+r+1}\Omega,\Xi ; \cdot\Uparrow \cdot \mathbin{\!/\mkern-5mu/^{i}\!} \cdot ; \cdot\Uparrow L$
where
![]() $k=|\Omega_1,\Psi_1|$
and
$k=|\Omega_1,\Psi_1|$
and
![]() $r=|\Omega|$
.
$r=|\Omega|$
.
It is also interesting to revisit the two different promotion rules: ![]() and
and ![]() . The following theorem shows that they coincide when
. The following theorem shows that they coincide when
![]() $\{\mathsf{C},\mathsf{W},\mathsf{T}\}\subseteq\mathcal{U}(i)$
.
$\{\mathsf{C},\mathsf{W},\mathsf{T}\}\subseteq\mathcal{U}(i)$
.
Theorem 3.4. Let i be unbounded and
![]() $\mathsf{T} \in\mathcal{U}(i)$
. If
$\mathsf{T} \in\mathcal{U}(i)$
. If ![]() then
then
![]() $\vdash_{n-1} \Theta; \cdot\Uparrow P $
.
$\vdash_{n-1} \Theta; \cdot\Uparrow P $
.
Cut-rules and reductions. The five cut-rules admissible in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
are presented in Figure 6. In all cases,
$\mathsf{LNS}_\mathsf{FMLL}$
are presented in Figure 6. In all cases,
![]() $\Lambda$
contains only unbounded subexponentials whereas
$\Lambda$
contains only unbounded subexponentials whereas
![]() $\Theta=(\Theta_1,\Theta_2)$
is a linear context. Below we explain the interdependencies between these rules during the cut-elimination procedure. For the sake of readability, in most of the derivations, we omit the unbounded context
$\Theta=(\Theta_1,\Theta_2)$
is a linear context. Below we explain the interdependencies between these rules during the cut-elimination procedure. For the sake of readability, in most of the derivations, we omit the unbounded context
![]() $\Lambda$
.
$\Lambda$
.
Elimination of
![]() $\Uparrow$
C. Since the cut formula is the first element in the list of formulas in the left premise, it must be necessarily principal. Take for instance the following case:
$\Uparrow$
C. Since the cut formula is the first element in the list of formulas in the left premise, it must be necessarily principal. Take for instance the following case:

When the cut formula has the shape ![]() (resp. a positive formula or a literal), a shorter cut using
(resp. a positive formula or a literal), a shorter cut using
![]() $\Uparrow$
CC (resp.
$\Uparrow$
CC (resp.
![]() $\Uparrow$
LC*) is used. For example:
$\Uparrow$
LC*) is used. For example:

When the cut formula is an atom, the right premise of the cut must necessarily finish with the initial rule. We show below the case where A is in the (linear) subexponential context i (where, necessarily,
![]() $\mathsf{T} \in \mathcal{U}(i)$
) and we use the admissible rule (T3), which is is justified by the respective statement in Theorem 3.1.
$\mathsf{T} \in \mathcal{U}(i)$
) and we use the admissible rule (T3), which is is justified by the respective statement in Theorem 3.1.

In the following, we will adopt the same procedure of reading the results in Theorem 3.2 as rules.
Elimination of
![]() $\Uparrow$
CC. The elimination of this rule is easy when the list L is not empty: it suffices to permute down the application of the introduction rule.
$\Uparrow$
CC. The elimination of this rule is easy when the list L is not empty: it suffices to permute down the application of the introduction rule.
When L is empty, the left premise necessarily starts with a decision rule or an application of
![]() ${\mathsf{D_d}}$
. We show below the case where Q is taken from the linear subexponential context a and, necessarily,
${\mathsf{D_d}}$
. We show below the case where Q is taken from the linear subexponential context a and, necessarily,
![]() $\mathsf{T}\in \mathcal{U}(a)$
. We proceed with a (smaller) application of
$\mathsf{T}\in \mathcal{U}(a)$
. We proceed with a (smaller) application of
![]() $\Downarrow$
CC:
$\Downarrow$
CC:

Consider now the case where the left premise starts with an application of
![]() ${\mathsf{D_d}}$
. Assume that
${\mathsf{D_d}}$
. Assume that
![]() $\mathsf{D} \in \mathcal{U}(a)$
,
$\mathsf{D} \in \mathcal{U}(a)$
,
![]() $a \preceq i$
and
$a \preceq i$
and
![]() $4 \in \mathcal{U}(i)$
. Moreover, let
$4 \in \mathcal{U}(i)$
. Moreover, let
![]() $\Psi=(\Psi_1^u,\Psi_2^l)$
and
$\Psi=(\Psi_1^u,\Psi_2^l)$
and
![]() $\Omega=(\Omega_1^u,\Omega_2^l,\Omega_3^l)$
. Hence
$\Omega=(\Omega_1^u,\Omega_2^l,\Omega_3^l)$
. Hence

The leaves in the above derivation are obtained from Theorem 3.3. The notation
![]() $\Omega_1^{\succeq a}$
represents the subset of formulas in
$\Omega_1^{\succeq a}$
represents the subset of formulas in
![]() $\Omega_1$
whose indices are above a and that were not weakened in the end of the subexponential phase. Note that, due to the upwardly closeness condition, the linear context
$\Omega_1$
whose indices are above a and that were not weakened in the end of the subexponential phase. Note that, due to the upwardly closeness condition, the linear context
![]() $\Psi_2$
must necessarily be moved to the left premise (since
$\Psi_2$
must necessarily be moved to the left premise (since
![]() $\mathsf{4}$
is not present in
$\mathsf{4}$
is not present in
![]() $\Psi$
). Also,
$\Psi$
). Also,
![]() $\Psi_1$
is necessarily weakened in the right premise after applying the release rule. The reduction consists in cutting with
$\Psi_1$
is necessarily weakened in the right premise after applying the release rule. The reduction consists in cutting with ![]() instead of
instead of ![]() as follows:
as follows:

In the above derivation,
![]() $\Omega'$
contains all the formulas in both
$\Omega'$
contains all the formulas in both
![]() $\Omega_1^{\succeq a}$
and
$\Omega_1^{\succeq a}$
and
![]() $\Omega_1^{\succeq i}$
, i.e., the formulas from
$\Omega_1^{\succeq i}$
, i.e., the formulas from
![]() $\Omega_1$
that were not weakened in neither of the derivations. Note that
$\Omega_1$
that were not weakened in neither of the derivations. Note that
![]() $a \preceq i$
and then, the application of
$a \preceq i$
and then, the application of
![]() $\mathsf{D_d}$
can preserve all the formulas in
$\mathsf{D_d}$
can preserve all the formulas in
![]() $\Omega_1^{\succeq i}$
(similarly for
$\Omega_1^{\succeq i}$
(similarly for
![]() $\Omega_3$
). Derivations
$\Omega_3$
). Derivations
![]() $\pi_i^w$
for
$\pi_i^w$
for
![]() $i\in\{1,2\}$
are obtained from
$i\in\{1,2\}$
are obtained from
![]() $\pi_i$
by weakening the formulas in
$\pi_i$
by weakening the formulas in
![]() $\Omega_1'$
not needed in each derivation.
$\Omega_1'$
not needed in each derivation.
Elimination of
![]() $\Downarrow$
CC. When the focused formula on the left premise is principal and focus cannot be lost, an invertibility lemma is used. Below a representative case using the invertibility lemma
$\Downarrow$
CC. When the focused formula on the left premise is principal and focus cannot be lost, an invertibility lemma is used. Below a representative case using the invertibility lemma
![]() $(\mathcal{L}\oplus):$
If
$(\mathcal{L}\oplus):$
If
![]() $\vdash \Theta;\ \Delta \Uparrow L,F$
then
$\vdash \Theta;\ \Delta \Uparrow L,F$
then
![]() $\vdash \Theta;\ \Delta,F\oplus G \Uparrow L$
.
$\vdash \Theta;\ \Delta,F\oplus G \Uparrow L$
.

When the left premise starts with the promotion rule, we also have several cases depending on the axioms of the introduced subexponential. Consider the case where i is unbounded and
![]() $\mathsf{4} \notin \mathcal{U}(i)$
. Let
$\mathsf{4} \notin \mathcal{U}(i)$
. Let
![]() $\Psi=(\Psi_1^u,\Psi_2^l)$
and
$\Psi=(\Psi_1^u,\Psi_2^l)$
and
![]() $\Omega=(\Omega_1^u,\Omega_2^l)$
:
$\Omega=(\Omega_1^u,\Omega_2^l)$
:

Note that H is stored in the context
![]() $\texttt{c}$
. The reduction considers a cut with
$\texttt{c}$
. The reduction considers a cut with ![]() (instead of
(instead of ![]() ):
):

![]() $\Psi_1'$
contains all the formulas in both
$\Psi_1'$
contains all the formulas in both
![]() $\Psi_1^{\succeq a}$
and
$\Psi_1^{\succeq a}$
and
![]() $\Psi_1^{\succeq i}$
(the same with
$\Psi_1^{\succeq i}$
(the same with
![]() $\Omega'$
). Since i is unbounded, note that the application of
$\Omega'$
). Since i is unbounded, note that the application of ![]() above is valid.
above is valid.
Another interesting case, similar to the previous one, is when
![]() $ \{\mathsf{C},\mathsf{W},\mathsf{4}\}\subseteq\mathcal{U}(i)$
. Hence, H is moved to the context
$ \{\mathsf{C},\mathsf{W},\mathsf{4}\}\subseteq\mathcal{U}(i)$
. Hence, H is moved to the context
![]() $i+$
and the reduction considers a (smaller) cut with
$i+$
and the reduction considers a (smaller) cut with
![]() $i+$
(instead of i).
$i+$
(instead of i).
Elimination of
![]() $\Uparrow$
C*. When the list
$\Uparrow$
C*. When the list
![]() $L_1$
is not empty, the first formula in
$L_1$
is not empty, the first formula in
![]() $L_1$
is necessarily principal in the left premise. Hence, we simply permute down the application of that rule.
$L_1$
is necessarily principal in the left premise. Hence, we simply permute down the application of that rule.
When
![]() $L_1$
is empty, we consider two cases: either the cut formula is stored in the left premise, or it is necessarily stored in the right premise. The reductions for these cases are as follows:
$L_1$
is empty, we consider two cases: either the cut formula is stored in the left premise, or it is necessarily stored in the right premise. The reductions for these cases are as follows:

Elimination of
![]() $\Uparrow$
LC* Similarly to the previous case, when the list
$\Uparrow$
LC* Similarly to the previous case, when the list
![]() $L_1$
is not empty the reduction is easy. When this is not the case, the left premise must start with a decision rule. When the focus is on the cut formula, the reduction is as follows:
$L_1$
is not empty the reduction is easy. When this is not the case, the left premise must start with a decision rule. When the focus is on the cut formula, the reduction is as follows:

When the proof continues by focusing on a formula different from the cut formula, an invertibility result is needed. Here, the case of
![]() $\oplus$
when F is a positive formula and
$\oplus$
when F is a positive formula and
![]() $F\oplus G$
was taken from the unbounded context
$F\oplus G$
was taken from the unbounded context
![]() $\Lambda$
(omitted in the derivation):
$\Lambda$
(omitted in the derivation):

where
![]() $\mathcal{L}U$
is the following lemma: if F is a positive formula and
$\mathcal{L}U$
is the following lemma: if F is a positive formula and
![]() $\vdash \Theta;\ \Delta,F \Uparrow L$
then
$\vdash \Theta;\ \Delta,F \Uparrow L$
then
![]() $\vdash \Theta;\ \Delta \Uparrow L,F$
.
$\vdash \Theta;\ \Delta \Uparrow L,F$
.
![]() $\mathcal{L'}\oplus$
is a tailored version of the invertibility result we have already seen (
$\mathcal{L'}\oplus$
is a tailored version of the invertibility result we have already seen (
![]() $\mathcal{L}\oplus$
) when
$\mathcal{L}\oplus$
) when
![]() $F\oplus G$
is stored in a unbounded context.
$F\oplus G$
is stored in a unbounded context.
Theorem 3.5. (Admissibility of Cut). The cut rules in Figure 6 are admissible.
3.3 Discussion
Before concluding this section, let us explain some further motivations on the design of the five rules in Figure 6, as well as the proof of the above theorem in Coq.
Cut-rules. The Rule
![]() $\Uparrow\! C$
is the starting point of the procedure since the cut-formula H is principal in both premises. The other rules appear during the elimination process. For instance, as we already know, the elimination of
$\Uparrow\! C$
is the starting point of the procedure since the cut-formula H is principal in both premises. The other rules appear during the elimination process. For instance, as we already know, the elimination of
![]() $\Uparrow$
C depends on
$\Uparrow$
C depends on
![]() $\Uparrow$
LC* when H is stored. Notice that the same case can be also solved with an application of
$\Uparrow$
LC* when H is stored. Notice that the same case can be also solved with an application of
![]() $\Uparrow$
C*. In fact, one may inline the elimination procedure of
$\Uparrow$
C*. In fact, one may inline the elimination procedure of
![]() $\Uparrow$
LC* directly in the elimination of
$\Uparrow$
LC* directly in the elimination of
![]() $\Uparrow$
C and
$\Uparrow$
C and
![]() $\Uparrow$
C* and hence, only four rules will be needed. However, this implies replicating the same procedure several times during the proof. In particular, during the elimination of
$\Uparrow$
C* and hence, only four rules will be needed. However, this implies replicating the same procedure several times during the proof. In particular, during the elimination of
![]() $\Uparrow C^{\ast}$
, we need to consider whether H or
$\Uparrow C^{\ast}$
, we need to consider whether H or
![]() $H^\perp$
is stored when
$H^\perp$
is stored when
![]() $L_1$
is empty and, in each case, we have to apply a similar procedure from
$L_1$
is empty and, in each case, we have to apply a similar procedure from
![]() $\Uparrow$
LC*. The inclusion of
$\Uparrow$
LC*. The inclusion of
![]() $\Uparrow$
LC* thus makes easier to understand the elimination process (and more amenable for mechanization).
$\Uparrow$
LC* thus makes easier to understand the elimination process (and more amenable for mechanization).
The set of rules we have chosen is not the only possible alternative. For instance, instead of
![]() $\Uparrow$
LC*, one may think in reducing the same case in
$\Uparrow$
LC*, one may think in reducing the same case in
![]() $\Uparrow$
C (when H is stored) with the following rule:
$\Uparrow$
C (when H is stored) with the following rule:

In this case,
![]() $H^{\bot}$
is a negative atom or it must lose focus. In the first case, the cut can be eliminated without any additional cut. In the second case, we obtain an instance of
$H^{\bot}$
is a negative atom or it must lose focus. In the first case, the cut can be eliminated without any additional cut. In the second case, we obtain an instance of
![]() $\Uparrow$
LC*. Therefore,
$\Uparrow$
LC*. Therefore,
![]() $\Uparrow$
LC can be seen as an instance of
$\Uparrow$
LC can be seen as an instance of
![]() $\Uparrow$
LC*.
$\Uparrow$
LC*.
Consider now the elimination of
![]() $\Uparrow$
CC when the list L is empty and the left premise focuses on some formula F. One may eliminate this case by applying the following rule:
$\Uparrow$
CC when the list L is empty and the left premise focuses on some formula F. One may eliminate this case by applying the following rule:

However, this rule requires a side condition: H cannot be a positive atom. Without that condition, the (nonprovable) sequent
![]() $\vdash i:\top;\cdot\Downarrow \, A^\perp$
can be proved by using
$\vdash i:\top;\cdot\Downarrow \, A^\perp$
can be proved by using
![]() $\Downarrow$
CC* with
$\Downarrow$
CC* with
![]() $H=A$
. Hence, the atomic case in the elimination of
$H=A$
. Hence, the atomic case in the elimination of
![]() $\Uparrow$
CC must be treated separately and some additional lemmas need to be proved. In particular, it is required to show that if
$\Uparrow$
CC must be treated separately and some additional lemmas need to be proved. In particular, it is required to show that if
![]() $\vdash \Lambda,\Theta_1,(i:A);\Gamma\Downarrow \, F$
and
$\vdash \Lambda,\Theta_1,(i:A);\Gamma\Downarrow \, F$
and ![]() then
then
![]() $\vdash \Lambda,\Theta; \Uparrow \ \Gamma{F}$
. Note that this lemma is an instance of the rule
$\vdash \Lambda,\Theta; \Uparrow \ \Gamma{F}$
. Note that this lemma is an instance of the rule
![]() $\Downarrow$
CC.
$\Downarrow$
CC.
Mechanization in Coq. Besides the inherent complexity of dealing with the several cases appearing during the cut-elimination procedure, in this formalization we have to cope also with the problem of encoding the higher-order quantifiers. There are several alternatives for representing binders in proof assistants (see e.g., Chlipala Reference Chlipala2008; Heberlin et al. Reference Heberlin, Kim and Lee2017; Laurent Reference Laurent2021; Pitts Reference Pitts2003). The current formalization builds on our previous work (Felty et al. Reference Felty, Olarte and Xavier2021), where the Hybrid system (Felty and Momigliano Reference Felty and Momigliano2009) is used to represent the syntax. From the positive side, this choice has the immediate effect of allowing us to define binders at two levels: the meta-logic (specification logic in the terminology of the two-level approach in Hybrid) and the object logic, the logical system to be encoded as a theory in the specification logic. This separation reflects the different logics defined here: the specification logic is
![]() $\mathsf{MMLL}$
(and its system
$\mathsf{MMLL}$
(and its system
![]() $\mathsf{LNS}_\mathsf{FMLL}$
) used to reason about different object logics (more on this in the next section). From the negative side, sequents cannot be defined as an inductive
$\mathsf{LNS}_\mathsf{FMLL}$
) used to reason about different object logics (more on this in the next section). From the negative side, sequents cannot be defined as an inductive
![]() $\texttt{Type}$
but as an inductive proposition (
$\texttt{Type}$
but as an inductive proposition (
![]() $\texttt{Prop}$
). Hence, we cannot manipulate derivations as objects (due to the impossibility of doing pattern matching on a
$\texttt{Prop}$
). Hence, we cannot manipulate derivations as objects (due to the impossibility of doing pattern matching on a
![]() $\texttt{Prop}$
value). Therefore, we cannot extract a program (the cut-elimination procedure) from the proof of the theorem above and what we have is a proof of cut admissibility. The work of Laurent (Reference Laurent2021) allows for defining first-order binders and sequents in
$\texttt{Prop}$
value). Therefore, we cannot extract a program (the cut-elimination procedure) from the proof of the theorem above and what we have is a proof of cut admissibility. The work of Laurent (Reference Laurent2021) allows for defining first-order binders and sequents in
![]() $\texttt{Type}$
. However, such binders cannot do pattern matching as in
$\texttt{Type}$
. However, such binders cannot do pattern matching as in
![]() $\exists F, G. P(F \star G)$
, where
$\exists F, G. P(F \star G)$
, where
![]() $P(\!\cdot\!)$
is a predicate symbol and
$P(\!\cdot\!)$
is a predicate symbol and
![]() $\star$
is a connective of the OL, nor to encode first-order object logics. As far as we know, it is not possible to represent in Coq quantifiers at the specification level and also at the object level and keep the definition of sequents in
$\star$
is a connective of the OL, nor to encode first-order object logics. As far as we know, it is not possible to represent in Coq quantifiers at the specification level and also at the object level and keep the definition of sequents in
![]() $\texttt{Type}$
. The reader can find in Felty et al. (Reference Felty, Olarte and Xavier2021) details about the representation of syntax in Hybrid. The repository (Xavier and Olarte Reference Xavier and Olarte2021) also includes further documentation on how to define the subexponential signature in
$\texttt{Type}$
. The reader can find in Felty et al. (Reference Felty, Olarte and Xavier2021) details about the representation of syntax in Hybrid. The repository (Xavier and Olarte Reference Xavier and Olarte2021) also includes further documentation on how to define the subexponential signature in
![]() $\mathsf{MMLL}$
as well as some tactics to improve automatization when using the library in Coq.
$\mathsf{MMLL}$
as well as some tactics to improve automatization when using the library in Coq.
It is worth noticing that there are some recent advances towards providing native support in Coq for reasoning about binders. Frameworks, mainly using de Bruijn terms, have been developed to automatize some of the tasks in such reasoning. The work of Stark (Reference Stark2020) covers the mechanization of binders and it makes use of the Autosubst 2 framework, that translates second-order HOAS specifications into potentially mutual inductive term sorts (Stark et al. Reference Stark, Schäfer and Kaiser2019). We also refer the reader to Forster (Reference Forster2021), that uses de Bruijn terms to formalize Computability Theory in the Calculus of Inductive Constructions.
4.
 $\mathsf{LNS}$
Systems as
$\mathsf{LNS}$
Systems as
 $\mathsf{MMLL}$
Theories
$\mathsf{MMLL}$
Theories
This section dwells on the specification of a class of
![]() $\mathsf{LNS}$
systems as
$\mathsf{LNS}$
systems as
![]() $\mathsf{MMLL}$
theories. More precisely, we encode the inference rules of a given OL as an
$\mathsf{MMLL}$
theories. More precisely, we encode the inference rules of a given OL as an
![]() $\mathsf{MMLL}$
theory. The encoding is modular and it allows for the specification of multimodal logics in a uniform way. We prove that the resulting specifications are adequate in the sense that an OL-sequent
$\mathsf{MMLL}$
theory. The encoding is modular and it allows for the specification of multimodal logics in a uniform way. We prove that the resulting specifications are adequate in the sense that an OL-sequent
![]() $\mathcal{S}$
is provable iff the encoding of
$\mathcal{S}$
is provable iff the encoding of
![]() $\mathcal{S}$
together with the resulting theory given by OL’s rules is also provable in
$\mathcal{S}$
together with the resulting theory given by OL’s rules is also provable in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
. This level of adequacy (Nigam and Miller Reference Nigam and Miller2010) is usually known as FCP (full completeness of proofs).
$\mathsf{LNS}_\mathsf{FMLL}$
. This level of adequacy (Nigam and Miller Reference Nigam and Miller2010) is usually known as FCP (full completeness of proofs).
In Miller and Pimentel (Reference Miller and Pimentel2013),
![]() $\mathsf{LL}$
was used as a logical framework for specifying a number of logical systems. Here we shall proceed similarly, but with
$\mathsf{LL}$
was used as a logical framework for specifying a number of logical systems. Here we shall proceed similarly, but with
![]() $\mathsf{MMLL}$
as the meta-level system. In what follows, we assume that the subexponential signature of
$\mathsf{MMLL}$
as the meta-level system. In what follows, we assume that the subexponential signature of
![]() $\mathsf{MMLL}$
includes a distinguished label
$\mathsf{MMLL}$
includes a distinguished label
![]() $\omega$
for storing theories, such that
$\omega$
for storing theories, such that
![]() $i\preceq \omega$
for all
$i\preceq \omega$
for all
![]() $i\in\mathcal{I}$
, and
$i\in\mathcal{I}$
, and
![]() $\mathcal{U}({\omega}) =\{\mathsf{C},\mathsf{W}, \mathsf{K}, \mathsf{T}, \mathsf{D},\mathsf{4}\}$
. Other subexponentials will be added to the base signature depending on the logical system encoded.
$\mathcal{U}({\omega}) =\{\mathsf{C},\mathsf{W}, \mathsf{K}, \mathsf{T}, \mathsf{D},\mathsf{4}\}$
. Other subexponentials will be added to the base signature depending on the logical system encoded.
OL formulas are specified using the meta-level predicates
![]() $\lfloor \cdot \rfloor$
and
$\lfloor \cdot \rfloor$
and
![]() $\lceil \cdot \rceil$
, that identify the occurrence of such formulas on the left and on the right side of the sequent respectively. Hence, OL sequents of the form
$\lceil \cdot \rceil$
, that identify the occurrence of such formulas on the left and on the right side of the sequent respectively. Hence, OL sequents of the form
![]() ${F_1,\ldots,F_n}\vdash{G_1,\ldots,G_m}$
,
${F_1,\ldots,F_n}\vdash{G_1,\ldots,G_m}$
,
![]() $n,m\ge0$
, are specified as the multiset of atomic
$n,m\ge0$
, are specified as the multiset of atomic
![]() $\mathsf{MMLL}$
formulas
$\mathsf{MMLL}$
formulas
![]() $\lfloor F_1 \rfloor,\ldots,\lfloor F_n \rfloor,\lceil G_1 \rceil,\ldots,\lceil G_m \rceil$
. As a mnemonic, formulas on the (L)eft side of OL sequents are specified with the predicate starting with
$\lfloor F_1 \rfloor,\ldots,\lfloor F_n \rfloor,\lceil G_1 \rceil,\ldots,\lceil G_m \rceil$
. As a mnemonic, formulas on the (L)eft side of OL sequents are specified with the predicate starting with
![]() ${\lfloor}$
. Given a set of OL-formulas
${\lfloor}$
. Given a set of OL-formulas
![]() $\Gamma$
, we shall use
$\Gamma$
, we shall use
![]() $\lfloor \Gamma \rfloor$
to denote the set of
$\lfloor \Gamma \rfloor$
to denote the set of
![]() $\mathsf{MMLL}$
-formulas
$\mathsf{MMLL}$
-formulas
![]() $\{\lfloor F \rfloor \mid F \in \Gamma\}$
, similarly for
$\{\lfloor F \rfloor \mid F \in \Gamma\}$
, similarly for
![]() $\lceil \Gamma \rceil$
.
$\lceil \Gamma \rceil$
.
OL- Inference rules are specified as rewriting clauses that replace the principal formula in the conclusion of the rule by the active formulas in the premises. The
![]() $\mathsf{LL}$
connectives indicate how these OL-formulas are connected: contexts are copied (
$\mathsf{LL}$
connectives indicate how these OL-formulas are connected: contexts are copied (
![]() $\mathbin{\&}$
) or split (
$\mathbin{\&}$
) or split (
![]() $\otimes$
), in different inference rules (
$\otimes$
), in different inference rules (
![]() $\oplus$
) or in the same sequent
$\oplus$
) or in the same sequent ![]() . Such clauses are members of the
. Such clauses are members of the
![]() $\mathsf{MMLL}$
theory
$\mathsf{MMLL}$
theory
![]() $\mathcal{T}_\mathcal{L}$
, specifying the behavior of the logical system
$\mathcal{T}_\mathcal{L}$
, specifying the behavior of the logical system
![]() $\mathcal{L}$
. Theories will be stored in the subexponential
$\mathcal{L}$
. Theories will be stored in the subexponential
![]() $\omega$
, since these clauses can be used as many times as needed and also copied to any component. Figure 7 presents the specification of the
$\omega$
, since these clauses can be used as many times as needed and also copied to any component. Figure 7 presents the specification of the
![]() $\mathsf{LNS}$
rules in Figure 1.
$\mathsf{LNS}$
rules in Figure 1.

Figure 7. Encoding of propositional rules of the system
![]() $\mathsf{LNS}_{\mathsf{G}}$
for classical logic. In all the specification clauses, there is an implicit existential quantification on F and G.
$\mathsf{LNS}_{\mathsf{G}}$
for classical logic. In all the specification clauses, there is an implicit existential quantification on F and G.
Consider the rules
![]() $\wedge_{Li}$
and
$\wedge_{Li}$
and
![]() $\wedge_{R}$
in Figure 1, and the corresponding clauses in Figure 7. The derivations in Figure 8 illustrate the behavior of these clauses once we focus on them. The first derivation in Figure 8 corresponds to focusing on the clause
$\wedge_{R}$
in Figure 1, and the corresponding clauses in Figure 7. The derivations in Figure 8 illustrate the behavior of these clauses once we focus on them. The first derivation in Figure 8 corresponds to focusing on the clause
![]() $\wedge_L$
from the theory
$\wedge_L$
from the theory
![]() $\mathcal{T}_\mathsf{G}$
where
$\mathcal{T}_\mathsf{G}$
where
![]() $\mathsf{I}=\mathsf{I_l}$
or
$\mathsf{I}=\mathsf{I_l}$
or
![]() $\mathsf{I}=\mathsf{I_s}$
and, accordingly,
$\mathsf{I}=\mathsf{I_s}$
and, accordingly,
![]() $\Gamma_1= \lfloor F\wedge G \rfloor$
, or
$\Gamma_1= \lfloor F\wedge G \rfloor$
, or
![]() $\Gamma_1=\emptyset$
and
$\Gamma_1=\emptyset$
and
![]() $\lfloor F\wedge G \rfloor\in \Theta$
. Bottom-up, the active formula
$\lfloor F\wedge G \rfloor\in \Theta$
. Bottom-up, the active formula
![]() $F \wedge G$
is taken from the linear or the classical context, and the whole positive phase (after the resulting negative phase) ends by storing the atom
$F \wedge G$
is taken from the linear or the classical context, and the whole positive phase (after the resulting negative phase) ends by storing the atom
![]() $\lfloor F \rfloor$
into the linear context. This derivation mimics exactly an application of the rule
$\lfloor F \rfloor$
into the linear context. This derivation mimics exactly an application of the rule
![]() $\wedge_{L1}$
at the object level. Similarly, if instead of
$\wedge_{L1}$
at the object level. Similarly, if instead of
![]() $\oplus_1$
we apply
$\oplus_1$
we apply
![]() $\oplus_2$
, the atom
$\oplus_2$
, the atom
![]() $\lfloor G \rfloor$
is stored, thus reflecting the behavior of
$\lfloor G \rfloor$
is stored, thus reflecting the behavior of
![]() $\wedge_{L2}$
. The second derivation in Figure 8 starts by focusing on the clause
$\wedge_{L2}$
. The second derivation in Figure 8 starts by focusing on the clause
![]() $\wedge_R$
, ending up with two premises corresponding exactly to the two premises of the OL-rule. The clauses for the other connectives and units work similarly. Moreover, when the clause corresponding to the initial rule is focused on, the proof must finish by showing that F is on the left and on the right of the OL-sequent. Given the identifier of a clause r (i.e., an OL-rule), we shall use [r] in
$\wedge_R$
, ending up with two premises corresponding exactly to the two premises of the OL-rule. The clauses for the other connectives and units work similarly. Moreover, when the clause corresponding to the initial rule is focused on, the proof must finish by showing that F is on the left and on the right of the OL-sequent. Given the identifier of a clause r (i.e., an OL-rule), we shall use [r] in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
derivations to collapse all the steps involved in the decomposition of the clause r. For instance:
$\mathsf{LNS}_\mathsf{FMLL}$
derivations to collapse all the steps involved in the decomposition of the clause r. For instance:


Figure 8. Examples of derivations focusing on the clauses
![]() $\wedge_L$
and
$\wedge_L$
and
![]() $\wedge_R$
.
$\wedge_R$
.
Regarding the structural rules of weakening and contraction, it may be the case that an OL admits some of them on the left, right, or both sides of sequents. We mimic those behaviors by adding the structural rules in Figure 9 according to each case. For instance, if
![]() $\mathsf{pos}_i$
(weakening/contraction for the left context) is in
$\mathsf{pos}_i$
(weakening/contraction for the left context) is in
![]() $\mathcal{T}_\mathcal{L}$
, we can prove the equivalence
$\mathcal{T}_\mathcal{L}$
, we can prove the equivalence ![]() . Hence, under the presence of
. Hence, under the presence of
![]() $\mathsf{pos}_i$
, formulas of the shape
$\mathsf{pos}_i$
, formulas of the shape
![]() $\lfloor F \rfloor$
can be stored in a unbounded subexponential context and they are free to be weakened and contracted (if i is unbounded). Similarly for
$\lfloor F \rfloor$
can be stored in a unbounded subexponential context and they are free to be weakened and contracted (if i is unbounded). Similarly for
![]() $\mathsf{neg}_i$
and right formulas. Observe that
$\mathsf{neg}_i$
and right formulas. Observe that
![]() $\mathsf{pos}_i$
and
$\mathsf{pos}_i$
and
![]() $\mathsf{neg}_i$
are parametric w.r.t. the subexponential label. For instance, if
$\mathsf{neg}_i$
are parametric w.r.t. the subexponential label. For instance, if
![]() $i=\texttt{c}$
, then the use of such clauses is restricted to a component (cf. Definition 4).
$i=\texttt{c}$
, then the use of such clauses is restricted to a component (cf. Definition 4).

Figure 9. Encoding of structural, intuitionistic implication, and modal rules.
Theorem 4.1. (Adequacy of
![]() $\mathcal{T}_\mathsf{G}$
) Let
$\mathcal{T}_\mathsf{G}$
) Let
![]() $\mathcal{T}_\mathsf{G}$
consist of the set of clauses in Figure 7 together with the structural rules
$\mathcal{T}_\mathsf{G}$
consist of the set of clauses in Figure 7 together with the structural rules
![]() $\mathsf{pos}_\texttt{c}$
and
$\mathsf{pos}_\texttt{c}$
and
![]() $\mathsf{neg}_\texttt{c}$
. Then
$\mathsf{neg}_\texttt{c}$
. Then
![]() $\mathcal{T}_\mathsf{G}$
is adequate FCP w.r.t.
$\mathcal{T}_\mathsf{G}$
is adequate FCP w.r.t.
![]() $\mathsf{LNS}_\mathsf{G}$
:
$\mathsf{LNS}_\mathsf{G}$
:
-
(1) Soundness: If the sequent
 $\Gamma \vdash \Delta$
is provable in
$\Gamma \vdash \Delta$
is provable in
 $\mathsf{LNS}_\mathsf{G}$
then the sequent
$\mathsf{LNS}_\mathsf{G}$
then the sequent
 $\vdash \omega:\mathcal{T}_\mathsf{G},\texttt{c}:(\lfloor \Gamma \rfloor,\lceil \Delta \rceil);\cdot \Uparrow \cdot$
is provable in
$\vdash \omega:\mathcal{T}_\mathsf{G},\texttt{c}:(\lfloor \Gamma \rfloor,\lceil \Delta \rceil);\cdot \Uparrow \cdot$
is provable in
 $\mathsf{LNS}_\mathsf{FMLL}$
.
$\mathsf{LNS}_\mathsf{FMLL}$
. -
(2) Completeness: If the sequent
 $\vdash \omega:\mathcal{T}_\mathsf{G},\texttt{c}:(\lfloor \Gamma \rfloor,\lceil \Delta \rceil);\lfloor \Gamma' \rfloor,\lceil \Delta' \rceil \Uparrow \cdot$
is provable in
$\vdash \omega:\mathcal{T}_\mathsf{G},\texttt{c}:(\lfloor \Gamma \rfloor,\lceil \Delta \rceil);\lfloor \Gamma' \rfloor,\lceil \Delta' \rceil \Uparrow \cdot$
is provable in
 $\mathsf{LNS}_\mathsf{FMLL}$
then the sequent
$\mathsf{LNS}_\mathsf{FMLL}$
then the sequent
 $\Gamma,\Gamma'\vdash \Delta,\Delta'$
is provable in
$\Gamma,\Gamma'\vdash \Delta,\Delta'$
is provable in
 $\mathsf{LNS}_\mathsf{G}$
.
$\mathsf{LNS}_\mathsf{G}$
.
Proof. As illustrated in Figure 8, we can prove that focusing on a clause is in one-to-one correspondence to the application of the corresponding rule in the OL. This is the case for all the rules introducing connectives. However, we cannot establish such a tight correspondence for the structural rules. In the proof of soundness, we are forced to use
![]() $\mathsf{pos}_\texttt{c}$
and
$\mathsf{pos}_\texttt{c}$
and
![]() $\mathsf{neg}_\texttt{c}$
to store all the atoms in the unbounded subexponential context
$\mathsf{neg}_\texttt{c}$
to store all the atoms in the unbounded subexponential context
![]() $\texttt{c}$
. Moreover, contraction and weakening at the object level are mimicked by a meta-level result in
$\texttt{c}$
. Moreover, contraction and weakening at the object level are mimicked by a meta-level result in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
(Theorem 3.2), but no clause in
$\mathsf{LNS}_\mathsf{FMLL}$
(Theorem 3.2), but no clause in
![]() $\mathcal{T}_\mathsf{G}$
is applied. For completeness, the applications of
$\mathcal{T}_\mathsf{G}$
is applied. For completeness, the applications of
![]() $\mathsf{pos}_\texttt{c}$
and
$\mathsf{pos}_\texttt{c}$
and
![]() $\mathsf{neg}_\texttt{c}$
do not have an object-level counterpart (since there is no linear/classical distinction at the object-level). Note that the images of the
$\mathsf{neg}_\texttt{c}$
do not have an object-level counterpart (since there is no linear/classical distinction at the object-level). Note that the images of the
![]() $\mathsf{LNS}_\mathsf{FMLL}$
sequents before and after the application of these rules are the same OL-sequent.
$\mathsf{LNS}_\mathsf{FMLL}$
sequents before and after the application of these rules are the same OL-sequent.
In the intuitionistic system
![]() $\mathsf{LNS}_{\mathsf{I}}$
(see Figures 1, 2 and 3), the rule
$\mathsf{LNS}_{\mathsf{I}}$
(see Figures 1, 2 and 3), the rule
![]() $\supset_R$
creates a new component while
$\supset_R$
creates a new component while
![]() $\texttt{lift}$
moves formulas across components. Such behavior will be specified with the subexponential t4 where
$\texttt{lift}$
moves formulas across components. Such behavior will be specified with the subexponential t4 where
![]() $\mathcal{U}(t4)=\{\mathsf{K},\mathsf{C},\mathsf{W}, \mathsf{T},\mathsf{4} \}$
. The encoding is thus obtained by considering the clauses in Figure 7 but replacing the rules for implication for those in Figure 9.
$\mathcal{U}(t4)=\{\mathsf{K},\mathsf{C},\mathsf{W}, \mathsf{T},\mathsf{4} \}$
. The encoding is thus obtained by considering the clauses in Figure 7 but replacing the rules for implication for those in Figure 9.
The proof of adequacy for this encoding requires an intermediary result. Consider the
![]() $\mathsf{LNS}_{\mathsf{I}}$
derivation on the left:
$\mathsf{LNS}_{\mathsf{I}}$
derivation on the left:

This OL-derivation does not have a corresponding
![]() $\mathsf{LNS}_\mathsf{FMLL}$
-derivation: once we focus on the clause
$\mathsf{LNS}_\mathsf{FMLL}$
-derivation: once we focus on the clause
![]() $\supset_R$
, necessarily the formula F is moved to the next component (
$\supset_R$
, necessarily the formula F is moved to the next component (
![]() $\mathtt{lift}$
) and, after finishing the subexponential phase, we are free to focus on the clause
$\mathtt{lift}$
) and, after finishing the subexponential phase, we are free to focus on the clause
![]() $\vee_{R1}$
. Hence, we shall show adequacy w.r.t. an alternative equivalent system, following the sequentialization procedure for
$\vee_{R1}$
. Hence, we shall show adequacy w.r.t. an alternative equivalent system, following the sequentialization procedure for
![]() $\mathsf{LNS}$
proposed in Pimentel et al. (Reference Pimentel, Ramanayake and Lellmann2019).
$\mathsf{LNS}$
proposed in Pimentel et al. (Reference Pimentel, Ramanayake and Lellmann2019).
More precisely, we consider the system
![]() $\mathsf{LNS}^{\texttt{S}}_{\mathsf{I}}$
which is as
$\mathsf{LNS}^{\texttt{S}}_{\mathsf{I}}$
which is as
![]() $\mathsf{LNS}_{\mathsf{I}}$
where the list
$\mathsf{LNS}_{\mathsf{I}}$
where the list
![]() $\mathcal{G}$
is empty in all the rules in Figures 1, 2 and 3 and the following release rule is added:
$\mathcal{G}$
is empty in all the rules in Figures 1, 2 and 3 and the following release rule is added:

The restriction on
![]() $\mathcal{G}$
guarantees that the introduction rules of connectives are applied only after the modal phase as in
$\mathcal{G}$
guarantees that the introduction rules of connectives are applied only after the modal phase as in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
. This strategy is complete (Pimentel et al. Reference Pimentel, Ramanayake and Lellmann2019) since it is always possible to organize
$\mathsf{LNS}_\mathsf{FMLL}$
. This strategy is complete (Pimentel et al. Reference Pimentel, Ramanayake and Lellmann2019) since it is always possible to organize
![]() $\mathsf{LNS}$
proofs by first applying all the lift operations to later apply the introduction rules on the last component. For that, it is shown that the application of rules (e.g.,
$\mathsf{LNS}$
proofs by first applying all the lift operations to later apply the introduction rules on the last component. For that, it is shown that the application of rules (e.g.,
![]() $\vee_{R_1}$
above) permutes down w.r.t the lift rule. See for instance the right derivation in (1).
$\vee_{R_1}$
above) permutes down w.r.t the lift rule. See for instance the right derivation in (1).
Theorem 4.2. (Adequacy of
![]() $\mathcal{T}_\mathsf{I}$
) Let
$\mathcal{T}_\mathsf{I}$
) Let
![]() $\mathcal{T}_\mathsf{I}$
contain
$\mathcal{T}_\mathsf{I}$
contain
![]() $\mathsf{pos}_{t4}$
,
$\mathsf{pos}_{t4}$
,
![]() $\mathsf{neg}_{\texttt{c}}$
plus the introduction clauses of
$\mathsf{neg}_{\texttt{c}}$
plus the introduction clauses of
![]() $\mathcal{T}_\mathsf{G}$
with the clauses for implication substituted by the clauses in Figure 9. Then
$\mathcal{T}_\mathsf{G}$
with the clauses for implication substituted by the clauses in Figure 9. Then
![]() $\mathcal{T}_\mathsf{I}$
is adequate FCP w.r.t.
$\mathcal{T}_\mathsf{I}$
is adequate FCP w.r.t.
![]() $\mathsf{LNS}^{\texttt{S}}_\mathsf{I}$
:
$\mathsf{LNS}^{\texttt{S}}_\mathsf{I}$
:
-
(1) Soundness: If the sequent
 $\Gamma \vdash \Delta$
is provable in
$\Gamma \vdash \Delta$
is provable in
 $\mathsf{LNS}^{\texttt{S}}_\mathsf{I}$
then the sequent
$\mathsf{LNS}^{\texttt{S}}_\mathsf{I}$
then the sequent
 $\vdash \omega:\mathcal{T}_\mathsf{I},t4: \lfloor \Gamma \rfloor, \texttt{c}: \lceil \Delta \rceil;\cdot \Uparrow \cdot$
is provable in
$\vdash \omega:\mathcal{T}_\mathsf{I},t4: \lfloor \Gamma \rfloor, \texttt{c}: \lceil \Delta \rceil;\cdot \Uparrow \cdot$
is provable in
 $\mathsf{LNS}_\mathsf{FMLL}$
.
$\mathsf{LNS}_\mathsf{FMLL}$
. -
(2) Completeness: If the sequent
 $\vdash \omega:\mathcal{T}_\mathsf{I},t4:\lfloor \Gamma \rfloor, \texttt{c}: \lceil \Delta \rceil;\lfloor \Gamma' \rfloor,\lceil \Delta' \rceil \Uparrow \cdot$
is provable in
$\vdash \omega:\mathcal{T}_\mathsf{I},t4:\lfloor \Gamma \rfloor, \texttt{c}: \lceil \Delta \rceil;\lfloor \Gamma' \rfloor,\lceil \Delta' \rceil \Uparrow \cdot$
is provable in
 $\mathsf{LNS}_\mathsf{FMLL}$
then the sequent
$\mathsf{LNS}_\mathsf{FMLL}$
then the sequent
 $\Gamma,\Gamma'\vdash \Delta,\Delta'$
is provable in
$\Gamma,\Gamma'\vdash \Delta,\Delta'$
is provable in
 $\mathsf{LNS}^{\texttt{S}}_\mathsf{I}$
.
$\mathsf{LNS}^{\texttt{S}}_\mathsf{I}$
.
Proof. For all the rules but implication right, the discussion is similar to the classical case. Consider the following derivation:

Here, the context
![]() $\Theta$
is split into
$\Theta$
is split into
![]() $\texttt{c}:\Theta$
and
$\texttt{c}:\Theta$
and
![]() $t4:\Theta$
. The former contains all the right formulas that will be forgotten in the subexponential phase. The latter contains all the left formulas that will be carried over the components. Note also that
$t4:\Theta$
. The former contains all the right formulas that will be forgotten in the subexponential phase. The latter contains all the left formulas that will be carried over the components. Note also that
![]() $\mathsf{T} \in \mathcal{U}(t4)$
and then,
$\mathsf{T} \in \mathcal{U}(t4)$
and then,
![]() $t4+=t4$
. Moreover, since
$t4+=t4$
. Moreover, since
![]() $t4\preceq \omega$
, the theory
$t4\preceq \omega$
, the theory
![]() $\mathcal{T}_\mathsf{I}$
always moves between components. This derivation corresponds, one-to-one, to an application of
$\mathcal{T}_\mathsf{I}$
always moves between components. This derivation corresponds, one-to-one, to an application of
![]() $\supset_R$
at the object level followed by zero or more application of
$\supset_R$
at the object level followed by zero or more application of
![]() $\mathtt{lift}$
and ending with the release rule
$\mathtt{lift}$
and ending with the release rule
![]() $\mathsf{R}$
in
$\mathsf{R}$
in
![]() $\mathsf{LNS}^{\texttt{S}}_\mathsf{I}$
.
$\mathsf{LNS}^{\texttt{S}}_\mathsf{I}$
. ![]()
We now analyze the specification of modal logics. In order to propose a parametric and modular encoding, we consider different subexponentials for each modal behavior. For that, the following notation will be handy:
-
the subexponential structure will include the set of labels
 $M=\{k, t, d, 4, t4, d4\}$
, where
$M=\{k, t, d, 4, t4, d4\}$
, where
 $\{\mathsf{K},\mathsf{C},\mathsf{W}\} \subseteq \mathcal{U}(l)$
for all
$\{\mathsf{K},\mathsf{C},\mathsf{W}\} \subseteq \mathcal{U}(l)$
for all
 $l\in M$
;
$l\in M$
; -
the name of each
 $l\in M$
matches the respective assumed axioms. For example,
$l\in M$
matches the respective assumed axioms. For example,
 $\mathcal{U}(d4)=\{\mathsf{K},\mathsf{C},\mathsf{W},\mathsf{D},\mathsf{4}\}$
.
$\mathcal{U}(d4)=\{\mathsf{K},\mathsf{C},\mathsf{W},\mathsf{D},\mathsf{4}\}$
.
The (parameterized) clauses specifying the rules for box are given in Figure 9. Remember that
![]() $\ell$
represents a (possibly empty) subset of
$\ell$
represents a (possibly empty) subset of
![]() $\mathcal{A} =\{\mathsf{T},\mathsf{D},\mathsf{4}\}$
and
$\mathcal{A} =\{\mathsf{T},\mathsf{D},\mathsf{4}\}$
and
![]() $\mathsf{K}\ell$
is the modal logic resulting from extending
$\mathsf{K}\ell$
is the modal logic resulting from extending
![]() $\mathsf{K}$
with the axioms in
$\mathsf{K}$
with the axioms in
![]() $\ell$
. The theory
$\ell$
. The theory
![]() $\mathcal{T}_{\mathsf{K}\ell}$
for
$\mathcal{T}_{\mathsf{K}\ell}$
for
![]() $\mathsf{K}\ell$
is given by the clauses of
$\mathsf{K}\ell$
is given by the clauses of
![]() $\mathcal{T}_\mathsf{G}$
(Figure 7) plus the clauses
$\mathcal{T}_\mathsf{G}$
(Figure 7) plus the clauses
![]() $\mathsf{neg}_\texttt{c}$
and
$\mathsf{neg}_\texttt{c}$
and
![]() $\mathsf{pos}_\texttt{c}$
(Figure 9) and the clauses
$\mathsf{pos}_\texttt{c}$
(Figure 9) and the clauses
![]() $\Box_{Ll}$
and
$\Box_{Ll}$
and
![]() $\Box_{Rl}$
(Figure 9), where
$\Box_{Rl}$
(Figure 9), where
![]() $l\in M$
is the subexponential corresponding to
$l\in M$
is the subexponential corresponding to
![]() $\ell$
. For example,
$\ell$
. For example,
![]() $\mathcal{T}_{\mathsf{K}\mathsf{T}\mathsf{4}}=\mathcal{T}_\mathsf{G}\cup\{\mathsf{neg}_\texttt{c},\mathsf{pos}_{\texttt{c}}\} \cup \{\Box_{Lt4},\Box_{Rt4}\}$
.
$\mathcal{T}_{\mathsf{K}\mathsf{T}\mathsf{4}}=\mathcal{T}_\mathsf{G}\cup\{\mathsf{neg}_\texttt{c},\mathsf{pos}_{\texttt{c}}\} \cup \{\Box_{Lt4},\Box_{Rt4}\}$
.
For adequacy, we also consider a sequentialized
![]() $\mathsf{LNS}$
system. As we did for the intuitionistic case, all the rules introducing the logical connectives rules in
$\mathsf{LNS}$
system. As we did for the intuitionistic case, all the rules introducing the logical connectives rules in
![]() $\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
assume that the history
$\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
assume that the history
![]() $\mathcal{G}$
is empty. Moreover, the release rule (2) is added to the system.
$\mathcal{G}$
is empty. Moreover, the release rule (2) is added to the system.
Theorem 4.3. (Adequacy of
![]() $\mathcal{T}_{\mathsf{K}\ell}$
)
$\mathcal{T}_{\mathsf{K}\ell}$
)
![]() $\mathcal{T}_{\mathsf{K}\ell}$
is adequate FCP w.r.t.
$\mathcal{T}_{\mathsf{K}\ell}$
is adequate FCP w.r.t.
![]() $\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
.
$\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
.
-
(1) Soundness: If the sequent
 $\Box\Phi,\Gamma \vdash \Delta$
is provable in
$\Box\Phi,\Gamma \vdash \Delta$
is provable in
 $\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
then the sequent
$\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
then the sequent
 $\vdash \omega:\mathcal{T}_{\mathsf{K}\ell}, l:\lfloor \Phi \rfloor,\texttt{c}: (\lfloor \Gamma \rfloor,\lceil \Delta \rceil);\cdot \Uparrow \cdot$
is provable in
$\vdash \omega:\mathcal{T}_{\mathsf{K}\ell}, l:\lfloor \Phi \rfloor,\texttt{c}: (\lfloor \Gamma \rfloor,\lceil \Delta \rceil);\cdot \Uparrow \cdot$
is provable in
 $\mathsf{LNS}_\mathsf{FMLL}$
.
$\mathsf{LNS}_\mathsf{FMLL}$
. -
(2) Completeness: If the sequent
 $\vdash \omega:\mathcal{T}_{\mathsf{K}\ell}, l:\lfloor \Phi \rfloor,\texttt{c}:(\lfloor \Gamma \rfloor, \lceil \Delta \rceil);\lfloor \Gamma' \rfloor,\lceil \Delta' \rceil \Uparrow \cdot$
is provable in
$\vdash \omega:\mathcal{T}_{\mathsf{K}\ell}, l:\lfloor \Phi \rfloor,\texttt{c}:(\lfloor \Gamma \rfloor, \lceil \Delta \rceil);\lfloor \Gamma' \rfloor,\lceil \Delta' \rceil \Uparrow \cdot$
is provable in
 $\mathsf{LNS}_\mathsf{FMLL}$
then the sequent
$\mathsf{LNS}_\mathsf{FMLL}$
then the sequent
 $\Box\Phi, \Gamma,\Gamma'\vdash \Delta,\Delta'$
is provable in
$\Box\Phi, \Gamma,\Gamma'\vdash \Delta,\Delta'$
is provable in
 $\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
.
$\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
.
Proof. Consider the following derivation.

The context
![]() $\Theta$
can be split into:
$\Theta$
can be split into:
![]() $\Theta(j)$
with subexponentials not related to l;
$\Theta(j)$
with subexponentials not related to l;
![]() $\Theta(k)$
containing subexponentials without
$\Theta(k)$
containing subexponentials without
![]() $\mathsf{4}$
;
$\mathsf{4}$
;
![]() $\Theta(4)$
containing subexponentials with
$\Theta(4)$
containing subexponentials with
![]() $\mathsf{4}$
and without
$\mathsf{4}$
and without
![]() $\mathsf{T}$
; and
$\mathsf{T}$
; and
![]() $\Theta(t4)$
is a context with subexponentials featuring both
$\Theta(t4)$
is a context with subexponentials featuring both
![]() $\mathsf{4}$
and
$\mathsf{4}$
and
![]() $\mathsf{T}$
. The context
$\mathsf{T}$
. The context
![]() $\Theta(j)$
contains all the right formulas, together with all the left formulas in contexts not related to i that will be “forgotten” after the application of the release rule; using the rule
$\Theta(j)$
contains all the right formulas, together with all the left formulas in contexts not related to i that will be “forgotten” after the application of the release rule; using the rule ![]() , the formulas in context
, the formulas in context
![]() $\Theta(4)$
are moved to the next component and the axiom
$\Theta(4)$
are moved to the next component and the axiom
![]() $\mathsf{T}$
is added. Using the same rule, the context
$\mathsf{T}$
is added. Using the same rule, the context
![]() $\Theta(t4)$
remains the same when passing to the next component. Moreover, the formulas in the context
$\Theta(t4)$
remains the same when passing to the next component. Moreover, the formulas in the context
![]() $\Theta(k)$
are moved without the box and then, stored in the subexponential
$\Theta(k)$
are moved without the box and then, stored in the subexponential
![]() $\texttt{c}$
(notation
$\texttt{c}$
(notation
![]() $\Theta(\texttt{c}/k)$
). Derivation
$\Theta(\texttt{c}/k)$
). Derivation
![]() $\pi$
continues by using
$\pi$
continues by using
![]() $\mathsf{neg}_\texttt{c}$
and storing
$\mathsf{neg}_\texttt{c}$
and storing
![]() $\lceil A \rceil$
in the context
$\lceil A \rceil$
in the context
![]() $\texttt{c}$
. This derivation adequately captures the behavior of
$\texttt{c}$
. This derivation adequately captures the behavior of
![]() $\Box$
in the logic
$\Box$
in the logic
![]() $\mathsf{LNS}_{\ell}$
.
$\mathsf{LNS}_{\ell}$
. ![]()
It is worth noticing the modularity of the encodings: all the modal systems have exactly the same encoding, only differing on the meta-level modality. This is a direct consequence of locality, granted by
![]() $\mathsf{LNS}$
. Therefore, we are able to spot the core characteristics of the logical systems, allowing punctual actions to be taken at the meta-level. This opens the possibility of being able to adequately encode a larger class of modal systems inside
$\mathsf{LNS}$
. Therefore, we are able to spot the core characteristics of the logical systems, allowing punctual actions to be taken at the meta-level. This opens the possibility of being able to adequately encode a larger class of modal systems inside
![]() $\mathsf{LNS}_\mathsf{FMLL}$
. For instance, if we are considering a (modal) substructural logic where formulas not necessarily behave classically, it suffices to remove
$\mathsf{LNS}_\mathsf{FMLL}$
. For instance, if we are considering a (modal) substructural logic where formulas not necessarily behave classically, it suffices to remove
![]() $\mathsf{pos}$
and/or
$\mathsf{pos}$
and/or
![]() $\mathsf{neg}$
accordingly and decree that
$\mathsf{neg}$
accordingly and decree that
![]() $\mathsf{U} \not\subset \mathcal{U}(l)$
for the context l storing left boxed formulas.
$\mathsf{U} \not\subset \mathcal{U}(l)$
for the context l storing left boxed formulas.
The method proposed here is also adequate for specifying simply dependent multimodal OL logics (see Definition 3). For each
![]() $i\in N$
, we consider a subexponential
$i\in N$
, we consider a subexponential
![]() $l_i$
and decree that
$l_i$
and decree that
![]() $l_i\preceq l_j$
iff
$l_i\preceq l_j$
iff
![]() $i \preccurlyeq j$
(and hence,
$i \preccurlyeq j$
(and hence, ![]() ). Moreover,
). Moreover,
![]() $\mathcal{U}(l_i)=f(i)$
. That is, each modal behavior specified by the indices in N is mapped to a subexponential with the same modal behavior. The system
$\mathcal{U}(l_i)=f(i)$
. That is, each modal behavior specified by the indices in N is mapped to a subexponential with the same modal behavior. The system
![]() $\mathsf{LNS}_{(N,\preccurlyeq,f)}$
can be then specified in
$\mathsf{LNS}_{(N,\preccurlyeq,f)}$
can be then specified in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
as the theory
$\mathsf{LNS}_\mathsf{FMLL}$
as the theory
![]() $\mathcal{T}_{\mathsf{K}\ell_N}$
as we did before for the one-modality case but considering a clause
$\mathcal{T}_{\mathsf{K}\ell_N}$
as we did before for the one-modality case but considering a clause
![]() $\Box_{L_i}$
(Figure 9) for each
$\Box_{L_i}$
(Figure 9) for each
![]() $i\in N$
. As expected, this clause stores F in the context
$i\in N$
. As expected, this clause stores F in the context
![]() $l_i$
when the atom
$l_i$
when the atom
![]() $\lfloor \Box_i F \rfloor$
is present in the linear or subexponential context. Similarly, we have an instance of
$\lfloor \Box_i F \rfloor$
is present in the linear or subexponential context. Similarly, we have an instance of
![]() $\Box_{R_i}$
in Figure 9 for each
$\Box_{R_i}$
in Figure 9 for each
![]() $i\in N$
that starts a subexponential phase indexed with
$i\in N$
that starts a subexponential phase indexed with
![]() $l_i$
.
$l_i$
.
Theorem 4.4. (Adequacy of multimodal systems)
![]() $\mathcal{T}_{\mathsf{K}\ell_N}$
is adequate FCP w.r.t.
$\mathcal{T}_{\mathsf{K}\ell_N}$
is adequate FCP w.r.t.
![]() $\mathsf{LNS}^{\texttt{S}}_{(N,\preccurlyeq,f)}$
.
$\mathsf{LNS}^{\texttt{S}}_{(N,\preccurlyeq,f)}$
.
-
(1) Soundness: If the sequent
 $\{\Box_{i}\Phi_i\},\Gamma \vdash \Delta$
is provable in
$\{\Box_{i}\Phi_i\},\Gamma \vdash \Delta$
is provable in
 $\mathsf{LNS}^{\texttt{S}}_{(N,\preccurlyeq,f)}$
then the sequent
$\mathsf{LNS}^{\texttt{S}}_{(N,\preccurlyeq,f)}$
then the sequent
 $\vdash \omega:\mathcal{T}_{\mathsf{K}\ell_N}, \{l_i: \lfloor \Phi_i \rfloor\},\texttt{c}: (\lfloor \Gamma \rfloor,\lceil \Delta \rceil);\cdot \Uparrow \cdot$
is provable in
$\vdash \omega:\mathcal{T}_{\mathsf{K}\ell_N}, \{l_i: \lfloor \Phi_i \rfloor\},\texttt{c}: (\lfloor \Gamma \rfloor,\lceil \Delta \rceil);\cdot \Uparrow \cdot$
is provable in
 $\mathsf{LNS}_\mathsf{FMLL}$
.
$\mathsf{LNS}_\mathsf{FMLL}$
. -
(2) Completeness: If the sequent
 $\vdash \omega:\mathcal{T}_{\mathsf{K}\ell_N}, \{l_i: \lfloor \Phi_i \rfloor\},\texttt{c}:(\lfloor \Gamma \rfloor, \lceil \Delta \rceil);\lfloor \Gamma' \rfloor,\lceil \Delta' \rceil \Uparrow \cdot$
is provable in
$\vdash \omega:\mathcal{T}_{\mathsf{K}\ell_N}, \{l_i: \lfloor \Phi_i \rfloor\},\texttt{c}:(\lfloor \Gamma \rfloor, \lceil \Delta \rceil);\lfloor \Gamma' \rfloor,\lceil \Delta' \rceil \Uparrow \cdot$
is provable in
 $\mathsf{LNS}_\mathsf{FMLL}$
then the sequent
$\mathsf{LNS}_\mathsf{FMLL}$
then the sequent
 $\{\Box_{i}\Phi_i\}, \Gamma,\Gamma'\vdash \Delta,\Delta'$
is provable in
$\{\Box_{i}\Phi_i\}, \Gamma,\Gamma'\vdash \Delta,\Delta'$
is provable in
 $\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
.
$\mathsf{LNS}^{\texttt{S}}_{\mathsf{K}\ell}$
.
Let us give a further example comparing derivations in the object- and meta-systems. In particular, we illustrate the reason of the apparently missing clause encoding the modal rule
![]() $\mathsf{T}$
, and the advantage, from the proof search perspective, of the stricter control of the modal rules in Figure 5, where applications of the rule
$\mathsf{T}$
, and the advantage, from the proof search perspective, of the stricter control of the modal rules in Figure 5, where applications of the rule
![]() $\mathsf{K}$
on a subexponential with
$\mathsf{K}$
on a subexponential with
![]() $\mathsf{4}$
are not allowed.
$\mathsf{4}$
are not allowed.
Example 4.1. Consider the following OL-derivations:

The underlying system in the first (resp. second) derivation is
![]() $\mathsf{LNS}_{\mathsf{K} \mathsf{T}}$
(resp.
$\mathsf{LNS}_{\mathsf{K} \mathsf{T}}$
(resp.
![]() $\mathsf{LNS}_{\mathsf{K} \mathsf{4}}$
). Below we show the corresponding meta-level derivations in the system
$\mathsf{LNS}_{\mathsf{K} \mathsf{4}}$
). Below we show the corresponding meta-level derivations in the system
![]() $\mathsf{LNS}_\mathsf{FMLL}$
. For simplicity, we omit the context
$\mathsf{LNS}_\mathsf{FMLL}$
. For simplicity, we omit the context
![]() $\omega$
containing the theory with the clauses of each system, and we do not use
$\omega$
containing the theory with the clauses of each system, and we do not use
![]() $\mathsf{pos}/\mathsf{neg}$
, keeping the
$\mathsf{pos}/\mathsf{neg}$
, keeping the
![]() $\lfloor \cdot \rfloor,\lceil \cdot \rceil$
atoms in the linear context:
$\lfloor \cdot \rfloor,\lceil \cdot \rceil$
atoms in the linear context:

It is worth noticing that we do not have an explicit clause for capturing the modal rule
![]() $\mathsf{T}$
. Instead, by storing the formula
$\mathsf{T}$
. Instead, by storing the formula
![]() $\lfloor A \supset B \rfloor$
into the context t, such atom can be used in the current context by applying the rule
$\lfloor A \supset B \rfloor$
into the context t, such atom can be used in the current context by applying the rule
![]() $\mathsf{I_s}$
, as in the leftmost leaf in the first derivation.
$\mathsf{I_s}$
, as in the leftmost leaf in the first derivation.
In the second meta-level derivation there is no explicit contraction, unlike in the OL derivation. The reason is the neater control of the rules for
![]() $\mathsf{4}$
and
$\mathsf{4}$
and
![]() $\mathsf{K}$
in
$\mathsf{K}$
in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
. Note that the formula
$\mathsf{LNS}_\mathsf{FMLL}$
. Note that the formula
![]() $\lfloor A \rfloor$
, after the application of
$\lfloor A \rfloor$
, after the application of
![]() $[\Box_R]$
, is located at
$[\Box_R]$
, is located at
![]() $4+$
. Due to the presence of
$4+$
. Due to the presence of
![]() $\mathsf{T}$
in
$\mathsf{T}$
in
![]() $4+$
, the left most application of
$4+$
, the left most application of
![]() $[\mathsf{init}]$
is valid. This branch of the derivation simulates the application of the rule
$[\mathsf{init}]$
is valid. This branch of the derivation simulates the application of the rule
![]() $\mathsf{K}$
at the object level. The topmost application of
$\mathsf{K}$
at the object level. The topmost application of
![]() $[\Box_R]$
(with the corresponding applications of
$[\Box_R]$
(with the corresponding applications of
![]() $?^4_\mathsf{4}$
) simulates the application of
$?^4_\mathsf{4}$
) simulates the application of
![]() $\mathsf{4}$
at the object level.
$\mathsf{4}$
at the object level.
The current version of the companion Coq library of this paper contains the mechanization of some of the adequacy results presented in this section. For each OL, there is a separated directory defining the derivability relation of the corresponding logic as an inductive proposition. Then, the clauses of the
![]() $\mathsf{MMLL}$
theory are introduced and the adequacy theorem is established. Defined tactics allow for some automation when dealing with the bipoles in the theory. In some cases, such tactics complete the decomposition of the bipole once the terms substituting the existential quantified variables have been chosen. For the time being of this publication, the adequacy results for classical (Theorem 4.1) and intuitionistic (Theorem 4.2) logics have been mechanized, as well as the instance
$\mathsf{MMLL}$
theory are introduced and the adequacy theorem is established. Defined tactics allow for some automation when dealing with the bipoles in the theory. In some cases, such tactics complete the decomposition of the bipole once the terms substituting the existential quantified variables have been chosen. For the time being of this publication, the adequacy results for classical (Theorem 4.1) and intuitionistic (Theorem 4.2) logics have been mechanized, as well as the instance
![]() $\ell=\{\mathsf{T},\mathsf{4}\}$
(i.e., the modal logic
$\ell=\{\mathsf{T},\mathsf{4}\}$
(i.e., the modal logic
![]() $\mathsf{S4}$
) for Theorem 4.3.
$\mathsf{S4}$
) for Theorem 4.3.
5. Cut Admissibility for Object Logics
In the previous section, we showed how to adequately encode a logical systems
![]() $\mathcal{L}$
as an
$\mathcal{L}$
as an
![]() $\mathsf{MMLL}$
theory
$\mathsf{MMLL}$
theory
![]() $\mathcal{T}_{\mathcal{L}}$
. In this section, we introduce clauses that adequately capture the cut rule at the object level, leading to the theory
$\mathcal{T}_{\mathcal{L}}$
. In this section, we introduce clauses that adequately capture the cut rule at the object level, leading to the theory
![]() $\mathcal{T}_{\mathcal{L}+\mathsf{cut}}$
. More interestingly, if the encoding satisfies a condition called cut-coherence, then both
$\mathcal{T}_{\mathcal{L}+\mathsf{cut}}$
. More interestingly, if the encoding satisfies a condition called cut-coherence, then both
![]() $\mathcal{T}_{\mathcal{L}}$
and
$\mathcal{T}_{\mathcal{L}}$
and
![]() $\mathcal{T}_{\mathcal{L}+\mathsf{cut}}$
prove the same (encoded) sequents, thus showing that the cut rule is admissible at the object level. This result is proved by relying on the meta-theory of
$\mathcal{T}_{\mathcal{L}+\mathsf{cut}}$
prove the same (encoded) sequents, thus showing that the cut rule is admissible at the object level. This result is proved by relying on the meta-theory of
![]() $\mathsf{MMLL}$
. As we shall see, testing cut-coherence is straightforward and hence,
$\mathsf{MMLL}$
. As we shall see, testing cut-coherence is straightforward and hence,
![]() $\mathsf{LNS}_\mathsf{FMLL}$
becomes a suitable logical framework for proving analyticity for a large class of systems, including several well known modal logical systems and also multi- and substructural-modal logics.
$\mathsf{LNS}_\mathsf{FMLL}$
becomes a suitable logical framework for proving analyticity for a large class of systems, including several well known modal logical systems and also multi- and substructural-modal logics.
We start by setting some requirements that OLs should comply in order to be amenable for the
![]() $\mathsf{MMLL}$
specification.
$\mathsf{MMLL}$
specification.
Definition 6. (Canonical-bipoles) A
![]() $\mathsf{MMLL}$
-formula is a bipole (Andreoli Reference Andreoli1992) if no positive connective is in the scope of a negative one, bangs have negative scope while question marks have atomic scope. A
$\mathsf{MMLL}$
-formula is a bipole (Andreoli Reference Andreoli1992) if no positive connective is in the scope of a negative one, bangs have negative scope while question marks have atomic scope. A
![]() $\mathsf{MMLL}$
-formula F is a canonical-bipole if F is a bipole built from
$\mathsf{MMLL}$
-formula F is a canonical-bipole if F is a bipole built from
![]() $\mathsf{MMLL}$
connectives and atomic formulas of the shape
$\mathsf{MMLL}$
connectives and atomic formulas of the shape
![]() $\lceil G \rceil,\lfloor G \rfloor$
where G is an OL-formula.
$\lceil G \rceil,\lfloor G \rfloor$
where G is an OL-formula.
Observe that all the clauses introducing connectives in Figures 7 and 9 have the shape
![]() $\exists \overline{F}. (H^\perp \otimes G)$
, where H is atomic and G a canonical-bipole,
$\exists \overline{F}. (H^\perp \otimes G)$
, where H is atomic and G a canonical-bipole, ![]() and
and ![]() . As seen in Section 4, focusing on this kind of formulas produces specific and controlled shapes of derivations in
. As seen in Section 4, focusing on this kind of formulas produces specific and controlled shapes of derivations in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
.
$\mathsf{LNS}_\mathsf{FMLL}$
.
Requirement 5.1. (Canonical theories and encodings). Let
![]() $\mathcal{C}$
be the set of connectives of the object logic
$\mathcal{C}$
be the set of connectives of the object logic
![]() $\mathcal{L}$
. The encoding of
$\mathcal{L}$
. The encoding of
![]() $\mathcal{L}$
as an
$\mathcal{L}$
as an
![]() $\mathsf{MMLL}$
theory is a pair of functions
$\mathsf{MMLL}$
theory is a pair of functions ![]() and
and ![]() from
from
![]() $\mathcal{C}$
to
$\mathcal{C}$
to
![]() $\mathsf{MMLL}$
canonical-bipoles. The encoding of left and right introduction rules for a given n-ary connective
$\mathsf{MMLL}$
canonical-bipoles. The encoding of left and right introduction rules for a given n-ary connective
![]() $\star\in\mathcal{C}$
is defined as, respectively
$\star\in\mathcal{C}$
is defined as, respectively
The canonical theory for
![]() $\mathcal{L}$
is the least set
$\mathcal{L}$
is the least set
![]() $\mathcal{T}_\mathcal{L}$
s.t. (1) for each
$\mathcal{T}_\mathcal{L}$
s.t. (1) for each
![]() $\star \in \mathcal{C}$
,
$\star \in \mathcal{C}$
, ![]() ; (2)
; (2)
![]() $\mathsf{pos}_i,\mathsf{neg}_j$
may belong to
$\mathsf{pos}_i,\mathsf{neg}_j$
may belong to
![]() $\mathcal{T}_\mathcal{L}$
; and (3)
$\mathcal{T}_\mathcal{L}$
; and (3)
![]() $\mathsf{init} \in\mathcal{T}_\mathcal{L}$
(see Figure 7). Moreover, the theory
$\mathsf{init} \in\mathcal{T}_\mathcal{L}$
(see Figure 7). Moreover, the theory
![]() $\mathcal{T}_\mathcal{L}$
must be adequate for the OL
$\mathcal{T}_\mathcal{L}$
must be adequate for the OL
![]() $\mathcal{L}$
: a sequent is provable in
$\mathcal{L}$
: a sequent is provable in
![]() $\mathcal{L}$
iff its encoding is provable in
$\mathcal{L}$
iff its encoding is provable in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
with the clauses
$\mathsf{LNS}_\mathsf{FMLL}$
with the clauses
![]() $\mathcal{T}_\mathcal{L}$
.
$\mathcal{T}_\mathcal{L}$
.
In words,
![]() $\mathcal{T}_{\mathcal{L}}$
includes the encoding of left and right introduction rules as well as the initial rule. Depending on the structural behavior of the OL,
$\mathcal{T}_{\mathcal{L}}$
includes the encoding of left and right introduction rules as well as the initial rule. Depending on the structural behavior of the OL,
![]() $\mathcal{T}_{\mathcal{L}} $
may include also the encoding of the rules for weakening and contraction. As already shown in the previous section, the encoded inference rules determine completely the shape of derivations in
$\mathcal{T}_{\mathcal{L}} $
may include also the encoding of the rules for weakening and contraction. As already shown in the previous section, the encoded inference rules determine completely the shape of derivations in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
. Also, we have showed that the proposed encodings are adequate.
$\mathsf{LNS}_\mathsf{FMLL}$
. Also, we have showed that the proposed encodings are adequate.
Regarding the specification of structural rules via
![]() $\mathsf{pos}_i$
and
$\mathsf{pos}_i$
and
![]() $\mathsf{neg}_j$
clauses, recall that, in intuitionistic and modal systems, the right formulas never move between components. This explains why
$\mathsf{neg}_j$
clauses, recall that, in intuitionistic and modal systems, the right formulas never move between components. This explains why
![]() $\mathsf{neg}$
should be instantiated with
$\mathsf{neg}$
should be instantiated with
![]() $\texttt{c}$
. Hence, as an invariant, the use of the rules in the theory
$\texttt{c}$
. Hence, as an invariant, the use of the rules in the theory
![]() $\mathcal{T}_\mathcal{L}$
can only store atoms of the form
$\mathcal{T}_\mathcal{L}$
can only store atoms of the form
![]() $\lceil F \rceil$
in the context
$\lceil F \rceil$
in the context
![]() $\texttt{c}$
(if
$\texttt{c}$
(if
![]() $\mathsf{neg}_\texttt{c}$
is part of the theory).
$\mathsf{neg}_\texttt{c}$
is part of the theory).
In
![]() $\mathsf{LNS}_{\mathsf{I}}$
, left formulas can always be moved to the next component. Moreover, besides
$\mathsf{LNS}_{\mathsf{I}}$
, left formulas can always be moved to the next component. Moreover, besides
![]() $\texttt{c}$
and
$\texttt{c}$
and
![]() $\omega$
, the encoding requires only an extra subexponential: t4 (Theorem 4.2). Hence,
$\omega$
, the encoding requires only an extra subexponential: t4 (Theorem 4.2). Hence,
![]() $\mathsf{pos}_i$
is instantiated with t4. On the other hand, in modal systems, only boxed formulas on the left can be moved between components. Hence, in these logical systems,
$\mathsf{pos}_i$
is instantiated with t4. On the other hand, in modal systems, only boxed formulas on the left can be moved between components. Hence, in these logical systems,
![]() $\mathsf{pos}_i$
must be instantiated with
$\mathsf{pos}_i$
must be instantiated with
![]() $i=\texttt{c}$
(and unboxed formulas cannot be moved between components).
$i=\texttt{c}$
(and unboxed formulas cannot be moved between components).
In any case, the following technical requirement, needed in the proof of Theorem 5.2, is valid.
Requirement 5.2. (
![]() $\mathsf{pos}$
and
$\mathsf{pos}$
and
![]() $\mathsf{neg}$
) If
$\mathsf{neg}$
) If
![]() $\mathsf{neg}_j \in \mathcal{T}_\mathcal{L}$
then
$\mathsf{neg}_j \in \mathcal{T}_\mathcal{L}$
then
![]() $j=\texttt{c}$
. Moreover, if
$j=\texttt{c}$
. Moreover, if
![]() $\mathsf{pos}_i \in \mathcal{T}_\mathcal{L}$
then
$\mathsf{pos}_i \in \mathcal{T}_\mathcal{L}$
then
![]() $\{\mathsf{C},\mathsf{W},\mathsf{T}\}\subseteq\mathcal{U}(i)$
and either: (1)
$\{\mathsf{C},\mathsf{W},\mathsf{T}\}\subseteq\mathcal{U}(i)$
and either: (1)
![]() $i=\texttt{c}$
or (2)
$i=\texttt{c}$
or (2)
![]() $i \neq \texttt{c}$
and
$i \neq \texttt{c}$
and
![]() $i \preceq m$
for all
$i \preceq m$
for all
![]() $m\in\mathcal{I},m\neq \texttt{c}$
.
$m\in\mathcal{I},m\neq \texttt{c}$
.
5.1 Cut rules, cut coherence, and admissibility of cut
The (multiplicative) OL-cut rule can be specified as the bipole
![]() $\mathsf{cut} = \exists F. (\lfloor F \rfloor \otimes \lceil F \rceil)$
. In fact, focusing on that formula mimics exactly the behavior of the cut rule at the object level:
$\mathsf{cut} = \exists F. (\lfloor F \rfloor \otimes \lceil F \rceil)$
. In fact, focusing on that formula mimics exactly the behavior of the cut rule at the object level:

We shall use
![]() $\mathsf{cut}_n$
to denote the rule
$\mathsf{cut}_n$
to denote the rule
![]() $\mathsf{cut}$
applied to (OL-) formulas of size strictly smaller than n. For instance, if
$\mathsf{cut}$
applied to (OL-) formulas of size strictly smaller than n. For instance, if
![]() $G = G_1 \star G_2$
, a valid application of
$G = G_1 \star G_2$
, a valid application of
![]() $\mathsf{cut}_{|G|}$
can instantiate the existentially quantified variable F in
$\mathsf{cut}_{|G|}$
can instantiate the existentially quantified variable F in
![]() $\mathsf{cut}$
with either
$\mathsf{cut}$
with either
![]() $G_1$
or
$G_1$
or
![]() $G_2$
(but not with G).
$G_2$
(but not with G).
Using the formulas
![]() $\mathsf{cut}$
and
$\mathsf{cut}$
and
![]() $\mathsf{init}$
, we can prove that
$\mathsf{init}$
, we can prove that
![]() $\lfloor \cdot \rfloor$
and
$\lfloor \cdot \rfloor$
and
![]() $\lceil \cdot \rceil$
are duals in the sense that the
$\lceil \cdot \rceil$
are duals in the sense that the
![]() $\mathsf{LNS}_\mathsf{FMLL}$
sequent
$\mathsf{LNS}_\mathsf{FMLL}$
sequent
![]() $\vdash \omega:\{\mathsf{cut},\mathsf{init}\}; \Uparrow \lfloor F \rfloor \equiv \lceil F \rceil^\perp$
is provable. More interestingly, this duality can be generalized to the right and left bodies of OL rules as well. More precisely,
$\vdash \omega:\{\mathsf{cut},\mathsf{init}\}; \Uparrow \lfloor F \rfloor \equiv \lceil F \rceil^\perp$
is provable. More interestingly, this duality can be generalized to the right and left bodies of OL rules as well. More precisely,
Definition 7. (Cut coherence). Let
![]() $\mathcal{T}_\mathcal{L}$
be the canonical theory of the OL
$\mathcal{T}_\mathcal{L}$
be the canonical theory of the OL
![]() $\mathcal{L}$
. We say that
$\mathcal{L}$
. We say that
![]() $\mathcal{T}_\mathcal{L}$
is cut-coherent if, for each connective
$\mathcal{T}_\mathcal{L}$
is cut-coherent if, for each connective
![]() $\star \in \mathcal{C}$
, and
$\star \in \mathcal{C}$
, and
![]() $F=\star(F_1,...,F_n)$
, the sequent below is provable
$F=\star(F_1,...,F_n)$
, the sequent below is provable
Theorem 5.1. All the encodings in Section 4 are cut coherent.
Proof. Proving this kind of sequents in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
is almost immediate. Here the example for the encoding of the rules introducing
$\mathsf{LNS}_\mathsf{FMLL}$
is almost immediate. Here the example for the encoding of the rules introducing
![]() $\Box$
in the logic
$\Box$
in the logic
![]() $\mathsf{K}$
:
$\mathsf{K}$
:

Note that
![]() $\mathsf{cut}$
is instantiated with F (a subformula of
$\mathsf{cut}$
is instantiated with F (a subformula of
![]() $\Box F$
).
$\Box F$
).
We now state the main result of the section. Consider two cut-free proof derivations from the object-level point of view (i.e., using only
![]() $\mathcal{T}_\mathcal{L}$
) introducing the cut formula F. It is possible to prove the same sequent using the rule
$\mathcal{T}_\mathcal{L}$
) introducing the cut formula F. It is possible to prove the same sequent using the rule
![]() $\mathsf{cut}$
(at the object-level) with strict subformulas of F.
$\mathsf{cut}$
(at the object-level) with strict subformulas of F.
Theorem 5.2. (OL cut admissibility). Let
![]() $\mathcal{T}_\mathcal{L}$
be the canonical theory of a given OL
$\mathcal{T}_\mathcal{L}$
be the canonical theory of a given OL
![]() $\mathcal{L}$
,
$\mathcal{L}$
,
![]() $\Gamma,\Delta$
be multisets,
$\Gamma,\Delta$
be multisets,
![]() $\Theta_1,\Theta_2$
bounded and
$\Theta_1,\Theta_2$
bounded and
![]() $\Lambda$
unbounded subexponential contexts containing only atoms of the form
$\Lambda$
unbounded subexponential contexts containing only atoms of the form
![]() $\lceil \cdot \rceil$
and
$\lceil \cdot \rceil$
and
![]() $\lfloor \cdot \rfloor$
. If the sequents
$\lfloor \cdot \rfloor$
. If the sequents
![]() $\vdash \omega:\mathcal{T}_\mathcal{L}, \Lambda,\Theta_1;\Gamma,\lfloor F \rfloor \Uparrow \cdot$
and
$\vdash \omega:\mathcal{T}_\mathcal{L}, \Lambda,\Theta_1;\Gamma,\lfloor F \rfloor \Uparrow \cdot$
and
![]() $\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_2;\Delta,\lceil F \rceil \Uparrow \cdot$
are both provable, then the sequent
$\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_2;\Delta,\lceil F \rceil \Uparrow \cdot$
are both provable, then the sequent
![]() $\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|}\},\Lambda,\Theta_1,\Theta_2;\Gamma,\Delta \Uparrow \cdot$
is also provable.
$\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|}\},\Lambda,\Theta_1,\Theta_2;\Gamma,\Delta \Uparrow \cdot$
is also provable.
Proof. When the theory includes the structural rules
![]() $\mathsf{pos}_i$
and/or
$\mathsf{pos}_i$
and/or
![]() $\mathsf{neg}_\texttt{c}$
, the proof of this theorem requires to count the number of times a formula stored in a unbounded subexponential context is used in a derivation. Since this is difficult to formalize, we introduce two additional clauses (depending on the structural behavior of the OL at hand):
$\mathsf{neg}_\texttt{c}$
, the proof of this theorem requires to count the number of times a formula stored in a unbounded subexponential context is used in a derivation. Since this is difficult to formalize, we introduce two additional clauses (depending on the structural behavior of the OL at hand):
-
(a)
 (when both
(when both
 $\mathsf{pos}_i$
and
$\mathsf{pos}_i$
and
 $\mathsf{neg}_\texttt{c}$
are present)
$\mathsf{neg}_\texttt{c}$
are present) -
(b)
 (when only
(when only
 $\mathsf{pos}_i$
is present)
$\mathsf{pos}_i$
is present)
We will write
![]() $\mathsf{cutC}_n, \mathsf{cutN}_n$
to denote the rules
$\mathsf{cutC}_n, \mathsf{cutN}_n$
to denote the rules
![]() $\mathsf{cutC}, \mathsf{cutN}$
applied to (OL) formulas of size strictly smaller than n. Observe that, in the presence of the corresponding structural rules,
$\mathsf{cutC}, \mathsf{cutN}$
applied to (OL) formulas of size strictly smaller than n. Observe that, in the presence of the corresponding structural rules,
![]() $\mathsf{cutC}$
and
$\mathsf{cutC}$
and
![]() $\mathsf{cutN}$
are equivalent to
$\mathsf{cutN}$
are equivalent to
![]() $\mathsf{cut}$
(remember that with
$\mathsf{cut}$
(remember that with
![]() $\mathsf{pos}_i$
, it is possible to prove the equivalences
$\mathsf{pos}_i$
, it is possible to prove the equivalences ![]() and
and ![]() ).
).
Assume that the OL features both,
![]() $\mathsf{pos}_i$
and
$\mathsf{pos}_i$
and
![]() $\mathsf{neg}_\texttt{c}$
. Hence, we consider the rules
$\mathsf{neg}_\texttt{c}$
. Hence, we consider the rules
![]() $\mathsf{cut}$
and
$\mathsf{cut}$
and
![]() $\mathsf{cutC}$
and we show, simultaneously, both:
$\mathsf{cutC}$
and we show, simultaneously, both:
-
(1) if
 $\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_1;\Omega,\lfloor F \rfloor \Uparrow \cdot$
and
$\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_1;\Omega,\lfloor F \rfloor \Uparrow \cdot$
and
 $\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_2;\Psi,\lceil F \rceil \Uparrow \cdot$
are both provable then the sequent
$\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_2;\Psi,\lceil F \rceil \Uparrow \cdot$
are both provable then the sequent
 $\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|},\mathsf{cutC}_{|F|}\},\Lambda,\Theta_1,\Theta_2;\Omega,\Psi \Uparrow \cdot$
is also provable; and
$\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|},\mathsf{cutC}_{|F|}\},\Lambda,\Theta_1,\Theta_2;\Omega,\Psi \Uparrow \cdot$
is also provable; and -
(2) if
 $\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_1,i:\lfloor F \rfloor;\Omega \Uparrow \cdot$
and
$\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_1,i:\lfloor F \rfloor;\Omega \Uparrow \cdot$
and
 $\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_2,\texttt{c}:\lceil F \rceil;\Psi \Uparrow \cdot$
are both provable then the sequent
$\vdash \omega:\mathcal{T}_\mathcal{L},\Lambda,\Theta_2,\texttt{c}:\lceil F \rceil;\Psi \Uparrow \cdot$
are both provable then the sequent
 $\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|},\mathsf{cutC}_{|F|}\},\Lambda,\Theta_1,\Theta_2;\Omega,\Psi \Uparrow \cdot$
is also provable.
$\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|},\mathsf{cutC}_{|F|}\},\Lambda,\Theta_1,\Theta_2;\Omega,\Psi \Uparrow \cdot$
is also provable.
In the proof of (1), if the structural rules are used on
![]() $\lfloor F \rfloor$
or
$\lfloor F \rfloor$
or
![]() $\lceil F \rceil$
, we produce a shorter derivation with (2), i.e., with
$\lceil F \rceil$
, we produce a shorter derivation with (2), i.e., with
![]() $\mathsf{cutC}$
.
$\mathsf{cutC}$
.
For the proof of (2), consider the case where
![]() $\lfloor F \rfloor$
and
$\lfloor F \rfloor$
and
![]() $\lceil F \rceil$
are principal in both premises thus using, respectively, the left and right introduction rules for the same connective:
$\lceil F \rceil$
are principal in both premises thus using, respectively, the left and right introduction rules for the same connective:

Here, ![]() means that the existential quantifiers of the clause were instantiated with the formula F. As we already know, the bodies
means that the existential quantifiers of the clause were instantiated with the formula F. As we already know, the bodies ![]() and
and ![]() produce well controlled forms of derivations. They can either end the proof (e.g., with the clause
produce well controlled forms of derivations. They can either end the proof (e.g., with the clause
![]() $\texttt{f}_{L}$
) or produce derivations with one or two premises.
$\texttt{f}_{L}$
) or produce derivations with one or two premises.
The resulting generated premises, after focusing on the body of the clause, can only add new atoms to the linear or classical context before ending the negative phase. For simplicity, consider that both
![]() $\pi$
and
$\pi$
and
![]() $\pi'$
produce one premise. We then have
$\pi'$
produce one premise. We then have
-
–
 $\Pi$
produces a sequent of the form
$\Pi$
produces a sequent of the form
 $\vdash \omega:\mathcal{T}_\mathcal{L}, \Lambda',\Theta_1', i:\lfloor F \rfloor;\Omega' \Uparrow \cdot$
.
$\vdash \omega:\mathcal{T}_\mathcal{L}, \Lambda',\Theta_1', i:\lfloor F \rfloor;\Omega' \Uparrow \cdot$
. -
–
 $\Pi'$
produces a sequent of the form
$\Pi'$
produces a sequent of the form
 $\vdash \omega:\mathcal{T}_\mathcal{L}, \Lambda'',\Theta_2', \texttt{c}:\lceil F \rceil;\Psi' \Uparrow \cdot$
.
$\vdash \omega:\mathcal{T}_\mathcal{L}, \Lambda'',\Theta_2', \texttt{c}:\lceil F \rceil;\Psi' \Uparrow \cdot$
.
The primed contexts are extensions of the original ones with atoms of the form
![]() $\lfloor \cdot \rfloor,\lceil \cdot \rceil$
. By induction, the sequents:
$\lfloor \cdot \rfloor,\lceil \cdot \rceil$
. By induction, the sequents:
-
–
 $\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|},\mathsf{cutC}_{|F|}\},\Lambda',\Theta_1';\Omega' \Uparrow \cdot$
; and
$\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|},\mathsf{cutC}_{|F|}\},\Lambda',\Theta_1';\Omega' \Uparrow \cdot$
; and -
–
 $\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|},\mathsf{cutC}_{|F|}\}, \Lambda'',\Theta_2';\Psi' \Uparrow \cdot$
$\vdash \omega:\{\mathcal{T}_\mathcal{L},\mathsf{cut}_{|F|},\mathsf{cutC}_{|F|}\}, \Lambda'',\Theta_2';\Psi' \Uparrow \cdot$
are both provable. Hence, the sequents below are also provable:
-
–
 ; and
; and -
–
 .
.
At this point, we rely on cut coherence (see Definition 7) and cut admissibility in
![]() $\mathsf{LNS}_\mathsf{FMLL}$
:
$\mathsf{LNS}_\mathsf{FMLL}$
:

where
![]() $\mathcal{T} = \mathcal{T}_{\mathcal{L}} \cup \{\mathsf{cut}_{|F|}, \mathsf{cutC}_{|F|}\}$
.
$\mathcal{T} = \mathcal{T}_{\mathcal{L}} \cup \{\mathsf{cut}_{|F|}, \mathsf{cutC}_{|F|}\}$
.
Now let us illustrate a nonprincipal case involving modal behaviors. Consider a derivation where the left and right premises introduce, respectively, the modal formulas
![]() $G_n$
and
$G_n$
and
![]() $F_m$
$F_m$

where
![]() $\Gamma_F,\Delta_f$
(resp.
$\Gamma_F,\Delta_f$
(resp.
![]() $\Gamma_G,\Delta_G$
) represent the atomic subformulas appearing in the decomposition of
$\Gamma_G,\Delta_G$
) represent the atomic subformulas appearing in the decomposition of
![]() $\lceil F_m \rceil$
(resp.
$\lceil F_m \rceil$
(resp.
![]() $\lceil G_n \rceil$
). In each case, the subindices n and m denote the underlying modalities of these formulas. Note that n and m cannot be
$\lceil G_n \rceil$
). In each case, the subindices n and m denote the underlying modalities of these formulas. Note that n and m cannot be
![]() $\texttt{c}$
since modalities of the OL are not mapped to this index. Also,
$\texttt{c}$
since modalities of the OL are not mapped to this index. Also,
![]() $i\neq \texttt{c}$
, otherwise,
$i\neq \texttt{c}$
, otherwise,
![]() $\lfloor F_m \rfloor$
must be necessarily weakened in the left derivation (and the end sequent is provable by using
$\lfloor F_m \rfloor$
must be necessarily weakened in the left derivation (and the end sequent is provable by using
![]() $[G_n]$
). We then have
$[G_n]$
). We then have
![]() $n \preceq i$
and, by Requirement 5.2,
$n \preceq i$
and, by Requirement 5.2,
![]() $i \preceq n$
,
$i \preceq n$
,
![]() $i\preceq m$
and hence,
$i\preceq m$
and hence,
![]() $n \preceq m$
. Since
$n \preceq m$
. Since
![]() $\mathsf{T}\in \mathcal{U}(i)$
, such axiom is also present in n and m and Theorem 3.1 applies on the context
$\mathsf{T}\in \mathcal{U}(i)$
, such axiom is also present in n and m and Theorem 3.1 applies on the context
![]() $\Lambda,\Theta_i$
. We conclude that
$\Lambda,\Theta_i$
. We conclude that
![]() $\Lambda,\Theta_i\supseteq \{\Lambda,\Theta_i\}^{\succeq n} \supseteq \{\Lambda,\Theta_i\}^{\succeq m}$
and the resulting reduction is:
$\Lambda,\Theta_i\supseteq \{\Lambda,\Theta_i\}^{\succeq n} \supseteq \{\Lambda,\Theta_i\}^{\succeq m}$
and the resulting reduction is:

![]() $\Pi$
is obtained by Theorem 3.1 and
$\Pi$
is obtained by Theorem 3.1 and
![]() $\Psi$
is the same as the derivation introducing
$\Psi$
is the same as the derivation introducing
![]() $F_m$
but weakening the formulas in
$F_m$
but weakening the formulas in
![]() $\Gamma_G$
and
$\Gamma_G$
and
![]() $\Delta_G$
in the release rule.
$\Delta_G$
in the release rule.
Since for every OL formula F,
![]() $|F| > 0$
, by induction we conclude the following.
$|F| > 0$
, by induction we conclude the following.
Corollary 8. Let
![]() $\mathcal{T}_\mathcal{L}$
be the theory of a given OL
$\mathcal{T}_\mathcal{L}$
be the theory of a given OL
![]() $\mathcal{L}$
, and let
$\mathcal{L}$
, and let
![]() $\Psi$
be a multiset and
$\Psi$
be a multiset and
![]() $\Theta$
a subexponential context containing only atoms of the form
$\Theta$
a subexponential context containing only atoms of the form
![]() $\lceil \cdot \rceil$
and
$\lceil \cdot \rceil$
and
![]() $\lfloor \cdot \rfloor$
. The sequent
$\lfloor \cdot \rfloor$
. The sequent
![]() $\vdash \omega:\{\mathcal{T}_\mathcal{L}, \mathsf{cut}\},\Theta;\Psi \Uparrow \cdot$
is provable iff
$\vdash \omega:\{\mathcal{T}_\mathcal{L}, \mathsf{cut}\},\Theta;\Psi \Uparrow \cdot$
is provable iff
![]() $\vdash \omega:\mathcal{T}_\mathcal{L},\Theta;\Psi \Uparrow \cdot$
is provable.
$\vdash \omega:\mathcal{T}_\mathcal{L},\Theta;\Psi \Uparrow \cdot$
is provable.
The mechanization of Theorem 5.1 is unfortunately not feasible due to the impossibility of reasoning about derivations (see discussion in the end of Section 3). For instance, it is not possible to specify, in a general way, the number of premises resulting after the decomposition of a bipole. The current version of the library offers definitions, in the form of class types, for cut coherence of constants, connectives, and OL binders. Hence, the clauses encoding OL rules must be instances of such classes (thus satisfying cut coherence). The proof of OL cut admissibility, for each specific case, follows the proof shown above: the principal cases rely on cut coherence and cut-admissibility of
![]() $\mathsf{MMLL}$
. The current version of the repository exemplifies this procedure for classical and intuitionistic logics, as well as for the logic
$\mathsf{MMLL}$
. The current version of the repository exemplifies this procedure for classical and intuitionistic logics, as well as for the logic
![]() $\mathsf{S4}$
.
$\mathsf{S4}$
.
6. Discussion and Conclusion
In this paper, we have extended the sufficient criterion for cut admissibility of object logical systems given in Miller and Pimentel (Reference Miller and Pimentel2013). For that, we moved from
![]() $\mathsf{LL}$
to a variant of linear logic with subexponentials called
$\mathsf{LL}$
to a variant of linear logic with subexponentials called
![]() $\mathsf{MMLL}$
, where different modal behaviors were embodied into the subexponential connectives. This allowed to establish a simple yet powerful criterion – cut-coherence – for proving analyticity for a large class of systems. This criterion neatly captures the duality of inference rules. In fact, checking cut coherence is equivalent to checking
$\mathsf{MMLL}$
, where different modal behaviors were embodied into the subexponential connectives. This allowed to establish a simple yet powerful criterion – cut-coherence – for proving analyticity for a large class of systems. This criterion neatly captures the duality of inference rules. In fact, checking cut coherence is equivalent to checking ![]() , and vice versa. And this is the spirit of cut admissibility.
, and vice versa. And this is the spirit of cut admissibility.
We start the discussion by exploring the similarities and differences between
![]() $\mathsf{MMLL}$
and other
$\mathsf{MMLL}$
and other
![]() $\mathsf{LL}$
based frameworks. First of all, since
$\mathsf{LL}$
based frameworks. First of all, since
![]() $\mathsf{LL}$
is a resource conscious logic, it is natural representing OL rules as meta-level rewriting clauses. The proposal in Miller and Pimentel (Reference Miller and Pimentel2013) explores this in a very elegant way, with natural and direct encodings, together with an extremely simple sufficient condition for cut-admissibility of the specified OLs. For broadening the spectrum of systems amenable for specification, Nigam et al. (Reference Nigam, Pimentel and Reis2016) considered an extension of linear logic with subexponentials (
$\mathsf{LL}$
is a resource conscious logic, it is natural representing OL rules as meta-level rewriting clauses. The proposal in Miller and Pimentel (Reference Miller and Pimentel2013) explores this in a very elegant way, with natural and direct encodings, together with an extremely simple sufficient condition for cut-admissibility of the specified OLs. For broadening the spectrum of systems amenable for specification, Nigam et al. (Reference Nigam, Pimentel and Reis2016) considered an extension of linear logic with subexponentials (
![]() $\mathsf{SELL}$
, Nigam and Miller Reference Nigam and Miller2010) as the logical framework. However, encoding modalities different from those in
$\mathsf{SELL}$
, Nigam and Miller Reference Nigam and Miller2010) as the logical framework. However, encoding modalities different from those in
![]() $\mathsf{LL}$
remained difficult (or even impossible) using only the linear logic exponentials. In Olarte et al. (Reference Olarte, Pimentel and Xavier2020), we approached this problem by adopting a framework (
$\mathsf{LL}$
remained difficult (or even impossible) using only the linear logic exponentials. In Olarte et al. (Reference Olarte, Pimentel and Xavier2020), we approached this problem by adopting a framework (
![]() $\mathsf{SLL}$
) allowing a finite set of unbounded subexponentials with different modal characteristics, giving a partial solution to the specification of modal systems.
$\mathsf{SLL}$
) allowing a finite set of unbounded subexponentials with different modal characteristics, giving a partial solution to the specification of modal systems.
![]() $\mathsf{MMLL}$
intends to close this series of works, enabling not only the specification of an infinite set of bounded or unbounded OL systems (e.g., multimodal normal logics) but also keeping the simplicity of the cut admissibility characterization given in Miller and Pimentel (Reference Miller and Pimentel2013). As a side effect, we obtained a system (
$\mathsf{MMLL}$
intends to close this series of works, enabling not only the specification of an infinite set of bounded or unbounded OL systems (e.g., multimodal normal logics) but also keeping the simplicity of the cut admissibility characterization given in Miller and Pimentel (Reference Miller and Pimentel2013). As a side effect, we obtained a system (
![]() $\mathsf{LNS}_\mathsf{FMLL}$
), with a more efficient proof search strategy when compared with
$\mathsf{LNS}_\mathsf{FMLL}$
), with a more efficient proof search strategy when compared with
![]() $\mathsf{SLL}$
, and more general than
$\mathsf{SLL}$
, and more general than
![]() $\mathsf{SELL}$
.
$\mathsf{SELL}$
.
Cut elimination and focusing are central for the development of logical frameworks. For this reason, the above series of works have been followed by different system implementations and formalizations in proof assistants. For instance, cut elimination and invertibility lemmas were proved for several linear logic calculi in Abella (Chaudhuri et al. Reference Chaudhuri, Lima and Reis2019). The library YALLA
Footnote 3
also formalizes several meta-properties of different variants of
![]() $\mathsf{LL}$
in Coq. Linear nested systems have been formalized in D’Abrera et al. (Reference D’Abrera, Dawson and Goré2021), together with a cut elimination procedure for the tense logic
$\mathsf{LL}$
in Coq. Linear nested systems have been formalized in D’Abrera et al. (Reference D’Abrera, Dawson and Goré2021), together with a cut elimination procedure for the tense logic
![]() $\mathsf{K}\mathsf{t}$
. The works by Nigam et al. (Reference Nigam, Reis and Lima2014) and ; Olarte et al. (Reference Olarte, Pimentel and Rocha2018) allow for proving, semi-automatically, invertibility and cut admissibility theorems for different logical systems, including
$\mathsf{K}\mathsf{t}$
. The works by Nigam et al. (Reference Nigam, Reis and Lima2014) and ; Olarte et al. (Reference Olarte, Pimentel and Rocha2018) allow for proving, semi-automatically, invertibility and cut admissibility theorems for different logical systems, including
![]() $\mathsf{LL}$
-based systems. The aforementioned work by Nigam et al. (Reference Nigam, Pimentel and Reis2016) is also supported by a tool that automatically checks the cut-coherence conditions proposed there. The work by Xavier et al. (Reference Xavier, Olarte, Reis and Nigam2017) was the first formalization of completeness of focusing and cut admissibility for first-order linear logic in Coq. The representation of the binders, needed for the quantifiers, followed the technique PHOAS (parametric higher order abstract syntax, Chlipala Reference Chlipala2008). That work also formalized the adequacy of the encoding of different logical systems as theories in
$\mathsf{LL}$
-based systems. The aforementioned work by Nigam et al. (Reference Nigam, Pimentel and Reis2016) is also supported by a tool that automatically checks the cut-coherence conditions proposed there. The work by Xavier et al. (Reference Xavier, Olarte, Reis and Nigam2017) was the first formalization of completeness of focusing and cut admissibility for first-order linear logic in Coq. The representation of the binders, needed for the quantifiers, followed the technique PHOAS (parametric higher order abstract syntax, Chlipala Reference Chlipala2008). That work also formalized the adequacy of the encoding of different logical systems as theories in
![]() $\mathsf{LL}$
. This formalization effort was extended in Felty et al. (Reference Felty, Olarte and Xavier2021), by introducing first-order object logics and using the cut coherence criteria in Miller and Pimentel (Reference Miller and Pimentel2013) to show cut admissibility for some OLs. Defining quantifiers at the
$\mathsf{LL}$
. This formalization effort was extended in Felty et al. (Reference Felty, Olarte and Xavier2021), by introducing first-order object logics and using the cut coherence criteria in Miller and Pimentel (Reference Miller and Pimentel2013) to show cut admissibility for some OLs. Defining quantifiers at the
![]() $\mathsf{LL}$
-level and also at the OL level was only possible by replacing the PHOAS representation of syntax with a definitional representation using a de Bruijn style supported by the Hybrid library (Felty and Momigliano Reference Felty and Momigliano2012).
$\mathsf{LL}$
-level and also at the OL level was only possible by replacing the PHOAS representation of syntax with a definitional representation using a de Bruijn style supported by the Hybrid library (Felty and Momigliano Reference Felty and Momigliano2012).
Logical frameworks, based on type systems, have also been used for characterizing and proving cut-elimination theorems of object logics (see e.g., Licata et al. Reference Licata, Shulman and Riley2017; Pfenning Reference Pfenning2000). Usually, the embedding of the OL into the logical framework is not simple/direct. The approach followed here is rather different: we provide easy-to-check conditions that guarantee that the property holds.
The key feature for achieving all this is modularity. Everywhere. Starting from the choice of
![]() $\mathsf{LNS}$
, a generalization of sequent systems, as the base framework. This allows for the locality of rules, enabling the central behavior of connectives to be shared among several different logics and leaving to the subexponentials the work of separating modal behaviors. That is, modalities reflect modalities, while (vanilla)
$\mathsf{LNS}$
, a generalization of sequent systems, as the base framework. This allows for the locality of rules, enabling the central behavior of connectives to be shared among several different logics and leaving to the subexponentials the work of separating modal behaviors. That is, modalities reflect modalities, while (vanilla)
![]() $\mathsf{LL}$
captures rules as rewriting clauses (as it should be). Second, structural rules are parametric w.r.t. subexponentials, allowing for a clear separation between modals and local structural behaviors. And last, but not least, since subexponentials in
$\mathsf{LL}$
captures rules as rewriting clauses (as it should be). Second, structural rules are parametric w.r.t. subexponentials, allowing for a clear separation between modals and local structural behaviors. And last, but not least, since subexponentials in
![]() $\mathsf{MMLL}$
also reflect Kripke models, logics having the same semantic behavior share the same modal characteristics.
$\mathsf{MMLL}$
also reflect Kripke models, logics having the same semantic behavior share the same modal characteristics.
As future work, it would be interesting to analyze the case of non-normal modal logics (Lellmann and Pimentel Reference Lellmann and Pimentel2019), as well as to explore the failure cases: is it possible, at the meta-level, to identify the reasons for the lack of analyticity? This would push the line of investigation towards finding necessary conditions for cut admissibility.
Acknowledgements
We thank the anonymous reviewers for the very detailed revision of our work and the Coq formalization. Their comments and suggestions greatly helped us to improve the material of this paper. The work of Olarte was funded by the Minciencias (Ministerio de Ciencia Tecnología e Innovación, Colombia) project PROMUEVA (BPIN 2021000100160). The work of Pimentel has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skł odowska-Curie grant agreement No 101007627.