Investigating electromagnetic scattering characteristics based on a nonlinear sea surface

Abstract

Establishing a precise electromagnetic scattering model of surfaces is of great significance for comprehending the underlying mechanics of synthetic aperture radar (SAR) imaging. To describe surface electromagnetic scattering more comprehensively, this paper established a nonlinear integral equation model with the Creamer model and bispectrum (IEM-C). Based on the IEM-C model, the effect of parameters, such as radar wave incidence angle, wind speed and direction of sea surfaces, and different polarization modes on the backscattering coefficients of C-band radar waves, was systematically evaluated. The results show that the IEM-C model can characterize both the vertical nonlinear features due to wave interactions and the horizontal nonlinear features due to the wind direction. The sensitivity of the sea surface backscattering coefficient in the IEM-C model to nonlinear effects varies with different incident angles. At the incident angle of 30°, the IEM-C model exhibits the most significant nonlinear effects. The nonlinear effects of the IEM-C model vary under different wind speeds. By comparing with the measured data, it is proved that the IEM-C model is closer to the real sea surface scattering situation than the IEM model.

Introduction

Sea currents have a significant impact on human production and life. It is imperative to acquire comprehensive oceanic information and comprehend the intricacies of its processes and causality [1]. Sea current observation methods are divided into two categories: in situ detection and remote-sensing detection. In situ detection methods offer high measurement accuracy but are limited in terms of equipment cost and detection range. On the other hand, remote-sensing detection methods have the advantages of wide coverage, high resolution, and near real-time data, providing a large amount of oceanic information [2]. Among various remote-sensing detection methods, synthetic aperture radar (SAR) stands out due to its advantages, such as all-time and all-weather imaging capabilities, comprehensive coverage, and high resolution, making it a valuable method for ocean sensing and detection [3]. SAR obtains images of the target area by transmitting microwave signals and receiving signals reflected from the sea surface. The morphology, roughness, and other features of the sea surface affect the scattering process of the sea surface and electromagnetic waves. By analyzing the scattering process, the morphology and structure of the sea surface can be inverted, which in turn generates high-resolution SAR images. Therefore, the establishment of an accurate electromagnetic scattering model of the sea surface is of great significance for understanding the SAR imaging mechanism and optimizing the SAR imaging algorithm.

Electromagnetic scattering models of surfaces can be divided into two categories: numerical calculation models and approximate analytical models. Numerical calculation models directly employ Maxwell’s equations to numerically solve differential or integral equations [4]. While these models provide very accurate results, a large amount of computational effort is required to compute large-scale problems [5]. In addition, these methods do not consider the physical context of ocean dynamics. Analytical approximation models, on the other hand, by physically approximating the problem under specific conditions, simplify the complex calculations providing a more intuitive physical explanation, which contributes to a better understanding of the scattering process [6]. Due to different physical approximation conditions, approximate analytical models are divided into the Kirchhoff approximation [7], the small perturbation model [8], the small slope approximation [9], and the integral equation model (IEM) [10]. The IEM has been widely recognized and applied in research because of its wide applicability of roughness [11–14].

Electromagnetic scattering calculations based on random rough surfaces are the key to studying electromagnetic scattering from surfaces [15]. The ocean’s surface can be described as a disorderly rough surface. In early electromagnetic scattering studies, it was often assumed that the sea surface was a superposition of a series of linear waves to simplify calculations. However, there are many nonlinear effects in the real sea surface, which make the surface appear nonlinear characteristics. Therefore, many scholars have developed nonlinear sea surface models to improve the accuracy of electromagnetic scattering from the sea surface. In 1989, Creamer proposed an improved linear representation to translate linear surfaces into the nonlinear surfaces, due to the fact that surface height and velocity potential can be expressed as a pair of standard Hamiltonian variables [16]. However, due to its computational complexity and usability challenges, the Creamer model has not been widely used. In response to the limitation, Soriano developed the second-order Creamer model by expanding the Creamer formulation using a Taylor series up to the second order [17]. By employing the fast inverse Fourier transform, the second-order Creamer model is computed significantly faster than the initial Creamer model, which greatly improves the simulation efficiency. In 2020, Su investigated the backscattering characteristics of a nonlinear surface under flow field modulation using the second-order Creamer model [18]. In 2022, Hwang conducted research on the swell factor of waves, with a particular focus on the impacts of linear and nonlinear sea surface Doppler spectral inversion using the second-order Creamer model [19].

In summary, the Creamer model can describe the vertical nonlinearity characteristics in the sea surface. However, there are also other nonlinearity characteristics in the sea surface. According to Aquarius satellite data, the backscatter coefficient of the sea surface exhibits significant variations with different wind directions, indicating that wind direction is a nonlinear influencing factor on the sea surface [20]. In 1992, Chen and Fung integrated the bispectrum into the IEM model, offering enhanced comprehension of how wind conditions affect the surface [12].

The wave spectrum is a mathematical function used to describe the distribution of energy carried by sea waves. It serves as a statistical instrument that captures the interplay among wave height, wave period, direction, and energy distribution [21]. Specifically, it is obtained by applying the Fourier transform to the autocorrelation function of the sea surface. The wave bispectrum refers to the Fourier transform of the bicorrelation function of the sea surface elevation. It serves as a third-order statistical measure that characterizes the nonlinearity and skewness features of the sea surface [13]. Hence, Xie developed a bistatic scattering model for non-Gaussian surfaces based on the bispectrum and analyzed the sensitivity of the model to the wind field [14]. At present, most studies consider the nonlinear scattering in one case. The Creamer model only considers the vertical direction’s nonlinearity characteristics, while the bispectrum only considers the horizontal direction’s nonlinearity characteristics. There are few studies of electromagnetic scattering from surfaces that consider both horizontal and vertical nonlinear properties.

The nonlinearity of the surface affects the distribution of roughness, which in turn affects the inversion of radar echo signals. Consequently, investigating the effects of the nonlinear properties of two-dimensional surfaces on the computation of electromagnetic scattering is of significant value. In this paper, the nonlinear integral equation model incorporating the Creamer nonlinearity (IEM-C) is developed based on the IEM model by combining the second-order Creamer nonlinear surface and bispectrum theory. The IEM-C model incorporates nonlinear corrections to linear sea surfaces and the bispectrum function is further added. These improvements enrich the discussion of nonlinear scattering factors at the surface and improve the computational accuracy. Based on the IEM-C model, the backscattering coefficients under different parameters were simulated, and the effects of the variations of parameters such as wind speed, wind angle, polarization mode, and radar wave incidence angle on the nonlinear scattering characteristics of sea surfaces were analyzed. Furthermore, the simulation results of the IEM-C model were compared with measured data, providing validation for its accuracy and reliability [22, 23].

Establishment of the IEM-C model

The sea surface is composed of large-scale structures and microstructures, with small-scale bubbles, breaking waves, and swells superimposed on large-scale quasi-periodic waves. Most early scattering studies have focused on linear surface scattering characteristics, which assume that the sea surface is a composite of linear waves. However, due to the presence of effects such as wave–wave interactions and the modulating influence of wind direction, the actual sea surface is nonlinear. Common nonlinear characteristics include vertical and horizontal nonlinearity. Vertical nonlinearity refers to the interaction between waves resulting in modulation at the crest and trough. Horizontal nonlinearity refers to the variation in backscattering coefficients between downwind and upwind conditions, which arises from the tilting of the sea surface caused by wind direction [17].

Introduction of vertical nonlinear features

The linear surface model is the prerequisite for nonlinear surface models. Common methods for modeling sea surfaces include fractal, bilinear superposition, and linear filtering [15]. The linear filtering method treats the surface as a superposition of different harmonics, with the amplitude of the harmonics being independent Gaussian random variables that are specifically proportional to the wave spectrum. The linear sea surface can be realized by Fourier transform of the spectrum. The spatial Fourier components of the linear surface can be expressed as follows:

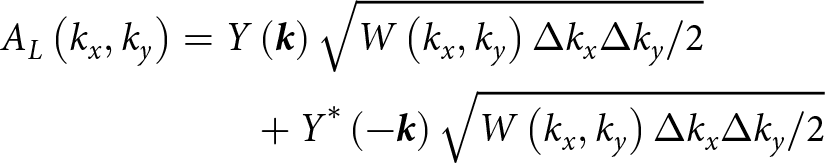(1)\begin{align}{A_L}\left( {{k_x},{k_y}} \right) & = Y \left( {{k}} \right)\sqrt {W\left( {{k_x},{k_y}} \right)\Delta {k_x}\Delta {k_y}/2} \nonumber \\ & \qquad + {Y ^*}\left( { - {{\bf {k}}}} \right)\sqrt {W\left( {{k_x},{k_y}} \right)\Delta {k_x}\Delta {k_y}/2} \end{align}

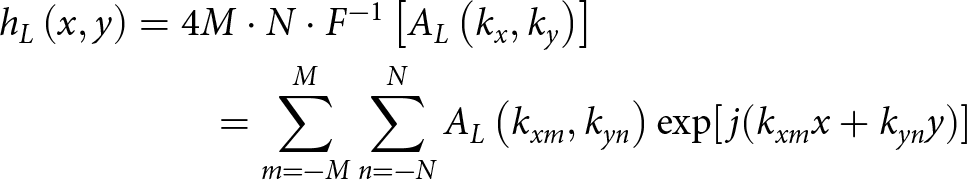(2)\begin{align}{h_L}\left( {x,y} \right) & = 4M \cdot N \cdot {F^{ - 1}}\left[ {{A_L}\left( {{k_x},{k_y}} \right)} \right] \nonumber \\ & \qquad = \sum\limits_{m = - M}^M {\sum\limits_{n = - N}^N {{A_L}\left( {{k_{xm}},{k_{yn}}} \right)} } \exp [\,j({k_{xm}}x + {k_{yn}}y)]\end{align}

where k represents the wave vector of the sea surface; ${k_x},{k_y}$ represent the wave vectors along the x-, y-direction, respectively; Y(k) is the independent Gaussian random variables; the * denotes the Hermitian form, which insures that ${h_L}(x,y)$is real; and ${h_L}(x,y)$ is the sea height at different points. The number of grid points along the surface in x- and y-directions are defined as 2 M and 2 N, respectively. ${F^{ - 1}}[ \cdot ]$ represents the inverse two-dimensional Fourier transform. $W\left( {{k_x},{k_y}} \right)$ represents the two-dimensional wave spectrum, composed of an omnidirectional and a directional spectrum. The wave spectrum describes the distribution of energy on the ocean surface with respect to wavelength and wave direction.

The sea surface height and velocity potential can be formulated as a pair of typical Hamiltonian variables. The nonlinear term of the second-order Creamer model can be written as the Hilbert transform of the linear surface [16]. In the two-dimensional case, the Hilbert transform vector of the linear term is

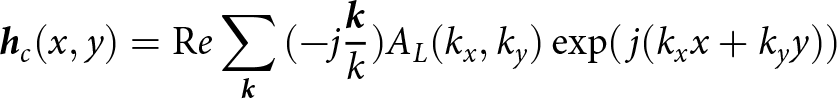(3)\begin{equation}{{\bf \it {h}}_c}(x,y) = {\mathop{\textrm Re}\nolimits} \sum\limits_{\bf \it {k}} {( - j{{\bf \it {k}} \over k})} {A_L}({k_x},{k_y})\exp (\,j({k_x}x + {k_y}y))\end{equation}

where $k = \sqrt {k_x^2 + k_y^2} $, and the components of its Hilbert vector in the x-, y-directions are as follows:

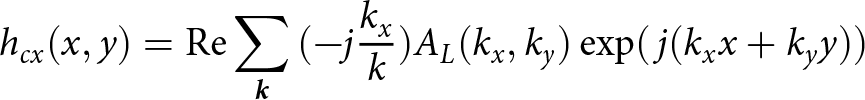(4)\begin{equation}{h_{cx}}(x,y) = {\mathop{\textrm {Re}}\nolimits} \sum\limits_{\bf \it {k}} {( - j{{{k_x}} \over k})} {A_L}({k_x},{k_y})\exp (\,j({k_x}x + {k_y}y))\end{equation}

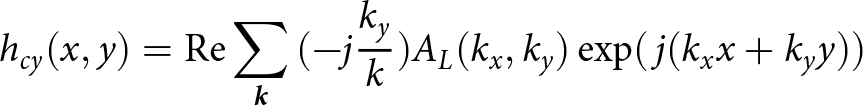(5)\begin{equation}{h_{cy}}(x,y) = {\mathop{\textrm {Re}}\nolimits} \sum\limits_{\bf \it {k}} {( - j{{{k_y}} \over k})} {A_L}({k_x},{k_y})\exp (\,j({k_x}x + {k_y}y))\end{equation}

The Creamer nonlinear Fourier components can be calculated by Equation (6) [12].

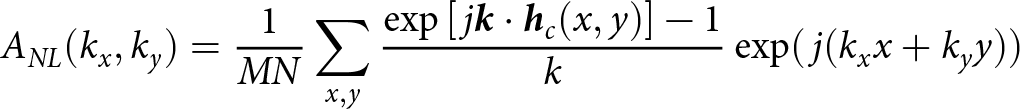(6)\begin{equation}{A_{NL}}({k_x},{k_y}) = {1 \over {MN}}\sum\limits_{x,y} {{{\exp \left[ {\,j{\bf \it {k}} \cdot {{\bf \it {h}}_c}(x,y)} \right] - 1} \over k}} \exp (\,j({k_x}x + {k_y}y))\end{equation}

where the exponential term in Equation (6) is dependent not only on k but also on the parameter ${{\boldsymbol{h}}_c}(x,y)$, which leads to complex model calculations. Soriano et al. retained the first two approximations by expanding the exponential term using Taylor series, which effectively reduces the computational complexity while preserving the nonlinear interaction between waves [17]. The first term of the Taylor expansion is equivalent to the Fourier transform of the linear ocean surface, designated as ${A_L}\left( {{k_x},{k_y}} \right)$. The second term characterizes weakly nonlinear effects:

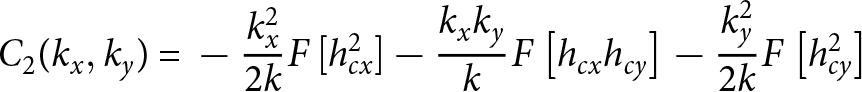(7)\begin{equation}{C_2}{\textrm{(}}{k_x},{k_y}{\textrm{) = }} - {{k_x^2} \over {2k}}F\left[ {h_{cx}^2} \right] - {{{k_x}{k_y}} \over k}F\left[ {{h_{cx}}{h_{cy}}} \right] - {{k_y^2} \over {2k}}F\left[ {h_{cy}^2} \right]\end{equation}

where $F[ \cdot ]$ represents the Fourier transform, and ${C_2}\left( {{k_x},{k_y}} \right)$ defines the second term of Creamer model expansion. Then the Fourier transform of the nonlinear surface can be expressed as follows:

(8)\begin{equation}{A_{NL}}({k_x},{k_y}) = {A_L}({k_x},{k_y}) + {C_2}{\textrm{(}}{k_x},{k_y}{\textrm{)}}\end{equation}

The nonlinear sea surface of the second-order Creamer model can be obtained by replacing the ${A_L}\left( {{k_x},{k_y}} \right)$ of Equation (2) with the ${A_{NL}}({k_x},{k_y})$ and performing a Fourier inverse transform.

The shape of the sea surface will be different under different wind conditions. The wind serves as a significant environmental parameter in simulating the sea surface. It can be described by the wind speed at 10 m above sea level and the wind direction ($\phi $). Figure 1 shows the two-dimensional linear and nonlinear sea surfaces established using the Elfouhaily spectrum with a wind speed of 5 m/s and wind direction along the x-direction [21].

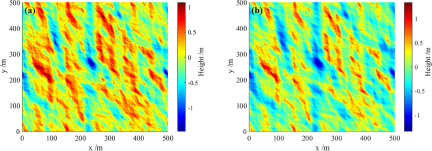
Figure 1. Two-dimensional sea surface of (a) linear (b) nonlinear.

To facilitate a more detailed examination of the disparity between linear and nonlinear surfaces, a one-dimensional surface can be derived by sampling from a two-dimensional surface. In this study, Fig. 2(a) displays the one-dimensional linear and nonlinear surfaces obtained by sampling from Fig. 1 at y = 250 m along the x-direction. Additionally, Fig. 2(b) illustrates the cumulative distribution function of the slopes computed from the linear and nonlinear surfaces depicted in Fig. 2(a).

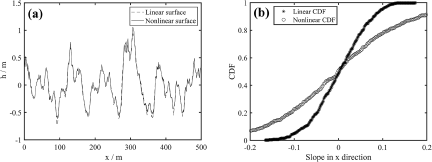
Figure 2. One-dimensional sea surface: (a) Height distribution; (b) Slope distribution.

Figure 2(a) shows that the nonlinear sea surface is sharper, with steeper crests and gentler troughs than the linear sea surface. The sea surface is commonly regarded as a superposition of waves with different wavelengths, which can be classified into shorter wavelength short waves and longer wavelength long waves. Wavelengths of short waves are usually less than 1 m, which is close to radar wavelengths and has a strong correlation with remote-sensing imaging results. On the other hand, wavelengths of long waves range from a few meters to several hundred meters. Due to the interaction between the waves in the sea surface, short waves are suppressed at the troughs of long waves and enhanced at the crests. By analyzing the cumulative distribution characteristics of the slope for linear and nonlinear sea surfaces in Fig. 2(b), it can be observed that the slope distribution of the nonlinear sea surface is steeper compared to the linear surface.

Introduction of horizontal nonlinear features

The sea surface is a randomly rough surface affected by wind and waves, with different height at different positions. The sea surface height $h(x,y)$ is a random variable that can be described by the probability density function of the sea surface height. A random variable can be characterized by its statistical distribution by using moments. Let the surface function $h(x,y)$ be a real stationary random process with zero mean. The first-order moments of the random variable represent its mathematical expectation $\left\langle h \right\rangle = 0$, the second-order moments represent the variance $\left\langle {{h^2}} \right\rangle = {\delta ^2}$, and the third-order moments represent the skewness $\left\langle {{h^3}} \right\rangle = {\mu _3}$ [18]. The second-order moments of the sea surface height are related to the autocorrelation function of the sea surface.

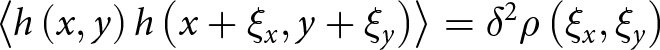(9)\begin{equation}\left\langle {h\left( {x,y} \right)h\left( {x + {\xi _x},y + {\xi _y}} \right)} \right\rangle = {\delta ^2}\rho \left( {{\xi _x},{\xi _y}} \right)\end{equation}

(10)\begin{equation}W\left( {{k_x},{k_y}} \right) = {1 \over {2\pi }}\int {{\delta ^2}\rho \left( {{\xi _x},{\xi _y}} \right)\exp \left( { - j{k_x}{\xi _x} - j{k_y}{\xi _y}} \right)} d{\xi _x}d{\xi _y}\end{equation}

where $\delta $ is the root mean square height of the surface, ${\xi _x}$ represents the displacement in the x-direction, and ${\xi _y}$ represents the displacement in the y-direction, $\rho ({\xi _x},{\xi _y})$ is the autocorrelation function of surface.

Equation (10) shows that the wave spectrum $W({k_x},{k_y})$ is the Fourier transform of the autocorrelation function $\rho ({\xi _x},{\xi _y})$. The autocorrelation function is the second-order statistic that characterizes the statistical distribution of sea surface height. The third-order moments of the sea surface height are related to the bicorrelation function of the sea surface. The bispectrum is defined as the Fourier transform of the bicorrelation function.

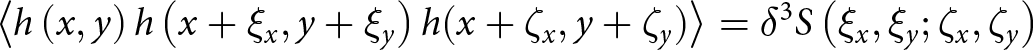(11)\begin{equation}\left\langle {h\left( {x,y} \right)h\left( {x + {\xi _x},y + {\xi _y}} \right)h(x + {\zeta _x},y + {\zeta _y})} \right\rangle = {\delta ^3}S\left( {{\xi _x},{\xi _y};{\zeta _x},{\zeta _y}} \right)\end{equation}

where ${\xi _x},{\zeta _x}$ denotes the displacement in the x-direction and ${\xi _y},{\zeta _y}$ denotes the displacement in the y-direction, and $S\left( {{\xi _x},{\xi _y};{\zeta _x},{\zeta _y}} \right)$ is the bicorrelation function, which can characterize both the linear and nonlinear features of the sea surface [13].

when ${\zeta _x} = {\xi _x}$, ${\zeta _y} = {\xi _y}$, we have

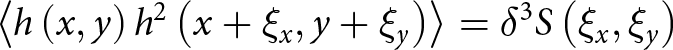(12)\begin{equation}\left\langle {h\left( {x,y} \right){h^2}\left( {x + {\xi _x},y + {\xi _y}} \right)} \right\rangle = {\delta ^3}S\left( {{\xi _x},{\xi _y}} \right)\end{equation}

and when ${\zeta _x} = 0$, ${\zeta _y} = 0$, we have

(13)\begin{align}\left\langle {{h^2}\left( {x,y} \right)h\left( {x + {\xi _x},y + {\xi _y}} \right)} \right\rangle & = \left\langle {{h^2}\left( {x' - {\xi _x},y' - {\xi _y}} \right)h\left( {x',y'} \right)} \right\rangle \nonumber \\ & \quad = {\delta ^3}S\left( { - {\xi _x}, - {\xi _y}} \right)\end{align}

The variables have reduced from four to two. The bicorrelation function $S\left( {{\xi _x},{\xi _y}} \right)$ can be decomposed into a symmetric part and an asymmetric part.

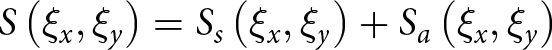(14)\begin{equation}S\left( {{\xi _x},{\xi _y}} \right) = {S_s}\left( {{\xi _x},{\xi _y}} \right) + {S_a}\left( {{\xi _x},{\xi _y}} \right)\end{equation}

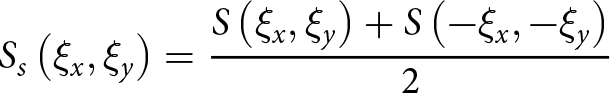(15)\begin{equation}{S_s}\left( {{\xi _x},{\xi _y}} \right) = {{S\left( {{\xi _x},{\xi _y}} \right) + S\left( { - {\xi _x}, - {\xi _y}} \right)} \over 2}\end{equation}

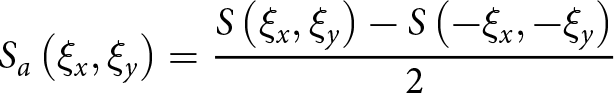(16)\begin{equation}{S_a}\left( {{\xi _x},{\xi _y}} \right) = {{S\left( {{\xi _x},{\xi _y}} \right) - S\left( { - {\xi _x}, - {\xi _y}} \right)} \over 2}\end{equation}

According to the properties of Fourier transforms, the Fourier transform of an even function is a real-valued even function, and the Fourier transform of an odd function is a purely imaginary odd function. The bispectrum $B({k_x},{k_y})$ can be divided into real and imaginary parts.

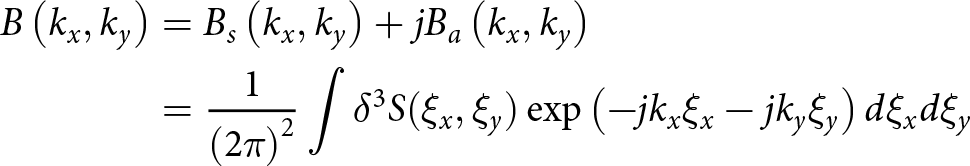(17)\begin{align} B\left( {{k_x},{k_y}} \right) & = {B_s}\left( {{k_x},{k_y}} \right) + j{B_a}\left( {{k_x},{k_y}} \right) \nonumber \\ & = {1 \over {{{\left( {2\pi } \right)}^2}}}\int {{\delta ^3}} S({\xi _x},{\xi _y})\exp \left( { - j{k_x}{\xi _x} - j{k_y}{\xi _y}} \right)d{\xi _x}d{\xi _y} \end{align}

where ${B_{\textrm{s}}}({k_x},{k_y})$ is the real part of the bispectrum, which is the Fourier transform of ${S_s}\left( {{\xi _x},{\xi _y}} \right)$, and ${B_{\textrm{a}}}({k_x},{k_y})$ is the imaginary part of the bispectrum, which is the Fourier transform of ${S_a}\left( {{\xi _x},{\xi _y}} \right)$.

In the IEM model, ${B_{\textrm{s}}}({k_x},{k_y})$ does not contribute to backscattering, while ${B_{\textrm{a}}}({k_x},{k_y})$ can be derived from Equation (18) [12–14].

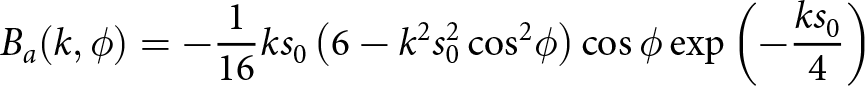(18)\begin{equation}{B_a}(k,\phi ) = - {1 \over {16}}k{s_0}\left( {6 - {k^2}s_0^2{{\,\cos }^2}\phi } \right)\cos \phi \exp \left( { - {{k{s_0}} \over 4}} \right)\end{equation}

where ${s_0}$ is the correlation distance of the bispectrum function [16].

Establishment of nonlinear electromagnetic scattering model

In the electromagnetic scattering model of the random rough surface, radar waves are incident to the sea surface and received by the radar after undergoing scattering from the sea surface. In this paper, the IEM-C model is developed based on the IEM model, combining the Creamer nonlinear sea-surface and bispectrum, to calculate the backscattering coefficients. The backscattering coefficients of the IEM-C model can be divided into the contributions of the wave spectrum and bispectrum, as shown in Equation (19).

(19)\begin{equation}\sigma _{pp}^0 = \sigma _{pp}^0(N) + \sigma _{pp}^0(S)\end{equation}

The $\sigma _{pp}^0(N)$ represents the contribution from the wave spectrum, while the $\sigma _{pp}^0(S)$ represents the contribution from the bispectrum [13]. The backscattering coefficient generated by the wave spectrum$\sigma _{pp}^0(N)$ is given by Equation (20).

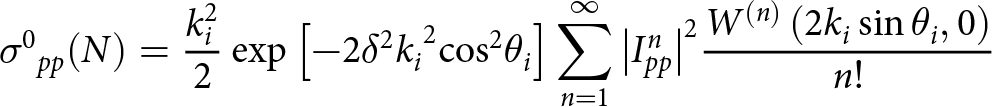(20)\begin{equation}{\sigma ^0}_{pp}(N) = {{k_i^2} \over 2}\exp \left[ { - 2{\delta ^2}{k_i}^2{{\cos }^2}{\theta _i}} \right]\sum\limits_{n = 1}^\infty {{{\left| {I_{pp}^n} \right|}^2}{{{W^{\left( n \right)}}\left( {2{k_i}\sin {\theta _i},0} \right)} \over {n!}}} \end{equation}

(21)\begin{equation}I_{pp}^n = {\left( {2{k_i}\cos {\theta _i}\delta } \right)^n}{f_{pp}}\exp ( - k_i^2{\delta ^2}{\cos ^2}{\theta _i}) + {({k_i}\delta \cos {\theta _i})^n}{F_{pp}}\end{equation}

where ${k_i}$ is the wave number of incident radar, ${\theta _i}$ is the incidence angle of radar wave, ${f_{pp}}$ is Kirchhoff field coefficient, and ${F_{pp}}$ is the compensation field coefficient [10]. The subscript pp represents the polarization state of radar waves. $W_{}^{(n)}(2{k_i}\sin {\theta _i},0)$ is the nth-order wave spectrum which is the Fourier transform of the nth autocorrelation function ${\rho ^{(n)}}(x,y)$.

$\sigma _{pp}^0(S)$ consists of three components representing the contribution of the bispectrum to the Kirchhoff field, the cross-field, and in the compensating field, as shown in Equation (22). The detailed derivation process can be found in paper [12], specifically equations (31)–(53).

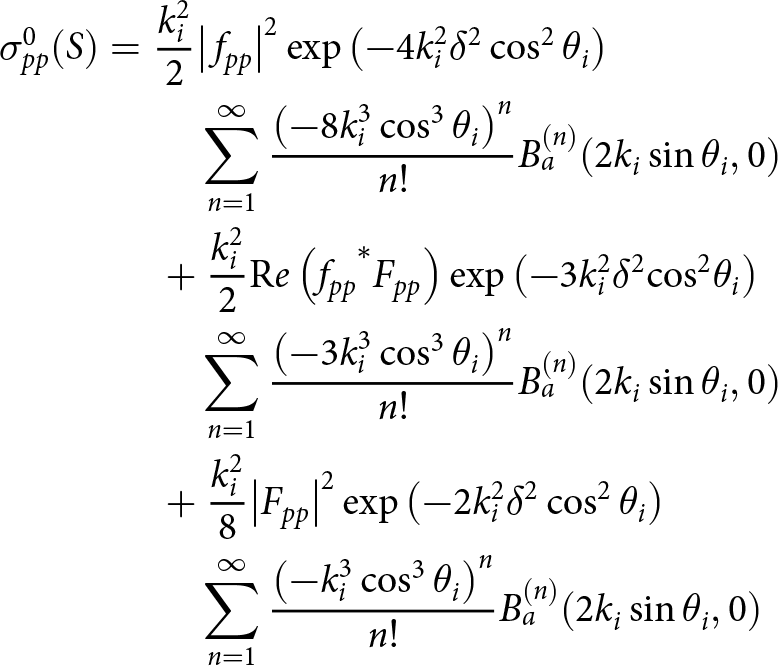(22)\begin{align}& \sigma _{pp}^0(S) = {{k_i^2} \over 2}{\left| {{\,f_{pp}}} \right|^2}\exp \left( { - 4k_i^2{\delta ^2}{{\,\cos }^2}{\,\theta _i}} \right) \nonumber \\ & \qquad \qquad \quad \sum\limits_{n = 1}^\infty {{{{{\left( { - 8k_i^3{{\,\cos }^3}{\,\theta _i}} \right)}^n}} \over {n!}}} B_a^{(n)}(2{k_i}\sin {\theta _i},0) \nonumber \\ & \qquad \qquad + {{k_i^2} \over 2}{\mathop{\textrm Re}\nolimits} \left( {{f_{pp}}^*{F_{pp}}} \right)\exp \left( { - 3k_i^2{\delta ^2}{{\cos }^2}{\theta _i}} \right)\nonumber \\ & \qquad \qquad \quad \sum\limits_{n = 1}^\infty {{{{{\left( { - 3k_i^3{{\,\cos }^3}{\,\theta _i}} \right)}^n}} \over {n!}}B_a^{(n)}(2{k_i}\sin {\theta _i},0)} \nonumber \\ & \qquad\qquad + {{k_i^2} \over 8}{\left| {{F_{pp}}} \right|^2}\exp \left( { - 2k_i^2{\delta ^2}{{\,\cos }^2}{\,\theta _i}} \right)\nonumber \\ & \qquad \qquad \quad \sum\limits_{n = 1}^\infty {{{{{\left( { - k_i^3{{\,\cos }^3}{\,\theta _i}} \right)}^n}} \over {n!}}} B_a^{(n)}(2{k_i}\sin {\theta _i},0)\end{align}

where $B_a^{(n)}(2{k_i}\sin {\theta _i},0)$ represents the nth-order bispectrum, which is the Fourier transform of the nth-order bicorrelation function.

Simulation analysis

The simulated sea surface has a size of 500 m × 500 m with a resolution of 1 m. The radar wave frequency is 5.3 GHz, and the sea surface roughness parameter is kδ = 4.75. The analysis compares the differences in backscattering coefficients between the IEM model and the IEM-C model in the C-band for different polarizations, radar incidence angles, wind speeds, and wind directions.

Different wind angles

First, the variation of the backscattering coefficient of the IEM-C model with the wind direction is analyzed. The wind direction angle ϕ is defined as the angle between the wind direction and the radar line of sight direction. With a fixed radar wave frequency of 5.3 GHz, an incident angle of 30°, the wind speed of 4 m/s, and the wind direction of 0° (north), the relationship between the backscattering coefficient of the sea surface and the wind direction angle is illustrated in Fig. 3.

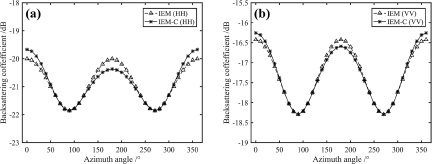
Figure 3. Backscattering coefficients for different wind directions: (a) HH polarization; (b) VV polarization.

From Fig. 3, it can be observed that the backscattering coefficients of HH polarization and VV polarization exhibit cosine-like variations with respect to ϕ. The backscattering coefficients of the IEM model are the same in upwind (ϕ = 0°) and downwind (ϕ = 180°) conditions. The backscattering coefficients of the IEM-C model exhibit differences in upwind (ϕ = 0°) and downwind (ϕ = 180°) conditions, with a 0.6 dB increase in upwind compared to downwind. The IEM-C model demonstrates differences in the backscattering coefficients between upwind and downwind conditions, which are not present in the IEM model. For 0 < ϕ < 90°, the backscattering coefficient of the IEM-C model is greater than that of the IEM model. At ϕ = 90°, the backscattering coefficient of the IEM-C model is the same as the IEM model. For 90 < ϕ < 270°, the backscattering coefficient of the IEM-C model is smaller than that of the IEM model. The IEM-C model adds the bispectrum of the surface on the basis of the second-order Creamer nonlinear sea surface, considering the nonlinear skewness characteristics in the horizontal direction caused by wind direction. In upwind cases, the roughness increases, leading to an enhancement the backscattering coefficient. In downwind cases, the roughness decreases, reducing the backscattering coefficient. The model simulation results show that the IEM-C model exhibits wind-dependent characteristics that are closer to the real sea surface scattering conditions.

Based on Fig. 3(a), it is evident that the disparity between the backscattering coefficients of the IEM-C model and the IEM model decreases as ϕ increases from 0° to 90°. Conversely, the disparity between the backscattering coefficients of the IEM-C model and the IEM model gradually increases as ϕ increases from 90° to 180°.

The closer the wind direction, the stronger the nonlinear scattering due to the wind direction. The nonlinear scattering properties are most pronounced in the case of upwind and downwind, while they have no effect in the case of crosswind. The variation of nonlinear scattering contributions observed in VV polarization shows the same trend as in HH polarization. Comparing Fig. 3(a), (b), the backscattering coefficient of HH polarization (0.31 dB) is larger than that of VV polarization (0.15 dB) for the same wind angle. In the IEM-C model, the difference of backscattering coefficients due to wind direction is more pronounced in HH polarization.

Different radar wave incidence angles

Under the premise of wind speed at 5 m/s and radar frequency at 5.3 GHz, the backscattering coefficient of the IEM-C model and the IEM model was calculated for upwind and downwind conditions with different incidence angles. The results are shown in Fig. 4.

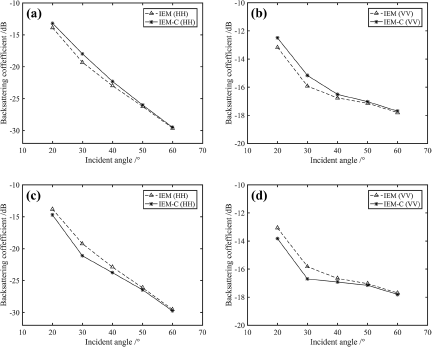
Figure 4. Backscattering coefficients at different incidence angles (a) HH – upwind; (b) VV – upwind; (c) HH – downwind; (d) VV – downwind.

Figure 4 illustrates a gradual decrease in the backscattering coefficients of both the IEM model and the IEM-C model as the incident angle increases. At small incidence angles, the dominant mechanism responsible for the backscattering is specular reflection, contributing to a higher backscatter coefficient. As the incidence angle increases, the contribution of specular reflection decreases, and Bragg scattering becomes dominant. As the angle of incidence increases further, the Bragg scattering decreases.

Based on the data presented in Fig. 4(a), (b), it can be observed that the backscattering coefficient of the IEM-C model is higher than that of the IEM model under upwind conditions. Similarly, from the observations in Fig. 4(c), (d), it is evident that the backscattering coefficient of the IEM-C model is lower compared to the IEM model under downwind conditions. As the incident angle increases, the difference of backscattering coefficients between the IEM-C model and the IEM model initially increases and then decreases, with the most significant difference (2.3 dB) observed at an incident angle of 30°.

Different wind speeds

Figure 5 illustrates the relationship between the wind speed and backscattering coefficient (upwind and downwind) for the radar wave frequency of 5.3 GHz and incident angle of 30°.

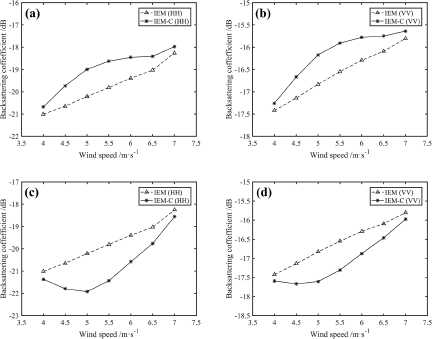
Figure 5. Backscattering coefficients at different wind speeds (a) HH – upwind; (b) VV – upwind; (c) HH – downwind; (d) VV – downwind.

A comprehensive analysis of Fig. 5 reveals that, irrespective of the polarization mode or the specific model employed, there is a discernible upward trend in the backscattering coefficient of the sea surface with increasing wind speed. This observed behavior can be attributed to the heightened instability of the sea surface as wind speed escalates. This leads to the increase in the roughness of the sea surface and the consequent increase in the backscattering coefficient.

By analyzing the backscattering results of the IEM and IEM-C models under the same polarization and wind direction conditions depicted in Fig. 5, it becomes evident that the IEM model exhibits a linear increase in the backscattering coefficient with increasing wind speed. Conversely, the backscattering coefficient of the IEM-C model demonstrates a nonlinear variation with wind speed. As the wind speed intensifies, the disparity between the IEM-C and IEM models initially enlarges and then diminishes, reaching its most pronounced level at a wind speed of 5 m/s.

Observing the backscattering coefficients for different polarizations and wind directions in Fig. 5(a), (c) and Fig. 5(b), (d), significant differences are observed. The backscattering coefficients of the IEM-C model for the downwind case are smaller than those of the IEM model for the same wind speeds. The scattering coefficients of the IEM model are smaller than those of the IEM-C model for the upwind case. Under the same wind speed conditions, the difference in backscattering coefficients between the IEM-C model and the IEM model is larger in the HH polarization compared to the VV polarization.

Model verification

To validate the IEM-C model proposed in this paper, a comparison was conducted between its simulation results and the measured data. The measured data were obtained from airborne radar measurements conducted by the United States Naval Research Laboratory (NRL) [22]. The operating bands of the radar are the X band (8910 MHz), C band (4455 MHz), L band (1228 MHz), and P band (428 MHz). This paper compares C band (4455 MHz) measurement data with simulation results.

Figure 6 illustrates the variation of backscattering coefficients with incident angles under HH and VV polarization. The backscattering coefficient decreases as the angle of incidence increases. It can be seen in the Fig. 6 that compared with the IEM model, the IEM-C model has stronger backscattering coefficients, which is closer to the airborne radar measured data. That is because the IEM-C model considers the wave–wave interaction and modifies the slope distribution, generating more large local steep surfaces that enhance the backscattering. Compared to the IEM model, the mean absolute deviation of the backscattering coefficient of IEM-C model decreases from 2.77 to 1.17 dB and the standard deviation from 1.06 to 0.75 dB for HH polarization.

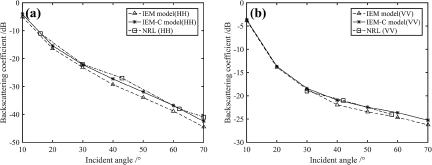
Figure 6. Backscattering coefficients of simulation and measurement for (a) HH polarization; (b) VV polarization.

Conclusion

Based on the IEM model, this study establishes the IEM-C model that considered the vertical and horizontal nonlinear characteristics of the sea surface, and analyzed the differences in the backscattering coefficients between the IEM-C model and the IEM model under different parameters.

By comparing the backscattering coefficients of the IEM-C model and the IEM model under different wind directions and speeds, it was observed that, under upwind and downwind conditions, the IEM-C model exhibited differences in the backscattering coefficients, while the IEM model did not show such differences. Under crosswind conditions, the backscattering coefficients of the IEM model were identical to those of the IEM-C model. Under downwind conditions, the backscattering coefficients of the IEM-C model were higher than those of the IEM model, while under upwind conditions, the backscattering coefficients of the IEM-C model were lower than those of the IEM model. Both the IEM-C model and the IEM model demonstrated a decreasing trend of the backscattering coefficients of the sea surface as the incident angle of the radar wave increased.

The nonlinear difference between the IEM-C model and the IEM model shows a tendency of increasing and then decreasing with increasing incidence angle. The nonlinear scattering feature of the IEM-C model is most significant at an incidence angle of 30°. The backscattering coefficients of the IEM-C model and the IEM model show some differences with the change of wind speed. The effect of the nonlinear scattering feature is most significant at a wind speed of 5 m/s.

Through comparison with measured data, the reliability of the IEM-C model is validated, demonstrating its closer approximation to the actual sea surface scattering characteristics. This highlights the importance of incorporating nonlinear features in the study of electromagnetic scattering from the sea surface.

In conclusion, the IEM-C model accounts for both vertical and horizontal nonlinear scattering characteristics of the surface, explaining the differences in surface backscattering coefficient under upwind and downwind conditions. Compared to the IEM model, the IEM-C model is more representative of actual sea surface conditions. The study of sea surface electromagnetic scattering contributes to a better understanding of the sea surface electromagnetic scattering mechanism and provides theoretical guidance for SAR imaging and ocean parameter retrieval.