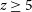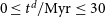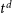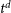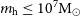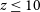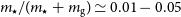1. Introduction
Recent observations with the JWST have revealed a potential overabundance of massive galaxies (
![]() $M_{\star}\sim 10^{10.5-11} \mathrm{M}_{\odot}$
) in the high-redshift Universe (
$M_{\star}\sim 10^{10.5-11} \mathrm{M}_{\odot}$
) in the high-redshift Universe (
![]() $z\gtrsim 7$
) when compared to the predictions of theoretical models of galaxy formation (e.g. Finkelstein et al. Reference Finkelstein2023a; Labbé et al. Reference Labbé2023). This has prompted questions about the validity of the standard cosmological model and the early growth of dark matter halos (e.g. Boylan-Kolchin Reference Boylan-Kolchin2023, but see Kragh Jespersen et al. Reference Kragh Jespersen, Steinhardt, Somerville and Lovell2024), as well as questions about our understanding of the interplay between gas reservoirs, star formation, and feedback at early times (e.g. Dekel et al. Reference Dekel, Sarkar, Birnboim, Mandelker and Li2023; Boyett et al. Reference Boyett2024). Whether or not there is an actual overabundance of massive galaxies when compared to theoretical model predictions (see discussion in, e.g. Finkelstein et al. Reference Finkelstein2023b), the questions these observations have prompted highlight the fundamental time limit imposed by the age of the Universe at early cosmic times when assessing galaxy properties, given the rate at which the highest mass dark matter halos can grow and consequently the stellar masses of the galaxies that they contain.
$z\gtrsim 7$
) when compared to the predictions of theoretical models of galaxy formation (e.g. Finkelstein et al. Reference Finkelstein2023a; Labbé et al. Reference Labbé2023). This has prompted questions about the validity of the standard cosmological model and the early growth of dark matter halos (e.g. Boylan-Kolchin Reference Boylan-Kolchin2023, but see Kragh Jespersen et al. Reference Kragh Jespersen, Steinhardt, Somerville and Lovell2024), as well as questions about our understanding of the interplay between gas reservoirs, star formation, and feedback at early times (e.g. Dekel et al. Reference Dekel, Sarkar, Birnboim, Mandelker and Li2023; Boyett et al. Reference Boyett2024). Whether or not there is an actual overabundance of massive galaxies when compared to theoretical model predictions (see discussion in, e.g. Finkelstein et al. Reference Finkelstein2023b), the questions these observations have prompted highlight the fundamental time limit imposed by the age of the Universe at early cosmic times when assessing galaxy properties, given the rate at which the highest mass dark matter halos can grow and consequently the stellar masses of the galaxies that they contain.
A similar time limit exists at lower halo masses. It has been understood for some time that the presence of photo-ionising backgrounds should inhibit the formation of galaxies in low-mass dark matter halos (e.g. Efstathiou Reference Efstathiou1992; Thoul & Weinberg Reference Thoul and Weinberg1996). For example, the presence of an ultraviolet (UV) background will photo-ionise warm diffuse gas in the inter-galactic medium (IGM), preventing its accretion onto low-mass dark matter halos while also preventing gas already present in halos from cooling (e.g. Efstathiou Reference Efstathiou1992). Such a UV background emerged during cosmological reionisation driven by high-mass stars (e.g. Barkana & Loeb Reference Barkana and Loeb2001; Wyithe & Loeb Reference Wyithe and Loeb2003), leading to the suppression of galaxy formation in lower mass halos (e.g. Gnedin Reference Gnedin2000; Wyithe & Loeb Reference Wyithe and Loeb2006; Okamoto, Gao, & Theuns Reference Okamoto, Gao and Theuns2008; Kravtsov & Manwadkar Reference Kravtsov and Manwadkar2022). Therefore, for lower mass halos to host galaxies, we might argue that there is a time limit imposed by the requirement that they form their stars prior to cosmological reionisation, at
![]() $z\gtrsim 6$
.
$z\gtrsim 6$
.
In this paper, we investigate the consequences of the time limit imposed by cosmological reionisation for the baryon content – the stellar mass,
![]() $m_\ast$
, and gas mass,
$m_\ast$
, and gas mass,
![]() $m_\mathrm{g}$
– of dark matter halos at high redshifts. In particular, we examine the interplay between the UV background-driven suppression of gas accretion onto lower dark matter halos, stellar feedback driven by star formation in these halos, and their baryon mass content –
$m_\mathrm{g}$
– of dark matter halos at high redshifts. In particular, we examine the interplay between the UV background-driven suppression of gas accretion onto lower dark matter halos, stellar feedback driven by star formation in these halos, and their baryon mass content –
![]() $m_\ast$
and
$m_\ast$
and
![]() $m_\mathrm{g}$
. Galaxies embedded within low-mass halos will experience episodes of supernova-driven feedback that deplete their reservoir of star forming gas via powerful winds (e.g. Dekel & Silk Reference Dekel and Silk1986; Efstathiou Reference Efstathiou2000) and prevent further stellar mass assembly and gas accretion. It’s interesting to note that the main sequence lifetimes of the high-mass stars (
$m_\mathrm{g}$
. Galaxies embedded within low-mass halos will experience episodes of supernova-driven feedback that deplete their reservoir of star forming gas via powerful winds (e.g. Dekel & Silk Reference Dekel and Silk1986; Efstathiou Reference Efstathiou2000) and prevent further stellar mass assembly and gas accretion. It’s interesting to note that the main sequence lifetimes of the high-mass stars (
![]() $M \geq 8\,\mathrm{M}_{\odot}$
) that result in supernovae are relatively short – of order
$M \geq 8\,\mathrm{M}_{\odot}$
) that result in supernovae are relatively short – of order
![]() $10^7$
yrs – which, at
$10^7$
yrs – which, at
![]() $z\gtrsim 6$
, is an appreciable fraction – approximately 10% – of a dark matter halo’s dynamical time. This means that a common assumption of galaxy formation models – that the time between star formation and supernova feedback is short and be treated as instantaneous – should break down in the high-redshift Universe. Instead, feedback is delayed, leading to episodic or bursty star formation (e.g. Scalo & Struck-Marcell Reference Scalo and Struck-Marcell1986; Faucher-Giguère Reference Faucher-Giguère2018; Orr, Hayward, & Hopkins Reference Orr, Hayward and Hopkins2019; Furlanetto & Mirocha Reference Furlanetto and Mirocha2022; Pallottini & Ferrara Reference Pallottini and Ferrara2023; Shen et al. Reference Shen, Vogelsberger, Boylan-Kolchin, Tacchella and Kannan2023; Sun et al. Reference Sun, Faucher-Giguère, Hayward, Shen, Wetzel and Cochrane2023).
$z\gtrsim 6$
, is an appreciable fraction – approximately 10% – of a dark matter halo’s dynamical time. This means that a common assumption of galaxy formation models – that the time between star formation and supernova feedback is short and be treated as instantaneous – should break down in the high-redshift Universe. Instead, feedback is delayed, leading to episodic or bursty star formation (e.g. Scalo & Struck-Marcell Reference Scalo and Struck-Marcell1986; Faucher-Giguère Reference Faucher-Giguère2018; Orr, Hayward, & Hopkins Reference Orr, Hayward and Hopkins2019; Furlanetto & Mirocha Reference Furlanetto and Mirocha2022; Pallottini & Ferrara Reference Pallottini and Ferrara2023; Shen et al. Reference Shen, Vogelsberger, Boylan-Kolchin, Tacchella and Kannan2023; Sun et al. Reference Sun, Faucher-Giguère, Hayward, Shen, Wetzel and Cochrane2023).
Faucher-Giguère (Reference Faucher-Giguère2018) modelled such bursty star formation and showed that it can arise when the effective equilibrium between the self-gravity of gas in a galaxy and stellar feedback following star formation cannot be maintained. This should be commonplace in galaxies at high redshifts and in lower mass galaxies across cosmic time. Indeed, there is observational evidence for bursty star formation in galaxies at high redshifts (e.g. Faisst et al. Reference Faisst, Capak, Emami, Tacchella and Larson2019; Looser et al. Reference Looser2023; Strait et al. Reference Strait2023). Faisst et al. (Reference Faisst, Capak, Emami, Tacchella and Larson2019) concluded from a statistical sample of
![]() $z\!\sim$
4.5 galaxies that the significant scatter in UV and H
$z\!\sim$
4.5 galaxies that the significant scatter in UV and H
![]() $\alpha$
luminosities and star formation rates implied episodes of bursty star formation during the prior 50 Myr. Drawing on JWST/NIRSpec data, Strait et al. (Reference Strait2023) found star formation is in the process of being shut down in a
$\alpha$
luminosities and star formation rates implied episodes of bursty star formation during the prior 50 Myr. Drawing on JWST/NIRSpec data, Strait et al. (Reference Strait2023) found star formation is in the process of being shut down in a
![]() $z=5.2$
galaxy, while Looser et al. (Reference Looser2023) found star formation has been quenched in a
$z=5.2$
galaxy, while Looser et al. (Reference Looser2023) found star formation has been quenched in a
![]() $z=7.3$
galaxy; both are consistent with galaxy formation model predictions that incorporate bursty star formation (Dome et al. Reference Dome, Tacchella, Fialkov, Dekel, Ginzburg, Lapiner and Looser2023). Similarly, there is observational evidence for bursty star formation in dwarf galaxies (e.g. Weisz et al. Reference Weisz2012; Emami et al. Reference Emami, Siana, Weisz and Johnson2019), based on the distributions of UV and H
$z=7.3$
galaxy; both are consistent with galaxy formation model predictions that incorporate bursty star formation (Dome et al. Reference Dome, Tacchella, Fialkov, Dekel, Ginzburg, Lapiner and Looser2023). Similarly, there is observational evidence for bursty star formation in dwarf galaxies (e.g. Weisz et al. Reference Weisz2012; Emami et al. Reference Emami, Siana, Weisz and Johnson2019), based on the distributions of UV and H
![]() $_{\alpha}$
that probe their star formation histories. Such bursty star formation arises naturally in hydrodynamical galaxy formation simulations that can track resolved star formation and feedback (e.g. Hopkins et al. Reference Hopkins2023), especially in lower mass galaxies (e.g. Oñorbe et al. Reference Oñorbe, Boylan-Kolchin, Bullock, Hopkins, Kereš, Faucher-Giguère, Quataert and Murray2015; Muratov et al. Reference Muratov, Kereš, Faucher-Giguère, Hopkins, Quataert and Murray2015; Sparre et al. Reference Sparre, Hayward, Feldmann, Faucher-Giguère, Muratov, Kereš and Hopkins2017) and during the epoch probed by JWST (e.g. Pallottini & Ferrara Reference Pallottini and Ferrara2023; Shen et al. Reference Shen, Vogelsberger, Boylan-Kolchin, Tacchella and Kannan2023; Sun et al. Reference Sun, Faucher-Giguère, Hayward, Shen, Wetzel and Cochrane2023).
$_{\alpha}$
that probe their star formation histories. Such bursty star formation arises naturally in hydrodynamical galaxy formation simulations that can track resolved star formation and feedback (e.g. Hopkins et al. Reference Hopkins2023), especially in lower mass galaxies (e.g. Oñorbe et al. Reference Oñorbe, Boylan-Kolchin, Bullock, Hopkins, Kereš, Faucher-Giguère, Quataert and Murray2015; Muratov et al. Reference Muratov, Kereš, Faucher-Giguère, Hopkins, Quataert and Murray2015; Sparre et al. Reference Sparre, Hayward, Feldmann, Faucher-Giguère, Muratov, Kereš and Hopkins2017) and during the epoch probed by JWST (e.g. Pallottini & Ferrara Reference Pallottini and Ferrara2023; Shen et al. Reference Shen, Vogelsberger, Boylan-Kolchin, Tacchella and Kannan2023; Sun et al. Reference Sun, Faucher-Giguère, Hayward, Shen, Wetzel and Cochrane2023).
Using a lightweight semi-analytical model that we have written, we examine how the combination of UV suppression of gas accretion from cosmological scales and bursty star formation driven by delayed feedback influence the baryon content of dark matter halos at high redshifts. We model the assembly histories of these halos using Monte Carlo merger trees that have been calibrated against cosmological N-body simulations (cf. Parkinson, Cole, & Helly Reference Parkinson, Cole and Helly2008) and therefore capture plausible variations in their growth over cosmic time. We assume that cosmological gas accretion tracks halo growth, modulated by the presence of the UV background, following the approach of Kravtsov & Manwadkar (Reference Kravtsov and Manwadkar2022). We parameterise star formation and feedback efficiencies, allowing for delayed feedback following the approach of Furlanetto & Mirocha (Reference Furlanetto and Mirocha2022). In this way, we can assess how local factors (star formation efficiency, onset and strength of stellar feedback, variation in dark matter halo assembly history) and global factors (onset of a UV ionising background and the suppression of cosmological gas accretion) influence the baryon content of halos at
![]() $z\geq 5$
.
$z\geq 5$
.
In the following sections, we describe the main features of our model (Section 2); we present our results for the baryon content of halos as a function of cosmic time and halo mass (Section 3.1), showing how they are sensitive to the assumptions of our model (instantaneous versus delayed feedback, absence or presence of UV background), model parameters (e.g. star formation efficiency, delayed feedback time interval), and variations in dark matter halo assembly history; and we summarise our key findings and their implications for our understanding of galaxy formation and evolution in the low-mass halo regime (Section 4). We use the cosmological parameter values
![]() $\Omega_\mathrm{b}=0.0484$
,
$\Omega_\mathrm{b}=0.0484$
,
![]() $\Omega_\mathrm{m}=0.308$
,
$\Omega_\mathrm{m}=0.308$
,
![]() $\Omega_\Lambda=0.692$
,
$\Omega_\Lambda=0.692$
,
![]() $h=0.678$
,
$h=0.678$
,
![]() $\sigma_8=0.815$
, and
$\sigma_8=0.815$
, and
![]() $n_\mathrm{s}=0.968$
, which are consistent with the results obtained by the Planck Collaboration et al. (2020).
$n_\mathrm{s}=0.968$
, which are consistent with the results obtained by the Planck Collaboration et al. (2020).
2. Theoretical model
We have written a lightweight semi-analytical modelFootnote a for studying the growth of gas and stellar mass in dark matter halos, which is motivated by the philosophy of equilibrium models set out in Davé, Finlator, & Oppenheimer (Reference Davé, Finlator and Oppenheimer2012). We track the mass assembly of dark matter halos and the corresponding cosmological accretion of gas from the IGM; the accumulation of a cold gas reservoir at the centre of the halo; star formation; and the expulsion of gas via stellar feedback (supernovae-driven winds). In particular, we follow Furlanetto & Mirocha (Reference Furlanetto and Mirocha2022) and introduce a delay between when stars form and when they produce feedback, and we adopt a time-dependent suppression of cosmological gas accretion that reflects the growth of a UV ionising background, following Kravtsov & Manwadkar (Reference Kravtsov and Manwadkar2022).
Note that we do not account for the growth of the seeds of supermassive black holes and the feedback they produce. We expect this to be important in more massive galaxies – star formation will be preferred at the expense of black hole growth in lower mass galaxies because black hole growth is limited to occur on a Salpeter timescale (see, e.g. Nayakshin, Wilkinson, & King Reference Nayakshin, Wilkinson and King2009; Bourne & Power Reference Bourne and Power2016). This difference in timescales on which stellar and black hole-driven feedback acts (e.g. Power et al. Reference Power, Zubovas, Nayakshin and King2011) should give rise to more complex bursty star formation histories in more massive galaxies; we will investigate this in a future paper.
2.1 Evolutionary equations
We track the time rate of change of gas (
![]() $\dot{m}_{\mathrm{g}}$
), star formation (
$\dot{m}_{\mathrm{g}}$
), star formation (
![]() $\dot{m}_{\star}$
), and supernova-driven wind mass loss (
$\dot{m}_{\star}$
), and supernova-driven wind mass loss (
![]() $\dot{m}_{w}$
) at time t via a set of coupled differential equations:
$\dot{m}_{w}$
) at time t via a set of coupled differential equations:
It is straightforward to convert between t and redshift z for our adopted cosmology, which is important for evaluating the contribution of the UV background. The various parameters are now described in the following subsections.
2.1.1 Growth of the gas reservoir
Equation (1) tracks the gas reservoir in a galaxy, accounting for the accretion rate of gas from cosmological scales (
![]() $\dot{m}_\mathrm{c,g}$
), gas that is converted to stars via
$\dot{m}_\mathrm{c,g}$
), gas that is converted to stars via
![]() $\dot{m}_{\star}$
, and gas that is lost via winds (
$\dot{m}_{\star}$
, and gas that is lost via winds (
![]() $\dot{m}_w$
). As is commonly assumed (e.g. White & Frenk Reference White and Frenk1991),
$\dot{m}_w$
). As is commonly assumed (e.g. White & Frenk Reference White and Frenk1991),
![]() $\dot{m}_{\mathrm{c,g}}$
tracks the accretion rate of the dark matter halo that hosts the galaxy, with
$\dot{m}_{\mathrm{c,g}}$
tracks the accretion rate of the dark matter halo that hosts the galaxy, with
![]() $\dot{m}_\mathrm{h}$
representing the halo mass growth rate;
$\dot{m}_\mathrm{h}$
representing the halo mass growth rate;
Here the quantities
![]() $\Omega_\mathrm{b}$
and
$\Omega_\mathrm{b}$
and
![]() $\Omega_\mathrm{m}$
refer to the total baryon and matter densities of the Universe, respectively, and the assumption is that the halo accretes a baryon mass equivalent to the cosmic fraction (
$\Omega_\mathrm{m}$
refer to the total baryon and matter densities of the Universe, respectively, and the assumption is that the halo accretes a baryon mass equivalent to the cosmic fraction (
![]() $\Omega_\mathrm{b}/\Omega_\mathrm{m}$
) per unit dark matter accreted. We also use a pre-factor
$\Omega_\mathrm{b}/\Omega_\mathrm{m}$
) per unit dark matter accreted. We also use a pre-factor
![]() $0 \leq \unicode{x025B}_\mathrm{in} \leq 1$
, such that
$0 \leq \unicode{x025B}_\mathrm{in} \leq 1$
, such that
![]() $\unicode{x025B}_\mathrm{in}=1$
corresponds to the accretion of the cosmic baryon fraction and
$\unicode{x025B}_\mathrm{in}=1$
corresponds to the accretion of the cosmic baryon fraction and
![]() $\unicode{x025B}_\mathrm{in}=0$
corresponds to complete suppression of baryon accretion. We discuss this further in the context of UV suppression of cosmological accretion below.
$\unicode{x025B}_\mathrm{in}=0$
corresponds to complete suppression of baryon accretion. We discuss this further in the context of UV suppression of cosmological accretion below.
2.1.2 Growth of stellar mass
Equation (2),
links the star formation rate to the mass of the gas reservoir,
![]() $m_\mathrm{g}$
, a star formation timescale,
$m_\mathrm{g}$
, a star formation timescale,
![]() $\tau_\mathrm{sf}$
, and an efficiency factor,
$\tau_\mathrm{sf}$
, and an efficiency factor,
![]() $\unicode{x025B}_\mathrm{sf}$
. We assume that
$\unicode{x025B}_\mathrm{sf}$
. We assume that
![]() $\tau_\mathrm{sf}$
is proportional to the dynamical time,
$\tau_\mathrm{sf}$
is proportional to the dynamical time,
where R and
![]() $\sigma$
are the characteristic radius and velocity dispersion of the system respectively. If we adopt the dynamical time of the halo as characterising this timescale, we expect that
$\sigma$
are the characteristic radius and velocity dispersion of the system respectively. If we adopt the dynamical time of the halo as characterising this timescale, we expect that
where
![]() $\Delta_\mathrm{vir} \simeq 178$
is the virial overdensity of the halo and
$\Delta_\mathrm{vir} \simeq 178$
is the virial overdensity of the halo and
is the Hubble parameter at cosmic time,
![]() $t\equiv~t(z)$
. We assume that
$t\equiv~t(z)$
. We assume that
and expect that
![]() $f_\mathrm{sf} \gtrsim 1$
. We take
$f_\mathrm{sf} \gtrsim 1$
. We take
![]() $\unicode{x025B}_\mathrm{sf}=0.015$
as our fiducial value, following Furlanetto & Mirocha (Reference Furlanetto and Mirocha2022) and motivated by Murray (Reference Murray2011) and Leroy et al. (Reference Leroy2017), but we allow this parameter to vary between
$\unicode{x025B}_\mathrm{sf}=0.015$
as our fiducial value, following Furlanetto & Mirocha (Reference Furlanetto and Mirocha2022) and motivated by Murray (Reference Murray2011) and Leroy et al. (Reference Leroy2017), but we allow this parameter to vary between
![]() $\unicode{x025B}_\mathrm{sf}=0.0015$
(low efficiency) and
$\unicode{x025B}_\mathrm{sf}=0.0015$
(low efficiency) and
![]() $\unicode{x025B}_\mathrm{sf}=0.1$
(high efficiency) to gauge its influence on our results.
$\unicode{x025B}_\mathrm{sf}=0.1$
(high efficiency) to gauge its influence on our results.
2.1.3 Supernovae-driven wind mass loss
Equation (3),
links the rate of mass loss driven by supernovae to
![]() $\dot{m}_\star$
at some time
$\dot{m}_\star$
at some time
![]() $t-t^\mathrm{d}$
, where
$t-t^\mathrm{d}$
, where
![]() $t^\mathrm{d}$
is the delayed feedback timescale. If
$t^\mathrm{d}$
is the delayed feedback timescale. If
![]() $t^\mathrm{d}=0$
, then this mass loss rate is driven by the instantaneous star formation rate; however, if
$t^\mathrm{d}=0$
, then this mass loss rate is driven by the instantaneous star formation rate; however, if
![]() $t^\mathrm{d}>0$
, then it depends on star formation at some earlier time and corresponds to delayed feedback. We adopt
$t^\mathrm{d}>0$
, then it depends on star formation at some earlier time and corresponds to delayed feedback. We adopt
![]() $t^\mathrm{d}$
=0.015 Gyr (15 Myr) as our fiducial value, but have explored values of
$t^\mathrm{d}$
=0.015 Gyr (15 Myr) as our fiducial value, but have explored values of
![]() $0 \leq t^\mathrm{d} \leq 0.03$
Gyr.
$0 \leq t^\mathrm{d} \leq 0.03$
Gyr.
We follow Furlanetto et al. (Reference Furlanetto, Mirocha, Mebane and Sun2017) in defining our choice of feedback efficiency parameter; they model momentum-regulated supernova feedback and assume that supernovae accelerate the wind to the escape velocity of the halo. This gives
where
![]() $\unicode{x025B}_\mathrm{fb}$
parameterises feedback efficiency and corresponds to the momentum injected by the supernovae driving the wind, and
$\unicode{x025B}_\mathrm{fb}$
parameterises feedback efficiency and corresponds to the momentum injected by the supernovae driving the wind, and
![]() $\pi_{\mathrm{p}}$
is the total amount of momentum from each supernova. We follow Furlanetto & Mirocha (Reference Furlanetto and Mirocha2022) in adopting
$\pi_{\mathrm{p}}$
is the total amount of momentum from each supernova. We follow Furlanetto & Mirocha (Reference Furlanetto and Mirocha2022) in adopting
![]() $\unicode{x025B}_\mathrm{fb}=5$
as our fiducial value, but we also consider values in the range
$\unicode{x025B}_\mathrm{fb}=5$
as our fiducial value, but we also consider values in the range
![]() $2\leq \unicode{x025B}_\mathrm{fb}\leq 7$
. Following Furlanetto et al. (Reference Furlanetto, Mirocha, Mebane and Sun2017), we assume
$2\leq \unicode{x025B}_\mathrm{fb}\leq 7$
. Following Furlanetto et al. (Reference Furlanetto, Mirocha, Mebane and Sun2017), we assume
![]() $\pi_{\mathrm{p}}$
, to be of the order unity.
$\pi_{\mathrm{p}}$
, to be of the order unity.
2.1.4 UV suppression of cosmological gas accretion
We follow the approach of Kravt
sov & Manwadkar (Reference Kravtsov and Manwadkar2022) by noting that the gas mass within a dark matter halo may be a function of both mass and redshift (e.g. Okamoto, Gao, & Theuns Reference Okamoto, Gao and Theuns2008),
The quantity
![]() $f_\mathrm{b}(m_\mathrm{h},z)$
is related to
$f_\mathrm{b}(m_\mathrm{h},z)$
is related to
![]() $\unicode{x025B}_\mathrm{in}$
in Equation (1), as we make clear below. Following Gnedin (Reference Gnedin2000), Okamoto, Gao, & Theuns (Reference Okamoto, Gao and Theuns2008), we write
$\unicode{x025B}_\mathrm{in}$
in Equation (1), as we make clear below. Following Gnedin (Reference Gnedin2000), Okamoto, Gao, & Theuns (Reference Okamoto, Gao and Theuns2008), we write
where
![]() $\Omega_\mathrm{b}/\Omega_\mathrm{m}$
is the cosmic baryon fraction and s(x,y) is defined as:
$\Omega_\mathrm{b}/\Omega_\mathrm{m}$
is the cosmic baryon fraction and s(x,y) is defined as:
![]() $\unicode{x03BC}_\mathrm{c}=m_\mathrm{h}/M_\mathrm{c}(z)$
, where
$\unicode{x03BC}_\mathrm{c}=m_\mathrm{h}/M_\mathrm{c}(z)$
, where
![]() $M_\mathrm{c}(z)$
is a characteristic mass below which
$M_\mathrm{c}(z)$
is a characteristic mass below which
![]() $s(\unicode{x03BC}_\mathrm{c},\unicode{x03C9}) \rightarrow 0$
. Following Kravtsov & Manwadkar (Reference Kravtsov and Manwadkar2022), we adopt
$s(\unicode{x03BC}_\mathrm{c},\unicode{x03C9}) \rightarrow 0$
. Following Kravtsov & Manwadkar (Reference Kravtsov and Manwadkar2022), we adopt
where
![]() $\unicode{x03B3}=15$
and
$\unicode{x03B3}=15$
and
![]() $\unicode{x03B2}$
is given by:
$\unicode{x03B2}$
is given by:
here
![]() $z_\mathrm{rei}$
is the redshift of reionisation. We adopt as our fiducial value
$z_\mathrm{rei}$
is the redshift of reionisation. We adopt as our fiducial value
![]() $z_\mathrm{rei}=7$
but have checked the sensitivity of our results to this choice.
$z_\mathrm{rei}=7$
but have checked the sensitivity of our results to this choice.
If we consider the time rate of change of Equations (10) and (11), we see that
 \begin{align} \dot{m}_\mathrm{g}(t)=\dot{f}_\mathrm{b}m_\mathrm{h}+f_\mathrm{b}\dot{m}_\mathrm{h}&=\left(f_\mathrm{b}+\dot{f}_\mathrm{b}\frac{m_\mathrm{h}}{\dot{m}_\mathrm{h}}\right)\dot{m}_\mathrm{h}\nonumber\\ &=\left(s+\dot{s}\frac{m_\mathrm{h}}{\dot{m}_\mathrm{h}}\right)\left(\frac{\Omega_\mathrm{b}}{\Omega_\mathrm{m}}\right)\dot{m}_\mathrm{h}\nonumber, \end{align}
\begin{align} \dot{m}_\mathrm{g}(t)=\dot{f}_\mathrm{b}m_\mathrm{h}+f_\mathrm{b}\dot{m}_\mathrm{h}&=\left(f_\mathrm{b}+\dot{f}_\mathrm{b}\frac{m_\mathrm{h}}{\dot{m}_\mathrm{h}}\right)\dot{m}_\mathrm{h}\nonumber\\ &=\left(s+\dot{s}\frac{m_\mathrm{h}}{\dot{m}_\mathrm{h}}\right)\left(\frac{\Omega_\mathrm{b}}{\Omega_\mathrm{m}}\right)\dot{m}_\mathrm{h}\nonumber, \end{align}
which is equivalent to Equation (4), and so we can evaluate
![]() $\unicode{x025B}_\mathrm{in}$
, given the form of Equation (12).Footnote b We write,
$\unicode{x025B}_\mathrm{in}$
, given the form of Equation (12).Footnote b We write,
where
 \begin{align*} \unicode{x025B}(z,\unicode{x03B3})&=\frac{0.63}{1+e^{(z/\unicode{x03B2})^{\unicode{x03B3}}}}+\frac{\unicode{x03B3} z^{\unicode{x03B3}-1}}{\unicode{x03B2}^{\unicode{x03B3}}}\frac{e^{(z/\unicode{x03B2})^{\unicode{x03B3}}}}{(1+e^{(z/\unicode{x03B2})^{\unicode{x03B3}}})^2},\\[4pt] X&=\frac{3c_{\unicode{x03C9}} M_{\unicode{x03C9}}}{1+c_{\unicode{x03C9}} M_{\unicode{x03C9}}},\quad c_{\unicode{x03C9}}=2^{\unicode{x03C9}/3}-1,\\[4pt] M_{\unicode{x03C9}}&= \left(\frac{M_\mathrm{c}(z)}{M_\mathrm{h}}\right)^{\unicode{x03C9}},\quad\unicode{x03C9}=2. \end{align*}
\begin{align*} \unicode{x025B}(z,\unicode{x03B3})&=\frac{0.63}{1+e^{(z/\unicode{x03B2})^{\unicode{x03B3}}}}+\frac{\unicode{x03B3} z^{\unicode{x03B3}-1}}{\unicode{x03B2}^{\unicode{x03B3}}}\frac{e^{(z/\unicode{x03B2})^{\unicode{x03B3}}}}{(1+e^{(z/\unicode{x03B2})^{\unicode{x03B3}}})^2},\\[4pt] X&=\frac{3c_{\unicode{x03C9}} M_{\unicode{x03C9}}}{1+c_{\unicode{x03C9}} M_{\unicode{x03C9}}},\quad c_{\unicode{x03C9}}=2^{\unicode{x03C9}/3}-1,\\[4pt] M_{\unicode{x03C9}}&= \left(\frac{M_\mathrm{c}(z)}{M_\mathrm{h}}\right)^{\unicode{x03C9}},\quad\unicode{x03C9}=2. \end{align*}
This has the effect of suppressing gas accretion at halo masses below the threshold mass
![]() $M_\mathrm{c}(z)$
at
$M_\mathrm{c}(z)$
at
![]() $z<z_\mathrm{rei}$
, with
$z<z_\mathrm{rei}$
, with
![]() $M_\mathrm{c}(z)$
increasing with decreasing z (i.e. accretion is suppressed onto progressively higher mass halos). For redshifts
$M_\mathrm{c}(z)$
increasing with decreasing z (i.e. accretion is suppressed onto progressively higher mass halos). For redshifts
![]() $z>z_\mathrm{rei}$
, there is no suppression of gas accretion. We refer the interested reader to Figure 1 of Kravtsov & Manwadkar (Reference Kravtsov and Manwadkar2022) for an illustration of this behaviour.
$z>z_\mathrm{rei}$
, there is no suppression of gas accretion. We refer the interested reader to Figure 1 of Kravtsov & Manwadkar (Reference Kravtsov and Manwadkar2022) for an illustration of this behaviour.

Figure 1. Mass assembly history of a sample of 100 dark matter halos with a halo mass of
![]() $m_\mathrm{h}=10^8\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^8\,\mathrm{M}_{\odot}$
at
![]() $z=5$
generated using the Parkinson, Cole, & Helly (Reference Parkinson, Cole and Helly2008) Monte Carlo merger tree algorithm. The upper and lower panels show
$z=5$
generated using the Parkinson, Cole, & Helly (Reference Parkinson, Cole and Helly2008) Monte Carlo merger tree algorithm. The upper and lower panels show
![]() $m_\mathrm{h}$
(in
$m_\mathrm{h}$
(in
![]() $\mathrm{M}_{\odot}$
) and
$\mathrm{M}_{\odot}$
) and
![]() $\dot{m}_\mathrm{h}$
(in
$\dot{m}_\mathrm{h}$
(in
![]() $\mathrm{M}_{\odot}/{\mathrm{Gyr}}$
) against cosmic time (in Gyrs; lower horizontal axis) and redshift (upper horizontal axis); red solid and dotted curves indicate the median, 10th, and 90th percentiles of the distributions at a given time.
$\mathrm{M}_{\odot}/{\mathrm{Gyr}}$
) against cosmic time (in Gyrs; lower horizontal axis) and redshift (upper horizontal axis); red solid and dotted curves indicate the median, 10th, and 90th percentiles of the distributions at a given time.
2.2 Modelling dark matter halo growth
We have used the algorithm of Parkinson, Cole, & Helly (Reference Parkinson, Cole and Helly2008) to generate Monte Carlo dark matter halo merger trees based on Extended Press-Schechter theory (e.g. Bond et al. Reference Bond, Cole, Efstathiou and Kaiser1991; Lacey & Cole Reference Lacey and Cole1993). This has been calibrated to provide predicted halo masses as a function of cosmic time that are consistent with merger trees derived from the Millennium Simulation (cf. Springel et al. Reference Springel2005). For each of the 11 halo mass bins equally spaced (linearly) in the interval
![]() $10^6\,\mathrm{M}_{\odot} \leq m_\mathrm{h} \leq 10^{11}\,\mathrm{M}_{\odot}$
, we sample 100 realisations following mass assembly histories in the redshift range
$10^6\,\mathrm{M}_{\odot} \leq m_\mathrm{h} \leq 10^{11}\,\mathrm{M}_{\odot}$
, we sample 100 realisations following mass assembly histories in the redshift range
![]() $5 \leq z \leq 25$
equally spaced in the logarithm of the expansion factor,
$5 \leq z \leq 25$
equally spaced in the logarithm of the expansion factor,
![]() $a=1/(1+z)$
. This provides us with
$a=1/(1+z)$
. This provides us with
![]() $m_\mathrm{h}$
as a function of z; we calculate
$m_\mathrm{h}$
as a function of z; we calculate
![]() $\dot{m}_\mathrm{h}$
as a function of t(z) by constructing a smooth spline interpolant, which we differentiate numerically.
$\dot{m}_\mathrm{h}$
as a function of t(z) by constructing a smooth spline interpolant, which we differentiate numerically.
In Fig. 1, we show the mass assembly histories of a sample of dark matter halos that have masses of
![]() $m_\mathrm{h}=10^8\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^8\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. Each individual halo is represented by a light grey curve; the median, 10th, and 90th percentiles are indicated by the red solid and dotted curves. The upper panel shows the variation of
$z=5$
. Each individual halo is represented by a light grey curve; the median, 10th, and 90th percentiles are indicated by the red solid and dotted curves. The upper panel shows the variation of
![]() $m_\mathrm{h}$
with cosmic time (lower horizontal axis) and redshift (upper horizontal axis), starting at
$m_\mathrm{h}$
with cosmic time (lower horizontal axis) and redshift (upper horizontal axis), starting at
![]() $z=25$
, while the lower panel shows the corresponding values of
$z=25$
, while the lower panel shows the corresponding values of
![]() $\dot{m}_\mathrm{h}$
. This shows that our Monte Carlo merger trees produce a diversity of assembly histories and that halos that have the same value of
$\dot{m}_\mathrm{h}$
. This shows that our Monte Carlo merger trees produce a diversity of assembly histories and that halos that have the same value of
![]() $m_\mathrm{h}$
at
$m_\mathrm{h}$
at
![]() $z=5$
can differ by up to an order of magnitude in
$z=5$
can differ by up to an order of magnitude in
![]() $m_\mathrm{h}$
and
$m_\mathrm{h}$
and
![]() $\dot{m}_\mathrm{h}$
at earlier times. This allows us to explore how such variation in
$\dot{m}_\mathrm{h}$
at earlier times. This allows us to explore how such variation in
![]() $\dot{m}_\mathrm{h}$
and the corresponding influence on
$\dot{m}_\mathrm{h}$
and the corresponding influence on
![]() $\dot{m}_\mathrm{c,g}$
and
$\dot{m}_\mathrm{c,g}$
and
![]() $\dot{m}_\star$
affect the halos’ baryon mass content.
$\dot{m}_\star$
affect the halos’ baryon mass content.

Figure 2. Baryon mass assembly history of an example halo with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. The upper and middle panels show
$z=5$
. The upper and middle panels show
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
(in
$m_\star$
(in
![]() $\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs); solid (dotted) curves correspond to instantaneous star formation and feedback without (with) UV suppression of accretion (instantaneous + No UV, instantaneous + UV), while dashed (dot-dashed) curves correspond to bursty star formation from delayed feedback without (with) UV suppression of accretion (delayed + No UV, delayed + UV). For comparison, we show also the growth of
$\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs); solid (dotted) curves correspond to instantaneous star formation and feedback without (with) UV suppression of accretion (instantaneous + No UV, instantaneous + UV), while dashed (dot-dashed) curves correspond to bursty star formation from delayed feedback without (with) UV suppression of accretion (delayed + No UV, delayed + UV). For comparison, we show also the growth of
![]() $m_\mathrm{h}$
with cosmic time in the lower panel.
$m_\mathrm{h}$
with cosmic time in the lower panel.
3. Results
3.1 Bursty star formation & UV suppression of accretion
We begin by considering the growth of gas mass (upper panel), stellar mass (middle panel), and halo mass (lower panel; for comparison) in Fig. 2, focusing on an example halo with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
, drawn from the sample of 100 halos in this mass bin. We choose this halo mass bin because it marks the transition between low-mass halos that can be efficiently quenched via delayed feedback alone and high-mass halos that continue to accrete and form stars after the onset of UV suppression; we show examples of low- and high-mass systems’ assembly histories in Appendix 1. To illustrate the effects of bursty star formation and UV suppression on the growth of gas and stellar mass as a function of cosmic time, we consider the cases of instantaneous star formation and feedback and no UV suppression of accretion (hereafter instantaneous + No UV; solid curves); instantaneous star formation feedback and UV suppression of gas accretion with
$z=5$
, drawn from the sample of 100 halos in this mass bin. We choose this halo mass bin because it marks the transition between low-mass halos that can be efficiently quenched via delayed feedback alone and high-mass halos that continue to accrete and form stars after the onset of UV suppression; we show examples of low- and high-mass systems’ assembly histories in Appendix 1. To illustrate the effects of bursty star formation and UV suppression on the growth of gas and stellar mass as a function of cosmic time, we consider the cases of instantaneous star formation and feedback and no UV suppression of accretion (hereafter instantaneous + No UV; solid curves); instantaneous star formation feedback and UV suppression of gas accretion with
![]() $z_\mathrm{rei}=7$
(hereafter instantaneous + UV; dotted curves); bursty star formation from delayed feedback and no UV suppression of accretion (hereafter delayed + No UV; dashed curves); and bursty star formation and feedback and UV suppression of accretion with
$z_\mathrm{rei}=7$
(hereafter instantaneous + UV; dotted curves); bursty star formation from delayed feedback and no UV suppression of accretion (hereafter delayed + No UV; dashed curves); and bursty star formation and feedback and UV suppression of accretion with
![]() $z_\mathrm{rei}=7$
(hereafter delayed + UV; dot-dashed curves). We adopt our fiducial parameters of
$z_\mathrm{rei}=7$
(hereafter delayed + UV; dot-dashed curves). We adopt our fiducial parameters of
![]() $\unicode{x025B}_\mathrm{sf}=0.015$
and
$\unicode{x025B}_\mathrm{sf}=0.015$
and
![]() $\unicode{x025B}_\mathrm{fb}=5$
.
$\unicode{x025B}_\mathrm{fb}=5$
.
In the instantaneous + No UV case, we find that both
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
show an initial steep rise at early times (
$m_\star$
show an initial steep rise at early times (
![]() $\leq$
$\leq$
![]() $0.5$
Gyr), and continue to grow but at a slower at later times (up to 2 Gyr). There are noticeable increases in
$0.5$
Gyr), and continue to grow but at a slower at later times (up to 2 Gyr). There are noticeable increases in
![]() $m_\mathrm{g}$
at approximately 0.5 and 0.6 Gyr; these correlate with increases in
$m_\mathrm{g}$
at approximately 0.5 and 0.6 Gyr; these correlate with increases in
![]() $m_\mathrm{h}$
evident in the lower panel, which translate into increases in
$m_\mathrm{h}$
evident in the lower panel, which translate into increases in
![]() $m_\mathrm{g}$
given our assumption that
$m_\mathrm{g}$
given our assumption that
![]() $\dot{m}_\mathrm{c,g}$
tracks
$\dot{m}_\mathrm{c,g}$
tracks
![]() $\dot{m}_\mathrm{h}$
. In contrast, for instantaneous + UV, we find that
$\dot{m}_\mathrm{h}$
. In contrast, for instantaneous + UV, we find that
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
show a similar initial steep rise at early times but the effect of the UV background shutting off cosmological accretion is evident –
$m_\star$
show a similar initial steep rise at early times but the effect of the UV background shutting off cosmological accretion is evident –
![]() $m_\mathrm{g}$
peaks after 0.75 Gyr and then declines with increasing time, while
$m_\mathrm{g}$
peaks after 0.75 Gyr and then declines with increasing time, while
![]() $m_\star$
plateaus. Because
$m_\star$
plateaus. Because
![]() $m_\mathrm{g}$
is linked to
$m_\mathrm{g}$
is linked to
![]() $\dot{m}_\mathrm{h}$
and the magnitude of UV suppression is both halo mass and redshift-dependent, we see that
$\dot{m}_\mathrm{h}$
and the magnitude of UV suppression is both halo mass and redshift-dependent, we see that
![]() $m_\mathrm{g}$
shows an initial sharp decline but plateaus after 1.5 Gyr. For the delayed + No UV case, we see the characteristic strong oscillations in
$m_\mathrm{g}$
shows an initial sharp decline but plateaus after 1.5 Gyr. For the delayed + No UV case, we see the characteristic strong oscillations in
![]() $m_\mathrm{g}$
– and to a lesser extent in
$m_\mathrm{g}$
– and to a lesser extent in
![]() $m_\star$
– evident during the initial 0.5 Gyr, but as the halo grows, these oscillations damp away, and both quantities are indistinguishable from the case with instantaneous star formation and feedback. Similarly, for the delayed + UV case, we see these oscillations in
$m_\star$
– evident during the initial 0.5 Gyr, but as the halo grows, these oscillations damp away, and both quantities are indistinguishable from the case with instantaneous star formation and feedback. Similarly, for the delayed + UV case, we see these oscillations in
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
repeated.
$m_\star$
repeated.
3.2 Halo mass assembly history
In Fig. 3, we show the variation in
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
with cosmic time for a sample of 100 halos, each with
$m_\star$
with cosmic time for a sample of 100 halos, each with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. We now focus on models with the UV suppression of accretion of gas from the IGM. The dotted (dot-dashed) curves correspond to the median values of
$z=5$
. We now focus on models with the UV suppression of accretion of gas from the IGM. The dotted (dot-dashed) curves correspond to the median values of
![]() $m_\mathrm{g}$
(upper panel) and
$m_\mathrm{g}$
(upper panel) and
![]() $m_\star$
(lower) for the instantaneous + UV (delayed +UV) case, while the coloured bands indicate the range of the 10th and 90th percentiles. This shows how variations in the assembly history of the underlying dark matter halo, whose growth rate
$m_\star$
(lower) for the instantaneous + UV (delayed +UV) case, while the coloured bands indicate the range of the 10th and 90th percentiles. This shows how variations in the assembly history of the underlying dark matter halo, whose growth rate
![]() $\dot{m}_\mathrm{h}$
governs the growth rate of the gas mass and consequently the stellar mass. The variations introduced by the diversity of halo assembly histories correspond to approximately
$\dot{m}_\mathrm{h}$
governs the growth rate of the gas mass and consequently the stellar mass. The variations introduced by the diversity of halo assembly histories correspond to approximately
![]() $0.5-1$
dex in both
$0.5-1$
dex in both
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
. The variations in
$m_\star$
. The variations in
![]() $m_\mathrm{g}$
are larger for the delayed + UV case, as we might expect, while we see that the variations in
$m_\mathrm{g}$
are larger for the delayed + UV case, as we might expect, while we see that the variations in
![]() $m_\star$
are similar in magnitude for both the instantaneous + UV and delayed + UV cases (
$m_\star$
are similar in magnitude for both the instantaneous + UV and delayed + UV cases (
![]() $\sim$
$\sim$
![]() $0.5$
dex at early times,
$0.5$
dex at early times,
![]() $\sim$
1 dex at later times).
$\sim$
1 dex at later times).

Figure 3.
Influence of halo mass assembly history: Baryon mass assembly history of a sample of 100 halos with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. The upper and lower panels show the median values of
$z=5$
. The upper and lower panels show the median values of
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
(in
$m_\star$
(in
![]() $\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs); dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles.
$\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs); dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles.
3.3 Efficiency of star formation,
 $\unicode{x025B}_\mathrm{sf}$
, and feedback,
$\unicode{x025B}_\mathrm{sf}$
, and feedback,
 $\unicode{x025B}_\mathrm{fb}$
$\unicode{x025B}_\mathrm{fb}$
We now examine how our choices of star formation and feedback efficiency affect the growth of gas mass (upper panel) and stellar mass (lower panel) in Figs. 4 and 5. As in Fig. 3, we focus on a sample of 100 halos with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
, but for cases of low and high star formation and feedback efficiencies,
$z=5$
, but for cases of low and high star formation and feedback efficiencies,
![]() $\unicode{x025B}_\mathrm{sf}$
and
$\unicode{x025B}_\mathrm{sf}$
and
![]() $\unicode{x025B}_\mathrm{fb}$
, respectively. We keep
$\unicode{x025B}_\mathrm{fb}$
, respectively. We keep
![]() $z_\mathrm{rei}=7$
fixed and look at the cases of low (high) efficiency in the upper (lower) panels, with reference curves corresponding to our fiducial values plotted in light grey (
$z_\mathrm{rei}=7$
fixed and look at the cases of low (high) efficiency in the upper (lower) panels, with reference curves corresponding to our fiducial values plotted in light grey (
![]() $\unicode{x025B}_\mathrm{sf}$
=0.015 and
$\unicode{x025B}_\mathrm{sf}$
=0.015 and
![]() $\unicode{x025B}_\mathrm{fb}$
=5).
$\unicode{x025B}_\mathrm{fb}$
=5).

Figure 4.
Influence of star formation efficiency: Baryon mass assembly history of a sample of 100 halos with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. The upper and lower panels show the median values of
$z=5$
. The upper and lower panels show the median values of
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
(in
$m_\star$
(in
![]() $\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs) for
$\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs) for
![]() $\unicode{x025B}_\mathrm{sf}$
=0.0015 (inefficient) and
$\unicode{x025B}_\mathrm{sf}$
=0.0015 (inefficient) and
![]() $\unicode{x025B}_\mathrm{sf}$
=0.1 (efficient) respectively. Dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles. The greyed bands and curves correspond to the counterpart cases with the fiducial value of
$\unicode{x025B}_\mathrm{sf}$
=0.1 (efficient) respectively. Dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles. The greyed bands and curves correspond to the counterpart cases with the fiducial value of
![]() $\unicode{x025B}_\mathrm{sf}$
=0.015.
$\unicode{x025B}_\mathrm{sf}$
=0.015.

Figure 5.
Influence of feedback efficiency: Baryon mass assembly history of a sample of 100 halos with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. The upper and lower panels show the median values of
$z=5$
. The upper and lower panels show the median values of
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
(in
$m_\star$
(in
![]() $\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs) for
$\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs) for
![]() $\unicode{x025B}_\mathrm{fb}$
=2 (inefficient) and
$\unicode{x025B}_\mathrm{fb}$
=2 (inefficient) and
![]() $\unicode{x025B}_\mathrm{fb}$
=7 (efficient) respectively. Dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles. The greyed bands and curves correspond to the counterpart cases with the fiducial value of
$\unicode{x025B}_\mathrm{fb}$
=7 (efficient) respectively. Dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles. The greyed bands and curves correspond to the counterpart cases with the fiducial value of
![]() $\unicode{x025B}_\mathrm{fb}$
=5.
$\unicode{x025B}_\mathrm{fb}$
=5.
As before, we focus on the cases of instantaneous + UV (dotted curves) and delayed + UV (dot-dashed curves). By reducing (increasing) the star formation efficiency, we expect the number of stars to be formed over a fixed interval to be lower (higher) than in the fiducial case; however, the coupling of star formation to feedback means that a higher star formation efficiency should boost the strength of the feedback, which, in the case of delayed feedback, should lead to stronger oscillations in the
![]() ${m}_\mathrm{g}$
and
${m}_\mathrm{g}$
and
![]() ${m}_\star$
(see, e.g. Furlanetto & Mirocha Reference Furlanetto and Mirocha2022). We anticipate that stronger (weaker) feedback efficiency should impact
${m}_\star$
(see, e.g. Furlanetto & Mirocha Reference Furlanetto and Mirocha2022). We anticipate that stronger (weaker) feedback efficiency should impact
![]() $\dot{m}_\mathrm{c,g}$
and consequently
$\dot{m}_\mathrm{c,g}$
and consequently
![]() $m_\mathrm{g}$
, but it’s likely the that the difference with respect to the fiducial run will be more pronounced for weaker feedback – it may evacuate the halo of gas more quickly, but the accretion rate onto the halo is unchanged.
$m_\mathrm{g}$
, but it’s likely the that the difference with respect to the fiducial run will be more pronounced for weaker feedback – it may evacuate the halo of gas more quickly, but the accretion rate onto the halo is unchanged.
In Fig. 4, we fix feedback efficiency at
![]() $\unicode{x025B}_\mathrm{fb}$
=5 and look at star formation efficiencies of
$\unicode{x025B}_\mathrm{fb}$
=5 and look at star formation efficiencies of
![]() $\unicode{x025B}_\mathrm{sf}$
=0.0015 (low efficiency, upper panel) and
$\unicode{x025B}_\mathrm{sf}$
=0.0015 (low efficiency, upper panel) and
![]() $\unicode{x025B}_\mathrm{sf}$
=0.1 (high efficiency, lower panel). As expected, in the case of higher star formation efficiency, we see evidence for enhanced star formation efficiency driving enhanced feedback. Consider the instantaneous + UV case. At a given time, we see that
$\unicode{x025B}_\mathrm{sf}$
=0.1 (high efficiency, lower panel). As expected, in the case of higher star formation efficiency, we see evidence for enhanced star formation efficiency driving enhanced feedback. Consider the instantaneous + UV case. At a given time, we see that
![]() $m_\mathrm{g}$
is smaller by approximately 0.5 dex compared to the fiducial run up to the point at which the effect of UV suppression kicks in, following which
$m_\mathrm{g}$
is smaller by approximately 0.5 dex compared to the fiducial run up to the point at which the effect of UV suppression kicks in, following which
![]() $m_\mathrm{g}$
rapidly declines as its converted to stars; the evolution of
$m_\mathrm{g}$
rapidly declines as its converted to stars; the evolution of
![]() $m_\star$
is relatively unchanged from the fiducial case. In contrast, the delayed + UV case shows some interesting changes compared to the fiducial case; the initial evolution of
$m_\star$
is relatively unchanged from the fiducial case. In contrast, the delayed + UV case shows some interesting changes compared to the fiducial case; the initial evolution of
![]() $m_\mathrm{g}$
is similar but from approximately 0.2 Gyr it experiences 3 longer periods in which
$m_\mathrm{g}$
is similar but from approximately 0.2 Gyr it experiences 3 longer periods in which
![]() $m_\mathrm{g}\rightarrow 0$
, while we also note that the typical system forms more stars at a given time, and
$m_\mathrm{g}\rightarrow 0$
, while we also note that the typical system forms more stars at a given time, and
![]() $m_\star$
is
$m_\star$
is
![]() $\sim 1$
dex higher after 1.2 Gyr. For the low star formation efficiency case, we see that the differences between the two models are dramatically reduced. In particular, the strong oscillations apparent in the fiducial delayed + UV case are very weak – only a dip in
$\sim 1$
dex higher after 1.2 Gyr. For the low star formation efficiency case, we see that the differences between the two models are dramatically reduced. In particular, the strong oscillations apparent in the fiducial delayed + UV case are very weak – only a dip in
![]() $m_\mathrm{g}$
is evident at 0.2 Gyr – and the evolution in
$m_\mathrm{g}$
is evident at 0.2 Gyr – and the evolution in
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
are very similar, with the delayed + UV case having higher values of
$m_\star$
are very similar, with the delayed + UV case having higher values of
![]() $m_\mathrm{g}$
by
$m_\mathrm{g}$
by
![]() $\sim$
$\sim$
![]() $0.1$
dex and lower values of
$0.1$
dex and lower values of
![]() $m_\star$
by
$m_\star$
by
![]() $\sim$
$\sim$
![]() $0.1$
dex, when compared to the instantaneous + UV case.
$0.1$
dex, when compared to the instantaneous + UV case.
In Fig. 5, we fix star formation efficiency at
![]() $\unicode{x025B}_\mathrm{sf}$
=0.015 and look at feedback efficiencies of
$\unicode{x025B}_\mathrm{sf}$
=0.015 and look at feedback efficiencies of
![]() $\unicode{x025B}_\mathrm{fb}$
=2 (low efficiency, upper panel) and
$\unicode{x025B}_\mathrm{fb}$
=2 (low efficiency, upper panel) and
![]() $\unicode{x025B}_\mathrm{fb}$
=7 (high efficiency, lower panel). As anticipated, stronger feedback acts to accelerate when the median halo loses its gas mass (i.e.
$\unicode{x025B}_\mathrm{fb}$
=7 (high efficiency, lower panel). As anticipated, stronger feedback acts to accelerate when the median halo loses its gas mass (i.e.
![]() $m_\mathrm{g}\rightarrow 0$
), especially following the onset of UV suppression, and the spread in times when this occurs is larger than in the fiducial model (0.3 Gyr compared to 0.2 Gyr in the fiducial case); however, it has little effect on the evolution of the stellar mass. We find that weaker feedback has a dramatic effect on the evolution of
$m_\mathrm{g}\rightarrow 0$
), especially following the onset of UV suppression, and the spread in times when this occurs is larger than in the fiducial model (0.3 Gyr compared to 0.2 Gyr in the fiducial case); however, it has little effect on the evolution of the stellar mass. We find that weaker feedback has a dramatic effect on the evolution of
![]() $m_\mathrm{g}$
in the delayed +UV model; the initial oscillations seen in the fiducial case are present, but after 0.3 Gyrs
$m_\mathrm{g}$
in the delayed +UV model; the initial oscillations seen in the fiducial case are present, but after 0.3 Gyrs
![]() $m_\mathrm{g}$
grows up to the onset of UV suppression, before showing a slow decline; the total gas mass in this model is larger than in the instantaneous feedback case after the initial oscillations have damped away. The behaviour of the instantaneous +UV models in both the strong and weak feedback cases track that in the fiducial case, with the key difference being in the rate of decline of
$m_\mathrm{g}$
grows up to the onset of UV suppression, before showing a slow decline; the total gas mass in this model is larger than in the instantaneous feedback case after the initial oscillations have damped away. The behaviour of the instantaneous +UV models in both the strong and weak feedback cases track that in the fiducial case, with the key difference being in the rate of decline of
![]() $m_\mathrm{g}$
after the onset of UV suppression – the halo retains more (less) gas mass at a given time when feedback is strong (weak).
$m_\mathrm{g}$
after the onset of UV suppression – the halo retains more (less) gas mass at a given time when feedback is strong (weak).
3.4 Delayed feedback timescale,
 $t^\mathrm{d}$
$t^\mathrm{d}$
In Fig. 6 we assess how our choice of the delayed feedback timescale,
![]() $t^\mathrm{d}$
, influences the growth of
$t^\mathrm{d}$
, influences the growth of
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
with cosmic time. We focus on a sample of 100 halos with
$m_\star$
with cosmic time. We focus on a sample of 100 halos with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
, with
$z=5$
, with
![]() $z_\mathrm{rei}=7$
fixed and our fiducial values of star formation and feedback efficiency of
$z_\mathrm{rei}=7$
fixed and our fiducial values of star formation and feedback efficiency of
![]() $\unicode{x025B}_\mathrm{sf}$
=0.015 and
$\unicode{x025B}_\mathrm{sf}$
=0.015 and
![]() $\unicode{x025B}_\mathrm{fb}$
=5. According to our formulation, the instantaneous star formation and feedback model corresponds to
$\unicode{x025B}_\mathrm{fb}$
=5. According to our formulation, the instantaneous star formation and feedback model corresponds to
![]() $t^\mathrm{d}$
=0, while our fiducial delayed feedback model assumes
$t^\mathrm{d}$
=0, while our fiducial delayed feedback model assumes
![]() $t^\mathrm{d}$
=0.015 Gyr; we consider two further cases, with
$t^\mathrm{d}$
=0.015 Gyr; we consider two further cases, with
![]() $t^\mathrm{d}$
=0.0075 Gyr (upper panel) and 0.03 Gyr (lower panel).
$t^\mathrm{d}$
=0.0075 Gyr (upper panel) and 0.03 Gyr (lower panel).

Figure 6.
Influence of delayed feedback timescale: Baryon mass assembly history of a sample of 100 halos with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. The upper and lower panels show the median values of
$z=5$
. The upper and lower panels show the median values of
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
(in
$m_\star$
(in
![]() $\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs) for
$\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs) for
![]() $t^\mathrm{d}$
=0.0075 Gyr and
$t^\mathrm{d}$
=0.0075 Gyr and
![]() $t^\mathrm{d}$
=0.03 Gyr respectively. Dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles. The greyed bands and curves correspond to the counterpart cases with the fiducial value of
$t^\mathrm{d}$
=0.03 Gyr respectively. Dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles. The greyed bands and curves correspond to the counterpart cases with the fiducial value of
![]() $t^\mathrm{d}$
=0.015 Gyr.
$t^\mathrm{d}$
=0.015 Gyr.
Compared to our fiducial model with
![]() $t^\mathrm{d}$
=0.015 Gyr, we see that a shorter (longer) time delay increases (decreases) the number of initial oscillations in both
$t^\mathrm{d}$
=0.015 Gyr, we see that a shorter (longer) time delay increases (decreases) the number of initial oscillations in both
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
, and the peak median masses are similar. There are two noticeable differences – in the lengths of the intervals when
$m_\star$
, and the peak median masses are similar. There are two noticeable differences – in the lengths of the intervals when
![]() $m_\mathrm{g}\rightarrow 0$
at early times, with
$m_\mathrm{g}\rightarrow 0$
at early times, with
![]() $t^\mathrm{d}$
=0.03 Gyr experiencing longer intervals when
$t^\mathrm{d}$
=0.03 Gyr experiencing longer intervals when
![]() $m_\mathrm{g}\simeq 0$
; and in the evolution of
$m_\mathrm{g}\simeq 0$
; and in the evolution of
![]() $m_\mathrm{g}$
after the onset of UV suppression of gas accretion, such that
$m_\mathrm{g}$
after the onset of UV suppression of gas accretion, such that
![]() $m_\mathrm{g}$
plateaus close to its peak value in the model with the long time delay through to 1.2 Gyr, whereas
$m_\mathrm{g}$
plateaus close to its peak value in the model with the long time delay through to 1.2 Gyr, whereas
![]() $m_\mathrm{g}\rightarrow 0$
after the onset of UV suppression as in the fiducial case, albeit with a delay of
$m_\mathrm{g}\rightarrow 0$
after the onset of UV suppression as in the fiducial case, albeit with a delay of
![]() $\sim$
$\sim$
![]() $0.1$
Gyr. These trends highlight the complex interplay between gas accretion, star formation, and delayed feedback – especially the manner in which gas mass is retained at later times when
$0.1$
Gyr. These trends highlight the complex interplay between gas accretion, star formation, and delayed feedback – especially the manner in which gas mass is retained at later times when
![]() $t^\mathrm{d}$
=0.03 Gyr.
$t^\mathrm{d}$
=0.03 Gyr.
3.5 Redshift of reionisation,
 $z_\mathrm{rei}$
$z_\mathrm{rei}$
In Fig. 7, we assess how our choice of the redshift of reionisation,
![]() $z_\mathrm{rei}$
, influences the growth of
$z_\mathrm{rei}$
, influences the growth of
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
with cosmic time. Again we focus on a sample of 100 halos with
$m_\star$
with cosmic time. Again we focus on a sample of 100 halos with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
, with our fiducial values of star formation and feedback efficiency of
$z=5$
, with our fiducial values of star formation and feedback efficiency of
![]() $\unicode{x025B}_\mathrm{sf}$
=0.015,
$\unicode{x025B}_\mathrm{sf}$
=0.015,
![]() $\unicode{x025B}_\mathrm{fb}$
=5 fixed. We look at the case of
$\unicode{x025B}_\mathrm{fb}$
=5 fixed. We look at the case of
![]() $z_\mathrm{rei}$
=10, which corresponds to the time when the Universes was approximately 60% of its age at
$z_\mathrm{rei}$
=10, which corresponds to the time when the Universes was approximately 60% of its age at
![]() $z=$
7 (our fiducial redshift of reionisation). The trends are qualitatively similar to those we see when
$z=$
7 (our fiducial redshift of reionisation). The trends are qualitatively similar to those we see when
![]() $z_\mathrm{rei}$
=7; the peak values of
$z_\mathrm{rei}$
=7; the peak values of
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
are lower, and the rate at which
$m_\star$
are lower, and the rate at which
![]() $m_\mathrm{g}\rightarrow 0$
is more rapid in the case of instantaneous feedback with UV suppression, as we would expect because of the shorter dynamical times in these systems.
$m_\mathrm{g}\rightarrow 0$
is more rapid in the case of instantaneous feedback with UV suppression, as we would expect because of the shorter dynamical times in these systems.

Figure 7.
Influence of redshift of reionisation: Baryon mass assembly history of a sample of 100 halos with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. We show the median values of
$z=5$
. We show the median values of
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
(in
$m_\star$
(in
![]() $\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs) for
$\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs) for
![]() $z_\mathrm{rei}$
=10. Dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles. The greyed bands and curves correspond to the counterpart cases with the fiducial value of
$z_\mathrm{rei}$
=10. Dotted curves correspond to the instantaneous + UV case, while dot-dashed curves correspond to the delayed + UV case. The coloured bands indicate the range of the 10th and 90th percentiles. The greyed bands and curves correspond to the counterpart cases with the fiducial value of
![]() $z_\mathrm{rei}$
=7.
$z_\mathrm{rei}$
=7.
3.6 Baryon mass content – variation with halo mass
We have explored how local factors – star formation and feedback efficiencies, burstiness of star formation, variation in dark matter halo assembly histories – and global factors – the onset of UV suppression arising from cosmological reionisation – influence the time evolution of the gas and stellar masses of halos. We focused on a halo mass scale –
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
– that we argued is transitional, being sufficiently massive enough not to experience early truncation of gas accretion and star formation, but not overly massive that it’s unaffected by delayed feedback and UV suppression of gas accretion from the IGM. We have this information for halos spanning a mass range
$z=5$
– that we argued is transitional, being sufficiently massive enough not to experience early truncation of gas accretion and star formation, but not overly massive that it’s unaffected by delayed feedback and UV suppression of gas accretion from the IGM. We have this information for halos spanning a mass range
![]() $10^6\,\mathrm{M}_\odot\leq m_\mathrm{h} \leq 10^{11}\,\mathrm{M}_\odot$
at that epoch, as we show in Appendix 1.
$10^6\,\mathrm{M}_\odot\leq m_\mathrm{h} \leq 10^{11}\,\mathrm{M}_\odot$
at that epoch, as we show in Appendix 1.
In Fig. 8 we quantify how
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
vary with
$m_\star$
vary with
![]() $m_\mathrm{h}$
, looking at three epochs – z=10, 7, and 5 (from right to left). Because we are interested in relative trends, we plot the quantity
$m_\mathrm{h}$
, looking at three epochs – z=10, 7, and 5 (from right to left). Because we are interested in relative trends, we plot the quantity
![]() $m_\star/(m_\star+m_\mathrm{g})$
against
$m_\star/(m_\star+m_\mathrm{g})$
against
![]() $m_\mathrm{h}$
at that epoch. As the system becomes gas depleted, we expect that
$m_\mathrm{h}$
at that epoch. As the system becomes gas depleted, we expect that
![]() $m_\star/(m_\star+m_\mathrm{g})\rightarrow 1$
because
$m_\star/(m_\star+m_\mathrm{g})\rightarrow 1$
because
![]() $m_\mathrm{g}\rightarrow 0$
, which we expect at lower halo masses and should move to a higher mass scale following the onset of the UV suppression of gas accretion from the IGM.
$m_\mathrm{g}\rightarrow 0$
, which we expect at lower halo masses and should move to a higher mass scale following the onset of the UV suppression of gas accretion from the IGM.

Figure 8. Baryon mass assembly history of a
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. The upper and lower panels show
$z=5$
. The upper and lower panels show
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
(in
$m_\star$
(in
![]() $\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs); solid (dotted) curves correspond to instantaneous star formation and feedback without (with) UV suppression of accretion, while dashed (dot-dashed) curves correspond to bursty star formation without (with) UV suppression of accretion.
$\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs); solid (dotted) curves correspond to instantaneous star formation and feedback without (with) UV suppression of accretion, while dashed (dot-dashed) curves correspond to bursty star formation without (with) UV suppression of accretion.
At
![]() $z=10$
, we see that this ratio shows little variation across the mass range, with the median
$z=10$
, we see that this ratio shows little variation across the mass range, with the median
![]() $m_\star/(m_\star+m_\mathrm{g})\simeq 0.05$
in the instantaneous + UV case, compared to
$m_\star/(m_\star+m_\mathrm{g})\simeq 0.05$
in the instantaneous + UV case, compared to
![]() $m_\star/(m_\star+m_\mathrm{g})\simeq 0.03$
in the delayed + UV case. There is a weak trend for
$m_\star/(m_\star+m_\mathrm{g})\simeq 0.03$
in the delayed + UV case. There is a weak trend for
![]() $m_\star/(m_\star+m_\mathrm{g})$
to decrease (increase) with increasing mass in the instantaneous (delayed) + UV case. Interestingly, we see an enhancement
$m_\star/(m_\star+m_\mathrm{g})$
to decrease (increase) with increasing mass in the instantaneous (delayed) + UV case. Interestingly, we see an enhancement
![]() $m_\star/(m_\star+m_\mathrm{g})$
in the delayed + UV case in the halo mass range
$m_\star/(m_\star+m_\mathrm{g})$
in the delayed + UV case in the halo mass range
![]() $10^7 \mathrm{M}_\odot \leq m_\mathrm{h} \leq 10^8 \mathrm{M}_\odot$
– this reflects the transitional nature of this halo mass range and how halo mass assembly histories interact with burstiness in star formation and delayed feedback to produce a range in gas mass.
$10^7 \mathrm{M}_\odot \leq m_\mathrm{h} \leq 10^8 \mathrm{M}_\odot$
– this reflects the transitional nature of this halo mass range and how halo mass assembly histories interact with burstiness in star formation and delayed feedback to produce a range in gas mass.
By
![]() $z=7$
, we now see a marked variation across the mass range. At higher masses, the median
$z=7$
, we now see a marked variation across the mass range. At higher masses, the median
![]() $m_\star/(m_\star+m_\mathrm{g})\simeq 0.05$
in the instantaneous + UV case, unchanged from
$m_\star/(m_\star+m_\mathrm{g})\simeq 0.05$
in the instantaneous + UV case, unchanged from
![]() $z=10$
; in contrast,
$z=10$
; in contrast,
![]() $m_\star/(m_\star+m_\mathrm{g})\simeq 0.02$
in the delayed + UV case, which has is lower than at
$m_\star/(m_\star+m_\mathrm{g})\simeq 0.02$
in the delayed + UV case, which has is lower than at
![]() $z=10$
. The ratio increases smoothly towards lower masses in the instantaneous + UV case, whereas the ratio is flat down to
$z=10$
. The ratio increases smoothly towards lower masses in the instantaneous + UV case, whereas the ratio is flat down to
![]() $m_\mathrm{h} \simeq 10^7\,\mathrm{M}_\odot$
before sharply turning up to
$m_\mathrm{h} \simeq 10^7\,\mathrm{M}_\odot$
before sharply turning up to
![]() $m_\star/(m_\star+m_\mathrm{g})\simeq 1$
. At
$m_\star/(m_\star+m_\mathrm{g})\simeq 1$
. At
![]() $z=5$
, the marked variation with mass has strengthened. At higher masses, the median
$z=5$
, the marked variation with mass has strengthened. At higher masses, the median
![]() $m_\star/(m_\star+m_\mathrm{g})\simeq 0.05$
in the instantaneous + UV case is unchanged from z=10, whereas
$m_\star/(m_\star+m_\mathrm{g})\simeq 0.05$
in the instantaneous + UV case is unchanged from z=10, whereas
![]() $m_\star/(m_\star+m_\mathrm{g})\simeq 0.01$
in the delayed + UV case, which is marginally lower than at
$m_\star/(m_\star+m_\mathrm{g})\simeq 0.01$
in the delayed + UV case, which is marginally lower than at
![]() $z=7$
. We now see a gradual rise in
$z=7$
. We now see a gradual rise in
![]() $m_\star/(m_\star+m_\mathrm{g})$
towards lower
$m_\star/(m_\star+m_\mathrm{g})$
towards lower
![]() $m_\mathrm{h}$
becoming evident at
$m_\mathrm{h}$
becoming evident at
![]() $m_\mathrm{h} \simeq 10^{10}\,\mathrm{M}_\odot$
; by
$m_\mathrm{h} \simeq 10^{10}\,\mathrm{M}_\odot$
; by
![]() $m_\star/(m_\star+m_\mathrm{g})$
=1 by
$m_\star/(m_\star+m_\mathrm{g})$
=1 by
![]() $m_\mathrm{h} \simeq 10^7\,\mathrm{M}_\odot$
in both the instantaneous + UV and delayed + UV cases.
$m_\mathrm{h} \simeq 10^7\,\mathrm{M}_\odot$
in both the instantaneous + UV and delayed + UV cases.
At the three epochs we have considered, we see a general trend for
![]() $m_\star/(m_\star+m_\mathrm{g})$
to be approximately a factor of 3–5 larger in the instantaneous + UV case compared to the delayed + UV case. Depending on epoch and mass scale, this can mean both a relative enhancement in stellar mass or a relative deficit in gas mass in the instantaneous + UV model. However, the trend is for the lower mass galaxies to have higher stellar masses in the delayed + UV case, while – in the context of this particular physical model – higher mass galaxies can retain their gas reservoirs. Physically, we would expect seed supermassive black hole growth and associated feedback to reduce gas mass in these high-mass galaxies. We will revisit this in a future paper.
$m_\star/(m_\star+m_\mathrm{g})$
to be approximately a factor of 3–5 larger in the instantaneous + UV case compared to the delayed + UV case. Depending on epoch and mass scale, this can mean both a relative enhancement in stellar mass or a relative deficit in gas mass in the instantaneous + UV model. However, the trend is for the lower mass galaxies to have higher stellar masses in the delayed + UV case, while – in the context of this particular physical model – higher mass galaxies can retain their gas reservoirs. Physically, we would expect seed supermassive black hole growth and associated feedback to reduce gas mass in these high-mass galaxies. We will revisit this in a future paper.
4. Conclusions
We have investigated how the baryon mass content (i.e. the stellar and gas mass) of dark matter halos in the early Universe (
![]() $z \geq 5$
) is affected by the complex interplay between bursty star formation – arising from delayed feedback – and the UV suppression of gas accretion from the IGM driven by cosmological reionisation. Using a lightweight semi-analytical model that we have written, we have assessed how global factors – the emergence of an ionising UV radiation background – and local factors – star formation and feedback efficiency, time delayed feedback, and variations in dark matter halo assembly histories – influence the evolution of baryon mass content as a function of cosmic time (
$z \geq 5$
) is affected by the complex interplay between bursty star formation – arising from delayed feedback – and the UV suppression of gas accretion from the IGM driven by cosmological reionisation. Using a lightweight semi-analytical model that we have written, we have assessed how global factors – the emergence of an ionising UV radiation background – and local factors – star formation and feedback efficiency, time delayed feedback, and variations in dark matter halo assembly histories – influence the evolution of baryon mass content as a function of cosmic time (
![]() $z \geq 5$
) and dark matter halo mass (
$z \geq 5$
) and dark matter halo mass (
![]() $10^6\,\mathrm{M}_\odot \leq m_\mathrm{h} \leq 10^{11}\,\mathrm{M}_\odot$
).
$10^6\,\mathrm{M}_\odot \leq m_\mathrm{h} \leq 10^{11}\,\mathrm{M}_\odot$
).
Using the assembly histories of baryons in a sample of halos with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_\odot$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_\odot$
at
![]() $z=5$
to illustrate the relative importance of physical processes, we investigated how star formation efficiency, the strength of feedback, and the delayed feedback timescale influenced the stellar and gas masses over cosmic time. As shown by previous studies, delayed feedback leads to oscillations in gas mass, evident more subtly in the stellar mass, as a function of cosmic time. If star formation is inefficient, gas and stellar mass growth histories are similar regardless of whether or not feedback is instantaneous or delayed; in contrast, highly efficient star formation can drive strong oscillations, as we would anticipate given that this population produces feedback via supernovae winds. Weaker delayed feedback cannot suppress the oscillatory behaviour in lower mass systems and these systems can retain their gas for a more extended period, whereas the main effect of stronger feedback is to drive
$z=5$
to illustrate the relative importance of physical processes, we investigated how star formation efficiency, the strength of feedback, and the delayed feedback timescale influenced the stellar and gas masses over cosmic time. As shown by previous studies, delayed feedback leads to oscillations in gas mass, evident more subtly in the stellar mass, as a function of cosmic time. If star formation is inefficient, gas and stellar mass growth histories are similar regardless of whether or not feedback is instantaneous or delayed; in contrast, highly efficient star formation can drive strong oscillations, as we would anticipate given that this population produces feedback via supernovae winds. Weaker delayed feedback cannot suppress the oscillatory behaviour in lower mass systems and these systems can retain their gas for a more extended period, whereas the main effect of stronger feedback is to drive
![]() $m_\mathrm{g} \rightarrow 0$
more quickly. Longer delayed feedback timescales reduce the number of oscillations in
$m_\mathrm{g} \rightarrow 0$
more quickly. Longer delayed feedback timescales reduce the number of oscillations in
![]() $m_\mathrm{g}$
and can result in more gas being retained at later times, whereas an earlier redshift of reionisation has the simple effect of nudging the evolutionary trends in
$m_\mathrm{g}$
and can result in more gas being retained at later times, whereas an earlier redshift of reionisation has the simple effect of nudging the evolutionary trends in
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
(i.e.
$m_\star$
(i.e.
![]() $m_\mathrm{g} \rightarrow 0)$
, plateauing of
$m_\mathrm{g} \rightarrow 0)$
, plateauing of
![]() $m_\star$
to the correspondingly earlier time.
$m_\star$
to the correspondingly earlier time.
If we consider the variation of baryon mass content – which we parameterise by the ratio
![]() $m_\star/(m_\star+m_\mathrm{g})$
– with halo mass, we find at earlier times that the median trend is for the ratio to be relatively flat and small in both the instantaneous and delayed feedback cases – of order
$m_\star/(m_\star+m_\mathrm{g})$
– with halo mass, we find at earlier times that the median trend is for the ratio to be relatively flat and small in both the instantaneous and delayed feedback cases – of order
![]() $0.01-0.1$
– but with
$0.01-0.1$
– but with
![]() $m_\star/(m_\star+m_\mathrm{g})$
to be approximately a factor of 3–5 larger in the instantaneous case. At later times, we find that the ratio increases with decreasing halo mass such that
$m_\star/(m_\star+m_\mathrm{g})$
to be approximately a factor of 3–5 larger in the instantaneous case. At later times, we find that the ratio increases with decreasing halo mass such that
![]() $m_\star/(m_\star+m_\mathrm{g})\rightarrow 1$
in the lowest mass systems. Higher mass systems retain their gas reservoirs in both cases considered because they are sufficiently massive to continue accreting gas from the IGM in a way that less massive systems cannot during cosmological reionisation.
$m_\star/(m_\star+m_\mathrm{g})\rightarrow 1$
in the lowest mass systems. Higher mass systems retain their gas reservoirs in both cases considered because they are sufficiently massive to continue accreting gas from the IGM in a way that less massive systems cannot during cosmological reionisation.
The relative gas richness of massive systems is at odds with both observations and theoretical expectations (e.g. Moster, Naab, & White Reference Moster, Naab and White2018; Labbé et al. Reference Labbé2023), but we would expect feedback from supermassive black holes in these massive galaxies to expel gas and quench star formation. As noted in Section 2, we do not model seed supermassive black growth or its associated feedback; we expect this to be important (e.g. Power et al. Reference Power, Zubovas, Nayakshin and King2011) in an interesting, mass scale-dependent manner (cf. Nayakshin, Wilkinson, & King Reference Nayakshin, Wilkinson and King2009) and we shall explore it in a future paper.
We have not explicitly considered the influence of metallicity in this paper, although we have investigated straightforward extensions to our model to do this (e.g. Kravtsov & Manwadkar Reference Kravtsov and Manwadkar2022). We expect that feedback efficiency should depend on metallicity (e.g. Jecmen & Oey Reference Jecmen and Oey2023; Sugimura et al. Reference Sugimura, Ricotti, Park, Garcia and Yajima2024). For example, the ability of massive stars to drive stellar winds depends on the interaction cross section of energetic photons with gas in stellar atmospheres, which depends on the presence of heavier elements (cf. Lamers & Cassinelli Reference Lamers1999). This will introduce another mass scale dependence, reflecting the number of generations of stars and metal enrichment events, and we shall explore it in future work.
Acknowledgement
AM and CP thank the anonymous referee for their very positive report. CP acknowledges the support of the ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013.
Data availability
Not applicable.
Appendix 1. Evolution of Baryon Mass Content at Low and High Halo Masses
In Fig. A1, we show the variation in
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
with cosmic time for a sample of 100 halos, each with
$m_\star$
with cosmic time for a sample of 100 halos, each with
![]() $m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
$m_\mathrm{h}=10^7\,\mathrm{M}_{\odot}$
at
![]() $z=5$
. The dotted (dot-dashed) curves correspond to the median values of
$z=5$
. The dotted (dot-dashed) curves correspond to the median values of
![]() $m_\mathrm{g}$
(upper panel) and
$m_\mathrm{g}$
(upper panel) and
![]() $m_\star$
(lower) for instantaneous (bursty) star formation and feedback with UV suppression of accretion, while the coloured bands indicate the range of the 10th and 90th percentiles. This shows how variations in the assembly history of the underlying dark matter halo, whose growth rate
$m_\star$
(lower) for instantaneous (bursty) star formation and feedback with UV suppression of accretion, while the coloured bands indicate the range of the 10th and 90th percentiles. This shows how variations in the assembly history of the underlying dark matter halo, whose growth rate
![]() $\dot{m}_\mathrm{h}$
governs the growth rate of the gas mass and consequently the stellar mass. Interestingly we see a large variation in gas mass at late times for the lower mass system – although the median
$\dot{m}_\mathrm{h}$
governs the growth rate of the gas mass and consequently the stellar mass. Interestingly we see a large variation in gas mass at late times for the lower mass system – although the median
![]() $m_\mathrm{g}=0$
, there is a large number of systems with
$m_\mathrm{g}=0$
, there is a large number of systems with
![]() $m_\mathrm{g}$
=10–100
$m_\mathrm{g}$
=10–100
![]() $\mathrm{M}_\odot$
.
$\mathrm{M}_\odot$
.

Figure A1. Baryon mass assembly history of a sample of 100 halos with
![]() $m_\mathrm{h}=10^6\,\mathrm{M}_{\odot}$
(upper panel) and
$m_\mathrm{h}=10^6\,\mathrm{M}_{\odot}$
(upper panel) and
![]() $m_\mathrm{h}=10^{11}\,\mathrm{M}_{\odot}$
(lower panel) at
$m_\mathrm{h}=10^{11}\,\mathrm{M}_{\odot}$
(lower panel) at
![]() $z=5$
. The upper and lower panels show the median values of
$z=5$
. The upper and lower panels show the median values of
![]() $m_\mathrm{g}$
and
$m_\mathrm{g}$
and
![]() $m_\star$
(in
$m_\star$
(in
![]() $\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs); dotted curves correspond to instantaneous star formation and feedback with UV suppression of accretion, while dot-dashed curves correspond to bursty star formation with UV suppression of accretion. The coloured ‘bands indicate the range of the 10th and 90th percentiles.
$\mathrm{M}_{\odot}$
) against cosmic time (in Gyrs); dotted curves correspond to instantaneous star formation and feedback with UV suppression of accretion, while dot-dashed curves correspond to bursty star formation with UV suppression of accretion. The coloured ‘bands indicate the range of the 10th and 90th percentiles.