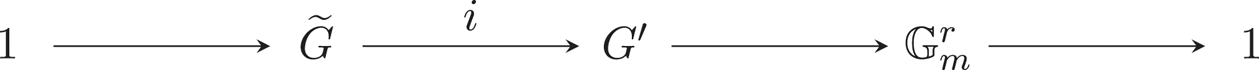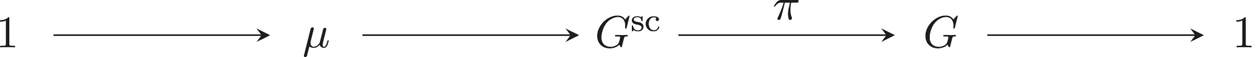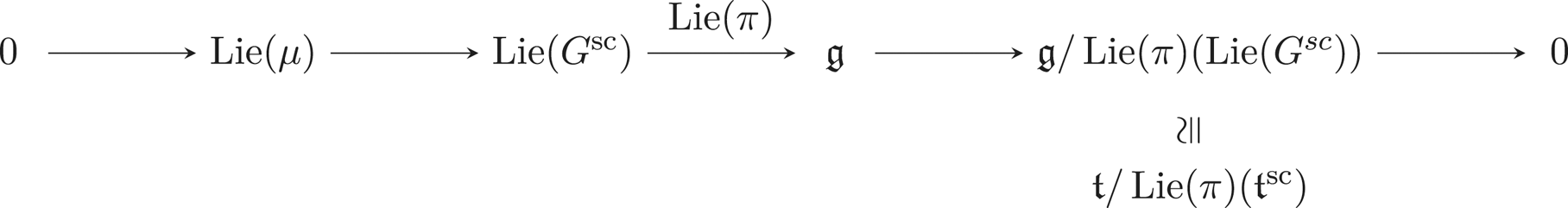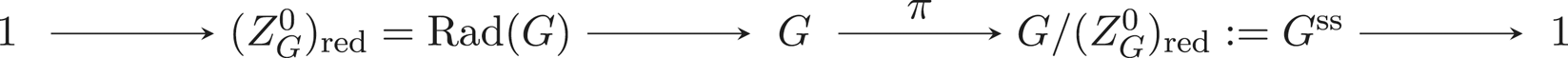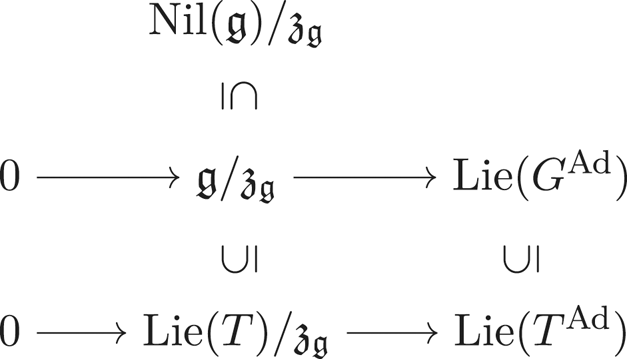1. Introduction
Let  $k$ be an algebraically closed field and let
$k$ be an algebraically closed field and let  $G$ be a
$G$ be a  $k$-group. We use the notation:
$k$-group. We use the notation:
−
 $\mathfrak {g}$ for its Lie algebra;
$\mathfrak {g}$ for its Lie algebra;−
 $G^0$ for the connected component of identity;
$G^0$ for the connected component of identity;−
 $G_{\mathrm {red}}$ for the reduced part of
$G_{\mathrm {red}}$ for the reduced part of  $G$.
$G$.
Assume that  $G$ is a reductive group. When
$G$ is a reductive group. When  $k$ is of characteristic zero, the classical theory comes with the well-defined exponential map which allows one to integrate any nilpotent element
$k$ is of characteristic zero, the classical theory comes with the well-defined exponential map which allows one to integrate any nilpotent element ![]() $x \in \mathfrak {g}$ into a unipotent element
$x \in \mathfrak {g}$ into a unipotent element  $\exp (x) \in G$. This enables one to define the Baker–Campbell–Hausdorff law which is useful to endow any nilpotent Lie subalgebra of
$\exp (x) \in G$. This enables one to define the Baker–Campbell–Hausdorff law which is useful to endow any nilpotent Lie subalgebra of  $\mathfrak {g}$ with a group law. By this process, the aforementioned Lie subalgebra becomes a unipotent group isomorphic to a unipotent subgroup of
$\mathfrak {g}$ with a group law. By this process, the aforementioned Lie subalgebra becomes a unipotent group isomorphic to a unipotent subgroup of  $G$. To summarise, when
$G$. To summarise, when  $k$ is of characteristic zero:
$k$ is of characteristic zero:
(i) any nilpotent subalgebra of
 $\mathfrak {g}$ can be integrated into a unipotent smooth connected subgroup
$\mathfrak {g}$ can be integrated into a unipotent smooth connected subgroup  $U \subseteq G$ (meaning that
$U \subseteq G$ (meaning that  $\operatorname {Lie}(U) \cong \mathfrak {u}$ as Lie algebras);
$\operatorname {Lie}(U) \cong \mathfrak {u}$ as Lie algebras);(ii) the exponential map induces an equivalence of categories between the category of finite-dimensional nilpotent
 $k$-Lie algebras and the category of unipotent algebraic
$k$-Lie algebras and the category of unipotent algebraic  $k$-groups (see, for example, [Reference Demazure and GabrielDG70, IV, § 2, n
$k$-groups (see, for example, [Reference Demazure and GabrielDG70, IV, § 2, n $^{\circ }$4, Corollaire 4.5]).
$^{\circ }$4, Corollaire 4.5]).
If now the field ![]() $k$ is of characteristic
$k$ is of characteristic ![]() $p>0$, one should try to determine whether it is possible to define analogues of the previously mentioned tools in order to integrate
$p>0$, one should try to determine whether it is possible to define analogues of the previously mentioned tools in order to integrate ![]() $p$-nil subalgebras of
$p$-nil subalgebras of ![]() $\mathfrak {g}$. As we explain in § 2.2, these
$\mathfrak {g}$. As we explain in § 2.2, these ![]() $p$-nil subalgebras are the adequate objects to consider in characteristic
$p$-nil subalgebras are the adequate objects to consider in characteristic ![]() $p>0$ for integration questions. The first step would be to get a punctual integration, that is, to find a way to integrate
$p>0$ for integration questions. The first step would be to get a punctual integration, that is, to find a way to integrate ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\mathfrak {g}$ into unipotent elements of
$\mathfrak {g}$ into unipotent elements of ![]() $G$. This is ensured as soon as there exists a
$G$. This is ensured as soon as there exists a ![]() $G$-equivariant isomorphism of reduced schemes between the reduced nilpotent scheme of
$G$-equivariant isomorphism of reduced schemes between the reduced nilpotent scheme of ![]() $\mathfrak {g}$ (denoted by
$\mathfrak {g}$ (denoted by ![]() $\mathcal {N}_{\mathrm {red}}(\mathfrak {g})$) and the reduced unipotent scheme of
$\mathcal {N}_{\mathrm {red}}(\mathfrak {g})$) and the reduced unipotent scheme of ![]() $G$ (denoted by
$G$ (denoted by ![]() $\mathcal {V}_{\mathrm {red}}(G)$). Such a map
$\mathcal {V}_{\mathrm {red}}(G)$). Such a map ![]() $\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ is called a Springer isomorphism. There is a technical subtlety here, which is detailed in § 3.1.1. For the purpose of this introduction, it is only required to have in mind that in separably good characteristics (which is the framework of this article), the nilpotent scheme is reduced, whereas in non-separably good characteristics neither the nilpotent nor the unipotent schemes are reduced. Moreover, a definition of separably good integers is provided in § 2.1.
$\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ is called a Springer isomorphism. There is a technical subtlety here, which is detailed in § 3.1.1. For the purpose of this introduction, it is only required to have in mind that in separably good characteristics (which is the framework of this article), the nilpotent scheme is reduced, whereas in non-separably good characteristics neither the nilpotent nor the unipotent schemes are reduced. Moreover, a definition of separably good integers is provided in § 2.1.
Using [Reference McNinchMcN05, Reference McNinch and TestermanMT09], one can show that such an isomorphism always exists in separably good characteristics for ![]() $G$. This has been observed by Sobaje in [Reference SobajeSob15]. Furthermore, the non-separably good characteristics case is addressed in [Reference SobajeSob18, § 7]. The author explains there why Springer isomorphisms fail to exist without this assumption. Moreover, and even if this is actually not a requirement here, one might wonder whether Springer isomorphisms are compatible with the
$G$. This has been observed by Sobaje in [Reference SobajeSob15]. Furthermore, the non-separably good characteristics case is addressed in [Reference SobajeSob18, § 7]. The author explains there why Springer isomorphisms fail to exist without this assumption. Moreover, and even if this is actually not a requirement here, one might wonder whether Springer isomorphisms are compatible with the ![]() $p$-power of the restricted Lie subalgebra one considers. We come back to this point later in the article (see the preamble of § 3.1.2 and Remark 3.10(ii)) but let us briefly explain the situation: such a compatibility is not always satisfied by Springer isomorphisms. Nevertheless, under mild conditions on
$p$-power of the restricted Lie subalgebra one considers. We come back to this point later in the article (see the preamble of § 3.1.2 and Remark 3.10(ii)) but let us briefly explain the situation: such a compatibility is not always satisfied by Springer isomorphisms. Nevertheless, under mild conditions on ![]() $p$ and
$p$ and ![]() $G$, there is always a Springer isomorphism compatible with the
$G$, there is always a Springer isomorphism compatible with the ![]() $p$-structure (see [Reference McNinchMcN03, Appendix 7]).
$p$-structure (see [Reference McNinchMcN03, Appendix 7]).
Unfortunately, the existence of a punctual integration is not sufficient to ensure a priori that any restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra can be integrated into a unipotent smooth connected subgroup of
$p$-subalgebra can be integrated into a unipotent smooth connected subgroup of ![]() $G$. If one tries to mimic the characteristic-zero framework, this would actually require the Springer isomorphism
$G$. If one tries to mimic the characteristic-zero framework, this would actually require the Springer isomorphism ![]() $\phi$ to come with a well-defined analogue of the Baker–Campbell–Hausdorff law. This analogue would allow one to make any
$\phi$ to come with a well-defined analogue of the Baker–Campbell–Hausdorff law. This analogue would allow one to make any ![]() $p$-nil subalgebra into a unipotent algebraic group. In order to exist, such a law requires even stronger conditions on
$p$-nil subalgebra into a unipotent algebraic group. In order to exist, such a law requires even stronger conditions on ![]() $p$: let us denote by
$p$: let us denote by ![]() $\operatorname {h}(G)$ the Coxeter number of
$\operatorname {h}(G)$ the Coxeter number of ![]() $G$. In [Reference SerreSer96], Serre showed that when
$G$. In [Reference SerreSer96], Serre showed that when ![]() $p\geqslant \operatorname {h}(G)$, the Baker–Campbell–Hausdorff law is well-defined. Note that under this assumption on
$p\geqslant \operatorname {h}(G)$, the Baker–Campbell–Hausdorff law is well-defined. Note that under this assumption on ![]() $p$, the series that defines the classical exponential map stops at the
$p$, the series that defines the classical exponential map stops at the ![]() $p$-power for any nilpotent element. This is a consequence of McNinch's article [Reference McNinchMcN02] in which the author shows that when
$p$-power for any nilpotent element. This is a consequence of McNinch's article [Reference McNinchMcN02] in which the author shows that when ![]() $p>\operatorname {h}(G)$, any
$p>\operatorname {h}(G)$, any ![]() $p$-nilpotent element has
$p$-nilpotent element has ![]() $p$-nilpotency order
$p$-nilpotency order ![]() $1$. Let us briefly remind the reader of the proof: one actually shows that any nilpotent element satisfies
$1$. Let us briefly remind the reader of the proof: one actually shows that any nilpotent element satisfies ![]() $\operatorname {ad}^{\operatorname {h}(G)}(x)=0$. As the regular nilpotent elements (those with centraliser of minimal dimension) are dense in
$\operatorname {ad}^{\operatorname {h}(G)}(x)=0$. As the regular nilpotent elements (those with centraliser of minimal dimension) are dense in ![]() $\mathcal {N}_{\mathrm {red}}(\mathfrak {g})$, it is enough to show this equality when the nilpotent element
$\mathcal {N}_{\mathrm {red}}(\mathfrak {g})$, it is enough to show this equality when the nilpotent element ![]() $x$ is regular. In this case the result can be obtained by looking at the weights of an associated cocharacter for which the corresponding weight spaces
$x$ is regular. In this case the result can be obtained by looking at the weights of an associated cocharacter for which the corresponding weight spaces ![]() $\mathfrak {g}_m$ are non-trivial. There are at most
$\mathfrak {g}_m$ are non-trivial. There are at most ![]() $\operatorname {h}(G)$ such weights
$\operatorname {h}(G)$ such weights ![]() $m$ and
$m$ and ![]() $\operatorname {ad}(x)(\mathfrak {g}_m) \subseteq \mathfrak {g}_{m+2}$, hence the result. This implies, in particular, that when
$\operatorname {ad}(x)(\mathfrak {g}_m) \subseteq \mathfrak {g}_{m+2}$, hence the result. This implies, in particular, that when ![]() $p>\operatorname {h}(G)$, the
$p>\operatorname {h}(G)$, the ![]() $p$-power (thus, the restricted
$p$-power (thus, the restricted ![]() $p$-algebra structure) is compatible with the exponential map. Otherwise stated, if
$p$-algebra structure) is compatible with the exponential map. Otherwise stated, if ![]() $x \in \mathfrak {g}$ is a
$x \in \mathfrak {g}$ is a ![]() $p$-nilpotent element, one indeed has
$p$-nilpotent element, one indeed has ![]() $\exp (x^{[p]}) = (\exp (x))^{[p]}$ (as
$\exp (x^{[p]}) = (\exp (x))^{[p]}$ (as ![]() $x^{[p]} = 0$).
$x^{[p]} = 0$).
Making use of this, Balaji et al. detail in [Reference Balaji, Deligne and ParameswaranBDP17, § 6] the proof of the existence of an isomorphism of algebraic groups induced by the exponential map between the Lie algebra of the unipotent radical of a Borel subgroup and this unipotent radical (there, the Lie algebra is endowed with an algebraic group structure induced by the Baker–Campbell–Hausdorff law). The existence of this isomorphism implies the existence of the desired integration when ![]() $p>\operatorname {h}(G)$. The authors attribute this result to Serre (see [Reference SerreSer96]). Note that Serre's result has been refined by Seitz in [Reference SeitzSei00, Proposition 5.3], when
$p>\operatorname {h}(G)$. The authors attribute this result to Serre (see [Reference SerreSer96]). Note that Serre's result has been refined by Seitz in [Reference SeitzSei00, Proposition 5.3], when ![]() $G$ is semisimple. There, the author establishes the existence of an isomorphism of algebraic groups induced by the exponential map between the Lie algebra of the unipotent radical of a parabolic subgroup and the corresponding unipotent radical
$G$ is semisimple. There, the author establishes the existence of an isomorphism of algebraic groups induced by the exponential map between the Lie algebra of the unipotent radical of a parabolic subgroup and the corresponding unipotent radical ![]() $U$ when
$U$ when ![]() $p$ is greater than the nilpotent class of
$p$ is greater than the nilpotent class of ![]() $U$ (which is smaller than
$U$ (which is smaller than ![]() $\operatorname {h}(G)$).
$\operatorname {h}(G)$).
Once the result of Balaji et al. has been established, one could have expected that the existence of this integration would induce, as in the characteristic-zero framework, an equivalence of categories (this time between the category of ![]() $p$-nil Lie algebras and the category of unipotent algebraic groups). This unfortunately breaks down and justifies the introduction of the notion of infinitesimal saturation as defined by Deligne in [Reference DeligneDel14] and attributed to Serre. Actually, if
$p$-nil Lie algebras and the category of unipotent algebraic groups). This unfortunately breaks down and justifies the introduction of the notion of infinitesimal saturation as defined by Deligne in [Reference DeligneDel14] and attributed to Serre. Actually, if ![]() $p>\operatorname {h}(G)$ the exponential map induces a bijective correspondence between the restricted
$p>\operatorname {h}(G)$ the exponential map induces a bijective correspondence between the restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie subalgebras of
$p$-Lie subalgebras of ![]() $\mathfrak {g}$ and the infinitesimally saturated unipotent algebraic subgroups of
$\mathfrak {g}$ and the infinitesimally saturated unipotent algebraic subgroups of ![]() $G$. All this content is explained in more detail in § 3.1.2.
$G$. All this content is explained in more detail in § 3.1.2.
In this article, we focus on integration of ![]() $p$-nil subalgebras of
$p$-nil subalgebras of ![]() $\mathfrak {g}$ when the characteristic
$\mathfrak {g}$ when the characteristic ![]() $p$ is separably good for
$p$ is separably good for ![]() $G$, which is a weaker assumption than the characteristic
$G$, which is a weaker assumption than the characteristic ![]() $p>\operatorname {h}(G)$ condition. As we show in §§ 3 and 4, the
$p>\operatorname {h}(G)$ condition. As we show in §§ 3 and 4, the ![]() $\operatorname {fppf}$-formalism introduced by Deligne in [Reference Demazure and GrothendieckSGA3I, VIB, Proposition 7.1 and Remark 7.6.1] provides a way of associating a smooth connected unipotent subgroup
$\operatorname {fppf}$-formalism introduced by Deligne in [Reference Demazure and GrothendieckSGA3I, VIB, Proposition 7.1 and Remark 7.6.1] provides a way of associating a smooth connected unipotent subgroup ![]() $J_{\mathfrak {u}} \subset G$ to any restricted
$J_{\mathfrak {u}} \subset G$ to any restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra
$p$-subalgebra ![]() $\mathfrak {u} \subseteq \mathfrak {g}$. Unfortunately, even if this subgroup is a natural candidate to integrate
$\mathfrak {u} \subseteq \mathfrak {g}$. Unfortunately, even if this subgroup is a natural candidate to integrate ![]() $\mathfrak {u}$, it is, in general, too big. One can indeed only expect the inclusion
$\mathfrak {u}$, it is, in general, too big. One can indeed only expect the inclusion ![]() $\mathfrak {u} \subseteq \mathfrak {j_u} := \operatorname {Lie}(J_{\mathfrak {u}})$ to hold true. We provide in § 3.3 a counter-example to the existence of a general integration of restricted
$\mathfrak {u} \subseteq \mathfrak {j_u} := \operatorname {Lie}(J_{\mathfrak {u}})$ to hold true. We provide in § 3.3 a counter-example to the existence of a general integration of restricted ![]() $p$-Lie algebras under the separably good characteristic assumption.
$p$-Lie algebras under the separably good characteristic assumption.
Notwithstanding this observation, and as we show in § 5, this technique still allows one to integrate some restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie algebras, for example the
$p$-Lie algebras, for example the ![]() $p$-radicals of Lie algebras whose normalisers are
$p$-radicals of Lie algebras whose normalisers are ![]() $\phi$-infinitesimally saturated (for
$\phi$-infinitesimally saturated (for ![]() $\phi$ a Springer isomorphism for
$\phi$ a Springer isomorphism for ![]() $G$). The notion of
$G$). The notion of ![]() $\phi$-infinitesimal saturation here extends the notion of infinitesimal saturation when the punctual integration comes from a Springer isomorphism that is not necessarily the truncated exponential map (as it happens, for instance, for small separably good characteristics for
$\phi$-infinitesimal saturation here extends the notion of infinitesimal saturation when the punctual integration comes from a Springer isomorphism that is not necessarily the truncated exponential map (as it happens, for instance, for small separably good characteristics for ![]() $G$).
$G$).
In § 4 we introduce this extended notion and show how, together with the aforementioned ![]() $\operatorname {fppf}$-formalism, this allows us to obtain a variation, in separably good characteristics, of a theorem of Deligne on the reduced part of infinitesimally saturated subgroups. More precisely, we show the following statement.
$\operatorname {fppf}$-formalism, this allows us to obtain a variation, in separably good characteristics, of a theorem of Deligne on the reduced part of infinitesimally saturated subgroups. More precisely, we show the following statement.
Theorem 1.1 Let ![]() $G$ be a reductive group over an algebraically closed field
$G$ be a reductive group over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is assumed to be separably good for
$p>0$ which is assumed to be separably good for ![]() $G$. Let
$G$. Let ![]() $\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ be a Springer isomorphism for
$\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ be a Springer isomorphism for ![]() $G$ and let
$G$ and let ![]() $N\subseteq G$ be a
$N\subseteq G$ be a ![]() $\phi$-infinitesimally saturated subgroup. Then:
$\phi$-infinitesimally saturated subgroup. Then:
(i) the subgroups
 $N_{\mathrm {red}}^0$ and
$N_{\mathrm {red}}^0$ and  $\operatorname {Rad}_U(N^0_{\mathrm {red}})$ are normal in
$\operatorname {Rad}_U(N^0_{\mathrm {red}})$ are normal in  $N$; moreover, the quotient
$N$; moreover, the quotient  $N/N^0_{\mathrm {red}}$ is a
$N/N^0_{\mathrm {red}}$ is a  $k$-group of multiplicative type;
$k$-group of multiplicative type;(ii) in addition, suppose that the connected reduced subgroup
 $N^0_{\mathrm {red}}$ is reductive, then there exists in
$N^0_{\mathrm {red}}$ is reductive, then there exists in  $N^0$ a central subscheme
$N^0$ a central subscheme  $M$ of multiplicative type such that
$M$ of multiplicative type such that  $(M^0\times N_{\mathrm {red}}^0)/\mu \cong N^0$, where
$(M^0\times N_{\mathrm {red}}^0)/\mu \cong N^0$, where  $\mu$ is the kernel of
$\mu$ is the kernel of  $M^0 \times N_{\mathrm {red}}^0 \rightarrow N^0$.
$M^0 \times N_{\mathrm {red}}^0 \rightarrow N^0$.
Section 6, finally, is a miscellany of technical results used in the proofs of several statements of this paper.
Let us, moreover, stress that even if after reading this introduction an integration seems to be possible only under very specific and restrictive conditions on the restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebras, the results presented in this article still allow one to extend theorems classically known in characteristic zero to the characteristic-
$p$-subalgebras, the results presented in this article still allow one to extend theorems classically known in characteristic zero to the characteristic-![]() $p$ framework. For instance, analogues of the Morozov theorem can be obtained with these techniques (see [Reference JeanninJea20]; this will also be developed in more detail in a future article). The latter states the following: let
$p$ framework. For instance, analogues of the Morozov theorem can be obtained with these techniques (see [Reference JeanninJea20]; this will also be developed in more detail in a future article). The latter states the following: let ![]() $G$ be a reductive group over a field
$G$ be a reductive group over a field ![]() $k$ of characteristic zero, if
$k$ of characteristic zero, if ![]() $\mathfrak {u}\subset \mathfrak {g}$ is a nilpotent algebra which is the nilradical of its normaliser
$\mathfrak {u}\subset \mathfrak {g}$ is a nilpotent algebra which is the nilradical of its normaliser ![]() $N_{\mathfrak {g}}(\mathfrak {u})$, this normaliser is the Lie algebra of a parabolic subgroup of
$N_{\mathfrak {g}}(\mathfrak {u})$, this normaliser is the Lie algebra of a parabolic subgroup of ![]() $G$. Obtaining analogues of this statement was the first motivation to study the questions raised in this paper. A subsidiary part of the content of this article comes from the author's PhD thesis [Reference JeanninJea20].
$G$. Obtaining analogues of this statement was the first motivation to study the questions raised in this paper. A subsidiary part of the content of this article comes from the author's PhD thesis [Reference JeanninJea20].
2. Context
2.1 Hypotheses on the characteristic
Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $p>0$ and
$p>0$ and ![]() $G$ be a reductive
$G$ be a reductive ![]() $k$-group. This section is dedicated to discuss usual assumptions made on the characteristic of
$k$-group. This section is dedicated to discuss usual assumptions made on the characteristic of ![]() $k$. We refer the reader to [Reference SteinbergSte75] and [Reference SpringerSpr69, § 0.3] for a definition and an exhaustive list of torsion characteristics for
$k$. We refer the reader to [Reference SteinbergSte75] and [Reference SpringerSpr69, § 0.3] for a definition and an exhaustive list of torsion characteristics for ![]() $G$. Good and very good characteristics are discussed, for instance, in the preamble of [Reference Levy, McNinch and TestermanLMT09] or in [Reference HerpelHer13, § 2]. We only recall here some useful facts.
$G$. Good and very good characteristics are discussed, for instance, in the preamble of [Reference Levy, McNinch and TestermanLMT09] or in [Reference HerpelHer13, § 2]. We only recall here some useful facts.
In what follows, ![]() $k$ is assumed to be algebraically closed. When
$k$ is assumed to be algebraically closed. When ![]() $G$ is a semisimple
$G$ is a semisimple ![]() $k$-group the following statement is a consequence of [Reference Levy, McNinch and TestermanLMT09, Theorem 2.2 and Remark (a)].
$k$-group the following statement is a consequence of [Reference Levy, McNinch and TestermanLMT09, Theorem 2.2 and Remark (a)].
Corollary 2.1 (Corollary of [Reference Levy, McNinch and TestermanLMT09, Theorem 2.2])
Let ![]() $G$ be a semisimple group over an algebraically closed field
$G$ be a semisimple group over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is not of torsion for
$p>0$ which is not of torsion for ![]() $G$. Let
$G$. Let ![]() $\mathfrak {u} \subseteq \mathfrak {g}$ be a restricted
$\mathfrak {u} \subseteq \mathfrak {g}$ be a restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra (see § 2.2). Then there exists a Borel subgroup
$p$-subalgebra (see § 2.2). Then there exists a Borel subgroup ![]() $B\subset G$ such that
$B\subset G$ such that ![]() $\mathfrak {u}$ is a subalgebra of
$\mathfrak {u}$ is a subalgebra of ![]() $\mathfrak {b}:=\operatorname {Lie}(B)$.
$\mathfrak {b}:=\operatorname {Lie}(B)$.
Remarks 2.2 The following remarks are of main importance in the integration process described in this article.
(i) The subalgebra ![]() $\mathfrak {u}$ is actually contained in the Lie algebra of the unipotent radical of a Borel subgroup
$\mathfrak {u}$ is actually contained in the Lie algebra of the unipotent radical of a Borel subgroup ![]() $B \subseteq G$. Indeed
$B \subseteq G$. Indeed ![]() $\mathfrak {b}$ is nothing but the semidirect sum of the Lie algebra of the unipotent radical of
$\mathfrak {b}$ is nothing but the semidirect sum of the Lie algebra of the unipotent radical of ![]() $B$, denoted by
$B$, denoted by ![]() $\operatorname {\mathfrak {rad_u}}(B)$, and the Lie algebra of a maximal torus of
$\operatorname {\mathfrak {rad_u}}(B)$, and the Lie algebra of a maximal torus of ![]() $G$, denoted by
$G$, denoted by ![]() $\mathfrak {t}$. This last factor contains no
$\mathfrak {t}$. This last factor contains no ![]() $p$-nilpotent element (see the preamble of § 2.2), whence the inclusion
$p$-nilpotent element (see the preamble of § 2.2), whence the inclusion ![]() $\mathfrak {u} \subset \operatorname {\mathfrak {rad_u}}(B)$.
$\mathfrak {u} \subset \operatorname {\mathfrak {rad_u}}(B)$.
(ii) The first point of this remark actually allows one to generalise the corollary to any reductive ![]() $k$-group
$k$-group ![]() $G$, when
$G$, when ![]() $k$ is an algebraically closed field of characteristic
$k$ is an algebraically closed field of characteristic ![]() $p>0$ that is not a torsion integer for
$p>0$ that is not a torsion integer for ![]() $G$. Let
$G$. Let ![]() $Z(G)$ be the centre of
$Z(G)$ be the centre of ![]() $G$. Also let also
$G$. Also let also ![]() $\pi : G \rightarrow G' := G/Z^0_{\mathrm {red}}(G)$ be the quotient map and set
$\pi : G \rightarrow G' := G/Z^0_{\mathrm {red}}(G)$ be the quotient map and set ![]() $\mathfrak {u}':= \operatorname {Lie}(\pi )(\mathfrak {u})$. As
$\mathfrak {u}':= \operatorname {Lie}(\pi )(\mathfrak {u})$. As ![]() $\operatorname {Lie}(Z^0_{\mathrm {red}}(G))$ is the Lie algebra of a torus it has no
$\operatorname {Lie}(Z^0_{\mathrm {red}}(G))$ is the Lie algebra of a torus it has no ![]() $p$-nilpotent element (this is detailed at the end of the proof of Lemma 2.6; note that the assumption made in the statement of this lemma is not necessary to prove this specific fact). Therefore, one has
$p$-nilpotent element (this is detailed at the end of the proof of Lemma 2.6; note that the assumption made in the statement of this lemma is not necessary to prove this specific fact). Therefore, one has ![]() $\mathfrak {u} \cong \mathfrak {u'}$. By what precedes, there exists a Borel subgroup
$\mathfrak {u} \cong \mathfrak {u'}$. By what precedes, there exists a Borel subgroup ![]() $B' \subset G'$ such that
$B' \subset G'$ such that ![]() $\mathfrak {u'} \subseteq \operatorname {\mathfrak {rad_u}}(B') \subset \mathfrak {b'}$. Let
$\mathfrak {u'} \subseteq \operatorname {\mathfrak {rad_u}}(B') \subset \mathfrak {b'}$. Let ![]() $B= \pi ^{-1}(B')$ be the preimage of
$B= \pi ^{-1}(B')$ be the preimage of ![]() $B'$. As
$B'$. As ![]() $\operatorname {\mathfrak {rad_u}}(B') \cong \operatorname {\mathfrak {rad_u}}(B)$ one can always assume that
$\operatorname {\mathfrak {rad_u}}(B') \cong \operatorname {\mathfrak {rad_u}}(B)$ one can always assume that ![]() $\mathfrak {u}$ is the subalgebra of the Lie algebra of the unipotent radical of a Borel subgroup of
$\mathfrak {u}$ is the subalgebra of the Lie algebra of the unipotent radical of a Borel subgroup of ![]() $\mathfrak {b} \subseteq \mathfrak {g}$.
$\mathfrak {b} \subseteq \mathfrak {g}$.
Separably good characteristics are defined by Pevtsova and Stark in [Reference Pevtsova and StarkPS18, Definition 2.2].
(i) When
 $G$ is semisimple, let
$G$ is semisimple, let  $G^{\operatorname {sc}}$ be the simply connected cover of
$G^{\operatorname {sc}}$ be the simply connected cover of  $G$. The characteristic
$G$. The characteristic  $p$ is separably good for
$p$ is separably good for  $G$ if
$G$ if  $p$ is good for
$p$ is good for  $G$ and if the isogeny
$G$ and if the isogeny  $G^{\operatorname {sc}} \rightarrow G$ is separable.
$G^{\operatorname {sc}} \rightarrow G$ is separable.(ii) When
 $G$ is reductive, the characteristic
$G$ is reductive, the characteristic  $p$ is separably good for
$p$ is separably good for  $G$ if it is separably good for its derived group
$G$ if it is separably good for its derived group  $[G,G]$.
$[G,G]$.
As underlined by Pevtsova and Stark, if ![]() $p$ is very good for
$p$ is very good for ![]() $G$, it is also separably good. Nevertheless, this last condition is only restrictive for type
$G$, it is also separably good. Nevertheless, this last condition is only restrictive for type ![]() $A$, which is the only type for which very good and separably good characteristics do not coincide. As an example,
$A$, which is the only type for which very good and separably good characteristics do not coincide. As an example, ![]() $p$ is separably good but not very good for
$p$ is separably good but not very good for ![]() $\operatorname {SL}_p$ or
$\operatorname {SL}_p$ or ![]() $\operatorname {GL}_p$. However, it is not separably good nor very good for
$\operatorname {GL}_p$. However, it is not separably good nor very good for ![]() $\operatorname {PGL}_p$.
$\operatorname {PGL}_p$.
Moreover, let ![]() $G$ be a reductive algebraic group over an algebraically closed field
$G$ be a reductive algebraic group over an algebraically closed field ![]() $k= \bar {k}$ and consider a maximal torus
$k= \bar {k}$ and consider a maximal torus ![]() $T \subsetneq G$. The tuple
$T \subsetneq G$. The tuple ![]() $\mathcal {R}(G) = (X(T), \Phi, Y(T), \Phi ^{\vee })$ whose components are respectively the associated group of characters, the root system, the group of cocharacters and the coroot system, is a root datum for
$\mathcal {R}(G) = (X(T), \Phi, Y(T), \Phi ^{\vee })$ whose components are respectively the associated group of characters, the root system, the group of cocharacters and the coroot system, is a root datum for ![]() $G$. This root datum is unique up to isomorphism (see [Reference Demazure and GrothendieckSGA3III, XXII, 2.6]). A prime number is pretty good for
$G$. This root datum is unique up to isomorphism (see [Reference Demazure and GrothendieckSGA3III, XXII, 2.6]). A prime number is pretty good for ![]() $G$ if, given any subset
$G$ if, given any subset ![]() $\Phi '\subseteq \Phi$ both the groups
$\Phi '\subseteq \Phi$ both the groups ![]() $X(T)/\mathbb {Z}\Phi '$ and
$X(T)/\mathbb {Z}\Phi '$ and ![]() $Y(T)/\mathbb {Z}\Phi '^{\vee }$ have no
$Y(T)/\mathbb {Z}\Phi '^{\vee }$ have no ![]() $p$-torsion. Note that these definitions still make sense when
$p$-torsion. Note that these definitions still make sense when ![]() $k$ is no longer algebraically closed but this goes beyond the framework of this article. Once again, this condition answers type
$k$ is no longer algebraically closed but this goes beyond the framework of this article. Once again, this condition answers type ![]() $A$-phenomenon. It is studied by Herpel in [Reference HerpelHer13]. In particular, pretty good and very good primes are the same when
$A$-phenomenon. It is studied by Herpel in [Reference HerpelHer13]. In particular, pretty good and very good primes are the same when ![]() $G$ is semisimple (see [Reference HerpelHer13, Lemma 2.12]). For instance,
$G$ is semisimple (see [Reference HerpelHer13, Lemma 2.12]). For instance, ![]() $p$ is not pretty good for
$p$ is not pretty good for ![]() $\operatorname {SL}_p$. However, if
$\operatorname {SL}_p$. However, if ![]() $G$ is an arbitrary group, being a very good prime is a more restrictive condition, indeed
$G$ is an arbitrary group, being a very good prime is a more restrictive condition, indeed ![]() $p$ is pretty good but not very good for
$p$ is pretty good but not very good for ![]() $\operatorname {GL}_p$ (see [Reference HerpelHer13, Example 2.13]). Finally, as explained in [Reference SteinbergSte75, 2.4], if
$\operatorname {GL}_p$ (see [Reference HerpelHer13, Example 2.13]). Finally, as explained in [Reference SteinbergSte75, 2.4], if ![]() $p$ does not divide the order of
$p$ does not divide the order of ![]() $X(T)/\mathbb {Z}\Phi$, then
$X(T)/\mathbb {Z}\Phi$, then ![]() $p$ is separably good for
$p$ is separably good for ![]() $G$. Hence, any pretty good prime is separably good for
$G$. Hence, any pretty good prime is separably good for ![]() $G$. In particular, as
$G$. In particular, as ![]() $p$ is not separably good for
$p$ is not separably good for ![]() $\operatorname {PGL}_p$ it is not pretty good either. To summarise, one has the following chain of implications:
$\operatorname {PGL}_p$ it is not pretty good either. To summarise, one has the following chain of implications:
2.2 From characteristic zero to positive characteristics, defining the good analogues: sorites on restricted  $p$-Lie algebras
$p$-Lie algebras
Before going any further, one needs to introduce the good analogues in characteristic ![]() $p>0$ for the objects involved in the characteristic-zero setting. This is done in this section. The results presented in the following are stated in the most general way. In particular, we do not assume a priori (and unless explicitly stated) in this subsection that the field
$p>0$ for the objects involved in the characteristic-zero setting. This is done in this section. The results presented in the following are stated in the most general way. In particular, we do not assume a priori (and unless explicitly stated) in this subsection that the field ![]() $k$ is algebraically closed.
$k$ is algebraically closed.
Let ![]() $\mathfrak {g}$ be a finite-dimensional restricted
$\mathfrak {g}$ be a finite-dimensional restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie algebra over
$p$-Lie algebra over ![]() $k$. In what follows, we denote by
$k$. In what follows, we denote by ![]() $[p]$ the
$[p]$ the ![]() $p$-structure for
$p$-structure for ![]() $\mathfrak {g}$. Let us stress that, in particular, the Lie algebra of any
$\mathfrak {g}$. Let us stress that, in particular, the Lie algebra of any ![]() $k$-group scheme
$k$-group scheme ![]() $G$ is endowed with such a
$G$ is endowed with such a ![]() $p$-structure (see [Reference Demazure and GabrielDG70, II, § 7, n
$p$-structure (see [Reference Demazure and GabrielDG70, II, § 7, n![]() $^{\circ }$3.4]). Moreover, for any algebraic subgroup
$^{\circ }$3.4]). Moreover, for any algebraic subgroup ![]() $H \subset G$, the
$H \subset G$, the ![]() $p$-structure on
$p$-structure on ![]() $\operatorname {Lie}(H) := \mathfrak {h}$ inherited from the group is compatible with that on
$\operatorname {Lie}(H) := \mathfrak {h}$ inherited from the group is compatible with that on ![]() $\mathfrak {g}$. In other words,
$\mathfrak {g}$. In other words, ![]() $\mathfrak {h}$ is a restricted
$\mathfrak {h}$ is a restricted ![]() $p$-subalgebra of
$p$-subalgebra of ![]() $\mathfrak {g}$. We refer the reader to [Reference Strade and FarnsteinerSF88, § 2, Définition] for general theory of restricted
$\mathfrak {g}$. We refer the reader to [Reference Strade and FarnsteinerSF88, § 2, Définition] for general theory of restricted ![]() $p$-Lie algebras.
$p$-Lie algebras.
Let ![]() $k$ be a field and let
$k$ be a field and let ![]() $\mathfrak {g}$ be a
$\mathfrak {g}$ be a ![]() $k$-Lie algebra. As a reminder:
$k$-Lie algebra. As a reminder:
(i) the solvable radical (or radical) of
 $\mathfrak {g}$, denoted by
$\mathfrak {g}$, denoted by  $\operatorname {rad}(\mathfrak {g})$, is the largest solvable ideal of
$\operatorname {rad}(\mathfrak {g})$, is the largest solvable ideal of  $\mathfrak {g}$ (see [Reference Strade and FarnsteinerSF88, § 1.7, Definition]);
$\mathfrak {g}$ (see [Reference Strade and FarnsteinerSF88, § 1.7, Definition]);(ii) the nilradical of
 $\mathfrak {g}$, denoted by
$\mathfrak {g}$, denoted by  $\operatorname {Nil}(\mathfrak {g})$, is the largest nilpotent ideal of
$\operatorname {Nil}(\mathfrak {g})$, is the largest nilpotent ideal of  $\mathfrak {g}$; in particular, all its elements are
$\mathfrak {g}$; in particular, all its elements are  $\operatorname {ad}$-nilpotent, by a corollary of Engel Theorem (see, for example, [Reference BourbakiBou71, § 4, n
$\operatorname {ad}$-nilpotent, by a corollary of Engel Theorem (see, for example, [Reference BourbakiBou71, § 4, n $^{\circ }$2 Corollaire 1]); when
$^{\circ }$2 Corollaire 1]); when  $k$ is of characteristic zero, the nilradical is nothing but the set of
$k$ is of characteristic zero, the nilradical is nothing but the set of  $\operatorname {ad}$-nilpotent elements of the radical of
$\operatorname {ad}$-nilpotent elements of the radical of  $\mathfrak {g}$ (see [Reference Strade and FarnsteinerSF88, § 1, Corollary 3.10] and [Reference BourbakiBou71, § 5, Corollaire 7]); let us stress that the equality
$\mathfrak {g}$ (see [Reference Strade and FarnsteinerSF88, § 1, Corollary 3.10] and [Reference BourbakiBou71, § 5, Corollaire 7]); let us stress that the equality  $\operatorname {Nil}(\mathfrak {g}/\operatorname {Nil}(\mathfrak {g}))= 0$ is not always satisfied when
$\operatorname {Nil}(\mathfrak {g}/\operatorname {Nil}(\mathfrak {g}))= 0$ is not always satisfied when  $k$ is of characteristic
$k$ is of characteristic  $p>0$ (see [Reference Strade and FarnsteinerSF88, p. 20] for a counter-example);
$p>0$ (see [Reference Strade and FarnsteinerSF88, p. 20] for a counter-example);(iii) a subalgebra
 $\mathfrak {h} \subseteq \mathfrak {g}$ is nil if any element of
$\mathfrak {h} \subseteq \mathfrak {g}$ is nil if any element of  $\mathfrak {h}$ is
$\mathfrak {h}$ is  $\operatorname {ad}$-nilpotent for the bracket on
$\operatorname {ad}$-nilpotent for the bracket on  $\mathfrak {g}$; any nil and finite-dimensional
$\mathfrak {g}$; any nil and finite-dimensional  $k$-Lie algebra is nilpotent.
$k$-Lie algebra is nilpotent.
One may wonder whether these classical objects inherit a ![]() $p$-structure compatible with that of
$p$-structure compatible with that of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Lemma 2.3 Let ![]() $\mathfrak {h}$ be a restricted
$\mathfrak {h}$ be a restricted ![]() $p$-Lie algebra over
$p$-Lie algebra over ![]() $k$. Then
$k$. Then ![]() $\operatorname {rad}(\mathfrak {h})$ is a restricted
$\operatorname {rad}(\mathfrak {h})$ is a restricted ![]() $p$-subalgebra of
$p$-subalgebra of ![]() $\mathfrak {h}$.
$\mathfrak {h}$.
Proof. Let us consider the morphism of Lie algebras ![]() $\mathfrak {h} \twoheadrightarrow \mathfrak {h/\operatorname {rad}(h)}$. According to [Reference Strade and FarnsteinerSF88, 1, § 7, Theorem 7.2] one has
$\mathfrak {h} \twoheadrightarrow \mathfrak {h/\operatorname {rad}(h)}$. According to [Reference Strade and FarnsteinerSF88, 1, § 7, Theorem 7.2] one has ![]() $\operatorname {rad}(\mathfrak {h/\operatorname {rad}(h)}) = 0$, thus the centre
$\operatorname {rad}(\mathfrak {h/\operatorname {rad}(h)}) = 0$, thus the centre ![]() $\mathfrak {z}_{\operatorname {rad}(\mathfrak {h/\operatorname {rad}(h)})}$ is trivial (because
$\mathfrak {z}_{\operatorname {rad}(\mathfrak {h/\operatorname {rad}(h)})}$ is trivial (because ![]() $\mathfrak {z_g} \subseteq \operatorname {rad}(\mathfrak {g})$, see, for instance, the first lines of the proof of Lemma 2.6). By [Reference Strade and FarnsteinerSF88, 2.3, Exercise 7], the radical of
$\mathfrak {z_g} \subseteq \operatorname {rad}(\mathfrak {g})$, see, for instance, the first lines of the proof of Lemma 2.6). By [Reference Strade and FarnsteinerSF88, 2.3, Exercise 7], the radical of ![]() $\mathfrak {h}$ is a
$\mathfrak {h}$ is a ![]() $p$-Lie subalgebra.
$p$-Lie subalgebra.
Assume the Lie algebra ![]() $\mathfrak {g}$ derives from an affine algebraic
$\mathfrak {g}$ derives from an affine algebraic ![]() $k$-group. Let
$k$-group. Let ![]() $\rho : G \rightarrow \operatorname {GL}(V)$ be a faithful representation of finite dimension. An element
$\rho : G \rightarrow \operatorname {GL}(V)$ be a faithful representation of finite dimension. An element ![]() $x \in \mathfrak {g}$ is nilpotent, or
$x \in \mathfrak {g}$ is nilpotent, or ![]() $\mathfrak {g}$-nilpotent, if
$\mathfrak {g}$-nilpotent, if ![]() $\operatorname {Lie}(\rho )(x)$ is a nilpotent element of
$\operatorname {Lie}(\rho )(x)$ is a nilpotent element of ![]() $\mathfrak {\operatorname {\mathfrak {gl}}}(V)$ (let us stress that
$\mathfrak {\operatorname {\mathfrak {gl}}}(V)$ (let us stress that ![]() $\operatorname {Lie}(\rho )$ is still injective because the Lie functor is left exact (see [Reference Demazure and GabrielDG70, II, § 4, 1.5])). In the same way, an element
$\operatorname {Lie}(\rho )$ is still injective because the Lie functor is left exact (see [Reference Demazure and GabrielDG70, II, § 4, 1.5])). In the same way, an element ![]() $x \in \mathfrak {g}$ is semisimple if
$x \in \mathfrak {g}$ is semisimple if ![]() $\operatorname {Lie}(\rho )(x)$ is a semisimple element of
$\operatorname {Lie}(\rho )(x)$ is a semisimple element of ![]() $\mathfrak {\operatorname {\mathfrak {gl}}}(V)$. These notions are independent from the choice of the faithful representation
$\mathfrak {\operatorname {\mathfrak {gl}}}(V)$. These notions are independent from the choice of the faithful representation ![]() $\rho$ (see [Reference BorelBor91, I.4.4, Theorem]). Let us emphasise that when
$\rho$ (see [Reference BorelBor91, I.4.4, Theorem]). Let us emphasise that when ![]() $k$ is perfect any
$k$ is perfect any ![]() $x \in \mathfrak {g}$ has a Jordan decomposition in
$x \in \mathfrak {g}$ has a Jordan decomposition in ![]() $\mathfrak {g}$ (see, for example, [Reference BorelBor91, I.4.4, Theorem]).
$\mathfrak {g}$ (see, for example, [Reference BorelBor91, I.4.4, Theorem]).
More generally, if one does no longer consider that ![]() $\mathfrak {g}$ is the Lie algebra of an algebraic group, then:
$\mathfrak {g}$ is the Lie algebra of an algebraic group, then:
− if
 $\mathfrak {g}$ is a semisimple Lie algebra over a field of characteristic zero (whatever the characteristic, semisimple Lie algebras are those with trivial solvable radical), any element
$\mathfrak {g}$ is a semisimple Lie algebra over a field of characteristic zero (whatever the characteristic, semisimple Lie algebras are those with trivial solvable radical), any element  $x \in \mathfrak {g}$ has a unique Jordan decomposition (see, for example, [Reference BourbakiBou71, § 6, n
$x \in \mathfrak {g}$ has a unique Jordan decomposition (see, for example, [Reference BourbakiBou71, § 6, n $^{\circ }$3, Théorème 3]);
$^{\circ }$3, Théorème 3]);− similarly, if
 $k$ is a perfect field of characteristic
$k$ is a perfect field of characteristic  $p>0$ and
$p>0$ and  $\mathfrak {g}$ is finitely generated restricted
$\mathfrak {g}$ is finitely generated restricted  $p$-Lie algebra, a decomposition
$p$-Lie algebra, a decomposition  $x = x_s + x_n$ (with
$x = x_s + x_n$ (with  $x_s$ semisimple and
$x_s$ semisimple and  $x_n$ nilpotent) always exists, with the additional condition for the nilpotent part to be
$x_n$ nilpotent) always exists, with the additional condition for the nilpotent part to be  $p$-nilpotent (see [Reference Strade and FarnsteinerSF88, 2.3, Theorem 3.5]).
$p$-nilpotent (see [Reference Strade and FarnsteinerSF88, 2.3, Theorem 3.5]).
An element ![]() $x \in \mathfrak {g}$ is
$x \in \mathfrak {g}$ is ![]() $p$-nilpotent if there exists an integer
$p$-nilpotent if there exists an integer ![]() $m \in \mathbb {N}$ such that
$m \in \mathbb {N}$ such that ![]() $x^{[p^m]}=0$. When it exists, the smallest
$x^{[p^m]}=0$. When it exists, the smallest ![]() $m \in \mathbb {N}$ such that
$m \in \mathbb {N}$ such that ![]() $x^{[p^m]}=0$ is called the order of
$x^{[p^m]}=0$ is called the order of ![]() $p$-nilpotency of
$p$-nilpotency of ![]() $x$. In this framework, an element
$x$. In this framework, an element ![]() $x \in \mathfrak {g}$ is
$x \in \mathfrak {g}$ is ![]() $p$-semisimple if
$p$-semisimple if ![]() $x$ belongs to the restricted
$x$ belongs to the restricted ![]() $p$-Lie algebra generated by
$p$-Lie algebra generated by ![]() $x^{[p]}$. Finally, an element
$x^{[p]}$. Finally, an element ![]() $x \in \mathfrak {g}$ is toral if
$x \in \mathfrak {g}$ is toral if ![]() $x^{[p]} = x$. According to [Reference Strade and FarnsteinerSF88, § 2, Proposition 3.3] and the remark that follows this proposition, both definitions of semisimplicity are equivalent. In what follows, an element is thus said to be
$x^{[p]} = x$. According to [Reference Strade and FarnsteinerSF88, § 2, Proposition 3.3] and the remark that follows this proposition, both definitions of semisimplicity are equivalent. In what follows, an element is thus said to be ![]() $p$-semisimple (respectively,
$p$-semisimple (respectively, ![]() $p$-nilpotent) if it is semisimple (respectively,
$p$-nilpotent) if it is semisimple (respectively, ![]() $\mathfrak {g}$-nilpotent). This equivalence of definitions is a consequence of the Iwasawa theorem (see [Reference IwasawaIwa48]) which ensures that any Lie subalgebra of finite dimension over a field of characteristic
$\mathfrak {g}$-nilpotent). This equivalence of definitions is a consequence of the Iwasawa theorem (see [Reference IwasawaIwa48]) which ensures that any Lie subalgebra of finite dimension over a field of characteristic ![]() $p>0$ has a faithful representation. This result has afterwards been extended by Jacobson to the framework of finite-dimensional restricted
$p>0$ has a faithful representation. This result has afterwards been extended by Jacobson to the framework of finite-dimensional restricted ![]() $p$-Lie algebras with the additional constraint that the involved representation is compatible with the
$p$-Lie algebras with the additional constraint that the involved representation is compatible with the ![]() $p$-structure (see [Reference JacobsonJac52] and [Reference SeligmanSel67, I, § 4, Theorem I.4.2]).
$p$-structure (see [Reference JacobsonJac52] and [Reference SeligmanSel67, I, § 4, Theorem I.4.2]).
Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $p>0$. Let
$p>0$. Let ![]() $\mathfrak {h}$ be a restricted
$\mathfrak {h}$ be a restricted ![]() $p$-algebra (as mentioned previously this is the case, in particular, if
$p$-algebra (as mentioned previously this is the case, in particular, if ![]() $\mathfrak {h}$ derives from a subgroup
$\mathfrak {h}$ derives from a subgroup ![]() $H \subset G$). The restricted
$H \subset G$). The restricted ![]() $p$-subalgebra
$p$-subalgebra ![]() $\mathfrak {h}$ is
$\mathfrak {h}$ is ![]() $p$-nilpotent if there exists an integer
$p$-nilpotent if there exists an integer ![]() $n \in \mathbb {N}$ such that
$n \in \mathbb {N}$ such that ![]() $\mathfrak {h}^{[p^n]} = 0$. When
$\mathfrak {h}^{[p^n]} = 0$. When ![]() $\mathfrak {g}$ is of finite dimension any restricted
$\mathfrak {g}$ is of finite dimension any restricted ![]() $p$-subalgebra which is
$p$-subalgebra which is ![]() $p$-nilpotent is also
$p$-nilpotent is also ![]() $p$-nil (that is, any of its elements are
$p$-nil (that is, any of its elements are ![]() $p$-nilpotent).
$p$-nilpotent).
It is worth noting that the study of ideals of ![]() $\mathfrak {g}$ that consist only of semisimple elements can also be very instructive. Let us recall the following result as an illustration (see [Reference Borel and TitsBT72, Proposition 2.13]): let
$\mathfrak {g}$ that consist only of semisimple elements can also be very instructive. Let us recall the following result as an illustration (see [Reference Borel and TitsBT72, Proposition 2.13]): let ![]() $\mathfrak {g}$ be the Lie algebra of a reductive
$\mathfrak {g}$ be the Lie algebra of a reductive ![]() $k$-group
$k$-group ![]() $G$. We consider the action of
$G$. We consider the action of ![]() $G$ on
$G$ on ![]() $\mathfrak {g}$ by conjugation. Let
$\mathfrak {g}$ by conjugation. Let ![]() $\mathfrak {j} \subseteq \mathfrak {g}$ be an ideal which in
$\mathfrak {j} \subseteq \mathfrak {g}$ be an ideal which in ![]() $G$-stable. Then
$G$-stable. Then ![]() $\mathfrak {j}$ consists only of semisimple elements if and only if
$\mathfrak {j}$ consists only of semisimple elements if and only if ![]() $\mathfrak {j} \subseteq \mathfrak {z_g}$.
$\mathfrak {j} \subseteq \mathfrak {z_g}$.
Let us finally underline that, although in positive characteristic the nilradical of a restricted ![]() $p$-algebra is well-defined, it no longer satisfies the properties it had in characteristic zero. Hence, we need to introduce the following object which appears to be, under some additional hypotheses, the good analogue to consider in characteristic
$p$-algebra is well-defined, it no longer satisfies the properties it had in characteristic zero. Hence, we need to introduce the following object which appears to be, under some additional hypotheses, the good analogue to consider in characteristic ![]() $p>0$.
$p>0$.
Definition 2.4 Let ![]() $\mathfrak {h}$ be a restricted
$\mathfrak {h}$ be a restricted ![]() $p$-algebra. The
$p$-algebra. The ![]() $p$-radical of
$p$-radical of ![]() $\mathfrak {h}$, denoted by
$\mathfrak {h}$, denoted by ![]() $\operatorname {rad}_p(\mathfrak {h})$, is the maximal
$\operatorname {rad}_p(\mathfrak {h})$, is the maximal ![]() $p$-nilpotent
$p$-nilpotent ![]() $p$-ideal of
$p$-ideal of ![]() $\mathfrak {h}$ (such an object exists; see, for instance, [Reference Strade and FarnsteinerSF88, 2.1, Corollary 1.6]).
$\mathfrak {h}$ (such an object exists; see, for instance, [Reference Strade and FarnsteinerSF88, 2.1, Corollary 1.6]).
Let us also stress that the Lie algebra of the unipotent radical of a connected algebraic group ![]() $H$, denoted by
$H$, denoted by ![]() $\mathfrak {\operatorname {\mathfrak {rad_u}}}(H)$, is an ideal of
$\mathfrak {\operatorname {\mathfrak {rad_u}}}(H)$, is an ideal of ![]() $\operatorname {Nil}(\mathfrak {h})$ (as
$\operatorname {Nil}(\mathfrak {h})$ (as ![]() $U$ is a unipotent normal subgroup of
$U$ is a unipotent normal subgroup of ![]() $\operatorname {Rad}(H)$). We aim to compare these different objects.
$\operatorname {Rad}(H)$). We aim to compare these different objects.
Lemma 2.5 Let ![]() $\mathfrak {h}$ be a restricted
$\mathfrak {h}$ be a restricted ![]() $p$-algebra. Then:
$p$-algebra. Then:
(i) the inclusions
 $\operatorname {rad}_p(\mathfrak {h}) \subseteq \operatorname {Nil}(\mathfrak {h}) \subseteq \operatorname {rad}(\mathfrak {h})$ are satisfied;
$\operatorname {rad}_p(\mathfrak {h}) \subseteq \operatorname {Nil}(\mathfrak {h}) \subseteq \operatorname {rad}(\mathfrak {h})$ are satisfied;(ii) the
 $p$-radical of
$p$-radical of  $\mathfrak {h}$ is a subset of the set of all
$\mathfrak {h}$ is a subset of the set of all  $p$-nilpotent elements of
$p$-nilpotent elements of  $\operatorname {rad}(\mathfrak {h})$;
$\operatorname {rad}(\mathfrak {h})$;(iii) let us denote by
 $\mathfrak {z_h}$ the centre of
$\mathfrak {z_h}$ the centre of  $\mathfrak {h}$; the equality
$\mathfrak {h}$; the equality  $\operatorname {rad}_p(\mathfrak {h}) = \operatorname {Nil}(\mathfrak {h})$ holds true if and only if the inclusion
$\operatorname {rad}_p(\mathfrak {h}) = \operatorname {Nil}(\mathfrak {h})$ holds true if and only if the inclusion  $\mathfrak {z_h} \subseteq \operatorname {rad}_p(\mathfrak {h})$ is satisfied.
$\mathfrak {z_h} \subseteq \operatorname {rad}_p(\mathfrak {h})$ is satisfied.
Proof. We show each point of the lemma separately.
(i) The inclusion ![]() $\operatorname {rad}_p(\mathfrak {h}) \subseteq \operatorname {Nil}(\mathfrak {h})$ is clear as
$\operatorname {rad}_p(\mathfrak {h}) \subseteq \operatorname {Nil}(\mathfrak {h})$ is clear as ![]() $\operatorname {rad}_p(\mathfrak {h})$ is a nil ideal of
$\operatorname {rad}_p(\mathfrak {h})$ is a nil ideal of ![]() $\mathfrak {h}$ (because it is
$\mathfrak {h}$ (because it is ![]() $p$-nil). Hence, it is a nilpotent ideal of
$p$-nil). Hence, it is a nilpotent ideal of ![]() $\mathfrak {h}$ because the Lie algebras involved here are of finite dimension.
$\mathfrak {h}$ because the Lie algebras involved here are of finite dimension.
The second inclusion is also direct as any nilpotent ideal is in particular solvable (see, for example, [Reference Strade and FarnsteinerSF88, §1.5 Remark]). Hence, the first point of the lemma is shown.
(ii) This last inclusion being satisfied and ![]() $\operatorname {rad}_p(\mathfrak {h})$ being
$\operatorname {rad}_p(\mathfrak {h})$ being ![]() $p$-nil, the restricted
$p$-nil, the restricted ![]() $p$-ideal is necessarily contained in the set of all
$p$-ideal is necessarily contained in the set of all ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\operatorname {rad}(\mathfrak {h})$. This ends the proof of part (ii).
$\operatorname {rad}(\mathfrak {h})$. This ends the proof of part (ii).
(iii) The centre of ![]() $\mathfrak {h}$ is an abelian ideal of
$\mathfrak {h}$ is an abelian ideal of ![]() $\mathfrak {h}$. It is, therefore, contained in the nilradical of
$\mathfrak {h}$. It is, therefore, contained in the nilradical of ![]() $\mathfrak {h}$. Thus, if one has the equality
$\mathfrak {h}$. Thus, if one has the equality ![]() $\operatorname {Nil}(\mathfrak {h})=\operatorname {rad}_p(\mathfrak {h})$, one also has the inclusion
$\operatorname {Nil}(\mathfrak {h})=\operatorname {rad}_p(\mathfrak {h})$, one also has the inclusion ![]() $\mathfrak {z_h}\subseteq \operatorname {rad}_p(\mathfrak {h})$.
$\mathfrak {z_h}\subseteq \operatorname {rad}_p(\mathfrak {h})$.
Reciprocally, assume the inclusion ![]() $\mathfrak {z_h} \subseteq \operatorname {rad}_p(\mathfrak {h})$ to be satisfied and let us show that any
$\mathfrak {z_h} \subseteq \operatorname {rad}_p(\mathfrak {h})$ to be satisfied and let us show that any ![]() $x \in \operatorname {Nil}(\mathfrak {h})$ is
$x \in \operatorname {Nil}(\mathfrak {h})$ is ![]() $p$-nilpotent. First, it is
$p$-nilpotent. First, it is ![]() $\operatorname {ad}$-nilpotent according to Corollary [Reference BourbakiBou71, § 4, n
$\operatorname {ad}$-nilpotent according to Corollary [Reference BourbakiBou71, § 4, n![]() $^{\circ }$2, Corollaire 1] because the ideal
$^{\circ }$2, Corollaire 1] because the ideal ![]() $\operatorname {Nil}(\mathfrak {h})$ is nilpotent. Moreover, as the Lie algebra
$\operatorname {Nil}(\mathfrak {h})$ is nilpotent. Moreover, as the Lie algebra ![]() $\mathfrak {h}$ is endowed with a
$\mathfrak {h}$ is endowed with a ![]() $p$-structure, there exists an integer
$p$-structure, there exists an integer ![]() $n$ such that
$n$ such that ![]() $\operatorname {ad}(x)^{p^n}= 0 = \operatorname {ad}(x^{[p^n]}).$ In other words
$\operatorname {ad}(x)^{p^n}= 0 = \operatorname {ad}(x^{[p^n]}).$ In other words ![]() $x^{[p^n]}$ belongs to the centre of
$x^{[p^n]}$ belongs to the centre of ![]() $\mathfrak {h}$. As we assumed the inclusion
$\mathfrak {h}$. As we assumed the inclusion ![]() $\mathfrak {z_h} \subseteq \operatorname {rad}_p(\mathfrak {h})$ to hold true, the element
$\mathfrak {z_h} \subseteq \operatorname {rad}_p(\mathfrak {h})$ to hold true, the element ![]() $x^{[p^n]}$ is actually
$x^{[p^n]}$ is actually ![]() $p$-nilpotent (the
$p$-nilpotent (the ![]() $p$-radical being
$p$-radical being ![]() $p$-nil). Hence, there exists an integer
$p$-nil). Hence, there exists an integer ![]() $m$ such that
$m$ such that ![]() $(x^{[p^n]})^{[p^m]} = (x ^{[p^{n+m}]}) =0$, whence the
$(x^{[p^n]})^{[p^m]} = (x ^{[p^{n+m}]}) =0$, whence the ![]() $p$-nilpotency of any element of
$p$-nilpotency of any element of ![]() $\operatorname {Nil}(\mathfrak {h})$. This implies that
$\operatorname {Nil}(\mathfrak {h})$. This implies that ![]() $\operatorname {Nil}(\mathfrak {h})$ is a restricted
$\operatorname {Nil}(\mathfrak {h})$ is a restricted ![]() $p$-ideal
$p$-ideal ![]() $p$-nil of
$p$-nil of ![]() $\mathfrak {h}$, because the nilradical of
$\mathfrak {h}$, because the nilradical of ![]() $\mathfrak {h}$ is a restricted
$\mathfrak {h}$ is a restricted ![]() $p$-ideal according to Lemma [Reference Strade and FarnsteinerSF88, 2.3, Exercise 5d]. This leads to the desired equality. Thus, we have shown part (iii).
$p$-ideal according to Lemma [Reference Strade and FarnsteinerSF88, 2.3, Exercise 5d]. This leads to the desired equality. Thus, we have shown part (iii).
When ![]() $\mathfrak {g}$ derives from a smooth connected algebraic
$\mathfrak {g}$ derives from a smooth connected algebraic ![]() $k$-group
$k$-group ![]() $G$, these objects should be compared with the Lie algebra of the radical (respectively of the unipotent radical) of
$G$, these objects should be compared with the Lie algebra of the radical (respectively of the unipotent radical) of ![]() $G$.
$G$.
Lemma 2.6 Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $p \geqslant 3$ and
$p \geqslant 3$ and ![]() $G$ be a reductive
$G$ be a reductive ![]() $k$-group. Then the equalities
$k$-group. Then the equalities ![]() $\mathfrak {z_g} = \operatorname {rad}(\mathfrak {g}) = \operatorname {Nil}(\mathfrak {g})$ hold true.
$\mathfrak {z_g} = \operatorname {rad}(\mathfrak {g}) = \operatorname {Nil}(\mathfrak {g})$ hold true.
Remark 2.7 The assumption on the characteristic allows a uniform proof of the above lemma. Notwithstanding this point, it is worth noting that the characteristic-two case can be handled by a case-by-case analysis (by making use of [Reference HogeweijHog82, Table 1]). Moreover, Lemma 2.10 provides the equality ![]() $\mathfrak {z_g} = \operatorname {Nil}(\mathfrak {g})$ (which is a weaker result) in any characteristic
$\mathfrak {z_g} = \operatorname {Nil}(\mathfrak {g})$ (which is a weaker result) in any characteristic ![]() $p>0$. This last statement appears as a Corollary of [Reference VasiuVas05, Lemma 2.1].
$p>0$. This last statement appears as a Corollary of [Reference VasiuVas05, Lemma 2.1].
The following lemma is useful in the proof of Lemma 2.6.
Lemma 2.8 Let ![]() $\widetilde {G}$ and
$\widetilde {G}$ and ![]() $G$ be two reductive
$G$ be two reductive ![]() $k$-groups and let us consider the following central exact sequence of algebraic groups:
$k$-groups and let us consider the following central exact sequence of algebraic groups:
Also let ![]() $\widetilde {T} \subseteq \widetilde {G}$ be a maximal
$\widetilde {T} \subseteq \widetilde {G}$ be a maximal ![]() $k$-torus and set
$k$-torus and set ![]() $T:=\widetilde {T} /S$. Then
$T:=\widetilde {T} /S$. Then ![]() $\operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is an ideal of
$\operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is an ideal of ![]() $\mathfrak {g}$ and the quotient
$\mathfrak {g}$ and the quotient ![]() $\mathfrak {g}/ \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is isomorphic to
$\mathfrak {g}/ \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is isomorphic to ![]() $\mathfrak {t}/ \operatorname {Lie}(\pi )(\widetilde {\mathfrak {t}})$ as a
$\mathfrak {t}/ \operatorname {Lie}(\pi )(\widetilde {\mathfrak {t}})$ as a ![]() $k$-Lie algebra. In particular, if
$k$-Lie algebra. In particular, if ![]() $k$ is of characteristic
$k$ is of characteristic ![]() $p>0$, the restricted
$p>0$, the restricted ![]() $p$-Lie algebra
$p$-Lie algebra ![]() $\mathfrak {g}/ \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is toral.
$\mathfrak {g}/ \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is toral.
Proof. The centre of a reductive group is a diagonalisable subgroup (see, for instance, [Reference Demazure and GrothendieckSGA3III, XXII, Corollaire 4.1.6]). The exact sequence of the lemma being central, the ![]() $k$-group
$k$-group ![]() $S$ is diagonalisable. Indeed any subgroup of a diagonalisable group defined over a field is diagonalisable (see [Reference Demazure and GrothendieckSGA3II, IX, Proposition 8.1]). Let
$S$ is diagonalisable. Indeed any subgroup of a diagonalisable group defined over a field is diagonalisable (see [Reference Demazure and GrothendieckSGA3II, IX, Proposition 8.1]). Let ![]() $E$ be a
$E$ be a ![]() $k$-torus such that
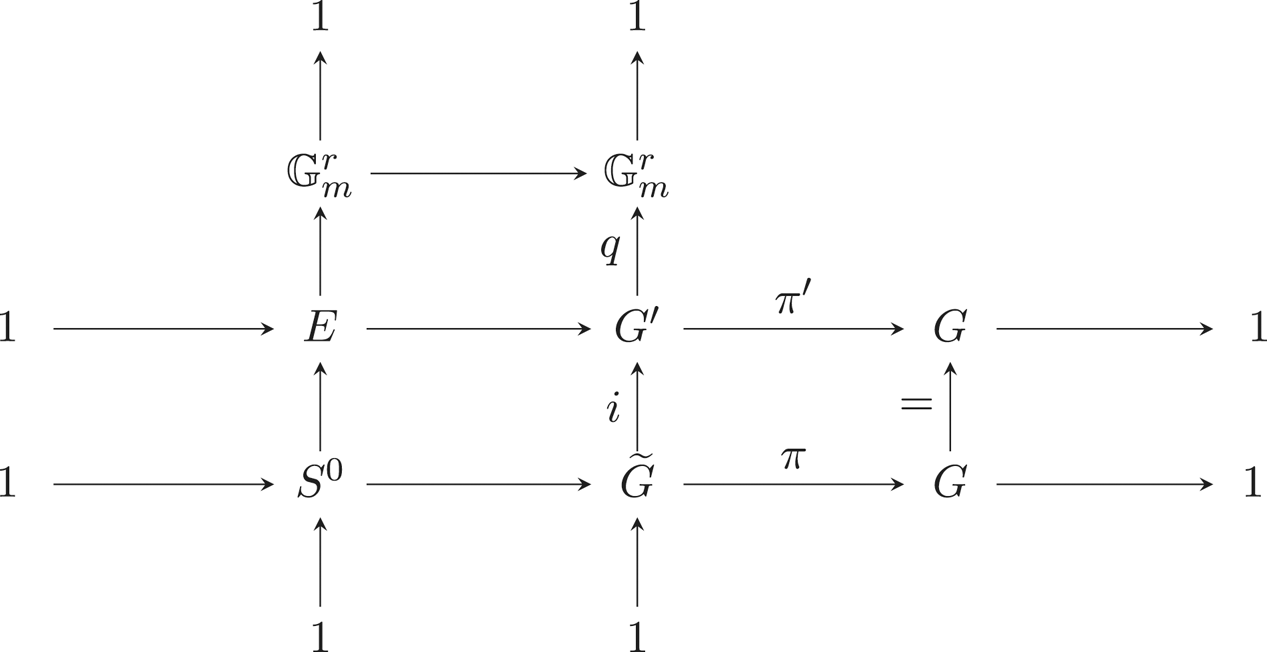
$k$-torus such that ![]() $S^0 \subseteq E$. Let us stress that such an object always exists because the maximal connected subgroups of multiplicative type of a reductive group over a field are the maximal tori (see Corollary 4.10). Consider the following commutative diagram of algebraic
$S^0 \subseteq E$. Let us stress that such an object always exists because the maximal connected subgroups of multiplicative type of a reductive group over a field are the maximal tori (see Corollary 4.10). Consider the following commutative diagram of algebraic ![]() $k$-groups:
$k$-groups:

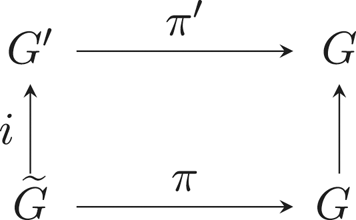
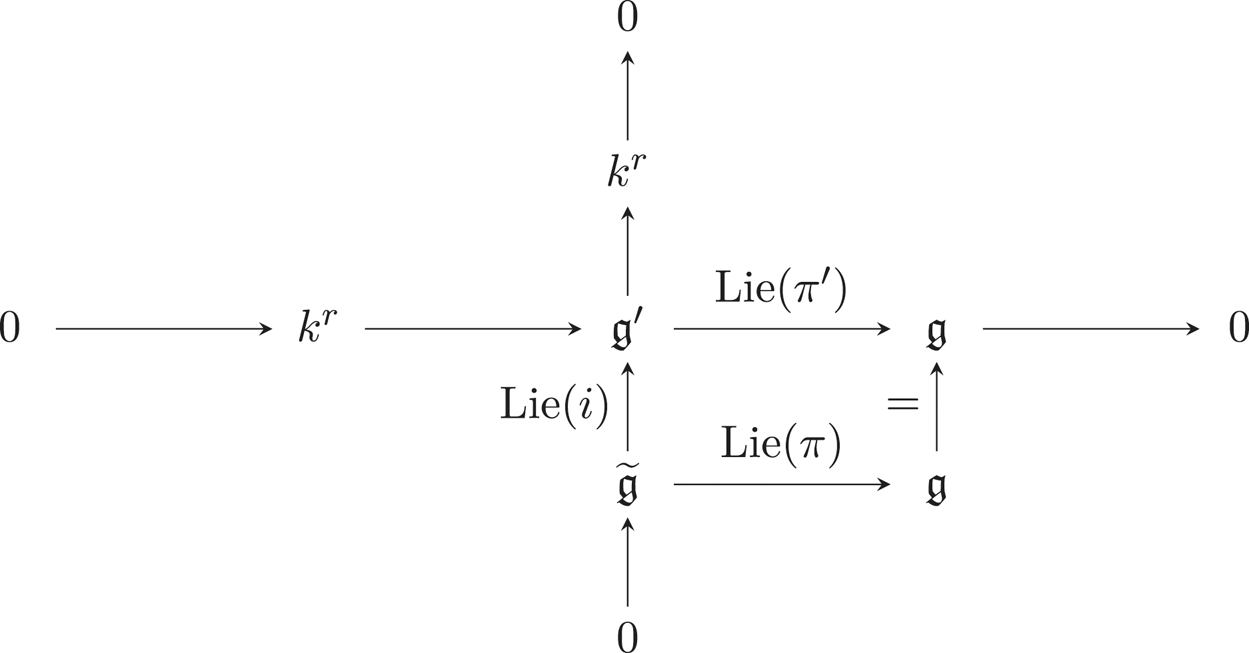
where ![]() $G'$ is defined for the lower left square to be commutative. It induces by derivation the following commutative diagram of Lie algebras.
$G'$ is defined for the lower left square to be commutative. It induces by derivation the following commutative diagram of Lie algebras.

Note that the right-exactness of the second line comes from the smoothness of ![]() $\operatorname {Ker}(\pi ')$ (see [Reference Demazure and GabrielDG70, II, §5, n
$\operatorname {Ker}(\pi ')$ (see [Reference Demazure and GabrielDG70, II, §5, n![]() $^{\circ}$5, Proposition 5.3]).
$^{\circ}$5, Proposition 5.3]).
We show that ![]() $\operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is an ideal of
$\operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is an ideal of ![]() $\mathfrak {g}$: let
$\mathfrak {g}$: let ![]() $y \in \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}}) \subseteq \mathfrak {g}$ and pick
$y \in \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}}) \subseteq \mathfrak {g}$ and pick ![]() $g \in \mathfrak {g}$. Also let
$g \in \mathfrak {g}$. Also let ![]() $x \in \widetilde {\mathfrak {g}}$ be such that
$x \in \widetilde {\mathfrak {g}}$ be such that ![]() $\operatorname {Lie}(\pi )(x) = y$. As
$\operatorname {Lie}(\pi )(x) = y$. As ![]() $\operatorname {Lie}(\pi ')$ is surjective there exists
$\operatorname {Lie}(\pi ')$ is surjective there exists ![]() $g' \in \mathfrak {g}'$ such that
$g' \in \mathfrak {g}'$ such that ![]() $\operatorname {Lie}(\pi )(g') = g$. This provides the equality:
$\operatorname {Lie}(\pi )(g') = g$. This provides the equality:
The Lie algebra ![]() $\widetilde {\mathfrak {g}}$ is isomorphic to the kernel of
$\widetilde {\mathfrak {g}}$ is isomorphic to the kernel of ![]() $\operatorname {Lie}(q) : \mathfrak {g}'\rightarrow k^r$ which is an ideal of
$\operatorname {Lie}(q) : \mathfrak {g}'\rightarrow k^r$ which is an ideal of ![]() $\mathfrak {g'}$. The commutativity of the diagram thus allows us to conclude that
$\mathfrak {g'}$. The commutativity of the diagram thus allows us to conclude that ![]() $[y,g] \in \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$. Therefore,
$[y,g] \in \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$. Therefore, ![]() $\operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is an ideal of
$\operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is an ideal of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
It remains to prove that the inclusion ![]() $\operatorname {Lie}(\pi )(\widetilde {\mathfrak {t}}) \subseteq \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}}) \cap \mathfrak {t}$ is actually an equality. This being established, one will only need to apply [Reference Borel and TitsBT72, Corollaire 2.17] to end the proof (as this corollary states that
$\operatorname {Lie}(\pi )(\widetilde {\mathfrak {t}}) \subseteq \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}}) \cap \mathfrak {t}$ is actually an equality. This being established, one will only need to apply [Reference Borel and TitsBT72, Corollaire 2.17] to end the proof (as this corollary states that ![]() $\mathfrak {t} \twoheadrightarrow \mathfrak {g}/\operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is surjective). Let us thus show the equality
$\mathfrak {t} \twoheadrightarrow \mathfrak {g}/\operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}})$ is surjective). Let us thus show the equality ![]() $\operatorname {Lie}(\pi )(\widetilde {\mathfrak {t}}) = \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}}) \cap \mathfrak {t}$. It comes from the study of the right lower square of the above commutative diagram of groups: the morphism
$\operatorname {Lie}(\pi )(\widetilde {\mathfrak {t}}) = \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}}) \cap \mathfrak {t}$. It comes from the study of the right lower square of the above commutative diagram of groups: the morphism ![]() $\pi '$ being surjective with toric kernel
$\pi '$ being surjective with toric kernel ![]() $E$, the group
$E$, the group ![]() $T$ is the image of a torus
$T$ is the image of a torus ![]() $T' \subseteq G'$ (by [Reference Demazure and GrothendieckSGA3II, IX, Proposition 8.2(ii)]). Hence, the equalities
$T' \subseteq G'$ (by [Reference Demazure and GrothendieckSGA3II, IX, Proposition 8.2(ii)]). Hence, the equalities ![]() $T = T'/E = \widetilde {T}/S$ hold true. The following square is commutative.
$T = T'/E = \widetilde {T}/S$ hold true. The following square is commutative.

The image ![]() $i(\widetilde {T})$ is thus contained in
$i(\widetilde {T})$ is thus contained in ![]() $T'$. Hence, the exact sequence
$T'$. Hence, the exact sequence
induces an exact sequence of tori:
Note that the subgroup ![]() $T''$ is indeed a torus as it is:
$T''$ is indeed a torus as it is:
− diagonalisable according to [Reference Demazure and GrothendieckSGA3II, IX, Proposition 8.1];
− smooth by [Reference Balaji, Deligne and ParameswaranBDP17, II, § 5, n
 $^{\circ }$5, Proposition 5.3(ii)]).
$^{\circ }$5, Proposition 5.3(ii)]).
The exactness is here preserved by derivation as ![]() $\widetilde {T}$ is smooth.
$\widetilde {T}$ is smooth.
Let us now consider the right lower square of the above commutative diagram of Lie algebras:

The kernel ![]() $E$ being smooth, the derived morphism
$E$ being smooth, the derived morphism ![]() $\operatorname {Lie}(\pi ')$ is still surjective. Hence, one still has
$\operatorname {Lie}(\pi ')$ is still surjective. Hence, one still has ![]() $\mathfrak {t} = \mathfrak {t'}/k^r$. According to what precedes any
$\mathfrak {t} = \mathfrak {t'}/k^r$. According to what precedes any ![]() $y \in \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}}) \cap \mathfrak {t}$ is the image of a certain
$y \in \operatorname {Lie}(\pi )(\widetilde {\mathfrak {g}}) \cap \mathfrak {t}$ is the image of a certain ![]() $x \in \widetilde {\mathfrak {g}}$ such that
$x \in \widetilde {\mathfrak {g}}$ such that ![]() $\operatorname {Lie}(i)(x) \in \mathfrak {t}'$. This, combined with the exactness of the following derived exact sequence,
$\operatorname {Lie}(i)(x) \in \mathfrak {t}'$. This, combined with the exactness of the following derived exact sequence,
allows us to conclude. The exactness indeed ensures that ![]() $x \in \widetilde {\mathfrak {t}}$. Moreover, because one has that
$x \in \widetilde {\mathfrak {t}}$. Moreover, because one has that ![]() $y = \operatorname {Lie}(\pi )(x)= \operatorname {Lie}(\pi ')(i(x)) \in \operatorname {Lie}(\pi )(\widetilde {\mathfrak {t}})$, the expected inclusion, thus the equality, are obtained.
$y = \operatorname {Lie}(\pi )(x)= \operatorname {Lie}(\pi ')(i(x)) \in \operatorname {Lie}(\pi )(\widetilde {\mathfrak {t}})$, the expected inclusion, thus the equality, are obtained.
Proof of Lemma 2.6 The centre ![]() $\mathfrak {z_g}$ is a nilpotent ideal of
$\mathfrak {z_g}$ is a nilpotent ideal of ![]() $\mathfrak {g}$, it is therefore solvable. The inclusions
$\mathfrak {g}$, it is therefore solvable. The inclusions ![]() $\mathfrak {z_g}\subseteq \operatorname {Nil}(\mathfrak {g}) \subseteq \operatorname {rad}(\mathfrak {g})$ follow. One thus only needs to show that
$\mathfrak {z_g}\subseteq \operatorname {Nil}(\mathfrak {g}) \subseteq \operatorname {rad}(\mathfrak {g})$ follow. One thus only needs to show that ![]() $\operatorname {rad}(\mathfrak {g}) \subseteq \mathfrak {z_g}$. The involved objects being all compatible with base change we can without loss of generality assume
$\operatorname {rad}(\mathfrak {g}) \subseteq \mathfrak {z_g}$. The involved objects being all compatible with base change we can without loss of generality assume ![]() $k$ to be algebraically closed.
$k$ to be algebraically closed.
A dévissage argument allows us to reduce ourselves to prove the statement for ![]() $G$ connected and semisimple: the reductive case can be deduced from the semisimple case, whereas the latter is ruled by the semisimple and simply connected case.
$G$ connected and semisimple: the reductive case can be deduced from the semisimple case, whereas the latter is ruled by the semisimple and simply connected case.
(i) Assume the ![]() $k$-group
$k$-group ![]() $G$ to be semisimple and simply connected. It thus decomposes into a product of almost simple groups (see [Reference TitsTit66, 3.1.1, p. 55]) and one can assume without loss of generality that
$G$ to be semisimple and simply connected. It thus decomposes into a product of almost simple groups (see [Reference TitsTit66, 3.1.1, p. 55]) and one can assume without loss of generality that ![]() $G$ is almost simple. There are two options:
$G$ is almost simple. There are two options:
(a) either
 $G$ is not of type
$G$ is not of type  $G_2$ when
$G_2$ when  $p= 3$, then according to [Reference HissHis84, Haupsatz], the quotient
$p= 3$, then according to [Reference HissHis84, Haupsatz], the quotient  $\mathfrak {g/z_g}$ is a simple
$\mathfrak {g/z_g}$ is a simple  $G$-module; hence, the radical
$G$-module; hence, the radical  $\operatorname {rad}(\mathfrak {g/z_g})$ is trivial;
$\operatorname {rad}(\mathfrak {g/z_g})$ is trivial;(b) or
 $G$ is a
$G$ is a  $k$-group of type
$k$-group of type  $G_2$ and
$G_2$ and  $k$ is of characteristic three; according to [Reference HogeweijHog82, Table 1] there are then only two possibilities for
$k$ is of characteristic three; according to [Reference HogeweijHog82, Table 1] there are then only two possibilities for  $\operatorname {rad}(\mathfrak {g})$, it is either trivial or the Lie algebra of a
$\operatorname {rad}(\mathfrak {g})$, it is either trivial or the Lie algebra of a  $\operatorname {PGL}_3$ factor; this last option cannot occur because the Lie algebra
$\operatorname {PGL}_3$ factor; this last option cannot occur because the Lie algebra  $\mathfrak {pgl}_3$ is not solvable, so one can conclude that
$\mathfrak {pgl}_3$ is not solvable, so one can conclude that  $\operatorname {rad}(\mathfrak {g})=0$.
$\operatorname {rad}(\mathfrak {g})=0$.
(ii) Assume now that ![]() $G$ is semisimple. It then admits a universal covering, denoted by
$G$ is semisimple. It then admits a universal covering, denoted by ![]() $G^{\operatorname {sc}}$ (see, for example, [Reference TitsTit66, 1.1.2, Theorem 1, p. 43]), and one can consider the following associated central extension.
$G^{\operatorname {sc}}$ (see, for example, [Reference TitsTit66, 1.1.2, Theorem 1, p. 43]), and one can consider the following associated central extension.
Let ![]() $T^{\operatorname {sc}}$ be a maximal
$T^{\operatorname {sc}}$ be a maximal ![]() $k$-torus of
$k$-torus of ![]() $G^{\operatorname {sc}}$ and set
$G^{\operatorname {sc}}$ and set ![]() $T=T^{\operatorname {sc}}/\mu$ (the corresponding Lie algebras will be denoted by
$T=T^{\operatorname {sc}}/\mu$ (the corresponding Lie algebras will be denoted by ![]() $\mathfrak {t}^{\operatorname {sc}}$, respectively
$\mathfrak {t}^{\operatorname {sc}}$, respectively ![]() $\mathfrak {t}$). The above lemma ensures that
$\mathfrak {t}$). The above lemma ensures that ![]() $\operatorname {Lie}(\pi )(\operatorname {Lie}(G^{\operatorname {sc}}))$ is an ideal of
$\operatorname {Lie}(\pi )(\operatorname {Lie}(G^{\operatorname {sc}}))$ is an ideal of ![]() $\mathfrak {g}$ and one has the following exact sequence of restricted
$\mathfrak {g}$ and one has the following exact sequence of restricted ![]() $p$-Lie algebras.
$p$-Lie algebras.

The extension being central, the preimage of ![]() $\operatorname {rad}(\mathfrak {g})$ is a solvable ideal of
$\operatorname {rad}(\mathfrak {g})$ is a solvable ideal of ![]() $\operatorname {Lie}(G^{\operatorname {sc}})$ (this is a consequence of [Reference Strade and FarnsteinerSF88, 1.5, Theorem 5.1(2)]). Hence, it is contained in
$\operatorname {Lie}(G^{\operatorname {sc}})$ (this is a consequence of [Reference Strade and FarnsteinerSF88, 1.5, Theorem 5.1(2)]). Hence, it is contained in ![]() $\operatorname {rad}(\operatorname {Lie}(G^{\operatorname {sc}})) = \mathfrak {z}_{\operatorname {Lie}(G^{\operatorname {sc}})}$. Composing with
$\operatorname {rad}(\operatorname {Lie}(G^{\operatorname {sc}})) = \mathfrak {z}_{\operatorname {Lie}(G^{\operatorname {sc}})}$. Composing with ![]() $\operatorname {Lie}(\pi )$, one can then deduce that the inclusion
$\operatorname {Lie}(\pi )$, one can then deduce that the inclusion
is satisfied, whence the desired equality
The above exact sequence thus induces the following one:

where ![]() $\mathfrak {h}$ is a restricted
$\mathfrak {h}$ is a restricted ![]() $p$-subalgebra of
$p$-subalgebra of ![]() $\mathfrak {t}/ \operatorname {Lie}(\pi )( \mathfrak {t}^{\operatorname {sc}})$, which is toral so has no
$\mathfrak {t}/ \operatorname {Lie}(\pi )( \mathfrak {t}^{\operatorname {sc}})$, which is toral so has no ![]() $p$-nilpotent elements. In other words, the
$p$-nilpotent elements. In other words, the ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\operatorname {rad}(\mathfrak {g})$ are trivial. Hence,
$\operatorname {rad}(\mathfrak {g})$ are trivial. Hence, ![]() $\operatorname {rad}(\mathfrak {g})$ only has semisimple elements. According to [Reference Borel and TitsBT72, Proposition 2.13], it only remains to show the equality
$\operatorname {rad}(\mathfrak {g})$ only has semisimple elements. According to [Reference Borel and TitsBT72, Proposition 2.13], it only remains to show the equality ![]() $N_{G}(\operatorname {rad}(\mathfrak {g})) =G$ to get the desired inclusion
$N_{G}(\operatorname {rad}(\mathfrak {g})) =G$ to get the desired inclusion ![]() $\operatorname {rad}(\mathfrak {g}) \subseteq \mathfrak {z_g}$. Note also that all the other assumptions of the proposition are trivially satisfied as
$\operatorname {rad}(\mathfrak {g}) \subseteq \mathfrak {z_g}$. Note also that all the other assumptions of the proposition are trivially satisfied as ![]() $\operatorname {rad}(\mathfrak {g})$ is a proper ideal of
$\operatorname {rad}(\mathfrak {g})$ is a proper ideal of ![]() $\mathfrak {g}$ (because
$\mathfrak {g}$ (because ![]() $G$ is a reductive
$G$ is a reductive ![]() $k$-group).
$k$-group).
Let us thus show the equality ![]() $N_{G}(\operatorname {rad}(\mathfrak {g})) =G$. According to [Reference Demazure and GabrielDG70, II, § 5, n
$N_{G}(\operatorname {rad}(\mathfrak {g})) =G$. According to [Reference Demazure and GabrielDG70, II, § 5, n![]() $^{\circ }$3.2, Proposition] this can be shown on
$^{\circ }$3.2, Proposition] this can be shown on ![]() $\bar {k}$-points (as the group
$\bar {k}$-points (as the group ![]() $G$ is smooth and of finite presentation and the Lie algebra
$G$ is smooth and of finite presentation and the Lie algebra ![]() $\operatorname {rad}(\mathfrak {g})$ is reduced and closed in
$\operatorname {rad}(\mathfrak {g})$ is reduced and closed in ![]() $\mathfrak {g}$). This is clear as
$\mathfrak {g}$). This is clear as ![]() $\operatorname {rad}(\mathfrak {g})(\bar {k})$ is stable under conjugation: the image of
$\operatorname {rad}(\mathfrak {g})(\bar {k})$ is stable under conjugation: the image of ![]() $\operatorname {rad}(\mathfrak {g})(\bar {k})$ by
$\operatorname {rad}(\mathfrak {g})(\bar {k})$ by ![]() $G(\bar {k})$-conjugation is a solvable ideal of
$G(\bar {k})$-conjugation is a solvable ideal of ![]() $\mathfrak {g}(\bar {k})$, its maximality can be deduced by applying the inverse morphism.
$\mathfrak {g}(\bar {k})$, its maximality can be deduced by applying the inverse morphism.
(iii) If ![]() $G$ is any reductive
$G$ is any reductive ![]() $k$-group, the following exact sequence allows to reduce ourselves to the preceding cases (see for example [Reference Demazure and GrothendieckSGA3III, XXII Définition 4.3.6]):
$k$-group, the following exact sequence allows to reduce ourselves to the preceding cases (see for example [Reference Demazure and GrothendieckSGA3III, XXII Définition 4.3.6]):
Indeed, as the subgroup ![]() $\operatorname {Rad}(G)$ is smooth, this exact sequence induces after derivation an exact sequence of Lie algebras (see [Reference Demazure and GabrielDG70, § 5, n
$\operatorname {Rad}(G)$ is smooth, this exact sequence induces after derivation an exact sequence of Lie algebras (see [Reference Demazure and GabrielDG70, § 5, n![]() $^{\circ }$5, Proposition 5.3])
$^{\circ }$5, Proposition 5.3])

The morphism ![]() $\operatorname {Lie}(\pi )$ is surjective, its image
$\operatorname {Lie}(\pi )$ is surjective, its image ![]() $\operatorname {Lie}(\pi )(\operatorname {rad}(\mathfrak {g}))$ is therefore a solvable ideal of
$\operatorname {Lie}(\pi )(\operatorname {rad}(\mathfrak {g}))$ is therefore a solvable ideal of ![]() $\operatorname {Lie}(G^{\operatorname {ss}})$. By what precedes it is then contained in the centre of
$\operatorname {Lie}(G^{\operatorname {ss}})$. By what precedes it is then contained in the centre of ![]() $\operatorname {Lie}(G^{\operatorname {ss}})$. Let
$\operatorname {Lie}(G^{\operatorname {ss}})$. Let ![]() $x \in \operatorname {rad}(\mathfrak {g})$. As
$x \in \operatorname {rad}(\mathfrak {g})$. As ![]() $k$ may be assumed to be algebraically closed, the element
$k$ may be assumed to be algebraically closed, the element ![]() $x$ admits a Jordan decomposition, say
$x$ admits a Jordan decomposition, say ![]() $x = x_{s} + x_n$, with
$x = x_{s} + x_n$, with ![]() $x_{s}$ semisimple and
$x_{s}$ semisimple and ![]() $x_n$ a
$x_n$ a ![]() $p$-nilpotent element of
$p$-nilpotent element of ![]() $\operatorname {rad}(\mathfrak {g})$ (for the existence of such see for example [Reference Strade and FarnsteinerSF88, 2.3, Theorem 3.5]). As
$\operatorname {rad}(\mathfrak {g})$ (for the existence of such see for example [Reference Strade and FarnsteinerSF88, 2.3, Theorem 3.5]). As ![]() $\pi (x) \in \mathfrak {z_g}$ one necessarily has
$\pi (x) \in \mathfrak {z_g}$ one necessarily has ![]() $\pi (x_n) = 0$, meaning that
$\pi (x_n) = 0$, meaning that ![]() $x_n \in \operatorname {Lie}((Z^0_G)_{\mathrm {red}})$ which is toral. Hence
$x_n \in \operatorname {Lie}((Z^0_G)_{\mathrm {red}})$ which is toral. Hence ![]() $x_n = 0$. So
$x_n = 0$. So ![]() $\operatorname {rad}(\mathfrak {g})$ only has semisimple elements. According to [Reference Borel and TitsBT72, Proposition 2.13] we just have shown that
$\operatorname {rad}(\mathfrak {g})$ only has semisimple elements. According to [Reference Borel and TitsBT72, Proposition 2.13] we just have shown that ![]() $\operatorname {rad}(\mathfrak {g}) \subseteq \mathfrak {z_g}$ because
$\operatorname {rad}(\mathfrak {g}) \subseteq \mathfrak {z_g}$ because ![]() $\operatorname {rad}(\mathfrak {g})$ is a proper
$\operatorname {rad}(\mathfrak {g})$ is a proper ![]() $G$-sub-module of
$G$-sub-module of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Remarks 2.9 It is worth mentioning the following points.
(i) Lemma 2.6 in particular allows one to measure the potential lack of smoothness of the centre of ![]() $G$. More precisely, one has:
$G$. More precisely, one has:
where the first isomorphism comes from Remark 6.2(ii). According to the proof of Lemma 2.6 this quotient is a restricted toral ![]() $p$-algebra.
$p$-algebra.
(ii) A careful study of the proof shows that the only difficulty one would have when trying to extend the above result to the characteristic-two framework relies on the fact that the ![]() $G$-module
$G$-module ![]() $\mathfrak {g/z_g}$ might not be simple. According to [Reference HissHis84, Haupsatz] for an algebraically closed field
$\mathfrak {g/z_g}$ might not be simple. According to [Reference HissHis84, Haupsatz] for an algebraically closed field ![]() $k$ of characteristic two this is not an issue if the root system of
$k$ of characteristic two this is not an issue if the root system of ![]() $G$ only has irreducible components of
$G$ only has irreducible components of ![]() $A_n$-type. This is always satisfied in this article.
$A_n$-type. This is always satisfied in this article.
As mentioned in Remark 2.7 the following result allows one to slightly refine the hypotheses on ![]() $p$ in the study of the nilradical of the Lie algebra of a reductive group.
$p$ in the study of the nilradical of the Lie algebra of a reductive group.
Lemma 2.10 (Corollary of [Reference VasiuVas05, Lemma 2.1])
Let ![]() $G$ be a reductive
$G$ be a reductive ![]() $k$-group. If
$k$-group. If ![]() $k$ is of characteristic two, assume that
$k$ is of characteristic two, assume that ![]() $G^{\operatorname {Ad}}_{k^s}$ has no direct factor
$G^{\operatorname {Ad}}_{k^s}$ has no direct factor ![]() $G_1$ isomorphic to
$G_1$ isomorphic to ![]() $\operatorname {SO}_{2n+1}$ for an integer
$\operatorname {SO}_{2n+1}$ for an integer ![]() $n>0$. Under these assumptions,
$n>0$. Under these assumptions, ![]() $\operatorname {Nil}(\mathfrak {g})$ is the centre of
$\operatorname {Nil}(\mathfrak {g})$ is the centre of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Proof. One inclusion is clear and does not require any additional assumption on the characteristic of ![]() $k$: the centre of
$k$: the centre of ![]() $\mathfrak {g}$ is a nilpotent ideal of
$\mathfrak {g}$ is a nilpotent ideal of ![]() $\mathfrak {g}$ so it is contained in the nilradical of
$\mathfrak {g}$ so it is contained in the nilradical of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
To show the reverse inclusion, one only needs to prove that ![]() $\operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g} = 0$. The inclusion
$\operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g} = 0$. The inclusion ![]() $\mathfrak {g/z_g} \subseteq \operatorname {Lie}(G^{\operatorname {Ad}})$ is provided by the exact sequence of Lie algebras of Remark 6.2(ii):
$\mathfrak {g/z_g} \subseteq \operatorname {Lie}(G^{\operatorname {Ad}})$ is provided by the exact sequence of Lie algebras of Remark 6.2(ii):
Assume that ![]() $\operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g} \neq 0$. We show that this implies [Reference VasiuVas05, Lemma 2.1] to hold true, leading to a contradiction (as it would imply
$\operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g} \neq 0$. We show that this implies [Reference VasiuVas05, Lemma 2.1] to hold true, leading to a contradiction (as it would imply ![]() $p = 2$ and
$p = 2$ and ![]() $G$ to be such as excluded in the assumptions).
$G$ to be such as excluded in the assumptions).
We therefore have to check that:
(i) the quotient
 $\operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g}$ is a
$\operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g}$ is a  $G^{\operatorname {Ad}}$-sub-module of
$G^{\operatorname {Ad}}$-sub-module of  $\operatorname {Lie}(G^{\operatorname {Ad}})$;
$\operatorname {Lie}(G^{\operatorname {Ad}})$;(ii) for any maximal torus
 $T^{\operatorname {Ad}}\subseteq G^{\operatorname {Ad}}$ the intersection
$T^{\operatorname {Ad}}\subseteq G^{\operatorname {Ad}}$ the intersection  $\mathfrak {\operatorname {Nil}(g)/z_g} \cap \operatorname {Lie}(T^{\operatorname {Ad}})$ is trivial.
$\mathfrak {\operatorname {Nil}(g)/z_g} \cap \operatorname {Lie}(T^{\operatorname {Ad}})$ is trivial.
To check that condition (i) is satisfied, we first show that ![]() $\operatorname {Nil}(\mathfrak {g/z_g}) = \operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g}$. The preimage of
$\operatorname {Nil}(\mathfrak {g/z_g}) = \operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g}$. The preimage of ![]() $\operatorname {Nil}(\mathfrak {g/z_g})$ is a nilpotent ideal of
$\operatorname {Nil}(\mathfrak {g/z_g})$ is a nilpotent ideal of ![]() $\mathfrak {g}$, as the following considered extension of Lie algebras is central.
$\mathfrak {g}$, as the following considered extension of Lie algebras is central.
It is thus contained in ![]() $\operatorname {Nil}(\mathfrak {g}/\mathfrak {z_g})$ because the quotient
$\operatorname {Nil}(\mathfrak {g}/\mathfrak {z_g})$ because the quotient ![]() $\operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g}$ is a nilpotent ideal of
$\operatorname {Nil}(\mathfrak {g})/\mathfrak {z_g}$ is a nilpotent ideal of ![]() $\mathfrak {g/z_g}$. Hence, we have shown the desired equality. Thus, we are reduced to showing that
$\mathfrak {g/z_g}$. Hence, we have shown the desired equality. Thus, we are reduced to showing that ![]() $\operatorname {Nil}(\mathfrak {g}/\mathfrak {z_g})$ is a
$\operatorname {Nil}(\mathfrak {g}/\mathfrak {z_g})$ is a ![]() $G^{\operatorname {Ad}}$-sub-module of
$G^{\operatorname {Ad}}$-sub-module of ![]() $\operatorname {Lie}(G^{\operatorname {Ad}})$, or in other words that
$\operatorname {Lie}(G^{\operatorname {Ad}})$, or in other words that ![]() $N_{G^{\operatorname {Ad}}}(\operatorname {Nil}(\mathfrak {g/z_g})) =G^{\operatorname {Ad}}$. Once again as:
$N_{G^{\operatorname {Ad}}}(\operatorname {Nil}(\mathfrak {g/z_g})) =G^{\operatorname {Ad}}$. Once again as:
− the group
 $G^{\operatorname {Ad}}$ is smooth of finite presentation; and
$G^{\operatorname {Ad}}$ is smooth of finite presentation; and−
 $\mathfrak {g/z_g}$ is reduced and closed in
$\mathfrak {g/z_g}$ is reduced and closed in  $\operatorname {Lie}(G^{\operatorname {Ad}})$;
$\operatorname {Lie}(G^{\operatorname {Ad}})$;
one only needs to check this equality on ![]() $\bar {k}$-points (see [Reference Demazure and GabrielDG70, II, § 5, n
$\bar {k}$-points (see [Reference Demazure and GabrielDG70, II, § 5, n![]() $^{\circ }$3.2, Proposition]). Recall that the quotient
$^{\circ }$3.2, Proposition]). Recall that the quotient ![]() $\operatorname {Nil}(\mathfrak {g/z_g}(\bar {k}))$ is stable for the adjoint action as the image of
$\operatorname {Nil}(\mathfrak {g/z_g}(\bar {k}))$ is stable for the adjoint action as the image of ![]() $\operatorname {Nil}(\mathfrak {g/z_g})(\bar {k})$ under the
$\operatorname {Nil}(\mathfrak {g/z_g})(\bar {k})$ under the ![]() $G^{\operatorname {Ad}}(\bar {k})$-conjugation is a nilpotent ideal of
$G^{\operatorname {Ad}}(\bar {k})$-conjugation is a nilpotent ideal of ![]() $\mathfrak {g/z_g}(\bar {k})$. Its maximality follows by considering the reverse morphism. Thus, we have shown the equality.
$\mathfrak {g/z_g}(\bar {k})$. Its maximality follows by considering the reverse morphism. Thus, we have shown the equality.
To check that condition (ii) is indeed satisfied, first note that any maximal torus ![]() $T^{\operatorname {Ad}} \subset G^{\operatorname {Ad}}$ comes from a maximal torus
$T^{\operatorname {Ad}} \subset G^{\operatorname {Ad}}$ comes from a maximal torus ![]() $T\subset G$. At the Lie algebras level one can summarise the situation with the following commutative diagram.
$T\subset G$. At the Lie algebras level one can summarise the situation with the following commutative diagram.

Assume that the intersection ![]() $\mathfrak {\operatorname {Nil}(g)/z_g} \cap \operatorname {Lie}(T^{\operatorname {Ad}})$ is not trivial. This implies, in particular, that neither is the intersection
$\mathfrak {\operatorname {Nil}(g)/z_g} \cap \operatorname {Lie}(T^{\operatorname {Ad}})$ is not trivial. This implies, in particular, that neither is the intersection ![]() $\mathfrak {\operatorname {Nil}(g)/z_g} \cap \operatorname {Lie}(T)/\mathfrak {z_g}$ as any element of the first intersection occurs as an element of the image of
$\mathfrak {\operatorname {Nil}(g)/z_g} \cap \operatorname {Lie}(T)/\mathfrak {z_g}$ as any element of the first intersection occurs as an element of the image of ![]() $\mathfrak {g} \rightarrow \mathfrak {g/z_g}$. Remember that we have already shown that
$\mathfrak {g} \rightarrow \mathfrak {g/z_g}$. Remember that we have already shown that ![]() $\mathfrak {z_g}$ is contained in
$\mathfrak {z_g}$ is contained in ![]() $\operatorname {Nil}(\mathfrak {g})$. According to Remark 6.2(ii), it is nothing but the Lie algebra of
$\operatorname {Nil}(\mathfrak {g})$. According to Remark 6.2(ii), it is nothing but the Lie algebra of ![]() $Z_G$, whence the inclusion
$Z_G$, whence the inclusion ![]() $\mathfrak {z_g} \subseteq \operatorname {Lie}(T)$.
$\mathfrak {z_g} \subseteq \operatorname {Lie}(T)$.
The non-triviality of the intersection ![]() $\mathfrak {\operatorname {Nil}(g)/z_g} \cap \operatorname {Lie}(T)/\mathfrak {z_g}$ is therefore equivalent to suppose that the inclusion
$\mathfrak {\operatorname {Nil}(g)/z_g} \cap \operatorname {Lie}(T)/\mathfrak {z_g}$ is therefore equivalent to suppose that the inclusion ![]() $\mathfrak {z_g} \subsetneq \operatorname {Lie}(T)\cap \operatorname {Nil}(\mathfrak {g})$ is strict. This leads to a contradiction. Indeed, any element of the nilradical is
$\mathfrak {z_g} \subsetneq \operatorname {Lie}(T)\cap \operatorname {Nil}(\mathfrak {g})$ is strict. This leads to a contradiction. Indeed, any element of the nilradical is ![]() $\operatorname {ad}$-nilpotent (according to the second point of the preamble of this section) and any
$\operatorname {ad}$-nilpotent (according to the second point of the preamble of this section) and any ![]() $\operatorname {ad}$-nilpotent element of the Lie algebra of a torus is central. This can be shown as follows: let
$\operatorname {ad}$-nilpotent element of the Lie algebra of a torus is central. This can be shown as follows: let ![]() $n$ be the order of
$n$ be the order of ![]() $\operatorname {ad}$-nilpotency of
$\operatorname {ad}$-nilpotency of ![]() $x \in \operatorname {Lie}(T)$ and
$x \in \operatorname {Lie}(T)$ and ![]() $y \in \mathfrak {g}$. Passing to the algebraic closure of
$y \in \mathfrak {g}$. Passing to the algebraic closure of ![]() $k$ if necessary, the Lie algebra
$k$ if necessary, the Lie algebra ![]() $\mathfrak {g}$ has a weight space decomposition for the action of the maximal torus
$\mathfrak {g}$ has a weight space decomposition for the action of the maximal torus ![]() $T$ (which is locally splittable). Let
$T$ (which is locally splittable). Let ![]() $R$ be an associated root system. One has
$R$ be an associated root system. One has ![]() $\mathfrak {g} = \mathfrak {t} \oplus \bigoplus _{\alpha \in R} \mathfrak {g}^{\alpha }$. Thus,
$\mathfrak {g} = \mathfrak {t} \oplus \bigoplus _{\alpha \in R} \mathfrak {g}^{\alpha }$. Thus, ![]() $y$ can be written as
$y$ can be written as ![]() $y = y_0 + \sum _{\alpha \in R} y^{\alpha }$ for
$y = y_0 + \sum _{\alpha \in R} y^{\alpha }$ for ![]() $y^0 \in \mathfrak {t}$ and
$y^0 \in \mathfrak {t}$ and ![]() $y^{\alpha } \in \mathfrak {g}^{\alpha }$, with
$y^{\alpha } \in \mathfrak {g}^{\alpha }$, with ![]() $\alpha \in R$. This leads to
$\alpha \in R$. This leads to
 \[ 0 = \operatorname{ad}^n(x)(y) = \operatorname{ad}^n(x)\bigg(y^0 + \sum_{\alpha \in R} y^{\alpha}\bigg) = \sum_{\alpha \in R} \alpha^n(x)y^{\alpha}, \]
\[ 0 = \operatorname{ad}^n(x)(y) = \operatorname{ad}^n(x)\bigg(y^0 + \sum_{\alpha \in R} y^{\alpha}\bigg) = \sum_{\alpha \in R} \alpha^n(x)y^{\alpha}, \]
where we have made use of the vanishing condition ![]() $\operatorname {ad}(x)(y^0)=0$ as
$\operatorname {ad}(x)(y^0)=0$ as ![]() $x \in \mathfrak {t}$. This equality being satisfied if and only if
$x \in \mathfrak {t}$. This equality being satisfied if and only if ![]() $\operatorname {ad}(x)(y^{\alpha }) = 0$ for any
$\operatorname {ad}(x)(y^{\alpha }) = 0$ for any ![]() $\alpha \in R$, this implies that
$\alpha \in R$, this implies that ![]() $x \in \mathfrak {z_g}$.
$x \in \mathfrak {z_g}$.
Remark 2.11 In this article, we always require that ![]() $p$ is not of torsion for
$p$ is not of torsion for ![]() $G$. This implies, in particular, that
$G$. This implies, in particular, that ![]() $p$ is strictly greater than two if
$p$ is strictly greater than two if ![]() $G$ has any factor of
$G$ has any factor of ![]() $B_n$ type. The above lemma then tells us that the equality
$B_n$ type. The above lemma then tells us that the equality ![]() $\operatorname {Nil}(\mathfrak {g}) = \mathfrak {z_g}$ is always satisfied here.
$\operatorname {Nil}(\mathfrak {g}) = \mathfrak {z_g}$ is always satisfied here.
Lemma 2.12 Let ![]() $U$ be a unipotent algebraic
$U$ be a unipotent algebraic ![]() $k$-group, then its Lie algebra
$k$-group, then its Lie algebra ![]() $\mathfrak {u}$ is
$\mathfrak {u}$ is ![]() $p$-nil. In particular, the Lie algebra of the unipotent radical of a smooth connected
$p$-nil. In particular, the Lie algebra of the unipotent radical of a smooth connected ![]() $k$-group
$k$-group ![]() $G$ is a restricted
$G$ is a restricted ![]() $p$-nil
$p$-nil ![]() $p$-ideal of
$p$-ideal of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Proof. As ![]() $k$ is a field, it follows from [Reference Demazure and GabrielDG70, IV, § 2, n
$k$ is a field, it follows from [Reference Demazure and GabrielDG70, IV, § 2, n![]() $^{\circ }$2, Proposition 2.5(vi)] that the unipotent
$^{\circ }$2, Proposition 2.5(vi)] that the unipotent ![]() $k$-group
$k$-group ![]() $U$ is embeddable into the subgroup
$U$ is embeddable into the subgroup ![]() $U_{n,k}$ of upper triangular matrices of
$U_{n,k}$ of upper triangular matrices of ![]() $\operatorname {GL}_n$ for a certain
$\operatorname {GL}_n$ for a certain ![]() $n \in \mathbb {N}$. This leads to the following inclusion of restricted
$n \in \mathbb {N}$. This leads to the following inclusion of restricted ![]() $p$-Lie algebras (all of them coming from algebraic
$p$-Lie algebras (all of them coming from algebraic ![]() $k$-groups)
$k$-groups) ![]() $\mathfrak {u} \subseteq \mathfrak {u}_{n,k}$. Note that the
$\mathfrak {u} \subseteq \mathfrak {u}_{n,k}$. Note that the ![]() $p$-structure on
$p$-structure on ![]() $\mathfrak {u}_{n,k}$ is given by taking the
$\mathfrak {u}_{n,k}$ is given by taking the ![]() $p$-power of matrices. This makes
$p$-power of matrices. This makes ![]() $\mathfrak {u}_{n,k}$ into a restricted
$\mathfrak {u}_{n,k}$ into a restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra, so is
$p$-subalgebra, so is ![]() $\mathfrak {u}$.
$\mathfrak {u}$.
If now ![]() $U$ is the unipotent radical of a smooth connected
$U$ is the unipotent radical of a smooth connected ![]() $k$-group
$k$-group ![]() $G$, its Lie algebra is an ideal of
$G$, its Lie algebra is an ideal of ![]() $\mathfrak {g}$ because it is the Lie algebra of a normal subgroup of
$\mathfrak {g}$ because it is the Lie algebra of a normal subgroup of ![]() $G$. As it derives from an algebraic
$G$. As it derives from an algebraic ![]() $k$-subgroup of
$k$-subgroup of ![]() $G$, it is endowed with a
$G$, it is endowed with a ![]() $p$-structure compatible with the
$p$-structure compatible with the ![]() $p$-structure of
$p$-structure of ![]() $G$. Hence, it is a restricted
$G$. Hence, it is a restricted ![]() $p$-ideal of
$p$-ideal of ![]() $\mathfrak {g}$. It is
$\mathfrak {g}$. It is ![]() $p$-nil by what precedes.
$p$-nil by what precedes.
Lemma 2.13 Let ![]() $k$ be a perfect field and let
$k$ be a perfect field and let ![]() $H$ be a smooth connected algebraic
$H$ be a smooth connected algebraic ![]() $k$-group. Then:
$k$-group. Then:
(i) if the reductive
 $k$-group
$k$-group  $\underline {H} := H/\operatorname {Rad}_U(H)$ satisfies the conditions of Lemma 2.10, the Lie algebra of the unipotent radical of
$\underline {H} := H/\operatorname {Rad}_U(H)$ satisfies the conditions of Lemma 2.10, the Lie algebra of the unipotent radical of  $H$ is the
$H$ is the  $p$-radical of
$p$-radical of  $\mathfrak {h}$; in other words, the equality
$\mathfrak {h}$; in other words, the equality  $\mathfrak {\operatorname {\mathfrak {rad_u}}}(H) = \operatorname {rad}_p(\mathfrak {h})$ holds true;
$\mathfrak {\operatorname {\mathfrak {rad_u}}}(H) = \operatorname {rad}_p(\mathfrak {h})$ holds true;(ii) if
 $k$ is of characteristic
$k$ is of characteristic  $p\geqslant 3$, the
$p\geqslant 3$, the  $p$-radical of
$p$-radical of  $\mathfrak {h}$ is the set of
$\mathfrak {h}$ is the set of  $p$-nilpotent elements of
$p$-nilpotent elements of  $\operatorname {rad}(\mathfrak {h})$.
$\operatorname {rad}(\mathfrak {h})$.
Remark 2.14 In particular, let ![]() $k$ be a perfect field. Consider a reductive
$k$ be a perfect field. Consider a reductive ![]() $k$-group
$k$-group ![]() $G$ and a parabolic subgroup
$G$ and a parabolic subgroup ![]() $P \subseteq G$. If
$P \subseteq G$. If ![]() $P$ is such that the reductive quotient
$P$ is such that the reductive quotient ![]() $P/\operatorname {Rad}_U(P)$ it defines satisfies the assumptions of Lemma 2.10, then:
$P/\operatorname {Rad}_U(P)$ it defines satisfies the assumptions of Lemma 2.10, then:
− the Lie algebra of its unipotent radical is the
 $p$-radical of
$p$-radical of  $\mathfrak {p} := \operatorname {Lie}(P)$;
$\mathfrak {p} := \operatorname {Lie}(P)$;− it is the set of all
 $p$-nilpotent elements of
$p$-nilpotent elements of  $\operatorname {rad}(\mathfrak {p})$.
$\operatorname {rad}(\mathfrak {p})$.
As a reminder (see [Reference Demazure and GrothendieckSGA3III, XXVI, Proposition 1.21(ii)]), if ![]() $L \subseteq P$ is a Levi subgroup, the solvable radical
$L \subseteq P$ is a Levi subgroup, the solvable radical ![]() $\operatorname {Rad}(P)$ is the semidirect product of the unipotent radical of
$\operatorname {Rad}(P)$ is the semidirect product of the unipotent radical of ![]() $P$ with the radical of
$P$ with the radical of ![]() $L$. This implies, in particular, that
$L$. This implies, in particular, that ![]() $\operatorname {Lie}(Z_L^0)\subseteq \operatorname {rad}(\mathfrak {p})$ for
$\operatorname {Lie}(Z_L^0)\subseteq \operatorname {rad}(\mathfrak {p})$ for ![]() $Z_L^0$ being the centre of
$Z_L^0$ being the centre of ![]() $L$.
$L$.
Proof. We show each point separately.
(i) We start by showing part (i). An implication is clear: according to Lemma 2.12, the Lie algebra ![]() $\mathfrak {\operatorname {\mathfrak {rad_u}}}(H)$ is a restricted
$\mathfrak {\operatorname {\mathfrak {rad_u}}}(H)$ is a restricted ![]() $p$-nil
$p$-nil ![]() $p$-ideal. In particular, the inclusion
$p$-ideal. In particular, the inclusion ![]() $\mathfrak {\operatorname {\mathfrak {rad_u}}}(H)\subseteq \operatorname {rad}_p(\mathfrak {h})$ holds true.
$\mathfrak {\operatorname {\mathfrak {rad_u}}}(H)\subseteq \operatorname {rad}_p(\mathfrak {h})$ holds true.
Let us show the reverse inclusion. The radical of ![]() $H$ being a smooth subgroup, the following exact sequence of algebraic
$H$ being a smooth subgroup, the following exact sequence of algebraic ![]() $k$-groups,
$k$-groups,
induces an exact sequence of ![]() $k$-Lie algebras (see [Reference Demazure and GabrielDG70, II, § 5, n
$k$-Lie algebras (see [Reference Demazure and GabrielDG70, II, § 5, n![]() $^{\circ }$5, Proposition 5.3]):
$^{\circ }$5, Proposition 5.3]):

This is an exact sequence of restricted ![]() $p$-Lie algebras (see [Reference Demazure and GabrielDG70, II, § 7, n
$p$-Lie algebras (see [Reference Demazure and GabrielDG70, II, § 7, n![]() $^{\circ }$2.1 and n
$^{\circ }$2.1 and n![]() $^{\circ }$3.4] for the compatibility with the
$^{\circ }$3.4] for the compatibility with the ![]() $p$-structure). The derived morphism
$p$-structure). The derived morphism ![]() $\operatorname {Lie}(\pi )$ being surjective, the image of
$\operatorname {Lie}(\pi )$ being surjective, the image of ![]() $\operatorname {Nil}(\mathfrak {h})$ under
$\operatorname {Nil}(\mathfrak {h})$ under ![]() $\operatorname {Lie}(\pi )$ is still an ideal. It is nilpotent as
$\operatorname {Lie}(\pi )$ is still an ideal. It is nilpotent as ![]() $\operatorname {Lie}(\pi )$ is a morphism of restricted
$\operatorname {Lie}(\pi )$ is a morphism of restricted ![]() $p$-Lie algebras, whence the inclusion
$p$-Lie algebras, whence the inclusion ![]() $\operatorname {Lie}(\pi )(\operatorname {Nil}(\mathfrak {h})) \subseteq \operatorname {Nil}(\underline {\mathfrak {h}})$. As
$\operatorname {Lie}(\pi )(\operatorname {Nil}(\mathfrak {h})) \subseteq \operatorname {Nil}(\underline {\mathfrak {h}})$. As ![]() $\underline {\mathfrak {h}}$ derives from a reductive
$\underline {\mathfrak {h}}$ derives from a reductive ![]() $k$-group which does not fit into the pathological case raised by Vasiu in [Reference VasiuVas05, Lemma 2.1], Lemma 2.10 applies. This leads to the equality
$k$-group which does not fit into the pathological case raised by Vasiu in [Reference VasiuVas05, Lemma 2.1], Lemma 2.10 applies. This leads to the equality ![]() $\operatorname {Nil}(\underline {\mathfrak {h}}) = \mathfrak {z}_{\underline {\mathfrak {h}}}$, thus one has
$\operatorname {Nil}(\underline {\mathfrak {h}}) = \mathfrak {z}_{\underline {\mathfrak {h}}}$, thus one has ![]() $\operatorname {Lie}(\pi )(\operatorname {Nil}(\mathfrak {h})) = \mathfrak {z}_{\underline {\mathfrak {h}}}$.
$\operatorname {Lie}(\pi )(\operatorname {Nil}(\mathfrak {h})) = \mathfrak {z}_{\underline {\mathfrak {h}}}$.
According to Lemma 2.5(i) one has ![]() $\operatorname {rad}_p(\mathfrak {h}) \subseteq \operatorname {Nil}(\mathfrak {h})$, hence any
$\operatorname {rad}_p(\mathfrak {h}) \subseteq \operatorname {Nil}(\mathfrak {h})$, hence any ![]() $x \in \operatorname {rad}_p(\mathfrak {h})$ is mapped to the centre of
$x \in \operatorname {rad}_p(\mathfrak {h})$ is mapped to the centre of ![]() $\mathfrak {z}_{\underline {\mathfrak {h}}}$. The restricted
$\mathfrak {z}_{\underline {\mathfrak {h}}}$. The restricted ![]() $p$-ideal
$p$-ideal ![]() $\operatorname {rad}_p(\mathfrak {h})$ being
$\operatorname {rad}_p(\mathfrak {h})$ being ![]() $p$-nil, the element
$p$-nil, the element ![]() $x$ is
$x$ is ![]() $p$-nilpotent, so is
$p$-nilpotent, so is ![]() $\operatorname {Lie}(\pi )(x)$ (as
$\operatorname {Lie}(\pi )(x)$ (as ![]() $\operatorname {Lie}(\pi )$ is compatible with the
$\operatorname {Lie}(\pi )$ is compatible with the ![]() $p$-structures on
$p$-structures on ![]() $\mathfrak {h}$ and
$\mathfrak {h}$ and ![]() $\underline {\mathfrak {h}}$). In other words,
$\underline {\mathfrak {h}}$). In other words, ![]() $\operatorname {Lie}(\pi )(x)$ is a
$\operatorname {Lie}(\pi )(x)$ is a ![]() $p$-nilpotent element of
$p$-nilpotent element of ![]() $\mathfrak {z}_{\underline {\mathfrak {h}}}$, which is, according to Remark 6.2(ii), the Lie algebra of the centre of the reductive
$\mathfrak {z}_{\underline {\mathfrak {h}}}$, which is, according to Remark 6.2(ii), the Lie algebra of the centre of the reductive ![]() $k$-group
$k$-group ![]() $\underline {H}$. This centre is thus a toral restricted
$\underline {H}$. This centre is thus a toral restricted ![]() $p$-subalgebra (see, for example, [Reference Demazure and GrothendieckSGA3III, XXII, Corollaire 4.1.7]), hence the equality
$p$-subalgebra (see, for example, [Reference Demazure and GrothendieckSGA3III, XXII, Corollaire 4.1.7]), hence the equality ![]() $\operatorname {Lie}(\pi )(x)= 0$. In other words, we just have shown that
$\operatorname {Lie}(\pi )(x)= 0$. In other words, we just have shown that ![]() $x \in \operatorname {\mathfrak {rad_u}}(H)$, whence the equality
$x \in \operatorname {\mathfrak {rad_u}}(H)$, whence the equality ![]() $\operatorname {rad}_p(\mathfrak {h}) = \operatorname {\mathfrak {rad_u}}(H)$. This concludes the proof of part (i).
$\operatorname {rad}_p(\mathfrak {h}) = \operatorname {\mathfrak {rad_u}}(H)$. This concludes the proof of part (i).
(ii) Let us then prove the second point of the statement. Once again an inclusion is clear: the ![]() $p$-radical
$p$-radical ![]() $\operatorname {rad}_p(\mathfrak {h})$ is a restricted
$\operatorname {rad}_p(\mathfrak {h})$ is a restricted ![]() $p$-nil
$p$-nil ![]() $p$-ideal of
$p$-ideal of ![]() $\mathfrak {h}$ and is therefore contained in the set of all
$\mathfrak {h}$ and is therefore contained in the set of all ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\mathfrak {h}$. Let us show the converse inclusion: let
$\mathfrak {h}$. Let us show the converse inclusion: let ![]() $x \in \operatorname {rad}(\mathfrak {h})$. The morphism
$x \in \operatorname {rad}(\mathfrak {h})$. The morphism ![]() $\operatorname {Lie}(\pi )$ being surjective, the image
$\operatorname {Lie}(\pi )$ being surjective, the image ![]() $\operatorname {Lie}(\pi (x))$ belongs to
$\operatorname {Lie}(\pi (x))$ belongs to ![]() $\operatorname {rad}(\underline {\mathfrak {h}})$, which is the centre of
$\operatorname {rad}(\underline {\mathfrak {h}})$, which is the centre of ![]() $\underline {\mathfrak {h}}$ according to Lemma 2.6 (which holds true as
$\underline {\mathfrak {h}}$ according to Lemma 2.6 (which holds true as ![]() $p\geqslant 3$). It necessarily vanishes because the centre of
$p\geqslant 3$). It necessarily vanishes because the centre of ![]() $\underline {\mathfrak {h}}$ is toral and
$\underline {\mathfrak {h}}$ is toral and ![]() $\operatorname {Lie}(\pi )(x)$ is also a
$\operatorname {Lie}(\pi )(x)$ is also a ![]() $p$-nilpotent element. In other words, we have shown that
$p$-nilpotent element. In other words, we have shown that ![]() $x\in \operatorname {\mathfrak {rad_u}}(\mathfrak {h})$ which is the
$x\in \operatorname {\mathfrak {rad_u}}(\mathfrak {h})$ which is the ![]() $p$-radical of
$p$-radical of ![]() $\mathfrak {h}$ according to the first point of the lemma. Hence, any
$\mathfrak {h}$ according to the first point of the lemma. Hence, any ![]() $p$-nilpotent of
$p$-nilpotent of ![]() $\operatorname {rad}(\mathfrak {h})$ belongs to
$\operatorname {rad}(\mathfrak {h})$ belongs to ![]() $\operatorname {rad}_p(\mathfrak {h})$, whence the desired equality.
$\operatorname {rad}_p(\mathfrak {h})$, whence the desired equality.
3. Springer isomorphisms and  $\operatorname {fppf}$-formalism
$\operatorname {fppf}$-formalism
3.1 Integrating  $p$-nilpotent elements: a starting point
$p$-nilpotent elements: a starting point
In what follows, the field ![]() $k$ is algebraically closed of characteristic
$k$ is algebraically closed of characteristic ![]() $p>0$ and
$p>0$ and ![]() $G$ is a reductive
$G$ is a reductive ![]() $k$-group. The notation used here is that same as used in [Reference Demazure and GrothendieckSGA3I, II, Définition 4.6.1]: let
$k$-group. The notation used here is that same as used in [Reference Demazure and GrothendieckSGA3I, II, Définition 4.6.1]: let ![]() $S$ be an affine scheme with ring of coordinates
$S$ be an affine scheme with ring of coordinates ![]() $\mathcal {O}_S$. For any
$\mathcal {O}_S$. For any ![]() $\mathcal {O}_S$-module
$\mathcal {O}_S$-module ![]() $F$, denote by
$F$, denote by ![]() $W(F)$ the following contravariant functor over the category of
$W(F)$ the following contravariant functor over the category of ![]() $S$-schemes:
$S$-schemes:
where ![]() $\Gamma$ identifies with the set of
$\Gamma$ identifies with the set of ![]() $F\otimes _{\mathcal {O}_S} \mathcal {O}_{S'}$-sections over
$F\otimes _{\mathcal {O}_S} \mathcal {O}_{S'}$-sections over ![]() $S'$. Moreover, let
$S'$. Moreover, let ![]() $H$ be a
$H$ be a ![]() $k$-algebraic group, and denote by
$k$-algebraic group, and denote by ![]() $\mathfrak {h}$ its Lie algebra. By [Reference Demazure and GrothendieckSGA3I, II, Lemme 4.11.7] the equality
$\mathfrak {h}$ its Lie algebra. By [Reference Demazure and GrothendieckSGA3I, II, Lemme 4.11.7] the equality ![]() $\mathfrak {h} = W(\mathfrak {h})$ is satisfied. In particular,
$\mathfrak {h} = W(\mathfrak {h})$ is satisfied. In particular, ![]() $\mathfrak {h}$ is smooth and connected.
$\mathfrak {h}$ is smooth and connected.
3.1.1 Reduced part of the nilpotent and unipotent schemes
The reductive group ![]() $G$ acts on
$G$ acts on ![]() $\mathfrak {g}$ via the adjoint action. Let us denote by
$\mathfrak {g}$ via the adjoint action. Let us denote by ![]() $\mathcal {O}_{\mathfrak {g}}$ the coordinate ring of
$\mathcal {O}_{\mathfrak {g}}$ the coordinate ring of ![]() $\mathfrak {g}$, and by
$\mathfrak {g}$, and by ![]() $\mathcal {O}_{\mathfrak {g}}^G$ the fixed points under the induced action. When
$\mathcal {O}_{\mathfrak {g}}^G$ the fixed points under the induced action. When ![]() $k$ is a field the affine quotient
$k$ is a field the affine quotient ![]() $[\mathfrak {g}/G]:= \operatorname {Spec}(\mathcal {O}_{\mathfrak {g}}^G)$ is universal and the nilpotent scheme
$[\mathfrak {g}/G]:= \operatorname {Spec}(\mathcal {O}_{\mathfrak {g}}^G)$ is universal and the nilpotent scheme ![]() $\mathcal {N}(\mathfrak {g})$ is the fibre
$\mathcal {N}(\mathfrak {g})$ is the fibre ![]() $\pi ^{-1}\pi (0)$, where
$\pi ^{-1}\pi (0)$, where ![]() $\pi : \mathfrak {g}\rightarrow [\mathfrak {g}/G]$ is the quotient morphism and
$\pi : \mathfrak {g}\rightarrow [\mathfrak {g}/G]$ is the quotient morphism and ![]() $0 \in \mathfrak {g}(k)$ is the zero section. This is explained in detail in a more general framework in [Reference HesselinkHes76, (2.4), (2.5) and (2.6)]. The reduced part of the nilpotent scheme, denoted by
$0 \in \mathfrak {g}(k)$ is the zero section. This is explained in detail in a more general framework in [Reference HesselinkHes76, (2.4), (2.5) and (2.6)]. The reduced part of the nilpotent scheme, denoted by ![]() $\mathcal {N}_{\mathrm {red}}(\mathfrak {g})$, coincides with the reduced subscheme of
$\mathcal {N}_{\mathrm {red}}(\mathfrak {g})$, coincides with the reduced subscheme of ![]() $\mathfrak {g}$ whose
$\mathfrak {g}$ whose ![]() $k$-points are the
$k$-points are the ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\mathfrak {g}$ (see, for instance, [Reference Bardsley and RichardsonBR85, 9.2.1]).
$\mathfrak {g}$ (see, for instance, [Reference Bardsley and RichardsonBR85, 9.2.1]).
Similarly, ![]() $G$ acts on itself via the adjoint action. When
$G$ acts on itself via the adjoint action. When ![]() $k$ is a field the affine quotient
$k$ is a field the affine quotient ![]() $[G/{\rm Ad}(G)]$ is universal and the unipotent scheme
$[G/{\rm Ad}(G)]$ is universal and the unipotent scheme ![]() $\mathcal {V}(G)$ is the fibre
$\mathcal {V}(G)$ is the fibre ![]() $\pi ^{-1}\pi (e)$, where
$\pi ^{-1}\pi (e)$, where ![]() $\pi : G\rightarrow [G/{\rm Ad}(G)]$ is the quotient morphism and
$\pi : G\rightarrow [G/{\rm Ad}(G)]$ is the quotient morphism and ![]() $e \in G(k)$ is the neutral element. The reduced part of the unipotent scheme, denoted by
$e \in G(k)$ is the neutral element. The reduced part of the unipotent scheme, denoted by ![]() $\mathcal {V}_{\mathrm {red}}(G)$, coincides with the reduced subscheme of
$\mathcal {V}_{\mathrm {red}}(G)$, coincides with the reduced subscheme of ![]() $G$ whose
$G$ whose ![]() $k$-points are the unipotent elements of
$k$-points are the unipotent elements of ![]() $G$ (see, for instance, [Reference Bardsley and RichardsonBR85, 9.1]).
$G$ (see, for instance, [Reference Bardsley and RichardsonBR85, 9.1]).
The literature on Springer isomorphisms mainly considers the so-called nilpotent and unipotent varieties (under the convention that varieties are reduced). When the terminology of schemes is adopted, as in the article of Balaji et al. [Reference Balaji, Deligne and ParameswaranBDP17], the authors insist on the necessity of considering the reduced part of both nilpotent and unipotent schemes (as the proof of existence of Springer isomorphisms is constructive and based on a reasoning on points). One might then wonder whether under the framework of this article these schemes are reduced or not. For the nilpotent scheme this is given by 3.1 which is a corollary of Riche's work [Reference RicheRic17, Lemma 3.3.3]. The following notions will be necessary in what follows.
− An element
 $x \in \mathfrak {g}$ is regular if its centraliser
$x \in \mathfrak {g}$ is regular if its centraliser  $C_G(x)$ is of minimal dimension. This lower bound exists, equals the rank of the reductive group
$C_G(x)$ is of minimal dimension. This lower bound exists, equals the rank of the reductive group  $G$ and is attained. This is detailed, for instance, in § 2.3 of Riche's paper. We denote by
$G$ and is attained. This is detailed, for instance, in § 2.3 of Riche's paper. We denote by  $\mathfrak {g}_{\operatorname {reg}}$ the subset of
$\mathfrak {g}_{\operatorname {reg}}$ the subset of  $\mathfrak {g}$ consisting of all regular nilpotent elements.
$\mathfrak {g}$ consisting of all regular nilpotent elements.− The intersection
 $\mathcal {N}(\mathfrak {g})\cap \mathfrak {g}_{\operatorname {reg}} \in W(\mathfrak {g})$ is denoted
$\mathcal {N}(\mathfrak {g})\cap \mathfrak {g}_{\operatorname {reg}} \in W(\mathfrak {g})$ is denoted  $\mathcal {N}(\mathfrak {g}_{\operatorname {reg}})$ and is the scheme whose points are regular nilpotent elements of
$\mathcal {N}(\mathfrak {g}_{\operatorname {reg}})$ and is the scheme whose points are regular nilpotent elements of  $\mathfrak {g}$.
$\mathfrak {g}$.
Proposition 3.1 (Corollary of [Reference RicheRic17, Lemma 3.3.3])
Let ![]() $G$ be a connected reductive group defined over a field
$G$ be a connected reductive group defined over a field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is assumed to be pretty good for
$p>0$ which is assumed to be pretty good for ![]() $G$. Then the nilpotent scheme
$G$. Then the nilpotent scheme ![]() $\mathcal {N}(\mathfrak {g})$ is reduced.
$\mathcal {N}(\mathfrak {g})$ is reduced.
Remark 3.2 Pretty good characteristics are those that satisfy Riche's (C3) condition in [Reference RicheRic17, 2.2, p. 227]. Integration and related questions often come with the assumption that the reductive group ![]() $G$ is standard (see, for instance, [Reference JantzenJan04, 2.9]). Namely, this means that:
$G$ is standard (see, for instance, [Reference JantzenJan04, 2.9]). Namely, this means that:
(i) the derived group
 $G$ is simply connected;
$G$ is simply connected;(ii) the characteristic is good for
 $G$;
$G$;(iii) there exists a
 $G$-equivariant non-degenerate bilinear form on
$G$-equivariant non-degenerate bilinear form on  $\mathfrak {g}$.
$\mathfrak {g}$.
As underlined in [Reference RicheRic17, 2.2], this is a stronger condition than the pretty good characteristic assumption. Thus, in particular, Proposition 3.1 ensures that the nilpotent scheme of a reductive group that satisfies the standard hypotheses is reduced.
Proof. Let us first remind the reader that the nilpotent scheme is irreducible, as already shown, for instance, in [Reference JantzenJan04, Lemma 6.2]. Note that in the article the proof is made for the reduced part of the nilpotent scheme (by the definition of the nilpotent variety); this is not an issue here, as being irreducible is a property of the underlying topological space.
The subset of regular elements of ![]() $\mathfrak {g}$ is open (this is shown, for instance, in [Reference HumphreysHum95, 1.4 Corollary]) and non-empty [Reference RicheRic17, Lemma 3.3.1], therefore
$\mathfrak {g}$ is open (this is shown, for instance, in [Reference HumphreysHum95, 1.4 Corollary]) and non-empty [Reference RicheRic17, Lemma 3.3.1], therefore ![]() $\mathcal {N}(\mathfrak {g}_{\operatorname {reg}})$ is also open (and non-empty) in
$\mathcal {N}(\mathfrak {g}_{\operatorname {reg}})$ is also open (and non-empty) in ![]() $\mathcal {N}(\mathfrak {g})$. The situation is that of the following diagram:
$\mathcal {N}(\mathfrak {g})$. The situation is that of the following diagram:

which is cartesian and where the morphism ![]() $\chi _{\operatorname {reg}}$ is smooth according to [Reference RicheRic17, Lemma 3.3.3] (as we have assumed the characteristic to be pretty good for
$\chi _{\operatorname {reg}}$ is smooth according to [Reference RicheRic17, Lemma 3.3.3] (as we have assumed the characteristic to be pretty good for ![]() $G$). Thus, the morphism
$G$). Thus, the morphism ![]() $\mathcal {N}(\mathfrak {g}_{\operatorname {reg}}) \rightarrow \operatorname {Spec}(k)$ is smooth (see, for instance, [Reference Demazure and GabrielDG70, I, § 4, n
$\mathcal {N}(\mathfrak {g}_{\operatorname {reg}}) \rightarrow \operatorname {Spec}(k)$ is smooth (see, for instance, [Reference Demazure and GabrielDG70, I, § 4, n![]() $^{\circ }$4.1]). As any smooth scheme over a field is geometrically reduced (see [Sta22, Tag 056T]), what precedes tells us that
$^{\circ }$4.1]). As any smooth scheme over a field is geometrically reduced (see [Sta22, Tag 056T]), what precedes tells us that ![]() $\mathcal {N}(\mathfrak {g}_{\operatorname {reg}})$ is indeed reduced. As this is an open subset of
$\mathcal {N}(\mathfrak {g}_{\operatorname {reg}})$ is indeed reduced. As this is an open subset of ![]() $\mathcal {N}(\mathfrak {g})$ it is dense in
$\mathcal {N}(\mathfrak {g})$ it is dense in ![]() $\mathcal {N}(\mathfrak {g})$ (the latter being irreducible) and its scheme theoretic closure is the nilpotent scheme itself. Hence,
$\mathcal {N}(\mathfrak {g})$ (the latter being irreducible) and its scheme theoretic closure is the nilpotent scheme itself. Hence, ![]() $\mathcal {N}(\mathfrak {g}_{\operatorname {reg}})$ is a reduced open subset which is scheme theoretically dense in
$\mathcal {N}(\mathfrak {g}_{\operatorname {reg}})$ is a reduced open subset which is scheme theoretically dense in ![]() $\mathcal {N}(\mathfrak {g})$ so the nilpotent scheme itself is reduced (see [Sta22, Tag 056E]).
$\mathcal {N}(\mathfrak {g})$ so the nilpotent scheme itself is reduced (see [Sta22, Tag 056E]).
Remark 3.3 To conclude that the nilpotent scheme is reduced in separably good characteristics, it remains to investigate what happens for ![]() $\operatorname {SL}_{mp}$ in characteristic
$\operatorname {SL}_{mp}$ in characteristic ![]() $p>0$, with
$p>0$, with ![]() $m\in \mathbb {N}^{*}$. This case is actually governed by the case of
$m\in \mathbb {N}^{*}$. This case is actually governed by the case of ![]() $\operatorname {GL}_{mp}$. Indeed, a matrix
$\operatorname {GL}_{mp}$. Indeed, a matrix ![]() $M \in \operatorname {\mathfrak {gl}}_{mp}$ is nilpotent if and only if its characteristic polynomial is of the form
$M \in \operatorname {\mathfrak {gl}}_{mp}$ is nilpotent if and only if its characteristic polynomial is of the form ![]() $t^{mp}$, thus if and only if
$t^{mp}$, thus if and only if ![]() $\operatorname {Tr}(\bigwedge ^i M) = 0$ for
$\operatorname {Tr}(\bigwedge ^i M) = 0$ for ![]() $0\leqslant i \leqslant mp$ where
$0\leqslant i \leqslant mp$ where ![]() $\bigwedge ^i M$ is the
$\bigwedge ^i M$ is the ![]() $i{\text {th}}$ exterior power of
$i{\text {th}}$ exterior power of ![]() $M$. In particular, they have trace zero, whence the isomorphism of coordinate rings
$M$. In particular, they have trace zero, whence the isomorphism of coordinate rings
 \[ \mathcal{O}_{\mathcal{N}(\operatorname{\mathfrak{gl}}_{mp})} = \mathcal{O}_{\operatorname{\mathfrak{gl}}_{mp}}\bigg/\bigg\langle {\rm Tr}\bigg(\bigwedge^i M\bigg)\bigg\rangle_{i=1, \ldots, mp} \cong \mathcal{O}_{\operatorname{\mathfrak{sl}}_{mp}}\bigg/\bigg\langle {\rm Tr}\bigg(\bigwedge^i M\bigg)\bigg\rangle_{i=1,\ldots mp}=\mathcal{O}_{\mathcal{N}(\operatorname{\mathfrak{sl}}_{mp})}. \]
\[ \mathcal{O}_{\mathcal{N}(\operatorname{\mathfrak{gl}}_{mp})} = \mathcal{O}_{\operatorname{\mathfrak{gl}}_{mp}}\bigg/\bigg\langle {\rm Tr}\bigg(\bigwedge^i M\bigg)\bigg\rangle_{i=1, \ldots, mp} \cong \mathcal{O}_{\operatorname{\mathfrak{sl}}_{mp}}\bigg/\bigg\langle {\rm Tr}\bigg(\bigwedge^i M\bigg)\bigg\rangle_{i=1,\ldots mp}=\mathcal{O}_{\mathcal{N}(\operatorname{\mathfrak{sl}}_{mp})}. \]
As ![]() $\mathcal {N}(\operatorname {\mathfrak {gl}}_{mp})$ is reduced in characteristic
$\mathcal {N}(\operatorname {\mathfrak {gl}}_{mp})$ is reduced in characteristic ![]() $p$ (according to 3.1 as
$p$ (according to 3.1 as ![]() $p$ is pretty good for
$p$ is pretty good for ![]() $\operatorname {GL}_{mp}$) so is its coordinate ring
$\operatorname {GL}_{mp}$) so is its coordinate ring ![]() $\mathcal {O}_{\mathcal {N}(\operatorname {\mathfrak {gl}}_{mp})}$, hence the reducedness of
$\mathcal {O}_{\mathcal {N}(\operatorname {\mathfrak {gl}}_{mp})}$, hence the reducedness of ![]() $\mathcal {N}(\operatorname {\mathfrak {sl}}_{mp})$. Therefore,
$\mathcal {N}(\operatorname {\mathfrak {sl}}_{mp})$. Therefore, ![]() $\mathcal {N}(\mathfrak {g})$ is reduced when the characteristic is separably good for the reductive group
$\mathcal {N}(\mathfrak {g})$ is reduced when the characteristic is separably good for the reductive group ![]() $G$.
$G$.
Remark 3.4 In non-separably good characteristics both unipotent and nilpotent schemes might be non-reduced as underlined, for instance, in [Reference SlodowySlo80, 3.9, Remark] in which the author studies the unipotent scheme of ![]() $\operatorname {PGL}_2$ in characteristic two. From this, one can derive the same counter-example for the nilpotent scheme of
$\operatorname {PGL}_2$ in characteristic two. From this, one can derive the same counter-example for the nilpotent scheme of ![]() $\operatorname {\mathfrak {pgl}}_2$:
$\operatorname {\mathfrak {pgl}}_2$:
 \[ \mathcal{N} (\operatorname{\mathfrak{pgl}}_2) = \left\lbrace \begin{pmatrix} x_1 & 0 & 0 \\ x_2 & 0 & x_3\\ 0 & 0 & x_1 \end{pmatrix}\right\rbrace \in \operatorname{\mathfrak{gl}}_3, \]
\[ \mathcal{N} (\operatorname{\mathfrak{pgl}}_2) = \left\lbrace \begin{pmatrix} x_1 & 0 & 0 \\ x_2 & 0 & x_3\\ 0 & 0 & x_1 \end{pmatrix}\right\rbrace \in \operatorname{\mathfrak{gl}}_3, \]
and a matrix ![]() $M$ of this Lie algebra (as described previously) is nilpotent if and only if its characteristic polynomial is
$M$ of this Lie algebra (as described previously) is nilpotent if and only if its characteristic polynomial is ![]() $t^3$. Hence, the nilpotent scheme of
$t^3$. Hence, the nilpotent scheme of ![]() $\operatorname {\mathfrak {pgl}}_2$ has coordinate ring
$\operatorname {\mathfrak {pgl}}_2$ has coordinate ring ![]() $k[x_1, x_2, x_3]/\langle (x_1^2), (2x_1)\rangle$, which is not reduced in characteristic two.
$k[x_1, x_2, x_3]/\langle (x_1^2), (2x_1)\rangle$, which is not reduced in characteristic two.
3.1.2 Springer isomorphisms
As explained in the introduction, the existence of a ![]() $G$-equivariant isomorphism
$G$-equivariant isomorphism ![]() $\phi :\mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ is necessary to obtain a punctual integration. When
$\phi :\mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ is necessary to obtain a punctual integration. When ![]() $G$ is a simply connected
$G$ is a simply connected ![]() $k$-group and
$k$-group and ![]() $p$ is good for
$p$ is good for ![]() $G$, Springer establishes in [Reference SpringerSpr69, Theorem 3.1] the existence of homeomorphisms between these schemes. As pointed out by the author himself, these homeomorphisms would be isomorphisms of varieties (with the convention of the article, hence of reduced schemes) if the reduced part of the nilpotent scheme were known to be normal (which had not been shown at the time of the paper). This result has been studied and refined by many mathematicians, among those Bardsley and Richardson in [Reference Bardsley and RichardsonBR85, 9.3.2] who established the normality of
$G$, Springer establishes in [Reference SpringerSpr69, Theorem 3.1] the existence of homeomorphisms between these schemes. As pointed out by the author himself, these homeomorphisms would be isomorphisms of varieties (with the convention of the article, hence of reduced schemes) if the reduced part of the nilpotent scheme were known to be normal (which had not been shown at the time of the paper). This result has been studied and refined by many mathematicians, among those Bardsley and Richardson in [Reference Bardsley and RichardsonBR85, 9.3.2] who established the normality of ![]() $\mathcal {N}(\mathfrak {g})$ in pretty good characteristic (under this assumption the nilpotent scheme is reduced according to Proposition 3.1) and extended the existence of such isomorphisms to any reductive
$\mathcal {N}(\mathfrak {g})$ in pretty good characteristic (under this assumption the nilpotent scheme is reduced according to Proposition 3.1) and extended the existence of such isomorphisms to any reductive ![]() $k$-group which satisfies the standard hypotheses (as defined by Jantzen, see Remark 3.2). Let us also mention here the work of Herpel who showed in [Reference HerpelHer13] the existence of Springer isomorphisms for any reductive
$k$-group which satisfies the standard hypotheses (as defined by Jantzen, see Remark 3.2). Let us also mention here the work of Herpel who showed in [Reference HerpelHer13] the existence of Springer isomorphisms for any reductive ![]() $k$-groups in pretty good characteristic. This mainly uses previous results from McNinch and Testerman (see [Reference McNinch and TestermanMT09, Theorem 3.3]).
$k$-groups in pretty good characteristic. This mainly uses previous results from McNinch and Testerman (see [Reference McNinch and TestermanMT09, Theorem 3.3]).
From now on, and unless otherwise stated, the characteristic of ![]() $k$ is separably good for
$k$ is separably good for ![]() $G$. In particular, nilpotent and unipotent schemes are reduced, hence the subscripts are removed everywhere Springer isomorphisms are considered.
$G$. In particular, nilpotent and unipotent schemes are reduced, hence the subscripts are removed everywhere Springer isomorphisms are considered.
Let us insist on the following point: there exist several Springer isomorphisms but they all induce the same bijection between the ![]() $G$-orbits of
$G$-orbits of ![]() $\mathcal {N}_{\mathrm {red}}(\mathfrak {g})$ and those of
$\mathcal {N}_{\mathrm {red}}(\mathfrak {g})$ and those of ![]() $\mathcal {V}_{\mathrm {red}}(G)$, as shown by Serre in [Reference McNinchMcN05, 10, Appendix]. To fix better the reader's idea on such variety of Springer isomorphisms one might have a look at the preamble of the aforementioned appendix. There Serre considers the example
$\mathcal {V}_{\mathrm {red}}(G)$, as shown by Serre in [Reference McNinchMcN05, 10, Appendix]. To fix better the reader's idea on such variety of Springer isomorphisms one might have a look at the preamble of the aforementioned appendix. There Serre considers the example ![]() $G = \operatorname {SL}_n$ and picks a nilpotent element
$G = \operatorname {SL}_n$ and picks a nilpotent element ![]() $e \in \operatorname {\mathfrak {sl}}_n$ of order
$e \in \operatorname {\mathfrak {sl}}_n$ of order ![]() $n$. He then explains that in this case a Springer isomorphism
$n$. He then explains that in this case a Springer isomorphism ![]() $\phi$ is of the form:
$\phi$ is of the form:
where the ![]() $a_i$ are elements of
$a_i$ are elements of ![]() $k$ such that
$k$ such that ![]() $a_1 \neq 0$. Moreover, any
$a_1 \neq 0$. Moreover, any ![]() $n$-tuple
$n$-tuple ![]() $(a_1, \cdots, a_{n-1})$ with
$(a_1, \cdots, a_{n-1})$ with ![]() $a_1\neq 0$ defines a unique Springer isomorphism.
$a_1\neq 0$ defines a unique Springer isomorphism.
When ![]() $G$ is simple, Sobaje reminds the reader of the existence of Springer isomorphisms in separably good characteristics (see [Reference SobajeSob15, Theorem 1.1 and Remark 2]). Moreover, in [Reference SobajeSob18, § 7] the author investigates the non-separably good characteristic case. He also emphasises that in separably good characteristics one can always find an isomorphism
$G$ is simple, Sobaje reminds the reader of the existence of Springer isomorphisms in separably good characteristics (see [Reference SobajeSob15, Theorem 1.1 and Remark 2]). Moreover, in [Reference SobajeSob18, § 7] the author investigates the non-separably good characteristic case. He also emphasises that in separably good characteristics one can always find an isomorphism ![]() $\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ that restricts to an isomorphism of reduced schemes
$\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ that restricts to an isomorphism of reduced schemes ![]() $W(\operatorname {\mathfrak {rad_u}}(B)) \cong \operatorname {\mathfrak {rad_u}}(B) \rightarrow \operatorname {Rad}_U(B)$ for any Borel subgroup
$W(\operatorname {\mathfrak {rad_u}}(B)) \cong \operatorname {\mathfrak {rad_u}}(B) \rightarrow \operatorname {Rad}_U(B)$ for any Borel subgroup ![]() $B\subset G$. The author then stresses that the differential of this restriction at
$B\subset G$. The author then stresses that the differential of this restriction at ![]() $0$ is a scalar multiple of the identity (this does not depend on the considered Borel subgroup). More precisely, the situation is the following (note that the two vertical arrows are closed immersions):
$0$ is a scalar multiple of the identity (this does not depend on the considered Borel subgroup). More precisely, the situation is the following (note that the two vertical arrows are closed immersions):

and ![]() $\tilde {\phi }$ is such that
$\tilde {\phi }$ is such that ![]() $(\operatorname {d}\tilde {\phi })_0 = \lambda \operatorname {id}$ with
$(\operatorname {d}\tilde {\phi })_0 = \lambda \operatorname {id}$ with ![]() $\lambda \in k^{*}$. Note that the fact that the restriction
$\lambda \in k^{*}$. Note that the fact that the restriction ![]() $\tilde {\phi }$ maps to
$\tilde {\phi }$ maps to ![]() $\operatorname {Lie}(\operatorname {Rad}_U(B))$ is actually a consequence of the
$\operatorname {Lie}(\operatorname {Rad}_U(B))$ is actually a consequence of the ![]() $\phi$-infinitesimal saturation of the unipotent radical of Borel subgroups (see Definition 4.1 for a definition of this notion as well as Remark 4.2 for a proof of this fact). Sobaje attributes the existence of such specific Springer isomorphisms to McNinch and Testerman (see [Reference McNinch and TestermanMT09, Theorem E]). This can be generalised to any reductive
$\phi$-infinitesimal saturation of the unipotent radical of Borel subgroups (see Definition 4.1 for a definition of this notion as well as Remark 4.2 for a proof of this fact). Sobaje attributes the existence of such specific Springer isomorphisms to McNinch and Testerman (see [Reference McNinch and TestermanMT09, Theorem E]). This can be generalised to any reductive ![]() $k$-group in separably good characteristic. Indeed the properties required for
$k$-group in separably good characteristic. Indeed the properties required for ![]() $\phi$ are preserved under separable isogenies for
$\phi$ are preserved under separable isogenies for ![]() $G$ (see [Reference HerpelHer13, Corollary 5.5] and [Reference McNinchMcN05, Proposition 9]). This allows us to consider semisimple groups rather than simple ones. The reductive case follows because ‘Springer isomorphisms are insensitive to the centre’. Indeed the radical of
$G$ (see [Reference HerpelHer13, Corollary 5.5] and [Reference McNinchMcN05, Proposition 9]). This allows us to consider semisimple groups rather than simple ones. The reductive case follows because ‘Springer isomorphisms are insensitive to the centre’. Indeed the radical of ![]() $\mathfrak {g}$ is the Lie algebra of the centre of
$\mathfrak {g}$ is the Lie algebra of the centre of ![]() $G$, thus is toral and does not contain any
$G$, thus is toral and does not contain any ![]() $p$-nilpotent elements (see Lemma 2.6 and Remark 6.2(ii)).
$p$-nilpotent elements (see Lemma 2.6 and Remark 6.2(ii)).
Let ![]() $P$ be a so-called restricted parabolic subgroup, that is, a parabolic subgroup for which the Lie algebra of the unipotent radical has
$P$ be a so-called restricted parabolic subgroup, that is, a parabolic subgroup for which the Lie algebra of the unipotent radical has ![]() $p$-nilpotency order equal to
$p$-nilpotency order equal to ![]() $1$. For instance, when
$1$. For instance, when ![]() $p>\operatorname {h}(G)$ (where
$p>\operatorname {h}(G)$ (where ![]() $\operatorname {h}(G)$ is the Coxeter number of
$\operatorname {h}(G)$ is the Coxeter number of ![]() $G$) any Borel subgroup of
$G$) any Borel subgroup of ![]() $G$ is restricted (because then, as explained in the introduction, any
$G$ is restricted (because then, as explained in the introduction, any ![]() $p$-nilpotent element of
$p$-nilpotent element of ![]() $G$ has
$G$ has ![]() $p$-nilpotent order equal to
$p$-nilpotent order equal to ![]() $1$; see [Reference McNinchMcN02] for more details). We denote:
$1$; see [Reference McNinchMcN02] for more details). We denote:
− the Lie algebra of the unipotent radical of
 $P$ by
$P$ by  $\operatorname {\mathfrak {rad_u}}(P)$; and
$\operatorname {\mathfrak {rad_u}}(P)$; and− the unipotent radical of
 $P$ by
$P$ by  $\operatorname {Rad}_U(P)$.
$\operatorname {Rad}_U(P)$.
In [Reference SeitzSei00, Proposition 5.3] (credited by Seiz to Serre), the author explains how to obtain a ![]() $P$-equivariant isomorphism of algebraic groups
$P$-equivariant isomorphism of algebraic groups ![]() $\exp _P: \mathfrak {rad_u(p)} \rightarrow \operatorname {Rad}_U(P)$ by base-changing the usual exponential map in characteristic zero. Note that here
$\exp _P: \mathfrak {rad_u(p)} \rightarrow \operatorname {Rad}_U(P)$ by base-changing the usual exponential map in characteristic zero. Note that here ![]() $\mathfrak {rad_u(p)}$ is endowed with the group law induced by the Baker–Campbell–Hausdorff law (which is well-defined, see the preamble of [Reference SeitzSei00, § 5]). When
$\mathfrak {rad_u(p)}$ is endowed with the group law induced by the Baker–Campbell–Hausdorff law (which is well-defined, see the preamble of [Reference SeitzSei00, § 5]). When ![]() $p>\operatorname {h}(G)$, Sobaje explains in [Reference SobajeSob18, Theorem 6.0.2] that there exists a unique Springer isomorphism
$p>\operatorname {h}(G)$, Sobaje explains in [Reference SobajeSob18, Theorem 6.0.2] that there exists a unique Springer isomorphism ![]() $\phi$ that restricts to
$\phi$ that restricts to ![]() $\exp _P$, whose tangent map is the identity and that is compatible with the
$\exp _P$, whose tangent map is the identity and that is compatible with the ![]() $p$-power. Note that when
$p$-power. Note that when ![]() $p<\operatorname {h}(G)$, maps satisfying the three aforementioned requirements still exist, but this time, there are many of such maps. Sobaje study and classify in [Reference SobajeSob18, Theorem 6.0.2] a specific class of such maps, the so-called generalised exponential maps.
$p<\operatorname {h}(G)$, maps satisfying the three aforementioned requirements still exist, but this time, there are many of such maps. Sobaje study and classify in [Reference SobajeSob18, Theorem 6.0.2] a specific class of such maps, the so-called generalised exponential maps.
Let us first consider the case ![]() $p>\operatorname {h}(G)$ to remind the reader of the construction of such group isomorphisms
$p>\operatorname {h}(G)$ to remind the reader of the construction of such group isomorphisms ![]() $\exp _B$ where
$\exp _B$ where ![]() $B \subset G$ is a Borel subgroup, and how this leads to integration results. In this setting, the reader might also refer to a recent article of Balaji et al. (see [Reference Balaji, Deligne and ParameswaranBDP17, § 6]) for a detailed construction of the group isomorphism
$B \subset G$ is a Borel subgroup, and how this leads to integration results. In this setting, the reader might also refer to a recent article of Balaji et al. (see [Reference Balaji, Deligne and ParameswaranBDP17, § 6]) for a detailed construction of the group isomorphism ![]() $\exp _B : \mathfrak {u_b}\rightarrow U_B$. This, combined with Corollary 2.1, actually allows to integrate restricted
$\exp _B : \mathfrak {u_b}\rightarrow U_B$. This, combined with Corollary 2.1, actually allows to integrate restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie subalgebras of
$p$-Lie subalgebras of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Proposition 3.5 Let ![]() $G$ be a reductive
$G$ be a reductive ![]() $k$-group over an algebraically closed field of characteristic
$k$-group over an algebraically closed field of characteristic ![]() $p> \operatorname {h}(G)$. Let
$p> \operatorname {h}(G)$. Let ![]() $\mathfrak {u} \subset \mathfrak {g}$ be a restricted
$\mathfrak {u} \subset \mathfrak {g}$ be a restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie subalgebra. Then
$p$-Lie subalgebra. Then ![]() $\mathfrak {u}$ can be integrated into a smooth connected unipotent subgroup of
$\mathfrak {u}$ can be integrated into a smooth connected unipotent subgroup of ![]() $G$. Namely there exists a smooth connected unipotent subgroup
$G$. Namely there exists a smooth connected unipotent subgroup ![]() $U \subset G$ such that
$U \subset G$ such that ![]() $\operatorname {Lie}(U) \cong \mathfrak {u}$ as Lie algebras.
$\operatorname {Lie}(U) \cong \mathfrak {u}$ as Lie algebras.
Proposition 3.6 will be useful to show the above statement. In the aforementioned framework and as underlined by Serre in [Reference SerreSer96, 2.2], if ![]() $B\subset G$ is a Borel subgroup, the group law on
$B\subset G$ is a Borel subgroup, the group law on ![]() $\mathfrak {\operatorname {\mathfrak {rad_u}}}(B)$ comes from the characteristic-zero framework by lifting and specialisation.
$\mathfrak {\operatorname {\mathfrak {rad_u}}}(B)$ comes from the characteristic-zero framework by lifting and specialisation.
More precisely, if we denote:
(i) by
 $G_{\mathbb {Z}}$ a reductive
$G_{\mathbb {Z}}$ a reductive  $\mathbb {Z}$-group and by
$\mathbb {Z}$-group and by  $B_{\mathbb {Z}} \subset G_{\mathbb {Z}}$ a Borel subgroup such that
$B_{\mathbb {Z}} \subset G_{\mathbb {Z}}$ a Borel subgroup such that  $G=G_{\mathbb {Z}}\otimes _{\mathbb {Z}} k$ and
$G=G_{\mathbb {Z}}\otimes _{\mathbb {Z}} k$ and  $B= B_{\mathbb {Z}}\otimes _{\mathbb {Z}} k$ (such groups both exist according to [Reference Demazure and GrothendieckSGA3III, XXV, Corollaire 1.3]);
$B= B_{\mathbb {Z}}\otimes _{\mathbb {Z}} k$ (such groups both exist according to [Reference Demazure and GrothendieckSGA3III, XXV, Corollaire 1.3]);(ii) by
 $G_\mathbb {Q}$ and
$G_\mathbb {Q}$ and  $B_{\mathbb {Q}}$ the groups obtained from
$B_{\mathbb {Q}}$ the groups obtained from  $G_{\mathbb {Z}}$ and
$G_{\mathbb {Z}}$ and  $B_{\mathbb {Z}}$ by base change from
$B_{\mathbb {Z}}$ by base change from  $\mathbb {Z}$ to
$\mathbb {Z}$ to  $\mathbb {Q}$;
$\mathbb {Q}$;
then we have the following result.
Proposition 3.6 [Reference SerreSer96, 2.2]
The law making ![]() $\operatorname {\mathfrak {rad_u}}(B)$ into an algebraic
$\operatorname {\mathfrak {rad_u}}(B)$ into an algebraic ![]() $k$-group comes from that on
$k$-group comes from that on ![]() $\operatorname {\mathfrak {rad_u}}(B)_{\mathbb {Q}}$: it is defined over
$\operatorname {\mathfrak {rad_u}}(B)_{\mathbb {Q}}$: it is defined over ![]() $\mathbb {Q}$, extends on
$\mathbb {Q}$, extends on ![]() $\operatorname {\mathfrak {rad_u}}(B)_{\mathbb {Z}_{(p)}}\!\!$ and induces a group law on
$\operatorname {\mathfrak {rad_u}}(B)_{\mathbb {Z}_{(p)}}\!\!$ and induces a group law on ![]() $\operatorname {\mathfrak {rad_u}}(B)_{\mathbb {F}_p}\!\!$ then on
$\operatorname {\mathfrak {rad_u}}(B)_{\mathbb {F}_p}\!\!$ then on ![]() $\operatorname {\mathfrak {rad_u}}(B)$ by specialisation. Namely, the situation can be read on the following diagram, the point being the existence of the dotted arrow. In other words, the Baker–Campbell–Hausdorff law has
$\operatorname {\mathfrak {rad_u}}(B)$ by specialisation. Namely, the situation can be read on the following diagram, the point being the existence of the dotted arrow. In other words, the Baker–Campbell–Hausdorff law has ![]() $\mathbb {Z}_{(p)}$-integral coefficients.
$\mathbb {Z}_{(p)}$-integral coefficients.

We refer the reader to [Reference JeanninJea20, Annexe D] for a proof of Proposition 3.6 stated in these terms. We are now able to show Proposition 3.5.
Proof of Proposition 3.5 According to [Reference SerreSer94, II, Lecture 2, Theorem 3], when ![]() $p>\operatorname {h}(G)$ the Lie algebra of the unipotent radical of any Borel subgroup
$p>\operatorname {h}(G)$ the Lie algebra of the unipotent radical of any Borel subgroup ![]() $B \subset G$ is endowed with a group structure induced by the Baker–Campbell–Hausdorff law (which has
$B \subset G$ is endowed with a group structure induced by the Baker–Campbell–Hausdorff law (which has ![]() $p$-integral coefficients as shown, for example, in [Reference SerreSer96, 2.2, Propositon 1]). This law being defined with iterated Lie brackets, it reduces to any subalgebra of
$p$-integral coefficients as shown, for example, in [Reference SerreSer96, 2.2, Propositon 1]). This law being defined with iterated Lie brackets, it reduces to any subalgebra of ![]() $\operatorname {\mathfrak {rad_u}}(B)$, endowing it with a group structure. As, by assumption, one has
$\operatorname {\mathfrak {rad_u}}(B)$, endowing it with a group structure. As, by assumption, one has ![]() $p>\operatorname {h}(G)$, the characteristic of
$p>\operatorname {h}(G)$, the characteristic of ![]() $k$ is not of torsion for
$k$ is not of torsion for ![]() $G$. Thus, there exists a Borel subgroup
$G$. Thus, there exists a Borel subgroup ![]() $B \subset G$ such that
$B \subset G$ such that ![]() $\mathfrak {u}$ is a Lie subalgebra of
$\mathfrak {u}$ is a Lie subalgebra of ![]() $\operatorname {\mathfrak {rad_u}}(B)$ (according to Corollary 2.1). Hence, what precedes implies, in particular, that
$\operatorname {\mathfrak {rad_u}}(B)$ (according to Corollary 2.1). Hence, what precedes implies, in particular, that ![]() $\mathfrak {u}$ is an algebraic group for the Baker–Campbell–Hausdorff law.
$\mathfrak {u}$ is an algebraic group for the Baker–Campbell–Hausdorff law.
The isomorphism of groups ![]() $\exp _{\mathfrak {b}} : \operatorname {\mathfrak {rad_u}}(B) \rightarrow \operatorname {Rad}_U(B)$ defined by Serre in [Reference SerreSer94, Part II, Lecture 2, Theorem 3] thus restricts to
$\exp _{\mathfrak {b}} : \operatorname {\mathfrak {rad_u}}(B) \rightarrow \operatorname {Rad}_U(B)$ defined by Serre in [Reference SerreSer94, Part II, Lecture 2, Theorem 3] thus restricts to ![]() $\mathfrak {u}$. Denote by
$\mathfrak {u}$. Denote by ![]() $U$ the image of the restricted morphism. It is a smooth connected unipotent subgroup of
$U$ the image of the restricted morphism. It is a smooth connected unipotent subgroup of ![]() $G$.
$G$.
It remains to show that ![]() $\operatorname {Lie}(U) \cong \mathfrak {u}$.
$\operatorname {Lie}(U) \cong \mathfrak {u}$.
The algebraic groups ![]() $\mathfrak {u}$ and
$\mathfrak {u}$ and ![]() $U$ being smooth, the isomorphism of algebraic groups
$U$ being smooth, the isomorphism of algebraic groups ![]() $(\exp _{\mathfrak {b}})_{\mid \mathfrak {u}}$ induces an isomorphism
$(\exp _{\mathfrak {b}})_{\mid \mathfrak {u}}$ induces an isomorphism ![]() $\operatorname {Lie}(U) \cong \operatorname {Lie}(\mathfrak {u})$ (see [Reference Demazure and GrothendieckSGA3I, VIIA Proposition 8.2]). As
$\operatorname {Lie}(U) \cong \operatorname {Lie}(\mathfrak {u})$ (see [Reference Demazure and GrothendieckSGA3I, VIIA Proposition 8.2]). As ![]() $\mathfrak {u}$ is a vector space over a field one has
$\mathfrak {u}$ is a vector space over a field one has ![]() $\operatorname {Lie}(\mathfrak {u}) \cong \mathfrak {u}$, hence
$\operatorname {Lie}(\mathfrak {u}) \cong \mathfrak {u}$, hence ![]() $\operatorname {Lie}(U) \cong \mathfrak {u}$ as Lie algebras. In other words, the map
$\operatorname {Lie}(U) \cong \mathfrak {u}$ as Lie algebras. In other words, the map ![]() $\exp _{\mathfrak {b}}$ induces the identity on tangent spaces. Therefore, the restricted
$\exp _{\mathfrak {b}}$ induces the identity on tangent spaces. Therefore, the restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra
$p$-subalgebra ![]() $\mathfrak {u}$ integrates into a smooth connected unipotent subgroup
$\mathfrak {u}$ integrates into a smooth connected unipotent subgroup ![]() $U$ of
$U$ of ![]() $G$.
$G$.
Remarks 3.7 The following points should help the reader to better understand the issues that are specific to the characteristic ![]() $p>0$ framework.
$p>0$ framework.
(i) What precedes ensures that when ![]() $p>\operatorname {h}(G)$, any restricted
$p>\operatorname {h}(G)$, any restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra of
$p$-subalgebra of ![]() $\mathfrak {g}$ can be integrated into a smooth unipotent connected subgroup of
$\mathfrak {g}$ can be integrated into a smooth unipotent connected subgroup of ![]() $G$. In particular, under this assumption on
$G$. In particular, under this assumption on ![]() $p$, any restricted
$p$, any restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra of an integrable
$p$-subalgebra of an integrable ![]() $p$-nil subalgebra of
$p$-nil subalgebra of ![]() $\mathfrak {g}$ can be integrated. This is not true in general, as shown in § 3.11 (see, in particular, Remark 3.13).
$\mathfrak {g}$ can be integrated. This is not true in general, as shown in § 3.11 (see, in particular, Remark 3.13).
(ii) Note that the work of Seitz mentioned in the preamble of this section (see [Reference SeitzSei00, § 5], in particular, Proposition 5.3) allows one to relax assumptions on ![]() $p$ and to still obtain an integration when
$p$ and to still obtain an integration when ![]() $G$ is semisimple (this should extend easily to arbitrary reductive groups): let
$G$ is semisimple (this should extend easily to arbitrary reductive groups): let ![]() $P \subsetneq G$ be a proper parabolic subgroup and let
$P \subsetneq G$ be a proper parabolic subgroup and let ![]() $\mathfrak {p}$ be its Lie algebra. Denote by
$\mathfrak {p}$ be its Lie algebra. Denote by ![]() $\operatorname {cl}(\mathfrak {u_p})$ the nilpotent index of the Lie algebra of
$\operatorname {cl}(\mathfrak {u_p})$ the nilpotent index of the Lie algebra of ![]() $U_P$, the unipotent radical of
$U_P$, the unipotent radical of ![]() $P$. Results of Seitz ensure that there exists an isomorphism of algebraic groups between
$P$. Results of Seitz ensure that there exists an isomorphism of algebraic groups between ![]() $\exp _P : \mathfrak {u_p} \rightarrow U_P$, where the Lie algebra is endowed with an algebraic group structure given by the Baker–Campbell–Hausdorff law (which is well-defined here as shown by the author). This result, coupled with works of McNinch [Reference McNinchMcN07] allows us to integrate several nil Lie subalgebras in characteristic
$\exp _P : \mathfrak {u_p} \rightarrow U_P$, where the Lie algebra is endowed with an algebraic group structure given by the Baker–Campbell–Hausdorff law (which is well-defined here as shown by the author). This result, coupled with works of McNinch [Reference McNinchMcN07] allows us to integrate several nil Lie subalgebras in characteristic ![]() $p<\operatorname {h}(G)$. Indeed, when
$p<\operatorname {h}(G)$. Indeed, when ![]() $p$ is not of torsion for
$p$ is not of torsion for ![]() $G$, given a
$G$, given a ![]() $p$-nil subalgebra
$p$-nil subalgebra ![]() $\mathfrak {u} \subsetneq \mathfrak {g}$ there exists a so-called optimal parabolic subgroup
$\mathfrak {u} \subsetneq \mathfrak {g}$ there exists a so-called optimal parabolic subgroup ![]() $P_{\mathfrak {u}}(G)$ such that
$P_{\mathfrak {u}}(G)$ such that ![]() $\mathfrak {u}$ is a Lie subalgebra of
$\mathfrak {u}$ is a Lie subalgebra of ![]() $\mathfrak {u_{p_u}}$ (see also [Reference JeanninJea20, II.3] for more details on this paper and the aforementioned construction, with the same notation as used here). Therefore, a precise bound for 3.5 would be to consider
$\mathfrak {u_{p_u}}$ (see also [Reference JeanninJea20, II.3] for more details on this paper and the aforementioned construction, with the same notation as used here). Therefore, a precise bound for 3.5 would be to consider ![]() $p> \operatorname {cl}(\mathfrak {u_{p_u}})$. However, this does not help to get rid of the difficulties that occur for small separably good characteristics
$p> \operatorname {cl}(\mathfrak {u_{p_u}})$. However, this does not help to get rid of the difficulties that occur for small separably good characteristics ![]() $p$, hence we preferred a ‘rough’ statement which avoids getting lost in technical details here.
$p$, hence we preferred a ‘rough’ statement which avoids getting lost in technical details here.
(iii) The situation might seem to be quite similar to the characteristic-zero framework. Unfortunately, and contrary to what happens in characteristic zero, the adjoint representation is not compatible with this integration in general. Namely it is not always true that ![]() ${\exp (t\operatorname {ad}(x))= \operatorname {Ad}(\exp (tx))}$ for any
${\exp (t\operatorname {ad}(x))= \operatorname {Ad}(\exp (tx))}$ for any ![]() $x \in \mathfrak {g}$ (where we denote by
$x \in \mathfrak {g}$ (where we denote by ![]() $\operatorname {ad}$ the derived representation
$\operatorname {ad}$ the derived representation ![]() ${\operatorname {Lie}(\operatorname {Ad})}$). Nevertheless, this is automatically satisfied if the adjoint representation
${\operatorname {Lie}(\operatorname {Ad})}$). Nevertheless, this is automatically satisfied if the adjoint representation ![]() $\operatorname {Ad}$ is of low height according to [Reference Balaji, Deligne and ParameswaranBDP17, 4.6]. The authors mention this result as a corollary of [Reference SerreSer98, Lecture 4, Theorem 5].
$\operatorname {Ad}$ is of low height according to [Reference Balaji, Deligne and ParameswaranBDP17, 4.6]. The authors mention this result as a corollary of [Reference SerreSer98, Lecture 4, Theorem 5].
(iv) Let us emphasise another property that is lost in characteristic ![]() $p>0$ and already mentioned in the introduction (see [Reference Demazure and GabrielDG70, IV, § 2, 4.5] for more details on the characteristic-zero case): even in characteristic
$p>0$ and already mentioned in the introduction (see [Reference Demazure and GabrielDG70, IV, § 2, 4.5] for more details on the characteristic-zero case): even in characteristic ![]() $p>\operatorname {h}(G)$ the integration process no longer induces an equivalence of categories between the category of restricted
$p>\operatorname {h}(G)$ the integration process no longer induces an equivalence of categories between the category of restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie algebras and the category of smooth connected unipotent algebraic groups. More precisely, we have the following.
$p$-Lie algebras and the category of smooth connected unipotent algebraic groups. More precisely, we have the following.
− Let
 $U$ be a unipotent subgroup of
$U$ be a unipotent subgroup of  $G$ and denote by
$G$ and denote by  $\mathfrak {u} := \operatorname {Lie}(U)$ its Lie algebra. The field
$\mathfrak {u} := \operatorname {Lie}(U)$ its Lie algebra. The field  $k$ is algebraically closed, thus perfect. The subgroup
$k$ is algebraically closed, thus perfect. The subgroup  $U$ is therefore
$U$ is therefore  $k$-embeddable into the unipotent radical of a Borel subgroup
$k$-embeddable into the unipotent radical of a Borel subgroup  $B \subset G$.
$B \subset G$.− Let
 $\log _B : \operatorname {Rad}_U(B) \rightarrow \operatorname {\mathfrak {rad_u}}(B)$ be the inverse isomorphism of algebraic groups of the morphism
$\log _B : \operatorname {Rad}_U(B) \rightarrow \operatorname {\mathfrak {rad_u}}(B)$ be the inverse isomorphism of algebraic groups of the morphism  $\exp _{\mathfrak {b}}$, see [Reference Balaji, Deligne and ParameswaranBDP17, § 6] for an explicit construction. As for
$\exp _{\mathfrak {b}}$, see [Reference Balaji, Deligne and ParameswaranBDP17, § 6] for an explicit construction. As for  $\exp _{\mathfrak {b}}$ it is induced by an isomorphism of reduced
$\exp _{\mathfrak {b}}$ it is induced by an isomorphism of reduced  $k$-schemes
$k$-schemes  $\log : \mathcal {V}_{\mathrm {red}}(G) \rightarrow \mathcal {N}_{\mathrm {red}}(\mathfrak {g})$.
$\log : \mathcal {V}_{\mathrm {red}}(G) \rightarrow \mathcal {N}_{\mathrm {red}}(\mathfrak {g})$.
In general, one cannot expect the integrated group ![]() $\exp (\mathfrak {u})$ to be the starting group
$\exp (\mathfrak {u})$ to be the starting group ![]() $U$. Equivalently, the equality
$U$. Equivalently, the equality ![]() $\log _B(U) \neq \mathfrak {u}$ needs not being satisfied a priori.
$\log _B(U) \neq \mathfrak {u}$ needs not being satisfied a priori.
For example, let ![]() $G = \operatorname {SL}_3$ and
$G = \operatorname {SL}_3$ and ![]() $p>3$. We consider the unipotent connected smooth subgroups of
$p>3$. We consider the unipotent connected smooth subgroups of ![]() $G$ generated respectively by the matrices
$G$ generated respectively by the matrices
 \[ \begin{pmatrix} 1 & t & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\quad {\rm and}\quad \begin{pmatrix} 1 & t & t^p \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}. \]
\[ \begin{pmatrix} 1 & t & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\quad {\rm and}\quad \begin{pmatrix} 1 & t & t^p \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}. \]
As ![]() $U_1 \neq U_2$, the restricted
$U_1 \neq U_2$, the restricted ![]() $p$-nil
$p$-nil ![]() $p$-algebras
$p$-algebras ![]() $\log (U_1)$ and
$\log (U_1)$ and ![]() $\log (U_2)$ do not coincide, even though the Lie algebras
$\log (U_2)$ do not coincide, even though the Lie algebras ![]() $\mathfrak {u_1} = \mathfrak {u_2}$ are the same; namely it is the restricted
$\mathfrak {u_1} = \mathfrak {u_2}$ are the same; namely it is the restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie algebra generated by
$p$-Lie algebra generated by
 \[ \begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}. \]
\[ \begin{pmatrix} 0 & 1 & 0\\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}. \]
3.2 From Lie algebras to groups: a natural candidate
Let ![]() $G$ be a reductive group over an algebraically closed field
$G$ be a reductive group over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is assumed to be separably good for
$p>0$ which is assumed to be separably good for ![]() $G$. Let
$G$. Let ![]() $\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ be a Springer isomorphism for
$\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ be a Springer isomorphism for ![]() $G$ such that for any Borel subgroup
$G$ such that for any Borel subgroup ![]() $B\subset G$ the differential of
$B\subset G$ the differential of ![]() $\phi$ restricted to
$\phi$ restricted to ![]() $\operatorname {\mathfrak {rad_u}}(B)$ is the identity at zero (this last assumption is allowed by [Reference SobajeSob15, Theorem 1.1 and Remark 2] as explained in § 3.1.2). It defines for any
$\operatorname {\mathfrak {rad_u}}(B)$ is the identity at zero (this last assumption is allowed by [Reference SobajeSob15, Theorem 1.1 and Remark 2] as explained in § 3.1.2). It defines for any ![]() $p$-nilpotent element of
$p$-nilpotent element of ![]() $\mathfrak {g}$ a
$\mathfrak {g}$ a ![]() $t$-power map:
$t$-power map:
Let ![]() $\mathfrak {u}$ be a restricted
$\mathfrak {u}$ be a restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie subalgebra of
$p$-Lie subalgebra of ![]() $\mathfrak {g}$. The
$\mathfrak {g}$. The ![]() $t$-power map
$t$-power map ![]() $\phi _x$ induces the following morphism:
$\phi _x$ induces the following morphism:
where the notation is that of [Reference Demazure and GrothendieckSGA3I, I, 4.6] (see also [Reference Demazure and GrothendieckSGA3I, II, Lemme 4.11.7]). Denote by ![]() $J_\mathfrak {u}$ the subgroup of
$J_\mathfrak {u}$ the subgroup of ![]() $G$ generated by
$G$ generated by ![]() $\psi _{\mathfrak {u}}$ as a
$\psi _{\mathfrak {u}}$ as a ![]() $\operatorname {fppf}$-sheaf (see [Reference Demazure and GrothendieckSGA3I, VIB, Proposition 7.1 and Remark 7.6.1]). This is:
$\operatorname {fppf}$-sheaf (see [Reference Demazure and GrothendieckSGA3I, VIB, Proposition 7.1 and Remark 7.6.1]). This is:
(i) a connected subgroup by [Reference Demazure and GrothendieckSGA3I, VIB, Corollaire 7.2.1] as
 $W(\mathfrak {u})$ is geometrically reduced and geometrically connected;
$W(\mathfrak {u})$ is geometrically reduced and geometrically connected;(ii) smooth (according to [Reference Demazure and GrothendieckSGA3I, VIB, Proposition 7.1(i)] as
 $G$ is locally of finite type over the field
$G$ is locally of finite type over the field  $k$);
$k$);
One thus needs to compare ![]() $\mathfrak {u}$ with the Lie algebra of
$\mathfrak {u}$ with the Lie algebra of ![]() $J_{\mathfrak {u}}$, denoted by
$J_{\mathfrak {u}}$, denoted by ![]() $\mathfrak {j_u}$. We show that when the restricted
$\mathfrak {j_u}$. We show that when the restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie subalgebra
$p$-Lie subalgebra ![]() $\mathfrak {u}\subseteq \mathfrak {g}$ satisfies some maximality properties (such as that required in the statements of Lemmas 5.1 and 5.3), it is integrable by
$\mathfrak {u}\subseteq \mathfrak {g}$ satisfies some maximality properties (such as that required in the statements of Lemmas 5.1 and 5.3), it is integrable by ![]() $J_{\mathfrak {u}}$. Before going any further, let us stress that when this integration holds true the normalisers
$J_{\mathfrak {u}}$. Before going any further, let us stress that when this integration holds true the normalisers ![]() $N_G(J_{\mathfrak {u}})$ and
$N_G(J_{\mathfrak {u}})$ and ![]() $N_G(\mathfrak {u})$ turn out to be the same. More precisely, we have the following.
$N_G(\mathfrak {u})$ turn out to be the same. More precisely, we have the following.
Lemma 3.8 Let ![]() $\mathfrak {u}$ be a restricted
$\mathfrak {u}$ be a restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie subalgebra of
$p$-Lie subalgebra of ![]() $\mathfrak {g}$. The subgroup
$\mathfrak {g}$. The subgroup ![]() $N_G(\mathfrak {u})$ normalises
$N_G(\mathfrak {u})$ normalises ![]() $J_\mathfrak {u}$.
$J_\mathfrak {u}$.
Proof. First note that ![]() $\phi$ is
$\phi$ is ![]() $G$-equivariant (because it is a Springer isomorphism), so is
$G$-equivariant (because it is a Springer isomorphism), so is ![]() $\phi _x$. Hence, the morphism
$\phi _x$. Hence, the morphism ![]() $\psi _{\mathfrak {u}}$ is compatible with the
$\psi _{\mathfrak {u}}$ is compatible with the ![]() $G$-action on
$G$-action on ![]() $\mathfrak {u}$. In other words, for any
$\mathfrak {u}$. In other words, for any ![]() $g \in G$ and any
$g \in G$ and any ![]() $(x,t) \in \mathfrak {u} \times \mathbb {G}_a$ the equality
$(x,t) \in \mathfrak {u} \times \mathbb {G}_a$ the equality ![]() $\operatorname {Ad}(g)\psi _{\mathfrak {u}}(x,t) = \psi _{\mathfrak {u}} \big ({\rm Ad}(g)x,t\big )$ is satisfied.
$\operatorname {Ad}(g)\psi _{\mathfrak {u}}(x,t) = \psi _{\mathfrak {u}} \big ({\rm Ad}(g)x,t\big )$ is satisfied.
Let ![]() $R$ be a
$R$ be a ![]() $k$-algebra, and consider
$k$-algebra, and consider ![]() $g \in N_G(\mathfrak {u})(R)$ and
$g \in N_G(\mathfrak {u})(R)$ and ![]() $h \in J_{\mathfrak {u}}(R)$. By the definition of
$h \in J_{\mathfrak {u}}(R)$. By the definition of ![]() $J_{\mathfrak {u}}$, there exists an
$J_{\mathfrak {u}}$, there exists an ![]() $\operatorname {fppf}$-covering
$\operatorname {fppf}$-covering ![]() $S \rightarrow R$ such that
$S \rightarrow R$ such that ![]() $h_S =\psi _{\mathfrak {u}}(x_1,s_1) \cdots \psi _{\mathfrak {u}}(x_n,s_n)$ for
$h_S =\psi _{\mathfrak {u}}(x_1,s_1) \cdots \psi _{\mathfrak {u}}(x_n,s_n)$ for ![]() $x_i \in \mathfrak {u}_R \otimes _R S$ and
$x_i \in \mathfrak {u}_R \otimes _R S$ and ![]() $s_i \in S$ (so that
$s_i \in S$ (so that ![]() $\psi _{\mathfrak {u}}(x_i,s_i) \in J_{\mathfrak {u}}(S)$). However, then one has
$\psi _{\mathfrak {u}}(x_i,s_i) \in J_{\mathfrak {u}}(S)$). However, then one has ![]() $({\rm Ad}(g)h)_S = \prod _{i=1}^n \operatorname {Ad}(g_S)\psi _{\mathfrak {u}}(x_i,s_i)$. The morphism
$({\rm Ad}(g)h)_S = \prod _{i=1}^n \operatorname {Ad}(g_S)\psi _{\mathfrak {u}}(x_i,s_i)$. The morphism ![]() $\psi _{\mathfrak {u}}$ being compatible with the
$\psi _{\mathfrak {u}}$ being compatible with the ![]() $G$-action, this can be rewritten as follows:
$G$-action, this can be rewritten as follows:
 \[ ({\rm Ad}(g)h)_S = \prod_{i=1}^n \operatorname{Ad}(g_S)\psi_{\mathfrak{u}}(x_i,s_i) = \prod_{i=1}^n \psi_{\mathfrak{u}}\big({\rm Ad}(g_S)x_i,s_i\big) \in J_{\mathfrak{u}}(S)\cap G(R) = J_{\mathfrak{u}}(R), \]
\[ ({\rm Ad}(g)h)_S = \prod_{i=1}^n \operatorname{Ad}(g_S)\psi_{\mathfrak{u}}(x_i,s_i) = \prod_{i=1}^n \psi_{\mathfrak{u}}\big({\rm Ad}(g_S)x_i,s_i\big) \in J_{\mathfrak{u}}(S)\cap G(R) = J_{\mathfrak{u}}(R), \]
where the equality ![]() $J_{\mathfrak {u}}(S)\cap G(R) = J_{\mathfrak {u}}(R)$ follows from the fact that
$J_{\mathfrak {u}}(S)\cap G(R) = J_{\mathfrak {u}}(R)$ follows from the fact that ![]() $J_{\mathfrak {u}}$ is generated by
$J_{\mathfrak {u}}$ is generated by ![]() $\psi _{\mathfrak {u}}$ as a
$\psi _{\mathfrak {u}}$ as a ![]() $\operatorname {fppf}$-sheaf.
$\operatorname {fppf}$-sheaf.
We thus have shown that ![]() $\operatorname {Ad}(g)h \in J_{\mathfrak {u}}(R)$ for all
$\operatorname {Ad}(g)h \in J_{\mathfrak {u}}(R)$ for all ![]() $g \in N_{\mathfrak {g}}(\mathfrak {u})(R)$. In other words, we have shown the inclusion
$g \in N_{\mathfrak {g}}(\mathfrak {u})(R)$. In other words, we have shown the inclusion ![]() $N_G(\mathfrak {u})(R) \subseteq N_G(J_\mathfrak {u})(R)$ for any
$N_G(\mathfrak {u})(R) \subseteq N_G(J_\mathfrak {u})(R)$ for any ![]() $k$-algebra
$k$-algebra ![]() $R$. Yoneda's lemma then leads to the desired inclusion
$R$. Yoneda's lemma then leads to the desired inclusion ![]() $N_G(\mathfrak {u}) \subseteq N_G(J_\mathfrak {u})$.
$N_G(\mathfrak {u}) \subseteq N_G(J_\mathfrak {u})$.
Lemma 3.9 When ![]() $J_{\mathfrak {u}}$ integrates
$J_{\mathfrak {u}}$ integrates ![]() $\mathfrak {u}$, the equality
$\mathfrak {u}$, the equality ![]() $N_G(J_{\mathfrak {u}}) = N_G(\mathfrak {u})$ is satisfied.
$N_G(J_{\mathfrak {u}}) = N_G(\mathfrak {u})$ is satisfied.
Proof. By Lemma 3.8 one only needs to show the inclusion ![]() $N_G(J_{\mathfrak {u}}) \subseteq N_G(\mathfrak {u})$. This is direct according to Lemma 6.3 as the equality
$N_G(J_{\mathfrak {u}}) \subseteq N_G(\mathfrak {u})$. This is direct according to Lemma 6.3 as the equality ![]() $\operatorname {Lie}(J_{\mathfrak {u}}) = \mathfrak {u}$ is satisfied by assumption.
$\operatorname {Lie}(J_{\mathfrak {u}}) = \mathfrak {u}$ is satisfied by assumption.
Remarks 3.10 Let us emphasise the following points.
(i) The assumptions on normalisers in Lemma 3.9 hold true, in particular, when ![]() $\mathfrak {u}$ is a subalgebra of
$\mathfrak {u}$ is a subalgebra of ![]() $\mathfrak {g}$ made of all the
$\mathfrak {g}$ made of all the ![]() $p$-nilpotent elements of the radical of
$p$-nilpotent elements of the radical of ![]() $N_{\mathfrak {g}}(\mathfrak {u})$. This is shown in Lemma 5.1.
$N_{\mathfrak {g}}(\mathfrak {u})$. This is shown in Lemma 5.1.
(ii) As mentioned in the introduction, no Springer isomorphism is compatible with the ![]() $p$-structure of the restricted
$p$-structure of the restricted ![]() $p$-nil
$p$-nil ![]() $p$-algebra. This is actually not a requirement here. Indeed one considers the image of all
$p$-algebra. This is actually not a requirement here. Indeed one considers the image of all ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\mathfrak {u}$ so
$\mathfrak {u}$ so ![]() $x$ and all its
$x$ and all its ![]() $p$-powers are taken into account in the integration process. Moreover, one only needs to compare the subalgebras
$p$-powers are taken into account in the integration process. Moreover, one only needs to compare the subalgebras ![]() $\mathfrak {u}$ and
$\mathfrak {u}$ and ![]() $\mathfrak {j_u}$ and both of them inherit their
$\mathfrak {j_u}$ and both of them inherit their ![]() $p$-structure from that of
$p$-structure from that of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
3.3 Obstructions to the existence of an integration for embedded restricted  $p$-nil
$p$-nil  $p$-subalgebras
$p$-subalgebras
3.3.1 Witt vectors and family of counter-examples
In what follows, we make use of some general results on Witt vectors to construct a family of counter-examples to the existence of an integration of morphisms and restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie algebras in general.
$p$-Lie algebras in general.
Example 3.11 Let ![]() $k$ be a perfect field of characteristic
$k$ be a perfect field of characteristic ![]() $p>0$ and let us consider the following commutative diagram of algebraic groups,
$p>0$ and let us consider the following commutative diagram of algebraic groups,

where:
− we denote the absolute Frobenius automorphism by
 $\operatorname {Frob}$;
$\operatorname {Frob}$;− the central term of the lower sequence is the pushout of the morphisms
 $i$ and
$i$ and  $\operatorname {Frob}$.
$\operatorname {Frob}$.
The group ![]() $\mathbb {G}_a$ being smooth, the exactness of the two horizontal sequences is preserved by derivation (see [Reference Demazure and GrothendieckSGA3I, II, § 5, Proposition 5.3] and [Reference Demazure and GabrielDG70, II, § 7, n
$\mathbb {G}_a$ being smooth, the exactness of the two horizontal sequences is preserved by derivation (see [Reference Demazure and GrothendieckSGA3I, II, § 5, Proposition 5.3] and [Reference Demazure and GabrielDG70, II, § 7, n![]() $^{\circ }$3, Proposition 3.4]). This leads to the following commutative diagram of restricted
$^{\circ }$3, Proposition 3.4]). This leads to the following commutative diagram of restricted ![]() $p$-Lie algebras and
$p$-Lie algebras and ![]() $p$-morphisms.
$p$-morphisms.

As ![]() $\operatorname {Lie}(\operatorname {Frob}) = 0$ the
$\operatorname {Lie}(\operatorname {Frob}) = 0$ the ![]() $p$-morphism
$p$-morphism ![]() $\mathfrak {w}_2' \rightarrow k$ is split (as a
$\mathfrak {w}_2' \rightarrow k$ is split (as a ![]() $p$-morphism). Let
$p$-morphism). Let ![]() $s :\operatorname {Lie}(\mathbb {G}_a) \rightarrow \mathfrak {w}_2'$ be the resulting splitting.
$s :\operatorname {Lie}(\mathbb {G}_a) \rightarrow \mathfrak {w}_2'$ be the resulting splitting.
Even though ![]() $\operatorname {Lie}(\mathbb {G}_a)$ and
$\operatorname {Lie}(\mathbb {G}_a)$ and ![]() $\mathfrak {w}_2$ are integrable, this splitting does not lift into a morphism of algebraic
$\mathfrak {w}_2$ are integrable, this splitting does not lift into a morphism of algebraic ![]() $k$-groups. The field
$k$-groups. The field ![]() $k$ being perfect, one only needs to check this on
$k$ being perfect, one only needs to check this on ![]() $k$ points. As the vertical morphisms induce the identity morphism on
$k$ points. As the vertical morphisms induce the identity morphism on ![]() $k$-points if the lifting
$k$-points if the lifting ![]() $s : \operatorname {Lie}(\mathbb {G}_a) \rightarrow \mathfrak{w}_2'$ were integrable into a morphism of algebraic groups
$s : \operatorname {Lie}(\mathbb {G}_a) \rightarrow \mathfrak{w}_2'$ were integrable into a morphism of algebraic groups ![]() $\sigma : \mathbb {G}_a(k) \rightarrow W'_2(k)$ such that
$\sigma : \mathbb {G}_a(k) \rightarrow W'_2(k)$ such that ![]() ${\operatorname {Lie}(\sigma )_k = s_k}$, the lower exact sequence of the above commutative diagram of algebraic groups would be split (because the
${\operatorname {Lie}(\sigma )_k = s_k}$, the lower exact sequence of the above commutative diagram of algebraic groups would be split (because the ![]() $\operatorname {Lie}$-functor is left exact). According to the previous remark on
$\operatorname {Lie}$-functor is left exact). According to the previous remark on ![]() $k$-points, the following exact sequence would then also be split.
$k$-points, the following exact sequence would then also be split.

This leads to a contradiction as ![]() $W_2$ would appear as a vector group, while it has
$W_2$ would appear as a vector group, while it has ![]() $p^2$-torsion (see for example [Reference SerreSer88, VII, § 2, n
$p^2$-torsion (see for example [Reference SerreSer88, VII, § 2, n![]() $^{\circ }$10, Proposition 9]: the construction of
$^{\circ }$10, Proposition 9]: the construction of ![]() $W_2'$ is explained in the proof of the proposition, see also [Reference RosenlichtRos58] for a reminder of vector groups).
$W_2'$ is explained in the proof of the proposition, see also [Reference RosenlichtRos58] for a reminder of vector groups).
Remark 3.12 As pointed out by the referee, connected abelian unipotent subgroups of dimension two over a field are classified, up to isomorphism, by a pair of invariants (see the paragraph after [Reference SerreSer88, VII, § 2, 11, Proposition 11]). Let ![]() $U$ be such a group and denote by
$U$ be such a group and denote by ![]() $U''$ the subgroup of
$U''$ the subgroup of ![]() $U$ whose elements have order dividing
$U$ whose elements have order dividing ![]() $p$. The group law is denoted additively. As explained in the aforementioned reference, the purely inseparable isogeny
$p$. The group law is denoted additively. As explained in the aforementioned reference, the purely inseparable isogeny ![]() $U/pU \rightarrow U'' : x \mapsto px$ has degree
$U/pU \rightarrow U'' : x \mapsto px$ has degree ![]() $p^h$ and
$p^h$ and ![]() $h$ is the second invariant of the above pair. This invariant could also be used to show that the splitting
$h$ is the second invariant of the above pair. This invariant could also be used to show that the splitting ![]() $s$ is not integrable in Example 3.11 (as this would imply that
$s$ is not integrable in Example 3.11 (as this would imply that ![]() $W_2$ has
$W_2$ has ![]() $h=2$ while it is actually equal to
$h=2$ while it is actually equal to ![]() $1$).
$1$).
3.3.2 Obstructions in the reductive framework
Let us go back to the framework we are interested in: let ![]() $G$ be a reductive group over an algebraically closed field of characteristic
$G$ be a reductive group over an algebraically closed field of characteristic ![]() $p>0$ which is assumed to be separably good for
$p>0$ which is assumed to be separably good for ![]() $G$. Let
$G$. Let ![]() $U$ and
$U$ and ![]() $V \subset G$ be two subgroups. What precedes tells us, in particular, that if
$V \subset G$ be two subgroups. What precedes tells us, in particular, that if ![]() $f : \mathfrak {u}=\operatorname {Lie}(U) \rightarrow \mathfrak {v}=\operatorname {Lie}(V)$ is a morphism of restricted
$f : \mathfrak {u}=\operatorname {Lie}(U) \rightarrow \mathfrak {v}=\operatorname {Lie}(V)$ is a morphism of restricted ![]() $p$-Lie algebras, it is not true in general that there exists a morphism of groups
$p$-Lie algebras, it is not true in general that there exists a morphism of groups ![]() $U \rightarrow V$ such that
$U \rightarrow V$ such that ![]() $\operatorname {Lie}(\phi ) = f$. Namely the map
$\operatorname {Lie}(\phi ) = f$. Namely the map ![]() $\operatorname {Hom}(G, \mathbb {G}_a) \rightarrow \operatorname {Hom}_{p-\operatorname {Lie}}(\mathfrak {g}, k)$ is not surjective. In what follows, a morphism of restricted
$\operatorname {Hom}(G, \mathbb {G}_a) \rightarrow \operatorname {Hom}_{p-\operatorname {Lie}}(\mathfrak {g}, k)$ is not surjective. In what follows, a morphism of restricted ![]() $p$-Lie algebras is integrable if it lifts into a morphism of algebraic groups with smooth kernel.
$p$-Lie algebras is integrable if it lifts into a morphism of algebraic groups with smooth kernel.
Remarks 3.13 One can make the following important remarks on integration of ![]() $p$-nil subalgebras.
$p$-nil subalgebras.
(i) Let ![]() $\mathfrak {u}\subset \mathfrak {g}$ be a restricted
$\mathfrak {u}\subset \mathfrak {g}$ be a restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra which is integrable into a unipotent smooth connected subgroup
$p$-subalgebra which is integrable into a unipotent smooth connected subgroup ![]() $U\subseteq G$. Example 3.11 together with Lemma 3.14 also shows that not any restricted
$U\subseteq G$. Example 3.11 together with Lemma 3.14 also shows that not any restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra
$p$-subalgebra ![]() $\mathfrak {v} \subseteq \mathfrak {u}$ of a restricted
$\mathfrak {v} \subseteq \mathfrak {u}$ of a restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie algebra is integrable into a smooth connected unipotent group
$p$-Lie algebra is integrable into a smooth connected unipotent group ![]() $V$ such that
$V$ such that ![]() $\operatorname {Lie}(V) = \mathfrak {v}$. Nevertheless, if we require the inclusion
$\operatorname {Lie}(V) = \mathfrak {v}$. Nevertheless, if we require the inclusion ![]() $\mathfrak {v} \subseteq \mathfrak {u}$ to be integrable into a morphism of algebraic groups with smooth kernel, then
$\mathfrak {v} \subseteq \mathfrak {u}$ to be integrable into a morphism of algebraic groups with smooth kernel, then ![]() $\mathfrak {v}$ is integrable into a smooth unipotent subgroup of
$\mathfrak {v}$ is integrable into a smooth unipotent subgroup of ![]() $U$ (by virtue of [Reference Demazure and GabrielDG70, II, § 5, Proposition 5.3]). Hence, in what follows a morphism of
$U$ (by virtue of [Reference Demazure and GabrielDG70, II, § 5, Proposition 5.3]). Hence, in what follows a morphism of ![]() $p$-Lie algebras
$p$-Lie algebras ![]() $f : \mathfrak {h} \rightarrow \mathfrak {h}'$ is said to be integrable if there exists a morphism of algebraic groups
$f : \mathfrak {h} \rightarrow \mathfrak {h}'$ is said to be integrable if there exists a morphism of algebraic groups ![]() $\phi : H \rightarrow H'$ with smooth kernel such that
$\phi : H \rightarrow H'$ with smooth kernel such that ![]() $\operatorname {Lie}(\phi )=f$.
$\operatorname {Lie}(\phi )=f$.
(ii) Let us stress that only the restricted ![]() $p$-subalgebras
$p$-subalgebras ![]() $\mathfrak {h} \subseteq \mathfrak {g}$ can pretend to derive from an algebraic group (as this last property automatically implies that
$\mathfrak {h} \subseteq \mathfrak {g}$ can pretend to derive from an algebraic group (as this last property automatically implies that ![]() $\mathfrak {h}$ is endowed with a
$\mathfrak {h}$ is endowed with a ![]() $p$-structure inherited from the group; see, for example, [Reference Demazure and GabrielDG70, II, § 7, n
$p$-structure inherited from the group; see, for example, [Reference Demazure and GabrielDG70, II, § 7, n![]() $^{\circ }$3, Proposition 3.4]). Moreover, as underlined by the example presented in Remark 3.7(iii) the integration of restricted
$^{\circ }$3, Proposition 3.4]). Moreover, as underlined by the example presented in Remark 3.7(iii) the integration of restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebras of
$p$-subalgebras of ![]() $\mathfrak {g}$ does no longer induce a bijective correspondence with unipotent subgroups of
$\mathfrak {g}$ does no longer induce a bijective correspondence with unipotent subgroups of ![]() $G$. This implies, in particular, that the integration of morphisms of restricted
$G$. This implies, in particular, that the integration of morphisms of restricted ![]() $p$-Lie algebras depends on the integration of the Lie algebra one starts with.
$p$-Lie algebras depends on the integration of the Lie algebra one starts with.
The following lemma makes a connection between integration of morphisms and integration of subalgebras.
Lemma 3.14 Let ![]() $G$ and
$G$ and ![]() $H$ be two algebraic smooth
$H$ be two algebraic smooth ![]() $k$-groups with Lie algebras
$k$-groups with Lie algebras ![]() $\mathfrak {g}:= \operatorname {Lie}(G)$, respectively
$\mathfrak {g}:= \operatorname {Lie}(G)$, respectively ![]() $\mathfrak {h}:=\operatorname {Lie}(H)$. Assume that
$\mathfrak {h}:=\operatorname {Lie}(H)$. Assume that ![]() $f : \mathfrak {g} \rightarrow \mathfrak {h}$ is a morphism of restricted
$f : \mathfrak {g} \rightarrow \mathfrak {h}$ is a morphism of restricted ![]() $p$-nil
$p$-nil ![]() $p$-Lie algebras which is integrable into a morphism of groups with smooth kernel. Let us denote by
$p$-Lie algebras which is integrable into a morphism of groups with smooth kernel. Let us denote by ![]() $\phi : G \rightarrow H$ the resulting integrated morphism, then
$\phi : G \rightarrow H$ the resulting integrated morphism, then ![]() $f(\mathfrak {g})$ is integrable into an algebraic smooth connected
$f(\mathfrak {g})$ is integrable into an algebraic smooth connected ![]() $k$-group.
$k$-group.
Proof. Denote by ![]() $\mathfrak {v} := f(\mathfrak {g})$ the image of the morphism
$\mathfrak {v} := f(\mathfrak {g})$ the image of the morphism ![]() $f$, which is assumed to be integrable into a morphism
$f$, which is assumed to be integrable into a morphism ![]() $\phi : G \rightarrow H$ with smooth kernel. One can a priori only expect the inclusions
$\phi : G \rightarrow H$ with smooth kernel. One can a priori only expect the inclusions ![]() $f(\mathfrak {g}) \subseteq \operatorname {Lie}(\phi (G)) \subseteq \mathfrak {h}$ to hold true. However, as
$f(\mathfrak {g}) \subseteq \operatorname {Lie}(\phi (G)) \subseteq \mathfrak {h}$ to hold true. However, as ![]() $k$ is a field and
$k$ is a field and ![]() $\ker (\phi )$ and
$\ker (\phi )$ and ![]() $G$ are smooth so is
$G$ are smooth so is ![]() $\phi (G)$. As a consequence, the restricted morphism
$\phi (G)$. As a consequence, the restricted morphism ![]() $f = \operatorname {Lie}(\phi ) : \mathfrak {g} \rightarrow \operatorname {Lie}(\phi (G))$ is surjective (see [Reference Demazure and GabrielDG70, II, § 5, Proposition 5.3]), whence the equality
$f = \operatorname {Lie}(\phi ) : \mathfrak {g} \rightarrow \operatorname {Lie}(\phi (G))$ is surjective (see [Reference Demazure and GabrielDG70, II, § 5, Proposition 5.3]), whence the equality ![]() $\mathfrak {v} = \operatorname {Lie}(\phi (G))$. In particular, the restricted
$\mathfrak {v} = \operatorname {Lie}(\phi (G))$. In particular, the restricted ![]() $p$-Lie algebra
$p$-Lie algebra ![]() $\mathfrak {v}$ is integrable into an algebraic smooth connected
$\mathfrak {v}$ is integrable into an algebraic smooth connected ![]() $k$-group.
$k$-group.
Remark 3.15 Let ![]() $\phi : G\rightarrow H$ be a smooth morphism of algebraic
$\phi : G\rightarrow H$ be a smooth morphism of algebraic ![]() $k$-groups. Assume that the derived morphism
$k$-groups. Assume that the derived morphism ![]() $\operatorname {Lie}(\phi ) : \mathfrak {g} \rightarrow \mathfrak {h}$ has a splitting
$\operatorname {Lie}(\phi ) : \mathfrak {g} \rightarrow \mathfrak {h}$ has a splitting ![]() $s:\mathfrak {h} \rightarrow \mathfrak {g}$ which is also a morphism of restricted
$s:\mathfrak {h} \rightarrow \mathfrak {g}$ which is also a morphism of restricted ![]() $p$-Lie algebras. It is worth noting that this splitting does not necessarily lift into a splitting of algebraic groups: consider, for instance, the Artin–Schreier covering of
$p$-Lie algebras. It is worth noting that this splitting does not necessarily lift into a splitting of algebraic groups: consider, for instance, the Artin–Schreier covering of ![]() $\mathbb {G}_a \rightarrow \mathbb {G}_a : t \mapsto t^p-t$, its derived morphism is nothing but the identity, whence it admits a splitting that does not lift to a splitting of algebraic groups.
$\mathbb {G}_a \rightarrow \mathbb {G}_a : t \mapsto t^p-t$, its derived morphism is nothing but the identity, whence it admits a splitting that does not lift to a splitting of algebraic groups.
4.  $\phi$-infinitesimal saturation and proof of Theorem 1.1
$\phi$-infinitesimal saturation and proof of Theorem 1.1
In what follows, ![]() $G$ is a reductive group over an algebraically closed field
$G$ is a reductive group over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is assumed to be separably good for
$p>0$ which is assumed to be separably good for ![]() $G$. Let
$G$. Let ![]() $\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ be a Springer isomorphism for
$\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ be a Springer isomorphism for ![]() $G$ such that for any Borel subgroup
$G$ such that for any Borel subgroup ![]() $B\subseteq G$ the differential at
$B\subseteq G$ the differential at ![]() $0$ of
$0$ of ![]() $\phi$ restricted to
$\phi$ restricted to ![]() $\operatorname {rad}_U(B)$ is the identity.
$\operatorname {rad}_U(B)$ is the identity.
4.1  $\phi$-infinitesimal saturation
$\phi$-infinitesimal saturation
The following definition extends the notion of infinitesimal saturation to the separably good characteristics.
Definition 4.1 A subgroup ![]() $G' \subseteq G$ is
$G' \subseteq G$ is ![]() $\phi$-infinitesimally saturated if for any
$\phi$-infinitesimally saturated if for any ![]() $p$-nilpotent element
$p$-nilpotent element ![]() $x \in \mathfrak {g'} := \operatorname {Lie}(G')$ the
$x \in \mathfrak {g'} := \operatorname {Lie}(G')$ the ![]() $t$-power map
$t$-power map
factorises through ![]() $G'$. In other words we ask for the following diagram to commute.
$G'$. In other words we ask for the following diagram to commute.

It follows from the definition that the group ![]() $G$ is itself
$G$ is itself ![]() $\phi$-infinitesimally saturated. Let us stress that there are non-trivial examples of
$\phi$-infinitesimally saturated. Let us stress that there are non-trivial examples of ![]() $\phi$-infinitesimally saturated subgroups of
$\phi$-infinitesimally saturated subgroups of ![]() $G$, as follows.
$G$, as follows.
Lemma 4.2 Any parabolic subgroup of ![]() $G$ is
$G$ is ![]() $\phi$-infinitesimally saturated, so are the Levi subgroups and the unipotent radical of any parabolic subgroup
$\phi$-infinitesimally saturated, so are the Levi subgroups and the unipotent radical of any parabolic subgroup ![]() $P \subset G$.
$P \subset G$.
Proof. In order to show this result, we make use of the dynamic method introduced in [Reference ConradCon14, 4] and [Reference Conrad, Gabber and PrasadCGP15, § 2.1]. Let ![]() $T \subset P \subset G$ be a maximal torus and a parabolic subgroup of
$T \subset P \subset G$ be a maximal torus and a parabolic subgroup of ![]() $G$, respectively. As
$G$, respectively. As ![]() $k$ is a field, there exists a non-necessarily unique cocharacter of
$k$ is a field, there exists a non-necessarily unique cocharacter of ![]() $T$, denoted here by
$T$, denoted here by ![]() $\lambda : \mathbb {G}_m \rightarrow G$ such that
$\lambda : \mathbb {G}_m \rightarrow G$ such that ![]() $P = P_G(\lambda )$ (see [Reference Conrad, Gabber and PrasadCGP15, Proposition 2.2.9]). We aim to show that for any
$P = P_G(\lambda )$ (see [Reference Conrad, Gabber and PrasadCGP15, Proposition 2.2.9]). We aim to show that for any ![]() $p$-nilpotent element
$p$-nilpotent element ![]() $x \in \mathfrak {p}$ the image of the
$x \in \mathfrak {p}$ the image of the ![]() $t$-power map
$t$-power map ![]() $\phi _x$ belongs to
$\phi _x$ belongs to ![]() $P= P_G(\lambda )$. The field
$P= P_G(\lambda )$. The field ![]() $k$ being algebraically closed, this is enough to show it on
$k$ being algebraically closed, this is enough to show it on ![]() $k$-points. As a reminder, when
$k$-points. As a reminder, when ![]() $P$ is of the form
$P$ is of the form ![]() $P_G(\lambda )$ the
$P_G(\lambda )$ the ![]() $k$-points of
$k$-points of ![]() $P$ are nothing but the set
$P$ are nothing but the set
Hence, one only needs to prove that ![]() $\lim _{s\to 0} \lambda (s)\cdot \phi (tx)$ exists. This can be done by making use of the
$\lim _{s\to 0} \lambda (s)\cdot \phi (tx)$ exists. This can be done by making use of the ![]() $G$-equivariance of
$G$-equivariance of ![]() $\phi$. This leads to the equality
$\phi$. This leads to the equality ![]() $\lambda (s)\cdot \phi (tx) = \phi (\lambda (s) \cdot tx)$. Moreover, as
$\lambda (s)\cdot \phi (tx) = \phi (\lambda (s) \cdot tx)$. Moreover, as ![]() $x \in \mathfrak {p_g(\lambda )}:= \operatorname {Lie}(P_G(\lambda ))$ the limit
$x \in \mathfrak {p_g(\lambda )}:= \operatorname {Lie}(P_G(\lambda ))$ the limit ![]() $\lim _{s\to 0} \lambda (s) \cdot x$ exists by definition. We deduce from the above equality that
$\lim _{s\to 0} \lambda (s) \cdot x$ exists by definition. We deduce from the above equality that ![]() $\lim _{s\to 0} \lambda (s)\cdot \phi (tx)$ exists, meaning that
$\lim _{s\to 0} \lambda (s)\cdot \phi (tx)$ exists, meaning that ![]() $\phi (tx)\in P_G(\lambda )= P$, whence the result.
$\phi (tx)\in P_G(\lambda )= P$, whence the result.
The same reasoning as before, together with [Reference Conrad, Gabber and PrasadCGP15, Lemma 2.1.5], allows us to show that:
− the unipotent radical of any parabolic subgroup
 $P \subseteq G$ is
$P \subseteq G$ is  $\phi$-infinitesimally saturated as
$\phi$-infinitesimally saturated as
 \[ \operatorname{Rad}_U(P_G(\lambda))(k) = \Big\{g \in G(k) \,\Big| \lim_{s\to 0} \lambda(s)\cdot g =1\Big.\Big\}; \]
\[ \operatorname{Rad}_U(P_G(\lambda))(k) = \Big\{g \in G(k) \,\Big| \lim_{s\to 0} \lambda(s)\cdot g =1\Big.\Big\}; \]
− the Levi subgroups of any parabolic subgroup
 $P \subseteq G$ are
$P \subseteq G$ are  $\phi$-infinitesimally saturated as
$\phi$-infinitesimally saturated as
 \[ Z_G(P_G(\lambda))(k) = P_G(\lambda)\cap P_G(-\lambda). \]
\[ Z_G(P_G(\lambda))(k) = P_G(\lambda)\cap P_G(-\lambda). \]
Remark 4.3 As mentioned in the preamble of § 3.1.2 when ![]() $p>\operatorname {h}(G)$ the only Springer isomorphism for
$p>\operatorname {h}(G)$ the only Springer isomorphism for ![]() $G$ that restricts to
$G$ that restricts to ![]() $\exp _B: \mathfrak {u_b} \rightarrow U_B$, whose tangent map is the identity and that is compatible with the
$\exp _B: \mathfrak {u_b} \rightarrow U_B$, whose tangent map is the identity and that is compatible with the ![]() $p$-power is nothing but the classical exponential map truncated at the power
$p$-power is nothing but the classical exponential map truncated at the power ![]() $p$ (this last condition is not necessary here). In this framework, being
$p$ (this last condition is not necessary here). In this framework, being ![]() $\phi$-infinitesimally saturated is nothing but being
$\phi$-infinitesimally saturated is nothing but being ![]() $\exp$-saturated, that is, being infinitesimally saturated as defined by Deligne in [Reference DeligneDel14, Définition 1.5]).
$\exp$-saturated, that is, being infinitesimally saturated as defined by Deligne in [Reference DeligneDel14, Définition 1.5]).
Having introduced this, we can show the following lemma which states that the generated subgroup ![]() $J_{\mathfrak {u}}$ seems to be the good candidate to integrate
$J_{\mathfrak {u}}$ seems to be the good candidate to integrate ![]() $\mathfrak {u}$ in general.
$\mathfrak {u}$ in general.
Lemma 4.4 Let ![]() $\mathfrak {u} \subseteq \mathfrak {g}$ be a restricted
$\mathfrak {u} \subseteq \mathfrak {g}$ be a restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra. Then:
$p$-subalgebra. Then:
(i) the generated subgroup
 $J_{\mathfrak {u}}$ is unipotent;
$J_{\mathfrak {u}}$ is unipotent;(ii) the inclusion
 $\mathfrak {u} \subseteq \operatorname {Lie}(J_{\mathfrak {u}}): = \mathfrak {j_u}$ is satisfied.
$\mathfrak {u} \subseteq \operatorname {Lie}(J_{\mathfrak {u}}): = \mathfrak {j_u}$ is satisfied.
Proof. With the Lie algebra ![]() $\mathfrak {u}$ being a restricted
$\mathfrak {u}$ being a restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra of
$p$-subalgebra of ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $p$ being separably good for
$p$ being separably good for ![]() $G$ (thus, not of torsion), Corollary 2.1 allows to embed
$G$ (thus, not of torsion), Corollary 2.1 allows to embed ![]() $\mathfrak {u}$ into the Lie algebra of the unipotent radical of a Borel subgroup
$\mathfrak {u}$ into the Lie algebra of the unipotent radical of a Borel subgroup ![]() $B\subset G$. Let us remind the reader of the notation introduced in § 3.2:
$B\subset G$. Let us remind the reader of the notation introduced in § 3.2:
− the Springer isomorphism
 $\phi$ being fixed, we define
where
$\phi$ being fixed, we define
where \begin{alignat*}{5} \psi_{\mathfrak{u}} : W\: &(\mathfrak{u}) \times \: & \mathbb{G}_a\: & \: & \rightarrow \: & G \\ \: & (x, \: & t)\: & \:& \mapsto \: & \phi_x(t), \end{alignat*}
\begin{alignat*}{5} \psi_{\mathfrak{u}} : W\: &(\mathfrak{u}) \times \: & \mathbb{G}_a\: & \: & \rightarrow \: & G \\ \: & (x, \: & t)\: & \:& \mapsto \: & \phi_x(t), \end{alignat*}
 $\phi _x(t):= \phi (tx)$ is the
$\phi _x(t):= \phi (tx)$ is the  $t$-power map;
$t$-power map;− we then denote by
 $J_{\mathfrak {u}}$ the subgroup of
$J_{\mathfrak {u}}$ the subgroup of  $G$ obtained by considering the
$G$ obtained by considering the  $\operatorname {fppf}$-sheaf generated by the image of
$\operatorname {fppf}$-sheaf generated by the image of  $\psi _{\mathfrak {u}}$.
$\psi _{\mathfrak {u}}$.
What precedes, in particular, tells us that ![]() $J_{\mathfrak {u}}$ is
$J_{\mathfrak {u}}$ is ![]() $k$-embeddable into the unipotent radical of a Borel subgroup. This is because
$k$-embeddable into the unipotent radical of a Borel subgroup. This is because ![]() $B$ is
$B$ is ![]() $\phi$-infinitesimally saturated according to Lemma 4.2. In other words,
$\phi$-infinitesimally saturated according to Lemma 4.2. In other words, ![]() $J_{\mathfrak {u}}$ is unipotent (see, for example, [Reference Demazure and GabrielDG70, IV, § 2, n
$J_{\mathfrak {u}}$ is unipotent (see, for example, [Reference Demazure and GabrielDG70, IV, § 2, n![]() $^{\circ}$2, Proposition 2.5(vi)]).
$^{\circ}$2, Proposition 2.5(vi)]).
We still denote by ![]() $\phi$ the restriction of the Springer isomorphism to
$\phi$ the restriction of the Springer isomorphism to ![]() $\operatorname {\mathfrak {rad_u}}(B)$. Recall that:
$\operatorname {\mathfrak {rad_u}}(B)$. Recall that:
− this restriction maps to
 $\operatorname {Rad}_U(B)$;
$\operatorname {Rad}_U(B)$;− its differential satisfies
 $(\operatorname {d}\phi )_0 = \operatorname {id}$ by assumption.
$(\operatorname {d}\phi )_0 = \operatorname {id}$ by assumption.
The subgroup ![]() $J_{\mathfrak {u}}$ being generated by the images of the
$J_{\mathfrak {u}}$ being generated by the images of the ![]() $t$-power maps
$t$-power maps ![]() $\phi _x$ for all
$\phi _x$ for all ![]() $x\in \mathfrak {u}$, the Lie algebra
$x\in \mathfrak {u}$, the Lie algebra ![]() $\mathfrak {j_u}$ contains the differential at
$\mathfrak {j_u}$ contains the differential at ![]() $0$ of all such maps, hence the expected inclusion.
$0$ of all such maps, hence the expected inclusion.
It is worth noting that the inclusion ![]() $\mathfrak {u}\subseteq \mathfrak {j_u}$ is strict in general, as underlined by the following lemma which is a variation of [Reference Demazure and GrothendieckSGA3I, VIB, Proposition 7.6]. Notwithstanding this, it is shown in § 5 that
$\mathfrak {u}\subseteq \mathfrak {j_u}$ is strict in general, as underlined by the following lemma which is a variation of [Reference Demazure and GrothendieckSGA3I, VIB, Proposition 7.6]. Notwithstanding this, it is shown in § 5 that ![]() $J_{\mathfrak {u}}$ does actually integrate
$J_{\mathfrak {u}}$ does actually integrate ![]() $\mathfrak {u}$ when the latter satisfies some maximality hypotheses (see Lemmas 5.1 and 5.3).
$\mathfrak {u}$ when the latter satisfies some maximality hypotheses (see Lemmas 5.1 and 5.3).
Proposition 4.5 Let ![]() $k$ be a separably closed field and let
$k$ be a separably closed field and let ![]() $(G_i)_{i \in \{1, \ldots, n\}}$ and
$(G_i)_{i \in \{1, \ldots, n\}}$ and ![]() $G$ be smooth connected
$G$ be smooth connected ![]() $k$-groups. For any
$k$-groups. For any ![]() $i \in \{1, \ldots, n\}$, consider a smooth morphism of
$i \in \{1, \ldots, n\}$, consider a smooth morphism of ![]() $k$-groups
$k$-groups ![]() $f_i: G_i \rightarrow G$. Then set
$f_i: G_i \rightarrow G$. Then set
 \begin{alignat*}{4} f := \prod_{i=1}^n \: & f_i : \: & \bigg(\prod_{i=1}^n G_i\bigg) \: & \rightarrow \: & G\:&\\ \: & \: & (g_1, \ldots, g_n) \:& \mapsto \: & f_1\: &(g_1) \cdots f_n(g_n) \end{alignat*}
\begin{alignat*}{4} f := \prod_{i=1}^n \: & f_i : \: & \bigg(\prod_{i=1}^n G_i\bigg) \: & \rightarrow \: & G\:&\\ \: & \: & (g_1, \ldots, g_n) \:& \mapsto \: & f_1\: &(g_1) \cdots f_n(g_n) \end{alignat*}
and for any ![]() $N \in \mathbb {N}_{>0}$ define
$N \in \mathbb {N}_{>0}$ define
 \begin{alignat*}{3} f_N := f \times \cdots \times f : \: & \bigg(\prod_{i=1}^n G_i \bigg)^{\times N} \: & \rightarrow \: & G \\ \: & (x_1, \ldots, x_N) \: & \mapsto \: & f(x_1) \cdots f(x_N) \end{alignat*}
\begin{alignat*}{3} f_N := f \times \cdots \times f : \: & \bigg(\prod_{i=1}^n G_i \bigg)^{\times N} \: & \rightarrow \: & G \\ \: & (x_1, \ldots, x_N) \: & \mapsto \: & f(x_1) \cdots f(x_N) \end{alignat*}
given by taking ![]() $N$ times the morphism
$N$ times the morphism ![]() $f$. The following assertions are equivalent:
$f$. The following assertions are equivalent:
(i) there exists an integer
 $N\geqslant 1$ for which the morphism
$N\geqslant 1$ for which the morphism  $f_N$ is surjective and smooth over a non-empty open subset of
$f_N$ is surjective and smooth over a non-empty open subset of  $(\prod _{i=1}^n G_i)^{\times N}$;
$(\prod _{i=1}^n G_i)^{\times N}$;(ii) for
 $N\geqslant 1$ large enough the morphism
$N\geqslant 1$ large enough the morphism  $f_N$ is surjective and separable;
$f_N$ is surjective and separable;(iii) the Lie algebra of
 $G$ decomposes as a
$G$ decomposes as a  $k$-vector space as follows,
where
$k$-vector space as follows,
where \[ \operatorname{Lie}(G) = \sum_{j=1}^n\operatorname{Ad}(h_j) \big( {\rm Lie}(f_j(G_j))\big), \]
\[ \operatorname{Lie}(G) = \sum_{j=1}^n\operatorname{Ad}(h_j) \big( {\rm Lie}(f_j(G_j))\big), \]
 $h_j \in M(k)$ for
$h_j \in M(k)$ for  $M = \langle f_i(G_i) \rangle _{i\in \{1, \ldots, n\}}$, the subgroup generated by the
$M = \langle f_i(G_i) \rangle _{i\in \{1, \ldots, n\}}$, the subgroup generated by the  $f_i(G_i)$;
$f_i(G_i)$;(iv) the group
 $G$ is generated by the images of the
$G$ is generated by the images of the  $G_j$ on the big étale site.
$G_j$ on the big étale site.
Remark 4.6 If the equivalent conditions of Lemma 4.5 are satisfied, then, in particular, the ![]() $k$-group
$k$-group ![]() $G$ is generated by the images of the
$G$ is generated by the images of the ![]() $G_j$ for the
$G_j$ for the ![]() $\operatorname {fppf}$-topology.
$\operatorname {fppf}$-topology.
Proof. We show

In order to avoid heavy notation, we only focus on the case ![]() $n=2$ in the statement of the lemma, the general proof follows by induction.
$n=2$ in the statement of the lemma, the general proof follows by induction.
(i) ![]() $\implies$ (ii) Let
$\implies$ (ii) Let ![]() $N\geqslant 1$ be an integer such that
$N\geqslant 1$ be an integer such that ![]() $f_N : (G_1 \times G_2)^{\times N} \rightarrow G$ is smooth and surjective over a non-empty open subset of
$f_N : (G_1 \times G_2)^{\times N} \rightarrow G$ is smooth and surjective over a non-empty open subset of ![]() $(\prod _{i=1}^n G_i)^{\times N}$. Denote by
$(\prod _{i=1}^n G_i)^{\times N}$. Denote by ![]() $U$ the image of this open set under
$U$ the image of this open set under ![]() $f_N$. It is open in
$f_N$. It is open in ![]() $G$ as
$G$ as ![]() $f$ is open. One first needs to obtain the surjectivity on the whole product of
$f$ is open. One first needs to obtain the surjectivity on the whole product of ![]() $m$ terms (for
$m$ terms (for ![]() $m$ large enough). We remark that because we are working with algebraic groups, it is enough to consider
$m$ large enough). We remark that because we are working with algebraic groups, it is enough to consider ![]() $f_{2N}$ (thus,
$f_{2N}$ (thus, ![]() $m = 2N$) rather than
$m = 2N$) rather than ![]() $f_N$ to obtain this property. This is so because the natural morphism
$f_N$ to obtain this property. This is so because the natural morphism ![]() $U(k) \cdot U(k) \rightarrow G(k)$ is surjective as
$U(k) \cdot U(k) \rightarrow G(k)$ is surjective as ![]() $G$ is a
$G$ is a ![]() $k$-algebraic group).
$k$-algebraic group).
Now, as being separated is nothing but being generically smooth, one only needs to show that ![]() $f_{2N}$ is smooth on a dense open subset of
$f_{2N}$ is smooth on a dense open subset of ![]() $G$. It suffices to show that there exists
$G$. It suffices to show that there exists ![]() $z \in (G_1\times G_2)^{\times 2N}$ such that
$z \in (G_1\times G_2)^{\times 2N}$ such that ![]() $(df_{2N})_z$ is surjective because the source and the target of
$(df_{2N})_z$ is surjective because the source and the target of ![]() $f_{2N}$ are smooth varieties (see [Reference Demazure and GabrielDG70, I, § 4, Corollaire 4.14]). The map
$f_{2N}$ are smooth varieties (see [Reference Demazure and GabrielDG70, I, § 4, Corollaire 4.14]). The map ![]() $f_N$ being smooth over a non-empty open subset of
$f_N$ being smooth over a non-empty open subset of ![]() $(G_1 \times G_2)^{\times N}$, one can find an element
$(G_1 \times G_2)^{\times N}$, one can find an element ![]() $x \in (G_1 \times G_2)^{\times N}$ such that
$x \in (G_1 \times G_2)^{\times N}$ such that ![]() $(df_N)_x$ is surjective. This implies that so is
$(df_N)_x$ is surjective. This implies that so is ![]() $(df_{2N})_{(1,x)}$ and allows us to conclude that
$(df_{2N})_{(1,x)}$ and allows us to conclude that ![]() $f_{2N}$ is smooth over an open neighbourhood of
$f_{2N}$ is smooth over an open neighbourhood of ![]() $(1,x)$.
$(1,x)$.
(ii) ![]() $\implies$ (iii) Let
$\implies$ (iii) Let ![]() $N \in \mathbb {N}_{>0}$ be such that the morphism
$N \in \mathbb {N}_{>0}$ be such that the morphism ![]() $f_N$ is separable and surjective. These two assumptions together ensure that there exists an element
$f_N$ is separable and surjective. These two assumptions together ensure that there exists an element
such that ![]() $(d f_N)_{h} : T\big ((G_1 \times G_2)^N\big )_h \rightarrow T(G)_g$ is surjective for
$(d f_N)_{h} : T\big ((G_1 \times G_2)^N\big )_h \rightarrow T(G)_g$ is surjective for ![]() $g=f_N(h)$. Set
$g=f_N(h)$. Set ![]() $g_{1,i} = h_{1,1}h_{1,2}\cdots h_{1,i}$ and
$g_{1,i} = h_{1,1}h_{1,2}\cdots h_{1,i}$ and ![]() $g_{2,i} = h_{2,1}h_{2,2}\cdots h_{2,i}$ and consider the map
$g_{2,i} = h_{2,1}h_{2,2}\cdots h_{2,i}$ and consider the map
 \begin{alignat*}{3} \alpha : \: & (G_1 \times G_2)^{\times N} \: & \rightarrow \: & (G_1 \times G_2)^{\times N}\\ \: & (x_{1,1}, \cdots x_{2,N}) \: & \mapsto \: & (h_{1,1}x_{1,1}, \cdots, h_{2,N}x_{2,N}). \end{alignat*}
\begin{alignat*}{3} \alpha : \: & (G_1 \times G_2)^{\times N} \: & \rightarrow \: & (G_1 \times G_2)^{\times N}\\ \: & (x_{1,1}, \cdots x_{2,N}) \: & \mapsto \: & (h_{1,1}x_{1,1}, \cdots, h_{2,N}x_{2,N}). \end{alignat*}
This allows us to translate ![]() $f_N$ to the origin as illustrated by the following diagram that can be shown to be commutative:
$f_N$ to the origin as illustrated by the following diagram that can be shown to be commutative:

where ![]() $\operatorname {Ad}^N(g_{j,i}): = \prod _{i=1}^N({\rm Ad}(g_{1,i}), \operatorname {Ad}(g_{2,i}))$ is the diagonal conjugation by the
$\operatorname {Ad}^N(g_{j,i}): = \prod _{i=1}^N({\rm Ad}(g_{1,i}), \operatorname {Ad}(g_{2,i}))$ is the diagonal conjugation by the ![]() $g_{j,i}$ for
$g_{j,i}$ for ![]() $j \in \{1,2\}$ and
$j \in \{1,2\}$ and ![]() $\rho (g^{-1})$ is the right multiplication. This implies, in particular, that the differential
$\rho (g^{-1})$ is the right multiplication. This implies, in particular, that the differential ![]() $d \big (f_N'' \circ \operatorname {Ad}^N(g_{j,i})\big )_e : T\big ((G_1 \times G_2)^{\times N} \big )_e \rightarrow \operatorname {Lie}(G)=:\mathfrak {g}$ is surjective. Thus, any
$d \big (f_N'' \circ \operatorname {Ad}^N(g_{j,i})\big )_e : T\big ((G_1 \times G_2)^{\times N} \big )_e \rightarrow \operatorname {Lie}(G)=:\mathfrak {g}$ is surjective. Thus, any ![]() $z \in \mathfrak {g}$ occurs as
$z \in \mathfrak {g}$ occurs as
 \[ d(f_N'' \circ \big({\rm Ad}^N(g_{j,i})\big))_e (x_{1,1},\cdots, x_{2,N}) = \sum_{i=1}^N \big({\rm Ad}(h_{1,i})(x_{1,i}) + \operatorname{Ad}(h_{2,i})(x_{2,i})\big) \]
\[ d(f_N'' \circ \big({\rm Ad}^N(g_{j,i})\big))_e (x_{1,1},\cdots, x_{2,N}) = \sum_{i=1}^N \big({\rm Ad}(h_{1,i})(x_{1,i}) + \operatorname{Ad}(h_{2,i})(x_{2,i})\big) \]
for an element ![]() $(x_{1,1},\cdots, x_{2,N}) \in T\big ((G_1 \times G_2)^{\times N} \big )_e$, whence the desired equality of vector spaces.
$(x_{1,1},\cdots, x_{2,N}) \in T\big ((G_1 \times G_2)^{\times N} \big )_e$, whence the desired equality of vector spaces.
(iii) ![]() $\implies$ (i) Let
$\implies$ (i) Let ![]() $x \in \mathfrak {g}$, by assumption there exist natural integers
$x \in \mathfrak {g}$, by assumption there exist natural integers ![]() $n$ and
$n$ and ![]() $m$ such that
$m$ such that
 \begin{align*} x & = \sum_{i=1}^{n}\big({\rm Ad}(h^{1,i})(x_{1,i}) + \operatorname{Ad}(h^{2,i})(x_{2,i})\big)\\ & = \sum_{i=1}^{n} \bigg({\rm Ad}\bigg(\prod_{j=1}^m g^{1,i}_{1,j}g^{1,i}_{2,j}\bigg)(x_{1,i}) + \operatorname{Ad}\bigg(\prod_{l=1}^m g^{2,i}_{1,l}g^{2,i}_{2,l} \bigg) (x_{2,i})\bigg), \end{align*}
\begin{align*} x & = \sum_{i=1}^{n}\big({\rm Ad}(h^{1,i})(x_{1,i}) + \operatorname{Ad}(h^{2,i})(x_{2,i})\big)\\ & = \sum_{i=1}^{n} \bigg({\rm Ad}\bigg(\prod_{j=1}^m g^{1,i}_{1,j}g^{1,i}_{2,j}\bigg)(x_{1,i}) + \operatorname{Ad}\bigg(\prod_{l=1}^m g^{2,i}_{1,l}g^{2,i}_{2,l} \bigg) (x_{2,i})\bigg), \end{align*}
where:
− for
 $q \in \{1,2\}$, the
$q \in \{1,2\}$, the  $h^{q,i}$ belong to
$h^{q,i}$ belong to  $\langle f_1(G_1)(k), f_2(G_2)(k) \rangle$, hence decompose into products of
$\langle f_1(G_1)(k), f_2(G_2)(k) \rangle$, hence decompose into products of  $g^{q,i}_{r,j} \in f_r(G_r)(k)$ for
$g^{q,i}_{r,j} \in f_r(G_r)(k)$ for  $r \in \{1,2\}$ and
$r \in \{1,2\}$ and  $j \in \{1,\cdots, m\}$; note that they may be equal to
$j \in \{1,\cdots, m\}$; note that they may be equal to  $1$;
$1$;− the
 $x_{q,i} = f(z_{q,i})$ are elements of
$x_{q,i} = f(z_{q,i})$ are elements of  $\operatorname {Lie}(f_q(G_q))$.
$\operatorname {Lie}(f_q(G_q))$.
Recall that, as noted previously (in the proof of the last implication), for any ![]() $g \in G$ the tangent space of
$g \in G$ the tangent space of ![]() $G$ at
$G$ at ![]() $g$ identifies with the Lie algebra of
$g$ identifies with the Lie algebra of ![]() $G$. Hence, the surjectivity of
$G$. Hence, the surjectivity of ![]() $(df_{N}\!)_e$ (as for any
$(df_{N}\!)_e$ (as for any ![]() $x \in \mathfrak {g}$, the
$x \in \mathfrak {g}$, the ![]() $N$-tuple
$N$-tuple ![]() $(z_{1,i}, z_{2,i})$ is an antecedent for
$(z_{1,i}, z_{2,i})$ is an antecedent for ![]() $(df_{N}\!)_e$). The derived morphism
$(df_{N}\!)_e$). The derived morphism ![]() $(df_N)_e$ being surjective and
$(df_N)_e$ being surjective and ![]() $G$ and
$G$ and ![]() $(G_1 \times G_2)^{\times N}$ being smooth, the morphism
$(G_1 \times G_2)^{\times N}$ being smooth, the morphism ![]() $f_N$ is smooth over a non-empty open subset
$f_N$ is smooth over a non-empty open subset ![]() $U \subset (G_1 \times G_2)^{N}$ (according to [Reference Demazure and GabrielDG70, I, § 4, Corollaire 4.14]). It remains to show the surjectivity of
$U \subset (G_1 \times G_2)^{N}$ (according to [Reference Demazure and GabrielDG70, I, § 4, Corollaire 4.14]). It remains to show the surjectivity of ![]() $f_N$ which is direct from the natural morphism
$f_N$ which is direct from the natural morphism ![]() $U(k) \cdot U(k) \rightarrow G(k)$ being surjective (because
$U(k) \cdot U(k) \rightarrow G(k)$ being surjective (because ![]() $G$ is an algebraic group).
$G$ is an algebraic group).
(i) ![]() $\implies$ (iv) For any
$\implies$ (iv) For any ![]() $k$-algebra
$k$-algebra ![]() $R$ and any
$R$ and any ![]() $g \in G(R)$ one needs to show that there exists an étale cover
$g \in G(R)$ one needs to show that there exists an étale cover ![]() $S \rightarrow R$ on which
$S \rightarrow R$ on which ![]() $g$ writes
$g$ writes ![]() $g_S = g_{1,1} g_{2,1} \cdots g_{1,N}g_{2,N}$, where
$g_S = g_{1,1} g_{2,1} \cdots g_{1,N}g_{2,N}$, where ![]() $g_{1,i} \in f_1(G_1)(S)$ and
$g_{1,i} \in f_1(G_1)(S)$ and ![]() $g_{2,i} \in f_2(G_2)(S)$ for
$g_{2,i} \in f_2(G_2)(S)$ for ![]() $i \in \{1, \ldots, N\}$. This is, therefore, actually enough to prove the statement when
$i \in \{1, \ldots, N\}$. This is, therefore, actually enough to prove the statement when ![]() $R$ is strictly henselian. One thus only needs to prove it on the residue field
$R$ is strictly henselian. One thus only needs to prove it on the residue field ![]() $\kappa$, as the Hensel lemma holds true allowing one to lift the desired property. The morphism
$\kappa$, as the Hensel lemma holds true allowing one to lift the desired property. The morphism ![]() $f_N$ is surjective and smooth over an open cover of
$f_N$ is surjective and smooth over an open cover of ![]() $(G_1\times G_2)^{\times N}$ so its image is a dense open subset
$(G_1\times G_2)^{\times N}$ so its image is a dense open subset ![]() $U \subset G$, hence the result as
$U \subset G$, hence the result as ![]() $U(\kappa ) \cdot U(\kappa ) \rightarrow G(\kappa )$ is surjective.
$U(\kappa ) \cdot U(\kappa ) \rightarrow G(\kappa )$ is surjective.
(iv) ![]() $\implies$ (iii) By assumption, there exists an integer
$\implies$ (iii) By assumption, there exists an integer ![]() $N \geqslant 1$ for which the morphism
$N \geqslant 1$ for which the morphism ![]() $f_N$ is a covering (see [Reference Demazure and GrothendieckSGA3I, VIB, Propositions 7.4 and 7.6]), hence its surjectivity. Any
$f_N$ is a covering (see [Reference Demazure and GrothendieckSGA3I, VIB, Propositions 7.4 and 7.6]), hence its surjectivity. Any ![]() $g \in G(k[\epsilon _1, \epsilon '_1, \cdots, \epsilon _N, \epsilon '_{N}])$ thus writes
$g \in G(k[\epsilon _1, \epsilon '_1, \cdots, \epsilon _N, \epsilon '_{N}])$ thus writes ![]() $g = \prod _{j=1}^N (h_{1,j} + \epsilon _j x_{1,j})(h_{2,j} + \epsilon '_j x_{2,j})$ for
$g = \prod _{j=1}^N (h_{1,j} + \epsilon _j x_{1,j})(h_{2,j} + \epsilon '_j x_{2,j})$ for ![]() $h_{i,j} \in f_{i}(G_i)(k)$ with
$h_{i,j} \in f_{i}(G_i)(k)$ with ![]() $i \in \{1,2\}$, and
$i \in \{1,2\}$, and ![]() $x_{i,j} \in \operatorname {Lie}(f_i(G_i))$. Hence, the map
$x_{i,j} \in \operatorname {Lie}(f_i(G_i))$. Hence, the map
is surjective, for ![]() $h=(h_{1,j}, h_{2,j})_{j \in \{1, \ldots, N\}}$. We now run exactly the same reasoning as in the proof (ii)
$h=(h_{1,j}, h_{2,j})_{j \in \{1, \ldots, N\}}$. We now run exactly the same reasoning as in the proof (ii) ![]() $\implies$ (iii): set
$\implies$ (iii): set ![]() $g_{1,i} = h_{1,1}h_{1,2}\cdots h_{1,i}$ and
$g_{1,i} = h_{1,1}h_{1,2}\cdots h_{1,i}$ and ![]() $g_{2,i} = h_{2,1}h_{2,2}\cdots h_{2,i}$. That leads to considering the map
$g_{2,i} = h_{2,1}h_{2,2}\cdots h_{2,i}$. That leads to considering the map
 \begin{alignat*}{3} \alpha : \: & (G_1 \times G_2)^{\times N} \: & \rightarrow \: & (G_1 \times G_2)^{\times N}\\ \: & (x_{1,1}, \cdots x_{2,N}) \: & \mapsto \: & (h_{1,1}x_{1,1}, \cdots, h_{2,N}x_{2,N}). \end{alignat*}
\begin{alignat*}{3} \alpha : \: & (G_1 \times G_2)^{\times N} \: & \rightarrow \: & (G_1 \times G_2)^{\times N}\\ \: & (x_{1,1}, \cdots x_{2,N}) \: & \mapsto \: & (h_{1,1}x_{1,1}, \cdots, h_{2,N}x_{2,N}). \end{alignat*}
This allows us to translate ![]() $f_N$ to the origin, as this can be read on the following diagram (which is commutative):
$f_N$ to the origin, as this can be read on the following diagram (which is commutative):

where ![]() $\operatorname {Ad}^N(g_{j,i}): = \prod _{i=1}^N({\rm Ad}(g_{1,i}), \operatorname {Ad}(g_{2,i}))$ is the diagonal conjugation by the
$\operatorname {Ad}^N(g_{j,i}): = \prod _{i=1}^N({\rm Ad}(g_{1,i}), \operatorname {Ad}(g_{2,i}))$ is the diagonal conjugation by the ![]() $g_{j,i}$ for
$g_{j,i}$ for ![]() $j \in \{1,2\}$. This implies, in particular, that the differential
$j \in \{1,2\}$. This implies, in particular, that the differential
is surjective. Thus, any ![]() $z \in \mathfrak {g}$ can be rewritten as
$z \in \mathfrak {g}$ can be rewritten as
 \[ d(f_N'' \circ \big({\rm Ad}^N(g_{j,i})\big))_e (x_{1,1},\cdots, x_{2,N}) = \sum_{i=1}^N \big({\rm Ad}(h_{1,i})(x_{1,i}) + \operatorname{Ad}(h_{2,i})(x_{2,i})\big) \]
\[ d(f_N'' \circ \big({\rm Ad}^N(g_{j,i})\big))_e (x_{1,1},\cdots, x_{2,N}) = \sum_{i=1}^N \big({\rm Ad}(h_{1,i})(x_{1,i}) + \operatorname{Ad}(h_{2,i})(x_{2,i})\big) \]
for an element ![]() $(x_{1,1},\cdots, x_{2,N}) \in T\big ((G_1 \times G_2)^{\times N} \big )_e$, whence the desired equality of vector spaces.
$(x_{1,1},\cdots, x_{2,N}) \in T\big ((G_1 \times G_2)^{\times N} \big )_e$, whence the desired equality of vector spaces.
Remark 4.7 Let ![]() $G$ be a reductive
$G$ be a reductive ![]() $k$-group of finite presentation and let
$k$-group of finite presentation and let ![]() $H \subseteq G$ be the
$H \subseteq G$ be the ![]() $k$-subgroup of
$k$-subgroup of ![]() $G$ generated by the
$G$ generated by the ![]() $f_i(G_i)$ as chosen in the previous lemma. Note that
$f_i(G_i)$ as chosen in the previous lemma. Note that ![]() $H$ is smooth and connected because so are the
$H$ is smooth and connected because so are the ![]() $G_i$. Under some extra assumptions such as:
$G_i$. Under some extra assumptions such as:
(i) the smoothness of all normalisers
 $N_G(\mathfrak {v})$ of all subspaces
$N_G(\mathfrak {v})$ of all subspaces  $\mathfrak {v}$ of
$\mathfrak {v}$ of  $\mathfrak {g}$ (which is ensured under very strict conditions on
$\mathfrak {g}$ (which is ensured under very strict conditions on  $p$, as described in [Reference Herpel and StewartHS16, Theorem A]);
$p$, as described in [Reference Herpel and StewartHS16, Theorem A]);(ii) the smoothness of
 $N_G(\langle \operatorname {Lie}(f_i(G_i))\rangle _{i=1}^n)$;
$N_G(\langle \operatorname {Lie}(f_i(G_i))\rangle _{i=1}^n)$;
the third point of the above lemma also allows us to conclude that ![]() $\operatorname {Lie}(G)$ is generated by the
$\operatorname {Lie}(G)$ is generated by the ![]() $\operatorname {Lie}(f_i(G_i))$ as a restricted
$\operatorname {Lie}(f_i(G_i))$ as a restricted ![]() $p$-Lie algebra. Indeed one only needs to obtain the inclusion
$p$-Lie algebra. Indeed one only needs to obtain the inclusion ![]() $H \subseteq N_G(\langle \operatorname {Lie}(f_i(G_i))\rangle )$. As the
$H \subseteq N_G(\langle \operatorname {Lie}(f_i(G_i))\rangle )$. As the ![]() $f_i$ are morphisms of groups, one actually only needs to show that
$f_i$ are morphisms of groups, one actually only needs to show that ![]() $f_i(G_i) \subset N_G(\langle \operatorname {Lie}(f_i(G_i))\rangle )$. Under the above assumptions the proof is the same as that in characteristic zero (that can be found, for instance, in [Reference BorelBor91, II, 7.6]).
$f_i(G_i) \subset N_G(\langle \operatorname {Lie}(f_i(G_i))\rangle )$. Under the above assumptions the proof is the same as that in characteristic zero (that can be found, for instance, in [Reference BorelBor91, II, 7.6]).
This remark provides some examples under which the Lie algebra of ![]() $H$ is the restricted
$H$ is the restricted ![]() $p$-Lie algebra generated by the Lie algebras of the
$p$-Lie algebra generated by the Lie algebras of the ![]() $f_i$. The following remark, however, illustrates the necessity of assumptions made in Proposition 4.5, by providing examples for which its conclusion does not hold true.
$f_i$. The following remark, however, illustrates the necessity of assumptions made in Proposition 4.5, by providing examples for which its conclusion does not hold true.
Remark 4.8 Let ![]() $G$ be an algebraic group over a separably closed field
$G$ be an algebraic group over a separably closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ and let
$p>0$ and let ![]() $(f_i: G_i \rightarrow G)_{i=1, \ldots, n}$ be a family of
$(f_i: G_i \rightarrow G)_{i=1, \ldots, n}$ be a family of ![]() $n$ smooth morphisms of
$n$ smooth morphisms of ![]() $k$-groups, where the
$k$-groups, where the ![]() $G_i$ are assumed to be smooth and connected. Assume that
$G_i$ are assumed to be smooth and connected. Assume that ![]() $G$ is generated by the
$G$ is generated by the ![]() $f_i(G_i)$. In general, it is not true that
$f_i(G_i)$. In general, it is not true that ![]() $\operatorname {Lie}(G)$ is generated by the
$\operatorname {Lie}(G)$ is generated by the ![]() $\operatorname {Lie}(f_i(G_i))$, as shown in the following two examples.
$\operatorname {Lie}(f_i(G_i))$, as shown in the following two examples.
(i) Assume
 $G = (\mathbb {G}_a)^2$. Set
$G = (\mathbb {G}_a)^2$. Set
 \begin{alignat*}{3} f_1: G_1:=\: &\mathbb{G}_a \: & \rightarrow \: & G\\ \: & x \: & \mapsto \: & (x,0), \end{alignat*}
so
\begin{alignat*}{3} f_1: G_1:=\: &\mathbb{G}_a \: & \rightarrow \: & G\\ \: & x \: & \mapsto \: & (x,0), \end{alignat*}
so \begin{alignat*}{3} f_2:G_2:=\: & \mathbb{G}_a \: & \rightarrow \: & G\\ \:& x \: & \mapsto \: & (x, x^p), \end{alignat*}
\begin{alignat*}{3} f_2:G_2:=\: & \mathbb{G}_a \: & \rightarrow \: & G\\ \:& x \: & \mapsto \: & (x, x^p), \end{alignat*}
 $G = \langle f_1(G_1), f_2(G_2)\rangle$. Note that
$G = \langle f_1(G_1), f_2(G_2)\rangle$. Note that  $\operatorname {Lie}(f_1(G_1)) = \operatorname {Lie}(f_2(G_2)) = k$, hence,
$\operatorname {Lie}(f_1(G_1)) = \operatorname {Lie}(f_2(G_2)) = k$, hence,
 \[ \langle \operatorname{Lie}(f_1(G_1)), \operatorname{Lie}(f_2(G_2)) \rangle= k \neq \operatorname{Lie}(G). \]
\[ \langle \operatorname{Lie}(f_1(G_1)), \operatorname{Lie}(f_2(G_2)) \rangle= k \neq \operatorname{Lie}(G). \]
(ii) The Lie algebra of
 $[G,G]$ (for
$[G,G]$ (for  $[G,G]$ the derived group of
$[G,G]$ the derived group of  $G$) does not necessarily coincide with the derived Lie algebra
$G$) does not necessarily coincide with the derived Lie algebra  $[\mathfrak {g}, \mathfrak {g}]$. For example, if
$[\mathfrak {g}, \mathfrak {g}]$. For example, if  $G = \operatorname {SL}_p = [\operatorname {GL}_p, \operatorname {GL}_p]$, then
$G = \operatorname {SL}_p = [\operatorname {GL}_p, \operatorname {GL}_p]$, then  $\operatorname {\mathfrak {sl}}_p$ is nothing but the matrices of size
$\operatorname {\mathfrak {sl}}_p$ is nothing but the matrices of size  $p \times p$ with trace zero, which does not coincide with
$p \times p$ with trace zero, which does not coincide with  $[\mathfrak {gl}_p, \mathfrak {gl}_p]$ due to the assumption on the characteristic.
$[\mathfrak {gl}_p, \mathfrak {gl}_p]$ due to the assumption on the characteristic.
The notion of ![]() $\phi$-infinitesimal saturation introduced here also allows us to extend theorems [Reference DeligneDel14, Théorème 1.7] and [Reference Balaji, Deligne and ParameswaranBDP17, Theorem 2.5] to
$\phi$-infinitesimal saturation introduced here also allows us to extend theorems [Reference DeligneDel14, Théorème 1.7] and [Reference Balaji, Deligne and ParameswaranBDP17, Theorem 2.5] to ![]() $\phi$-infinitesimally reductive
$\phi$-infinitesimally reductive ![]() $k$-groups
$k$-groups ![]() $N$ over an algebraically closed field
$N$ over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is assumed to be separably good for
$p>0$ which is assumed to be separably good for ![]() $G$. This is the point of Theorem 1.1. Let us first remark that points (i) and (iii) of [Reference DeligneDel14, Lemme 2.3] are still valid in the aforementioned framework and allow us to reduce ourselves to show the result for connected
$G$. This is the point of Theorem 1.1. Let us first remark that points (i) and (iii) of [Reference DeligneDel14, Lemme 2.3] are still valid in the aforementioned framework and allow us to reduce ourselves to show the result for connected ![]() $N$. More precisely, we have the following.
$N$. More precisely, we have the following.
Lemma 4.9 Let ![]() $G$ be a reductive group over an algebraically closed field
$G$ be a reductive group over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is assumed to be separably good for
$p>0$ which is assumed to be separably good for ![]() $G$, and let
$G$, and let ![]() $N \subset G$ be a subgroup of
$N \subset G$ be a subgroup of ![]() $G$. The following assertions hold true:
$G$. The following assertions hold true:
(i) if
 $N$ is
$N$ is  $\phi$-infinitesimally saturated in
$\phi$-infinitesimally saturated in  $G$, then so is
$G$, then so is  $N^0$;
$N^0$;(ii) if the reduced part
 $N^0_{\mathrm {red}}$ of
$N^0_{\mathrm {red}}$ of  $N^0$ and its unipotent radical
$N^0$ and its unipotent radical  $\operatorname {Rad}_U(N^0_{\mathrm {red}})$ are normal subgroups of
$\operatorname {Rad}_U(N^0_{\mathrm {red}})$ are normal subgroups of  $N^0$, then they are normal in
$N^0$, then they are normal in  $N$.
$N$.
Proof. See [Reference DeligneDel14, Lemme 2.3] for a proof as the notion of ![]() $\phi$-infinitesimal saturation is nothing but a generalisation of those of infinitesimal saturation to the framework described previously (see Remark 4.3).
$\phi$-infinitesimal saturation is nothing but a generalisation of those of infinitesimal saturation to the framework described previously (see Remark 4.3).
In what follows, the ![]() $\phi$-infinitesimally saturated group
$\phi$-infinitesimally saturated group ![]() $N$ is therefore assumed to be connected. In order to state and show the
$N$ is therefore assumed to be connected. In order to state and show the ![]() $\phi$-infinitesimal version of Deligne's result stated in the introduction of this article (see Theorem 1.1), one will need a fundamental result on maximal
$\phi$-infinitesimal version of Deligne's result stated in the introduction of this article (see Theorem 1.1), one will need a fundamental result on maximal ![]() $k$-groups of multiplicative type, which is stated and shown in § 4.2.
$k$-groups of multiplicative type, which is stated and shown in § 4.2.
4.2 A preliminary result on maximal  $k$-groups of multiplicative type
$k$-groups of multiplicative type
Corollary 4.10 (Corollary of [Reference Conrad, Gabber and PrasadCGP15, Proposition A.2.11])
Let ![]() $k$ be a field and let
$k$ be a field and let ![]() $G$ be an affine smooth algebraic
$G$ be an affine smooth algebraic ![]() $k$-group. The maximal connected subgroups of multiplicative type of
$k$-group. The maximal connected subgroups of multiplicative type of ![]() $G$ are the maximal tori of
$G$ are the maximal tori of ![]() $G$.
$G$.
Proof. Without loss of generality, one can assume ![]() $G$ to be connected (as any maximal connected subgroup of
$G$ to be connected (as any maximal connected subgroup of ![]() $G$ is contained in the identity component
$G$ is contained in the identity component ![]() $G^0$). Let
$G^0$). Let ![]() $H \subset G$ be a maximal connected subgroup of multiplicative type.
$H \subset G$ be a maximal connected subgroup of multiplicative type.
Note that, as explained in the proof of [Reference Balaji, Deligne and ParameswaranBDP17, Corollaire 3.3], the connected centraliser of ![]() $H$ in
$H$ in ![]() $G$, denoted by
$G$, denoted by ![]() $Z_G^0(H)$, is a smooth subgroup of
$Z_G^0(H)$, is a smooth subgroup of ![]() $G$. This is an immediate consequence of the smoothness theorem for centralisers (see for example [Reference Demazure and GabrielDG70, II, § 5, 2.8]): the group
$G$. This is an immediate consequence of the smoothness theorem for centralisers (see for example [Reference Demazure and GabrielDG70, II, § 5, 2.8]): the group ![]() $G$ being smooth, the set of
$G$ being smooth, the set of ![]() $H$-fixed points of
$H$-fixed points of ![]() $G$ (for the
$G$ (for the ![]() $H$-conjugation) is smooth over
$H$-conjugation) is smooth over ![]() $k$.
$k$.
We proceed by induction on the dimension of ![]() $G$, the case of dimension zero being trivial.
$G$, the case of dimension zero being trivial.
If now the group ![]() $G$ is of strictly positive dimension, then one of the following holds.
$G$ is of strictly positive dimension, then one of the following holds.
(i) Either the inclusion
 $Z_G^0(H) \subset G$ is strict and then
$Z_G^0(H) \subset G$ is strict and then  $H$ is a maximal connected subgroup of
$H$ is a maximal connected subgroup of  $Z_G^0(H)$ of multiplicative type, thus
$Z_G^0(H)$ of multiplicative type, thus  $H$ is a
$H$ is a  $k$-torus (of
$k$-torus (of  $Z_G^0(H)$, hence of
$Z_G^0(H)$, hence of  $G$) by induction.
$G$) by induction.(ii) Or
 $Z_G^0(H)= G$ and
$Z_G^0(H)= G$ and  $H$ is central in
$H$ is central in  $G$. Then, by [Reference Conrad, Gabber and PrasadCGP15, Proposition A.2.11] (applied to
$G$. Then, by [Reference Conrad, Gabber and PrasadCGP15, Proposition A.2.11] (applied to  $G$) one has the following exact sequence:
where
$G$) one has the following exact sequence:
where
 $V$ is a unipotent smooth connected group and
$V$ is a unipotent smooth connected group and  $G_t$ is the
$G_t$ is the  $k$-subgroup of
$k$-subgroup of  $G$ generated by the
$G$ generated by the  $k$-tori of
$k$-tori of  $G$. The subgroup
$G$. The subgroup  $H \subseteq G$ is maximal and connected of multiplicative type in
$H \subseteq G$ is maximal and connected of multiplicative type in  $G$. It thus fulfils the same conditions in
$G$. It thus fulfils the same conditions in  $G_t$. The quotient
$G_t$. The quotient  $G/G_t = U$ is indeed unipotent, thus the subgroup of multiplicative type
$G/G_t = U$ is indeed unipotent, thus the subgroup of multiplicative type  $H$ intersects
$H$ intersects  $U$ trivially. It is therefore included in
$U$ trivially. It is therefore included in  $G_t$. If
$G_t$. If  $V \neq 1$, then
$V \neq 1$, then  $H$ is a
$H$ is a  $k$-torus by induction. Otherwise one has
$k$-torus by induction. Otherwise one has  $G_t = G$ and if
$G_t = G$ and if  $T$ is a
$T$ is a  $k$-torus of
$k$-torus of  $G$ the subgroup
$G$ the subgroup  $H\cdot T \subset G$ is connected of multiplicative type and contains
$H\cdot T \subset G$ is connected of multiplicative type and contains  $H$ so it is equal to
$H$ so it is equal to  $H$ (as
$H$ (as  $H$ is assumed to be maximal). Finally, one actually has
$H$ is assumed to be maximal). Finally, one actually has  $T \subset H$, hence
$T \subset H$, hence  $G_t \subset H$, so we have shown that
$G_t \subset H$, so we have shown that  $H = G_t$. This implies, in particular, the smoothness of
$H = G_t$. This implies, in particular, the smoothness of  $H$ which turns out to be a
$H$ which turns out to be a  $k$-torus.
$k$-torus.
4.3 An infinitesimal version of Theorem 1.1
Let ![]() $H\subseteq N \subseteq G$ be a maximal connected subgroup of multiplicative type of the
$H\subseteq N \subseteq G$ be a maximal connected subgroup of multiplicative type of the ![]() $\phi$-infinitesimally saturated subgroup
$\phi$-infinitesimally saturated subgroup ![]() $N$. The
$N$. The ![]() $k$-group
$k$-group ![]() $H$ is the direct product of a
$H$ is the direct product of a ![]() $k$-torus
$k$-torus ![]() $T$ together with a diagonalisable
$T$ together with a diagonalisable ![]() $k$-group
$k$-group ![]() $D$. The latter is a product of subgroups of the form
$D$. The latter is a product of subgroups of the form ![]() $\mu _{p^i}$, with
$\mu _{p^i}$, with ![]() $i \in \mathbb {N}$. Moreover, the
$i \in \mathbb {N}$. Moreover, the ![]() $k$-torus
$k$-torus ![]() $T$ is nothing but the intersection
$T$ is nothing but the intersection ![]() $H\cap N_{\mathrm {red}}$ and it is a maximal torus of
$H\cap N_{\mathrm {red}}$ and it is a maximal torus of ![]() $N$ and
$N$ and ![]() $N_{\mathrm {red}}$ (according to Corollary 4.10).
$N_{\mathrm {red}}$ (according to Corollary 4.10).
Let ![]() $Z:=Z^0_{N_{\mathrm {red}}}(T)$ be the connected centraliser of
$Z:=Z^0_{N_{\mathrm {red}}}(T)$ be the connected centraliser of ![]() $T$ for the action of
$T$ for the action of ![]() $N_{\mathrm {red}}$ and set
$N_{\mathrm {red}}$ and set ![]() $W = Z/T$. This is a unipotent subgroup of
$W = Z/T$. This is a unipotent subgroup of ![]() $N$, the reasoning is the same as that of [Reference DeligneDel14, § 2.5]): according to [Reference Demazure and GrothendieckSGA3II, XVII, Proposition 4.3.1(iv)] as the field
$N$, the reasoning is the same as that of [Reference DeligneDel14, § 2.5]): according to [Reference Demazure and GrothendieckSGA3II, XVII, Proposition 4.3.1(iv)] as the field ![]() $k$ is algebraically closed, one only needs to show that this quotient has no subgroup of
$k$ is algebraically closed, one only needs to show that this quotient has no subgroup of ![]() $\mu _p$-type. This is clear: if such a factor would exist its inverse image in
$\mu _p$-type. This is clear: if such a factor would exist its inverse image in ![]() $Z$ would be an extension of
$Z$ would be an extension of ![]() $\mu _p$ by
$\mu _p$ by ![]() $T$ in
$T$ in ![]() $N_{\mathrm {red}}$, hence of multiplicative type. This is absurd as the maximal connected subgroups of multiplicative type of a smooth algebraic group over a field are the maximal tori (by Corollary 4.10). Moreover:
$N_{\mathrm {red}}$, hence of multiplicative type. This is absurd as the maximal connected subgroups of multiplicative type of a smooth algebraic group over a field are the maximal tori (by Corollary 4.10). Moreover:
− the groups
 $T$ and
$T$ and  $Z$ being smooth, so is
$Z$ being smooth, so is  $W$ according to [Reference Demazure and GabrielDG70, II, § 5, n
$W$ according to [Reference Demazure and GabrielDG70, II, § 5, n $^{\circ }$5, Proposition 5.3(ii)];
$^{\circ }$5, Proposition 5.3(ii)];− the group
 $W$ is also unipotent according to what precedes.
$W$ is also unipotent according to what precedes.
The field ![]() $k$ being perfect [Reference Demazure and GrothendieckSGA3II, exposé XVII, Théorème 6.1.1] holds true and implies the exactness of the following exact sequence.
$k$ being perfect [Reference Demazure and GrothendieckSGA3II, exposé XVII, Théorème 6.1.1] holds true and implies the exactness of the following exact sequence.
To summarise, we have an isomorphism ![]() $Z_{N_{\mathrm {red}}}(T)\cong T \times W$. Let
$Z_{N_{\mathrm {red}}}(T)\cong T \times W$. Let ![]() $X$ be the reduced
$X$ be the reduced ![]() $k$-subscheme of
$k$-subscheme of ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\mathfrak {n}^0 = W(\mathfrak {n}^0) = \operatorname {Lie}(Z_{N_{\mathrm {red}}}(T))$.
$\mathfrak {n}^0 = W(\mathfrak {n}^0) = \operatorname {Lie}(Z_{N_{\mathrm {red}}}(T))$.
Lemma 4.11 The centraliser ![]() $Z^0_{N_{\mathrm {red}}}(T)$ is the subgroup of
$Z^0_{N_{\mathrm {red}}}(T)$ is the subgroup of ![]() $N$ generated by
$N$ generated by ![]() $T$ and the morphism:
$T$ and the morphism:
It is normalised by ![]() $H$.
$H$.
Proof. Let ![]() $J_X \subseteq G$ be the subgroup of
$J_X \subseteq G$ be the subgroup of ![]() $N$ generated by the image of
$N$ generated by the image of ![]() $\psi _X$. The subgroup
$\psi _X$. The subgroup ![]() $N$ being
$N$ being ![]() $\phi$-infinitesimally saturated, the
$\phi$-infinitesimally saturated, the ![]() $t$-power map induced by
$t$-power map induced by ![]() $\phi$ maps any
$\phi$ maps any ![]() $p$-nilpotent element of
$p$-nilpotent element of ![]() $\operatorname {Lie}(Z_{N}(T))$ to
$\operatorname {Lie}(Z_{N}(T))$ to ![]() $N$. Thus,
$N$. Thus, ![]() $\psi _X$ factorises through
$\psi _X$ factorises through ![]() $N$. Moreover, as
$N$. Moreover, as ![]() $J_X$ is the image of a reduced
$J_X$ is the image of a reduced ![]() $k$-scheme it is reduced, hence smooth (as
$k$-scheme it is reduced, hence smooth (as ![]() $k$ is algebraically closed). Thus, the inclusion
$k$ is algebraically closed). Thus, the inclusion ![]() $J_X \subset N_{\mathrm {red}}$ holds true. Finally,
$J_X \subset N_{\mathrm {red}}$ holds true. Finally, ![]() $\phi$ is
$\phi$ is ![]() $G$-equivariant because it is a Springer isomorphism. This implies that the image of
$G$-equivariant because it is a Springer isomorphism. This implies that the image of ![]() $\psi _X$ commutes with any element of
$\psi _X$ commutes with any element of ![]() $T$. We just have shown that
$T$. We just have shown that ![]() $J_X \subset Z_{N_{\mathrm {red}}}(T)$.
$J_X \subset Z_{N_{\mathrm {red}}}(T)$.
Also let ![]() $E_{T,J^0_X}$ be the subgroup generated by
$E_{T,J^0_X}$ be the subgroup generated by ![]() $T$ and
$T$ and ![]() $J^0_X$ as a
$J^0_X$ as a ![]() $\operatorname {fppf}$-sheaf. It is:
$\operatorname {fppf}$-sheaf. It is:
− a smooth subgroup of
 $Z_{N_\mathrm {red}}(T)$ as
$Z_{N_\mathrm {red}}(T)$ as  $T \in Z^0_{N_{\mathrm {red}}}(T)$ is smooth and
$T \in Z^0_{N_{\mathrm {red}}}(T)$ is smooth and  $J^0_X \subset Z^0_{N_{\mathrm {red}}}(T)$ by what precedes;
$J^0_X \subset Z^0_{N_{\mathrm {red}}}(T)$ by what precedes;− connected according to [Reference Demazure and GrothendieckSGA3I, VIB, Corollaire 7.2.1], the torus
 $T$ being geometrically connected and geometrically reduced.
$T$ being geometrically connected and geometrically reduced.
Thus, ![]() $E_{T,J^0_X}$ is actually contained in the identity component of the reduced centraliser. At the Lie algebras level this leads to the following inclusion:
$E_{T,J^0_X}$ is actually contained in the identity component of the reduced centraliser. At the Lie algebras level this leads to the following inclusion:
As ![]() $W$ is a unipotent subgroup of
$W$ is a unipotent subgroup of ![]() $Z^0_{N_{\mathrm {red}}}(T) \cong T \times W$ the Lie algebra
$Z^0_{N_{\mathrm {red}}}(T) \cong T \times W$ the Lie algebra ![]() $\mathfrak {w} : = \operatorname {Lie}(W)$ is a restricted
$\mathfrak {w} : = \operatorname {Lie}(W)$ is a restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra of
$p$-subalgebra of ![]() $Z^0_{N_{\mathrm {red}}}(T)$, hence is contained in the reduced subscheme
$Z^0_{N_{\mathrm {red}}}(T)$, hence is contained in the reduced subscheme ![]() $X$. The latter is the set of
$X$. The latter is the set of ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\operatorname {Lie}(Z_N(T))$ so it is contained in the set of all
$\operatorname {Lie}(Z_N(T))$ so it is contained in the set of all ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\mathfrak {g}$. This set coincides with
$\mathfrak {g}$. This set coincides with ![]() $\operatorname {rad}_p(\mathfrak {g})$ by Lemma 2.13, which holds true as either
$\operatorname {rad}_p(\mathfrak {g})$ by Lemma 2.13, which holds true as either ![]() $p\geqslant 3$ or if
$p\geqslant 3$ or if ![]() $p=2$ the conditions defined in Remark 2.9(ii) are satisfied. As
$p=2$ the conditions defined in Remark 2.9(ii) are satisfied. As ![]() $p$ is not of torsion for
$p$ is not of torsion for ![]() $G$, Corollary 2.1 holds true and allows to embed
$G$, Corollary 2.1 holds true and allows to embed ![]() $\operatorname {rad}_p(\mathfrak {g})$, thus
$\operatorname {rad}_p(\mathfrak {g})$, thus ![]() $X$, into the Lie algebra of the unipotent radical of a Borel subgroup
$X$, into the Lie algebra of the unipotent radical of a Borel subgroup ![]() $B\subseteq G$. Remember that the differential at
$B\subseteq G$. Remember that the differential at ![]() $0$ of the restriction of
$0$ of the restriction of ![]() $\phi$ to this subalgebra satisfies
$\phi$ to this subalgebra satisfies ![]() $(\operatorname {d}\phi )_0 = \operatorname {id}$. The group
$(\operatorname {d}\phi )_0 = \operatorname {id}$. The group ![]() $J_X$ being generated by the image of
$J_X$ being generated by the image of ![]() $\psi _X$, this property ensures that the differential at
$\psi _X$, this property ensures that the differential at ![]() $0$ of any
$0$ of any ![]() $\phi (tx)$, for any
$\phi (tx)$, for any ![]() $t \in \mathbb {G}_a$ and
$t \in \mathbb {G}_a$ and ![]() $x \in X$, belongs to
$x \in X$, belongs to ![]() $\mathfrak {j}_X:=\operatorname {Lie}(J_X)=\operatorname {Lie}(J_X)^0$. In other words, one has the following inclusions
$\mathfrak {j}_X:=\operatorname {Lie}(J_X)=\operatorname {Lie}(J_X)^0$. In other words, one has the following inclusions ![]() $\mathfrak {w}\subseteq X \subseteq \operatorname {Lie}(J_X^0)$. Moreover, the inclusion
$\mathfrak {w}\subseteq X \subseteq \operatorname {Lie}(J_X^0)$. Moreover, the inclusion ![]() $T\subseteq E_{T,J^0_X}$ induces an inclusion of Lie algebras
$T\subseteq E_{T,J^0_X}$ induces an inclusion of Lie algebras ![]() $\mathfrak {t} := \operatorname {Lie}(T) \subseteq \operatorname {Lie}(E_{T,J^0_X})= \operatorname {Lie}(E_{T,J^0_X})$.
$\mathfrak {t} := \operatorname {Lie}(T) \subseteq \operatorname {Lie}(E_{T,J^0_X})= \operatorname {Lie}(E_{T,J^0_X})$.
As one has ![]() $Z_{N_{\mathrm {red}}}(T) \cong T \times W$, what precedes leads to the following inclusion:
$Z_{N_{\mathrm {red}}}(T) \cong T \times W$, what precedes leads to the following inclusion:
thus to the equality ![]() $\operatorname {Lie}(Z^0_{N_{\mathrm {red}}}(T)) = \operatorname {Lie}(E_{T,J^0_X})$. As the groups involved here are smooth and connected this equality of Lie algebras lifts to the group level according to [Reference Demazure and GabrielDG70, II, § 5, n
$\operatorname {Lie}(Z^0_{N_{\mathrm {red}}}(T)) = \operatorname {Lie}(E_{T,J^0_X})$. As the groups involved here are smooth and connected this equality of Lie algebras lifts to the group level according to [Reference Demazure and GabrielDG70, II, § 5, n![]() $^{\circ }$5.5], whence the equality
$^{\circ }$5.5], whence the equality ![]() $Z^0_{N_{\mathrm {red}}}(T) = E_{T,J^0_X}$.
$Z^0_{N_{\mathrm {red}}}(T) = E_{T,J^0_X}$.
It then remains to show that ![]() $E_{T,J^0_X}$ is normalised by
$E_{T,J^0_X}$ is normalised by ![]() $H$. Recall that it is the subgroup generated by
$H$. Recall that it is the subgroup generated by ![]() $T\subseteq H$ (which is normal in
$T\subseteq H$ (which is normal in ![]() $H$) and
$H$) and ![]() $J^0_X$ (which is characteristic in
$J^0_X$ (which is characteristic in ![]() $J_X$, see [Reference Demazure and GabrielDG70, II, § 5, n
$J_X$, see [Reference Demazure and GabrielDG70, II, § 5, n![]() $^{\circ }$1.1]). Hence, one only needs to show that
$^{\circ }$1.1]). Hence, one only needs to show that ![]() $J_X$ is
$J_X$ is ![]() $H$-stable. First remark that
$H$-stable. First remark that ![]() $X$ is stabilised by
$X$ is stabilised by ![]() $H$ because the latter stabilises
$H$ because the latter stabilises ![]() $\operatorname {Lie}(Z_{N}(T))$ and the
$\operatorname {Lie}(Z_{N}(T))$ and the ![]() $p$-nilpotency is preserved by the adjoint action. The
$p$-nilpotency is preserved by the adjoint action. The ![]() $G$-equivariance of
$G$-equivariance of ![]() $\phi$ (thus, its
$\phi$ (thus, its ![]() $H$-equivariance) then allows us to conclude: let
$H$-equivariance) then allows us to conclude: let ![]() $R$ be a
$R$ be a ![]() $k$-algebra. For any
$k$-algebra. For any ![]() $j \in J_X(R)$ and
$j \in J_X(R)$ and ![]() $h \in H(R)$ there is an
$h \in H(R)$ there is an ![]() $\operatorname {fppf}$-covering
$\operatorname {fppf}$-covering ![]() $S \rightarrow R$ such that
$S \rightarrow R$ such that ![]() $j_S = \psi _{X}(x_1,t_1) \cdots \psi _{X}(x_n,t_n)$ where
$j_S = \psi _{X}(x_1,t_1) \cdots \psi _{X}(x_n,t_n)$ where ![]() $x_i \in X_R \otimes _R S$ and
$x_i \in X_R \otimes _R S$ and ![]() $s_i \in S$. However, then one has
$s_i \in S$. However, then one has
 \[ ({\rm Ad}(h)j)_S = \prod_{i=1}^n \operatorname{Ad}(h_S)\psi_{X}(x_i,s_i) = \prod_{i=1}^n \psi_{X}\big( {\rm Ad}(h_S)x_i,s_i\big) \in J_{X}(S)\cap G(R) = J_{X}(R), \]
\[ ({\rm Ad}(h)j)_S = \prod_{i=1}^n \operatorname{Ad}(h_S)\psi_{X}(x_i,s_i) = \prod_{i=1}^n \psi_{X}\big( {\rm Ad}(h_S)x_i,s_i\big) \in J_{X}(S)\cap G(R) = J_{X}(R), \]
and by the Yoneda lemma ![]() $E_{T,J^0_X}$ is stable under the
$E_{T,J^0_X}$ is stable under the ![]() $H$-action.
$H$-action.
Lemma 4.12 The restricted ![]() $p$-Lie algebra
$p$-Lie algebra ![]() $\mathfrak {n}_{\mathrm {red}} := \operatorname {Lie}(N_{\mathrm {red}})$ is an ideal of
$\mathfrak {n}_{\mathrm {red}} := \operatorname {Lie}(N_{\mathrm {red}})$ is an ideal of ![]() $\mathfrak {n}$ acted on by
$\mathfrak {n}$ acted on by ![]() $H$.
$H$.
Proof. According to the proof of [Reference Balaji, Deligne and ParameswaranBDP17, Lemma 2.14] the morphism of ![]() $k$-schemes
$k$-schemes ![]() $N_{\mathrm {red}}\times H \rightarrow N$ is faithfully flat. This being said
$N_{\mathrm {red}}\times H \rightarrow N$ is faithfully flat. This being said ![]() $N$ appears as the
$N$ appears as the ![]() $\operatorname {fppf}$-sheaf generated by
$\operatorname {fppf}$-sheaf generated by ![]() $N_{\mathrm {red}}$ and
$N_{\mathrm {red}}$ and ![]() $H$. Thus, in order to show that
$H$. Thus, in order to show that ![]() $\mathfrak {n}_{\mathrm {red}}$ is actually
$\mathfrak {n}_{\mathrm {red}}$ is actually ![]() $N$-stable one only needs to show that
$N$-stable one only needs to show that ![]() $\mathfrak {n}_{\mathrm {red}}$ is
$\mathfrak {n}_{\mathrm {red}}$ is ![]() $H$-stable. The torus
$H$-stable. The torus ![]() $T = H \cap N_{\mathrm {red}}$ acts on
$T = H \cap N_{\mathrm {red}}$ acts on ![]() $N_{\mathrm {red}}$, respectively on
$N_{\mathrm {red}}$, respectively on ![]() $N$, leading to the following decompositions:
$N$, leading to the following decompositions:
and
where ![]() $X(T)^*$ stands for the group of non-trivial characters of
$X(T)^*$ stands for the group of non-trivial characters of ![]() $T$. Any factor in the decomposition of
$T$. Any factor in the decomposition of ![]() $\operatorname {Lie}(N)$ is stable for
$\operatorname {Lie}(N)$ is stable for ![]() $H$ as
$H$ as ![]() $T$ is normal in
$T$ is normal in ![]() $H$ and we need to show that so is any factor of the decomposition of
$H$ and we need to show that so is any factor of the decomposition of ![]() $\mathfrak {n}_{\mathrm {red}}$. Let us first study the positive weight spaces. The group
$\mathfrak {n}_{\mathrm {red}}$. Let us first study the positive weight spaces. The group ![]() $N$ being generated as a
$N$ being generated as a ![]() $\operatorname {fppf}$-sheaf by
$\operatorname {fppf}$-sheaf by ![]() $N_{\mathrm {red}}$ and the subgroup of multiplicative type
$N_{\mathrm {red}}$ and the subgroup of multiplicative type ![]() $H$ (whose Lie algebra is toral) the
$H$ (whose Lie algebra is toral) the ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\operatorname {Lie}(N)$ are the
$\operatorname {Lie}(N)$ are the ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\operatorname {Lie}(N_{\mathrm {red}})$. This being observed, as for any
$\operatorname {Lie}(N_{\mathrm {red}})$. This being observed, as for any ![]() $\alpha \neq 0$ the weight space
$\alpha \neq 0$ the weight space ![]() $\mathfrak {n}^{\alpha }$ has only
$\mathfrak {n}^{\alpha }$ has only ![]() $p$-nilpotent elements (because we consider the action of a torus here) the equality
$p$-nilpotent elements (because we consider the action of a torus here) the equality ![]() $\mathfrak {n}_{\mathrm {red}}^{\alpha }:= \mathfrak {n}^{\alpha } \cap \mathfrak {n}_{\mathrm {red}} = \mathfrak {n}^{\alpha }$ is satisfied, whence the desired
$\mathfrak {n}_{\mathrm {red}}^{\alpha }:= \mathfrak {n}^{\alpha } \cap \mathfrak {n}_{\mathrm {red}} = \mathfrak {n}^{\alpha }$ is satisfied, whence the desired ![]() $H$-stability.
$H$-stability.
It remains to show that ![]() $\operatorname {Lie}(Z_{N_{\mathrm {red}}}(T))$ is
$\operatorname {Lie}(Z_{N_{\mathrm {red}}}(T))$ is ![]() $H$-stable. According to Lemma 4.11 the subgroup
$H$-stable. According to Lemma 4.11 the subgroup ![]() $H$ normalises
$H$ normalises ![]() $Z_{N_{\mathrm {red}}}(T)^0$, thus the stability of
$Z_{N_{\mathrm {red}}}(T)^0$, thus the stability of ![]() $\operatorname {Lie}(Z_{N_{\mathrm {red}}}(T)^0) = \operatorname {Lie}(Z_{N_{\mathrm {red}}}(T))$.
$\operatorname {Lie}(Z_{N_{\mathrm {red}}}(T)^0) = \operatorname {Lie}(Z_{N_{\mathrm {red}}}(T))$.
According to what precedes ![]() $\mathfrak {n}_{\mathrm {red}}$ is stable for the action of
$\mathfrak {n}_{\mathrm {red}}$ is stable for the action of ![]() $H$ on
$H$ on ![]() $\mathfrak {n}$, hence this subalgebra is invariant for the action of
$\mathfrak {n}$, hence this subalgebra is invariant for the action of ![]() $N$. Reasoning on the
$N$. Reasoning on the ![]() $R[\epsilon ]$-points for any
$R[\epsilon ]$-points for any ![]() $k$-algebra
$k$-algebra ![]() $R$, one can shows that
$R$, one can shows that ![]() $\mathfrak {n_{\mathrm {red}}}$ is an ideal of
$\mathfrak {n_{\mathrm {red}}}$ is an ideal of ![]() $\mathfrak {n}$.
$\mathfrak {n}$.
The proof of the following lemma is the same as the proof of [Reference DeligneDel14, Lemma 2.22] because relaxing the hypotheses had no consequences on the involved arguments. We reproduce the proof here to ensure consistency in notation.
Lemma 4.13 (Deligne [Reference DeligneDel14, 2.22])
Let ![]() $V$ be the unipotent radical of
$V$ be the unipotent radical of ![]() $N_{\mathrm {red}}$. The action of
$N_{\mathrm {red}}$. The action of ![]() $H$ on
$H$ on ![]() $\operatorname {Lie}(N_{\mathrm {red}}) = \mathfrak {n}_{\mathrm {red}}$ leaves
$\operatorname {Lie}(N_{\mathrm {red}}) = \mathfrak {n}_{\mathrm {red}}$ leaves ![]() $\operatorname {Lie}(V) := \mathfrak {v}$ invariant.
$\operatorname {Lie}(V) := \mathfrak {v}$ invariant.
Proof. The torus ![]() $T$ acts on
$T$ acts on ![]() $\mathfrak {n}_{\mathrm {red}}$ thus on
$\mathfrak {n}_{\mathrm {red}}$ thus on ![]() $\mathfrak {v}$. The Lie algebras
$\mathfrak {v}$. The Lie algebras ![]() $\mathfrak {n}_{\mathrm {red}}$ and
$\mathfrak {n}_{\mathrm {red}}$ and ![]() $\mathfrak {v}$ have a weight space decomposition for this action, namely
$\mathfrak {v}$ have a weight space decomposition for this action, namely ![]() $\mathfrak {n}_{\mathrm {red}} =\mathfrak {n}_{\mathrm {red}}^0 \oplus \bigoplus _{\alpha \in X(T)^*} \mathfrak {n}_{\mathrm {red}}^{\alpha }$ and
$\mathfrak {n}_{\mathrm {red}} =\mathfrak {n}_{\mathrm {red}}^0 \oplus \bigoplus _{\alpha \in X(T)^*} \mathfrak {n}_{\mathrm {red}}^{\alpha }$ and ![]() $\mathfrak {v} = \mathfrak {v}^0 \oplus \bigoplus _{\alpha \in X(T)^*} \mathfrak {v}^{\alpha }$. According to the proof of Lemma 4.12 the decomposition of
$\mathfrak {v} = \mathfrak {v}^0 \oplus \bigoplus _{\alpha \in X(T)^*} \mathfrak {v}^{\alpha }$. According to the proof of Lemma 4.12 the decomposition of ![]() $\mathfrak {n}_{\mathrm {red}}$ is
$\mathfrak {n}_{\mathrm {red}}$ is ![]() $H$-stable. It remains to show that so is any
$H$-stable. It remains to show that so is any ![]() $\mathfrak {v}^{\alpha }$.
$\mathfrak {v}^{\alpha }$.
Consider the following commutative diagram. As a reminder as ![]() $Z = T \times W$ and
$Z = T \times W$ and ![]() $T$ and
$T$ and ![]() $Z$ are normal in
$Z$ are normal in ![]() $N_{\mathrm {red}}$, so is the subgroup
$N_{\mathrm {red}}$, so is the subgroup ![]() $W\subseteq N_{\mathrm {red}}$. Moreover,
$W\subseteq N_{\mathrm {red}}$. Moreover, ![]() $W$ is also unipotent smooth and connected so it is contained in
$W$ is also unipotent smooth and connected so it is contained in ![]() $V:= \operatorname {Rad}_U(N_{\mathrm {red}})$.
$V:= \operatorname {Rad}_U(N_{\mathrm {red}})$.

Let us first study the ![]() $H$-stability of the weight-zero part of
$H$-stability of the weight-zero part of ![]() $\mathfrak {v}$. As the diagram above is cartesian, one has
$\mathfrak {v}$. As the diagram above is cartesian, one has ![]() $\mathfrak {v}^0 = \mathfrak {n}_{\mathrm {red}}^0 \cap \mathfrak {v} = \mathfrak {z} \cap \mathfrak {v} = \mathfrak {w}$. However,
$\mathfrak {v}^0 = \mathfrak {n}_{\mathrm {red}}^0 \cap \mathfrak {v} = \mathfrak {z} \cap \mathfrak {v} = \mathfrak {w}$. However, ![]() $\mathfrak {w}$ is
$\mathfrak {w}$ is ![]() $H$-stable as the subgroups
$H$-stable as the subgroups ![]() $T$ and
$T$ and ![]() $Z$ are (for
$Z$ are (for ![]() $Z$ this has been shown in Lemma 4.11) and the sequence is split.
$Z$ this has been shown in Lemma 4.11) and the sequence is split.
Let us now focus on the positive weights. Let ![]() $\mathfrak {q}$ be the Lie algebra of the reductive quotient
$\mathfrak {q}$ be the Lie algebra of the reductive quotient ![]() $N_{\mathrm {red}}/V$. The torus
$N_{\mathrm {red}}/V$. The torus ![]() $T$ acts on this Lie algebra which writes
$T$ acts on this Lie algebra which writes ![]() $\mathfrak {q} = \mathfrak {q}^0 \oplus \bigoplus _{\alpha \in X^*(T)} \mathfrak {q}^{\alpha }$. There are two possible situations.
$\mathfrak {q} = \mathfrak {q}^0 \oplus \bigoplus _{\alpha \in X^*(T)} \mathfrak {q}^{\alpha }$. There are two possible situations.
− Either
 $\alpha$ is not a weight of
$\alpha$ is not a weight of  $T$ on
$T$ on  $\mathfrak {q}$. Then one has
$\mathfrak {q}$. Then one has  $\mathfrak {v}^{\alpha } = \mathfrak {n}_{\mathrm {red}}^{\alpha }$, whence the
$\mathfrak {v}^{\alpha } = \mathfrak {n}_{\mathrm {red}}^{\alpha }$, whence the  $H$-stability of
$H$-stability of  $\mathfrak {v}^{\alpha }$.
$\mathfrak {v}^{\alpha }$.− Or
 $\alpha$ is a non-trivial weight of
$\alpha$ is a non-trivial weight of  $T$ on
$T$ on  $\mathfrak {q}$. Then the weight spaces
$\mathfrak {q}$. Then the weight spaces  $\mathfrak {q}^{\alpha }$ and
$\mathfrak {q}^{\alpha }$ and  $\mathfrak {q}^{-\alpha }$ are of dimension one (according to [Reference Demazure and GrothendieckSGA3III, XIX, Proposition 1.12(iii)]). As
$\mathfrak {q}^{-\alpha }$ are of dimension one (according to [Reference Demazure and GrothendieckSGA3III, XIX, Proposition 1.12(iii)]). As  $p>2$ (because it is separably good for
$p>2$ (because it is separably good for  $G$), the pairing
induced by the bracket on
$G$), the pairing
induced by the bracket on \begin{alignat*}{3} \mathfrak{q}^{\alpha} \times \mathfrak{q}^{-\alpha} \:& \rightarrow \:& \mathfrak{q}^0 := \operatorname{Lie}(\:& T_Q) \\ (X_{\alpha},X_{-\alpha}) \:& \mapsto \:& [X_{\alpha}, X_{-\alpha}]\:& \end{alignat*}
\begin{alignat*}{3} \mathfrak{q}^{\alpha} \times \mathfrak{q}^{-\alpha} \:& \rightarrow \:& \mathfrak{q}^0 := \operatorname{Lie}(\:& T_Q) \\ (X_{\alpha},X_{-\alpha}) \:& \mapsto \:& [X_{\alpha}, X_{-\alpha}]\:& \end{alignat*}
 $\mathfrak {q}$ is non-degenerate (see [Reference Demazure and GrothendieckSGA3III, XXIII, Corollaire 6.5]), thus maps to a one-dimensional subspace
$\mathfrak {q}$ is non-degenerate (see [Reference Demazure and GrothendieckSGA3III, XXIII, Corollaire 6.5]), thus maps to a one-dimensional subspace  $h_{\alpha }$.
$h_{\alpha }$.
Likewise, the bracket on
 $\mathfrak {n}_{\mathrm {red}}$ induces a non-degenerate pairing of
$\mathfrak {n}_{\mathrm {red}}$ induces a non-degenerate pairing of  $\mathfrak {n}_{\mathrm {red}}^{\alpha }$ and
$\mathfrak {n}_{\mathrm {red}}^{\alpha }$ and  $\mathfrak {n}_{\mathrm {red}}^{-\alpha }$, and one has the following commutative diagram.
Denote by
$\mathfrak {n}_{\mathrm {red}}^{-\alpha }$, and one has the following commutative diagram.
Denote by
 $d$ the image of the pairing of
$d$ the image of the pairing of  $\mathfrak {n}_{\mathrm {red}}^{\alpha }$ and
$\mathfrak {n}_{\mathrm {red}}^{\alpha }$ and  $\mathfrak {n}_{\mathrm {red}}^{-\alpha }$ composed with the projection
$\mathfrak {n}_{\mathrm {red}}^{-\alpha }$ composed with the projection  $\mathfrak {n}_{\mathrm {red}}^0 \rightarrow \mathfrak {n}_{\mathrm {red}}^0/\mathfrak {w}$. According to what precedes this is a line of
$\mathfrak {n}_{\mathrm {red}}^0 \rightarrow \mathfrak {n}_{\mathrm {red}}^0/\mathfrak {w}$. According to what precedes this is a line of  $\mathfrak {n}_{\mathrm {red}}^0/\mathfrak {w}$.
$\mathfrak {n}_{\mathrm {red}}^0/\mathfrak {w}$.
The situation can be summarised as in the following commutative diagram.
In other words, one has
 $\mathfrak {v}^{\pm \alpha } = \ker \big (\mathfrak {v}^{\pm \alpha } \rightarrow \operatorname {Hom}(\mathfrak {n}_{\mathrm {red}}^{\mp \alpha },d)\big )$ and
$\mathfrak {v}^{\pm \alpha } = \ker \big (\mathfrak {v}^{\pm \alpha } \rightarrow \operatorname {Hom}(\mathfrak {n}_{\mathrm {red}}^{\mp \alpha },d)\big )$ and  $\mathfrak {v}^{\pm \alpha }$ is a sub-representation of the representation defined by the action of
$\mathfrak {v}^{\pm \alpha }$ is a sub-representation of the representation defined by the action of  $H$ on
$H$ on  $\mathfrak {n}_{\mathrm {red}}$, thus it is
$\mathfrak {n}_{\mathrm {red}}$, thus it is  $H$-stable.
$H$-stable.
Combining Lemmas 4.12 and 4.13 one can show an infinitesimal version of [Reference Balaji, Deligne and ParameswaranBDP17, Théorème 2.5].
Proposition 4.14 Let ![]() $G$ be a reductive group over an algebraically closed field
$G$ be a reductive group over an algebraically closed field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is assumed to be separably good for
$p>0$ which is assumed to be separably good for ![]() $G$. Let
$G$. Let ![]() $\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ be a Springer isomorphism for
$\phi : \mathcal {N}_{\mathrm {red}}(\mathfrak {g}) \rightarrow \mathcal {V}_{\mathrm {red}}(G)$ be a Springer isomorphism for ![]() $G$. If
$G$. If ![]() $N \subseteq G$ is a
$N \subseteq G$ is a ![]() $\phi$-infinitesimally saturated subgroup, then:
$\phi$-infinitesimally saturated subgroup, then:
(i) the Lie algebra
 $\mathfrak {n}_{\mathrm {red}}$ is an ideal of
$\mathfrak {n}_{\mathrm {red}}$ is an ideal of  $\mathfrak {n}$;
$\mathfrak {n}$;(ii) the Lie algebra of the unipotent radical of
 $N_{\mathrm {red}}$ is an ideal of
$N_{\mathrm {red}}$ is an ideal of  $\mathfrak {n}$.
$\mathfrak {n}$.
Proof. The first point is provided by Lemma 4.12. The second point follows from a direct application of Lemma 4.13 combined with [Reference Balaji, Deligne and ParameswaranBDP17, Lemma 2.14]: with the subgroup ![]() $N$ being generated as an
$N$ being generated as an ![]() $\operatorname {fppf}$-sheaf by
$\operatorname {fppf}$-sheaf by ![]() $H$ and
$H$ and ![]() $N_{\mathrm {red}}$, one only needs to show that
$N_{\mathrm {red}}$, one only needs to show that ![]() $\operatorname {\mathfrak {rad_u}}(N_{\mathrm {red}})$ is
$\operatorname {\mathfrak {rad_u}}(N_{\mathrm {red}})$ is ![]() $H$-stable. This has been shown by the aforementioned lemma. A reasoning on
$H$-stable. This has been shown by the aforementioned lemma. A reasoning on ![]() $R[\epsilon ]$-points for any
$R[\epsilon ]$-points for any ![]() $k$-algebra
$k$-algebra ![]() $R$ then leads to obtaining that
$R$ then leads to obtaining that ![]() $\operatorname {\mathfrak {rad_u}}(N_{\mathrm {red}})$ is an ideal of
$\operatorname {\mathfrak {rad_u}}(N_{\mathrm {red}})$ is an ideal of ![]() $\mathfrak {n}$.
$\mathfrak {n}$.
4.4 Proof of Theorem 1.1
We can now prove Theorem 1.1.
We start by showing that ![]() $N_{\mathrm {red}}$ is a normal subgroup of
$N_{\mathrm {red}}$ is a normal subgroup of ![]() $N$. The latter being generated by
$N$. The latter being generated by ![]() $H$ and
$H$ and ![]() $N_{\mathrm {red}}$ as an
$N_{\mathrm {red}}$ as an ![]() $\operatorname {fppf}$-sheaf, one actually needs to show that
$\operatorname {fppf}$-sheaf, one actually needs to show that ![]() $N_{\mathrm {red}}$ is
$N_{\mathrm {red}}$ is ![]() $H$-stable. The reasoning follows the proof of Lemma 4.12: we consider the subgroup
$H$-stable. The reasoning follows the proof of Lemma 4.12: we consider the subgroup ![]() $E_{Z^0, J_{\mathfrak {n}^{\alpha }}}$ generated by
$E_{Z^0, J_{\mathfrak {n}^{\alpha }}}$ generated by ![]() $Z^0 := Z^0_{N_{\mathrm {red}}}(T)$ and
$Z^0 := Z^0_{N_{\mathrm {red}}}(T)$ and ![]() $J_{\mathfrak {n}^{\alpha }}$ for
$J_{\mathfrak {n}^{\alpha }}$ for ![]() $\alpha \in X(T)^*$. Recall that the
$\alpha \in X(T)^*$. Recall that the ![]() $J_{\mathfrak {n}^{\alpha }}$ are themselves the subgroups generated as
$J_{\mathfrak {n}^{\alpha }}$ are themselves the subgroups generated as ![]() $\operatorname {fppf}$-sheaves by the image of the morphisms
$\operatorname {fppf}$-sheaves by the image of the morphisms
Note that ![]() $\psi _{\alpha }$ is well-defined for any
$\psi _{\alpha }$ is well-defined for any ![]() $\alpha \in X(T)^*$:
$\alpha \in X(T)^*$:
− any weight space
 $\mathfrak {n}^{\alpha }$ consists of
$\mathfrak {n}^{\alpha }$ consists of  $p$-nilpotent elements because we consider the action of a torus;
$p$-nilpotent elements because we consider the action of a torus;− any weight space
 $\mathfrak {n}^{\alpha }$ is geometrically reduced and geometrically connected as it is a vector space.
$\mathfrak {n}^{\alpha }$ is geometrically reduced and geometrically connected as it is a vector space.
Thus, the groups ![]() $J_{\mathfrak {n}^{\alpha }}$ are smooth and connected (this last point is ensured by [Reference Demazure and GrothendieckSGA3I, VIB, Corollaire 7.2.1]).
$J_{\mathfrak {n}^{\alpha }}$ are smooth and connected (this last point is ensured by [Reference Demazure and GrothendieckSGA3I, VIB, Corollaire 7.2.1]).
The arguments of the proof of Lemma 4.11 apply and allow us to show that the ![]() $k$-subgroup
$k$-subgroup ![]() $E_{Z^0, J_{\mathfrak {n}^{\alpha }}}$ is contained in
$E_{Z^0, J_{\mathfrak {n}^{\alpha }}}$ is contained in ![]() $N$ (this subgroup being
$N$ (this subgroup being ![]() $\phi$-infinitesimally saturated), and even in
$\phi$-infinitesimally saturated), and even in ![]() $N_{\mathrm {red}}$ as it is smooth. Moreover, recall that
$N_{\mathrm {red}}$ as it is smooth. Moreover, recall that ![]() $p$ is not of torsion for
$p$ is not of torsion for ![]() $G$ and that for any non-zero weight the corresponding weight space is
$G$ and that for any non-zero weight the corresponding weight space is ![]() $p$-nil. Therefore, they are all embeddable into the Lie algebra of the unipotent radical of a Borel subgroup
$p$-nil. Therefore, they are all embeddable into the Lie algebra of the unipotent radical of a Borel subgroup ![]() $B\subseteq G$. The weight spaces
$B\subseteq G$. The weight spaces ![]() $\mathfrak {n}^{\alpha }$ are all contained in
$\mathfrak {n}^{\alpha }$ are all contained in ![]() $\operatorname {Lie}(E_{Z^0, J_{\mathfrak {n}^{\alpha }}}) =: \mathfrak {e}$ because the differential at
$\operatorname {Lie}(E_{Z^0, J_{\mathfrak {n}^{\alpha }}}) =: \mathfrak {e}$ because the differential at ![]() $0$ of the restriction of
$0$ of the restriction of ![]() $\phi$ to the Lie algebra of the unipotent radical of any Borel subgroup is the identity. The Lie algebra
$\phi$ to the Lie algebra of the unipotent radical of any Borel subgroup is the identity. The Lie algebra ![]() $\operatorname {Lie}(Z^0)$ also satisfies this inclusion as
$\operatorname {Lie}(Z^0)$ also satisfies this inclusion as ![]() $Z^0 \subset E_{Z^0, J_{\mathfrak {n}^{\alpha }}}$.
$Z^0 \subset E_{Z^0, J_{\mathfrak {n}^{\alpha }}}$.
To summarise, we have shown that ![]() $\mathfrak {n}_{\mathrm {red}} = \operatorname {Lie}(Z^0) \oplus \bigoplus _{\alpha \in X(T)^*} \mathfrak {n}^{\alpha } \subseteq \mathfrak {e}$. With the groups involved here being smooth and connected, the equality of Lie algebras lifts to an equality of groups (see [Reference Demazure and GabrielDG70, II, § 5, n
$\mathfrak {n}_{\mathrm {red}} = \operatorname {Lie}(Z^0) \oplus \bigoplus _{\alpha \in X(T)^*} \mathfrak {n}^{\alpha } \subseteq \mathfrak {e}$. With the groups involved here being smooth and connected, the equality of Lie algebras lifts to an equality of groups (see [Reference Demazure and GabrielDG70, II, § 5, n![]() $^{\circ }$5.5]), hence the identity
$^{\circ }$5.5]), hence the identity ![]() $E_{Z^0, J_{\mathfrak {n}^{\alpha }}}= N^0_{\mathrm {red}}$.
$E_{Z^0, J_{\mathfrak {n}^{\alpha }}}= N^0_{\mathrm {red}}$.
Thus, the problem restricts to showing the ![]() $H$-stability of
$H$-stability of ![]() $E_{Z^0, J_{\mathfrak {n}^{\alpha }}}$. By Lemma 4.11 the centraliser
$E_{Z^0, J_{\mathfrak {n}^{\alpha }}}$. By Lemma 4.11 the centraliser ![]() $Z^0$ is
$Z^0$ is ![]() $H$-invariant, so one only has to show the
$H$-invariant, so one only has to show the ![]() $H$-stability of the
$H$-stability of the ![]() $J_{\mathfrak {n}^{\alpha }}$. As
$J_{\mathfrak {n}^{\alpha }}$. As ![]() $H$ normalises
$H$ normalises ![]() $T$ and as
$T$ and as ![]() $\phi$ is
$\phi$ is ![]() $G$-equivariant, any
$G$-equivariant, any ![]() $\mathfrak {n}^{\alpha }$ is
$\mathfrak {n}^{\alpha }$ is ![]() $H$-invariant. Hence,
$H$-invariant. Hence, ![]() $N_{\mathrm {red}}$ is a normal subgroup of
$N_{\mathrm {red}}$ is a normal subgroup of ![]() $N$.
$N$.
Recall that in the preamble of § 4.3 we have explained that ![]() $H$ is actually equal to the product
$H$ is actually equal to the product ![]() $T \times D$ (for
$T \times D$ (for ![]() $D$ a
$D$ a ![]() $k$-diagonalisable group). To prove that
$k$-diagonalisable group). To prove that ![]() $N/N_{\mathrm {red}}$ is of multiplicative type we show that it is isomorphic to the group
$N/N_{\mathrm {red}}$ is of multiplicative type we show that it is isomorphic to the group ![]() $D$. As:
$D$. As:
− the group
 $H$ normalises
$H$ normalises  $N_{\mathrm {red}}$ (which is normal in
$N_{\mathrm {red}}$ (which is normal in  $N$);
$N$);− the equality
 $HN_{\mathrm {red}} = N$ is satisfied as well as the following isomorphism
$HN_{\mathrm {red}} = N$ is satisfied as well as the following isomorphism  $N_{\mathrm {red}} \cong H \cap N_{\mathrm {red}}$;
$N_{\mathrm {red}} \cong H \cap N_{\mathrm {red}}$;
one has an isomorphism of ![]() $\operatorname {fppf}$-sheaves which turns out to be an isomorphism of algebraic groups
$\operatorname {fppf}$-sheaves which turns out to be an isomorphism of algebraic groups ![]() $H/H_{\mathrm {red}} \cong N/N_{\mathrm {red}} \cong D$.
$H/H_{\mathrm {red}} \cong N/N_{\mathrm {red}} \cong D$.
To end the proof of the first point of the theorem it remains to show that the unipotent radical of ![]() $N_{\mathrm {red}}$, denoted by
$N_{\mathrm {red}}$, denoted by ![]() $V$, is normal in
$V$, is normal in ![]() $N$. Once again, the
$N$. Once again, the ![]() $\operatorname {fppf}$-formalism reduces the problem to showing the
$\operatorname {fppf}$-formalism reduces the problem to showing the ![]() $H$-invariance of
$H$-invariance of ![]() $V$, the unipotent radical
$V$, the unipotent radical ![]() $\operatorname {Rad}_U(N_{\mathrm {red}})$ being normal in
$\operatorname {Rad}_U(N_{\mathrm {red}})$ being normal in ![]() $N_{\mathrm {red}}$. The reasoning follows the proof of the normality of
$N_{\mathrm {red}}$. The reasoning follows the proof of the normality of ![]() $N_{\mathrm {red}}$ in
$N_{\mathrm {red}}$ in ![]() $N$: we consider the subgroup
$N$: we consider the subgroup ![]() $E_{W,J_{\mathfrak {v}}^{\alpha }}$ generated by
$E_{W,J_{\mathfrak {v}}^{\alpha }}$ generated by ![]() $W$ and
$W$ and ![]() $J_{\mathfrak {v}^{\alpha }}$ for
$J_{\mathfrak {v}^{\alpha }}$ for ![]() $\alpha \in X(T)^*$. As
$\alpha \in X(T)^*$. As ![]() $W$ and
$W$ and ![]() $J_{\mathfrak {v}^{\alpha }}$ are normal in
$J_{\mathfrak {v}^{\alpha }}$ are normal in ![]() $N_{\mathrm {red}}$, the subgroup
$N_{\mathrm {red}}$, the subgroup ![]() $E_{W,J_{\mathfrak {v}^{\alpha }}}$ is a unipotent smooth connected normal subgroup of
$E_{W,J_{\mathfrak {v}^{\alpha }}}$ is a unipotent smooth connected normal subgroup of ![]() $N$, thus it is contained in the unipotent radical of
$N$, thus it is contained in the unipotent radical of ![]() $N_{\mathrm {red}}$.
$N_{\mathrm {red}}$.
Moreover, for any non-zero weight, the corresponding weight space can be embedded into the Lie algebra of the unipotent radical of a Borel subgroup (as ![]() $p$ is not of torsion for
$p$ is not of torsion for ![]() $G$ and the considered weight space is
$G$ and the considered weight space is ![]() $p$-nil). Once again we make use of the properties of the differential of
$p$-nil). Once again we make use of the properties of the differential of ![]() $\phi$ at
$\phi$ at ![]() $0$ to conclude that
$0$ to conclude that ![]() $\mathfrak {v}= \mathfrak {w} \oplus \bigoplus _{\alpha \in X(T)^*} \mathfrak {v}^{\alpha }$ is contained in
$\mathfrak {v}= \mathfrak {w} \oplus \bigoplus _{\alpha \in X(T)^*} \mathfrak {v}^{\alpha }$ is contained in ![]() $\operatorname {Lie}(E_{W,J_{\mathfrak {v}}^{\alpha }})$. This implies the equality
$\operatorname {Lie}(E_{W,J_{\mathfrak {v}}^{\alpha }})$. This implies the equality ![]() $V= E_{W,J_{\mathfrak {v}}^{\alpha }}$ for the same reasons as previously. This equality being satisfied, the result follows from stability properties established in the proof of Lemma 4.13. Indeed, we have shown that then
$V= E_{W,J_{\mathfrak {v}}^{\alpha }}$ for the same reasons as previously. This equality being satisfied, the result follows from stability properties established in the proof of Lemma 4.13. Indeed, we have shown that then ![]() $W$ as well as any
$W$ as well as any ![]() $J_{\mathfrak {v}}^{\alpha }$, for non-trivial
$J_{\mathfrak {v}}^{\alpha }$, for non-trivial ![]() $\alpha$, are
$\alpha$, are ![]() $H$-stable. Combining this with the
$H$-stable. Combining this with the ![]() $G$-equivariance of
$G$-equivariance of ![]() $\phi$ leads to the conclusion that
$\phi$ leads to the conclusion that ![]() $V$ is a normal subgroup of
$V$ is a normal subgroup of ![]() $N$.
$N$.
It remains to show the last point of Theorem 1.1 which is a generalised version of [Reference DeligneDel14, Theorem 1.7(iii)] (see also [Reference Balaji, Deligne and ParameswaranBDP17, Theorem 2.5(ii)]). A careful reading of the proof of this latter shows that it does not depend on the additional assumptions made by the author (that, in practice, reduce the range of allowed characteristics). The arguments are, hence, the same as that provided by Deligne in the framework of [Reference DeligneDel14, 2.25] (see also [Reference Balaji, Deligne and ParameswaranBDP17, Corollary 2.15]) and the proof is reproduced here only for the sake of clarity.
The reduced part ![]() $N_{\mathrm {red}} \subseteq N$ is now assumed to be reductive. We show that the connected component of the identity
$N_{\mathrm {red}} \subseteq N$ is now assumed to be reductive. We show that the connected component of the identity ![]() $M^0$ of
$M^0$ of ![]() $M= \ker \big (H\rightarrow \operatorname {Aut}(N_{\mathrm {red}})\big )$ is the central connected subgroup of multiplicative type we are seeking. It is clearly of multiplicative type as it is a closed subgroup of
$M= \ker \big (H\rightarrow \operatorname {Aut}(N_{\mathrm {red}})\big )$ is the central connected subgroup of multiplicative type we are seeking. It is clearly of multiplicative type as it is a closed subgroup of ![]() $H$ (see [Reference Demazure and GabrielDG70, IV, § 1, Corollaire 2.4(a)]). Thus, we need to show that it is central and that
$H$ (see [Reference Demazure and GabrielDG70, IV, § 1, Corollaire 2.4(a)]). Thus, we need to show that it is central and that ![]() $M^0 \times N_{\mathrm {red}} \rightarrow N$ is an epimorphism. The first assertion is clear as:
$M^0 \times N_{\mathrm {red}} \rightarrow N$ is an epimorphism. The first assertion is clear as:
− the connected group
 $M^0$ centralises
$M^0$ centralises  $N_{\mathrm {red}}$; and
$N_{\mathrm {red}}$; and−
 $N$ is generated by
$N$ is generated by  $H$ and
$H$ and  $N_{\mathrm {red}}$ as a
$N_{\mathrm {red}}$ as a  $\operatorname {fppf}$-sheaf (as shown previously).
$\operatorname {fppf}$-sheaf (as shown previously).
To show that ![]() $M^0 \times N_{\mathrm {red}} \rightarrow N$ is an epimorphism, one proves that
$M^0 \times N_{\mathrm {red}} \rightarrow N$ is an epimorphism, one proves that ![]() $N$ is generated by
$N$ is generated by ![]() $M^0$ and
$M^0$ and ![]() $N_{\mathrm {red}}$ as a
$N_{\mathrm {red}}$ as a ![]() $\operatorname {fppf}$-sheaf. We already know that
$\operatorname {fppf}$-sheaf. We already know that ![]() $N$ is generated by
$N$ is generated by ![]() $N_{\mathrm {red}}$ and
$N_{\mathrm {red}}$ and ![]() $H$. To conclude we show:
$H$. To conclude we show:
− that
 $M$ is generated by
$M$ is generated by  $M_{\mathrm {red}}\subset N_{\mathrm {red}}$ and
$M_{\mathrm {red}}\subset N_{\mathrm {red}}$ and  $M^0$;
$M^0$;− that
 $H$ is generated by
$H$ is generated by  $M$ and
$M$ and  $T$.
$T$.
The assertion for ![]() $M$ is the consequence of structural properties of groups multiplicative type: the field
$M$ is the consequence of structural properties of groups multiplicative type: the field ![]() $k$ being algebraically closed, any group of multiplicative type is diagonalisable. Hence,
$k$ being algebraically closed, any group of multiplicative type is diagonalisable. Hence, ![]() $M$ is isomorphic to a product of
$M$ is isomorphic to a product of ![]() $\mathbb {G}_m$,
$\mathbb {G}_m$, ![]() $\mu _{q}$ and
$\mu _{q}$ and ![]() $\mu _{p^i}$ (for
$\mu _{p^i}$ (for ![]() $(q,p) =1$) (see the proof of [Reference Demazure and GrothendieckSGA3I, VIII, Proposition 2.1]). Its reduced component being smooth of multiplicative type, the order of its torsion part is coprime with
$(q,p) =1$) (see the proof of [Reference Demazure and GrothendieckSGA3I, VIII, Proposition 2.1]). Its reduced component being smooth of multiplicative type, the order of its torsion part is coprime with ![]() $p$ (see [Reference Demazure and GrothendieckSGA3I, VIII, Proposition 2.1]). Hence,
$p$ (see [Reference Demazure and GrothendieckSGA3I, VIII, Proposition 2.1]). Hence, ![]() $M/M_{\mathrm {red}}$ is a product of groups of the form
$M/M_{\mathrm {red}}$ is a product of groups of the form ![]() $\mu _{p^i}$ for
$\mu _{p^i}$ for ![]() $i \in \mathbb {N}$. Conversely, the quotient
$i \in \mathbb {N}$. Conversely, the quotient ![]() $M/M^0$ is a product of
$M/M^0$ is a product of ![]() $\mu _{q}$ with
$\mu _{q}$ with ![]() $(p,q) = 1$, hence the result.
$(p,q) = 1$, hence the result.
One still has to show that ![]() $H$ is generated by
$H$ is generated by ![]() $M$ and
$M$ and ![]() $T$. Recall that we have shown previously that
$T$. Recall that we have shown previously that ![]() $N_{\mathrm {red}}$ is stable under the action of
$N_{\mathrm {red}}$ is stable under the action of ![]() $H$-conjugation on
$H$-conjugation on ![]() $N$. Note that this action fixes
$N$. Note that this action fixes ![]() $T$, hence we have the following diagram (according to [Reference Demazure and GrothendieckSGA3III, XXIV, Proposition 2.11], the group
$T$, hence we have the following diagram (according to [Reference Demazure and GrothendieckSGA3III, XXIV, Proposition 2.11], the group ![]() $N_{\mathrm {red}}$ being reductive).
$N_{\mathrm {red}}$ being reductive).

The action of ![]() $H$ on
$H$ on ![]() $N_{\mathrm {red}}$ thus factors through
$N_{\mathrm {red}}$ thus factors through ![]() $T^{\operatorname {Ad}}$. Thus, we have the following exact sequence.
$T^{\operatorname {Ad}}$. Thus, we have the following exact sequence.
Hence, ![]() $H$ is generated as a
$H$ is generated as a ![]() $\operatorname {fppf}$-sheaf by
$\operatorname {fppf}$-sheaf by ![]() $M$ and
$M$ and ![]() $T^{\operatorname {Ad}}$, whence by
$T^{\operatorname {Ad}}$, whence by ![]() $M$ and
$M$ and ![]() $T$ as
$T$ as ![]() $T^{\operatorname {Ad}}$ is a quotient of
$T^{\operatorname {Ad}}$ is a quotient of ![]() $T$.
$T$.
5. Integration of some maximal  $p$-nil
$p$-nil  $p$-subalgebras
$p$-subalgebras  $\mathfrak {g}$
$\mathfrak {g}$
Let us start with the very specific case which has motivated our interest in the questions studied in this article: assume ![]() $\mathfrak {u}\subseteq \mathfrak {g}$ to be a restricted
$\mathfrak {u}\subseteq \mathfrak {g}$ to be a restricted ![]() $p$-subalgebra which is the set of
$p$-subalgebra which is the set of ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {u}))$. Note that
$\operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {u}))$. Note that ![]() $N_{\mathfrak {g}}(\mathfrak {u})$ is a restricted
$N_{\mathfrak {g}}(\mathfrak {u})$ is a restricted ![]() $p$-Lie algebra (according to Lemma 6.4 as it derives from an algebraic
$p$-Lie algebra (according to Lemma 6.4 as it derives from an algebraic ![]() $k$-group, namely
$k$-group, namely ![]() $N_G(\mathfrak {u})$). Moreover,
$N_G(\mathfrak {u})$). Moreover, ![]() $\mathfrak {u}$ is a restricted
$\mathfrak {u}$ is a restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra of
$p$-subalgebra of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Lemma 5.1 Let ![]() $G$ be a reductive group over a field
$G$ be a reductive group over a field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is assumed to be separably good for
$p>0$ which is assumed to be separably good for ![]() $G$ and let
$G$ and let ![]() $\mathfrak {u} \subseteq \mathfrak {g}$ be a subalgebra. If
$\mathfrak {u} \subseteq \mathfrak {g}$ be a subalgebra. If ![]() $\mathfrak {u}$ is the set of
$\mathfrak {u}$ is the set of ![]() $p$-nilpotent elements of the radical of its normaliser in
$p$-nilpotent elements of the radical of its normaliser in ![]() $\mathfrak {g}$, denoted by
$\mathfrak {g}$, denoted by ![]() $N_{\mathfrak {g}}(\mathfrak {u})$, the subalgebra
$N_{\mathfrak {g}}(\mathfrak {u})$, the subalgebra ![]() $\mathfrak {u}$ is integrable by
$\mathfrak {u}$ is integrable by ![]() $J_{\mathfrak {u}}$.
$J_{\mathfrak {u}}$.
Proof. According to Lemma 4.4, there is a unipotent smooth connected subgroup ![]() $J_{\mathfrak {u}}\subset G$ such that the inclusion
$J_{\mathfrak {u}}\subset G$ such that the inclusion ![]() $\mathfrak {u}\subseteq \mathfrak {j_u}:= \operatorname {Lie}(J_{\mathfrak {u}})$ holds true. Moreover, as according to Lemma 6.3 one has
$\mathfrak {u}\subseteq \mathfrak {j_u}:= \operatorname {Lie}(J_{\mathfrak {u}})$ holds true. Moreover, as according to Lemma 6.3 one has ![]() $J_{\mathfrak {u}} \subseteq N_G(J_{\mathfrak {u}}) \subseteq N_G(\mathfrak {j_u})$, at the Lie algebra level the following inclusions are satisfied:
$J_{\mathfrak {u}} \subseteq N_G(J_{\mathfrak {u}}) \subseteq N_G(\mathfrak {j_u})$, at the Lie algebra level the following inclusions are satisfied:
Assume the inclusion ![]() $\mathfrak {u} \subset \mathfrak {j_u}$ to be strict, then
$\mathfrak {u} \subset \mathfrak {j_u}$ to be strict, then ![]() $\mathfrak {u}$ is a proper subalgebra of its normaliser in
$\mathfrak {u}$ is a proper subalgebra of its normaliser in ![]() $\mathfrak {j_u}$ (this is a corollary of the Engel theorem; see, for example, [Reference BourbakiBou71, § 4, n
$\mathfrak {j_u}$ (this is a corollary of the Engel theorem; see, for example, [Reference BourbakiBou71, § 4, n![]() $^{\circ }$1, Proposition 3]). In other words, one has
$^{\circ }$1, Proposition 3]). In other words, one has ![]() $\mathfrak {u} \subsetneq N_{\mathfrak {j_u}}(\mathfrak {u}):= \mathfrak {j_u}\cap N_{\mathfrak {g}}(\mathfrak {u}).$ However, according to Lemma 3.8 the group
$\mathfrak {u} \subsetneq N_{\mathfrak {j_u}}(\mathfrak {u}):= \mathfrak {j_u}\cap N_{\mathfrak {g}}(\mathfrak {u}).$ However, according to Lemma 3.8 the group ![]() $J_{\mathfrak {u}}$ is normalised by
$J_{\mathfrak {u}}$ is normalised by ![]() $N_G(\mathfrak {u})$, hence
$N_G(\mathfrak {u})$, hence ![]() $N_{\mathfrak {j_u}}(\mathfrak {u}) \subseteq N_{\mathfrak {g}}(\mathfrak {u})$ is an ideal of
$N_{\mathfrak {j_u}}(\mathfrak {u}) \subseteq N_{\mathfrak {g}}(\mathfrak {u})$ is an ideal of ![]() $N_{\mathfrak {g}}(\mathfrak {u})$. It is:
$N_{\mathfrak {g}}(\mathfrak {u})$. It is:
− a restricted
 $p$-algebra (as it derives from an algebraic group according to Lemma 6.4);
$p$-algebra (as it derives from an algebraic group according to Lemma 6.4);− a restricted
 $p$-ideal (as the restriction of the
$p$-ideal (as the restriction of the  $p$-structure of
$p$-structure of  $N_{\mathfrak {g}}(\mathfrak {u})$ coincides with that inherited from
$N_{\mathfrak {g}}(\mathfrak {u})$ coincides with that inherited from  $N_{J_\mathfrak {u}}(\mathfrak {u})$); and
$N_{J_\mathfrak {u}}(\mathfrak {u})$); and− even a
 $p$-nil
$p$-nil  $p$-ideal (as
$p$-ideal (as  $\mathfrak {j_u}$ is
$\mathfrak {j_u}$ is  $p$-nil according to Lemma 2.12).
$p$-nil according to Lemma 2.12).
In particular, it is a solvable ideal of ![]() $N_{\mathfrak {g}}(\mathfrak {u})$ whence the inclusion
$N_{\mathfrak {g}}(\mathfrak {u})$ whence the inclusion ![]() $N_{\mathfrak {j_u}}(\mathfrak {u}) \subseteq \operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {u}))$. To summarise: the set
$N_{\mathfrak {j_u}}(\mathfrak {u}) \subseteq \operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {u}))$. To summarise: the set ![]() $\mathfrak {u}$ of
$\mathfrak {u}$ of ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {u}))$ is contained in a
$\operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {u}))$ is contained in a ![]() $p$-nil ideal of this radical (namely,
$p$-nil ideal of this radical (namely, ![]() $N_{\mathfrak {j_u}}(\mathfrak {u})$), hence is equal to the latter. This contradicts the strictness of the inclusion, whence the equality
$N_{\mathfrak {j_u}}(\mathfrak {u})$), hence is equal to the latter. This contradicts the strictness of the inclusion, whence the equality ![]() $\mathfrak {u} = \mathfrak {j_u}$. This, in particular, means that there exists a unipotent smooth connected subgroup
$\mathfrak {u} = \mathfrak {j_u}$. This, in particular, means that there exists a unipotent smooth connected subgroup ![]() $J_{\mathfrak {u}} \subseteq G$ such that
$J_{\mathfrak {u}} \subseteq G$ such that ![]() $\operatorname {Lie}(J_{\mathfrak {u}}) = \mathfrak {u}$. Thus
$\operatorname {Lie}(J_{\mathfrak {u}}) = \mathfrak {u}$. Thus ![]() $\mathfrak {u}$ is integrable.
$\mathfrak {u}$ is integrable.
Now let ![]() $\mathfrak {h} \subseteq \mathfrak {g}$ be a subalgebra, and denote by
$\mathfrak {h} \subseteq \mathfrak {g}$ be a subalgebra, and denote by ![]() $\mathfrak {u}$ the
$\mathfrak {u}$ the ![]() $p$-radical of
$p$-radical of ![]() $N_{\mathfrak {g}}(\mathfrak {h})$. The
$N_{\mathfrak {g}}(\mathfrak {h})$. The ![]() $p$-radical of
$p$-radical of ![]() $N_{\mathfrak {g}}(\mathfrak {h})$ being a restricted
$N_{\mathfrak {g}}(\mathfrak {h})$ being a restricted ![]() $p$-nil
$p$-nil ![]() $p$-ideal, the work done in § 4 allows us to associate to
$p$-ideal, the work done in § 4 allows us to associate to ![]() $\mathfrak {u}$ a unipotent, smooth, connected subgroup
$\mathfrak {u}$ a unipotent, smooth, connected subgroup ![]() $J_{\mathfrak {u}} \subset G$.
$J_{\mathfrak {u}} \subset G$.
Lemma 5.2 The subgroup ![]() $N_G(\mathfrak {h})$ normalises
$N_G(\mathfrak {h})$ normalises ![]() $J_\mathfrak {u}$.
$J_\mathfrak {u}$.
Proof. One only needs to apply verbatim the proof of Lemma 3.8 as, by assumption, ![]() $\mathfrak {u}$ is an ideal of
$\mathfrak {u}$ is an ideal of ![]() $N_{\mathfrak {g}}(\mathfrak {h})$.
$N_{\mathfrak {g}}(\mathfrak {h})$.
Lemma 5.3 Let ![]() $G$ be a reductive group over a field
$G$ be a reductive group over a field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$ which is assumed to be separably good for
$p>0$ which is assumed to be separably good for ![]() $G$ and let
$G$ and let ![]() $\mathfrak {h} \subseteq \mathfrak {g}$ be a subalgebra such that the normaliser
$\mathfrak {h} \subseteq \mathfrak {g}$ be a subalgebra such that the normaliser ![]() $N_{G}(\mathfrak {h})$ is
$N_{G}(\mathfrak {h})$ is ![]() $\phi$-infinitesimally saturated. If
$\phi$-infinitesimally saturated. If ![]() $\mathfrak {u}:=\operatorname {rad}_p(N_{\mathfrak {g}}(\mathfrak {h}))$, then the subalgebra
$\mathfrak {u}:=\operatorname {rad}_p(N_{\mathfrak {g}}(\mathfrak {h}))$, then the subalgebra ![]() $\mathfrak {u}$ is integrable.
$\mathfrak {u}$ is integrable.
Proof. Recall that according to Lemma 4.4 one has the inclusion ![]() $\mathfrak {u}\subseteq \mathfrak {j_u}$. Moreover,
$\mathfrak {u}\subseteq \mathfrak {j_u}$. Moreover, ![]() $N_G(\mathfrak {h})$ being
$N_G(\mathfrak {h})$ being ![]() $\phi$-infinitesimally saturated, the group
$\phi$-infinitesimally saturated, the group ![]() $J_{\mathfrak {u}}$ is a subgroup of
$J_{\mathfrak {u}}$ is a subgroup of ![]() $N_G(\mathfrak {h})$. At the Lie algebra level this leads to the following inclusions
$N_G(\mathfrak {h})$. At the Lie algebra level this leads to the following inclusions ![]() $\mathfrak {u} \subset \mathfrak {j_u} \subseteq \operatorname {Lie}(N_{G}(\mathfrak {h})) = N_{\mathfrak {g}}(\mathfrak {h})$.
$\mathfrak {u} \subset \mathfrak {j_u} \subseteq \operatorname {Lie}(N_{G}(\mathfrak {h})) = N_{\mathfrak {g}}(\mathfrak {h})$.
Assume the inclusion ![]() $\mathfrak {u} \subsetneq \mathfrak {j_u}$ to be strict. Then
$\mathfrak {u} \subsetneq \mathfrak {j_u}$ to be strict. Then ![]() $\mathfrak {u}$ is a proper subalgebra of its normaliser in
$\mathfrak {u}$ is a proper subalgebra of its normaliser in ![]() $\mathfrak {j_u}$ (according to [Reference BourbakiBou71, § 4, n
$\mathfrak {j_u}$ (according to [Reference BourbakiBou71, § 4, n![]() $^{\circ }$1, Proposition 3]). In other words, one has
$^{\circ }$1, Proposition 3]). In other words, one has
However, according to Lemma 5.2 the subgroup ![]() $J_{\mathfrak {u}}$ is normalised by
$J_{\mathfrak {u}}$ is normalised by ![]() $N_G(\mathfrak {h})$, hence
$N_G(\mathfrak {h})$, hence ![]() $N_{\mathfrak {j_u}}(\mathfrak {u}) \subseteq N_{\mathfrak {g}}(\mathfrak {h})$ is an ideal of
$N_{\mathfrak {j_u}}(\mathfrak {u}) \subseteq N_{\mathfrak {g}}(\mathfrak {h})$ is an ideal of ![]() $N_{\mathfrak {g}}(\mathfrak {h})$. The same arguments as those developed in the proof of Lemma 5.1 allow us to show that it is a restricted
$N_{\mathfrak {g}}(\mathfrak {h})$. The same arguments as those developed in the proof of Lemma 5.1 allow us to show that it is a restricted ![]() $p$-nil
$p$-nil ![]() $p$-ideal of
$p$-ideal of ![]() $N_{\mathfrak {g}}(\mathfrak {h})$ such that
$N_{\mathfrak {g}}(\mathfrak {h})$ such that ![]() $N_{\mathfrak {j_u}}(\mathfrak {u}) \subseteq \operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {h}))$. This leads to the equality
$N_{\mathfrak {j_u}}(\mathfrak {u}) \subseteq \operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {h}))$. This leads to the equality ![]() $N_{\mathfrak {j_u}}(\mathfrak {h})=\mathfrak {u}$ as
$N_{\mathfrak {j_u}}(\mathfrak {h})=\mathfrak {u}$ as ![]() $\mathfrak {u}$ is nothing but the set of
$\mathfrak {u}$ is nothing but the set of ![]() $p$-nilpotent elements of
$p$-nilpotent elements of ![]() $\operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {h}))$. This contradicts the strictness of the inclusion, whence the equality
$\operatorname {rad}(N_{\mathfrak {g}}(\mathfrak {h}))$. This contradicts the strictness of the inclusion, whence the equality ![]() $\mathfrak {u} = \mathfrak {j_u}$. In particular,
$\mathfrak {u} = \mathfrak {j_u}$. In particular, ![]() $\mathfrak {u}$ is integrable.
$\mathfrak {u}$ is integrable.
Remarks 5.4 Let us make more explicit the above condition of ![]() $\phi$-infinitesimal saturation with the two following remarks.
$\phi$-infinitesimal saturation with the two following remarks.
(i) In the particular case when ![]() $\mathfrak {h} = \mathfrak {u}$, namely when
$\mathfrak {h} = \mathfrak {u}$, namely when ![]() $\mathfrak {u} := \operatorname {rad}_p(\operatorname {N}_{\mathfrak {g}}(\mathfrak {u}))$ is the
$\mathfrak {u} := \operatorname {rad}_p(\operatorname {N}_{\mathfrak {g}}(\mathfrak {u}))$ is the ![]() $p$-radical of its normaliser in
$p$-radical of its normaliser in ![]() $\mathfrak {g}$, the
$\mathfrak {g}$, the ![]() $\phi$-infinitesimal saturation assumption is superfluous as in this case the inclusion
$\phi$-infinitesimal saturation assumption is superfluous as in this case the inclusion ![]() $J_{\mathfrak {u}}\subseteq N_G(J_{\mathfrak {u}})$ is clear.
$J_{\mathfrak {u}}\subseteq N_G(J_{\mathfrak {u}})$ is clear.
(ii) The condition of ![]() $\phi$-infinitesimal saturation of normalisers might seem to be extremely restrictive. Let us stress that there exist non-trivial examples of
$\phi$-infinitesimal saturation of normalisers might seem to be extremely restrictive. Let us stress that there exist non-trivial examples of ![]() $\phi$-infinitesimally saturated normalisers: any parabolic subgroup satisfies this condition (according to Lemma 4.2) and such subgroup appears to be the normaliser of its Lie algebra. Moreover, if
$\phi$-infinitesimally saturated normalisers: any parabolic subgroup satisfies this condition (according to Lemma 4.2) and such subgroup appears to be the normaliser of its Lie algebra. Moreover, if ![]() $p>\operatorname {h}(G)$, one can show that the normaliser for the adjoint action of
$p>\operatorname {h}(G)$, one can show that the normaliser for the adjoint action of ![]() $G$ of any restricted
$G$ of any restricted ![]() $p$-nil
$p$-nil ![]() $p$-subalgebra is
$p$-subalgebra is ![]() $\exp$-infinitesimally saturated (or infinitesimally saturated).
$\exp$-infinitesimally saturated (or infinitesimally saturated).
6. Added in proof: technical results on normalisers and centralisers
The formalism used in this section is developed in [Reference Demazure and GabrielDG70, II, § 4]. We refer the reader, in particular, to [Reference Demazure and GabrielDG70, II, § 4, 3.7] for notation. Let ![]() $A$ be a ring and
$A$ be a ring and ![]() $G$ be an affine
$G$ be an affine ![]() $A$-group functor. Let us recall the following.
$A$-group functor. Let us recall the following.
(i) If ![]() $R$ is an
$R$ is an ![]() $A$-algebra
$A$-algebra ![]() $R$, we denote by
$R$, we denote by ![]() $R[t]$ the algebra of polynomials in
$R[t]$ the algebra of polynomials in ![]() $t$ and by
$t$ and by ![]() $\epsilon$ the image of
$\epsilon$ the image of ![]() $t$ via the projection
$t$ via the projection ![]() $R[t] \rightarrow R[t]/(t^2)=:R[\epsilon ]$. We associate to
$R[t] \rightarrow R[t]/(t^2)=:R[\epsilon ]$. We associate to ![]() $G$ a functor in Lie algebras denoted by
$G$ a functor in Lie algebras denoted by ![]() $\mathfrak {Lie}(G)$ and which is the kernel of the following exact sequence.
$\mathfrak {Lie}(G)$ and which is the kernel of the following exact sequence.

For any ![]() $y \in \mathfrak {Lie}(G)(R)$ we denote by
$y \in \mathfrak {Lie}(G)(R)$ we denote by ![]() $\operatorname {e}^{\epsilon y}$ the image of
$\operatorname {e}^{\epsilon y}$ the image of ![]() $y$ in
$y$ in ![]() $G(R[\epsilon ])$. In what follows, the notation
$G(R[\epsilon ])$. In what follows, the notation ![]() $\mathfrak {Lie}(G)(R)$ refers both to the kernel of
$\mathfrak {Lie}(G)(R)$ refers both to the kernel of ![]() $p$ as well and to its image in
$p$ as well and to its image in ![]() $G(R[\epsilon ])$. The Lie-algebra of
$G(R[\epsilon ])$. The Lie-algebra of ![]() $G$ is given by the
$G$ is given by the ![]() $k$-algebra
$k$-algebra ![]() $\mathfrak {Lie}(G)(A)$ and is denoted by
$\mathfrak {Lie}(G)(A)$ and is denoted by ![]() $\operatorname {Lie}(G) := \mathfrak {g}$. According to [Reference Demazure and GabrielDG70, II, § 4, n
$\operatorname {Lie}(G) := \mathfrak {g}$. According to [Reference Demazure and GabrielDG70, II, § 4, n![]() $^{\circ }$4.8, Proposition] when
$^{\circ }$4.8, Proposition] when ![]() $G$ is smooth or when
$G$ is smooth or when ![]() $A$ is a field and
$A$ is a field and ![]() $G$ is locally of finite presentation over
$G$ is locally of finite presentation over ![]() $A$, the equality
$A$, the equality ![]() $\operatorname {Lie}(G) \otimes _A R = \mathfrak {Lie}(G)(A)\otimes _A R = \mathfrak {Lie}(G)(R) = \operatorname {Lie}(G_R)$ holds true for any
$\operatorname {Lie}(G) \otimes _A R = \mathfrak {Lie}(G)(A)\otimes _A R = \mathfrak {Lie}(G)(R) = \operatorname {Lie}(G_R)$ holds true for any ![]() $A$-algebra
$A$-algebra ![]() $R$ (these are sufficient conditions). When the aforementioned equality is satisfied, the
$R$ (these are sufficient conditions). When the aforementioned equality is satisfied, the ![]() $A$-functor
$A$-functor ![]() $\mathfrak {Lie}(G)$ is representable by
$\mathfrak {Lie}(G)$ is representable by ![]() $W(\mathfrak {g})$, where for any
$W(\mathfrak {g})$, where for any ![]() $A$-module
$A$-module ![]() $M$ and any
$M$ and any ![]() $A$-algebra
$A$-algebra ![]() $R$ we set
$R$ we set ![]() $W(M)(R) := M \otimes _A R$.
$W(M)(R) := M \otimes _A R$.
(ii) For any ![]() $A$-algebra
$A$-algebra ![]() $R$ we use the additive notation to describe the group law of
$R$ we use the additive notation to describe the group law of ![]() $\mathfrak {Lie}(G)(R)$.
$\mathfrak {Lie}(G)(R)$.
(iii) The ![]() $A$-group functor
$A$-group functor ![]() $G$ acts on
$G$ acts on ![]() $\mathfrak {Lie}(G)$ as follows: for any
$\mathfrak {Lie}(G)$ as follows: for any ![]() $A$-algebra
$A$-algebra ![]() $R$ the induced morphism is
$R$ the induced morphism is
 \begin{alignat*}{3} \operatorname{Ad}_R : \: & G_R\: &\rightarrow \: & \operatorname{Aut}(\mathfrak{Lie}(G))(R),\\ \: & g \: & \mapsto \: & \operatorname{Ad}_R(g) : \mathfrak{Lie}(G)(R) \rightarrow \mathfrak{Lie}(G)(R) : x \mapsto i(g)xi(g)^{-1}. \end{alignat*}
\begin{alignat*}{3} \operatorname{Ad}_R : \: & G_R\: &\rightarrow \: & \operatorname{Aut}(\mathfrak{Lie}(G))(R),\\ \: & g \: & \mapsto \: & \operatorname{Ad}_R(g) : \mathfrak{Lie}(G)(R) \rightarrow \mathfrak{Lie}(G)(R) : x \mapsto i(g)xi(g)^{-1}. \end{alignat*}
When ![]() $G$ is smooth (in particular, when
$G$ is smooth (in particular, when ![]() $\mathfrak {Lie}(G)$ is representable) the
$\mathfrak {Lie}(G)$ is representable) the ![]() $G$-action on
$G$-action on ![]() $\mathfrak {Lie}(G)$ defines a linear representation
$\mathfrak {Lie}(G)$ defines a linear representation ![]() $G \rightarrow \operatorname {GL}(\mathfrak {g})$ (see [Reference Demazure and GabrielDG70, II, § 4, n
$G \rightarrow \operatorname {GL}(\mathfrak {g})$ (see [Reference Demazure and GabrielDG70, II, § 4, n![]() $^{\circ }$4.8, Proposition]).
$^{\circ }$4.8, Proposition]).
6.1 Centralisers
Lemma 6.1 Let ![]() $A$ be a ring and set
$A$ be a ring and set ![]() $S = \operatorname {Spec}(A)$. If
$S = \operatorname {Spec}(A)$. If ![]() $G$ is a smooth affine
$G$ is a smooth affine ![]() $S$-group scheme, the equality
$S$-group scheme, the equality ![]() $\operatorname {Lie}(Z_G(\mathfrak {h})) = Z_{\mathfrak {g}}(\mathfrak {h})$ is satisfied for any subspace
$\operatorname {Lie}(Z_G(\mathfrak {h})) = Z_{\mathfrak {g}}(\mathfrak {h})$ is satisfied for any subspace ![]() $\mathfrak {h}\subset \mathfrak {g}$.
$\mathfrak {h}\subset \mathfrak {g}$.
Proof. By definition, one has
The last identity can be rewritten as ![]() $e^{\epsilon g}e^{\epsilon ' x}e^{-\epsilon g}e^{-\epsilon ' x} = e^{\epsilon \epsilon '[g,x]} = 1$ in
$e^{\epsilon g}e^{\epsilon ' x}e^{-\epsilon g}e^{-\epsilon ' x} = e^{\epsilon \epsilon '[g,x]} = 1$ in ![]() $G(A[\epsilon, \epsilon '])$, whence the vanishing of the Lie bracket
$G(A[\epsilon, \epsilon '])$, whence the vanishing of the Lie bracket ![]() $[g,x]$ (which is a condition in
$[g,x]$ (which is a condition in ![]() $G(A[\epsilon ])$). This leads to the following equality:
$G(A[\epsilon ])$). This leads to the following equality:
Remarks 6.2 Let us emphasise some very particular behaviours of the centre.
(i) Let ![]() $Z_G(\mathfrak {h})_{\mathrm {red}}$ be the reduced part of the centraliser. Even when
$Z_G(\mathfrak {h})_{\mathrm {red}}$ be the reduced part of the centraliser. Even when ![]() $k$ is an algebraically closed field, the equality
$k$ is an algebraically closed field, the equality ![]() $\operatorname {Lie}(Z_G(\mathfrak {h})_{\mathrm {red}}) = Z_{\mathfrak {g}}(\mathfrak {h})$ is a priori not satisfied (see, for example, [Reference JantzenJan04, 2.3]).
$\operatorname {Lie}(Z_G(\mathfrak {h})_{\mathrm {red}}) = Z_{\mathfrak {g}}(\mathfrak {h})$ is a priori not satisfied (see, for example, [Reference JantzenJan04, 2.3]).
(ii) Let ![]() $S:= \operatorname {Spec}(A)$ be an affine scheme and let
$S:= \operatorname {Spec}(A)$ be an affine scheme and let ![]() $G$ be a
$G$ be a ![]() $S$-group scheme. Assume
$S$-group scheme. Assume ![]() $Z_G$ to be representable (this condition is, in particular, satisfied when
$Z_G$ to be representable (this condition is, in particular, satisfied when ![]() $G$ is locally free and separated (see [Reference Demazure and GabrielDG70, II, § 1, n
$G$ is locally free and separated (see [Reference Demazure and GabrielDG70, II, § 1, n![]() $^{\circ }$3.6(c), Théorème]). As mentioned in [Reference Demazure and GrothendieckSGA3I, II, 5.3.3] the algebra
$^{\circ }$3.6(c), Théorème]). As mentioned in [Reference Demazure and GrothendieckSGA3I, II, 5.3.3] the algebra ![]() $\operatorname {Lie}(Z_G):= \mathfrak {Lie}(Z_G)(A)$ is a subalgebra of
$\operatorname {Lie}(Z_G):= \mathfrak {Lie}(Z_G)(A)$ is a subalgebra of ![]() $\mathfrak {z_g}$.
$\mathfrak {z_g}$.
According to [Reference Demazure and GrothendieckSGA3II, XII Théorème 4.7(d) and Proposition 4.11] when ![]() $G$ is smooth affine of connected fibres and of zero unipotent rank over
$G$ is smooth affine of connected fibres and of zero unipotent rank over ![]() $S$, the centre of
$S$, the centre of ![]() $G$ is the kernel of the adjoint representation
$G$ is the kernel of the adjoint representation ![]() $\operatorname {Ad} : G \rightarrow \operatorname {GL}(\mathfrak {g})$. Under these assumptions the equality
$\operatorname {Ad} : G \rightarrow \operatorname {GL}(\mathfrak {g})$. Under these assumptions the equality ![]() $\operatorname {Lie}(Z_G)= \mathfrak {z_g}$ holds true. Indeed the exact sequence of algebraic groups
$\operatorname {Lie}(Z_G)= \mathfrak {z_g}$ holds true. Indeed the exact sequence of algebraic groups
induces by derivation an exact sequence (see [Reference Demazure and GabrielDG70, II, § 4, n![]() $^{\circ }$1.5]) as follows.
$^{\circ }$1.5]) as follows.

The desired equality follows as, by definition, ![]() $\mathfrak {z_g}:= \ker (\operatorname {ad})$. Let us emphasise that this applies, in particular, to any reductive
$\mathfrak {z_g}:= \ker (\operatorname {ad})$. Let us emphasise that this applies, in particular, to any reductive ![]() $S$-group
$S$-group ![]() $G$ and to any parabolic subgroup
$G$ and to any parabolic subgroup ![]() $P\subseteq G$ (as any Cartan subgroup of
$P\subseteq G$ (as any Cartan subgroup of ![]() $P$ is a Cartan subgroup of
$P$ is a Cartan subgroup of ![]() $G$).
$G$).
6.2 Normalisers
Let ![]() $S=\operatorname {Spec}(A)$ be an affine scheme and let
$S=\operatorname {Spec}(A)$ be an affine scheme and let ![]() $G$ be a smooth
$G$ be a smooth ![]() $S$-group scheme of finite presentation. In what follows,
$S$-group scheme of finite presentation. In what follows, ![]() $H \subseteq G$ is a closed locally free subgroup. Let us stress that under these conditions the normaliser
$H \subseteq G$ is a closed locally free subgroup. Let us stress that under these conditions the normaliser ![]() $N_G(H)$ is representable by a closed group sub-functor of
$N_G(H)$ is representable by a closed group sub-functor of ![]() $G$ according to [Reference Demazure and GabrielDG70, II, § 1, n
$G$ according to [Reference Demazure and GabrielDG70, II, § 1, n![]() $^{\circ }$3, Théorème 3.6(b)]. Moreover, if
$^{\circ }$3, Théorème 3.6(b)]. Moreover, if ![]() $H$ is smooth, the aforementioned theorem provides the representability of
$H$ is smooth, the aforementioned theorem provides the representability of ![]() $N_G(\mathfrak {Lie}(H))= N_G(\mathfrak {h})$ as then
$N_G(\mathfrak {Lie}(H))= N_G(\mathfrak {h})$ as then ![]() $\mathfrak {Lie}(H)$ is representable by
$\mathfrak {Lie}(H)$ is representable by ![]() $W(\mathfrak {h})$ which is locally free.
$W(\mathfrak {h})$ which is locally free.
Lemma 6.3 If ![]() $H \subseteq G$ is a closed subgroup, then the inclusion
$H \subseteq G$ is a closed subgroup, then the inclusion ![]() $N_G(H) \subseteq N_G(\mathfrak {Lie}(H))$ is satisfied. In particular, if
$N_G(H) \subseteq N_G(\mathfrak {Lie}(H))$ is satisfied. In particular, if ![]() $H$ is smooth this leads to the inclusion
$H$ is smooth this leads to the inclusion ![]() $N_G(H)(R) \subseteq N_G(\mathfrak {h}_R)$ for any
$N_G(H)(R) \subseteq N_G(\mathfrak {h}_R)$ for any ![]() $A$-algebra
$A$-algebra ![]() $R$.
$R$.
Proof. Let us recall that ![]() $G$ acts on
$G$ acts on ![]() $\mathfrak {Lie}(G)$ via the adjoint representation. Namely, for any
$\mathfrak {Lie}(G)$ via the adjoint representation. Namely, for any ![]() $A$-algebra
$A$-algebra ![]() $R$ one has
$R$ one has
 \begin{alignat*}{3} \operatorname{Ad}_R : \: & G_R\: &\rightarrow \: & \operatorname{GL}(\mathfrak{Lie}(G))(R),\\ \: & g \: & \mapsto \: & \operatorname{Ad}_R(g) : \mathfrak{Lie}(G)(R) \rightarrow \mathfrak{Lie}(G)(R) : x \mapsto i(g)xi(g)^{-1}. \end{alignat*}
\begin{alignat*}{3} \operatorname{Ad}_R : \: & G_R\: &\rightarrow \: & \operatorname{GL}(\mathfrak{Lie}(G))(R),\\ \: & g \: & \mapsto \: & \operatorname{Ad}_R(g) : \mathfrak{Lie}(G)(R) \rightarrow \mathfrak{Lie}(G)(R) : x \mapsto i(g)xi(g)^{-1}. \end{alignat*}
Let ![]() $g \in N_G(H)(R):= \{g' \in G(R) \mid \operatorname {Ad}(g')(H\otimes _A R) = H\otimes _A R\}$ (see, for example, [Reference Demazure and GabrielDG70, II, § 1, n
$g \in N_G(H)(R):= \{g' \in G(R) \mid \operatorname {Ad}(g')(H\otimes _A R) = H\otimes _A R\}$ (see, for example, [Reference Demazure and GabrielDG70, II, § 1, n![]() $^{\circ }$3.4, Definition]). In particular, for any
$^{\circ }$3.4, Definition]). In particular, for any ![]() $x \in \mathfrak {Lie}(H)(R)$, one has
$x \in \mathfrak {Lie}(H)(R)$, one has
hence the inclusion ![]() $N_G(H) \subseteq N_G(\mathfrak {Lie}(H))$.
$N_G(H) \subseteq N_G(\mathfrak {Lie}(H))$.
If now ![]() $H$ is smooth, then
$H$ is smooth, then ![]() $\mathfrak {Lie}(H)$ is representable by a
$\mathfrak {Lie}(H)$ is representable by a ![]() $A$-functor of Lie algebras and one has
$A$-functor of Lie algebras and one has
for any ![]() $A$-algebra
$A$-algebra ![]() $R$.
$R$.
Lemma 6.4 Let ![]() $\mathfrak {h} \subseteq \mathfrak {g}$ be a Lie subalgebra. Then one has
$\mathfrak {h} \subseteq \mathfrak {g}$ be a Lie subalgebra. Then one has ![]() $\operatorname {Lie}(\operatorname {N}_G(\mathfrak {h})) = \operatorname {N}_{\mathfrak {g}}(\mathfrak {h})$.
$\operatorname {Lie}(\operatorname {N}_G(\mathfrak {h})) = \operatorname {N}_{\mathfrak {g}}(\mathfrak {h})$.
Proof. By definition, one has that
The last relation can be written
in ![]() $G(A[\epsilon, \epsilon '])$, because
$G(A[\epsilon, \epsilon '])$, because ![]() $\epsilon ^2 =0$. In other words, one has
$\epsilon ^2 =0$. In other words, one has
 \begin{align*} \operatorname{Lie}(N_G(\mathfrak{h})) & = \{g \in \mathfrak{g} \mid x + \epsilon[g,x] \in \mathfrak{h}_{A[\epsilon]}, \forall x \in \mathfrak{h}(A[\epsilon])\}\\ & = \{g \in \mathfrak{g} \mid \epsilon[g,x] \in \mathfrak{h}_{A[\epsilon]}, \forall x \in \mathfrak{h}(A[\epsilon])\}\\ & = \{g \in \mathfrak{g} \mid [g,x] \in \mathfrak{h}_{A[\epsilon]}, \forall x \in \mathfrak{h}(A[\epsilon])\}\\ &= N_{\mathfrak{g}}(\mathfrak{h}). \end{align*}
\begin{align*} \operatorname{Lie}(N_G(\mathfrak{h})) & = \{g \in \mathfrak{g} \mid x + \epsilon[g,x] \in \mathfrak{h}_{A[\epsilon]}, \forall x \in \mathfrak{h}(A[\epsilon])\}\\ & = \{g \in \mathfrak{g} \mid \epsilon[g,x] \in \mathfrak{h}_{A[\epsilon]}, \forall x \in \mathfrak{h}(A[\epsilon])\}\\ & = \{g \in \mathfrak{g} \mid [g,x] \in \mathfrak{h}_{A[\epsilon]}, \forall x \in \mathfrak{h}(A[\epsilon])\}\\ &= N_{\mathfrak{g}}(\mathfrak{h}). \end{align*}
The second part of the following lemma is shown in the proof of [Reference Conrad, Gabber and PrasadCGP15, Proposition 3.5.7] when ![]() $k$ is a separably closed field. The study of the proof shows that one actually only needs
$k$ is a separably closed field. The study of the proof shows that one actually only needs ![]() $H(k)$ to be Zariski-dense in
$H(k)$ to be Zariski-dense in ![]() $H$ for the result to hold true. Let us stress that this is especially verified when:
$H$ for the result to hold true. Let us stress that this is especially verified when:
(i) the field
 $k$ is perfect and the subgroup
$k$ is perfect and the subgroup  $H$ is connected (see [Reference BorelBor91, Corollary 18.2]);
$H$ is connected (see [Reference BorelBor91, Corollary 18.2]);(ii) the field
 $k$ is infinite and the subgroup
$k$ is infinite and the subgroup  $H$ is reductive (see [Reference BorelBor91, Corollary 18.2]);
$H$ is reductive (see [Reference BorelBor91, Corollary 18.2]);(iii) the subgroup
 $H$ is unipotent smooth connected and split.
$H$ is unipotent smooth connected and split.
Indeed, under these assumptions ![]() $H$ is isomorphic to a product of
$H$ is isomorphic to a product of ![]() $\mathbb {G}_a$. These conditions are satisfied, in particular, when
$\mathbb {G}_a$. These conditions are satisfied, in particular, when ![]() $k$ is perfect and
$k$ is perfect and ![]() $H$ is unipotent smooth and connected (which is a special case of assumption (i)).
$H$ is unipotent smooth and connected (which is a special case of assumption (i)).
Lemma 6.5 Let ![]() $H\subseteq G$ be a closed and smooth subgroup. Then:
$H\subseteq G$ be a closed and smooth subgroup. Then:
(i) in general, only the inclusion
 $\operatorname {Lie}(N_G(H)) \subseteq N_{\mathfrak {g}}(\mathfrak {h})$ holds true;
$\operatorname {Lie}(N_G(H)) \subseteq N_{\mathfrak {g}}(\mathfrak {h})$ holds true;(ii) if
 $H(k)$ is Zariski-dense in
$H(k)$ is Zariski-dense in  $H$, then
$H$, then
 \[ \operatorname{Lie}(N_G(H)) = \lbrace x \in \mathfrak{g} \mid \operatorname{Ad}(h)(x) - x \in \mathfrak{h} \ \forall h \in H(k)\rbrace. \]
\[ \operatorname{Lie}(N_G(H)) = \lbrace x \in \mathfrak{g} \mid \operatorname{Ad}(h)(x) - x \in \mathfrak{h} \ \forall h \in H(k)\rbrace. \]
Proof. The inclusion ![]() $N_G(H) \subseteq N_{G}(\mathfrak {Lie}(H))$ is provided by Lemma 6.3. Combining this with the equality obtained in Lemma 6.5, one obtains
$N_G(H) \subseteq N_{G}(\mathfrak {Lie}(H))$ is provided by Lemma 6.3. Combining this with the equality obtained in Lemma 6.5, one obtains
As already mentioned, the second assertion of the lemma is shown in [Reference Conrad, Gabber and PrasadCGP15, Proposition 3.5.7].
Remarks 6.6 The first point of the above lemma provides a strict inclusion of Lie algebras in the general case. This is actually a positive characteristic phenomenon (see [Reference HumphreysHum75, 10.5, Corollary B] and the remark that follows Corollary B).
(i) When ![]() $k$ is of characteristic zero, the aforementioned inclusion is always an equality (see [Reference HumphreysHum75, 13, Exercise 1]).
$k$ is of characteristic zero, the aforementioned inclusion is always an equality (see [Reference HumphreysHum75, 13, Exercise 1]).
(ii) When ![]() $k$ is of characteristic
$k$ is of characteristic ![]() $p>0$, the inclusion may be strict as shown in the following example (see [Reference HumphreysHum75, 10, Exercise 4]): assume
$p>0$, the inclusion may be strict as shown in the following example (see [Reference HumphreysHum75, 10, Exercise 4]): assume ![]() $p=2$. Set
$p=2$. Set ![]() $G = \operatorname {SL}_2$ and consider the Borel subgroup
$G = \operatorname {SL}_2$ and consider the Borel subgroup ![]() $B$ of upper triangular matrices. With the group
$B$ of upper triangular matrices. With the group ![]() $B$ being parabolic, it is its self-normaliser. In other words, one has
$B$ being parabolic, it is its self-normaliser. In other words, one has ![]() $N_G(B) = B$. However, at the Lie algebra level one has
$N_G(B) = B$. However, at the Lie algebra level one has ![]() $\operatorname {Lie}(N_G(B)) = \mathfrak {g}$ (as
$\operatorname {Lie}(N_G(B)) = \mathfrak {g}$ (as ![]() $k$ is of characteristic two). Indeed
$k$ is of characteristic two). Indeed ![]() $\operatorname {\mathfrak {sl}}_2$ is generated by
$\operatorname {\mathfrak {sl}}_2$ is generated by ![]() $\big (\begin {smallmatrix} 1 & 0\\ 0 & 1 \end {smallmatrix}\big )$,
$\big (\begin {smallmatrix} 1 & 0\\ 0 & 1 \end {smallmatrix}\big )$, ![]() $\big (\begin {smallmatrix} 0 & 1\\ 0 & 0 \end {smallmatrix}\big )$,
$\big (\begin {smallmatrix} 0 & 1\\ 0 & 0 \end {smallmatrix}\big )$, ![]() $\big (\begin {smallmatrix} 0 & 0\\ 1 & 0 \end {smallmatrix}\big )$ and one only needs to show that the bracket of the two matrices
$\big (\begin {smallmatrix} 0 & 0\\ 1 & 0 \end {smallmatrix}\big )$ and one only needs to show that the bracket of the two matrices ![]() $\big (\begin {smallmatrix} 0 & 0\\ 1 & 0 \end {smallmatrix}\big )$ and
$\big (\begin {smallmatrix} 0 & 0\\ 1 & 0 \end {smallmatrix}\big )$ and ![]() $\big (\begin {smallmatrix} 0 & 1\\ 0 & 0 \end {smallmatrix}\big )$ still belongs to
$\big (\begin {smallmatrix} 0 & 1\\ 0 & 0 \end {smallmatrix}\big )$ still belongs to ![]() $\mathfrak {b}$. One has
$\mathfrak {b}$. One has ![]() $\big [\big (\begin {smallmatrix} 0 & 1\\ 0 & 0 \end {smallmatrix}\big ), \big (\begin {smallmatrix} 0 & 0\\ 1 & 0 \end {smallmatrix}\big )\big ] = \operatorname {id} \in \mathfrak {b}$.
$\big [\big (\begin {smallmatrix} 0 & 1\\ 0 & 0 \end {smallmatrix}\big ), \big (\begin {smallmatrix} 0 & 0\\ 1 & 0 \end {smallmatrix}\big )\big ] = \operatorname {id} \in \mathfrak {b}$.
Acknowledgements
The author would like to thank: Philippe Gille for all the fruitful discussions they had which go beyond the framework of this paper, his availability and his multiple reviews and corrections of this article; Benoît Dejoncheere for his supportive help, his several reviews and useful advice; Matthieu Romagny for conversations on the nilpotent scheme; and both reviewers of the author's PhD manuscript, Anne-Marie Aubert and Vikraman Balaji, for their corrections and remarks. Finally, many thanks should go to the anonymous referee of this article for raising many interesting points that definitely helped to improve its content. Any critical remarks must be addressed exclusively to the author of this paper.