Introduction
Radar calculates depths based on reflection-time measurements. The conversion of time to depth has two main components: the velocity of the electromagnetic wave in solid ice, and a firn compensation which corrects for the higher velocity in the snow. For solid natural ice, a laboratory-measured permittivity of 3.17, corresponding to a wave velocity of 168.4 m μs−1, was used (Reference EvansEvans, 1965). With improved equipment Reference Paren and RobinParen and Robin (1975) observed internal layers in polar ice, and it was deduced that the origin of the internal layer reflections was due to changes in loss tangent. Changes in the density could not be the cause for the observed internal reflections in the deeper part of the ice cap. Also, it was observed that radar reflecting layers correlated to ice-core measurements (δ 18O) and thus could provide additional glaciological information (Reference GudmandsenGudmandsen, 1975). A major problem was the difference between the vertical resolution of the ice-core record and that of the radar profile: in the ice core the resolution is at the cm level, whereas a 250 ns long radar pulse spans 42 m of ice. As a result, in the radar picture we observe different layer patterns depending on the pulse length used, because the observed reflection is a combination of several reflections. Even with this uncertainty, it was clear that the radar returns contained glaciological information, although the mechanism was not known.
The development of the electrical conductivity measurement (ECM) method (Reference HammerHammer, 1980) was a significant step forward in interpreting the source of the radar echoes. In the ECM method, conductive horizons due to the presence of acidity (H+) are recorded, and it is these horizons that give rise to radar reflections. Although some events were identified by this method, it was not very successful. The reason was, again, that the difference in resolution between the two records made correlation difficult. Besides, the radar horizons were isochrons and, as such, used for cross-correlation between ice cores from different polar regions (Reference Jacobel and HodgeJacobel and Hodge, 1995; Reference Dahl-JensenDahl-Jensen and others, 1997; Reference Legarsky, Wong, Akins and GogineniLegarsky and others, 1998; Reference Tabacco, Passerini, Corbelli and GormanTabacco and others, 1998).
In this paper, a high-resolution radar record of the upper 800 m near the Greenland Ice Core Project (GRIP) drilling site in central Greenland is compared with the ECM record of the ice core from the GRIP site. Also, the depth of the reflecting layers, and thereby the firn correction, is determined using a seismic method, which requires no information on the firn density. The firn correction and the radar wave velocity in solid ice are determined.
The Instrument
A 35 MHz high-resolution monopulse radio-echo system was used to record the radar profile. The system consisted of components developed at the Geophysical Institute, University of Munster, and described by Reference BlindowBlindow (1986). It was enhanced to record reflections over a 10 μs time interval, without losing the resolution, in the depth range to 800 m. The radar base frequency is relatively low (35 MHz), and the transmitted wavelet is short and corresponds almost to a quarter of a wavelength. Figure 1 shows the amplitude reflection coefficient for a step change in loss tangent. Several sample waveforms are shown, including a typical transmitted wavelet. The reflected amplitude is nearly proportional to layer thickness for layers up to 1 m. The waveform also illustrates that a relative resolution in the order of 0.5 m is possible. For a radar with a base frequency of 35 MHz, this resolution is unique, and it can be obtained only with a broad-band antenna. The reflections with this waveform are further discussed in the Appendix. The radar was operated along the reconstructed Expédition Glaciologique International au Groenland (EGIG) line between Camp VI (T1) and Jarl Joset (T53), on the north–south traverse from the ice-core drill site GRIP to the point Crête (T43) of the EGIG line (Reference HofmannHofmann, 1964) and between the two central Greenland drill sites GRIP and Greenland Ice Sheet Project Two (GISP2).

Fig. 1. Relation between reflection coefficient and layer thickness. The amplitude reflection coefficient is shown as a function of layer thickness for a step change in loss tangent of tan δ = 0.0018. The following waveforms are used: sine, Gaussian pulse and a typical wavelet as transmitted by the pulse radar.
To obtain the internal structure of the upper 800 m of the ice sheet, a shot was recorded every 10 m. The distance between transmitter and receiver antenna was 10–20 m except when the equipment was used for common depth point (CDP) measurements (see later). Because the recording of the radar returns is digitized, and all processing is performed digitally, the measurements are very accurate. Calibration traces help to eliminate any drift. After resampling, recalibration, filtering and gain control, single reflections are accurate to within 1 m, and the relative accuracy between two such reflections is even higher.
CDP measurements were performed at regular intervals along the traverse to determine the velocity–depth function.
ECM and Ice-Core Logging
The main cause for the larger reflections of electromagnetic waves in ice is acid deposits from the atmosphere, which change the electrical conductivity and the loss angle of the ice. The resulting dielectric change can be measured on the ice core by two different methods. The permittivity is measured by dielectrical profiling (DEP) equipment (Reference Moore and ParenMoore and Paren, 1987) on an ice core. The surface conductivity (ECM) is measured by two electrodes moving along the core; these have a potential difference of about 1 kV, and the current is recorded while the electrodes are moved. This method mainly records the acidity. Because volcanic eruptions cause acid precipitation (Reference HammerHammer, 1980; Reference MillarMillar, 1982), the ECM method is useful for detecting volcanic fallout. In the Greenland ice cores, mainly major eruptions in the Northern Hemisphere are detected, i.e. volcanoes located in Iceland (Laki, Eldga), in the Mediterranean (Thera) or in Indonesia (Tambora) (Reference Hammer, Clausen, Friedrich and TauberHammer and others, 1987; Reference Clausen and HammerClausen and Hammer, 1988). The basic resolution of an ECM record is 1 mm, and acid layers typically span a few cm to dm of ice. In order to make the resolution of the ECM profile compatible with the radar records, this paper presents the ECM profile as 10 cm averages. The depth and age of the volcanic horizons in the top 800 m of the GRIP ice core are presented in Reference ClausenClausen and others (1997).
The absolute depth of the ice-core record is recorded with high precision. The top of the GRIP ice core is referenced to the undisturbed surface during summer 1989. This reference may have a relatively large error, 0.5 m in the worst case, because it is difficult to preserve the “undisturbed surface” when construction takes place around the drilling site. Unfortunately the undisturbed surface was not measured later using a global positioning system (GPS) or similar means. Also, the thickness of the upper layers varies significantly from year to year and from place to place. The depth reference, however, has been cross-checked with several nearby shallow cores, so 0.5 m is a worst-case limit. During drilling, the bottom part of a core is always kept on the logging table so it can be fitted to the next core. This fit is normally perfect, and with no missing cores the accuracy of the depth scale is estimated to be 1‰ (Reference Hammer, Clausen, Hardy and RenfrewHammer and Clausen, 1991).
CDP Layer-Depth Measurements
Although the radar horizons can be related to the ECM profile, this relation requires a correction for the higher velocity in the firn, as well as knowledge of the electromagnetic wave speed in the ice. These parameters can be found by the CDP technique, commonly used in seismic processing, whereby receivers placed at increasing distances from the transmitter record the seismic echoes simultaneously. In the ice-radar version, the centre point between transmitter and receiver is kept stationary, and the transmitter and receiver are moved symmetrically relative to this point. Therefore, the active reflective point in the ice cap remains the same as the reflection angles are changed. This procedure ensures the most accurate measurements.
A CDP measurement was recorded at a distance of approximately 1 km from the drillhole at GRIP. Transmitter and receiver were separated up to 400 m, increasing the reflection time from 800 m depth by about 0.3 μs or ten periods at the 35 MHz signal frequency. This is sufficient for a velocity analysis with the usual algorithms. The analysis follows a procedure (Reference Garotta and MichonGarotta and Michon, 1967) which sums up the traces of the CDP along calculated hyperbolas for each velocity in question. A maximum amplitude in this stacked trace is found at a certain reflection time corresponding to the correct matching of the stacked velocity.
Figure 2 shows the velocity–depth function of an ice sheet with a firn layer that is compacted continuously with increasing depth up to the final density of ice. Although the recording time was only 10 μs, the first half is shown because the final velocity of electromagnetic waves is reached at about 2 μs reflection time. To check the sensitivity of the solution, the calculated velocity is varied ±1 m μs−1 around the mean. The stacked velocities are nearly equal to the rms velocities from which interval velocities, or just the velocity vs depth, can be calculated:

where
![]() and t
1 are the rms velocity and the reflection time, respectively, from the surface down to the upper layer boundary,
and t
1 are the rms velocity and the reflection time, respectively, from the surface down to the upper layer boundary,
![]() and t
2 are the rms velocity and the reflection time, respectively, from the surface down to the lower layer boundary, and v
int is the velocity within the layer in question.
and t
2 are the rms velocity and the reflection time, respectively, from the surface down to the lower layer boundary, and v
int is the velocity within the layer in question.

Fig. 2. rms velocity and interval velocity vs depth. The rms velocity is calculated from CDP measurements, and the interval velocity, or point velocity, from the rms values.
This velocity is plotted as the left curve in Figure 2.
Firn Correction and Wave Velocity
Figure 2 shows the radar wave velocity in solid ice to be close to 168 m μs−1 This result was obtained without knowledge of the layer depths, using only the known distance between transmitter and receiver and the time delay of the radar echoes. In fact, the depths of several layers are known from the core logging, and using this knowledge the velocity obtained from the CDP measurements can be refined. Only layers below 100 m depth are used because layers closer to the surface are more difficult to identify. Since we want to determine the electromagnetic wave speed in solid ice, the layers < 100 m deep do not contribute to the solution anyway.
Using the preliminary velocity from the CDP measurements, and adding a bias to the height to compensate for the difference between the vertical reference of the radar and the ice core, seven pronounced volcanic layers are identified and used to refine the velocity determination. Next, the speed of the electromagnetic wave is varied from 167 to 169.5 m μs−1. Changing the speed changes the apparent depth of the layer. The sensitivity of the depth change vs wave speed increases with layer depth, the deepest layers being most sensitive to the changes in speed. Figure 3 shows the difference between the radar depth and the depth determined by core logging for seven layers. With a wave speed of 168.1 m μs−1, all seven layers have the same offset, 3.5 m. The wave-velocity error is estimated to be 0.5 m μs−1. The 3.5 m offset has several causes:
-
(1) The depth reference for the ice-core logging is the 1989 surface, and the radar measurements are made in 1990
-
(2) The radar measurements were performed 1 km from the drill site
-
(3) Errors in the 1989 reference surface
-
(4) Uncorrected cable-length errors in the radar system.

Fig. 3. Vertical offset for several layers in the ice vs radar-wave velocity. The x axis has 168 m μs−1 as zero. With a wave speed of 168.l m μs−1 layers at 130–802 m depth agree better than 1 m or within the limits of the accuracy.
Resulting Profiles
The velocity correction in the firn was determined from CDP measurements. For most radar soundings this is not a practical possibility, so the density profile is used to estimate the firn correction. We will check the firn correction calculated by two different equations and compare the result to the CDP measurements. Reference Gudmandsen and WaitGudmandsen (1971) used the equation:
Adjusting the constant to give a velocity of 168.1 m μs−1 with an ice density of 918 kg m3, we obtain the relation:
For a heterogeneous mixture of ice and air as found in the firn, Reference LooyengaLooyenga (1965) gives the equation
Figure 4 shows the measured density profile at GRIP, and the modelled density profile using the equation by Reference Herron and LangwayHerron and Langway (1980). The firn correction is the change in depth due to the higher velocity of the radar wave in the upper layers. Using the measured density profile down to 141 m, and extending it with the modelled density curve, the firn correction is shown for the Looyenga model. The total firn correction is 11.6 m; it is 10.9 m for the Gudmandsen correction, compared to 13.4 m for the CDP measurements. Although the difference between the Looyenga equation and the CDP measurements is greater than the accuracy of the measurements, even higher accuracy of the radar measurements would be required in order to resolve the reason for the difference. In any case, a difference of 1.8 m has little significance for measurements of the deeper ice sheets.

Fig. 4. Density and electromagnetic wave-speed firn correction based on the density. The measured and the modelled density, as well as the firn corrections based on Reference LooyengaLooyenga (1965), are shown.
Figure 5 shows the radar profile over a 10 km horizontal distance, ending at the right at the GRIP drilling site. Next to the radar profile is the ECM profile, with 10 cm averaging, converted to the radar-wave travel time-scale using the Looyenga equation. There is excellent correlation between ECM peaks and radar layers. For the stronger echoes in the upper layers, there is some tendency for double signals, caused by multiple reflections.

Fig. 5. Radar profile for a 10 km long track ending to the right at GRIP. The 10 cm averaged ECM profile is shown to the right of the radar profile. The depth scale for the ECM curve is converted to radar time-scale using the Looyenga equation (Equation (4)).
The wave-speed measurements have been performed at a temperature of −32°C and pressures of 10–80 bars. The results can, with care, be extended to other conditions. One problem in extending the results is the absolute accuracy of the measurements. However, assuming that the primary error in the measurements is a bias, and that relative measurements are more accurate, Figure 6 shows the wave-speed variations with temperature. The figure is based on measurements by Reference GoughGough (1972) for temperatures between −40° and −60°C, and by Reference Johari and CharetteJohari and Charette (1975) for temperatures between −1° and −25°C. Gough used frequencies up to 1 MHz, and Johari and Charette 35–60 MHz. The low frequencies used by Gough will introduce some extra error, especially at higher temperatures (Reference Fitzgerald and ParenFitzgerald and Paren, 1975). Both datasets have been adjusted to give 168.1 m μs −1 at −32°C. Although the fitting of two different datasets produces a slight bump in the curve, they fit well. For temperatures below −10°C, the changes are small.

Fig. 6. Wave-speed variation with temperature, based on data from Reference GoughGough (1972) and adjusted to give 168.1 m μs−1 at −32°C.
There is some wave-speed dependency on density and therefore on pressure. For this effect, the Looyenga equation cannot be used since it assumes a mixture between two substances with different permittivity. Therefore, as an approximation, the permittivity can be assumed to be proportional to density. Using a compressibility of 12 × 10−1 bar−1 (Reference DorseyDorsey, 1940), the density will increase 3.3 kg m−3 at 300 bar, corresponding to a wave speed of 168.4 μm s−1. Interestingly, this increase will be compensated by the higher temperatures deeper down in the ice caps.
Conclusion
We have determined the speed of a 35 MHz electromagnetic wave in solid ice to be 168.1 ±0.5 m μs−1. Other measured values are 169 m μs−1 (Reference RobinRobin, 1975a), 168.17 m μs−1 (Reference Johari and CharetteJohari and Charette, 1975), 168.2 m μs−1 (Reference Gudmandsen and WaitGudmandsen, 1971) and 167.7 m μs−1 (Reference RobinRobin, 1975b). Our result is based on the highly accurate logging of ice cores. Also, we have shown that for Holocene ice the strong radar reflections are caused by acid fallout from volcanic eruptions. For more alkaline ice, like the cold parts of the Greenland Wisconsin ice, the radar reflection signal from the eruptions may be masked by the alkalinity of the ice in the same way it is for EGMs, i.e. the ice seldom becomes acidic. Also, the commonly used equations for calculating electromagnetic wave speed in the firn give reasonable results, although higher-resolution measurements could improve the correction.
The combination of in situ measurements of velocities of electromagnetic waves in ice and true depths of many acid layers in ice cores results in a precise velocity in compacted ice of the Greenland ice sheet of 168.1 m μs−1 at −32°C. The comparison of radio-echo soundings converted with a velocity–depth function and the conductivity profile of the GRIP ice core shows an impressive correlation between EGM peaks and radar reflecting layers. Estimates for the wave speed with varying temperature and pressure have been presented.
Acknowledgements
This work is a contribution to the Greenland Ice Gore Project (GRIP), a European Science Foundation programme involving a collaborative effort by eight nations and the European Union to drill through the central Greenland ice sheet. It has been supported by “Bundesministerium für Bildung und Forschung” FKz. 03F0544A.
Appendix
Figure 1 shows the relative reflection coefficient of a thin layer depending on its relative thickness. The amplitude reflection coefficient for a layer less than one wavelength thick can be calculated from power reflection coefficients by Reference Paren and RobinParen and Robin (1975) which give:

where l is the layer thickness, λ is the wavelength, and Δ tan δ is the difference in loss tangent between the layer and the surrounding ice. As the reflection at the top of a thin layer is overlaid by the bottom reflection, the amplitude reflection coefficient must be superimposed by a cosine term:

with
where r 1 is the amplitude reflection coefficient at the top, r 2 = −r 1 is the amplitude reflection coefficient at the bottom, t 1 = 1 + r 1 is the transmission coefficient at the top and E 0 is the initial amplitude. For a non-continuous wavelet the reflection coefficient is calculated as the integral over the frequency range with spectral weight of the wavelet:
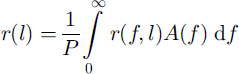
with normalization

Figure 1 shows the reflection coefficients of the half-continuum without special signal, of a sine wave, of a synthetic Gaussian wavelet and of a typical transmitted wavelet over the layer thickness. The layer has a difference in loss tangent of tan δ = 0.0018 which is typical for a volcanic layer. For the sine wave the reflection coefficient changes periodically between 0 and twice the value of the half-continuum according to constructive and destructive interference. The dependence for the wavelets is nearly linear for layers below 1 m thickness. This has the same effect as a high-pass filter of the signal which is expected for thin layers (Reference BlindowBlindow, 1986). At 2 m thicknesses it reaches the value of the half-continuum. This shows the high dependency of reflection coefficients on layer thickness below 1 m thickness.








