Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T15:26:20.287Z Has data issue: false hasContentIssue false
  • English
  • Français

New Ideas for Celestial Navigation in the Third Millennium

Published online by Cambridge University Press:  23 February 2010

Boris Vulfovich  and
Vasily Fogilev
Rights & Permissions [Opens in a new window]

Abstract

This paper reports on innovative mathematical and analytical approaches to celestial navigation. Beyond the common-sense recommendation for automation of the calculations, it is necessary to consider the specific algorithms used. The advantages of these new algorithms become evident when navigational practice is extended beyond the usual twilight round of sights or the noon Sun line. But exploiting the full advantages of the algorithms would probably require new software. This leads us to consider the prospects of applying new information technologies to the task of taking celestial observations.

Keywords

celestial navigation
Type
Forum
Information
The Journal of Navigation , Volume 63 , Issue 2 , April 2010 , pp. 373 - 378
Copyright
Copyright © The Royal Institute of Navigation 2010

1. INTRODUCTION

It is not much of an exaggeration to say that today navigation is virtually synonymous with GPS. This is a development of the present decade, which has seen the completion of the GPS satellite constellation, the shutdown of other electronic means of navigation, and a drastic reduction in the prices of GPS receivers.

Yet GPS has operational characteristics and vulnerabilities that may render it unusable or unreliable under certain conditions. Much work is being devoted to the development of strategies for dealing with GPS outages. Operational plans now must provide for the contingency that GPS may not be available at the most critical times. In order to prevent an over-reliance on a single type of “black box” navigation, every user/platform with a validated requirement has a primary and at least one alternate means of position determination so as to increase reliability. Furthermore, the alternate means must be independent of the primary [Reference Kaplan5].

Some kind of alternative to GPS is needed to provide redundancy for navigational systems. Unfortunately, alternative electronic navigation systems such as Omega have been decommissioned and long-term operational support for others, such as LORAN, is not guaranteed; in any event, LORAN is not available worldwide.

The stellar reference frame is an alternative to GPS that could be used to determine a ship's position. Nowadays celestial navigation is in great decline. Ship's officers, although they must learn celestial navigation, seldom use it. They rely on GPS, the accurate DR available aboard a large ship with a gyrocompass, an accurate shaft tachometer or revolution counter, and the relative luxury of a large chart table and good plotting instruments. While thousands of merchant marine officers have demonstrated proficiency in celestial navigation, the number of them who are actually using sextants for navigation is very small – according to information primarily from interviews with ship pilots and ship's officers. These officers seem unaware of the hazards of total reliance on one electronic aid to navigation, despite numerous accidents. Modern ships have automated navigation systems that rely on GPS. The great drive behind automated navigation systems has not been to increase reliability by cross-checking aids to navigation, but to reduce operator workload. This has succeeded beyond anyone's wildest dreams, in this case reducing the watch officer's navigation workload to zero. But one wonders what he is doing now that is more important than navigating the ship. The primary use of celestial navigation aboard large merchant ships seems to be as a backup to GPS, and each ship continues to carry equipment and tables to allow celestial navigation should it be needed. Coastwise or offshore, it is never desirable to be totally dependent on one electronic aid to navigation [Reference Kaplan5].

Celestial navigation is practiced on a daily basis on training vessels. Standard practice relies on quartermasters skilled in the use of handheld marine sextants and paper-and-pencil sight-reduction techniques. The basic method has not changed much in a hundred years, although almanacs and other sight-reduction tools have become more convenient to use. Observations are limited to a few Sun sights during the day and a few star sights during twilight. Because observations with hand-held sextants have typical uncertainties of about one arc minute, celestial fixes are rarely more accurate than several nautical miles [Reference Feldman, Seidelmann and Barton6]. This kind of celestial navigation may be good for “reality checks” on GPS fixes, and may be useful in an emergency [Reference Fogilev4]. However, if we are willing to think a bit more broadly about how celestial navigation could be performed, we find that these problems with celestial fixes have technical solutions. In fact, as we shall see, most of the necessary solutions are available “off the shelf”. Significant improvement to accuracy and availability of celestial navigation will require changes in both the observational hardware and the computational procedure used to obtain a fix. Let us look at the mathematical situation.

2. ESTIMATION OF THE SMALL SELECTION

In the earlier work [Reference Vulfovich3], there are published results of astronavigational measurments:

(1)
x_{\setnum{1}} \comma x_{\setnum{2}} \comma \ldots \comma x_{i} \comma \ldots \comma x_{n} {\rm \comma }\quad {3}\les {\rm n}\les {\rm 9\comma }

which has normal (Gauss) distribution.

Up to now, in order to estimate the assembly average M(x) we use the arithmetical mean of volumes xi

(2)
\tilde{M}\lpar x\rpar \approx \bar{X} \equals {1 \over n}\sum\limits_{i \equals \setnum{1}}^{n} {x_{i} }.

This approach assumes that all volumes x i have equal possibilities (weights) p i

(3)
p_{i} \equals {1 \over n} \equals const.

But let us suppose that condition (3) does not correspond with the nature of the Gauss distribution. Let us suppose, on the contrary, that their probabilities (weights) are not equal:

(4)
p_{i} \ne const.

The estimation of the assembly average must be calculated with the fundamental formulae:

(5)
\tilde{M}\lpar x\rpar \equals \sum\limits_{i \equals \setnum{1}}^{n} {p_{i} x_{i} }.

It is proposed that the probability (weight) p i of every volume x i is in inverse ratio with sum d i of squares of diversions of volume x i from every other x j:

(6)
d_{i} \equals \sum\limits_{j \equals \setnum{1}}^{n \minus \setnum{1}} {\lpar x_{j} \minus x_{i} \rpar ^{\setnum{2}} }

and therefore:

(7)
p_{i} \equals {K \over {d_{i} }}.

The coefficient K is:

(8)
K \equals {1 \over {\sum\limits_{i \equals \setnum{1}}^{n} {{1 \over {d_{i} }}} }}.

It is necessary for normalization of all weights:

(9)
\sum\limits_{i \equals \setnum{1}}^{n} {p_{i} \equals 1}.

So, in the traditional method all volumes x i have equal probabilities (weights), whereas in the proposed method all volumes are not equal: those which lie closer have greater weights.

Example: x=(x 1=2; x 2=5; x 3=9), n=3.

Using the traditional method: p i=1/3=const

(10)
\tilde{M}\lpar x\rpar \equals \bar{X} \equals {1 \over 3}\lpar 2 \plus 5 \plus 9\rpar \equals 5{\cdot}33.

Using the new method:

(11)
K \equals {1 \over {{1 \over {58}} \plus {1 \over {25}} \plus {1 \over {65}}}} \equals 13{\cdot}77.

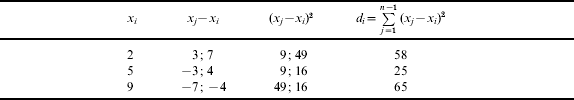
Then we find according to (7):

p_{\setnum{1}} \equals {{13{\cdot}77} \over {58}} \equals 0{\cdot}24\semi \quad p_{\setnum{2}} \equals {{13{\cdot}77} \over {25}} \equals 0{\cdot}55\semi \quad p_{\setnum{3}} \equals {{13{\cdot}77} \over {65}} \equals 0{\cdot}21.

So we calculate using (5), M=0·24×2+0·55×5+0·21×9=5·12.

The volume 5·12 more closely corresponds to given volumes, than does 5·33, since volume x 2=5 is nearer to volume x 1=2 than it is to x 3=9.

In order to estimate the standard σ(x) we propose to use a posteriori σapost(x) and a priori σapr(x) volumes and their weights a(n) and (1−a(n)), consequently:

(12)
\tilde{\sigma }\lpar x\rpar \equals a\lpar n\rpar \sigma ^{apost} \lpar x\rpar \plus \lpar 1 \minus a\lpar n\rpar \rpar \sigma ^{apr} \lpar x\rpar.

Volume of σapost(x) must be calculated using the formula:

(13)
\sigma ^{apost} \lpar x\rpar \equals \sqrt {\sum\limits_{i \equals \setnum{1}}^{n} {p_{i} \lpar x_{i} \minus \tilde{M}\lpar x\rpar \rpar ^{\setnum{2}} } } \comma

where expressions (7) and (5) are used.

Formula (13) is used instead of the well known expression:

(14)
\sigma ^{apost} \lpar x\rpar \equals \sqrt {{{\sum {\lpar x_{i} \minus \bar{X}\rpar ^{\setnum{2}} } } \over {n \minus 1}}}.

Volume of σapr(x) must be chosen from official instructions for accuracy in measuring the main navigation parameters.

As to weights a(n), we propose to calculate them using the formula:

(15)
a\lpar n\rpar \equals 0{\cdot}012 \times n^{\setnum{1}{\cdot}\setnum{893}}.

This gives us: a(3)=0·1 if n=3 and a(9)=0·8 if n=9. These volumes: 0·1 and 0·9 are merely for the sake of discussion, but the method of derivation seems quite useful.

So the obtained estimates &Mtilde;(x) and &sigmatilde;(x) as points then permit us to obtain the estimates &Mtilde;(x) and &sigmatilde;(x) as intervals.

For this it is necessary to use Student's distribution with desired confidential probability γ.

3. ITERATION MODE

Lastly let us mention the iteration mode where the DR ship's position Mc is taken as initial, as seen in Figure 1 [Reference Vulfovich1], [Reference Vulfovich2], [Reference Fogilev4].

Figure 1. Main idea of the iteration method.

Let us put the DR (computed) latitude ϕ=ϕc, the first altitude h 1 and the Body's C1 coordinates (δ1; t Gr1) into the expression “sinh”:

(16)
\sinh \equals \sin \varphi \sin \delta \plus \cos \varphi \cos \delta \cos \lpar t_{Gr} \plus \lambda \rpar

So we obtain the first iteration for the longitude λ1:

(17)
\left. \eqalign{ \cos \lpar t_{Gr\setnum{1}} \plus \lambda _{\setnum{1}} \rpar \equals \tab {{\sinh _{\setnum{1}} \minus \sin \varphi _{c} \sin \delta _{\setnum{1}} } \over {\cos \varphi _{c} \cos \delta _{\setnum{1}} }} \cr \lambda _{\setnum{1}} \equals \tab \lpar t_{Gr\setnum{1}} \plus \lambda _{\setnum{1}} \rpar \minus t_{Gr\setnum{1}} \cr} \right].

In this way we have obtained the first iteration – point M 1(ϕc; λ1).

Then we put in the equation (16) the found longitude λ=λ1, the altitude of the second Body h and its coordinates (δ2; t Gr2). The first iteration for the latitude ϕ=ϕ1 we can find using the algorithm:

(18)
\left. \eqalign{ tgQ \equals \tab ctg\delta _{\setnum{2}} \cos \lpar t_{Gr\setnum{2}} \plus \lambda _{\setnum{1}} \rpar \cr \sin \lpar \varphi _{\setnum{1}} \plus Q\rpar \equals \tab \cos \delta _{\setnum{2}} \sinh _{\setnum{2}} \cos Q \cr \varphi _{\setnum{1}} \equals \tab \lpar \varphi _{\setnum{1}} \plus Q\rpar \minus Q \cr} \right].

As a result we have obtained the second iteration – the ship's position M 2(ϕ1; λ1), Figure 1.

Using by turns the altitudes h 1 and h 2 and the algorithms (17), (18) we will find the following iterations – M 3(ϕ1; λ2); M 4(ϕ2; λ2); M 5(ϕ2; λ3); …; M o(ϕo; λo), Figure 1.

The iteration process will continue up to executing the conditions:

(19)
\left.{\matrix{ {\varphi _{i \plus \setnum{1}} \minus \varphi _{i} \les \varepsilon} \cr {\lambda _{i \plus \setnum{1}} \minus \lambda _{i} \les \varepsilon}\cr} } \right]\comma

Where ε is taken as the criterion for the coordinates' accuracy, the convergence of this process is proved; its algorithms (17, 18, 19) are quite suitable for computer calculation [Reference Vulfovich1], [Reference Vulfovich2].

4. CONCLUSION

The calculations that are required for the reduction of a celestial sight, if performed by hand, are slow and error-prone and discourage the human navigator from taking sights because of the tedious work involved. The traditional procedure imposes several other not-so-obvious limitations on observations. For example, because observations of the Moon and planets require a parallax correction, many navigators avoid these objects, despite the fact that in marginal conditions they may be the only ones visible. Because the Moon is so seldom used, the possibility of Sun-Moon fixes is effectively precluded. All of this argues, if argument is needed, for a computer program to do the calculations. Any reasonably accurate algorithm, implemented in a user-friendly program, would encourage navigators to broaden their observational habits and obtain more sights.

When navigation methods are combined, the objective is to use the strengths of one method to compensate for the weaknesses of another in a way that results in significantly higher accuracy and reliability. As our defence forces rely increasingly on GPS, it is important that this dependence does not become a single-point-failure risk for maritime safety. Independent alternatives to GPS are needed and are required by official policy. Imaginative application of available technology can ensure that celestial navigation has as much of a role to play in the future as it has had in the past in helping to provide safe passage for our seafaring worldwide.

References

REFERENCES

1.Vulfovich, B. (1998). The elements of celestial navigation, Murmansk State Technical University, 156–160.Google Scholar
2.Vulfovich, B. (2007). Fundamental navigation, Murmansk State Technical University, 109–145.Google Scholar
3.Vulfovich, B. (1995). Parameters of the low sets of observations, Hydrographic notes, 232, 20–25.Google Scholar
4.Fogilev, V. (2008). Capabilities of using alternative methods of celestial fix by stars processing at sea, Exploitation of sea transport, 53, 41–44.Google Scholar
5.Kaplan, G. H. (1995). Determining the Position and Motion of a Vessel from Celestial Observations, Navigation, Journal of the Institute of Navigation, 42, 631–648.CrossRefGoogle Scholar
6.Feldman, S., Seidelmann, P. K., Barton, G. G. (1974). Advances in Celestial Navigation, Naval Engineers Journal (August), 65–76.CrossRefGoogle Scholar
Figure 0

Figure 1. Main idea of the iteration method.