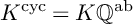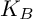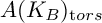1 Introduction
Suppose A is an abelian variety defined over a number field K. The celebrated Mordell–Weil theorem states that for any number field L containing K, the subgroup
![]() $A(L)_{\operatorname {\mathrm {tors}}}$
of torsion points of A defined over L is finite (e.g., [Reference Mumford24, Appendix II]). At the opposite extreme, over the algebraic closure
$A(L)_{\operatorname {\mathrm {tors}}}$
of torsion points of A defined over L is finite (e.g., [Reference Mumford24, Appendix II]). At the opposite extreme, over the algebraic closure
![]() $\overline {K}$
of K, using the geometry of A, one easily sees that the geometric torsion group
$\overline {K}$
of K, using the geometry of A, one easily sees that the geometric torsion group
![]() $A(\overline {K})_{\operatorname {\mathrm {tors}}}$
is infinite. Then it is natural to ask whether the finiteness property of the torsion subgroup
$A(\overline {K})_{\operatorname {\mathrm {tors}}}$
is infinite. Then it is natural to ask whether the finiteness property of the torsion subgroup
![]() $A(L)_{\operatorname {\mathrm {tors}}}$
is still preserved for various infinite algebraic extensions
$A(L)_{\operatorname {\mathrm {tors}}}$
is still preserved for various infinite algebraic extensions
![]() $L/K$
. This kind of question can be traced back at least to [Reference Mazur18], in which Mazur asked whether the group
$L/K$
. This kind of question can be traced back at least to [Reference Mazur18], in which Mazur asked whether the group
![]() $A(K^{\operatorname {\mathrm {cyc}},p})$
, where
$A(K^{\operatorname {\mathrm {cyc}},p})$
, where
![]() $K^{\operatorname {\mathrm {cyc}},p} = K(\cup _n \zeta _{p^n})$
is the field obtained by adjoining all p-power roots of unity to K, is still finitely generated. The torsion part
$K^{\operatorname {\mathrm {cyc}},p} = K(\cup _n \zeta _{p^n})$
is the field obtained by adjoining all p-power roots of unity to K, is still finitely generated. The torsion part
![]() $A(K^{\operatorname {\mathrm {cyc}},p})_{\mathrm{tors}}$
of this group is then proved to be finite by Imai [Reference Imai11] and Serre [Reference Serre34] independently. Their results are then generalized by Ribet in his article [Reference Katz and Lang12, Appendix]. Let
$A(K^{\operatorname {\mathrm {cyc}},p})_{\mathrm{tors}}$
of this group is then proved to be finite by Imai [Reference Imai11] and Serre [Reference Serre34] independently. Their results are then generalized by Ribet in his article [Reference Katz and Lang12, Appendix]. Let
![]() $K^{\textrm {cyc}}:= \cup _p K^{\operatorname {\mathrm {cyc}},p} = K(\cup _{n} \zeta _n)$
be the infinite extension of K obtained by adjoining all roots of unity. Then Ribet showed that for every abelian variety A defined over the number field K, one has
$K^{\textrm {cyc}}:= \cup _p K^{\operatorname {\mathrm {cyc}},p} = K(\cup _{n} \zeta _n)$
be the infinite extension of K obtained by adjoining all roots of unity. Then Ribet showed that for every abelian variety A defined over the number field K, one has
Zarhin then further generalized this result [Reference Zarhin46] by showing that if A is a simple abelian variety over its ground field K, then over the maximal abelian extension
![]() $K^{\textrm ab}$
of K, the torsion group
$K^{\textrm ab}$
of K, the torsion group
![]() $A(K^{\textrm ab})_{\mathrm{tors}}$
is finite if and only if A is not of CM type over K, that is, if and only if the K-endomorphism algebra
$A(K^{\textrm ab})_{\mathrm{tors}}$
is finite if and only if A is not of CM type over K, that is, if and only if the K-endomorphism algebra ![]() is not a number field of degree
is not a number field of degree
![]() $2\dim A$
. As a cohomological generalization of Ribet’s result, Rössler and Szamuely [Reference Rössler and Szamuely33] proved that for any projective, smooth, and geometrically connected variety X over a number field K, the groups
$2\dim A$
. As a cohomological generalization of Ribet’s result, Rössler and Szamuely [Reference Rössler and Szamuely33] proved that for any projective, smooth, and geometrically connected variety X over a number field K, the groups ![]() are finite for all odd positive integers i and all integers j. In contrast, when K is a p-adic field, then the analog of Imai and Serre’s result is generalized by Ozeki in [Reference Ozeki27]. In addition, an analog of Zarhin’s result is proved for Drinfeld modules by Li [Reference Li15]. Quite recently, Lombardo studied a problem which, while perhaps superficially different, turns out to be closely related [Reference Lombardo17]; we discuss his work at the end of this introduction.
are finite for all odd positive integers i and all integers j. In contrast, when K is a p-adic field, then the analog of Imai and Serre’s result is generalized by Ozeki in [Reference Ozeki27]. In addition, an analog of Zarhin’s result is proved for Drinfeld modules by Li [Reference Li15]. Quite recently, Lombardo studied a problem which, while perhaps superficially different, turns out to be closely related [Reference Lombardo17]; we discuss his work at the end of this introduction.
In this article, we focus on the generalization of (1.1) in another direction. Notice that by the Kronecker–Weber theorem, the cyclotomic extension
![]() $K^{\operatorname {\mathrm {cyc}}} =K({\mathbb G}_{m, \mathrm {tors}})$
is exactly the extension of K obtained by adjoining all the geometric torsion points of the algebraic torus
$K^{\operatorname {\mathrm {cyc}}} =K({\mathbb G}_{m, \mathrm {tors}})$
is exactly the extension of K obtained by adjoining all the geometric torsion points of the algebraic torus
![]() $\mathbb G_{m}$
. Due to the fact that there is no nontrivial isogeny, or even nonconstant geometric morphism, between
$\mathbb G_{m}$
. Due to the fact that there is no nontrivial isogeny, or even nonconstant geometric morphism, between
![]() $\mathbb G_m$
and an abelian variety, one is naturally led to ask the following question.
$\mathbb G_m$
and an abelian variety, one is naturally led to ask the following question.
Question 1.1. Suppose two abelian varieties A and B are defined over a number field K; assume that over
![]() ${\overline {K}}$
they share no common nontrivial isogeny factor. Let
${\overline {K}}$
they share no common nontrivial isogeny factor. Let
![]() $K_{B}$
denote the infinite extension of K obtained by adjoining the coordinates of all the geometric torsion points of B. Is the torsion group of A over
$K_{B}$
denote the infinite extension of K obtained by adjoining the coordinates of all the geometric torsion points of B. Is the torsion group of A over
![]() $K_B$
finite, that is, is
$K_B$
finite, that is, is
We answer this question in the present article, up to a finite extension of the base field and under the Mumford–Tate conjecture. We state our results after introducing a few definitions.
Definition 1.2. Given two abelian varieties A and B defined over a number field K, we say that A is torsion finite for B over K if
![]() $A(K_B)_{\operatorname {\mathrm {tors}}}$
is finite. Otherwise, we say that A is torsion infinite for B over K.
$A(K_B)_{\operatorname {\mathrm {tors}}}$
is finite. Otherwise, we say that A is torsion infinite for B over K.
Moreover, if there is a finite extension
![]() $L/K$
such that
$L/K$
such that
![]() $A(L_B)_{\operatorname {\mathrm {tors}}}$
is infinite, we say A is potentially torsion infinite for B. If such L does not exist, we will say that A is essentially torsion finite for B.
$A(L_B)_{\operatorname {\mathrm {tors}}}$
is infinite, we say A is potentially torsion infinite for B. If such L does not exist, we will say that A is essentially torsion finite for B.
Although not stated in this language, Serre gave a positive answer to Question 1.1 in [Reference Serre35, théoremè 6 and 7] when A and B are both elliptic curves which are not geometrically isogenous. In fact, Serre proved that for such A and B, the image of the adelic representation induced by
![]() $A\times B$
equals the product of the images induced by A and B, up to a finite index; the claim readily follows. Our strategy is inspired by Serre’s work. However, one of the advantages of working with elliptic curves, as opposed to higher-dimensional abelian varieties, is the open image theorem [Reference Serre34, Reference Serre35]. This theorem, together with its analog for CM elliptic curves [Reference Serre and Tate39], classifies the
$A\times B$
equals the product of the images induced by A and B, up to a finite index; the claim readily follows. Our strategy is inspired by Serre’s work. However, one of the advantages of working with elliptic curves, as opposed to higher-dimensional abelian varieties, is the open image theorem [Reference Serre34, Reference Serre35]. This theorem, together with its analog for CM elliptic curves [Reference Serre and Tate39], classifies the
![]() $\ell $
-adic representation images of elliptic curves in terms of
$\ell $
-adic representation images of elliptic curves in terms of
![]() ${\mathbb {Q}}$
-algebraic groups. With the help of these algebraic groups, the answer to Question 1.1 is essentially (but nontrivially) a consequence of Goursat’s lemma.
${\mathbb {Q}}$
-algebraic groups. With the help of these algebraic groups, the answer to Question 1.1 is essentially (but nontrivially) a consequence of Goursat’s lemma.
The open image theorem for higher-dimensional abelian varieties is not known in general—indeed, it cannot hold for an abelian variety which is not Hodge maximal. Nonetheless, the Mumford–Tate conjecture claims that, for an abelian variety A over a sufficiently large number field, its
![]() $\ell $
-adic Galois representation images are still classified by a
$\ell $
-adic Galois representation images are still classified by a
![]() ${\mathbb {Q}}$
-algebraic group, the Mumford–Tate group
${\mathbb {Q}}$
-algebraic group, the Mumford–Tate group
![]() $\operatorname {\mathrm {MT}}(A)$
, which is defined in terms of the Hodge structure
$\operatorname {\mathrm {MT}}(A)$
, which is defined in terms of the Hodge structure
![]() $H_1(A(\mathbb C), {\mathbb {Q}})$
. (For a quick review of the Mumford–Tate group and the related conjecture, see §3.2. For an abelian variety A defined over a subfield
$H_1(A(\mathbb C), {\mathbb {Q}})$
. (For a quick review of the Mumford–Tate group and the related conjecture, see §3.2. For an abelian variety A defined over a subfield
![]() $K\subset {\mathbb {C}}$
, we will often abuse notation and write
$K\subset {\mathbb {C}}$
, we will often abuse notation and write
![]() $H_1(A,{\mathbb {Q}})$
for the homology group
$H_1(A,{\mathbb {Q}})$
for the homology group
![]() $H_1((A\times _{\operatorname {\mathrm {Spec}} K} \operatorname {\mathrm {Spec}} {\mathbb {C}})({\mathbb {C}})^{\mathrm {an}},{\mathbb {Q}})$
, endowed with its Hodge structure, and define
$H_1((A\times _{\operatorname {\mathrm {Spec}} K} \operatorname {\mathrm {Spec}} {\mathbb {C}})({\mathbb {C}})^{\mathrm {an}},{\mathbb {Q}})$
, endowed with its Hodge structure, and define
![]() $H^1(A,{\mathbb {Q}})$
in an analogous fashion.)
$H^1(A,{\mathbb {Q}})$
in an analogous fashion.)
In this article, assuming the Mumford–Tate conjecture, using Galois theory, and generalizing Serre’s idea to algebraic groups beyond
![]() $\operatorname {\mathrm {GL}}_2$
, we are able to prove a criterion for the essential torsion finiteness of pairs of abelian varieties.
$\operatorname {\mathrm {GL}}_2$
, we are able to prove a criterion for the essential torsion finiteness of pairs of abelian varieties.
Theorem 1.3 (See Theorem 4.10 for a more detailed version).
Suppose A and B are two absolutely simple abelian varieties defined over a number field K, and suppose that the Mumford–Tate conjecture holds for A and B.
Then A is potentially torsion infinite for B if and only if
When this holds, for each prime
![]() $\ell $
, there exists a finite extension
$\ell $
, there exists a finite extension
![]() $L_\ell /K$
such that
$L_\ell /K$
such that
Insofar as (the image of) the action of Galois on torsion points is constrained by the Mumford–Tate group, it is not surprising that a relation on Mumford–Tate groups can force a resonance among torsion fields. What is perhaps more interesting is that just the presence of infinite torsion—for example, if
![]() $A[\ell ](K_B)$
is nontrivial for an infinite, but sparse, set of primes—is enough to constrain the relation between
$A[\ell ](K_B)$
is nontrivial for an infinite, but sparse, set of primes—is enough to constrain the relation between
![]() $\operatorname {\mathrm {MT}}(A\times B)$
and
$\operatorname {\mathrm {MT}}(A\times B)$
and
![]() $\operatorname {\mathrm {MT}}(B)$
. In particular, we will see that the existence of
$\operatorname {\mathrm {MT}}(B)$
. In particular, we will see that the existence of
![]() $\ell $
-torsion for infinitely many
$\ell $
-torsion for infinitely many
![]() $\ell $
forces the presence of
$\ell $
forces the presence of
![]() $\ell $
-torsion for
$\ell $
-torsion for
![]() $\ell $
in a set of positive density.
$\ell $
in a set of positive density.
The Mumford–Tate group
![]() $\operatorname {\mathrm {MT}}(A)$
is canonically an extension of
$\operatorname {\mathrm {MT}}(A)$
is canonically an extension of
![]() $\mathbb G_m$
by the Hodge group, or special Mumford–Tate group,
$\mathbb G_m$
by the Hodge group, or special Mumford–Tate group,
![]() $\operatorname {\mathrm {sMT}}(A)$
. Ichikawa [Reference Ichikawa10] and Lombardo [Reference Lombardo16] have investigated conditions under which
$\operatorname {\mathrm {sMT}}(A)$
. Ichikawa [Reference Ichikawa10] and Lombardo [Reference Lombardo16] have investigated conditions under which
(For example, this holds if A and B satisfy a certain odd relative dimension condition and at least one is not of Type IV in the Albert classification.) When A and B satisfy (1.3), we have
Theorem 1.3 then immediately implies that A and B are mutually essentially torsion finite. (See the last part of §4.4 for more details.)
Taken together with our main theorem, Ichikawa and Lombardo’s results often imply a positive answer to our main question 1.1, except when both A and B are of Type IV. Thus, Question 1.1 is particularly interesting when both A and B are of Type IV, such as when both A and B have complex multiplication (CM) over
![]() ${\overline {K}}$
.
${\overline {K}}$
.
In fact, there do exist examples where Question 1.1 has a negative answer. For instance, the Jacobian of a certain genus
![]() $4$
curve [Reference Shioda40, Exam. 6.1] decomposes into a product of a potentially CM elliptic curve and a simple potentially CM abelian threefold. However, one can check that the elliptic curve is torsion infinite for the threefold (see [Reference Lombardo17, Th. 1.2]). In addition, Lombardo [Reference Lombardo17] constructed infinitely many pairs of nonisogenous CM abelian varieties for which the answer to Question 1.1 is again negative. As a complement to Lombardo’s work, we give a sufficient and necessary condition for answering our main question for CM pairs, as follows.
$4$
curve [Reference Shioda40, Exam. 6.1] decomposes into a product of a potentially CM elliptic curve and a simple potentially CM abelian threefold. However, one can check that the elliptic curve is torsion infinite for the threefold (see [Reference Lombardo17, Th. 1.2]). In addition, Lombardo [Reference Lombardo17] constructed infinitely many pairs of nonisogenous CM abelian varieties for which the answer to Question 1.1 is again negative. As a complement to Lombardo’s work, we give a sufficient and necessary condition for answering our main question for CM pairs, as follows.
Let A be an isotypic abelian variety over a number field K with CM by a CM field E, and suppose that K contains E. (Recall that an abelian variety is said to be isotypic if it is isogenous to some power of a simple abelian variety.) We see in §5.1 that there is a surjection of algebraic tori
which induces an inclusion of character groups
In fact,
![]() $\operatorname {\mathrm {MT}}(A)$
only depends on the CM type of A. With this reminder, we can state a version of our main theorem for abelian varieties with complex multiplication. For a torus T, let
$\operatorname {\mathrm {MT}}(A)$
only depends on the CM type of A. With this reminder, we can state a version of our main theorem for abelian varieties with complex multiplication. For a torus T, let
![]() $X^*(T)_{\mathbb {Q}} = X^*(T)\otimes {\mathbb {Q}}$
.
$X^*(T)_{\mathbb {Q}} = X^*(T)\otimes {\mathbb {Q}}$
.
Theorem 1.4 (See Theorem 5.4 for a more detailed version).
Let
![]() $A_1$
and
$A_1$
and
![]() $A_2$
be isotypic potentially CM abelian varieties over a sufficiently large number field K, with respective Mumford–Tate groups
$A_2$
be isotypic potentially CM abelian varieties over a sufficiently large number field K, with respective Mumford–Tate groups
![]() $T_1$
and
$T_1$
and
![]() $T_2$
. Using the inclusions
$T_2$
. Using the inclusions
![]() $X^*(T_i) \hookrightarrow X^*(T^K)$
, either:
$X^*(T_i) \hookrightarrow X^*(T^K)$
, either:
-
(a)
 $X^*(T_1)_{\mathbb {Q}} \subset X^*(T_2)_{\mathbb {Q}}$
. Then
$X^*(T_1)_{\mathbb {Q}} \subset X^*(T_2)_{\mathbb {Q}}$
. Then
 $A_1$
is potentially torsion infinite for
$A_1$
is potentially torsion infinite for
 $A_2$
.
$A_2$
.Moreover, if
 $X^*(T_1) \subset X^*(T_2)$
and if
$X^*(T_1) \subset X^*(T_2)$
and if
 $A_1$
is simple with nondegenerate CM (5.1.3), then
$A_1$
is simple with nondegenerate CM (5.1.3), then
 $A_1(K_{A_2})_{\operatorname {\mathrm {tors}}} = A_1({\overline {K}})_{\operatorname {\mathrm {tors}}}$
.
$A_1(K_{A_2})_{\operatorname {\mathrm {tors}}} = A_1({\overline {K}})_{\operatorname {\mathrm {tors}}}$
. -
(b)
 $X^*(T_1)_{\mathbb {Q}} \not \subset X^*(T_2)_{\mathbb {Q}}$
. Then
$X^*(T_1)_{\mathbb {Q}} \not \subset X^*(T_2)_{\mathbb {Q}}$
. Then
 $A_1$
is essentially torsion finite for
$A_1$
is essentially torsion finite for
 $A_2$
.
$A_2$
.
Theorem 1.4 is unconditional because the Mumford–Tate conjecture is known for CM abelian varieties (see Lemma 5.1).
We briefly compare this result to Zarhin’s work [Reference Zarhin46]. Suppose B has complex multiplication over K, but A does not even have potential complex multiplication. Note that
![]() $K_B$
is an abelian extension of K. Zarhin’s result implies that
$K_B$
is an abelian extension of K. Zarhin’s result implies that
![]() $A(K^{\operatorname {ab}})_{\operatorname {\mathrm {tors}}}$
is finite; a fortiori, A is essentially torsion finite for B. However, if A is also of CM type, then Theorem 1.4 gives finer information on whether A is essentially torsion finite for B.
$A(K^{\operatorname {ab}})_{\operatorname {\mathrm {tors}}}$
is finite; a fortiori, A is essentially torsion finite for B. However, if A is also of CM type, then Theorem 1.4 gives finer information on whether A is essentially torsion finite for B.
A morphism
![]() $A \to B$
induces a map of homology groups
$A \to B$
induces a map of homology groups
![]() $H_1(A,{\mathbb {Q}}) \to H_1(B,{\mathbb {Q}})$
, and thus a morphism of Tannakian categories
$H_1(A,{\mathbb {Q}}) \to H_1(B,{\mathbb {Q}})$
, and thus a morphism of Tannakian categories
![]() ${\langle {H_1(A,{\mathbb {Q}})} \rangle } \to {\langle {H_1(B,{\mathbb {Q}})} \rangle }$
and ultimately of Mumford–Tate groups
${\langle {H_1(A,{\mathbb {Q}})} \rangle } \to {\langle {H_1(B,{\mathbb {Q}})} \rangle }$
and ultimately of Mumford–Tate groups
![]() $\operatorname {\mathrm {MT}}(B) \to \operatorname {\mathrm {MT}}(A)$
. More generally, a correspondence between
$\operatorname {\mathrm {MT}}(B) \to \operatorname {\mathrm {MT}}(A)$
. More generally, a correspondence between
![]() $A^m$
and
$A^m$
and
![]() $B^n$
induces a relation between
$B^n$
induces a relation between
![]() $\operatorname {\mathrm {MT}}(A)$
and
$\operatorname {\mathrm {MT}}(A)$
and
![]() $\operatorname {\mathrm {MT}}(B)$
; and the class of such a correspondence is a Hodge class on
$\operatorname {\mathrm {MT}}(B)$
; and the class of such a correspondence is a Hodge class on
![]() $A^m \times B^n$
.
$A^m \times B^n$
.
In §5.2, we will see that if the CM abelian variety A is torsion infinite for the CM abelian variety B, then there is a nonempty
![]() ${\mathbb {Q}}$
-vector space of interesting Hodge classes on some product
${\mathbb {Q}}$
-vector space of interesting Hodge classes on some product
![]() $A^m \times B^n$
; perhaps not surprisingly, we call such a class a torsion infinite class. These Hodge classes are extra, in the sense that they are not in the span of classes pulled back from
$A^m \times B^n$
; perhaps not surprisingly, we call such a class a torsion infinite class. These Hodge classes are extra, in the sense that they are not in the span of classes pulled back from
![]() $A^m$
and
$A^m$
and
![]() $B^n$
. Conversely, we show that the presence of such a class implies that A is torsion infinite for B.
$B^n$
. Conversely, we show that the presence of such a class implies that A is torsion infinite for B.
Of course, the Hodge conjecture predicts that torsion infinite classes are actually the classes of cycles on
![]() $A^m \times B^n$
. It would be interesting to see, even in special cases, if one can geometrically realize torsion infinite classes.
$A^m \times B^n$
. It would be interesting to see, even in special cases, if one can geometrically realize torsion infinite classes.
In addition to the above applications, thanks to the work of Moonen and Zarhin on the Hodge groups of abelian varieties of low dimension [Reference Moonen and Zarhin23], one can compare the Mumford–Tate groups of every possible pair of absolutely simple abelian varieties up to dimension
![]() $3$
. As a consequence, we give a positive answer to Question 1.1 for most pairs of such abelian varieties. Precisely, following the classification in their article, we prove the following theorem.
$3$
. As a consequence, we give a positive answer to Question 1.1 for most pairs of such abelian varieties. Precisely, following the classification in their article, we prove the following theorem.
Theorem 1.5 (Also Theorem 5.14).
Suppose A and B are absolutely simple abelian varieties over a common number field, and assume that they are nonisogenous over
![]() $\mathbb C$
. Suppose that
$\mathbb C$
. Suppose that
![]() $\dim A \le \dim B \le 3$
. Then A and B are mutually essentially torsion finite except for the following cases:
$\dim A \le \dim B \le 3$
. Then A and B are mutually essentially torsion finite except for the following cases:
-
(a) A is a CM elliptic curve, and B is a CM abelian threefold. Then B is essentially torsion finite for A, and A is potentially torsion infinite for B exactly when there is an embedding of
 ${\mathbb {Q}}$
-algebras
${\mathbb {Q}}$
-algebras  .
. -
(b) A is a CM elliptic curve, and B is an abelian threefold of type IV but not CM. Then B is essentially torsion finite for A, and A is potentially torsion infinite for B exactly when there is an isomorphism of
 ${\mathbb {Q}}$
-algebras
${\mathbb {Q}}$
-algebras  .
. -
(c) A and B are both CM abelian threefolds.
(In (c), the essential torsion finiteness depends on the CM types of A and B as in Theorem 5.4.)
Again, this result is unconditional since the Mumford–Tate conjecture is known to hold for simple abelian varieties of dimensions less than
![]() $4$
[Reference Moonen and Zarhin23].
$4$
[Reference Moonen and Zarhin23].
This article is structured as follows: in §2, we collect some basic results on representations of algebraic groups. In particular, we introduce the notion of a collection of subgroups of bounded index (of the
![]() ${\mathbb {F}}_\ell $
-points of a group scheme over
${\mathbb {F}}_\ell $
-points of a group scheme over
![]() ${\mathbb {Z}}[1/N]$
); this allows us to infer information about a representation of an algebraic group from data about the behavior of abstract subgroups of its finite-field-valued points. In §3, we establish notation and review facts (and conjectures) concerning the Galois representations attached to abelian varieties. We finally turn to the torsion-finiteness question itself in §4.1, establishing our main result (Theorem 1.3) in §4.4. The article concludes with a detailed analysis of CM (§5.1) and low-dimensional (§5.3) pairs of abelian varieties, and of certain extra Hodge classes which are the hallmark of torsion-infinite pairs of CM abelian varieties (§5.2).
${\mathbb {Z}}[1/N]$
); this allows us to infer information about a representation of an algebraic group from data about the behavior of abstract subgroups of its finite-field-valued points. In §3, we establish notation and review facts (and conjectures) concerning the Galois representations attached to abelian varieties. We finally turn to the torsion-finiteness question itself in §4.1, establishing our main result (Theorem 1.3) in §4.4. The article concludes with a detailed analysis of CM (§5.1) and low-dimensional (§5.3) pairs of abelian varieties, and of certain extra Hodge classes which are the hallmark of torsion-infinite pairs of CM abelian varieties (§5.2).
It turns out that while we were working out these results, Lombardo studied a similar problem with somewhat stronger restrictions [Reference Lombardo17]. Two abelian varieties A and B over a number field K are said to be strongly iso-Kummerian if for each positive integer d we have
that is, if the d-torsion points of A and B generate the same extension of K. Using the theory of the (special) Mumford–Tate group and assuming the Mumford–Tate conjecture, Lombardo proves that condition (1.4) puts a strong restriction on the Hodge groups of A, B and
![]() $A\times B$
. This constraint forces A to have the same isogeny factors as B when either
$A\times B$
. This constraint forces A to have the same isogeny factors as B when either
![]() $\dim A\leq 3$
and
$\dim A\leq 3$
and
![]() $\dim B\leq 3$
[Reference Lombardo17, Th. 1.2]; or every simple factor of A or B has dimension
$\dim B\leq 3$
[Reference Lombardo17, Th. 1.2]; or every simple factor of A or B has dimension
![]() $\leq 2$
, or is of odd relative dimension and not of type IV [Reference Lombardo17, Th. 1.4]. As a complement, by studying certain simple CM types on cyclic CM fields, Lombardo also constructs infinitely many nonisogenous iso-Kummerian pairs [Reference Lombardo17, Th. 1.1]. In spite of the obvious similarities, our work is differs from Lombardo’s in its emphasis and results.
$\leq 2$
, or is of odd relative dimension and not of type IV [Reference Lombardo17, Th. 1.4]. As a complement, by studying certain simple CM types on cyclic CM fields, Lombardo also constructs infinitely many nonisogenous iso-Kummerian pairs [Reference Lombardo17, Th. 1.1]. In spite of the obvious similarities, our work is differs from Lombardo’s in its emphasis and results.
-
1. Condition (1.4) is much stronger than our (potentially) torsion-infinite condition. In fact, (1.4) forces
 $K_A=K_B$
, so
$K_A=K_B$
, so
 $K_AK_B/K_B$
is a trivial extension. However, even if A is torsion-infinite for B,
$K_AK_B/K_B$
is a trivial extension. However, even if A is torsion-infinite for B,
 $K_AK_B/K_B$
can still be infinite (Example 5.7).
$K_AK_B/K_B$
can still be infinite (Example 5.7). -
2. In assumption (1.4), by taking
 $d=\ell ^n$
and letting
$d=\ell ^n$
and letting
 $n\to \infty $
, one can directly deduce
$n\to \infty $
, one can directly deduce
 $A[\ell ^{\infty }](K_{B,\ell ^{\infty }})=A_{\ell ^{\infty }}$
. However, if one only assumes that A is torsion-infinite for B, it is possible that the subgroup
$A[\ell ^{\infty }](K_{B,\ell ^{\infty }})=A_{\ell ^{\infty }}$
. However, if one only assumes that A is torsion-infinite for B, it is possible that the subgroup
 $A[\ell ^{\infty }](K_{B,\ell ^{\infty }})$
is finite for every
$A[\ell ^{\infty }](K_{B,\ell ^{\infty }})$
is finite for every
 $\ell $
, but nontrivial for infinitely many
$\ell $
, but nontrivial for infinitely many
 $\ell $
. One of our main contributions in this article is to rule out this possibility (under the Mumford–Tate conjecture, as usual).
$\ell $
. One of our main contributions in this article is to rule out this possibility (under the Mumford–Tate conjecture, as usual). -
3. Lombardo shows that if A and B are strongly iso-Kummerian, then the natural projections
 $\operatorname {\mathrm {MT}}(A\times B)\to \operatorname {\mathrm {MT}}(A)$
and
$\operatorname {\mathrm {MT}}(A\times B)\to \operatorname {\mathrm {MT}}(A)$
and
 $\operatorname {\mathrm {MT}}(A\times B) \to \operatorname {\mathrm {MT}}(B)$
are isogenies [Reference Lombardo17, Lem. 3.2]. We are able to deduce this conclusion from the weaker hypothesis that A and B are mutually potentially torsion infinite (Corollary 4.14).
$\operatorname {\mathrm {MT}}(A\times B) \to \operatorname {\mathrm {MT}}(B)$
are isogenies [Reference Lombardo17, Lem. 3.2]. We are able to deduce this conclusion from the weaker hypothesis that A and B are mutually potentially torsion infinite (Corollary 4.14).
2 Preliminaries
2.1 Reminders on algebraic groups
We collect some standard, useful facts on algebraic groups.
Lemma 2.1 (Goursat’s lemma).
Let
![]() $G_1$
,
$G_1$
,
![]() $G_2$
, and
$G_2$
, and
![]() $G_{12}$
be either abstract groups or algebraic groups over a field. Suppose
$G_{12}$
be either abstract groups or algebraic groups over a field. Suppose
![]() $G_{12}$
is endowed with an inclusion
$G_{12}$
is endowed with an inclusion
![]() $\iota \colon G_{12}\hookrightarrow G_1\times G_2$
such that
$\iota \colon G_{12}\hookrightarrow G_1\times G_2$
such that
![]() $\pi _i \circ \iota $
is surjective for
$\pi _i \circ \iota $
is surjective for
![]() $i=1,2$
:
$i=1,2$
:

Let
![]() $M_{12} = \ker (\pi _2\circ \iota )$
, and let
$M_{12} = \ker (\pi _2\circ \iota )$
, and let
![]() $H_{12} \cong M_{12}$
be the image of
$H_{12} \cong M_{12}$
be the image of
![]() $M_{12}$
under the isomorphism
$M_{12}$
under the isomorphism
![]() $G_1 \times {\left \{ e\right \}} \cong G_1 $
; define
$G_1 \times {\left \{ e\right \}} \cong G_1 $
; define
![]() $M_{21}$
and
$M_{21}$
and
![]() $H_{21}$
analogously.
$H_{21}$
analogously.
Then, under the composite map
![]() $G_{12}$
is the inverse image in
$G_{12}$
is the inverse image in
![]() $G_1 \times G_2$
of the graph of an isomorphism
$G_1 \times G_2$
of the graph of an isomorphism
![]() $\frac {G_1}{H_{12}} \to \frac {G_2}{H_{21}}$
.
$\frac {G_1}{H_{12}} \to \frac {G_2}{H_{21}}$
.
Proof. This is standard (see, e.g., [Reference Ribet31, Lem. 5.2.1] for the case of abstract groups). The constructions of
![]() $H_{ij}$
and
$H_{ij}$
and
![]() $M_{ij}$
also make sense in the category of algebraic groups, and the asserted properties may be verified pointwise, as in [Reference Ribet31].
$M_{ij}$
also make sense in the category of algebraic groups, and the asserted properties may be verified pointwise, as in [Reference Ribet31].
Remark 2.2. Under the hypotheses of Lemma 2.1, suppose
![]() $H_{12} = G_{1}$
. Then, clearly,
$H_{12} = G_{1}$
. Then, clearly,
![]() $H_{21} = G_2$
, and thus
$H_{21} = G_2$
, and thus
![]() $G_{12} \cong G_1 \times G_2$
. At the opposite extreme, if
$G_{12} \cong G_1 \times G_2$
. At the opposite extreme, if
![]() $H_{12}$
and
$H_{12}$
and
![]() $H_{21}$
are trivial, then, up to a choice of isomorphism
$H_{21}$
are trivial, then, up to a choice of isomorphism
![]() $G_1 \cong G_2$
,
$G_1 \cong G_2$
,
![]() $\iota : G_{12}\hookrightarrow G_1\times G_2$
is the diagonal embedding.
$\iota : G_{12}\hookrightarrow G_1\times G_2$
is the diagonal embedding.
Lemma 2.3. Assume
![]() $G_1$
,
$G_1$
,
![]() $G_2$
, and
$G_2$
, and
![]() $G_{12}$
are reductive groups over a field K of characteristic zero and satisfy a diagram (2.1). Then the following are equivalent:
$G_{12}$
are reductive groups over a field K of characteristic zero and satisfy a diagram (2.1). Then the following are equivalent:
-
(a)
 $\dim G_{12}=\dim G_2$
;
$\dim G_{12}=\dim G_2$
; -
(b)
 $\operatorname {\mathrm {rank}} G_{12}=\operatorname {\mathrm {rank}} G_2$
; and
$\operatorname {\mathrm {rank}} G_{12}=\operatorname {\mathrm {rank}} G_2$
; and -
(c) the surjection
 $G_{12} \twoheadrightarrow G_2$
is an isogeny.
$G_{12} \twoheadrightarrow G_2$
is an isogeny.
Proof. The short exact sequence of algebraic groups
induces a corresponding exact sequence on Lie algebras. Since K has characteristic zero, the rank and dimension of a reductive group can be read off from its Lie algebra. Note that
![]() $\operatorname {Lie}(M_{12}) = \operatorname {Lie}(M_{12}^\circ )$
and that
$\operatorname {Lie}(M_{12}) = \operatorname {Lie}(M_{12}^\circ )$
and that
![]() $M_{12}^\circ $
, being a connected normal (Lemma 2.4) subgroup of a reductive group, is also reductive (e.g., [Reference Milne19, Cor. 21.53]). In particular, either (a) or (b) holds if and only if
$M_{12}^\circ $
, being a connected normal (Lemma 2.4) subgroup of a reductive group, is also reductive (e.g., [Reference Milne19, Cor. 21.53]). In particular, either (a) or (b) holds if and only if
![]() $\operatorname {Lie}(M_{12})= (0)$
, that is,
$\operatorname {Lie}(M_{12})= (0)$
, that is,
![]() $\dim M_{12}=0$
and thus
$\dim M_{12}=0$
and thus
![]() $\pi _2\circ \iota $
is an isogeny.
$\pi _2\circ \iota $
is an isogeny.
Lemma 2.4. Let G be a connected algebraic group, and let
![]() $M\subset G$
be a normal algebraic subgroup. Then
$M\subset G$
be a normal algebraic subgroup. Then
![]() $M^\circ $
is normal in G.
$M^\circ $
is normal in G.
Proof. Since G and
![]() $M^\circ $
are connected, the image of
$M^\circ $
are connected, the image of
![]() $M^\circ $
under conjugation by G is connected and contains the identity element of G. Since this image is a subgroup of M, which is normal in G, it is contained in
$M^\circ $
under conjugation by G is connected and contains the identity element of G. Since this image is a subgroup of M, which is normal in G, it is contained in
![]() $M^\circ $
, and thus
$M^\circ $
, and thus
![]() $M^\circ $
is stable under conjugation by G.
$M^\circ $
is stable under conjugation by G.
Finally, when studying CM abelian varieties in §5, we will need to work with algebraic tori.
Let K be a perfect field. An algebraic torus
![]() $T/K$
is an algebraic group such that
$T/K$
is an algebraic group such that
![]() $T_{{\overline {K}}} \cong \mathbb G_{m,{\overline {K}}}^{\oplus \dim T}$
. Let
$T_{{\overline {K}}} \cong \mathbb G_{m,{\overline {K}}}^{\oplus \dim T}$
. Let
![]() $X^*(T)$
be the (absolute) character group
$X^*(T)$
be the (absolute) character group ![]() , and let
, and let
![]() $X^*(T)_{\mathbb {Q}} = X^*(T)\otimes {\mathbb {Q}}$
; then
$X^*(T)_{\mathbb {Q}} = X^*(T)\otimes {\mathbb {Q}}$
; then
![]() $T\mapsto X^*(T)$
gives a contravariant equivalence between the category of algebraic tori over K and the category of finite free
$T\mapsto X^*(T)$
gives a contravariant equivalence between the category of algebraic tori over K and the category of finite free
![]() ${\mathbb {Z}}$
-modules with a continuous action by the absolute Galois group
${\mathbb {Z}}$
-modules with a continuous action by the absolute Galois group
![]() $\operatorname {\mathrm {Gal}}(K) := \operatorname {\mathrm {Gal}}({\overline {K}}/K)$
. This extends to a contravariant equivalence between the category of K-groups of multiplicative type and the category of finitely generated
$\operatorname {\mathrm {Gal}}(K) := \operatorname {\mathrm {Gal}}({\overline {K}}/K)$
. This extends to a contravariant equivalence between the category of K-groups of multiplicative type and the category of finitely generated
![]() ${\mathbb {Z}}$
-modules with continuous
${\mathbb {Z}}$
-modules with continuous
![]() $\operatorname {\mathrm {Gal}}(K)$
action. We have
$\operatorname {\mathrm {Gal}}(K)$
action. We have
![]() $\dim T = \operatorname {\mathrm {rank}}_{{\mathbb {Z}}}X^*(T) = \dim _{{\mathbb {Q}}} X^*(T)_{\mathbb {Q}}$
. If
$\dim T = \operatorname {\mathrm {rank}}_{{\mathbb {Z}}}X^*(T) = \dim _{{\mathbb {Q}}} X^*(T)_{\mathbb {Q}}$
. If
![]() $\alpha \colon S \to T$
is a morphism of algebraic tori, then
$\alpha \colon S \to T$
is a morphism of algebraic tori, then
![]() $\dim \ker (\alpha ) = \dim _{\mathbb {Q}} X^*(T)_{\mathbb {Q}}/ \alpha ^*X^*(S)_{\mathbb {Q}}$
, and
$\dim \ker (\alpha ) = \dim _{\mathbb {Q}} X^*(T)_{\mathbb {Q}}/ \alpha ^*X^*(S)_{\mathbb {Q}}$
, and
![]() $\alpha $
has connected kernel if and only if
$\alpha $
has connected kernel if and only if
![]() $X^*(T)/\alpha ^*X^*(S)$
is torsion-free.
$X^*(T)/\alpha ^*X^*(S)$
is torsion-free.
If
![]() $F/{\mathbb {Q}}$
is a finite extension, we let
$F/{\mathbb {Q}}$
is a finite extension, we let
![]() $T^F$
denote
$T^F$
denote
![]() $\operatorname {Res}_{F/{\mathbb {Q}}}{\mathbb {G}}_{m,F}$
, the Weil restriction of the multiplicative group, and let
$\operatorname {Res}_{F/{\mathbb {Q}}}{\mathbb {G}}_{m,F}$
, the Weil restriction of the multiplicative group, and let
![]() $T^{F,1}$
denote the norm one torus
$T^{F,1}$
denote the norm one torus
![]() $\operatorname {Res}_{F/{\mathbb {Q}}}^{(1)}{\mathbb {G}}_{m,F}$
, which is the kernel of the norm map
$\operatorname {Res}_{F/{\mathbb {Q}}}^{(1)}{\mathbb {G}}_{m,F}$
, which is the kernel of the norm map
![]() $\operatorname {N}_{F/{\mathbb {Q}}}\colon T^F \to {\mathbb {G}}_m$
.
$\operatorname {N}_{F/{\mathbb {Q}}}\colon T^F \to {\mathbb {G}}_m$
.
2.2 Representations of algebraic groups
2.2.1 Fixed spaces
Let
![]() $G/K$
be an algebraic group over a field. Let
$G/K$
be an algebraic group over a field. Let
![]() $V/K$
be a finite-dimensional representation of G, that is, a finite-dimensional vector space V equipped with a morphism
$V/K$
be a finite-dimensional representation of G, that is, a finite-dimensional vector space V equipped with a morphism
![]() $G \to \operatorname {\mathrm {GL}}_V$
of algebraic groups. The schematic fixed space of V under G is
$G \to \operatorname {\mathrm {GL}}_V$
of algebraic groups. The schematic fixed space of V under G is
where
![]() $v_R$
is the image of v under
$v_R$
is the image of v under
![]() $V\hookrightarrow V\otimes _KR$
[Reference Milne19, §4i].
$V\hookrightarrow V\otimes _KR$
[Reference Milne19, §4i].
We define the naïve fixed space as
More generally, if
![]() $\Gamma \subset G(K)$
is an abstract subgroup, the subspace fixed by
$\Gamma \subset G(K)$
is an abstract subgroup, the subspace fixed by
![]() $\Gamma $
is
$\Gamma $
is
Lemma 2.5. We have
![]() $V^G \subseteq V^{G(K)}$
, with equality if K is infinite and
$V^G \subseteq V^{G(K)}$
, with equality if K is infinite and
![]() $G/G^\circ $
is a split étale group.
$G/G^\circ $
is a split étale group.
Proof. The first statement is trivial; for the second, use the fact that under the stated hypotheses,
![]() $G(K)$
is Zariski dense in G.
$G(K)$
is Zariski dense in G.
Lemma 2.6. Let
![]() $\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a morphism of algebraic groups over K, and let
$\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a morphism of algebraic groups over K, and let
![]() $M\subset G$
be a normal algebraic subgroup. Then
$M\subset G$
be a normal algebraic subgroup. Then
![]() $V^M$
is stable under G, and thus is a sub-G-representation of G.
$V^M$
is stable under G, and thus is a sub-G-representation of G.
Proof. It suffices to verify this after passage to the algebraic closure of K, so we may and do assume that
![]() $G(K)$
is dense in G, and that
$G(K)$
is dense in G, and that
![]() $M(K)$
is dense in M. It now suffices to show that, for each
$M(K)$
is dense in M. It now suffices to show that, for each
![]() $g\in G(K)$
,
$g\in G(K)$
,
![]() $gW \subset W$
. Since W is fixed by the normal subgroup M,
$gW \subset W$
. Since W is fixed by the normal subgroup M,
![]() $gW$
is fixed by
$gW$
is fixed by
![]() $gMg^{-1} = M$
, and so
$gMg^{-1} = M$
, and so
![]() $gW \subset V^M = W$
.
$gW \subset V^M = W$
.
Lemma 2.7. Let
![]() $V/{\mathbb {F}}_\ell $
be a finite-dimensional vector space, and let
$V/{\mathbb {F}}_\ell $
be a finite-dimensional vector space, and let
![]() $\mathtt G$
be an abstract group equipped with a representation
$\mathtt G$
be an abstract group equipped with a representation
![]() $\rho : \mathtt G \to \operatorname {\mathrm {GL}}_V({\mathbb {F}}_\ell )$
. Let
$\rho : \mathtt G \to \operatorname {\mathrm {GL}}_V({\mathbb {F}}_\ell )$
. Let
![]() ${\mathtt H} \trianglelefteq \mathtt G$
be a normal subgroup such that
${\mathtt H} \trianglelefteq \mathtt G$
be a normal subgroup such that
![]() $V^{\rho ({\mathtt H})}\supsetneq (0)$
and
$V^{\rho ({\mathtt H})}\supsetneq (0)$
and
![]() $[\mathtt G: {\mathtt H}]$
is a power of
$[\mathtt G: {\mathtt H}]$
is a power of
![]() $\ell $
. Then
$\ell $
. Then
![]() $V^{\rho (\mathtt G)}\supsetneq (0)$
.
$V^{\rho (\mathtt G)}\supsetneq (0)$
.
Proof. Choose some
![]() $w \in V^{\rho ({\mathtt H}_\ell )}\smallsetminus {\left \{ 0\right \}}$
, and let
$w \in V^{\rho ({\mathtt H}_\ell )}\smallsetminus {\left \{ 0\right \}}$
, and let
![]() $W = {\mathbb {F}}_\ell [\mathtt G]w$
be the subspace spanned by its
$W = {\mathbb {F}}_\ell [\mathtt G]w$
be the subspace spanned by its
![]() $\mathtt G$
-orbit. The representation
$\mathtt G$
-orbit. The representation
![]() $\rho _W$
of
$\rho _W$
of
![]() $\mathtt G$
on
$\mathtt G$
on
![]() $W\subseteq V$
factors as
$W\subseteq V$
factors as
![]() $\mathtt G \to \mathtt G/{\mathtt H} \to \operatorname {\mathrm {GL}}_W({\mathbb {F}}_\ell )$
. Since
$\mathtt G \to \mathtt G/{\mathtt H} \to \operatorname {\mathrm {GL}}_W({\mathbb {F}}_\ell )$
. Since
![]() $\mathtt G/{\mathtt H}$
is an
$\mathtt G/{\mathtt H}$
is an
![]() $\ell $
-group, by the Sylow theorem,
$\ell $
-group, by the Sylow theorem,
![]() $\rho _W(\mathtt G)$
is contained in the
$\rho _W(\mathtt G)$
is contained in the
![]() ${\mathbb {F}}_\ell $
-points of a maximal unipotent subgroup U of
${\mathbb {F}}_\ell $
-points of a maximal unipotent subgroup U of
![]() $\operatorname {\mathrm {GL}}_W$
. (Differently put, after a suitable choice of basis, the image of
$\operatorname {\mathrm {GL}}_W$
. (Differently put, after a suitable choice of basis, the image of
![]() $\mathtt G$
in
$\mathtt G$
in
![]() $\operatorname {\mathrm {GL}}_W$
is contained in the
$\operatorname {\mathrm {GL}}_W$
is contained in the
![]() ${\mathbb {F}}_\ell $
-points of the group U of unipotent upper-triangular matrices.) Since U has a nontrivial fixed vector, so does
${\mathbb {F}}_\ell $
-points of the group U of unipotent upper-triangular matrices.) Since U has a nontrivial fixed vector, so does
![]() $\mathtt G$
.
$\mathtt G$
.
2.2.2 Bounded subgroups
Let
![]() $H/{\mathbb {Z}}[1/N]$
be a smooth affine algebraic group scheme with geometrically connected fibers. Suppose that for each
$H/{\mathbb {Z}}[1/N]$
be a smooth affine algebraic group scheme with geometrically connected fibers. Suppose that for each
![]() $\ell \nmid N$
, an abstract group
$\ell \nmid N$
, an abstract group
![]() ${\mathtt H}_\ell \subset H({\mathbb {F}}_\ell )$
is specified.
${\mathtt H}_\ell \subset H({\mathbb {F}}_\ell )$
is specified.
Definition 2.8. The collection
![]() ${\left \{{{\mathtt H}_\ell }\right \}}_\ell $
is bounded (in H, independently of
${\left \{{{\mathtt H}_\ell }\right \}}_\ell $
is bounded (in H, independently of
![]() $\ell $
) if there exists some finite B such that, for each
$\ell $
) if there exists some finite B such that, for each
![]() $\ell $
,
$\ell $
,
Equivalently, there is some positive
![]() $C = 1/B$
such that
$C = 1/B$
such that
![]() $\#{\mathtt H}_\ell> C \#H({\mathbb {F}}_\ell )$
.
$\#{\mathtt H}_\ell> C \#H({\mathbb {F}}_\ell )$
.
Lemma 2.9. Let
![]() $\alpha \colon H \to G$
be a surjective morphism of smooth algebraic groups over
$\alpha \colon H \to G$
be a surjective morphism of smooth algebraic groups over
![]() ${\mathbb {Z}}[1/N]$
, with G connected. Then
${\mathbb {Z}}[1/N]$
, with G connected. Then
![]() ${\left \{{\alpha (H({\mathbb {F}}_\ell ))}\right \}}_\ell $
is bounded in G.
${\left \{{\alpha (H({\mathbb {F}}_\ell ))}\right \}}_\ell $
is bounded in G.
Proof. Let
![]() $P = \ker (\alpha )$
. Its formation commutes with base change, and it is the extension of a finite group scheme D by a connected group
$P = \ker (\alpha )$
. Its formation commutes with base change, and it is the extension of a finite group scheme D by a connected group
![]() $P^\circ $
. Taking
$P^\circ $
. Taking
![]() ${\mathbb {F}}_\ell $
-points, we have
${\mathbb {F}}_\ell $
-points, we have
It suffices to show that
![]() $H^1({\mathbb {F}}_\ell ,P)$
is bounded independently of
$H^1({\mathbb {F}}_\ell ,P)$
is bounded independently of
![]() $\ell $
. By Lang’s theorem,
$\ell $
. By Lang’s theorem,
![]() $H^1({\mathbb {F}}_\ell , P^\circ )$
is trivial, and so it suffices to show that
$H^1({\mathbb {F}}_\ell , P^\circ )$
is trivial, and so it suffices to show that
![]() $H^1({\mathbb {F}}_\ell , D)$
is bounded. Now, use the fact that D is finite and
$H^1({\mathbb {F}}_\ell , D)$
is bounded. Now, use the fact that D is finite and
![]() $\#H^1({\mathbb {F}}_\ell ,D) = \#D({\mathbb {F}}_\ell )$
(see [Reference Platonov and Rapinchuk29, p. 290]).
$\#H^1({\mathbb {F}}_\ell ,D) = \#D({\mathbb {F}}_\ell )$
(see [Reference Platonov and Rapinchuk29, p. 290]).
Lemma 2.10. Let
be an exact sequence of algebraic groups over
![]() ${\mathbb {Z}}[1/N]$
. Suppose that
${\mathbb {Z}}[1/N]$
. Suppose that
![]() ${\left \{{{\mathtt H}_\ell }\right \}}_\ell $
has bounded index in H. Then:
${\left \{{{\mathtt H}_\ell }\right \}}_\ell $
has bounded index in H. Then:
-
(a)
 ${\left \{{\alpha ({\mathtt H}_\ell )}\right \}}_\ell $
has bounded index in G, and
${\left \{{\alpha ({\mathtt H}_\ell )}\right \}}_\ell $
has bounded index in G, and -
(b)
 ${\left \{{ (\ker \alpha |_{{\mathtt H}_\ell })\cap P^\circ ({\mathbb {F}}_\ell )}\right \}}_\ell $
has bounded index in
${\left \{{ (\ker \alpha |_{{\mathtt H}_\ell })\cap P^\circ ({\mathbb {F}}_\ell )}\right \}}_\ell $
has bounded index in
 $P^\circ $
.
$P^\circ $
.
Proof. Suppose
![]() $\#{\mathtt H}_\ell> C_{{\mathtt H}}\cdot \#H({\mathbb {F}}_\ell )$
and (using Lemma 2.9)
$\#{\mathtt H}_\ell> C_{{\mathtt H}}\cdot \#H({\mathbb {F}}_\ell )$
and (using Lemma 2.9)
![]() $\#\alpha (H({\mathbb {F}}_\ell ))> C_\alpha \cdot \#G({\mathbb {F}}_\ell )$
for
$\#\alpha (H({\mathbb {F}}_\ell ))> C_\alpha \cdot \#G({\mathbb {F}}_\ell )$
for
![]() $\ell \gg 0$
. We then have the easy estimates
$\ell \gg 0$
. We then have the easy estimates

This proves (a).
Let
![]() $\mathtt P_\ell = \ker \alpha |_{{\mathtt H}_\ell }$
. Then
$\mathtt P_\ell = \ker \alpha |_{{\mathtt H}_\ell }$
. Then

Let
![]() $P'$
be any irreducible component of
$P'$
be any irreducible component of
![]() $P_{{\mathbb {F}}_\ell }$
. Then
$P_{{\mathbb {F}}_\ell }$
. Then
![]() $\mathtt P_\ell \cap P'({\mathbb {F}}_\ell )$
, if nonempty, is a torsor under
$\mathtt P_\ell \cap P'({\mathbb {F}}_\ell )$
, if nonempty, is a torsor under
![]() $\mathtt P_\ell \cap P^\circ ({\mathbb {F}}_\ell )$
, and so
$\mathtt P_\ell \cap P^\circ ({\mathbb {F}}_\ell )$
, and so

2.2.3 Representations of connected groups
Let
![]() $G/{\mathbb {Z}}[1/N]$
be a smooth affine algebraic group with connected fibers. Let V be a free
$G/{\mathbb {Z}}[1/N]$
be a smooth affine algebraic group with connected fibers. Let V be a free
![]() ${\mathbb {Z}}[1/N]$
-module of rank n, and let
${\mathbb {Z}}[1/N]$
-module of rank n, and let
![]() $\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a representation. For a field k equipped with a ring map
$\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a representation. For a field k equipped with a ring map
![]() ${\mathbb {Z}}[1/N]\to k$
, let
${\mathbb {Z}}[1/N]\to k$
, let
![]() $r_k(G,\rho )$
be the multiplicity of the trivial representation of
$r_k(G,\rho )$
be the multiplicity of the trivial representation of
![]() $G(k)$
:
$G(k)$
:
Let
![]() $V_\ell = V\otimes {\mathbb {F}}_\ell $
, and let
$V_\ell = V\otimes {\mathbb {F}}_\ell $
, and let
![]() $r_\ell (G,\rho ) = r_{{\mathbb {F}}_\ell }(G,\rho )$
. Note that, when
$r_\ell (G,\rho ) = r_{{\mathbb {F}}_\ell }(G,\rho )$
. Note that, when
![]() $\ell \gg 0$
, by specialization, we always have
$\ell \gg 0$
, by specialization, we always have
![]() $r_{\mathbb {Q}}(G,\rho ) \leq r_\ell (G,\rho )$
.
$r_{\mathbb {Q}}(G,\rho ) \leq r_\ell (G,\rho )$
.
If
![]() $g\in G(k)$
, let
$g\in G(k)$
, let
![]() $m(g,\rho ) = m_k(g,\rho )$
be the multiplicity of
$m(g,\rho ) = m_k(g,\rho )$
be the multiplicity of
![]() $1$
as a root of the characteristic polynomial of
$1$
as a root of the characteristic polynomial of
![]() $\rho (g)$
. Let
$\rho (g)$
. Let
![]() $G_{\rho , \ge m}$
be the locus of those g for which
$G_{\rho , \ge m}$
be the locus of those g for which
![]() $m(g,\rho ) \ge m$
. (Schematically,
$m(g,\rho ) \ge m$
. (Schematically,
![]() $G_{\rho , \ge 1}$
may be constructed by pulling back the composite morphism
$G_{\rho , \ge 1}$
may be constructed by pulling back the composite morphism
by the zero section
![]() $\operatorname {\mathrm {Spec}}\ {\mathbb {Z}}[1/N] \to \mathbb G_a$
, where the map
$\operatorname {\mathrm {Spec}}\ {\mathbb {Z}}[1/N] \to \mathbb G_a$
, where the map
![]() $\text {eval}_1$
means evaluating the characteristic polynomial at
$\text {eval}_1$
means evaluating the characteristic polynomial at
![]() $1$
; for other values of m,
$1$
; for other values of m,
![]() $G_{\rho ,\ge m}$
may be constructed by considering higher derivatives of the characteristic polynomial.)
$G_{\rho ,\ge m}$
may be constructed by considering higher derivatives of the characteristic polynomial.)
Lemma 2.11. Suppose that there is an infinite collection of primes
![]() ${\mathbb L}$
such that, if
${\mathbb L}$
such that, if
![]() $\ell \in {\mathbb L}$
, then
$\ell \in {\mathbb L}$
, then
![]() $r_\ell (G,\rho ) = r$
. Then we have:
$r_\ell (G,\rho ) = r$
. Then we have:
-
(a) for each
 $g\in G({\mathbb {Q}})$
,
$g\in G({\mathbb {Q}})$
,
 $m(g,\rho ) \ge r$
;
$m(g,\rho ) \ge r$
; -
(b)
 $r_{\mathbb {Q}}(G, \rho ) = r$
; and
$r_{\mathbb {Q}}(G, \rho ) = r$
; and -
(c)
 $\dim V_{\mathbb {Q}}^{G_{\mathbb {Q}}} = r$
.
$\dim V_{\mathbb {Q}}^{G_{\mathbb {Q}}} = r$
.
Proof. We assume
![]() $r>0$
, since (by specialization) the statement is trivial if
$r>0$
, since (by specialization) the statement is trivial if
![]() $r=0$
.
$r=0$
.
For (a), it suffices to apply, to the characteristic polynomial of
![]() $\rho (g)$
, the following elementary observation. Let
$\rho (g)$
, the following elementary observation. Let
![]() $f(T) \in {\mathbb {Q}}[T]$
be any polynomial; since clearing denominators does not alter the roots of f, we may and do assume
$f(T) \in {\mathbb {Q}}[T]$
be any polynomial; since clearing denominators does not alter the roots of f, we may and do assume
![]() $f(T) \in {\mathbb {Z}}[T]$
. Suppose
$f(T) \in {\mathbb {Z}}[T]$
. Suppose
![]() $\lambda \in {\mathbb {Z}}$
. If
$\lambda \in {\mathbb {Z}}$
. If
![]() $\ell $
is sufficiently large, relative to the coefficients of f and to
$\ell $
is sufficiently large, relative to the coefficients of f and to
![]() $\lambda $
, then
$\lambda $
, then
![]() $f(\lambda ) = 0$
if and only if
$f(\lambda ) = 0$
if and only if
![]() $f(\lambda ) \equiv 0 \bmod \ell $
; and, by taking the first
$f(\lambda ) \equiv 0 \bmod \ell $
; and, by taking the first
![]() $r-1$
derivatives of f, a similar result holds for roots of higher multiplicity.
$r-1$
derivatives of f, a similar result holds for roots of higher multiplicity.
We now prove (b). For each
![]() $\ell \in {\mathbb L}$
, let
$\ell \in {\mathbb L}$
, let
![]() $Y_\ell \subset V_\ell $
be the subspace fixed by
$Y_\ell \subset V_\ell $
be the subspace fixed by
![]() $G_{{\mathbb {F}}_\ell }$
.
$G_{{\mathbb {F}}_\ell }$
.
Let
![]() $m_0$
be the integer such that
$m_0$
be the integer such that
![]() $G_{\mathbb {Q}}= {G_{\mathbb {Q}}}_{\rho , \ge m_0} \supsetneq {G_{\mathbb {Q}}}_{\rho , \ge m_0+1}$
; by (a), we have
$G_{\mathbb {Q}}= {G_{\mathbb {Q}}}_{\rho , \ge m_0} \supsetneq {G_{\mathbb {Q}}}_{\rho , \ge m_0+1}$
; by (a), we have
![]() $m_0 \ge r \ge 1$
. Let
$m_0 \ge r \ge 1$
. Let
![]() ${G_{\mathbb {Q}}}^{ss}$
be the open and dense semisimple locus (e.g., [Reference Humphreys9, Th. 22.2]), and let
${G_{\mathbb {Q}}}^{ss}$
be the open and dense semisimple locus (e.g., [Reference Humphreys9, Th. 22.2]), and let
![]() $G^* = {G_{\mathbb {Q}}}^{ss} \smallsetminus {G_{{\mathbb {Q}}}}_{\rho , \ge m_0+1}$
. Since
$G^* = {G_{\mathbb {Q}}}^{ss} \smallsetminus {G_{{\mathbb {Q}}}}_{\rho , \ge m_0+1}$
. Since
![]() $G_{\mathbb {Q}}$
is connected,
$G_{\mathbb {Q}}$
is connected,
![]() $G^*$
is open and dense in
$G^*$
is open and dense in
![]() $G_{\mathbb {Q}}$
. Like any connected affine algebraic group,
$G_{\mathbb {Q}}$
. Like any connected affine algebraic group,
![]() $G_{\mathbb {Q}}$
is unirational. Consequently,
$G_{\mathbb {Q}}$
is unirational. Consequently,
![]() $G^*({\mathbb {Q}})$
is Zariski dense in
$G^*({\mathbb {Q}})$
is Zariski dense in
![]() $G_{\mathbb {Q}}$
.
$G_{\mathbb {Q}}$
.
For
![]() $g\in G^*({\mathbb {Q}})$
, let
$g\in G^*({\mathbb {Q}})$
, let
![]() $W_g \subset V_{\mathbb {Q}}$
be the
$W_g \subset V_{\mathbb {Q}}$
be the
![]() $m_0$
-dimensional subspace fixed by g. After choosing an integral model of
$m_0$
-dimensional subspace fixed by g. After choosing an integral model of
![]() $W_g$
, for all but finitely many
$W_g$
, for all but finitely many
![]() $\ell $
, the reductions
$\ell $
, the reductions
![]() $g_\ell \in G({\mathbb {F}}_\ell )$
and
$g_\ell \in G({\mathbb {F}}_\ell )$
and
![]() $W_{g,\ell } \subset V_\ell $
are well defined; and for
$W_{g,\ell } \subset V_\ell $
are well defined; and for
![]() $\ell \in {\mathbb L}$
, we have
$\ell \in {\mathbb L}$
, we have
![]() $W_{g,\ell } \supseteq Y_\ell $
.
$W_{g,\ell } \supseteq Y_\ell $
.
Let
![]() $W = \cap _{g\in G^*({\mathbb {Q}})} W_g$
; since
$W = \cap _{g\in G^*({\mathbb {Q}})} W_g$
; since
![]() $V_{\mathbb {Q}}$
is finite-dimensional, there is a finite list of elements
$V_{\mathbb {Q}}$
is finite-dimensional, there is a finite list of elements
![]() $g_1, \dots , g_n \in G^*({\mathbb {Q}})$
such that
$g_1, \dots , g_n \in G^*({\mathbb {Q}})$
such that
![]() $W = \cap _i W_{g_i}$
. If
$W = \cap _i W_{g_i}$
. If
![]() $\ell $
is sufficiently large as to avoid the finitely many primes of bad reduction for the
$\ell $
is sufficiently large as to avoid the finitely many primes of bad reduction for the
![]() $W_{g_i}$
, then
$W_{g_i}$
, then
![]() $W\otimes {\mathbb {F}}_\ell $
contains
$W\otimes {\mathbb {F}}_\ell $
contains
![]() $Y_\ell $
. This shows that
$Y_\ell $
. This shows that
![]() $\dim _{\mathbb {Q}} W \ge \dim _{{\mathbb {F}}_\ell } Y_\ell = r$
. By the density of
$\dim _{\mathbb {Q}} W \ge \dim _{{\mathbb {F}}_\ell } Y_\ell = r$
. By the density of
![]() $G^*({\mathbb {Q}})$
, W is fixed by all of
$G^*({\mathbb {Q}})$
, W is fixed by all of
![]() $G_{\mathbb {Q}}$
, and so
$G_{\mathbb {Q}}$
, and so
![]() $r_{\mathbb {Q}}(G,\rho ) \ge r$
; again, by specialization, we find that equality holds. This proves (b). Since
$r_{\mathbb {Q}}(G,\rho ) \ge r$
; again, by specialization, we find that equality holds. This proves (b). Since
![]() $W = V_{\mathbb {Q}}^{G_{\mathbb {Q}}}$
, we may conclude (c), as well.
$W = V_{\mathbb {Q}}^{G_{\mathbb {Q}}}$
, we may conclude (c), as well.
Now, let
![]() ${\left \{{\mathtt G_\ell }\right \}}$
be a collection of bounded subgroups of G, and let
${\left \{{\mathtt G_\ell }\right \}}$
be a collection of bounded subgroups of G, and let
In the statement below, sufficiently large depends only on
![]() $\dim V$
and the constant in (2.2); however, in our applications, we do not have control over this constant.
$\dim V$
and the constant in (2.2); however, in our applications, we do not have control over this constant.
Lemma 2.12. Let
![]() ${\left \{{\mathtt G_\ell }\right \}}$
be a collection of bounded subgroups of G. If
${\left \{{\mathtt G_\ell }\right \}}$
be a collection of bounded subgroups of G. If
![]() $r_\ell (\mathtt G_\ell ,\rho ) = r$
for some sufficiently large
$r_\ell (\mathtt G_\ell ,\rho ) = r$
for some sufficiently large
![]() $\ell $
, then
$\ell $
, then
![]() $r_\ell ({G},\rho ) = r$
.
$r_\ell ({G},\rho ) = r$
.
Proof. For any
![]() $\ell $
, let
$\ell $
, let
![]() $W_\ell \subset V\otimes {\mathbb {F}}_\ell $
be a subspace of dimension r, and let
$W_\ell \subset V\otimes {\mathbb {F}}_\ell $
be a subspace of dimension r, and let
![]() $\operatorname {\mathrm {Fix}}_{G,W_\ell }\subset G_{{\mathbb {F}}_\ell }$
be the subgroup scheme which fixes
$\operatorname {\mathrm {Fix}}_{G,W_\ell }\subset G_{{\mathbb {F}}_\ell }$
be the subgroup scheme which fixes
![]() $W_\ell $
. By Bézout’s theorem, since
$W_\ell $
. By Bézout’s theorem, since
![]() $\operatorname {\mathrm {Fix}}_{G,W_\ell }$
is the intersection of G and
$\operatorname {\mathrm {Fix}}_{G,W_\ell }$
is the intersection of G and
![]() $\operatorname {\mathrm {Fix}}_{\operatorname {\mathrm {GL}}_{V,{\mathbb {F}}_\ell },W_\ell }$
in
$\operatorname {\mathrm {Fix}}_{\operatorname {\mathrm {GL}}_{V,{\mathbb {F}}_\ell },W_\ell }$
in
![]() $\operatorname {\mathrm {GL}}_{V,{\mathbb {F}}_\ell }$
, there is a constant B such that
$\operatorname {\mathrm {GL}}_{V,{\mathbb {F}}_\ell }$
, there is a constant B such that
![]() $\#\pi _0(\operatorname {\mathrm {Fix}}_{G,W_\ell }) \le B$
, independent of the choice of
$\#\pi _0(\operatorname {\mathrm {Fix}}_{G,W_\ell }) \le B$
, independent of the choice of
![]() $W_\ell $
and of
$W_\ell $
and of
![]() $\ell $
.
$\ell $
.
For any connected group H of dimension d over a finite field
![]() ${\mathbb {F}}$
, we have
${\mathbb {F}}$
, we have
![]() $(\#{\mathbb {F}}-1)^d \le \#H({\mathbb {F}}) \le (\# {\mathbb {F}}+1)^d$
(see [Reference Nori25, Lem. 3.5] or [Reference Larsen and Pink14, Prop. 3.1]). Fix a prime
$(\#{\mathbb {F}}-1)^d \le \#H({\mathbb {F}}) \le (\# {\mathbb {F}}+1)^d$
(see [Reference Nori25, Lem. 3.5] or [Reference Larsen and Pink14, Prop. 3.1]). Fix a prime
![]() $\ell $
, and suppose that
$\ell $
, and suppose that
![]() $r_\ell (\mathtt G_\ell ,\rho ) = r$
; let
$r_\ell (\mathtt G_\ell ,\rho ) = r$
; let
![]() $W_\ell \subset V\otimes {\mathbb {F}}_\ell $
be the subspace fixed by
$W_\ell \subset V\otimes {\mathbb {F}}_\ell $
be the subspace fixed by
![]() $\mathtt G_\ell $
. We then have
$\mathtt G_\ell $
. We then have
If
![]() $\ell \gg _{d,C/B} 0$
, this forces
$\ell \gg _{d,C/B} 0$
, this forces
![]() $\dim \operatorname {\mathrm {Fix}}_{G,W_\ell } = \dim G_{{\mathbb {F}}_\ell }$
, so that
$\dim \operatorname {\mathrm {Fix}}_{G,W_\ell } = \dim G_{{\mathbb {F}}_\ell }$
, so that
![]() $\operatorname {\mathrm {Fix}}_{G,W_\ell } =G_{{\mathbb {F}}_\ell }$
.
$\operatorname {\mathrm {Fix}}_{G,W_\ell } =G_{{\mathbb {F}}_\ell }$
.
Lemma 2.13. Let
![]() ${\left \{{\mathtt G_\ell }\right \}}$
be a collection of bounded subgroups of G. Suppose that there is an infinite collection of primes
${\left \{{\mathtt G_\ell }\right \}}$
be a collection of bounded subgroups of G. Suppose that there is an infinite collection of primes
![]() ${\mathbb L}$
such that, if
${\mathbb L}$
such that, if
![]() $\ell \in {\mathbb L}$
, then
$\ell \in {\mathbb L}$
, then
![]() $r_\ell (\mathtt G_\ell ,\rho ) \ge r$
. Then:
$r_\ell (\mathtt G_\ell ,\rho ) \ge r$
. Then:
-
(a)
 $r_{{\mathbb {Q}}}(G,\rho )\ge r$
and
$r_{{\mathbb {Q}}}(G,\rho )\ge r$
and -
(b)
 $r_\ell (G,\rho ) \ge r$
for all but finitely many
$r_\ell (G,\rho ) \ge r$
for all but finitely many
 $\ell $
.
$\ell $
.
Proof. By Lemma 2.12, we find that for
![]() $\ell \gg 0$
, we have
$\ell \gg 0$
, we have
![]() $r_\ell ({G}_\ell ,\rho ) \ge r$
. Lemma 2.11 then shows that
$r_\ell ({G}_\ell ,\rho ) \ge r$
. Lemma 2.11 then shows that
![]() $r_{\mathbb {Q}}(G,\rho ) \ge r$
. This proves (a); then (b) follows by specialization.
$r_{\mathbb {Q}}(G,\rho ) \ge r$
. This proves (a); then (b) follows by specialization.
Lemma 2.14. Let
![]() $\mathtt G_{\ell _0^{\infty }}$
be a Zariski dense subgroup of
$\mathtt G_{\ell _0^{\infty }}$
be a Zariski dense subgroup of
![]() $G_{{\mathbb {Q}}_{\ell _0}}$
. Suppose
$G_{{\mathbb {Q}}_{\ell _0}}$
. Suppose
![]() $r(\mathtt G_{\ell _0^{\infty }},\rho ) \ge r$
. Then:
$r(\mathtt G_{\ell _0^{\infty }},\rho ) \ge r$
. Then:
-
(a)
 $r_{{\mathbb {Q}}}(G,\rho )\ge r$
and
$r_{{\mathbb {Q}}}(G,\rho )\ge r$
and -
(b)
 $r_\ell (G,\rho ) \ge r$
for all but finitely many
$r_\ell (G,\rho ) \ge r$
for all but finitely many
 $\ell $
.
$\ell $
.
Proof. Under the hypothesis,
![]() $r(G_{{\mathbb {Q}}_{\ell _0}}, \rho ) \geq r$
; for (a), it then suffices to note that, since
$r(G_{{\mathbb {Q}}_{\ell _0}}, \rho ) \geq r$
; for (a), it then suffices to note that, since
![]() $G_{\mathbb {Q}}$
is connected, the formation of the fixed points of the action of G is stable under the base change
$G_{\mathbb {Q}}$
is connected, the formation of the fixed points of the action of G is stable under the base change
![]() ${\mathbb {Q}} \hookrightarrow {\mathbb {Q}}_{\ell _0}$
(§2.2.1). Part (b) follows by specialization.
${\mathbb {Q}} \hookrightarrow {\mathbb {Q}}_{\ell _0}$
(§2.2.1). Part (b) follows by specialization.
2.2.4 Interlude on étale group schemes
If
![]() $(S,{\overline {s}})$
is a geometrically pointed connected scheme, then a (not necessarily connected) finite étale group scheme
$(S,{\overline {s}})$
is a geometrically pointed connected scheme, then a (not necessarily connected) finite étale group scheme
![]() $G \to S$
is tantamount to an action, by group automorphisms, of
$G \to S$
is tantamount to an action, by group automorphisms, of
![]() $\pi _1(S,{\overline {s}})$
on the abstract finite group
$\pi _1(S,{\overline {s}})$
on the abstract finite group
![]() $G_{{\overline {s}}}$
. We will say that G is split if this action is trivial.
$G_{{\overline {s}}}$
. We will say that G is split if this action is trivial.
Lemma 2.15. Let
![]() $G/{\mathbb {Z}}[1/N]$
be an étale group scheme, and let
$G/{\mathbb {Z}}[1/N]$
be an étale group scheme, and let
![]() $M\subset G$
be a normal sub-group scheme. Suppose that there exists an
$M\subset G$
be a normal sub-group scheme. Suppose that there exists an
![]() $\ell _0 \nmid N$
such that
$\ell _0 \nmid N$
such that
![]() $M({\mathbb {F}}_{\ell _0}) = G({\mathbb {F}}_{\ell _0})$
. Then, for
$M({\mathbb {F}}_{\ell _0}) = G({\mathbb {F}}_{\ell _0})$
. Then, for
![]() $\ell $
in a set of positive density,
$\ell $
in a set of positive density,
![]() $M({\mathbb {F}}_\ell ) = G({\mathbb {F}}_\ell )$
; and if G is split, then
$M({\mathbb {F}}_\ell ) = G({\mathbb {F}}_\ell )$
; and if G is split, then
![]() $M({\mathbb {F}}_\ell ) = G({\mathbb {F}}_\ell )$
for every
$M({\mathbb {F}}_\ell ) = G({\mathbb {F}}_\ell )$
for every
![]() $\ell \nmid N$
.
$\ell \nmid N$
.
Proof. Let
![]() $\operatorname {\mathrm {Spec}}(R) \to \operatorname {\mathrm {Spec}}({\mathbb {Z}}[1/N])$
be a Galois étale cover which trivializes G and M; let
$\operatorname {\mathrm {Spec}}(R) \to \operatorname {\mathrm {Spec}}({\mathbb {Z}}[1/N])$
be a Galois étale cover which trivializes G and M; let
![]() $K = \operatorname {Frac}(R)$
. Let
$K = \operatorname {Frac}(R)$
. Let
![]() $\ell \nmid N$
be a prime, and let
$\ell \nmid N$
be a prime, and let
![]() $\lambda $
be a prime of R lying over
$\lambda $
be a prime of R lying over
![]() $\ell $
. The Artin symbol
$\ell $
. The Artin symbol
![]() $(\lambda , K/{\mathbb {Q}})$
determines
$(\lambda , K/{\mathbb {Q}})$
determines
![]() $G({\mathbb {F}}_\ell )$
and
$G({\mathbb {F}}_\ell )$
and
![]() $M({\mathbb {F}}_\ell )$
as abstract groups, and the equality
$M({\mathbb {F}}_\ell )$
as abstract groups, and the equality
![]() $M({\mathbb {F}}_\ell ) = G({\mathbb {F}}_\ell )$
depends only on the conjugacy class
$M({\mathbb {F}}_\ell ) = G({\mathbb {F}}_\ell )$
depends only on the conjugacy class
![]() $(\ell , K/{\mathbb {Q}})$
.
$(\ell , K/{\mathbb {Q}})$
.
Under the hypotheses, for any
![]() $\ell $
in the set of positive density for which
$\ell $
in the set of positive density for which
![]() $(\ell , K/{\mathbb {Q}})= (\ell _0,K/{\mathbb {Q}})$
, we have
$(\ell , K/{\mathbb {Q}})= (\ell _0,K/{\mathbb {Q}})$
, we have
![]() $M({\mathbb {F}}_\ell ) = G({\mathbb {F}}_\ell )$
.
$M({\mathbb {F}}_\ell ) = G({\mathbb {F}}_\ell )$
.
The claim when G is split is trivially true, since then M is split, too, and
![]() $M({\mathbb {F}}_\ell ) = M({\mathbb {Z}}[1/N])$
and
$M({\mathbb {F}}_\ell ) = M({\mathbb {Z}}[1/N])$
and
![]() $G({\mathbb {F}}_\ell ) = G({\mathbb {Z}}[1/N])$
.
$G({\mathbb {F}}_\ell ) = G({\mathbb {Z}}[1/N])$
.
2.2.5 Representations of group schemes
We now turn to working with a smooth group scheme
![]() $G/{\mathbb {Z}}[1/N]$
. We will often assume that G has reductive connected component of identity, that is, that for each
$G/{\mathbb {Z}}[1/N]$
. We will often assume that G has reductive connected component of identity, that is, that for each
![]() $s \in \operatorname {\mathrm {Spec}} {\mathbb {Z}}[1/N]$
,
$s \in \operatorname {\mathrm {Spec}} {\mathbb {Z}}[1/N]$
,
![]() $(G_s)^\circ $
is reductive. With this hypothesis,
$(G_s)^\circ $
is reductive. With this hypothesis,
![]() $G^\circ $
is a reductive group scheme over
$G^\circ $
is a reductive group scheme over
![]() ${\mathbb {Z}}[1/N]$
, and
${\mathbb {Z}}[1/N]$
, and
![]() $G/G^\circ $
is étale [Reference Conrad7, Prop. 3.1.3]. (In fact, we will use the same nomenclature, and deduce the same conclusions, for group schemes over an arbitrary base.) (Without this assumption, it is known that
$G/G^\circ $
is étale [Reference Conrad7, Prop. 3.1.3]. (In fact, we will use the same nomenclature, and deduce the same conclusions, for group schemes over an arbitrary base.) (Without this assumption, it is known that
![]() $G/G^\circ $
is an étale algebraic space [Reference Ancona, Huber and Pepin Lehalleur1, Lem. 2.1], but one may need to enlarge N to ensure that
$G/G^\circ $
is an étale algebraic space [Reference Ancona, Huber and Pepin Lehalleur1, Lem. 2.1], but one may need to enlarge N to ensure that
![]() $G/G^\circ $
is representable by a scheme [Reference Behrend2, Prop. 5.1.1].)
$G/G^\circ $
is representable by a scheme [Reference Behrend2, Prop. 5.1.1].)
Lemma 2.16. Let
![]() $G/{\mathbb {Z}}[1/N]$
be a smooth affine algebraic group scheme with reductive connected component of identity. Let V be a free
$G/{\mathbb {Z}}[1/N]$
be a smooth affine algebraic group scheme with reductive connected component of identity. Let V be a free
![]() ${\mathbb {Z}}[1/N]$
-module of finite rank, and let
${\mathbb {Z}}[1/N]$
-module of finite rank, and let
![]() $\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a homomorphism of algebraic groups. Let
$\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a homomorphism of algebraic groups. Let
![]() ${\left \{{\mathtt G_\ell }\right \}}$
be a collection of bounded subgroups of G. Suppose that there is an infinite collection of primes
${\left \{{\mathtt G_\ell }\right \}}$
be a collection of bounded subgroups of G. Suppose that there is an infinite collection of primes
![]() ${\mathbb L}$
such that, if
${\mathbb L}$
such that, if
![]() $\ell \in {\mathbb L}$
, then
$\ell \in {\mathbb L}$
, then
![]() $r_\ell (\mathtt G_\ell , \rho ) \ge r$
.
$r_\ell (\mathtt G_\ell , \rho ) \ge r$
.
-
(a) Then
 $r_{\mathbb {Q}}(G^\circ ,\rho ) \ge r$
.
$r_{\mathbb {Q}}(G^\circ ,\rho ) \ge r$
. -
(b) Suppose that for some
 $\ell _0 \in {\mathbb L}$
,
$\ell _0 \in {\mathbb L}$
,
 $\mathtt G_{\ell _0}$
meets every geometrically irreducible component of
$\mathtt G_{\ell _0}$
meets every geometrically irreducible component of
 $G_{\ell _0}$
. Then, for
$G_{\ell _0}$
. Then, for
 $\ell $
in a set of positive density,
$\ell $
in a set of positive density,
 $r_\ell (G,\rho ) \ge r$
.
$r_\ell (G,\rho ) \ge r$
. -
(c) In the setting of (b), suppose that
 $G/G^\circ $
is split. Then
$G/G^\circ $
is split. Then
 $r_\ell (G,\rho ) \ge r$
for all
$r_\ell (G,\rho ) \ge r$
for all
 $\ell \nmid N$
.
$\ell \nmid N$
.
Proof. By Lemma 2.13, applied to the bounded subgroups
![]() ${\mathtt G_\ell \cap G^\circ ({\mathbb {F}}_\ell )}$
of
${\mathtt G_\ell \cap G^\circ ({\mathbb {F}}_\ell )}$
of
![]() $G^\circ $
, we find that
$G^\circ $
, we find that
![]() $r(G^\circ _{\mathbb {Q}},\rho ) \ge r$
; this proves (a).
$r(G^\circ _{\mathbb {Q}},\rho ) \ge r$
; this proves (a).
Now suppose that there is some
![]() $\ell _0\in {\mathbb L}$
for which
$\ell _0\in {\mathbb L}$
for which
![]() $\mathtt G_{\ell _0}$
meets every geometrically irreducible component of
$\mathtt G_{\ell _0}$
meets every geometrically irreducible component of
![]() $G_{\ell _0}$
. Let
$G_{\ell _0}$
. Let
![]() ${\overline {G}} = G/G^\circ $
. The image of
${\overline {G}} = G/G^\circ $
. The image of
![]() $\mathtt G_{\ell _0}$
in
$\mathtt G_{\ell _0}$
in
![]() ${\overline {G}}({\mathbb {F}}_{\ell _0})$
is all of
${\overline {G}}({\mathbb {F}}_{\ell _0})$
is all of
![]() ${\overline {G}}({\mathbb {F}}_{\ell _0})$
. Replace V with the eigenspace where
${\overline {G}}({\mathbb {F}}_{\ell _0})$
. Replace V with the eigenspace where
![]() $G^\circ $
acts with eigenvalue one; then V has rank at least r. The representation
$G^\circ $
acts with eigenvalue one; then V has rank at least r. The representation
![]() $\rho \colon G \to \operatorname {\mathrm {GL}}_V$
factors through
$\rho \colon G \to \operatorname {\mathrm {GL}}_V$
factors through
![]() $\bar \rho \colon {\overline {G}} \to \operatorname {\mathrm {GL}}_W$
. There is some subrepresentation
$\bar \rho \colon {\overline {G}} \to \operatorname {\mathrm {GL}}_W$
. There is some subrepresentation
![]() $\bar \rho _W\colon {\overline {G}} \to \operatorname {\mathrm {GL}}_W \subset \operatorname {\mathrm {GL}}_V$
of rank at least r such that
$\bar \rho _W\colon {\overline {G}} \to \operatorname {\mathrm {GL}}_W \subset \operatorname {\mathrm {GL}}_V$
of rank at least r such that
![]() $\mathtt G_{\ell _0}$
acts trivially on
$\mathtt G_{\ell _0}$
acts trivially on
![]() $W\otimes {\mathbb {F}}_{\ell _0}$
.
$W\otimes {\mathbb {F}}_{\ell _0}$
.
Let M be the group scheme
![]() $M = \ker (\bar \rho _W) \subset {\overline {G}}$
. We have
$M = \ker (\bar \rho _W) \subset {\overline {G}}$
. We have
![]() $\mathtt G_{\ell _0} \subseteq M({\mathbb {F}}_{\ell _0})$
. Parts (b) and (c) now follow from Lemma 2.15.
$\mathtt G_{\ell _0} \subseteq M({\mathbb {F}}_{\ell _0})$
. Parts (b) and (c) now follow from Lemma 2.15.
Lemma 2.17. Let
![]() $G/{\mathbb {Z}}_\ell $
be a smooth affine group scheme with reductive connected component of identity, and suppose that
$G/{\mathbb {Z}}_\ell $
be a smooth affine group scheme with reductive connected component of identity, and suppose that
![]() $\ell \nmid [G:G^\circ ]$
. Let V be a free
$\ell \nmid [G:G^\circ ]$
. Let V be a free
![]() ${\mathbb {Z}}_\ell $
-module of finite rank, and let
${\mathbb {Z}}_\ell $
-module of finite rank, and let
![]() $\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a homomorphism of algebraic groups. Suppose that
$\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a homomorphism of algebraic groups. Suppose that
![]() $\dim V_{{\mathbb {Q}}_\ell }^{G^\circ _{{\mathbb {Q}}_\ell }} \ge r$
and
$\dim V_{{\mathbb {Q}}_\ell }^{G^\circ _{{\mathbb {Q}}_\ell }} \ge r$
and
![]() $r_\ell (G,\rho ) \ge r$
. Then
$r_\ell (G,\rho ) \ge r$
. Then
![]() $r(G_{{\mathbb {Q}}_\ell },\rho ) \ge r$
.
$r(G_{{\mathbb {Q}}_\ell },\rho ) \ge r$
.
Proof. Replacing V with the subspace fixed by
![]() $G^\circ ({\mathbb {Q}}_\ell )$
, we assume that the representation
$G^\circ ({\mathbb {Q}}_\ell )$
, we assume that the representation
![]() $G \to \operatorname {\mathrm {GL}}_V$
factors through
$G \to \operatorname {\mathrm {GL}}_V$
factors through
![]() ${\overline {G}} := (G/G^\circ )$
. Since
${\overline {G}} := (G/G^\circ )$
. Since
![]() ${\overline {G}}$
is étale, specialization of sections gives a bijection
${\overline {G}}$
is étale, specialization of sections gives a bijection
![]() ${\overline {G}}({\mathbb {Z}}_\ell ) \to {\overline {G}}({\mathbb {Z}}/\ell )$
. Moreover, by Lang’s theorem,
${\overline {G}}({\mathbb {Z}}_\ell ) \to {\overline {G}}({\mathbb {Z}}/\ell )$
. Moreover, by Lang’s theorem,
![]() ${\overline {G}}({\mathbb {Z}}/\ell ) = G({\mathbb {Z}}/\ell )/G^\circ ({\mathbb {Z}}/\ell )$
and
${\overline {G}}({\mathbb {Z}}/\ell ) = G({\mathbb {Z}}/\ell )/G^\circ ({\mathbb {Z}}/\ell )$
and
![]() ${\overline {G}}({\mathbb {Z}}_\ell ) = G({\mathbb {Z}}_\ell )/G^\circ ({\mathbb {Z}}_\ell )$
.
${\overline {G}}({\mathbb {Z}}_\ell ) = G({\mathbb {Z}}_\ell )/G^\circ ({\mathbb {Z}}_\ell )$
.
Since
![]() $\ell \nmid [G:G^\circ ]$
, we may write V uniquely as a direct sum of irreducible
$\ell \nmid [G:G^\circ ]$
, we may write V uniquely as a direct sum of irreducible
![]() ${\overline {G}}$
representations over
${\overline {G}}$
representations over
![]() ${\mathbb {Z}}_\ell $
. By hypothesis, there is a free
${\mathbb {Z}}_\ell $
. By hypothesis, there is a free
![]() ${\mathbb {Z}}_\ell $
-module
${\mathbb {Z}}_\ell $
-module
![]() $W\subset V$
, stable under G and of rank at least r, such that
$W\subset V$
, stable under G and of rank at least r, such that
![]() $G({\mathbb {F}}_\ell )$
acts trivially on
$G({\mathbb {F}}_\ell )$
acts trivially on
![]() $W\otimes {\mathbb {F}}_\ell $
. We have a commutative diagram:
$W\otimes {\mathbb {F}}_\ell $
. We have a commutative diagram:

Suppose
![]() $g \in G({\mathbb {Z}}_\ell )$
, and let
$g \in G({\mathbb {Z}}_\ell )$
, and let
![]() $\alpha $
be any eigenvalue of
$\alpha $
be any eigenvalue of
![]() $\rho _W(g)$
. On one hand,
$\rho _W(g)$
. On one hand,
![]() $\alpha $
is an mth root of unity for some
$\alpha $
is an mth root of unity for some
![]() $m|[G:G^\circ ]$
. On the other hand, by the commutativity of the diagram,
$m|[G:G^\circ ]$
. On the other hand, by the commutativity of the diagram,
![]() $\alpha \equiv 1 \bmod \ell $
. Consequently,
$\alpha \equiv 1 \bmod \ell $
. Consequently,
![]() $\alpha =1$
. Since
$\alpha =1$
. Since
![]() $\rho _W(g)\in \operatorname {\mathrm {GL}}_W({\mathbb {Z}}_\ell )$
has finite order, it is semisimple, and we conclude that
$\rho _W(g)\in \operatorname {\mathrm {GL}}_W({\mathbb {Z}}_\ell )$
has finite order, it is semisimple, and we conclude that
![]() $\rho _W(g) = \operatorname {\mathrm {id}}_W$
.
$\rho _W(g) = \operatorname {\mathrm {id}}_W$
.
Lemma 2.18. Let
![]() $G/{\mathbb {Z}}[1/N]$
be a smooth affine group scheme with reductive connected component of identity. Let V be a free
$G/{\mathbb {Z}}[1/N]$
be a smooth affine group scheme with reductive connected component of identity. Let V be a free
![]() ${\mathbb {Z}}[1/N]$
-module of finite rank, and let
${\mathbb {Z}}[1/N]$
-module of finite rank, and let
![]() $\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a homomorphism of algebraic groups. Let
$\rho \colon G \to \operatorname {\mathrm {GL}}_V$
be a homomorphism of algebraic groups. Let
![]() $\mathtt G_{\ell _0^{\infty }}$
be a Zariski dense subgroup of
$\mathtt G_{\ell _0^{\infty }}$
be a Zariski dense subgroup of
![]() $G_{{\mathbb {Q}}_{\ell _0}}$
. If
$G_{{\mathbb {Q}}_{\ell _0}}$
. If
![]() $r(\mathtt G_{\ell _0^{\infty }},\rho ) \ge r$
, then
$r(\mathtt G_{\ell _0^{\infty }},\rho ) \ge r$
, then
![]() $r_{{\mathbb {Q}}_\ell }(G,\rho ) \ge r$
for
$r_{{\mathbb {Q}}_\ell }(G,\rho ) \ge r$
for
![]() $\ell $
in a set of positive density. If
$\ell $
in a set of positive density. If
![]() $G/G^\circ $
is split, then this holds for all
$G/G^\circ $
is split, then this holds for all
![]() $\ell $
.
$\ell $
.
Proof. By Lemma 2.14,
![]() $r_\ell (G^\circ ,\rho ) \ge r$
for all
$r_\ell (G^\circ ,\rho ) \ge r$
for all
![]() $\ell $
. Using the same technique as in the proof of Lemma 2.16 to move from
$\ell $
. Using the same technique as in the proof of Lemma 2.16 to move from
![]() $G^\circ $
to G, we find that
$G^\circ $
to G, we find that
![]() $r_{\mathbb {Q}}(G,\rho ) \ge r$
; for
$r_{\mathbb {Q}}(G,\rho ) \ge r$
; for
![]() $\ell $
in a set of positive density,
$\ell $
in a set of positive density,
![]() $r_\ell (G,\rho ) \ge r$
; and that this holds for all sufficiently large
$r_\ell (G,\rho ) \ge r$
; and that this holds for all sufficiently large
![]() $\ell $
if
$\ell $
if
![]() $G/G^\circ $
is split. In particular, by Lemma 2.11(c),
$G/G^\circ $
is split. In particular, by Lemma 2.11(c),
![]() $\dim V_{\mathbb {Q}}^{G^\circ _{\mathbb {Q}}} \ge r$
.
$\dim V_{\mathbb {Q}}^{G^\circ _{\mathbb {Q}}} \ge r$
.
Now, let
![]() $\ell $
be any prime for which
$\ell $
be any prime for which
![]() $r_\ell (G,\rho ) \ge r$
and
$r_\ell (G,\rho ) \ge r$
and
![]() $\ell \nmid [G:G^\circ ]$
; by Lemma 2.17,
$\ell \nmid [G:G^\circ ]$
; by Lemma 2.17,
![]() $r_{{\mathbb {Q}}_\ell }(G,\rho ) \ge r$
.
$r_{{\mathbb {Q}}_\ell }(G,\rho ) \ge r$
.
3 Torsion points on abelian varieties
3.1 Torsion points and Galois representations
For the purpose of establishing notation, let
![]() $A/K$
be an abelian variety over a perfect field. For a natural number N, we let
$A/K$
be an abelian variety over a perfect field. For a natural number N, we let
![]() $K_{A, N}$
be the field of definition of the N-torsion of A. We further let
$K_{A, N}$
be the field of definition of the N-torsion of A. We further let
![]() $K_{A, \ell ^{\infty }} = \bigcup _n K_{A, \ell ^n}$
, and let
$K_{A, \ell ^{\infty }} = \bigcup _n K_{A, \ell ^n}$
, and let
![]() $K_A = \bigcup _N K_{A, N}$
be the field obtained by adjoining the coordinates of all torsion points of A. Finally, we let
$K_A = \bigcup _N K_{A, N}$
be the field obtained by adjoining the coordinates of all torsion points of A. Finally, we let
![]() $A_N = A[N]({\overline {K}})$
be the geometric N-torsion, and
$A_N = A[N]({\overline {K}})$
be the geometric N-torsion, and
![]() $A_{\ell ^{\infty }} = \cup _n A_{\ell ^n}$
.
$A_{\ell ^{\infty }} = \cup _n A_{\ell ^n}$
.
For a fixed prime
![]() $\ell $
, we have the usual representations
$\ell $
, we have the usual representations

with respective images
![]() $\Gamma _{A/K,\ell }$
and
$\Gamma _{A/K,\ell }$
and
![]() $\Gamma _{A/K,\ell ^{\infty }}$
.
$\Gamma _{A/K,\ell ^{\infty }}$
.
3.1.1 Independence
Serre has shown that, while the
![]() $\ell $
-adic representations attached to an abelian variety are compatible, they are also independent.
$\ell $
-adic representations attached to an abelian variety are compatible, they are also independent.
For an abelian variety
![]() $A/K$
and a prime
$A/K$
and a prime
![]() $\ell $
, briefly let
$\ell $
, briefly let ![]() . Say that
. Say that
![]() $A/K$
has independent torsion fields if, for each prime
$A/K$
has independent torsion fields if, for each prime
![]() $\ell $
, the Galois extensions
$\ell $
, the Galois extensions
![]() $K_{A,\ell ^{\infty }}$
and
$K_{A,\ell ^{\infty }}$
and
![]() $K^{\prime }_{A,\ell }$
are linearly disjoint over K. (Note that the compositum
$K^{\prime }_{A,\ell }$
are linearly disjoint over K. (Note that the compositum
![]() $K_{A,\ell ^{\infty }} K^{\prime }_{A,\ell }$
is simply
$K_{A,\ell ^{\infty }} K^{\prime }_{A,\ell }$
is simply
![]() $K_A$
, the field generated by the torsion points of A.)
$K_A$
, the field generated by the torsion points of A.)
Lemma 3.1. Let
![]() $A/K$
be an abelian variety over a number field.
$A/K$
be an abelian variety over a number field.
-
(a) There exists a finite extension
 $K^{\operatorname {ind}}/K$
such that
$K^{\operatorname {ind}}/K$
such that
 $A/K^{\operatorname {ind}}$
has independent torsion fields.
$A/K^{\operatorname {ind}}$
has independent torsion fields. -
(b) If
 $L/K^{\operatorname {ind}}$
is any algebraic extension, then
$L/K^{\operatorname {ind}}$
is any algebraic extension, then
 $A/L$
has independent torsion fields.
$A/L$
has independent torsion fields.
Proof. See [Reference Serre38, théorème 1 and §3] or [Reference Böckle, Gajda and Petersen3, §1].
Lemma 3.2. Let A and B be abelian varieties over a number field K, and suppose that
![]() $A\times B$
has independent torsion fields. Then
$A\times B$
has independent torsion fields. Then
Proof. It suffices to show that
![]() $A[\ell ^{\infty }](K_B) \subset A[\ell ^{\infty }](K_{B,\ell ^{\infty }})$
. Assuming that
$A[\ell ^{\infty }](K_B) \subset A[\ell ^{\infty }](K_{B,\ell ^{\infty }})$
. Assuming that
![]() $P\in A[\ell ^{\infty }](K_{B})$
, we denote by
$P\in A[\ell ^{\infty }](K_{B})$
, we denote by
![]() $K(P)$
the extension of K by adjoining the coordinates of P. Then
$K(P)$
the extension of K by adjoining the coordinates of P. Then
![]() $K(P)\subset K_{A\times B, \ell ^{\infty }}$
. We also have
$K(P)\subset K_{A\times B, \ell ^{\infty }}$
. We also have
![]() $K(P)\subset K_B=K_{B, \ell ^{\infty }}\cdot K^{\prime }_{B, \ell }$
. Notice that
$K(P)\subset K_B=K_{B, \ell ^{\infty }}\cdot K^{\prime }_{B, \ell }$
. Notice that
![]() $A\times B$
has independent torsion fields, so
$A\times B$
has independent torsion fields, so
![]() $K\subset K_{A\times B, \ell ^{\infty }}\cap K^{\prime }_{B, \ell }\subset K_{A\times B, \ell ^{\infty }}\cap K^{\prime }_{A\times B,\ell }=K$
, which tells us that every inclusion here is actually an equality. Hence, one has that
$K\subset K_{A\times B, \ell ^{\infty }}\cap K^{\prime }_{B, \ell }\subset K_{A\times B, \ell ^{\infty }}\cap K^{\prime }_{A\times B,\ell }=K$
, which tells us that every inclusion here is actually an equality. Hence, one has that
This means that
![]() $P\in A[\ell ^{\infty }](K_{B, \ell ^{\infty }})$
.
$P\in A[\ell ^{\infty }](K_{B, \ell ^{\infty }})$
.
3.1.2 Connectedness
We let
![]() $\mathcal G_{A/K,\ell }$
be the Zariski closure of
$\mathcal G_{A/K,\ell }$
be the Zariski closure of
![]() $\Gamma _{A/K,\ell ^{\infty }}$
in
$\Gamma _{A/K,\ell ^{\infty }}$
in
![]() $\operatorname {\mathrm {GL}}_{H_1(A_{\overline {K}}, {\mathbb {Q}}_{\ell })} = \operatorname {\mathrm {GL}}_{T_\ell A \otimes {\mathbb {Q}}_\ell }$
, with connected component
$\operatorname {\mathrm {GL}}_{H_1(A_{\overline {K}}, {\mathbb {Q}}_{\ell })} = \operatorname {\mathrm {GL}}_{T_\ell A \otimes {\mathbb {Q}}_\ell }$
, with connected component
![]() $\mathcal G_{A/K,\ell }^{\circ }$
. In general,
$\mathcal G_{A/K,\ell }^{\circ }$
. In general,
![]() $\mathcal G_{A/K,\ell }$
does not have to be connected, but when K is a number field,
$\mathcal G_{A/K,\ell }$
does not have to be connected, but when K is a number field,
![]() $\mathcal G_{A/K,\ell }$
will be connected after a finite extension of K which is independent of
$\mathcal G_{A/K,\ell }$
will be connected after a finite extension of K which is independent of
![]() $\ell $
.
$\ell $
.
Lemma 3.3. Suppose
![]() $K/{\mathbb {Q}}$
is a finite extension. Then:
$K/{\mathbb {Q}}$
is a finite extension. Then:
-
(a) The finite quotient group
 $\mathcal G_{A/K,\ell }/\mathcal G_{A/K,\ell }^\circ $
is independent of
$\mathcal G_{A/K,\ell }/\mathcal G_{A/K,\ell }^\circ $
is independent of
 $\ell $
.
$\ell $
. -
(b) There exists a finite extension
 $K^{\operatorname {conn}}$
of K such that, if L is any finite extension of
$K^{\operatorname {conn}}$
of K such that, if L is any finite extension of
 $K^{\operatorname {conn}}$
and
$K^{\operatorname {conn}}$
and
 $\ell $
is any prime number, the corresponding
$\ell $
is any prime number, the corresponding
 $\mathcal G_{A/L,\ell }$
is connected.
$\mathcal G_{A/L,\ell }$
is connected.
Proof. See [Reference Serre37] or [Reference Larsen and Pink13, Prop. 6.14].
(In contrast, Example 5.7 will show that if K is algebraic but infinite, then such a finite connectedness extension need not exist.)
3.2 Mumford–Tate conjecture
This section is devoted to recalling the Mumford–Tate conjecture. In particular, we will review a result of Cadoret and Moonen [Reference Cadoret and Moonen4, §1] and of Hindry and Ratazzi [Reference Hindry and Ratazzi8] which states that as
![]() $\ell $
varies, the
$\ell $
varies, the
![]() $\ell $
-adic image of the Galois group is a bounded index subgroup of the
$\ell $
-adic image of the Galois group is a bounded index subgroup of the
![]() $\mathbb Z_{\ell }$
-points of the Mumford–Tate group.
$\mathbb Z_{\ell }$
-points of the Mumford–Tate group.
Let K be a number field, embedded in
![]() ${\mathbb {C}}$
. To ease notation slightly, we write
${\mathbb {C}}$
. To ease notation slightly, we write
![]() $\operatorname {\mathrm {MT}}(A)$
for the Mumford–Tate group of an abelian variety A over K, that is,
$\operatorname {\mathrm {MT}}(A)$
for the Mumford–Tate group of an abelian variety A over K, that is, ![]() (cf. §4.1). This is a connected
(cf. §4.1). This is a connected
![]() ${\mathbb {Q}}$
-algebraic group. Let
${\mathbb {Q}}$
-algebraic group. Let
![]() $G_A$
be the Zariski closure of
$G_A$
be the Zariski closure of
![]() $\operatorname {\mathrm {MT}}(A)$
in
$\operatorname {\mathrm {MT}}(A)$
in
![]() $\operatorname {\mathrm {GL}}_{H_1(A_{\mathbb {C}},{\mathbb {Z}})}$
; it is a group scheme over
$\operatorname {\mathrm {GL}}_{H_1(A_{\mathbb {C}},{\mathbb {Z}})}$
; it is a group scheme over
![]() ${\mathbb {Z}}$
. Then
${\mathbb {Z}}$
. Then
![]() $G_A$
is smooth over
$G_A$
is smooth over
![]() ${\mathbb {Z}}[1/N_A]$
for some positive integer
${\mathbb {Z}}[1/N_A]$
for some positive integer
![]() $N_A$
, and
$N_A$
, and
![]() $G_{A,{\mathbb {Q}}} = \operatorname {\mathrm {MT}}(A)$
.
$G_{A,{\mathbb {Q}}} = \operatorname {\mathrm {MT}}(A)$
.
If
![]() $K =K^{\textrm {conn}}$
, then it is known that there is a natural inclusion
$K =K^{\textrm {conn}}$
, then it is known that there is a natural inclusion
![]() $\Gamma _{A/K,\ell ^{\infty }} \subset \operatorname {\mathrm {MT}}(A)({\mathbb {Q}}_\ell )$
, and thus an inclusion
$\Gamma _{A/K,\ell ^{\infty }} \subset \operatorname {\mathrm {MT}}(A)({\mathbb {Q}}_\ell )$
, and thus an inclusion
![]() $G_{A/K,\ell ^{\infty }} \hookrightarrow \operatorname {\mathrm {MT}}(A)_{{\mathbb {Q}}_\ell }$
of algebraic groups over
$G_{A/K,\ell ^{\infty }} \hookrightarrow \operatorname {\mathrm {MT}}(A)_{{\mathbb {Q}}_\ell }$
of algebraic groups over
![]() ${\mathbb {Q}}_\ell $
. The Mumford–Tate conjecture asserts that this inclusion is actually an isomorphism. More precisely, for every prime
${\mathbb {Q}}_\ell $
. The Mumford–Tate conjecture asserts that this inclusion is actually an isomorphism. More precisely, for every prime
![]() $\ell \nmid N$
, both
$\ell \nmid N$
, both ![]() and
and
![]() $\mathcal {G}_{A/K, \ell }^{\circ }$
are subgroup schemes of
$\mathcal {G}_{A/K, \ell }^{\circ }$
are subgroup schemes of
![]() $\operatorname {\mathrm {GL}}_{H^1(A, {\mathbb {Z}}_\ell )}$
. The following conjecture claims the comparison result of the two group schemes.
$\operatorname {\mathrm {GL}}_{H^1(A, {\mathbb {Z}}_\ell )}$
. The following conjecture claims the comparison result of the two group schemes.
Conjecture 3.4 [Reference Cadoret and Moonen4, Mumford–Tate conjecture].
With the above notations,
![]() $G_{A, \ell }=\mathcal {G}_{A/K, \ell }^{\circ }$
.
$G_{A, \ell }=\mathcal {G}_{A/K, \ell }^{\circ }$
.
Remark 3.5. Conjecture 3.4 is equivalent to the usual statement
for every prime
![]() $\ell $
[Reference Cadoret and Moonen4].
$\ell $
[Reference Cadoret and Moonen4].
In this article, the Mumford–Tate conjecture is a standing assumption we require in order to make any significant progress. The conjecture is known to be true for large classes of abelian varieties. For example, it is known that an absolutely simple abelian variety A of dimension g satisfies the Mumford–Tate conjecture in any of the following settings:
-
1. g is prime [Reference Ribet32, Reference Tankeev42, Reference Tankeev43];
-
2.
 $g \le 3$
[Reference Moonen and Zarhin23];
$g \le 3$
[Reference Moonen and Zarhin23]; -
3.
 , and g satisfies certain numerical conditions (e.g., g is odd) [Reference Pink28];
, and g satisfies certain numerical conditions (e.g., g is odd) [Reference Pink28]; -
4. A has complex multiplication [Reference Pohlmann30, Reference Yu45].
Our list is far from complete. See also [Reference Vasiu44] and the discussion in [Reference Moonen22, §2.4.] for additional references and known results. Moreover, if the Mumford–Tate conjecture is true for abelian varieties A and B, then it is also true for their product
![]() $A\times B$
[Reference Commelin6].
$A\times B$
[Reference Commelin6].
In the presence of the Mumford–Tate conjecture, we have good control over
![]() $\Gamma _{A/K,\ell ^{\infty }}$
.
$\Gamma _{A/K,\ell ^{\infty }}$
.
Theorem 3.6 [Reference Cadoret and Moonen4, Th. A], [Reference Hindry and Ratazzi8, théorème 10.1].
Let A be an abelian variety defined over K, assume
![]() $K=K^{\mathrm{conn}}$
, and assume that the Mumford–Tate conjecture is true for A. Then the index
$K=K^{\mathrm{conn}}$
, and assume that the Mumford–Tate conjecture is true for A. Then the index
![]() $[G_A({\mathbb {Z}}_\ell ): \Gamma _{A/K, \ell ^{\infty }}]$
is bounded when
$[G_A({\mathbb {Z}}_\ell ): \Gamma _{A/K, \ell ^{\infty }}]$
is bounded when
![]() $\ell $
varies.
$\ell $
varies.
In particular,
![]() ${\left \{{\Gamma _{A/K,\ell }}\right \}}$
is a collection of bounded subgroups of
${\left \{{\Gamma _{A/K,\ell }}\right \}}$
is a collection of bounded subgroups of
![]() $G_A$
.
$G_A$
.
4 Torsion-finite pairs of abelian varieties
4.1 Mumford–Tate groups for a pair of abelian varieties
Let A and B be abelian varieties over a subfield K of
![]() ${\mathbb {C}}$
. Let
${\mathbb {C}}$
. Let
![]() $G_A$
,
$G_A$
,
![]() $G_B$
, and
$G_B$
, and
![]() $G_{A\times B}$
denote the (
$G_{A\times B}$
denote the (
![]() ${\mathbb {Z}}$
-models of) the Mumford–Tate groups of, respectively, A, B, and
${\mathbb {Z}}$
-models of) the Mumford–Tate groups of, respectively, A, B, and
![]() $A\times B$
, and let
$A\times B$
, and let
![]() $sG_A$
,
$sG_A$
,
![]() $sG_B$
, and
$sG_B$
, and
![]() $sG_{A\times B}$
denote their respective Hodge groups. Recall that the Mumford–Tate group
$sG_{A\times B}$
denote their respective Hodge groups. Recall that the Mumford–Tate group
![]() $G_C$
of a complex abelian variety C is the
$G_C$
of a complex abelian variety C is the
![]() ${\mathbb {Q}}$
-algebraic hull of the morphism
${\mathbb {Q}}$
-algebraic hull of the morphism ![]() defining the Hodge structure on
defining the Hodge structure on
![]() $H_1(C,{\mathbb {Q}})$
. Equivalently, it is the Tannakian fundamental group (really, the group which represents automorphisms of the fiber functor which sends a Hodge structure V to its underlying vector space
$H_1(C,{\mathbb {Q}})$
. Equivalently, it is the Tannakian fundamental group (really, the group which represents automorphisms of the fiber functor which sends a Hodge structure V to its underlying vector space
![]() $|V|$
) of
$|V|$
) of
![]() ${\langle {H_1(C,{\mathbb {Q}})} \rangle }$
, the tensor category generated by the Hodge structure
${\langle {H_1(C,{\mathbb {Q}})} \rangle }$
, the tensor category generated by the Hodge structure
![]() $H_1(C,{\mathbb {Q}})$
. Since
$H_1(C,{\mathbb {Q}})$
. Since
![]() $H^1(C,{\mathbb {Q}})$
is dual to
$H^1(C,{\mathbb {Q}})$
is dual to
![]() $H_1(C,{\mathbb {Q}})$
, the tensor categories
$H_1(C,{\mathbb {Q}})$
, the tensor categories
![]() ${\langle {H_1(C,{\mathbb {Q}})} \rangle }$
and
${\langle {H_1(C,{\mathbb {Q}})} \rangle }$
and
![]() ${\langle {H^1(C,{\mathbb {Q}})} \rangle }$
coincide, and we may use either description to compute
${\langle {H^1(C,{\mathbb {Q}})} \rangle }$
coincide, and we may use either description to compute
![]() $\operatorname {\mathrm {MT}}(C)$
. We have
$\operatorname {\mathrm {MT}}(C)$
. We have
![]() $G_C/sG_C \cong {\mathbb {G}}_m$
.
$G_C/sG_C \cong {\mathbb {G}}_m$
.
Since
![]() $H_1(A\times B,{\mathbb {Q}}) \cong H_1(A,{\mathbb {Q}})\oplus H_1(B,{\mathbb {Q}})$
is an object of
$H_1(A\times B,{\mathbb {Q}}) \cong H_1(A,{\mathbb {Q}})\oplus H_1(B,{\mathbb {Q}})$
is an object of
![]() ${\langle {H_1(A,{\mathbb {Q}}),H_1(B,{\mathbb {Q}})} \rangle }$
, there is a canonical inclusion
${\langle {H_1(A,{\mathbb {Q}}),H_1(B,{\mathbb {Q}})} \rangle }$
, there is a canonical inclusion
![]() $\iota \colon G_{A\times B} \hookrightarrow G_A\times G_B$
. Moreover,
$\iota \colon G_{A\times B} \hookrightarrow G_A\times G_B$
. Moreover,
![]() $H_1(A,{\mathbb {Q}})$
and
$H_1(A,{\mathbb {Q}})$
and
![]() $H_1(B,{\mathbb {Q}})$
are both objects of
$H_1(B,{\mathbb {Q}})$
are both objects of
![]() ${\langle {H_1(A\times B,{\mathbb {Q}})} \rangle }$
. The corresponding inclusions
${\langle {H_1(A\times B,{\mathbb {Q}})} \rangle }$
. The corresponding inclusions
![]() ${\langle {H_1(A,{\mathbb {Q}})} \rangle } \hookrightarrow {\langle {H_1(A\times B,{\mathbb {Q}})} \rangle }$
and
${\langle {H_1(A,{\mathbb {Q}})} \rangle } \hookrightarrow {\langle {H_1(A\times B,{\mathbb {Q}})} \rangle }$
and
![]() ${\langle {H_1(B,{\mathbb {Q}})} \rangle }\hookrightarrow {\langle {H_1(A\times B,{\mathbb {Q}})} \rangle }$
yield surjections
${\langle {H_1(B,{\mathbb {Q}})} \rangle }\hookrightarrow {\langle {H_1(A\times B,{\mathbb {Q}})} \rangle }$
yield surjections
![]() $G_{A\times B} \twoheadrightarrow G_A$
and
$G_{A\times B} \twoheadrightarrow G_A$
and
![]() $G_{A\times B}\twoheadrightarrow G_B$
. Thus, the three algebraic groups
$G_{A\times B}\twoheadrightarrow G_B$
. Thus, the three algebraic groups
![]() $G_A$
,
$G_A$
,
![]() $G_B$
, and
$G_B$
, and
![]() $G_{A\times B}$
satisfy the hypotheses of Goursat’s lemma (Lemma 2.1), and fit in a diagram as follows.
$G_{A\times B}$
satisfy the hypotheses of Goursat’s lemma (Lemma 2.1), and fit in a diagram as follows.

Let
![]() $M_{A,B} = \ker (\pi _B\circ \iota )$
; under the isomorphism
$M_{A,B} = \ker (\pi _B\circ \iota )$
; under the isomorphism
![]() $G_A\times {\left \{e\right \}} \cong G_A$
, it is isomorphic to a normal algebraic subgroup
$G_A\times {\left \{e\right \}} \cong G_A$
, it is isomorphic to a normal algebraic subgroup
![]() $H_{A,B}$
of
$H_{A,B}$
of
![]() $G_A$
. Define
$G_A$
. Define
![]() $M_{B,A}$
and
$M_{B,A}$
and
![]() $H_{B, A}$
in an analogous fashion. Because
$H_{B, A}$
in an analogous fashion. Because
![]() $H_1(A,{\mathbb {Q}})$
and
$H_1(A,{\mathbb {Q}})$
and
![]() $H_1(B,{\mathbb {Q}})$
have the same nonzero weight,
$H_1(B,{\mathbb {Q}})$
have the same nonzero weight,
![]() $H_{A,B} \subset sG_A$
and
$H_{A,B} \subset sG_A$
and
![]() $H_{B,A} \subset sG_B$
. Consequently, the Hodge groups also satisfy the hypotheses of Goursat’s lemma, that is, fit in a diagram:
$H_{B,A} \subset sG_B$
. Consequently, the Hodge groups also satisfy the hypotheses of Goursat’s lemma, that is, fit in a diagram:

In particular,
![]() $sG_{A\times B}$
is the inverse image in
$sG_{A\times B}$
is the inverse image in
![]() $sG_A\times sG_B$
of the graph of an isomorphism
$sG_A\times sG_B$
of the graph of an isomorphism
For future use, we record the following observation.
Lemma 4.1. Let A and B be complex abelian varieties. The following are equivalent.
-
(a) A and B are isogenous.
-
(b)
 $H_1(A,{\mathbb {Q}})$
and
$H_1(A,{\mathbb {Q}})$
and
 $H_1(B,{\mathbb {Q}})$
are isomorphic representations of
$H_1(B,{\mathbb {Q}})$
are isomorphic representations of
 $\operatorname {\mathrm {sMT}}(A \times B)$
.
$\operatorname {\mathrm {sMT}}(A \times B)$
. -
(c) The canonical surjections
 $\operatorname {\mathrm {sMT}}(A\times B) \twoheadrightarrow \operatorname {\mathrm {sMT}}(A)$
and
$\operatorname {\mathrm {sMT}}(A\times B) \twoheadrightarrow \operatorname {\mathrm {sMT}}(A)$
and
 $\operatorname {\mathrm {sMT}}(A\times B) \twoheadrightarrow \operatorname {\mathrm {sMT}}(B)$
are isomorphisms, and
$\operatorname {\mathrm {sMT}}(A\times B) \twoheadrightarrow \operatorname {\mathrm {sMT}}(B)$
are isomorphisms, and
 $H_1(A,{\mathbb {Q}})$
and
$H_1(A,{\mathbb {Q}})$
and
 $H_1(B,{\mathbb {Q}})$
are isomorphic representations of this common group.
$H_1(B,{\mathbb {Q}})$
are isomorphic representations of this common group.
Proof. The category
![]() ${\langle {H_1(A\times B,{\mathbb {Q}})} \rangle }$
is equivalent to the category of representations of
${\langle {H_1(A\times B,{\mathbb {Q}})} \rangle }$
is equivalent to the category of representations of
![]() $\operatorname {\mathrm {MT}}(A\times B)$
. So
$\operatorname {\mathrm {MT}}(A\times B)$
. So
![]() $H_1(A,{\mathbb {Q}})$
and
$H_1(A,{\mathbb {Q}})$
and
![]() $H_1(B,{\mathbb {Q}})$
are isomorphic in the category of Hodge structures, or equivalently in the full subcategory generated by
$H_1(B,{\mathbb {Q}})$
are isomorphic in the category of Hodge structures, or equivalently in the full subcategory generated by
![]() $H_1(A\times B,{\mathbb {Q}})$
, if and only if they are isomorphic representations of
$H_1(A\times B,{\mathbb {Q}})$
, if and only if they are isomorphic representations of
![]() $\operatorname {\mathrm {MT}}(A\times B)$
. For weight reasons, it suffices to verify this for the Hodge group
$\operatorname {\mathrm {MT}}(A\times B)$
. For weight reasons, it suffices to verify this for the Hodge group
![]() $\operatorname {\mathrm {sMT}}(A\times B)$
. Riemann’s theorem—that the isogeny class of an abelian variety is determined by its Hodge structure—proves the equivalence of (a) and (b).
$\operatorname {\mathrm {sMT}}(A\times B)$
. Riemann’s theorem—that the isogeny class of an abelian variety is determined by its Hodge structure—proves the equivalence of (a) and (b).
If A and B are isogenous, it is well known that
![]() $\operatorname {\mathrm {MT}}(A\times B) \cong \operatorname {\mathrm {MT}}(A) \cong \operatorname {\mathrm {MT}}(B)$
(e.g., [Reference Moonen21, Rem. 1.8]). Conversely, under the hypothesis of (c), weight considerations show that the corresponding hypothesis holds for Mumford–Tate groups, too. Now, use the fact that
$\operatorname {\mathrm {MT}}(A\times B) \cong \operatorname {\mathrm {MT}}(A) \cong \operatorname {\mathrm {MT}}(B)$
(e.g., [Reference Moonen21, Rem. 1.8]). Conversely, under the hypothesis of (c), weight considerations show that the corresponding hypothesis holds for Mumford–Tate groups, too. Now, use the fact that
![]() $\operatorname {\mathrm {MT}}(A)$
is canonically isomorphic to the image of
$\operatorname {\mathrm {MT}}(A)$
is canonically isomorphic to the image of
![]() $\operatorname {\mathrm {MT}}(A\times B)$
in
$\operatorname {\mathrm {MT}}(A\times B)$
in
![]() $\operatorname {\mathrm {GL}}_{H_1(A,{\mathbb {Q}})}$
and the analogous statement for B in order to deduce (b).
$\operatorname {\mathrm {GL}}_{H_1(A,{\mathbb {Q}})}$
and the analogous statement for B in order to deduce (b).
Now, suppose that A and B have complex multiplication (see §5.1 for a review of this concept). Then
![]() $A\times B$
does, too, and the Mumford–Tate groups
$A\times B$
does, too, and the Mumford–Tate groups
![]() $G_A$
,
$G_A$
,
![]() $G_B$
, and
$G_B$
, and
![]() $G_{A\times B}$
are all tori. Taking character groups in (4.1) yields a diagram of
$G_{A\times B}$
are all tori. Taking character groups in (4.1) yields a diagram of
![]() ${\mathbb {Z}}$
-modules
${\mathbb {Z}}$
-modules

In particular, we may use this diagram to compute
![]() $H_{A, B}$
, a group of multiplicative type; it is the group whose character group is
$H_{A, B}$
, a group of multiplicative type; it is the group whose character group is

If we identify
![]() $X^*(G_A)$
and
$X^*(G_A)$
and
![]() $X^*(G_B)$
with their images under, respectively, the inclusions
$X^*(G_B)$
with their images under, respectively, the inclusions
![]() $(\pi _A\circ \iota )^*$
and
$(\pi _A\circ \iota )^*$
and
![]() $(\pi _B\circ \iota )^*$
, we may rewrite this as
$(\pi _B\circ \iota )^*$
, we may rewrite this as

4.2 Galois representations for a pair of abelian varieties
Now, further suppose that K is finitely generated over
![]() ${\mathbb {Q}}$
, and assume that A and B satisfy the Mumford–Tate conjecture.
${\mathbb {Q}}$
, and assume that A and B satisfy the Mumford–Tate conjecture.
Since our main results concern potentially infinite torsion, we will assume that
![]() $A\times B$
has connected, independent Galois representations.
$A\times B$
has connected, independent Galois representations.
For a positive integer N, we identify the Galois group
![]() $\Gamma _{A/K,N}$
with a subgroup
$\Gamma _{A/K,N}$
with a subgroup
![]() $\mathtt G_{A,N}$
of
$\mathtt G_{A,N}$
of
![]() $G_A({\mathbb {Z}}/N)$
, and make similar identifications of the image of
$G_A({\mathbb {Z}}/N)$
, and make similar identifications of the image of
![]() $\operatorname {\mathrm {Gal}}(K)$
acting on the N-torsion of B and of
$\operatorname {\mathrm {Gal}}(K)$
acting on the N-torsion of B and of
![]() $A\times B$
. The N-torsion fields of A and B are then arranged in the following tower, where each extension is labeled with its corresponding Galois group.
$A\times B$
. The N-torsion fields of A and B are then arranged in the following tower, where each extension is labeled with its corresponding Galois group.

Let
![]() ${\mathtt H}_{A,B,\ell ^{\infty }} = \varprojlim _{n}{\mathtt H}_{A,B,\ell ^n} \subset H_{A,B}({\mathbb {Z}}_\ell )$
.
${\mathtt H}_{A,B,\ell ^{\infty }} = \varprojlim _{n}{\mathtt H}_{A,B,\ell ^n} \subset H_{A,B}({\mathbb {Z}}_\ell )$
.
We have
![]() $\operatorname {\mathrm {Gal}}(K_{B,\ell } K_{A,\ell }/K_{B,\ell }) = \mathtt M_{A,B,\ell } \cong {\mathtt H}_{A,B,\ell } \subseteq H_{A,B}({\mathbb {F}}_\ell )$
, and
$\operatorname {\mathrm {Gal}}(K_{B,\ell } K_{A,\ell }/K_{B,\ell }) = \mathtt M_{A,B,\ell } \cong {\mathtt H}_{A,B,\ell } \subseteq H_{A,B}({\mathbb {F}}_\ell )$
, and
![]() $A[\ell ](K_{B,\ell })$
is the set of elements of
$A[\ell ](K_{B,\ell })$
is the set of elements of
![]() $A_\ell $
fixed by
$A_\ell $
fixed by
![]() ${{\mathtt H}}_{A,B,\ell }$
.
${{\mathtt H}}_{A,B,\ell }$
.
Lemma 4.2. Let A and B be abelian varieties over a number field K. Suppose that
![]() $A\times B$
has independent Galois representations. Then, for each prime
$A\times B$
has independent Galois representations. Then, for each prime
![]() $\ell $
,
$\ell $
,
![]() $A[\ell ](K_B)$
is nontrivial if and only if
$A[\ell ](K_B)$
is nontrivial if and only if
![]() $A[\ell ](K_{B,\ell })$
is nontrivial.
$A[\ell ](K_{B,\ell })$
is nontrivial.
Proof. By independence,
![]() $A[\ell ](K_B) = A[\ell ](K_{B,\ell ^{\infty }})$
(Lemma 3.2). Suppose that, for some
$A[\ell ](K_B) = A[\ell ](K_{B,\ell ^{\infty }})$
(Lemma 3.2). Suppose that, for some
![]() $n> 1$
,
$n> 1$
,
![]() $\#A[\ell ](K_{B,\ell ^n})> 1$
; equivalently,
$\#A[\ell ](K_{B,\ell ^n})> 1$
; equivalently,
![]() $\operatorname {\mathrm {Gal}}(K_{B,\ell ^n})$
has a nontrivial fixed point in
$\operatorname {\mathrm {Gal}}(K_{B,\ell ^n})$
has a nontrivial fixed point in
![]() $A_\ell $
. By Lemma 2.7, in order to show that
$A_\ell $
. By Lemma 2.7, in order to show that
![]() $\operatorname {\mathrm {Gal}}(K_{B,\ell })$
has a nontrivial fixed point in
$\operatorname {\mathrm {Gal}}(K_{B,\ell })$
has a nontrivial fixed point in
![]() $A_\ell $
, it suffices to show that
$A_\ell $
, it suffices to show that
![]() $[\operatorname {\mathrm {Gal}}(K_{B,\ell ^n}):\operatorname {\mathrm {Gal}}(K_{B,\ell })]$
is a power of
$[\operatorname {\mathrm {Gal}}(K_{B,\ell ^n}):\operatorname {\mathrm {Gal}}(K_{B,\ell })]$
is a power of
![]() $\ell $
. This last claim follows from the inclusions
$\ell $
. This last claim follows from the inclusions
Lemma 4.3. Let A and B be abelian varieties over a number field K. Suppose that A and B satisfy the Mumford–Tate conjecture, and that
![]() $A\times B$
has connected Galois representations. Then:
$A\times B$
has connected Galois representations. Then:
-
(a)
 ${\left \{{ {\mathtt H}_{A,B,\ell }\cap H_{A,B}^\circ ({\mathbb {F}}_\ell )}\right \}}$
is a collection of bounded subgroups of
${\left \{{ {\mathtt H}_{A,B,\ell }\cap H_{A,B}^\circ ({\mathbb {F}}_\ell )}\right \}}$
is a collection of bounded subgroups of
 $H_{A,B}^\circ $
; and
$H_{A,B}^\circ $
; and -
(b)
 ${\mathtt H}_{A,B,\ell ^{\infty }}\cap H_{A,B}^\circ ({\mathbb {Z}}_\ell )$
is Zariski dense in
${\mathtt H}_{A,B,\ell ^{\infty }}\cap H_{A,B}^\circ ({\mathbb {Z}}_\ell )$
is Zariski dense in
 $H_{A,B,{\mathbb {Q}}_\ell }^\circ $
.
$H_{A,B,{\mathbb {Q}}_\ell }^\circ $
.
Proof. Since
![]() $A\times B$
satisfies the Mumford–Tate conjecture,
$A\times B$
satisfies the Mumford–Tate conjecture,
![]() ${\left \{{\mathtt G_{A\times B,\ell }}\right \}}$
is bounded in
${\left \{{\mathtt G_{A\times B,\ell }}\right \}}$
is bounded in
![]() $G_{A\times B}$
(Theorem 3.6). Now, apply Lemma 2.10(b) to the exact sequence
$G_{A\times B}$
(Theorem 3.6). Now, apply Lemma 2.10(b) to the exact sequence
to deduce (a).
For a fixed
![]() $\ell $
, there exists an
$\ell $
, there exists an
![]() $n = n_\ell $
such that
$n = n_\ell $
such that
![]() $\mathtt G_{A,\ell ^{\infty }}$
contains
$\mathtt G_{A,\ell ^{\infty }}$
contains
![]() $\ker (G_A({\mathbb {Z}}_\ell )\to G_A({\mathbb {Z}}_\ell /\ell ^n))$
, and so
$\ker (G_A({\mathbb {Z}}_\ell )\to G_A({\mathbb {Z}}_\ell /\ell ^n))$
, and so
![]() ${\mathtt H}_{A,B,\ell ^{\infty }}\cap H_{A,B}^\circ ({\mathbb {Z}}_\ell )$
contains
${\mathtt H}_{A,B,\ell ^{\infty }}\cap H_{A,B}^\circ ({\mathbb {Z}}_\ell )$
contains
![]() $\ker (H_{A,B}^\circ ({\mathbb {Z}}_\ell ) \to H_{A,B}^\circ ({\mathbb {Z}}_\ell /\ell ^n))$
. Then counting points (with values in
$\ker (H_{A,B}^\circ ({\mathbb {Z}}_\ell ) \to H_{A,B}^\circ ({\mathbb {Z}}_\ell /\ell ^n))$
. Then counting points (with values in
![]() ${\mathbb {Z}}_\ell /\ell ^{m+n}$
for
${\mathbb {Z}}_\ell /\ell ^{m+n}$
for
![]() $m\gg 0$
) shows that the Zariski closure of
$m\gg 0$
) shows that the Zariski closure of
![]() ${\mathtt H}_{A,B,\ell ^{\infty }}\cap H_{A,B}^\circ ({\mathbb {Z}}_\ell )$
, a closed subgroup of the irreducible variety
${\mathtt H}_{A,B,\ell ^{\infty }}\cap H_{A,B}^\circ ({\mathbb {Z}}_\ell )$
, a closed subgroup of the irreducible variety
![]() $H_{A,B,{\mathbb {Q}}_\ell }^\circ $
, must be all of
$H_{A,B,{\mathbb {Q}}_\ell }^\circ $
, must be all of
![]() $H^\circ _{A,B,{\mathbb {Q}}_\ell }$
.
$H^\circ _{A,B,{\mathbb {Q}}_\ell }$
.
4.3 Preliminaries on torsion finiteness
If two abelian varieties are isomorphic, or more generally isogenous, then it is easy to see that each is torsion infinite for the other:
Lemma 4.4. Let A and B be abelian varieties over a number field K.
-
(a) If A and
 $A'$
are isogenous over K, and if B and
$A'$
are isogenous over K, and if B and
 $B'$
are isogenous over K, then A is torsion finite for B over K if and only if
$B'$
are isogenous over K, then A is torsion finite for B over K if and only if
 $A'$
is torsion finite for
$A'$
is torsion finite for
 $B'$
over K.
$B'$
over K. -
(b) If
 $L/K$
is a finite extension, and if
$L/K$
is a finite extension, and if
 $A_L$
is torsion finite for
$A_L$
is torsion finite for
 $B_L$
over L, then A is torsion finite for B over K.
$B_L$
over L, then A is torsion finite for B over K. -
(c) If m and n are two positive integers, then A is torsion finite for B over K if and only if
 $A^{m}$
is torsion finite for
$A^{m}$
is torsion finite for
 $B^{n}$
over K.
$B^{n}$
over K.
Proof. Let
![]() $g\colon B \to B'$
be an isogeny of exponent N; there is an isogeny
$g\colon B \to B'$
be an isogeny of exponent N; there is an isogeny
![]() $g'\colon B' \to B$
such that
$g'\colon B' \to B$
such that
![]() $g'\circ g = [N]_B$
. Then, for any (not necessarily finite) field extension
$g'\circ g = [N]_B$
. Then, for any (not necessarily finite) field extension
![]() $F/K$
, one has
$F/K$
, one has
In particular,
![]() $B(F)_{\mathrm{tors}}$
and
$B(F)_{\mathrm{tors}}$
and
![]() $B'(F)_{\mathrm{tors}}$
are either both finite or infinite. Moreover, one can also deduce that
$B'(F)_{\mathrm{tors}}$
are either both finite or infinite. Moreover, one can also deduce that
![]() $K_B=K_{B'}$
. We deduce (a) after applying the same argument to A and
$K_B=K_{B'}$
. We deduce (a) after applying the same argument to A and
![]() $A'$
.
$A'$
.
Part (b) is obvious since
![]() $L_B$
contains
$L_B$
contains
![]() $K_B$
.
$K_B$
.
Part (c) follows from the observation that
![]() $K_{C,N}=K_{C^{r}, N}$
for any abelian variety
$K_{C,N}=K_{C^{r}, N}$
for any abelian variety
![]() $C/K$
and any natural numbers r and N.
$C/K$
and any natural numbers r and N.
Lemma 4.5. Suppose A and B are abelian varieties over a field K. There exist a finite extension L and an isogeny of L-abelian varieties
![]() $\oplus _{i=1}^r A_i^{m_i} \to A_L$
with each
$\oplus _{i=1}^r A_i^{m_i} \to A_L$
with each
![]() $A_i$
absolutely simple; and A is essentially torsion finite for B if and only if each
$A_i$
absolutely simple; and A is essentially torsion finite for B if and only if each
![]() $A_i$
is essentially torsion finite for
$A_i$
is essentially torsion finite for
![]() $B_L$
.
$B_L$
.
Proof. The existence of such an L and a factorization of
![]() $A_L$
is standard; since we are only concerned with essential torsion finiteness, we may and do assume
$A_L$
is standard; since we are only concerned with essential torsion finiteness, we may and do assume
![]() $L=K$
. Then A is essentially torsion finite for B if and only if
$L=K$
. Then A is essentially torsion finite for B if and only if
![]() $\oplus _i A_i^{m_i}$
is (Lemma 4.4(a)), which obviously holds if and only if each summand
$\oplus _i A_i^{m_i}$
is (Lemma 4.4(a)), which obviously holds if and only if each summand
![]() $A_i^{m_i}$
is essentially torsion finite for B. By Lemma 4.4(c), this holds if and only if each
$A_i^{m_i}$
is essentially torsion finite for B. By Lemma 4.4(c), this holds if and only if each
![]() $A_i$
is essentially torsion finite for B.
$A_i$
is essentially torsion finite for B.
4.4 Potentially torsion-infinite pairs
If
![]() $H_{A,B}$
is connected and if A acquires infinite torsion over
$H_{A,B}$
is connected and if A acquires infinite torsion over
![]() $K_B$
, then A acquires
$K_B$
, then A acquires
![]() $\ell $
-power torsion for all
$\ell $
-power torsion for all
![]() $\ell $
:
$\ell $
:
Lemma 4.6. Let A and B be abelian varieties over a number field K. Suppose that A and B satisfy the Mumford–Tate conjecture, and that
![]() $A\times B$
has connected independent Galois representations.
$A\times B$
has connected independent Galois representations.
Suppose that
![]() $H_{A,B}$
is connected. Then the following are equivalent:
$H_{A,B}$
is connected. Then the following are equivalent:
-
(a)
 $A(K_B)_{\operatorname {\mathrm {tors}}}$
is infinite.
$A(K_B)_{\operatorname {\mathrm {tors}}}$
is infinite. -
(b) For all
 $\ell $
,
$\ell $
,
 $A[\ell ](K_B)$
is nontrivial.
$A[\ell ](K_B)$
is nontrivial. -
(c) For all
 $\ell $
,
$\ell $
,
 $A[\ell ^{\infty }](K_B)$
is infinite.
$A[\ell ^{\infty }](K_B)$
is infinite.
Proof. It suffices to show that (a) implies each of (b) and (c). Note that, since
![]() $A\times B$
has independent representations,
$A\times B$
has independent representations,
![]() $A[\ell ^{\infty }](K_B) = A[\ell ^{\infty }](K_{B,\ell ^{\infty }})$
.
$A[\ell ^{\infty }](K_B) = A[\ell ^{\infty }](K_{B,\ell ^{\infty }})$
.
By Lemma 4.3,
![]() ${\left \{{{\mathtt H}_{A,B,\ell }}\right \}}$
is a collection of bounded subgroups of the connected group
${\left \{{{\mathtt H}_{A,B,\ell }}\right \}}$
is a collection of bounded subgroups of the connected group
![]() $H_{A,B}$
, and each
$H_{A,B}$
, and each
![]() ${\mathtt H}_{A,B,\ell ^{\infty }}$
is Zariski dense in
${\mathtt H}_{A,B,\ell ^{\infty }}$
is Zariski dense in
![]() $H_{A,B,{\mathbb {Q}}_\ell }$
.
$H_{A,B,{\mathbb {Q}}_\ell }$
.
Suppose that (a) holds; then
![]() $A[\ell ](K_{B,\ell ^{\infty }})$
is nontrivial for infinitely many
$A[\ell ](K_{B,\ell ^{\infty }})$
is nontrivial for infinitely many
![]() $\ell $
, or
$\ell $
, or
![]() $A[\ell _0^{\infty }](K_{B,\ell _0^{\infty }})$
is infinite for some
$A[\ell _0^{\infty }](K_{B,\ell _0^{\infty }})$
is infinite for some
![]() $\ell _0$
. In the former case,
$\ell _0$
. In the former case,
![]() $A[\ell ](K_{B,\ell })$
is nontrivial for infinitely many
$A[\ell ](K_{B,\ell })$
is nontrivial for infinitely many
![]() $\ell $
(Lemma 4.2), and thus
$\ell $
(Lemma 4.2), and thus
![]() $r_\ell (H_{A,B},\rho _A)$
is positive for infinitely many
$r_\ell (H_{A,B},\rho _A)$
is positive for infinitely many
![]() $\ell $
; in the latter,
$\ell $
; in the latter,
![]() $r_{{\mathbb {Q}}_{\ell _0}}(H_{A,B},\rho _A)$
is positive. Thus, by Lemma 2.13 or 2.14,
$r_{{\mathbb {Q}}_{\ell _0}}(H_{A,B},\rho _A)$
is positive. Thus, by Lemma 2.13 or 2.14,
![]() $\rho _{\mathbb {Q}}(H_{A,B},\rho _A)$
is positive; therefore, so is
$\rho _{\mathbb {Q}}(H_{A,B},\rho _A)$
is positive; therefore, so is
![]() $\rho _\ell (H_{A,B},\rho _A)$
and
$\rho _\ell (H_{A,B},\rho _A)$
and
![]() $\rho _{{\mathbb {Q}}_{\ell }}(H_{A,B},\rho _A)$
for each
$\rho _{{\mathbb {Q}}_{\ell }}(H_{A,B},\rho _A)$
for each
![]() $\ell $
. Therefore, both (b) and (c) hold.
$\ell $
. Therefore, both (b) and (c) hold.
In the absence of a connectedness hypothesis on
![]() $H_{A,B}$
, our results are less balanced. Moreover, the Mumford–Tate conjecture does not immediately imply that
$H_{A,B}$
, our results are less balanced. Moreover, the Mumford–Tate conjecture does not immediately imply that
![]() ${\mathtt H}_{A,B,\ell }$
meets every geometrically irreducible component of
${\mathtt H}_{A,B,\ell }$
meets every geometrically irreducible component of
![]() $H_{A,B,\ell }$
. In situations where this is known, however, we can deduce the following statement.
$H_{A,B,\ell }$
. In situations where this is known, however, we can deduce the following statement.
Lemma 4.7. Let A and B be abelian varieties over a number field K. Suppose that A and B satisfy the Mumford–Tate conjecture and that
![]() $A\times B$
has connected, independent Galois representations.
$A\times B$
has connected, independent Galois representations.
Suppose that
![]() $A(K_B)_{\operatorname {\mathrm {tors}}}$
is infinite, and that there exists some
$A(K_B)_{\operatorname {\mathrm {tors}}}$
is infinite, and that there exists some
![]() $\ell _0$
such that
$\ell _0$
such that
![]() $A[\ell _0](K_{B,\ell _0})$
is nontrivial. Additionally, assume that
$A[\ell _0](K_{B,\ell _0})$
is nontrivial. Additionally, assume that
![]() ${\mathtt H}_{A,B,\ell _0}$
meets every geometrically irreducible component of
${\mathtt H}_{A,B,\ell _0}$
meets every geometrically irreducible component of
![]() $H_{A,B,\ell _0}$
, and
$H_{A,B,\ell _0}$
, and
![]() $H_{A,B,{\mathbb {Z}}_{\ell _{0}}}$
is smooth. Then, for
$H_{A,B,{\mathbb {Z}}_{\ell _{0}}}$
is smooth. Then, for
![]() $\ell $
in a set of positive density,
$\ell $
in a set of positive density,
![]() $A[\ell ](K_B)$
is nontrivial and
$A[\ell ](K_B)$
is nontrivial and
![]() $A[\ell ^{\infty }](K_B)$
is infinite.
$A[\ell ^{\infty }](K_B)$
is infinite.
Proof. If
![]() $A[\ell ](K_B)$
is nontrivial for infinitely many
$A[\ell ](K_B)$
is nontrivial for infinitely many
![]() $\ell $
, this follows from Lemma 2.16, applied to the collection of bounded subgroups
$\ell $
, this follows from Lemma 2.16, applied to the collection of bounded subgroups
![]() ${\left \{{{\mathtt H}_{A,B,\ell }}\right \}}$
of
${\left \{{{\mathtt H}_{A,B,\ell }}\right \}}$
of
![]() $H_{A,B}$
. If instead there exists some
$H_{A,B}$
. If instead there exists some
![]() $\ell _1$
such that
$\ell _1$
such that
![]() $A[\ell _1^{\infty }](K_B)$
is infinite, then as in the proof of Lemma 2.18, we find that
$A[\ell _1^{\infty }](K_B)$
is infinite, then as in the proof of Lemma 2.18, we find that
![]() $r_{\mathbb {Q}}(H_{A,B}^\circ ,\rho _A)$
is positive; and that for
$r_{\mathbb {Q}}(H_{A,B}^\circ ,\rho _A)$
is positive; and that for
![]() $\ell $
in a set of positive density (namely, the set of
$\ell $
in a set of positive density (namely, the set of
![]() $\ell $
relatively prime to
$\ell $
relatively prime to
![]() $[H_{A,B}:H_{A,B}^\circ ]$
and with the same Artin symbol as
$[H_{A,B}:H_{A,B}^\circ ]$
and with the same Artin symbol as
![]() $\ell _0$
in some finite splitting field for
$\ell _0$
in some finite splitting field for
![]() $H_{A,B}/H_{A,B}^\circ $
),
$H_{A,B}/H_{A,B}^\circ $
),
![]() $r_\ell (H_{A,B},\rho _A)$
is also positive.
$r_\ell (H_{A,B},\rho _A)$
is also positive.
The hypothesis on
![]() $\ell _0$
in Lemma 4.7 seems difficult to work with abstractly, although in explicit examples one can compute
$\ell _0$
in Lemma 4.7 seems difficult to work with abstractly, although in explicit examples one can compute
![]() $H_{A,B}/H_{A,B}^\circ $
(e.g., Example 5.7) and thereby make progress. However, we can still make a uniform statement purely in terms of torsion, at the cost of surrendering some control of the precise field over which A acquires infinite
$H_{A,B}/H_{A,B}^\circ $
(e.g., Example 5.7) and thereby make progress. However, we can still make a uniform statement purely in terms of torsion, at the cost of surrendering some control of the precise field over which A acquires infinite
![]() $\ell $
-torsion.
$\ell $
-torsion.
Lemma 4.8. Let A and B be abelian varieties over a number field K. Suppose that A and B satisfy the Mumford–Tate conjecture and that
![]() $A\times B$
has connected independent Galois representations.
$A\times B$
has connected independent Galois representations.
Suppose that
![]() $A(K_B)_{\operatorname {\mathrm {tors}}}$
is infinite. Let
$A(K_B)_{\operatorname {\mathrm {tors}}}$
is infinite. Let
![]() $N_{A,B} = [H_{A,B}:H^\circ _{A,B}]$
.
$N_{A,B} = [H_{A,B}:H^\circ _{A,B}]$
.
-
(a) We have
 $r_{\mathbb {Q}}(H^\circ _{A,B},\rho _A)>0$
.
$r_{\mathbb {Q}}(H^\circ _{A,B},\rho _A)>0$
. -
(b) For each
 $\ell $
, there exists a finite extension
$\ell $
, there exists a finite extension
 $\widetilde {K_{B,\ell ^{\infty }}}$
of
$\widetilde {K_{B,\ell ^{\infty }}}$
of
 $K_{B,\ell ^{\infty }}$
such that
$K_{B,\ell ^{\infty }}$
such that
 $[\widetilde {K_{B,\ell ^{\infty }}}: K_{B,\ell ^{\infty }}] | N_{A,B}$
and
$[\widetilde {K_{B,\ell ^{\infty }}}: K_{B,\ell ^{\infty }}] | N_{A,B}$
and
 $A[\ell ^{\infty }](\widetilde {K_{B,\ell ^{\infty }}})$
is infinite.
$A[\ell ^{\infty }](\widetilde {K_{B,\ell ^{\infty }}})$
is infinite. -
(c) For each
 $\ell $
, there exists some
$\ell $
, there exists some
 $n_\ell $
such that
$n_\ell $
such that
 $A[\ell ^{\infty }](K_{B,\ell ^{\infty }}K_{A,\ell ^{n_\ell }})$
is infinite; and if
$A[\ell ^{\infty }](K_{B,\ell ^{\infty }}K_{A,\ell ^{n_\ell }})$
is infinite; and if
 $\ell \nmid N_{A,B}$
, then we may take
$\ell \nmid N_{A,B}$
, then we may take
 $n_\ell =1$
. (In fact,
$n_\ell =1$
. (In fact,
 $K_{B,\ell ^{\infty }}\subseteq \widetilde {K_{B,\ell ^{\infty }}}\subseteq K_{B,\ell ^{\infty }}K_{A,\ell ^{n_\ell }}$
.)
$K_{B,\ell ^{\infty }}\subseteq \widetilde {K_{B,\ell ^{\infty }}}\subseteq K_{B,\ell ^{\infty }}K_{A,\ell ^{n_\ell }}$
.)
Proof. Since
![]() $A(K_B)_{\operatorname {\mathrm {tors}}}$
is infinite, there exist infinitely many
$A(K_B)_{\operatorname {\mathrm {tors}}}$
is infinite, there exist infinitely many
![]() $\ell $
such that
$\ell $
such that
![]() $A[\ell ](K_B)$
is nontrivial, or there is some
$A[\ell ](K_B)$
is nontrivial, or there is some
![]() $\ell _0$
such that
$\ell _0$
such that
![]() $A[\ell _0^{\infty }](K_B)$
is infinite. By Lemma 2.16 or 2.14 as appropriate,
$A[\ell _0^{\infty }](K_B)$
is infinite. By Lemma 2.16 or 2.14 as appropriate,
![]() $r := r_{\mathbb {Q}}(H_{A,B}^\circ ,\rho _A)>0$
.
$r := r_{\mathbb {Q}}(H_{A,B}^\circ ,\rho _A)>0$
.
Now, fix a prime
![]() $\ell $
. Let
$\ell $
. Let
![]() $\widetilde {K_{B,\ell ^{\infty }}}$
be the smallest extension of
$\widetilde {K_{B,\ell ^{\infty }}}$
be the smallest extension of
![]() $K_{B,\ell ^{\infty }}$
for which
$K_{B,\ell ^{\infty }}$
for which
![]() $\rho _{A,\ell ^{\infty }}(\operatorname {\mathrm {Gal}}(\widetilde {K_{B,\ell ^{\infty }}})) \subseteq H^\circ _{A,B}({\mathbb {Z}}_\ell )$
. Then
$\rho _{A,\ell ^{\infty }}(\operatorname {\mathrm {Gal}}(\widetilde {K_{B,\ell ^{\infty }}})) \subseteq H^\circ _{A,B}({\mathbb {Z}}_\ell )$
. Then
![]() $[\widetilde {K_{B,\ell ^{\infty }}}:K_{B,\ell ^{\infty }}] | N_{A,B}$
, and
$[\widetilde {K_{B,\ell ^{\infty }}}:K_{B,\ell ^{\infty }}] | N_{A,B}$
, and
![]() $\operatorname {\mathrm {rank}}_{{\mathbb {Z}}_\ell } A[\ell ^{\infty }](\widetilde {K_{B,\ell ^{\infty }}}) \ge r>0$
.
$\operatorname {\mathrm {rank}}_{{\mathbb {Z}}_\ell } A[\ell ^{\infty }](\widetilde {K_{B,\ell ^{\infty }}}) \ge r>0$
.
Moreover, we have inclusions
![]() $K_{B,\ell ^{\infty }} \subseteq \widetilde {K_{B,\ell ^{\infty }}} \subseteq (K_{B,\ell ^{\infty }})_{A,\ell ^{\infty }}$
. Since the first extension is finite, there exists some n such that
$K_{B,\ell ^{\infty }} \subseteq \widetilde {K_{B,\ell ^{\infty }}} \subseteq (K_{B,\ell ^{\infty }})_{A,\ell ^{\infty }}$
. Since the first extension is finite, there exists some n such that
![]() $\widetilde {K_{B,\ell ^{\infty }}} \subseteq (K_{B,\ell ^{\infty }})_{A,\ell ^n}$
. Now, if
$\widetilde {K_{B,\ell ^{\infty }}} \subseteq (K_{B,\ell ^{\infty }})_{A,\ell ^n}$
. Now, if
![]() $n\ge 2$
, then
$n\ge 2$
, then
![]() $\operatorname {\mathrm {Gal}}((K_{B,\ell ^{\infty }})_{A,\ell ^n} / (K_{B,\ell ^{\infty }})_{A,\ell })$
is a group whose order is a power of
$\operatorname {\mathrm {Gal}}((K_{B,\ell ^{\infty }})_{A,\ell ^n} / (K_{B,\ell ^{\infty }})_{A,\ell })$
is a group whose order is a power of
![]() $\ell $
. Consequently, if
$\ell $
. Consequently, if
![]() $\ell \nmid N_{A,B}$
, then
$\ell \nmid N_{A,B}$
, then
![]() $\widetilde {K_{B,\ell ^{\infty }}} \subseteq (K_{B,\ell ^{\infty }})_{A,\ell }= K_{A,\ell }K_{B,\ell ^{\infty }}$
.
$\widetilde {K_{B,\ell ^{\infty }}} \subseteq (K_{B,\ell ^{\infty }})_{A,\ell }= K_{A,\ell }K_{B,\ell ^{\infty }}$
.
Remark 4.9. In the context of Lemma 4.8(b), one might hope that there is a finite extension
![]() $L_B$
of
$L_B$
of
![]() $K_B$
such that
$K_B$
such that
![]() $A[\ell ](L_B)$
is nontrivial for each
$A[\ell ](L_B)$
is nontrivial for each
![]() $\ell $
. (Even more optimistically, one might hope that such an
$\ell $
. (Even more optimistically, one might hope that such an
![]() $L_B$
is the compositum of
$L_B$
is the compositum of
![]() $K_B$
and a finite extension of K.) However, there is no independence-of-
$K_B$
and a finite extension of K.) However, there is no independence-of-
![]() $\ell $
connectedness result for Galois representations of infinite algebraic extensions of
$\ell $
connectedness result for Galois representations of infinite algebraic extensions of
![]() ${\mathbb {Q}}$
to which one might appeal. In fact, we will see below (5.7) that in general, no such uniform-in-
${\mathbb {Q}}$
to which one might appeal. In fact, we will see below (5.7) that in general, no such uniform-in-
![]() $\ell $
finite extension exists. In this sense, Lemma 4.8(b) is optimal without additional hypotheses.
$\ell $
finite extension exists. In this sense, Lemma 4.8(b) is optimal without additional hypotheses.
Theorem 4.10. Let A and B be abelian varieties over a number field K. Suppose that A and B satisfy the Mumford–Tate conjecture and that A is absolutely simple. Then the following are equivalent:
-
(a) A is potentially torsion infinite for B;
-
(b)
 $\dim H_{A,B} = 0$
;
$\dim H_{A,B} = 0$
; -
(c)
 $\dim G_{A\times B} = \dim G_B$
;
$\dim G_{A\times B} = \dim G_B$
; -
(d)
 $\operatorname {\mathrm {rank}} G_{A\times B} = \operatorname {\mathrm {rank}} G_B$
; and
$\operatorname {\mathrm {rank}} G_{A\times B} = \operatorname {\mathrm {rank}} G_B$
; and -
(e) there exists a finite extension
 $K'$
of K such that for all sufficiently large
$K'$
of K such that for all sufficiently large
 $\ell $
,
$\ell $
,
 $K^{\prime }_{A,\ell ^{\infty }} \subset K_B K^{\prime }_{A,\ell }$
, and thus
$K^{\prime }_{A,\ell ^{\infty }} \subset K_B K^{\prime }_{A,\ell }$
, and thus
 $A[\ell ^{\infty }](K_B K^{\prime }_{A,\ell }) = A_{\ell ^{\infty }}$
.
$A[\ell ^{\infty }](K_B K^{\prime }_{A,\ell }) = A_{\ell ^{\infty }}$
.
Proof. Suppose that A is potentially torsion infinite for B. Then, possibly after replacing K with a finite extension, we find that
![]() $r := r_{\mathbb {Q}}(H^\circ _{A,B},\rho _A)>0$
(Lemma 4.8(a)). Note that
$r := r_{\mathbb {Q}}(H^\circ _{A,B},\rho _A)>0$
(Lemma 4.8(a)). Note that
![]() $H_{A,B}$
, and thus
$H_{A,B}$
, and thus
![]() $H^\circ _{A,B}$
, are normal subgroups of
$H^\circ _{A,B}$
, are normal subgroups of
![]() $\operatorname {\mathrm {MT}}(A)$
(Lemma 2.4).
$\operatorname {\mathrm {MT}}(A)$
(Lemma 2.4).
Because A is absolutely simple and
![]() $\operatorname {\mathrm {MT}}(A)$
is reductive,
$\operatorname {\mathrm {MT}}(A)$
is reductive,
![]() $H_1(A,{\mathbb {Q}})$
is an irreducible representation of
$H_1(A,{\mathbb {Q}})$
is an irreducible representation of
![]() $\operatorname {\mathrm {MT}}(A)$
. Now,
$\operatorname {\mathrm {MT}}(A)$
. Now,
![]() $H_1(A,{\mathbb {Q}})^{H^\circ _{A,B}}$
is a sub-
$H_1(A,{\mathbb {Q}})^{H^\circ _{A,B}}$
is a sub-
![]() $\operatorname {\mathrm {MT}}(A)$
-representation (Lemma 2.6) of
$\operatorname {\mathrm {MT}}(A)$
-representation (Lemma 2.6) of
![]() $H_1(A,{\mathbb {Q}})$
. Since
$H_1(A,{\mathbb {Q}})$
. Since
![]() $\dim H_1(A,{\mathbb {Q}})^{H_{A,B}^\circ } = r>0$
and
$\dim H_1(A,{\mathbb {Q}})^{H_{A,B}^\circ } = r>0$
and
![]() $H_1(A,{\mathbb {Q}})$
is irreducible, it follows that
$H_1(A,{\mathbb {Q}})$
is irreducible, it follows that
![]() $H_1(A,{\mathbb {Q}})^{H_{A,B}^\circ } = H_1(A,{\mathbb {Q}})$
. This implies that
$H_1(A,{\mathbb {Q}})^{H_{A,B}^\circ } = H_1(A,{\mathbb {Q}})$
. This implies that
![]() $H_{A,B}^\circ $
is trivial, and thus
$H_{A,B}^\circ $
is trivial, and thus
![]() $\dim H_{A,B} = 0$
.
$\dim H_{A,B} = 0$
.
The converse, that (b) implies (a), is easy. Indeed, suppose
![]() $\dim H_{A,B} = 0$
, and fix a prime
$\dim H_{A,B} = 0$
, and fix a prime
![]() $\ell $
. Then
$\ell $
. Then
![]() $\operatorname {\mathrm {Gal}}(K_B)$
acts on
$\operatorname {\mathrm {Gal}}(K_B)$
acts on
![]() $T_\ell A$
through a subgroup of
$T_\ell A$
through a subgroup of
![]() $H_{A,B}({\mathbb {Z}}_\ell )$
, which is by hypothesis a finite group; after passage to a finite extension, the Galois group acts trivially on all
$H_{A,B}({\mathbb {Z}}_\ell )$
, which is by hypothesis a finite group; after passage to a finite extension, the Galois group acts trivially on all
![]() $\ell $
-power torsion points.
$\ell $
-power torsion points.
The equivalence of (b)–(d) is a standard observation about reductive groups (Lemma 2.3).
Now suppose (b) holds. After replacing K with a suitable finite extension, we may and do assume that
![]() $A\times B$
has connected independent Galois representations. Then Lemma 4.8(c) shows that there exists some
$A\times B$
has connected independent Galois representations. Then Lemma 4.8(c) shows that there exists some
![]() $n_\ell $
such that
$n_\ell $
such that
![]() $\operatorname {\mathrm {Gal}}(K_{B} K_{A,\ell ^{n_\ell }})$
acts trivially on
$\operatorname {\mathrm {Gal}}(K_{B} K_{A,\ell ^{n_\ell }})$
acts trivially on
![]() $T_\ell A$
and that if
$T_\ell A$
and that if
![]() $\ell \nmid [H_{A,B}:H^\circ _{A,B}]$
, then we may take
$\ell \nmid [H_{A,B}:H^\circ _{A,B}]$
, then we may take
![]() $n_\ell = 1$
.
$n_\ell = 1$
.
The proof is completed with the trivial observation that (e) implies (a).
Corollary 4.12. Let
![]() $B/K$
be an abelian variety over a number field for which the Mumford–Tate conjecture holds, and let
$B/K$
be an abelian variety over a number field for which the Mumford–Tate conjecture holds, and let
![]() $E/K$
be an elliptic curve with complex multiplication. Then either E is potentially torsion infinite for B or
$E/K$
be an elliptic curve with complex multiplication. Then either E is potentially torsion infinite for B or
![]() $sG_{E\times B} = sG_E \times sG_B$
.
$sG_{E\times B} = sG_E \times sG_B$
.
Proof. The Mumford–Tate conjecture holds for E and thus for
![]() $E\times B$
, and E is visibly absolutely simple; it therefore suffices to show that if E is essentially torsion finite for B, then the special Mumford–Tate group of the product is the product of the special Mumford–Tate groups. By Theorem 4.10,
$E\times B$
, and E is visibly absolutely simple; it therefore suffices to show that if E is essentially torsion finite for B, then the special Mumford–Tate group of the product is the product of the special Mumford–Tate groups. By Theorem 4.10,
![]() $\dim H_{E,B}>0$
. Since
$\dim H_{E,B}>0$
. Since
![]() $H_{E,B}$
is a positive-dimensional subgroup of the one-dimensional torus
$H_{E,B}$
is a positive-dimensional subgroup of the one-dimensional torus
![]() $sG_E$
, it follows that
$sG_E$
, it follows that
![]() $H_{E,B} = sG_E$
, and thus
$H_{E,B} = sG_E$
, and thus
![]() $sG_{E\times B} = sG_E \times sG_B$
(Remark 2.2).
$sG_{E\times B} = sG_E \times sG_B$
(Remark 2.2).
Corollary 4.13. Let A and B be abelian varieties over a number field, of respective dimensions
![]() $d_A$
and
$d_A$
and
![]() $d_B$
. Suppose that A and B satisfy the Mumford–Tate conjecture, that A is absolutely simple, and that
$d_B$
. Suppose that A and B satisfy the Mumford–Tate conjecture, that A is absolutely simple, and that
Then A is essentially torsion finite for B.
Proof. Let
![]() $r_A$
and
$r_A$
and
![]() $r_B$
denote the respective ranks of the Mumford–Tate groups of A and B. On one hand, we have the trivial bound
$r_B$
denote the respective ranks of the Mumford–Tate groups of A and B. On one hand, we have the trivial bound
![]() $r_B \le d+1$
. On the other hand, a weak form of [Reference Orr26, Th. 1.2] implies that
$r_B \le d+1$
. On the other hand, a weak form of [Reference Orr26, Th. 1.2] implies that
![]() $r_A \ge \frac 13(\log _2 d_A+2)$
. Therefore, hypothesis (4.6) implies that
$r_A \ge \frac 13(\log _2 d_A+2)$
. Therefore, hypothesis (4.6) implies that
![]() $r_A> r_B$
. Since
$r_A> r_B$
. Since
![]() $\operatorname {\mathrm {rank}}(G_A)-\operatorname {\mathrm {rank}}(G_B) = \operatorname {\mathrm {rank}}(H_{A,B})-\operatorname {\mathrm {rank}}(H_{B,A})$
, we find that the rank of
$\operatorname {\mathrm {rank}}(G_A)-\operatorname {\mathrm {rank}}(G_B) = \operatorname {\mathrm {rank}}(H_{A,B})-\operatorname {\mathrm {rank}}(H_{B,A})$
, we find that the rank of
![]() $H_{A,B}$
is positive, and thus
$H_{A,B}$
is positive, and thus
![]() $\dim H_{A,B}>0$
. Now, apply Theorem 4.10.
$\dim H_{A,B}>0$
. Now, apply Theorem 4.10.
Corollary 4.14. Suppose that A and B are two absolutely simple abelian varieties over K and that the Mumford–Tate conjecture holds for
![]() $A\times B$
. Then the following are equivalent.
$A\times B$
. Then the following are equivalent.
-
(a) A and B are mutually potentially torsion infinite.
-
(b) The natural surjections
 $G_{A\times B} \to G_A$
and
$G_{A\times B} \to G_A$
and
 $G_{A\times B} \to G_B$
are isogenies.
$G_{A\times B} \to G_B$
are isogenies. -
(c) The natural surjections
 $sG_{A\times B} \to sG_A$
and
$sG_{A\times B} \to sG_A$
and
 $sG_{A\times B} \to sG_B$
are isogenies.
$sG_{A\times B} \to sG_B$
are isogenies. -
(d)
 $\dim (G_{A\times B}) = \dim G_A = \dim G_B$
.
$\dim (G_{A\times B}) = \dim G_A = \dim G_B$
. -
(e)
 $\dim (sG_{A\times B}) = \dim sG_A = \dim sG_B$
.
$\dim (sG_{A\times B}) = \dim sG_A = \dim sG_B$
. -
(f)
 $\operatorname {\mathrm {rank}}(G_{A\times B}) = \operatorname {\mathrm {rank}} G_A = \operatorname {\mathrm {rank}} G_B$
.
$\operatorname {\mathrm {rank}}(G_{A\times B}) = \operatorname {\mathrm {rank}} G_A = \operatorname {\mathrm {rank}} G_B$
. -
(g)
 $\operatorname {\mathrm {rank}}(sG_{A\times B}) = \operatorname {\mathrm {rank}} sG_A = \operatorname {\mathrm {rank}} sG_B$
.
$\operatorname {\mathrm {rank}}(sG_{A\times B}) = \operatorname {\mathrm {rank}} sG_A = \operatorname {\mathrm {rank}} sG_B$
.
At the opposite extreme, we have the following corollary.
Corollary 4.15. Suppose that A and B are two absolutely simple abelian varieties over K and that the Mumford–Tate conjecture holds for
![]() $A\times B$
. If
$A\times B$
. If
![]() $sG_{A\times B} = sG_A \times sG_B$
, then A and B are mutually essentially torsion finite.
$sG_{A\times B} = sG_A \times sG_B$
, then A and B are mutually essentially torsion finite.
As we noted in the introduction, Ichikawa [Reference Ichikawa10] and Lombardo [Reference Lombardo16] have given sufficient criteria for a pair of abelian varieties
![]() $(A,B)$
to satisfy
$(A,B)$
to satisfy
![]() $sG_{A\times B} = sG_A \times sG_B$
; a typical example is when A and B are nonisogenous abelian varieties of odd dimension with absolute endomorphism ring
$sG_{A\times B} = sG_A \times sG_B$
; a typical example is when A and B are nonisogenous abelian varieties of odd dimension with absolute endomorphism ring
![]() ${\mathbb {Z}}$
.
${\mathbb {Z}}$
.
5 Applications
In this section, we apply Theorem 4.10 to the following two classes of abelian varieties:
-
(a) CM abelian varieties;
-
(b) abelian varieties with dimension smaller than 4.
Since the Mumford–Tate groups, and in fact the Mumford–Tate conjecture, are known for these classes of varieties, we are able to obtain some unconditional results.
More precisely, in §5.1, after a brief review of CM abelian varieties, we give a criterion (Theorem 5.4) to decide the essential torsion finiteness of a pair of CM abelian varieties in terms of their CM types. This criterion, compared with Theorem 4.10, has the advantage of being effective. In particular, one can use it to create examples of non-isogenous but potentially torsion-infinite pairs. This is demonstrated in Examples 5.12 and 5.7. Moreover, since the Mumford–Tate group of a CM abelian variety is a torus—indeed, this characterizes CM abelian varieties—our theorem indicates a way to describe the extra Hodge classes on the product of CM abelian varieties via relations among the characters of their Mumford–Tate groups. We also explore the relation between extra Hodge classes and torsion infiniteness in the CM case; this is the main content of §5.2.
In a different direction, thanks to the classification of Mumford–Tate groups of low-dimension abelian varieties (see [Reference Moonen and Zarhin23, §2] for instance), one is able to analyze the equivalent conditions in Theorem 4.10 for each pair of realizable Mumford–Tate groups. The result of this study is Theorem 5.14. In particular, this theorem allows the comparison of Type IV varieties, which is not covered by the result of [Reference Lombardo16]. Details are given in §5.3.
5.1 CM abelian varieties
5.1.1 CM types and Mumford–Tate groups
We start by briefly reviewing some background on CM abelian varieties. See [Reference Milne20] and [Reference Serre and Tate39] for more details.
Let A be a g-dimensional abelian variety over a number field K, and let E be a CM-algebra of dimension
![]() $2g$
. We say A has complex multiplication by E if there exists an embedding of algebras
$2g$
. We say A has complex multiplication by E if there exists an embedding of algebras ![]() . In this case, we call A a CM abelian variety and say that A has CM by E. (If there is some finite extension
. In this case, we call A a CM abelian variety and say that A has CM by E. (If there is some finite extension
![]() $L/K$
such that
$L/K$
such that
![]() $A_L$
has CM by E, we will say that A has potential CM by E.)
$A_L$
has CM by E, we will say that A has potential CM by E.)
The embedding i induces an E-action on the Lie algebra
![]() $\operatorname {\mathrm {Lie}}(A_{\mathbb C})$
. The character of this E-representation is given by
$\operatorname {\mathrm {Lie}}(A_{\mathbb C})$
. The character of this E-representation is given by
![]() $\sum _{\varphi \in \Phi }\varphi $
for some subset
$\sum _{\varphi \in \Phi }\varphi $
for some subset ![]() . Let c be the complex conjugation on
. Let c be the complex conjugation on
![]() $\mathbb C$
. Then
$\mathbb C$
. Then
where
![]() $\Phi ^{c} =\{c\circ \varphi |\varphi \in \Phi \}$
. The pair
$\Phi ^{c} =\{c\circ \varphi |\varphi \in \Phi \}$
. The pair
![]() $(E, \Phi )$
is called the CM type of A (or
$(E, \Phi )$
is called the CM type of A (or
![]() $(A, i)$
). Conversely, for any pair
$(A, i)$
). Conversely, for any pair
![]() $(E, \Phi )$
where E is a CM algebra and the subset
$(E, \Phi )$
where E is a CM algebra and the subset ![]() satisfies (5.1), there exists a CM abelian variety
satisfies (5.1), there exists a CM abelian variety
![]() $A_0$
defined over a number field equipped with an action
$A_0$
defined over a number field equipped with an action ![]() with CM type
with CM type
![]() $(E, \Phi )$
. The correspondence between CM types and isogeny classes of abelian varieties with action by a CM algebra is well understood (see, e.g., [Reference Milne20, Prop. 3.12]).
$(E, \Phi )$
. The correspondence between CM types and isogeny classes of abelian varieties with action by a CM algebra is well understood (see, e.g., [Reference Milne20, Prop. 3.12]).
Fix an embedding
![]() $K\hookrightarrow {\mathbb {C}}$
, and let
$K\hookrightarrow {\mathbb {C}}$
, and let
![]() ${\overline {K}}$
be the algebraic closure of K in
${\overline {K}}$
be the algebraic closure of K in
![]() ${\mathbb {C}}$
. Then any embedding
${\mathbb {C}}$
. Then any embedding
![]() $E \hookrightarrow {\mathbb {C}}$
factors through
$E \hookrightarrow {\mathbb {C}}$
factors through
![]() ${\overline {K}}$
, and we have a bijection
${\overline {K}}$
, and we have a bijection ![]() . Let
. Let
![]() $\widetilde {E}$
be a Galois extension of
$\widetilde {E}$
be a Galois extension of
![]() ${\mathbb Q}$
in
${\mathbb Q}$
in
![]() $\overline {K}$
which splits E. Then the Galois group
$\overline {K}$
which splits E. Then the Galois group
![]() $\operatorname {\mathrm {Gal}}(\widetilde {E}/{\mathbb Q})$
acts on
$\operatorname {\mathrm {Gal}}(\widetilde {E}/{\mathbb Q})$
acts on ![]() by left composition. Let
by left composition. Let
![]() $H = H_{(E,\Phi )}$
be the group
$H = H_{(E,\Phi )}$
be the group
![]() $\{\sigma \in \operatorname {\mathrm {Gal}}(\widetilde {E}/{\mathbb Q})| \Phi ^{\sigma }=\Phi \}$
. The fixed field
$\{\sigma \in \operatorname {\mathrm {Gal}}(\widetilde {E}/{\mathbb Q})| \Phi ^{\sigma }=\Phi \}$
. The fixed field
![]() $E^{\ast }:=\widetilde {E}^{H}$
of H is called the reflex field of the CM type
$E^{\ast }:=\widetilde {E}^{H}$
of H is called the reflex field of the CM type
![]() $(E, \Phi )$
.
$(E, \Phi )$
.
We now introduce the reflex norm associated with the CM abelian variety A. Recall (§2.1) that for any finite extension F of
![]() ${\mathbb Q}$
, we let
${\mathbb Q}$
, we let ![]() be the Weil restriction of the multiplicative group. We define
be the Weil restriction of the multiplicative group. We define ![]() . Since
. Since
![]() $\widetilde E/{\mathbb Q}$
is Galois,
$\widetilde E/{\mathbb Q}$
is Galois, ![]() is a torsor under
is a torsor under ![]() , and the choice of embedding
, and the choice of embedding
![]() $\widetilde E \hookrightarrow {\overline {K}}$
gives a bijection between these two sets. We use this to define, for
$\widetilde E \hookrightarrow {\overline {K}}$
gives a bijection between these two sets. We use this to define, for ![]() , the (group-theoretic) inverse
, the (group-theoretic) inverse ![]() .
.
Let
![]() $\widetilde {\Phi }^{-1}$
be the set
$\widetilde {\Phi }^{-1}$
be the set
![]() $\{\widetilde {\varphi }^{-1}\mid \widetilde {\varphi }\in \widetilde {\Phi }\}$
. The map
$\{\widetilde {\varphi }^{-1}\mid \widetilde {\varphi }\in \widetilde {\Phi }\}$
. The map
![]() $N_{\widetilde {\Phi }^{-1}}: \widetilde {E}^{\ast }\rightarrow \widetilde {E}^{\ast }$
given by
$N_{\widetilde {\Phi }^{-1}}: \widetilde {E}^{\ast }\rightarrow \widetilde {E}^{\ast }$
given by
![]() $N_{\widetilde {\Phi }^{-1}}(a)=\prod _{\sigma \in \widetilde {\Phi }^{-1}}\sigma (a)$
defines a map of algebraic tori
$N_{\widetilde {\Phi }^{-1}}(a)=\prod _{\sigma \in \widetilde {\Phi }^{-1}}\sigma (a)$
defines a map of algebraic tori
![]() $N_{\widetilde {\Phi }^{-1}}: T^{\widetilde {E}}\rightarrow T^{\widetilde {E}}.$
This map factors through
$N_{\widetilde {\Phi }^{-1}}: T^{\widetilde {E}}\rightarrow T^{\widetilde {E}}.$
This map factors through
![]() $T^{E^{\ast }}$
and has image contained in
$T^{E^{\ast }}$
and has image contained in
![]() $T^{E}$
. More precisely, we have a commutative diagram of
$T^{E}$
. More precisely, we have a commutative diagram of
![]() ${\mathbb Q}$
-tori
${\mathbb Q}$
-tori

where
![]() $N_{\widetilde {E}/E^{\ast }}$
is the usual norm map and
$N_{\widetilde {E}/E^{\ast }}$
is the usual norm map and
![]() $N_{\Phi }$
is called the reflex norm of
$N_{\Phi }$
is called the reflex norm of
![]() $(E, \Phi )$
. For any finite extension
$(E, \Phi )$
. For any finite extension
![]() $L/E^{\ast }$
, we define
$L/E^{\ast }$
, we define
![]() $N_{L, \Phi }=N_{\Phi }\circ N_{L/E^{\ast }}$
. We will call
$N_{L, \Phi }=N_{\Phi }\circ N_{L/E^{\ast }}$
. We will call
![]() $N_{L, \Phi }$
the L-reflex norm of
$N_{L, \Phi }$
the L-reflex norm of
![]() $(E, \Phi )$
. Note that
$(E, \Phi )$
. Note that
![]() $N_{L/E^{\ast }}$
is a surjective map. The image of the map
$N_{L/E^{\ast }}$
is a surjective map. The image of the map
![]() $N_{L,\Phi }: T^{L}\rightarrow T^{E}$
is independent of L, and we denote it by
$N_{L,\Phi }: T^{L}\rightarrow T^{E}$
is independent of L, and we denote it by
![]() $T_{\Phi }$
. See, for example, [Reference Yu45, Lem. 4.2] for an explicit calculation of
$T_{\Phi }$
. See, for example, [Reference Yu45, Lem. 4.2] for an explicit calculation of
![]() $X^*(T_\Phi )$
.
$X^*(T_\Phi )$
.
Consider the special case where E is a Galois extension of
![]() ${\mathbb {Q}}$
. Then E contains the reflex field
${\mathbb {Q}}$
. Then E contains the reflex field
![]() $E^*$
, and
$E^*$
, and
![]() $T_{\Phi }$
, as the image of
$T_{\Phi }$
, as the image of
![]() $T^E$
under
$T^E$
under
![]() $N_{E,\Phi }: T^E \to T^{E^*} \to T^E$
, is a quotient of
$N_{E,\Phi }: T^E \to T^{E^*} \to T^E$
, is a quotient of
![]() $T^E$
. Inside
$T^E$
. Inside
we find that

Lemma 5.1. If A is a CM abelian variety over a number field, then the Mumford–Tate conjecture holds for A. Moreover, if
![]() $(E,\Phi )$
is a CM-type for A, then
$(E,\Phi )$
is a CM-type for A, then
![]() $\operatorname {\mathrm {MT}}(A) \cong T_\Phi $
.
$\operatorname {\mathrm {MT}}(A) \cong T_\Phi $
.
Proof. This is due to Pohlmann [Reference Pohlmann30, Th. 5] (see also [Reference Yu45, Lem. 4.2] for a modern proof). (In fact, while [Reference Yu45] focuses on simple abelian varieties, the proof given there works verbatim in the non-simple case, too.)
Remark 5.2. Note in particular that (the character group of) the torus
![]() $\operatorname {\mathrm {MT}}(A)$
can be explicitly described using a CM type
$\operatorname {\mathrm {MT}}(A)$
can be explicitly described using a CM type
![]() $(E, \Phi )$
of A. It is usually more convenient to assume that E is Galois over
$(E, \Phi )$
of A. It is usually more convenient to assume that E is Galois over
![]() ${\mathbb Q}$
; and in studying the essential torsion finiteness problem for CM abelian varieties, we can always do this. Indeed, if
${\mathbb Q}$
; and in studying the essential torsion finiteness problem for CM abelian varieties, we can always do this. Indeed, if
![]() $E/{\mathbb Q}$
is not Galois, choose a CM Galois extension
$E/{\mathbb Q}$
is not Galois, choose a CM Galois extension
![]() $E'/{\mathbb Q}$
such that
$E'/{\mathbb Q}$
such that
![]() $E\subseteq E'$
, and let
$E\subseteq E'$
, and let
![]() $n=[E':E]$
. Then
$n=[E':E]$
. Then
![]() $A^n$
has a CM type
$A^n$
has a CM type
![]() $(E', \Phi ')$
where
$(E', \Phi ')$
where ![]() . Moreover,
. Moreover,
![]() $\operatorname {\mathrm {MT}}(A)\cong \operatorname {\mathrm {MT}} (A^n)$
; and if A is defined over a field K, then
$\operatorname {\mathrm {MT}}(A)\cong \operatorname {\mathrm {MT}} (A^n)$
; and if A is defined over a field K, then
![]() $K_A = K_{A^n}$
(Lemma 4.5). Thus, for our purposes, we may restrict our attention to Galois CM fields.
$K_A = K_{A^n}$
(Lemma 4.5). Thus, for our purposes, we may restrict our attention to Galois CM fields.
5.1.2 Galois representations
For use in later examples, we recall the calculation of the Galois representation of a CM abelian variety following [Reference Serre and Tate39, §7] and [Reference Yu45, §3]. Let
![]() $A/K$
be an abelian variety with complex multiplication by E. Let
$A/K$
be an abelian variety with complex multiplication by E. Let
![]() $\ell $
be a rational prime which does not divide the index
$\ell $
be a rational prime which does not divide the index ![]() . (This condition only rules out finitely many primes. Alternatively, for our applications, we may replace K by a finite extension and adjust A in its isogeny class, in which case we may assume that
. (This condition only rules out finitely many primes. Alternatively, for our applications, we may replace K by a finite extension and adjust A in its isogeny class, in which case we may assume that ![]() .) Then
.) Then
![]() $\mathcal O_{E_\ell } := \mathcal O_E \otimes {\mathbb {Z}}_\ell $
is a direct sum of discrete valuation rings, and the Tate module
$\mathcal O_{E_\ell } := \mathcal O_E \otimes {\mathbb {Z}}_\ell $
is a direct sum of discrete valuation rings, and the Tate module
![]() $T_\ell A$
is free of rank one over
$T_\ell A$
is free of rank one over
![]() $\mathcal O_{E_\ell }$
. The Galois group of K acts E-linearly on
$\mathcal O_{E_\ell }$
. The Galois group of K acts E-linearly on
![]() $T_\ell A$
, and so the Galois representation
$T_\ell A$
, and so the Galois representation
![]() $\rho _{A/K,\ell ^{\infty }}$
of
$\rho _{A/K,\ell ^{\infty }}$
of
![]() $\operatorname {\mathrm {Gal}}(K)$
factors through
$\operatorname {\mathrm {Gal}}(K)$
factors through
![]() $\operatorname {\mathrm {Gal}}(K)^{\textrm ab}$
. Composing the
$\operatorname {\mathrm {Gal}}(K)^{\textrm ab}$
. Composing the
![]() $\ell $
-adic representation with the Artin reciprocity map (in the idelic formulation of class field theory), one obtains a continuous group homomorphism which we still denote by
$\ell $
-adic representation with the Artin reciprocity map (in the idelic formulation of class field theory), one obtains a continuous group homomorphism which we still denote by
![]() $\rho _{A/K,\ell ^{\infty }}$
:
$\rho _{A/K,\ell ^{\infty }}$
:

After possibly replacing K with a finite extension, we now assume that K contains
![]() $E^*$
, the reflex field of the CM type of A, so that the reflex norm
$E^*$
, the reflex field of the CM type of A, so that the reflex norm
![]() $N_{K,\Phi }$
is defined (§5.1). Then, by [Reference Serre and Tate39, Ths. 10 and 11], we can concretely describe the representation
$N_{K,\Phi }$
is defined (§5.1). Then, by [Reference Serre and Tate39, Ths. 10 and 11], we can concretely describe the representation
![]() $\widetilde \rho _{A/K,\ell ^{\infty }}$
by
$\widetilde \rho _{A/K,\ell ^{\infty }}$
by

Here,
![]() $a_\ell =(a_v)_{v\mid \ell }$
denotes the component of a in
$a_\ell =(a_v)_{v\mid \ell }$
denotes the component of a in
![]() $K_{\ell }^\times =\prod _{v\mid \ell }K_v^\times $
; and the map
$K_{\ell }^\times =\prod _{v\mid \ell }K_v^\times $
; and the map
is induced by the reflex norm map from
![]() $T^K$
to
$T^K$
to
![]() $T^E$
; and
$T^E$
; and
is the unique homomorphism satisfying the following conditions:
-
(a) The restriction of
 $\varepsilon $
to
$\varepsilon $
to
 $K^{\times }$
is the reflex norm map
$K^{\times }$
is the reflex norm map
 $N_{K, \Phi }: K^{\times }\to E^{\times }$
.
$N_{K, \Phi }: K^{\times }\to E^{\times }$
. -
(b) The homomorphism
 $\varepsilon $
is continuous, in the sense that its kernel is open in
$\varepsilon $
is continuous, in the sense that its kernel is open in
 $ \mathbb {A}_K^{\times }$
.
$ \mathbb {A}_K^{\times }$
. -
(c) There is a finite set S of places of K, including the infinite ones and those where A has bad reduction, such that
where each
 $\pi _v$
is the Frobenius element attached to v [Reference Serre and Tate39, p. 511].
$\pi _v$
is the Frobenius element attached to v [Reference Serre and Tate39, p. 511].
5.1.3 Nondegenerate abelian varieties
Let
![]() $A/K$
be an abelian variety with CM type
$A/K$
be an abelian variety with CM type
![]() $(E,\Phi )$
. Recall that A is called nondegenerate if
$(E,\Phi )$
. Recall that A is called nondegenerate if
![]() $\dim \operatorname {\mathrm {MT}}(A)$
is maximal, that is,
$\dim \operatorname {\mathrm {MT}}(A)$
is maximal, that is,
![]() $\dim \operatorname {\mathrm {MT}}(A) = \dim A+1$
. Recall that
$\dim \operatorname {\mathrm {MT}}(A) = \dim A+1$
. Recall that
![]() $\mathcal G_{A/K,{\mathbb {Q}}_\ell } $
is the Zariski closure of the
$\mathcal G_{A/K,{\mathbb {Q}}_\ell } $
is the Zariski closure of the
![]() $\ell $
-adic representation image (cf. §3.1.2).
$\ell $
-adic representation image (cf. §3.1.2).
Lemma 5.3. Let
![]() $A/K$
be an abelian variety with nondegenerate CM type
$A/K$
be an abelian variety with nondegenerate CM type
![]() $(E,\Phi )$
. Then, for each
$(E,\Phi )$
. Then, for each
![]() $\ell $
,
$\ell $
,
![]() $\mathcal G_{A/K,{\mathbb {Q}}_\ell } = \operatorname {\mathrm {MT}}(A)\times _{\mathbb {Q}} {\mathbb {Q}}_\ell $
, that is,
$\mathcal G_{A/K,{\mathbb {Q}}_\ell } = \operatorname {\mathrm {MT}}(A)\times _{\mathbb {Q}} {\mathbb {Q}}_\ell $
, that is,
![]() $K = K^{\text {conn},A}$
.
$K = K^{\text {conn},A}$
.
Proof. By Lemma 3.3, it suffices to prove the statement for a single
![]() $\ell $
, and so we assume that
$\ell $
, and so we assume that ![]() . As we have seen above,
. As we have seen above,
![]() $T_\ell A$
admits commuting actions by
$T_\ell A$
admits commuting actions by
![]() $\mathcal O_{E_\ell }$
and
$\mathcal O_{E_\ell }$
and
![]() $\operatorname {\mathrm {Gal}}(K)$
, and thus the
$\operatorname {\mathrm {Gal}}(K)$
, and thus the
![]() $\ell $
-adic representation
$\ell $
-adic representation
![]() $\operatorname {\mathrm {Gal}}(K) \to \operatorname {\mathrm {Aut}}(T_\ell A)$
factors through
$\operatorname {\mathrm {Gal}}(K) \to \operatorname {\mathrm {Aut}}(T_\ell A)$
factors through
![]() $\mathcal O_{E_\ell }^\times $
. A choice of K-rational polarization on A induces a symplectic form
$\mathcal O_{E_\ell }^\times $
. A choice of K-rational polarization on A induces a symplectic form
![]() $\psi $
on
$\psi $
on
![]() $T_\ell A$
, which is also preserved by
$T_\ell A$
, which is also preserved by
![]() $\operatorname {\mathrm {Gal}}(K)$
up to a scaling. Thus, the image of
$\operatorname {\mathrm {Gal}}(K)$
up to a scaling. Thus, the image of
![]() $\operatorname {\mathrm {Gal}}(K)$
in
$\operatorname {\mathrm {Gal}}(K)$
in
![]() $\operatorname {\mathrm {Aut}}(T_\ell A)$
is contained in
$\operatorname {\mathrm {Aut}}(T_\ell A)$
is contained in
![]() $\mathcal O_{E_\ell }^\times \cap \operatorname {GSp}(T_\ell A, \psi )$
. Since these are the
$\mathcal O_{E_\ell }^\times \cap \operatorname {GSp}(T_\ell A, \psi )$
. Since these are the
![]() ${\mathbb {Z}}_\ell $
-points of a maximal torus in
${\mathbb {Z}}_\ell $
-points of a maximal torus in
![]() $\operatorname {GSp}_{2\dim A}$
—indeed, both
$\operatorname {GSp}_{2\dim A}$
—indeed, both
![]() $\operatorname {\mathrm {rank}} \operatorname {GSp}_{2\dim A}$
and
$\operatorname {\mathrm {rank}} \operatorname {GSp}_{2\dim A}$
and
![]() $\dim \operatorname {\mathrm {MT}}(A)$
are
$\dim \operatorname {\mathrm {MT}}(A)$
are
![]() $1+\dim A$
—the result follows.
$1+\dim A$
—the result follows.
5.1.4 Torsion finiteness
With this preparation, we can now use Theorem 4.10 to characterize the essential torsion finiteness of CM abelian varieties in terms of CM types.
Recall that an abelian variety A over a field K is called isotypic if it is isogenous to a power of a simple abelian variety over the same field K, that is, up to isogeny, A has a unique simple factor (see [Reference Chai, Conrad and Oort5, Defn. 1.2.5.2]). Any CM abelian variety is isogenous to a product of isotypic CM abelian varieties (see [Reference Chai, Conrad and Oort5, Prop. 1.3.2.1]), and an isotypic CM abelian variety is geometrically isotypic (see [Reference Chai, Conrad and Oort5, Cor. 1.3.7.2]).
To state our next result, it is more convenient to name our abelian varieties
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. In this case, we will change notation slightly and write, for example,
$A_2$
. In this case, we will change notation slightly and write, for example,
![]() $G_1$
and
$G_1$
and
![]() $H_{12}$
for
$H_{12}$
for
![]() $G_{A_1}$
and
$G_{A_1}$
and
![]() $H_{A_1,A_2}$
.
$H_{A_1,A_2}$
.
Theorem 5.4. Let
![]() $A_1$
and
$A_1$
and
![]() $A_2$
be two isotypic abelian varieties over a number field K, with
$A_2$
be two isotypic abelian varieties over a number field K, with
![]() $A_i$
of potential CM type
$A_i$
of potential CM type
![]() $(E_i, \Phi _i)$
. Let
$(E_i, \Phi _i)$
. Let
![]() $T_i = T_{\Phi _i} = \operatorname {\mathrm {MT}}(A_i)$
be the Mumford–Tate group of
$T_i = T_{\Phi _i} = \operatorname {\mathrm {MT}}(A_i)$
be the Mumford–Tate group of
![]() $A_i$
, and let
$A_i$
, and let
![]() $T_{12} = \operatorname {\mathrm {MT}}(A_1\times A_2)$
. Use the surjection
$T_{12} = \operatorname {\mathrm {MT}}(A_1\times A_2)$
. Use the surjection
![]() $T_{12} \twoheadrightarrow T_i$
to identify
$T_{12} \twoheadrightarrow T_i$
to identify
![]() $X^*(T_i)$
with a submodule of
$X^*(T_i)$
with a submodule of
![]() $X^*(T_{12})$
. Then either:
$X^*(T_{12})$
. Then either:
-
(a)
 $X^*(T_1)\otimes {\mathbb {Q}} \subseteq X^*(T_2)\otimes {\mathbb {Q}}$
. Then
$X^*(T_1)\otimes {\mathbb {Q}} \subseteq X^*(T_2)\otimes {\mathbb {Q}}$
. Then
 $A_1$
is potentially torsion infinite for
$A_1$
is potentially torsion infinite for
 $A_2$
. For each
$A_2$
. For each
 $\ell $
, there exists a finite extension
$\ell $
, there exists a finite extension
 $\widetilde K_\ell /K$
such that Moreover, if
$\widetilde K_\ell /K$
such that Moreover, if
 $X^*(T_1)\subseteq X^*(T_2)$
, and if
$X^*(T_1)\subseteq X^*(T_2)$
, and if
 $A_1$
is simple and nondegenerate, then
$A_1$
is simple and nondegenerate, then 
-
(b)
 $X^*(T_1)\otimes {\mathbb {Q}}\not \subseteq X^*(T_2)\otimes {\mathbb {Q}}$
. Then
$X^*(T_1)\otimes {\mathbb {Q}}\not \subseteq X^*(T_2)\otimes {\mathbb {Q}}$
. Then
 $A_1$
is essentially torsion finite for
$A_1$
is essentially torsion finite for
 $A_2$
.
$A_2$
.
Proof. By Theorem 4.10 and Remark 4.11,
![]() $A_1$
is potentially torsion infinite for
$A_1$
is potentially torsion infinite for
![]() $A_2$
if and only if
$A_2$
if and only if
![]() $\dim H_{12} = 0$
. Since
$\dim H_{12} = 0$
. Since
![]() $H_{12}$
is of multiplicative type, this happens if and only if
$H_{12}$
is of multiplicative type, this happens if and only if
![]() $\dim _{{\mathbb Q}} X^*(H_{12})\otimes {\mathbb Q} = 0$
. After tensoring both sides of (4.5) with
$\dim _{{\mathbb Q}} X^*(H_{12})\otimes {\mathbb Q} = 0$
. After tensoring both sides of (4.5) with
![]() ${\mathbb Q}$
, we find that this happens if and only if
${\mathbb Q}$
, we find that this happens if and only if
![]() $X^*(T_1)\otimes {\mathbb Q} \subseteq X^*(T_2)\otimes {\mathbb Q}$
.
$X^*(T_1)\otimes {\mathbb Q} \subseteq X^*(T_2)\otimes {\mathbb Q}$
.
If
![]() $A_1$
is potentially torsion infinite for
$A_1$
is potentially torsion infinite for
![]() $A_2$
, then the description of
$A_2$
, then the description of
![]() $\widetilde K_\ell $
, etc. is in Lemma 4.8.
$\widetilde K_\ell $
, etc. is in Lemma 4.8.
Finally, suppose that we have an inclusion of integral lattices
![]() $X^*(T_1)\subseteq X^*(T_2)$
and that
$X^*(T_1)\subseteq X^*(T_2)$
and that
![]() $A_1$
is simple and nondegenerate. The calculation (4.5) shows that
$A_1$
is simple and nondegenerate. The calculation (4.5) shows that
![]() $H_{12}$
is trivial. Briefly suppose that
$H_{12}$
is trivial. Briefly suppose that
![]() $A_1/K$
has CM actually defined over K, and thus (Lemma 5.3) has connected Galois representations. Then, for each natural number N, we have a containment
$A_1/K$
has CM actually defined over K, and thus (Lemma 5.3) has connected Galois representations. Then, for each natural number N, we have a containment
![]() $\Gamma _{A_1,N} \subset T_1({\mathbb {Z}}/N)$
, and thus
$\Gamma _{A_1,N} \subset T_1({\mathbb {Z}}/N)$
, and thus
![]() $\operatorname {\mathrm {Gal}}(K_{A_2})$
acts trivially on
$\operatorname {\mathrm {Gal}}(K_{A_2})$
acts trivially on
![]() $A_{1,N}$
.
$A_{1,N}$
.
Now, suppose that
![]() $A_1/K$
merely has potential complex multiplication. The surjection
$A_1/K$
merely has potential complex multiplication. The surjection
![]() $T_2 \to T_1$
means that the splitting field of
$T_2 \to T_1$
means that the splitting field of
![]() $T_2$
contains the splitting field of
$T_2$
contains the splitting field of
![]() $T_1$
; equivalently, we have an inclusion of reflex fields
$T_1$
; equivalently, we have an inclusion of reflex fields
![]() $E_1^* \subset E_2^*$
. Suppose
$E_1^* \subset E_2^*$
. Suppose
![]() $N\ge 3$
is an integer. Then all geometric endomorphisms of
$N\ge 3$
is an integer. Then all geometric endomorphisms of
![]() $A_2$
are defined over
$A_2$
are defined over
![]() $K_{A_2,N}$
[Reference Silverberg41]. Therefore,
$K_{A_2,N}$
[Reference Silverberg41]. Therefore,
![]() $K_{A_2,N}$
contains
$K_{A_2,N}$
contains
![]() $E_2^*$
, and thus
$E_2^*$
, and thus
![]() $E_1^*$
(see [Reference Milne20, Prop. 7.11]). Because
$E_1^*$
(see [Reference Milne20, Prop. 7.11]). Because
![]() $E_1^*$
is simple, all geometric endomorphisms of
$E_1^*$
is simple, all geometric endomorphisms of
![]() $A_1$
are defined over
$A_1$
are defined over
![]() $K_{A_2,N}$
. Therefore, the image of the action of
$K_{A_2,N}$
. Therefore, the image of the action of
![]() $\operatorname {\mathrm {Gal}}(K_{A_2,N})$
on
$\operatorname {\mathrm {Gal}}(K_{A_2,N})$
on
![]() $A_{1,N}$
, and a fortiori that of
$A_{1,N}$
, and a fortiori that of
![]() $\operatorname {\mathrm {Gal}}(K_{A_2})$
, is contained in
$\operatorname {\mathrm {Gal}}(K_{A_2})$
, is contained in
![]() $T_1({\mathbb {Z}}/N)$
(Lemma 5.3), and we conclude as before.
$T_1({\mathbb {Z}}/N)$
(Lemma 5.3), and we conclude as before.
Remark 5.5. In the context of Theorem 5.4, let
![]() $E/{\mathbb {Q}}$
be a Galois CM field containing
$E/{\mathbb {Q}}$
be a Galois CM field containing
![]() $E_1$
and
$E_1$
and
![]() $E_2$
, and assume that
$E_2$
, and assume that
![]() $A_1$
and
$A_1$
and
![]() $A_2$
share no common geometric isogeny factor. As in Remark 5.2, after replacing
$A_2$
share no common geometric isogeny factor. As in Remark 5.2, after replacing
![]() $A_1$
and
$A_1$
and
![]() $A_2$
by suitable powers, we may assume
$A_2$
by suitable powers, we may assume
![]() $A_1$
and
$A_1$
and
![]() $A_2$
have CM by the same field E, with respective CM types
$A_2$
have CM by the same field E, with respective CM types
![]() $\Phi _{E,1}$
and
$\Phi _{E,1}$
and
![]() $\Phi _{E,2}$
; then
$\Phi _{E,2}$
; then
![]() $A_1\times A_2$
has a CM type
$A_1\times A_2$
has a CM type
![]() $(E\times E, \Phi _{12})$
, where
$(E\times E, \Phi _{12})$
, where
![]() $\Phi _{12} = \Phi _{E,1}\sqcup \Phi _{E,2}$
. Then
$\Phi _{12} = \Phi _{E,1}\sqcup \Phi _{E,2}$
. Then
![]() $T_{\Phi _i} = T_{E,\Phi _i}$
, and the compatibility of the various (reflex) norm maps is expressed in the commutativity of the following diagram of tori:
$T_{\Phi _i} = T_{E,\Phi _i}$
, and the compatibility of the various (reflex) norm maps is expressed in the commutativity of the following diagram of tori:

In particular, in Theorem 5.4, we may compare
![]() $X^*(T_{\Phi _1})$
and
$X^*(T_{\Phi _1})$
and
![]() $X^*(T_{\Phi _2})$
inside
$X^*(T_{\Phi _2})$
inside
![]() $X^*(T^E)$
(or
$X^*(T^E)$
(or
![]() $X^{\ast }(T^{E})\otimes {\mathbb Q}$
).
$X^{\ast }(T^{E})\otimes {\mathbb Q}$
).
5.1.5 Examples
In concrete cases, Theorem 5.4 gives a way to explicitly analyze essential torsion finiteness for pairs of CM abelian varieties.
Example 5.6. Let
![]() $E = {\mathbb Q}(\zeta _{13})$
. Then
$E = {\mathbb Q}(\zeta _{13})$
. Then ![]() . There are exactly six isomorphism classes of CM types for E, with representatives
. There are exactly six isomorphism classes of CM types for E, with representatives

Let
![]() $A_i$
be an abelian sixfold with CM type
$A_i$
be an abelian sixfold with CM type
![]() $(E,\Phi _i)$
. Then any abelian variety with CM by E is geometrically isogenous to one of the
$(E,\Phi _i)$
. Then any abelian variety with CM by E is geometrically isogenous to one of the
![]() $A_i$
; and for
$A_i$
; and for
![]() $1 \le i \le 5$
,
$1 \le i \le 5$
,
![]() $A_i$
is geometrically simple. By an explicit computation, one can check that in
$A_i$
is geometrically simple. By an explicit computation, one can check that in
![]() $X^{\ast }(T^{E})\otimes {\mathbb Q}$
, we have
$X^{\ast }(T^{E})\otimes {\mathbb Q}$
, we have

Then, for any
![]() $i \leq 5$
,
$i \leq 5$
,
![]() $A_i$
is essentially torsion finite for
$A_i$
is essentially torsion finite for
![]() $A_6$
; and for any
$A_6$
; and for any
![]() $j \le 6$
,
$j \le 6$
,
![]() $A_j$
is potentially torsion infinite for
$A_j$
is potentially torsion infinite for
![]() $A_i$
.
$A_i$
.
We also can compute
![]() $X^{\ast }(H_{ij})$
explicitly. For example, consider
$X^{\ast }(H_{ij})$
explicitly. For example, consider
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. By (5.3),
$A_2$
. By (5.3),
![]() $X^{\ast }(T_{\Phi _1})$
is generated by the Galois orbit of
$X^{\ast }(T_{\Phi _1})$
is generated by the Galois orbit of
![]() $ 1+\sigma ^{-1}+\sigma ^{-2}+\sigma ^{-3}+\sigma ^{-4}+\sigma ^{-5}$
and
$ 1+\sigma ^{-1}+\sigma ^{-2}+\sigma ^{-3}+\sigma ^{-4}+\sigma ^{-5}$
and
![]() $X^{\ast }(T_{\Phi _2})$
is generated by the Galois orbit of
$X^{\ast }(T_{\Phi _2})$
is generated by the Galois orbit of
![]() $1+\sigma ^{-7}+\sigma ^{-2}+\sigma ^{-3}+\sigma ^{-4}+\sigma ^{-5}$
. Note that the Galois orbit of
$1+\sigma ^{-7}+\sigma ^{-2}+\sigma ^{-3}+\sigma ^{-4}+\sigma ^{-5}$
. Note that the Galois orbit of
![]() $ 1+\sigma ^{-1}+\sigma ^{-2}+\sigma ^{-3}+\sigma ^{-4}+\sigma ^{-5}$
(resp.
$ 1+\sigma ^{-1}+\sigma ^{-2}+\sigma ^{-3}+\sigma ^{-4}+\sigma ^{-5}$
(resp.
![]() $1+\sigma ^{-7}+\sigma ^{-2}+\sigma ^{-3}+\sigma ^{-4}+\sigma ^{-5}$
) equals the Galois orbit of
$1+\sigma ^{-7}+\sigma ^{-2}+\sigma ^{-3}+\sigma ^{-4}+\sigma ^{-5}$
) equals the Galois orbit of
![]() $1+\sigma ^{1}+\sigma ^{2}+\sigma ^{3}+\sigma ^{4}+\sigma ^{5}$
(resp.
$1+\sigma ^{1}+\sigma ^{2}+\sigma ^{3}+\sigma ^{4}+\sigma ^{5}$
(resp.
![]() $1+\sigma ^{7}+\sigma ^{2}+\sigma ^{3}+\sigma ^{4}+\sigma ^{5}$
). We compute
$1+\sigma ^{7}+\sigma ^{2}+\sigma ^{3}+\sigma ^{4}+\sigma ^{5}$
). We compute

Then
![]() $X^{\ast }(T_{\Phi _{2}})\subseteq X^{\ast }(T_{\Phi _{1}})$
. So, by (4.5),
$X^{\ast }(T_{\Phi _{2}})\subseteq X^{\ast }(T_{\Phi _{1}})$
. So, by (4.5),

The types
![]() $\Phi_1$
and
$\Phi_1$
and
![]() $\Phi_2$
are primitive. Then
$\Phi_2$
are primitive. Then
![]() $X^{\ast }(T_{\Phi _1})$
is a rank 7 free
$X^{\ast }(T_{\Phi _1})$
is a rank 7 free
![]() $\mathbb Z$
-module with a basis
$\mathbb Z$
-module with a basis
![]() $\{\sigma ^{i} + \sigma ^{i+1} + \sigma ^{i+2} + \sigma ^{i+3} + \sigma ^{i+4} +\sigma ^{i+5}\mid 0\leq i \leq 6\}$
and
$\{\sigma ^{i} + \sigma ^{i+1} + \sigma ^{i+2} + \sigma ^{i+3} + \sigma ^{i+4} +\sigma ^{i+5}\mid 0\leq i \leq 6\}$
and
![]() $X^{\ast }(T_{\Phi _2})$
is a rank 7 free
$X^{\ast }(T_{\Phi _2})$
is a rank 7 free
![]() $\mathbb Z$
-module with a basis
$\mathbb Z$
-module with a basis
![]() $\{\sigma ^{i} + \sigma ^{i+7} + \sigma ^{i+2} + \sigma ^{i+3} + \sigma ^{i+4} +\sigma ^{i+5}\mid 0\leq i \leq 6\}$
. A more detailed linear algebra calculation shows that
$\{\sigma ^{i} + \sigma ^{i+7} + \sigma ^{i+2} + \sigma ^{i+3} + \sigma ^{i+4} +\sigma ^{i+5}\mid 0\leq i \leq 6\}$
. A more detailed linear algebra calculation shows that

In Lemma 4.8, one might hope that
![]() $\widetilde {K}_{\ell }$
could be chosen independently of
$\widetilde {K}_{\ell }$
could be chosen independently of
![]() $\ell $
. To end this section, we will explain that this is impossible in general by considering the following example.
$\ell $
. To end this section, we will explain that this is impossible in general by considering the following example.
Example 5.7. Let E be
![]() ${\mathbb Q}(\zeta _{11})$
. Then
${\mathbb Q}(\zeta _{11})$
. Then ![]() . There are exactly four isomorphism classes of CM type for E, with representatives
. There are exactly four isomorphism classes of CM type for E, with representatives

Let K be a number field containing E (and, in particular, the reflex fields of each
![]() $\Phi _i$
), and let
$\Phi _i$
), and let
![]() $A_{i}/K$
be an abelian fivefold with CM type
$A_{i}/K$
be an abelian fivefold with CM type
![]() $(E, \Phi _{i})$
. Further, assume that each
$(E, \Phi _{i})$
. Further, assume that each
![]() $A_i$
has independent representations over K and that each
$A_i$
has independent representations over K and that each
![]() $A_i$
has everywhere good reduction. Let S be a sufficiently large finite set of primes of K so that the description of the Galois representations in §5.1.2 holds. Then any abelian variety with CM by E is geometrically isogenous to one of the
$A_i$
has everywhere good reduction. Let S be a sufficiently large finite set of primes of K so that the description of the Galois representations in §5.1.2 holds. Then any abelian variety with CM by E is geometrically isogenous to one of the
![]() $A_i$
. For
$A_i$
. For
![]() $2\leq i \leq 4$
,
$2\leq i \leq 4$
,
![]() $A_i$
is geometrically simple, while
$A_i$
is geometrically simple, while
![]() $A_1$
is geometrically isogenous to the cube of an elliptic curve with complex multiplication by
$A_1$
is geometrically isogenous to the cube of an elliptic curve with complex multiplication by
![]() ${\mathbb {Q}}(\sqrt {-11})$
. By an explicit computation, one can check that in
${\mathbb {Q}}(\sqrt {-11})$
. By an explicit computation, one can check that in
![]() $X^{\ast }(T^{E})\otimes {\mathbb Q}$
, we have
$X^{\ast }(T^{E})\otimes {\mathbb Q}$
, we have

For any
![]() $i\geq 2$
,
$i\geq 2$
,
![]() $A_i$
is essentially torsion finite for
$A_i$
is essentially torsion finite for
![]() $A_1$
; and for any
$A_1$
; and for any
![]() $j\leq 4$
,
$j\leq 4$
,
![]() $A_{j}$
is potentially torsion infinite for
$A_{j}$
is potentially torsion infinite for
![]() $A_{i}$
.
$A_{i}$
.
Now, we focus on
![]() $A_1$
and
$A_1$
and
![]() $A_2$
.
$A_2$
.
Identifying
![]() $X^*(T^E)$
with the group ring
$X^*(T^E)$
with the group ring
![]() ${\mathbb {Z}}[{\langle \sigma \rangle } ]$
, we may present
${\mathbb {Z}}[{\langle \sigma \rangle } ]$
, we may present
![]() $X^*(T_{\Phi _1})$
as
$X^*(T_{\Phi _1})$
as
![]() $X^*(T_{\Phi _1}) \cong {\mathbb {Z}}\oplus {\mathbb {Z}}$
, with basis elements
$X^*(T_{\Phi _1}) \cong {\mathbb {Z}}\oplus {\mathbb {Z}}$
, with basis elements
![]() $\sum _{0 \le j \le 5} \sigma ^{2j}$
and
$\sum _{0 \le j \le 5} \sigma ^{2j}$
and
![]() $\sum _{0 \le j \le 5} \sigma ^{2j+1}$
. The action of the generator
$\sum _{0 \le j \le 5} \sigma ^{2j+1}$
. The action of the generator
![]() $\sigma $
of
$\sigma $
of
![]() $\operatorname {\mathrm {Gal}}(E/{\mathbb {Q}})$
is to exchange these two basis vectors. In particular, the torus is split by the fixed field
$\operatorname {\mathrm {Gal}}(E/{\mathbb {Q}})$
is to exchange these two basis vectors. In particular, the torus is split by the fixed field
![]() ${\mathbb {Q}}(\zeta _{11})^{\sigma ^5} = {\mathbb {Q}}(\sqrt {-11})$
.
${\mathbb {Q}}(\zeta _{11})^{\sigma ^5} = {\mathbb {Q}}(\sqrt {-11})$
.
An explicit computation shows that
In particular,
![]() $X^*(H_{12}) = X^*(T_{\Phi _1})/3 X^*(T_{\Phi _1})$
. Thus,
$X^*(H_{12}) = X^*(T_{\Phi _1})/3 X^*(T_{\Phi _1})$
. Thus,
![]() ${H_{12}}_{\bar {\mathbb {Q}}} \cong ({\mathbb {Z}}/3)_{\bar {\mathbb {Q}}} \oplus ({\mathbb {Z}}/3)_{\bar {\mathbb {Q}}}$
, and the action of
${H_{12}}_{\bar {\mathbb {Q}}} \cong ({\mathbb {Z}}/3)_{\bar {\mathbb {Q}}} \oplus ({\mathbb {Z}}/3)_{\bar {\mathbb {Q}}}$
, and the action of
![]() $\operatorname {\mathrm {Gal}}({\mathbb {Q}}(\sqrt {-11})/{\mathbb {Q}})$
exchanges the two components.
$\operatorname {\mathrm {Gal}}({\mathbb {Q}}(\sqrt {-11})/{\mathbb {Q}})$
exchanges the two components.
On one hand,
![]() $H_{12}$
is zero-dimensional. Consequently, by Theorem 4.10 (and the following remark),
$H_{12}$
is zero-dimensional. Consequently, by Theorem 4.10 (and the following remark),
![]() $A_1$
is potentially torsion-infinite for
$A_1$
is potentially torsion-infinite for
![]() $A_2$
.
$A_2$
.
On the other hand,
![]() $H_{12}$
is not split over
$H_{12}$
is not split over
![]() ${\mathbb {Q}}$
, although it does admit
${\mathbb {Q}}$
, although it does admit
![]() ${\mathbb {Q}}$
-points. Indeed,
${\mathbb {Q}}$
-points. Indeed,
![]() $H_{12}({\mathbb {Q}}) = {\left \{{(0,0),(1,1),(2,2)}\right \}} \subsetneq ({\mathbb {Z}}/3)\oplus ({\mathbb {Z}}/3)$
. Consequently, Lemma 4.8 only implies that, for each
$H_{12}({\mathbb {Q}}) = {\left \{{(0,0),(1,1),(2,2)}\right \}} \subsetneq ({\mathbb {Z}}/3)\oplus ({\mathbb {Z}}/3)$
. Consequently, Lemma 4.8 only implies that, for each
![]() $\ell $
, there exists some finite extension
$\ell $
, there exists some finite extension
![]() $\widetilde K_{2,\ell ^{\infty }}$
of
$\widetilde K_{2,\ell ^{\infty }}$
of
![]() $K_{2,\ell ^{\infty }}$
such that
$K_{2,\ell ^{\infty }}$
such that
![]() $A_1[\ell ^{\infty }](\widetilde K_{2,\ell ^{\infty }})$
is infinite. We will now use the explicit calculation of the action of Galois to show that for any finite extension
$A_1[\ell ^{\infty }](\widetilde K_{2,\ell ^{\infty }})$
is infinite. We will now use the explicit calculation of the action of Galois to show that for any finite extension
![]() $L/K$
,
$L/K$
,
![]() $A_1[\ell ^{\infty }](L_{2,\ell ^{\infty }})$
is finite for all but finitely many primes
$A_1[\ell ^{\infty }](L_{2,\ell ^{\infty }})$
is finite for all but finitely many primes
![]() $\ell $
. This shows that Lemma 4.8 is essentially optimal.
$\ell $
. This shows that Lemma 4.8 is essentially optimal.
Let
![]() $\rho _{1 , \ell }$
and
$\rho _{1 , \ell }$
and
![]() $\rho _{2, \ell }$
denote
$\rho _{2, \ell }$
denote
![]() $\rho _{A_1/K,\ell ^{\infty }}$
and
$\rho _{A_1/K,\ell ^{\infty }}$
and
![]() $\rho _{A_2/K,\ell ^{\infty }}$
, respectively; and let
$\rho _{A_2/K,\ell ^{\infty }}$
, respectively; and let
![]() $\widetilde \rho _{i,\ell }$
be the pullback of
$\widetilde \rho _{i,\ell }$
be the pullback of
![]() $\rho _{i,\ell }$
to
$\rho _{i,\ell }$
to
![]() $\mathbb A_K^\times $
.
$\mathbb A_K^\times $
.
Now, suppose
![]() $\ell \not \in S$
, and embed
$\ell \not \in S$
, and embed
![]() $K_\ell ^{\times }=\prod _{v\mid \ell } K_{v}^{\times }$
naturally into the
$K_\ell ^{\times }=\prod _{v\mid \ell } K_{v}^{\times }$
naturally into the
![]() $\ell $
-adic component of
$\ell $
-adic component of
![]() $ \mathbb {A}_K^{\times }$
. Then the restriction of the
$ \mathbb {A}_K^{\times }$
. Then the restriction of the
![]() $\ell $
-adic representations (5.4) to
$\ell $
-adic representations (5.4) to
![]() $\mathcal O_{K_{\ell }}^{\times }$
reads as
$\mathcal O_{K_{\ell }}^{\times }$
reads as
Now, further assume that
![]() $\ell $
is a prime integer that totally splits in K, and use the fact that the reflex norm
$\ell $
is a prime integer that totally splits in K, and use the fact that the reflex norm
![]() $N_{K, \Phi _i}=N_{E, \Phi _i}\circ { N}_{K/E}$
, where
$N_{K, \Phi _i}=N_{E, \Phi _i}\circ { N}_{K/E}$
, where
![]() $N_{K/E}$
is the usual norm map of fields. Then
$N_{K/E}$
is the usual norm map of fields. Then
![]() $K_{\ell }$
is unramified over
$K_{\ell }$
is unramified over
![]() $E_{\ell }$
, and thus
$E_{\ell }$
, and thus
![]() $N_{K/E}(\mathcal O_{K_{\ell }}^{\times })=\mathcal O_{E_{\ell }}^{\times }$
[Reference Serre36, V, §2, Cor. of Prop. 3]. Hence, (5.6) factors through (which will still be denoted by
$N_{K/E}(\mathcal O_{K_{\ell }}^{\times })=\mathcal O_{E_{\ell }}^{\times }$
[Reference Serre36, V, §2, Cor. of Prop. 3]. Hence, (5.6) factors through (which will still be denoted by
![]() $\widetilde \rho _{i, \ell }$
to ease notation)
$\widetilde \rho _{i, \ell }$
to ease notation)
Since
![]() $\ell $
splits in K, it is also totally split in the subextension E. Recall that
$\ell $
splits in K, it is also totally split in the subextension E. Recall that ![]() , and hence
, and hence

With respect to this isomorphism, every element
![]() $a_{\ell }$
of
$a_{\ell }$
of
![]() $\mathcal O_{E_\ell }^{\times }$
can be expressed by a vector of the form
$\mathcal O_{E_\ell }^{\times }$
can be expressed by a vector of the form
![]() $a_{\ell }=(a_1, a_2, a_3,\ldots , a_{10})$
, and
$a_{\ell }=(a_1, a_2, a_3,\ldots , a_{10})$
, and ![]() acts on
acts on
![]() $a_{\ell }$
by cyclically permuting its coordinates. By definition,
$a_{\ell }$
by cyclically permuting its coordinates. By definition,

Fix
![]() $x,y \in {\mathbb {Z}}_\ell ^\times $
, and consider the element
$x,y \in {\mathbb {Z}}_\ell ^\times $
, and consider the element
![]() $a_\ell \in \mathcal O_{E_\ell }^\times $
with coordinates
$a_\ell \in \mathcal O_{E_\ell }^\times $
with coordinates
Direct computation then shows that

Now, suppose that
![]() $xy$
is a primitive third root of unity; this is possible, of course, exactly if
$xy$
is a primitive third root of unity; this is possible, of course, exactly if
![]() $\ell \equiv 1 \bmod 3$
. On one hand,
$\ell \equiv 1 \bmod 3$
. On one hand,
![]() $N_{E,\Phi _1}(a_\ell ) = 1$
; on the other hand, because
$N_{E,\Phi _1}(a_\ell ) = 1$
; on the other hand, because
![]() $xy\not \equiv 1 \bmod \ell $
and
$xy\not \equiv 1 \bmod \ell $
and
![]() $(xy)^2\not \equiv 1 \bmod \ell $
,
$(xy)^2\not \equiv 1 \bmod \ell $
,
![]() $N_{E,\Phi _2}(a_\ell )$
acts without fixed points on
$N_{E,\Phi _2}(a_\ell )$
acts without fixed points on
![]() $\mathcal O_E\otimes {\mathbb {Z}}/\ell $
. In particular,
$\mathcal O_E\otimes {\mathbb {Z}}/\ell $
. In particular,
![]() $a_\ell \in \ker \widetilde \rho _{2,\ell }\smallsetminus \ker \widetilde \rho _{1,\ell }$
. Let
$a_\ell \in \ker \widetilde \rho _{2,\ell }\smallsetminus \ker \widetilde \rho _{1,\ell }$
. Let
![]() $g\in \operatorname {\mathrm {Gal}}(K)$
be the image of
$g\in \operatorname {\mathrm {Gal}}(K)$
be the image of
![]() $a_\ell $
under the reciprocity map. By (5.6) and the formula of Serre-Tate,
$a_\ell $
under the reciprocity map. By (5.6) and the formula of Serre-Tate,
![]() $g\in \ker \rho _{2,\ell }\smallsetminus \ker \rho _{1,\ell }$
. Moreover, since
$g\in \ker \rho _{2,\ell }\smallsetminus \ker \rho _{1,\ell }$
. Moreover, since
![]() $\rho _{1,\ell }(g)= \widetilde \rho _{1,\ell }(a_{\ell })\in E^{\times }$
, we know that it does not have eigenvalue
$\rho _{1,\ell }(g)= \widetilde \rho _{1,\ell }(a_{\ell })\in E^{\times }$
, we know that it does not have eigenvalue
![]() $1$
, even when working with
$1$
, even when working with
![]() ${\mathbb {Z}}/\ell $
-coefficients. In particular,
${\mathbb {Z}}/\ell $
-coefficients. In particular,
![]() $A_1[\ell ](K_{A_2,\ell ^{\infty }})$
is trivial.
$A_1[\ell ](K_{A_2,\ell ^{\infty }})$
is trivial.
Finally, notice that we can produce such an
![]() $a_\ell $
for each
$a_\ell $
for each
![]() $\ell $
with
$\ell $
with
![]() $\ell \equiv 1 \bmod 3$
which is totally split in K. Since
$\ell \equiv 1 \bmod 3$
which is totally split in K. Since
![]() $A_1$
has independent extensions, there is not a finite extension
$A_1$
has independent extensions, there is not a finite extension
![]() $L/K$
on which each
$L/K$
on which each
![]() $\operatorname {art}(a_\ell )$
acts trivially. In particular, there is no finite extension
$\operatorname {art}(a_\ell )$
acts trivially. In particular, there is no finite extension
![]() $L/K$
such that, for each
$L/K$
such that, for each
![]() $\ell $
,
$\ell $
,
![]() $A_1[\ell ^{\infty }](L_{A_2,\ell ^{\infty }}) = A_1[\ell ^{\infty }]({\overline {L}})$
.
$A_1[\ell ^{\infty }](L_{A_2,\ell ^{\infty }}) = A_1[\ell ^{\infty }]({\overline {L}})$
.
Example 5.8. In [Reference Lombardo17, Th. 5.1], Lombardo gives a construction of an infinite family of iso-Kummerian CM pairs of abelian varieties. We briefly interpret his work in the framework developed here.
Given a CM field E which is the compositum of a cyclic totally real field of dimension g and a quadratic imaginary field, and the auxiliary choice of two integers r and h, Lombardo defines two different CM types
![]() $\Phi _1$
and
$\Phi _1$
and
![]() $\Phi _2$
, and chooses corresponding abelian varieties
$\Phi _2$
, and chooses corresponding abelian varieties
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. After passage to a suitably large common field of definition K, one shows that the kernels of the
$A_2$
. After passage to a suitably large common field of definition K, one shows that the kernels of the
![]() $\ell $
-adic representations
$\ell $
-adic representations
![]() $\widetilde \rho _{A_k,K,\ell ^{\infty }}$
coincide.
$\widetilde \rho _{A_k,K,\ell ^{\infty }}$
coincide.
This calculation shows that the characters of
![]() $T^E$
which vanish on the image of
$T^E$
which vanish on the image of
![]() $T^K$
under
$T^K$
under
![]() $N_{K,\Phi _1}$
are the same as those characters which vanish on the image of
$N_{K,\Phi _1}$
are the same as those characters which vanish on the image of
![]() $T^K$
under
$T^K$
under
![]() $N_{K,\Phi _2}$
. Consequently,
$N_{K,\Phi _2}$
. Consequently,
![]() $\operatorname {\mathrm {MT}}(A_1)$
and
$\operatorname {\mathrm {MT}}(A_1)$
and
![]() $\operatorname {\mathrm {MT}}(A_2)$
are the same subtorus of
$\operatorname {\mathrm {MT}}(A_2)$
are the same subtorus of
![]() $T_E$
, and thus
$T_E$
, and thus
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are mutually torsion-infinite.
$A_2$
are mutually torsion-infinite.
5.2 Extra Hodge classes and torsion infiniteness
Following the notation in the previous section, let
![]() $A_1$
and
$A_1$
and
![]() $A_2$
be two isotypic CM abelian varieties over K. In this section, we will see that if
$A_2$
be two isotypic CM abelian varieties over K. In this section, we will see that if
![]() $A_1$
is potentially torsion-infinite for
$A_1$
is potentially torsion-infinite for
![]() $A_2$
, then this is explained by a certain sort of Hodge class in some degree
$A_2$
, then this is explained by a certain sort of Hodge class in some degree
![]() $2w$
on some product
$2w$
on some product
![]() $A_1^m \times A_2^n$
. The particular values of w, m, and n are not unique; and even once these are specified, the class itself, or even its
$A_1^m \times A_2^n$
. The particular values of w, m, and n are not unique; and even once these are specified, the class itself, or even its
![]() ${\mathbb {Q}}$
-span is not canonical. Consequently, we will call any such Hodge class a torsion-infinite Hodge class from
${\mathbb {Q}}$
-span is not canonical. Consequently, we will call any such Hodge class a torsion-infinite Hodge class from
![]() $A_1$
to
$A_1$
to
![]() $A_2$
, even though it actually lives on some unspecified product
$A_2$
, even though it actually lives on some unspecified product
![]() $A_1^m \times A_2^n$
.
$A_1^m \times A_2^n$
.
Suppose that
![]() $A_i$
has a CM type
$A_i$
has a CM type
![]() $(E, \Phi _i)$
where E is a CM Galois extension of
$(E, \Phi _i)$
where E is a CM Galois extension of
![]() ${\mathbb Q}$
. We also assume that the base field K is sufficiently large (e.g., it contains E).
${\mathbb Q}$
. We also assume that the base field K is sufficiently large (e.g., it contains E).
We first describe the Hodge classes on
![]() $A_{1}^{m}\times A_{2}^{n}$
(see [Reference Pohlmann30] for more details). Let
$A_{1}^{m}\times A_{2}^{n}$
(see [Reference Pohlmann30] for more details). Let
![]() $V_i=H^{1}(A_{i}, {\mathbb Q})$
. Recall that
$V_i=H^{1}(A_{i}, {\mathbb Q})$
. Recall that
![]() ${\langle {V_i} \rangle }$
, the tensor category generated by
${\langle {V_i} \rangle }$
, the tensor category generated by
![]() $V_i$
, is equivalent to the category
$V_i$
, is equivalent to the category
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb Q}}(\operatorname {\mathrm {MT}}(A_i))$
of representations of
$\operatorname {\mathrm {Rep}}_{{\mathbb Q}}(\operatorname {\mathrm {MT}}(A_i))$
of representations of
![]() $\operatorname {\mathrm {MT}}(A_i)$
. By Lemma 5.1 and our assumption for E, the reflex norm defines a quotient map
$\operatorname {\mathrm {MT}}(A_i)$
. By Lemma 5.1 and our assumption for E, the reflex norm defines a quotient map
![]() $N_{E, \Phi _i}: T^{E}\twoheadrightarrow \operatorname {\mathrm {MT}}(A_{i})$
, which induces a fully faithful map on the categories of representations
$N_{E, \Phi _i}: T^{E}\twoheadrightarrow \operatorname {\mathrm {MT}}(A_{i})$
, which induces a fully faithful map on the categories of representations
![]() $\operatorname {\mathrm {Rep}}_{{\mathbb Q}}(\operatorname {\mathrm {MT}}(A_i))\rightarrow \operatorname {\mathrm {Rep}}_{{\mathbb Q}}(T^{E})$
. This allows us to describe the Hodge classes on
$\operatorname {\mathrm {Rep}}_{{\mathbb Q}}(\operatorname {\mathrm {MT}}(A_i))\rightarrow \operatorname {\mathrm {Rep}}_{{\mathbb Q}}(T^{E})$
. This allows us to describe the Hodge classes on
![]() $A_{1}^{m}\times A_{2}^{n}$
using the representation theory of the algebraic torus
$A_{1}^{m}\times A_{2}^{n}$
using the representation theory of the algebraic torus
![]() $T^{E}$
for any positive integers m and n.
$T^{E}$
for any positive integers m and n.
We denote the representation
![]() $T^{E}\twoheadrightarrow \operatorname {\mathrm {MT}}(A_i) \hookrightarrow \operatorname {\mathrm {GL}}_{V_i}$
by
$T^{E}\twoheadrightarrow \operatorname {\mathrm {MT}}(A_i) \hookrightarrow \operatorname {\mathrm {GL}}_{V_i}$
by
![]() $\rho _i$
. Note that
$\rho _i$
. Note that ![]() , and the Galois group
, and the Galois group ![]() acts on it by left multiplication. Since
acts on it by left multiplication. Since
![]() $E/{\mathbb Q}$
is Galois, we can identify
$E/{\mathbb Q}$
is Galois, we can identify
![]() $\Phi _{i}$
with a subset of
$\Phi _{i}$
with a subset of ![]() .
.
For any representation
![]() $\rho :T^{E}\rightarrow \operatorname {\mathrm {GL}}_V$
, we let
$\rho :T^{E}\rightarrow \operatorname {\mathrm {GL}}_V$
, we let
![]() $\Xi _{V}$
(or
$\Xi _{V}$
(or
![]() $\Xi _{\rho }$
) be the collection of weights of this representation. The set
$\Xi _{\rho }$
) be the collection of weights of this representation. The set
![]() $\Xi _{V}$
is a finite submultiset of
$\Xi _{V}$
is a finite submultiset of
![]() $X^{\ast }(T^{E})$
; the support
$X^{\ast }(T^{E})$
; the support ![]() of
of
![]() $\Xi _V$
—that is, those elements of
$\Xi _V$
—that is, those elements of
![]() $X^*(T^E)$
with nonzero multiplicity—is finite, and all multiplicities are finite. For future use, we note that if
$X^*(T^E)$
with nonzero multiplicity—is finite, and all multiplicities are finite. For future use, we note that if
![]() $\Xi _V = {\left \{{\alpha _1, \dots , \alpha _d}\right \}}$
is a set of distinct characters, then
$\Xi _V = {\left \{{\alpha _1, \dots , \alpha _d}\right \}}$
is a set of distinct characters, then
![]() $\operatorname {supp}(\Xi _{V^{\oplus m}})$
is the same set, and each weight now occurs with multiplicity m. Moreover, the support of
$\operatorname {supp}(\Xi _{V^{\oplus m}})$
is the same set, and each weight now occurs with multiplicity m. Moreover, the support of
![]() $\Xi _{\wedge ^r(V^{\oplus m})}$
is then
$\Xi _{\wedge ^r(V^{\oplus m})}$
is then
By the definition of the reflex norm,

Since ![]() acts transitively on this set, we have
acts transitively on this set, we have

as Galois modules. We also denote the one-dimensional representation
![]() $\operatorname {\mathrm {Nm}} :T^{E}\rightarrow \mathbb G_{m}$
by
$\operatorname {\mathrm {Nm}} :T^{E}\rightarrow \mathbb G_{m}$
by
![]() ${\mathbb Q}(1)$
. The weight of the representation
${\mathbb Q}(1)$
. The weight of the representation
![]() ${\mathbb {Q}}(1)$
is
${\mathbb {Q}}(1)$
is ![]() . If
. If
![]() $n\ge 0$
, let
$n\ge 0$
, let
![]() ${\mathbb {Q}}(n) = {\mathbb {Q}}(1)^{\otimes n}$
, and if
${\mathbb {Q}}(n) = {\mathbb {Q}}(1)^{\otimes n}$
, and if
![]() $n < 0$
, set
$n < 0$
, set
![]() ${\mathbb {Q}}(n) = {\mathbb {Q}}(1)^{\vee , \otimes -n}$
. Finally, let
${\mathbb {Q}}(n) = {\mathbb {Q}}(1)^{\vee , \otimes -n}$
. Finally, let
![]() ${\mathbb {Q}}(0)$
denote the trivial representation of
${\mathbb {Q}}(0)$
denote the trivial representation of
![]() $T^E$
. If V is any representation of
$T^E$
. If V is any representation of
![]() $T^E$
, then we let
$T^E$
, then we let
![]() $V(n) = V\otimes {\mathbb {Q}}(n)$
. If
$V(n) = V\otimes {\mathbb {Q}}(n)$
. If
![]() $V=H^{1}(A, {\mathbb Q})$
for some abelian variety A, then
$V=H^{1}(A, {\mathbb Q})$
for some abelian variety A, then
![]() $V^{\vee }\cong V(1)$
.
$V^{\vee }\cong V(1)$
.
If V is any Hodge structure, the group of Hodge classes in V is ![]() , where
, where ![]() is the trivial Hodge structure. For an integer
is the trivial Hodge structure. For an integer
![]() $w\ge 0$
, we have
$w\ge 0$
, we have

So the
![]() ${\mathbb {Q}}$
-span of a Hodge class can be identified with an element
${\mathbb {Q}}$
-span of a Hodge class can be identified with an element
![]() $\alpha \in X^{\ast }(T^{E})$
such that
$\alpha \in X^{\ast }(T^{E})$
such that
Using the polarization on
![]() $V_1$
, we rewrite these conditions as
$V_1$
, we rewrite these conditions as
Moreover, the existence of a Hodge class in degree
![]() $2w$
on some product
$2w$
on some product
![]() $A_1^m \times A_2^n$
is equivalent to the existence of
$A_1^m \times A_2^n$
is equivalent to the existence of
![]() $\alpha \in X^{\ast }(T^{E})$
and r with
$\alpha \in X^{\ast }(T^{E})$
and r with
![]() $0 \le r \le 2w$
such that
$0 \le r \le 2w$
such that
![]() $\alpha $
is a
$\alpha $
is a
![]() ${\mathbb {Z}}_{\ge 0}$
-linear combination of the weights in
${\mathbb {Z}}_{\ge 0}$
-linear combination of the weights in
![]() $\Xi _{V_{1}}$
and
$\Xi _{V_{1}}$
and
![]() $\alpha +(w-r)\chi $
is a
$\alpha +(w-r)\chi $
is a
![]() ${\mathbb {Z}}_{\ge 0}$
-linear combination of the weights in
${\mathbb {Z}}_{\ge 0}$
-linear combination of the weights in
![]() $\Xi _{V_{2}}$
. Let
$\Xi _{V_{2}}$
. Let
![]() $s = 2w-r$
. The choices
$s = 2w-r$
. The choices
![]() $(r,s) = (0,2w)$
and
$(r,s) = (0,2w)$
and
![]() $(r,s) = (2w,0)$
correspond to Hodge classes which come from
$(r,s) = (2w,0)$
correspond to Hodge classes which come from
![]() $A_1^m$
and
$A_1^m$
and
![]() $A_2^n$
by pullback, while classes with r and s positive are conjecturally the classes of nontrivial correspondences between
$A_2^n$
by pullback, while classes with r and s positive are conjecturally the classes of nontrivial correspondences between
![]() $A_1^m$
and
$A_1^m$
and
![]() $A_2^n$
.
$A_2^n$
.
For such
![]() $\alpha \in \Xi _{\wedge ^{r} V_{1}^{ \oplus m}}$
, if moreover
$\alpha \in \Xi _{\wedge ^{r} V_{1}^{ \oplus m}}$
, if moreover
![]() $\alpha =r\alpha _{0}$
for some
$\alpha =r\alpha _{0}$
for some
![]() $\alpha _{0}\in \Xi _{V_{1}}$
and some positive integer r, that is,
$\alpha _{0}\in \Xi _{V_{1}}$
and some positive integer r, that is,
we call the related Hodge classes torsion-infinite Hodge classes from
![]() $A_{1}$
to
$A_{1}$
to
![]() $A_{2}$
, regardless of the choice of m and n (and of r and s). As a consequence of our definition, these classes are in
$A_{2}$
, regardless of the choice of m and n (and of r and s). As a consequence of our definition, these classes are in
![]() $H^{r,0}(A_{1}^{m})^{\vee }\otimes H^{s}(A_{2}^{n}, \mathbb C)(w-r)$
(or
$H^{r,0}(A_{1}^{m})^{\vee }\otimes H^{s}(A_{2}^{n}, \mathbb C)(w-r)$
(or
![]() $H^{0,r}(A_{1}^{m})^{\vee }\otimes H^{s}(A_{2}^{n}, \mathbb C)(w-r)$
). In particular, these classes are not in the
$H^{0,r}(A_{1}^{m})^{\vee }\otimes H^{s}(A_{2}^{n}, \mathbb C)(w-r)$
). In particular, these classes are not in the
![]() ${\mathbb {Q}}$
-span of those classes which are pulled back from
${\mathbb {Q}}$
-span of those classes which are pulled back from
![]() $A_1^m$
or
$A_1^m$
or
![]() $A_2^n$
, and thus the torsion-infinite Hodge classes are extra Hodge classes.
$A_2^n$
, and thus the torsion-infinite Hodge classes are extra Hodge classes.
Proposition 5.9. Let
![]() $A_1$
and
$A_1$
and
![]() $A_2$
be two isotypic CM abelian varieties over a number field K. Suppose that
$A_2$
be two isotypic CM abelian varieties over a number field K. Suppose that
![]() $\operatorname {Hom}_{{\overline {K}}}(A_1, A_2) =(0)$
, that is, that
$\operatorname {Hom}_{{\overline {K}}}(A_1, A_2) =(0)$
, that is, that
![]() $A_{1,{\overline {K}}}$
and
$A_{1,{\overline {K}}}$
and
![]() $A_{2,{\overline {K}}}$
have no common nontrivial isogeny factor.
$A_{2,{\overline {K}}}$
have no common nontrivial isogeny factor.
Then
![]() $A_1$
is potentially torsion-infinite for
$A_1$
is potentially torsion-infinite for
![]() $A_2$
if and only if there is a torsion-infinite Hodge class from
$A_2$
if and only if there is a torsion-infinite Hodge class from
![]() $A_{1}$
to
$A_{1}$
to
![]() $A_2$
.
$A_2$
.
Proof. Assume that
![]() $A_1$
is potentially torsion-infinite for
$A_1$
is potentially torsion-infinite for
![]() $A_2$
over K. By Theorem 5.4,
$A_2$
over K. By Theorem 5.4,
Suppose that
![]() $\alpha \in \Xi _{V_1}$
. Then
$\alpha \in \Xi _{V_1}$
. Then
![]() $\alpha =\sum _{\beta \in \Xi _{V_{2}}}c_{\beta } \beta $
for certain rational numbers
$\alpha =\sum _{\beta \in \Xi _{V_{2}}}c_{\beta } \beta $
for certain rational numbers
![]() $c_\beta $
. Note that, if
$c_\beta $
. Note that, if
![]() $\beta \in \Xi _{V_{2}}$
, then its complex conjugate
$\beta \in \Xi _{V_{2}}$
, then its complex conjugate
![]() $\beta \circ c = \chi -\beta $
is in
$\beta \circ c = \chi -\beta $
is in
![]() $\Xi _{V_2}$
, too. Using this fact, we can rewrite
$\Xi _{V_2}$
, too. Using this fact, we can rewrite
![]() $\alpha $
as
$\alpha $
as

where
![]() $c_{\beta }^{+}$
and
$c_{\beta }^{+}$
and
![]() $c_{\chi }^{+}$
are nonnegative rational numbers. Choose a positive integer m such that
$c_{\chi }^{+}$
are nonnegative rational numbers. Choose a positive integer m such that
![]() $mc_{\beta }^{+}$
and
$mc_{\beta }^{+}$
and
![]() $mc_{\chi }^{+}$
are integers. Then
$mc_{\chi }^{+}$
are integers. Then

Let
![]() $n=\sum _{\beta \in \Xi _{\rho _2}}mc_{\beta }^{+}$
.
$n=\sum _{\beta \in \Xi _{\rho _2}}mc_{\beta }^{+}$
.
Consider the embedding
![]() $\mathbb G_m \to T^E$
induced by
$\mathbb G_m \to T^E$
induced by
![]() ${\mathbb {Q}}\hookrightarrow E$
, and let
${\mathbb {Q}}\hookrightarrow E$
, and let
![]() $\tau $
be the standard (positive) generator of
$\tau $
be the standard (positive) generator of
![]() $X^*(\mathbb G_m)$
. Then
$X^*(\mathbb G_m)$
. Then
![]() $\gamma |_{\mathbb G_m} = g\tau $
for any
$\gamma |_{\mathbb G_m} = g\tau $
for any
![]() $\gamma \in \Xi _{V_1}\cup \Xi _{V_2}$
, while
$\gamma \in \Xi _{V_1}\cup \Xi _{V_2}$
, while
![]() $\chi |_{\mathbb G_m} = 2g\tau $
. Thus, restricting (5.8) to
$\chi |_{\mathbb G_m} = 2g\tau $
. Thus, restricting (5.8) to
![]() $\mathbb G_m$
and computing coefficients of
$\mathbb G_m$
and computing coefficients of
![]() $\tau $
yields
$\tau $
yields
In particular,
![]() $m+n=n-m +2m=2mc_{\chi }^{+}+2m=2(mc_{\chi }^{+}+m)$
is even. Then
$m+n=n-m +2m=2mc_{\chi }^{+}+2m=2(mc_{\chi }^{+}+m)$
is even. Then
![]() $H^{m}(A_{1}^{m},{\mathbb Q})\otimes H^{n}(A_{2}^{n},{\mathbb Q})(mc_{\chi }^{+}+m)$
contains a torsion-infinite Hodge class from
$H^{m}(A_{1}^{m},{\mathbb Q})\otimes H^{n}(A_{2}^{n},{\mathbb Q})(mc_{\chi }^{+}+m)$
contains a torsion-infinite Hodge class from
![]() $A_{1}$
to
$A_{1}$
to
![]() $A_{2}$
.
$A_{2}$
.
Conversely, if there is a torsion-infinite Hodge class from
![]() $A_{1}$
to
$A_{1}$
to
![]() $A_{2}$
, then there exists a weight
$A_{2}$
, then there exists a weight
![]() $\alpha _0\in \Xi _{V_{1}}$
which is a
$\alpha _0\in \Xi _{V_{1}}$
which is a
![]() ${\mathbb {Q}}$
-linear combination of the weights in
${\mathbb {Q}}$
-linear combination of the weights in
![]() $\Xi _{V_{2}}$
. Since
$\Xi _{V_{2}}$
. Since ![]() acts transitively on
acts transitively on
![]() $\Xi _{V_{1}}$
,
$\Xi _{V_{1}}$
,
![]() $X^{\ast }(T_{\Phi _{1}})\otimes {\mathbb Q}\subset X^{\ast }(T_{\Phi _{2}})\otimes {\mathbb Q} $
. By theorem 5.4,
$X^{\ast }(T_{\Phi _{1}})\otimes {\mathbb Q}\subset X^{\ast }(T_{\Phi _{2}})\otimes {\mathbb Q} $
. By theorem 5.4,
![]() $A_1$
is potentially torsion infinite for
$A_1$
is potentially torsion infinite for
![]() $A_2$
over K.
$A_2$
over K.
Remark 5.10. In the proof, we choose
![]() $r=m$
and
$r=m$
and
![]() $s=n=\sum _{\beta \in \Xi _{\rho _{2}}}mc_{\beta }^{+}$
for convenience. However, sometimes smaller m and n can be chosen. See Examples 5.12 and 5.7.
$s=n=\sum _{\beta \in \Xi _{\rho _{2}}}mc_{\beta }^{+}$
for convenience. However, sometimes smaller m and n can be chosen. See Examples 5.12 and 5.7.
Before displaying some concrete examples, let us prove the following lemma. Recall our discussion of nondegenerate abelian varieties (5.1.3).
Lemma 5.11. Let
![]() $A_1$
and
$A_1$
and
![]() $A_2$
be two CM abelian varieties. Suppose that
$A_2$
be two CM abelian varieties. Suppose that
![]() $A_i$
has a CM type
$A_i$
has a CM type
![]() $(E, \Phi _i)$
and
$(E, \Phi _i)$
and
![]() $A_{2}$
is nondegenerate. Then
$A_{2}$
is nondegenerate. Then
![]() $X^{\ast }(T_{\Phi _{1}})\otimes {\mathbb Q}\subseteq X^{\ast }(T_{\Phi _{2}})\otimes {\mathbb Q}$
. In particular, if
$X^{\ast }(T_{\Phi _{1}})\otimes {\mathbb Q}\subseteq X^{\ast }(T_{\Phi _{2}})\otimes {\mathbb Q}$
. In particular, if
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
are nondegenerate, then
$A_{2}$
are nondegenerate, then
![]() $X^{\ast }(T_{\Phi _{1}})\otimes {\mathbb Q}= X^{\ast }(T_{\Phi _{2}})\otimes {\mathbb Q}$
.
$X^{\ast }(T_{\Phi _{1}})\otimes {\mathbb Q}= X^{\ast }(T_{\Phi _{2}})\otimes {\mathbb Q}$
.
Proof. First, we let
![]() $E^+$
be the totally real subfield of E and let
$E^+$
be the totally real subfield of E and let
![]() $\mathbb {U}_1^{E^+}$
be the norm one subtorus of
$\mathbb {U}_1^{E^+}$
be the norm one subtorus of
![]() $T^{E^+}$
. For any CM type
$T^{E^+}$
. For any CM type
![]() $(E,\Phi )$
,
$(E,\Phi )$
,
because the restriction of
![]() $N_{E,\Phi }$
to
$N_{E,\Phi }$
to
![]() $T^{E^+}$
is simply
$T^{E^+}$
is simply
![]() $N_{E^+/{\mathbb {Q}}}$
; and a dimension count shows that equality holds if and only if
$N_{E^+/{\mathbb {Q}}}$
; and a dimension count shows that equality holds if and only if
![]() $(E,\Phi )$
is nondegenerate.
$(E,\Phi )$
is nondegenerate.
Under the hypotheses of the lemma, we have the following commutative diagram:

where the surjection f is induced by the inclusion
![]() $(\ker (N_{E, \Phi _2}))^{\circ }=\mathbb {U}_1^{E^+}\hookrightarrow (\ker (N_{E, \Phi _1}))^{\circ }$
. This implies that
$(\ker (N_{E, \Phi _2}))^{\circ }=\mathbb {U}_1^{E^+}\hookrightarrow (\ker (N_{E, \Phi _1}))^{\circ }$
. This implies that
![]() $X^{\ast }(T_{\Phi _{1}})\otimes {\mathbb Q}\subseteq X^{\ast }(T_{\Phi _{2}})\otimes {\mathbb Q}$
.
$X^{\ast }(T_{\Phi _{1}})\otimes {\mathbb Q}\subseteq X^{\ast }(T_{\Phi _{2}})\otimes {\mathbb Q}$
.
Example 5.12. Let E be
![]() ${\mathbb Q}(\zeta _{7})$
. Then
${\mathbb Q}(\zeta _{7})$
. Then ![]() . There are two isomorphism classes of CM types for E:
. There are two isomorphism classes of CM types for E:
Let
![]() $A_i$
be an abelian variety with CM type
$A_i$
be an abelian variety with CM type
![]() $(E,\Phi _i)$
. Then
$(E,\Phi _i)$
. Then
![]() $A_1$
is geometrically isogenous to the third power of an elliptic curve with CM by
$A_1$
is geometrically isogenous to the third power of an elliptic curve with CM by
![]() ${\mathbb Q}(\sqrt {-7})$
, while
${\mathbb Q}(\sqrt {-7})$
, while
![]() $A_2$
is nondegenerate. By Lemma 5.11,
$A_2$
is nondegenerate. By Lemma 5.11,
![]() $A_1$
is potentially torsion-infinite for
$A_1$
is potentially torsion-infinite for
![]() $A_2$
. In fact, we have
$A_2$
. In fact, we have

This means that
![]() $H^1(A_1,{\mathbb Q})^\vee \otimes H^3(A_2,{\mathbb Q})(1)$
contains a torsion-infinite Hodge class from
$H^1(A_1,{\mathbb Q})^\vee \otimes H^3(A_2,{\mathbb Q})(1)$
contains a torsion-infinite Hodge class from
![]() $A_1$
to
$A_1$
to
![]() $A_2$
.
$A_2$
.
Example 5.13. We return to the setting of Example 5.7, with
![]() $E = {\mathbb Q}(\zeta _{11})$
. Consider
$E = {\mathbb Q}(\zeta _{11})$
. Consider
![]() $A_2$
and
$A_2$
and
![]() $A_3$
with CM types
$A_3$
with CM types
![]() $(E, \Phi _2=\{1, \sigma ^6, \sigma ^2, \sigma ^3, \sigma ^4\})$
and
$(E, \Phi _2=\{1, \sigma ^6, \sigma ^2, \sigma ^3, \sigma ^4\})$
and
![]() $(E, \Phi _{3}=\{1, \sigma ^3, \sigma ^6, \sigma ^{9}, \sigma ^2\})$
. Since
$(E, \Phi _{3}=\{1, \sigma ^3, \sigma ^6, \sigma ^{9}, \sigma ^2\})$
. Since
![]() $A_2$
and
$A_2$
and
![]() $A_3$
are primitive, by Lemma 5.11,
$A_3$
are primitive, by Lemma 5.11,
![]() $X^{\ast }(T_{\Phi _2})\otimes {\mathbb Q}= X^{\ast }(T_{\Phi _3})\otimes {\mathbb Q}$
. Considering the relation between
$X^{\ast }(T_{\Phi _2})\otimes {\mathbb Q}= X^{\ast }(T_{\Phi _3})\otimes {\mathbb Q}$
. Considering the relation between
![]() $X^{\ast }(T_{\Phi _2})$
and
$X^{\ast }(T_{\Phi _2})$
and
![]() $X^{\ast }(T_{\Phi _3})$
, we have
$X^{\ast }(T_{\Phi _3})$
, we have
More precisely,

and

So
![]() $A_2$
and
$A_2$
and
![]() $A_3$
are potentially torsion-infinite for each other. Moreover,
$A_3$
are potentially torsion-infinite for each other. Moreover,
![]() $H^{1}(A_3, {\mathbb Q})^{\vee }\otimes H^{3}(A_2, {\mathbb Q})(1)$
contains a torsion-infinite Hodge class from
$H^{1}(A_3, {\mathbb Q})^{\vee }\otimes H^{3}(A_2, {\mathbb Q})(1)$
contains a torsion-infinite Hodge class from
![]() $A_3$
to
$A_3$
to
![]() $A_2$
, and
$A_2$
, and
![]() $H^{3}(A_2^3, {\mathbb Q})^{\vee }\otimes H^{7}(A_3^2, {\mathbb Q})(2)$
contains a torsion-infinite Hodge class from
$H^{3}(A_2^3, {\mathbb Q})^{\vee }\otimes H^{7}(A_3^2, {\mathbb Q})(2)$
contains a torsion-infinite Hodge class from
![]() $A_2^3$
to
$A_2^3$
to
![]() $A_3^2$
.
$A_3^2$
.
5.3 Low-dimensional abelian varieties
In [Reference Moonen and Zarhin23, §2], Moonen and Zarhin list all the possible Hodge groups for absolute simple abelian varieties with dimension
![]() $g \leq 3$
. We will follow their classification and use the notation
$g \leq 3$
. We will follow their classification and use the notation
![]() $(g, {\mathrm{Type}})$
to denote an absolutely simple abelian variety with dimension g and the indicated endomorphism type in the Albert classification. For instance,
$(g, {\mathrm{Type}})$
to denote an absolutely simple abelian variety with dimension g and the indicated endomorphism type in the Albert classification. For instance,
![]() $(2, {\textrm IV}(2,1))$
refers to an absolutely simple CM abelian surface.
$(2, {\textrm IV}(2,1))$
refers to an absolutely simple CM abelian surface.
Theorem 5.14. Suppose A and B are absolutely simple abelian varieties over a common number field, and assume that they are nonisogenous over
![]() $\mathbb C$
. Suppose that
$\mathbb C$
. Suppose that
![]() $\dim A \le \dim B \le 3$
. Then A and B are mutually essentially torsion finite except for the following cases:
$\dim A \le \dim B \le 3$
. Then A and B are mutually essentially torsion finite except for the following cases:
-
(a) A is a CM elliptic curve, and B is of type
 $(3, {\textrm IV}(3,1))$
, that is, B is a simple CM abelian threefold. Then B is essentially torsion finite for A; and A is potentially torsion infinite for B exactly when there is an embedding of
$(3, {\textrm IV}(3,1))$
, that is, B is a simple CM abelian threefold. Then B is essentially torsion finite for A; and A is potentially torsion infinite for B exactly when there is an embedding of
 ${\mathbb {Q}}$
-algebras
${\mathbb {Q}}$
-algebras  .
. -
(b) A is a CM elliptic curve, and B is of type
 $(3, {\textrm IV}(1,1))$
. Then B is essentially torsion finite for A; and A is potentially torsion infinite for B exactly when there is an isomorphism of
$(3, {\textrm IV}(1,1))$
. Then B is essentially torsion finite for A; and A is potentially torsion infinite for B exactly when there is an isomorphism of
 ${\mathbb {Q}}$
-algebras
${\mathbb {Q}}$
-algebras  .
. -
(c)
 $[A,B]$
is of type
$[A,B]$
is of type
 $[(3,{\textrm IV}(3,1)), (3,{\textrm IV}(3,1))]$
, that is, both of them are CM abelian threefolds. Then the essential torsion finiteness depends on the CM types of A and B as in Theorem 5.4.
$[(3,{\textrm IV}(3,1)), (3,{\textrm IV}(3,1))]$
, that is, both of them are CM abelian threefolds. Then the essential torsion finiteness depends on the CM types of A and B as in Theorem 5.4.
Proof. Our proof contains two parts. In the first part, we will assume that the pair
![]() $(A,B)$
is not one of the cases (a), (b), or (c). The analysis of the special situations is carried out in the second part.
$(A,B)$
is not one of the cases (a), (b), or (c). The analysis of the special situations is carried out in the second part.
Recall that, if
then A and B are mutually torsion finite (Corollary 4.15). Since
![]() $\dim A\leq \dim B$
, (5.9) holds in each of the following cases.
$\dim A\leq \dim B$
, (5.9) holds in each of the following cases.
-
1. Suppose both A and B are of odd relative dimension, and they are not both of type IV. Then [Reference Ichikawa10, Th. IA] states that (5.9) holds.
-
2. Suppose A is a CM elliptic curve and condition (a) does not hold. Then (5.9) is a consequence of [Reference Moonen and Zarhin23, Prop. (3.8)]. In particular, (5.9) holds if B is a surface (since a geometrically simple abelian surface in characteristic zero does not admit an action by a quadratic imaginary field—this result of Shimura informs [Reference Moonen and Zarhin23, (2.2)]) or a non-type IV threefold.
-
3. If
 $\dim A=\dim B=2$
, then (5.9) follows from [Reference Moonen and Zarhin23, (5.4) and (5.5)].
$\dim A=\dim B=2$
, then (5.9) follows from [Reference Moonen and Zarhin23, (5.4) and (5.5)]. -
4. If
 $\dim A=2$
and
$\dim A=2$
and
 $\dim B=3$
, then (5.9) follows from [Reference Moonen and Zarhin23, Th. (0.2)(iv)].
$\dim B=3$
, then (5.9) follows from [Reference Moonen and Zarhin23, Th. (0.2)(iv)].
Hence, we are left with two situations to discuss. For expository ease, we will let
![]() $A_1=A$
and
$A_1=A$
and
![]() $A_2=B$
in the following discussion.
$A_2=B$
in the following discussion.
Case 1. Suppose the pair is of type [(3,IV(1,1)), (3,IV(1,1))], and that
![]() $A_1$
is potentially torsion infinite for
$A_1$
is potentially torsion infinite for
![]() $A_2$
; we will show that
$A_2$
; we will show that
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are geometrically isogenous. We start by describing the Mumford–Tate groups of each
$A_2$
are geometrically isogenous. We start by describing the Mumford–Tate groups of each
![]() $A_i$
although ultimately we will analyze their special Mumford–Tate groups, in order to exploit the fact that isogenous one-dimensional algebraic tori are actually isomorphic. Recall that if G is a reductive group with derived group
$A_i$
although ultimately we will analyze their special Mumford–Tate groups, in order to exploit the fact that isogenous one-dimensional algebraic tori are actually isomorphic. Recall that if G is a reductive group with derived group
![]() $G'$
and connected center
$G'$
and connected center
![]() $Z $
, then Z is a torus and G is canonically isomorphic to
$Z $
, then Z is a torus and G is canonically isomorphic to
![]() $G'\times Z/(G'\cap Z)$
.
$G'\times Z/(G'\cap Z)$
.
For
![]() $i = 1,2$
, the endomorphism algebra
$i = 1,2$
, the endomorphism algebra ![]() is an imaginary quadratic field. The Mumford–Tate group
is an imaginary quadratic field. The Mumford–Tate group
![]() $G_i$
of
$G_i$
of
![]() $A_i$
is a unitary similitude group in three variables attached to the quadratic extension
$A_i$
is a unitary similitude group in three variables attached to the quadratic extension
![]() $F_i/{\mathbb {Q}}$
, which we denote
$F_i/{\mathbb {Q}}$
, which we denote
![]() $\operatorname {\mathrm {GU}}_{F_i}(3)$
, and the Hodge group
$\operatorname {\mathrm {GU}}_{F_i}(3)$
, and the Hodge group
![]() $sG_i$
is the unitary group
$sG_i$
is the unitary group
![]() $\operatorname {\mathrm {U}}_{F_i}(3)$
. The center of
$\operatorname {\mathrm {U}}_{F_i}(3)$
. The center of
![]() $G_i$
is
$G_i$
is
![]() $T^{F_i} = \operatorname {\mathrm {Res}}_{F_i/{\mathbb {Q}}}{\mathbb {G}}_m$
; the connected center
$T^{F_i} = \operatorname {\mathrm {Res}}_{F_i/{\mathbb {Q}}}{\mathbb {G}}_m$
; the connected center
![]() $Z_i$
of
$Z_i$
of
![]() $sG_i$
is the norm one torus
$sG_i$
is the norm one torus
![]() $T^{F_i,1} =\operatorname {\mathrm {Res}}^{(1)}_{F_i/{\mathbb {Q}}}{\mathbb {G}}_m \cong \operatorname {\mathrm {U}}_{F_i}(1)$
; and we have exact sequences
$T^{F_i,1} =\operatorname {\mathrm {Res}}^{(1)}_{F_i/{\mathbb {Q}}}{\mathbb {G}}_m \cong \operatorname {\mathrm {U}}_{F_i}(1)$
; and we have exact sequences

The restriction
![]() $\delta _i := \det |_{Z_i}$
is
$\delta _i := \det |_{Z_i}$
is
![]() $[3]_{Z_i}$
, the cubing map. Moreover,
$[3]_{Z_i}$
, the cubing map. Moreover,
![]() $H_1(A_i,{\mathbb {Q}})$
is the standard representation of
$H_1(A_i,{\mathbb {Q}})$
is the standard representation of
![]() $G_i$
(see, e.g., [Reference Moonen and Zarhin23, (2.3)]).
$G_i$
(see, e.g., [Reference Moonen and Zarhin23, (2.3)]).
Note that
![]() $\dim G_1 = \dim G_2$
. Under the assumption that
$\dim G_1 = \dim G_2$
. Under the assumption that
![]() $A_1$
is potentially torsion-infinite for
$A_1$
is potentially torsion-infinite for
![]() $A_2$
, we have
$A_2$
, we have
![]() $\dim G_{12} = \dim G_2$
(Theorem 4.10). Therefore,
$\dim G_{12} = \dim G_2$
(Theorem 4.10). Therefore,
![]() $\dim G_{12} = \dim G_1$
as well, and thus
$\dim G_{12} = \dim G_1$
as well, and thus
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are mutually potentially torsion-infinite.
$A_2$
are mutually potentially torsion-infinite.
The isogenies
![]() $\pi _i: G_{12} \to G_i$
induce isomorphisms of Lie algebras
$\pi _i: G_{12} \to G_i$
induce isomorphisms of Lie algebras
![]() $\mathfrak g_{12} \to \mathfrak g_{i}$
. We thus have an isomorphism of
$\mathfrak g_{12} \to \mathfrak g_{i}$
. We thus have an isomorphism of
![]() ${\mathbb {Q}}$
-Lie algebras
${\mathbb {Q}}$
-Lie algebras
![]() $\mathfrak {gu}_{F_1}(3) \cong \mathfrak {gu}_{F_2}(3)$
, and so
$\mathfrak {gu}_{F_1}(3) \cong \mathfrak {gu}_{F_2}(3)$
, and so
![]() $F_1 \cong F_2$
. We relabel this common quadratic field F and proceed.
$F_1 \cong F_2$
. We relabel this common quadratic field F and proceed.
For each i, the inclusion
![]() $H_1(A_i,{\mathbb {Q}})\hookrightarrow H_1(A_1\times A_2,{\mathbb {Q}})$
is F-linear. Therefore, we have commutative diagrams
$H_1(A_i,{\mathbb {Q}})\hookrightarrow H_1(A_1\times A_2,{\mathbb {Q}})$
is F-linear. Therefore, we have commutative diagrams

where the right-hand diagram is the restriction of the left-hand diagram to Hodge groups.
Fix some i, and consider the isogeny of Hodge groups
![]() $\pi _i: sG_{12} \to sG_i$
. Let
$\pi _i: sG_{12} \to sG_i$
. Let
![]() $M_i = \pi _i^{-1}(\operatorname {\mathrm {SU}}_F(3))^\circ $
. Since
$M_i = \pi _i^{-1}(\operatorname {\mathrm {SU}}_F(3))^\circ $
. Since
![]() $\operatorname {\mathrm {SU}}_F(3)$
is simply connected,
$\operatorname {\mathrm {SU}}_F(3)$
is simply connected,
![]() $M_i \cong \operatorname {\mathrm {SU}}_F(3)$
maps isomorphically onto its image. Let
$M_i \cong \operatorname {\mathrm {SU}}_F(3)$
maps isomorphically onto its image. Let
![]() $d_{12}\colon sG_{12} \to sG_{12}/M_i$
be the projection. The quotient
$d_{12}\colon sG_{12} \to sG_{12}/M_i$
be the projection. The quotient
![]() $sG_{12}/M_i$
is a smooth geometrically connected group which is isogenous to the one-dimensional torus
$sG_{12}/M_i$
is a smooth geometrically connected group which is isogenous to the one-dimensional torus
![]() $T^{F,1}$
, and thus is isomorphic to
$T^{F,1}$
, and thus is isomorphic to
![]() $T^{F,1}$
. Similarly, the connected center
$T^{F,1}$
. Similarly, the connected center
![]() $Z_{12}$
of
$Z_{12}$
of
![]() $sG_{12}$
is isomorphic to
$sG_{12}$
is isomorphic to
![]() $T^{F,1}$
, and we have a commutative diagram:
$T^{F,1}$
, and we have a commutative diagram:

Let
![]() $\delta _{12}= d_{12}|_{Z_{12}}$
, and note that
$\delta _{12}= d_{12}|_{Z_{12}}$
, and note that
![]() $\ker \delta _{12} = Z_{12} \cap \operatorname {\mathrm {SU}}_F(3)$
. Since
$\ker \delta _{12} = Z_{12} \cap \operatorname {\mathrm {SU}}_F(3)$
. Since
![]() $\bar \pi _i \circ \delta _{12} = \delta _1=[3]$
and
$\bar \pi _i \circ \delta _{12} = \delta _1=[3]$
and
![]() $\ker [3]$
is simple, exactly one of
$\ker [3]$
is simple, exactly one of
![]() $\bar \pi _i$
and
$\bar \pi _i$
and
![]() $\delta _{12}$
is an isomorphism. So either:
$\delta _{12}$
is an isomorphism. So either:
-
•
 $\delta _{12}$
is an isomorphism. Then
$\delta _{12}$
is an isomorphism. Then
 $Z_{12}\cap \operatorname {\mathrm {SU}}_F(3) = {\left \{{1}\right \}}$
, and so
$Z_{12}\cap \operatorname {\mathrm {SU}}_F(3) = {\left \{{1}\right \}}$
, and so
 $sG_{12} \cong \operatorname {\mathrm {SU}}_F(3)\times \operatorname {\mathrm {U}}_F(1)$
, and
$sG_{12} \cong \operatorname {\mathrm {SU}}_F(3)\times \operatorname {\mathrm {U}}_F(1)$
, and
 $\pi _i$
is the canonical projection; or
$\pi _i$
is the canonical projection; or -
•
 $\bar \pi _i$
is an isomorphism. Then
$\bar \pi _i$
is an isomorphism. Then
 $Z_{12}\cap \operatorname {\mathrm {SU}}_F(3) = \ker [3]$
,
$Z_{12}\cap \operatorname {\mathrm {SU}}_F(3) = \ker [3]$
,
 $sG_{12} \cong \operatorname {\mathrm {U}}_F(3)$
, and
$sG_{12} \cong \operatorname {\mathrm {U}}_F(3)$
, and
 $\pi _i$
is an isomorphism.
$\pi _i$
is an isomorphism.
Of course, the isomorphism class of
![]() $sG_{12}$
is independent of the choice of i; and we have seen that each
$sG_{12}$
is independent of the choice of i; and we have seen that each
![]() $\pi _i$
is determined, up to isomorphism, by the isomorphism class of
$\pi _i$
is determined, up to isomorphism, by the isomorphism class of
![]() $sG_{12}$
. Therefore,
$sG_{12}$
. Therefore,
![]() $sG_{12} \to sG_i \to \operatorname {\mathrm {GL}}_{V_i}$
is independent of i, and so
$sG_{12} \to sG_i \to \operatorname {\mathrm {GL}}_{V_i}$
is independent of i, and so
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are isogenous (Lemma 4.1). (After the fact, using Lemma 4.1(c), we recognize that the second case happens, that is, that
$A_2$
are isogenous (Lemma 4.1). (After the fact, using Lemma 4.1(c), we recognize that the second case happens, that is, that
![]() $sG_{12} \cong U_F(3)$
.)
$sG_{12} \cong U_F(3)$
.)
Case 2. If the pair is of type
![]() $[(3, {\mathrm{IV}}(1,1)), (3, {\mathrm{IV}}(3,1))]$
, then the Hodge group of
$[(3, {\mathrm{IV}}(1,1)), (3, {\mathrm{IV}}(3,1))]$
, then the Hodge group of
![]() $A_1$
has been explained in Case 1. Note in particular that the center of
$A_1$
has been explained in Case 1. Note in particular that the center of
![]() $\operatorname {\mathrm {sMT}}(A_1)$
is
$\operatorname {\mathrm {sMT}}(A_1)$
is
![]() $U_{F_1}(1)$
, a one-dimensional torus.
$U_{F_1}(1)$
, a one-dimensional torus.
Now consider
![]() $A_2$
. It has complex multiplication by a CM field
$A_2$
. It has complex multiplication by a CM field
![]() $E_2$
. Since
$E_2$
. Since
![]() $\dim A_2 = 3$
is prime, the CM type is nondegenerate, that is,
$\dim A_2 = 3$
is prime, the CM type is nondegenerate, that is,
![]() $\dim \operatorname {\mathrm {sMT}}(A_2) = 3$
.
$\dim \operatorname {\mathrm {sMT}}(A_2) = 3$
.
In particular, there is no isogeny from the center of
![]() $\operatorname {\mathrm {sMT}}(A_1)$
to
$\operatorname {\mathrm {sMT}}(A_1)$
to
![]() $\operatorname {\mathrm {sMT}}(A_2)$
. By [Reference Moonen and Zarhin23, Lem. 3.6],
$\operatorname {\mathrm {sMT}}(A_2)$
. By [Reference Moonen and Zarhin23, Lem. 3.6],
![]() $A_1$
and
$A_1$
and
![]() $A_2$
satisfy (5.9), and thus are mutually essentially torsion finite. This finishes the first part of the proof.
$A_2$
satisfy (5.9), and thus are mutually essentially torsion finite. This finishes the first part of the proof.
It remains to discuss cases (a)–and (c). Of course, there is nothing to prove for case (c). As for (a) and (b), since
we immediately deduce that
![]() $A_2$
is essentially torsion finite for
$A_2$
is essentially torsion finite for
![]() $A_1$
.
$A_1$
.
Moreover, by [Reference Moonen and Zarhin23, Prop. (3.8)],
![]() $\operatorname {\mathrm {sMT}}(A_1\times A_2) = \operatorname {\mathrm {sMT}}(A_1)\times \operatorname {\mathrm {sMT}}(A_2)$
if and only if there is no embedding
$\operatorname {\mathrm {sMT}}(A_1\times A_2) = \operatorname {\mathrm {sMT}}(A_1)\times \operatorname {\mathrm {sMT}}(A_2)$
if and only if there is no embedding ![]() ; and this is equivalent to the essential torsion finiteness of
; and this is equivalent to the essential torsion finiteness of
![]() $A_1$
for
$A_1$
for
![]() $A_2$
(Corollary 4.12).
$A_2$
(Corollary 4.12).
Acknowledgments
We thank Yuan Ren for bringing this interesting question to our attention. Lian Duan thanks Ken Ribet for useful suggestions; Xiyuan Wang thanks Stefan Patrikis for many enlightening discussions; and we all thank Davide Lombardo for helpful comments on a draft of this article. This article benefited greatly from a referee’s extraordinarily close reading; we are grateful for their efforts.