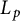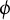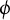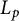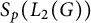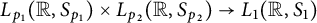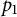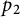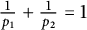1 Introduction
In recent years, the analysis of Fourier multipliers on noncommutative
![]() $L_p$
-spaces has seen a rapid development. In particular, several multiplier theorems have been established for the noncommutative
$L_p$
-spaces has seen a rapid development. In particular, several multiplier theorems have been established for the noncommutative
![]() $L_p$
-spaces of a group von Neumann algebra (see, e.g., [Reference Cadilhac, Conde-Alonso and ParcetCCP22, Reference Conde-Alonso, González-Pérez, Parcet and TablateCGPTb, Reference Junge, Mei and ParcetJMP14, Reference Mei and RicardMeRi17, Reference Mei, Ricard and XuMRX22, Reference Parcet, Ricard and de la SallePRS22]). Here, the symbol of the multiplier is a function on a locally compact group and the multiplier acts on the noncommutative
$L_p$
-spaces of a group von Neumann algebra (see, e.g., [Reference Cadilhac, Conde-Alonso and ParcetCCP22, Reference Conde-Alonso, González-Pérez, Parcet and TablateCGPTb, Reference Junge, Mei and ParcetJMP14, Reference Mei and RicardMeRi17, Reference Mei, Ricard and XuMRX22, Reference Parcet, Ricard and de la SallePRS22]). Here, the symbol of the multiplier is a function on a locally compact group and the multiplier acts on the noncommutative
![]() $L_p$
-space. In particular, the group plays the role of the frequency side.
$L_p$
-space. In particular, the group plays the role of the frequency side.
In several of these approaches, Schur multipliers are used to estimate the bounds of Fourier multipliers and vice versa. For instance, upper bounds on the norms of Fourier multipliers in terms of Schur multipliers play a crucial role in [Reference Parcet, Ricard and de la SallePRS22]. Conversely, transference from Fourier to Schur multipliers was used by Pisier [Reference PisierPi98] to provide examples of bounded multipliers on
![]() $L_p$
-spaces that are not completely bounded. In [Reference Lafforgue and de la SalleLaSa11], analogous transference techniques were used to provide examples of noncommutative
$L_p$
-spaces that are not completely bounded. In [Reference Lafforgue and de la SalleLaSa11], analogous transference techniques were used to provide examples of noncommutative
![]() $L_p$
-spaces without the completely bounded approximation property. Furthermore, the use of multilinear Schur multipliers and operator integrals led to several surprising results such as the resolution of Koplienko’s conjecture on higher-order spectral shift [Reference Potapov, Skripka and SukochevPSS13] (see also [Reference Potapov, Skripka, Sukochev and TomskovaPSST17]).
$L_p$
-spaces without the completely bounded approximation property. Furthermore, the use of multilinear Schur multipliers and operator integrals led to several surprising results such as the resolution of Koplienko’s conjecture on higher-order spectral shift [Reference Potapov, Skripka and SukochevPSS13] (see also [Reference Potapov, Skripka, Sukochev and TomskovaPSST17]).
Bo
![]() $\dot{\rm z}$
ejko and Fendler proved the following in [Reference Bozejko and FendlerBoFe84]. Let G be a locally compact group. Let
$\dot{\rm z}$
ejko and Fendler proved the following in [Reference Bozejko and FendlerBoFe84]. Let G be a locally compact group. Let
![]() $\phi \in C_b(G)$
and set
$\phi \in C_b(G)$
and set
![]() $\widetilde {\phi }(s,t) = \phi (s t^{-1}), s,t \in G$
. Then the Schur multiplier
$\widetilde {\phi }(s,t) = \phi (s t^{-1}), s,t \in G$
. Then the Schur multiplier
![]() $M_{\widetilde {\phi }}: B(L_2(G)) \rightarrow B(L_2(G))$
is bounded if and only if it is completely bounded if and only if the Fourier multiplier
$M_{\widetilde {\phi }}: B(L_2(G)) \rightarrow B(L_2(G))$
is bounded if and only if it is completely bounded if and only if the Fourier multiplier
![]() $T_{\phi }: \mathcal {L}G \rightarrow \mathcal {L}G$
is completely bounded.
$T_{\phi }: \mathcal {L}G \rightarrow \mathcal {L}G$
is completely bounded.
Several papers have treated the extension of the Bo
![]() $\dot{\rm z}$
ejko–Fendler result to noncommutative
$\dot{\rm z}$
ejko–Fendler result to noncommutative
![]() $L_p$
-spaces. In particular, in [Reference Neuwirth and RicardNeRi11], Neuwirth and Ricard proved for a discrete group G that
$L_p$
-spaces. In particular, in [Reference Neuwirth and RicardNeRi11], Neuwirth and Ricard proved for a discrete group G that
If G is moreover amenable, then this is an equality. The same result was then obtained for G a locally compact group in [Reference Caspers and de la SalleCaSa15]. An analogous result was obtained for actions and crossed products by González-Perez [Reference Gonzalez-PerezGon18], and in an ad hoc way in the bilinear discrete setting, a similar result was obtained for the discrete Heisenberg group in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Section 7].
The purpose of this paper is to prove transference results for Fourier and Schur multipliers in the multilinear setting for arbitrary unimodular locally compact groups. We confine ourselves to the unimodular setting for reasons further discussed in Remark 4.4.
Now, we describe in more detail the contents of the paper. Our first main result (Theorem 3.1) is the following multilinear extension of [Reference Caspers and de la SalleCaSa15, Theorem 4.2]. The definition of
![]() $(p_1, \dots , p_n)$
-multiplicatively bounded maps is given in Section 2.7. If
$(p_1, \dots , p_n)$
-multiplicatively bounded maps is given in Section 2.7. If
![]() $n=1$
, then we are in the linear case and by a well-known theorem of Pisier [Reference PisierPi98] a map is “p-multiplicatively bounded” if and only if it is completely bounded as a map on the
$n=1$
, then we are in the linear case and by a well-known theorem of Pisier [Reference PisierPi98] a map is “p-multiplicatively bounded” if and only if it is completely bounded as a map on the
![]() $L_p$
-space with the natural operator space structure that was also introduced in [Reference PisierPi98].
$L_p$
-space with the natural operator space structure that was also introduced in [Reference PisierPi98].
Theorem A Let G be a locally compact second countable unimodular group, and let
![]() $1 \leq p \leq \infty $
,
$1 \leq p \leq \infty $
,
![]() $1<p_1, \ldots , p_n \leq \infty $
be such that
$1<p_1, \ldots , p_n \leq \infty $
be such that
![]() $p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
$p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
![]() $\phi \in C_b(G^{\times n})$
and set
$\phi \in C_b(G^{\times n})$
and set
![]() $\widetilde {\phi } \in C_b(G^{\times n + 1})$
by
$\widetilde {\phi } \in C_b(G^{\times n + 1})$
by
If
![]() $\phi $
is the symbol of a
$\phi $
is the symbol of a
![]() $(p_1, \ldots , p_n)$
-multiplicatively bounded Fourier multiplier
$(p_1, \ldots , p_n)$
-multiplicatively bounded Fourier multiplier
![]() $T_{\phi }$
of G, then
$T_{\phi }$
of G, then
![]() $\widetilde {\phi }$
is the symbol of a
$\widetilde {\phi }$
is the symbol of a
![]() $(p_1, \ldots , p_n)$
-multiplicatively bounded Schur multiplier
$(p_1, \ldots , p_n)$
-multiplicatively bounded Schur multiplier
![]() $M_{\widetilde {\phi }}$
of G. Moreover,
$M_{\widetilde {\phi }}$
of G. Moreover,
 $$\begin{align*}\begin{aligned} & \Vert M_{\widetilde{\phi}}: S_{p_1}(L_2(G)) \times \cdots \times S_{p_n}(L_2(G)) \rightarrow S_{p}(L_2(G)) \Vert_{(p_1,\ldots,p_n)-mb}\\ & \qquad \leq \Vert T_{\phi}: L_{p_1}(\mathcal{L}G ) \times \cdots \times L_{p_n}(\mathcal{L}G ) \rightarrow L_{p}(\mathcal{L}G ) \Vert_{(p_1,\ldots,p_n)-mb}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} & \Vert M_{\widetilde{\phi}}: S_{p_1}(L_2(G)) \times \cdots \times S_{p_n}(L_2(G)) \rightarrow S_{p}(L_2(G)) \Vert_{(p_1,\ldots,p_n)-mb}\\ & \qquad \leq \Vert T_{\phi}: L_{p_1}(\mathcal{L}G ) \times \cdots \times L_{p_n}(\mathcal{L}G ) \rightarrow L_{p}(\mathcal{L}G ) \Vert_{(p_1,\ldots,p_n)-mb}. \end{aligned} \end{align*}$$
Note that in the linear (unimodular, second countable) case of
![]() $n=1$
, this result is actually a strengthening of [Reference Caspers and de la SalleCaSa15, Theorem 4.2]. Namely, the symbol here is only assumed to define an
$n=1$
, this result is actually a strengthening of [Reference Caspers and de la SalleCaSa15, Theorem 4.2]. Namely, the symbol here is only assumed to define an
![]() $L_p$
-Fourier multiplier at a single exponent p, whereas [Reference Caspers and de la SalleCaSa15, Theorem 4.2] requires that the multiplier is (completely) bounded for all
$L_p$
-Fourier multiplier at a single exponent p, whereas [Reference Caspers and de la SalleCaSa15, Theorem 4.2] requires that the multiplier is (completely) bounded for all
![]() $1 \leq p \leq \infty $
simultaneously. The current proof takes a different route and uses results that appeared after [Reference Caspers and de la SalleCaSa15] in the papers [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Reference Caspers, Parcet, Perrin and RicardCPPR15, Reference Conde-Alonso, Parcet and RicardCPR18].
$1 \leq p \leq \infty $
simultaneously. The current proof takes a different route and uses results that appeared after [Reference Caspers and de la SalleCaSa15] in the papers [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Reference Caspers, Parcet, Perrin and RicardCPPR15, Reference Conde-Alonso, Parcet and RicardCPR18].
For transference in the other direction, we need our group G to be amenable, just as in [Reference Caspers and de la SalleCaSa15, Reference Neuwirth and RicardNeRi11]. In fact, amenability is a necessary requirement for our proof strategy (see [Reference Caspers and de la SalleCaSa15, Theorem 2.1]). The following is our second main result (Corollary 4.2). Note here the strict bounds
![]() $1 < p < \infty $
, caused by the requirement that the maps
$1 < p < \infty $
, caused by the requirement that the maps
![]() $i_q$
from Theorem 4.1 are complete isometries.
$i_q$
from Theorem 4.1 are complete isometries.
Theorem B Let G be a locally compact unimodular amenable group, and let
![]() $1 < p,p_1,\ldots ,p_n < \infty $
be such that
$1 < p,p_1,\ldots ,p_n < \infty $
be such that
![]() $p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Let
$p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Let
![]() $\phi \in C_b(G^{\times n})$
and define
$\phi \in C_b(G^{\times n})$
and define
![]() $\widetilde {\phi }$
as in (1.1). If
$\widetilde {\phi }$
as in (1.1). If
![]() $\widetilde {\phi }$
is the symbol of a
$\widetilde {\phi }$
is the symbol of a
![]() $(p_1, \ldots , p_n)$
-bounded (resp. multiplicatively bounded) Schur multiplier, then
$(p_1, \ldots , p_n)$
-bounded (resp. multiplicatively bounded) Schur multiplier, then
![]() $\phi $
is the symbol of a
$\phi $
is the symbol of a
![]() $(p_1, \dots , p_n)$
-bounded (resp. multiplicatively bounded) Fourier multiplier. Moreover,
$(p_1, \dots , p_n)$
-bounded (resp. multiplicatively bounded) Fourier multiplier. Moreover,
with equality in the
![]() $(p_1,\ldots ,p_n)$
-
$(p_1,\ldots ,p_n)$
-
![]() $mb$
norm when G is second countable.
$mb$
norm when G is second countable.
The proof is a multilinear version of the ultraproduct techniques from [Reference Caspers and de la SalleCaSa15, Theorem 5.2] and [Reference Neuwirth and RicardNeRi11].
In the final section, which can mostly be read separately from the rest of the paper, we consider the case of vector-valued bilinear Fourier multipliers on
![]() ${\operatorname {\mathbb {R}}}$
. Lacey and Thiele have shown in [Reference Lacey and ThieleLaTh99] that the bilinear Hilbert transform is bounded from
${\operatorname {\mathbb {R}}}$
. Lacey and Thiele have shown in [Reference Lacey and ThieleLaTh99] that the bilinear Hilbert transform is bounded from
![]() $L_{p_1}(\mathbb {R}) \times L_{p_2}(\mathbb {R}) \to L_p(\mathbb {R})$
, when
$L_{p_1}(\mathbb {R}) \times L_{p_2}(\mathbb {R}) \to L_p(\mathbb {R})$
, when
![]() $\frac {2}{3} < p < \infty $
and
$\frac {2}{3} < p < \infty $
and
![]() $\frac {1}{p}=\frac {1}{p_1}+\frac {1}{p_2}$
. The vector-valued bilinear Hilbert transform is bounded as a map from
$\frac {1}{p}=\frac {1}{p_1}+\frac {1}{p_2}$
. The vector-valued bilinear Hilbert transform is bounded as a map from
whenever
![]() $1<\frac {1}{\max \{q,q'\}} + \frac {1}{\max \{q_1,q_1'\} }+ \frac {1}{\max \{q_2,q_2'\}}$
, as shown by Amenta and Uraltsev in [Reference Amenta and UraltsevAmUr20] and Di Plinio et al. in [Reference DiPlinio, Li, Martikainen and VuorinenDMLV22]. In particular, this class does not include Hölder combinations of
$1<\frac {1}{\max \{q,q'\}} + \frac {1}{\max \{q_1,q_1'\} }+ \frac {1}{\max \{q_2,q_2'\}}$
, as shown by Amenta and Uraltsev in [Reference Amenta and UraltsevAmUr20] and Di Plinio et al. in [Reference DiPlinio, Li, Martikainen and VuorinenDMLV22]. In particular, this class does not include Hölder combinations of
![]() $q_i$
. We show that this result does not extend to the case when
$q_i$
. We show that this result does not extend to the case when
![]() $p_i=q_i,p=q=1$
, using a transference method similar to the ones used in earlier sections. To be precise, we prove the following result (Theorem 5.2).
$p_i=q_i,p=q=1$
, using a transference method similar to the ones used in earlier sections. To be precise, we prove the following result (Theorem 5.2).
Theorem C Let
![]() $1 < p_1, p_2 < \infty $
be such that
$1 < p_1, p_2 < \infty $
be such that
![]() $\frac {1}{p_1} + \frac {1}{p_2} = 1$
and set
$\frac {1}{p_1} + \frac {1}{p_2} = 1$
and set
![]() $h(s,t) = \chi _{\geq 0}(s-t)$
. There exists an absolute constant
$h(s,t) = \chi _{\geq 0}(s-t)$
. There exists an absolute constant
![]() $C>0$
such that, for every
$C>0$
such that, for every
![]() $N \in \mathbb {N}_{\geq 1}$
, we have
$N \in \mathbb {N}_{\geq 1}$
, we have
Additionally, we show a similar result for Calderón–Zygmund operators. Here, Grafakos and Torres [Reference Grafakos and TorresGrTo02] have shown that for a class of Calderón–Zygmund operators, we have boundedness
![]() $L_1 \times L_1 \rightarrow L_{\frac {1}{2}, \infty }$
in the Euclidean case. Later, a vector-valued extension was obtained in [Reference DiPlinio, Li, Martikainen and VuorinenDLMV20]. Here, for a class of Calderón–Zygmund operators, the boundedness of the vector-valued map was obtained for
$L_1 \times L_1 \rightarrow L_{\frac {1}{2}, \infty }$
in the Euclidean case. Later, a vector-valued extension was obtained in [Reference DiPlinio, Li, Martikainen and VuorinenDLMV20]. Here, for a class of Calderón–Zygmund operators, the boundedness of the vector-valued map was obtained for
![]() $L_{p_1} \times L_{p_2} \rightarrow L_p$
with
$L_{p_1} \times L_{p_2} \rightarrow L_p$
with
![]() $1 < p, p_1, p_2 < \infty $
and
$1 < p, p_1, p_2 < \infty $
and
![]() $\frac {1}{p}=\frac {1}{p_1}+\frac {1}{p_2}$
. Theorem 5.3 shows that the latter result cannot be extended to the case when
$\frac {1}{p}=\frac {1}{p_1}+\frac {1}{p_2}$
. Theorem 5.3 shows that the latter result cannot be extended to the case when
![]() $p=1$
.
$p=1$
.
The structure of this paper is as follows. In Section 2, we treat the necessary preliminaries and establish the definitions of multilinear Fourier and Schur multipliers. We also look briefly at transference in the case that
![]() $p_i = \infty $
for all i. In Section 3, we prove the transference from Fourier to Schur multipliers for general
$p_i = \infty $
for all i. In Section 3, we prove the transference from Fourier to Schur multipliers for general
![]() $p_i$
; the other direction for amenable G is proved in Section 4. Finally, in Section 5, we give the counterexamples for the vector-valued bilinear Hilbert transform and Calderón–Zygmund operators.
$p_i$
; the other direction for amenable G is proved in Section 4. Finally, in Section 5, we give the counterexamples for the vector-valued bilinear Hilbert transform and Calderón–Zygmund operators.
2 Preliminaries
2.1 Notational conventions
![]() $\mathbb {N}$
denotes the natural numbers starting from 0, and
$\mathbb {N}$
denotes the natural numbers starting from 0, and
![]() $\mathbb {N}_{\geq 1}$
denotes
$\mathbb {N}_{\geq 1}$
denotes
![]() $\mathbb {N} \backslash \{ 0 \}$
.
$\mathbb {N} \backslash \{ 0 \}$
.
![]() $M_n := M_n(\mathbb {C})$
denotes the complex
$M_n := M_n(\mathbb {C})$
denotes the complex
![]() $n \times n$
matrices. We denote
$n \times n$
matrices. We denote
![]() $B(H)$
for the bounded operators on a Hilbert space H. We denote by
$B(H)$
for the bounded operators on a Hilbert space H. We denote by
![]() $E_{st}, 1 \leq s,t \leq n$
, the matrix units of
$E_{st}, 1 \leq s,t \leq n$
, the matrix units of
![]() $M_n$
. Likewise,
$M_n$
. Likewise,
![]() $E_{st}$
,
$E_{st}$
,
![]() $s,t \in F$
denote the matrix units of
$s,t \in F$
denote the matrix units of
![]() $B(\ell _2(F))$
whenever F is a finite set. We also use
$B(\ell _2(F))$
whenever F is a finite set. We also use
![]() $1_F$
to denote the indicator function on the set F.
$1_F$
to denote the indicator function on the set F.
2.2 Locally compact groups
Let G be a locally compact group, which we assume to be unimodular with Haar measure
![]() $\mu _G$
(see Remark 4.4). Integration against the Haar measure is denoted by
$\mu _G$
(see Remark 4.4). Integration against the Haar measure is denoted by
![]() $\int \cdot \: ds$
. For
$\int \cdot \: ds$
. For
![]() $1 \leq p <\infty $
, we let
$1 \leq p <\infty $
, we let
![]() $L_p(G)$
be the p-integrable functions with norm determined by
$L_p(G)$
be the p-integrable functions with norm determined by
![]() $\Vert f \Vert _p^p = \int \vert f(s) \vert ^p ds$
.
$\Vert f \Vert _p^p = \int \vert f(s) \vert ^p ds$
.
![]() $C_c(G)$
denotes the continuous and compactly supported functions on G.
$C_c(G)$
denotes the continuous and compactly supported functions on G.
![]() $L_1(G)$
is a
$L_1(G)$
is a
![]() $\ast $
-algebra with multiplication given by convolution
$\ast $
-algebra with multiplication given by convolution
![]() $(f\ast g)(t) = \int f(s) g(s^{-1} t) ds$
and involution given by
$(f\ast g)(t) = \int f(s) g(s^{-1} t) ds$
and involution given by
![]() $f^{\ast }(s) = \overline { f(s^{-1})}$
.
$f^{\ast }(s) = \overline { f(s^{-1})}$
.
![]() $\lambda $
denotes the left regular representation of G on
$\lambda $
denotes the left regular representation of G on
![]() $L_2(G)$
, i.e.,
$L_2(G)$
, i.e.,
![]() $(\lambda _s f)(t) = f(s^{-1}t)$
.
$(\lambda _s f)(t) = f(s^{-1}t)$
.
![]() $\lambda $
also determines a representation of
$\lambda $
also determines a representation of
![]() $L_1(G)$
by the strongly convergent integral
$L_1(G)$
by the strongly convergent integral
![]() $\lambda (f) = \int f(s) \lambda _s ds$
. The Fourier algebra [Reference EymardEym64] is defined as
$\lambda (f) = \int f(s) \lambda _s ds$
. The Fourier algebra [Reference EymardEym64] is defined as
Set the group von Neumann algebra
It comes equipped with a natural weight
![]() $\varphi $
called the Plancherel weight that is given, for
$\varphi $
called the Plancherel weight that is given, for
![]() $x \in \mathcal {L} G$
, by
$x \in \mathcal {L} G$
, by
 $$\begin{align*}\varphi(x^{\ast} x) = \left\{ \begin{array}{ll} \Vert f \Vert_2^2, & \textrm{ if } \exists f \in L_2(G) \textrm { s.t. } \forall \xi \in C_{c}(G): x \xi = f \ast \xi, \\ \infty, & \textrm{ otherwise}. \end{array} \right. \end{align*}$$
$$\begin{align*}\varphi(x^{\ast} x) = \left\{ \begin{array}{ll} \Vert f \Vert_2^2, & \textrm{ if } \exists f \in L_2(G) \textrm { s.t. } \forall \xi \in C_{c}(G): x \xi = f \ast \xi, \\ \infty, & \textrm{ otherwise}. \end{array} \right. \end{align*}$$
![]() $\varphi $
is tracial since (in fact if and only if) G is unimodular, i.e.,
$\varphi $
is tracial since (in fact if and only if) G is unimodular, i.e.,
![]() $\varphi (x^{\ast } x ) = \varphi (x x^{\ast })$
.
$\varphi (x^{\ast } x ) = \varphi (x x^{\ast })$
.
2.3 Noncommutative
 $L_p$
-spaces
$L_p$
-spaces
Let
![]() $L_p(\mathcal {L} G)$
denote the noncommutative
$L_p(\mathcal {L} G)$
denote the noncommutative
![]() $L_p$
-space associated with
$L_p$
-space associated with
![]() $\mathcal {L} G$
and the Plancherel weight
$\mathcal {L} G$
and the Plancherel weight
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $\varphi $
is a trace, this space can be viewed as the completion of the set of elements in
$\varphi $
is a trace, this space can be viewed as the completion of the set of elements in
![]() $\mathcal {L} G$
with finite
$\mathcal {L} G$
with finite
![]() $\|.\|_{L_p(\mathcal {L} G)}$
norm:
$\|.\|_{L_p(\mathcal {L} G)}$
norm:
Let
![]() $C_c(G) \star C_c(G)$
denote the span of the set of functions of the form
$C_c(G) \star C_c(G)$
denote the span of the set of functions of the form
![]() $f_1 \ast f_2, f_i \in C_c(G)$
. Then
$f_1 \ast f_2, f_i \in C_c(G)$
. Then
![]() $\lambda (C_c(G)\star C_c(G))$
is dense in
$\lambda (C_c(G)\star C_c(G))$
is dense in
![]() $L_p(\mathcal {L} G)$
for every
$L_p(\mathcal {L} G)$
for every
![]() $1\leq p <\infty $
and is weak* dense in
$1\leq p <\infty $
and is weak* dense in
![]() $L_{\infty }(\mathcal {L} G)=\mathcal {L} G$
.
$L_{\infty }(\mathcal {L} G)=\mathcal {L} G$
.
2.4 Multilinear Fourier multipliers
Let
![]() $\phi \in C_b(G^{\times n})$
. The Fourier multiplier
$\phi \in C_b(G^{\times n})$
. The Fourier multiplier
![]() $T_{\phi }$
associated with the symbol
$T_{\phi }$
associated with the symbol
![]() $\phi $
is the multilinear map defined for
$\phi $
is the multilinear map defined for
![]() $\lambda (f_i), f_i \in C_c(G)\star C_c(G)$
by
$\lambda (f_i), f_i \in C_c(G)\star C_c(G)$
by
Let
![]() $1\leq p_1, \ldots , p_n, p < \infty $
with
$1\leq p_1, \ldots , p_n, p < \infty $
with
![]() $p^{-1}=\sum _i p_i^{-1}$
. Assume that
$p^{-1}=\sum _i p_i^{-1}$
. Assume that
![]() $T_{\phi }$
maps
$T_{\phi }$
maps
![]() $\lambda (C_c(G)\star C_c(G)) \times \cdots \times \lambda (C_c(G)\ast C_c(G))$
into
$\lambda (C_c(G)\star C_c(G)) \times \cdots \times \lambda (C_c(G)\ast C_c(G))$
into
![]() $L_p(\mathcal {L} G)$
. Equip the ith copy of
$L_p(\mathcal {L} G)$
. Equip the ith copy of
![]() $\lambda (C_c(G)\star C_c(G))$
with the
$\lambda (C_c(G)\star C_c(G))$
with the
![]() $\|.\|_{L_{p_i}(\mathcal {L} G)}$
topology. If
$\|.\|_{L_{p_i}(\mathcal {L} G)}$
topology. If
![]() $T_{\phi }$
is a continuous multilinear map with respect to the above topologies, we extend
$T_{\phi }$
is a continuous multilinear map with respect to the above topologies, we extend
![]() $T_{\phi }$
to a map
$T_{\phi }$
to a map
![]() $L_{p_1}(\mathcal {L} G)\times \cdots \times L_{p_n}(\mathcal {L} G) \to L_p (\mathcal {L} G)$
. By mild abuse of notation, we also denote this map by
$L_{p_1}(\mathcal {L} G)\times \cdots \times L_{p_n}(\mathcal {L} G) \to L_p (\mathcal {L} G)$
. By mild abuse of notation, we also denote this map by
![]() $T_{\phi }$
, and call it the
$T_{\phi }$
, and call it the
![]() $(p_1,\ldots ,p_n)$
-Fourier multiplier associated with
$(p_1,\ldots ,p_n)$
-Fourier multiplier associated with
![]() $\phi $
. When some or all of the
$\phi $
. When some or all of the
![]() $p_i, p$
are equal to
$p_i, p$
are equal to
![]() $\infty $
, we equip the corresponding copy of
$\infty $
, we equip the corresponding copy of
![]() $\lambda (C_c(G) \star C_c(G))$
with the norm topology from
$\lambda (C_c(G) \star C_c(G))$
with the norm topology from
![]() $C^{\ast }_{\lambda }(G)$
, and replace
$C^{\ast }_{\lambda }(G)$
, and replace
![]() $L_{p_i}(\mathcal {L} G)$
by
$L_{p_i}(\mathcal {L} G)$
by
![]() $C^{\ast }_{\lambda }(G)$
.
$C^{\ast }_{\lambda }(G)$
.
By a closed graph argument,
![]() $T_{\phi }$
is then a bounded multilinear map, and we denote its norm by
$T_{\phi }$
is then a bounded multilinear map, and we denote its norm by
![]() $\Vert T_{\phi } \Vert _{(p_1,\ldots ,p_n)}$
.
$\Vert T_{\phi } \Vert _{(p_1,\ldots ,p_n)}$
.
2.5 Schatten
 $p $
-operators
$p $
-operators
For
![]() $1\leq p< \infty $
, let
$1\leq p< \infty $
, let
![]() $S_p(H)$
denote the Schatten p-operators on a Hilbert space H consisting of all
$S_p(H)$
denote the Schatten p-operators on a Hilbert space H consisting of all
![]() $x \in B(H)$
such that
$x \in B(H)$
such that
![]() $\Vert x \Vert _{S_p} := \mathrm {Tr}(\vert x \vert ^p)^{1/p} <\infty $
where
$\Vert x \Vert _{S_p} := \mathrm {Tr}(\vert x \vert ^p)^{1/p} <\infty $
where
![]() $\mathrm {Tr}$
is the usual trace on
$\mathrm {Tr}$
is the usual trace on
![]() $B(H)$
.
$B(H)$
.
![]() $S_{\infty }(H)$
denotes the compact operators on H. For
$S_{\infty }(H)$
denotes the compact operators on H. For
![]() $1 \leq p \leq q \leq \infty $
, we have the dense inclusions
$1 \leq p \leq q \leq \infty $
, we have the dense inclusions
![]() $S_p(H) \subseteq S_q(H)$
.
$S_p(H) \subseteq S_q(H)$
.
Again, let G be a unimodular locally compact group. For
![]() $F \subset G$
a relatively compact set with positive measure, let
$F \subset G$
a relatively compact set with positive measure, let
![]() $P_F:L_2(G)\to L_2(F)$
be the orthogonal projection. Then, for
$P_F:L_2(G)\to L_2(F)$
be the orthogonal projection. Then, for
![]() $1\leq p \leq \infty $
, and
$1\leq p \leq \infty $
, and
![]() $x \in L_{2p}( \mathcal {L} G)$
,
$x \in L_{2p}( \mathcal {L} G)$
,
![]() $x P_F$
defines an operator in
$x P_F$
defines an operator in
![]() $S_{2p}(L_2(G))$
(see [Reference Caspers and de la SalleCaSa15, Proposition 3.1]). For
$S_{2p}(L_2(G))$
(see [Reference Caspers and de la SalleCaSa15, Proposition 3.1]). For
![]() $x \in L_{p}(\mathcal {L} G)$
with polar decomposition
$x \in L_{p}(\mathcal {L} G)$
with polar decomposition
![]() $x = u \vert x \vert $
, we will abusively denote by
$x = u \vert x \vert $
, we will abusively denote by
![]() $P_F x P_F$
the operator
$P_F x P_F$
the operator
![]() $ ( \vert x \vert ^{1/2} u^{\ast } P_F)^{\ast } \vert x \vert ^{1/2} P_F $
, which lies in
$ ( \vert x \vert ^{1/2} u^{\ast } P_F)^{\ast } \vert x \vert ^{1/2} P_F $
, which lies in
![]() $S_p(L_2(G))$
whenever
$S_p(L_2(G))$
whenever
![]() $x \in L_p(\mathcal {L} G)$
. We will additionally use the fact that the map
$x \in L_p(\mathcal {L} G)$
. We will additionally use the fact that the map
defines a contraction from
![]() $L_p(\mathcal {L} G)$
to
$L_p(\mathcal {L} G)$
to
![]() $S_p(L_2(G))$
[Reference Caspers and de la SalleCaSa15, Theorem 5.1].
$S_p(L_2(G))$
[Reference Caspers and de la SalleCaSa15, Theorem 5.1].
Let E be an operator space. For
![]() $N \in \mathbb {N}_{\geq 1}$
, and
$N \in \mathbb {N}_{\geq 1}$
, and
![]() $1\leq p \leq \infty $
,
$1\leq p \leq \infty $
,
![]() $S_p^N[E]$
will denote the space
$S_p^N[E]$
will denote the space
![]() $M_N(E)$
equipped with the “operator-valued Schatten p-norm.” When
$M_N(E)$
equipped with the “operator-valued Schatten p-norm.” When
![]() $E={\operatorname {\mathbb {C}}}$
, this is the Schatten p-class associated with a Hilbert space of dimension n, or equivalently, the noncommutative
$E={\operatorname {\mathbb {C}}}$
, this is the Schatten p-class associated with a Hilbert space of dimension n, or equivalently, the noncommutative
![]() $L_p$
-space associated with
$L_p$
-space associated with
![]() $M_N$
equipped with the normalized trace, and is denoted by just
$M_N$
equipped with the normalized trace, and is denoted by just
![]() $S_p^N$
. When
$S_p^N$
. When
![]() $p=\infty $
, the norm on
$p=\infty $
, the norm on
![]() $S_p[E]$
is the operator space norm on
$S_p[E]$
is the operator space norm on
![]() $M_N(E)$
; for
$M_N(E)$
; for
![]() $p=1$
, this is the projective operator space norm on
$p=1$
, this is the projective operator space norm on
![]() $S_1^N\otimes E$
. The rest are constructed via interpolation. The particulars will not be used in what follows; we refer to [Reference PisierPi98] for the details. If E is the noncommutative
$S_1^N\otimes E$
. The rest are constructed via interpolation. The particulars will not be used in what follows; we refer to [Reference PisierPi98] for the details. If E is the noncommutative
![]() $L_p$
-space associated with some tracial von Neumann algebra
$L_p$
-space associated with some tracial von Neumann algebra
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $S_p^N[E]$
can be identified with the noncommutative
$S_p^N[E]$
can be identified with the noncommutative
![]() $L_p$
-space corresponding to
$L_p$
-space corresponding to
![]() $M_N \otimes \mathcal {M}$
.
$M_N \otimes \mathcal {M}$
.
2.6 Multilinear Schur multipliers
Let X be some measure space. We identify
![]() $S_2(L_2(X))$
linearly and isometrically with the integral operators given by kernels in
$S_2(L_2(X))$
linearly and isometrically with the integral operators given by kernels in
![]() $L_2(X\times X)$
. This way
$L_2(X\times X)$
. This way
![]() $A \in L_2(X\times X)$
corresponds to
$A \in L_2(X\times X)$
corresponds to
![]() $(A \xi )(t) = \int A(t,s) \xi (s) ds$
. Throughout what follows, we will make no distinction between a Hilbert–Schmidt operator on
$(A \xi )(t) = \int A(t,s) \xi (s) ds$
. Throughout what follows, we will make no distinction between a Hilbert–Schmidt operator on
![]() $L_2(X)$
and its kernel in
$L_2(X)$
and its kernel in
![]() $L_2(X \times X)$
.
$L_2(X \times X)$
.
For
![]() $\phi \in L_{\infty }(X^{\times n+1})$
, the associated Schur multiplier is the multilinear map
$\phi \in L_{\infty }(X^{\times n+1})$
, the associated Schur multiplier is the multilinear map
![]() $S_2(L_2(X))\times \cdots \times S_2(L_2(X)) \to S_2(L_2(X))$
determined by
$S_2(L_2(X))\times \cdots \times S_2(L_2(X)) \to S_2(L_2(X))$
determined by
 $$\begin{align*}&M_{\phi}( A_1,\ldots, A_n)(t_0,t_n) \\&\quad= \int_{X^{\times n-1}} \phi(t_0,\ldots,t_n) A_1(t_0,t_1)A_2(t_1,t_2)\ldots A_n(t_{n-1},t_n) dt_1 \ldots dt_{n-1}. \end{align*}$$
$$\begin{align*}&M_{\phi}( A_1,\ldots, A_n)(t_0,t_n) \\&\quad= \int_{X^{\times n-1}} \phi(t_0,\ldots,t_n) A_1(t_0,t_1)A_2(t_1,t_2)\ldots A_n(t_{n-1},t_n) dt_1 \ldots dt_{n-1}. \end{align*}$$
That
![]() $M_{\phi }$
indeed takes values in
$M_{\phi }$
indeed takes values in
![]() $S_2(L_2(X))$
, or rather
$S_2(L_2(X))$
, or rather
![]() $L_2(X \times X)$
, is an easy application of the Cauchy–Schwarz inequality, as we show here in the case of
$L_2(X \times X)$
, is an easy application of the Cauchy–Schwarz inequality, as we show here in the case of
![]() $n=2$
:
$n=2$
:
 $$\begin{align*}\begin{aligned} &\iint_{X^2} \left| \int_X \phi(r,s,t) A(r,s) B(s,t) ds\right|{}^2 drdt \\&\quad\leq \|\phi\|_{\infty}^2 \int_X \int_X \left( \int_X |A(r,s)|^2 ds\right) dr \left( \int_X |B(s,t)|^2 ds\right) dt \\ &\quad= \|\phi\|_{\infty}^2 \|A\|_2^2 \|B\|_2^2. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\iint_{X^2} \left| \int_X \phi(r,s,t) A(r,s) B(s,t) ds\right|{}^2 drdt \\&\quad\leq \|\phi\|_{\infty}^2 \int_X \int_X \left( \int_X |A(r,s)|^2 ds\right) dr \left( \int_X |B(s,t)|^2 ds\right) dt \\ &\quad= \|\phi\|_{\infty}^2 \|A\|_2^2 \|B\|_2^2. \end{aligned} \end{align*}$$
The case of higher-order n is similar to [Reference Potapov, Skripka, Sukochev and TomskovaPSST17, Lemma 2.1].
Let
![]() $1\leq p,p_1,\ldots ,p_n \leq \infty $
, with
$1\leq p,p_1,\ldots ,p_n \leq \infty $
, with
![]() $p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Consider the restriction of
$p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Consider the restriction of
![]() $M_{\phi }$
where its ith input is restricted to
$M_{\phi }$
where its ith input is restricted to
![]() $S_2(L_2(X)) \cap S_{p_i}(L_2(X))$
. If the resulting restriction takes values in
$S_2(L_2(X)) \cap S_{p_i}(L_2(X))$
. If the resulting restriction takes values in
![]() $S_p(L_2(X))$
and has a bounded extension to
$S_p(L_2(X))$
and has a bounded extension to
![]() $S_{p_1}(L_2(X)) \times \cdots \times S_{p_n}(L_2(X))$
, its extension, also denoted by
$S_{p_1}(L_2(X)) \times \cdots \times S_{p_n}(L_2(X))$
, its extension, also denoted by
![]() $M_{\phi }$
, is called the
$M_{\phi }$
, is called the
![]() $(p_1, \dots , p_n)$
-Schur multiplier.
$(p_1, \dots , p_n)$
-Schur multiplier.
2.7 Norms for multilinear maps
If
![]() $E_1,\ldots , E_n, E$
are Banach spaces and
$E_1,\ldots , E_n, E$
are Banach spaces and
![]() $T: E_1 \times \cdots \times E_n \to E$
is a multilinear map, we recall that
$T: E_1 \times \cdots \times E_n \to E$
is a multilinear map, we recall that
![]() $\| T \|$
is the quantity
$\| T \|$
is the quantity
![]() $\sup _{x_i \in E_i, \| x_i \| =1} \| T(x_1,\ldots ,x_n)\|$
.
$\sup _{x_i \in E_i, \| x_i \| =1} \| T(x_1,\ldots ,x_n)\|$
.
If
![]() $E_1, \ldots , E_n, E$
are operator spaces, T is a multilinear map, and
$E_1, \ldots , E_n, E$
are operator spaces, T is a multilinear map, and
![]() $N \in \mathbb {N}_{\geq 1}$
, the multiplicative amplification of T refers to the map
$N \in \mathbb {N}_{\geq 1}$
, the multiplicative amplification of T refers to the map
which sends
![]() $x_i = \alpha _i \otimes v_i$
where
$x_i = \alpha _i \otimes v_i$
where
![]() $\alpha _i \in M_N, v_i \in E_i$
, to
$\alpha _i \in M_N, v_i \in E_i$
, to
![]() $(\alpha _1 \ldots \alpha _n) \otimes T(v_1,\ldots ,v_n)$
.
$(\alpha _1 \ldots \alpha _n) \otimes T(v_1,\ldots ,v_n)$
.
![]() $T^{(N)}$
is viewed as a multilinear map on the space
$T^{(N)}$
is viewed as a multilinear map on the space
![]() $M_N(E_i)$
, which is equipped with the matrix norm from the operator space structure of
$M_N(E_i)$
, which is equipped with the matrix norm from the operator space structure of
![]() $E_i$
. We say T is multiplicatively bounded if
$E_i$
. We say T is multiplicatively bounded if
![]() $\|T\|_{mb}=\sup _N \| T^{(N)}\| < \infty $
.
$\|T\|_{mb}=\sup _N \| T^{(N)}\| < \infty $
.
Let
![]() $1\leq p, p_1, \ldots , p_n \leq \infty $
with
$1\leq p, p_1, \ldots , p_n \leq \infty $
with
![]() $p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Generalizing a definition by [Reference XuXu06], we will say a multilinear map
$p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Generalizing a definition by [Reference XuXu06], we will say a multilinear map
![]() $T: E_1 \times \cdots \times E_n \to E $
is
$T: E_1 \times \cdots \times E_n \to E $
is
![]() $(p_1,\ldots ,p_n)$
-multiplicatively bounded if the multiplicative extensions
$(p_1,\ldots ,p_n)$
-multiplicatively bounded if the multiplicative extensions
have uniformly bounded norms. The
![]() $(p_1,\ldots ,p_n)$
-multiplicatively bounded norm of T is then
$(p_1,\ldots ,p_n)$
-multiplicatively bounded norm of T is then
![]() $\sup _N \Vert T^{(N)} \Vert $
. It is denoted by
$\sup _N \Vert T^{(N)} \Vert $
. It is denoted by
![]() $\|T\|_{(p_1, \dots , p_n)-mb}$
.
$\|T\|_{(p_1, \dots , p_n)-mb}$
.
Remark 2.1 It is unclear if this definition of
![]() $(p_1, \ldots , p_n)$
-multiplicative boundedness corresponds to complete boundedness of some linear map on some appropriate tensor product of the
$(p_1, \ldots , p_n)$
-multiplicative boundedness corresponds to complete boundedness of some linear map on some appropriate tensor product of the
![]() $E_i$
’s. In the special case that the range space is
$E_i$
’s. In the special case that the range space is
![]() ${\operatorname {\mathbb {C}}}$
and
${\operatorname {\mathbb {C}}}$
and
![]() $n=2$
, such a tensor product has been constructed in [Reference XuXu06, Remark 2.7]. However, this tensor norm does not seem to admit a natural operator space structure, nor does it seem to work in the multilinear case.
$n=2$
, such a tensor product has been constructed in [Reference XuXu06, Remark 2.7]. However, this tensor norm does not seem to admit a natural operator space structure, nor does it seem to work in the multilinear case.
The norms of multilinear Schur multipliers are determined by the restriction of the symbol to finite sets. This is the multilinear version of [Reference Lafforgue and de la SalleLaSa11, Theorem 1.19] and [Reference Caspers and de la SalleCaSa15, Theorem 3.1].
Theorem 2.2 Let
![]() $\mu $
be a Radon measure on a locally compact space X, and let
$\mu $
be a Radon measure on a locally compact space X, and let
![]() $\phi : X^{n+1} \to {\operatorname {\mathbb {C}}}$
be a continuous function. Let
$\phi : X^{n+1} \to {\operatorname {\mathbb {C}}}$
be a continuous function. Let
![]() $K>0$
. The following are equivalent for
$K>0$
. The following are equivalent for
![]() $1 \leq p_1, \dots , p_n, p \leq \infty $
:
$1 \leq p_1, \dots , p_n, p \leq \infty $
:
-
(i)
 $\phi $
defines a bounded Schur multiplier
$\phi $
defines a bounded Schur multiplier
 $S_{p_1}(L_2(X)) \times \cdots \times S_{p_n}(L_2(X)) \to S_p(L_2(X))$
with norm less than K.
$S_{p_1}(L_2(X)) \times \cdots \times S_{p_n}(L_2(X)) \to S_p(L_2(X))$
with norm less than K. -
(ii) For every
 $\sigma $
-finite measurable subset
$\sigma $
-finite measurable subset
 $X_0$
in X,
$X_0$
in X,
 $\phi $
restricts to a bounded Schur multiplier
$\phi $
restricts to a bounded Schur multiplier
 $S_{p_1}(L_2(X_0)) \times \cdots \times S_{p_n}(L_2(X_0)) \to S_p(L_2(X_0))$
with norm less than K.
$S_{p_1}(L_2(X_0)) \times \cdots \times S_{p_n}(L_2(X_0)) \to S_p(L_2(X_0))$
with norm less than K. -
(iii) For any finite subset
 $F = \{s_1, \dots , s_N\} \subset X$
belonging to the support of
$F = \{s_1, \dots , s_N\} \subset X$
belonging to the support of
 $\mu $
, the symbol
$\mu $
, the symbol
 $\phi |_{F^{\times (n+1)}}$
defines a bounded Schur multiplier
$\phi |_{F^{\times (n+1)}}$
defines a bounded Schur multiplier
 $S_{p_1}(\ell _2(F)) \times \cdots \times S_{p_2}(\ell _2(F)) \to S_p(\ell _2(F))$
with norm less than K.
$S_{p_1}(\ell _2(F)) \times \cdots \times S_{p_2}(\ell _2(F)) \to S_p(\ell _2(F))$
with norm less than K.
The same equivalence is true for the
![]() $(p_1, \ldots , p_n)-mb$
norms.
$(p_1, \ldots , p_n)-mb$
norms.
Proof
![]() $(i) \Rightarrow (ii)$
is trivial. The implication
$(i) \Rightarrow (ii)$
is trivial. The implication
![]() $(ii) \Rightarrow (i)$
remains exactly the same as in [Reference Caspers and de la SalleCaSa15, Theorem 3.1] except for the fact that we have to take
$(ii) \Rightarrow (i)$
remains exactly the same as in [Reference Caspers and de la SalleCaSa15, Theorem 3.1] except for the fact that we have to take
![]() $x_i \in S_{p_i}(L_2(X))$
and take into account the support projections of
$x_i \in S_{p_i}(L_2(X))$
and take into account the support projections of
![]() $x_1, x_1^*, \ldots , x_n, x_n^*$
when choosing
$x_1, x_1^*, \ldots , x_n, x_n^*$
when choosing
![]() $X_0$
. The equivalence
$X_0$
. The equivalence
![]() $(ii) \Leftrightarrow (iii)$
is mutatis mutandis the same as in [Reference Lafforgue and de la SalleLaSa11, Theorem 1.19]. For the
$(ii) \Leftrightarrow (iii)$
is mutatis mutandis the same as in [Reference Lafforgue and de la SalleLaSa11, Theorem 1.19]. For the
![]() $(p_1, \ldots , p_n)-mb$
norms, we apply the theorem on the space
$(p_1, \ldots , p_n)-mb$
norms, we apply the theorem on the space
![]() ${X_N = X \times \{1, \dots , N\}}$
and function
${X_N = X \times \{1, \dots , N\}}$
and function
![]() $\phi _N((s_0, i_0), \dots , (s_n, i_n)) = \phi (s_0, \dots , s_n)$
and use the isometric identifications
$\phi _N((s_0, i_0), \dots , (s_n, i_n)) = \phi (s_0, \dots , s_n)$
and use the isometric identifications
and the fact that under these identifications, we have
2.8 Transference for
 $p_i = \infty $
$p_i = \infty $
Let G be a locally compact group which in this subsection is not required to be unimodular. The following Proposition 2.3 (based on [Reference Effros and RuanEfRu90, Theorem 4.1]) was proved in [Reference Todorov and TurowskaToTu10, Theorem 5.5]. This is a multilinear version of the Bo
![]() $\dot{\rm z}$
ejko–Fendler result [Reference Bozejko and FendlerBoFe84], and it yields a transference result between Fourier and Schur multipliers for the case
$\dot{\rm z}$
ejko–Fendler result [Reference Bozejko and FendlerBoFe84], and it yields a transference result between Fourier and Schur multipliers for the case
![]() $p_1 = \cdots = p_n = \infty $
. We give a proof of the ‘if’ direction that is slightly different from [Reference Todorov and TurowskaToTu10] by using the transference techniques from Theorem 3.1, which simplify in the current setup.
$p_1 = \cdots = p_n = \infty $
. We give a proof of the ‘if’ direction that is slightly different from [Reference Todorov and TurowskaToTu10] by using the transference techniques from Theorem 3.1, which simplify in the current setup.
Proposition 2.3 For
![]() $\phi \in C_b(G^{\times n})$
, set
$\phi \in C_b(G^{\times n})$
, set
Then
![]() $M_{\widetilde {\phi }}$
is multiplicatively bounded on
$M_{\widetilde {\phi }}$
is multiplicatively bounded on
![]() $S_{\infty }(L_2(G))^{\times n} \to S_{\infty }(L_2(G))$
iff
$S_{\infty }(L_2(G))^{\times n} \to S_{\infty }(L_2(G))$
iff
![]() $T_{\phi }$
defines a multiplicatively bounded multilinear map on
$T_{\phi }$
defines a multiplicatively bounded multilinear map on
![]() $\mathcal {L} G^{\times n} \to \mathcal {L} G$
. In this case, we have
$\mathcal {L} G^{\times n} \to \mathcal {L} G$
. In this case, we have
Proof of the “if” direction
Assume that
![]() $T_{\phi }$
is multiplicatively bounded. Let
$T_{\phi }$
is multiplicatively bounded. Let
![]() $F \subseteq G$
be finite with
$F \subseteq G$
be finite with
![]() $|F| = N$
. Let
$|F| = N$
. Let
![]() $p_s \in B(\ell _2(F))$
be the projection on the one-dimensional space spanned by the delta function
$p_s \in B(\ell _2(F))$
be the projection on the one-dimensional space spanned by the delta function
![]() $\delta _s$
. Let
$\delta _s$
. Let
![]() $\widetilde {\phi }_F := \widetilde {\phi }|_{F^{\times n+1}}$
. By Theorem 2.2 (using that
$\widetilde {\phi }_F := \widetilde {\phi }|_{F^{\times n+1}}$
. By Theorem 2.2 (using that
![]() $\phi $
is continuous), it suffices to prove that
$\phi $
is continuous), it suffices to prove that
and its matrix amplifications are bounded by
![]() $\|T_{\phi }\|_{mb}$
. Define the unitary
$\|T_{\phi }\|_{mb}$
. Define the unitary
![]() $U = \sum _{s \in F} p_s \otimes \lambda _s \in B(\ell _2(F)) \otimes \mathcal {L} G$
and the isometry
$U = \sum _{s \in F} p_s \otimes \lambda _s \in B(\ell _2(F)) \otimes \mathcal {L} G$
and the isometry
Note that
![]() $\pi $
satisfies
$\pi $
satisfies
![]() $\pi (E_{st}) = E_{st} \otimes \lambda _{st^{-1}}$
. For
$\pi (E_{st}) = E_{st} \otimes \lambda _{st^{-1}}$
. For
![]() $s_0, \dots , s_n \in F$
,
$s_0, \dots , s_n \in F$
,
 $$\begin{align*}\begin{aligned} \pi(M_{\widetilde{\phi}_F}(E_{s_0 s_1}, E_{s_1 s_2}, \ldots, E_{s_{n-1} s_n})) &= \pi( \widetilde{\phi}(s_0, \ldots, s_n)E_{s_0 s_n}) \\ &= \phi(s_0 s_1^{-1}, \ldots, s_{n-1} s_n^{-1}) E_{s_0 s_n} \otimes \lambda_{s_0 s_n^{-1}}, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \pi(M_{\widetilde{\phi}_F}(E_{s_0 s_1}, E_{s_1 s_2}, \ldots, E_{s_{n-1} s_n})) &= \pi( \widetilde{\phi}(s_0, \ldots, s_n)E_{s_0 s_n}) \\ &= \phi(s_0 s_1^{-1}, \ldots, s_{n-1} s_n^{-1}) E_{s_0 s_n} \otimes \lambda_{s_0 s_n^{-1}}, \end{aligned} \end{align*}$$
whereas
 $$\begin{align*}\begin{aligned} T_{\phi}^{(N)}(\pi(E_{s_0 s_1}), \ldots, \pi(E_{s_{n-1} s_n})) &= T_{\phi}^{(N)}(E_{s_0s_1} \otimes \lambda_{s_0 s_1}^{-1}, \ldots, E_{s_{n-1} s_n} \otimes \lambda_{s_{n-1} s_n^{-1}})\\ &= E_{s_0 s_n} \otimes T_{\phi}(\lambda_{s_0 s_1^{-1}}, \ldots, \lambda_{s_{n-1} s_n^{-1}}) \\ &= \phi(s_0 s_1^{-1}, \ldots, s_{n-1} s_n^{-1}) E_{s_0 s_n} \otimes \lambda_{s_0 s_n^{-1}}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} T_{\phi}^{(N)}(\pi(E_{s_0 s_1}), \ldots, \pi(E_{s_{n-1} s_n})) &= T_{\phi}^{(N)}(E_{s_0s_1} \otimes \lambda_{s_0 s_1}^{-1}, \ldots, E_{s_{n-1} s_n} \otimes \lambda_{s_{n-1} s_n^{-1}})\\ &= E_{s_0 s_n} \otimes T_{\phi}(\lambda_{s_0 s_1^{-1}}, \ldots, \lambda_{s_{n-1} s_n^{-1}}) \\ &= \phi(s_0 s_1^{-1}, \ldots, s_{n-1} s_n^{-1}) E_{s_0 s_n} \otimes \lambda_{s_0 s_n^{-1}}. \end{aligned} \end{align*}$$
It follows that
![]() $T_{\phi }^{(N)} \circ \pi ^{\times n} = \pi \circ M_{\widetilde {\phi }_F}$
. This implies that
$T_{\phi }^{(N)} \circ \pi ^{\times n} = \pi \circ M_{\widetilde {\phi }_F}$
. This implies that
By taking matrix amplifications, we prove similarly that
![]() $\| M_{\widetilde {\phi }_F}\|_{mb} \leq \|T_{\phi }\|_{mb}$
.
$\| M_{\widetilde {\phi }_F}\|_{mb} \leq \|T_{\phi }\|_{mb}$
.
Remark 2.4 A multilinear map on the product of some operator spaces is multiplicatively bounded iff its linearization is completely bounded as a map on the corresponding Haagerup tensor product. However, as [Reference Juschenko, Todorov and TurowskaJTT09, Lemma 3.3] shows, for Schur multipliers
![]() $M_{\widetilde {\phi }}$
on
$M_{\widetilde {\phi }}$
on
![]() $S_{\infty }(L_2(G))^{\times n}$
, just boundedness on the Haagerup tensor product is sufficient to guarantee that
$S_{\infty }(L_2(G))^{\times n}$
, just boundedness on the Haagerup tensor product is sufficient to guarantee that
![]() $M_{\widetilde {\phi }}$
is multiplicatively bounded. Note that even in the linear case, when
$M_{\widetilde {\phi }}$
is multiplicatively bounded. Note that even in the linear case, when
![]() $p<\infty $
, it is unknown whether a bounded Schur multiplier on
$p<\infty $
, it is unknown whether a bounded Schur multiplier on
![]() $S_p(L_2({\operatorname {\mathbb {R}}}))$
is necessarily completely bounded unless
$S_p(L_2({\operatorname {\mathbb {R}}}))$
is necessarily completely bounded unless
![]() $\phi $
has continuous symbol (we refer to [Reference PisierPi98, Conjecture 8.1.12], [Reference Lafforgue and de la SalleLaSa11, Theorem 1.19], and [Reference Caspers and WildschutCaWi19]).
$\phi $
has continuous symbol (we refer to [Reference PisierPi98, Conjecture 8.1.12], [Reference Lafforgue and de la SalleLaSa11, Theorem 1.19], and [Reference Caspers and WildschutCaWi19]).
3 Transference from Fourier to Schur multipliers
Let G be a locally compact group, which is again assumed to be unimodular. We will prove that symbols of
![]() $(p_1, \dots , p_n)$
-Fourier multipliers are also symbols of
$(p_1, \dots , p_n)$
-Fourier multipliers are also symbols of
![]() $(p_1, \dots , p_n)$
-Schur multipliers using a multilinear transference method. This yields a multilinear version of [Reference Caspers and de la SalleCaSa15, Theorem 4.2]. We stipulate that in the proofs of [Reference Caspers and de la SalleCaSa15, Section 4], the transference is carried out for rational exponents p. In order to treat the general multilinear case, we present an alternative proof that transfers multipliers directly for every real exponent
$(p_1, \dots , p_n)$
-Schur multipliers using a multilinear transference method. This yields a multilinear version of [Reference Caspers and de la SalleCaSa15, Theorem 4.2]. We stipulate that in the proofs of [Reference Caspers and de la SalleCaSa15, Section 4], the transference is carried out for rational exponents p. In order to treat the general multilinear case, we present an alternative proof that transfers multipliers directly for every real exponent
![]() $p \in [1, \infty )$
. In fact, this gives an improvement of [Reference Caspers and de la SalleCaSa15, Theorem 4.2], which is stated under the stronger assumption that the multiplier acts boundedly on the Fourier algebra (equivalently is a p-multiplier at
$p \in [1, \infty )$
. In fact, this gives an improvement of [Reference Caspers and de la SalleCaSa15, Theorem 4.2], which is stated under the stronger assumption that the multiplier acts boundedly on the Fourier algebra (equivalently is a p-multiplier at
![]() $p=1$
). The fundamental difference in the proof is that we base ourselves on the methods from [Reference Caspers, Parcet, Perrin and RicardCPPR15, Claim B, p. 24] and [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6].
$p=1$
). The fundamental difference in the proof is that we base ourselves on the methods from [Reference Caspers, Parcet, Perrin and RicardCPPR15, Claim B, p. 24] and [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6].
As before, for
![]() $\phi \in C_b(G^{\times n})$
, we set
$\phi \in C_b(G^{\times n})$
, we set
![]() $\widetilde {\phi } \in C_b(G^{\times n+1})$
by
$\widetilde {\phi } \in C_b(G^{\times n+1})$
by
Theorem 3.1 Let G be a locally compact, second-countable, unimodular group, and let
![]() $1 \leq p \leq \infty , 1 < p_1, \ldots , p_n \leq \infty $
be such that
$1 \leq p \leq \infty , 1 < p_1, \ldots , p_n \leq \infty $
be such that
![]() $p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
$p^{-1} = \sum _{i=1}^n p_i^{-1}$
. Let
![]() $\phi \in C_b(G^{\times n})$
be the symbol of a
$\phi \in C_b(G^{\times n})$
be the symbol of a
![]() $(p_1, \ldots , p_n)$
-multiplicatively bounded Fourier multiplier of G. Then
$(p_1, \ldots , p_n)$
-multiplicatively bounded Fourier multiplier of G. Then
![]() $\widetilde {\phi }$
is the symbol of a
$\widetilde {\phi }$
is the symbol of a
![]() $(p_1, \ldots , p_n)$
-multiplicatively bounded Schur multiplier of G. Moreover,
$(p_1, \ldots , p_n)$
-multiplicatively bounded Schur multiplier of G. Moreover,
 $$\begin{align*}\begin{aligned} & \Vert M_{\widetilde{\phi}}: S_{p_1}(L_2(G)) \times \cdots \times S_{p_n}(L_2(G)) \rightarrow S_{p}(L_2(G)) \Vert_{(p_1,\ldots,p_n)-mb}\\ & \qquad \leq \Vert T_{\phi}: L_{p_1}(\mathcal{L}G ) \times \cdots \times L_{p_n}(\mathcal{L}G ) \rightarrow L_{p}(\mathcal{L}G ) \Vert_{(p_1,\ldots,p_n)-mb}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} & \Vert M_{\widetilde{\phi}}: S_{p_1}(L_2(G)) \times \cdots \times S_{p_n}(L_2(G)) \rightarrow S_{p}(L_2(G)) \Vert_{(p_1,\ldots,p_n)-mb}\\ & \qquad \leq \Vert T_{\phi}: L_{p_1}(\mathcal{L}G ) \times \cdots \times L_{p_n}(\mathcal{L}G ) \rightarrow L_{p}(\mathcal{L}G ) \Vert_{(p_1,\ldots,p_n)-mb}. \end{aligned} \end{align*}$$
Proof Let
![]() $F \subseteq G$
be finite. Consider the Hilbert space
$F \subseteq G$
be finite. Consider the Hilbert space
![]() $\ell _2(F)$
, and for
$\ell _2(F)$
, and for
![]() $s \in F$
, let
$s \in F$
, let
![]() $p_s$
be the orthogonal projection onto the one-dimensional space spanned by the delta function
$p_s$
be the orthogonal projection onto the one-dimensional space spanned by the delta function
![]() $\delta _s$
. By Theorem 2.2, it suffices to show that the norm of
$\delta _s$
. By Theorem 2.2, it suffices to show that the norm of
and its matrix amplifications are bounded by
![]() $\Vert T_{\phi } \Vert _{(p_1,\ldots ,p_n)-mb}$
.
$\Vert T_{\phi } \Vert _{(p_1,\ldots ,p_n)-mb}$
.
The proof requires the introduction of coordinatewise convolutions as follows. Fix functions
![]() $\varphi _k \in A(G)$
such that
$\varphi _k \in A(G)$
such that
![]() $\varphi _k \geq 0$
,
$\varphi _k \geq 0$
,
![]() $\Vert \varphi _k \Vert _{L_1(G)} = 1$
and such that the support of
$\Vert \varphi _k \Vert _{L_1(G)} = 1$
and such that the support of
![]() $\varphi _k$
shrinks to the identity of G; from (2.1), it is clear that such functions exist. Then, for any function
$\varphi _k$
shrinks to the identity of G; from (2.1), it is clear that such functions exist. Then, for any function
![]() $\phi \in C_b( G^{\times n} )$
, we set
$\phi \in C_b( G^{\times n} )$
, we set
 $$ \begin{align} \begin{aligned} & \phi_k(s_1, \ldots, s_n) \\ := & \int_{G^{\times n}} \phi(t_1^{-1} s_1 t_2, t_2^{-1} s_2 t_3, \ldots , t_{n-2}^{-1} s_{n-2} t_{n-1} , t_{n-1}^{-1} s_{n-1}, s_n t_{n}^{-1} ) \left( \prod_{j=1}^{n} \varphi_k(t_j) \right) dt_1 \ldots dt_n. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \phi_k(s_1, \ldots, s_n) \\ := & \int_{G^{\times n}} \phi(t_1^{-1} s_1 t_2, t_2^{-1} s_2 t_3, \ldots , t_{n-2}^{-1} s_{n-2} t_{n-1} , t_{n-1}^{-1} s_{n-1}, s_n t_{n}^{-1} ) \left( \prod_{j=1}^{n} \varphi_k(t_j) \right) dt_1 \ldots dt_n. \end{aligned} \end{align} $$
For the particular case
![]() $n = 1$
, this expression becomes by definition
$n = 1$
, this expression becomes by definition
Let
![]() $(U_{\alpha })_{\alpha }$
be a symmetric neighborhood basis of the identity of G consisting of relatively compact sets. Set
$(U_{\alpha })_{\alpha }$
be a symmetric neighborhood basis of the identity of G consisting of relatively compact sets. Set
with polar decomposition
![]() $k_{\alpha } = u_{\alpha } h_{\alpha }$
. Then
$k_{\alpha } = u_{\alpha } h_{\alpha }$
. Then
![]() $k_{\alpha }$
is an element in
$k_{\alpha }$
is an element in
![]() $L_2(\mathcal {L} G)$
with
$L_2(\mathcal {L} G)$
with
![]() $\Vert k_{\alpha } \Vert _2 = 1$
. Consequently,
$\Vert k_{\alpha } \Vert _2 = 1$
. Consequently,
![]() $h_{\alpha }^{2/q}$
is in
$h_{\alpha }^{2/q}$
is in
![]() $L_q(\mathcal {L} G)$
for
$L_q(\mathcal {L} G)$
for
![]() $1 \leq q < \infty $
with
$1 \leq q < \infty $
with
![]() $\Vert h_{\alpha }^{2/q} \Vert = 1$
. In case
$\Vert h_{\alpha }^{2/q} \Vert = 1$
. In case
![]() $q = \infty $
by mild abuse of notation, we set
$q = \infty $
by mild abuse of notation, we set
![]() $h_{\alpha }^{2/q} =1$
. Set the unitary
$h_{\alpha }^{2/q} =1$
. Set the unitary
Now, let
![]() $a_i \in S_{p_i}(\ell _2(F))$
. Since
$a_i \in S_{p_i}(\ell _2(F))$
. Since
![]() $\phi _k$
converges to
$\phi _k$
converges to
![]() $\phi $
pointwise, we have
$\phi $
pointwise, we have
So, with
![]() $N = \vert F \vert $
,
$N = \vert F \vert $
,
 $$ \begin{align} \begin{aligned} \Vert M_{\widetilde{\phi}}(a_1, \ldots, a_n ) \Vert_{S_p^N} = & \lim_k \limsup_{\alpha} \Vert M_{\widetilde{\phi_k}}(a_1, \ldots, a_n ) { \otimes h_{\alpha}^{\frac2p}} \Vert_{S_p^N{ \otimes L_p(\mathcal{L} G)}} \\ = & \lim_k \limsup_{\alpha} \Vert U ( M_{\widetilde{\phi_k}}(a_1, \ldots, a_n ) \otimes h_{\alpha}^{\frac{2}{p}} ) U^{\ast} \Vert_{S_p^N \otimes L_p(\mathcal{L} G)} \\ \leq & \; A+ B, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \Vert M_{\widetilde{\phi}}(a_1, \ldots, a_n ) \Vert_{S_p^N} = & \lim_k \limsup_{\alpha} \Vert M_{\widetilde{\phi_k}}(a_1, \ldots, a_n ) { \otimes h_{\alpha}^{\frac2p}} \Vert_{S_p^N{ \otimes L_p(\mathcal{L} G)}} \\ = & \lim_k \limsup_{\alpha} \Vert U ( M_{\widetilde{\phi_k}}(a_1, \ldots, a_n ) \otimes h_{\alpha}^{\frac{2}{p}} ) U^{\ast} \Vert_{S_p^N \otimes L_p(\mathcal{L} G)} \\ \leq & \; A+ B, \end{aligned} \end{align} $$
where
 $$ \begin{align} \begin{aligned} &A = \limsup_k \limsup_{\alpha} \Vert T_{\phi_k}^{ (N) }( U ( a_1 \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast}, \ldots, U ( a_n \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} ) \Vert_{S_p^N \otimes L_p(\mathcal{L} G)}, \\ &B =\limsup_k \limsup_{\alpha} \Vert T_{\phi_k}^{ (N) }( U ( a_1 \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast}, \ldots, U ( a_n \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} ) - \\ & \hspace{5cm} U ( M_{\widetilde{\phi_k}}(a_1, \ldots, a_n) \otimes h_{\alpha}^{\frac{2}{p}} ) U^{\ast} \Vert_{S_p^N \otimes L_p(\mathcal{L} G)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &A = \limsup_k \limsup_{\alpha} \Vert T_{\phi_k}^{ (N) }( U ( a_1 \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast}, \ldots, U ( a_n \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} ) \Vert_{S_p^N \otimes L_p(\mathcal{L} G)}, \\ &B =\limsup_k \limsup_{\alpha} \Vert T_{\phi_k}^{ (N) }( U ( a_1 \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast}, \ldots, U ( a_n \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} ) - \\ & \hspace{5cm} U ( M_{\widetilde{\phi_k}}(a_1, \ldots, a_n) \otimes h_{\alpha}^{\frac{2}{p}} ) U^{\ast} \Vert_{S_p^N \otimes L_p(\mathcal{L} G)}. \end{aligned} \end{align} $$
Below, we prove that
![]() $B=0$
. Therefore,
$B=0$
. Therefore,
 $$ \begin{align} \begin{aligned} &\Vert M_{\widetilde{\phi}} (a_1, \ldots, a_n ) \Vert_{S_p^N} \\&\quad\leq \limsup_k \limsup_{\alpha} \Vert T_{\phi_k}^{(N)}( U ( a_1 \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast}, \ldots, U ( a_n \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} ) \Vert_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &\quad\leq \limsup_k \limsup_{\alpha} \Vert T_{\phi_k}^{(N)} \Vert \Vert U ( a_1 \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast} \Vert_{S_{p_1}^N \otimes L_{p_1}(\mathcal{L} G)} \ldots \Vert U ( a_n \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} \Vert_{S_{p_n}^N \otimes L_{p_n}(\mathcal{L} G)}\\ &\quad= \limsup_k \Vert T_{\phi_k}^{(N)} \Vert \Vert a_1 \Vert_{S_{p_1}^N} \ldots \Vert a_n \Vert_{S_{p_n}^N}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\Vert M_{\widetilde{\phi}} (a_1, \ldots, a_n ) \Vert_{S_p^N} \\&\quad\leq \limsup_k \limsup_{\alpha} \Vert T_{\phi_k}^{(N)}( U ( a_1 \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast}, \ldots, U ( a_n \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} ) \Vert_{S_p^N \otimes L_p(\mathcal{L} G)} \\ &\quad\leq \limsup_k \limsup_{\alpha} \Vert T_{\phi_k}^{(N)} \Vert \Vert U ( a_1 \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast} \Vert_{S_{p_1}^N \otimes L_{p_1}(\mathcal{L} G)} \ldots \Vert U ( a_n \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} \Vert_{S_{p_n}^N \otimes L_{p_n}(\mathcal{L} G)}\\ &\quad= \limsup_k \Vert T_{\phi_k}^{(N)} \Vert \Vert a_1 \Vert_{S_{p_1}^N} \ldots \Vert a_n \Vert_{S_{p_n}^N}, \end{aligned} \end{align} $$
where the norm of
![]() $T_{\phi _k}^{(N)}$
is understood as in (2.2) for the map
$T_{\phi _k}^{(N)}$
is understood as in (2.2) for the map
![]() $T_{\phi _k}: L_{p_1}(\mathcal {L} G) \times \cdots \times L_{p_n}(\mathcal {L} G) \rightarrow L_{p}(\mathcal {L} G)$
. By [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.3] and the fact that
$T_{\phi _k}: L_{p_1}(\mathcal {L} G) \times \cdots \times L_{p_n}(\mathcal {L} G) \rightarrow L_{p}(\mathcal {L} G)$
. By [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.3] and the fact that
![]() $\Vert \varphi _k \Vert _{L_1(G)} = 1$
, it follows then that
$\Vert \varphi _k \Vert _{L_1(G)} = 1$
, it follows then that
![]() $\Vert T_{\phi _k}^{(N)} \Vert \leq \Vert T_{\phi }^{(N)}\Vert $
. Hence,
$\Vert T_{\phi _k}^{(N)} \Vert \leq \Vert T_{\phi }^{(N)}\Vert $
. Hence,
This finishes the proof. The multiplicatively bounded case follows by taking matrix amplifications.
Now, let us prove that the last term in (3.2) goes to 0. By the triangle inequality, it suffices to prove that the limits of the following terms are 0. For
![]() $r_0, \ldots , r_n \in F$
with matrix units
$r_0, \ldots , r_n \in F$
with matrix units
![]() $E_{r_i, r_{i+1}}$
,
$E_{r_i, r_{i+1}}$
,
 $$ \begin{align} \begin{aligned} & T_{\phi_k}^{ (N) }( U ( E_{r_0,r_1} \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast}, \ldots, U ( E_{r_{n-1},r_n} \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} ) \kern1.5pt{-}\kern1.5pt U ( M_{\widetilde{\phi_k}}(E_{r_0,r_1}, \ldots, E_{r_{n-1}, r_{n}}) \otimes h_{\alpha}^{\frac{2}{p}} ) U^{\ast} \\ & \quad = E_{r_0, r_n} \otimes \left( T_{\phi_k}( \lambda_{r_0} h_{\alpha}^{\frac{2}{p_1}} \lambda_{r_1}^{\ast}, \ldots, \lambda_{r_{n-1}} h_{\alpha}^{\frac{2}{p_n}} \lambda_{r_n}^{\ast} ) - \phi_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) \lambda_{r_0} h_{\alpha}^{\frac{2}{p}} \lambda_{r_n}^{\ast}\right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & T_{\phi_k}^{ (N) }( U ( E_{r_0,r_1} \otimes h_{\alpha}^{\frac{2}{p_1}} ) U^{\ast}, \ldots, U ( E_{r_{n-1},r_n} \otimes h_{\alpha}^{\frac{2}{p_n}} ) U^{\ast} ) \kern1.5pt{-}\kern1.5pt U ( M_{\widetilde{\phi_k}}(E_{r_0,r_1}, \ldots, E_{r_{n-1}, r_{n}}) \otimes h_{\alpha}^{\frac{2}{p}} ) U^{\ast} \\ & \quad = E_{r_0, r_n} \otimes \left( T_{\phi_k}( \lambda_{r_0} h_{\alpha}^{\frac{2}{p_1}} \lambda_{r_1}^{\ast}, \ldots, \lambda_{r_{n-1}} h_{\alpha}^{\frac{2}{p_n}} \lambda_{r_n}^{\ast} ) - \phi_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) \lambda_{r_0} h_{\alpha}^{\frac{2}{p}} \lambda_{r_n}^{\ast}\right). \end{aligned} \end{align} $$
Applying the transformation formula [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.3] to the
![]() $T_{\phi _k}$
term,
$T_{\phi _k}$
term,
Taking the norm of the expression in equation (3.6),
 $$ \begin{align} &\Vert (3.6) \Vert_{S_p^N \otimes L_p(\mathcal{L} G)}\\& \quad= \Vert T_{\phi_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) - \phi_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) h_{\alpha}^{\frac{2}{p}} \Vert_{L_p(\mathcal{L} G)}. \nonumber\end{align} $$
$$ \begin{align} &\Vert (3.6) \Vert_{S_p^N \otimes L_p(\mathcal{L} G)}\\& \quad= \Vert T_{\phi_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) - \phi_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) h_{\alpha}^{\frac{2}{p}} \Vert_{L_p(\mathcal{L} G)}. \nonumber\end{align} $$
We now claim that
![]() $\lim _k \limsup _{\alpha }$
of this expression yields 0, by almost identical arguments as those used in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6]. Since we have a couple of differences, namely that we have a translated function
$\lim _k \limsup _{\alpha }$
of this expression yields 0, by almost identical arguments as those used in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6]. Since we have a couple of differences, namely that we have a translated function
![]() $\phi _k(r_0 \: \cdot \: r_1^{-1}, \ldots , r_{n-1} \: \cdot \: r_{n}^{-1} )$
and we do not use the small almost invariant neighborhoods (SAIN) condition (see [Reference Caspers, Parcet, Perrin and RicardCPPR15, Definition 3.1]), we spell out some of the details here.
$\phi _k(r_0 \: \cdot \: r_1^{-1}, \ldots , r_{n-1} \: \cdot \: r_{n}^{-1} )$
and we do not use the small almost invariant neighborhoods (SAIN) condition (see [Reference Caspers, Parcet, Perrin and RicardCPPR15, Definition 3.1]), we spell out some of the details here.
Let
![]() $\zeta :G \to {\operatorname {\mathbb {R}}}_{\geq 0}$
be a continuous compactly supported positive definite function in
$\zeta :G \to {\operatorname {\mathbb {R}}}_{\geq 0}$
be a continuous compactly supported positive definite function in
![]() $A(G)$
with
$A(G)$
with
![]() $\zeta (e)=1$
, so that
$\zeta (e)=1$
, so that
![]() $T_{\zeta }$
is contractive. For
$T_{\zeta }$
is contractive. For
![]() $1\leq j\leq n$
, let
$1\leq j\leq n$
, let
![]() $\zeta _j(s)=\zeta (r_{j-1}^{-1} s r_j)$
and let
$\zeta _j(s)=\zeta (r_{j-1}^{-1} s r_j)$
and let
![]() $\phi (\zeta _1,\ldots ,\zeta _n)(s_1,\ldots ,s_n)= \phi (s_1,\ldots ,s_n)\zeta _1(s_1)\ldots \zeta _n(s_n)$
. Then
$\phi (\zeta _1,\ldots ,\zeta _n)(s_1,\ldots ,s_n)= \phi (s_1,\ldots ,s_n)\zeta _1(s_1)\ldots \zeta _n(s_n)$
. Then
 $$\begin{align*}\begin{aligned} &\Vert T_{\phi_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) - \phi_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) h_{\alpha}^{\frac{2}{p}} \Vert_{L_p(\mathcal{L} G)} \\ & \leq \Vert \left( (\phi(\zeta_1,\ldots,\zeta_n))_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_{n}^{-1}) - \phi_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) \right) h_{\alpha}^{\frac{2}{p}} \Vert_{L_p(\mathcal{L} G)} \\ &\quad{+}\kern1.5pt \Vert T_{(\phi(\zeta_1,\ldots,\zeta_n))_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) \kern1.5pt{-}\kern1.5pt (\phi(\zeta_1,\ldots,\zeta_n))_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) h_{\alpha}^{\frac{2}{p}} \Vert_{L_p(\kern-0.2pt\mathcal{L} G)} \\ &\quad{+}\kern1.5pt \Vert T_{(\phi(\zeta_1,\ldots,\zeta_n))_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) \kern1.5pt{-}\kern1.5pt T_{\phi_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) \Vert_{L_p(\mathcal{L} G)} \\ &= A_{k,\alpha} + B_{k,\alpha} + C_{k,\alpha}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} &\Vert T_{\phi_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) - \phi_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) h_{\alpha}^{\frac{2}{p}} \Vert_{L_p(\mathcal{L} G)} \\ & \leq \Vert \left( (\phi(\zeta_1,\ldots,\zeta_n))_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_{n}^{-1}) - \phi_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) \right) h_{\alpha}^{\frac{2}{p}} \Vert_{L_p(\mathcal{L} G)} \\ &\quad{+}\kern1.5pt \Vert T_{(\phi(\zeta_1,\ldots,\zeta_n))_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) \kern1.5pt{-}\kern1.5pt (\phi(\zeta_1,\ldots,\zeta_n))_k(r_0 r_1^{-1}, \ldots, r_{n-1} r_n^{-1}) h_{\alpha}^{\frac{2}{p}} \Vert_{L_p(\kern-0.2pt\mathcal{L} G)} \\ &\quad{+}\kern1.5pt \Vert T_{(\phi(\zeta_1,\ldots,\zeta_n))_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) \kern1.5pt{-}\kern1.5pt T_{\phi_k(r_0 \: \cdot \: r_1^{-1}, \ldots, r_{n-1} \: \cdot \: r_{n}^{-1} ) }( h_{\alpha}^{\frac{2}{p_1}}, \ldots, h_{\alpha}^{\frac{2}{p_n}} ) \Vert_{L_p(\mathcal{L} G)} \\ &= A_{k,\alpha} + B_{k,\alpha} + C_{k,\alpha}. \end{aligned} \end{align*}$$
The terms
![]() $A_{k,\alpha }$
,
$A_{k,\alpha }$
,
![]() $B_{k,\alpha }$
, and
$B_{k,\alpha }$
, and
![]() $C_{k,\alpha }$
should be compared to the terms occurring in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, equation (4.7)]. Since
$C_{k,\alpha }$
should be compared to the terms occurring in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, equation (4.7)]. Since
![]() $\varphi _k$
have support shrinking to e, and
$\varphi _k$
have support shrinking to e, and
![]() $\zeta _j(r_{j-1}r_j^{-1})=1$
, it follows that
$\zeta _j(r_{j-1}r_j^{-1})=1$
, it follows that
![]() $\lim _k A_{k,\alpha } = 0$
.
$\lim _k A_{k,\alpha } = 0$
.
For fixed
![]() $t_1,\ldots , t_n \in G$
, define
$t_1,\ldots , t_n \in G$
, define
and for
![]() $1\leq j \leq n-2$
,
$1\leq j \leq n-2$
,
 $$\begin{align*}\begin{aligned} y_{j, \alpha} &= \lambda_{t_j^{-1} r_{j-1}} h_{\alpha}^{\frac{2}{p_j}} \lambda_{r_j^{-1}t_{j+1}}, \\ y_{n-1, \alpha} &= \lambda_{t_{n-1}^{-1} r_{n-2}} h_{\alpha}^{\frac{2}{p_{n-1}}} \lambda_{r_{n-1}^{-1}}, \\ y_{n, \alpha} &= \lambda_{r_{n-1}} h_{\alpha}^{\frac{2}{p_n}} \lambda_{r_n^{-1} t_n^{-1}}. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} y_{j, \alpha} &= \lambda_{t_j^{-1} r_{j-1}} h_{\alpha}^{\frac{2}{p_j}} \lambda_{r_j^{-1}t_{j+1}}, \\ y_{n-1, \alpha} &= \lambda_{t_{n-1}^{-1} r_{n-2}} h_{\alpha}^{\frac{2}{p_{n-1}}} \lambda_{r_{n-1}^{-1}}, \\ y_{n, \alpha} &= \lambda_{r_{n-1}} h_{\alpha}^{\frac{2}{p_n}} \lambda_{r_n^{-1} t_n^{-1}}. \end{aligned} \end{align*}$$
By the same arguments as in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6, after equation (4.8)], we get, for
![]() $1 \leq j \leq n-2$
,
$1 \leq j \leq n-2$
,
 $$ \begin{align} \begin{aligned} \lim_{\alpha } \Vert (T_{\zeta_j }- \operatorname{\mathrm{id}})( y_{j, \alpha} ) \Vert_{L_{p_j}(\mathcal{L}G )} = & \vert \zeta( r_{j-1}^{-1} t_j^{-1} r_{j-1} r_j^{-1} t_{j+1} t_j ) - 1 \vert, \\ \lim_{\alpha } \Vert (T_{\zeta_{n-1} }- \operatorname{\mathrm{id}})( y_{n-1, \alpha} ) \Vert_{L_{p_{n-1}}(\mathcal{L}G )} = & \vert \zeta( r_{n-2}^{-1} t_{n-1}^{-1} r_{n-2} ) - 1 \vert, \\ \lim_{\alpha } \Vert (T_{\zeta_n }- \operatorname{\mathrm{id}})( y_{n, \alpha} ) \Vert_{L_{p_n}(\mathcal{L}G )} = & \vert \zeta( r_n^{-1} t_{n}^{-1} r_n ) - 1 \vert. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \lim_{\alpha } \Vert (T_{\zeta_j }- \operatorname{\mathrm{id}})( y_{j, \alpha} ) \Vert_{L_{p_j}(\mathcal{L}G )} = & \vert \zeta( r_{j-1}^{-1} t_j^{-1} r_{j-1} r_j^{-1} t_{j+1} t_j ) - 1 \vert, \\ \lim_{\alpha } \Vert (T_{\zeta_{n-1} }- \operatorname{\mathrm{id}})( y_{n-1, \alpha} ) \Vert_{L_{p_{n-1}}(\mathcal{L}G )} = & \vert \zeta( r_{n-2}^{-1} t_{n-1}^{-1} r_{n-2} ) - 1 \vert, \\ \lim_{\alpha } \Vert (T_{\zeta_n }- \operatorname{\mathrm{id}})( y_{n, \alpha} ) \Vert_{L_{p_n}(\mathcal{L}G )} = & \vert \zeta( r_n^{-1} t_{n}^{-1} r_n ) - 1 \vert. \end{aligned} \end{align} $$
Crucially, here we require this argument from [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6, after equation (4.8)] only for
![]() $x_j=1$
. Hence, we do not require the use of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 3.15], which uses the SAIN condition. Furthermore, note that in this case, the above equalities are trivially true when
$x_j=1$
. Hence, we do not require the use of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 3.15], which uses the SAIN condition. Furthermore, note that in this case, the above equalities are trivially true when
![]() $p_j=\infty $
(as
$p_j=\infty $
(as
![]() $h_{\alpha }^{2/p_j} = 1$
in that case), so we do not require the use of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Proposition 3.9], which holds only for
$h_{\alpha }^{2/p_j} = 1$
in that case), so we do not require the use of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Proposition 3.9], which holds only for
![]() $1<p_j<\infty $
. Integrating
$1<p_j<\infty $
. Integrating
![]() $C_{\alpha }(t_1,\ldots ,t_n)$
against
$C_{\alpha }(t_1,\ldots ,t_n)$
against
![]() $\prod _{j=1}^n \varphi _k (t_j)$
, we can show that
$\prod _{j=1}^n \varphi _k (t_j)$
, we can show that
![]() $\lim _k \limsup _{\alpha } C_{k,\alpha } = 0$
, just as in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6].
$\lim _k \limsup _{\alpha } C_{k,\alpha } = 0$
, just as in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6].
To show that
![]() $\lim _k \lim _{\alpha } B_{k,\alpha }=0$
, we only note the modifications from [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6]. As before,
$\lim _k \lim _{\alpha } B_{k,\alpha }=0$
, we only note the modifications from [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6]. As before,
![]() $x_j=1$
in the proof of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6]. The operators
$x_j=1$
in the proof of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6]. The operators
![]() $T_j$
appearing in that proof are to be replaced with
$T_j$
appearing in that proof are to be replaced with
![]() $T_{\varphi _k (r_{j-1} \: \cdot \: r_{j}^{-1} t_j)}$
for
$T_{\varphi _k (r_{j-1} \: \cdot \: r_{j}^{-1} t_j)}$
for
![]() $1\leq j \leq n-1$
and
$1\leq j \leq n-1$
and
![]() $T_{n}$
is
$T_{n}$
is
![]() $T_{\varphi _k(t_n r_{n-1} \: \cdot \: r_n^{-1})}$
. Since all
$T_{\varphi _k(t_n r_{n-1} \: \cdot \: r_n^{-1})}$
. Since all
![]() $x_j$
are
$x_j$
are
![]() $1$
, the term
$1$
, the term
![]() $S_{j+1}(x_{j+1} S_{j+2}(x_{j+2} \ldots S_{n-1}(x_{n-1}) \ldots ))$
in the definition of
$S_{j+1}(x_{j+1} S_{j+2}(x_{j+2} \ldots S_{n-1}(x_{n-1}) \ldots ))$
in the definition of
![]() $R_{j,V}$
that appears in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6] is now just the scalar
$R_{j,V}$
that appears in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.6] is now just the scalar
 $$\begin{align*}\prod_{i=j+1}^{n-1} \varphi_k (r_{i-1} r_{i}^{-1} t_i). \end{align*}$$
$$\begin{align*}\prod_{i=j+1}^{n-1} \varphi_k (r_{i-1} r_{i}^{-1} t_i). \end{align*}$$
Now, in equation (4.13) of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM], the commutator terms vanish, as one of the terms in every case is a scalar. Additionally, since the
![]() $\widetilde {S_j}$
in the estimate for the first summand in equation (4.14) of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM] is a scalar, we can once more avoid [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 3.15] and the SAIN condition. Once again, note that since
$\widetilde {S_j}$
in the estimate for the first summand in equation (4.14) of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM] is a scalar, we can once more avoid [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 3.15] and the SAIN condition. Once again, note that since
![]() $x_j=1$
, the proof remains valid even when some of the
$x_j=1$
, the proof remains valid even when some of the
![]() $p_j=\infty $
.
$p_j=\infty $
.
Remark 3.2 Theorem 3.1 assumes G to be second-countable since its proof relies on [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM], which assumes second countability.
Remark 3.3 Fix
![]() $1 \leq i \leq n$
. In case
$1 \leq i \leq n$
. In case
![]() $p_i = p = 1$
and
$p_i = p = 1$
and
![]() $p_j = \infty $
for all
$p_j = \infty $
for all
![]() $1 \leq j \leq n, i \not = j$
, we do not know whether Theorem 3.1 holds. The reason is that we do not know whether the limits (3.8) (at index i) hold and neither do we know if the two further applications of Proposition 3.9 in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Proof of Lemma 4.6] hold.
$1 \leq j \leq n, i \not = j$
, we do not know whether Theorem 3.1 holds. The reason is that we do not know whether the limits (3.8) (at index i) hold and neither do we know if the two further applications of Proposition 3.9 in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Proof of Lemma 4.6] hold.
4 Amenable groups: transference from Schur to Fourier multipliers
Recall [Reference Bekka, de la Harpe and ValetteBHV08, Section G] that G is amenable iff it satisfies the Følner condition: for any
![]() $\varepsilon>0$
and any compact set
$\varepsilon>0$
and any compact set
![]() $K\subseteq G$
, there exists a compact set F with nonzero measure such that
$K\subseteq G$
, there exists a compact set F with nonzero measure such that
![]() $\frac {\mu _G(s.F \Delta F)}{\mu _G(F)} < \varepsilon $
for all
$\frac {\mu _G(s.F \Delta F)}{\mu _G(F)} < \varepsilon $
for all
![]() $s\in K$
. Here,
$s\in K$
. Here,
![]() $\Delta $
is the symmetric difference. This allows us to construct a net
$\Delta $
is the symmetric difference. This allows us to construct a net
![]() $F_{(\varepsilon ,K)}$
of such Følner sets using the ordering
$F_{(\varepsilon ,K)}$
of such Følner sets using the ordering
![]() $( \varepsilon _1, K_1) \leq (\varepsilon _2,K_2)$
if
$( \varepsilon _1, K_1) \leq (\varepsilon _2,K_2)$
if
![]() $\varepsilon _1 \geq \varepsilon _2, K_1 \subseteq K_2$
.
$\varepsilon _1 \geq \varepsilon _2, K_1 \subseteq K_2$
.
Theorem 4.1 Let G be a locally compact, unimodular, amenable group, and let
![]() $1\leq p,p_1,\ldots ,p_n \leq \infty $
be such that
$1\leq p,p_1,\ldots ,p_n \leq \infty $
be such that
![]() $p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Let
$p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Let
![]() $\phi \in C_b(G^{\times n})$
be such that
$\phi \in C_b(G^{\times n})$
be such that
![]() $\widetilde {\phi }$
is the symbol of a
$\widetilde {\phi }$
is the symbol of a
![]() $(p_1,\ldots ,p_n)$
-Schur multiplier of G. Then there is an ultrafilter
$(p_1,\ldots ,p_n)$
-Schur multiplier of G. Then there is an ultrafilter
![]() $\mathcal {U}$
on a set I and there are complete contractions (resp. complete isometries if
$\mathcal {U}$
on a set I and there are complete contractions (resp. complete isometries if
![]() $1 < q < \infty $
)
$1 < q < \infty $
)
![]() $i_q: L_q(\mathcal {L} G) \to \prod _{\mathcal {U}} S_q(L_2(G))$
such that, for all
$i_q: L_q(\mathcal {L} G) \to \prod _{\mathcal {U}} S_q(L_2(G))$
such that, for all
![]() $f_i,f \in C_c(G)\star C_c(G)$
,
$f_i,f \in C_c(G)\star C_c(G)$
,
where
![]() $x_i = \lambda (f_i), y = \lambda (f)$
, and
$x_i = \lambda (f_i), y = \lambda (f)$
, and
![]() $\frac {1}{p'}+\frac {1}{p}=1$
. In a similar way, the matrix amplifications of
$\frac {1}{p'}+\frac {1}{p}=1$
. In a similar way, the matrix amplifications of
![]() $i_q$
intertwine the multiplicative amplifications of the Fourier and Schur multipliers.
$i_q$
intertwine the multiplicative amplifications of the Fourier and Schur multipliers.
Proof Let
![]() $F_{\alpha }, \alpha \in I$
be a Følner net for G, where I is the index set consisting of pairs
$F_{\alpha }, \alpha \in I$
be a Følner net for G, where I is the index set consisting of pairs
![]() $(\varepsilon , K)$
for
$(\varepsilon , K)$
for
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
![]() $K \subseteq G$
compact. It has the ordering as described above. Let
$K \subseteq G$
compact. It has the ordering as described above. Let
![]() $P_{\alpha }=P_{F_{\alpha }}$
be the projection onto
$P_{\alpha }=P_{F_{\alpha }}$
be the projection onto
![]() $L_2(F_{\alpha })$
. Let
$L_2(F_{\alpha })$
. Let
![]() $\mathcal {U}$
be an ultrafilter refining the net I, and consider the map
$\mathcal {U}$
be an ultrafilter refining the net I, and consider the map
![]() $i_p: L_p(\mathcal {L} G)\to \prod _{\mathcal {U}} S_p(L_2(G))$
defined by
$i_p: L_p(\mathcal {L} G)\to \prod _{\mathcal {U}} S_p(L_2(G))$
defined by
![]() $i_p(x) = (i_{p,\alpha }(x))_{\alpha \in I} = (\frac {1}{\mu _G(F_{\alpha })^{1/p}}P_{\alpha }x P_{\alpha })_{\alpha \in I}$
. From [Reference Caspers and de la SalleCaSa15, Theorem 5.1],
$i_p(x) = (i_{p,\alpha }(x))_{\alpha \in I} = (\frac {1}{\mu _G(F_{\alpha })^{1/p}}P_{\alpha }x P_{\alpha })_{\alpha \in I}$
. From [Reference Caspers and de la SalleCaSa15, Theorem 5.1],
![]() $i_p$
is a complete contraction (and even a complete isometry for
$i_p$
is a complete contraction (and even a complete isometry for
![]() $1< p < \infty $
[Reference Caspers and de la SalleCaSa15, Theorem 5.2]); here, the Følner condition is used.
$1< p < \infty $
[Reference Caspers and de la SalleCaSa15, Theorem 5.2]); here, the Følner condition is used.
Fix
![]() $\alpha $
and let
$\alpha $
and let
![]() $f \in C_c(G)\ast C_c(G)$
. We first observe that by [Reference Caspers and de la SalleCaSa15, Theorem 5.1] applied to the bounded operator
$f \in C_c(G)\ast C_c(G)$
. We first observe that by [Reference Caspers and de la SalleCaSa15, Theorem 5.1] applied to the bounded operator
![]() $x = \lambda (f)$
we have
$x = \lambda (f)$
we have
![]() $P_{F_{\alpha }} \lambda (f) P_{F_{\alpha }} \in S_q(L_2(G))$
for all
$P_{F_{\alpha }} \lambda (f) P_{F_{\alpha }} \in S_q(L_2(G))$
for all
![]() $1\leq q \leq \infty $
and the kernel of this operator is given by the function
$1\leq q \leq \infty $
and the kernel of this operator is given by the function
So we have
 $$ \begin{align*} M_{\widetilde{\phi}} (i_{p_1, \alpha}(x_1),\ldots,i_{p_n, \alpha}(x_n)) (t_0,t_{n}) & \\ = \frac{1}{\mu_G(F_{\alpha})^{1/p}} 1_{F_{\alpha}}(t_0)1_{F_{\alpha}}(t_n) \int_{F_{\alpha}^{\times n-1}} & \phi(t_0t_1^{-1},\ldots, t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) dt_1 \ldots dt_{n-1}. \end{align*} $$
$$ \begin{align*} M_{\widetilde{\phi}} (i_{p_1, \alpha}(x_1),\ldots,i_{p_n, \alpha}(x_n)) (t_0,t_{n}) & \\ = \frac{1}{\mu_G(F_{\alpha})^{1/p}} 1_{F_{\alpha}}(t_0)1_{F_{\alpha}}(t_n) \int_{F_{\alpha}^{\times n-1}} & \phi(t_0t_1^{-1},\ldots, t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) dt_1 \ldots dt_{n-1}. \end{align*} $$
Moreover, after some change of variables, we see that
![]() $P_{F_{\alpha }} T_{\phi }(x_1,\ldots ,x_n)P_{F_{\alpha }}$
is given by the kernel
$P_{F_{\alpha }} T_{\phi }(x_1,\ldots ,x_n)P_{F_{\alpha }}$
is given by the kernel
 $$ \begin{align*} &(t_0,t_n) \\&\quad\mapsto 1_{F_{\alpha}}(t_0) \int_{G^{\times n-1}} \phi(t_0t_1^{-1},\ldots,t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) 1_F(t_n) dt_1\ldots dt_{n-1}. \end{align*} $$
$$ \begin{align*} &(t_0,t_n) \\&\quad\mapsto 1_{F_{\alpha}}(t_0) \int_{G^{\times n-1}} \phi(t_0t_1^{-1},\ldots,t_{n-1}t_n^{-1}) f_1(t_0t_1^{-1})\ldots f_n(t_{n-1}t_n^{-1}) 1_F(t_n) dt_1\ldots dt_{n-1}. \end{align*} $$
Let
![]() $\Phi $
denote the function
$\Phi $
denote the function
and let
![]() $\Psi _{\alpha }$
be defined by
$\Psi _{\alpha }$
be defined by
Let K be some compact set such that
![]() $\operatorname {\mathrm {supp}}(f_j),\operatorname {\mathrm {supp}}(f)\subseteq K$
. Let
$\operatorname {\mathrm {supp}}(f_j),\operatorname {\mathrm {supp}}(f)\subseteq K$
. Let
![]() $t_0, \dots , t_n$
be such that both
$t_0, \dots , t_n$
be such that both
![]() $\Phi (t_0, \dots , t_n)$
and
$\Phi (t_0, \dots , t_n)$
and
![]() $\Psi _{\alpha }(t_0, \dots , t_n)$
are nonzero. Since
$\Psi _{\alpha }(t_0, \dots , t_n)$
are nonzero. Since
![]() $\Psi _{\alpha }(t_0, \dots , t_n)$
is nonzero, we must have
$\Psi _{\alpha }(t_0, \dots , t_n)$
is nonzero, we must have
![]() $t_0, t_n \in F_{\alpha }$
and
$t_0, t_n \in F_{\alpha }$
and
![]() $t_1, \ldots ,t_{n-1} \notin F_{\alpha }$
. Since
$t_1, \ldots ,t_{n-1} \notin F_{\alpha }$
. Since
![]() $\Phi (t_0, \dots , t_n)$
is nonzero, there are
$\Phi (t_0, \dots , t_n)$
is nonzero, there are
![]() $k_1,\ldots ,k_n \in K$
such that
$k_1,\ldots ,k_n \in K$
such that
![]() $t_{n-1} = k_n t_n,\ t_{n-2} = k_{n-1}k_n t_n,\ \ldots ,\ t_0 = k_1 \ldots k_n t_n$
. Hence, we find that
$t_{n-1} = k_n t_n,\ t_{n-2} = k_{n-1}k_n t_n,\ \ldots ,\ t_0 = k_1 \ldots k_n t_n$
. Hence, we find that
![]() $t_n$
belongs to the set
$t_n$
belongs to the set
Using these facts, along with some change of variables, we get
 $$ \begin{align} \begin{aligned} &\vert \langle i_{p,\alpha}(T_{\phi}(x_1,\ldots,x_n)),i_{p',\alpha}(y^*) \rangle_{p,p'} - \langle M_{\widetilde{\phi}}( i_{p_1,\alpha}(x_1),\ldots,i_{p_n,\alpha}(x_n) ) , i_{p',\alpha}(y^*) \rangle_{p,p'} \vert \\ &= \left\vert \frac{1}{\mu_G(F_{\alpha})} \int_{G^{n+1}} \Phi(t_0,\ldots,t_n) \Psi_{\alpha}(t_0,\ldots,t_n) dt_0 \ldots dt_n \right\vert \\ &= \left\vert \frac{1}{\mu_G(F_{\alpha})} \int_{K^{n}} \int_{G} \Phi(k_1\ldots k_n t_n, \ldots , k_n t_n, t_n) \Psi_{\alpha}(k_1\ldots k_nt_n,\ldots ,k_nt_n, t_n)dk_1 \ldots dk_n dt_n \right\vert \\ &\leq \| \Phi \|_{\infty} \int_{K^n} \frac{1}{\mu_G(F_{\alpha})}\mu_G\\&\quad\times\left(F_{\alpha} \cap (F_{\alpha}.(k_1\ldots k_n)^{-1}) \cap (F_{\alpha}.(k_2\ldots k_n)^{-1})^c \cap \ldots \cap (F_{\alpha}.(k_n)^{-1})^c\right) dk_1 \ldots dk_n \\ & \leq \| \Phi \|_{\infty} \int_{K^n} \frac{1}{\mu_G(F_{\alpha})}\mu_G\left(F_{\alpha} \cap(F_{\alpha}.(k_n)^{-1})^c \right) dk_1 \ldots dk_n. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\vert \langle i_{p,\alpha}(T_{\phi}(x_1,\ldots,x_n)),i_{p',\alpha}(y^*) \rangle_{p,p'} - \langle M_{\widetilde{\phi}}( i_{p_1,\alpha}(x_1),\ldots,i_{p_n,\alpha}(x_n) ) , i_{p',\alpha}(y^*) \rangle_{p,p'} \vert \\ &= \left\vert \frac{1}{\mu_G(F_{\alpha})} \int_{G^{n+1}} \Phi(t_0,\ldots,t_n) \Psi_{\alpha}(t_0,\ldots,t_n) dt_0 \ldots dt_n \right\vert \\ &= \left\vert \frac{1}{\mu_G(F_{\alpha})} \int_{K^{n}} \int_{G} \Phi(k_1\ldots k_n t_n, \ldots , k_n t_n, t_n) \Psi_{\alpha}(k_1\ldots k_nt_n,\ldots ,k_nt_n, t_n)dk_1 \ldots dk_n dt_n \right\vert \\ &\leq \| \Phi \|_{\infty} \int_{K^n} \frac{1}{\mu_G(F_{\alpha})}\mu_G\\&\quad\times\left(F_{\alpha} \cap (F_{\alpha}.(k_1\ldots k_n)^{-1}) \cap (F_{\alpha}.(k_2\ldots k_n)^{-1})^c \cap \ldots \cap (F_{\alpha}.(k_n)^{-1})^c\right) dk_1 \ldots dk_n \\ & \leq \| \Phi \|_{\infty} \int_{K^n} \frac{1}{\mu_G(F_{\alpha})}\mu_G\left(F_{\alpha} \cap(F_{\alpha}.(k_n)^{-1})^c \right) dk_1 \ldots dk_n. \end{aligned} \end{align} $$
Using the ordering described earlier, if the index
![]() $\alpha \geq (\varepsilon \times \left (\|\Phi \|_{\infty } \mu _G(K^n)\right )^{-1}, K^{-1})$
, then the Følner condition implies that (4.2) is less than
$\alpha \geq (\varepsilon \times \left (\|\Phi \|_{\infty } \mu _G(K^n)\right )^{-1}, K^{-1})$
, then the Følner condition implies that (4.2) is less than
![]() $\varepsilon $
, and hence equation (4.1) is true.
$\varepsilon $
, and hence equation (4.1) is true.
A direct modification of this argument now shows that the
![]() $i_p$
also intertwine the multiplicative amplifications of the Fourier and Schur multipliers. That is, for
$i_p$
also intertwine the multiplicative amplifications of the Fourier and Schur multipliers. That is, for
![]() $\beta _i \in S_{p_i}^N, \beta \in S_{p'}^{N}$
, we have
$\beta _i \in S_{p_i}^N, \beta \in S_{p'}^{N}$
, we have
 $$ \begin{align} \begin{aligned} \langle \operatorname{\mathrm{id}} \otimes & i_p(T^{(N)}_{\phi}(\beta_1\otimes x_1,\ldots,\beta_n \otimes x_n)), \operatorname{\mathrm{id}}\otimes i_{p'}(\beta \otimes y^*) \rangle_{p,p'} = \\ &\left\langle \left( M^{(N)}_{\widetilde{\phi}}(\operatorname{\mathrm{id}}\otimes i_{p_1,\alpha}(\beta_1 \otimes x_1),\ldots,\operatorname{\mathrm{id}}\otimes i_{p_n,\alpha}(\beta_n \otimes x_n) ) \right)_{\alpha} , \operatorname{\mathrm{id}}\otimes i_{p'}(\beta\otimes y^*) \right\rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle \operatorname{\mathrm{id}} \otimes & i_p(T^{(N)}_{\phi}(\beta_1\otimes x_1,\ldots,\beta_n \otimes x_n)), \operatorname{\mathrm{id}}\otimes i_{p'}(\beta \otimes y^*) \rangle_{p,p'} = \\ &\left\langle \left( M^{(N)}_{\widetilde{\phi}}(\operatorname{\mathrm{id}}\otimes i_{p_1,\alpha}(\beta_1 \otimes x_1),\ldots,\operatorname{\mathrm{id}}\otimes i_{p_n,\alpha}(\beta_n \otimes x_n) ) \right)_{\alpha} , \operatorname{\mathrm{id}}\otimes i_{p'}(\beta\otimes y^*) \right\rangle. \end{aligned} \end{align} $$
Combining this with Theorem 3.1, we get the multilinear version of [Reference Caspers and de la SalleCaSa15, Corollary 5.3]
Corollary 4.2 Let
![]() $1 < p,p_1,\ldots ,p_n < \infty $
be such that
$1 < p,p_1,\ldots ,p_n < \infty $
be such that
![]() $p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Let
$p^{-1}=\sum _{i=1}^n p_i^{-1}$
. Let
![]() $\phi \in C_b(G^{\times n})$
and assume that G is amenable. If
$\phi \in C_b(G^{\times n})$
and assume that G is amenable. If
![]() $\widetilde {\phi }$
is the symbol of a
$\widetilde {\phi }$
is the symbol of a
![]() $(p_1, \ldots , p_n)$
-bounded (resp. multiplicatively bounded) Schur multiplier, then
$(p_1, \ldots , p_n)$
-bounded (resp. multiplicatively bounded) Schur multiplier, then
![]() $\phi $
is the symbol of a
$\phi $
is the symbol of a
![]() $(p_1, \dots , p_n)$
-bounded (resp. multiplicatively bounded) Fourier multiplier. Moreover,
$(p_1, \dots , p_n)$
-bounded (resp. multiplicatively bounded) Fourier multiplier. Moreover,
with equality in the
![]() $(p_1,\ldots ,p_n)$
-
$(p_1,\ldots ,p_n)$
-
![]() $mb$
norm when G is second-countable.
$mb$
norm when G is second-countable.
Proof For
![]() $1<p<\infty $
,
$1<p<\infty $
,
![]() $i_p$
is a (complete) isometry. Hence, for
$i_p$
is a (complete) isometry. Hence, for
![]() $x_i$
as in the hypothesis of Theorem 4.1, we get
$x_i$
as in the hypothesis of Theorem 4.1, we get
 $$\begin{align*} &\Vert T_{\phi} (x_1,\ldots,x_n) \Vert_{L_p(\mathcal{L} G)} \\&\quad= \Vert i_p \circ T_{\phi} (x_1,\ldots,x_n) \Vert_{L_p(\mathcal{L} G)} = \Vert M_{\widetilde{\phi}} (i_{p_1}(x_1),\ldots,i_{p_n}(x_n)) \Vert_{L_p(\mathcal{L} G)} \\ &\quad\leq \Vert M_{\widetilde{\phi}} \Vert_{(p_1,\ldots p_n)} \prod_{i=1}^n \Vert x_i \Vert_{L_{p_i}(\mathcal{L} G)}. \end{align*}$$
$$\begin{align*} &\Vert T_{\phi} (x_1,\ldots,x_n) \Vert_{L_p(\mathcal{L} G)} \\&\quad= \Vert i_p \circ T_{\phi} (x_1,\ldots,x_n) \Vert_{L_p(\mathcal{L} G)} = \Vert M_{\widetilde{\phi}} (i_{p_1}(x_1),\ldots,i_{p_n}(x_n)) \Vert_{L_p(\mathcal{L} G)} \\ &\quad\leq \Vert M_{\widetilde{\phi}} \Vert_{(p_1,\ldots p_n)} \prod_{i=1}^n \Vert x_i \Vert_{L_{p_i}(\mathcal{L} G)}. \end{align*}$$
For
![]() $1<p_i<\infty $
, such
$1<p_i<\infty $
, such
![]() $x_i$
are norm-dense in
$x_i$
are norm-dense in
![]() $L_{p_i}(\mathcal {L} G)$
, so we get the bound on
$L_{p_i}(\mathcal {L} G)$
, so we get the bound on
![]() $\Vert T_{\phi } \Vert _{(p_1,\ldots ,p_n)}$
. The multiplicatively bounded version follows similarly, with the other inequality coming from Theorem 3.1.
$\Vert T_{\phi } \Vert _{(p_1,\ldots ,p_n)}$
. The multiplicatively bounded version follows similarly, with the other inequality coming from Theorem 3.1.
Let
![]() $H\leq G$
be a subgroup. Clearly, from Theorem 2.2, the restriction of
$H\leq G$
be a subgroup. Clearly, from Theorem 2.2, the restriction of
![]() $\phi $
to H also determines a bounded Schur multiplier, with
$\phi $
to H also determines a bounded Schur multiplier, with
Combining this observation with Corollary 4.2 gives us the multiplicatively bounded version of the multilinear de Leeuw restriction theorem [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Theorem 4.5] for amenable discrete subgroups of second-countable groups. Note that the SAIN condition used in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Theorem 4.5] is implicit here since the subgroup is amenable.
Corollary 4.3 Let G be a locally compact, unimodular, second-countable group, and let
![]() $1<p,p_1,\ldots ,p_n<\infty $
with
$1<p,p_1,\ldots ,p_n<\infty $
with
![]() $p^{-1}=\sum _i p_i^{-1}$
. Let
$p^{-1}=\sum _i p_i^{-1}$
. Let
![]() $\phi \in C_b(G^{\times n})$
be a symbol of a
$\phi \in C_b(G^{\times n})$
be a symbol of a
![]() $(p_1,\ldots ,p_n)$
-multiplicatively bounded Fourier multiplier. If H is an amenable discrete subgroup of G, then we have
$(p_1,\ldots ,p_n)$
-multiplicatively bounded Fourier multiplier. If H is an amenable discrete subgroup of G, then we have
Remark 4.4 We now discuss some difficulties one encounters when modifying the above methods to the nonunimodular case, meaning that the Plancherel weight
![]() $\varphi $
is no longer a trace. In this case,
$\varphi $
is no longer a trace. In this case,
![]() $\lambda (C_c(G) \star C_c(G))$
is no longer a common dense subset of the
$\lambda (C_c(G) \star C_c(G))$
is no longer a common dense subset of the
![]() $L_p(\mathcal {L} G)$
. Rather, we have embeddings
$L_p(\mathcal {L} G)$
. Rather, we have embeddings
![]() $\eta _{t,p}: \lambda (C_c(G) \star C_c(G)) \to L_p(\mathcal {L} G)$
with dense image given by
$\eta _{t,p}: \lambda (C_c(G) \star C_c(G)) \to L_p(\mathcal {L} G)$
with dense image given by
![]() $\lambda (f) \mapsto \Delta ^{(1-t)/p} \lambda (f) \Delta ^{t/p}$
, where
$\lambda (f) \mapsto \Delta ^{(1-t)/p} \lambda (f) \Delta ^{t/p}$
, where
![]() $0 \leq t \leq 1$
and
$0 \leq t \leq 1$
and
![]() $\Delta $
is the multiplication operator with the modular function, which we denote also by
$\Delta $
is the multiplication operator with the modular function, which we denote also by
![]() $\Delta $
(see [Reference TerpTer81, Reference TerpTer82] for details).
$\Delta $
(see [Reference TerpTer81, Reference TerpTer82] for details).
This raises the question how to define the
![]() $(p_1, \dots , p_n)$
-Fourier multiplier. A possible choice would be to take some
$(p_1, \dots , p_n)$
-Fourier multiplier. A possible choice would be to take some
![]() $t \in [0,1]$
and define
$t \in [0,1]$
and define
However, with this definition, the intertwining property in the ultralimit of (4.2) will no longer hold. This can be illustrated by considering the case
![]() $n=2$
and
$n=2$
and
![]() $\phi (x,y) = \phi _1(x) \phi _2(y)$
. In order for the intertwining property to hold, the Fourier multiplier would have to satisfy
$\phi (x,y) = \phi _1(x) \phi _2(y)$
. In order for the intertwining property to hold, the Fourier multiplier would have to satisfy
where on the right-hand side we use the linear definition of the Fourier multiplier from [Reference Caspers and de la SalleCaSa15]. This is not the case with the above definition. As a consequence, we no longer have nice relations between nested linear Fourier multipliers and multilinear Fourier multipliers, as in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.4]. As the proof of the multilinear restriction theorem in [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM] repeatedly uses such formulae, it is also unclear if these de Leeuw-type theorems are still valid in the nonunimodular case.
5 Domain of the completely bounded bilinear Hilbert transform and Calderón–Zygmund operators
In this final section, we prove a result about nonboundedness of the bilinear Hilbert transform based on our multilinear transference techniques. We prove an analogous result for examples of Calderón–Zygmund operators. This shows that the main results from [Reference Amenta and UraltsevAmUr20, Reference DiPlinio, Li, Martikainen and VuorinenDMLV22] about
![]() $L_p$
-boundedness of certain Fourier multipliers cannot be extended to range spaces with
$L_p$
-boundedness of certain Fourier multipliers cannot be extended to range spaces with
![]() $p \leq 1$
. This is in contrast with the Euclidean (nonvector-valued) case.
$p \leq 1$
. This is in contrast with the Euclidean (nonvector-valued) case.
5.1 Lower bounds for the vector-valued bilinear Hilbert transform
For
![]() $0 < p < \infty $
, let
$0 < p < \infty $
, let
![]() $S_p^N = S_p(\mathbb {C}^N)$
be the Schatten
$S_p^N = S_p(\mathbb {C}^N)$
be the Schatten
![]() $L_p$
-space associated with linear operators on
$L_p$
-space associated with linear operators on
![]() $\mathbb {C}^N$
. For
$\mathbb {C}^N$
. For
![]() $ 0 < p < 1$
, we have that
$ 0 < p < 1$
, we have that
![]() $S_p^N$
is a quasi-Banach space satisfying the quasi-triangle inequality:
$S_p^N$
is a quasi-Banach space satisfying the quasi-triangle inequality:
We set
The first statement of the following theorem is the main result of [Reference Lacey and ThieleLaTh99], and the latter statement of this theorem for
![]() $1 < p < \infty $
was proved in [Reference Amenta and UraltsevAmUr20, Reference DiPlinio, Li, Martikainen and VuorinenDMLV22].
$1 < p < \infty $
was proved in [Reference Amenta and UraltsevAmUr20, Reference DiPlinio, Li, Martikainen and VuorinenDMLV22].
Theorem 5.1 For every
![]() $1 < q_1,q_2,q, p_1, p_2 < \infty , \frac {2}{3} < p < \infty $
with
$1 < q_1,q_2,q, p_1, p_2 < \infty , \frac {2}{3} < p < \infty $
with
![]() $\frac {1}{p} = \frac {1}{p_1} + \frac {1}{p_2}$
and
$\frac {1}{p} = \frac {1}{p_1} + \frac {1}{p_2}$
and
![]() $N \in \mathbb {N}_{\geq 1}$
, there exists a bounded linear map
$N \in \mathbb {N}_{\geq 1}$
, there exists a bounded linear map
which is determined by
where
![]() $s \in \mathbb {R}$
and
$s \in \mathbb {R}$
and
![]() $f_i, i =1,2$
are functions in
$f_i, i =1,2$
are functions in
![]() $L_{p_i}(\mathbb {R}, S_{q_i}^N )$
whose Fourier transforms
$L_{p_i}(\mathbb {R}, S_{q_i}^N )$
whose Fourier transforms
![]() $\widehat {f_i}$
are continuous compactly supported functions
$\widehat {f_i}$
are continuous compactly supported functions
![]() $\mathbb {R} \rightarrow S_{q_i}^N$
. If
$\mathbb {R} \rightarrow S_{q_i}^N$
. If
![]() $1 < p := (\frac {1}{p_1} + \frac {1}{p_2})^{-1} < \infty $
and
$1 < p := (\frac {1}{p_1} + \frac {1}{p_2})^{-1} < \infty $
and
![]() $\frac {1}{\max \{q,q'\}}+\frac {1}{\max \{q_1,q_1'\}}+\frac {1}{\max \{q_2,q_2'\}}> 1$
, we have that this operator is moreover uniformly bounded in N.
$\frac {1}{\max \{q,q'\}}+\frac {1}{\max \{q_1,q_1'\}}+\frac {1}{\max \{q_2,q_2'\}}> 1$
, we have that this operator is moreover uniformly bounded in N.
Note that the map
![]() $T_h^{(N)}$
as defined above coincides with the multiplicative amplification of the map
$T_h^{(N)}$
as defined above coincides with the multiplicative amplification of the map
![]() $T_h := T_h^{(1)}$
as defined in Section 2.7, so this notation is consistent.
$T_h := T_h^{(1)}$
as defined in Section 2.7, so this notation is consistent.
Our aim is to show that the results of [Reference Amenta and UraltsevAmUr20, Reference DiPlinio, Li, Martikainen and VuorinenDMLV22] cannot be extended to the case
![]() $p_i=q_i$
,
$p_i=q_i$
,
![]() $q=p = 1=\frac {1}{p_1}+\frac {1}{p_2}$
; i.e., the bound of (5.1) is not uniform in N. In particular, we show that the bound can be estimated from below by
$q=p = 1=\frac {1}{p_1}+\frac {1}{p_2}$
; i.e., the bound of (5.1) is not uniform in N. In particular, we show that the bound can be estimated from below by
![]() $C \log (N)$
for some constant C independent of N.
$C \log (N)$
for some constant C independent of N.
For a function
![]() $\phi : \mathbb {R}^2 \rightarrow \mathbb {C}$
, we recall the definition
$\phi : \mathbb {R}^2 \rightarrow \mathbb {C}$
, we recall the definition
Theorem 5.2 Let
![]() $1 < p_1, p_2 < \infty $
be such that
$1 < p_1, p_2 < \infty $
be such that
![]() $\frac {1}{p_1} + \frac {1}{p_2} = 1$
. There exists an absolute constant
$\frac {1}{p_1} + \frac {1}{p_2} = 1$
. There exists an absolute constant
![]() $C>0$
such that, for every
$C>0$
such that, for every
![]() $N \in \mathbb {N}_{\geq 1}$
, we have
$N \in \mathbb {N}_{\geq 1}$
, we have
Proof In the proof, let
![]() $\mathbb {Z}_N = [-N, N] \cap \mathbb {Z}$
. We may naturally identify
$\mathbb {Z}_N = [-N, N] \cap \mathbb {Z}$
. We may naturally identify
![]() $S_p^{2N+1}$
with
$S_p^{2N+1}$
with
![]() $S_p( \ell _2(\mathbb {Z}_N) )$
. Let
$S_p( \ell _2(\mathbb {Z}_N) )$
. Let
![]() $\varphi \in C_c(\mathbb {R}), \varphi \geq 0$
be such that
$\varphi \in C_c(\mathbb {R}), \varphi \geq 0$
be such that
![]() $\varphi (t) = \varphi (-t), t\in \mathbb {R}$
,
$\varphi (t) = \varphi (-t), t\in \mathbb {R}$
,
![]() $\Vert \varphi \Vert _{L_1(G)} = 1$
and its support is contained in
$\Vert \varphi \Vert _{L_1(G)} = 1$
and its support is contained in
![]() $[-\frac {1}{2}, \frac {1}{2}]$
. Set, for
$[-\frac {1}{2}, \frac {1}{2}]$
. Set, for
![]() $s_1, s_2 \in \mathbb {R}$
,
$s_1, s_2 \in \mathbb {R}$
,
Then H is continuous and H equals h on
![]() $\mathbb {Z} \times \mathbb {Z}$
. As a consequence of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.3], we find
$\mathbb {Z} \times \mathbb {Z}$
. As a consequence of [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.3], we find
By the multilinear De Leeuw restriction theorem [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Theorem C], we have
Let
![]() $\zeta _l(z) = z^l, z\in \mathbb {T}, l \in \mathbb {Z}$
. Set the unitary
$\zeta _l(z) = z^l, z\in \mathbb {T}, l \in \mathbb {Z}$
. Set the unitary
![]() $U = \sum _{l=-N}^N p_l \otimes \zeta _l$
and for any
$U = \sum _{l=-N}^N p_l \otimes \zeta _l$
and for any
![]() $1 < p < \infty $
the isometric map
$1 < p < \infty $
the isometric map
Then,
This together with (5.2) implies that
Now, set
![]() $H_j(s,t) = \widetilde { H } \vert _{\mathbb {Z} \times \mathbb {Z}}(s, j, t), s,t \in \mathbb {Z}$
. Note that
$H_j(s,t) = \widetilde { H } \vert _{\mathbb {Z} \times \mathbb {Z}}(s, j, t), s,t \in \mathbb {Z}$
. Note that
By [Reference Potapov, Skripka, Sukochev and TomskovaPSST17, Theorem 2.3], we find that
For
![]() $j = 0$
, we have that
$j = 0$
, we have that
![]() $M_{ H_j }$
is the triangular truncation map and therefore by [Reference DaviesDav88, Proof of Lemma 10] (apply
$M_{ H_j }$
is the triangular truncation map and therefore by [Reference DaviesDav88, Proof of Lemma 10] (apply
![]() $M_{H_0}$
to the matrix consisting of only 1’s) there is a constant
$M_{H_0}$
to the matrix consisting of only 1’s) there is a constant
![]() $C>0$
such that
$C>0$
such that
Combining (5.3)–(5.5) yields the result for
![]() $2N+1$
. Since the norm of
$2N+1$
. Since the norm of
![]() $T_h^{(N)}$
is increasing in N, the result for even N also follows.
$T_h^{(N)}$
is increasing in N, the result for even N also follows.
5.2 Lower bounds for Calderón–Zygmund operators
The aim of this section is to show a result similar to Theorem 5.2 for Calderón–Zygmund operators by considering an example. This shows that the results from [Reference DiPlinio, Li, Martikainen and VuorinenDLMV20] cannot be extended to the case where the range space is
![]() $p=1$
. This is in contrast with the commutative situation where Grafakos and Torres [Reference Grafakos and TorresGrTo02] have shown boundedness of a class of Calderón–Zygmund operators with natural size and smoothness conditions as maps
$p=1$
. This is in contrast with the commutative situation where Grafakos and Torres [Reference Grafakos and TorresGrTo02] have shown boundedness of a class of Calderón–Zygmund operators with natural size and smoothness conditions as maps
![]() $L_p \times \cdots \times L_p \rightarrow L_{p/n}$
for
$L_p \times \cdots \times L_p \rightarrow L_{p/n}$
for
![]() $p \in (1, \infty )$
.
$p \in (1, \infty )$
.
Consider any symbol m that is smooth on
![]() $\mathbb {R}^2 \backslash \{ 0 \}$
, homogeneous, and which is determined on one of the quadrants by
$\mathbb {R}^2 \backslash \{ 0 \}$
, homogeneous, and which is determined on one of the quadrants by
Here, homogeneous means that
![]() $m(\lambda s, \lambda t) = m(s,t), s,t \in \mathbb {R}, \lambda>0$
. We assume moreover that m is regulated at 0, by which we mean that
$m(\lambda s, \lambda t) = m(s,t), s,t \in \mathbb {R}, \lambda>0$
. We assume moreover that m is regulated at 0, by which we mean that
As m is homogeneous, this expression is independent of r. This type of symbol m is important as it occurs naturally in the analysis of divided difference functions; for instance, it plays a crucial role in [Reference Caspers, Sukochev and ZaninCSZ21].
Theorem 5.3 Let
![]() $1 < p_1, p_2 < \infty $
be such that
$1 < p_1, p_2 < \infty $
be such that
![]() $\frac {1}{p_1} + \frac {1}{p_2} = 1$
. There exists an absolute constant
$\frac {1}{p_1} + \frac {1}{p_2} = 1$
. There exists an absolute constant
![]() $C>0$
such that
$C>0$
such that
Proof By [Reference DaviesDav88, Lemma 10] (and the proof of [Reference DaviesDav88, Corollary 11]), there exist constants
![]() $0 = \lambda _0 < \lambda _1 < \cdots < \lambda _N$
such that the function
$0 = \lambda _0 < \lambda _1 < \cdots < \lambda _N$
such that the function
 $$\begin{align*}\phi(i,j) = \frac{\lambda_i - \lambda_j}{\lambda_i + \lambda_j}, \qquad 1 \leq i,j \leq N, \end{align*}$$
$$\begin{align*}\phi(i,j) = \frac{\lambda_i - \lambda_j}{\lambda_i + \lambda_j}, \qquad 1 \leq i,j \leq N, \end{align*}$$
is the symbol of a linear Schur multiplier
![]() $M_{\phi }: S_1^{N} \rightarrow S_1^N$
whose norm is at least
$M_{\phi }: S_1^{N} \rightarrow S_1^N$
whose norm is at least
![]() $C \log (N)$
for some absolute constant
$C \log (N)$
for some absolute constant
![]() $C> 0$
. Without loss of generality, we may assume that
$C> 0$
. Without loss of generality, we may assume that
![]() $\lambda _i \in K_N^{-1} \mathbb {Z}$
for some
$\lambda _i \in K_N^{-1} \mathbb {Z}$
for some
![]() $K_N \in \mathbb {N}_{\geq 1}$
by an approximation argument. Then, in this proof, let
$K_N \in \mathbb {N}_{\geq 1}$
by an approximation argument. Then, in this proof, let
![]() $\Lambda _N = \{ \lambda _0, \lambda _1, \ldots , \lambda _N \}$
. We may naturally identify
$\Lambda _N = \{ \lambda _0, \lambda _1, \ldots , \lambda _N \}$
. We may naturally identify
![]() $S_p^{N+1}$
with
$S_p^{N+1}$
with
![]() $S_p( \ell _2(\Lambda _N))$
by identifying
$S_p( \ell _2(\Lambda _N))$
by identifying
![]() $E_{i,j}$
with
$E_{i,j}$
with
![]() $E_{\lambda _i, \lambda _j}$
. We proceed as in the proof of Theorem 5.2.
$E_{\lambda _i, \lambda _j}$
. We proceed as in the proof of Theorem 5.2.
For
![]() $\lambda \in K_N^{-1} \mathbb {Z}$
, let
$\lambda \in K_N^{-1} \mathbb {Z}$
, let
![]() $p_{\lambda }$
be the orthogonal projection of
$p_{\lambda }$
be the orthogonal projection of
![]() $\ell _2(K_N^{-1} \mathbb {Z})$
onto
$\ell _2(K_N^{-1} \mathbb {Z})$
onto
![]() $\mathbb {C} \delta _{\lambda }$
. Furthermore, for
$\mathbb {C} \delta _{\lambda }$
. Furthermore, for
![]() $\lambda \in K_N^{-1} \mathbb {Z}$
, set
$\lambda \in K_N^{-1} \mathbb {Z}$
, set
![]() $\zeta _{\lambda }: \mathbb {T} \rightarrow \mathbb {C}$
by
$\zeta _{\lambda }: \mathbb {T} \rightarrow \mathbb {C}$
by
![]() $\zeta _{\lambda }(z) = z^{ K_N \lambda }, \theta \in \mathbb {R}$
. This way every
$\zeta _{\lambda }(z) = z^{ K_N \lambda }, \theta \in \mathbb {R}$
. This way every
![]() ${z \in \mathbb {T}}$
determines a representation
${z \in \mathbb {T}}$
determines a representation
![]() $\lambda \mapsto \zeta _{\lambda }(z)$
of
$\lambda \mapsto \zeta _{\lambda }(z)$
of
![]() $K_N^{-1} \mathbb {Z}$
and this identifies
$K_N^{-1} \mathbb {Z}$
and this identifies
![]() $\mathbb {T}$
with the Pontrjagin dual of
$\mathbb {T}$
with the Pontrjagin dual of
![]() $K_N^{-1} \mathbb {Z}$
. Set the unitary
$K_N^{-1} \mathbb {Z}$
. Set the unitary
![]() $U = \sum _{\lambda \in \Lambda _N} p_{\lambda } \otimes \zeta _{\lambda }$
and for any
$U = \sum _{\lambda \in \Lambda _N} p_{\lambda } \otimes \zeta _{\lambda }$
and for any
![]() $1 < p < \infty $
the isometric map
$1 < p < \infty $
the isometric map
For
![]() $r>0$
, consider the function
$r>0$
, consider the function
This function is continuous and bounded, and hence we may apply the bilinear De Leeuw restriction theorem [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Theorem C] to get
 $$ \begin{align} \begin{aligned} & \Vert T_{ m_r\vert_{ (K_N^{-1} \mathbb{Z})^2} }^{(N+1)}: L_{p_1}(\mathbb{T}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{T}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{T}, S_{1}^{N+1}) \Vert\\ &\qquad \leq \Vert T_{ m_r }^{(N+1)}: L_{p_1}(\mathbb{R}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{R}, S_{p_2}^{N+1}) \rightarrow L_{1}(\mathbb{R}, S_{1}^{N+1} ) \Vert. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \Vert T_{ m_r\vert_{ (K_N^{-1} \mathbb{Z})^2} }^{(N+1)}: L_{p_1}(\mathbb{T}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{T}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{T}, S_{1}^{N+1}) \Vert\\ &\qquad \leq \Vert T_{ m_r }^{(N+1)}: L_{p_1}(\mathbb{R}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{R}, S_{p_2}^{N+1}) \rightarrow L_{1}(\mathbb{R}, S_{1}^{N+1} ) \Vert. \end{aligned} \end{align} $$
Since
![]() $ m_r\vert _{ (K_N^{-1} \mathbb {Z})^2}$
converges to
$ m_r\vert _{ (K_N^{-1} \mathbb {Z})^2}$
converges to
![]() $m \vert _{ (K_N^{-1} \mathbb {Z})^2}$
pointwise, we obtain (by considering the action of the multiplier on functions with finite frequency support)
$m \vert _{ (K_N^{-1} \mathbb {Z})^2}$
pointwise, we obtain (by considering the action of the multiplier on functions with finite frequency support)
 $$ \begin{align} \begin{aligned} & \lim_{r\searrow 0} \Vert T_{ m_r\vert _{ (K_N^{-1} \mathbb{Z})^2 } }^{(N+1)}: L_{p_1}(\mathbb{T}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{T}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{T}, S_{1}^{N+1}) \Vert \\ & \qquad = \Vert T_{ m\vert_{ (K_N^{-1} \mathbb{Z})^2} }^{(N+1)}: L_{p_1}(\mathbb{T}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{T}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{T}, S_{1}^{N+1})\Vert. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \lim_{r\searrow 0} \Vert T_{ m_r\vert _{ (K_N^{-1} \mathbb{Z})^2 } }^{(N+1)}: L_{p_1}(\mathbb{T}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{T}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{T}, S_{1}^{N+1}) \Vert \\ & \qquad = \Vert T_{ m\vert_{ (K_N^{-1} \mathbb{Z})^2} }^{(N+1)}: L_{p_1}(\mathbb{T}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{T}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{T}, S_{1}^{N+1})\Vert. \end{aligned} \end{align} $$
Furthermore, viewing
![]() $m_r$
as a convolution of m with an
$m_r$
as a convolution of m with an
![]() $L_1(\mathbb {R}^2)$
function, from [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.3],
$L_1(\mathbb {R}^2)$
function, from [Reference Caspers, Janssens, Krishnaswamy-Usha and MiaskiwskyiCJKM, Lemma 4.3],
 $$ \begin{align} \begin{aligned} &\Vert T_{ m_r }^{(N+1)}: L_{p_1}(\mathbb{R}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{R}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{R}, S_{1}^{N+1}) \Vert \\ &\qquad \leq \Vert T_{ m}^{(N+1)}: L_{p_1}(\mathbb{R}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{R}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{R}, S_{1}^{N+1}) \Vert = B_{p_1, p_2,N}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\Vert T_{ m_r }^{(N+1)}: L_{p_1}(\mathbb{R}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{R}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{R}, S_{1}^{N+1}) \Vert \\ &\qquad \leq \Vert T_{ m}^{(N+1)}: L_{p_1}(\mathbb{R}, S_{p_1}^{N+1}) \times L_{p_2}(\mathbb{R}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{R}, S_{1}^{N+1}) \Vert = B_{p_1, p_2,N}. \end{aligned} \end{align} $$
Combining the estimates (5.7)–(5.9), we find that
We view
![]() $\widetilde {m} \vert _{\Lambda _N \times \Lambda _N \times \Lambda _N}$
as the symbol of a Schur multiplier
$\widetilde {m} \vert _{\Lambda _N \times \Lambda _N \times \Lambda _N}$
as the symbol of a Schur multiplier
![]() $M_{ \widetilde { m} \vert _{\Lambda _N \times \Lambda _N \times \Lambda _N} }: S_{p_1}^{N+1} \times S_{p_2}^{N+1} \rightarrow S_{1}^{N+1}$
. Then,
$M_{ \widetilde { m} \vert _{\Lambda _N \times \Lambda _N \times \Lambda _N} }: S_{p_1}^{N+1} \times S_{p_2}^{N+1} \rightarrow S_{1}^{N+1}$
. Then,
It follows with (5.10) that
 $$ \begin{align} \begin{aligned} & \Vert M_{ \widetilde{m} \vert_{\Lambda_N \times \Lambda_N \times \Lambda_N} }: S_{p_1}^{N+1} \times S_{p_2}^{N+1} \rightarrow S_{1}^{N+1} \Vert \\ \leq & \Vert T_{ m\vert_{K_N^{-1} \mathbb{Z}}}^{(N+1)}: L_{p_1}(\mathbb{T}, S_{p_1}^{N+1} ) \times L_{p_2}(\mathbb{T}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{T}, S_{p}^{N+1} ) \Vert \leq B_{p_1, p_2,N+1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \Vert M_{ \widetilde{m} \vert_{\Lambda_N \times \Lambda_N \times \Lambda_N} }: S_{p_1}^{N+1} \times S_{p_2}^{N+1} \rightarrow S_{1}^{N+1} \Vert \\ \leq & \Vert T_{ m\vert_{K_N^{-1} \mathbb{Z}}}^{(N+1)}: L_{p_1}(\mathbb{T}, S_{p_1}^{N+1} ) \times L_{p_2}(\mathbb{T}, S_{p_2}^{N+1} ) \rightarrow L_{1}(\mathbb{T}, S_{p}^{N+1} ) \Vert \leq B_{p_1, p_2,N+1}. \end{aligned} \end{align} $$
By [Reference Potapov, Skripka, Sukochev and TomskovaPSST17, Theorem 2.3], we find that
Now, for
![]() $s,t \in \mathbb {R}_{> 0}$
, we find
$s,t \in \mathbb {R}_{> 0}$
, we find
It follows therefore by the first paragraph that for some constant
![]() $C>0$
,
$C>0$
,
The combination of the latter estimate with (5.11) yields the result.
Remark 5.4 In [Reference Grafakos and TorresGrTo02] it is shown that for a natural class of Calderón–Zygmund operators, the associated convolution operator is bounded as a map
![]() $L_1 \times L_1 \rightarrow L_{\frac {1}{2}, \infty }$
as well as
$L_1 \times L_1 \rightarrow L_{\frac {1}{2}, \infty }$
as well as
![]() $L_{p_1} \times L_{p_2} \rightarrow L_p$
with
$L_{p_1} \times L_{p_2} \rightarrow L_p$
with
![]() $\frac {1}{p} = \frac {1}{p_1} + \frac {1}{p_2}$
and
$\frac {1}{p} = \frac {1}{p_1} + \frac {1}{p_2}$
and
![]() $\frac {1}{2} < p < \infty , 1<p_1,p_2<\infty $
. This applies in particular to the map
$\frac {1}{2} < p < \infty , 1<p_1,p_2<\infty $
. This applies in particular to the map
![]() $T_m$
with symbol m as in (5.6) (see [Reference Grafakos and TorresGrTo02, Proposition 6]). Our example shows that this result does not extend to the vector-valued setting in case
$T_m$
with symbol m as in (5.6) (see [Reference Grafakos and TorresGrTo02, Proposition 6]). Our example shows that this result does not extend to the vector-valued setting in case
![]() $\frac {1}{2} < p \leq 1$
. On the other hand, affirmative results in case
$\frac {1}{2} < p \leq 1$
. On the other hand, affirmative results in case
![]() $1 < p < \infty $
and
$1 < p < \infty $
and
![]() $\frac {1}{p}=\frac {1}{p_1}+\frac {1}{p_2}$
were obtained in [Reference DiPlinio, Li, Martikainen and VuorinenDLMV20]. The question remains open whether a weak
$\frac {1}{p}=\frac {1}{p_1}+\frac {1}{p_2}$
were obtained in [Reference DiPlinio, Li, Martikainen and VuorinenDLMV20]. The question remains open whether a weak
![]() $L_1$
-bound
$L_1$
-bound
![]() $L_{p_1} \times L_{p_2} \rightarrow L_{1, \infty }, \frac {1}{p_1} + \frac {1}{p_2} = 1$
holds, even in the case
$L_{p_1} \times L_{p_2} \rightarrow L_{1, \infty }, \frac {1}{p_1} + \frac {1}{p_2} = 1$
holds, even in the case
![]() $p_1 = p_2 = 2$
.
$p_1 = p_2 = 2$
.
Acknowledgment
We would like to thank Clément Coine, Francesco Di Plinio, Christian Le Merdy, Éric Ricard, Lyudmyla Turowska, and Gennady Uraltsev for useful discussions, feedback, and/or communication about the contents of this paper.