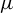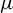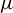1 Introduction
By a topological dynamical system (t.d.s. for short), we mean a pair
![]() $(X,T)$
, where X is a compact metric space with a metric d and T is a homeomorphism from X to itself. A point
$(X,T)$
, where X is a compact metric space with a metric d and T is a homeomorphism from X to itself. A point
![]() $x\in X$
is called a transitive point if
$x\in X$
is called a transitive point if
![]() ${\mathrm {Orb}(x,T)}=\{x,Tx,\ldots \}$
is dense in X. A t.d.s.
${\mathrm {Orb}(x,T)}=\{x,Tx,\ldots \}$
is dense in X. A t.d.s.
![]() $(X,T)$
is called minimal if all points in X are transitive points. Denote by
$(X,T)$
is called minimal if all points in X are transitive points. Denote by
![]() $\mathcal B_X$
all Borel measurable subsets of X. A Borel (probability) measure
$\mathcal B_X$
all Borel measurable subsets of X. A Borel (probability) measure
![]() $\mu $
on X is called T-invariant if
$\mu $
on X is called T-invariant if
![]() $\mu (T^{-1}A)=\mu (A)$
for any
$\mu (T^{-1}A)=\mu (A)$
for any
![]() $A\in \mathcal {B}_X$
. A T-invariant measure
$A\in \mathcal {B}_X$
. A T-invariant measure
![]() $\mu $
on X is called ergodic if
$\mu $
on X is called ergodic if
![]() $B\in \mathcal {B}_X$
with
$B\in \mathcal {B}_X$
with
![]() $T^{-1}B=B$
implies
$T^{-1}B=B$
implies
![]() $\mu (B)=0$
or
$\mu (B)=0$
or
![]() $\mu (B)=1$
. Denote by
$\mu (B)=1$
. Denote by
![]() $M(X, T)$
(respectively
$M(X, T)$
(respectively
![]() $M^e(X, T)$
) the collection of all T-invariant measures (respectively all ergodic measures) on X. For
$M^e(X, T)$
) the collection of all T-invariant measures (respectively all ergodic measures) on X. For
![]() $\mu \in M(X,T)$
, the support of
$\mu \in M(X,T)$
, the support of
![]() $\mu $
is defined by
$\mu $
is defined by
![]() $\operatorname {\mathrm {supp}}(\mu )=\{x\in X\colon \mu (U)>0\text { for any neighborhood }U\text { of }x\}$
. Each measure
$\operatorname {\mathrm {supp}}(\mu )=\{x\in X\colon \mu (U)>0\text { for any neighborhood }U\text { of }x\}$
. Each measure
![]() $\mu \in M(X,T)$
induces a measure-preserving system (m.p.s. for short)
$\mu \in M(X,T)$
induces a measure-preserving system (m.p.s. for short)
![]() $(X,\mathcal B_X,\mu , T)$
.
$(X,\mathcal B_X,\mu , T)$
.
It is well known that the entropy can be used to measure the local complexity of the structure of orbits in a given system. One may naturally ask how to characterize the entropy in a local way. The related research started from the series of pioneering papers of Blanchard et al [Reference Blanchard1–Reference Blanchard, Host, Maass, Martinez and Rudolph4], in which the notions of entropy pairs and entropy pairs for a measure were introduced. From then on, entropy pairs have been intensively studied by many researchers. Huang and Ye [Reference Huang and Ye16] extended the notions from pairs to finite tuples, and showed that if the entropy of a given system is positive, then there are entropy n-tuples for any
![]() $n\in \mathbb {N}$
in both topological and measurable settings.
$n\in \mathbb {N}$
in both topological and measurable settings.
The sequence entropy was introduced by Kušhnirenko [Reference Kušhnirenko22] to establish the relation between spectrum theory and entropy theory. As in classical local entropy theory, the sequence entropy can also be localized. In [Reference Huang, Li, Shao and Ye12, Reference Huang, Maass and Ye15], the authors investigated the sequence entropy pairs, sequence entropy tuples, and sequence entropy tuples for a measure. Using tools from combinatorics, Kerr and Li [Reference Kerr and Li18, Reference Kerr and Li19] studied (sequence) entropy tuples, (sequence) entropy tuples for a measure, and IT-tuples via independence sets. Huang and Ye [Reference Huang and Ye17] showed that a system has a sequence entropy n-tuple if and only if its maximal pattern entropy is no less than
![]() $\log n$
in both topological and measurable settings. More introductions and applications of the local entropy theory can refer to a survey [Reference Glasner and Ye10].
$\log n$
in both topological and measurable settings. More introductions and applications of the local entropy theory can refer to a survey [Reference Glasner and Ye10].
In addition to the entropy, the sensitivity is another candidate to describe the complexity of a system, which was first used by Ruelle [Reference Ruelle, Dell'Antonio, Doplicher and Jona-Lasinio30]. In [Reference Xiong31], Xiong introduced a multi-variant version of the sensitivity, called the n-sensitivity. Motivated by the local entropy theory, Ye and Zhang [Reference Ye and Zhang32] introduced the notion of sensitive tuples. Particularly, they showed that a transitive t.d.s. is n-sensitive if and only if it has a sensitive n-tuple; and a sequence entropy n-tuple of a minimal t.d.s. is a sensitive n-tuple. For the converse, Maass and Shao [Reference Maass and Shao29] showed that in a minimal t.d.s., if a sensitive n-tuple is a minimal point of the n-fold product t.d.s., then it is a sequence entropy n-tuple.
Recently, Li, Tu, and Ye [Reference Li, Tu and Ye25] studied the sensitivity in the mean form. Li, Ye, and Yu [Reference Li, Ye and Yu27, Reference Li and Yu28] further studied the multi-version of mean sensitivity and its local representation, namely, the mean n-sensitivity and the mean n-sensitive tuple. One naturally wonders if there is still a characterization of sequence entropy tuples via mean sensitive tuples. By the results of [Reference Fuhrmann, Glasner, Jäger and Oertel6, Reference García-Ramos, Jäger and Ye8, Reference Kerr and Li18, Reference Li, Ye and Yu27], one can see that a sequence entropy tuple is not always a mean sensitive tuple even in a minimal t.d.s. Nonetheless, the works of [Reference Downarowicz and Glasner5, Reference Huang11, Reference Li, Tu and Ye25] yield that every minimal mean sensitive t.d.s. (that is, has a mean sensitive pair by [Reference Li, Ye and Yu27]) is not tame (that is, exists an IT pair by [Reference Kerr and Li18]). So generally, we conjecture that for any minimal t.d.s., a mean sensitive n-tuple is an IT n-tuple and so a sequence entropy n-tuple by [Reference Kerr and Li18, Theorem 5.9]. Now we can answer this question under an additional condition. Namely, the following theorem.
Theorem 1.1. Let
![]() $(X,T)$
be a minimal t.d.s. and
$(X,T)$
be a minimal t.d.s. and
![]() $\pi : (X,T)\rightarrow (X_{eq},T_{eq})$
be the factor map to its maximal equicontinuous factor which is almost one to one. Then for
$\pi : (X,T)\rightarrow (X_{eq},T_{eq})$
be the factor map to its maximal equicontinuous factor which is almost one to one. Then for
![]() $2\le n\in \mathbb {N}$
,
$2\le n\in \mathbb {N}$
,
where
![]() $MS_n(X,T)$
denotes all the mean sensitive n-tuples and
$MS_n(X,T)$
denotes all the mean sensitive n-tuples and
![]() $IT_n(X,T)$
denotes all the IT n-tuples.
$IT_n(X,T)$
denotes all the IT n-tuples.
In the parallel measure-theoretical setting, Huang, Lu, and Ye [Reference Huang, Lu and Ye14] studied measurable sensitivity and its local representation. The notion of
![]() $\mu $
-mean sensitivity for an invariant measure
$\mu $
-mean sensitivity for an invariant measure
![]() $\mu $
on a t.d.s. was studied by García-Ramos [Reference García-Ramos7]. Li [Reference Li23] introduced the notion of the
$\mu $
on a t.d.s. was studied by García-Ramos [Reference García-Ramos7]. Li [Reference Li23] introduced the notion of the
![]() $\mu $
-mean n-sensitivity, and showed that an ergodic m.p.s. is
$\mu $
-mean n-sensitivity, and showed that an ergodic m.p.s. is
![]() $\mu $
-mean n-sensitive if and only if its maximal pattern entropy is no less than
$\mu $
-mean n-sensitive if and only if its maximal pattern entropy is no less than
![]() $\log n$
. The authors in [Reference Li, Ye and Yu27] introduced the notion of the
$\log n$
. The authors in [Reference Li, Ye and Yu27] introduced the notion of the
![]() $\mu $
-n-sensitivity in the mean, which was proved to be equivalent to the
$\mu $
-n-sensitivity in the mean, which was proved to be equivalent to the
![]() $\mu $
-mean n-sensitivity in the ergodic case.
$\mu $
-mean n-sensitivity in the ergodic case.
Using the idea of localization, the authors [Reference Li and Yu28] introduced the notion of the
![]() $\mu $
-mean sensitive tuple and showed that every
$\mu $
-mean sensitive tuple and showed that every
![]() $\mu $
-entropy tuple of an ergodic m.p.s. is a
$\mu $
-entropy tuple of an ergodic m.p.s. is a
![]() $\mu $
-mean sensitive tuple. A natural question is left open in [Reference Li and Yu28].
$\mu $
-mean sensitive tuple. A natural question is left open in [Reference Li and Yu28].
Question 1.2. Is there a characterization of
![]() $\mu $
-sequence entropy tuples via
$\mu $
-sequence entropy tuples via
![]() $\mu $
-mean sensitive tuples?
$\mu $
-mean sensitive tuples?
The authors in [Reference Li and Tu24] introduced a weaker notion named the density-sensitive tuple and showed that every
![]() $\mu $
-sequence entropy tuple of an ergodic m.p.s. is a
$\mu $
-sequence entropy tuple of an ergodic m.p.s. is a
![]() $\mu $
-density-sensitive tuple. In this paper, we give a positive answer to this question. Namely, the following theorem.
$\mu $
-density-sensitive tuple. In this paper, we give a positive answer to this question. Namely, the following theorem.
Theorem 1.3. Let
![]() $(X,T)$
be a t.d.s.,
$(X,T)$
be a t.d.s.,
![]() $\mu \in M^e(X,T)$
and
$\mu \in M^e(X,T)$
and
![]() $2\le n\in \mathbb {N}$
. Then the
$2\le n\in \mathbb {N}$
. Then the
![]() $\mu $
-sequence entropy n-tuple, the
$\mu $
-sequence entropy n-tuple, the
![]() $\mu $
-mean sensitive n-tuple and the
$\mu $
-mean sensitive n-tuple and the
![]() $\mu $
-n-sensitive in the mean tuple coincide.
$\mu $
-n-sensitive in the mean tuple coincide.
By the definitions, it is easy to see that a
![]() $\mu $
-mean sensitive n-tuple must be a
$\mu $
-mean sensitive n-tuple must be a
![]() $\mu $
-n-sensitive in the mean tuple. Thus, Theorem 1.3 is a direct corollary of the following two theorems.
$\mu $
-n-sensitive in the mean tuple. Thus, Theorem 1.3 is a direct corollary of the following two theorems.
Theorem 1.4. Let
![]() $(X,T)$
be a t.d.s.,
$(X,T)$
be a t.d.s.,
![]() $\mu \in M(X,T)$
, and
$\mu \in M(X,T)$
, and
![]() $2\le n\in \mathbb {N}$
. Then each
$2\le n\in \mathbb {N}$
. Then each
![]() $\mu $
-n-sensitive in the mean tuple is a
$\mu $
-n-sensitive in the mean tuple is a
![]() $\mu $
-sequence entropy n-tuple.
$\mu $
-sequence entropy n-tuple.
Theorem 1.5. Let
![]() $(X,T)$
be a t.d.s.,
$(X,T)$
be a t.d.s.,
![]() $\mu \in M^e(X,T)$
, and
$\mu \in M^e(X,T)$
, and
![]() $2\le n\in \mathbb {N}$
. Then each
$2\le n\in \mathbb {N}$
. Then each
![]() $\mu $
-sequence entropy n-tuple is a
$\mu $
-sequence entropy n-tuple is a
![]() $\mu $
-mean sensitive n-tuple.
$\mu $
-mean sensitive n-tuple.
In fact, Theorem 1.4 shows a bit more than Theorem 1.3, as for a T-invariant measure
![]() $\mu $
which is not ergodic, every
$\mu $
which is not ergodic, every
![]() $\mu $
-n-sensitive in the mean tuple is still a
$\mu $
-n-sensitive in the mean tuple is still a
![]() $\mu $
-sequence entropy n-tuple. However, the following result shows that ergodicity of
$\mu $
-sequence entropy n-tuple. However, the following result shows that ergodicity of
![]() $\mu $
in Theorem 1.5 is necessary.
$\mu $
in Theorem 1.5 is necessary.
Theorem 1.6. For every
![]() $2\le n\in \mathbb {N}$
, there exist a t.d.s.
$2\le n\in \mathbb {N}$
, there exist a t.d.s.
![]() $(X,T)$
and
$(X,T)$
and
![]() $\mu \in M(X,T)$
such that there is a
$\mu \in M(X,T)$
such that there is a
![]() $\mu $
-sequence entropy n-tuple but it is not a
$\mu $
-sequence entropy n-tuple but it is not a
![]() $\mu $
-n-sensitive in the mean tuple.
$\mu $
-n-sensitive in the mean tuple.
It is fair to note that García-Ramos informed us that at the same time, he with Muñoz-López also reported a completely independent proof of the equivalence of the sequence entropy pair and the mean sensitive pair in the ergodic case [Reference García-Ramos and Muñoz-López9]. Their proof relies on the deep equivalent characterization of measurable sequence entropy pairs developed by Kerr and Li [Reference Kerr and Li19] using the combinatorial notion of independence. Our results provide more information in the general case, and the proofs work on the classical definition of sequence entropy pairs introduced in [Reference Huang, Maass and Ye15]. It is worth noting that the proofs depend on a new interesting ergodic measure decomposition result (Lemma 4.3), which was applied to prove the profound Erdös’s conjectures in the number theory by Kra et al [Reference Kra, Moreira, Richter and Robertson20, Reference Kra, Moreira, Richter and Robertson21]. This decomposition may have more applications because it has the hybrid topological and Borel structures.
The outline of the paper is the following. In §2, we recall some basic notions that we will use in the paper. In §3, we prove Theorem 1.4. In §4, we show Theorems 1.5 and 1.6. In §5, we study the mean sensitive tuple and the sequence entropy in the topological sense and show Theorem 1.1.
2 Preliminaries
Throughout the paper, denote by
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() ${\mathbb {Z}}_{+}$
the collections of natural numbers
${\mathbb {Z}}_{+}$
the collections of natural numbers
![]() $\{1,2,\ldots \}$
and non-negative integers
$\{1,2,\ldots \}$
and non-negative integers
![]() $\{0,1,2,\ldots \}$
, respectively.
$\{0,1,2,\ldots \}$
, respectively.
For
![]() $F\subset \mathbb {Z}_+$
, denote by
$F\subset \mathbb {Z}_+$
, denote by
![]() $\#\{F\}$
(or simply write
$\#\{F\}$
(or simply write
![]() $\#F$
when it is clear from the context) the cardinality of F. The upper density
$\#F$
when it is clear from the context) the cardinality of F. The upper density
![]() $\overline {D}(F)$
of F is defined by
$\overline {D}(F)$
of F is defined by
Similarly, the lower density
![]() $\underline {D}(F)$
of F can be given by
$\underline {D}(F)$
of F can be given by
If
![]() $\overline {D}(F)=\underline {D}(F)$
, we say that the density of F exists and is equal to the common value, which is written as
$\overline {D}(F)=\underline {D}(F)$
, we say that the density of F exists and is equal to the common value, which is written as
![]() $D(F)$
.
$D(F)$
.
Given a t.d.s.
![]() $(X,T)$
and
$(X,T)$
and
![]() $n\in \mathbb {N}$
, denote by
$n\in \mathbb {N}$
, denote by
![]() $X^{(n)}$
the n-fold product of X. Let
$X^{(n)}$
the n-fold product of X. Let
![]() $\Delta _n(X)=\{(x,x,\ldots , x)\in X^{(n)}\colon x\in X\}$
be the diagonal of
$\Delta _n(X)=\{(x,x,\ldots , x)\in X^{(n)}\colon x\in X\}$
be the diagonal of
![]() $ X^{(n)}$
and
$ X^{(n)}$
and
![]() $\Delta _n^\prime (X)=\{(x_1,x_2,\ldots ,x_n)\in X^{(n)}: x_i=x_j \text { for some } 1\le i\neq j\le n \}$
.
$\Delta _n^\prime (X)=\{(x_1,x_2,\ldots ,x_n)\in X^{(n)}: x_i=x_j \text { for some } 1\le i\neq j\le n \}$
.
If a closed subset
![]() $Y\subset X$
is T-invariant in the sense of
$Y\subset X$
is T-invariant in the sense of
![]() $TY= Y$
, then the restriction
$TY= Y$
, then the restriction
![]() $(Y, T|_Y)$
(or simply write
$(Y, T|_Y)$
(or simply write
![]() $(Y,T)$
when it is clear from the context) is also a t.d.s., which is called a subsystem of
$(Y,T)$
when it is clear from the context) is also a t.d.s., which is called a subsystem of
![]() $(X,T)$
.
$(X,T)$
.
Let
![]() $(X,T)$
be a t.d.s.,
$(X,T)$
be a t.d.s.,
![]() $x\in X$
, and
$x\in X$
, and
![]() $U,V\subset X$
. Denote by
$U,V\subset X$
. Denote by
A t.d.s.
![]() $(X,T)$
is called transitive if
$(X,T)$
is called transitive if
![]() $N(U,V)\neq \emptyset $
for all non-empty open subsets
$N(U,V)\neq \emptyset $
for all non-empty open subsets
![]() $U,V$
of X. It is well known that the set of all transitive points in a transitive t.d.s. forms a dense
$U,V$
of X. It is well known that the set of all transitive points in a transitive t.d.s. forms a dense
![]() $G_\delta $
subset of X .
$G_\delta $
subset of X .
Given two t.d.s.
![]() $(X, T)$
and
$(X, T)$
and
![]() $(Y,S)$
, a map
$(Y,S)$
, a map
![]() $\pi \colon X\to Y$
is called a factor map if
$\pi \colon X\to Y$
is called a factor map if
![]() $\pi $
is surjective and continuous such that
$\pi $
is surjective and continuous such that
![]() $\pi \circ T=S\circ \pi $
, and in which case
$\pi \circ T=S\circ \pi $
, and in which case
![]() $(Y,S)$
is referred to be a factor of
$(Y,S)$
is referred to be a factor of
![]() $(X, T)$
. Furthermore, if
$(X, T)$
. Furthermore, if
![]() $\pi $
is a homeomorphism, we say that
$\pi $
is a homeomorphism, we say that
![]() $(X,T)$
is conjugate to
$(X,T)$
is conjugate to
![]() $(Y,S)$
.
$(Y,S)$
.
A t.d.s.
![]() $(X,T)$
is called equicontinuous (respectively mean equicontinuous) if for any
$(X,T)$
is called equicontinuous (respectively mean equicontinuous) if for any
![]() $\epsilon>0$
, there is
$\epsilon>0$
, there is
![]() $\delta>0$
such that if
$\delta>0$
such that if
![]() $x,y\in X$
with
$x,y\in X$
with
![]() $d(x,y)<\delta $
, then
$d(x,y)<\delta $
, then
![]() $\max _{k\in \mathbb {Z}_+}d(T^kx,T^ky)<\epsilon $
(respectively
$\max _{k\in \mathbb {Z}_+}d(T^kx,T^ky)<\epsilon $
(respectively
![]() $\limsup _{n\to \infty }({1}/{n})\sum _{k=0}^{n-1}d(T^kx,T^ky)<\epsilon $
). Every t.d.s.
$\limsup _{n\to \infty }({1}/{n})\sum _{k=0}^{n-1}d(T^kx,T^ky)<\epsilon $
). Every t.d.s.
![]() $(X, T)$
is known to have a maximal equicontinuous factor (or a maximal mean equicontinuous factor [Reference Li, Tu and Ye25]). More studies on mean equicontinuous systems can be seen in the recent survey [Reference Li, Ye and Yu26].
$(X, T)$
is known to have a maximal equicontinuous factor (or a maximal mean equicontinuous factor [Reference Li, Tu and Ye25]). More studies on mean equicontinuous systems can be seen in the recent survey [Reference Li, Ye and Yu26].
In the remainder of this section, we fix a t.d.s.
![]() $(X,T)$
with a measure
$(X,T)$
with a measure
![]() $\mu \in M(X,T)$
. The entropy of a finite measurable partition
$\mu \in M(X,T)$
. The entropy of a finite measurable partition
![]() $\alpha =\{A_1, A_2, \ldots , A_k\}$
of X is defined by
$\alpha =\{A_1, A_2, \ldots , A_k\}$
of X is defined by
![]() $ H_\mu (\alpha )=-\sum _{i=1}^k \mu (A_i) \log \mu (A_i), $
where
$ H_\mu (\alpha )=-\sum _{i=1}^k \mu (A_i) \log \mu (A_i), $
where
![]() $0 \log 0$
is defined to be 0. Moreover, we define the sequence entropy of T with respect to
$0 \log 0$
is defined to be 0. Moreover, we define the sequence entropy of T with respect to
![]() $\alpha $
along an increasing sequence
$\alpha $
along an increasing sequence
![]() $S=\{s_i\}_{i=1}^{\infty }$
of
$S=\{s_i\}_{i=1}^{\infty }$
of
![]() $\mathbb {Z}_+$
by
$\mathbb {Z}_+$
by
 $$ \begin{align*} h_\mu^{S}(T, \alpha)=\limsup _{n\rightarrow \infty} \frac{1}{n} H_\mu\bigg(\bigvee_{i=1}^n T^{-s_i} \alpha\bigg). \end{align*} $$
$$ \begin{align*} h_\mu^{S}(T, \alpha)=\limsup _{n\rightarrow \infty} \frac{1}{n} H_\mu\bigg(\bigvee_{i=1}^n T^{-s_i} \alpha\bigg). \end{align*} $$
The sequence entropy of T along the sequence S is
where the supremum takes over all finite measurable partitions. Correspondingly, the topological sequence entropy of T with respect to S and a finite open cover
![]() $\mathcal {U}$
is
$\mathcal {U}$
is
 $$ \begin{align*} h^{S}(T, \mathcal{U})=\limsup _{n \rightarrow\infty} \frac{1}{n} \log N\bigg(\bigvee_{i=1}^n T^{-s_i} \mathcal{U}\bigg), \end{align*} $$
$$ \begin{align*} h^{S}(T, \mathcal{U})=\limsup _{n \rightarrow\infty} \frac{1}{n} \log N\bigg(\bigvee_{i=1}^n T^{-s_i} \mathcal{U}\bigg), \end{align*} $$
where
![]() $N(\bigvee _{i=1}^n T^{-s_i} \mathcal {U})$
is the minimum among the cardinalities of all sub-families of
$N(\bigvee _{i=1}^n T^{-s_i} \mathcal {U})$
is the minimum among the cardinalities of all sub-families of
![]() $\bigvee _{i=1}^n T^{-s_i} \mathcal {U}$
covering X. The topological sequence entropy of T with respect to S is defined by
$\bigvee _{i=1}^n T^{-s_i} \mathcal {U}$
covering X. The topological sequence entropy of T with respect to S is defined by
where the supremum takes over all finite open covers.
Let
![]() $(x_i)_{i=1}^n\in X^{(n)}$
. A finite cover
$(x_i)_{i=1}^n\in X^{(n)}$
. A finite cover
![]() $\mathcal {U}=\{U_1,U_2,\ldots ,U_k\}$
of X is said to be an admissible cover with respect to
$\mathcal {U}=\{U_1,U_2,\ldots ,U_k\}$
of X is said to be an admissible cover with respect to
![]() $(x_i)_{i=1}^n$
if for each
$(x_i)_{i=1}^n$
if for each
![]() $1\leq j\leq k$
, there exists
$1\leq j\leq k$
, there exists
![]() $1\leq i_j\leq n$
such that
$1\leq i_j\leq n$
such that
![]() $x_{i_j}\notin \overline {U_j}$
. Analogously, we define admissible partitions with respect to
$x_{i_j}\notin \overline {U_j}$
. Analogously, we define admissible partitions with respect to
![]() $(x_i)_{i=1}^n$
.
$(x_i)_{i=1}^n$
.
Definition 2.1. [Reference Huang, Maass and Ye15, Reference Maass and Shao29]
An n-tuple
![]() $(x_i)_{i=1}^n\in X^{(n)}\setminus \Delta _n(X)$
,
$(x_i)_{i=1}^n\in X^{(n)}\setminus \Delta _n(X)$
,
![]() $n\geq 2$
is called the following.
$n\geq 2$
is called the following.
-
• A sequence entropy n-tuple for
 $\mu $
if for any admissible finite Borel measurable partition
$\mu $
if for any admissible finite Borel measurable partition
 $\alpha $
with respect to
$\alpha $
with respect to
 $(x_i)_{i=1}^n$
, there exists a sequence
$(x_i)_{i=1}^n$
, there exists a sequence
 $S=\{m_i\}_{i=1}^{\infty }$
of
$S=\{m_i\}_{i=1}^{\infty }$
of
 $\mathbb {Z}_+$
such that
$\mathbb {Z}_+$
such that
 $h^{S}_{\mu }(T,\alpha )>0$
. Denote by
$h^{S}_{\mu }(T,\alpha )>0$
. Denote by
 $SE_n^{\mu }(X,T)$
the set of all sequence entropy n-tuples for
$SE_n^{\mu }(X,T)$
the set of all sequence entropy n-tuples for
 $\mu $
.
$\mu $
. -
• A sequence entropy n-tuple if for any admissible finite open cover
 $\mathcal {U}$
with respect to
$\mathcal {U}$
with respect to
 $(x_i)_{i=1}^n$
, there exists a sequence
$(x_i)_{i=1}^n$
, there exists a sequence
 $S=\{m_i\}_{i=1}^{\infty }$
of
$S=\{m_i\}_{i=1}^{\infty }$
of
 $\mathbb {Z}_+$
such that
$\mathbb {Z}_+$
such that
 $h^{S}(T,\mathcal {U})>0$
. Denote by
$h^{S}(T,\mathcal {U})>0$
. Denote by
 $SE_n(X,T)$
the set of all sequence entropy n-tuples.
$SE_n(X,T)$
the set of all sequence entropy n-tuples.
We say that
![]() $f\in L^2(X,\mathcal B_X,\mu )$
is almost periodic if
$f\in L^2(X,\mathcal B_X,\mu )$
is almost periodic if
![]() $\{f\circ T^n : n\in \mathbb {Z}_+\}$
is precompact in
$\{f\circ T^n : n\in \mathbb {Z}_+\}$
is precompact in
![]() $L^2(X,\mathcal B_X,\mu )$
. The set of all almost periodic functions is denoted by
$L^2(X,\mathcal B_X,\mu )$
. The set of all almost periodic functions is denoted by
![]() $H_c$
, and there exists a T-invariant
$H_c$
, and there exists a T-invariant
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {K}_\mu \subset \mathcal B_X$
such that
$\mathcal {K}_\mu \subset \mathcal B_X$
such that
![]() $H_c= L^2(X,\mathcal {K}_\mu ,\mu )$
, where
$H_c= L^2(X,\mathcal {K}_\mu ,\mu )$
, where
![]() $\mathcal {K}_\mu $
is called the Kronecker algebra of
$\mathcal {K}_\mu $
is called the Kronecker algebra of
![]() $(X, \mathcal B_X,\mu , T )$
. The product
$(X, \mathcal B_X,\mu , T )$
. The product
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $X^{(n)}$
is denoted by
$X^{(n)}$
is denoted by
![]() $\mathcal {B}_X^{(n)}$
. Define the measure
$\mathcal {B}_X^{(n)}$
. Define the measure
![]() $\unicode{x3bb} _n(\mu )$
on
$\unicode{x3bb} _n(\mu )$
on
![]() $\mathcal {B}_X^{(n)}$
by letting
$\mathcal {B}_X^{(n)}$
by letting
 $$ \begin{align*}\unicode{x3bb}_n(\mu)\bigg(\prod_{i=1}^nA_i\bigg)=\int_{X}\prod_{i=1}^n\mathbb{E}(1_{A_i}|\mathcal{K}_\mu)\,d\mu.\end{align*} $$
$$ \begin{align*}\unicode{x3bb}_n(\mu)\bigg(\prod_{i=1}^nA_i\bigg)=\int_{X}\prod_{i=1}^n\mathbb{E}(1_{A_i}|\mathcal{K}_\mu)\,d\mu.\end{align*} $$
Note that
![]() $SE_n^{\mu }(X,T)=\operatorname {\mathrm {supp}}(\unicode{x3bb} _n(\mu ))\setminus \Delta _n(X)$
[Reference Huang, Maass and Ye15, Theorem 3.4].
$SE_n^{\mu }(X,T)=\operatorname {\mathrm {supp}}(\unicode{x3bb} _n(\mu ))\setminus \Delta _n(X)$
[Reference Huang, Maass and Ye15, Theorem 3.4].
3 Proof of Theorem 1.4
Definition 3.1. [Reference Li and Yu28]
For
![]() $2\le n\in \mathbb {N}$
and a t.d.s.
$2\le n\in \mathbb {N}$
and a t.d.s.
![]() $(X,T)$
with
$(X,T)$
with
![]() $\mu \in M(X,T)$
, we say that the n-tuple
$\mu \in M(X,T)$
, we say that the n-tuple
![]() $(x_1,x_2,\dotsc ,x_n)\in X^{(n)}\setminus \Delta _n(X)$
is
$(x_1,x_2,\dotsc ,x_n)\in X^{(n)}\setminus \Delta _n(X)$
is
-
(1) a
 $\mu $
-mean n-sensitive tuple if for any open neighborhoods
$\mu $
-mean n-sensitive tuple if for any open neighborhoods
 $U_i$
of
$U_i$
of
 $x_i$
with
$x_i$
with
 $i=1,2,\dotsc ,n$
, there is
$i=1,2,\dotsc ,n$
, there is
 $\delta> 0$
such that for any
$\delta> 0$
such that for any
 $A\in \mathcal B_X$
with
$A\in \mathcal B_X$
with
 $\mu (A)>0$
, there are
$\mu (A)>0$
, there are
 $y_1,y_2,\dotsc ,y_n\in A$
and a subset F of
$y_1,y_2,\dotsc ,y_n\in A$
and a subset F of
 $\mathbb {Z}_+$
with
$\mathbb {Z}_+$
with
 $\overline {D}(F)>\delta $
such that
$\overline {D}(F)>\delta $
such that
 $T^k y_i \in U_i$
for all
$T^k y_i \in U_i$
for all
 $i=1,2,\ldots ,n$
and
$i=1,2,\ldots ,n$
and
 $k\in F$
;
$k\in F$
; -
(2) a
 $\mu $
-n-sensitive in the mean tuple if for any
$\mu $
-n-sensitive in the mean tuple if for any
 $\tau>0$
, there is
$\tau>0$
, there is
 $\delta =\delta (\tau )> 0$
such that for any
$\delta =\delta (\tau )> 0$
such that for any
 $A\in \mathcal B_X$
with
$A\in \mathcal B_X$
with
 $\mu (A)>0$
, there is
$\mu (A)>0$
, there is
 $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
 $y_1^m,y_2^m,\dotsc ,y_n^m\in A$
such that
$y_1^m,y_2^m,\dotsc ,y_n^m\in A$
such that  $$ \begin{align*} \frac{\#\{0\le k\le m-1: T^ky_i^m\in B(x_i,\tau), i=1,2,\ldots,n\}}{m}>\delta. \end{align*} $$
$$ \begin{align*} \frac{\#\{0\le k\le m-1: T^ky_i^m\in B(x_i,\tau), i=1,2,\ldots,n\}}{m}>\delta. \end{align*} $$
We denote the set of all
![]() $\mu $
-mean n-sensitive tuples (respectively
$\mu $
-mean n-sensitive tuples (respectively
![]() $\mu $
-n-sensitive in the mean tuples) by
$\mu $
-n-sensitive in the mean tuples) by
![]() $MS_n^\mu (X,T)$
(respectively
$MS_n^\mu (X,T)$
(respectively
![]() $SM_n^\mu (X,T)$
). We call an n-tuple
$SM_n^\mu (X,T)$
). We call an n-tuple
![]() $(x_1,x_2,\dotsc ,x_n)\in X^{(n)}$
essential if
$(x_1,x_2,\dotsc ,x_n)\in X^{(n)}$
essential if
![]() $x_i\neq x_j$
for each
$x_i\neq x_j$
for each
![]() $1\le i<j\le n$
and at this time, we write the collection of all essential n-tuples in
$1\le i<j\le n$
and at this time, we write the collection of all essential n-tuples in
![]() $MS_n^\mu (X,T)$
(respectively
$MS_n^\mu (X,T)$
(respectively
![]() $SM_n^\mu (X,T)$
) as
$SM_n^\mu (X,T)$
) as
![]() $MS_n^{\mu ,e}(X,T)$
(respectively
$MS_n^{\mu ,e}(X,T)$
(respectively
![]() $SM_n^{\mu ,e}(X,T)$
).
$SM_n^{\mu ,e}(X,T)$
).
Proof of Theorem 1.4
It suffices to prove
![]() $SM_n^{\mu ,e}(X,T)\subset SE_n^{\mu ,e}(X,T)$
. Let
$SM_n^{\mu ,e}(X,T)\subset SE_n^{\mu ,e}(X,T)$
. Let
![]() $(x_1,\ldots ,x_n) \in SM_n^{\mu ,e}(X,T)$
. Take
$(x_1,\ldots ,x_n) \in SM_n^{\mu ,e}(X,T)$
. Take
![]() $\alpha =\{A_1,\ldots ,A_l\}$
as an admissible partition of
$\alpha =\{A_1,\ldots ,A_l\}$
as an admissible partition of
![]() $(x_1,\ldots ,x_n)$
. Then for each
$(x_1,\ldots ,x_n)$
. Then for each
![]() $1\le k\le l$
, there is
$1\le k\le l$
, there is
![]() $i_k\in \{1,\ldots ,n\}$
such that
$i_k\in \{1,\ldots ,n\}$
such that
![]() $x_{i_k}\notin \overline {A_k}$
. Put
$x_{i_k}\notin \overline {A_k}$
. Put
![]() $E_i=\{1\le k\le l: x_i\not \in \overline {A_k}\}$
for
$E_i=\{1\le k\le l: x_i\not \in \overline {A_k}\}$
for
![]() $1\le i\le n$
. Obviously,
$1\le i\le n$
. Obviously,
![]() $\bigcup _{i=1}^n E_i=\{1,\ldots ,l\}$
. Set
$\bigcup _{i=1}^n E_i=\{1,\ldots ,l\}$
. Set
 $$ \begin{align*}B_1=\bigcup_{k\in E_1}A_k, B_2=\bigcup_{k\in E_2\setminus E_1}A_k, \ldots, B_n=\bigcup_{k\in E_n\setminus(\bigcup_{j=1}^{n-1}E_j)}A_k. \end{align*} $$
$$ \begin{align*}B_1=\bigcup_{k\in E_1}A_k, B_2=\bigcup_{k\in E_2\setminus E_1}A_k, \ldots, B_n=\bigcup_{k\in E_n\setminus(\bigcup_{j=1}^{n-1}E_j)}A_k. \end{align*} $$
Then,
![]() $\beta =\{B_1,\ldots ,B_n\}$
is also an admissible partition of
$\beta =\{B_1,\ldots ,B_n\}$
is also an admissible partition of
![]() $(x_1,\ldots ,x_n)$
such that
$(x_1,\ldots ,x_n)$
such that
![]() $x_i\notin \overline {B_i}$
for all
$x_i\notin \overline {B_i}$
for all
![]() $1\le i\le n$
. Without loss of generality, we assume
$1\le i\le n$
. Without loss of generality, we assume
![]() $B_i\neq \emptyset $
for
$B_i\neq \emptyset $
for
![]() $1\le i\le n$
. It suffices to show that there exists a sequence
$1\le i\le n$
. It suffices to show that there exists a sequence
![]() $S=\{m_i\}_{i=1}^{\infty }$
of
$S=\{m_i\}_{i=1}^{\infty }$
of
![]() $\mathbb {Z}_+$
such that
$\mathbb {Z}_+$
such that
![]() $h^{S}_{\mu }(T,\beta )>0,$
as
$h^{S}_{\mu }(T,\beta )>0,$
as
![]() $\alpha \succ \beta $
. Let
$\alpha \succ \beta $
. Let
By [Reference Huang, Maass and Ye15, Lemma 2.2 and Theorem 2.3], we have
![]() $h^*_\mu (T,\beta )=H_\mu (\beta |\mathcal {K}_\mu )$
, where
$h^*_\mu (T,\beta )=H_\mu (\beta |\mathcal {K}_\mu )$
, where
![]() $\mathcal {K}_\mu $
is the Kronecker algebra of
$\mathcal {K}_\mu $
is the Kronecker algebra of
![]() $(X,\mathcal B_X,\mu ,T)$
. So it suffices to show
$(X,\mathcal B_X,\mu ,T)$
. So it suffices to show
![]() $\beta \nsubseteq \mathcal {K}_\mu $
.
$\beta \nsubseteq \mathcal {K}_\mu $
.
We prove it by contradiction. Now we assume that
![]() $\beta \subseteq \mathcal {K}_\mu $
. Then for each
$\beta \subseteq \mathcal {K}_\mu $
. Then for each
![]() $i=1,\ldots ,n$
,
$i=1,\ldots ,n$
,
![]() $1_{B_i}$
is an almost periodic function. By [Reference Yu33, Theorems 4.7 and 5.2],
$1_{B_i}$
is an almost periodic function. By [Reference Yu33, Theorems 4.7 and 5.2],
![]() $1_{B_i}$
is a
$1_{B_i}$
is a
![]() $\mu $
-equicontinuous in the mean function. That is, for each
$\mu $
-equicontinuous in the mean function. That is, for each
![]() $1\le i\le n$
and any
$1\le i\le n$
and any
![]() $\tau>0$
, there is a compact
$\tau>0$
, there is a compact
![]() $K\subset X$
with
$K\subset X$
with
![]() $\mu (K)>1-\tau $
such that for any
$\mu (K)>1-\tau $
such that for any
![]() $\epsilon '>0$
, there is
$\epsilon '>0$
, there is
![]() $\delta '>0$
such that for all
$\delta '>0$
such that for all
![]() $m\in \mathbb {N}$
, whenever
$m\in \mathbb {N}$
, whenever
![]() $x,y\in K$
with
$x,y\in K$
with
![]() $d(x,y)<\delta '$
,
$d(x,y)<\delta '$
,
 $$ \begin{align} \frac{1}{m}\sum_{t=0}^{m-1}|1_{B_i}(T^tx)- 1_{B_i}(T^ty)|<\epsilon'. \end{align} $$
$$ \begin{align} \frac{1}{m}\sum_{t=0}^{m-1}|1_{B_i}(T^tx)- 1_{B_i}(T^ty)|<\epsilon'. \end{align} $$
However, take
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
![]() $B_\epsilon (x_i)\cap B_i=\emptyset $
for
$B_\epsilon (x_i)\cap B_i=\emptyset $
for
![]() $i=1,\ldots ,n$
. Since
$i=1,\ldots ,n$
. Since
![]() $(x_1,\ldots ,x_n)\in SM_n^{\mu ,e}(X,T)$
, there is
$(x_1,\ldots ,x_n)\in SM_n^{\mu ,e}(X,T)$
, there is
![]() $\delta :=\delta (\epsilon )>0$
such that for any
$\delta :=\delta (\epsilon )>0$
such that for any
![]() $A\in \mathcal B_X$
with
$A\in \mathcal B_X$
with
![]() $\mu (A)>0$
, there are
$\mu (A)>0$
, there are
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $y_1^m,\ldots ,y_n^m\in A$
such that if we denote
$y_1^m,\ldots ,y_n^m\in A$
such that if we denote
![]() $C_m=\{0\le t\le m-1:T^ty_i^m\in B_\epsilon (x_i)\text { for all }i=1,2,\ldots ,n\}$
, then
$C_m=\{0\le t\le m-1:T^ty_i^m\in B_\epsilon (x_i)\text { for all }i=1,2,\ldots ,n\}$
, then
![]() $\#C_m \ge m\delta $
. Since
$\#C_m \ge m\delta $
. Since
![]() $ B_\epsilon (x_1)\cap B_1=\emptyset $
, then
$ B_\epsilon (x_1)\cap B_1=\emptyset $
, then
![]() $ B_\epsilon (x_1)\subset \bigcup _{i=2}^nB_i$
. This implies that there is
$ B_\epsilon (x_1)\subset \bigcup _{i=2}^nB_i$
. This implies that there is
![]() $i_0\in \{2,\ldots ,n\}$
such that
$i_0\in \{2,\ldots ,n\}$
such that
For any
![]() $t\in C_m$
, we have
$t\in C_m$
, we have
![]() $T^ty_{i_0}^m\in B_\epsilon (x_{i_0})$
, and then
$T^ty_{i_0}^m\in B_\epsilon (x_{i_0})$
, and then
![]() $T^ty_{i_0}^m\notin B_{i_0}$
, as
$T^ty_{i_0}^m\notin B_{i_0}$
, as
![]() $B_\epsilon (x_{i_0})\cap B_{i_0}=\emptyset $
. This implies that
$B_\epsilon (x_{i_0})\cap B_{i_0}=\emptyset $
. This implies that
 $$ \begin{align} \frac{1}{m}\sum_{t=0}^{m-1}|1_{B_{i_0}}(T^ty_1^m)-1_{B_{i_0}}(T^ty_{i_0}^m)|\ge\frac{\#C_m}{m(n-1)}\ge \frac{\delta}{n-1}. \end{align} $$
$$ \begin{align} \frac{1}{m}\sum_{t=0}^{m-1}|1_{B_{i_0}}(T^ty_1^m)-1_{B_{i_0}}(T^ty_{i_0}^m)|\ge\frac{\#C_m}{m(n-1)}\ge \frac{\delta}{n-1}. \end{align} $$
Choose a measurable subset
![]() $A\subset K$
such that
$A\subset K$
such that
![]() $\mu (A)>0$
and
$\mu (A)>0$
and
![]() $\operatorname {\mathrm {diam}}(A)=\sup \{d(x,y):x,y\in A\}<\delta '$
, and
$\operatorname {\mathrm {diam}}(A)=\sup \{d(x,y):x,y\in A\}<\delta '$
, and
![]() $\epsilon '={\delta }/{2(n-1)}$
. Then by equation (3.1), for any
$\epsilon '={\delta }/{2(n-1)}$
. Then by equation (3.1), for any
![]() $m\in \mathbb {N}$
and
$m\in \mathbb {N}$
and
![]() $x,y\in A$
,
$x,y\in A$
,
 $$ \begin{align*} \frac{1}{m}\sum_{t=0}^{m-1}|1_{B_{i_0}}(T^tx)- 1_{B_{i_0}}(T^ty)|<\frac{\delta}{2(n-1)}, \end{align*} $$
$$ \begin{align*} \frac{1}{m}\sum_{t=0}^{m-1}|1_{B_{i_0}}(T^tx)- 1_{B_{i_0}}(T^ty)|<\frac{\delta}{2(n-1)}, \end{align*} $$
which is a contradiction with equation (3.2). Thus,
![]() $SM_n^{\mu ,e}(X,T)\subset SE_n^{\mu ,e}(X,T)$
.
$SM_n^{\mu ,e}(X,T)\subset SE_n^{\mu ,e}(X,T)$
.
4 Proof of Theorem 1.5
In §4.1, we first reduce Theorem 1.5 to just prove that it is true for the ergodic m.p.s. with a continuous factor map to its Kronecker factor, and then we finish the proof of Theorem 1.5 under this assumption. In §4.2, we show the condition that
![]() $\mu $
is ergodic is necessary.
$\mu $
is ergodic is necessary.
4.1 Ergodic case
Throughout this section, we will use the following two types of factor maps between two m.p.s.
![]() $(X, \mathcal B_X,\mu , T)$
and
$(X, \mathcal B_X,\mu , T)$
and
![]() $(Z, \mathcal B_Z,\nu , S)$
.
$(Z, \mathcal B_Z,\nu , S)$
.
-
(1) Measurable factor maps: a measurable map
 $\pi : X \rightarrow Z$
such that
$\pi : X \rightarrow Z$
such that
 $\mu \circ \pi ^{-1}=\nu $
and
$\mu \circ \pi ^{-1}=\nu $
and
 $\pi \circ T=S \circ \pi $
$\pi \circ T=S \circ \pi $
 $\mu $
-almost everywhere;
$\mu $
-almost everywhere; -
(2) Continuous factor maps: a topological factor map
 $\pi {\kern-1pt}:{\kern-1pt} X {\kern-1pt}\rightarrow{\kern-1pt} Z$
such that
$\pi {\kern-1pt}:{\kern-1pt} X {\kern-1pt}\rightarrow{\kern-1pt} Z$
such that
 $\mu \circ \pi ^{-1}=\nu $
.
$\mu \circ \pi ^{-1}=\nu $
.
If a continuous factor map
![]() $\pi $
such that
$\pi $
such that
![]() $\pi ^{-1}(\mathcal B_Z)=\mathcal {K}_\mu $
,
$\pi ^{-1}(\mathcal B_Z)=\mathcal {K}_\mu $
,
![]() $\pi $
is called a continuous factor map to its Kronecker factor.
$\pi $
is called a continuous factor map to its Kronecker factor.
The following result is a weaker version in [Reference Kra, Moreira, Richter and Robertson20, Proposition 3.20].
Lemma 4.1. Let
![]() $(X, \mathcal {B}_X,\mu , T)$
be an ergodic m.p.s. Then there exists an ergodic m.p.s.
$(X, \mathcal {B}_X,\mu , T)$
be an ergodic m.p.s. Then there exists an ergodic m.p.s.
![]() $(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
and a continuous factor map
$(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
and a continuous factor map
![]() $\tilde {\pi }: \tilde {X} \rightarrow X$
such that
$\tilde {\pi }: \tilde {X} \rightarrow X$
such that
![]() $(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
has a continuous factor map to its Kronecker factor.
$(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
has a continuous factor map to its Kronecker factor.
The following result shows that we only need to prove
![]() $SE_n^{\mu }(X,T)\subset MS_n^{\mu }(X,T)$
for all ergodic m.p.s. with a continuous factor map to its Kronecker factor.
$SE_n^{\mu }(X,T)\subset MS_n^{\mu }(X,T)$
for all ergodic m.p.s. with a continuous factor map to its Kronecker factor.
Lemma 4.2. If
![]() $SE_n^{\tilde {\mu }}(\tilde {X},\tilde T)\subset MS_n^{\tilde {\mu }}(\tilde {X},\tilde T)$
for all ergodic m.p.s.
$SE_n^{\tilde {\mu }}(\tilde {X},\tilde T)\subset MS_n^{\tilde {\mu }}(\tilde {X},\tilde T)$
for all ergodic m.p.s.
![]() $(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
with a continuous factor map to its Kronecker factor, then
$(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
with a continuous factor map to its Kronecker factor, then
![]() $SE_n^{\mu }(X,T)\subset MS_n^{\mu }(X,T)$
for all ergodic m.p.s.
$SE_n^{\mu }(X,T)\subset MS_n^{\mu }(X,T)$
for all ergodic m.p.s.
![]() $(X, \mathcal {B}_X,\mu , T)$
.
$(X, \mathcal {B}_X,\mu , T)$
.
Proof. By Lemma 4.1, there exists an ergodic m.p.s.
![]() $(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
and a continuous factor map
$(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
and a continuous factor map
![]() $\tilde {\pi }: \tilde {X} \rightarrow X$
such that
$\tilde {\pi }: \tilde {X} \rightarrow X$
such that
![]() $(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
has a continuous factor map to its Kronecker factor. Thus,
$(\tilde {X},\tilde {B}, \tilde {\mu }, \tilde {T})$
has a continuous factor map to its Kronecker factor. Thus,
![]() $SE_n^{\tilde \mu }(\tilde {X},\tilde T)\subset MS_n^{\tilde \mu }(\tilde {X},\tilde T)$
, by the assumption.
$SE_n^{\tilde \mu }(\tilde {X},\tilde T)\subset MS_n^{\tilde \mu }(\tilde {X},\tilde T)$
, by the assumption.
For any
![]() $(x_1,\dotsc ,x_n)\in SE_n^{\mu }(X,T)\setminus \Delta _n'(X)$
, by [Reference Huang, Maass and Ye15, Theorem 3.7], there exists an n-tuple
$(x_1,\dotsc ,x_n)\in SE_n^{\mu }(X,T)\setminus \Delta _n'(X)$
, by [Reference Huang, Maass and Ye15, Theorem 3.7], there exists an n-tuple
![]() $(\tilde {x_1},\ldots ,\tilde {x_n})\in SE_n^{\tilde \mu }(\tilde {X},\tilde T)\setminus \Delta _n'(\tilde {X})$
such that
$(\tilde {x_1},\ldots ,\tilde {x_n})\in SE_n^{\tilde \mu }(\tilde {X},\tilde T)\setminus \Delta _n'(\tilde {X})$
such that
![]() $\tilde \pi (\tilde {x_i})=x_i$
. For any open neighborhood
$\tilde \pi (\tilde {x_i})=x_i$
. For any open neighborhood
![]() $U_1\times \cdots \times U_n$
of
$U_1\times \cdots \times U_n$
of
![]() $(x_1,\dotsc ,x_n)$
with
$(x_1,\dotsc ,x_n)$
with
![]() $U_i\cap U_j=\emptyset $
for
$U_i\cap U_j=\emptyset $
for
![]() $i\neq j$
, then
$i\neq j$
, then
![]() $\tilde \pi ^{-1}(U_1)\times \cdots \times \tilde \pi ^{-1}(U_n)$
is an open neighborhood of
$\tilde \pi ^{-1}(U_1)\times \cdots \times \tilde \pi ^{-1}(U_n)$
is an open neighborhood of
![]() $(\tilde {x_1},\ldots ,\tilde {x_n})$
. Since
$(\tilde {x_1},\ldots ,\tilde {x_n})$
. Since
![]() $(\tilde {x_1},\ldots ,\tilde {x_n})\in SE_n^{\tilde \mu }(\tilde {X},\tilde T)\setminus \Delta _n'(\tilde {X})\subset MS_n^{\tilde \mu }(\tilde {X},\tilde T)\setminus \Delta _n'(\tilde {X})$
, there exists
$(\tilde {x_1},\ldots ,\tilde {x_n})\in SE_n^{\tilde \mu }(\tilde {X},\tilde T)\setminus \Delta _n'(\tilde {X})\subset MS_n^{\tilde \mu }(\tilde {X},\tilde T)\setminus \Delta _n'(\tilde {X})$
, there exists
![]() $\delta>0$
such that for any
$\delta>0$
such that for any
![]() $A\in \mathcal {B}_X$
with
$A\in \mathcal {B}_X$
with
![]() $\tilde {\mu }(\tilde \pi ^{-1}(A))=\mu (A)>0$
, there exist
$\tilde {\mu }(\tilde \pi ^{-1}(A))=\mu (A)>0$
, there exist
![]() $F\subset \mathbb {N}$
with
$F\subset \mathbb {N}$
with
![]() $\overline {D}(F)\ge \delta $
and
$\overline {D}(F)\ge \delta $
and
![]() $\tilde {y_1},\ldots ,\tilde {y_n}\in \tilde \pi ^{-1}(A)$
such that for any
$\tilde {y_1},\ldots ,\tilde {y_n}\in \tilde \pi ^{-1}(A)$
such that for any
![]() $m\in F$
,
$m\in F$
,
and hence
![]() $(T^m\tilde \pi (\tilde {y_1}),\ldots ,T^m\tilde \pi (\tilde {y_n}))\in U_1\times \cdots \times U_n$
. Note that
$(T^m\tilde \pi (\tilde {y_1}),\ldots ,T^m\tilde \pi (\tilde {y_n}))\in U_1\times \cdots \times U_n$
. Note that
![]() $\tilde \pi (\tilde {y_i})\in A$
for each
$\tilde \pi (\tilde {y_i})\in A$
for each
![]() $i=1,2,\ldots ,n$
. Thus we have
$i=1,2,\ldots ,n$
. Thus we have
![]() $(x_1,\dotsc ,x_n)\in MS_n^{\mu }(X,T)$
.
$(x_1,\dotsc ,x_n)\in MS_n^{\mu }(X,T)$
.
According to the above-mentioned lemma, in the rest of this section, we fix an ergodic m.p.s. with a continuous factor map
![]() $\pi :(X,\mathcal {B}_X, \mu , T)\rightarrow (Z,\mathcal {B}_Z, \nu , R)$
to its Kronecker factor. Moreover, we fix a measure disintegration
$\pi :(X,\mathcal {B}_X, \mu , T)\rightarrow (Z,\mathcal {B}_Z, \nu , R)$
to its Kronecker factor. Moreover, we fix a measure disintegration
![]() $z \to \eta _{z}$
of
$z \to \eta _{z}$
of
![]() $\mu $
over
$\mu $
over
![]() $\pi $
, that is,
$\pi $
, that is,
![]() $\mu = \int _Z \eta _{z} \,d\nu (z)$
.
$\mu = \int _Z \eta _{z} \,d\nu (z)$
.
The following lemma plays a crucial role in our proof. In [Reference Kra, Moreira, Richter and Robertson20, Proposition 3.11], the authors proved it for
![]() $n=2$
, but general cases are similar in idea. For readability, we move the complicated proof to Appendix A.
$n=2$
, but general cases are similar in idea. For readability, we move the complicated proof to Appendix A.
Lemma 4.3. Let
![]() $\pi :(X,\mathcal {B}_X, \mu , T)\rightarrow (Z,\mathcal {B}_Z, \nu , R)$
be a continuous factor map to its Kronecker factor. Then for each
$\pi :(X,\mathcal {B}_X, \mu , T)\rightarrow (Z,\mathcal {B}_Z, \nu , R)$
be a continuous factor map to its Kronecker factor. Then for each
![]() $n\in \mathbb {N}$
, there exists a continuous map
$n\in \mathbb {N}$
, there exists a continuous map
![]() $\textbf {x}\mapsto \unicode{x3bb} _{\textbf {x}}^n$
from
$\textbf {x}\mapsto \unicode{x3bb} _{\textbf {x}}^n$
from
![]() $X^{(n)}$
to
$X^{(n)}$
to
![]() $M(X^{(n)})$
such that the map
$M(X^{(n)})$
such that the map
![]() $\textbf {x} \mapsto \unicode{x3bb} _{\textbf {x}}^n$
is an ergodic decomposition of
$\textbf {x} \mapsto \unicode{x3bb} _{\textbf {x}}^n$
is an ergodic decomposition of
![]() $\mu ^{(n)}$
, where
$\mu ^{(n)}$
, where
![]() $\mu ^{(n)}$
is the n-fold product of
$\mu ^{(n)}$
is the n-fold product of
![]() $\mu $
and
$\mu $
and
The following two lemmas can be viewed as generalizations of Lemma 3.3 and Theorem 3.4 in [Reference Huang, Maass and Ye15], respectively.
Lemma 4.4. Let
![]() $\pi :(X,\mathcal {B}_X, \mu , T)\rightarrow (Z,\mathcal {B}_Z, \nu , R)$
be a continuous factor map to its Kronecker factor. Assume that
$\pi :(X,\mathcal {B}_X, \mu , T)\rightarrow (Z,\mathcal {B}_Z, \nu , R)$
be a continuous factor map to its Kronecker factor. Assume that
![]() $\mathcal {U}=\{U_1, U_2, \ldots , U_n\}$
is a measurable cover of X. Then for any measurable partition
$\mathcal {U}=\{U_1, U_2, \ldots , U_n\}$
is a measurable cover of X. Then for any measurable partition
![]() $\alpha $
finer than
$\alpha $
finer than
![]() $\mathcal {U}$
as a cover, there exists an increasing sequence
$\mathcal {U}$
as a cover, there exists an increasing sequence
![]() $S\subset \mathbb {Z}_+$
with
$S\subset \mathbb {Z}_+$
with
![]() $h_{\mu }^{S}(T,\alpha )>0$
if and only if
$h_{\mu }^{S}(T,\alpha )>0$
if and only if
![]() $\unicode{x3bb} _{\textbf {x}}^n (U_1^c\times \cdots \times U_n^c)>0$
for all
$\unicode{x3bb} _{\textbf {x}}^n (U_1^c\times \cdots \times U_n^c)>0$
for all
![]() $\textbf {x}=(x_1,\dotsc , x_n)\in X^{(n)}$
.
$\textbf {x}=(x_1,\dotsc , x_n)\in X^{(n)}$
.
Proof.
![]() $(\Rightarrow )$
In contrast, we may assume that
$(\Rightarrow )$
In contrast, we may assume that
![]() $\unicode{x3bb} _{\textbf {x}}^n(U_1^c\times \cdots \times U_n^c)=0$
for some
$\unicode{x3bb} _{\textbf {x}}^n(U_1^c\times \cdots \times U_n^c)=0$
for some
![]() $\textbf {x}=(x_1,\dotsc , x_n)\in X^{(n)}$
. Let
$\textbf {x}=(x_1,\dotsc , x_n)\in X^{(n)}$
. Let
![]() $C_i=\{z\in Z: \eta _{z+\pi (x_i)}(U_i^c)>0\}$
for
$C_i=\{z\in Z: \eta _{z+\pi (x_i)}(U_i^c)>0\}$
for
![]() $i=1,\dotsc ,n$
. Then
$i=1,\dotsc ,n$
. Then
Put
![]() $D_i=\pi ^{-1}(C_i)\cup (U_i^c\setminus \pi ^{-1}(C_i))$
. Then
$D_i=\pi ^{-1}(C_i)\cup (U_i^c\setminus \pi ^{-1}(C_i))$
. Then
![]() $D_i\in \pi ^{-1}(\mathcal {B}_Z)= \mathcal {K}_\mu $
and
$D_i\in \pi ^{-1}(\mathcal {B}_Z)= \mathcal {K}_\mu $
and
![]() $D_i^c\subset U_i$
, where
$D_i^c\subset U_i$
, where
![]() $\mathcal {K}_\mu $
is the Kronecker factor of X.
$\mathcal {K}_\mu $
is the Kronecker factor of X.
For any
![]() $\textbf {s}=(s(1),\dotsc ,s(n))\in \{0,1\}^n$
, let
$\textbf {s}=(s(1),\dotsc ,s(n))\in \{0,1\}^n$
, let
![]() $D_{\textbf {s}}=\bigcap _{i=1}^nD_i(s(i))$
, where
$D_{\textbf {s}}=\bigcap _{i=1}^nD_i(s(i))$
, where
![]() $D_i(0)=D_i$
and
$D_i(0)=D_i$
and
![]() $D_i(1)=D_i^c$
. Set
$D_i(1)=D_i^c$
. Set
![]() $E_1=(\bigcap _{i=1}^nD_i)\cap U_1 $
and
$E_1=(\bigcap _{i=1}^nD_i)\cap U_1 $
and
![]() $E_j=(\bigcap _{i=1}^nD_i)\cap ( U_j\setminus \bigcup _{i=1}^{j-1}U_i)$
for
$E_j=(\bigcap _{i=1}^nD_i)\cap ( U_j\setminus \bigcup _{i=1}^{j-1}U_i)$
for
![]() $j=2,\dotsc ,n$
.
$j=2,\dotsc ,n$
.
Consider the measurable partition
For any
![]() $\textbf {s}\in \{0,1\}^n\setminus \{(0,\dotsc ,0)\}$
, we have
$\textbf {s}\in \{0,1\}^n\setminus \{(0,\dotsc ,0)\}$
, we have
![]() $s(i)=1$
for some
$s(i)=1$
for some
![]() $i=1,\dotsc ,n$
, then
$i=1,\dotsc ,n$
, then
![]() $D_{\textbf {s}}\subset D_i^c\subset U_i$
. It is straightforward that for all
$D_{\textbf {s}}\subset D_i^c\subset U_i$
. It is straightforward that for all
![]() $1\leq j\leq n$
,
$1\leq j\leq n$
,
![]() $E_j\subset U_j$
. Thus,
$E_j\subset U_j$
. Thus,
![]() $\alpha $
is finer than
$\alpha $
is finer than
![]() $\mathcal {U}$
and by hypothesis, there exists an increasing sequence S of
$\mathcal {U}$
and by hypothesis, there exists an increasing sequence S of
![]() $\mathbb {Z}_+$
with
$\mathbb {Z}_+$
with
![]() $h_{\mu }^{S}(T,\alpha )>0$
.
$h_{\mu }^{S}(T,\alpha )>0$
.
However, since
![]() $\unicode{x3bb} _{\textbf {x}}^n(U_1^c\times \cdots \times U_n^c)=0$
, we deduce
$\unicode{x3bb} _{\textbf {x}}^n(U_1^c\times \cdots \times U_n^c)=0$
, we deduce
![]() $\nu (\bigcap _{i=1}^nC_i)=0$
and hence
$\nu (\bigcap _{i=1}^nC_i)=0$
and hence
![]() $\mu (\bigcap _{i=1}^nD_i)=0$
. Thus, we have
$\mu (\bigcap _{i=1}^nD_i)=0$
. Thus, we have
![]() $E_1,\dotsc , E_n\in \mathcal {K}_\mu $
. It is also clear that
$E_1,\dotsc , E_n\in \mathcal {K}_\mu $
. It is also clear that
![]() $D_{\textbf {s}}\in \mathcal {K}_\mu $
for all
$D_{\textbf {s}}\in \mathcal {K}_\mu $
for all
![]() $\textbf {s}\in \{0,1\}^n\setminus \{(0,\dotsc ,0)\}$
, as
$\textbf {s}\in \{0,1\}^n\setminus \{(0,\dotsc ,0)\}$
, as
![]() $D_1,\dotsc ,D_n\in \mathcal {K}_\mu .$
Therefore, each element of
$D_1,\dotsc ,D_n\in \mathcal {K}_\mu .$
Therefore, each element of
![]() $\alpha $
is
$\alpha $
is
![]() $\mathcal {K}_\mu $
-measurable, by [Reference Huang, Maass and Ye15, Lemma 2.2],
$\mathcal {K}_\mu $
-measurable, by [Reference Huang, Maass and Ye15, Lemma 2.2],
which is a contradiction.
![]() $(\Leftarrow )$
Assume
$(\Leftarrow )$
Assume
![]() $\unicode{x3bb} _{\textbf {x}}^n(U_1^c\times \cdots \times U_n^c)>0$
for any
$\unicode{x3bb} _{\textbf {x}}^n(U_1^c\times \cdots \times U_n^c)>0$
for any
![]() $\textbf {x}\in X^{(n)}$
. In particular, we take
$\textbf {x}\in X^{(n)}$
. In particular, we take
![]() $\textbf {x}=(x,\ldots ,x)$
such that
$\textbf {x}=(x,\ldots ,x)$
such that
![]() $\pi (x)$
is the identity element of group Z. Without loss of generality, we may assume that any finite measurable partition
$\pi (x)$
is the identity element of group Z. Without loss of generality, we may assume that any finite measurable partition
![]() $\alpha $
which is finer than
$\alpha $
which is finer than
![]() $\mathcal {U}$
as a cover is of the type
$\mathcal {U}$
as a cover is of the type
![]() $\alpha =\{A_1, A_2, \ldots , A_n\}$
with
$\alpha =\{A_1, A_2, \ldots , A_n\}$
with
![]() $A_i \subset U_i$
, for
$A_i \subset U_i$
, for
![]() $1 \leqslant i \leqslant n$
. Let
$1 \leqslant i \leqslant n$
. Let
![]() $\alpha $
be one of such partitions. We observe that
$\alpha $
be one of such partitions. We observe that
Therefore,
![]() $A_j \notin \mathcal {K}_\mu $
for some
$A_j \notin \mathcal {K}_\mu $
for some
![]() $1 \leqslant j \leqslant n$
. It follows from [Reference Huang, Maass and Ye15, Theorem 2.3] that there exists a sequence
$1 \leqslant j \leqslant n$
. It follows from [Reference Huang, Maass and Ye15, Theorem 2.3] that there exists a sequence
![]() $S \subset \mathbb {Z}_+$
such that
$S \subset \mathbb {Z}_+$
such that
![]() $h_\mu ^{S}(T, \alpha )=H_\mu (\alpha \mid \mathcal {K}_\mu )>0$
. This finishes the proof.
$h_\mu ^{S}(T, \alpha )=H_\mu (\alpha \mid \mathcal {K}_\mu )>0$
. This finishes the proof.
Lemma 4.5. For any
![]() $\textbf {x}=(x_1,\dotsc ,x_n)\in X^{(n)}$
,
$\textbf {x}=(x_1,\dotsc ,x_n)\in X^{(n)}$
,
Proof. On the one hand, let
![]() $\textbf {y}=(y_1,\dotsc ,y_n)\in SE_n^{\mu }(X,T)$
. We show that
$\textbf {y}=(y_1,\dotsc ,y_n)\in SE_n^{\mu }(X,T)$
. We show that
![]() $\textbf {y}\in \operatorname {supp}\unicode{x3bb} _{\textbf {x}}^n\setminus \Delta _n(X)$
. It suffices to prove that for any measurable neighborhood
$\textbf {y}\in \operatorname {supp}\unicode{x3bb} _{\textbf {x}}^n\setminus \Delta _n(X)$
. It suffices to prove that for any measurable neighborhood
![]() $U_1\times \cdots \times U_n$
of
$U_1\times \cdots \times U_n$
of
![]() $\textbf {y}$
,
$\textbf {y}$
,
Without loss of generality, we assume that
![]() $U_i\cap U_j=\emptyset $
if
$U_i\cap U_j=\emptyset $
if
![]() $y_i\not = y_j$
. Then
$y_i\not = y_j$
. Then
![]() $\mathcal {U}=\{U_1^c, U_2^c, \ldots , U_n^c\}$
is a finite cover of X. It is clear that any finite measurable partition
$\mathcal {U}=\{U_1^c, U_2^c, \ldots , U_n^c\}$
is a finite cover of X. It is clear that any finite measurable partition
![]() $\alpha $
finer than
$\alpha $
finer than
![]() $\mathcal {U}$
as a cover is an admissible partition with respect to
$\mathcal {U}$
as a cover is an admissible partition with respect to
![]() $\textbf {y}$
. Therefore, there exists an increasing sequence
$\textbf {y}$
. Therefore, there exists an increasing sequence
![]() $S\subset \mathbb {Z}_+$
with
$S\subset \mathbb {Z}_+$
with
![]() $h_{\mu }^{S}(T,\alpha )>0$
. By Lemma 4.4, we obtain that
$h_{\mu }^{S}(T,\alpha )>0$
. By Lemma 4.4, we obtain that
which implies that
![]() $\textbf {y}\in \operatorname {supp}\unicode{x3bb} _{\textbf {x}}^n$
. Since
$\textbf {y}\in \operatorname {supp}\unicode{x3bb} _{\textbf {x}}^n$
. Since
![]() $\textbf {y}\notin \Delta _n(X)$
,
$\textbf {y}\notin \Delta _n(X)$
,
![]() $\textbf {y}\in \operatorname {supp}\unicode{x3bb} _{\textbf {x}}^n\setminus \Delta _n(X)$
.
$\textbf {y}\in \operatorname {supp}\unicode{x3bb} _{\textbf {x}}^n\setminus \Delta _n(X)$
.
On the other hand, let
![]() $\textbf {y}=(y_1,\ldots ,y_n) \in \operatorname {supp}\unicode{x3bb} _{\textbf {x}}^n\setminus \Delta _n(X)$
. We show that for any admissible partition
$\textbf {y}=(y_1,\ldots ,y_n) \in \operatorname {supp}\unicode{x3bb} _{\textbf {x}}^n\setminus \Delta _n(X)$
. We show that for any admissible partition
![]() $\alpha =\{A_1, A_2, \ldots , A_k\}$
with respect to
$\alpha =\{A_1, A_2, \ldots , A_k\}$
with respect to
![]() $\textbf {y}$
, there exists an increasing sequence
$\textbf {y}$
, there exists an increasing sequence
![]() $S \subset \mathbb {Z}_+$
such that
$S \subset \mathbb {Z}_+$
such that
![]() $h_\mu ^{S}(T, \alpha )>0$
. Since
$h_\mu ^{S}(T, \alpha )>0$
. Since
![]() $\alpha $
is an admissible partition with respect to
$\alpha $
is an admissible partition with respect to
![]() $\textbf {y}$
, there exist closed neighborhoods
$\textbf {y}$
, there exist closed neighborhoods
![]() $U_i$
of
$U_i$
of
![]() $y_i, 1 \leqslant i \leqslant n$
, such that for each
$y_i, 1 \leqslant i \leqslant n$
, such that for each
![]() $j \in \{1,2, \ldots , k\}$
, we find
$j \in \{1,2, \ldots , k\}$
, we find
![]() $i_j \in \{1,2, \ldots , n\}$
with
$i_j \in \{1,2, \ldots , n\}$
with
![]() $A_j \subset U_{i_j}^c$
. That is,
$A_j \subset U_{i_j}^c$
. That is,
![]() $\alpha $
is finer than
$\alpha $
is finer than
![]() $\mathcal {U}=\{U_1^c, U_2^c, \ldots , U_n^c\}$
as a cover. Since
$\mathcal {U}=\{U_1^c, U_2^c, \ldots , U_n^c\}$
as a cover. Since
by Lemma 4.4, there exists an increasing sequence
![]() $S \subset \mathbb {Z}_+$
such that
$S \subset \mathbb {Z}_+$
such that
![]() $h_\mu ^{S}(T, \alpha )>0$
.
$h_\mu ^{S}(T, \alpha )>0$
.
Now we are ready to give the proof of Theorem 1.5.
Proof of Theorem 1.5
We only need to prove that
![]() $SE_n^{\mu ,e}(X,T)\subset MS_n^{\mu ,e}(X,T)$
. We let
$SE_n^{\mu ,e}(X,T)\subset MS_n^{\mu ,e}(X,T)$
. We let
![]() $\pi :(X,\mathcal {B}_X, \mu , T)\rightarrow (Z,\mathcal {B}_Z, \nu , R)$
be a continuous factor map to its Kronecker factor. For any
$\pi :(X,\mathcal {B}_X, \mu , T)\rightarrow (Z,\mathcal {B}_Z, \nu , R)$
be a continuous factor map to its Kronecker factor. For any
![]() $\textbf {y}=(y_1,\ldots ,y_n)\in SE_n^{\mu ,e}(X,T)$
, let
$\textbf {y}=(y_1,\ldots ,y_n)\in SE_n^{\mu ,e}(X,T)$
, let
![]() $U_1\times U_2\times \cdots \times U_n$
be an open neighborhood of
$U_1\times U_2\times \cdots \times U_n$
be an open neighborhood of
![]() $\textbf {y}$
such that
$\textbf {y}$
such that
![]() $U_i\cap U_j=\emptyset $
for
$U_i\cap U_j=\emptyset $
for
![]() $1\le i\not =j \le n$
. By Lemma 4.5, one has
$1\le i\not =j \le n$
. By Lemma 4.5, one has
![]() $\unicode{x3bb} _{\textbf {x}}^n(U_1\times U_2\times \cdots \times U_n)> 0$
for any
$\unicode{x3bb} _{\textbf {x}}^n(U_1\times U_2\times \cdots \times U_n)> 0$
for any
![]() $\textbf {x}=(x_1,\dotsc ,x_n)\in X^{(n)}$
. Since the map
$\textbf {x}=(x_1,\dotsc ,x_n)\in X^{(n)}$
. Since the map
![]() $\textbf {x} \mapsto \unicode{x3bb} _{\textbf {x}}^n$
is continuous, X is compact, and
$\textbf {x} \mapsto \unicode{x3bb} _{\textbf {x}}^n$
is continuous, X is compact, and
![]() $U_1, U_2, \dotsc , U_n$
are open sets, it follows that there exists
$U_1, U_2, \dotsc , U_n$
are open sets, it follows that there exists
![]() $\delta>0$
such that for any
$\delta>0$
such that for any
![]() $\textbf {x}\in X^{(n)}$
,
$\textbf {x}\in X^{(n)}$
,
![]() $\unicode{x3bb} _{\textbf {x}}^n(U_1\times U_2\times \cdots \times U_n)\ge \delta $
. As the map
$\unicode{x3bb} _{\textbf {x}}^n(U_1\times U_2\times \cdots \times U_n)\ge \delta $
. As the map
![]() $\textbf {x} \mapsto \unicode{x3bb} _{\textbf {x}}^n$
is an ergodic decomposition of
$\textbf {x} \mapsto \unicode{x3bb} _{\textbf {x}}^n$
is an ergodic decomposition of
![]() $\mu ^{(n)}$
, there exists
$\mu ^{(n)}$
, there exists
![]() $B\subset X^{(n)}$
with
$B\subset X^{(n)}$
with
![]() $\mu ^{(n)}(B)=1$
such that
$\mu ^{(n)}(B)=1$
such that
![]() $\unicode{x3bb} _{\textbf {x}}^n$
is ergodic on
$\unicode{x3bb} _{\textbf {x}}^n$
is ergodic on
![]() $X^{(n)}$
for any
$X^{(n)}$
for any
![]() $\textbf {x}\in B$
.
$\textbf {x}\in B$
.
For any
![]() $A\in \mathcal {B}_X$
with
$A\in \mathcal {B}_X$
with
![]() $\mu (A)>0$
, there exists a subset C of
$\mu (A)>0$
, there exists a subset C of
![]() $X^{(n)}$
with
$X^{(n)}$
with
![]() $\mu ^{(n)}(C)>0$
such that for any
$\mu ^{(n)}(C)>0$
such that for any
![]() $\textbf {x}\in C$
,
$\textbf {x}\in C$
,
Take
![]() $\textbf {x}\in B\cap C$
, by the Birkhoff pointwise ergodic theorem, for
$\textbf {x}\in B\cap C$
, by the Birkhoff pointwise ergodic theorem, for
![]() $\unicode{x3bb} _{\textbf {x}}^n$
-almost every (a.e.)
$\unicode{x3bb} _{\textbf {x}}^n$
-almost every (a.e.)
![]() $(x_1',\dotsc ,x_n')\in X^{(n)}$
,
$(x_1',\dotsc ,x_n')\in X^{(n)}$
,
 $$ \begin{align*}\lim_{N\to \infty}\frac{1}{N}\sum_{m=0}^{N-1}1_{U_1\times U_2\times\cdots\times U_n}(T^mx_1',\dotsc,T^mx_n')=\unicode{x3bb}_{\textbf{x}}^n(U_1\times U_2\times\cdots\times U_n)\ge \delta.\end{align*} $$
$$ \begin{align*}\lim_{N\to \infty}\frac{1}{N}\sum_{m=0}^{N-1}1_{U_1\times U_2\times\cdots\times U_n}(T^mx_1',\dotsc,T^mx_n')=\unicode{x3bb}_{\textbf{x}}^n(U_1\times U_2\times\cdots\times U_n)\ge \delta.\end{align*} $$
Since
![]() $\unicode{x3bb} _{\textbf {x}}^n(A^n)>0$
, there exists
$\unicode{x3bb} _{\textbf {x}}^n(A^n)>0$
, there exists
![]() $(x_1",\dotsc ,x_n")\in A^n$
such that
$(x_1",\dotsc ,x_n")\in A^n$
such that
 $$ \begin{align*} \begin{split} &\lim_{N\to \infty}\frac{1}{N}\#\{m\in[0,N-1]:(T^mx_1",\dotsc,T^mx_n")\in U_1\times U_2\times\cdots\times U_n\}\\& \quad =\lim_{N\to \infty}\frac{1}{N}\sum_{m=0}^{N-1}1_{U_1\times U_2\times\cdots\times U_n}(T^mx_1",\dotsc,T^mx_n")\\& \quad =\unicode{x3bb}_{\textbf{x}}^n(U_1\times U_2\times\cdots\times U_n)\ge \delta. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} &\lim_{N\to \infty}\frac{1}{N}\#\{m\in[0,N-1]:(T^mx_1",\dotsc,T^mx_n")\in U_1\times U_2\times\cdots\times U_n\}\\& \quad =\lim_{N\to \infty}\frac{1}{N}\sum_{m=0}^{N-1}1_{U_1\times U_2\times\cdots\times U_n}(T^mx_1",\dotsc,T^mx_n")\\& \quad =\unicode{x3bb}_{\textbf{x}}^n(U_1\times U_2\times\cdots\times U_n)\ge \delta. \end{split} \end{align*} $$
Let
![]() $F=\{m\in \mathbb {Z}_+:(T^mx_1",\dotsc ,T^mx_n")\in U_1\times U_2\times \cdots \times U_n\}$
. Then
$F=\{m\in \mathbb {Z}_+:(T^mx_1",\dotsc ,T^mx_n")\in U_1\times U_2\times \cdots \times U_n\}$
. Then
![]() $D(F)\ge \delta $
and hence
$D(F)\ge \delta $
and hence
![]() $\textbf {y}\in MS_n^{\mu ,e}(X,T).$
This finishes the proof.
$\textbf {y}\in MS_n^{\mu ,e}(X,T).$
This finishes the proof.
4.2 Non-ergodic case
Lemma 4.6.
Let
![]() $(X,T)$
be a t.d.s. For any
$(X,T)$
be a t.d.s. For any
![]() $\mu \in M(X,T)$
with the form
$\mu \in M(X,T)$
with the form
![]() $\mu =\sum _{i=1}^{m}\unicode{x3bb} _i\nu _i$
, where
$\mu =\sum _{i=1}^{m}\unicode{x3bb} _i\nu _i$
, where
![]() $\nu _i\in M^e(X,T)$
,
$\nu _i\in M^e(X,T)$
,
![]() $\sum _{i=1}^m\unicode{x3bb} _i=1$
, and
$\sum _{i=1}^m\unicode{x3bb} _i=1$
, and
![]() $\unicode{x3bb} _i>0$
, one has
$\unicode{x3bb} _i>0$
, one has
 $$ \begin{align} \bigcup_{i=1}^mSE_n^{\nu_i}(X,T)\subset SE_n^{\mu}(X,T) \end{align} $$
$$ \begin{align} \bigcup_{i=1}^mSE_n^{\nu_i}(X,T)\subset SE_n^{\mu}(X,T) \end{align} $$
and
 $$ \begin{align} \bigcap_{i=1}^mSM_n^{\nu_i}(X,T)= SM_n^{\mu}(X,T). \end{align} $$
$$ \begin{align} \bigcap_{i=1}^mSM_n^{\nu_i}(X,T)= SM_n^{\mu}(X,T). \end{align} $$
Proof. We first prove equation (4.1). For any
![]() $\textbf {x}=(x_1,\dotsc ,x_n)\in \bigcup _{i=1}^mSE_n^{\nu _i}(X,T)$
, there exists
$\textbf {x}=(x_1,\dotsc ,x_n)\in \bigcup _{i=1}^mSE_n^{\nu _i}(X,T)$
, there exists
![]() $i\in \{1,2,\ldots ,m\}$
such that
$i\in \{1,2,\ldots ,m\}$
such that
![]() $\textbf {x}\in SE_n^{\nu _i}(X,T)$
and then for any admissible partition
$\textbf {x}\in SE_n^{\nu _i}(X,T)$
and then for any admissible partition
![]() $\alpha $
with respect to
$\alpha $
with respect to
![]() $\textbf {x}$
, there exists
$\textbf {x}$
, there exists
![]() $S=\{s_j\}_{j=1}^\infty $
such that
$S=\{s_j\}_{j=1}^\infty $
such that
![]() $h_{\nu _i}^S(T,\alpha )>0.$
By the definition of the sequence entropy,
$h_{\nu _i}^S(T,\alpha )>0.$
By the definition of the sequence entropy,
 $$ \begin{align*}h_{\mu}^S(T,\alpha)=\limsup_{N\to \infty}\sum_{i=1}^m\unicode{x3bb}_i\frac{1}{N}H_{\nu_i}(\bigvee_{j=0}^{N-1}T^{-s_j}\alpha)\ge \unicode{x3bb}_ih_{\nu_i}^S(T,\alpha)>0.\end{align*} $$
$$ \begin{align*}h_{\mu}^S(T,\alpha)=\limsup_{N\to \infty}\sum_{i=1}^m\unicode{x3bb}_i\frac{1}{N}H_{\nu_i}(\bigvee_{j=0}^{N-1}T^{-s_j}\alpha)\ge \unicode{x3bb}_ih_{\nu_i}^S(T,\alpha)>0.\end{align*} $$
So
![]() $\textbf {x}\in SE_n^{\mu }(X,T)$
, which finishes the proof of equation (4.1).
$\textbf {x}\in SE_n^{\mu }(X,T)$
, which finishes the proof of equation (4.1).
Next, we show equation (4.2). For this, we only need to note that for any
![]() $A\in \mathcal {B}_X$
,
$A\in \mathcal {B}_X$
,
![]() $\mu (A)>0$
if and only if
$\mu (A)>0$
if and only if
![]() $\nu _j(A)>0$
for some
$\nu _j(A)>0$
for some
![]() $j\in \{1,2,\ldots m\}.$
$j\in \{1,2,\ldots m\}.$
Proof of Theorem 1.6
We first claim that there is a t.d.s.
![]() $(X,T)$
with
$(X,T)$
with
![]() $\mu _1,\mu _2\in M^e(X,T)$
such that
$\mu _1,\mu _2\in M^e(X,T)$
such that
![]() $SE_n^{\mu _1}(X,T)\neq SE_n^{\mu _2}(X,T)$
. For example, we recall that the full shift on two symbols with the measure is defined by the probability vector
$SE_n^{\mu _1}(X,T)\neq SE_n^{\mu _2}(X,T)$
. For example, we recall that the full shift on two symbols with the measure is defined by the probability vector
![]() $(1/2,1/2)$
. It has completely positive entropy and the measure has the full support. Thus, every non-diagonal n-tuple is a sequence entropy n-tuple for this measure. In particular, we consider two such full shifts
$(1/2,1/2)$
. It has completely positive entropy and the measure has the full support. Thus, every non-diagonal n-tuple is a sequence entropy n-tuple for this measure. In particular, we consider two such full shifts
![]() $(X_1,T_1,\mu _1)=(\{0,1\}^{\mathbb {Z}},\sigma _1,\mu _1)$
and
$(X_1,T_1,\mu _1)=(\{0,1\}^{\mathbb {Z}},\sigma _1,\mu _1)$
and
![]() $(X_2,T_2,\mu _2)=(\{2,3\}^{\mathbb {Z}},\sigma _2,\mu _2)$
, and define a new system
$(X_2,T_2,\mu _2)=(\{2,3\}^{\mathbb {Z}},\sigma _2,\mu _2)$
, and define a new system
![]() $(X,T)$
as
$(X,T)$
as
![]() $X=X_1\bigsqcup X_2$
,
$X=X_1\bigsqcup X_2$
,
![]() $T|_{X_i}=T_i, i=1,2$
. Then,
$T|_{X_i}=T_i, i=1,2$
. Then,
![]() $\mu _1,\mu _2\in M^e(X,T)$
and
$\mu _1,\mu _2\in M^e(X,T)$
and
![]() $SE_n^{\mu _1}(X,T)=X_1^{(n)}\setminus \Delta _n(X_1)\neq X_2^{(n)}\setminus \Delta _n(X_2)=SE_n^{\mu _2}(X,T).$
$SE_n^{\mu _1}(X,T)=X_1^{(n)}\setminus \Delta _n(X_1)\neq X_2^{(n)}\setminus \Delta _n(X_2)=SE_n^{\mu _2}(X,T).$
Let
![]() $\mu =\tfrac 12\mu _1+\tfrac 12\mu _2\in M(X,T)$
. By Lemma 4.6, if
$\mu =\tfrac 12\mu _1+\tfrac 12\mu _2\in M(X,T)$
. By Lemma 4.6, if
![]() $SE_n^\mu (X,T)=SM_n^\mu (X,T)$
, then we have
$SE_n^\mu (X,T)=SM_n^\mu (X,T)$
, then we have
 $$ \begin{align*}\bigcup_{i=1}^2SE_n^{\mu_i}(X,T)\subset SE_n^{\mu}(X,T)=SM_n^\mu(X,T)=\bigcap_{i=1}^2SM_n^{\mu_i}(X,T).\end{align*} $$
$$ \begin{align*}\bigcup_{i=1}^2SE_n^{\mu_i}(X,T)\subset SE_n^{\mu}(X,T)=SM_n^\mu(X,T)=\bigcap_{i=1}^2SM_n^{\mu_i}(X,T).\end{align*} $$
However, applying Theorem 1.3 to each
![]() $\mu _i\in M^e(X,T)$
, one has
$\mu _i\in M^e(X,T)$
, one has
So
![]() $SE_n^{\mu _1}(X,T)= SE_n^{\mu _2}(X,T)$
, which is a contradiction with our assumption.
$SE_n^{\mu _1}(X,T)= SE_n^{\mu _2}(X,T)$
, which is a contradiction with our assumption.
5 Topological sequence entropy and mean sensitive tuples
This section is devoted to providing some partial evidence for the conjecture that in a minimal system, every mean sensitive tuple is a topological sequence entropy tuple.
It is known that the topological sequence entropy tuple has lift property [Reference Maass and Shao29]. We can show that under the minimality condition, the mean sensitive tuple also has lift property. Let us begin with some notions. For
![]() $2\le n\in \mathbb {N}$
, we say that
$2\le n\in \mathbb {N}$
, we say that
![]() $(x_1,x_2,\dotsc ,x_n)\in X^{(n)}\setminus \Delta _n(X)$
(respectively
$(x_1,x_2,\dotsc ,x_n)\in X^{(n)}\setminus \Delta _n(X)$
(respectively
![]() $(x_1,x_2,\dotsc ,x_n)\in X^{(n)}\setminus \Delta ^{\prime }_n(X)$
) is a mean n-sensitive tuple (respectively an essential mean n-sensitive tuple) if for any
$(x_1,x_2,\dotsc ,x_n)\in X^{(n)}\setminus \Delta ^{\prime }_n(X)$
) is a mean n-sensitive tuple (respectively an essential mean n-sensitive tuple) if for any
![]() $\tau>0$
, there is
$\tau>0$
, there is
![]() $\delta =\delta (\tau )> 0$
such that for any non-empty open set
$\delta =\delta (\tau )> 0$
such that for any non-empty open set
![]() $U\subset X$
, there exist
$U\subset X$
, there exist
![]() $y_1,y_2,\dotsc ,y_n\in U$
such that if we denote
$y_1,y_2,\dotsc ,y_n\in U$
such that if we denote
![]() $F=\{k\in \mathbb {Z}_+\colon T^ky_i\in B(x_i,\tau ),i=1,2,\ldots ,n\}$
, then
$F=\{k\in \mathbb {Z}_+\colon T^ky_i\in B(x_i,\tau ),i=1,2,\ldots ,n\}$
, then
![]() $\overline {D}(F)>\delta $
. Denote the set of all mean n-sensitive tuples (respectively essential mean n-sensitive tuples) by
$\overline {D}(F)>\delta $
. Denote the set of all mean n-sensitive tuples (respectively essential mean n-sensitive tuples) by
![]() $MS_n(X,T)$
(respectively
$MS_n(X,T)$
(respectively
![]() $MS^e_n(X,T)$
).
$MS^e_n(X,T)$
).
Theorem 5.1. Let
![]() $\pi : (X,T)\rightarrow (Y,S)$
be a factor map between two t.d.s. Then,
$\pi : (X,T)\rightarrow (Y,S)$
be a factor map between two t.d.s. Then,
-
(1)
 $\pi ^{(n)} ( MS_n(X,T))\subset MS_n(Y,S)\cup \Delta _n(Y)$
for every
$\pi ^{(n)} ( MS_n(X,T))\subset MS_n(Y,S)\cup \Delta _n(Y)$
for every
 $n\geq 2$
;
$n\geq 2$
; -
(2)
 $\pi ^{(n)}(MS_n(X, T) \cup \Delta _n(X))= MS_n(Y,S)\cup \Delta _n(Y)$
for every
$\pi ^{(n)}(MS_n(X, T) \cup \Delta _n(X))= MS_n(Y,S)\cup \Delta _n(Y)$
for every
 $n\geq 2$
, provided that
$n\geq 2$
, provided that
 $(X,T)$
is minimal.
$(X,T)$
is minimal.
Proof. Item (1) is easy to be proved by the definition. We only prove item (2).
Supposing that
![]() $(y_1,y_2,\ldots ,y_n)\in MS_n(Y,S)$
, we will show that there exists
$(y_1,y_2,\ldots ,y_n)\in MS_n(Y,S)$
, we will show that there exists
![]() $(z_1,z_2,\ldots ,z_n)\in MS_n(X,T)$
such that
$(z_1,z_2,\ldots ,z_n)\in MS_n(X,T)$
such that
![]() $\pi (z_i)=y_i$
for each
$\pi (z_i)=y_i$
for each
![]() $i=1,2,\ldots,n$
. Fix
$i=1,2,\ldots,n$
. Fix
![]() $x\in X$
and let
$x\in X$
and let
![]() $U_m=B(x,{1}/{m})$
. Since
$U_m=B(x,{1}/{m})$
. Since
![]() $(X,T)$
is minimal,
$(X,T)$
is minimal,
![]() $\operatorname {int}(\pi (U_m))\not = \emptyset $
, where
$\operatorname {int}(\pi (U_m))\not = \emptyset $
, where
![]() $\operatorname {int}(\pi (U_m))$
is the interior of
$\operatorname {int}(\pi (U_m))$
is the interior of
![]() $\pi (U_m)$
. Since
$\pi (U_m)$
. Since
![]() $(y_1,y_2,\ldots ,y_n)\in MS_n(Y,S)$
, there exists
$(y_1,y_2,\ldots ,y_n)\in MS_n(Y,S)$
, there exists
![]() $\delta>0$
and
$\delta>0$
and
![]() $y_m^1, \ldots , y_m^n\in \operatorname {int}(\pi (U_m))$
such that
$y_m^1, \ldots , y_m^n\in \operatorname {int}(\pi (U_m))$
such that
Then there exist
![]() $x_m^1, \ldots , x_m^n\in U_m$
with
$x_m^1, \ldots , x_m^n\in U_m$
with
![]() $\pi (x_m^i)=y_m^i$
such that for any
$\pi (x_m^i)=y_m^i$
such that for any
![]() $m\in \mathbb {N}$
,
$m\in \mathbb {N}$
,
Put
 $$ \begin{align*} A=\prod_{i=1}^n \pi^{-1}(\overline{B(y_i, 1)}), \end{align*} $$
$$ \begin{align*} A=\prod_{i=1}^n \pi^{-1}(\overline{B(y_i, 1)}), \end{align*} $$
and it is clear that A is a compact subset of
![]() $X^{(n)}$
.
$X^{(n)}$
.
We can cover A with finite non-empty open sets of diameter less than
![]() $1$
, that is,
$1$
, that is,
![]() $A \subset \bigcup _{i=1}^{N_1}A_1^i$
and
$A \subset \bigcup _{i=1}^{N_1}A_1^i$
and
![]() $\operatorname {\mathrm {diam}}(A_1^i)<1$
. Then for each
$\operatorname {\mathrm {diam}}(A_1^i)<1$
. Then for each
![]() $m\in \mathbb {N}$
, there is
$m\in \mathbb {N}$
, there is
![]() $1\leq N_1^m\leq N_1$
such that
$1\leq N_1^m\leq N_1$
such that
Without loss of generality, we assume
![]() $N_1^m=1$
for all
$N_1^m=1$
for all
![]() $m\in \mathbb {N}$
. Namely,
$m\in \mathbb {N}$
. Namely,
Repeating the above procedure, for
![]() $l\ge 1$
, we can cover
$l\ge 1$
, we can cover
![]() $\overline {A_l^{1}}\cap A$
with finite non-empty open sets of diameter less than
$\overline {A_l^{1}}\cap A$
with finite non-empty open sets of diameter less than
![]() ${1}/({l+1})$
, that is,
${1}/({l+1})$
, that is,
![]() $\overline {A_l^{1}}\cap A \subset \bigcup _{i=1}^{N_{l+1}}A_{l+1}^i$
and
$\overline {A_l^{1}}\cap A \subset \bigcup _{i=1}^{N_{l+1}}A_{l+1}^i$
and
![]() $\operatorname {\mathrm {diam}}(A_{l+1}^i)<{1}/({l+1})$
. Then for each
$\operatorname {\mathrm {diam}}(A_{l+1}^i)<{1}/({l+1})$
. Then for each
![]() $m\in \mathbb {N}$
, there is
$m\in \mathbb {N}$
, there is
![]() $1\leq N_{l+1}^m\leq N_{l+1}$
such that
$1\leq N_{l+1}^m\leq N_{l+1}$
such that
 $$ \begin{align*} \overline{D}(\{k\in \mathbb{Z}_+: (T^kx_m^1,\ldots, T^kx_m^n)\in \overline{A_{l+1}^{N_{l+1}^m} }\cap A \}) \ge \frac{\delta}{N_1N_2\cdots N_{l+1}}. \end{align*} $$
$$ \begin{align*} \overline{D}(\{k\in \mathbb{Z}_+: (T^kx_m^1,\ldots, T^kx_m^n)\in \overline{A_{l+1}^{N_{l+1}^m} }\cap A \}) \ge \frac{\delta}{N_1N_2\cdots N_{l+1}}. \end{align*} $$
Without loss of generality, we assume
![]() $N_{l+1}^m=1$
for all
$N_{l+1}^m=1$
for all
![]() $m\in \mathbb {N}$
. Namely,
$m\in \mathbb {N}$
. Namely,
It is clear that there is a unique point
![]() $(z_1^1,\ldots ,z_n^1)\in \bigcap _{l=1}^{\infty } \overline {A_l^{1}}\cap A $
. We claim that
$(z_1^1,\ldots ,z_n^1)\in \bigcap _{l=1}^{\infty } \overline {A_l^{1}}\cap A $
. We claim that
![]() $(z_1^1,\ldots ,z_n^1)\in MS_n(X, T)$
. In fact, for any
$(z_1^1,\ldots ,z_n^1)\in MS_n(X, T)$
. In fact, for any
![]() $\tau>0$
, there is
$\tau>0$
, there is
![]() $l\in \mathbb {N}$
such that
$l\in \mathbb {N}$
such that
![]() $\overline {A_{l}^{1}}\cap A \subset V_{1}\times \cdots \times V_{n}$
, where
$\overline {A_{l}^{1}}\cap A \subset V_{1}\times \cdots \times V_{n}$
, where
![]() $V_i=B(z_i^1,\tau )$
for
$V_i=B(z_i^1,\tau )$
for
![]() $i=1,\ldots ,n$
. By the construction, for any
$i=1,\ldots ,n$
. By the construction, for any
![]() $m\in \mathbb {N}$
, there are
$m\in \mathbb {N}$
, there are
![]() $x_m^1,\ldots , x_m^n\in U_m$
such that
$x_m^1,\ldots , x_m^n\in U_m$
such that
and so
for all
![]() $m\in \mathbb {N}$
. For any non-empty open set
$m\in \mathbb {N}$
. For any non-empty open set
![]() $U\subset X$
, since x is a transitive point, there is
$U\subset X$
, since x is a transitive point, there is
![]() $s\in \mathbb {Z}$
such that
$s\in \mathbb {Z}$
such that
![]() $T^sx\in U$
. We can choose
$T^sx\in U$
. We can choose
![]() $m\in \mathbb {Z}$
such that
$m\in \mathbb {Z}$
such that
![]() $T^sU_{m}\subset U$
. This implies that
$T^sU_{m}\subset U$
. This implies that
![]() $T^sx_{m}^1,\ldots , T^sx_{m}^n\in U$
and
$T^sx_{m}^1,\ldots , T^sx_{m}^n\in U$
and
So we have
![]() $(z_1^1,\ldots ,z_n^1)\in MS_n(X, T)$
.
$(z_1^1,\ldots ,z_n^1)\in MS_n(X, T)$
.
Similarly, for each
![]() $p\in \mathbb {N}$
, there exists
$p\in \mathbb {N}$
, there exists
![]() $(z_1^p,\ldots ,z_n^p)\in MS_n(X, T)\cap \prod _{i=1}^n \pi ^{-1} (\overline {B(y_i, {1}/{p})})$
. Set
$(z_1^p,\ldots ,z_n^p)\in MS_n(X, T)\cap \prod _{i=1}^n \pi ^{-1} (\overline {B(y_i, {1}/{p})})$
. Set
![]() $z_i^p\rightarrow z_i$
as
$z_i^p\rightarrow z_i$
as
![]() $p\rightarrow \infty $
. Then
$p\rightarrow \infty $
. Then
![]() $(z_1,\ldots ,z_n)\in MS_n(X, T)\cup \Delta _n(X)$
and
$(z_1,\ldots ,z_n)\in MS_n(X, T)\cup \Delta _n(X)$
and
![]() $\pi (z_i)=y_i$
.
$\pi (z_i)=y_i$
.
Denote by
![]() $\mathcal {A}(MS_2(X, T))$
the smallest closed
$\mathcal {A}(MS_2(X, T))$
the smallest closed
![]() $T\times T$
-invariant equivalence relation containing
$T\times T$
-invariant equivalence relation containing
![]() $MS_2(X, T)$
.
$MS_2(X, T)$
.
Corollary 5.2. Let
![]() $(X,T)$
be a minimal t.d.s. Then
$(X,T)$
be a minimal t.d.s. Then
![]() $X/\mathcal {A}(MS_2(X, T))$
is the maximal mean equicontinuous factor of
$X/\mathcal {A}(MS_2(X, T))$
is the maximal mean equicontinuous factor of
![]() $(X,T)$
.
$(X,T)$
.
Proof. Let
![]() $Y=X/\mathcal {A}(MS_2(X, T))$
and
$Y=X/\mathcal {A}(MS_2(X, T))$
and
![]() $\pi :(X,T)\to (Y,S)$
be the corresponding factor map. We show that
$\pi :(X,T)\to (Y,S)$
be the corresponding factor map. We show that
![]() $(Y,S)$
is mean equicontinuous. Assume that
$(Y,S)$
is mean equicontinuous. Assume that
![]() $(Y,S)$
is not mean equicontinuous, by [Reference Li, Tu and Ye25, Corollary 5.5],
$(Y,S)$
is not mean equicontinuous, by [Reference Li, Tu and Ye25, Corollary 5.5],
![]() $(Y,S)$
is mean sensitive. Then by [Reference Li, Ye and Yu27, Theorem 4.4],
$(Y,S)$
is mean sensitive. Then by [Reference Li, Ye and Yu27, Theorem 4.4],
![]() $MS_2(Y,S)\not =\emptyset $
. By Theorem 5.1, there exists
$MS_2(Y,S)\not =\emptyset $
. By Theorem 5.1, there exists
![]() $(x_1,x_2)\in MS_2(X, T)$
such that
$(x_1,x_2)\in MS_2(X, T)$
such that
![]() $(\pi (x_1),\pi (x_2))\in MS_2(Y,S)$
. Then
$(\pi (x_1),\pi (x_2))\in MS_2(Y,S)$
. Then
![]() $(x_1,x_2)\not \in R_\pi :=\{(x,x')\in X\times X:\pi (x)=\pi (x')\}$
, which is a contradiction with
$(x_1,x_2)\not \in R_\pi :=\{(x,x')\in X\times X:\pi (x)=\pi (x')\}$
, which is a contradiction with
![]() $R_\pi =\mathcal {A}(MS_2(X, T))$
.
$R_\pi =\mathcal {A}(MS_2(X, T))$
.
Let
![]() $(Z,W)$
be a mean equicontinuous t.d.s. and
$(Z,W)$
be a mean equicontinuous t.d.s. and
![]() $\theta : (X,T)\to (Z,W)$
be a factor map. Since
$\theta : (X,T)\to (Z,W)$
be a factor map. Since
![]() $(X,T)$
is minimal, so is
$(X,T)$
is minimal, so is
![]() $(Z,W)$
. Then by [Reference Li, Tu and Ye25, Corollary 5.5] and [Reference Li, Ye and Yu27, Theorem 4.4],
$(Z,W)$
. Then by [Reference Li, Tu and Ye25, Corollary 5.5] and [Reference Li, Ye and Yu27, Theorem 4.4],
![]() $MS_2(Z,W)=\emptyset $
. By Theorem 5.1,
$MS_2(Z,W)=\emptyset $
. By Theorem 5.1,
![]() $MS_2(X,T)\subset R_\theta $
, where
$MS_2(X,T)\subset R_\theta $
, where
![]() $R_\theta $
is the corresponding equivalence relation with respect to
$R_\theta $
is the corresponding equivalence relation with respect to
![]() $\theta $
. This implies that
$\theta $
. This implies that
![]() $(Z,W)$
is a factor of
$(Z,W)$
is a factor of
![]() $(Y,S)$
and so
$(Y,S)$
and so
![]() $(Y,S)$
is the maximal mean equicontinuous factor of
$(Y,S)$
is the maximal mean equicontinuous factor of
![]() $(X,T)$
.
$(X,T)$
.
In the following, we show Theorem 1.1. Let us begin with some preparations.
Definition 5.3. [Reference Kerr and Li18]
Let
![]() $(X,T)$
be a t.d.s.
$(X,T)$
be a t.d.s.
-
• For a tuple
 $(A_1,A_2,\ldots , A_n)$
of subsets of X, we say that a set
$(A_1,A_2,\ldots , A_n)$
of subsets of X, we say that a set
 $J\subseteq \mathbb {Z}_+$
is an independence set for A if for every non-empty finite subset
$J\subseteq \mathbb {Z}_+$
is an independence set for A if for every non-empty finite subset
 $I\subseteq J$
and function
$I\subseteq J$
and function
 $\sigma : I\rightarrow \{1,2,\ldots , n\}$
, we have
$\sigma : I\rightarrow \{1,2,\ldots , n\}$
, we have
 $\bigcap _{k\in I} T^{-k} A_{\sigma (k)}\neq \emptyset .$
$\bigcap _{k\in I} T^{-k} A_{\sigma (k)}\neq \emptyset .$
-
• For
 $n\ge 2$
, we call a tuple
$n\ge 2$
, we call a tuple
 $\textbf {x}=(x_1,\ldots ,x_n)\in X^{(n)}$
an IT-tuple if for any product neighborhood
$\textbf {x}=(x_1,\ldots ,x_n)\in X^{(n)}$
an IT-tuple if for any product neighborhood
 $U_1\times U_2\times \cdots \times U_n$
of
$U_1\times U_2\times \cdots \times U_n$
of
 $\textbf {x}$
in
$\textbf {x}$
in
 $X^{(n)}$
, the tuple
$X^{(n)}$
, the tuple
 $(U_1,U_2,\ldots , U_n)$
has an infinite independence set. We denote the set of IT-tuples of length n by
$(U_1,U_2,\ldots , U_n)$
has an infinite independence set. We denote the set of IT-tuples of length n by
 $\mathrm {IT}_n (X, T)$
.
$\mathrm {IT}_n (X, T)$
. -
• For
 $n\ge 2$
, we call an IT-tuple
$n\ge 2$
, we call an IT-tuple
 $\textbf {x}=(x_1,\ldots ,x_n)\in X^{(n)}$
an essential IT-tuple if
$\textbf {x}=(x_1,\ldots ,x_n)\in X^{(n)}$
an essential IT-tuple if
 $x_i\neq x_j$
for any
$x_i\neq x_j$
for any
 $i\neq j$
. We denote the set of all essential IT-tuples of length n by
$i\neq j$
. We denote the set of all essential IT-tuples of length n by
 $\mathrm {IT}^e_n (X, T)$
.
$\mathrm {IT}^e_n (X, T)$
.
Proposition 5.4. [Reference Huang, Lian, Shao and Ye13, Proposition 3.2]
Let X be a compact metric topological group with the left Haar measure
![]() $\mu $
, and let
$\mu $
, and let
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n\ge 2$
. Suppose that
$n\ge 2$
. Suppose that
![]() $V_{1},\ldots ,V_{n}\subset X$
are compact subsets satisfying that
$V_{1},\ldots ,V_{n}\subset X$
are compact subsets satisfying that
-
(i)
 $\overline {\operatorname {int} V_i}=V_i$
for
$\overline {\operatorname {int} V_i}=V_i$
for
 $i=1,2,\ldots ,n$
;
$i=1,2,\ldots ,n$
; -
(ii)
 $\operatorname {int}(V_{i})\cap \operatorname {int}(V_{j})=\emptyset $
for all
$\operatorname {int}(V_{i})\cap \operatorname {int}(V_{j})=\emptyset $
for all
 $1\le i\neq j\le n$
;
$1\le i\neq j\le n$
; -
(iii)
 $\mu (\bigcap _{1\leq i\leq n}V_{i})>0$
.
$\mu (\bigcap _{1\leq i\leq n}V_{i})>0$
.
Further, assume that
![]() $T: X\rightarrow X$
is a minimal rotation and
$T: X\rightarrow X$
is a minimal rotation and
![]() $\mathcal {G}\subset X$
is a residual set. Then there exists an infinite set
$\mathcal {G}\subset X$
is a residual set. Then there exists an infinite set
![]() $I\subset \mathbb {Z}_+$
such that for all
$I\subset \mathbb {Z}_+$
such that for all
![]() $a\in \{1,2,\ldots ,n\}^{I}$
, there exists
$a\in \{1,2,\ldots ,n\}^{I}$
, there exists
![]() $x \in \mathcal {G}$
with the property that
$x \in \mathcal {G}$
with the property that
A subset
![]() $Z\subset X$
is called proper if Z is a compact subset with
$Z\subset X$
is called proper if Z is a compact subset with
![]() $\overline {\operatorname {int}(Z)} = Z$
. The following lemma can help us to complete the proof of Theorem 1.1.
$\overline {\operatorname {int}(Z)} = Z$
. The following lemma can help us to complete the proof of Theorem 1.1.
Lemma 5.5. Let
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,S)$
be two t.d.s., and
$(Y,S)$
be two t.d.s., and
![]() $\pi :(X,T)\to (Y,S)$
be a factor map. Suppose that
$\pi :(X,T)\to (Y,S)$
be a factor map. Suppose that
![]() $(X,T)$
is minimal. Then the image of proper subsets of X under
$(X,T)$
is minimal. Then the image of proper subsets of X under
![]() $\pi $
is a proper subset of Y.
$\pi $
is a proper subset of Y.
Proof. Given a proper subset Z of X, we will show
![]() $\pi (Z)$
is also proper. It is clear that
$\pi (Z)$
is also proper. It is clear that
![]() $\pi (Z)$
is compact, as
$\pi (Z)$
is compact, as
![]() $\pi $
is continuous. Now we prove
$\pi $
is continuous. Now we prove
![]() $\overline {\operatorname {int}(\pi (Z))} = \pi (Z)$
.
$\overline {\operatorname {int}(\pi (Z))} = \pi (Z)$
.
It follows from the closeness of
![]() $\pi (Z)$
that
$\pi (Z)$
that
![]() $\overline {\operatorname {int}(\pi (Z))} \subset \pi (Z)$
. However, for any
$\overline {\operatorname {int}(\pi (Z))} \subset \pi (Z)$
. However, for any
![]() $y\in \pi (Z), $
take
$y\in \pi (Z), $
take
![]() $x\in \pi ^{-1}(y)\cap Z$
. Since
$x\in \pi ^{-1}(y)\cap Z$
. Since
![]() $\pi ^{-1}(y)\cap Z=\pi ^{-1}(y)\cap \overline {\operatorname {int}(Z)}$
, there exists a sequence
$\pi ^{-1}(y)\cap Z=\pi ^{-1}(y)\cap \overline {\operatorname {int}(Z)}$
, there exists a sequence
![]() $\{x_n\}_{n\in \mathbb {N}}$
such that
$\{x_n\}_{n\in \mathbb {N}}$
such that
![]() $x_n\in \operatorname {int}(Z)$
for each
$x_n\in \operatorname {int}(Z)$
for each
![]() $n\in \mathbb{N}$
, and
$n\in \mathbb{N}$
, and
![]() $\lim _{n\to \infty }x_n=x$
. Let
$\lim _{n\to \infty }x_n=x$
. Let
![]() $\{r_n\}_{n\in \mathbb {N}}$
be a sequence of
$\{r_n\}_{n\in \mathbb {N}}$
be a sequence of
![]() $\mathbb {R}$
satisfying
$\mathbb {R}$
satisfying
By the minimality of
![]() $(X,T)$
, we have
$(X,T)$
, we have
![]() $\pi $
is semi-open, and hence
$\pi $
is semi-open, and hence
![]() $\operatorname {int}(\pi (B(x_n,r_n)))\neq \emptyset $
. Thus, there exists
$\operatorname {int}(\pi (B(x_n,r_n)))\neq \emptyset $
. Thus, there exists
![]() $x_n'\in B(x_n,r_n)$
such that
$x_n'\in B(x_n,r_n)$
such that
![]() $\pi (x_n')\in \operatorname {int}(\pi (B(x_n,r_n)))\subset \operatorname {int}(\pi (Z))$
. Since
$\pi (x_n')\in \operatorname {int}(\pi (B(x_n,r_n)))\subset \operatorname {int}(\pi (Z))$
. Since
![]() $x_n'\in B(x_n,r_n)$
and
$x_n'\in B(x_n,r_n)$
and
![]() $\lim _{n\to \infty }x_n=x$
, one has
$\lim _{n\to \infty }x_n=x$
, one has
![]() $\lim _{n\to \infty }x_n'=x$
, and hence
$\lim _{n\to \infty }x_n'=x$
, and hence
![]() $\lim _{n\to \infty }\pi (x_n')= \pi (x)=y.$
This implies that
$\lim _{n\to \infty }\pi (x_n')= \pi (x)=y.$
This implies that
![]() $y\in \overline {\operatorname {int}(\pi (Z))}$
, which finishes the proof.
$y\in \overline {\operatorname {int}(\pi (Z))}$
, which finishes the proof.
Inspired by [Reference Huang, Lian, Shao and Ye13, Proposition 3.7], we can give the proof of Theorem 1.1.
Proof of Theorem 1.1
It suffices to prove
![]() $MS^e_n(X,T)\subset IT_n^e(X,T)$
. Given
$MS^e_n(X,T)\subset IT_n^e(X,T)$
. Given
![]() $\textbf {x}=(x_1,\ldots ,x_n)\in MS^e_n(X,T)$
, we will show that
$\textbf {x}=(x_1,\ldots ,x_n)\in MS^e_n(X,T)$
, we will show that
![]() $\textbf {x}\in IT^e_n(X,T).$
$\textbf {x}\in IT^e_n(X,T).$
Since the minimal t.d.s.
![]() $(X_{eq},T_{eq})$
is the maximal equicontinuous factor of
$(X_{eq},T_{eq})$
is the maximal equicontinuous factor of
![]() $(X,T)$
, then
$(X,T)$
, then
![]() $X_{eq}$
can be viewed as a compact metric group with a
$X_{eq}$
can be viewed as a compact metric group with a
![]() $T_{eq}$
-invariant metric
$T_{eq}$
-invariant metric
![]() $d_{eq}$
. Let
$d_{eq}$
. Let
![]() $\mu $
be the left Haar probability measure of
$\mu $
be the left Haar probability measure of
![]() $X_{eq}$
, which is also the unique
$X_{eq}$
, which is also the unique
![]() $T_{eq}$
-invariant probability measure of
$T_{eq}$
-invariant probability measure of
![]() $(X_{eq},T_{eq})$
. Let
$(X_{eq},T_{eq})$
. Let
Then
![]() $Y_1$
is a dense
$Y_1$
is a dense
![]() $G_\delta $
-set as
$G_\delta $
-set as
![]() $\pi $
is almost one to one.
$\pi $
is almost one to one.
Without loss of generality, assume that
![]() $\epsilon =\tfrac 14 \min _{1\le i\neq j\le n}d(x_i,x_j)$
. Let
$\epsilon =\tfrac 14 \min _{1\le i\neq j\le n}d(x_i,x_j)$
. Let
![]() $U_i=\overline {B_\epsilon (x_i)}$
for
$U_i=\overline {B_\epsilon (x_i)}$
for
![]() $1\le i\le n$
. Then
$1\le i\le n$
. Then
![]() $U_i$
is proper for each
$U_i$
is proper for each
![]() $1\le i\le n$
. We will show that
$1\le i\le n$
. We will show that
![]() $U_1,U_2,\ldots ,U_n$
is an infinite independent tuple of
$U_1,U_2,\ldots ,U_n$
is an infinite independent tuple of
![]() $(X,T)$
, that is, there is some infinite set
$(X,T)$
, that is, there is some infinite set
![]() $I\subseteq \mathbb {Z}_+$
such that
$I\subseteq \mathbb {Z}_+$
such that
Let
![]() $V_i=\pi (U_i)$
for
$V_i=\pi (U_i)$
for
![]() $1\le i\le n$
. By Lemma 5.5,
$1\le i\le n$
. By Lemma 5.5,
![]() $V_i$
is proper for each
$V_i$
is proper for each
![]() $i\in \{1,2,\ldots ,n\}$
. We claim that
$i\in \{1,2,\ldots ,n\}$
. We claim that
![]() $\mathrm {int }(V_i)\cap \mathrm {int}(V_j)=\emptyset $
for all
$\mathrm {int }(V_i)\cap \mathrm {int}(V_j)=\emptyset $
for all
![]() $1\le i\neq j\le n$
. In fact, if there is some
$1\le i\neq j\le n$
. In fact, if there is some
![]() $1\le i\neq j\le n$
such that
$1\le i\neq j\le n$
such that
![]() $\mathrm {int }(V_i)\cap \mathrm {int}(V_j)\not =\emptyset $
, then
$\mathrm {int }(V_i)\cap \mathrm {int}(V_j)\not =\emptyset $
, then
as
![]() $Y_1$
is a dense
$Y_1$
is a dense
![]() $G_\delta $
-set. Let
$G_\delta $
-set. Let
![]() $y\in \mathrm {int }(V_i)\cap \mathrm {int}(V_j)\cap Y_1$
. Then there are
$y\in \mathrm {int }(V_i)\cap \mathrm {int}(V_j)\cap Y_1$
. Then there are
![]() $x_i\in U_i$
and
$x_i\in U_i$
and
![]() $x_j\in U_j$
such that
$x_j\in U_j$
such that
![]() $y=\pi (x_i)=\pi (x_j)$
, which contradicts with
$y=\pi (x_i)=\pi (x_j)$
, which contradicts with
![]() $y\in Y_1$
.
$y\in Y_1$
.
Choose a non-empty open set
![]() $W_m\subset X$
with
$W_m\subset X$
with
![]() $\operatorname {diam}(\pi (W_m))<{1}/{m}$
for each
$\operatorname {diam}(\pi (W_m))<{1}/{m}$
for each
![]() $m\in \mathbb {N}$
. Since
$m\in \mathbb {N}$
. Since
![]() $\textbf {x}\in MS^e_n(X,T)$
, there exist
$\textbf {x}\in MS^e_n(X,T)$
, there exist
![]() $\delta>0$
and
$\delta>0$
and
![]() $\textbf {x}^m=(x_1^m, x_2^m,\ldots , x_n^m)\in W_m\times \cdots \times W_m$
such that
$\textbf {x}^m=(x_1^m, x_2^m,\ldots , x_n^m)\in W_m\times \cdots \times W_m$
such that
![]() $\overline {D}(N(\textbf {x}^m, U_1\times U_2\times \cdots \times U_n))\ge \delta .$
Let
$\overline {D}(N(\textbf {x}^m, U_1\times U_2\times \cdots \times U_n))\ge \delta .$
Let
![]() $\textbf {y}^m=(y_1^m,y_2^m,\ldots ,y_n^m)=\pi ^{(n)} (\textbf {x}^m)$
. Then,
$\textbf {y}^m=(y_1^m,y_2^m,\ldots ,y_n^m)=\pi ^{(n)} (\textbf {x}^m)$
. Then,
For
![]() $p\in \overline {D}(N(\textbf {y}^m, V_1\times V_2\times \cdots \times V_n))$
,
$p\in \overline {D}(N(\textbf {y}^m, V_1\times V_2\times \cdots \times V_n))$
,
![]() $T_{eq}^py_i^m\in V_i$
for each
$T_{eq}^py_i^m\in V_i$
for each
![]() $i=1,2,\ldots,n$
. As
$i=1,2,\ldots,n$
. As
![]() $\operatorname {diam}(\pi (W_m))<{1}/{m}$
,
$\operatorname {diam}(\pi (W_m))<{1}/{m}$
,
![]() $d_{eq}(y_1^m, y_i^m)<{1}/{m}$
for
$d_{eq}(y_1^m, y_i^m)<{1}/{m}$
for
![]() $1\le i\le n$
. Note that
$1\le i\le n$
. Note that
Let
![]() $V_i^m=B_{{1}/{m}}(V_i)=\{y\in X_{eq}:d_{eq}(y,V_i)<{1}/{m}\}$
. Then,
$V_i^m=B_{{1}/{m}}(V_i)=\{y\in X_{eq}:d_{eq}(y,V_i)<{1}/{m}\}$
. Then,
![]() $T_{eq}^py_1^m\in \bigcap _{i=1}^n V_i^m$
and
$T_{eq}^py_1^m\in \bigcap _{i=1}^n V_i^m$
and
 $$ \begin{align*}\overline{D}(N(y_1^m, \bigcap_{i=1}^n V_i^m))\ge \delta.\end{align*} $$
$$ \begin{align*}\overline{D}(N(y_1^m, \bigcap_{i=1}^n V_i^m))\ge \delta.\end{align*} $$
Since
![]() $(X_{eq},T_{eq})$
is uniquely ergodic with respect to a measure
$(X_{eq},T_{eq})$
is uniquely ergodic with respect to a measure
![]() $\mu $
,
$\mu $
,
![]() $\mu (\bigcap _{i=1}^n V_i^m)\ge \delta $
. Letting
$\mu (\bigcap _{i=1}^n V_i^m)\ge \delta $
. Letting
![]() $m\to \infty $
, one has
$m\to \infty $
, one has
![]() $\mu (\bigcap _{i=1}^n V_i)\ge \delta>0.$
$\mu (\bigcap _{i=1}^n V_i)\ge \delta>0.$
By Proposition 5.4, there is an infinite
![]() $I\subseteq \mathbb {Z}_+$
such that for all
$I\subseteq \mathbb {Z}_+$
such that for all
![]() $a\in \{1,2,\ldots ,n\}^{I}$
, there exists
$a\in \{1,2,\ldots ,n\}^{I}$
, there exists
![]() $y_0\in Y_1$
with the property that
$y_0\in Y_1$
with the property that
Set
![]() $\pi ^{-1}(y_0)=\{x_0\}$
. Then
$\pi ^{-1}(y_0)=\{x_0\}$
. Then
which implies that
![]() $(x_1,x_2,\ldots ,x_n)\in IT_n(X,T)$
.
$(x_1,x_2,\ldots ,x_n)\in IT_n(X,T)$
.
Acknowledgments
We thank the referee for a very careful reading and many useful comments, which helped us to improve the paper. Research of J.L. is supported by NNSF of China (Grant No. 12031019); C.L. is partially supported by NNSF of China (Grant No. 12090012); S.T. is supported by NNSF of China (Grants No. 11801584 and No. 12171175); and T.Y. is supported by NNSF of China (Grant No. 12001354) and STU Scientific Research Foundation for Talents (Grant No. NTF19047).
A Appendix. Proof of Lemma 4.3
In this section, we give the proof of Lemma 4.3.
Lemma A.1. For an m.p.s.
![]() $(X,\mathcal {B}_X,\mu ,T)$
with
$(X,\mathcal {B}_X,\mu ,T)$
with
![]() $\mathcal {K}_\mu $
its Kronecker factor,
$\mathcal {K}_\mu $
its Kronecker factor,
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $f_i\in L^\infty (X,\mu )$
,
$f_i\in L^\infty (X,\mu )$
,
![]() $i=1,\dotsc ,n$
, we have
$i=1,\dotsc ,n$
, we have
 $$ \begin{align*} \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n} f_i( T^m x_i) = \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n}\mathbb{E}(f_i | \mathcal{K}_\mu)(T^m x_i). \end{align*} $$
$$ \begin{align*} \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n} f_i( T^m x_i) = \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n}\mathbb{E}(f_i | \mathcal{K}_\mu)(T^m x_i). \end{align*} $$
Proof. On the one hand, by the Birkhoff ergodic theorem, for
![]() $\textbf {x}=(x_1,\dotsc ,x_n)\in X^{(n)}$
, let
$\textbf {x}=(x_1,\dotsc ,x_n)\in X^{(n)}$
, let
![]() $F(\textbf {x})=F(x_1,\ldots ,x_n)=\prod _{i=1}^{n} f_i(x_i)$
,
$F(\textbf {x})=F(x_1,\ldots ,x_n)=\prod _{i=1}^{n} f_i(x_i)$
,
 $$ \begin{align*}\lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n} f_i( T^m x_i) =\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} F((T^{(n)})^m\textbf{x})= \mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|I_{\mu^{(n)}}\bigg)(\textbf{x}),\end{align*} $$
$$ \begin{align*}\lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n} f_i( T^m x_i) =\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} F((T^{(n)})^m\textbf{x})= \mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|I_{\mu^{(n)}}\bigg)(\textbf{x}),\end{align*} $$
where
![]() $I_{\mu ^{(n)}}=\{A\in \mathcal {B}^{(n)}_X: T^{(n)}A=A\}$
.
$I_{\mu ^{(n)}}=\{A\in \mathcal {B}^{(n)}_X: T^{(n)}A=A\}$
.
On the other hand, following [Reference Huang, Maass and Ye15, Lemma 4.4], we have
![]() $(\mathcal {K}_\mu )^{\bigotimes n}=\mathcal {K}_{\mu ^{(n)}}$
. Then for
$(\mathcal {K}_\mu )^{\bigotimes n}=\mathcal {K}_{\mu ^{(n)}}$
. Then for
![]() $\textbf {x}=(x_1,\dotsc ,x_n)\in X^{(n)}$
,
$\textbf {x}=(x_1,\dotsc ,x_n)\in X^{(n)}$
,
 $$ \begin{align*}\prod_{i=1}^{n}\mathbb{E}_{\mu}(f_i|\mathcal{K}_\mu)(x_i) =\mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|(\mathcal{K}_\mu)^{\bigotimes n}\bigg)(\textbf{x}) =\mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|\mathcal{K}_{\mu^{(n)}}\bigg)(\textbf{x}).\end{align*} $$
$$ \begin{align*}\prod_{i=1}^{n}\mathbb{E}_{\mu}(f_i|\mathcal{K}_\mu)(x_i) =\mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|(\mathcal{K}_\mu)^{\bigotimes n}\bigg)(\textbf{x}) =\mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|\mathcal{K}_{\mu^{(n)}}\bigg)(\textbf{x}).\end{align*} $$
This implies that
 $$ \begin{align*} \lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} \prod_{i=1}^{n} \mathbb{E}_{\mu}(f_i|\mathcal{K}_\mu)(T^mx_i) &= \mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}\mathbb{E}_{\mu}(f_i|\mathcal{K}_\mu)|I_{\mu^{(n)}}\bigg)(\textbf{x})\\ &= \mathbb{E}_{\mu^{(n)}}(\mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|\mathcal{K}_{\mu^{(n)}}\bigg)|I_{\mu^{(n)}})(\textbf{x})\\ &= \mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|I_{\mu^{(n)}}\bigg)(\textbf{x}), \end{align*} $$
$$ \begin{align*} \lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} \prod_{i=1}^{n} \mathbb{E}_{\mu}(f_i|\mathcal{K}_\mu)(T^mx_i) &= \mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}\mathbb{E}_{\mu}(f_i|\mathcal{K}_\mu)|I_{\mu^{(n)}}\bigg)(\textbf{x})\\ &= \mathbb{E}_{\mu^{(n)}}(\mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|\mathcal{K}_{\mu^{(n)}}\bigg)|I_{\mu^{(n)}})(\textbf{x})\\ &= \mathbb{E}_{\mu^{(n)}}\bigg(\prod_{i=1}^{n}f_i|I_{\mu^{(n)}}\bigg)(\textbf{x}), \end{align*} $$
where the last equality follows from the fact that
![]() $I_{\mu ^{(n)}}\subset \mathcal {K}_{\mu ^{(n)}}.$
$I_{\mu ^{(n)}}\subset \mathcal {K}_{\mu ^{(n)}}.$
Lemma A.2. Let
![]() $(Z,\mathcal B_Z,\nu ,R)$
be a minimal rotation on a compact abelian group. Then for any
$(Z,\mathcal B_Z,\nu ,R)$
be a minimal rotation on a compact abelian group. Then for any
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\phi _i\in L^\infty (Z,\nu )$
,
$\phi _i\in L^\infty (Z,\nu )$
,
![]() $i=1,\dotsc ,n$
,
$i=1,\dotsc ,n$
,
 $$ \begin{align*}\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} \prod_{i=1}^{n} \phi_i (R^mz_i) = \int_Z \prod_{i=1}^{n} \phi_i (z_i+z)\,d \nu(z) \quad\text{for }\nu^{(n)}\text{-a.e. }(z_1,\ldots, z_n). \end{align*} $$
$$ \begin{align*}\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} \prod_{i=1}^{n} \phi_i (R^mz_i) = \int_Z \prod_{i=1}^{n} \phi_i (z_i+z)\,d \nu(z) \quad\text{for }\nu^{(n)}\text{-a.e. }(z_1,\ldots, z_n). \end{align*} $$
Proof. Since
![]() $(Z,\mathcal B_Z,\nu ,R)$
is a minimal rotation on a compact abelian group, there exists
$(Z,\mathcal B_Z,\nu ,R)$
is a minimal rotation on a compact abelian group, there exists
![]() $a\in Z$
such that
$a\in Z$
such that
![]() $R^mz=z+ma$
for any
$R^mz=z+ma$
for any
![]() $z\in Z$
.
$z\in Z$
.
Let
![]() $F(z)=\prod _{i=1}^{n} \phi _i (z_i+z)$
. Then
$F(z)=\prod _{i=1}^{n} \phi _i (z_i+z)$
. Then
![]() $F(R^me_Z)=F(ma)$
, where
$F(R^me_Z)=F(ma)$
, where
![]() $e_Z$
is the identity element of Z. Since
$e_Z$
is the identity element of Z. Since
![]() $(Z,R)$
is minimal equicontinuous,
$(Z,R)$
is minimal equicontinuous,
![]() $(Z,\mathcal B_Z,\nu ,R)$
is uniquely ergodic. By an approximation argument, we have, for
$(Z,\mathcal B_Z,\nu ,R)$
is uniquely ergodic. By an approximation argument, we have, for
![]() $\nu ^{(n)}$
-a.e.
$\nu ^{(n)}$
-a.e.
![]() $(z_1,\ldots , z_n)$
,
$(z_1,\ldots , z_n)$
,
 $$ \begin{align*} \lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M}\prod_{i=1}^{n} \phi_i(R^mz_i) =&\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M}\prod_{i=1}^{n} \phi_i (z_i+ma)\\ =&\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} F(ma) =\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} F(R^me_Z)\\ =&\int_Z F(z) \,d \nu(z) = \int_Z \prod_{i=1}^{n} \phi_i (z_i+z) d \nu(z). \end{align*} $$
$$ \begin{align*} \lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M}\prod_{i=1}^{n} \phi_i(R^mz_i) =&\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M}\prod_{i=1}^{n} \phi_i (z_i+ma)\\ =&\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} F(ma) =\lim_{M\to\infty}\dfrac{1}{M} \sum_{m=1}^{M} F(R^me_Z)\\ =&\int_Z F(z) \,d \nu(z) = \int_Z \prod_{i=1}^{n} \phi_i (z_i+z) d \nu(z). \end{align*} $$
The proof is completed.
Proof of Lemma 4.3
Let
![]() $z \mapsto \eta _z$
be the disintegration of
$z \mapsto \eta _z$
be the disintegration of
![]() $\mu $
over the continuous factor map
$\mu $
over the continuous factor map
![]() $\pi $
from
$\pi $
from
![]() $(X,\mathcal B_X,\mu ,T)$
to its Kronecker factor
$(X,\mathcal B_X,\mu ,T)$
to its Kronecker factor
![]() $(Z,\mathcal B_Z,\nu ,R)$
. For
$(Z,\mathcal B_Z,\nu ,R)$
. For
![]() $n\in \mathbb {N}$
, define
$n\in \mathbb {N}$
, define
for every
![]() $\textbf {x}=(x_1,\dotsc ,x_n) \in X^{(n)}$
.
$\textbf {x}=(x_1,\dotsc ,x_n) \in X^{(n)}$
.
We first note that for each
![]() $\textbf {x} \in X^{(n)}$
, the measures
$\textbf {x} \in X^{(n)}$
, the measures
![]() $\eta _{z + \pi (x_i)}$
are defined for
$\eta _{z + \pi (x_i)}$
are defined for
![]() $\nu $
-a.e.
$\nu $
-a.e.
![]() $z \in Z$
and therefore is well defined. To prove that
$z \in Z$
and therefore is well defined. To prove that
![]() $\textbf {x} \mapsto \unicode{x3bb} ^n_{\textbf {x}}$
is continuous, first note that uniform continuity implies
$\textbf {x} \mapsto \unicode{x3bb} ^n_{\textbf {x}}$
is continuous, first note that uniform continuity implies
 $$ \begin{align*} (u_1,\dotsc,u_n) \mapsto \int_Z \prod_{i=1}^{n}f_i(z + u_i) \,d\nu(z) \end{align*} $$
$$ \begin{align*} (u_1,\dotsc,u_n) \mapsto \int_Z \prod_{i=1}^{n}f_i(z + u_i) \,d\nu(z) \end{align*} $$
from
![]() $Z^{(n)}$
to
$Z^{(n)}$
to
![]() $\mathbb {C}$
is continuous whenever
$\mathbb {C}$
is continuous whenever
![]() $f_i \colon Z \to \mathbb {C}$
are continuous. An approximation argument then gives continuity for every
$f_i \colon Z \to \mathbb {C}$
are continuous. An approximation argument then gives continuity for every
![]() $f_i \in L^\infty (Z,\nu )$
. In particular,
$f_i \in L^\infty (Z,\nu )$
. In particular,
 $$ \begin{align*} \textbf{x} \mapsto \int_Z \prod_{i=1}^{n}\mathbb{E}(f_i \mid \mathcal B_Z)(z + \pi(x_i)) \,d\nu(z) \end{align*} $$
$$ \begin{align*} \textbf{x} \mapsto \int_Z \prod_{i=1}^{n}\mathbb{E}(f_i \mid \mathcal B_Z)(z + \pi(x_i)) \,d\nu(z) \end{align*} $$
from
![]() $X^{(n)}$
to
$X^{(n)}$
to
![]() $\mathbb {C}$
is continuous whenever
$\mathbb {C}$
is continuous whenever
![]() $f_i \in L^{\infty}(X,\mu)$
, which in turn implies continuity of
$f_i \in L^{\infty}(X,\mu)$
, which in turn implies continuity of
![]() $\textbf {x} \mapsto \unicode{x3bb} _{\textbf {x}}^n$
.
$\textbf {x} \mapsto \unicode{x3bb} _{\textbf {x}}^n$
.
To prove that
![]() $\textbf {x}\mapsto \unicode{x3bb} _{\textbf {x}}^n$
is an ergodic decomposition, we first calculate
$\textbf {x}\mapsto \unicode{x3bb} _{\textbf {x}}^n$
is an ergodic decomposition, we first calculate
 $$ \begin{align*} \int_{X^{(n)}} \int_Z \prod_{i=1}^{n}\eta_{z + \pi(x_i)}\,d \nu(z) \,d \mu^{(n)}(\textbf{x}) =\int_Z \prod_{i=1}^{n}\int_X \eta_{z + \pi(x_i)} \,d \mu(x_i) \,d \nu(z), \end{align*} $$
$$ \begin{align*} \int_{X^{(n)}} \int_Z \prod_{i=1}^{n}\eta_{z + \pi(x_i)}\,d \nu(z) \,d \mu^{(n)}(\textbf{x}) =\int_Z \prod_{i=1}^{n}\int_X \eta_{z + \pi(x_i)} \,d \mu(x_i) \,d \nu(z), \end{align*} $$
which is equal to
![]() $\mu ^{(n)}$
because all inner integrals are equal to
$\mu ^{(n)}$
because all inner integrals are equal to
![]() $\mu $
. We conclude that
$\mu $
. We conclude that
which shows
![]() $\textbf {x} \mapsto \unicode{x3bb} ^n_{\textbf {x}}$
is a disintegration of
$\textbf {x} \mapsto \unicode{x3bb} ^n_{\textbf {x}}$
is a disintegration of
![]() $\mu ^{(n)}$
.
$\mu ^{(n)}$
.
We are left with verifying that
for
![]() $\mu ^{(n)}$
-a.e.
$\mu ^{(n)}$
-a.e.
![]() $\textbf {x}\in X^{(n)}$
whenever
$\textbf {x}\in X^{(n)}$
whenever
![]() $F \colon X^{(n)} \to \mathbb {C}$
is measurable and bounded. Recall that
$F \colon X^{(n)} \to \mathbb {C}$
is measurable and bounded. Recall that
![]() $I_{\mu ^{(n)}}$
denotes the
$I_{\mu ^{(n)}}$
denotes the
![]() $\sigma $
-algebra of
$\sigma $
-algebra of
![]() $T^{(n)}$
-invariant sets. Fix such an F. It follows from the pointwise ergodic theorem that
$T^{(n)}$
-invariant sets. Fix such an F. It follows from the pointwise ergodic theorem that
 $$ \begin{align*} \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M F( T^m x_1,\dotsc, T^m x_n) = \mathbb{E}_{\mu^{(n)}}(F \mid I_{\mu^{(n)}})(\textbf{x}) \end{align*} $$
$$ \begin{align*} \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M F( T^m x_1,\dotsc, T^m x_n) = \mathbb{E}_{\mu^{(n)}}(F \mid I_{\mu^{(n)}})(\textbf{x}) \end{align*} $$
for
![]() $\mu ^{(n)}$
-a.e.
$\mu ^{(n)}$
-a.e.
![]() $\textbf {x}\in X^{(n)}$
. We therefore wish to prove that
$\textbf {x}\in X^{(n)}$
. We therefore wish to prove that
 $$ \begin{align*} \int_{X^{(n)}} F \,d \unicode{x3bb}^n_{\textbf{x}} = \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M F( T^m x_1,\dotsc, T^m x_n) \end{align*} $$
$$ \begin{align*} \int_{X^{(n)}} F \,d \unicode{x3bb}^n_{\textbf{x}} = \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M F( T^m x_1,\dotsc, T^m x_n) \end{align*} $$
holds for
![]() $\mu ^{(n)}$
-a.e.
$\mu ^{(n)}$
-a.e.
![]() $\textbf {x} \in X^{(n)}$
.
$\textbf {x} \in X^{(n)}$
.
By an approximation argument, it suffices to verify that
 $$ \begin{align*} \int_{X^{(n)}} f_1 \otimes\cdots\otimes f_n \,d \unicode{x3bb}^n_{\textbf{x}} = \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n} f_i( T^m x_i) \end{align*} $$
$$ \begin{align*} \int_{X^{(n)}} f_1 \otimes\cdots\otimes f_n \,d \unicode{x3bb}^n_{\textbf{x}} = \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n} f_i( T^m x_i) \end{align*} $$
holds for
![]() $\mu ^{(n)}$
-a.e.
$\mu ^{(n)}$
-a.e.
![]() $\textbf {x} \in X^{(n)}$
whenever
$\textbf {x} \in X^{(n)}$
whenever
![]() $f_i$
belongs to
$f_i$
belongs to
![]() $L^\infty (X,\mu )$
for
$L^\infty (X,\mu )$
for
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
By Lemma A.1,
 $$ \begin{align*} \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n} f_i( T^m x_i) = \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n}\mathbb{E}(f_i \mid \mathcal B_Z)(T^m x_i) \end{align*} $$
$$ \begin{align*} \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n} f_i( T^m x_i) = \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n}\mathbb{E}(f_i \mid \mathcal B_Z)(T^m x_i) \end{align*} $$
for
![]() $\mu ^{(n)}$
-a.e.
$\mu ^{(n)}$
-a.e.
![]() $\textbf {x}\in X^{(n)}$
. By Lemma A.2, for every
$\textbf {x}\in X^{(n)}$
. By Lemma A.2, for every
![]() $\phi _i$
in
$\phi _i$
in
![]() $L^\infty (Z,\nu )$
,
$L^\infty (Z,\nu )$
,
 $$ \begin{align*}\lim_{M \to \infty}\dfrac{1}{M} \sum_{m=1}^{M} \prod_{i=1}^{n} \phi_i (R^mz_i) = \int_Z \prod_{i=1}^{n} \phi_i (z_i+z)\,d \nu(z)\end{align*} $$
$$ \begin{align*}\lim_{M \to \infty}\dfrac{1}{M} \sum_{m=1}^{M} \prod_{i=1}^{n} \phi_i (R^mz_i) = \int_Z \prod_{i=1}^{n} \phi_i (z_i+z)\,d \nu(z)\end{align*} $$
for
![]() $\nu ^{(n)}$
-a.e.
$\nu ^{(n)}$
-a.e.
![]() $\textbf {z}\in Z^{(n)}$
. Taking
$\textbf {z}\in Z^{(n)}$
. Taking
![]() $\phi _i = \mathbb {E}(f_i \mid \mathcal B_Z)$
gives
$\phi _i = \mathbb {E}(f_i \mid \mathcal B_Z)$
gives
 $$ \begin{align*} \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n}\mathbb{E}(f_i \mid \mathcal B_Z)(T^m x_i) = \int_{X^{(n)}} f_1 \otimes \cdots \otimes f_n \,d \unicode{x3bb}^n_{\textbf{x}} \end{align*} $$
$$ \begin{align*} \lim_{M \to \infty} \dfrac{1}{M} \sum_{m=1}^M \prod_{i=1}^{n}\mathbb{E}(f_i \mid \mathcal B_Z)(T^m x_i) = \int_{X^{(n)}} f_1 \otimes \cdots \otimes f_n \,d \unicode{x3bb}^n_{\textbf{x}} \end{align*} $$
for
![]() $\mu ^{(n)}$
-a.e.
$\mu ^{(n)}$
-a.e.
![]() $\textbf {x}\in X^{(n)}$
.
$\textbf {x}\in X^{(n)}$
.