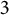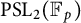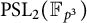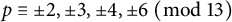1 Introduction
The Inverse Galois Problem asks whether every finite group is isomorphic to the Galois group of some extension of
![]() ${\mathbb Q}$
. There has been much work on using modular forms to realize explicit simple groups of the form
${\mathbb Q}$
. There has been much work on using modular forms to realize explicit simple groups of the form
![]() $\operatorname {PSL}_2({\mathbb F}_{\ell ^r})$
as Galois groups of extensions of
$\operatorname {PSL}_2({\mathbb F}_{\ell ^r})$
as Galois groups of extensions of
![]() ${\mathbb Q}$
(cf. [Reference Dieulefait4–Reference Dieulefait and Vila6, Reference Reverter and Vila13, Reference Ribet14]). For example, [Reference Dieulefait and Vila6, Section 3.2] shows that
${\mathbb Q}$
(cf. [Reference Dieulefait4–Reference Dieulefait and Vila6, Reference Reverter and Vila13, Reference Ribet14]). For example, [Reference Dieulefait and Vila6, Section 3.2] shows that
![]() $\operatorname {PSL}_2({\mathbb F}_{\ell ^2})$
occurs as a Galois group of an extension of
$\operatorname {PSL}_2({\mathbb F}_{\ell ^2})$
occurs as a Galois group of an extension of
![]() ${\mathbb Q}$
for all primes
${\mathbb Q}$
for all primes
![]() $\ell $
in an explicit set of density
$\ell $
in an explicit set of density
![]() $1-1/2^{10}$
(and for primes
$1-1/2^{10}$
(and for primes
![]() $\ell \leq 5,000,000$
). Furthermore, it is shown in [Reference Dieulefait and Vila6] that
$\ell \leq 5,000,000$
). Furthermore, it is shown in [Reference Dieulefait and Vila6] that
![]() $\operatorname {PSL}_2({\mathbb F}_{\ell ^4})$
occurs as a Galois group of an extension of
$\operatorname {PSL}_2({\mathbb F}_{\ell ^4})$
occurs as a Galois group of an extension of
![]() ${\mathbb Q}$
when
${\mathbb Q}$
when
![]() $\ell \equiv 2,3 \ \pmod {5}$
or
$\ell \equiv 2,3 \ \pmod {5}$
or
![]() $\ell \equiv \pm 3,\pm 5,\pm 6,\pm 7 \ \pmod {17}$
.
$\ell \equiv \pm 3,\pm 5,\pm 6,\pm 7 \ \pmod {17}$
.
The goal of this paper is to try to realize more groups of the form
![]() $\operatorname {PSL}_2({\mathbb F}_{\ell ^r})$
for odd r. We will achieve this by working with newforms of odd weight; the papers mentioned above focus on even weight modular forms (usual weight
$\operatorname {PSL}_2({\mathbb F}_{\ell ^r})$
for odd r. We will achieve this by working with newforms of odd weight; the papers mentioned above focus on even weight modular forms (usual weight
![]() $2$
). We will give background and describe the general situation in Section 1.1. In Sections 1.2 and 1.3, we will use specific newforms of weight
$2$
). We will give background and describe the general situation in Section 1.1. In Sections 1.2 and 1.3, we will use specific newforms of weight
![]() $3$
to realize many groups of the form
$3$
to realize many groups of the form
![]() $\operatorname {PSL}_2({\mathbb F}_{\ell ^r})$
with r equal to
$\operatorname {PSL}_2({\mathbb F}_{\ell ^r})$
with r equal to
![]() $1$
and
$1$
and
![]() $3$
, respectively.
$3$
, respectively.
Throughout the paper, we fix an algebraic closure
![]() ${\overline {\mathbb Q}}$
of
${\overline {\mathbb Q}}$
of
![]() ${\mathbb Q}$
and define the group
${\mathbb Q}$
and define the group
![]() $G:= \operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}/{\mathbb Q})$
. For a ring R, we let
$G:= \operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}/{\mathbb Q})$
. For a ring R, we let
![]() $\operatorname {PSL}_2(R)$
and
$\operatorname {PSL}_2(R)$
and
![]() $\operatorname {PGL}_2(R)$
be the quotients of
$\operatorname {PGL}_2(R)$
be the quotients of
![]() $\operatorname {SL}_2(R)$
and
$\operatorname {SL}_2(R)$
and
![]() $\operatorname {GL}_2(R)$
, respectively, by its subgroup of scalar matrices (in particular, this notation may disagree with the R-points of the corresponding group scheme
$\operatorname {GL}_2(R)$
, respectively, by its subgroup of scalar matrices (in particular, this notation may disagree with the R-points of the corresponding group scheme
![]() $\operatorname {PSL}_2$
or
$\operatorname {PSL}_2$
or
![]() $\operatorname {PGL}_2$
).
$\operatorname {PGL}_2$
).
1.1 General results
Fix a newform
![]() $f(\tau )=\sum _{n=1}^\infty a_n q^n$
of weight
$f(\tau )=\sum _{n=1}^\infty a_n q^n$
of weight
![]() $k>1$
on
$k>1$
on
![]() $\Gamma _1(N)$
without complex multiplication, where the
$\Gamma _1(N)$
without complex multiplication, where the
![]() $a_n$
are complex numbers and
$a_n$
are complex numbers and
![]() $q=e^{2\pi i \tau }$
with
$q=e^{2\pi i \tau }$
with
![]() $\tau $
a variable of the complex upper half-plane. Let
$\tau $
a variable of the complex upper half-plane. Let
![]() $\varepsilon \colon\ ({\mathbb Z}/N{\mathbb Z})^\times \to {\mathbb C}^\times $
be the nebentypus of f.
$\varepsilon \colon\ ({\mathbb Z}/N{\mathbb Z})^\times \to {\mathbb C}^\times $
be the nebentypus of f.
Let E be the subfield of
![]() ${\mathbb C}$
generated by the coefficients
${\mathbb C}$
generated by the coefficients
![]() $a_n$
; it is also generated by the coefficients
$a_n$
; it is also generated by the coefficients
![]() $a_p$
with primes
$a_p$
with primes
![]() $p\nmid N$
. The field E is a number field, and all the
$p\nmid N$
. The field E is a number field, and all the
![]() $a_n$
are known to lie in its ring of integers
$a_n$
are known to lie in its ring of integers
![]() ${\mathcal O}$
. The image of
${\mathcal O}$
. The image of
![]() $\varepsilon $
lies in
$\varepsilon $
lies in
![]() $E^\times $
. Let K be the subfield of E generated by the algebraic integers
$E^\times $
. Let K be the subfield of E generated by the algebraic integers
![]() $r_p:=a_p^2/\varepsilon (p)$
for primes
$r_p:=a_p^2/\varepsilon (p)$
for primes
![]() $p\nmid N$
; denote its ring of integers by R.
$p\nmid N$
; denote its ring of integers by R.
Take any nonzero prime ideal
![]() $\Lambda $
of
$\Lambda $
of
![]() ${\mathcal O}$
and denote by
${\mathcal O}$
and denote by
![]() $\ell =\ell (\Lambda )$
the rational prime lying under
$\ell =\ell (\Lambda )$
the rational prime lying under
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $E_\Lambda $
and
$E_\Lambda $
and
![]() ${\mathcal O}_\Lambda $
be the completions of E and
${\mathcal O}_\Lambda $
be the completions of E and
![]() ${\mathcal O}$
, respectively, at
${\mathcal O}$
, respectively, at
![]() $\Lambda $
. From [Reference Deligne3], we know that there is a continuous representation
$\Lambda $
. From [Reference Deligne3], we know that there is a continuous representation
such that for each prime
![]() $p\nmid N\ell $
, the representation
$p\nmid N\ell $
, the representation
![]() $\rho _\Lambda $
is unramified at p and satisfies
$\rho _\Lambda $
is unramified at p and satisfies
The representation
![]() $\rho _\Lambda $
is uniquely determined by the conditions (1.1) up to conjugation by an element of
$\rho _\Lambda $
is uniquely determined by the conditions (1.1) up to conjugation by an element of
![]() $\operatorname {GL}_2(E_\Lambda )$
. By composing
$\operatorname {GL}_2(E_\Lambda )$
. By composing
![]() $\rho _\Lambda $
with the natural projection arising from the reduction map
$\rho _\Lambda $
with the natural projection arising from the reduction map
![]() ${\mathcal O}_\Lambda \to {\mathbb F}_\Lambda :={\mathcal O}/\Lambda $
, we obtain a representation
${\mathcal O}_\Lambda \to {\mathbb F}_\Lambda :={\mathcal O}/\Lambda $
, we obtain a representation
Composing
with the natural quotient map
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )\to \operatorname {PGL}_2({\mathbb F}_\Lambda )$
, we obtain a homomorphism
$\operatorname {GL}_2({\mathbb F}_\Lambda )\to \operatorname {PGL}_2({\mathbb F}_\Lambda )$
, we obtain a homomorphism
Define the field
![]() ${\mathbb F}_\lambda :=R/\lambda $
, where
${\mathbb F}_\lambda :=R/\lambda $
, where
![]() $\lambda := \Lambda \cap R$
. There are natural injective homomorphisms
$\lambda := \Lambda \cap R$
. There are natural injective homomorphisms
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda ) \hookrightarrow \operatorname {PGL}_2({\mathbb F}_\lambda ) \hookrightarrow \operatorname {PGL}_2({\mathbb F}_\Lambda )$
and
$\operatorname {PSL}_2({\mathbb F}_\lambda ) \hookrightarrow \operatorname {PGL}_2({\mathbb F}_\lambda ) \hookrightarrow \operatorname {PGL}_2({\mathbb F}_\Lambda )$
and
![]() $\operatorname {PSL}_2({\mathbb F}_\Lambda ) \hookrightarrow \operatorname {PGL}_2({\mathbb F}_\Lambda )$
that we shall view as inclusions.
$\operatorname {PSL}_2({\mathbb F}_\Lambda ) \hookrightarrow \operatorname {PGL}_2({\mathbb F}_\Lambda )$
that we shall view as inclusions.
The main task of this paper is to describe the group
![]() for all
for all
![]() $\Lambda $
outside of some explicit set. The following theorem of Ribet gives two possibilities for
$\Lambda $
outside of some explicit set. The following theorem of Ribet gives two possibilities for
![]() for all but finitely many
for all but finitely many
![]() $\Lambda $
.
$\Lambda $
.
Theorem 1.1 (Ribet)
There is a finite set S of nonzero prime ideals of R such that if
![]() $\Lambda $
is a nonzero prime ideal of
$\Lambda $
is a nonzero prime ideal of
![]() ${\mathcal O}$
with
${\mathcal O}$
with
![]() $\lambda :=R\cap \Lambda \notin S$
, then the group
$\lambda :=R\cap \Lambda \notin S$
, then the group
![]() is conjugate in
is conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to either
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to either
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
![]() $\operatorname {PGL}_2({\mathbb F}_\lambda )$
.
$\operatorname {PGL}_2({\mathbb F}_\lambda )$
.
Proof As noted in Section 3 of [Reference Dieulefait and Wiese7], this is an easy consequence of [Reference Ribet16].
We will give a proof of Theorem 1.1 in Section 4 that allows one to compute such a set S. There are several related results in the literature; for example, Billerey and Dieulefait [Reference Billerey and Dieulefait1] give a version of Theorem 1.1 when the nebentypus
![]() $\varepsilon $
is trivial.
$\varepsilon $
is trivial.
We now explain how to distinguish the two possibilities from Theorem 1.1. Let
![]() $L\subseteq {\mathbb C}$
be the extension of K generated by the square roots of the values
$L\subseteq {\mathbb C}$
be the extension of K generated by the square roots of the values
![]() $r_p=a_p^2/\varepsilon (p)$
with
$r_p=a_p^2/\varepsilon (p)$
with
![]() $p\nmid N$
; it is a finite extension of K (moreover, it is contained in a finite cyclotomic extension of E).
$p\nmid N$
; it is a finite extension of K (moreover, it is contained in a finite cyclotomic extension of E).
Theorem 1.2 Let
![]() $\Lambda $
be a nonzero prime ideal of
$\Lambda $
be a nonzero prime ideal of
![]() ${\mathcal O}$
such that
${\mathcal O}$
such that
![]() is conjugate to
is conjugate to
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
![]() $\operatorname {PGL}_2({\mathbb F}_\lambda )$
, where
$\operatorname {PGL}_2({\mathbb F}_\lambda )$
, where
![]() $\lambda =\Lambda \cap R$
. After conjugating
$\lambda =\Lambda \cap R$
. After conjugating
![]() , we may assume that
, we may assume that
![]() . Let
. Let
![]() $\ell $
be the rational prime lying under
$\ell $
be the rational prime lying under
![]() $\Lambda $
.
$\Lambda $
.
-
(i) If k is odd, then
 if and only if
if and only if
 $\lambda $
splits completely in L.
$\lambda $
splits completely in L. -
(ii) If k is even and
 $[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is even, then
$[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is even, then
 if and only if
if and only if
 $\lambda $
splits completely in L.
$\lambda $
splits completely in L. -
(iii) If k is even,
 $[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is odd, and
$[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is odd, and
 $\ell \nmid N$
, then
$\ell \nmid N$
, then
 .
.
Remark 1.3
-
(i) From Theorem 1.2, we see that it is more challenging to produce Galois extensions of
 ${\mathbb Q}$
with Galois group
${\mathbb Q}$
with Galois group
 $\operatorname {PSL}_2({\mathbb F}_{\ell ^r})$
with odd r if we focus solely on newforms with k even. However, it is still possible to obtain such groups in the excluded case
$\operatorname {PSL}_2({\mathbb F}_{\ell ^r})$
with odd r if we focus solely on newforms with k even. However, it is still possible to obtain such groups in the excluded case
 $\ell | N$
.
$\ell | N$
. -
(ii) Parts (ii) and (iii) of Theorem 1.2 are included for completeness (see [Reference Dieulefait4, Proposition 1.5] for an equivalent version in the case
 $k=2$
due to Dieulefait). Surprisingly, there has been very little attention in the literature given to the case where k is odd (commenting on a preprint of this work, Dieulefait has shared several explicit examples worked out with Tsaknias and Vila). In Sections 1.2 and 1.3, we give examples with
$k=2$
due to Dieulefait). Surprisingly, there has been very little attention in the literature given to the case where k is odd (commenting on a preprint of this work, Dieulefait has shared several explicit examples worked out with Tsaknias and Vila). In Sections 1.2 and 1.3, we give examples with
 $k=3$
and
$k=3$
and
 $L=K$
(so
$L=K$
(so
 $\lambda $
splits in L for any
$\lambda $
splits in L for any
 $\lambda $
).
$\lambda $
).
1.2 An example realizing the groups
 $\text {PSL}_2({\mathbb F}_\ell )$
$\text {PSL}_2({\mathbb F}_\ell )$
We now give an example that realizes the simple groups
![]() $\operatorname {PSL}_2({\mathbb F}_\ell )$
as Galois groups of an extension of
$\operatorname {PSL}_2({\mathbb F}_\ell )$
as Galois groups of an extension of
![]() ${\mathbb Q}$
for all primes
${\mathbb Q}$
for all primes
![]() $\ell \geq 7$
. Let
$\ell \geq 7$
. Let
![]() $f=\sum _{n=1}^\infty a_n q^n$
be a newform of weight
$f=\sum _{n=1}^\infty a_n q^n$
be a newform of weight
![]() $3$
, level
$3$
, level
![]() $N=27$
, and nebentypus
$N=27$
, and nebentypus
![]() $\varepsilon (a)=\big (\frac {-3}{a}\big )$
; it is non-CM, i.e., it does not have complex multiplication. We can choose f so thatFootnote
1
$\varepsilon (a)=\big (\frac {-3}{a}\big )$
; it is non-CM, i.e., it does not have complex multiplication. We can choose f so thatFootnote
1
the other possibility for f is its complex conjugate
![]() .
.
The subfield E of
![]() ${\mathbb C}$
generated by the coefficients
${\mathbb C}$
generated by the coefficients
![]() $a_n$
is
$a_n$
is
![]() ${\mathbb Q}(i)$
. Take any prime
${\mathbb Q}(i)$
. Take any prime
![]() $p\neq 3$
. We will see that
$p\neq 3$
. We will see that
![]() . Therefore,
. Therefore,
![]() $a_p$
or
$a_p$
or
![]() $i a_p$
belongs to
$i a_p$
belongs to
![]() ${\mathbb Z}$
when
${\mathbb Z}$
when
![]() $\varepsilon (p)$
is
$\varepsilon (p)$
is
![]() $1$
or
$1$
or
![]() $-1$
, respectively, and hence
$-1$
, respectively, and hence
![]() $r_p=a_p^2/\varepsilon (p)$
is a square in
$r_p=a_p^2/\varepsilon (p)$
is a square in
![]() ${\mathbb Z}$
. Therefore,
${\mathbb Z}$
. Therefore,
![]() $L=K={\mathbb Q}$
.
$L=K={\mathbb Q}$
.
In Section 6.1, we shall verify that Theorem 1.1 holds with
![]() $S=\{2,3,5\}$
. Take any prime
$S=\{2,3,5\}$
. Take any prime
![]() $\ell \geq 7$
and prime
$\ell \geq 7$
and prime
![]() $\Lambda \subseteq {\mathbb Z}[i]$
dividing
$\Lambda \subseteq {\mathbb Z}[i]$
dividing
![]() $\ell $
. Theorem 1.2 with
$\ell $
. Theorem 1.2 with
![]() $L=K={\mathbb Q}$
implies that
$L=K={\mathbb Q}$
implies that
![]() is isomorphic to
is isomorphic to
![]() $\operatorname {PSL}_2({\mathbb F}_\ell )$
. The following theorem is now an immediate consequence (it is easy to prove directly for the group
$\operatorname {PSL}_2({\mathbb F}_\ell )$
. The following theorem is now an immediate consequence (it is easy to prove directly for the group
![]() $\operatorname {PSL}_2({\mathbb F}_5)\cong A_5$
).
$\operatorname {PSL}_2({\mathbb F}_5)\cong A_5$
).
Theorem 1.4 For each prime
![]() $\ell \geq 5$
, there is a Galois extension
$\ell \geq 5$
, there is a Galois extension
![]() $K/{\mathbb Q}$
such that
$K/{\mathbb Q}$
such that
![]() $\operatorname {\mathrm {Gal}}(K/{\mathbb Q})$
is isomorphic to the simple group
$\operatorname {\mathrm {Gal}}(K/{\mathbb Q})$
is isomorphic to the simple group
![]() $\operatorname {PSL}_2({\mathbb F}_\ell )$
.■
$\operatorname {PSL}_2({\mathbb F}_\ell )$
.■
Remark 1.5
-
(i) In Section 5.5 of [Reference Serre17], Serre describes the image of
 and proves that it gives rise to a
and proves that it gives rise to a
 $\operatorname {PSL}_2({\mathbb F}_7)$
-extension of
$\operatorname {PSL}_2({\mathbb F}_7)$
-extension of
 ${\mathbb Q}$
; however, he does not consider the image modulo other primes. Note that Serre was actually giving an example of his conjecture, so he started with the
${\mathbb Q}$
; however, he does not consider the image modulo other primes. Note that Serre was actually giving an example of his conjecture, so he started with the
 $\operatorname {PSL}_2({\mathbb F}_7)$
-extension and then found the newform f.
$\operatorname {PSL}_2({\mathbb F}_7)$
-extension and then found the newform f. -
(ii) Theorem 1.4 was first proved by the author in [Reference Zywina18] by considering the Galois action on the second
 $\ell $
-adic étale cohomology of a specific surface. One can show that the Galois extensions of [Reference Zywina18] could also be constructed by first starting with an appropriate newform of weight
$\ell $
-adic étale cohomology of a specific surface. One can show that the Galois extensions of [Reference Zywina18] could also be constructed by first starting with an appropriate newform of weight
 $3$
and level
$3$
and level
 $32$
.
$32$
.
1.3 Another example
We now give an example with
![]() $K\neq {\mathbb Q}$
. Additional details will be provided in Section 6.2. Let
$K\neq {\mathbb Q}$
. Additional details will be provided in Section 6.2. Let
![]() $f=\sum _n a_n q^n$
be a non-CM newform of weight
$f=\sum _n a_n q^n$
be a non-CM newform of weight
![]() $3$
, level
$3$
, level
![]() $N=160$
, and nebentypus
$N=160$
, and nebentypus
![]() $\varepsilon (a)=\big (\frac {-5}{a}\big )$
.
$\varepsilon (a)=\big (\frac {-5}{a}\big )$
.
Take E, K, L, R, and
![]() ${\mathcal O}$
as in Section 1.1. We will see in Section 6.2 that
${\mathcal O}$
as in Section 1.1. We will see in Section 6.2 that
![]() $E=K(i)$
and that K is the unique cubic field in
$E=K(i)$
and that K is the unique cubic field in
![]() ${\mathbb Q}(\zeta _{13})$
. We will also observe that
${\mathbb Q}(\zeta _{13})$
. We will also observe that
![]() $L=K$
.
$L=K$
.
Take any odd prime
![]() $\ell $
congruent to
$\ell $
congruent to
![]() $\pm 2$
,
$\pm 2$
,
![]() $\pm 3$
,
$\pm 3$
,
![]() $\pm 4$
, or
$\pm 4$
, or
![]() $\pm 6$
modulo
$\pm 6$
modulo
![]() $13$
. Let
$13$
. Let
![]() $\Lambda $
be any prime ideal of
$\Lambda $
be any prime ideal of
![]() ${\mathcal O}$
dividing
${\mathcal O}$
dividing
![]() $\ell $
, and set
$\ell $
, and set
![]() $\lambda = \Lambda \cap R$
. The assumption on
$\lambda = \Lambda \cap R$
. The assumption on
![]() $\ell $
modulo
$\ell $
modulo
![]() $13$
implies that
$13$
implies that
![]() $\lambda = \ell R$
and that
$\lambda = \ell R$
and that
![]() ${\mathbb F}_\lambda \cong {\mathbb F}_{\ell ^3}$
. In Section 6.2, we shall compute a set S as in Theorem 1.1 which does not contain
${\mathbb F}_\lambda \cong {\mathbb F}_{\ell ^3}$
. In Section 6.2, we shall compute a set S as in Theorem 1.1 which does not contain
![]() $\lambda $
. Theorem 1.2 with
$\lambda $
. Theorem 1.2 with
![]() $L=K$
implies that
$L=K$
implies that
![]() is isomorphic to
is isomorphic to
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )\cong \operatorname {PSL}_2({\mathbb F}_{\ell ^3})$
. The following is an immediate consequence.
$\operatorname {PSL}_2({\mathbb F}_\lambda )\cong \operatorname {PSL}_2({\mathbb F}_{\ell ^3})$
. The following is an immediate consequence.
Theorem 1.6 If
![]() $\ell $
is an odd prime congruent to
$\ell $
is an odd prime congruent to
![]() $\pm 2$
,
$\pm 2$
,
![]() $\pm 3$
,
$\pm 3$
,
![]() $\pm 4$
, or
$\pm 4$
, or
![]() $\pm 6$
modulo
$\pm 6$
modulo
![]() $13$
, then the simple group
$13$
, then the simple group
![]() $\operatorname {PSL}_2({\mathbb F}_{\ell ^3})$
occurs as the Galois group of an extension of
$\operatorname {PSL}_2({\mathbb F}_{\ell ^3})$
occurs as the Galois group of an extension of
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
2 The fields K and L
Take a newform f with notation and assumptions as in Section 1.1.
2.1 The field K
Let
![]() $\Gamma $
be the set of automorphisms
$\Gamma $
be the set of automorphisms
![]() $\gamma $
of the field E for which there is a primitive Dirichlet character
$\gamma $
of the field E for which there is a primitive Dirichlet character
![]() $\chi _\gamma $
that satisfies
$\chi _\gamma $
that satisfies
for all primes
![]() $p\nmid N$
. The set of primes p with
$p\nmid N$
. The set of primes p with
![]() $a_p\neq 0$
has density
$a_p\neq 0$
has density
![]() $1$
since f is non-CM, so the image of
$1$
since f is non-CM, so the image of
![]() $\chi _\gamma $
lies in
$\chi _\gamma $
lies in
![]() $E^\times $
and the character
$E^\times $
and the character
![]() $\chi _\gamma $
is uniquely determined from
$\chi _\gamma $
is uniquely determined from
![]() $\gamma $
.
$\gamma $
.
Define M to be N or
![]() $4N$
if N is odd or even, respectively. The conductor of
$4N$
if N is odd or even, respectively. The conductor of
![]() $\chi _\gamma $
divides M (cf. [Reference Momose12, Remark 1.6]). Moreover, there is a quadratic Dirichlet character
$\chi _\gamma $
divides M (cf. [Reference Momose12, Remark 1.6]). Moreover, there is a quadratic Dirichlet character
![]() $\alpha $
with conductor dividing M and an integer i such that
$\alpha $
with conductor dividing M and an integer i such that
![]() $\chi _\gamma $
is the primitive character coming from
$\chi _\gamma $
is the primitive character coming from
![]() $\alpha \varepsilon ^i$
(cf. [Reference Momose12, Lemma 1.5(i)]).
$\alpha \varepsilon ^i$
(cf. [Reference Momose12, Lemma 1.5(i)]).
For each prime
![]() $p\nmid N$
, we have
$p\nmid N$
, we have
![]() (cf. [Reference Ribet15, p. 21]), so complex conjugation induces an automorphism
(cf. [Reference Ribet15, p. 21]), so complex conjugation induces an automorphism
![]() $\gamma $
of E and
$\gamma $
of E and
![]() $\chi _\gamma $
is the primitive character coming from
$\chi _\gamma $
is the primitive character coming from
![]() $\varepsilon ^{-1}$
. In particular,
$\varepsilon ^{-1}$
. In particular,
![]() $\Gamma \neq 1$
if
$\Gamma \neq 1$
if
![]() $\varepsilon $
is nontrivial.
$\varepsilon $
is nontrivial.
Remark 2.1 More generally, we could have instead considered an embedding
![]() $\gamma \colon E \to {\mathbb C}$
and a Dirichlet character
$\gamma \colon E \to {\mathbb C}$
and a Dirichlet character
![]() $\chi _\gamma $
such that (2.1) holds for all sufficiently large primes p. This gives the same twists, since
$\chi _\gamma $
such that (2.1) holds for all sufficiently large primes p. This gives the same twists, since
![]() $\gamma (E)=E$
and the character
$\gamma (E)=E$
and the character
![]() $\chi _\gamma $
is unramified at primes
$\chi _\gamma $
is unramified at primes
![]() $p\nmid N$
(cf. [Reference Momose12, Remark 1.3]).
$p\nmid N$
(cf. [Reference Momose12, Remark 1.3]).
The set
![]() $\Gamma $
is in fact an abelian subgroup of
$\Gamma $
is in fact an abelian subgroup of
![]() $\operatorname {\mathrm {Aut}}(E)$
(cf. [Reference Momose12, Lemma 1.5(ii)]). Denote by
$\operatorname {\mathrm {Aut}}(E)$
(cf. [Reference Momose12, Lemma 1.5(ii)]). Denote by
![]() $E^{\Gamma }$
the fixed field of E by
$E^{\Gamma }$
the fixed field of E by
![]() $\Gamma $
.
$\Gamma $
.
Lemma 2.2
-
(i) We have
 $K=E^{\Gamma} $
, and hence
$K=E^{\Gamma} $
, and hence
 $\operatorname {\mathrm {Gal}}(E/K)=\Gamma $
.
$\operatorname {\mathrm {Gal}}(E/K)=\Gamma $
. -
(ii) There is a prime
 $p\nmid N$
such that
$p\nmid N$
such that
 $K={\mathbb Q}(r_p)$
.
$K={\mathbb Q}(r_p)$
.
Proof Take any
![]() $p\nmid N$
. For each
$p\nmid N$
. For each
![]() $\gamma \in \Gamma $
, we have
$\gamma \in \Gamma $
, we have
where we have used that
![]() $\chi _\gamma (p)^2 = \gamma (\varepsilon (p))/\varepsilon (p)$
(cf. [Reference Momose12, Proof of Lemma 1.5(ii)]). This shows that
$\chi _\gamma (p)^2 = \gamma (\varepsilon (p))/\varepsilon (p)$
(cf. [Reference Momose12, Proof of Lemma 1.5(ii)]). This shows that
![]() $r_p$
belong in
$r_p$
belong in
![]() $E^{\Gamma} $
and hence
$E^{\Gamma} $
and hence
![]() $K\subseteq E^{\Gamma} $
since
$K\subseteq E^{\Gamma} $
since
![]() $p\nmid N$
was arbitrary. To complete the proof of the lemma, it thus suffices to show that
$p\nmid N$
was arbitrary. To complete the proof of the lemma, it thus suffices to show that
![]() $E^{\Gamma} ={\mathbb Q}(r_p)$
for some prime
$E^{\Gamma} ={\mathbb Q}(r_p)$
for some prime
![]() $p\nmid N$
.
$p\nmid N$
.
For
![]() $\gamma \in \Gamma $
, let
$\gamma \in \Gamma $
, let
![]() $\widetilde \chi _\gamma \colon G \to {\mathbb C}^\times $
be the continuous character such that
$\widetilde \chi _\gamma \colon G \to {\mathbb C}^\times $
be the continuous character such that
![]() $\widetilde \chi _\gamma (\operatorname {\mathrm {Frob}}_p)=\chi _\gamma (p)$
for all
$\widetilde \chi _\gamma (\operatorname {\mathrm {Frob}}_p)=\chi _\gamma (p)$
for all
![]() $p\nmid N$
. Define the group
$p\nmid N$
. Define the group
![]() $H = \bigcap _{\gamma \in \Gamma } \ker \widetilde \chi _\gamma $
; it is an open normal subgroup of G with
$H = \bigcap _{\gamma \in \Gamma } \ker \widetilde \chi _\gamma $
; it is an open normal subgroup of G with
![]() $G/H$
is abelian. Let
$G/H$
is abelian. Let
![]() ${\mathcal K}$
be the subfield of
${\mathcal K}$
be the subfield of
![]() ${\overline {\mathbb Q}}$
fixed by H; it is a finite abelian extension of
${\overline {\mathbb Q}}$
fixed by H; it is a finite abelian extension of
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
Fix a prime
![]() $\ell $
and a prime ideal
$\ell $
and a prime ideal
![]() $\Lambda | \ell $
of
$\Lambda | \ell $
of
![]() ${\mathcal O}$
. In the proof of Theorem 3.1 of [Reference Ribet16], Ribet proved that
${\mathcal O}$
. In the proof of Theorem 3.1 of [Reference Ribet16], Ribet proved that
![]() $E^{\Gamma} ={\mathbb Q}(a_v^2)$
for a positive density set of finite place
$E^{\Gamma} ={\mathbb Q}(a_v^2)$
for a positive density set of finite place
![]() $v\nmid N\ell $
of
$v\nmid N\ell $
of
![]() ${\mathcal K}$
, where
${\mathcal K}$
, where
![]() $a_v:=\operatorname {\mathrm {tr}}(\rho _\Lambda (\operatorname {\mathrm {Frob}}_v))$
. There is thus a finite place
$a_v:=\operatorname {\mathrm {tr}}(\rho _\Lambda (\operatorname {\mathrm {Frob}}_v))$
. There is thus a finite place
![]() $v\nmid N\ell $
of
$v\nmid N\ell $
of
![]() ${\mathcal K}$
of degree
${\mathcal K}$
of degree
![]() $1$
such that
$1$
such that
![]() $E^{\Gamma} ={\mathbb Q}(a_v^2)$
. We have
$E^{\Gamma} ={\mathbb Q}(a_v^2)$
. We have
![]() $a_v=a_p$
, where p is the rational prime that v divides, so
$a_v=a_p$
, where p is the rational prime that v divides, so
![]() $E^{\Gamma} ={\mathbb Q}(a_p^2)$
. Since v has degree
$E^{\Gamma} ={\mathbb Q}(a_p^2)$
. Since v has degree
![]() $1$
and
$1$
and
![]() ${\mathcal K}/{\mathbb Q}$
is abelian, the prime p must split completely in
${\mathcal K}/{\mathbb Q}$
is abelian, the prime p must split completely in
![]() ${\mathcal K}$
and hence
${\mathcal K}$
and hence
![]() $\chi _\gamma (p)=1$
for all
$\chi _\gamma (p)=1$
for all
![]() $\gamma \in \Gamma $
; in particular,
$\gamma \in \Gamma $
; in particular,
![]() $\varepsilon (p)=1$
. Therefore,
$\varepsilon (p)=1$
. Therefore,
![]() $E^{\Gamma} ={\mathbb Q}(r_p)$
.
$E^{\Gamma} ={\mathbb Q}(r_p)$
.
2.2 The field L
Recall that we defined L to be the extension of K in
![]() ${\mathbb C}$
obtained by adjoining the square root of
${\mathbb C}$
obtained by adjoining the square root of
![]() $r_p = a_p^2/\varepsilon (p)$
for all
$r_p = a_p^2/\varepsilon (p)$
for all
![]() $p\nmid N$
. The following allows one to find a finite set of generators for the extension
$p\nmid N$
. The following allows one to find a finite set of generators for the extension
![]() $L/K$
and gives a way to check the criterion of Theorem 1.2.
$L/K$
and gives a way to check the criterion of Theorem 1.2.
Lemma 2.3
-
(i) Choose primes
 $p_1,\ldots , p_m \nmid N$
that generate the group
$p_1,\ldots , p_m \nmid N$
that generate the group
 $({\mathbb Z}/M{\mathbb Z})^\times $
and satisfy
$({\mathbb Z}/M{\mathbb Z})^\times $
and satisfy
 $r_{p_i}\neq 0$
for all
$r_{p_i}\neq 0$
for all
 $1\leq i\leq m$
. Then
$1\leq i\leq m$
. Then
 $L=K(\sqrt {r_{p_1}},\ldots ,\sqrt {r_{p_m}})$
.
$L=K(\sqrt {r_{p_1}},\ldots ,\sqrt {r_{p_m}})$
. -
(ii) Take any nonzero prime ideal
 $\lambda $
of R that does not divide
$\lambda $
of R that does not divide
 $2$
. Let
$2$
. Let
 $p_1,\ldots , p_m$
be primes as in (i). Then the following are equivalent:
$p_1,\ldots , p_m$
be primes as in (i). Then the following are equivalent:-
(a)
 $ \lambda $
splits completely in L.
$ \lambda $
splits completely in L. -
(b) For all
 $p\nmid N$
,
$p\nmid N$
,
 $r_p$
is a square in
$r_p$
is a square in
 $K_\lambda $
.
$K_\lambda $
. -
(c) For all
 $1\leq i \leq m$
,
$1\leq i \leq m$
,
 $r_{p_i}$
is a square in
$r_{p_i}$
is a square in
 $K_\lambda $
.
$K_\lambda $
.
-
Proof Take any prime
![]() $p\nmid N$
. To prove part (i), it suffices to show that
$p\nmid N$
. To prove part (i), it suffices to show that
![]() $\sqrt {r_p}$
belongs to the field
$\sqrt {r_p}$
belongs to the field
![]() $L':=K(\sqrt {r_{p_1}},\ldots ,\sqrt {r_{p_m}})$
. This is obvious if
$L':=K(\sqrt {r_{p_1}},\ldots ,\sqrt {r_{p_m}})$
. This is obvious if
![]() $r_p=0$
, so assume that
$r_p=0$
, so assume that
![]() $r_p\neq 0$
. Since the
$r_p\neq 0$
. Since the
![]() $p_i$
generate
$p_i$
generate
![]() $({\mathbb Z}/M{\mathbb Z})^\times $
by assumption, there are integers
$({\mathbb Z}/M{\mathbb Z})^\times $
by assumption, there are integers
![]() $e_i\geq 0$
such that
$e_i\geq 0$
such that
![]() $p\equiv p_1^{e_1} \cdots p_m^{e_m} \ \pmod {M}$
. Take any
$p\equiv p_1^{e_1} \cdots p_m^{e_m} \ \pmod {M}$
. Take any
![]() $\gamma \in \Gamma $
. Using that the conductor of
$\gamma \in \Gamma $
. Using that the conductor of
![]() $\chi _\gamma $
divides M and (2.1), we have
$\chi _\gamma $
divides M and (2.1), we have
 $$\begin{align*}\gamma\Big( \frac{a_p}{{\prod}_i a_{p_i}^{e_i}} \Big) =\frac{\chi_\gamma(p)}{\chi_\gamma({\prod}_i p_i^{e_i})} \cdot \frac{a_p}{{\prod}_i a_{p_i}^{e_i}} = \frac{\chi_\gamma(p)}{\chi_\gamma(p)}\cdot \frac{a_p}{{\prod}_i a_{p_i}^{e_i}} = \frac{a_p}{{\prod}_i a_{p_i}^{e_i}}. \end{align*}$$
$$\begin{align*}\gamma\Big( \frac{a_p}{{\prod}_i a_{p_i}^{e_i}} \Big) =\frac{\chi_\gamma(p)}{\chi_\gamma({\prod}_i p_i^{e_i})} \cdot \frac{a_p}{{\prod}_i a_{p_i}^{e_i}} = \frac{\chi_\gamma(p)}{\chi_\gamma(p)}\cdot \frac{a_p}{{\prod}_i a_{p_i}^{e_i}} = \frac{a_p}{{\prod}_i a_{p_i}^{e_i}}. \end{align*}$$
Since
![]() $E^{\Gamma} =K$
by Lemma 2.2(i), the value
$E^{\Gamma} =K$
by Lemma 2.2(i), the value
![]() $a_p/{\prod }_i a_{p_i}^{e_i}$
belongs to K; it is nonzero since
$a_p/{\prod }_i a_{p_i}^{e_i}$
belongs to K; it is nonzero since
![]() $r_p\neq 0$
and
$r_p\neq 0$
and
![]() $r_{p_i}\neq 0$
. We have
$r_{p_i}\neq 0$
. We have
![]() $\varepsilon (p) = \prod _i \varepsilon (p_i)^{e_i}$
since the conductor of
$\varepsilon (p) = \prod _i \varepsilon (p_i)^{e_i}$
since the conductor of
![]() $\varepsilon $
divides M. Therefore,
$\varepsilon $
divides M. Therefore,
 $$\begin{align*}\frac{r_p}{{\prod}_i r_{p_i}^{e_i}} = \frac{a_p^2}{{\prod}_i (a_{p_i}^2)^{e_i}} = \bigg(\frac{a_p}{{\prod}_i a_{p_i}^{e_i}}\bigg)^2 \in (K^\times)^2. \end{align*}$$
$$\begin{align*}\frac{r_p}{{\prod}_i r_{p_i}^{e_i}} = \frac{a_p^2}{{\prod}_i (a_{p_i}^2)^{e_i}} = \bigg(\frac{a_p}{{\prod}_i a_{p_i}^{e_i}}\bigg)^2 \in (K^\times)^2. \end{align*}$$
This shows that
![]() $\sqrt {r_p}$
is contained in
$\sqrt {r_p}$
is contained in
![]() $L'$
as desired. This proves (i); part (ii) is an easy consequence of (i).
$L'$
as desired. This proves (i); part (ii) is an easy consequence of (i).
Remark 2.4 Finding primes
![]() $p_i$
as in Lemma 2.3(i) is straightforward since
$p_i$
as in Lemma 2.3(i) is straightforward since
![]() $r_p\neq 0$
for all p outside a set of density
$r_p\neq 0$
for all p outside a set of density
![]() $0$
(and the primes representing each class
$0$
(and the primes representing each class
![]() $a\in ({\mathbb Z}/M{\mathbb Z})^\times $
have positive density). Lemma 2.3(ii) gives a straightforward way to check if
$a\in ({\mathbb Z}/M{\mathbb Z})^\times $
have positive density). Lemma 2.3(ii) gives a straightforward way to check if
![]() $\lambda $
splits completely in L. Let
$\lambda $
splits completely in L. Let
![]() $e_i$
be the
$e_i$
be the
![]() $\lambda $
-adic valuation of
$\lambda $
-adic valuation of
![]() $r_{p_i}$
, and let
$r_{p_i}$
, and let
![]() $\pi $
be a uniformizer of
$\pi $
be a uniformizer of
![]() $K_\lambda $
; then
$K_\lambda $
; then
![]() $r_{p_i}$
is a square in
$r_{p_i}$
is a square in
![]() $K_\lambda $
if and only if e is even and the image of
$K_\lambda $
if and only if e is even and the image of
![]() $r_{p_i}/\pi ^{e_i}$
in
$r_{p_i}/\pi ^{e_i}$
in
![]() ${\mathbb F}_\lambda $
is a square.
${\mathbb F}_\lambda $
is a square.
3 Proof of Theorem 1.2
We may assume that
![]() is
is
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
![]() $\operatorname {PGL}_2({\mathbb F}_\lambda )$
. For any
$\operatorname {PGL}_2({\mathbb F}_\lambda )$
. For any
![]() $n\geq 1$
, the group
$n\geq 1$
, the group
![]() $\operatorname {GL}_2({\mathbb F}_{2^n})$
is generated by
$\operatorname {GL}_2({\mathbb F}_{2^n})$
is generated by
![]() $\operatorname {SL}_2({\mathbb F}_{2^n})$
and its scalar matrices, so
$\operatorname {SL}_2({\mathbb F}_{2^n})$
and its scalar matrices, so
![]() $\operatorname {PSL}_2({\mathbb F}_{2^n})=\operatorname {PGL}_2({\mathbb F}_{2^n})$
. The theorem is thus trivial when
$\operatorname {PSL}_2({\mathbb F}_{2^n})=\operatorname {PGL}_2({\mathbb F}_{2^n})$
. The theorem is thus trivial when
![]() $\ell =2$
, so we may assume that
$\ell =2$
, so we may assume that
![]() $\ell $
is odd.
$\ell $
is odd.
Take any
![]() $\alpha \in \operatorname {PGL}_2({\mathbb F}_\lambda )\subseteq \operatorname {PGL}_2({\mathbb F}_\Lambda )$
and choose any matrix
$\alpha \in \operatorname {PGL}_2({\mathbb F}_\lambda )\subseteq \operatorname {PGL}_2({\mathbb F}_\Lambda )$
and choose any matrix
![]() $A\in \operatorname {GL}_2({\mathbb F}_\Lambda )$
whose image in
$A\in \operatorname {GL}_2({\mathbb F}_\Lambda )$
whose image in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
is
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
is
![]() $\alpha $
. The value
$\alpha $
. The value
![]() $\operatorname {\mathrm {tr}}(A)^2/\det (A)$
does not depend on the choice of A and lies in
$\operatorname {\mathrm {tr}}(A)^2/\det (A)$
does not depend on the choice of A and lies in
![]() ${\mathbb F}_\lambda $
(since we can choose A in
${\mathbb F}_\lambda $
(since we can choose A in
![]() $\operatorname {GL}_2({\mathbb F}_\lambda )$
); by abuse of notation, we denote this common value by
$\operatorname {GL}_2({\mathbb F}_\lambda )$
); by abuse of notation, we denote this common value by
![]() $\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha )$
.
$\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha )$
.
Lemma 3.1 Suppose that
![]() $p\nmid N\ell $
is a prime for which
$p\nmid N\ell $
is a prime for which
![]() $r_p \not \equiv 0\ \pmod {\lambda }$
. Then
$r_p \not \equiv 0\ \pmod {\lambda }$
. Then
![]() is contained in
is contained in
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
if and only if the image of
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
if and only if the image of
![]() $a_p^2/(\varepsilon (p) p^{k-1})=r_p/p^{k-1}$
in
$a_p^2/(\varepsilon (p) p^{k-1})=r_p/p^{k-1}$
in
![]() ${\mathbb F}_\lambda ^\times $
is a square.
${\mathbb F}_\lambda ^\times $
is a square.
Proof Define
![]() and
and
![]() ; the image of A in
; the image of A in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
is
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
is
![]() $\alpha $
. The value
$\alpha $
. The value
![]() $\xi _p:=\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha ) = \operatorname {\mathrm {tr}}(A)^2/\det (A)$
agrees with the image of
$\xi _p:=\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha ) = \operatorname {\mathrm {tr}}(A)^2/\det (A)$
agrees with the image of
![]() $a_p^2/(\varepsilon (p)p^{k-1})= r_p/p^{k-1}$
in
$a_p^2/(\varepsilon (p)p^{k-1})= r_p/p^{k-1}$
in
![]() ${\mathbb F}_\Lambda $
. Since
${\mathbb F}_\Lambda $
. Since
![]() $r_p \in R$
is nonzero modulo
$r_p \in R$
is nonzero modulo
![]() $\lambda $
by assumption, the value
$\lambda $
by assumption, the value
![]() $\xi _p$
lies in
$\xi _p$
lies in
![]() ${\mathbb F}_\lambda ^\times $
. Fix a matrix
${\mathbb F}_\lambda ^\times $
. Fix a matrix
![]() $A_0 \in \operatorname {GL}_2({\mathbb F}_\lambda )$
whose image in
$A_0 \in \operatorname {GL}_2({\mathbb F}_\lambda )$
whose image in
![]() $\operatorname {PGL}_2({\mathbb F}_\lambda )$
is
$\operatorname {PGL}_2({\mathbb F}_\lambda )$
is
![]() $\alpha $
; we have
$\alpha $
; we have
![]() $\xi _p = \operatorname {\mathrm {tr}}(A_0)^2/\det (A_0)$
. Since
$\xi _p = \operatorname {\mathrm {tr}}(A_0)^2/\det (A_0)$
. Since
![]() $\xi _p \neq 0$
, we find that
$\xi _p \neq 0$
, we find that
![]() $\xi _p$
and
$\xi _p$
and
![]() $\det (A_0)$
lie in the same coset in
$\det (A_0)$
lie in the same coset in
![]() ${\mathbb F}_\lambda ^\times /({\mathbb F}_\lambda ^\times )^2$
.
${\mathbb F}_\lambda ^\times /({\mathbb F}_\lambda ^\times )^2$
.
The determinant gives rise to a homomorphism
![]() $d\colon \operatorname {PGL}_2({\mathbb F}_\lambda ) \to {\mathbb F}_\lambda ^\times /( {\mathbb F}_\lambda ^\times )^2$
whose kernel is
$d\colon \operatorname {PGL}_2({\mathbb F}_\lambda ) \to {\mathbb F}_\lambda ^\times /( {\mathbb F}_\lambda ^\times )^2$
whose kernel is
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
. Define the character
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
. Define the character
We have
![]() $\xi (\operatorname {\mathrm {Frob}}_p) = \det (A_0) \cdot ( {\mathbb F}_\lambda ^\times )^2 = \xi _p \cdot ( {\mathbb F}_\lambda ^\times )^2$
. So
$\xi (\operatorname {\mathrm {Frob}}_p) = \det (A_0) \cdot ( {\mathbb F}_\lambda ^\times )^2 = \xi _p \cdot ( {\mathbb F}_\lambda ^\times )^2$
. So
![]() $\xi (\operatorname {\mathrm {Frob}}_p)=1$
, equivalently
$\xi (\operatorname {\mathrm {Frob}}_p)=1$
, equivalently
, if and only if
![]() $\xi _p \in {\mathbb F}_\lambda ^\times $
is a square.
$\xi _p \in {\mathbb F}_\lambda ^\times $
is a square.
Let M be the integer from Section 2.1.
Lemma 3.2 For each
![]() $a\in ({\mathbb Z}/M\ell {\mathbb Z})^\times $
, there is a prime
$a\in ({\mathbb Z}/M\ell {\mathbb Z})^\times $
, there is a prime
![]() $p\equiv a \ \pmod {M\ell }$
such that
$p\equiv a \ \pmod {M\ell }$
such that
![]() $r_p \not \equiv 0 \ \pmod {\lambda }$
.
$r_p \not \equiv 0 \ \pmod {\lambda }$
.
Proof Set
![]() ; it is
; it is
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
![]() $\operatorname {PGL}_2({\mathbb F}_\lambda )$
by assumption. Let
$\operatorname {PGL}_2({\mathbb F}_\lambda )$
by assumption. Let
![]() $H'$
be the commutator subgroup of H. We claim that for each coset
$H'$
be the commutator subgroup of H. We claim that for each coset
![]() $\kappa $
of
$\kappa $
of
![]() $H'$
in H, there exists an
$H'$
in H, there exists an
![]() $\alpha \in \kappa $
with
$\alpha \in \kappa $
with
![]() $\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha )\neq 0$
. If
$\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha )\neq 0$
. If
![]() $H'=\operatorname {PSL}_2({\mathbb F}_\lambda )$
, then the claim is easy; note that for any
$H'=\operatorname {PSL}_2({\mathbb F}_\lambda )$
, then the claim is easy; note that for any
![]() $t\in {\mathbb F}_\lambda $
and
$t\in {\mathbb F}_\lambda $
and
![]() $d\in {\mathbb F}_\lambda ^\times $
, there is a matrix in
$d\in {\mathbb F}_\lambda ^\times $
, there is a matrix in
![]() $\operatorname {GL}_2({\mathbb F}_\lambda )$
with trace t and determinant d. When
$\operatorname {GL}_2({\mathbb F}_\lambda )$
with trace t and determinant d. When
![]() $\#{\mathbb F}_\lambda \neq 3$
, the group
$\#{\mathbb F}_\lambda \neq 3$
, the group
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
is non-abelian and simple, so
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
is non-abelian and simple, so
![]() $H'=\operatorname {PSL}_2({\mathbb F}_\lambda )$
. When
$H'=\operatorname {PSL}_2({\mathbb F}_\lambda )$
. When
![]() $\#{\mathbb F}_\lambda =3$
and
$\#{\mathbb F}_\lambda =3$
and
![]() $H=\operatorname {PGL}_2({\mathbb F}_\lambda )$
, we have
$H=\operatorname {PGL}_2({\mathbb F}_\lambda )$
, we have
![]() $H'=\operatorname {PSL}_2({\mathbb F}_\lambda )$
. It thus suffices to prove the claim in the case where
$H'=\operatorname {PSL}_2({\mathbb F}_\lambda )$
. It thus suffices to prove the claim in the case where
![]() ${\mathbb F}_\lambda ={\mathbb F}_3$
and
${\mathbb F}_\lambda ={\mathbb F}_3$
and
![]() $H=\operatorname {PSL}_2({\mathbb F}_3)$
. In this case,
$H=\operatorname {PSL}_2({\mathbb F}_3)$
. In this case,
![]() $H'$
is the unique subgroup of H of index
$H'$
is the unique subgroup of H of index
![]() $3$
and the cosets of
$3$
and the cosets of
![]() $H/H'$
are represented by
$H/H'$
are represented by
![]() $\left (\begin {smallmatrix} 1 & b \\ 0 & 1 \end {smallmatrix}\right )$
with
$\left (\begin {smallmatrix} 1 & b \\ 0 & 1 \end {smallmatrix}\right )$
with
![]() $b\in {\mathbb F}_3$
. The claim is now immediate in this remaining case.
$b\in {\mathbb F}_3$
. The claim is now immediate in this remaining case.
Let
![]() $\chi \colon\ G\twoheadrightarrow ({\mathbb Z}/M\ell {\mathbb Z})^\times $
be the cyclotomic character that satisfies
$\chi \colon\ G\twoheadrightarrow ({\mathbb Z}/M\ell {\mathbb Z})^\times $
be the cyclotomic character that satisfies
![]() $\chi (\operatorname {\mathrm {Frob}}_p) \equiv p \ \pmod {M\ell }$
for all
$\chi (\operatorname {\mathrm {Frob}}_p) \equiv p \ \pmod {M\ell }$
for all
![]() $p\nmid M\ell $
. The set
$p\nmid M\ell $
. The set
![]() is thus the union of cosets of
is thus the union of cosets of
![]() $H'$
in H. By the claim above, there exists an
$H'$
in H. By the claim above, there exists an
![]() with
with
![]() $\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha )~\neq~0$
. By the Chebotarev density theorem, there is a prime
$\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha )~\neq~0$
. By the Chebotarev density theorem, there is a prime
![]() $p\nmid M\ell $
satisfying
$p\nmid M\ell $
satisfying
![]() $p\equiv a \ \pmod {M\ell }$
and
$p\equiv a \ \pmod {M\ell }$
and
![]() . The lemma follows since
. The lemma follows since
![]() $r_p/p^{k-1}$
modulo
$r_p/p^{k-1}$
modulo
![]() $\lambda $
agrees with
$\lambda $
agrees with
![]() $\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha )\neq 0$
.
$\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha )\neq 0$
.
Case 1: Assume that k is odd or
![]() $[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is even.
$[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is even.
First, suppose that
![]() . By Lemma 3.2, there are primes
. By Lemma 3.2, there are primes
![]() $p_1,\ldots , p_m \nmid N\ell $
that generate the group
$p_1,\ldots , p_m \nmid N\ell $
that generate the group
![]() $({\mathbb Z}/M{\mathbb Z})^\times $
and satisfy
$({\mathbb Z}/M{\mathbb Z})^\times $
and satisfy
![]() $r_{p_i}\not \equiv 0 \ \pmod {\lambda }$
for all
$r_{p_i}\not \equiv 0 \ \pmod {\lambda }$
for all
![]() $1\leq i\leq m$
. By Lemma 3.1 and the assumption
$1\leq i\leq m$
. By Lemma 3.1 and the assumption
![]() , the image of
, the image of
![]() $r_{p_i}/{p_i}^{k-1}$
in
$r_{p_i}/{p_i}^{k-1}$
in
![]() ${\mathbb F}_\lambda $
is a nonzero square for all
${\mathbb F}_\lambda $
is a nonzero square for all
![]() $1\leq i \leq m$
. For each
$1\leq i \leq m$
. For each
![]() $1\leq i \leq m$
, the assumption that k is odd or
$1\leq i \leq m$
, the assumption that k is odd or
![]() $[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is even implies that
$[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is even implies that
![]() $p_i^{k-1}$
is a square in
$p_i^{k-1}$
is a square in
![]() ${\mathbb F}_\lambda $
, and hence the image of
${\mathbb F}_\lambda $
, and hence the image of
![]() $r_{p_i}$
in
$r_{p_i}$
in
![]() ${\mathbb F}_\lambda $
is a nonzero square. Since
${\mathbb F}_\lambda $
is a nonzero square. Since
![]() $\lambda \nmid 2$
, we deduce that each
$\lambda \nmid 2$
, we deduce that each
![]() $r_{p_i}$
is a square in
$r_{p_i}$
is a square in
![]() $K_\lambda $
. By Lemma 2.3(ii), the prime
$K_\lambda $
. By Lemma 2.3(ii), the prime
![]() $\lambda $
splits completely in L.
$\lambda $
splits completely in L.
Now, suppose that
![]() . There exists an element
. There exists an element
![]() $\alpha \in \operatorname {PGL}_2({\mathbb F}_\lambda ) - \operatorname {PSL}_2({\mathbb F}_\lambda )$
with
$\alpha \in \operatorname {PGL}_2({\mathbb F}_\lambda ) - \operatorname {PSL}_2({\mathbb F}_\lambda )$
with
![]() $\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha ) \neq 0$
. By the Chebotarev density theorem, there is a prime
$\operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha ) \neq 0$
. By the Chebotarev density theorem, there is a prime
![]() $p\nmid N\ell $
such that
$p\nmid N\ell $
such that
![]() . We have
. We have
![]() $r_p \equiv \operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha ) \not \equiv 0\ \pmod {\lambda }$
. Since
$r_p \equiv \operatorname {\mathrm {tr}}(\alpha )^2/\det (\alpha ) \not \equiv 0\ \pmod {\lambda }$
. Since
![]() , Lemma 3.1 implies that the image of
, Lemma 3.1 implies that the image of
![]() $r_p/p^{k-1}$
in
$r_p/p^{k-1}$
in
![]() ${\mathbb F}_\lambda $
is not a square. Since k is odd or
${\mathbb F}_\lambda $
is not a square. Since k is odd or
![]() $[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is even, the image of
$[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is even, the image of
![]() $r_p$
in
$r_p$
in
![]() ${\mathbb F}_\lambda $
is not a square. Therefore,
${\mathbb F}_\lambda $
is not a square. Therefore,
![]() $r_p$
is not a square in
$r_p$
is not a square in
![]() $K_\lambda $
. By Lemma 2.3(ii), we deduce that
$K_\lambda $
. By Lemma 2.3(ii), we deduce that
![]() $\lambda $
does not split completely in L.
$\lambda $
does not split completely in L.
Case 2: Assume that k is even,
![]() $[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is odd, and
$[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is odd, and
![]() $\ell \nmid N$
.
$\ell \nmid N$
.
Since
![]() $\ell \nmid N$
, there is an integer
$\ell \nmid N$
, there is an integer
![]() $a\in {\mathbb Z}$
such that
$a\in {\mathbb Z}$
such that
![]() $a\equiv 1 \ \pmod {M}$
and a is not a square modulo
$a\equiv 1 \ \pmod {M}$
and a is not a square modulo
![]() $\ell $
. By Lemma 3.2, there is a prime
$\ell $
. By Lemma 3.2, there is a prime
![]() $p\equiv a \ \pmod {M\ell }$
such that
$p\equiv a \ \pmod {M\ell }$
such that
![]() $r_p\not \equiv 0 \ \pmod {\lambda }$
.
$r_p\not \equiv 0 \ \pmod {\lambda }$
.
We claim that
![]() $a_p\in R$
and
$a_p\in R$
and
![]() $\varepsilon (p)=1$
. With notation as in Section 2.1, take any
$\varepsilon (p)=1$
. With notation as in Section 2.1, take any
![]() $\gamma \in \Gamma $
. Since the conductor of
$\gamma \in \Gamma $
. Since the conductor of
![]() $\chi _\gamma $
divides M and
$\chi _\gamma $
divides M and
![]() $p\equiv 1 \ \pmod {M}$
, we have
$p\equiv 1 \ \pmod {M}$
, we have
![]() $\gamma (a_p)=\chi _\gamma (p) a_p =a_p$
. Since
$\gamma (a_p)=\chi _\gamma (p) a_p =a_p$
. Since
![]() $\gamma \in \Gamma $
was arbitrary, we have
$\gamma \in \Gamma $
was arbitrary, we have
![]() $a_p \in K$
by Lemma 2.2. Therefore,
$a_p \in K$
by Lemma 2.2. Therefore,
![]() $a_p\in R$
since it is an algebraic integer. We have
$a_p\in R$
since it is an algebraic integer. We have
![]() $\varepsilon (p)=1$
since
$\varepsilon (p)=1$
since
![]() $p\equiv 1\ \pmod {N}$
.
$p\equiv 1\ \pmod {N}$
.
Since
![]() $a_p\in R$
and
$a_p\in R$
and
![]() $r_p\not \equiv 0 \ \pmod {\lambda }$
, the image of
$r_p\not \equiv 0 \ \pmod {\lambda }$
, the image of
![]() $a_p^2$
in
$a_p^2$
in
![]() ${\mathbb F}_\lambda $
is a nonzero square. Since k is even,
${\mathbb F}_\lambda $
is a nonzero square. Since k is even,
![]() $p^k$
is a square in
$p^k$
is a square in
![]() ${\mathbb F}_\lambda $
. Since a, and hence p, is not a square modulo
${\mathbb F}_\lambda $
. Since a, and hence p, is not a square modulo
![]() $\ell $
and
$\ell $
and
![]() $[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is odd, the prime p is not a square in
$[{\mathbb F}_\lambda :{\mathbb F}_\ell ]$
is odd, the prime p is not a square in
![]() ${\mathbb F}_\lambda $
. So the image of
${\mathbb F}_\lambda $
. So the image of
in
![]() ${\mathbb F}_\lambda $
is not a square. Lemma 3.1 implies that
${\mathbb F}_\lambda $
is not a square. Lemma 3.1 implies that
![]() . Therefore,
. Therefore,
![]() .
.
4 An effective version of Theorem 1.1
Take a newform f with notation and assumptions as in Section 1.1. Let
![]() $\lambda $
be a nonzero prime ideal of R, and let
$\lambda $
be a nonzero prime ideal of R, and let
![]() $\ell $
be the prime lying under
$\ell $
be the prime lying under
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $k_\lambda $
be the subfield of
$k_\lambda $
be the subfield of
![]() ${\mathbb F}_\lambda $
generated by the image of
${\mathbb F}_\lambda $
generated by the image of
![]() $r_p$
modulo
$r_p$
modulo
![]() $\lambda $
with primes
$\lambda $
with primes
![]() $p\nmid N\ell $
. Take any prime ideal
$p\nmid N\ell $
. Take any prime ideal
![]() $\Lambda $
of
$\Lambda $
of
![]() ${\mathcal O}$
that divides
${\mathcal O}$
that divides
![]() $\lambda $
.
$\lambda $
.
In this section, we describe how to compute an explicit finite set S of prime ideals of R as in Theorem 1.1. First, some simple definitions:
-
• Let
 ${\mathbb F}$
be an extension of
${\mathbb F}$
be an extension of
 ${\mathbb F}_\Lambda $
of degree
${\mathbb F}_\Lambda $
of degree
 $\gcd (2,\ell )$
.
$\gcd (2,\ell )$
. -
• Let
 $e_0=0$
if
$e_0=0$
if
 $\ell \geq k-1$
and
$\ell \geq k-1$
and
 $\ell \nmid N$
, and
$\ell \nmid N$
, and
 $e_0=\ell -2$
otherwise.
$e_0=\ell -2$
otherwise. -
• Let
 $e_1=0$
if N is odd, and
$e_1=0$
if N is odd, and
 $e_1=1$
otherwise.
$e_1=1$
otherwise. -
• Let
 $e_2=0$
if
$e_2=0$
if
 $\ell \geq 2k$
, and
$\ell \geq 2k$
, and
 $e_2=1$
otherwise.
$e_2=1$
otherwise. -
• Define
 ${\mathcal M}=4^{e_1} \ell ^{e_2}\prod _{p|N} p$
.
${\mathcal M}=4^{e_1} \ell ^{e_2}\prod _{p|N} p$
.
We will prove the following in Section 5.
Theorem 4.1 Suppose that all the following conditions hold:
-
(a) For every integer
 $0\leq j \leq e_0$
and character
$0\leq j \leq e_0$
and character
 $\chi \colon\ ({\mathbb Z}/N{\mathbb Z})^\times \to {\mathbb F}^\times $
, there is a prime
$\chi \colon\ ({\mathbb Z}/N{\mathbb Z})^\times \to {\mathbb F}^\times $
, there is a prime
 $p\nmid N\ell $
such that
$p\nmid N\ell $
such that
 $\chi (p)p^j \in {\mathbb F}$
is not a root of the polynomial
$\chi (p)p^j \in {\mathbb F}$
is not a root of the polynomial
 $x^2 - a_px + \varepsilon (p)p^{k-1} \in {\mathbb F}_\Lambda [x]$
.
$x^2 - a_px + \varepsilon (p)p^{k-1} \in {\mathbb F}_\Lambda [x]$
. -
(b) For every nontrivial character
 $\chi \colon\ ({\mathbb Z}/{\mathcal M}{\mathbb Z})^\times \to \{\pm 1\}$
, there is a prime
$\chi \colon\ ({\mathbb Z}/{\mathcal M}{\mathbb Z})^\times \to \{\pm 1\}$
, there is a prime
 $p\nmid N\ell $
such that
$p\nmid N\ell $
such that
 $\chi (p)=-1$
and
$\chi (p)=-1$
and
 $r_p \not \equiv 0 \ \pmod {\lambda }$
.
$r_p \not \equiv 0 \ \pmod {\lambda }$
. -
(c) If
 $\#k_\lambda \notin \{4,5\}$
, then at least one of the following holds:
$\#k_\lambda \notin \{4,5\}$
, then at least one of the following holds:-
•
 $\ell> 5k-4$
and
$\ell> 5k-4$
and
 $\ell \nmid N$
,
$\ell \nmid N$
, -
•
 $\ell \equiv 0, \pm 1 \ \pmod {5}$
and
$\ell \equiv 0, \pm 1 \ \pmod {5}$
and
 $\#k_\lambda \neq \ell $
,
$\#k_\lambda \neq \ell $
, -
•
 $\ell \equiv \pm 2\ \pmod {5}$
and
$\ell \equiv \pm 2\ \pmod {5}$
and
 $\#k_\lambda \neq \ell ^2$
,
$\#k_\lambda \neq \ell ^2$
, -
• there is a prime
 $p\nmid N\ell $
such that the image of
$p\nmid N\ell $
such that the image of
 $a_{p}^2/(\varepsilon (p) p^{k-1})$
in
$a_{p}^2/(\varepsilon (p) p^{k-1})$
in
 ${\mathbb F}_\lambda $
is not equal to
${\mathbb F}_\lambda $
is not equal to
 $0$
,
$0$
,
 $1$
, and
$1$
, and
 $4$
, and is not a root of
$4$
, and is not a root of
 $x^2-3x+1$
.
$x^2-3x+1$
.
-
-
(d) If
 $\#k_\lambda \notin \{3,5,7\}$
, then at least one of the following holds:
$\#k_\lambda \notin \{3,5,7\}$
, then at least one of the following holds:-
•
 $\ell> 4k-3$
and
$\ell> 4k-3$
and
 $\ell \nmid N$
,
$\ell \nmid N$
, -
•
 $\#k_\lambda \neq \ell $
,
$\#k_\lambda \neq \ell $
, -
• there is a prime
 $p\nmid N\ell $
such that the image of
$p\nmid N\ell $
such that the image of
 $a_{p}^2/(\varepsilon (p) p^{k-1})$
in
$a_{p}^2/(\varepsilon (p) p^{k-1})$
in
 ${\mathbb F}_\lambda $
is not equal to
${\mathbb F}_\lambda $
is not equal to
 $0$
,
$0$
,
 $1$
,
$1$
,
 $2$
, and
$2$
, and
 $4$
.
$4$
.
-
-
(e) If
 $\#k_\lambda \in \{5,7\}$
, then for every nontrivial character
$\#k_\lambda \in \{5,7\}$
, then for every nontrivial character
 $\chi \colon\ ({\mathbb Z}/ 4^{e_1}\ell N{\mathbb Z})^\times \to \{\pm 1\}$
, there is a prime
$\chi \colon\ ({\mathbb Z}/ 4^{e_1}\ell N{\mathbb Z})^\times \to \{\pm 1\}$
, there is a prime
 $p\nmid N\ell $
such that
$p\nmid N\ell $
such that
 $\chi (p)=1$
and
$\chi (p)=1$
and
 $a_{p}^2/(\varepsilon (p) p^{k-1})\equiv 2 \ \pmod {\lambda }$
.
$a_{p}^2/(\varepsilon (p) p^{k-1})\equiv 2 \ \pmod {\lambda }$
.
Then the group
![]() is conjugate in
is conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
![]() $\operatorname {PSL}_2(k_\lambda )$
or
$\operatorname {PSL}_2(k_\lambda )$
or
![]() $\operatorname {PGL}_2(k_\lambda )$
.
$\operatorname {PGL}_2(k_\lambda )$
.
Remark 4.2 Note that the above conditions simplify greatly if one also assumes that
![]() $\ell \nmid N$
and
$\ell \nmid N$
and
![]() $\ell>5k-4$
.
$\ell>5k-4$
.
Although we will not prove it, Theorem 4.1 has been stated so that all the conditions (a)–(e) hold if and only if
![]() is conjugate to
is conjugate to
![]() $\operatorname {PSL}_2(k_\lambda )$
or
$\operatorname {PSL}_2(k_\lambda )$
or
![]() $\operatorname {PGL}_2(k_\lambda )$
. In particular, after considering enough primes p, one will obtain the minimal set S of Theorem 1.1 (one could use an effective version of Chebotarev density to make this a legitimate algorithm for computing this minimal set).
$\operatorname {PGL}_2(k_\lambda )$
. In particular, after considering enough primes p, one will obtain the minimal set S of Theorem 1.1 (one could use an effective version of Chebotarev density to make this a legitimate algorithm for computing this minimal set).
Let us now describe how to compute a set of exceptional primes as in Theorem 1.1. Define
![]() $M=N$
if N is odd and
$M=N$
if N is odd and
![]() $M=4N$
otherwise. Set
$M=4N$
otherwise. Set
![]() ${\mathcal M}':=4^{e_1} \prod _{p|N} p$
. We first choose some primes:
${\mathcal M}':=4^{e_1} \prod _{p|N} p$
. We first choose some primes:
-
• Let
 $q_1,\ldots , q_n$
be primes congruent to
$q_1,\ldots , q_n$
be primes congruent to
 $1$
modulo N.
$1$
modulo N. -
• Let
 $p_1,\ldots , p_m \nmid N$
be primes with
$p_1,\ldots , p_m \nmid N$
be primes with
 $r_{p_i}\neq 0$
such that for every nontrivial character
$r_{p_i}\neq 0$
such that for every nontrivial character
 $\chi \colon\ ({\mathbb Z}/{\mathcal M}' {\mathbb Z})^\times \to \{\pm 1\}$
, we have
$\chi \colon\ ({\mathbb Z}/{\mathcal M}' {\mathbb Z})^\times \to \{\pm 1\}$
, we have
 $\chi (p_i)=-1$
for some
$\chi (p_i)=-1$
for some
 $1\leq i \leq m$
.
$1\leq i \leq m$
. -
• Let
 $p_0 \nmid N$
be a prime such that
$p_0 \nmid N$
be a prime such that
 ${\mathbb Q}(r_{p_0})=K$
.
${\mathbb Q}(r_{p_0})=K$
.
That such primes
![]() $p_1,\ldots , p_m$
exist is clear since the set of primes p with
$p_1,\ldots , p_m$
exist is clear since the set of primes p with
![]() $r_p\neq 0$
has density
$r_p\neq 0$
has density
![]() $1$
. That such a prime q exists follows from Lemma 2.2 (the set of such q actually has positive density). Define the ring
$1$
. That such a prime q exists follows from Lemma 2.2 (the set of such q actually has positive density). Define the ring
![]() $R':={\mathbb Z}[a_{q}^2/\varepsilon (q)]$
; it is an order in R.
$R':={\mathbb Z}[a_{q}^2/\varepsilon (q)]$
; it is an order in R.
Define S to be the set of nonzero primes
![]() $\lambda $
of R, dividing a rational prime
$\lambda $
of R, dividing a rational prime
![]() $\ell $
, that satisfy one of the following conditions:
$\ell $
, that satisfy one of the following conditions:
-
•
 $\ell \leq 5k-4$
or
$\ell \leq 5k-4$
or
 $\ell \leq 7$
,
$\ell \leq 7$
, -
•
 $\ell | N$
,
$\ell | N$
, -
• for all
 $1\leq i \leq n$
, we have
$1\leq i \leq n$
, we have
 $\ell =q_i$
or
$\ell =q_i$
or
 $r_{q_i} \equiv (1+q_i^{k-1})^2 \ \pmod {\lambda }$
,
$r_{q_i} \equiv (1+q_i^{k-1})^2 \ \pmod {\lambda }$
, -
• for some
 $1\leq i \leq m$
, we have
$1\leq i \leq m$
, we have
 $\ell =p_i$
or
$\ell =p_i$
or
 $r_{p_i} \equiv 0 \ \pmod {\lambda }$
,
$r_{p_i} \equiv 0 \ \pmod {\lambda }$
, -
•
 $\ell =q$
or
$\ell =q$
or
 $\ell $
divides
$\ell $
divides
 $[R:R']$
.
$[R:R']$
.
Note that the set S is finite (the only part that is not immediate is that
![]() $r_{q_i} - (1+q_i^{k-1})^2\neq 0$
; this follows from Deligne’s bound
$r_{q_i} - (1+q_i^{k-1})^2\neq 0$
; this follows from Deligne’s bound
![]() $|r_{q_i}|=|a_{q_i}| \leq 2q_i^{(k-1)/2}$
and
$|r_{q_i}|=|a_{q_i}| \leq 2q_i^{(k-1)/2}$
and
![]() $k>1$
). The following is our effective version of Theorem 1.1.
$k>1$
). The following is our effective version of Theorem 1.1.
Theorem 4.3 Take any nonzero prime ideal
![]() $\lambda \notin S$
of R, and let
$\lambda \notin S$
of R, and let
![]() $\Lambda $
be any prime of
$\Lambda $
be any prime of
![]() ${\mathcal O}$
dividing
${\mathcal O}$
dividing
![]() $\lambda $
. Then the group
$\lambda $
. Then the group
![]() is conjugate in
is conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to either
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to either
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
![]() $\operatorname {PGL}_2({\mathbb F}_\lambda )$
.
$\operatorname {PGL}_2({\mathbb F}_\lambda )$
.
Proof Let
![]() $\ell $
be the rational prime lying under
$\ell $
be the rational prime lying under
![]() $\lambda $
. We shall verify the conditions of Theorem 4.1.
$\lambda $
. We shall verify the conditions of Theorem 4.1.
We first show that condition (a) of Theorem 4.1 holds. Take any integer
![]() $0\leq j \leq e_0$
and character
$0\leq j \leq e_0$
and character
![]() $\chi \colon\ ({\mathbb Z}/N{\mathbb Z})^\times \to {\mathbb F}^\times ={\mathbb F}_\Lambda ^\times $
. We have
$\chi \colon\ ({\mathbb Z}/N{\mathbb Z})^\times \to {\mathbb F}^\times ={\mathbb F}_\Lambda ^\times $
. We have
![]() $\ell>5k-4>k-1$
and
$\ell>5k-4>k-1$
and
![]() $\ell \nmid N$
since
$\ell \nmid N$
since
![]() $\lambda \notin S$
, so
$\lambda \notin S$
, so
![]() $e_0=0$
and hence
$e_0=0$
and hence
![]() $j=0$
. Take any
$j=0$
. Take any
![]() $1\leq i \leq n$
. Since
$1\leq i \leq n$
. Since
![]() $q_i\equiv 1\ \pmod {N}$
and
$q_i\equiv 1\ \pmod {N}$
and
![]() $j=0$
, we have
$j=0$
, we have
![]() $\chi (q_i)q_i^j=1$
and
$\chi (q_i)q_i^j=1$
and
![]() $\varepsilon (q_i)=1$
. Since
$\varepsilon (q_i)=1$
. Since
![]() $\lambda \notin S$
, we also have
$\lambda \notin S$
, we also have
![]() $q_i \nmid N \ell $
(
$q_i \nmid N \ell $
(
![]() $q_i\nmid N$
is immediate from the congruence imposed on
$q_i\nmid N$
is immediate from the congruence imposed on
![]() $q_i$
). If
$q_i$
). If
![]() $\chi (q_i)q_i^j=1$
was a root of
$\chi (q_i)q_i^j=1$
was a root of
![]() $x^2-a_{q_i}x+\varepsilon (q_i)q_i^{k-1}$
in
$x^2-a_{q_i}x+\varepsilon (q_i)q_i^{k-1}$
in
![]() ${\mathbb F}_\Lambda [x]$
, then we would have
${\mathbb F}_\Lambda [x]$
, then we would have
![]() $a_{q_i} \equiv 1 + q_i^{k-1} \ \pmod {\Lambda }$
; squaring and using that
$a_{q_i} \equiv 1 + q_i^{k-1} \ \pmod {\Lambda }$
; squaring and using that
![]() $\varepsilon (q_i)=1$
, we deduce that
$\varepsilon (q_i)=1$
, we deduce that
![]() $r_{q_i} \equiv (1+q_i^{k-1})^2 \ \pmod {\lambda }$
. Since
$r_{q_i} \equiv (1+q_i^{k-1})^2 \ \pmod {\lambda }$
. Since
![]() $\lambda \notin S$
, we have
$\lambda \notin S$
, we have
![]() $r_{q_i} \not \equiv (1+q_i^{k-1})^2 \ \pmod {\lambda }$
for some
$r_{q_i} \not \equiv (1+q_i^{k-1})^2 \ \pmod {\lambda }$
for some
![]() $1\leq i \leq n$
and hence
$1\leq i \leq n$
and hence
![]() $\chi (q_i)q_i^j$
is not a root of
$\chi (q_i)q_i^j$
is not a root of
![]() $x^2-a_{q_i}x+\varepsilon (q_i)q_i^{k-1}$
.
$x^2-a_{q_i}x+\varepsilon (q_i)q_i^{k-1}$
.
We now show that condition (b) of Theorem 4.1 holds. We have
![]() $e_2=0$
since
$e_2=0$
since
![]() $\lambda \notin S$
, and hence
$\lambda \notin S$
, and hence
![]() ${\mathcal M}'={\mathcal M}$
. Take any nontrivial character
${\mathcal M}'={\mathcal M}$
. Take any nontrivial character
![]() $\chi \colon\ ({\mathbb Z}/{\mathcal M}{\mathbb Z})^\times \to \{\pm 1\}$
. By our choice of primes
$\chi \colon\ ({\mathbb Z}/{\mathcal M}{\mathbb Z})^\times \to \{\pm 1\}$
. By our choice of primes
![]() $p_1,\ldots ,p_m$
, we have
$p_1,\ldots ,p_m$
, we have
![]() $\chi (p_i)=-1$
for some
$\chi (p_i)=-1$
for some
![]() $1\leq i \leq m$
. The prime
$1\leq i \leq m$
. The prime
![]() $p_i$
does not divide
$p_i$
does not divide
![]() $N\ell $
(that
$N\ell $
(that
![]() $p_i\neq \ell $
follows since
$p_i\neq \ell $
follows since
![]() $\lambda \notin S$
). Since
$\lambda \notin S$
). Since
![]() $\lambda \notin S$
, we have
$\lambda \notin S$
, we have
![]() $r_{p_i}\not \equiv 0 \ \pmod {\lambda }$
.
$r_{p_i}\not \equiv 0 \ \pmod {\lambda }$
.
Since
![]() $\lambda \notin S$
, the prime
$\lambda \notin S$
, the prime
![]() $\ell \nmid N$
is greater that
$\ell \nmid N$
is greater that
![]() $7$
,
$7$
,
![]() $4k-3$
, and
$4k-3$
, and
![]() $5k-4$
. Conditions (c)–(e) of Theorem 4.1 all hold.
$5k-4$
. Conditions (c)–(e) of Theorem 4.1 all hold.
Theorem 4.1 now implies that
![]() is conjugate in
is conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to either
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to either
![]() $\operatorname {PSL}_2(k_\lambda )$
or
$\operatorname {PSL}_2(k_\lambda )$
or
![]() $\operatorname {PGL}_2(k_\lambda )$
. It remains to prove that
$\operatorname {PGL}_2(k_\lambda )$
. It remains to prove that
![]() $k_\lambda ={\mathbb F}_\lambda $
. We have
$k_\lambda ={\mathbb F}_\lambda $
. We have
![]() $q\neq \ell $
since
$q\neq \ell $
since
![]() $\lambda \notin S$
. The image of the reduction map
$\lambda \notin S$
. The image of the reduction map
![]() $R' \to {\mathbb F}_\lambda $
thus lies in
$R' \to {\mathbb F}_\lambda $
thus lies in
![]() $k_\lambda $
. We have
$k_\lambda $
. We have
![]() $\ell \nmid [R:R']$
since
$\ell \nmid [R:R']$
since
![]() $\lambda \notin S$
, so the map
$\lambda \notin S$
, so the map
![]() $R'\to {\mathbb F}_\lambda $
is surjective. Therefore,
$R'\to {\mathbb F}_\lambda $
is surjective. Therefore,
![]() $k_\lambda ={\mathbb F}_\lambda $
.
$k_\lambda ={\mathbb F}_\lambda $
.
5 Proof of Theorem 4.1
5.1 Some group theory
Fix a prime
![]() $\ell $
and an integer
$\ell $
and an integer
![]() $r\geq 1$
. A Borel subgroup of
$r\geq 1$
. A Borel subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
is a subgroup conjugate to the subgroup of upper triangular matrices. A split Cartan subgroup of
$\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
is a subgroup conjugate to the subgroup of upper triangular matrices. A split Cartan subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
is a subgroup conjugate to the subgroup of diagonal matrices. A nonsplit Cartan subgroup of
$\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
is a subgroup conjugate to the subgroup of diagonal matrices. A nonsplit Cartan subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
is a subgroup that is cyclic of order
$\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
is a subgroup that is cyclic of order
![]() $(\ell ^r)^2-1$
. Fix a Cartan subgroup
$(\ell ^r)^2-1$
. Fix a Cartan subgroup
![]() ${\mathcal C}$
of
${\mathcal C}$
of
![]() $\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
. Let
$\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
. Let
![]() ${\mathcal N}$
be the normalizer of
${\mathcal N}$
be the normalizer of
![]() ${\mathcal C}$
in
${\mathcal C}$
in
![]() $\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
. One can show that
$\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
. One can show that
![]() $[{\mathcal N}:{\mathcal C}] = 2$
and that
$[{\mathcal N}:{\mathcal C}] = 2$
and that
![]() $\operatorname {\mathrm {tr}}(g)=0$
and
$\operatorname {\mathrm {tr}}(g)=0$
and
![]() $g^2$
is scalar for all
$g^2$
is scalar for all
![]() $g\in {\mathcal N}-{\mathcal C}$
.
$g\in {\mathcal N}-{\mathcal C}$
.
Lemma 5.1 Fix a prime
![]() $\ell $
and an integer
$\ell $
and an integer
![]() $r\geq 1$
. Let G be a subgroup of
$r\geq 1$
. Let G be a subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
, and let
$\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
, and let
![]() be its image in
be its image in
![]() $\operatorname {PGL}_2({\mathbb F}_{\ell ^r})$
. Then at least one of the following holds:
$\operatorname {PGL}_2({\mathbb F}_{\ell ^r})$
. Then at least one of the following holds:
-
(1) G is contained in a Borel subgroup of
 $\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
.
$\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
. -
(2) G is contained in the normalizer of a Cartan subgroup of
 $\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
.
$\operatorname {GL}_2({\mathbb F}_{\ell ^r})$
. -
(3)
 is isomorphic to
is isomorphic to
 $\mathfrak {A}_4$
.
$\mathfrak {A}_4$
. -
(4)
 is isomorphic to
is isomorphic to
 $\mathfrak {S}_4$
.
$\mathfrak {S}_4$
. -
(5)
 is isomorphic to
is isomorphic to
 $\mathfrak {A}_5$
.
$\mathfrak {A}_5$
. -
(6)
 is conjugate to
is conjugate to
 $\operatorname {PSL}_2({\mathbb F}_{\ell ^s})$
or
$\operatorname {PSL}_2({\mathbb F}_{\ell ^s})$
or
 $\operatorname {PGL}_2({\mathbb F}_{\ell ^s})$
for some integer s dividing r.
$\operatorname {PGL}_2({\mathbb F}_{\ell ^s})$
for some integer s dividing r.
Proof This can be deduced directly from a theorem of Dickson (cf. [Reference Huppert10, Satz 8.27]), which will give the finite subgroups of
![]() $\operatorname {PSL}_2(\overline {{\mathbb F}}_\ell ) = \operatorname {PGL}_2(\overline {{\mathbb F}}_\ell )$
. The finite subgroups of
$\operatorname {PSL}_2(\overline {{\mathbb F}}_\ell ) = \operatorname {PGL}_2(\overline {{\mathbb F}}_\ell )$
. The finite subgroups of
![]() $\operatorname {PGL}_2({\mathbb F}_{\ell ^r})$
have been worked out in [Reference Faber9].
$\operatorname {PGL}_2({\mathbb F}_{\ell ^r})$
have been worked out in [Reference Faber9].
Lemma 5.2 Fix a prime
![]() $\ell $
and an integer
$\ell $
and an integer
![]() $r\geq 1$
. Take a matrix
$r\geq 1$
. Take a matrix
![]() $A\in \operatorname {GL}_2({\mathbb F}_{\ell ^r})$
, and let m be its order in
$A\in \operatorname {GL}_2({\mathbb F}_{\ell ^r})$
, and let m be its order in
![]() $\operatorname {PGL}_2({\mathbb F}_{\ell ^r})$
.
$\operatorname {PGL}_2({\mathbb F}_{\ell ^r})$
.
-
(i) Suppose that
 $\ell \nmid m$
. If m is
$\ell \nmid m$
. If m is
 $1$
,
$1$
,
 $2$
,
$2$
,
 $3$
, or
$3$
, or
 $4$
, then
$4$
, then
 $\operatorname {\mathrm {tr}}(A)^2/\det (A)$
is
$\operatorname {\mathrm {tr}}(A)^2/\det (A)$
is
 $4$
,
$4$
,
 $0$
,
$0$
,
 $1$
, or
$1$
, or
 $2$
, respectively. If
$2$
, respectively. If
 $m=5$
, then
$m=5$
, then
 $\operatorname {\mathrm {tr}}(A)^2/\det (A)$
is a root of
$\operatorname {\mathrm {tr}}(A)^2/\det (A)$
is a root of
 $x^2-3x+1$
.
$x^2-3x+1$
. -
(ii) If
 $\ell | m$
, then
$\ell | m$
, then
 $\operatorname {\mathrm {tr}}(A)^2/\det (A) = 4$
.
$\operatorname {\mathrm {tr}}(A)^2/\det (A) = 4$
.
Proof The quantity
![]() $\operatorname {\mathrm {tr}}(A)^2/\det (A)$
does not change if we replace A by a scalar multiple or by a conjugate in
$\operatorname {\mathrm {tr}}(A)^2/\det (A)$
does not change if we replace A by a scalar multiple or by a conjugate in
![]() $\operatorname {GL}_2(\overline {{\mathbb F}}_\ell )$
. If
$\operatorname {GL}_2(\overline {{\mathbb F}}_\ell )$
. If
![]() $\ell \nmid m$
, then we may thus assume that
$\ell \nmid m$
, then we may thus assume that
![]() $A=\left (\begin {smallmatrix} \zeta & 0 \\ 0 & 1 \end {smallmatrix}\right )$
where
$A=\left (\begin {smallmatrix} \zeta & 0 \\ 0 & 1 \end {smallmatrix}\right )$
where
![]() $\zeta \in \overline {{\mathbb F}}_\ell $
has order m. We have
$\zeta \in \overline {{\mathbb F}}_\ell $
has order m. We have
![]() $\operatorname {\mathrm {tr}}(A)^2/\det (A) = \zeta +\zeta ^{-1} + 2$
, which is
$\operatorname {\mathrm {tr}}(A)^2/\det (A) = \zeta +\zeta ^{-1} + 2$
, which is
![]() $4$
,
$4$
,
![]() $0$
,
$0$
,
![]() $1$
, or
$1$
, or
![]() $2$
when m is
$2$
when m is
![]() $1$
,
$1$
,
![]() $2$
,
$2$
,
![]() $3$
, or
$3$
, or
![]() $4$
, respectively. If
$4$
, respectively. If
![]() $m=5$
, then
$m=5$
, then
![]() $ \zeta +\zeta ^{-1} + 2$
is a root of
$ \zeta +\zeta ^{-1} + 2$
is a root of
![]() $x^2-3x+1$
. If
$x^2-3x+1$
. If
![]() $\ell | m$
, then after conjugating and scaling, we may assume that
$\ell | m$
, then after conjugating and scaling, we may assume that
![]() $A=\left (\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right )$
and hence
$A=\left (\begin {smallmatrix} 1 & 1 \\ 0 & 1 \end {smallmatrix}\right )$
and hence
![]() $\operatorname {\mathrm {tr}}(A)^2/\det (A) =4$
.
$\operatorname {\mathrm {tr}}(A)^2/\det (A) =4$
.
5.2 Image of inertia at
 $\ell $
$\ell $
Fix an inertia subgroup
![]() ${\mathcal I}_\ell $
of
${\mathcal I}_\ell $
of
![]() $G=\operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}/{\mathbb Q})$
for the prime
$G=\operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}/{\mathbb Q})$
for the prime
![]() $\ell $
; it is uniquely defined up to conjugacy. The following gives important information concerning the representation
$\ell $
; it is uniquely defined up to conjugacy. The following gives important information concerning the representation
![]() for large
for large
![]() $\ell $
. Let
$\ell $
. Let
![]() $\chi _\ell \colon\ G\twoheadrightarrow {\mathbb F}_\ell ^\times $
be the character such that for each prime
$\chi _\ell \colon\ G\twoheadrightarrow {\mathbb F}_\ell ^\times $
be the character such that for each prime
![]() $p\nmid \ell $
,
$p\nmid \ell $
,
![]() $\chi _\ell $
is unramified at p and
$\chi _\ell $
is unramified at p and
![]() $\chi _\ell (\operatorname {\mathrm {Frob}}_p)\equiv p \ \pmod {\ell }$
.
$\chi _\ell (\operatorname {\mathrm {Frob}}_p)\equiv p \ \pmod {\ell }$
.
Lemma 5.3 Fix a prime
![]() $\ell \geq k-1$
for which
$\ell \geq k-1$
for which
![]() $\ell \nmid 2N$
. Let
$\ell \nmid 2N$
. Let
![]() $\Lambda $
be a prime ideal of
$\Lambda $
be a prime ideal of
![]() ${\mathcal O}$
dividing
${\mathcal O}$
dividing
![]() $\ell $
, and set
$\ell $
, and set
![]() $\lambda =\Lambda \cap R$
.
$\lambda =\Lambda \cap R$
.
-
(i) Suppose that
 $r_\ell \not \equiv 0 \ \pmod {\lambda }$
. After conjugating
$r_\ell \not \equiv 0 \ \pmod {\lambda }$
. After conjugating
 by a matrix in
by a matrix in
 $\operatorname {GL}_2({\mathbb F}_\Lambda )$
, we have In particular,
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
, we have In particular,
 contains a cyclic group of order
contains a cyclic group of order
 $(\ell -1)/\gcd (\ell -1,k-1)$
.
$(\ell -1)/\gcd (\ell -1,k-1)$
.
-
(ii) Suppose that
 $r_\ell \equiv 0 \ \pmod {\lambda }$
. Then
$r_\ell \equiv 0 \ \pmod {\lambda }$
. Then
 is absolutely irreducible and
is absolutely irreducible and
 is cyclic. Furthermore, the group
is cyclic. Furthermore, the group
 is cyclic of order
is cyclic of order
 $(\ell +1)/\gcd (\ell +1,k-1)$
.
$(\ell +1)/\gcd (\ell +1,k-1)$
.
Proof Parts (i) and (ii) follow from Theorems 2.5 and 2.6, respectively, of [Reference Edixhoven8]; they are theorems of Deligne and Fontaine, respectively. We have used that
![]() $r_\ell =a_\ell ^2/\varepsilon (\ell ) \in R$
is congruent to
$r_\ell =a_\ell ^2/\varepsilon (\ell ) \in R$
is congruent to
![]() $0$
modulo
$0$
modulo
![]() $\lambda $
if and only if
$\lambda $
if and only if
![]() $a_\ell \in {\mathcal O}$
is congruent to
$a_\ell \in {\mathcal O}$
is congruent to
![]() $0$
modulo
$0$
modulo
![]() $\Lambda $
.
$\Lambda $
.
5.3 Borel case
Suppose that
is a reducible subgroup of
![]() $\operatorname {GL}_2({\mathbb F})$
. There are, thus, characters
$\operatorname {GL}_2({\mathbb F})$
. There are, thus, characters
![]() $\psi _1,\psi _2 \colon\ G \to {\mathbb F}^\times $
such that after conjugating the
$\psi _1,\psi _2 \colon\ G \to {\mathbb F}^\times $
such that after conjugating the
![]() ${\mathbb F}$
-representation
${\mathbb F}$
-representation
, we have

The characters
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
are unramified at each prime
$\psi _2$
are unramified at each prime
![]() $p\nmid N\ell $
since
$p\nmid N\ell $
since
is unramified at such primes.
Lemma 5.4 For each
![]() $i\in \{1,2\}$
, there is a unique integer
$i\in \{1,2\}$
, there is a unique integer
![]() $0\leq m_i < \ell -1$
such that
$0\leq m_i < \ell -1$
such that
![]() $\psi _i\chi _\ell ^{-m_i} \colon\ G \to {\mathbb F}^\times $
is unramified at all primes
$\psi _i\chi _\ell ^{-m_i} \colon\ G \to {\mathbb F}^\times $
is unramified at all primes
![]() $p\nmid N$
. If
$p\nmid N$
. If
![]() $\ell \geq k-1$
and
$\ell \geq k-1$
and
![]() $\ell \nmid N$
, then
$\ell \nmid N$
, then
![]() $m_1$
or
$m_1$
or
![]() $m_2$
is
$m_2$
is
![]() $0$
.
$0$
.
Proof The existence and uniqueness of
![]() $m_i$
is an easy consequence of class field theory for
$m_i$
is an easy consequence of class field theory for
![]() ${\mathbb Q}_\ell $
. A choice of embedding
${\mathbb Q}_\ell $
. A choice of embedding
![]() ${\overline {\mathbb Q}}\subseteq {\overline {\mathbb Q}}_\ell $
induces an injective homomorphism
${\overline {\mathbb Q}}\subseteq {\overline {\mathbb Q}}_\ell $
induces an injective homomorphism
![]() $G_{{\mathbb Q}_\ell }:=\operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}_\ell /{\mathbb Q}_\ell ) \hookrightarrow G$
. Let
$G_{{\mathbb Q}_\ell }:=\operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}_\ell /{\mathbb Q}_\ell ) \hookrightarrow G$
. Let
![]() ${\mathbb Q}_\ell ^{\operatorname {ab}}$
be the maximal abelian extension of
${\mathbb Q}_\ell ^{\operatorname {ab}}$
be the maximal abelian extension of
![]() ${\mathbb Q}_\ell $
in
${\mathbb Q}_\ell $
in
![]() ${\overline {\mathbb Q}}_\ell $
. Restricting
${\overline {\mathbb Q}}_\ell $
. Restricting
![]() $\psi _i$
to
$\psi _i$
to
![]() $G_{{\mathbb Q}_\ell }$
, we obtain a representation
$G_{{\mathbb Q}_\ell }$
, we obtain a representation
![]() $\psi _i\colon\ G_{{\mathbb Q}_\ell }^{\operatorname {ab}}:=\operatorname {\mathrm {Gal}}({\mathbb Q}_\ell ^{\operatorname {ab}}/{\mathbb Q}_\ell ) \to {\mathbb F}^\times $
. By local class field, the inertia subgroup
$\psi _i\colon\ G_{{\mathbb Q}_\ell }^{\operatorname {ab}}:=\operatorname {\mathrm {Gal}}({\mathbb Q}_\ell ^{\operatorname {ab}}/{\mathbb Q}_\ell ) \to {\mathbb F}^\times $
. By local class field, the inertia subgroup
![]() ${\mathcal I}$
of
${\mathcal I}$
of
![]() $G_{{\mathbb Q}_\ell }^{\operatorname {ab}}$
is isomorphic to
$G_{{\mathbb Q}_\ell }^{\operatorname {ab}}$
is isomorphic to
![]() ${\mathbb Z}_\ell ^\times $
. Since
${\mathbb Z}_\ell ^\times $
. Since
![]() $\ell $
does not divide the cardinality of
$\ell $
does not divide the cardinality of
![]() ${\mathbb F}^\times $
, we find that
${\mathbb F}^\times $
, we find that
![]() $\psi _i|_{{\mathcal I}}$
factors through a group isomorphic to
$\psi _i|_{{\mathcal I}}$
factors through a group isomorphic to
![]() ${\mathbb F}_\ell ^\times $
. The character
${\mathbb F}_\ell ^\times $
. The character
![]() $\psi _i|_{{\mathcal I}}$
must agree with a power of
$\psi _i|_{{\mathcal I}}$
must agree with a power of
![]() $\chi _\ell |_{{\mathcal I}}$
since
$\chi _\ell |_{{\mathcal I}}$
since
![]() $\chi _\ell \colon\ G_{{\mathbb Q}_\ell } \to {\mathbb F}_\ell ^\times $
satisfies
$\chi _\ell \colon\ G_{{\mathbb Q}_\ell } \to {\mathbb F}_\ell ^\times $
satisfies
![]() $\chi _\ell ({\mathcal I})={\mathbb F}_\ell ^\times $
and
$\chi _\ell ({\mathcal I})={\mathbb F}_\ell ^\times $
and
![]() ${\mathbb F}_\ell ^\times $
is cyclic.
${\mathbb F}_\ell ^\times $
is cyclic.
The second part of the lemma follows immediately from Lemma 5.3.
Take any
![]() $i\in \{1,2\}$
. By Lemma 5.4, there is a unique
$i\in \{1,2\}$
. By Lemma 5.4, there is a unique
![]() $0\leq m_i < \ell -1$
such that the character
$0\leq m_i < \ell -1$
such that the character
is unramified at
![]() $\ell $
and at all primes
$\ell $
and at all primes
![]() $p\nmid N$
. There is a character
$p\nmid N$
. There is a character
![]() $\chi _i \colon\ ({\mathbb Z}/N_i{\mathbb Z})^\times \to {\mathbb F}^\times $
with
$\chi _i \colon\ ({\mathbb Z}/N_i{\mathbb Z})^\times \to {\mathbb F}^\times $
with
![]() $N_i\geq 1$
dividing some power of N and
$N_i\geq 1$
dividing some power of N and
![]() $\ell \nmid N_i$
such that
$\ell \nmid N_i$
such that
![]() $\tilde \psi _i(\operatorname {\mathrm {Frob}}_p) = \chi _i(p)$
for all
$\tilde \psi _i(\operatorname {\mathrm {Frob}}_p) = \chi _i(p)$
for all
![]() $p\nmid N\ell $
. We may assume that
$p\nmid N\ell $
. We may assume that
![]() $\chi _i$
is taken so that
$\chi _i$
is taken so that
![]() $N_i$
is minimal.
$N_i$
is minimal.
Lemma 5.5 The integer
![]() $N_i$
divides N.
$N_i$
divides N.
Proof We first recall the notion of an Artin conductor. Consider a representation
![]() $\rho \colon\ G\to \operatorname {\mathrm {Aut}}_{{\mathbb F}}(V)$
, where V is a finite-dimensional
$\rho \colon\ G\to \operatorname {\mathrm {Aut}}_{{\mathbb F}}(V)$
, where V is a finite-dimensional
![]() ${\mathbb F}$
-vector space. Take any prime
${\mathbb F}$
-vector space. Take any prime
![]() $p\neq \ell $
. A choice of embedding
$p\neq \ell $
. A choice of embedding
![]() ${\overline {\mathbb Q}}\subseteq {\overline {\mathbb Q}}_p$
induces an injective homomorphism
${\overline {\mathbb Q}}\subseteq {\overline {\mathbb Q}}_p$
induces an injective homomorphism
![]() $\operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}_p/{\mathbb Q}_p) \hookrightarrow G$
. Choose any finite Galois extension
$\operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}_p/{\mathbb Q}_p) \hookrightarrow G$
. Choose any finite Galois extension
![]() $L/{\mathbb Q}_p$
for which
$L/{\mathbb Q}_p$
for which
![]() $\rho (\operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}_p/L))=\{I\}$
. For each
$\rho (\operatorname {\mathrm {Gal}}({\overline {\mathbb Q}}_p/L))=\{I\}$
. For each
![]() $i\geq 0$
, let
$i\geq 0$
, let
![]() $H_i$
be the ith ramification subgroup of
$H_i$
be the ith ramification subgroup of
![]() $\operatorname {\mathrm {Gal}}(L/{\mathbb Q}_p)$
with respect to the lower numbering. Define the integer
$\operatorname {\mathrm {Gal}}(L/{\mathbb Q}_p)$
with respect to the lower numbering. Define the integer
The Artin conductor of
![]() $\rho $
is the integer
$\rho $
is the integer
![]() $N(\rho ):=\prod _{p\neq \ell } p^{f_p(\rho )}$
.
$N(\rho ):=\prod _{p\neq \ell } p^{f_p(\rho )}$
.
Using that the character
![]() $\tilde \psi _i\colon\ G \to {\mathbb F}^\times $
is unramified at
$\tilde \psi _i\colon\ G \to {\mathbb F}^\times $
is unramified at
![]() $\ell $
, one can verify that
$\ell $
, one can verify that
![]() $N(\tilde \psi _i)=N_i$
. Consider our representation
$N(\tilde \psi _i)=N_i$
. Consider our representation
![]() . For a fixed prime
. For a fixed prime
![]() $p\neq \ell $
, take L and
$p\neq \ell $
, take L and
![]() $H_i$
as above. The semisimplification of
$H_i$
as above. The semisimplification of
![]() is
is
![]() $V_1\oplus V_2$
, where
$V_1\oplus V_2$
, where
![]() $V_i$
is the one-dimensional representation given by
$V_i$
is the one-dimensional representation given by
![]() $\psi _i$
. We have
$\psi _i$
. We have
![]() since
since
![]() $\dim _{{\mathbb F}} V^{H_i} \leq \dim _{{\mathbb F}} V_1^{H_i} + \dim _{{\mathbb F}} V_2^{H_i}$
. By using this for all
$\dim _{{\mathbb F}} V^{H_i} \leq \dim _{{\mathbb F}} V_1^{H_i} + \dim _{{\mathbb F}} V_2^{H_i}$
. By using this for all
![]() $p\neq \ell $
, we deduce that
$p\neq \ell $
, we deduce that
![]() $N(\psi _1) N(\psi _2)=N_1 N_2$
divides
$N(\psi _1) N(\psi _2)=N_1 N_2$
divides
![]() . The lemma follows since
. The lemma follows since
![]() divides N (cf. [Reference Livné11, Proposition 0.1]).
divides N (cf. [Reference Livné11, Proposition 0.1]).
Fix an
![]() $i\in \{1,2\}$
; if
$i\in \{1,2\}$
; if
![]() $\ell \geq k-1$
and
$\ell \geq k-1$
and
![]() $\ell \nmid N$
, then we may suppose that
$\ell \nmid N$
, then we may suppose that
![]() $m_i=0$
by Lemma 5.4. Since the conductor of
$m_i=0$
by Lemma 5.4. Since the conductor of
![]() $\chi _i$
divides N by Lemma 5.5, assumption (a) implies that there is a prime
$\chi _i$
divides N by Lemma 5.5, assumption (a) implies that there is a prime
![]() $p\nmid N\ell $
for which
$p\nmid N\ell $
for which
![]() $\chi _i(p) p^{m_i} \in {\mathbb F}$
is not a root of
$\chi _i(p) p^{m_i} \in {\mathbb F}$
is not a root of
![]() $x^2-a_p x + \varepsilon (p)p^{k-1} \in {\mathbb F}[x]$
. However, this is a contradiction since
$x^2-a_p x + \varepsilon (p)p^{k-1} \in {\mathbb F}[x]$
. However, this is a contradiction since
is a root of
![]() $x^2-a_p x + \varepsilon (p)p^{k-1}$
.
$x^2-a_p x + \varepsilon (p)p^{k-1}$
.
Therefore, the
![]() ${\mathbb F}$
-representation
${\mathbb F}$
-representation
![]() is irreducible. In particular,
is irreducible. In particular,
![]() is not contained in a Borel subgroup of
is not contained in a Borel subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )$
.
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
.
5.4 Cartan case
Lemma 5.6 The group
![]() is not contained in a Cartan subgroup of
is not contained in a Cartan subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )$
.
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
.
Proof Suppose that
![]() is contained in a Cartan subgroup
is contained in a Cartan subgroup
![]() ${\mathcal C}$
of
${\mathcal C}$
of
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )$
. If
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
. If
![]() $\ell =2$
, then
$\ell =2$
, then
![]() ${\mathcal C}$
is reducible as a subgroup of
${\mathcal C}$
is reducible as a subgroup of
![]() $\operatorname {GL}_2({\mathbb F})$
since
$\operatorname {GL}_2({\mathbb F})$
since
![]() ${\mathbb F}/{\mathbb F}_\Lambda $
is a quadratic extension. However, we saw in Section 5.3 that
${\mathbb F}/{\mathbb F}_\Lambda $
is a quadratic extension. However, we saw in Section 5.3 that
![]() is an irreducible subgroup of
is an irreducible subgroup of
![]() $\operatorname {GL}_2({\mathbb F})$
. Therefore,
$\operatorname {GL}_2({\mathbb F})$
. Therefore,
![]() $\ell $
is odd. If
$\ell $
is odd. If
![]() ${\mathcal C}$
is split, then
${\mathcal C}$
is split, then
![]() is a reducible subgroup of
is a reducible subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )$
. This was ruled out in Section 5.3, so
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
. This was ruled out in Section 5.3, so
![]() ${\mathcal C}$
must be a nonsplit Cartan subgroup with
${\mathcal C}$
must be a nonsplit Cartan subgroup with
![]() $\ell $
odd.
$\ell $
odd.
Recall that the representation
![]() is odd, i.e., if
is odd, i.e., if
![]() $c\in G$
is an element corresponding to complex conjugation under some embedding
$c\in G$
is an element corresponding to complex conjugation under some embedding
![]() ${\overline {\mathbb Q}}\hookrightarrow {\mathbb C}$
, then
${\overline {\mathbb Q}}\hookrightarrow {\mathbb C}$
, then
![]() . Therefore,
. Therefore,
![]() has order
has order
![]() $2$
and determinant
$2$
and determinant
![]() $-1\neq 1$
(this last inequality uses that
$-1\neq 1$
(this last inequality uses that
![]() $\ell $
is odd). A nonsplit Cartan subgroup
$\ell $
is odd). A nonsplit Cartan subgroup
![]() ${\mathcal C}$
of
${\mathcal C}$
of
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )$
is cyclic and hence
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
is cyclic and hence
![]() $-I$
is the unique element of
$-I$
is the unique element of
![]() ${\mathcal C}$
of order
${\mathcal C}$
of order
![]() $2$
. Since
$2$
. Since
![]() $\det (-I)= 1$
, we find that
$\det (-I)= 1$
, we find that
![]() does not belong to
does not belong to
![]() ${\mathcal C}$
; this gives the desired contradiction.
${\mathcal C}$
; this gives the desired contradiction.
5.5 Normalizer of a Cartan case
Suppose that
is contained in the normalizer
![]() ${\mathcal N}$
of a Cartan subgroup
${\mathcal N}$
of a Cartan subgroup
![]() ${\mathcal C}$
of
${\mathcal C}$
of
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )$
. The group
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
. The group
![]() ${\mathcal C}$
has index
${\mathcal C}$
has index
![]() $2$
in
$2$
in
![]() ${\mathcal N}$
, so we obtain a character
${\mathcal N}$
, so we obtain a character
The character
![]() $\beta _\Lambda $
is nontrivial since
$\beta _\Lambda $
is nontrivial since
by Lemma 5.6.
Lemma 5.7 The character
![]() $\beta _\Lambda $
is unramified at all primes
$\beta _\Lambda $
is unramified at all primes
![]() $p\nmid N\ell $
. If
$p\nmid N\ell $
. If
![]() $\ell \geq 2k$
and
$\ell \geq 2k$
and
![]() $\ell \nmid N$
, then the character
$\ell \nmid N$
, then the character
![]() $\beta _\Lambda $
is also unramified at
$\beta _\Lambda $
is also unramified at
![]() $\ell $
.
$\ell $
.
Proof The character
![]() $\beta _\Lambda $
is unramified at each prime
$\beta _\Lambda $
is unramified at each prime
![]() $p\nmid N\ell $
since
$p\nmid N\ell $
since
![]() is unramified at such primes. Now, suppose that
is unramified at such primes. Now, suppose that
![]() $\ell \geq 2k$
and
$\ell \geq 2k$
and
![]() $\ell \nmid N$
. We have
$\ell \nmid N$
. We have
![]() $\ell>2$
, so
$\ell>2$
, so
![]() $\ell \nmid |{\mathcal N}|$
and hence Lemma 5.3 implies that
$\ell \nmid |{\mathcal N}|$
and hence Lemma 5.3 implies that
![]() is cyclic. Moreover, Lemma 5.3 implies that
is cyclic. Moreover, Lemma 5.3 implies that
![]() is cyclic of order
is cyclic of order
![]() $d\geq (\ell -1)/(k-1)$
. Our assumption
$d\geq (\ell -1)/(k-1)$
. Our assumption
![]() $\ell \geq 2k$
ensures that
$\ell \geq 2k$
ensures that
![]() $d>2$
.
$d>2$
.
Now, take a generator g of
![]() . Suppose that
. Suppose that
![]() $\beta _\Lambda $
is ramified at
$\beta _\Lambda $
is ramified at
![]() $\ell $
and hence g belongs to
$\ell $
and hence g belongs to
![]() ${\mathcal N}-{\mathcal C}$
. The condition
${\mathcal N}-{\mathcal C}$
. The condition
![]() $g\in {\mathcal N}-{\mathcal C}$
implies that
$g\in {\mathcal N}-{\mathcal C}$
implies that
![]() $g^2$
is a scalar matrix and hence
$g^2$
is a scalar matrix and hence
![]() is a group of order
is a group of order
![]() $1$
or
$1$
or
![]() $2$
. This contradicts
$2$
. This contradicts
![]() $d>2$
, so
$d>2$
, so
![]() $\beta _\Lambda $
is unramified at
$\beta _\Lambda $
is unramified at
![]() $\ell $
.
$\ell $
.
Let
![]() $\chi $
be the primitive Dirichlet character that satisfies
$\chi $
be the primitive Dirichlet character that satisfies
![]() $\beta _\Lambda (\operatorname {\mathrm {Frob}}_p)=\chi (p)$
for all primes
$\beta _\Lambda (\operatorname {\mathrm {Frob}}_p)=\chi (p)$
for all primes
![]() $p\nmid N\ell $
. Since
$p\nmid N\ell $
. Since
![]() $\beta _\Lambda $
is a quadratic character, Lemma 5.7 implies that the conductor of
$\beta _\Lambda $
is a quadratic character, Lemma 5.7 implies that the conductor of
![]() $\chi $
divides
$\chi $
divides
![]() ${\mathcal M}$
. The character
${\mathcal M}$
. The character
![]() $\chi $
is nontrivial since
$\chi $
is nontrivial since
![]() $\beta _\Lambda $
is nontrivial. Assumption (b) implies that there is a prime
$\beta _\Lambda $
is nontrivial. Assumption (b) implies that there is a prime
![]() $p\nmid N\ell $
satisfying
$p\nmid N\ell $
satisfying
![]() $\chi (p)=-1$
and
$\chi (p)=-1$
and
![]() $r_p \not \equiv 0 \ \pmod {\lambda }$
. We thus have
$r_p \not \equiv 0 \ \pmod {\lambda }$
. We thus have
![]() $g\in {\mathcal N}-{\mathcal C}$
and
$g\in {\mathcal N}-{\mathcal C}$
and
![]() $\operatorname {\mathrm {tr}}(g)\neq 0$
, where
$\operatorname {\mathrm {tr}}(g)\neq 0$
, where
![]() . However, this contradicts that
. However, this contradicts that
![]() $\operatorname {\mathrm {tr}}(A)=0$
for all
$\operatorname {\mathrm {tr}}(A)=0$
for all
![]() $A\in {\mathcal N}-{\mathcal C}$
.
$A\in {\mathcal N}-{\mathcal C}$
.
Therefore, the image of
![]() does not lie in the normalizer of a Cartan subgroup of
does not lie in the normalizer of a Cartan subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )$
.
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
.
5.6
 $\mathfrak {A}_5$
case
$\mathfrak {A}_5$
case
Assume that
![]() is isomorphic to
is isomorphic to
![]() $\mathfrak {A}_5$
with
$\mathfrak {A}_5$
with
![]() $\#k_\lambda \notin \{4,5\}$
.
$\#k_\lambda \notin \{4,5\}$
.
The image of
![]() $r_p/p^{k-1}= a_p^2/(\varepsilon (p)p^{k-1})$
in
$r_p/p^{k-1}= a_p^2/(\varepsilon (p)p^{k-1})$
in
![]() ${\mathbb F}_\lambda $
is equal to
${\mathbb F}_\lambda $
is equal to
![]() $\operatorname {\mathrm {tr}}(A)^2/\det (A)$
with
$\operatorname {\mathrm {tr}}(A)^2/\det (A)$
with
![]() . Every element of
. Every element of
![]() $\mathfrak {A}_5$
has order
$\mathfrak {A}_5$
has order
![]() $1$
,
$1$
,
![]() $2$
,
$2$
,
![]() $3$
, or
$3$
, or
![]() $5$
, so Lemma 5.2 implies that the image of
$5$
, so Lemma 5.2 implies that the image of
![]() $r_p/p^{k-1}$
in
$r_p/p^{k-1}$
in
![]() ${\mathbb F}_\lambda $
is
${\mathbb F}_\lambda $
is
![]() $0$
,
$0$
,
![]() $1$
,
$1$
,
![]() $4$
, or is a root of
$4$
, or is a root of
![]() $x^2-3x+1$
for all
$x^2-3x+1$
for all
![]() $p\nmid N\ell $
. If
$p\nmid N\ell $
. If
![]() $\lambda | 5$
, then Lemma 5.2 implies that
$\lambda | 5$
, then Lemma 5.2 implies that
![]() $k_\lambda ={\mathbb F}_5$
, which is excluded by our assumption on
$k_\lambda ={\mathbb F}_5$
, which is excluded by our assumption on
![]() $k_\lambda $
. So
$k_\lambda $
. So
![]() $\lambda \nmid 5$
and Lemma 5.2 ensures that
$\lambda \nmid 5$
and Lemma 5.2 ensures that
![]() $k_\lambda $
is the splitting field of
$k_\lambda $
is the splitting field of
![]() $x^2-3x+1$
over
$x^2-3x+1$
over
![]() ${\mathbb F}_\ell $
. So
${\mathbb F}_\ell $
. So
![]() $k_\lambda $
is
$k_\lambda $
is
![]() ${\mathbb F}_\ell $
if
${\mathbb F}_\ell $
if
![]() $\ell \equiv \pm 1 \ \pmod {5}$
and
$\ell \equiv \pm 1 \ \pmod {5}$
and
![]() ${\mathbb F}_{\ell ^2}$
if
${\mathbb F}_{\ell ^2}$
if
![]() $\ell \equiv \pm 2 \ \pmod {5}$
.
$\ell \equiv \pm 2 \ \pmod {5}$
.
From assumption (c), we find that
![]() $\ell> 5k-4$
and
$\ell> 5k-4$
and
![]() $\ell \nmid N$
. By Lemma 5.3, the group
$\ell \nmid N$
. By Lemma 5.3, the group
![]() contains an element of order at least
contains an element of order at least
![]() $(\ell -1)/(k-1)> ((5k-4)-1)/(k-1) = 5$
. This is a contradiction since
$(\ell -1)/(k-1)> ((5k-4)-1)/(k-1) = 5$
. This is a contradiction since
![]() $\mathfrak {A}_5$
has no elements with order greater than
$\mathfrak {A}_5$
has no elements with order greater than
![]() $5$
.
$5$
.
5.7
 $\mathfrak {A}_4$
and
$\mathfrak {A}_4$
and
 $\mathfrak {S}_4$
cases
$\mathfrak {S}_4$
cases
Suppose that
![]() is isomorphic to
is isomorphic to
![]() $\mathfrak {A}_4$
or
$\mathfrak {A}_4$
or
![]() $\mathfrak {S}_4$
with
$\mathfrak {S}_4$
with
![]() $\#k_\lambda \neq 3$
.
$\#k_\lambda \neq 3$
.
First suppose that
![]() $\#k_\lambda \notin \{5,7\}$
. The image of
$\#k_\lambda \notin \{5,7\}$
. The image of
![]() $r_p/p^{k-1}= a_p^2/(\varepsilon (p)p^{k-1})$
in
$r_p/p^{k-1}= a_p^2/(\varepsilon (p)p^{k-1})$
in
![]() ${\mathbb F}_\lambda $
is equal to
${\mathbb F}_\lambda $
is equal to
![]() $\operatorname {\mathrm {tr}}(A)^2/\det (A)$
with
$\operatorname {\mathrm {tr}}(A)^2/\det (A)$
with
![]() . Since every element of
. Since every element of
![]() $\mathfrak {S}_4$
has order at most
$\mathfrak {S}_4$
has order at most
![]() $4$
, Lemma 5.2 implies that
$4$
, Lemma 5.2 implies that
![]() $r_p/p^{k-1}$
is congruent to
$r_p/p^{k-1}$
is congruent to
![]() $0$
,
$0$
,
![]() $1$
,
$1$
,
![]() $2$
, or
$2$
, or
![]() $4$
modulo
$4$
modulo
![]() $\lambda $
for all primes
$\lambda $
for all primes
![]() $p\nmid N\ell $
. In particular,
$p\nmid N\ell $
. In particular,
![]() $k_\lambda ={\mathbb F}_\ell $
. By assumption (d), we must have
$k_\lambda ={\mathbb F}_\ell $
. By assumption (d), we must have
![]() $\ell>4k-3$
and
$\ell>4k-3$
and
![]() $\ell \nmid N$
. By Lemma 5.3, the group
$\ell \nmid N$
. By Lemma 5.3, the group
![]() contains an element of order at least
contains an element of order at least
![]() $(\ell -1)/(k-1)> ((4k-3)-1)/(k-1) = 4$
. This is a contradiction since
$(\ell -1)/(k-1)> ((4k-3)-1)/(k-1) = 4$
. This is a contradiction since
![]() $\mathfrak {S}_4$
has no elements with order greater than
$\mathfrak {S}_4$
has no elements with order greater than
![]() $4$
.
$4$
.
Now, suppose that
![]() $\#k_\lambda \in \{5,7\}$
. By assumption (e), with any
$\#k_\lambda \in \{5,7\}$
. By assumption (e), with any
![]() $\chi $
, there is a prime
$\chi $
, there is a prime
![]() $p\nmid N\ell $
such that
$p\nmid N\ell $
such that
![]() $a_p^2/(\varepsilon (p)p^{k-1}) \equiv 2 \ \pmod {\lambda }$
. The element
$a_p^2/(\varepsilon (p)p^{k-1}) \equiv 2 \ \pmod {\lambda }$
. The element
has order
![]() $1$
,
$1$
,
![]() $2$
,
$2$
,
![]() $3$
, or
$3$
, or
![]() $4$
. By Lemma 5.2, we deduce that g has order
$4$
. By Lemma 5.2, we deduce that g has order
![]() $4$
. Since
$4$
. Since
![]() $\mathfrak {A}_4$
has no elements of order
$\mathfrak {A}_4$
has no elements of order
![]() $4$
, we deduce that
$4$
, we deduce that
is isomorphic to
![]() $\mathfrak {S}_4$
. Let
$\mathfrak {S}_4$
. Let
![]() $H'$
be the unique index
$H'$
be the unique index
![]() $2$
subgroup of H; it is isomorphic to
$2$
subgroup of H; it is isomorphic to
![]() $\mathfrak {A}_4$
. Define the character
$\mathfrak {A}_4$
. Define the character
The quadratic character
![]() $\beta $
corresponds to a Dirichlet character
$\beta $
corresponds to a Dirichlet character
![]() $\chi $
whose conductor divides
$\chi $
whose conductor divides
![]() $4^e \ell N$
. By assumption (e), there is a prime
$4^e \ell N$
. By assumption (e), there is a prime
![]() $p\nmid N\ell $
such that
$p\nmid N\ell $
such that
![]() $\chi (p)=1$
and
$\chi (p)=1$
and
![]() $a_p^2/(\varepsilon (p)p^{k-1})\equiv 2 \ \pmod {\lambda }$
. Since
$a_p^2/(\varepsilon (p)p^{k-1})\equiv 2 \ \pmod {\lambda }$
. Since
![]() $\beta (\operatorname {\mathrm {Frob}}_p)=\chi (p)=1$
, we have
$\beta (\operatorname {\mathrm {Frob}}_p)=\chi (p)=1$
, we have
. Since
![]() $H'\cong \mathfrak {A}_4$
, Lemma 5.2 implies that the image of
$H'\cong \mathfrak {A}_4$
, Lemma 5.2 implies that the image of
![]() $a_p^2/(\varepsilon (p)p^{k-1})$
in
$a_p^2/(\varepsilon (p)p^{k-1})$
in
![]() ${\mathbb F}_\lambda $
is
${\mathbb F}_\lambda $
is
![]() $0$
,
$0$
,
![]() $1$
, or
$1$
, or
![]() $4$
. This contradicts
$4$
. This contradicts
![]() $a_p^2/(\varepsilon (p)p^{k-1})\equiv 2 \ \pmod {\lambda }$
.
$a_p^2/(\varepsilon (p)p^{k-1})\equiv 2 \ \pmod {\lambda }$
.
Therefore, the image of
![]() is not isomorphic to either of the groups
is not isomorphic to either of the groups
![]() $\mathfrak {A}_4$
or
$\mathfrak {A}_4$
or
![]() $\mathfrak {S}_4$
.
$\mathfrak {S}_4$
.
5.8 End of proof
In Section 5.3, we saw that
![]() is not contained in a Borel subgroup of
is not contained in a Borel subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )$
. In Section 5.5, we saw that
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
. In Section 5.5, we saw that
![]() is not contained in the normalizer of a Cartan subgroup of
is not contained in the normalizer of a Cartan subgroup of
![]() $\operatorname {GL}_2({\mathbb F}_\Lambda )$
.
$\operatorname {GL}_2({\mathbb F}_\Lambda )$
.
In Section 5.6, we showed that if
![]() $\#k_\lambda \notin \{4,5\}$
, then
$\#k_\lambda \notin \{4,5\}$
, then
![]() is not isomorphic to
is not isomorphic to
![]() $\mathfrak {A}_5$
. We want to exclude the cases
$\mathfrak {A}_5$
. We want to exclude the cases
![]() $\#k_\lambda \in \{4,5\}$
since
$\#k_\lambda \in \{4,5\}$
since
![]() $\operatorname {PSL}_2({\mathbb F}_4)$
and
$\operatorname {PSL}_2({\mathbb F}_4)$
and
![]() $\operatorname {PSL}_2({\mathbb F}_5)$
are both isomorphic to
$\operatorname {PSL}_2({\mathbb F}_5)$
are both isomorphic to
![]() $\mathfrak {A}_5$
.
$\mathfrak {A}_5$
.
In Section 5.7, we showed that if
![]() $\#k_\lambda \neq 3$
, then
$\#k_\lambda \neq 3$
, then
![]() is not isomorphic to
is not isomorphic to
![]() $\mathfrak {A}_4$
and not isomorphic to
$\mathfrak {A}_4$
and not isomorphic to
![]() $\mathfrak {S}_4$
. We want to exclude the case
$\mathfrak {S}_4$
. We want to exclude the case
![]() $\#k_\lambda =3$
since
$\#k_\lambda =3$
since
![]() $\operatorname {PSL}_2({\mathbb F}_3)$
and
$\operatorname {PSL}_2({\mathbb F}_3)$
and
![]() $\operatorname {PGL}_2({\mathbb F}_3)$
are isomorphic to
$\operatorname {PGL}_2({\mathbb F}_3)$
are isomorphic to
![]() $\mathfrak {A}_4$
and
$\mathfrak {A}_4$
and
![]() $\mathfrak {S}_4$
, respectively.
$\mathfrak {S}_4$
, respectively.
By Lemma 5.1, the group
![]() must be conjugate in
must be conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
![]() $\operatorname {PSL}_2({\mathbb F}')$
or
$\operatorname {PSL}_2({\mathbb F}')$
or
![]() $\operatorname {PGL}_2({\mathbb F}')$
, where
$\operatorname {PGL}_2({\mathbb F}')$
, where
![]() ${\mathbb F}'$
is a subfield of
${\mathbb F}'$
is a subfield of
![]() ${\mathbb F}_\Lambda $
. One can then show that
${\mathbb F}_\Lambda $
. One can then show that
![]() ${\mathbb F}'$
is the subfield of
${\mathbb F}'$
is the subfield of
![]() ${\mathbb F}_\Lambda $
generated by the set
${\mathbb F}_\Lambda $
generated by the set
![]() . By the Chebotarev density theorem, the field
. By the Chebotarev density theorem, the field
![]() ${\mathbb F}'$
is the subfield of
${\mathbb F}'$
is the subfield of
![]() ${\mathbb F}_\Lambda $
generated by the images of
${\mathbb F}_\Lambda $
generated by the images of
![]() $a_p^2/(\varepsilon (p) p^{k-1})=r_p/p^{k-1}$
with
$a_p^2/(\varepsilon (p) p^{k-1})=r_p/p^{k-1}$
with
![]() $p\nmid N\ell $
. Therefore,
$p\nmid N\ell $
. Therefore,
![]() ${\mathbb F}'=k_\lambda $
and hence
${\mathbb F}'=k_\lambda $
and hence
![]() is conjugate in
is conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
![]() $\operatorname {PSL}_2(k_\lambda )$
or
$\operatorname {PSL}_2(k_\lambda )$
or
![]() $\operatorname {PGL}_2(k_\lambda )$
.
$\operatorname {PGL}_2(k_\lambda )$
.
6 Examples
6.1 Example from Section 1.2
Let f be the newform from Section 1.2. We have
![]() $E={\mathbb Q}(i)$
. We know that
$E={\mathbb Q}(i)$
. We know that
![]() $\Gamma \neq 1$
since
$\Gamma \neq 1$
since
![]() $\varepsilon $
is nontrivial. Therefore,
$\varepsilon $
is nontrivial. Therefore,
![]() $\Gamma =\operatorname {\mathrm {Gal}}({\mathbb Q}(i)/{\mathbb Q})$
and
$\Gamma =\operatorname {\mathrm {Gal}}({\mathbb Q}(i)/{\mathbb Q})$
and
![]() $K=E^{\Gamma }$
equals
$K=E^{\Gamma }$
equals
![]() ${\mathbb Q}$
. So
${\mathbb Q}$
. So
![]() $\Gamma $
is generated by complex conjugation and we have
$\Gamma $
is generated by complex conjugation and we have
![]() for
for
![]() $p\nmid N$
. As noted in Section 1.2, this implies that
$p\nmid N$
. As noted in Section 1.2, this implies that
![]() $r_p$
is a square in
$r_p$
is a square in
![]() ${\mathbb Z}$
for all
${\mathbb Z}$
for all
![]() $p\nmid N$
and hence L equals
$p\nmid N$
and hence L equals
![]() $K={\mathbb Q}$
. Fix a prime
$K={\mathbb Q}$
. Fix a prime
![]() $\ell =\lambda $
and a prime ideal
$\ell =\lambda $
and a prime ideal
![]() $\Lambda | \ell $
of
$\Lambda | \ell $
of
![]() ${\mathcal O}={\mathbb Z}[i]$
.
${\mathcal O}={\mathbb Z}[i]$
.
Set
![]() $q_1=109$
and
$q_1=109$
and
![]() $q_2=379$
; they are primes that are congruent to
$q_2=379$
; they are primes that are congruent to
![]() $1$
modulo
$1$
modulo
![]() $27$
. Set
$27$
. Set
![]() $p_1=5$
, and we have
$p_1=5$
, and we have
![]() $\chi (p_1)=-1$
, where
$\chi (p_1)=-1$
, where
![]() $\chi $
is the unique nontrivial character
$\chi $
is the unique nontrivial character
![]() $({\mathbb Z}/3{\mathbb Z})^\times \to \{\pm 1\}$
. Set
$({\mathbb Z}/3{\mathbb Z})^\times \to \{\pm 1\}$
. Set
![]() $q=5$
; the field
$q=5$
; the field
![]() ${\mathbb Q}(r_q)$
equals
${\mathbb Q}(r_q)$
equals
![]() $K={\mathbb Q}$
and hence
$K={\mathbb Q}$
and hence
![]() ${\mathbb Z}[r_{q}]={\mathbb Z}$
.
${\mathbb Z}[r_{q}]={\mathbb Z}$
.
One can verify that
![]() $a_{109}=164$
,
$a_{109}=164$
,
![]() $a_{379}=704$
, and
$a_{379}=704$
, and
![]() $a_5=-3i$
, so
$a_5=-3i$
, so
![]() $r_{109}=164^2$
,
$r_{109}=164^2$
,
![]() $r_{379}=704^2$
, and
$r_{379}=704^2$
, and
![]() $r_5=3^2$
. We have
$r_5=3^2$
. We have
![]() $r_{109} - (1+109^2)^2 = -2^2\times 3^3\times 7\times 19\times 31\times 317$
and
$r_{109} - (1+109^2)^2 = -2^2\times 3^3\times 7\times 19\times 31\times 317$
and
![]() $r_{379} - (1+379^2)^2 = -2^2 \times 3^3\times 2,647 \times 72,173$
. So if
$r_{379} - (1+379^2)^2 = -2^2 \times 3^3\times 2,647 \times 72,173$
. So if
![]() $\ell \geq 11$
, then there is an
$\ell \geq 11$
, then there is an
![]() $i\in \{1,2\}$
such that
$i\in \{1,2\}$
such that
![]() $\ell \neq q_i$
and
$\ell \neq q_i$
and
![]() $r_{q_i}\not \equiv (1+q_i^2)^2\ \pmod {\ell }$
.
$r_{q_i}\not \equiv (1+q_i^2)^2\ \pmod {\ell }$
.
Let S be the set from Section 4 with the above choice of
![]() $q_1$
,
$q_1$
,
![]() $q_2$
,
$q_2$
,
![]() $p_1$
, and q. We find that
$p_1$
, and q. We find that
![]() $S = \{2,3,5,7,11\}$
. Theorem 4.3 implies that
$S = \{2,3,5,7,11\}$
. Theorem 4.3 implies that
![]() is conjugate in
is conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
![]() $\operatorname {PSL}_2({\mathbb F}_\ell )$
when
$\operatorname {PSL}_2({\mathbb F}_\ell )$
when
![]() $\ell>11$
.
$\ell>11$
.
Now, take
![]() $\ell \in \{7,11\}$
. Choose a prime ideal
$\ell \in \{7,11\}$
. Choose a prime ideal
![]() $\Lambda $
of
$\Lambda $
of
![]() ${\mathcal O}$
dividing
${\mathcal O}$
dividing
![]() $\ell $
. We have
$\ell $
. We have
![]() $e_0=e_1=e_2=0$
and
$e_0=e_1=e_2=0$
and
![]() ${\mathcal M}=3$
. The subfield
${\mathcal M}=3$
. The subfield
![]() $k_\ell $
generated over
$k_\ell $
generated over
![]() ${\mathbb F}_\ell $
by the images of
${\mathbb F}_\ell $
by the images of
![]() $r_p$
modulo
$r_p$
modulo
![]() $\ell $
with
$\ell $
with
![]() $p\nmid N\ell $
is of course
$p\nmid N\ell $
is of course
![]() ${\mathbb F}_\ell $
(since the
${\mathbb F}_\ell $
(since the
![]() $r_p$
are rational integers). We now verify the conditions of Theorem 4.1.
$r_p$
are rational integers). We now verify the conditions of Theorem 4.1.
We first check condition (a). Suppose there is a character
![]() $\chi \colon\ ({\mathbb Z}/27{\mathbb Z})^\times \to {\mathbb F}_\ell ^\times $
such that
$\chi \colon\ ({\mathbb Z}/27{\mathbb Z})^\times \to {\mathbb F}_\ell ^\times $
such that
![]() $\chi (q_2)$
is a root of
$\chi (q_2)$
is a root of
![]() $x^2-a_{q_2} x + \varepsilon (q_2) q_2^2$
modulo
$x^2-a_{q_2} x + \varepsilon (q_2) q_2^2$
modulo
![]() $\ell $
. Since
$\ell $
. Since
![]() $q_2\equiv 1\ \pmod {27}$
and
$q_2\equiv 1\ \pmod {27}$
and
![]() $a_{q_2}=704$
, we find that
$a_{q_2}=704$
, we find that
![]() $1$
is a root of
$1$
is a root of
![]() $x^2-a_{q_2} x + q_2^2 \in {\mathbb F}_\ell [x]$
. Therefore,
$x^2-a_{q_2} x + q_2^2 \in {\mathbb F}_\ell [x]$
. Therefore,
![]() $a_{q_2} \equiv 1+q_2^2 \ \pmod {\ell }$
and hence
$a_{q_2} \equiv 1+q_2^2 \ \pmod {\ell }$
and hence
![]() $r_{q_2}^2 = a_{q_2}^2 \equiv (1+ q_2^2)^2 \ \pmod {\ell }$
. However,
$r_{q_2}^2 = a_{q_2}^2 \equiv (1+ q_2^2)^2 \ \pmod {\ell }$
. However,
![]() $r_{379} - (1+379^2)^2 \not \equiv 0 \ \pmod {\ell }$
from the explicit value of it computed above. So the character
$r_{379} - (1+379^2)^2 \not \equiv 0 \ \pmod {\ell }$
from the explicit value of it computed above. So the character
![]() $\chi $
does not exist and we have verified condition (a).
$\chi $
does not exist and we have verified condition (a).
We now check condition (b). Let
![]() $\chi \colon\ ({\mathbb Z}/3{\mathbb Z})^\times \to \{\pm 1\}$
be the nontrivial character. We have
$\chi \colon\ ({\mathbb Z}/3{\mathbb Z})^\times \to \{\pm 1\}$
be the nontrivial character. We have
![]() $\chi (5)=-1$
and
$\chi (5)=-1$
and
![]() $r_5 = 9 \not \equiv 0 \ \pmod {\ell }$
. Therefore, condition (b) holds.
$r_5 = 9 \not \equiv 0 \ \pmod {\ell }$
. Therefore, condition (b) holds.
We now check condition (c). If
![]() $\ell =7$
, we have
$\ell =7$
, we have
![]() $\ell \equiv 2 \ \pmod {5}$
and
$\ell \equiv 2 \ \pmod {5}$
and
![]() $\#k_\ell = \ell \neq \ell ^2$
, so condition (c) holds. Take
$\#k_\ell = \ell \neq \ell ^2$
, so condition (c) holds. Take
![]() $\ell =11$
. We have
$\ell =11$
. We have
![]() $a_5^2/(\varepsilon (5) 5^2) = 9/5^2 \equiv 3 \ \pmod {11}$
, which verifies condition (c).
$a_5^2/(\varepsilon (5) 5^2) = 9/5^2 \equiv 3 \ \pmod {11}$
, which verifies condition (c).
Condition (d) holds since
![]() $\#k_\ell = 5$
if
$\#k_\ell = 5$
if
![]() $\ell = 7$
, and
$\ell = 7$
, and
![]() $\ell>4k-3=9$
and
$\ell>4k-3=9$
and
![]() $\ell \nmid N$
if
$\ell \nmid N$
if
![]() $\ell =11$
.
$\ell =11$
.
Finally, we explain why condition (e) holds when
![]() $\ell =7$
. Let
$\ell =7$
. Let
![]() $\chi \colon\ ({\mathbb Z}/7\cdot 27 {\mathbb Z})^\times \to \{\pm 1\}$
be any nontrivial character. A quick computation shows that there is a prime
$\chi \colon\ ({\mathbb Z}/7\cdot 27 {\mathbb Z})^\times \to \{\pm 1\}$
be any nontrivial character. A quick computation shows that there is a prime
![]() $p\in \{13,37,41\}$
such that
$p\in \{13,37,41\}$
such that
![]() $\chi (p)=1$
and that
$\chi (p)=1$
and that
![]() $a_p^2/(\varepsilon (p) p^2) \equiv 2 \ \pmod {7}$
.
$a_p^2/(\varepsilon (p) p^2) \equiv 2 \ \pmod {7}$
.
Theorem 4.1 implies that
![]() is conjugate in
is conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
![]() $\operatorname {PSL}_2({\mathbb F}_\ell )$
or
$\operatorname {PSL}_2({\mathbb F}_\ell )$
or
![]() $\operatorname {PGL}_2({\mathbb F}_\ell )$
. Since
$\operatorname {PGL}_2({\mathbb F}_\ell )$
. Since
![]() $L=K$
, the group
$L=K$
, the group
![]() isomorphic to
isomorphic to
![]() $\operatorname {PSL}_2({\mathbb F}_{\ell })$
by Theorem 1.2(i).
$\operatorname {PSL}_2({\mathbb F}_{\ell })$
by Theorem 1.2(i).
6.2 Example from §1.3
Let f be a newform as in Section 1.3; we have
![]() $k=3$
and
$k=3$
and
![]() $N=160$
. The Magma code below verifies that f is uniquely determined up to replacing by a quadratic twist and then a Galois conjugate. So the group
$N=160$
. The Magma code below verifies that f is uniquely determined up to replacing by a quadratic twist and then a Galois conjugate. So the group
![]() , up to isomorphism, does not depend on the choice of f.
, up to isomorphism, does not depend on the choice of f.

Define
![]() $b = \zeta _{13}^1 + \zeta _{13}^5+\zeta _{13}^8 +\zeta _{13}^{12}$
, where
$b = \zeta _{13}^1 + \zeta _{13}^5+\zeta _{13}^8 +\zeta _{13}^{12}$
, where
![]() $\zeta _{13}$
is a primitive
$\zeta _{13}$
is a primitive
![]() $13$
th root of unity in
$13$
th root of unity in
![]() ${\overline {\mathbb Q}}$
(note that
${\overline {\mathbb Q}}$
(note that
![]() $\{1,5,8,12\}$
is the unique index
$\{1,5,8,12\}$
is the unique index
![]() $3$
subgroup of
$3$
subgroup of
![]() ${\mathbb F}_{13}^\times $
). The characteristic polynomial of b is
${\mathbb F}_{13}^\times $
). The characteristic polynomial of b is
![]() $x^3 + x^2 - 4x + 1$
, and hence
$x^3 + x^2 - 4x + 1$
, and hence
![]() ${\mathbb Q}(b)$
is the unique cubic extension of
${\mathbb Q}(b)$
is the unique cubic extension of
![]() ${\mathbb Q}$
in
${\mathbb Q}$
in
![]() ${\mathbb Q}(\zeta _{13})$
. The code below shows that the coefficient field E is equal to
${\mathbb Q}(\zeta _{13})$
. The code below shows that the coefficient field E is equal to
![]() ${\mathbb Q}(b,i)$
(it is a degree
${\mathbb Q}(b,i)$
(it is a degree
![]() $6$
extension of
$6$
extension of
![]() ${\mathbb Q}$
that contains roots of
${\mathbb Q}$
that contains roots of
![]() $x^3 + x^2 - 4x + 1$
and
$x^3 + x^2 - 4x + 1$
and
![]() $x^2+1$
).
$x^2+1$
).

Fix notation as in Section 2.1. We have
![]() $\Gamma \neq 1$
since
$\Gamma \neq 1$
since
![]() $\varepsilon $
is nontrivial. The character
$\varepsilon $
is nontrivial. The character
![]() $\chi _\gamma ^2$
is trivial for
$\chi _\gamma ^2$
is trivial for
![]() $\gamma \in \Gamma $
(since
$\gamma \in \Gamma $
(since
![]() $\chi _\gamma $
is always a quadratic character times some power of
$\chi _\gamma $
is always a quadratic character times some power of
![]() $\varepsilon $
). Therefore,
$\varepsilon $
). Therefore,
![]() $\Gamma $
is a
$\Gamma $
is a
![]() $2$
-group. The field
$2$
-group. The field
![]() $K=E^{\Gamma} $
is thus
$K=E^{\Gamma} $
is thus
![]() ${\mathbb Q}(b)$
, which is the unique cubic extension of
${\mathbb Q}(b)$
, which is the unique cubic extension of
![]() ${\mathbb Q}$
in E. Therefore,
${\mathbb Q}$
in E. Therefore,
![]() $r_p = a_p^2/\varepsilon (p)$
lies in
$r_p = a_p^2/\varepsilon (p)$
lies in
![]() $K={\mathbb Q}(b)$
for all
$K={\mathbb Q}(b)$
for all
![]() $p\nmid N$
.
$p\nmid N$
.
The code below verifies that
![]() $r_3$
,
$r_3$
,
![]() $r_7$
, and
$r_7$
, and
![]() $r_{11}$
are squares in K that do not lie in
$r_{11}$
are squares in K that do not lie in
![]() ${\mathbb Q}$
(and, in particular, are nonzero). Since
${\mathbb Q}$
(and, in particular, are nonzero). Since
![]() $3$
,
$3$
,
![]() $7$
, and
$7$
, and
![]() $11$
generate the group
$11$
generate the group
![]() $({\mathbb Z}/40{\mathbb Z})^\times $
, we deduce from Lemma 2.3 that the field
$({\mathbb Z}/40{\mathbb Z})^\times $
, we deduce from Lemma 2.3 that the field
![]() $L=K(\{\sqrt {r_p}:p\nmid N\})$
is equal to K.
$L=K(\{\sqrt {r_p}:p\nmid N\})$
is equal to K.

Let
![]() $N_{K/{\mathbb Q}}\colon\ K\to {\mathbb Q}$
be the norm map. The following code verifies that
$N_{K/{\mathbb Q}}\colon\ K\to {\mathbb Q}$
be the norm map. The following code verifies that
![]() $N_{K/{\mathbb Q}}(r_3) = 2^6$
,
$N_{K/{\mathbb Q}}(r_3) = 2^6$
,
![]() $N_{K/{\mathbb Q}}(r_7) = 2^6$
,
$N_{K/{\mathbb Q}}(r_7) = 2^6$
,
![]() $N_{K/{\mathbb Q}}(r_{11}) = 2^{12}5^4$
,
$N_{K/{\mathbb Q}}(r_{11}) = 2^{12}5^4$
,
![]() $N_{K/{\mathbb Q}}(r_{13})=2^{12} 13^2$
,
$N_{K/{\mathbb Q}}(r_{13})=2^{12} 13^2$
,
![]() $N_{K/{\mathbb Q}}(r_{17}) = 2^{18}5^2$
, and that
$N_{K/{\mathbb Q}}(r_{17}) = 2^{18}5^2$
, and that

Set
![]() $q_1=641$
and
$q_1=641$
and
![]() $q_2=1,061$
; they are primes congruent to
$q_2=1,061$
; they are primes congruent to
![]() $1$
modulo
$1$
modulo
![]() $160$
. Let
$160$
. Let
![]() $\lambda $
be a prime ideal of R dividing a rational prime
$\lambda $
be a prime ideal of R dividing a rational prime
![]() $\ell>3$
. From (6.1), we find that
$\ell>3$
. From (6.1), we find that
![]() $\ell \neq q_i$
and
$\ell \neq q_i$
and
![]() $r_{q_i} \not \equiv (1+q_i^2)^2 \ \pmod {\lambda }$
for some
$r_{q_i} \not \equiv (1+q_i^2)^2 \ \pmod {\lambda }$
for some
![]() $i\in \{1,2\}$
(otherwise,
$i\in \{1,2\}$
(otherwise,
![]() $\lambda $
would divide
$\lambda $
would divide
![]() $2$
).
$2$
).
Set
![]() $p_1=3$
,
$p_1=3$
,
![]() $p_2= 7$
, and
$p_2= 7$
, and
![]() $p_3=11$
. For each nontrivial quadratic character
$p_3=11$
. For each nontrivial quadratic character
![]() $\chi \colon\ ({\mathbb Z}/40 {\mathbb Z})^\times \to \{\pm 1\}$
, we have
$\chi \colon\ ({\mathbb Z}/40 {\mathbb Z})^\times \to \{\pm 1\}$
, we have
![]() $\chi (p_i)=-1$
for some prime
$\chi (p_i)=-1$
for some prime
![]() $i\in \{1,2,3\}$
(since
$i\in \{1,2,3\}$
(since
![]() $3$
,
$3$
,
![]() $7$
, and
$7$
, and
![]() $11$
generate the group
$11$
generate the group
![]() $({\mathbb Z}/40{\mathbb Z})^\times $
). From the computed values of
$({\mathbb Z}/40{\mathbb Z})^\times $
). From the computed values of
![]() $N_{K/{\mathbb Q}}(r_p)$
, we find that
$N_{K/{\mathbb Q}}(r_p)$
, we find that
![]() $r_{p_i} \not \equiv 0 \ \pmod {\lambda }$
for all
$r_{p_i} \not \equiv 0 \ \pmod {\lambda }$
for all
![]() $i\in \{1,2,3\}$
and all nonzero prime ideals
$i\in \{1,2,3\}$
and all nonzero prime ideals
![]() $\lambda \nmid N$
of R.
$\lambda \nmid N$
of R.
Set
![]() $q=3$
. We have noted that
$q=3$
. We have noted that
![]() $r_{q}\in K-{\mathbb Q}$
, so
$r_{q}\in K-{\mathbb Q}$
, so
![]() $K={\mathbb Q}(r_{q})$
. The index of the order
$K={\mathbb Q}(r_{q})$
. The index of the order
![]() ${\mathbb Z}[r_{q}]$
in R is a power of
${\mathbb Z}[r_{q}]$
in R is a power of
![]() $2$
since
$2$
since
![]() $N_{K/{\mathbb Q}}(q)$
is a power of
$N_{K/{\mathbb Q}}(q)$
is a power of
![]() $2$
.
$2$
.
Let S be the set from Section 4 with the above choice of
![]() $q_1$
,
$q_1$
,
![]() $q_2$
,
$q_2$
,
![]() $p_1$
,
$p_1$
,
![]() $p_2$
,
$p_2$
,
![]() $p_3$
, and q. The above computations show that S consists of the prime ideals
$p_3$
, and q. The above computations show that S consists of the prime ideals
![]() $\lambda $
of R that divide a prime
$\lambda $
of R that divide a prime
![]() $\ell \leq 11$
.
$\ell \leq 11$
.
Now, let
![]() $\ell $
be an odd prime congruent to
$\ell $
be an odd prime congruent to
![]() $\pm 2$
,
$\pm 2$
,
![]() $\pm 3$
,
$\pm 3$
,
![]() $\pm 4$
, or
$\pm 4$
, or
![]() $\pm 6$
modulo
$\pm 6$
modulo
![]() $13$
. Since K is the unique cubic extension in
$13$
. Since K is the unique cubic extension in
![]() ${\mathbb Q}(\zeta _{13})$
, we find that the ideal
${\mathbb Q}(\zeta _{13})$
, we find that the ideal
![]() $\lambda := \ell R$
is prime in R and that
$\lambda := \ell R$
is prime in R and that
![]() ${\mathbb F}_\lambda \cong {\mathbb F}_{\ell ^3}$
. The above computations show that
${\mathbb F}_\lambda \cong {\mathbb F}_{\ell ^3}$
. The above computations show that
![]() $\lambda \notin S$
when
$\lambda \notin S$
when
![]() $\ell \notin \{3,7,11\}$
. Theorem 4.3 implies that if
$\ell \notin \{3,7,11\}$
. Theorem 4.3 implies that if
![]() $\ell \notin \{3,7,11\}$
, then
$\ell \notin \{3,7,11\}$
, then
![]() is conjugate in
is conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
![]() $\operatorname {PGL}_2({\mathbb F}_\lambda )$
, where
$\operatorname {PGL}_2({\mathbb F}_\lambda )$
, where
![]() $\Lambda $
is a prime ideal of
$\Lambda $
is a prime ideal of
![]() ${\mathcal O}$
dividing
${\mathcal O}$
dividing
![]() $\lambda $
. So if
$\lambda $
. So if
![]() $\ell \notin \{3,7,11\}$
, the group
$\ell \notin \{3,7,11\}$
, the group
![]() isomorphic to
isomorphic to
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )\cong \operatorname {PSL}_2({\mathbb F}_{\ell ^3})$
by Theorem 1.2(i) and the equality
$\operatorname {PSL}_2({\mathbb F}_\lambda )\cong \operatorname {PSL}_2({\mathbb F}_{\ell ^3})$
by Theorem 1.2(i) and the equality
![]() $L=K$
.
$L=K$
.
Now, take
![]() $\lambda = \ell R$
with
$\lambda = \ell R$
with
![]() $\ell \in \{3,7,11\}$
; it is a prime ideal. Choose a prime ideal
$\ell \in \{3,7,11\}$
; it is a prime ideal. Choose a prime ideal
![]() $\Lambda $
of
$\Lambda $
of
![]() ${\mathcal O}$
dividing
${\mathcal O}$
dividing
![]() $\lambda $
. We noted above that
$\lambda $
. We noted above that
![]() ${\mathbb Z}[r_3]$
is an order in R with index a power of
${\mathbb Z}[r_3]$
is an order in R with index a power of
![]() $2$
; the same argument shows that this also holds for the order
$2$
; the same argument shows that this also holds for the order
![]() ${\mathbb Z}[r_7]$
. Therefore, the field
${\mathbb Z}[r_7]$
. Therefore, the field
![]() $k_\lambda $
generated over
$k_\lambda $
generated over
![]() ${\mathbb F}_\ell $
by the images of
${\mathbb F}_\ell $
by the images of
![]() $r_p$
modulo
$r_p$
modulo
![]() $\lambda $
with
$\lambda $
with
![]() $p\nmid N\ell $
is equal to
$p\nmid N\ell $
is equal to
![]() ${\mathbb F}_\lambda $
. Since
${\mathbb F}_\lambda $
. Since
![]() $\#{\mathbb F}_\lambda =\ell ^3$
, we find that conditions (c)–(e) of Theorem 4.1 hold.
$\#{\mathbb F}_\lambda =\ell ^3$
, we find that conditions (c)–(e) of Theorem 4.1 hold.
We now show that condition (a) of Theorem 4.1 holds for our fixed
![]() $\Lambda $
. We have
$\Lambda $
. We have
![]() $e_0=0$
, so take any character
$e_0=0$
, so take any character
![]() $\chi \colon\ ({\mathbb Z}/N{\mathbb Z})^\times \to {\mathbb F}_\Lambda ^\times $
. We claim that
$\chi \colon\ ({\mathbb Z}/N{\mathbb Z})^\times \to {\mathbb F}_\Lambda ^\times $
. We claim that
![]() $\chi (q_i)\in {\mathbb F}_\Lambda $
is not a root of
$\chi (q_i)\in {\mathbb F}_\Lambda $
is not a root of
![]() $x^2-a_{q_i} x + \varepsilon (q_i) q_i^2$
for some
$x^2-a_{q_i} x + \varepsilon (q_i) q_i^2$
for some
![]() $i\in \{1,2\}$
. Since
$i\in \{1,2\}$
. Since
![]() $q_i\equiv 1\ \pmod {N}$
, the claim is equivalent to showing that
$q_i\equiv 1\ \pmod {N}$
, the claim is equivalent to showing that
![]() $a_{q_i} \not \equiv 1 + q_i^2 \ \pmod {\Lambda }$
for some
$a_{q_i} \not \equiv 1 + q_i^2 \ \pmod {\Lambda }$
for some
![]() $i\in \{1,2\}$
. So we need to prove that
$i\in \{1,2\}$
. So we need to prove that
![]() $r_{q_i} \equiv (1 + q_i^2)^2 \ \pmod {\lambda }$
for some
$r_{q_i} \equiv (1 + q_i^2)^2 \ \pmod {\lambda }$
for some
![]() $i\in \{1,2\}$
; this is clear since otherwise
$i\in \{1,2\}$
; this is clear since otherwise
![]() $\ell $
divides the quantity (6.1). This completes our verification of condition (a).
$\ell $
divides the quantity (6.1). This completes our verification of condition (a).
We now show that condition (b) of Theorem 4.1 holds. We have
![]() $r_p \not \equiv 0 \ \pmod {\lambda }$
for all primes
$r_p \not \equiv 0 \ \pmod {\lambda }$
for all primes
![]() $p\in \{3,7,11,13,17\}$
; this is a consequence of
$p\in \{3,7,11,13,17\}$
; this is a consequence of
![]() $N_{K/{\mathbb Q}}(r_p)\not \equiv 0 \ \pmod {\ell }$
. We have
$N_{K/{\mathbb Q}}(r_p)\not \equiv 0 \ \pmod {\ell }$
. We have
![]() ${\mathcal M}= 120$
if
${\mathcal M}= 120$
if
![]() $\ell =3$
and
$\ell =3$
and
![]() ${\mathcal M}=40$
otherwise. Condition (b) holds since
${\mathcal M}=40$
otherwise. Condition (b) holds since
![]() $({\mathbb Z}/{\mathcal M}{\mathbb Z})^\times $
is generated by the primes
$({\mathbb Z}/{\mathcal M}{\mathbb Z})^\times $
is generated by the primes
![]() $p\in \{3,7,11,13,17\}$
for which
$p\in \{3,7,11,13,17\}$
for which
![]() $p\nmid {\mathcal M}\ell $
.
$p\nmid {\mathcal M}\ell $
.
Theorem 4.1 implies that
![]() is conjugate in
is conjugate in
![]() $\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
$\operatorname {PGL}_2({\mathbb F}_\Lambda )$
to
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
$\operatorname {PSL}_2({\mathbb F}_\lambda )$
or
![]() $\operatorname {PGL}_2({\mathbb F}_\lambda )$
. Since
$\operatorname {PGL}_2({\mathbb F}_\lambda )$
. Since
![]() $L=K$
, the group
$L=K$
, the group
![]() is isomorphic to
is isomorphic to
![]() $\operatorname {PSL}_2({\mathbb F}_\lambda )\cong \operatorname {PSL}_2({\mathbb F}_{\ell ^3})$
by Theorem 1.2(i).
$\operatorname {PSL}_2({\mathbb F}_\lambda )\cong \operatorname {PSL}_2({\mathbb F}_{\ell ^3})$
by Theorem 1.2(i).
Acknowledgment
Thanks to Ravi Ramakrishna and Luis Dieulefait for their comments and corrections. Thanks also to Henri Darmon for suggesting that there should be a modular interpretation of the Galois representations in [Reference Zywina18]. Computations were performed with Magma [Reference Bosma, Cannon and Playoust2].