Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Quaife, Bryan D.
and
Moore, M. Nicholas J.
2018.
A boundary-integral framework to simulate viscous erosion of a porous medium.
Journal of Computational Physics,
Vol. 375,
Issue. ,
p.
1.
Favier, B.
Purseed, J.
and
Duchemin, L.
2019.
Rayleigh–Bénard convection with a melting boundary.
Journal of Fluid Mechanics,
Vol. 858,
Issue. ,
p.
437.
Amin, Khunsa
Huang, Jinzi Mac
Hu, Kevin J.
Zhang, Jun
and
Ristroph, Leif
2019.
The role of shape-dependent flight stability in the origin of oriented meteorites.
Proceedings of the National Academy of Sciences,
Vol. 116,
Issue. 33,
p.
16180.
Yang, JinHong
Yuan, QuanZi
and
Zhao, YaPu
2019.
Solute transport and interface evolution in dissolutive wetting.
Science China Physics, Mechanics & Astronomy,
Vol. 62,
Issue. 12,
Huang, Jinzi Mac
Tong, Joshua
Shelley, Michael
and
Ristroph, Leif
2020.
Ultra-sharp pinnacles sculpted by natural convective dissolution.
Proceedings of the National Academy of Sciences,
Vol. 117,
Issue. 38,
p.
23339.
Purseed, J.
Favier, B.
Duchemin, L.
and
Hester, E. W.
2020.
Bistability in Rayleigh-Bénard convection with a melting boundary.
Physical Review Fluids,
Vol. 5,
Issue. 2,
Pegler, Samuel S.
and
Davies Wykes, Megan S.
2020.
Shaping of melting and dissolving solids under natural convection.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Mena, Sarah E.
and
Curtis, Jennifer Sinclair
2020.
Experimental data for solid–liquid flows at intermediate and high Stokes numbers.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Lu, Cai-Lei
Luo, Kang
Zhou, Pu-Cheng
and
Yi, Hong-Liang
2021.
Rayleigh-Bénard convection in a dielectric fluid under an external electric field with a melting boundary.
Physical Review Fluids,
Vol. 6,
Issue. 6,
Huang, Jinzi Mac
Shelley, Michael J.
and
Stein, David B.
2021.
A stable and accurate scheme for solving the Stefan problem coupled with natural convection using the Immersed Boundary Smooth Extension method.
Journal of Computational Physics,
Vol. 432,
Issue. ,
p.
110162.
Pegler, Samuel S.
and
Davies Wykes, Megan S.
2021.
The convective Stefan problem: shaping under natural convection.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Jiang, Yunshan
and
McDonald, N.R.
2022.
Dissolution of plane surfaces by sources in potential flow.
Physica D: Nonlinear Phenomena,
Vol. 442,
Issue. ,
p.
133549.
Lu, Cailei
Zhang, Mengqi
Luo, Kang
Wu, Jian
and
Yi, Hongliang
2022.
Rayleigh–Bénard instability in the presence of phase boundary and shear.
Journal of Fluid Mechanics,
Vol. 948,
Issue. ,
Bayat, Elyce
Egan, Raphael
Bochkov, Daniil
Sauret, Alban
and
Gibou, Frederic
2022.
A sharp numerical method for the simulation of Stefan problems with convective effects.
Journal of Computational Physics,
Vol. 471,
Issue. ,
p.
111627.
Weady, Scott
Tong, Joshua
Zidovska, Alexandra
and
Ristroph, Leif
2022.
Anomalous Convective Flows Carve Pinnacles and Scallops in Melting Ice.
Physical Review Letters,
Vol. 128,
Issue. 4,
Yang, Rui
Chong, Kai Leong
Liu, Hao-Ran
Verzicco, Roberto
and
Lohse, Detlef
2022.
Abrupt transition from slow to fast melting of ice.
Physical Review Fluids,
Vol. 7,
Issue. 8,
Yang, Rui
Howland, Christopher J.
Liu, Hao-Ran
Verzicco, Roberto
and
Lohse, Detlef
2023.
Bistability in Radiatively Heated Melt Ponds.
Physical Review Letters,
Vol. 131,
Issue. 23,
Yang, Rui
Howland, Christopher J.
Liu, Hao-Ran
Verzicco, Roberto
and
Lohse, Detlef
2023.
Ice melting in salty water: layering and non-monotonic dependence on the mean salinity.
Journal of Fluid Mechanics,
Vol. 969,
Issue. ,
Yang, Rui
Howland, Christopher J.
Liu, Hao-Ran
Verzicco, Roberto
and
Lohse, Detlef
2023.
Morphology evolution of a melting solid layer above its melt heated from below.
Journal of Fluid Mechanics,
Vol. 956,
Issue. ,
Du, Yihong
Calzavarini, Enrico
and
Sun, Chao
2024.
The physics of freezing and melting in the presence of flows.
Nature Reviews Physics,
Vol. 6,
Issue. 11,
p.
676.

$\unicode[STIX]{x1D706}$ and amplitude
$A$. (b) The observed pattern may represent the most prominent amplitude (circle) on the boundary between growth and shrinking.
1 Flowing fluids and shapeable solids
It is an exciting time for two important research areas in fluid mechanics. On one hand, we have fluid–structure interactions, the classic example of which is aeroelastic phenomena such as the flapping of a flag. On the other, we have moving-boundary problems that focus on the interface between two phases of matter, for example a freezing and advancing ice-water front or its recession by melting. Where these two disciplines overlap are diverse problems unified by the interaction of flowing fluids with solid but shapeable boundaries. Many processes may drive changes in shape, such as erosion, dissolution, melting, corrosion and so on, and flows are inevitably present.
Upon more reflection, one gets the impression that cases for which a flow encounters a truly immovable solid are in the minority, even if these are the problems that fill up our fluid mechanics textbooks. Even mountains gradually slump and flow due to erosion. The field of geomorphology, which seeks to explain landforms and their development, provides many examples of boundary–flow interactions that yield stereotyped shapes and patterns. Given their beauty, it is perhaps no wonder that landscapes have inspired an entire class of paintings and that our art of sculpting borrows the natural media of stone, clay and ice.
Perhaps we fluid dynamicists are drawn to such shape–flow coupled problems because of their contrast with the textbook settings where flows must satisfy no-slip and no-penetration. In a process like erosion or dissolution, the fluid invades the solid by eating it away. The compliant fluid indeed gives way to the solid, but only on short time scales. Gradually and incrementally, but persistently, and always eventually, the flow leaves its imprint. What makes these problems physically and mathematically interesting is that the solid–fluid dynamics are interdependent, often leading to characteristic shapes or shape dynamics. In other words, complex feedback processes are at work, and better understanding translates to better control in chemical or pharmaceutical applications, for example.
2 Dissolution sculptures
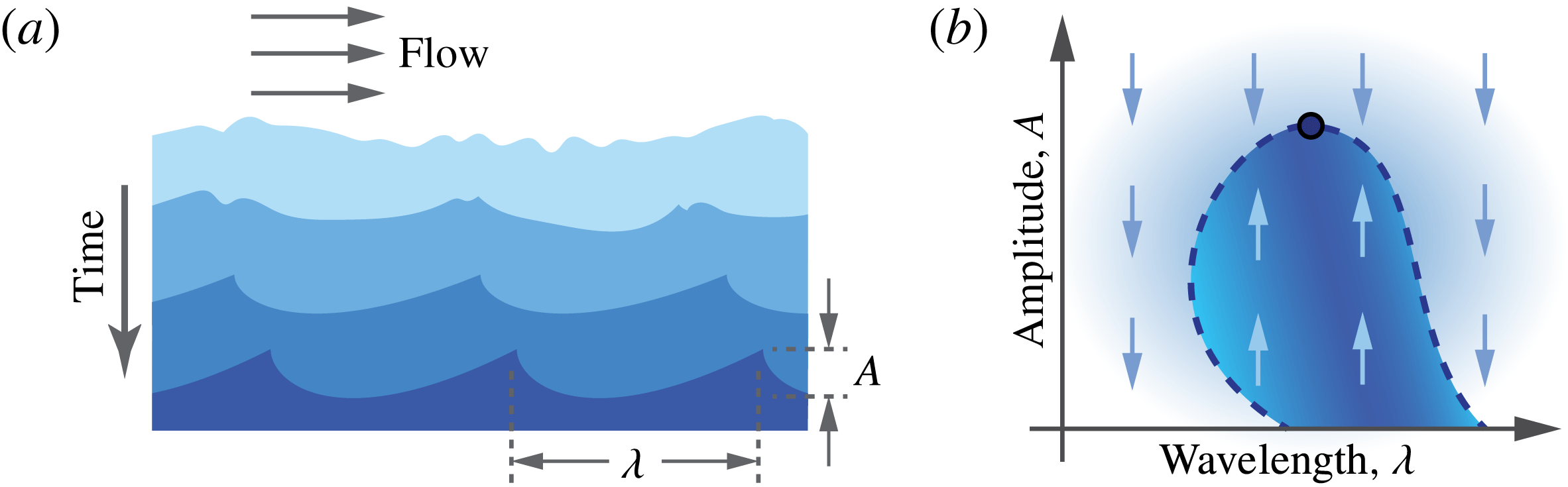
The work of Claudin, Durán & Andreotti (Reference Claudin, Durán and Andreotti2017) is a great example that illustrates some of the common threads in shape–flow problems. The team studies the flow of a fluid over a solid and flat but dissolvable bed, a setting whose simplicity conveys a sense of generality. The authors formulate a model that tracks the average and fluctuating components of a turbulent flow as well as the concentration of dissolved solute. Their stability analysis indicates that the fluid invades the solid not uniformly but such as to give rise to a wavy interface, and this evolution is shown schematically in figure 2(a).
Before digging deeper, we note that the authors are asking some form of the question ‘What’s in a shape?’ This is the key question for all studies in geomorphology that seek to understand the changing face of the Earth as well as other celestial surfaces. Shape is the first clue, and sometimes the only clue available, when we encounter a new topography, and we would like to read into shape to infer environmental conditions past and present. An example of such historical inference is the case for flowing water on Mars as suggested by erosion channels and characteristically shaped river islands.
This particular work follows others (Blumberg & Curl Reference Blumberg and Curl1974; Meakin & Jamtveit Reference Meakin and Jamtveit2009) aiming to understand the ripply and scalloped patterns seen in different situations such as the walls of ice caves carved by wind, the walls of mineral caves carved by flowing water, and the sides of melting icebergs (figure 1). This nicely illustrates the surprising convergence of form that is a theme of shape–flow interaction problems. The analogy between dissolution and melting is precise, as the concentration of the dissolved solid is akin to temperature. That gets us to the nature of the two-way interaction, which is given by a boundary evolution law, rather than just a boundary condition that the fluid must satisfy. In this case, the gradient of the solute concentration (or temperature) in the fluid near the interface dictates how fast material will exit the solid into the fluid, and thus determines the recession velocity of the boundary (Huang, Moore & Ristroph Reference Huang, Moore and Ristroph2015).
Figure 1. Natural patterning. (a) Water-driven mineral scallops (reproduced with permission from Johannes Lundberg). (b) and (c) Water-driven iceberg scallops, exposed by turnover (reproduced with permission from Phillip Colla).
About those ripples: for those of us steeped in fluid dynamics, the appearance of a wavy interface as the result of an instability is familiar from many hyphenated phenomena, Rayleigh–Plateau, Kelvin–Helmholtz, Saffman–Taylor and so on. But the authors do not simply declare victory at the appearance of an instability of the flat bed. Rather they have taken the next step of imposing even higher amplitude roughness and asking whether this too is amplified. This approach has led them to conclude that there is a finite amplitude to the roughness: shallower patterns are amplified and more deeply etched patterns are dissolved away (figure 2 b). These findings lead to predictions for the wavelength and amplitude or depth of the pattern that would be maintained as the surface recedes. A comparison with previous observations of ice scallops shows good correspondence.
Figure 2. Birth of a scalloped pattern. (a) Flow over a melting ice sheet or dissolving mineral bed. The initial bed may contain many ripples of various heights, and the shape evolution selects a specific wavelength $\unicode[STIX]{x1D706}$
and amplitude
$\unicode[STIX]{x1D706}$
and amplitude
 $A$
. (b) The observed pattern may represent the most prominent amplitude (circle) on the boundary between growth and shrinking.
$A$
. (b) The observed pattern may represent the most prominent amplitude (circle) on the boundary between growth and shrinking.
This study makes big strides towards understanding the steady state or terminal patterns seen in nature. Geomorphological problems often involve this emergence and persistence of stereotyped forms, which may be interpreted as stable attractors of the shape dynamics. In studying the growth of an icicle or stalactite (Short et al. Reference Short, Baygents, Beck, Stone, Toomey and Goldstein2005), for example, we believe that there is a fundamental form that would arise under ideal conditions, with natural sculptures being close but imperfect realizations. We seek these ideal forms by taking the problem out of nature and into the laboratory or, as this study does, packaging it into a model or simulation.
3 Outlook and future directions
The work of Claudin et al. (Reference Claudin, Durán and Andreotti2017) invites future study of this instability, and a controlled laboratory experiment may be informative. We also note that the authors’ approach does not explicitly evolve the shape nor exactly identify its ideal terminal form, but rather asks whether the amplitude of a sinusoidal waveform would tend to grow or shrink. The fully nonlinear and coupled problem awaits, as do three-dimensional formulations descriptive of the scalloping seen on mineral and ice surfaces. But this raises a good point: often we may consider a decoupled problem in which the flow field alone is first solved, then the boundary is incrementally moved according to the time-averaged effect of this flow. This quasistatic scheme works when the boundary speed is very slow compared to the flow speed. This means we should not toss out those fluid mechanics textbooks full of immovable-solid problems, as their solutions must be stitched together in time to get the boundary evolution.
I might also speculate that the mechanism identified here accounts for some but not all ripply patterns seen in nature. For example, the pocked surfaces of meteorites may be of different origin, as these are carved by ablative heating and melting during entry through the atmosphere (Feldman Reference Feldman1959). These may be more akin to the formation of water waves, with wind shear destabilizing the molten surface. Regardless, this again highlights the interesting similarities between disparate processes, a related example being the conical shapes assumed by both meteorites and bodies subject to fluidic erosion (Ristroph et al. Reference Ristroph, Moore, Childress, Shelley and Zhang2012). Further investigation is needed to say if such similarities are only superficial or something more.
More generally, future research might compare receding (e.g. erosion or melting) and advancing (deposition or freezing) processes and address the issue of reversibility. I am not aware of any scallops formed by advancing fronts. And I am excited to know what new themes and unifying principles will emerge in the future. Certainly, as this and other studies have shown, the ‘common wisdom’ that processes like dissolution and erosion are smoothers of shape is not to be taken literally. Here, a flat surface spontaneously develops curvature, and previous studies show that erosion carves sharp points, corners and edges from smooth initial geometries (Ristroph et al. Reference Ristroph, Moore, Childress, Shelley and Zhang2012). Progress will likely come from the detailed study of such archetypal problems, where clean and controlled experiments may make close contact with simulations (Mitchell & Spagnolie Reference Mitchell and Spagnolie2017) and mathematical models (Moore Reference Moore2017).
If more urgency is needed, we may appeal to a darker motivation for studying this class of problems: the looming consequences of our changing climate. Our oceans and water supplies are increasingly acidified, and with it comes increased dissolution and corrosion. Global temperatures are increasing, and with that comes increased melting of the polar ice. The sea levels are rising, and hence erosion of our coasts. So as we appreciate the inherent beauty in all these processes, we should respect their persistent power, the consequences of which may grow more dire in the near future.