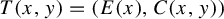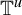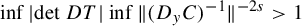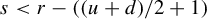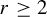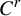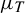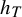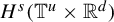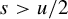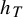Regularity and linear response formula of the SRB measures for solenoidal attractors

Abstract

We show that a class of higher-dimensional hyperbolic endomorphisms admit absolutely continuous invariant probabilities whose densities are regular and vary differentiably with respect to the dynamical system. The maps we consider are skew-products given by $T(x,y) = (E (x), C(x,y))$, where E is an expanding map of $\mathbb {T}^u$ and C is a contracting map on each fiber. If $\inf |\!\det DT| \inf \| (D_yC)^{-1}\| ^{-2s}>1$ for some ${s<r-(({u+d})/{2}+1)}$, $r \geq 2$, and T satisfies a transversality condition between overlaps of iterates of T (a condition which we prove to be $C^r$-generic under mild assumptions), then the SRB measure $\mu _T$ of T is absolutely continuous and its density $h_T$ belongs to the Sobolev space $H^s({\mathbb {T}}^u\times {\mathbb {R}}^d)$. When $s> {u}/{2}$, it is also valid that the density $h_T$ is differentiable with respect to T. Similar results are proved for thermodynamical quantities for potentials close to the geometric potential.

1 Introduction

The statistical point of view of dynamical systems is one of the most useful tools available for the study of the asymptotic behavior of chaotic dynamics. It has been noticed that several chaotic dynamical systems can be described statistically, and among the class of such chaotic systems are the hyperbolic ones. A central object of study in the ergodic theory of smooth dynamical systems are the SRB measures, named after the work of Sinai, Ruelle, and Bowen in the 1970s. A measure $\mu $ is called a SRB measure for the transformation T if for a positive Lebesgue measure set of points x, it is valid that

$$ \begin{align*} \lim_{n \to \infty} \frac{1}{n} \sum_{j=0}^{n-1} \phi(T^j(x)) = \int \phi\, d\mu \end{align*} $$

for all continuous real functions $\phi $ .

The classical theory of hyperbolic dynamics was initially developed for invertible dynamical systems. Sinai, Ruelle, and Bowen [18, 19, 48, 57] proved that transitive hyperbolic attractors for smooth diffeomorphisms admit a unique SRB measure, which means that these systems are physical observables by the SRB measure. The ergodic theory of uniformly hyperbolic diffeomorphisms is nowadays well understood. Hyperbolic transitive basic sets admit a unique equilibrium state for Hölder continuous potentials, and they satisfy exponential decay of correlations and central limit theorem [18]. Modern methods also prove that the SRB measure (and equilibrium states) depends differentiably with respect to the dynamical systems for hyperbolic diffeormorphisms [9, 11, 24, 25].

The notion of uniform hyperbolicity was extended to the non-invertible context (endomorphisms) [33, 42, 43, 54]. Several properties of invertible hyperbolic dynamical systems were proved to be true also for uniformly hyperbolic endomorphisms, such as the existence of SRB measures [46, 47, 60], existence and uniqueness of equilibrium states for Holder continuous potential [34, 35], and exponential decay of correlations and central limit theorem [36]. One difficulty is that in general there do not exist Markov partitions for hyperbolic sets like for diffeomorphism. This can be bypassed considering the natural extension of the endomorphism (seen as a hyperbolic homeomorphism). Notions as inverse topological pressure were introduced to study these systems [38, 39], and in [37], inverse SRB measures were studied for hyperbolic attractors of endomorphisms. It has also been proved that SRB measures for hyperbolic attractors of endomorphisms are equilibrium states for the geometric potential [47]. The ergodic theory of endomorphisms has been extended for more general non-hyperbolic systems, for example, for non-uniformly hyperbolic attractors [45] and partially hyperbolic systems [6, 21, 59].

Another difficulty that appears in the non-invertible setting is the non-existence of an unstable foliation, since every point can have more than one unstable direction. More precisely, each choice of preitinerary corresponds to one possibly distinct local unstable manifold. For diffeomorphisms that do not hold for endomorphisms, for example, there exists Anosov endomorphisms that are not structurally stable [35, 42].

Due to the existence of several unstable directions, the geometry of hyperbolic sets for endomorphisms can be more complicated. One very different phenomenon related to the geometry of a hyperbolic set for endomorphisms is the fact that hyperbolic attractors can have positive Lebesgue measure and can support an absolutely continuous invariant measure. This phenomenon does not occur in the invertible setting, because if the hyperbolic attractor for some diffeomorphism is proper, then its Lebesgue measure is zero [5, 19], so any invariant measure supported in the attractor (such as the SRB measure) must be singular with respect to the Lebesgue measure. For bidimensional endomorphisms, it was noticed in [3, 58, 59] that some bidimensional hyperbolic attractors can admit an absolutely continuous invariant measure (and so the Lebesgue measure of these attractors is non-zero). In [12], the existence of an absolutely continuous invariant measure was proved for certain higher-dimensional hyperbolic attractors in dimension greater than $2$ . It is interesting to note this phenomenon for hyperbolic maps because the absolute continuity of the SRB measure is usually associated to maps with all Lyapunov exponents being positive [2, 4, 49].

Motivated by statistical physics, some authors addressed the question of linear response, which corresponds to the differentiability of the SRB measure (or more general equilibrium states) with respect to the dynamical system. Recently, some authors proved linear response formulas for expanding maps [13, 49], non-uniformly expanding maps [14], of uniformly hyperbolic invertible dynamical systems [9, 11, 24, 29, 50]. The differentiability of the SRB measure was proved for some bidimensional partially hyperbolic endomorphism presenting a transversality condition similar to that in this work [61]. The survey [8] has a large list of classical references on linear response. To our knowledge, no result of linear response was proved for hyperbolic endomorphisms.

Two features of the dynamical systems in [7, 12, 58, 59] that allow to prove the absolute continuity of the SRB measure are volume expansion of the dynamical system and a geometrical condition of transversality between the images of unstable directions. Heuristically, one idea behind these phenomena is the fact that for hyperbolic attractors, the SRB measure is always regular with respect to directions that present expansion [41, 45]. For non-invertible maps, the dynamical system can spread the unstable (expanding) direction into several transversal directions and the good regularity of the SRB measure expected in these directions is scattered into a positive volume set.

Motivated by these facts, one can ask whether some hyperbolic attractors for endomorphisms satisfy other regular ergodic properties usually associated to expanding maps. The SRB measure for expanding maps is absolutely continuous, and its density is differentiable and varies differentiably with respect to the map [31, 49, 52].

Based on this, we are interested to prove that:

1. (1) the density of the SRB measure is smooth for certain volume expanding hyperbolic endomorphisms satisfying some transversality condition between its overlaps; and

2. (2) in such a case, it depends differentiably with respect to the dynamical system.

In this paper, we also give sufficient conditions under which the transversality condition holds generically.

We also mention that there have been many advances in the dimension theory of hyperbolic sets. Even for diffeomorphisms, the theory is not complete in dimension greater than $2$ (see for instance [10, 40, 56]). For conformal hyperbolic attractor, its dimension is the sum of its stable and unstable dimension, and both of them are the zero of a topological pressure usually known as Bowen’s equation [10, 40]. For non-conformal hyperbolic attractors, under a similar condition of transversality, the dimension can also be calculated as the sum of the unstable and the weak-stable dimension, and both of them are given by a Bowen’s equation [15–17, 55]. We are not focused on dimension theory because the hyperbolic attractors that we study here have positive Lebesgue measure (usually called fat attractors), so their dimension is the same dimension of the whole manifold.

The main contributions of this work are the proofs of the absolute continuity of the SRB measure, the smoothness of its density, and the differentiable dependence of this density with respect to the dynamical system. We conclude similar results for other potentials close to the geometric potential. Other ergodic properties of the SRB measure are already known, such as exponential mixing [36], statistical stability [21], and large deviation formulas [32]. Our methods also allow to obtain exponential mixing with uniform rates of decay and the stability (continuity) as a consequence of the differentiability.

In this work, we deal with hyperbolic skew-products, but we expect that the same kind of results are valid for hyperbolic attractors and partially hyperbolic attractors for endomorphisms satisfying a condition of weak contraction on central directions in comparison to the expansion on unstable directions and a similar condition of transversality between the images of unstable directions.

1.1 Statement of the results

In this work, we consider maps $T:{\mathbb {T}^u}\times {\mathbb {R}}^d \to {\mathbb {T}^u}\times {\mathbb {R}}^d $ given by

$$ \begin{align*} T(x,y) = ( E(x), C(x,y)), \end{align*} $$

where E is an expanding map of the torus ${\mathbb {T}^u}$ , $D_yC$ is a contraction of ${\mathbb {R}}^d$ for every $(x,y)\in {\mathbb {T}^u} \times {\mathbb {R}}^d$ , and T is of class $C^r$ , $r\geq 2$ .

Denote by $\mathcal {E}^r(u)$ the set of the $C^r$ expanding maps of ${\mathbb {T}}^u$ , and by $\mathcal {C}^r(u,d)$ the set of the maps $C:{\mathbb {T}^u} \times {\mathbb {R}}^d \to {\mathbb {R}}^d$ of class $C^r$ with bounded derivative such that $D_yC$ are contractions for every $(x,y)\in {\mathbb {T}^u} \times {\mathbb {R}}^d$ . Denote $T=T(E,C)$ for $E\in \mathcal {E}^r(u)$ , ${C\in \mathcal {C}^r(u,d)}$ .

Given $E\in \mathcal {E}^r(u)$ , denote by N the degree of E, and by $\underline {\mu }$ and $\overline {\mu }$ (respectively $\underline {\unicode{x3bb} }$ and $\overline {\unicode{x3bb} }$ ) the minimum (respectively maximum) rates of expansion of $DE$ (respectively of contraction of $D_yC$ ).

Two features are important in the skew-products that we are going to consider: volume-expansion ( $|\!\det DT|>1$ ) and a condition of transversality between the overlaps (see Definition 2.5). The remark and example below show that they are natural conditions for the existence of some absolutely continuous invariant measure.

Remark 1.1. If $\Lambda $ is a compact invariant set for the differentiable dynamical system T and T contracts volume ( $|\!\det DT| <1$ ), then $\Lambda $ has zero Lebesgue measure and every invariant measure supported in $\Lambda $ must be singular with respect to the Lebesgue measure.

Example 1.2. Given any Lipschitz function $f: \mathbb {T}^u \to {\mathbb {R}}^d$ , consider the skew-product $T(x,y) = (E(x), C(y)+f(E(x)) - C(f(x)))$ , where $C:{\mathbb {R}}^d\to {\mathbb {R}}^d$ is a contraction. In this case, the attractor $\Lambda $ is the graph of f and so it has zero Lebesgue measure.

In this work, we consider the set

(1) $$ \begin{align} \kern-95pt \mathcal{C}^r(s,d,E)=\bigg\{ C \in \mathcal{C}^r(u,d); &\inf_{x,y} |\!\det DT(x,y)| \underline{\unicode{x3bb}}^{2s}> 1 \text{ and } \end{align} $$

(2)

The first condition above is a few more than volume expansion by the map, actually condition (1) for $s= 0$ is equivalent to the expansion of volume everywhere by the dynamical system. By uniform continuity, if T expands volume, then condition (1) will be valid for some $s>0$ . The second condition is a technical condition under which the transversality condition is valid generically (see Theorem F).

In this section, we will state first the theorems under the assumption $C \in \mathcal {C}^r(s,d,E_0)$ . In §2, we will give a more precise statement of the theorems asking the transversality condition instead of condition (2).

One class of skew-products for which condition (2) is easier to verify is the following example.

Example 1.3. Consider $T:{\mathbb {T}^u} \times {\mathbb {R}} \to {\mathbb {T}^u} \times {\mathbb {R}}$ given by $T(x,y)=(E(x),\unicode{x3bb} y + f(x))$ , with E a linear conformal expanding endomorphism of the torus with $\mu =\| E\| $ and $f\in C^{\infty }({\mathbb {T}^u},{\mathbb {R}}^d)$ . In this setting, $\mathcal {C}^\infty (s,1,E) $ corresponds to the parameters $\unicode{x3bb} \in ( \mu ^{{-u}/({1+2s})} ,1)$ .

1.1.1 Smoothness of the density

The first theorem concerns the absolute continuity of the SRB measure and the smoothness of its density function. It states that the condition $C_0 \in C^r(s,d,E_0)$ is sufficient for the existence of pairs $(E,C)$ arbitrarily $C^r$ -close to $(E_0,C_0)$ so that the corresponding SRB measure is absolutely continuous and its density is Sobolev regular.

Theorem A. Fix integers $1 \leq d \leq u$ and a real number $0 \leq s < r-(({u+d})/{2} +~1)$ . Given $E_0 \in \mathcal {E}^r(u)$ and $C_0 \in C^r(s,d,E_0)$ , there exists an open neighborhood ${\mathcal {U} \subset \mathcal {E}^r(u) \times C^r({\mathbb {T}^u}, {\mathbb {R}}^d)}$ of $(E_0,C_0)$ and a $C^r$ -open and dense subset $\mathcal {W} \subset \mathcal {U}$ such that for each pair $(E,C) \in \mathcal {W}$ , the density $h_T$ of the SRB measure of the hyperbolic endomorphism $T=T(E,C)$ belongs to $H^s({\mathbb {T}^u} \times {\mathbb {R}}^d)$ .

The condition behind the subset $\mathcal {W}$ corresponds to a geometrical condition of transversal overlaps of the images. We define this condition in §2 and give a more explicit version of this theorem, denoted Theorem A $^{\prime }$ .

In the situation where $s> ({u+d})/{2}$ , Sobolev’s embedding theorem implies that any $h_T$ coincides almost everywhere with a $C^k$ function for every $k<s-({u+d})/{2}$ . In particular, $h_T$ is continuous almost everywhere, which implies that the attractor $\Lambda $ has non-empty interior.

Corollary B. Under the assumptions of Theorem A, if $r\geq u+d+2$ and $s>({u+d})/{2}$ , then the corresponding attractor $\Lambda _{T}$ has non-empty interior and the density $h_T$ of the SRB measure is a Hölder continuous function.

1.1.2 Spectral gap of the transfer operator

To prove Theorem A, we study the action of the transfer operator

(3) $$ \begin{align} {\mathcal L} h(z)= \sum_{T(w)=z}\frac{h(w)}{|\!\det DT(w)|} \end{align} $$

on an appropriate Banach space $\mathcal {B}$ adapted to the dynamical system. This Banach space is defined using the method developed in [24] (also used in [7]), defining an anisotropic norm of the function corresponding to its action in the space of regular functions supported in ‘almost stable manifolds’ (see Definition 3.1). We prove one Lasota–Yorke inequality for this anisotropic norm and another for the Sobolev norm.

In the linear setting in [12], the absolute continuity of the density was proved and that it is in the space $L^2$ . This followed through a Lasota–Yorke-like inequality for $L^2$ and $L^1$ norms. Due to lack of compactness of any immersion of $L^2$ into $L^1$ , such inequality does not lead to spectral gap properties for the operator acting in $L^2$ . Our new approach in this paper consider norms with higher regularity, which allow us to obtain more statistical properties.

We say that ${\mathcal L}$ has a spectral gap in a Banach space E if we can write the restriction ${\mathcal L}_{|E}= \unicode{x3bb} P + N$ , where P is a projection with $\dim \operatorname {Im}(P)=1$ , N is a bounded operator with spectral radius $\rho (N):= \underset {n \to \infty }{\lim }\sqrt [n]{\| L^n\| } \leq |\unicode{x3bb} |$ , and $PN=NP=0$ .

If $\mu $ is a T-invariant probability, we say that $(T,\mu )$ has exponential decay of correlations in a vector space $\mathcal {B} \subset L^1(\mu )$ with exponential rate at most $\zeta <1$ if for every $\phi \in \mathcal {B}$ and $\psi \in L^\infty (\mu )$ , there exists a constant $K(\phi ,\psi )>0$ such that

(4) $$ \begin{align} \bigg|\!\int \phi (\psi\circ T^n)\, d\mu - \int \phi \,d\mu \int \psi \,d\mu \bigg| \leq K(\phi,\psi) \zeta^n. \end{align} $$

For $s>u/2$ , we prove the ${\mathcal L}$ spectral gap and, thus, T has exponential decay of correlations in a Banach space containing smooth observables.

Theorem C. Fix integers $1 \leq d \leq u$ and a real number $u/2 < s < r-(({u+d})/{2}~+~1)$ . Given $E_0 \in \mathcal {E}^r(u)$ and $C_0 \in C^r(s,d,E_0)$ , there exists an open neighborhood $\mathcal {U} \subset \mathcal {E}^r(u) \times C^r({\mathbb {T}^u}, {\mathbb {R}}^d)$ of $(E_0,C_0)$ , and a $C^r$ -open and dense subset $\mathcal {W} \subset \mathcal {U}$ such that for each pair $(E,C) \in \mathcal {W}$ , there exists a Banach space $\mathcal {B}$ contained in $H^s({\mathbb {T}^u}\times {\mathbb {R}}^d)$ and containing $C^{r-1}(D)$ such that the corresponding transfer operator ${\mathcal L}$ of $T=T(E,C)$ has spectral gap in $\mathcal {B}$ with essential spectral radius at most $\zeta $ , where

(5) $$ \begin{align} \zeta \in (\max\{ \underline{\mu}^{{-1}/({1+\log{(1+{d}/{2}+u)}})},(\inf |\!\det DT| \underline{\unicode{x3bb}}^{2s})^{{-1}/{2}}\},1). \end{align} $$

In particular, $T=T(E,C)$ has exponential decay of correlations in some vector space $\hat{\mathcal{B}}$ with exponential rate $\zeta $ , where $\hat{\mathcal{B}}$ is contained in $\mathcal {B}$ and contains $C^{r-1}(D)$ .

Exponential decay of correlations of the SRB measure for Holder observables was already proved for hyperbolic endomorphisms [36] but with exponential rates that could depend on the rate of expansion/contraction of the dynamical system. What is new as a consequence of Theorem C is that in this setting, the rate of exponential decay of correlations for smooth observables can be taken to be uniform, even if the rate of contraction of the dynamical system tends to be weaker, e.g. as in the family of maps ${T_t=T(E,C +t (\operatorname {Id}-C) )}$ , $t \to 1^-$ . An interesting problem is to show that $T_1$ has exponential decay of correlations with the same rate $\zeta $ for a generic function f.

Remark 1.4. We believe that the condition $u/2 < s< r-(({u+d})/{2}+1)$ may not be optimal. It just seems to be a technical sufficient condition that appeared throughout the proof. Condition $s< r - (({u+d})/{2}) +1)$ was used to prove the second Lasota–Yorke inequality (Proposition 3.4) and condition $s> u/2$ was to establish a certain compactness of the norms considered in the proof of Theorem C $^{\prime }$ (see Claim 4.9).

1.1.3 Differentiability of the density of the SRB measure with respect to the dynamical system

We conclude the differentiability of the density $h_T$ with respect to the map T, this differentiability result has been referred to as the linear response formula (see e.g. [8, 51]).

One difficulty to prove such results is that we do not have the differentiability of the transfer operator as an operator acting on the same space, this is bypassed considering the transfer operator as a linear transformation from one Banach space into a larger space (defined by a weaker norm) and fitting it into a perturbative setting developed by Gouezel and Liverani in [24].

Denoting $h_T$ the density of the SRB measure, we have the following theorem.

Theorem D. Fix integers $1 \leq d \leq u$ and $u/2 < s < r-(({u+d})/{2}+1)$ . Given $E_0 \in \mathcal {E}^r(u)$ and $C_0 \in C^r(s,d,E_0)$ , there exists an open neighborhood ${\mathcal {U} \subset \mathcal {E}^r(u) \times C^r({\mathbb {T}^u}, {\mathbb {R}}^d)}$ of $(E_0,C_0)$ , and a $C^r$ -open and dense subset $\mathcal {W} \subset \mathcal {U}$ such that the mapping

$$ \begin{align*} \mathcal{W}\subset C^r({\mathbb{T}^u})\times \mathcal{C}^r(s,d,E) & \to H^s({\mathbb{T}^u} \times {\mathbb{R}}^d) \\(E,C) & \mapsto h_{T(E,C)} \end{align*} $$

is $C^{r-s-\lfloor ({u+d})/{2} \rfloor - 2 }$ in $ \mathcal {U}$ .

1.1.4 Differentiability for smooth potentials close to the geometrical potential

In the following, we deal with a more general transfer operator associated to other potentials. Given a continuous function $P: {\mathbb {T}^u} \times {\mathbb {R}}^d \to {\mathbb {R}}$ called potential, we denote the transfer operator with respect to P by

(6) $$ \begin{align} {\mathcal L}_{T,P} h(x)= \sum_{T(y)=x} e^{P(y)} h(y). \end{align} $$

Notice that the transfer operator ${\mathcal L}$ as defined before coincides with ${\mathcal L}_{T,P_0}$ for the geometrical potential $P_0=-\log |\!\det DT|$ .

We obtain the same conclusions for the transfer operator associated to potentials $\phi $ that are $C^r$ -close to the geometrical potential $P_0$ . To simplify the notation, we identify ${T = T(E,C)}$ with the pair $(E,C)$ .

Theorem E. Fix integers $1 \leq d \leq u$ and $u/2 < s < r-(({u+d})/{2}+1)$ . Given ${E_0 \in \mathcal {E}^r(u)}$ , $C_0 \in C^r(s,d,E_0)$ , and

$$ \begin{align*} \zeta \in (\max\{ \underline{\mu}^{{-1}/({1+\log{(1+{d}/{2}+u)}})},(\inf |\!\det DT| \underline{\unicode{x3bb}}^{2s})^{{-1}/{2}}\},1), \end{align*} $$

there exists open neighborhoods $\mathcal {U} \subset \mathcal {E}^r(u) \times C^r({\mathbb {T}^u}, {\mathbb {R}}^d)$ of $(E_0,C_0)$ , $\mathcal {Y} \subset C^{r-1}({\mathbb {T}^u} \times {\mathbb {R}}^d,{\mathbb {R}})$ of $P_0$ , and a $C^r$ -open and dense subset $\mathcal {W} \subset \mathcal {U}$ such that for each pair $(E,C) \in \mathcal {W}$ , there exists a Banach space $\mathcal {B}$ contained in $H^s({\mathbb {T}^u}\times {\mathbb {R}}^d)$ and containing $C^{r-1}(D)$ such that for every $P \in \mathcal {Y}$ , the action of the operator ${\mathcal L}_{T(E,C),P}$ in $\mathcal {B}$ has spectral gap with essential spectral radius at most $\zeta $ . So there exists a unique eigenfunction $h_{(T,P)}$ in $H^s$ associated to the spectral radius $\unicode{x3bb} _{(T,P)}$ for the transfer operator ${\mathcal L}_{(T,P)}$ . The following functions are of class $C^{ r-s-\lfloor ({u+d})/{2} \rfloor - 2}$ in $\mathcal {W} \times \mathcal {Z}$ and analytic with respect only to P:

1. (1) the spectral radius $(T,P) \to \unicode{x3bb} _{(T,P)} \in {\mathbb {R}}$ ;

2. (2) the eigenfunction $(T,P) \to h_{(T,P)} \in H^s({\mathbb {T}^u} \times {\mathbb {R}}^d)$ ;

3. (3) the eigenmeasure $(T,P) \to \nu _{(T,P)} \in \mathcal {B}^{*}$ ;

4. (4) the invariant measure $(T,P) \to \mu _{(T,P)}=h_{(T,P)} \nu _{(T,P)} \in \mathcal {B}^*$ ;

5. (5) the Lyapunov exponent functions,

   $$ \begin{align*} \!\!\!\!\!\!\!\!\!(T,P) \to \int \log \| DT\| \, d\mu_{(T,P)}, \int \log \| DT(x)^{1}\| ^{-1} \, d\mu_{(T,P)}, \int \log|\!\det DT|\, d\mu_{(T,P)}; \end{align*} $$

6. (6) the mean $(T,P) \to m_{(T,P)}(\psi ) := \int \psi \, d\mu _{(T,P)} \in {\mathbb {R}} $ , for any $\psi \in C^{r-1}(D) $ ;

7. (7) the variance $(T,{\kern-1pt}P) {\kern-1pt}\to{\kern-1pt} \sigma ^2_{(T,P)(\psi )} {\kern-1pt}:={\kern-2pt} \int \tilde \psi ^2\, d \mu _{(T,P)} {\kern-1pt}+{\kern-1pt} 2 {\kern-1pt}\sum _{n=1}^\infty {\kern-1pt}\int{\kern-1pt} \tilde \psi (\tilde \psi \circ T^n)\, d \mu _{(T,P)}$ , where $\tilde \psi = \psi - \int \psi \, d\mu _{(T,P)}$ , for any $\psi \in C^{r-1}(D)$ .

The mean and variance in items (6) and (7) appear in the central limit theorem. It is well known that the central limit theorem can be derived from exponential decay of correlations, in this case stated as the following corollary.

Corollary. (Exponential decay of correlations)

Under the hypothesis of Theorem E, $(T,\mu _{(T,P)})$ has exponential decay of correlations in a vector space $\mathcal {B} \subset L^1(\mu )$ with exponential rate at most $\zeta <1$ , for a vector space $\mathcal {B}$ contained in $H^s({\mathbb {T}^u} \times {\mathbb {R}}^d)$ and containing $C^{r-1}(D)$ .

Corollary. (Central limit theorem)

Under the hypothesis of Theorem E, for every $(E,C,P) \in \mathcal {W} \times \mathcal {Z}$ and for every function $\psi \in C^{r-1}(D) $ :

1. (1) either $\psi $ is cohomologous to a constant, that is, $\psi = u\circ T -u + \int \psi \,d\mu _{(T,P)}$ for some $u \in L^2(\mu _{(T,P)})$ ;

2. (2) or the convergence in distribution

   $$ \begin{align*} \frac{1}{\sqrt{n}}\sum_{j=0}^{n-1} \psi \circ T^j \to \mathcal{N}(m,\sigma^2) \end{align*} $$
   holds with mean $m=m_{(T,P)}$ and variance $\sigma ^2= \sigma ^2_{(T,P)}(\psi )>0 $ defined in items (6) and (7) in Theorem E.

1.1.5 Commentaries on the transversality condition

In all theorems A, C, D, and E, the condition behind $\mathcal {U}$ is a transversality condition that we define precisely in Definition 2.5. In §2, we give a more explicit version of each theorem (Theorems A $^{\prime }$ , C $^{\prime }$ , D $^{\prime }$ , and E $^{\prime }$ ) in terms of this transversality condition.

The tranversality condition plays a fundamental role in this work. Heuristically, it means that the dynamical system spreads the unstable direction into several complementary directions, and since the density of the SRB measure tends to be regular toward the unstable direction, it becomes regular in the whole ambient. A similar condition of transversality was formulated initially in [58, 59], in [7] for surface endomorphism, and in [12] for higher dimensions.

1.2 Organization of the paper

In §2, we give the basic definitions of the classes of dynamical systems considered, we define the main transversality condition, and give the precise statements of this work.

In §3, we introduce the two norms: the anisotropic norm and the Sobolev norm, and we state the two main Lasota–Yorke inequalities for the transfer operator in terms of these norms. Section 4 is dedicated to the proof of the two main Lasota–Yorke inequalities. One difficulty appears when dealing with the transversality in higher dimensions in the proof of the second main Lasota–Yorke inequality (Proposition 3.4). In §5, we put together the first and the second main inequalities and prove Theorems A $^{\prime }$ and C $^{\prime }$ .

In §6, we study the differentiability of the density and conclude Theorem D $^{\prime }$ . For this, we prove the differentiability of the transfer operator as a linear transformation from one Banach space into a larger space. In §7, we study the differentiability of the density with respect to other potentials close to the geometrical potential and obtain similar results for their equilibrium states, proving Theorems E $^{\prime }$ and F $^{\prime }$ . We also obtain as consequence the differentiability of the other statistical quantities stated in Corollaries G $^{\prime }$ and H $^{\prime }$ .

In §8, we give sufficient conditions for the genericity of the transversality condition. The proof consists in the construction of a parameterized family of perturbations for which the transversality is valid for almost every parameter.

2 Definitions and statements

Now we consider the map $T=T(E,C):{\mathbb {T}^u}\times {\mathbb {R}}^{d} \rightarrow {\mathbb {T}^u}\times {\mathbb {R}}^{d}$ given by $T(x,y) = ( E(x) , C(x,y) ), $ where $s>0$ , $E\in \mathcal {E}^r(u)$ is a expanding map of degree N, and $C\in ~\mathcal {C}^r ({\mathbb {T}^u} \times {\mathbb {R}}^d,{\mathbb {R}}^d)$ is a map that satisfies

(7) $$ \begin{align} 1< \underline{\mu} < \| DE^{-1}(x)\| ^{-1} \leq \| DE(x)\| < \overline{\mu}, \end{align} $$

(8) $$ \begin{align} 0<\underline{\unicode{x3bb}} < \| (D_yC(x,y))^{-1}\| ^{-1}\leq \| (D_yC(x,y))\| < \overline{\unicode{x3bb}}<1\quad \text{for every } (x,y), \end{align} $$

(9) $$ \begin{align} \| DC\| _{C^{r-1}} < \kappa, \end{align} $$

(10) $$ \begin{align} \inf_{x,y} |\!\det DT(x,y)| \underline{\unicode{x3bb}}^{2s}>1. \end{align} $$

Remark 2.1. We will consider $C^r$ open neighborhoods of $(E,C)$ such that equations (7), (8), (9), and (10) are valid for every $T=T(E, C)$ in the same neighborhood.

The attractor $\Lambda $ for T is given by $\Lambda =\bigcap _{n\geq 0}{T^n(D)}$ for $D= {\mathbb {T}^u} \times [-K_0,K_0]^d$ , where $K_0=(1-\bar {\unicode{x3bb} })^{-1} \kappa $ (notice that $T(D) \subset D$ ). Since the restriction of T to $\Lambda $ is a topologically mixing hyperbolic endomorphism, it admits a unique SRB measure $\mu _T$ supported on $\Lambda $ [60].

2.1 Codifying the dynamical system

Let us fix notation involving the partition of the base space ${\mathbb {T}^u}$ that codify the action of the expanding map E. This is essentially the same notation used in [12].

Fix $\mathcal {R}=\{\mathcal {R}(1),\ldots ,\mathcal {R}(r)\}$ a Markov partition for E, that is, $\mathcal {R}(i)$ are disjoint open sets, the interior of each $\overline {R(i)}$ coincides with $R(i)$ , $E_{|_{\mathcal {R}(i)}}$ is one-to-one, ${\bigcup }_i \overline {\mathcal {R}(i)}= {\mathbb {T}^u}$ , and $E({\mathcal {R}(i)}) \cap {\mathcal {R}(j)} \neq \emptyset $ implies that ${\mathcal {R}(j)}\subset E(\mathcal {R}(i))$ . Each $\mathcal {R}(i)$ is called a rectangle of the Markov partition. Markov partitions always exist for expanding maps with arbitrarily small diameter (see [44]). Suppose that $\operatorname {diam}(\mathcal {R}) < \gamma $ , where ${0<\gamma < 1/2}$ is a constant such that for every $x\in {\mathbb {T}^u}$ and $y\in E^{-1}(x)$ , there exists a unique inverse branch $h_{y,x}:B(x,\gamma ) \to B(y,\gamma )$ such that $ h_{y,x}(x)=y \quad \text {and}\quad E(h_{y,x}(z))=z $ for every $z \in B(x,\gamma )$ .

Consider the set $\overline {I}=\{ 1, \ldots , r\}$ and $\overline {I}^n$ the set of words of length n with letters in $\overline {I}$ , $1\leq n \leq \infty $ . Denoting by ${\textbf {a}} =(a_{i})_{i=1}^{n}$ a word in $\overline {I}^{n}$ , define $I^n$ the subset of admissible words ${\textbf {a}} =(a_{i})_{i=1}^{n}$ , that is, with the property that $E(\mathcal {R}(a_{i+1})) \cap \mathcal {R}(a_{i}) \neq \emptyset \text { for every} 0\leq i \leq n-1 \,. $ Consider the partition $\mathcal {R}^{n}:= \vee _{i=0}^{n-1} E^{-i}(\mathcal {R})$ and, for every ${\textbf {a}} \in \overline {I}^n$ , the set $\mathcal {R}({\textbf {a}}) = \bigcap _{i=0}^{n-1} E^{-i}(\mathcal {R}(a_{n-i}))$ in $ \mathcal {R}^n$ , which is non-empty if and only if ${\textbf {a}}\in I^n$ . The truncation of ${\textbf {a}}=(a_j)_{j=1}^{n}$ to length $1\le p\le n$ is denoted by $[{\textbf {a}}]_p=(a_j)_{j=1}^{p}$ .

For any $x{\kern-1pt}\in{\kern-1pt} {\mathbb {T}^u}$ , fix some $\pi (x) {\kern-1pt}\in{\kern-1pt} \overline {I}$ such that $x{\kern-1pt}\in{\kern-1pt} \overline {\mathcal {R}(\pi (x))}$ . For any ${\textbf {c}}\in I^p$ , $1\leq p < \infty $ , we consider $I^n({\textbf {c}})$ the set of words ${\textbf {a}}\in I^n$ such that $E^n(\mathcal {R}({\textbf {a}})) \cap \mathcal {R}({\textbf {c}}) \neq \emptyset $ . Define $I^n(x):=I^n(\pi (x))$ and, for ${\textbf {a}}\in I^{n}(x)$ , denote by ${\textbf {a}}(x)$ the point $y\in \mathcal {R}({\textbf {a}})$ that satisfies $E^{n}(y)= x$ . For any ${\textbf {a}}\in I^n$ and $1\leq n <\infty $ , we consider the set ${\mathbb {D}}({\textbf {a}}):=\{x\in {\mathbb {T}^u} | {\textbf {a}} \in I^n(x)\}=E^n({\mathcal R}({\textbf {a}}))=E({\mathcal R}([{\textbf {a}}]_1))$ , which is a union of rectangles of the Markov partition. The image of $\mathcal {R}({\textbf {a}})\times \{ y \}$ by $T^{n}$ is the graph of the function $S(\cdot ,({\textbf {a}},y)):{\mathbb {D}}({\textbf {a}}) \to {\mathbb {R}}^d$ given by

(11) $$ \begin{align} S(x,({\textbf{a}},y)) := C_{[{\textbf{a}}]_{1}(x)}\circ C_{[{\textbf{a}}]_{2}(x)}\circ \cdots \circ C_{ {\textbf{a}}(x)}(y), \end{align} $$

where we denote $C_x(y)= C(x,y)$ .

Consider the sets $I^\infty (x) = \{ {\textbf {a}} \in I^\infty $ such that $[{\textbf {a}}]_i \in I^i(x)$ for every $i\geq 1 \}$ and ${\mathbb {D}}({\textbf {a}}):=\{ x \in {\mathbb {T}^u} | {\textbf {a}}\in I^\infty (x)\}=\bigcap _{n=1}^{+\infty }E^n({\mathcal R}([{\textbf {a}}]_n)) =E({\mathcal R}([{\textbf {a}}]_1))$ for ${\textbf {a}}\in I^\infty $ . If ${\textbf {a}}\in I^{\infty }(x)$ , we define $S(x,({\textbf {a}},y)) = {\lim }_{n\to \infty } S(x,[{\textbf {a}}]_n) = \lim _n y_0^{[{\textbf {a}}]_n}(x,y)$ .

For any $p\geq 1$ and ${\textbf {c}}\in I^p$ , let us denote by $\mathcal {R}_{*}({\textbf {c}})$ the union of atoms $\mathcal {R}(\tilde {{\textbf {c}}})$ , $\tilde {{\textbf {c}}}\in I^p$ , that are adjacent to $\mathcal {R}({\textbf {c}})$ . We suppose that the diameter of the partition $\mathcal {R}$ is small enough such that the diameter of $\mathcal {R}_{*}({\textbf {c}})$ is smaller than $\gamma $ . For ${\textbf {a}} \in I^i$ , let us denote by $E^{-i}_{{\textbf {c}},{\textbf {a}}}$ the inverse branch of $E^i$ satisfying $E^{-i}_{{\textbf {c}},{\textbf {a}}}(\mathcal {R}({\textbf {c}}))\subset \mathcal {R}({\textbf {a}})$ (and so $E^{-i}_{{\textbf {c}},{\textbf {a}}}(\mathcal {R}_{*}({\textbf {c}}))\subset \mathcal {R}_{*}({\textbf {a}})$ ). We can extend $S(x,({\textbf {a}},y))$ to a ball $B_{\textbf {c}}$ of radius $\gamma $ containing $\mathcal {R}_{*}({\textbf {c}})$ by $ S_{\textbf {c}}(x,({\textbf {a}},y)) := C_{E^{-1}_{{\textbf {c}},{\textbf {a}}}(x)}\circ C_{E^{-2}_{{\textbf {c}},{\textbf {a}}}(x)}\circ \cdots \circ C_{ E^{-n}_{{\textbf {c}},{\textbf {a}}}(x)}(y). $

Consider also the constants $\theta =\overline {\unicode{x3bb} }\underline {\mu }^{-1}$ and $\alpha _0 = {\kappa }/({1-\overline {\unicode{x3bb} } })$ .

2.2 The smallest singular value

The smallest singular value shall be a useful tool to analyze the structure of the attractor close to the overlap between its images.

Definition 2.2. Given a linear transformation $A:\mathbb {R}^{u}\to \mathbb {R}^{d}$ , with $u\geq d$ , the smallest singular value of A is

(12) $$ \begin{align} \boldsymbol{m}(A):= \sup_{\dim(W)=d} \inf_{v\in W, \| v \| =1}\| A(v)\| , \end{align} $$

where the supremum is taken over the n-dimensional subspaces $W\subset \mathbb {R}^{m}$ .

Usually the singular values are defined as the non-negative square roots of the eigenvalues of $A^*A$ . Denoting $\sigma _1 \geq \cdots \geq \sigma _u$ the singular values of A, they satisfy the following max-min relation:

$$ \begin{align*} \sigma_j:= \sup_{\dim(W)=j} \inf_{v\in W, \| v \| =1}\| A(v)\|. \end{align*} $$

We call $\boldsymbol {m}(A)$ the smallest singular value because it is the smallest singular value that is not trivially null, since $\sigma _u=\cdots = \sigma _{u-d-1}=0$ and $\sigma _{u-d}=\boldsymbol{m}(A)$ .

A linear transformation $A:\mathbb {R}^u \to \mathbb {R}^d$ is surjective if and only if $\boldsymbol {m}(A)>0$ , this means that we can understand the smallest singular value as a way to measure how surjective the transformation is. So the value $\boldsymbol {m}(T_1-T_2)$ will be used to measure how transversal are the graphs of $T_1$ and $T_2$ .

One property of the smallest singular value that will be useful is the following triangular inequality:

(13) $$ \begin{align} \boldsymbol{m}(A) \leq \boldsymbol{m}(B) + \| A-B\|. \end{align} $$

2.3 The transversality condition

For each ${\textbf {a}} \in I^q$ and $B \subset {\mathbb {R}}^d$ , we think heuristically on the image $T^q(\mathcal {R}({\textbf {a}}) \times B )$ as a component of the attractor represented by ${\textbf {a}} \times B$ .

First let us define what it means for ${\textbf {a}}\times B_1$ and ${\textbf {b}} \times B_2$ to be geometrically transversal.

Definition 2.3. Let ${\textbf {a}}, {\textbf {b}} \in I^q({\textbf {c}})$ , ${\textbf {c}} \in I^p$ , $B_1, B_2 \subset [-K_0,K_0]^d$ . We say that ${\textbf {a}}\times B_1$ and ${\textbf {b}} \times B_2$ are geometrically transversal on ${\textbf {c}}$ if

(14) $$ \begin{align} \mathfrak{m}( D S_{{\textbf{c}}}(x_1,({\textbf{a}},y_1)) - D S_{{\textbf{c}}}(x_2,({\textbf{b}},y_2)) )> 3 \theta^q \alpha_{0} \end{align} $$

for every $x_1, x_2 \in \overline {\mathcal {R}_{*}({\textbf {c}})}$ , $y_1 \in B_1$ and $y_2 \in B_2$ .

We give another definition including the case when the distance between $T^q(\mathcal {R}({\textbf {a}}) \times B_1 )$ and $T^q(\mathcal {R}({\textbf {b}}) \times B_2 )$ is greater than $\delta $ .

Definition 2.4. Given $\delta>0$ , ${\textbf {c}}\in I^p$ , ${\textbf {a}}, {\textbf {b}} \in I^{q}({\textbf {c}})$ , and $B_1, B_2 \subset {\mathbb {R}}^d$ , we say that ${\textbf {a}}\times B_1$ and ${\textbf {b}} \times B_2$ are $\delta $ -transversal on ${\textbf {c}}$ if they are geometrically transversal or

(15) $$ \begin{align} \| S_{{\textbf{c}}}(x_1,({\textbf{a}},y_1)) - S_{{\textbf{c}}}(x_2,({\textbf{b}},y_2))\|> \delta \end{align} $$

for every $x_1, x_2 \in \overline {\mathcal {R}_{*}({\textbf {c}})}$ , $y_1 \in B_1$ and $y_2 \in B_2$ .

To give a definition of transversality considering all the attractor, let us fix for every p a finite covering ${\mathcal Y}_p$ of $[-K_0,K_0]^d$ by cubes of size $l(p) = {K_0}/{2^p}$ . We also suppose that ${\mathcal Y}_{p+1}$ refines ${\mathcal Y}_p$ .

Definition 2.5. Given $M>0$ , consider the integers $\tau _M(q,p)$ and $\tau _M(q)$ given by

$$ \begin{align*} \tau_{M}(q,p) = \max_{{\textbf{c}}\in I^{p}} \max_{{\textbf{a}}\in I^{q}({\textbf{c}})} \max_{B_1 \in {\mathcal Y}_p} \# \{& {\textbf{b}}\in I^{q}({\textbf{c}}) | \text{ } {\textbf{a}}\times B_1 \text{ is not } M^q\text{-transversal to } {\textbf{b}}\times B_2\\[-4pt] &\text{on } {\textbf{c}} \text{ for some } B_2 \in \mathcal{Y}_p \} \end{align*} $$

and

(16) $$ \begin{align} \tau_{M}(q) = \min_{p\geq 1} \tau_{M}(q,p). \end{align} $$

For $\beta>1$ , we say that it holds the $\beta $ -transversality condition if there exists some ${M \in (0,1)}$ such that

(17) $$ \begin{align} \limsup_{q\to\infty}\frac{1}{q}\log \tau_M(q) <\log \beta. \end{align} $$

The number $ \tau _{M}(q)$ is a way to count how many images by $T^q$ are not $\delta $ -transversal (meaning that they are not geometrically transversal and the distance between them is smaller than $\delta $ ) for $\delta =M^q$ , where M can be any very small auxiliary constant.

The condition of $\beta $ -transversality includes cases where $ \tau _{M}(q)$ can be exponentially large but growing with rate at most $\beta ^q$ .

Equation (2) in the definition of $ \mathcal {C}^r(s,d,E)$ is given so that for some $M\in (0,1)$ , the set of contractions $\tilde C$ ’s such that $({\log \tau _M(q)})/{q}<\log \beta $ for some q is open and dense in some neighborhood of C. Actually, we state that this condition is enough to construct a family of perturbations of C such that the transversality condition is valid for almost every perturbation.

Theorem F. Given $u \geq d$ , $E \in \mathcal {E}^r(u)$ , $s \geq 0$ , and $C \in \mathcal {C}^r(s,d,E)$ such that ${\beta =\inf |\!\det DT| \underline {\unicode{x3bb} }^{2s}>1}$ , there exists a finite-dimensional space $H \subset C^r({\mathbb {T}^u} \times {\mathbb {R}}^d, {\mathbb {R}}^d)$ such that the $\beta $ -transversality condition is valid for $T(E,C + f)$ for almost every $f \in H$ in a neighborhood of $\mathbf {0}$ .

2.4 Statements in terms of the transversality condition

Theorems A, C, D, and E are obtained putting together Theorem F with their more explicit formulations involving the transversality condition given below (Theorems A $^{\prime }$ , C $^{\prime }$ , D $^{\prime }$ , and E $^{\prime }$ ).

Theorem A′. For $0 \leq s < r-(({u+d})/{2}+1)$ , if $\beta =\inf |\!\det DT| \underline {\unicode{x3bb} }^{2s}>1$ and ${T=T(E,C)}$ satisfies the $\beta $ -transversality condition, then there exists a $C^r$ neighborhood $\mathcal {W}$ of $(E,C)$ such that the corresponding SRB measure $\mu _{\tilde T}$ is absolutely continuous with respect to the volume of ${\mathbb {T}^u}\times {\mathbb {R}}^d$ and its density is in $H^s({\mathbb {T}}^u\times {\mathbb {R}}^d)$ for every $(\tilde E, \tilde C) \in \mathcal {W}.$

Corollary B′. Under the assumptions of Theorem A $^{\prime }$ , if $r\geq u+d+2$ and ${s>({u+d})/{2}}$ , then the corresponding attractor $\Lambda _{T}$ has non-empty interior and the density $h_T$ of the SRB measure is Hölder continuous.

Theorem C′. Suppose that $u/2 < s< r-(({u+d})/{2}+1)$ , that $\inf |\!\det DT| \underline {\unicode{x3bb} }^{2s}>1$ , and $T=T(E,C)$ satisfies the $\beta $ -transversality condition. Then there exists a Banach space $\mathcal {B}$ contained in $H^s({\mathbb {T}^u}\times {\mathbb {R}}^d)$ and containing $C^{r-1}(D)$ such that for every

$$ \begin{align*} \zeta \in (\max\{ \underline{\mu}^{{-1}/({1+\log(1+{d}/{2}+u)})},(\inf |\!\det DT| \underline{\unicode{x3bb}}^{2s})^{{-1}/{2}}\},1), \end{align*} $$

there exists a $C^r$ neighborhood $\mathcal {W}$ of $(E,C)$ such that for every $\tilde T=T(\tilde {E}, \tilde C) \in \mathcal {W}$ , the action of ${\mathcal L}_{\tilde T}$ in $\mathcal {B}$ has spectral gap with essential spectral radius at most $\zeta $ .

In particular, $\tilde T$ has exponential decay of correlations in some linear space $\hat{\mathcal{B}}$ with exponential rate $\zeta $ , where $\hat{\mathcal{B}}$ is contained in $\mathcal {B}$ and contains $C^{r-1}(D)$ .

Theorem D′. Suppose that s is an integer with $u/2 < s< r-(({u+d})/{2}+1)$ , that $\inf |\!\det DT| \underline {\unicode{x3bb} }^{2s}>1$ , and T satisfies the $\beta $ -transversality condition, then there exists an open neighborhood $\mathcal {W}$ such that the mapping

$$ \begin{align*} \mathcal{W} \subset C^r({\mathbb{T}^u})\times C^r({\mathbb{T}^u},{\mathbb{R}}^d) & \to H^s({\mathbb{T}^u} \times {\mathbb{R}}^d) \\(E,C) & \mapsto h_{T(E,C)} \end{align*} $$

is $C^{r-s-\lfloor (({u+d})/{2}) \rfloor -2 }$ at $(E,C)$ .

Theorem E′. Suppose that s is an integer with $u/2 < s< r- (({u+d})/{2}+1)$ , that $\inf |\!\det DT| \underline {\unicode{x3bb} }^{2s}>1$ , $T=T(E_0,C_0)$ satisfies the $\beta $ -transversality condition, and

$$ \begin{align*} \zeta \in (\max\{ \underline{\mu}^{{-1}/({1+\log{(1+{d}/{2}+u)}})},(\inf |\!\det DT| \underline{\unicode{x3bb}}^{2s})^{{-1}/{2}}\},1). \end{align*} $$

Then there exists open sets $\mathcal {W} \subset C^{r}({\mathbb {T}^u}, {\mathbb {T}^u}) \times C^r({\mathbb {T}^u}\times {\mathbb {R}}^d, {\mathbb {R}}^d) $ containing $(E_0,C_0)$ and $\mathcal {Z} \subset C^{r-1}({\mathbb {T}^u} \times {\mathbb {R}}^d, {\mathbb {R}})$ containing $P_0$ and a Banach space $\mathcal {B}$ contained in $H^s({\mathbb {T}^u}\times {\mathbb {R}}^d)$ , and containing $C^{r-1}(D)$ such that for every $(E,C,P) \in \mathcal {W}$ , the action of the operator ${\mathcal L}_{T(E,C),P}$ in $\mathcal {B}$ has spectral gap with essential spectral radius at most $\zeta $ . So there exists a unique eigenfunction $h_{T(E,C),P}$ in $H^s$ associated to the spectral radius $\unicode{x3bb} _{T(E,C),P}$ for the transfer operator ${\mathcal L}_{T(E,C),P}$ . The following functions are of class $C^{ r-s-\lfloor (({u+d})/{2}) \rfloor -2 }$ at $(E,C,P)$ :

1. (1) the spectral radius $(E,C,P) \to \unicode{x3bb} _{T(E,C),P} \in {\mathbb {R}}$ ;

2. (2) the eigenfunction $(E,C,P) \to h_{T(E,C),P} \in H^s({\mathbb {T}^u} \times {\mathbb {R}}^d)$ ;

3. (3) the eigenmeasure $(E,C,P) \to \nu _{T(E,C),P} \in \mathcal {B}^{*}$ ;

4. (4) the equilibrium state $(E,C,P) \to \mu _{T(E,C),P}=h_{T(E,C),P} \nu _{T(E,C),P} \in \mathcal {B}^*$ ;

5. (5) the Lyapunov exponent functions,

   $$ \begin{align*} \!\!\!\!\!\!\!\!\!(T,P) \to \int \log \| DT\| \, d\mu_{(T,P)}, \int \log \| DT(x)^{1}\| ^{-1} \, d\mu_{(T,P)}, \int\! \log|\!\det DT|\, d\mu_{(T,P)}; \end{align*} $$

6. (6) the mean $(T,P) \to m_{(T,P)}(\psi ) := \int \psi \, d\mu _{(T,P)} \in {\mathbb {R}} $ , for any $\psi \in C^{r-1}(D) $ ;

7. (7) the variance $(T,{\kern-1.2pt}P) {\kern-1pt}\to \sigma ^2_{(T,P)(\psi )} {\kern-1pt}:={\kern-1.5pt} \int{\kern-1pt} \tilde \psi ^2\, d \mu _{(T,P)}{\kern-1pt} +{\kern-1pt} 2 {\kern-1pt}\sum _{n=1}^\infty {\kern-1pt}\int{\kern-1pt} \tilde \psi (\tilde \psi \circ T^n)\, d \mu _{(T,P)}$ , where $\tilde \psi = \psi - \int \psi \, d\mu _{(T,P)}$ , for any $\psi \in C^{r-1}(D)$ .

Remark 2.6. The set $\mathcal {W}$ in the statements of Theorems A, C, D, and E is the same set $\mathcal {W}$ of the Theorems A $^{\prime }$ , B $^{\prime }$ , C $^{\prime }$ , D $^{\prime }$ , and E $^{\prime }$ . It is interesting to notice that it contains pairs of the form $(E_0,C_n)$ with $C_n$ converging to $C_0$ in the $C^r$ -topology, since Theorem F holds only perturbing C by some $\tilde {C} = C+f$ .

3 Description of the norms $\| \cdot \| ^\dagger _\rho $ and $\| \cdot \| _{H^s}$

In this section, we define two norms that will be used in this work and state the main Lasota–Yorke inequalities of this paper (Propositions 3.2, 3.4, and 3.5), that are stated in terms of these norms.

3.1 The norm $\| \cdot \| ^\dagger _\rho $

Here we define a norm $\| \cdot \| ^\dagger _\rho $ similar to the anisotropic norms in [7, 24].

For each $x_0\in {\mathbb {T}}^u$ , there exist exactly N ( $=$ degree of E) $C^r$ -inverse branches of E denoted by $h_1, \ldots , h_N: B(x_o, \gamma ) \to {\mathbb {T}^u}$ and $C^r$ -inverse branches of T denoted by $H_j:B(x_0,\gamma )\times {\mathbb {R}}^d \to {\mathbb {T}}^u\times {\mathbb {R}}^d$ ( $j=1,\ldots ,N$ ). Denote the inverse branches of $T^n$ by $H^{n,j}$ ( $j=1,\ldots ,N^n$ ) and the first u components of $H^{n,j}$ by $h^{n,j}_i$ , $i=1, \ldots , u$ , which depend only on x and correspond to the inverse branches of the expanding map E.

Define $\mathcal {S}$ the set of maps $\psi :U_\psi \to {\mathbb {T}}^u$ of class $C^r$ such that $U_\psi $ is an open set contained in ${\mathbb {R}}^d$ , $\psi (U_\psi )$ is contained in some ball of radius $\gamma $ , and $\| D^\nu \psi \| \le k_\nu $ for $1\le \nu \le r$ , for constants $k_1,\ldots ,k_r$ that will be chosen appropriately. Given $\psi \in \mathcal {S}$ , we denote by $G_\psi = \{(\psi (y),y)\mid y \in U_\psi \}$ the graph of $\psi $ . Then $T^{-n}(G_\psi )$ is the disjoint union of the sets $H^{n,j}(G_\psi )$ , where each $H^{n,j}:B(x, \gamma )\times {\mathbb {R}}^d\to {\mathbb {T}}^u\times {\mathbb {R}}^d$ is an inverse branch of $T^n$ , $j=1, \ldots , N^{n}$ .

Taking some connected component $G_i$ of $T^{-n}(G_\psi )$ , we have $G_i=\{(\psi _i(y),y) \mid y\in U_{\psi _i} \}$ , where $T^n(\psi _i(y),y)=(E^n(\psi _i(y)), C^n(\psi _i(y),y))=(\psi (y),y)$ for $y\in U_{\psi _i}$ . We consider the map $g_j: U_\psi \to U_{\psi _i}$ given by $g_j(y)=\pi _2\circ H^{n,j}\circ (\psi ,I)(y)$ , where $\pi _2(x,y)=y$ and $I(y)=y$ .

Let us fix the cone field

(18) $$ \begin{align} \mathcal{C}=\{(u,v) \in T_{(x,y)}({\mathbb{T}^u}\times{\mathbb{R}}^d ) \mid \| u\| \le \alpha_0^{-1}\| v\| \}, \end{align} $$

which is invariant under $DT_{(x,y)}^{-1}$ for every $(x,y) \in {\mathbb {T}^u}\times {\mathbb {R}}^d$ .

We suppose that $k_1 \leq \alpha _0^{-1}/2$ and we increase the constants $k_2, \ldots , k_r>0$ so that the following is valid for every $\tilde {T}$ in a $C^r$ neighborhood $\mathcal {V}$ of T: if $\sigma $ is a u-dimensional ball contained in a u-dimensional plane of ${\mathbb {T}}^u\times {\mathbb {R}}^d$ and $\Gamma $ is a connected component of $\tilde {T}^{-q}(\sigma )$ such that its tangent vectors are all in $\mathcal {C}$ , then $\Gamma $ is the graph of an element of $\mathcal {S}$ .

For $h\in C^r(D)$ and multi-indexes $\alpha =(\alpha _1,\ldots ,\alpha _u)$ and $\beta =(\beta _1,\ldots ,\beta _d)$ , $|\alpha |+ |\beta | \leq ~r$ , we denote $ \partial ^\alpha _x\partial ^\beta _y h = { \partial ^{|\alpha |+|\beta |} h }/({\partial _{x_1}^{\alpha _1}\cdots \partial _{x_u}^{\alpha _u} \partial _{y_1}^{\beta _1} \cdots \partial _{y_d}^{\beta _d}}).$

Definition 3.1. For $h\in C^r(D)$ and an integer $0\le \rho \le r-1$ , we define

(19) $$ \begin{align} \| h\| _\rho^{\dagger}=\max_{|\alpha|+|\beta|\le \rho}\sup_{\psi\in {\mathcal S}}\sup_{\phi\in {\mathcal C}^{|\alpha|+|\beta|}(U_\psi)}\int\phi(y).\partial_x^{\alpha}\partial_y^{\beta}h(\psi(y),y)\,dy, \end{align} $$

where the first supremum is taken over functions $\phi $ with $\operatorname {supp}(\phi )\subset {\mbox {Int}}(U_\psi )$ and $\| \phi \| _{C^{|\alpha |+|\beta |}}\le 1.$

The first Lasota–Yorke inequality of this work is similar to those in [7, 24].

Proposition 3.2. (First Lasota–Yorke inequality (for $\| \cdot \| ^\dagger $ ))

If $\delta> \underline {\mu }^{-1}$ , there exists a constant $K_1>0$ and for any n, there exists $K_1(n)>0$ so that

(20) $$ \begin{align} \| {\mathcal L}^nh\| _{\rho}^{\dagger}\le K_1\delta^{\rho n}\| h\| _{\rho}^{\dagger}+K_1(n)\| h\| _{\rho-1}^{\dagger} \quad \text{for } 1\le \rho \le r-1, \end{align} $$

and

(21) $$ \begin{align} \| {\mathcal L}^nh\| _0^{\dagger}\le K_1\| h\| _0^{\dagger} \end{align} $$

for $n\ge 0$ and $h\in C^r(D)$ , where $K_1(n)$ depends on n but not on h.

Proposition 3.2 is proved in §4.1.

Remark 3.3. Through this paper, we will introduce several constants $K>0$ depending only on the objects that were fixed before, but for simplicity, we will keep denoting them as K. In the cases where the constant depends on other objects that are not fixed, we will emphasize this dependence (e.g. $K(n)$ ). Some constants that we shall mention further will be denoted by $K_1, K_2$ or $K_1(n), K_2(n),$ etc.

3.2 The Sobolev norm $\| \cdot \| _{H^s}$

The second norm that we will consider is the Sobolev norm. Here we remember some facts about the Fourier transform and the Sobolev norm that shall be used.

Given $u \in C^r(D)$ , the Fourier transform ${\mathcal F}(u): {\mathbb {Z}}^u\times {\mathbb {R}}^d \to \mathbb {C}$ is defined by

(22) $$ \begin{align} {\mathcal F}(u)(\xi,\eta) = \int_{{\mathbb{T}^u}\times{\mathbb{R}}^d} u(x,y) e^{- 2\pi i (\langle \xi, x \rangle + \langle \eta, y \rangle )}\, dxdy. \end{align} $$

The Sobolev norm of u is defined by $\| u\| _{H^s} = \sqrt {\langle u, u \rangle _{H^s}}$ , where

(23) $$ \begin{align} \langle u_1, u_2 \rangle_{H^s} := \sum_{\eta \in {\mathbb{Z}}^u} \int_{R^d} {\mathcal F}(u_1)(\eta,\xi) \overline{{\mathcal F}(u_2)(\eta,\xi)} (1+\| \xi\| ^2+\| \eta\| ^2)^s\, d\eta, \end{align} $$

and the Sobolev space $H^s$ is the completion of $C^r(D)$ with respect to this norm.

An equivalent definition is given by the $L^2$ norm of the derivatives. For multi-indexes $\alpha $ and $\beta $ , we denote $\sigma =(\alpha ,\beta )$ and $\partial ^\sigma _z h = \partial ^\alpha _x\partial ^\beta _y h$ . If s is an integer with $0\leq s\leq r$ and $u_1,u_2 \in C^r(D)$ , we define the inner product $ \langle u_1, u_2 \rangle _{\tilde H^s} = \sum _{|\sigma |\leq s} \langle \partial _z^\gamma u_1 , \partial ^\gamma _z u_2 \rangle _{L^2} $ and this inner product induces the norm $\| u\| _{\tilde H^s} = \sqrt { \langle u, u\rangle _{\tilde H^s}}$ . It is a standard fact that these norms are equivalent (see e.g [27, §7.9]).

The second Lasota–Yorke inequality of this work corresponds to the following proposition.

Proposition 3.4. (Second Lasota–Yorke inequality (for Sobolev norm))

There exist positive constants $K_2$ (independent of q and M) and $K_2(q,M)$ such that for every $\phi \in C^r(D)$ , every $M>0$ , and every integer $\rho _0$ with $s+ (({u+d})/{2}) < \rho _0 \leq r-1$ , we have

(24) $$ \begin{align} \| \mathcal{L}^q \phi\| _{H^s}^2 \leq K_2 \frac{\tau_M(q)}{(\inf |\!\det DT| \underline{\unicode{x3bb}}^{2s})^q} \| \phi\| ^2_{H^s} + K_2(q,M) \| \phi\| _{H^s} \| \phi\| ^{\dagger}_{\rho_0}. \end{align} $$

Proposition 3.4 is proved in §4.2.

3.3 The third norm

Finally, let us consider the following norm:

(25) $$ \begin{align} \| h\| _{\rho,s} = \| h\|_{\rho}^\dagger + \| h\| _{H^s}. \end{align} $$

Putting the last two inequalities together, we will obtain the third Lasota–Yorke inequality.

Proposition 3.5. (Third Lasota–Yorke inequality)

Given an integer q satisfying

(26) $$ \begin{align} K_2 \frac{ \tau_M(q)}{(|\!\det DT| {\underline{\unicode{x3bb}}^{2s}})^q} < 1 \end{align} $$

and integers $0 \leq \rho _1<\rho _0 \leq r-1$ with $s<\rho _0-u/2-d/2$ , consider $\nu =\nu (\rho _0,\rho _1) := \sum _{j=\rho _1+1}^{\rho _0} {1}/{j}$ and some

(27) $$ \begin{align} \zeta \in \bigg(\!\! \max \bigg\{ \underline{\mu}^{{{-1}/{\nu}}} , \bigg(\bigg\{K_2^{{1}/{q}} \frac{\tau(q)^{1/q}}{\inf |\!\det DT| {\underline{\unicode{x3bb}}^{2s}}}\bigg)^{{1}/{2}} \bigg\} , 1 \bigg). \end{align} $$

Then there exists a positive constant $K_3$ such that for all $n\in {\mathbb {N}}$ ,

(28) $$ \begin{align} \| {\mathcal L}^n \phi\| _{\rho_0,s} \leq K_3 \zeta^n \| \phi\| _{\rho_0,s} + K_3 \| \phi\| ^\dagger_{\rho_1}. \end{align} $$

The proposition inequality follows from Proposition 3.2 and Proposition 3.4 in the same lines of the proof of [7, Theorem 12].

4 Proof of the main inequalities

The proofs of the Lasota–Yorke inequalities stated before follow essentially from the same lines as in [7]. We will describe the main steps. The second Lasota–Yorke inequality needs a more careful look due to the nonlinearity and the transversality condition in higher dimensions.

4.1 First Lasota–Yorke inequality (for $\| \cdot \| ^\dagger $ )

First notice the following expression for the derivatives of ${\mathcal L}^n h $ as given below.

Claim 4.1. If $1\le |\alpha |+|\beta |=\rho \le r-1$ , then

(29) $$ \begin{align} \partial_x^{\alpha} \partial_{y}^{\beta}(\mathcal{L}^n h)(x,y) = \sum_{j=1}^{N^n} \sum_{|a|+|b| \leq \rho} \partial_x^{a} \partial_{y_1}^{b_1}\cdots \partial_{y_d}^{b_d} h (H^{n,j}(x,y)) \cdot Q_{\alpha,\beta,a,b,n;j}(x,y), \end{align} $$

where $Q_{\alpha ,\beta ,a,b,n;j}(x,y)$ is an homogeneous polynomial on the derivatives of order up to $|\alpha |+|\beta |-|a|-|b|+1$ of the components of $H^{n,j}$ and $\Theta _n\circ H^{n,j}$ at the point $(x,y)$ , where $\Theta _n(x,y)=|\!\det DE^n(x)|^{-1}|\!\det D_yC^n(x,y)|^{-1}$ . Also, if $|a|+|b|=|\alpha |+|\beta |$ and $|b|\geq |\beta |$ , then $Q_{\alpha ,\beta ,a,b,n;j}(x,y)=p(x,y)\Theta _n( H^{n,j}(x,y))$ , where p is an homogeneous polynomial of degree $|\alpha |+|\beta |$ on the partial derivatives of order 1 of $H^{n,j}$ . In fact, ${ p=\sum _{|a|+|b|= \rho }c_{a,b} p_{a,b},} $ where $c_{a,b}$ are positive integers and

(30) $$ \begin{align} p_{a,b}=\frac{\partial{h^{n,j}}}{\partial x_{i_1}}\cdots \frac{{\partial h^{n,j}}}{\partial x_{i_{|a|}}}\frac{{\partial H^{n,j}}}{\partial x_{i_{|a|+1}}}\cdots \frac{{\partial H^{n,j}}}{\partial y_{i_{|a|+|\alpha|-|a|}}}\frac{{\partial H^{n,j}}}{\partial y_{i_{|\alpha|-|a|+1}}}\cdots \frac{{\partial H^{n,j}}}{\partial y_{i_\rho}}. \end{align} $$

Proof. The proof follows by induction on $\rho $ , and we describe here the main steps. Iterating ${\mathcal L}$ in equation (3) and using the chain rule, we can write ${\mathcal L}^n$ as

(31) $$ \begin{align} {\mathcal L}^n h(x,y)= \sum_{j=1}^{N^n} h( H^{n,j}(x,y) ) \cdot \Theta_n \circ H^{n,j}(x,y), \end{align} $$

which corresponds to the case $\rho =0$ for $Q_{0,0,0,0,n;j} = Q_{n,j} = \Theta _n \circ H^{n,j}$ .

Consider the inverse branches $H^{n,j}$ of $T^n$ , $j=1,\ldots , N^n$ , and denote by $H_k^{n,j}$ its kth component. Here, $H^{n,j}$ are locally written as $ H^{n,j}(x,y)=(h^{n,j}(x),C^{n,j}(x,y) ). $

Suppose that equation (29) is valid for some $\rho $ and let us differentiate it with respect to some variable $u_\ell \in \{x_1,\ldots ,x_u, y_1,\ldots , y_d\}$ . Denote by $u_k$ the kth variable of $(x,y)$ , that is, $x_k$ for $1\leq k \leq u$ and $y_{k-u}$ for $u+1 \leq k \leq u+d$ . By the rule of product and chain rule, $\partial _{u_\ell } \partial ^\alpha _x\partial _y^\beta ({\mathcal L}^nh)$ is a sum of terms of the type:

(32) $$ \begin{align} \partial_{u_k}\partial_x^{a} \partial_{y_1}^{b_1}\cdots \partial_{y_d}^{b_d} h (H^{n,j}(x,y)) \cdot [\partial_{u_\ell} H_k^{n,j}(x,y) \cdot Q_{\alpha,\beta,a,b,n;j}(x,y)] \end{align} $$

and

(33) $$ \begin{align} \partial_x^{a} \partial_{y_1}^{b_1}\cdots \partial_{y_d}^{b_d} h (H^{n,j}(x,y)) \cdot \partial_{u_\ell} Q_{\alpha,\beta,a,b,n;j}(x,y). \end{align} $$

All the terms in the bracket in equation (32) are the product of $Q_{\alpha ,\beta ,a,b,n;j}$ with some derivative of some component of $H_k^{n,j}$ , so are also homogeneous polynomials on the derivatives of the components of $H^{n,j}$ and $\Theta _n \circ H^{n,j}$ of order 1 or of the same order of $Q_{\alpha , \beta , a, b, n;j}$ . In the case $|\alpha |+|\beta |=|a|+|b|$ and $|b|\geq |\beta |$ , since we do not differentiate $Q_{\alpha ,\beta ,a,b,n;j}$ , no derivatives of $\Theta _n \circ H^{n,j}$ will appear. Since $\partial _{y_i}H^{n,j}_k=0$ for $k=1,\ldots , u$ , in the polynomials $p_{a,b}$ , the derivatives of $h^{n,j}$ with respect to $y_i$ -variables are null.

For the terms of the type in equation (33), notice that $\partial _{u_\ell } Q_{\alpha ,\beta ,a,b,n;j}(x,y)$ is also an homogeneous polynomial on the derivatives of the components of $H^{n,j}$ and $\Theta _n\circ H^{n,j}$ of order increased by $1$ . Notice also that a and b are the same, and $|\alpha |+|\beta |$ increases by $1$ . In particular, these terms do not correspond to the case $|a|+|b|=|\alpha |+|\beta |$ .

Proof of Proposition 3.2

(First Lasota–Yorke inequality). Using the formula of Claim 4.1 for $\psi \in \mathcal {S}$ , $\phi \in C^r(\psi )$ with $\| \phi \| _{C^\rho }\leq 1$ , and considering $\psi _1,\ldots ,\psi _{N^n}$ , $g_1,\ldots ,g_{N^n}$ such that $T^n(\psi _i(g_i(y)),g_i(y))=(\psi (y),y)$ , we have

(34) $$ \begin{align} &\int \phi(y)\cdot \partial_x^{\alpha} \partial_{y}^{\beta} (\mathcal{L}^n h)(\psi(y),y)\, dy \nonumber \\ &\quad= \sum_{i=1}^{N^n} \int \sum_{|a|+|b|\leq \rho} \phi(y) \partial_x^{a} \partial_{y_1}^{b_1}\cdots \partial_{y_d}^{b_d} h(\psi_i(g_i(y)),g_i(y) )\cdot Q_{\alpha,\beta,a,b,n;i}(\psi(y),y)\, dy \nonumber \\ &\quad= \sum_{i=1}^{N^n}\sum_{|a|+|b|\leq \rho} \int \Psi_{i,\alpha,\beta,a,b,n;i}(y') \cdot \partial_x^{a} \partial_{y_1}^{b_1}\cdots \partial_{y_d}^{b_d} h(\psi_i(y'),y')\, dy', \end{align} $$

where $\Psi _{\alpha ,\beta ,a,b,n;i}(y')\!=\!\phi (g_i^{-1}(y'))\cdot Q_{\alpha ,\beta ,a,b,n;i}((\psi \circ g_i^{-1})(y'),g_i^{-1}(y'))\cdot \! |\!\det Dg_{i}^{-1}(y')|.$

Note that $\!\Psi _{\alpha ,\beta ,a,b,n;i}$ has $C^{|a|+|b|}$ -norm uniformly bounded by some constant $K(n)$ depending on the constants $k_1,k_2,\ldots ,k_r$ on the definition of $\mathcal {S}$ but not on h. Actually, we can bound from above its $C^0$ norm by

$$ \begin{align*}K_0(n)= \underset{\begin{subarray}{c} 1\leq i \leq N^n \\ \alpha|,|\beta|,|a|,|b| \leq r-1 \\ (x,y) \in T^{-n}({\mathbb{T}^u} \times [-K,K]^d) \end{subarray}}{\sup} |Q_{\alpha,\beta,a,b,n;i}(x,y)| \cdot |\!\det D_y C(x,y)|^{-n}. \end{align*} $$

To bound its $C^\ell $ -norm, we can differentiate $\ell $ times $\Psi _{\alpha ,\beta ,a,b,n;i}$ , using the chain rule and product rule, to obtain an expression involving derivatives of $\phi $ , derivatives of $g_i^{-1}$ , and derivatives of $\psi $ , and all of them are uniformly bounded.

In particular, we have

(35) $$ \begin{align} \sum_{i=1}^{N^n}\sum_{|a|+|b|< \rho} \int {\Psi_{\alpha,\beta,a,b,n;i}(y') \cdot \partial_x^{a} \partial_{y_1}^{b_1}\cdots \partial_{y_d}^{b_d} h(\psi_i(y'),y')}\, dy' \leq K_0(n) \| h\| ^\dagger_{\rho-1}. \end{align} $$

To estimate the sum of the terms with $|a|+|b|=\rho $ , we integrate by parts if $|b|>0$ . For this, we rewrite the integral as a surface integral over $G_{\psi _i}$ , $\partial _{y_j}h$ as a combination of Lie derivatives of $\partial _x h$ and ${\mathcal L}_{V_j}h$ , where $V_j$ are tangent vector fields, and apply the following integration by parts: $ \int _S {\mathcal L}_X(f)g = - \int _S f {\mathcal L}_X(g) + \int _S f g \operatorname {div} X.$ Integrating by parts repeatedly when $|b|>0$ , only expressions with at most $\rho -1$ derivatives with respect to x and y or $\rho $ derivatives only in the variable x will remain.

Denote by $S_1$ the sum corresponding to $\rho $ derivatives only on x and by $S_2$ the sum of the remaining terms. Here, $S_2$ is a sum of terms of the form $ \int _{U_{\psi _i}} \tilde {\phi } (y') {\mathcal L}_{V_j^{(i)}}(\tilde {h}) (\psi _i(y'),y')\, dy', $ where $\tilde {h}$ has at most $\rho -1$ derivatives of h. Since $\tilde {h}$ has at most $\rho -1$ derivatives of h, we have that $S_2 \leq K(n) \| h \| ^\dagger _{\rho -1}$ .

So now we only need to consider the terms for $|b|=0$ and $|a|=\rho $ . To estimate $\label {eq.estimate2.2} \int \Psi _{\alpha ,\beta ,a,b,n;i_0}(y') \cdot \partial _x^a h(y')\, dy', $ we write

(36) $$ \begin{align} \Psi_{\alpha,\beta,a,b,n;i_0}(y') \cdot \partial^a_x h(y')=\frac{\phi_1(y')\phi_2(y')\phi_3(y')\phi_4(y') }{\det DE^n(x_{i_0})}\partial_x^{a}h(\psi_{i_0}(y'),y'), \end{align} $$

where $\displaystyle \phi _1(y')=\phi \circ g_{i_0}^{-1}(y')$ , $ \phi _2(y')={\det DE^n(x_{i_0})}/({\det DE^n\circ \psi _{i_0}(y')})$ , $ \phi _3(y')= \det Dg_{i_0}^{-1}/({\det D_yC^n\circ (\psi _{i_0},I)})$ , and $ \phi _4=p\circ (\psi ,I)\circ g_{i_0}^{-1}. $ We can notice that there exists a constant $K>0$ such that

(37) $$ \begin{align} \| p\circ (\psi,I)\circ g_{i_0}^{-1}\| _{C^{\rho}} &\le K n^{\rho^2} \underline{\mu}^{-\rho n},\ \ \,\kern3pt\qquad\qquad\end{align} $$

(38) $$ \begin{align} \bigg\| \frac{\det Dg_{i_0}^{-1}}{\det D_yC^n\circ (\psi_{i_0},I)}\bigg\| _{C^\rho} &\le K,\qquad\qquad\qquad\qquad\kern1pt\qquad \end{align} $$

(39) $$ \begin{align} \| [\det\circ (DE^n)\circ \psi_{i_0}]^{-1}\| _{C^\rho}&\le K n^{r-1} \| \det\circ [DE^n(x_{i_0})]^{-1}\|, \end{align} $$

for all $ x_{i_0}\in h_{i_0}^n(\psi (U_\psi )).$ Actually, equation (37) follows from the expression of $p_{a,b}$ in equation (30) noticing that $b=0$ and $|\alpha |=|a|$ , so only derivatives of $h^{n,j}$ with respect to x variables appear that are bounded by $\underline {\mu }^{-n}$ . Equations (38) and (39) follow from the bounded distortion property, noticing that $ [DE^n \circ \psi _{i_0}]^{-1}(y) = Dh^{n,j}_{i_0}(\psi (g^{-1}_{i_0}(y) ))$ and that $h_{n,j}$ is a composition of inverse branches of E.

Then the $C^{\rho }$ norms of $\phi _1$ , $\phi _2$ , and $\phi _3$ are bounded for some constant independent on n. The $C^\rho $ norm of $\phi _4$ is bounded from above by $K n^{\rho ^2} \underline {\mu }^{-\rho n} $ . Then $\| \phi _1\phi _2\phi _3\phi _4\| _{C^\rho }$ is bounded by $K n^{\rho ^2+r-1}\underline {\mu }^{-\rho n}$ . So $ S_1 \le K n^{\rho ^2+r-1}\underline {\mu }^{-\rho n}\| h\| _\rho ^{\dagger }. $

Consequently, we conclude that equation (34) is bounded by $ K n^{\rho ^2+r-1}\underline {\mu }^{-\rho n}\| h\| _\rho ^{\dagger }+K(n)\| h\| _{\rho -1}^{\dagger } $ for some constant K independent on n.

The estimate in equation (21) is analogous and easier.

4.2 Second Lasota–Yorke inequality (for Sobolev norm)

Through this section, we fix an integer q and fix p such that $\tau (q,\tilde {p})=\tau (q)$ for every $\tilde {p} \geq p$ .

Let us consider the dual cone fields

(40) $$ \begin{align} {\mathcal C}^*=\{(u,v)\in {\mathbb{R}}^u\times{\mathbb{R}}^d\mid \| v\| \le \alpha_0^{-1} \| u\| \} \end{align} $$

and

(41) $$ \begin{align} {\mathcal C}^*_1 = \{ (u,v)\in {\mathbb{R}}^u\times{\mathbb{R}}^d\mid \| v\| \le \tfrac{9}{10} \alpha_0^{-1} \| u\| \}. \end{align} $$

Notice that for all $(\xi _0,\eta _0)\neq 0$ in ${\mathcal C}_1^*$ , there is a u-dimensional subspace $W_0$ contained in ${\mathcal C}_1^*$ such that $(\xi _0,\eta _0)\in W_0$ . Indeed, it is enough to take $W_0$ generated by $\{(\xi _0,\eta _0), (\xi _1,0), \ldots , (\xi _{u-1},0)\},$ where $\{{\xi _0}/{\| \xi _0\| },\xi _1,\ldots ,\xi _{u-1}\}$ is an orthonormal base of ${\mathbb {R}}^u$ .

By uniform continuity of $(x,y) \mapsto (DT^q_{(x,y)})^*$ , it follows that if $(DT^q_{(x_0,y_0)})^*(\xi ,\eta ) \in {\mathcal C}^*_1$ , then there exist a u-dimensional subspace W such that $(\xi ,\eta )\in W$ and a constant ${R=R(q)>0}$ such that $ (DT^q_{(x,y)})^*((DT^q_{(x_0,y_0)})^*)^{-1} {\mathcal C}_1^* \subset {\mathcal C}^* $ for every $(x,y)\in B(x_0,R) \times B(y_0,R)$ . Consider p sufficiently large such that ${\mathcal R}_{*}({\textbf {c}}{\textbf {a}})\subset B(x_0,R)$ , where $R=R(q)$ is given as above.

The following lemma is similar to [7, Lemma 8].

Lemma 4.2. Let $\rho _0$ be an integer with $s+1<\rho _0\le r-1$ . Consider ${\textbf {a}}\in I^{q}$ and ${\textbf {c}}\in I^{p}$ , and $\chi :{\mathbb {T}}^u\times {\mathbb {R}}^d \to {\mathbb {R}}$ a $C^\infty $ function supported on ${\mathcal R}({\textbf {c}}{\textbf {a}})\times B(y_0,R)$ . If $0\neq (\xi ,\eta )\in {\mathbb {Z}}^u\times {\mathbb {R}}^d$ satisfies $(DT^q_{(x_0,y_0)})^*(\xi ,\eta )\in {\mathcal C}_1^*$ for some $x_0\in {\mathcal R}({\textbf {c}}{\textbf {a}})$ , then, for any $\phi \in C^r(D)$ , it follows that

(42) $$ \begin{align} (1+\| \xi\| ^2+\| \eta\| ^2)^{{\rho_0}/{2}}|{\mathcal F}({\mathcal L}^q(\chi. \phi))(\xi,\eta)|\le K(\chi,q)\| \phi\| ^{\dagger}_{\rho_0}, \end{align} $$

where $K(\chi ,q)$ depends only on $\chi $ and q.

Proof. Consider W a u-dimensional subspace containing $(\xi ,\eta )$ as described above such that $(DT_{(x,y)}^q)^*W\subset {\mathcal C}^*$ for all $(x,y)\in B(x_0,R) \times B(y_0,R) \supset {\mathcal R}({\textbf {c}}{\textbf {a}})$ and $(\xi ,\eta )\in W$ . We have $|{\mathcal F}({\mathcal L}^q(\chi \phi ))(\xi ,\eta )| (\| \xi \| ^{\rho _0} + \| \eta \| ^{\rho _0}) \leq K |{\mathcal F}(\partial ^{\rho _0}_{x_j}{\mathcal L}^q(\chi \phi ))(\xi ,\eta )|, $ where the $\rho $ derivatives are taken with respect to the variable $x_j$ ( $\xi _j$ or $\eta _j$ ) that has greatest absolute value. Since the support of ${\mathcal L}^q(\chi \phi )$ is contained in $D\cap ({\mathcal R}({\textbf {c}})\times {\mathbb {R}}^d)$ , we have

$$ \begin{align*} |{\mathcal F}(\partial^{\rho_0}_{x_j}{\mathcal L}^q(\chi\phi))(\xi,\eta)| \leq \int_\Gamma \int_{\sigma } | \partial^{\rho_0}_{x_j}{\mathcal L}^q(\chi\phi)) |\, dm_\sigma \, d\hat{m} \leq K \sup_{\sigma \in \Gamma}\int_{\sigma} |\partial^{\rho_0}_{x_j}{\mathcal L}^q(\chi\phi) |\,dm_\sigma. \end{align*} $$

For each $\sigma \in \Gamma $ , there is a unique $\widetilde {\sigma }$ contained in ${\mathcal R}({\textbf {c}}{\textbf {a}})\times {\mathbb {R}}^d$ such that $T^q(\widetilde {\sigma })=~\sigma $ . For $x\in \widetilde {\sigma }$ and $(u,v)$ tangent to $\sigma $ at $T^q(x,y)$ , we have $ 0=\langle (u,v) ,(w_1,w_2) \rangle =\langle (DT^q_{(x,y)})^{-1}(u,v) ,(DT^q_{(x,y)})^*(w_1,w_2) \rangle $ for all $(w_1,w_2)\in W$ . Since $(DT^q_{(x,y)})^*W$ is a u-dimensional subspace contained in ${\mathcal C}^*$ , we have $(DT^q_{x})^{-1}(u,v)\in {\mathcal C}$ . So, we conclude that $\hat {\sigma }:=T^{-q} \sigma \cap ({\mathcal R}({\textbf {c}}{\textbf {a}})\times {\mathbb {R}}^d)$ is the graph of some $\tilde {\psi }$ in ${\mathcal S}$ . Since $\chi $ is supported in $\mathcal {R}({\textbf {c}}{\textbf {a}})\times B$ , we have that ${\mathcal L}^q(\chi \phi ) = ({(\chi \phi )}/{|\!\det DT^q|})\circ g$ for the inverse branch $g:{\mathcal R}({\textbf {c}})\times {\mathbb {R}}^d \to {\mathcal R}({\textbf {c}}{\textbf {a}})\times {\mathbb {R}}^d$ of the restriction of $T^{q}$ to ${\mathbb {R}}({\textbf {c}}{\textbf {a}})\times {\mathbb {R}}^d$ . Then,

$$ \begin{align*} |\partial^{\rho_0} {\mathcal L}^q(\chi\phi)(x,y)| \leq K(\chi, g) \sum_{|\beta|\leq \rho_0} {|\partial^{\beta}\phi(g(x,y))|}. \end{align*} $$

Integrating and changing variables, we obtain

$$ \begin{align*} \int_{\sigma} |\partial^{\rho_0} {\mathcal L}^q(\chi \phi)(x,y)|\,dm_{\sigma} \leq K(\chi,q) \sum_\beta \int_\sigma |\partial^\beta \phi(g(x,y))|\, dm_{\sigma} \leq K(\chi,q) \| \phi\| ^\dagger_{\rho_0}. \\[-30pt] \end{align*} $$

To make the local argument, we will consider a fixed partition of unity. For this, we consider $\{\chi _{{\textbf {c}}}:{\mathbb {T}^u} \to {\mathbb {R}}\}_{{\textbf {c}}\in \mathcal {A}^p}$ a family of $C^\infty $ functions that form a partition of unity subordinated to the covering $\{\mathcal {R}_{*}({\textbf {c}}) \}$ . Recall that a family of functions $\{f_i\}_{i \in \Lambda }$ is subordinated to an open covering $\{U_i\}_{i \in \Lambda }$ if the support of $f_\unicode{x3bb} $ is contained in $U_i$ for every $i\in \Lambda $ . We define $\{\chi _{{\textbf {c}},{\textbf {a}}}:{\mathbb {T}^u}\times {\mathbb {R}}^d \to {\mathbb {R}}\}_{{\textbf {c}}\in \mathcal {A}^p}$ by

(43) $$ \begin{align} \chi_{{\textbf{c}},{\textbf{a}}}(T^{-q}_{{\textbf{c}},{\textbf{a}}} (x,y) ) = \chi_{{\textbf{c}}}(x) \end{align} $$

if $x\in \mathcal {R}_{*}({\textbf {c}})$ and $0$ elsewhere. Notice that $\{\chi _{{\textbf {c}},{\textbf {a}}}\}$ is another partition of unity subordinated to $\{\mathcal {R}_{*}({\textbf {c}}{\textbf {a}}) \times {\mathbb {R}}^d\}$ . We also consider $\{\chi _{{\textbf {c}},{\textbf {a}},B}:{\mathbb {T}^u} \to {\mathbb {R}}\}_{{\textbf {c}}\in \mathcal {A}^p}$ a family of $C^\infty $ functions subordinated to $\{E_{{\textbf {c}}{\textbf {a}}}^{-q}(\mathcal {R}_{*}({\textbf {c}})) \times B_{*}\}$ with

(44) $$ \begin{align} \chi_{{\textbf{c}},{\textbf{a}}} = \displaystyle \sum_{B \in {\mathcal Y}_p} \chi_{{\textbf{c}},{\textbf{b}},B}, \end{align} $$

where $B_{*}$ is the union of the cubes of ${\mathcal Y}_p$ that are adjacent to B.

Lemma 4.3. For $\epsilon>0$ and $0 \leq t < s \leq r$ , there exist positive constants K, $K(\epsilon )$ , and $K(\epsilon , t, s)$ such that, for any $\phi \in C^r(D)$ ,

(45) $$ \begin{align} &\sum_{{\textbf{a}},{\textbf{c}},B}\| \chi_{{\textbf{c}},{\textbf{a}},B}\phi\| ^2_{H^s} \leq 2 \| \phi\| ^2_{H^s} + K \| \phi\| ^2_{L^1}, \end{align} $$

(46) $$ \begin{align} &\| \phi\| ^2_{H^s} \leq K \sum_{{\textbf{c}}} \| \chi_{{\textbf{c}}} \phi\| ^2_{H^s} + K \| \phi\| ^2_{L^1}, \end{align} $$

(47) $$ \begin{align} &\| \phi\| ^2_{H^t} \leq \epsilon \| \phi\| ^2_{H^s} + K(\epsilon, t, s) \| \phi\| ^2_{L^1}, \end{align} $$

(48) $$ \begin{align} &|\langle \phi_1,\phi_2 \rangle_{\tilde H^s} | \leq K(\epsilon,s) \| \phi_1\| _{L^1} \| \phi_2\| _{L^1} \end{align} $$

for every $\phi _1, \phi _2 \in C^r(D)$ whose distance between their supports is greater than $\epsilon $ .

Proof. The proofs are the same as [7, Lemmas 7 and 9].

Lemma 4.4. Given $0\le s\le r $ , ${\textbf {a}}\in \mathcal {A}^q$ , ${\textbf {c}}\in \mathcal {A}^p$ , and $B \in \mathcal {Y}_p$ , there exists a constant ${K>1}$ and other $K(q)$ such that

(49) $$ \begin{align} \| {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B}\phi)\| ^2_{H^s} \leq \frac{K }{ \inf |\!\det DT^q| \underline{\unicode{x3bb}}^{2qs} } \| \chi_{{\textbf{c}},{\textbf{a}},B}\phi\| ^2_{H^s} + K(q) \| \phi\| ^2_{L^1} \end{align} $$

for every $\phi \in C^r(D)$ .

Proof. Let us first consider the s integer. Recall that $T_{{\textbf {c}},{\textbf {a}}}^{-q}$ is an inverse branch defined over ${\mathcal R}({\textbf {c}}) \times {\mathbb {R}}^d$ by $T_{{\textbf {c}},{\textbf {a}}}^{-q}(x,y)=(E_{{\textbf {c}},{\textbf {a}}}^{-q}x,C^{-q}(x,y))$ . If we call by $g_1, g_2, \ldots , g_{u+d}$ the components of $T^{-q}_{{\textbf {c}},{\textbf {a}}}$ , then we may observe that $\| \partial ^{\sigma }g_j\| \le K \underline {\unicode{x3bb} }^{-q}$ for all $\sigma $ multi-index with $|\sigma | \le s $ . From this, we can write

$$ \begin{align*}\partial^{\sigma}[(\chi_{{\textbf{c}},{\textbf{a}},B}\phi)\circ T_{{\textbf{c}},{\textbf{a}}}^{-q}](z) = \sum_{|\sigma'|\le|\sigma|} \psi_{\sigma',\sigma}(z) (\partial^{\sigma'} \chi_{{\textbf{c}},{\textbf{a}},B}\phi)\circ T_{{\textbf{c}},{\textbf{a}}}^{-q}(z), \end{align*} $$

where $\psi _{\sigma ',\sigma }$ is a polynomial function of degree at most s in the variables $\partial ^{\gamma }g_j$ , and $\gamma $ goes through the multi-indexes with $|\gamma |\leq |\sigma '|$ and $j=1,2,\ldots ,u+d$ . Notice that $|\psi _{\sigma ',\sigma }(z)|\le K \underline {\unicode{x3bb} }^{-qs}$ for some constant K. So we have

$$ \begin{align*} \| {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B}\phi)\| ^2_{H^s}\!\leq\! K \!\!\!\sum_{ \substack{ |\sigma|{\le}s \\ |\sigma'|+|\sigma"|\le|\sigma|}} \!\! \int \bigg| \bigg( (\partial^{\sigma'}\! \chi_{{\textbf{c}},{\textbf{a}},B}\phi)\! \partial^{\sigma"}\bigg(\frac{1}{|\!\det DT^q| } \bigg) \bigg)\! \circ T_{{\textbf{c}},{\textbf{a}}}^{-q}(z)\! \psi_{\sigma',\sigma}(z) \bigg|\, dz. \end{align*} $$

Write this last sum above as $\mathcal {S}_1+\mathcal {S}_2$ , where $\mathcal {S}_1$ correspond to the terms with $\sigma "=0$ and $\mathcal {S}_2$ to terms with $|\sigma "|>0$ (which implies $|\sigma '|\leq s-1$ ). We deal with $\mathcal {S}_1$ making a change of variables and with $\mathcal {S}_2$ bounding it by the $H^{s-1}$ norm and using Young’s inequality to bound by the $H^s$ norm and $L^1$ norm. So

$$ \begin{align*} \mathcal{S}_1 &\leq K \underline{\unicode{x3bb}}^{-2qs} \sum_{|\sigma|{\le}s} \int \bigg(\sum_{|\sigma'|\le|\sigma|} \frac{|(\partial^{\sigma'} \chi_{{\textbf{c}},{\textbf{a}},B}\phi)\circ T_{{\textbf{c}},{\textbf{a}}}^{-q}(z)|}{|\!\det DT^q|\circ T_{{\textbf{c}},{\textbf{a}}}^{-q}(z)}\bigg)^2\, dz\\ &= K \underline{\unicode{x3bb}}^{-2qs} \inf|\!\det DT^q|^{-1} \| \chi_{{\textbf{c}},{\textbf{a}},B}\phi\| _{H^s}^2 \end{align*} $$

and

$$ \begin{align*}\mathcal{S}_2 \leq K_1(q) \| \chi_{{\textbf{c}},{\textbf{a}},B}\phi\| _{H^{s-1}} \leq \underline{\unicode{x3bb}}^{-2qs} \inf|\!\det DT^q|^{-1}\| \chi_{{\textbf{c}},{\textbf{a}},B}\phi\| _{H^{s}} + K(q) \| \chi_{{\textbf{c}},{\textbf{a}},B}\phi\| _{L^1} .\end{align*} $$

For non-integer values of s, we shall use interpolation of Hilbert spaces [20]. For $s=0$ , the estimative for $\mathcal {S}_1$ gives

$$ \begin{align*} \| \mathcal{L}^q (\chi_{{\textbf{c}},{\textbf{a}},B}\phi)\| ^2_{L^2} \leq \frac{K}{\inf |\!\det DT^q|} \| \chi_{{\textbf{c}},{\textbf{a}},B}\phi \| ^2_{L^2} =: {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert {\chi_{{\textbf{c}},{\textbf{a}},B}\phi} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{H_0}^2. \end{align*} $$

For every $s\leq r$ integer, since $\| h\| _{L^2} \leq K(D) \| u\| _{L^1}$ , we have

$$ \begin{align*} \| {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B}\phi)\| ^2_{H^s} \leq \frac{K }{ \inf |\!\det DT^q| \underline{\unicode{x3bb}}^{2qs} } \| \chi_{{\textbf{c}},{\textbf{a}},B}\phi\| ^2_{H^s} \kern1.3pt{+}\kern1.3pt K(q) \| \chi_{{\textbf{c}},{\textbf{a}},B} \phi\| ^2_{L^2} =: \kern-2pt{\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert {\chi_{{\textbf{c}},{\textbf{a}},B}\phi} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{H_1}^2. \end{align*} $$

This implies that

$$ \begin{align*} \| {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B}\phi)\| ^2_{H^{t}}\! \leq \! {\left\vert\kern-0.25ex\left\vert\kern-0.25ex\left\vert {\chi_{{\textbf{c}},{\textbf{a}},B}\phi} \right\vert\kern-0.25ex\right\vert\kern-0.25ex\right\vert}_{H_t}^2 = \frac{K }{ (\inf |\!\det DT^q| \underline{\unicode{x3bb}}^{2qt})} \| \chi_{{\textbf{c}},{\textbf{a}},B}\phi\| ^2_{H^{t}} + K(q) \| \chi_{{\textbf{c}},{\textbf{a}},B} \phi\| ^2_{L^2}. \end{align*} $$

Equation (49) follows using equation (47) for some small $\epsilon = \epsilon (q)$ .

One fact about the transversality that shall be used in the proof of the second Lasota–Yorke inequality is the following lemma.

Lemma 4.5. Let $(\xi ,\eta )\in {\mathbb {Z}}^u\times {\mathbb {R}}^d\setminus \{0\}$ . If ${\textbf {a}}\times B_1$ is geometrically transversal to ${\textbf {b}}\times B_2$ on ${\textbf {c}}$ , then either $(DT_x^q)^*(\xi ,\eta )\in ~{\mathcal C}_1^*$ for all $(x,y)\in E^{-q}_{{\textbf {c}},{\textbf {a}}}({\mathcal R}_{*}({\textbf {c}})) \times B_1$ or $(DT^q_x)^*(\xi ,\eta )\in {\mathcal C}_1^*$ for all $(x,y)\in E^{-q}_{{\textbf {c}},{\textbf {b}}}({\mathcal R}_{*}({\textbf {c}})) \times B_2$ .

Proof. Note that if $E^q(x_{\textbf {a}})=x$ for some $x_{\textbf {a}} \in E^{-q}_{{\textbf {c}},{\textbf {a}}}({\mathcal R}_{*}({\textbf {c}}))$ , then

$$ \begin{align*} (DT^q_{({\textbf{a}}(x),y) } )^*=\left( \begin{array}{@{}cc@{}} (DE^q_{{\textbf{a}}(x)})^* & (DE^q_{{\textbf{a}}(x)})^*(D_xC^q_{{\textbf{a}}(x)}(y))^* \\ 0 & (D_yC^q_{{\textbf{a}}(x)})^*\\ \end{array} \right)\!. \end{align*} $$

Supposing that $(DT^q_{({\textbf {a}}(x_{\textbf {a}}),y_{\textbf {a}})})^*(\xi ,\eta )\not \in {\mathcal C}_1^*$ for some ${\textbf {a}}(x_{\textbf {a}})\in E^{-q}_{{\textbf {c}},{\textbf {a}}}({\mathcal R}_{*}({\textbf {c}}))$ and $y \in B_{\textbf {a}}$ , then we claim that $(DT^q_{({\textbf {b}}(x_{\textbf {b}}),y_{\textbf {b}})})^*(\xi ,\eta )\in {\mathcal C}_1^*$ for all ${\textbf {b}}(x_{\textbf {b}})\in E^{-q}_{{\textbf {c}},{\textbf {b}}}({\mathcal R}_{*}({\textbf {c}}))$ and $y_{\textbf {b}}\in B_{\textbf {b}}$ . In fact, if both vectors are not in ${\mathcal C}_1^*$ , then

$$ \begin{align*}\| D_yC^q({\textbf{i}}(x_{\textbf{i}}),y_{\textbf{i}})^* \eta \|> \tfrac{9}{10}\alpha_0^{-1} \| DE^q({\textbf{i}}(x_{\textbf{i}}))^*\xi + D_xC^q({\textbf{i}}(x_{\textbf{i}}),y_{\textbf{i}})^*\eta\| \end{align*} $$

for ${\textbf {i}} \in \{{\textbf {a}}, {\textbf {b}}\}$ . Denoting $f_{\textbf {i}} = DE^q({\textbf {i}}(x_{\textbf {i}}))^*\xi + D_xC^q({\textbf {i}}(x_{\textbf {i}}),y_{\textbf {i}})^*\eta $ , it satisfies

$$ \begin{align*} \| (DE^q_{{\textbf{i}}(x_1)})^*)^{-1}f_{\textbf{i}} \| \leq \underline{\mu}^{-q} \| f_{\textbf{i}}\| < \tfrac{10}{9}\alpha_0 \underline{\mu}^{-q} \| D_yC^q({\textbf{i}}(x_{\textbf{i}}),y_{\textbf{i}})^*\eta\| \leq \tfrac{10}{9}\alpha_0 \theta^q \| \eta \|. \end{align*} $$

Reminding that $S(x,({\textbf {i}},y))= \pi _2 T^q (E_{\textbf {i}}^{-q}(x),y)$ , where $\pi _2(x,y)=y$ , we have

$$ \begin{align*} &\tfrac{20}{9} \alpha_0 \theta^q \| \eta\| \geq \| (DE^q_({\textbf{a}}(x_1))^*)^{-1}f_{\textbf{a}} - (DE^q_({\textbf{b}}(x_2))^*)^{-1}f_{\textbf{b}} \| \\ &\quad=\| (DE^q({\textbf{a}}(x_1))^*)^{-1} D_xC^q({\textbf{a}}(x_1),y_1)^*\eta - (DE^q({\textbf{b}}(x_2))^*)^{-1} D_xC^q({\textbf{b}}(x_2),y_2)^*\eta \| \\ &\quad=\| (DS(x_1,({\textbf{a}},y_1))-DS(x_2,({\textbf{b}},y_2)))^*\eta\| \geq 3 \alpha_0\theta^q\| \eta\| , \end{align*} $$

which is a contradiction.

Now we can proceed to the proof of Proposition 3.4.

Proof of Proposition 3.4

By Lemma 4.3, we have

$$ \begin{align*} \| {\mathcal L}^q \phi\| ^2_{H^s} &\leq K \sum_{{\textbf{c}} } \| \chi_{{\textbf{c}}} {\mathcal L}^q \phi\| ^2_{H^s} + K \| \phi\| ^2_{L^1} \leq K \sum_{{\textbf{c}}} \bigg\| \sum_{{\textbf{a}},B} {\mathcal L}^q (\chi_{{\textbf{c}},{\textbf{a}},B}\phi) \bigg\| ^2_{H^s} + K \| \phi\| ^2_{L^1} \\ &= K \sum_{{\textbf{c}}\in A^p,\,{\textbf{a}},{\textbf{b}} \in A^q, B_1,B_2 \in \mathcal{Y}_p} \langle {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi),{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi) \rangle_{H^s} + K \| \phi\| ^2_{L^1}. \end{align*} $$

Denote ${\textbf {a}} \pitchfork _{\textbf {c}} {\textbf {b}}$ if ${\textbf {a}}\times B_1$ is transversal to $ {\textbf {b}} \times B_2$ in ${\textbf {c}}$ for every $B_1, B_2 \in \mathcal {Y}_p$ , and denote ${\textbf {a}} \times B_1 \pitchfork _{\textbf {c}}^g {\textbf {b}} \times B_2$ if ${\textbf {a}}\times B_1$ is geometrically transversal to $ {\textbf {b}} \times B_2$ in ${\textbf {c}}$ .

For ${\textbf {a}} \pitchfork _{\textbf {c}} {\textbf {b}}$ , notice that

$$ \begin{align*} &\sum_{{\textbf{a}} \pitchfork_{\textbf{c}} {\textbf{b}}, B_1,B_2}\! \langle {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi),{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi)\! \rangle_{H^s} =\! \sum_{{\textbf{a}} \pitchfork_{\textbf{c}} {\textbf{b}}} \sum_{B_1, B_2 \in {\mathcal Y}_p}\! \langle {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi),{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi) \rangle_{H^s}\\ &\quad\leq \sum_{{\textbf{a}}\times B_1 \pitchfork_{\textbf{c}}^g {\textbf{b}}\times B_2} \langle {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi),{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi) \rangle_{H^s}\\ &\qquad + \sum_{d(B_1,B_2)> M^q } \langle {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi),{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi) \rangle_{H^s}. \end{align*} $$

If the distance between $B_1$ and $B_2$ is greater than $M^q$ , then by equation (48),

$$ \begin{align*} \langle {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi),{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi) \rangle_{H^s} &\leq K(q,M) \| \chi_{{\textbf{c}},{\textbf{a}},B_1} \phi\| _{L^1} \| \chi_{{\textbf{c}},{\textbf{b}},B_2} \phi\| _{L^1}\\ &\leq K(q,M) \| \phi\| ^\dagger_{\rho_0} \| \phi\| _{H^s}. \end{align*} $$

If ${\textbf {a}}\times B_1$ is geometrically transversal to $ {\textbf {b}} \times B_2$ in ${\textbf {c}}$ , then by Lemma 4.5, for every $(\xi ,\eta ) \neq (0,0)$ , we have either $(DT_{(x,y)}^q)^*(\xi ,\eta )\in {\mathcal C}_1^*$ for all ${(x,y)}\in {\mathcal R}({\textbf {c}}{\textbf {a}}) \times B_1$ or $(DT^q_{(x,y)})^*(\xi ,\eta )\in {\mathcal C}_1^*$ for all ${(x,y)}\in {\mathcal R}({\textbf {c}}{\textbf {b}}) \times B_2 $ . Denote by U the set of $(\xi ,\eta )$ such that the first occurs, and V the set such that the second occurs. Then, if $(\xi ,\eta )\in U$ , by Lemma 4.2, we have $ |{\mathcal F}({\mathcal L}^q(\chi _{{\textbf {c}},{\textbf {a}},B_1}\phi ))(\xi ,\eta )| \leq K ( 1+ |\xi |^2 + |\eta |^2)^{-{\rho _0}/{2}} \| \phi \| ^\dagger _{\rho _0}. $ So,

$$ \begin{align*} &\bigg| \sum_{\xi}\int_U (1+|\xi|^2+|\eta|^2)^s {\mathcal F}{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi)(\xi,\eta) \overline{{\mathcal F}{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi)}(\xi,\eta)\, d\eta \bigg| \\ &\quad \leq \bigg( \sum_{\xi}\int_U (1+|\xi|^2+|\eta|^2)^s |{\mathcal F}{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi)(\xi,\eta)|^2\, d\eta \bigg)^{1/2} \| {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi)\| _{H^s}\\ &\quad \leq K(q)\| \phi\| _{H^s} \sum_{\xi} \int (1+|\xi|^2+|\eta|^2)^{s-\rho_0} \| \phi\| ^\dagger_{\rho_0}\,d\,\eta \leq K(q) \| \phi\| ^\dagger_{\rho_0} \| \phi\| _{H^s}, \end{align*} $$

where we used that the integral is finite since $s-\rho _0<-(u+d)/2$ .

Summing it with the same integrals over V instead of U, we obtain that

(50) $$ \begin{align} \langle {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi),{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi) \rangle_{H^s} \leq K(q) \| \phi\| ^\dagger_{\rho_0} \| \phi\| _{H^s}. \end{align} $$

For ${\textbf {a}} \not \pitchfork _{\textbf {c}} {\textbf {b}}$ , we use $\langle u_1,u_2 \rangle _{H^s} \leq \tfrac 12 (\| u_1 \|^2_{H^s}+ \| u_2 \| ^2_{H^s} ) $ together with the definition of $\tau _M(q)$ to obtain

(51) $$ \begin{align} \sum_{{\textbf{a}} \not\pitchfork_{\textbf{c}} {\textbf{b}}, B_1,B_2} \langle {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi),{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi) \rangle_{H^s} \leq \tau_M(q) \sum_{{\textbf{a}}, B_1} \| {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi)\| ^2_{H^s}. \end{align} $$

Using it with Lemmas 4.3 and 4.4, we have

$$ \begin{align*} \sum_{{\textbf{c}}\in A^p,\,{\textbf{a}}\not\pitchfork_{\textbf{c}} {\textbf{b}}} \langle {\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{a}},B_1}\phi),{\mathcal L}^q(\chi_{{\textbf{c}},{\textbf{b}},B_2}\phi) \rangle_{H^s} \leq \frac{K \tau_M(q,p)}{(\inf |\!\det DT^q| \underline{\unicode{x3bb}}^{2sq}) } \| \phi \| ^2_{H^s} + K(q) \| \phi\| _{L^1}^2. \end{align*} $$

Then

$$ \begin{align*} \| \mathcal{L}^q \phi\| _{H^s}^2 &\leq \frac{K \tau_M(q,p)}{\inf |\!\det DT^q| \underline{\unicode{x3bb}}^{2sq}} \| \phi \| ^2_{H^s} +K \| \phi\| ^2_{L^1}+ K(q,M) \| \phi\| ^\dagger_{\rho_0} \| \phi\| _{H^s} \\ &\leq \frac{K \tau_M(q)}{\inf |\!\det DT^q| \underline{\unicode{x3bb}}^{2sq}} \| \phi\| ^2_{H^s} + K(q,M) \| \phi\| ^\dagger_{\rho_0} \| \phi\| _{H^s}.\\[-3.6pc] \end{align*} $$

4.3 Proof of Theorems A $^{\prime }$ and C $^{\prime }$

The proof of Theorems A $^{\prime }$ and C $^{\prime }$ are the same as those of [7, Theorems 1 and 3]. We will describe them briefly.

Proof of Theorem A $^{\prime }$

The transversality condition implies that we can consider q sufficiently large such that $\omega = ({K_2 \tau _M(q)}/{(|\!\det DT|{\underline {\unicode{x3bb} }}^{2s})^q}) <1$ . Consider $\rho _0 = r-1$ and $\rho _1=0$ . Since $s<r-u/2-d/2-1$ , we have that $s+u/2+d/2<\rho _0 $ , so we can apply Proposition 3.5 for some $\zeta $ between $\omega $ and $1$ .

Fix some non-negative function $\psi _0 \in C^r(D)$ with $\| \psi _0\| _{L^1}=1$ , $\nu _0=\psi _0 m$ , $\psi _n = ({1}/{n}) (\psi _0 + {\mathcal L}\psi _0 + \cdots + {\mathcal L}^{n-1}\psi _0)$ , and $\nu _n=\psi _n m$ , then $\nu _n = ({1}/{n}) \sum _{j=0}^{n-1}T^j_{*}\nu _0 \overset {*}{\to } \mu $ since $\mu $ is the SRB measure for T. It is easy to check that $\mu =\psi _{\infty }m$ , where $\psi _\infty $ is a weak* accumulation point of $\psi _n$ in $L^2$ , so $\mu $ is an absolutely continuous invariant probability.

The openness in $T{\kern-1.3pt}={\kern-1.3pt}T(E,{\kern-1pt}C)$ follows from the fact that $\tau _M(q)$ is upper semi-continuous on $(E,C)\in C^r({\mathbb {T}^u}) \times C^r({\mathbb {T}^u} \times {\mathbb {R}}^d, {\mathbb {R}}^d)$ , from the openness of the condition $K_{2}({\tau _M(q)}/ {\inf |\!\det DT^q|\underline {\unicode{x3bb} }^{2sq}})<1$ and because we are considering a $C^r$ neighborhood of maps T where the bounds in equations (7), (8), (9), and (10) hold with the same constants. This concludes the proof of Theorem A $^{\prime }$ .

Remark 4.6. We mention that the transversality condition defined in Definition 2.4 is not an open condition. What is open in $(E,C)$ is the condition

(52) $$ \begin{align} \displaystyle \frac{K_2 \tau_M(q)}{\inf|\!\det DT^q| \underline{\unicode{x3bb}}^{2sq}} <1 \end{align} $$

for fixed q, which is enough for the conclusion of Theorem A $^{\prime }$ .

When $s>u/2$ , we can obtain spectral properties of the action of the operator ${\mathcal L}$ in a Banach space $\mathcal {B}$ contained in $H^s$ and containing $C^{r-1}(D)$ . When we have a Lasota–Yorke inequality, the spectral gap can be obtained as a standard consequence of a theorem due to Hennion, and Ionescu-Tulcea and Marinescu [26, 28].

Let us denote the spectral radius of ${\mathcal L}:\mathcal {B}\to \mathcal {B}$ by $\rho ({\mathcal L})= \lim _{n\to \infty } \sqrt [n]{\| {\mathcal L}^n\| }$ . The essential spectral radius $\rho _{ess}({\mathcal L})$ is the supremum of the $\unicode{x3bb} $ such that the range of $T-\unicode{x3bb} I$ is not closed or the kernel of $T-\unicode{x3bb} I$ is infinite dimensional.

If the operator ${\mathcal L}$ has a spectral gap, then there exist bounded operators ${\mathcal P}$ and ${\mathcal N}$ such that ${\mathcal L}=\unicode{x3bb} {\mathcal P} +{\mathcal N}$ with $|\unicode{x3bb} |=\rho ({\mathcal L})$ , ${\mathcal P}^2={\mathcal P}$ , $\dim (\operatorname {im}({\mathcal P}))=1$ , $\rho ({\mathcal N})<|\unicode{x3bb} |$ , and ${{\mathcal P}{\mathcal N}={\mathcal N}{\mathcal P}=0}$ . In this case, the essential spectral radius of ${\mathcal L}$ satisfies $\rho _{ess}({\mathcal L}) \leq \rho ({\mathcal N})$ .

Theorem. (Hennion)

Let $L:(\mathcal {B},\| \cdot \| ) \to (\mathcal {B},\| \cdot \| )$ be a bounded operator and $\| \cdot \| '$ be a norm in $\mathcal {B}$ such that:

1. (1) $\| \cdot \| '$ is continuous in $\| \cdot \| $ ;

2. (2) for every bounded sequence $\{\phi _n\}\in \mathcal {B}$ , there exists a subsequence $\{\phi _{n_k}\}$ and $\psi \in \mathcal {B}$ such that $\| \phi _{n_k} - \psi \| '\to 0$ ;

3. (3) $\| L \phi \| ' \leq M \| \phi \| '$ for some $M>0$ and every $\phi \in \mathcal {B}$ ;

4. (4) there exists constants $r \in (0,\rho (L))$ , $K_1>0 $ and $K_2(n)> 0$ for all $n\in {\mathbb {N}}$ such that

   (53) $$ \begin{align} \| L^n \phi\| \leq K_1 r^n \| \phi\| + K_2(n) \| \phi\| ' \quad \text{for all } n; \end{align} $$

5. (5) there exists a unique eigenvalue $\unicode{x3bb} $ with $|\unicode{x3bb} |=\rho (L)$ and $\dim \operatorname {ker}(L-\unicode{x3bb} I)=1$ .

Then L has spectral gap with essential spectral radius at most r.

Proof. A proof of this theorem can be found in [53] (see also [22, Theorem B.14 B]). In [53, Appendix A.3], it is proved that conditions (1)–(4) imply that the operator is quasi-compact. In [53, Exercise 2.2], it is proved that if L is quasi-compact and satisfies condition (5), then L has a spectral gap.

Remark 4.7. The change of variables formula implies that

(54) $$ \begin{align} \| {\mathcal L}(h)\| _{L^1} \leq \| h \| _{L^1} \end{align} $$

for every $h \in L^1$ , then $\rho ({\mathcal L}) \leq 1$ . As consequence of Theorem A $^{\prime }$ , there exists a fixed point $\psi \in \mathcal {B}$ of ${\mathcal L}$ (the density of the absolutely continuous invariant probability), so $\rho ({\mathcal L}|\mathcal {B})=1$ in this case.

Moreover, if the transfer operator ${\mathcal L}$ has a spectral gap, then it follows that the dynamical system has exponential decay of correlations with respect to the SRB measure with exponential rate at most $\rho (\mathcal {N})<1$ , as below.

Proposition 4.8. Suppose that ${\mathcal L}$ has a spectral gap in some Banach space $\mathcal {B}$ embedded continuously in $L^2(\nu )$ with $\rho ({\mathcal L} |\mathcal {B})= \unicode{x3bb} $ and $\rho ({\mathcal N})=\zeta < \unicode{x3bb} $ , where $\nu $ is an eigenmeasure of ${\mathcal L}^*$ associated to the eigenvalue $\unicode{x3bb} $ . If $\phi _0\in \mathcal {B}$ is a non-negative eigenfunction of ${\mathcal L}$ associated to the eigenvalue $\unicode{x3bb} $ satisfying $\int \phi _0 \,d\nu =1$ , considering $\mu =\phi _0 \nu $ , it follows that $\mu $ is invariant and $(T,\mu )$ has exponential decay of correlations in $\tilde{\mathcal{B}}:=\{\phi \in \mathcal {B}, \phi \phi _0\in \mathcal {B}\}$ with exponential rate at most $\tilde \zeta =\zeta \unicode{x3bb} ^{-1}<1$ . Moreover, it follows that $\unicode{x3bb} ^{-n}{\mathcal L}^n(\phi )$ converges to $(\int \phi \, d\nu ) \phi _0$ .

In particular, if $\mathcal {B}$ is a Banach algebra, then $\tilde {\mathcal {B}}=\mathcal {B}$ , so $(T,\mu )$ has exponential decay of correlations in $\mathcal {B}$ .

Proof. It is standard to verify that $\mu $ is T-invariant, since for every bounded continuous function g, it holds

$$ \begin{align*} \int g\circ T d\mu &= \int (g\circ T) hd\nu = \unicode{x3bb}^{-1} \int (g \circ T) h\, d(\mathcal{L}^*\nu) \\ &= \unicode{x3bb}^{-1}\int \mathcal{L}((g\circ T) h)\, d\nu = \unicode{x3bb}^{-1} \int g \mathcal{L}(h)\, d\nu = \int g h\, d\nu = \int g \, d\mu. \end{align*} $$

Since ${\mathcal L}$ has spectral gap in $\mathcal {B}$ , for each $\phi \in \mathcal {B}$ , we write $\phi =a(\phi )\phi _0+ \phi _1$ with $\| \mathcal {L}^n\phi _1\| _{\mathcal {B}}\le \zeta ^n\| \phi _1\| _{\mathcal {B}}$ . Then the properties $\int {\mathcal L}^n u \, d\nu = \unicode{x3bb} ^n \int u \, d\nu $ and ${\mathcal L}^n \phi _0 = \unicode{x3bb} ^n \phi _0$ imply that for every n,

$$ \begin{align*} \bigg|\!\int \phi_1 \,d\nu\bigg| &=\bigg|\!\int \unicode{x3bb}^{-n}{\mathcal L}^n(\phi_1) \,d\nu\bigg| \leq C \unicode{x3bb}^{-n}\| {\mathcal L}^n(\phi_1)\| _{L^2(\nu)} \\ &\leq C\unicode{x3bb}^{-n}\| {\mathcal L}^n(\phi_1)\| _{{\mathcal B}} \leq C(\zeta \unicode{x3bb}^{-1})^n\| \phi_1\| _{{\mathcal B}} \to 0. \end{align*} $$

So it follows that $\int \phi _1\, d\nu =0$ . Since $\int \phi _0\, d\nu =1$ , we have $a(\phi )=\int \phi \,d\nu $ . In particular, $\unicode{x3bb} ^{-n}{\mathcal L}^n(\phi )=(\int \phi \,d\nu ) \phi _0 + \unicode{x3bb} ^{-n} {\mathcal L}^n\phi _1 $ converges to $(\int \phi \,d\nu ) \phi _0$ exponentially fast in ${\mathcal B}$ .

We also have the property ${\mathcal L}^n(\phi \cdot \psi \circ T^n)=\psi \cdot \mathcal {L}^n\phi $ and $\phi _1 = \mathcal {N}(\phi )$ implies that $\| \phi _1\| _{\mathcal {B}} \leq K \| \phi \| _{\mathcal {B}}$ for $K= \| \mathcal {N}\| $ .

Given $\psi \in L^\infty (\mu )$ and $\phi \in \tilde{\mathcal{B}}$ , it follows that

$$ \begin{align*} \bigg|\! \int\kern-1.3pt \phi(\psi\circ T^n)\,d\mu \kern1.3pt{-} \int\kern-1.5pt \phi\, d\mu \int\kern-1.5pt \psi\, d\mu \bigg| &=\bigg|\! \int \phi(\psi\circ T^n)\phi_0\,d\nu - \int \phi\phi_0 d\nu \int \psi\phi_0\, d\nu \bigg| \\&= \bigg|\! \int \bigg[\dfrac{{\mathcal L}^n (\phi\phi_0)}{\unicode{x3bb}^n} - \bigg(\!\int \phi \phi_0\,d\nu\bigg) \phi_0\bigg] \psi\, d\nu \bigg|\\ &= \bigg|\! \int \unicode{x3bb}^{-n}{\mathcal L}^n \bigg[ (\phi\phi_0)_1 \bigg] \psi\, dm \bigg|\\ &\le \unicode{x3bb}^{-n}\| \psi\| _{L^2(m)} \| {\mathcal L}^n (\phi\phi_0)_1 \| _{L^2(m)} \\ &\le K \unicode{x3bb}^{-n}\| \psi\| _{L^2(m)} \| {\mathcal L}^n (\phi\phi_0) \| _{\mathcal{B} } \\ &\le K \unicode{x3bb}^{-n}\| \psi\| _{L^2(m)} \| (\phi\phi_0)_1 \| _{\mathcal{B} } \zeta^n \kern1.2pt{=}\kern1.2pt K(\phi,\psi) \bigg(\kern-0.2pt\dfrac{\zeta}{\unicode{x3bb}}\kern-0.2pt\bigg)^{\kern-1pt n}\kern-0.1pt. \end{align*} $$

So $(T,\mu )$ has exponential decay of correlations in $\tilde{\mathcal{B}}$ .

Proof of Theorem C $^{\prime }$

Consider the smallest integer $\rho _0$ and the greatest integer $\rho _1$ such that $ \rho _1+ u/2 < s < \rho _0 - u/2-d/2. $ Consider $t \in ( \rho _1+u/2,s)$ and an integer q such that $K_2 \tau _M(q) < (\inf |\!\det DT|{\underline {\unicode{x3bb} }}^{2s})^q$ . Since $\rho _0 - \rho _1 \leq u + ({d}/{2}) +2 $ and $\sum _{j=1}^{n}1/j\le 1+\log (n-1)$ , we have $\nu \le 1+\log (u+({d}/{2})+1) := a$ .

Consider $\mathcal {B}$ the completion of $C^r(D)$ with respect to the norm $\| \cdot \| _{\rho _0,s}$ and $\mathcal {B}'$ the completion of $C^r(D)$ with respect to the norm $\| \cdot \| ^\dagger _{\rho _1}$ .

If $\zeta \in ( \max \{\underline {\mu }^{{-1}/{a}},({(K_2 \tau _M(q))^{1/q}}/{|\!\det DT| \underline {\unicode{x3bb} }^{2s}})\} , 1 )$ , then $\zeta $ is in the interval in equation (27).

We will verify that the conditions of Hennion’s theorem are satisfied. Obviously, $\| \cdot \| _{\rho _1} \leq \| \cdot \| _{\rho _0} \leq \| \cdot \| $ , which implies condition (1). Condition (3) is an immediate consequence of Lemma 3.2. Condition (4) follows from Lemma 3.5 with $r=\zeta < 1$ .

Condition (5) follows from the fact that $T|\Lambda $ is topologically mixing and that the SRB measure is a mixing absolutely continuous invariant probability (see e.g. [53, Exercise 2.3]).

To verify condition (2), we notice that the embedding of $\mathcal {B}$ in $\mathcal {B}'$ is compact. Actually, the embedding of $H^s(D)$ in $H^t(D)$ is compact and the embedding of $H^t(D)$ in $\mathcal {B}'$ is continuous, as we notice in the claim below.

So we can apply the theorem of Hennion and Proposition 4.8 to conclude the part of spectral gap and decay of correlations in Theorem C $^{\prime }$ .

It remains to notice that $C^{r-1}(D) \subset \mathcal {B}$ . The definition of $\| \cdot \| ^\dagger _\rho $ gives that

$$ \begin{align*}\bigg| \int_{U_\psi} \phi(y) \partial^\alpha_x \partial_y^\beta h(\psi(y),y)\, dy\bigg| \leq \int_{U_\psi} \bigg|\partial_x^\alpha \partial_y^\beta h (\psi(y),y)\bigg|\,dy \leq \operatorname{vol}(D) \| h\| _{C^{r-1}}\end{align*} $$

whenever $|\alpha |+|\beta | \leq \rho _0$ , $\psi \in \mathcal {S}$ , $\phi \in C^{|\alpha |+|\beta |}(U_\psi )$ , and $\| \phi \| _{C^{|\alpha |+|\beta |}}\leq 1$ . This implies immediately that $\| h\| _{\rho _0}^\dagger \leq K \| h\| _{C^{r-1}}$ and so $C^{r-1}(D) \subset \mathcal {B}$ . Since $C^{r-1}(D)$ is a Banach algebra, it follows that $C^{r-1}(D) \subset \hat {\mathcal {B}}$ .

Claim 4.9. The embedding of $H^t(D)$ in $\mathcal {B}'$ is continuous, that is, there exists a constant $K>0$ such that

(55) $$ \begin{align} \| u\| _{\rho_1}^{\dagger} \le K \| u\| _{H^t}. \end{align} $$

Proof of Claim 4.9

From the definition of $\| .\| _{\rho _1}^{\dagger }$ , it follows that $ \| u\| _{\rho _1}^\dagger $ is bounded by $ K \max _{|\gamma |\le \rho _1}\sup _{\psi \in {\mathcal S}}\| \partial ^{\gamma }u(\psi (\cdot ),\cdot )\| _{L^2({\mathbb {R}}^d)}. $ Define $v(x,y)=u(x+\psi (y),y)$ for ${y\in U_\psi }$ and $v(x,y)=0$ if $y\not \in U_{\psi }$ , then the norm of $\| \partial ^{\gamma }u(\psi (\cdot ),\cdot )\| _{L^2({\mathbb {R}}^d)}$ is bounded by $K\| v(0,\cdot )\| _{H^{\rho _1}}$ . Due to [1, Theorem 7.58(iii)] applied with $p=q=2$ , $\tilde {s}=\rho _1+u/2$ , $\chi =\rho _1$ , $k=d$ , $n=u+d$ , we have

(56) $$ \begin{align} \| v(0,\cdot)\| _{H^{\rho_1}} \leq K \| v\| _{H^{\tilde{s}}({\mathbb{R}}^{u+d})}. \end{align} $$

For any $0< t < r$ , it is easy to see that $ \| v\| _{H^t({\mathbb {R}}^{u+d})}\le K \| u\| _{H^t({\mathbb {R}}^{u+d})}, $ where K depends on only $k_1, k_2, \ldots , k_r$ . So, for $t>\rho _1 + ({u}/{2}) = \tilde {s}$ , we conclude that $ \| v\| _{H^{\tilde {s}}({\mathbb {R}}^{u+d})} \le K \| v\| _{H^t({\mathbb {R}}^{u+d})}\le K \| u\| _{H^t({\mathbb {R}}^{u+d})}. $

5 Linear response formula

This section is dedicated to the proof of Theorem D $^{\prime }$ . First we will prove in §5.1 the differentiability of the transfer operator ${\mathcal L}={\mathcal L}_{(E,C)}$ with respect to the map $T=T(E,C)$ .

We cannot guarantee that ${\mathcal L}_{T(E,C)}$ and $h_{T(E,C)}$ are smooth with respect to $(E,C)$ using the classical spectral theory, because it would only guarantee such differentiability if we had the differentiability of the transfer operator as an operator acting on the same space. To prove the differentiability, we will consider the Banach spaces $\mathcal {B}^{\rho ,s}$ defined as the completion of $C^r(D)$ with respect to the norm $\| \cdot \| _{\rho ,s}= \| \cdot \| _{H^s} + \| \cdot \| _{\rho }^\dagger $ and consider ${\mathcal L}_{T(E,C)}$ as a linear transformation from $B^{\rho ,s}$ to $B^{\rho -k,s-k}$ .

5.1 Differentiability of the transfer operator

The notion here used is the Fréchet differentiability: given Banach spaces E, F, an open set $\mathcal {V}\subset E$ , and a map $T:\mathcal {V} \to F$ , we say that T is Fréchet differentiable if for every $x_0 \in \mathcal {V}$ , there exists a continuous linear functional $DT(x_0): E \to F$ such that

(57) $$ \begin{align} \lim_{ \| h\| _{E}\to 0} \frac{\| T(x_0+h)-T(x_0)-DT(x_0)h \| _F}{\| h\| _{E}}=0. \end{align} $$

To study the differentiability of the transfer operator, we consider a constant $K>0$ and $\hat{\mathcal{K}}$ the space of $C^r$ skew-products $T:{\mathbb {T}}^u\times {\mathbb {R}}^d \to {\mathbb {T}}^u\times {\mathbb {R}}^d$ , $T(x,y)=(E(x),C(x,y))$ , such that $E:{\mathbb {T}}^u\to {\mathbb {T}}^u$ is a expanding map of degree N, $C(x,.):{\mathbb {R}}^d\to {\mathbb {R}}^d$ is an invertible contraction map, and $T({\mathbb {T}}^u\times [-K,K]^d)\subset {\mathbb {T}}^u\times (-K,K)^d$ . Consider the equivalence relation on $\hat{\mathcal{K}}$ given by $T\sim \hat {T}$ if and only if $T(x,y)=\hat {T}(x,y)$ for all $(x,y)\in {\mathbb {T}}^u\times [-K,K]^d$ . Finally, consider the quotient space $\mathcal {K}:=\hat{\mathcal{K}}/\sim $ equipped with the norm $\| T\| _{r,K}=\| T_{|K}\| _r$ .

For each $T\in \mathcal {K}$ , we associate the transfer operator with potential $P_T(x,y)=-\log |\!\det DT(x,y)|$ defined by

$$ \begin{align*} \mathcal{L}_T\varphi(z)=\sum_{T(z')=z}\exp\circ P_T(z')\varphi(z') \end{align*} $$

for $\varphi \in C^r({\mathbb {T}}^u\times [-K_0,K_0]^d,{\mathbb {R}})$ .

Theorem 5.1. Let $k\geq 1$ be an integer such that $k \leq \rho \leq r-1$ and $k \leq s \leq r-1$ , then the mapping

$$ \begin{align*} \Psi:\mathcal{K} &\to L(B^{\rho,s}, B^{\rho-k,s-k})\\ T &\mapsto \mathcal{L}_T \end{align*} $$

is $C^{\tilde k}$ , where $\tilde k=\min \{k-1,r-\rho -1, r-s-1\}$ .

This proposition can be reduced to a local version of it. Fix ${T}_0\in \mathcal {V}$ and consider a finite open covering of ${\mathbb {T}}^u$ by sets $B_j$ and another open set $\hat B_j$ ( $j=1, \ldots , m$ ) such that $\overline {B_j}\subset \hat B_j$ , $E^{-1}(\hat B_j)$ is the union of exactly $N=\deg E$ disjoint open sets $\hat U_{i,j}$ ( $i=1,\ldots , N$ ), and the restriction of E to each $\hat U_{i,j}$ is a $C^r$ -diffeomorphism over $\hat B_j$ . Consider $U_{i,j}$ open sets of ${\mathbb {T}}^u$ such that $\overline {U}_{i,j}\subset \hat U_{i,j}$ and $\overline {B}_j\subset E(U_{i,j})\subset \hat E(\overline {U}_{i,j})\subset \hat B_{j}$ . So there exists a smaller neighborhood (also denoted by $\mathcal {V}$ ) of $T_0$ such that $T_{|U_{i,j} \times (-K_0,K_0)^d}: U_{i,j} \times (-K_0,K_0)^d \to \hat B_j \times (-K_0,K_0)^d$ is a $C^r$ -diffeomorphism over the image for every $T\in \mathcal {V}$ .

Consider a $C^{\infty }$ partition of the unity $\{ \vartheta _j \}$ subordinated to the covering $\{ B_j \times (-K_0,K_0)^d \}_{j=1}^{m}$ of ${\mathbb {T}}^u\times (-K_0,K_0)^d$ . Denote by $\xi _{i,j}(T)$ the inverse diffeomorphism of $T_{|U_{i,j} \times {\mathbb {R}}^d}: U_{i,j} \times (-K_0,K_0)^d \to \hat B_j \times (-K_0,K_0)^d$ . Write $\mathcal {L}_T\varphi (z) =\sum _{j=1}^m\sum _{i=1}^{N} \mathcal {L}_T^{(i,j)}\varphi (z) $ for

(58) $$ \begin{align} \mathcal{L}_T^{(i,j)}\varphi(z)=\exp\circ P_T(\xi_{i,j}(T)(z))\varphi(\xi_{i,j}(T)(z))\vartheta_j(z) \end{align} $$

and denote $\Psi _{(i,j)}(T) = \mathcal {L}_T^{(i,j)} $ .

Also, observe that $\Psi _{(i,j)}(T)=F_{i,j}(T)G_{i,j}(T),$ where $F_{i,j}:\mathcal {V}\to C_b^{a}(B_j,U_{i,j}) $ is given by $F_{i,j}(T)=\exp \circ (-\log |DT\circ \xi _{i,j}(T)|)$ and $G_{i,j}:\mathcal {V} \to L(B^{\rho ,s},B^{\rho -k,s-k})$ is given by $G_{i,j}(T)\varphi =(\varphi \circ \xi _{i,j}(T))\vartheta _{j}.$

Proposition 5.2. (Local version of Proposition 5.1)

The mapping

$$ \begin{align*} \Psi_{(i,j)}:\mathcal{V} &\to L(B^{\rho,s}, B^{\rho-k,s-k})\\ T &\mapsto \mathcal{L}_T^{(i,j)} \end{align*} $$

is $C^{\tilde k}$ , where $\tilde k=\min \{k-1,r-\rho -1, r-s-1\}$ .

The rest of this section is dedicated to the proof of Proposition 5.2.

Given U, V, and $\tilde {V}$ open sets contained in ${\mathbb {T}}^u \times [-K_0,K_0]^d$ such that the restriction of T to U is a diffeomorphism into the image and $\overline {V}\subset T(U)\subset T(\overline {U})\subset \tilde {V}$ for every $T\in \mathcal {V}$ , denote by $C_{b}^{r-k}(V,U)$ the set of $C^{r-k}$ bounded mappings from V to U and define $\xi :\mathcal {V} \to C_{b}^{r-k}(V,U)$ , where $\xi (T)$ is the unique inverse branch of T defined on V such that $\xi (T)(V)\subset U$ .

Lemma 5.3. The mapping $\xi :\mathcal {V} \to C_{b}^{r-k}(V,U)$ is $C^{k}$ . Consequently, all the $\xi _{i,j}$ are $C^k$ .

Proof. Without loss of generality, we can suppose that U, V, and $\tilde {V}$ are bounded open sets of ${\mathbb {R}}^{u+d}$ . Let $F: C_b^{r}(U,\tilde {V}) \times C_b^{r-k}(V,U) \to C_b^{r-k}(V,\tilde {V})$ be given by $ F(T,S)=T\circ S. $ The same proof of [23, Theorem 3.1] shows that F is $C^k$ . Moreover, for $k\ge 1$ , $\partial _SF(T,S):C_b^{r-k}(V,{\mathbb {R}}^{u+d}) \to C_b^{r-k}(V,{\mathbb {R}}^{u+d})$ is given by

$$ \begin{align*} \partial_SF(T,S)H=(DT\circ S)\cdot H. \end{align*} $$

So, if $T\in \mathcal {V}$ and $S=\xi (T)$ , then $\partial _SF(T,S)$ is a continuous linear isomorphism with inverse $\partial _SF(T,S)^{-1}:C_b^{r-k}(V,{\mathbb {R}}^{u+d}) \to C_b^{r-k}(V,{\mathbb {R}}^{u+d})$ given by $ \partial _SF(T,S)^{-1} H=(DT\circ S)^{-1}\cdot H. $ Since $F(T,\xi (T))=\mathrm {id}_{V}$ , the implicit function theorem implies that $\xi $ is $C^k$ .

Lemma 5.4. Let $f:GL({\mathbb {R}}^{u+d}) \to {\mathbb {R}}$ be a $C^{\infty }$ function. Then the mapping $\alpha : \mathcal {V} \to C^{r-k}(U,{\mathbb {R}})$ given by $\alpha (T)=f\circ DT\circ \xi (T) $ is $C^{k-1}$ .

Proof. It is enough to show that $\gamma (T)=DT\circ \xi (T)$ is $C^{k-1}$ . Consider

$$ \begin{align*}F: C_b^{r}(U,\tilde V) \times C_b^{r-k}(V,U)\to C_b^{r-1}(U,L({\mathbb{R}}^{u+d},{\mathbb{R}}^{u+d}))\times C_b^{r-k}(V,U)\end{align*} $$

given by $ F(T,S)=(DT,S) $ and

$$ \begin{align*}G:C_b^{r-1}(U,L({\mathbb{R}}^{u+d},{\mathbb{R}}^{u+d}))\times C_b^{r-k}(V,U) \to C_b^{r-1}(V,L({\mathbb{R}}^{u+d},{\mathbb{R}}^{u+d}))\end{align*} $$

given by $ G(A,S)=A\circ S. $ Notice that F is a continuous linear mapping and, by the same argument of the previous lemma, G is of class $C^{k-1}$ . So, $\beta (T,S)=G\circ F(T,S)= DT\circ S$ is $C^{k-1}.$ Since $\gamma (T)=\beta (T,\xi (T))$ , it follows that $\gamma $ is $C^{k-1}$ .

Below we use that the determinant of a linear transformation A is a $C^\infty $ -smooth map with respect to A (since it can be written as an algebraic expression of its coefficients). Applying the previous lemma to $f(A)=\exp \circ (-\log |\!\det A|)$ , we obtain the following corollary.

Corollary 5.5. The mapping $T\in \mathcal {V} \mapsto \exp \circ (-\log |DT\circ \xi _{i,j}(T)|)$ is $C^{k-1}$ .

In the following, consider $\Theta : \mathcal {V} \to L(B^{\rho ,s}, B^{\rho -k,s-k}) $ given by $[\Theta (T)\varphi ](z)=\varphi \circ \xi (T)(z)$ . Consider also $F:\xi (\mathcal {V})\subset C^{a}_b(V,U) \to L(B^{\rho ,s}, B^{\rho -k,s-k})$ defined by $F(S)(\varphi )(z)=\varphi (S(z))$ .

For $\varphi \in B^{\rho ,s}$ , $S\in \xi (\mathcal {V})$ , and $H\in C^{a}_b(V,{\mathbb {R}}^{u+d})$ such that $S+H\in \xi (\mathcal {V})$ , we write

$$ \begin{align*} [F(S+H)\varphi](z) =\bigg[\varphi(S(z))+\sum_{j=1}^{\tilde k}\dfrac{D^{j}\varphi(S(z)).H(z)^j}{j!}\bigg]+R(S,H,z), \end{align*} $$

where $ R(S,H)(\varphi )(z)=\int _{0}^{1} ({(1-t)^{\tilde k}}/{(\tilde k)!}) D^{\tilde k +1}\varphi (S(z)+tH(z)).H(z)^{\tilde k +1}\,dt. $

Lemma 5.6. The mapping $ \omega _j: \xi (\mathcal {V})\to L^{j}_s(C_b^{a}(V,{\mathbb {R}}^{u+d}), L(B^{\rho ,s},B^{\rho -k,s-k})) $ given by

$$ \begin{align*}[\omega_j(S).(H_1,\ldots,H_j)(\varphi)](z)= D^{j}\varphi(S(z)).(H_1(z)\cdots{\kern-1pt},H_j(z)) \end{align*} $$

is continuous for each $j=1,2,\ldots ,\tilde k$ .

Proof. Consider $\tilde H=(H_1,\ldots ,H_j)\in (C_b^{a}(V,{\mathbb {R}}^{u+d})^j$ and write

$$ \begin{align*} &[(\omega_j(S+H)-\omega_j(S)).\tilde H](\varphi)(z) = (D^{j}\varphi(S(z)+H(z))-D^{j}\varphi(S(z))).\tilde H(z). \end{align*} $$

For each multi-index $\alpha $ with $|\alpha |\le a-k$ , we have

$$ \begin{align*} \partial^{\alpha}\kern-1pt[(\omega_j(S\kern1.3pt{+}\kern1.3ptH)\kern1.3pt{-}\kern1.3pt\omega_j(S)).\tilde{H}(\varphi)](z)\kern1pt{=}\kern1.3pt\sum_{\gamma_1+\tilde\gamma=\alpha}\![\partial^{\gamma_1}(D^{j} \varphi(S(z)\kern1.3pt{+}\kern1.3ptH(z))\kern1.3pt{-}\kern1.3ptD^{j}\varphi(S(z))).\partial^{\tilde \gamma}\tilde{H}(z)], \end{align*} $$

where $\tilde \gamma =\gamma _2+\cdots +\gamma _{j+1}$ and $\partial ^{\tilde \gamma }\tilde {H}(z)=(\partial ^{\gamma _2}H_1(z),\ldots ,\partial ^{\gamma _{j+1}}H_j(z))$ .

We can write

$$ \begin{align*} &\partial^{\gamma_1}(D^{j}\varphi(S(z)+H(z))-D^{j}\varphi(S(z))\\ &\quad=\sum_{1\le |\sigma|\le |\gamma_1|}(\partial^{\sigma}(D^{j}\varphi)(S(z)+H(z))-\partial^{\sigma}(D^{j}\varphi)(S(z))) Q_{\sigma,\gamma_1}(S+H;z)\\ &\qquad+ \partial^{\sigma}(D^{j}\varphi)(S(z))(Q_{\sigma,\gamma_1}(S+H;z)-Q_{\sigma,\gamma_1}(S;z)), \end{align*} $$

where $Q_{\sigma ,\gamma _1}(S;z)$ is a polynomial of degree $|\sigma |$ in the derivatives of $S_1, \ldots , S_{u+d}$ of order at most $|\gamma _1|$ .

For $\gamma _1\le \alpha $ and $|\sigma |\le |\gamma _1|$ , define

$$ \begin{align*} A_{S,H,\gamma_1,\sigma}(z)=(\partial^{\sigma} (D^{j}\varphi)(S(z)+H(z))-\partial^{\sigma}(D^{j}\varphi)(S(z))) Q_{\sigma,\gamma_1}(S+H;z) \end{align*} $$

and

$$ \begin{align*} B_{S,H,\gamma_1,\sigma}(z)=\partial^{\sigma}(D^{j}\varphi)(S(z)) (Q_{\sigma,\gamma_1}(S+H;z)-Q_{\sigma,\gamma_1}(S;z)). \end{align*} $$

Using the mean value theorem, we have

$$ \begin{align*} A_{S,H,\gamma_1,\sigma}(z)=\int_{0}^{1} (\partial^{\sigma}(D^{j+1}\varphi)(S(z)+tH(z))H(z))Q_{\sigma,\gamma_1}(S+H;z)\,dt. \end{align*} $$

Then, we can write

$$ \begin{align*} \partial^{\alpha}[(\omega_j(S+H)-\omega_j(S)).\tilde{H}(\varphi)](z) =\sum_{\gamma_1+\tilde\gamma=\alpha}\sum_{1\le |\sigma|\le |\gamma_1|} \mathcal{P}_1(z)+\mathcal{P}_2(z) \end{align*} $$

for $ \mathcal {P}_1(z)=(A_{S,H,\gamma _1,\sigma }(z)).\partial ^{\tilde \gamma }\tilde {H}(z) $ and $ \mathcal {P}_2(z)=(B_{S,H,\gamma _1,\sigma }(z)).\partial ^{\tilde \gamma }\tilde {H}(z). $

Now suppose that $|\alpha |\le \rho -k$ and let $\psi :D_\psi \subset {\mathbb {R}}^d \to {\mathbb {R}}^u$ in $\mathcal {S}$ (as in the definition of $\| \cdot \| _{\rho -k}^{\dagger }$ ) and $\eta :D_\psi \to {\mathbb {R}}$ a $C^{|\alpha |}$ function with compact support and $\| \eta \| _{|\alpha |}\le 1$ . Then

$$ \begin{align*} \int\eta(y)P_1(\psi(y),y)\,dy &=\int_0^1\int[(\eta(y)Q_{\sigma,\gamma_1}(S+H;(\psi(y),y)))\\&\qquad\times([\partial^{\sigma}(D^{j+1}\varphi)(S(\psi(y),y)+tH(\psi(y),y))]H(\psi(y),y))\\&\qquad \times (\partial^{\gamma_2}H_1(\psi(y),y),\ldots,\partial^{\gamma_{j+1}}H_j(\psi(y),y))]\,dy\,dt. \end{align*} $$

Recall that $S(\psi (y),y)+tH(\psi (y),y)=(\tilde \psi (g_t(y)),g_t(y))$ for some diffeomorphism $g_t:D_\psi \to \pi _2\circ (S+tH)(G_{\psi })$ . So, making the change of variable $y=g_t^{-1}(\tilde y)$ and writing $z(\tilde y)=(\psi (g_t^{-1}(\tilde y)),g_t^{-1}(\tilde y))$ , we obtain

$$ \begin{align*} \int\eta(y)P_1(\psi(y),y)\,dy \le K\| \varphi\| _{\rho}^{\dagger}\| H \| _{a}\| H_1\| _{a}\cdots\| H_j\| _{a}. \end{align*} $$

Since $Q_{\sigma ,\gamma _1}(S+H;z)-Q_{\sigma ,\gamma _1}(S;z)$ is bounded by $K \| H \| _a$ , we similarly prove that

$$ \begin{align*} \int\eta(y)P_2(\psi(y),y)\,dy \le K\| \varphi\| _{\rho}^{\dagger}\| H \| _{a}\| H_1\| _{a}\cdots\| H_j\| _{a}. \end{align*} $$

These estimates prove that

(59) $$ \begin{align} \| [(\omega_j(S+H)-\omega_j(S)).\tilde H](\varphi)\| _{\rho-k}^{\dagger}\le K\| \varphi\| _{\rho}^{\dagger}\| H \| _{a}\| H_1\| _{a}\cdots\| H_j\| _{a}. \end{align} $$

Now, for $|\alpha |\le s-k$ , we have

$$ \begin{align*} \| \mathcal{P}_1\| _{L^{2}}^2&=\int\bigg|\int_{0}^{1}D^{j+1} (\partial^{\sigma}\varphi)(S(z)+tH(z))\cdot\tilde H(z)Q_{\sigma,\gamma_1}(S+tH;z)\,dt\bigg|^2 \, dz. \end{align*} $$

Recall $S+tH$ is a diffeomorphism over V for all $t\in [0,1]$ . So, making the changing of variable $\tilde z=(S+tH)(z) $ and observing that $|Q_{\sigma ,\gamma _1}(S+tH;z)|$ is uniformly bounded, we conclude that

$$ \begin{align*}\| \mathcal{P}_1\| _{L^{2}}\le K \| \varphi\| _{H^{s}}\| H \| _a\| H_1\| _a\cdots \| H_j\| _a.\end{align*} $$

Analogously, we can check that

$$ \begin{align*} \| \mathcal{P}_2\| _{L^2} \leq K\| \varphi\| _{H^{s}}\| H \| _a\| H_1\| _a\cdots \| H_j\| _a. \end{align*} $$

Hence, we conclude

(60) $$ \begin{align} \| [(\omega_j(S+H)-\omega_j(S)).\tilde H](\varphi)\| _{H^{s-k}}\le K\| \varphi\| _{H^s}\| H \| _{a}\| H_1\| _{a}\cdots\| H_j\| _{a}. \end{align} $$

Equations (59) and (60) imply the continuity of $\omega _j$ .

Lemma 5.7. Given $S\in \xi (\mathcal {V})$ , we have

$$ \begin{align*} R(S,H)=o(H^{\tilde k}), \quad\text{that is, } \lim_{\| H \| _{r-k}\to 0}\dfrac{\| R(S,H)\| }{\| H \| _{a}^{\tilde k}}=0, \end{align*} $$

where $\| R(S,H)\| =\sup \{\| R(S,H)\varphi \| _{\rho -k,s-k}:\,\| \varphi \| _{\rho ,s}\le 1\}$ .

Proof. Denote $j=\tilde k+1$ , $S_t(z)=S(z)+tH(z)$ , $\hat R_t(z)=(D^{j}\varphi )(S_t(z)).(H(z))^{j}$ , $\tilde {H}=(H_1,\ldots ,H_j)$ , and let $\varphi $ be a function in $B^{\rho ,s}$ .

For $|\alpha |\le a-k$ , we have

$$ \begin{align*} \partial^{\alpha}\hat R_t(z)=\sum_{\gamma_1+\tilde{\gamma}=\alpha}\sum_{1\le |\sigma|\le |\gamma_1|}\partial^{\sigma}(D^{j}\varphi)(S_t(z)).\partial^{\tilde\gamma}\tilde{H}(z)Q_{\sigma,\gamma_1}(S_t;z). \end{align*} $$

Now suppose that $|\alpha |\le \rho -k$ and let $\psi :D_\psi \subset {\mathbb {R}}^d \to {\mathbb {R}}^u$ be in $\mathcal {S}$ (as in the definition of $\| \cdot \| _{\rho -k}^{\dagger }$ ) and $\eta :D_\psi \to {\mathbb {R}}$ a $C^{|\alpha |}$ function with compact support and $\| \eta \| _{|\alpha |}\le 1$ . Then, writing $\hat z(y)=(\psi (y),y)$ , we have

$$ \begin{align*} \int\eta(y)\partial^{\alpha}(R(S,H).\varphi)(\hat z(y))\,dy =\int_{0}^{1}\dfrac{(1-t)^{\tilde k}}{(\tilde k)!}\int\eta(y)\partial^{\alpha}\hat R_t(\hat z(y))\,dy\,dt. \end{align*} $$

Recall that $S_t(\psi (y),y)=(\tilde \psi (g_t(y)),g_t(y))$ for some diffeomorphism $g_t:D_\psi \to \pi _2\circ (S_t)(G_{\psi })$ . So, making the changing of variable $y=g_t^{-1}(\tilde y)$ and writing $ z(\tilde y)=(\psi (g_t^{-1}(\tilde y)),g_t^{-1}(\tilde y))$ , we obtain for each integral $\int \eta (y)\partial ^{\alpha }\hat R_t(\hat z(y))\,dy$ the estimate

$$ \begin{align*} \int\partial^{\sigma}(D^{j}\varphi)(\tilde\psi(\tilde y),\tilde y).\partial^{\tilde\gamma}\tilde{H}(z(\tilde y))Q_{\sigma,\gamma_1}(S_t;z(\tilde y))\,d\tilde y \le K\| \varphi\| _{\rho}^{\dagger}\| H \| _{a}^{j}. \end{align*} $$

Then

$$ \begin{align*} \int_{[-K,K]^{d}}\eta(y)\partial^{\alpha}(R(S,H).\varphi)(\hat z(y))\,dy\le K\| \varphi\| _{\rho}^{\dagger}\| H \| _{a}^{j}, \end{align*} $$

what means that

(61) $$ \begin{align} \| (R(S,H).\varphi)\| _{\rho-k}\le K\| \varphi\| _{\rho}^{\dagger}\| H \| _{a}^{j}. \end{align} $$

For $|\alpha |\le s-k$ , we have

$$ \begin{align*} \| \partial^{\alpha}(R(S,H).\varphi)\|_{L^2}^{2}\le K\! \int\! \bigg(\!\int_{0}^{1}\kern-2pt\partial^{\alpha}\hat R_t(z)\,dt\bigg)^2\,dz \le K \int_{[0,1]^2}\kern-1pt \| \partial^{\alpha}\hat R_t\| _{L^2}\| \partial^{\alpha}\hat R_{\tilde t}\| _{L^2}\,dt\,d\tilde t. \end{align*} $$

This implies that

(62) $$ \begin{align} \| (R(S,H).\varphi)\| _{H^{s-k}}\le K \| \varphi\| _{H^s}\| H \| _{a}^{j}. \end{align} $$

Putting together equations (61) and (62), the claim follows.

Lemma 5.8. The mapping $\Theta : \mathcal {V} \to L(B^{\rho ,s}, B^{\rho -k,s-k}) $ , given by $[\Theta (T)\varphi ](z)=\varphi \circ \xi (T)(z)$ , is of class $C^{\tilde k}$ , where $\tilde k=\min \{k-1,r-\rho -1, r-s-1\}$ . In particular, $G_{i,j}:\mathcal {V} \to L(B^{\rho ,s},B^{\rho -k,s-k})$ given by $G_{i,j}(T)\varphi =(\varphi \circ \xi _{i,j}(T))\vartheta _{j}$ is $C^{\tilde k}$ .

Proof. Define $a=\max \{\rho ,s\}$ , since $\xi $ is $C^{r-a}$ and $\Theta (T)=F\circ \xi (T)$ , it is sufficient to prove that F is $C^{\tilde k}$ . According to [23, Theorem 1.4] (converse of Taylor Formula), to prove that F is $C^{\tilde k}$ , it is sufficient to prove that each $\omega _j$ is continuous and $ R(S,H)=o(H^{\tilde k})$ , and this is exactly what was proved in the previous two lemmas.

Finally, it follows the differentiability of the transfer operator (Proposition 5.2).

Proof of Proposition 5.2

Let a be the maximum of $\rho $ and s. Observe that $\Psi _{(i,j)}(T)=F_{i,j}(T)G_{i,j}(T),$ where $F_{i,j}:\mathcal {V}\to C_b^{a}(B_j,U_{i,j}) $ is given by $F_{i,j}(T)=\exp \circ (-\log |DT\circ \xi _{i,j}(T)|)$ and $G_{i,j}:\mathcal {V} \to L(B^{\rho ,s},B^{\rho -k,s-k})$ is given by $G_{i,j}(T)\varphi =(\varphi \circ \xi _{i,j}(T))\vartheta _{j}.$ From Corollary 5.5, $F_{i,j}$ is $C^{r-a-1}$ and so is $C^{\tilde k}$ and, from Lemma 5.8, $G_{i,j}$ is $C^{\tilde k}$ , then we conclude that $\Psi _{i,j}$ is $C^{\tilde k}$ .

5.2 Differentiability of the resolvent

In the following, we will prove the differentiability of the resolvent $(zI-{\mathcal L}_{T})^{-1}$ with respect to $T=T(E,C)$ . Notice that ${\mathcal {R}(z)=(zI-{\mathcal L}_{T})^{-1}}$ is the inverse of the operator $zI-{\mathcal L}_{T}$ , but we are going to look to $\mathcal {R}(z)$ as a linear mapping from $\mathcal {B}^{\rho ,s} $ to $\mathcal {B}^{\rho -k,s-k} $ .

We prove this step in a more abstract setting, as in [24, Theorem 8.1]. Consider $q \geq 2$ , $\mathcal {B}^{0} \supset \dots \supset \mathcal {B}^{q}$ Banach spaces, I a Banach manifold, and $\{L_{t}\}_{t \in I}$ a family of bounded linear operators acting on each of the Banach spaces $\mathcal {B}^{i}$ and such that $I \ni t \mapsto L_{t} \in L(\mathcal {B}^{1}, \mathcal {B}^{0})$ is continuous. Assume that there exist constants $M>0$ and $\alpha < M$ such that for every $t \in I$ and $g\in \mathcal {B}^0$ :

(63) $$ \begin{align} \| L_{t}^{n}g\| _{\mathcal{B}^{0}} \leq C M^{n}\| g\| _{\mathcal{B}^{0}} \end{align} $$

and

(64) $$ \begin{align} \| L_{t}^{n}g\| _{\mathcal{B}^{1}} \leq C \alpha^{n}\| g\| _{\mathcal{B}^{1}} + C M^{n}\| g\| _{\mathcal{B}^{0}}. \end{align} $$

The continuity of the resolvent follows immediately from Liverani and Keller [30]: let $L_t$ be as above and suppose that $L_t \to L_{t_0}$ as $t \to t_0$ , then $(z- L_t)^{-1} \to (z- L_{t_0})^{-1} $ as $t \to t_0$ , where we see all operators acting from ${\mathcal B}^q$ to ${\mathcal B}^0$ .

Now we will deduce a differentiability result. For this, we can suppose, without loss of generality, that I is a neighborhood of $t_0=0$ in a Banach space. Denote also $L(\mathcal {B}^{i}, \mathcal {B}^{i-j})$ the space of bounded linear transformations from $B^{i}$ to $B^{i-j}$ .

For $\varrho> \alpha $ and $\delta>0$ , denote $V_{\varrho ,\delta }$ the set of complex numbers z such that $|z| \geq \varrho $ and, for all $1 \leq k \leq q$ , the distance from z to the spectrum of $L_0$ acting on $\mathcal {B}^k$ is greater than $\delta $ .

Theorem 5.9. Suppose that $L_t \to L_{0}$ and $(z- L_t)^{-1} \to (z- L_{0})^{-1}$ as $t \to 0$ (as operators acting from ${\mathcal B}^q$ to ${\mathcal B}^0$ ). Suppose that there exists $ Q_1: I \to {\mathcal L}(I; {\mathcal L}({\mathcal B}^q; {\mathcal B}^0))$ , $Q_2: I \to {\mathcal L}^{(2)}(I^2; {\mathcal L}({\mathcal B}^q; {\mathcal B}^0))$ , $\ldots $ , $Q_q: I \to {\mathcal L}^{(q)}(I^q; {\mathcal L}({\mathcal B}^q; {\mathcal B}^0)) $ continuous maps that are respectively the jth-derivatives of $L_t$ , for $j=1,2,\ldots ,q$ . Assume that for all i, $j\leq i \leq q$ , we have that $Q_{i}: I \to L^{(i)}(I^i; L(\mathcal {B}^{i} , \mathcal {B}^{i - j}))$ is uniformly bounded.

Then $(z,t) \in V_{\varrho ,\delta } \times I \to (z- L_t)^{-1} \in L(\mathcal {B}^q,\mathcal {B}^0)$ is $C^{q-1}$ .

Proof. It follows from [24, Theorem 8.1].

Remark 5.10. Under the same hypothesis of Theorem 5.9, it also follows from the calculations above that if $T_{i|(t,z)}$ denotes the ith derivative of $I \times V_{\varrho ,\delta } \ni (t,z) \mapsto (z - L_{t})^{-1} \in L(\mathcal {B}^{q} , \mathcal {B}^{0})$ in $(t , z)$ , then for fixed $t \in I$ , we have that

$$ \begin{align*} \frac{\|T_{i|(t+h_{1},z+h_{2})} - T_{i|(t,z)} - T_{i+1|(t , z)}\cdot (h_{1} , h_{2})\|}{\|(h_{1}, h_{2})\|} \end{align*} $$

converges to 0 uniformly in $z \in V_{\varrho ,\delta }$ , when $(h_{1} , h_{2})$ converges to 0.

5.3 Proof of Theorem D $^{\prime }$

Proof of the Theorem D $^{\prime }$

Consider $\rho _0 = s + \lfloor ({u+d})/{2} \rfloor + 1$ and $\rho _1< \rho _0$ as in the proof of Theorem C $^{\prime }$ . Then ${\mathcal L}$ has a spectral gap with a uniform bound for the essential spectral radius in a neighborhood of $(E,C)$ .

Actually, let $\zeta \in (0,1)$ and $K_3>0$ be as in the third Lasota–Yorke inequality (Proposition 3.5) for the Banach spaces $\mathcal {B}=\mathcal {B}^{\rho _0,s}$ and $\mathcal {B}'=\mathcal {B}^{\rho _1,0}$ . Fixing some $\tilde {\zeta }\in (\zeta ,1)$ , we consider $n_0$ large enough such that $K_3 \zeta ^{n_0} < \tilde {\zeta }^{n_0}$ , so equation (28) is valid for this fixed integer $n_0$ . Since $(E,C) \to {\mathcal L}_{T(E,C)}$ is continuous, we see that equation (28) is valid for the integer $n_0$ with the same constants for every $(\tilde {E},\tilde {C})$ in a neighborhood $\mathcal {V}$ of $(E,C)$ in $C^r({\mathbb {T}^u}) \times C^r({\mathbb {T}^u} \times {\mathbb {R}}^d)$ , then the theorem of Hennion implies that every ${\mathcal L}_{T(\tilde E,\tilde C)}$ has spectral gap with essential radius bounded by $\tilde {\zeta }$ for every $( \tilde E,\tilde C) \in \mathcal {V}$ . We keep denoting $(E,C)$ for any element in $\mathcal {V}$ .

Recall that the spectral radius of ${\mathcal L}_{T(E,C)}$ is equal to $1$ for every $(E,C) \in \mathcal {V}$ , by Remark 4.7. Consider $\delta>0$ small and $\varrho \in (\tilde \zeta + \delta , 1 - \delta )$ . Fix a closed $C^{\infty }$ -curve $\gamma $ contained in $V_{\varrho ,\delta }$ such that the bounded connected component determined by $\gamma $ contains the spectral radius $1$ and the unbounded connected component contains the ball centered in $0\in {\mathbb {C}}$ with radius $\tilde {\zeta }$ (which contains the rest of the spectrum of ${\mathcal L}_{T(E,C)}$ for any $(E,C) \in \mathcal {V}$ ). If $\Pi _{T(E,C)}$ is the spectral projection of $\mathcal {L}_{T(E,C)}|\mathcal {B}$ associated to its spectral radius, we know that

(65) $$ \begin{align} \Pi_{T(E,C)} = \frac{1}{2\pi i}\int_{\gamma}(zI - \mathcal{L}_{T(E,C)})^{-1}\,dz \end{align} $$

for all $(E,C) \in \mathcal {V}$ .

Consider the Banach spaces

(66) $$ \begin{align} \mathcal{B}^0 = \mathcal{B}^{\rho_1,0} (=\mathcal{B}), \,\, \mathcal{B}^1=\mathcal{B}^{\rho_0,s} (=\mathcal{B}'),\quad \text{and}\quad \mathcal{B}^j=\mathcal{B}^{\rho_0+j-1,s+j-1}\quad \kern-1.2pt \text{for all } 1 {\kern-1pt}\leq{\kern-1pt} j {\kern-1pt}\leq{\kern-1pt} q_{0}, \end{align} $$

the Banach manifold $I=\mathcal {V}$ , denote $t=(E,C)$ and $L_t= {\mathcal L}_{T(E,C)}$ . We consider $q_0$ such that $\rho _0 + q_{0} - 1 = r-1$ , that is, $q_{0}=r-\rho _0 = r - s - \lfloor ({u+d})/{2} \rfloor - 1$ .

Notice that equations (63) and (64) are valid since ${\mathcal L}_{T(E,C)}$ is uniformly bounded for every $(E,C)\in \mathcal {V}$ due to the choices of $\mathcal {V}$ , $\mathcal {B}^0=\mathcal {B}$ , and $\mathcal {B}^1=\mathcal {B}'$ , then we can apply Theorem 5.9 and Remark 5.9 due to Proposition 6.1, it follows that

$$ \begin{align*}\mathcal{V} \times \gamma \ni (E,C,z) \to (zI - \mathcal{L}_{T(E,C)})^{-1} \in L(\mathcal{B}^{q_{0}} , \mathcal{B}^{0})\end{align*} $$

is $C^{q_0 - 1}$ and that the rest of the $C^{q_0 -1 }$ -differentiability goes to 0 uniformly with respect to $z \in \gamma $ , when we fix $(E,C) \in \mathcal {V}$ .

So $\mathcal {V} \ni (E,C) \mapsto \Pi _{T(E,C)} \in L(\mathcal {B}^{q_0} , \mathcal {B}^{0})$ is $C^{r - s -\lfloor ({u+d})/{2}\rfloor - 2}$ .

Fixing a non-negative $C^{\infty }$ function h that is positive in ${\mathbb {T}}^u \times [-K,K]^d$ and ${\int h\, dm =1}$ , we have that $h_{T(E,C)} = \Pi _{T(E,C)}(h)$ , which finishes the proof of Theorem D $^{\prime }$ .

6 Differentiability of thermodynamical quantities for potentials close to $P_0$

In the continuation, we will also consider perturbations with respect to the potential ${P \in C^{r-1}(D)}$ .

6.1 Analyticity of the transfer operator with respect to the potential

We want to perturb the transfer operator also with respect to some potential $\psi \in C^{r-1}$ . The differentiability of the transfer operator with respect to the potential is ever better, since this mapping is analytic.

Theorem 6.1. Let $r\geq 1$ , $k \leq \rho \leq r$ , and $k \leq s \leq r$ , then the mapping

$$ \begin{align*} C^{r-1}({\mathbb{T}^u} \times {\mathbb{R}}^d, {\mathbb{R}}) &\to L(\mathcal{B}^{\rho,s}, \mathcal{B}^{\rho-k, s-k})\\P & \mapsto {\mathcal L}_{(T,P)} \end{align*} $$

is analytic.

Proof. Notice that for $P, H\in C^{r-1}({\mathbb {T}^u} \times {\mathbb {R}}^d, {\mathbb {R}})$ and $\varphi \in \mathcal {B}^{\rho ,s}$ :

(67) $$ \begin{align} \mathcal{L}_{T,P+H}(\varphi)(x) = \mathcal{L}_{T,P}(e^H \varphi)(x)= \sum_{j=0}^{\infty} \frac{1}{j!} \mathcal{L}_{T,P}(H^j\varphi)(x). \end{align} $$

Now using that

$$ \begin{align*} \| \mathcal{L}_{T,P}(H^j\varphi)\| ^{\dagger}_{\rho-k}\le K \| H^j\| _{C^{r-1}}\| \varphi\| ^{\dagger}_{\rho-k}\le K^j \| H \| ^j_{C^{r-1}}\| \varphi\| ^{\dagger}_{\rho-k} \end{align*} $$

and

$$ \begin{align*} \| \mathcal{L}_{T,P}(H^j\varphi)\| _{H^{s-k}}\le K \| H^j\| _{C^{r-1}}\| \varphi\| ^{\dagger}_{H^{s-k}}\le K^j \| H \| ^j_{C^{r-1}}\| \varphi\| _{H^{s-k}} \end{align*} $$

for some $K>0$ , we have that

$$ \begin{align*} \bigg\| \sum_{j=0}^{\infty} \frac{1}{j!} \mathcal{L}_{T,P}(H^j\varphi)\bigg\| _{\rho-k,s-k}\le e^{{K\| H\| _{C^{r-1}}}}\| \varphi\| _{\rho-k,s-k}. \end{align*} $$

Denote by $\mathcal {S}^j$ the space of symmetric j-linear maps from $C^{r-1}({\mathbb {T}^u} \times {\mathbb {R}}^d, {\mathbb {R}})^j$ to $L(\mathcal {B}^{\rho ,s}, \mathcal {B}^{\rho -k, s-k})$ .

The map $P\in C^{r-1}({\mathbb {T}^u} \times {\mathbb {R}}^d, {\mathbb {R}}) \mapsto \Psi (P) \in \mathcal {S}^j$ given by $\Psi (P)(H_1, \ldots , H_j)(H)=\mathcal {L}_{T,P}(H_1\cdots H_j H)$ is clearly continuous. Moreover, for each integer J, it is valid that

$$ \begin{align*} & \sup_{\| \varphi\| _{\rho,s}\le 1} \bigg\| \mathcal{L}_{T,P+H}(\varphi) - \sum_{j=0}^{J} \frac{1}{j!} \mathcal{L}_{T,P}(H^j\varphi)\bigg\| _{\rho-k,s-k} \\ &\qquad=\sup_{\| \varphi\| _{\rho,s}\le 1} \bigg\| \sum_{j=J+1}^{\infty} \frac{1}{j!} \mathcal{L}_{T,P}(H^j\varphi)\bigg\| _{\rho-k,s-k}\le {K^{J+1}}\| H \| _{C^{r-1}}^{J+1}e^{K\| H \| _{C^{r-1}}}. \end{align*} $$

From [23, Theorem 1.4] (converse of Taylor’s theorem), we conclude that $\mathcal {L}_{T,P}$ is of class $C^{J}$ for every J non-negative integer and

$$ \begin{align*} D^j_P\mathcal{L}_{T,P}(H,\ldots,H)(\varphi)=\mathcal{L}_{T,P}(H^j\varphi). \end{align*} $$

The same argument proves that $\mathcal {L}_{T,P}$ is analytic.

Putting together Theorems 5.1 and 6.1, we obtain the following corollary.

Corollary 6.2. Let $r\geq 1$ , $k\geq 1$ be an integer such that $k \leq \rho \leq r-1$ and $k \leq s \leq r-1$ , then the mapping

$$ \begin{align*} \Psi:\mathcal{K} \times C^{r-1}({\mathbb{T}^u} \times {\mathbb{R}}^d, {\mathbb{R}}) &\to L(B^{\rho,s}, B^{\rho-k,s-k})\\ (T,P) &\mapsto \mathcal{L}_{T,P} \end{align*} $$

is $C^{\tilde k}$ , where $\tilde k=\min \{k-1,r-\rho -1, r-s-1\}$ .

Proof. We use the equality

$$ \begin{align*}{\mathcal L}_{(T,P)}(\varphi)={\mathcal L}_{(T,\Theta(T))}(e^{P-\Theta(T)}\varphi),\end{align*} $$

where $\Theta (T)=-\log |\!\det DT|$ is the geometric potential of T. The result follows since $T\mapsto {\mathcal L}_{(T,\Theta (T))}$ is of class $C^{\tilde k}$ by Theorem 5.1, $X \mapsto e^{X}$ is analytic, and $T \in C^r({\mathbb {T}^u} \times {\mathbb {R}}^d) \mapsto P(T) = - \log |\!\det DT| \in C^{r-1}({\mathbb {T}^u} \times {\mathbb {R}}^d,{\mathbb {R}})$ is of class $C^\infty $ .

6.2 Regularity of the quantities with respect to other smooth potentials (Proof of Theorem E $^{\prime }$ )

As a consequence of the analyticity of the operator with respect to the potential, it follows similarly the regularity of the eigenfunction h, the eigenmeasure $\nu $ , the spectral radius $\unicode{x3bb} $ , etc., as stated in Theorem E $^{\prime }$ .

Proof of Theorem E $^{\prime }$

The proof of this theorem is similar to the proof of Theorem D $^{\prime }$ . We consider the same $\rho _1<\rho _0$ and, analogously, we see that ${\mathcal L}_{T(\tilde {E},\tilde {C}, \tilde {P})}$ has spectral gap with essential spectral radius bounded by $\tilde {\zeta }$ and a single dominant eigenvalue $\unicode{x3bb} _{(\tilde {E},\tilde {C}, \tilde {P})}$ close to $1$ for every $(\tilde {E},\tilde {C}, \tilde {P})$ in a neighborhood $\mathcal {W}$ of $(E,C,P_0)$ . We keep denoting $(\tilde {E},\tilde {C}, \tilde {P})$ as $(E,C,P)$ . Corollary 6.2 implies that the transfer operator is differentiable with respect to $(E,C,P)$ .

As before, we fix a closed curve $\gamma $ in $V_{\varrho , \delta }$ whose bounded component contains the spectral radius $\unicode{x3bb} _{(E,C,P)}$ and whose unbounded component contains the rest of the spectrum for every $(E,C,P)\in \mathcal {W}$ . Consider the spectral projection

(68) $$ \begin{align} P_{(E,C,P)} = \frac{1}{2\pi i}\int_{\gamma}(zI - \mathcal{L}_{T(E,C),P})^{-1}\,dz. \end{align} $$

So the spectral projection $\Pi _{T(E,C),P}$ is differentiable with respect to the map and the potential, that is,

$$ \begin{align*}\mathcal{W} \ni (E,C,P) \to \Pi_{T(E,C),P} \in L(\mathcal{B}^{q_0},\mathcal{B}^0)\end{align*} $$

is $C^{r - s -\lfloor ({u+d})/{2}\rfloor - 2}$ .

Fixing a function h as before and some $x_0$ with $ \Pi _{T(E,C),P}(h)(x_0) \neq 0$ , we have that

So they are also of class $C^{r - s -\lfloor ({u+d})/{2}\rfloor - 2}$ . It was proved in Proposition 4.8 that $\mu $ is actually invariant.

The differentiability of the Lyapunov exponent functions and of the mean $m_{(T,P)}$ follow immediately. The differentiability of the variance $\sigma _{(T,P)}^2$ follows in identical lines to [14, Corollary C and Theorem D].

7 Genericity of the transversality condition (Proof of Theorem F)

In this section, we prove Theorem F.

Given functions $\phi _1,\ldots , \phi _s \in C^\infty ({\mathbb {T}^u}, {\mathbb {R}}^d)$ and a parameter ${\textbf {t}}=(t_1,\ldots ,t_s) \in {\mathbb {R}}^s$ , we consider the corresponding $ C_{{\textbf {t}}}(x,y) := C(x,y) + \sum _{k=1}^{s} t_{k} \phi _{k} (x)$ , $ T_{\textbf {t}}:= T(E,C_{\textbf {t}})$ , and $ S(x,({\textbf {a}},y);{\textbf {t}}) := C_{\textbf {t}}( [{\textbf {a}}]_1(x), C_{\textbf {t}}([{\textbf {a}}]_2(x),\ldots ,C_{\textbf {t}}([{\textbf {a}}]_n(x),y)) \cdots ) $ for ${\textbf {a}}\in I^{n}(x)$ , $1\leq n <\infty $ .

Given points $x \in {\mathbb {T}^u}$ , sequences $\sigma = ({\textbf {a}}_{0}, {\textbf {a}}_{1}, \ldots , {\textbf {a}}_{\kappa })$ of $\kappa +1$ words in $I^{q}(x)$ , $q\leq +\infty $ , and $\gamma = (y_{0}, y_{1}, \ldots , y_{\kappa })$ of $\kappa +1$ points in ${\mathbb {R}}^d$ , we consider the mapping $\psi _{x,\sigma ,\gamma }:{\mathbb {R}}^{s}\rightarrow (M(d\times u))^\kappa $ defined by

(69) $$ \begin{align} \psi_{x,\sigma,\gamma}({\textbf{t}}) = ( D S(x,({\textbf{a}}_{i},y_i);{\textbf{t}}) - D S(x,({\textbf{a}}_{0},y_0);{\textbf{t}}) )_{i=1,\ldots,\kappa}. \end{align} $$

The Jacobian $\operatorname {Jac} \psi _{x,\sigma ,\gamma }({\textbf {t}})$ is the supremum of the Jacobian of the restrictions of $\psi _{x,\sigma ,\gamma }$ to $\kappa $ -dimensional subspaces:

(70) $$ \begin{align} \operatorname{Jac} (\psi_{x,\sigma,\gamma})({\textbf{t}}) = \sup_{\dim L=\kappa du} {|\!\det D_{\textbf{t}}\psi_{x,\sigma,\gamma} |_{L} ({\textbf{t}}) | }. \end{align} $$

Definition 7.1. For every integer $n\geq 1$ , we say that the family $T_{{\textbf {t}}}$ is $(n,\eta )$ -generic on $W\subset {\mathbb {T}^u} \times {\mathbb {R}}^d$ if the following holds: for any $(x,z) \in W$ , every $D\geq n^3$ , every $q> n$ , every sequence $({\textbf {a}}_{0},{\textbf {a}}_{1},\ldots ,{\textbf {a}}_{D})$ of $D+1$ words in $I^{q}(x)$ , and every sequence $(\tilde y_0, \tilde y_1,\ldots ,\tilde y_D)$ of points in $[-K_0,K_0]^d$ such that $[{\textbf {a}}_{0}]_{n},\ldots , [{\textbf {a}}_D]_n$ are mutually distinct, $(x,S(x,({\textbf {a}}_i,y_i))) \in W$ , and $\| S(x,({\textbf {a}}_i,y_i)) - z\| \leq \eta $ , taking $\kappa =\lfloor ({D}/{2n})\rfloor $ , there exists a subsequence $\sigma =({\textbf {b}}_{0}, {\textbf {b}}_{1}, \ldots , {\textbf {b}}_{\kappa })$ of $({\textbf {a}}_0,\ldots ,{\textbf {a}}_D)$ of length $\kappa + 1 $ such that ${\textbf {b}}_{0}={\textbf {a}}_{0}$ and for the corresponding subsequence of points $\gamma = (y_0,y_1,\ldots ,y_\kappa )$ , it is valid that $\operatorname {Jac} (\psi _{x,\sigma ,\gamma })(\textbf {t})>\tfrac 12$ for every ${\textbf {t}}\in B(0,\eta )$ .

The proof of Theorem F is divided into two parts: one corresponds to the construction of functions $\phi _1,\ldots ,\phi _s$ for which the family $T_{\textbf {t}}$ is n-generic for some large value of n (Proposition 7.2) and the other to check that the transversality condition is valid for almost every parameter ${\textbf {t}}$ in a neighborhood of $0$ for generic families (Proposition 7.3).

Proposition 7.2. Given $u\geq d$ , $E\in \mathcal {E}^r(u)$ , $C\in \mathcal {C}^r(u,d)$ , there exists an integer $n_0$ such that for every $n \geq n_0$ , there exist functions $\phi _k \in C^{\infty }({\mathbb {T}^u},{\mathbb {R}}^d)$ , $1\leq k \leq s$ , a neighborhood W of $\Lambda $ , and a constant $\eta>0$ such that the corresponding family $T_{{\textbf {t}}}$ is $(n,\eta )$ -generic on W.

In this section, we will denote $\tau _M$ as $\tau _{M,(E,C)}(q)$ to emphasize its dependence on $(E,C)$ . Define the set

(71) $$ \begin{align} \mathcal{NT}_{\beta}^{M} := \bigg\{ C \in C^r({\mathbb{T}^u} \times {\mathbb{R}}^d, {\mathbb{R}}^d) , \underset{q\to\infty}{\limsup} \frac{1}{q}\log \tau_{M,(E,C)}(q)> \log \beta \bigg\}. \end{align} $$

Proposition 7.3. Given integers $u\ge d $ , $E\in \mathcal {E}^r(u)$ , and $C\in \mathcal {C}^r(s,d,E)$ , there exist $C^\infty $ -functions $\phi _k:{\mathbb {T}}^u \to {\mathbb {R}}^d$ , $k=1,2,\ldots , s$ , a constant $M \in (0,1)$ , and $\eta>0$ such that for any $(n, \eta )$ -generic family $T_{\textbf {t}}$ , the set of parameters ${\textbf {t}}=(t_1,t_2,\ldots ,t_s)$ such that $f_{\textbf {t}} \notin \mathcal {NT}_{\beta }^{M}$ has full Lebesgue measure in $B(\textbf {0},\eta )$ for .

This section is dedicated to the proof of the two propositions above.

7.1 The construction of generic families

As in [12, §4], it is easy to see by compactness that Proposition 7.2 is immediate from a local version of it, so it is enough to prove the following proposition.

Proposition 7.4. (Local version of Proposition 7.2)

Given $u\geq d$ , $E\in \mathcal {E}^r(u)$ , $C\in \mathcal {C}^r(u,d)$ , for every point $p_0=(x_0,y_0)\in \Lambda $ , there exists an integer $n_0$ such that for every $n \geq n_0$ , there exist a neighborhood $U_{p_0}$ of $p_0$ , functions $\phi _k \in C^{\infty }({\mathbb {T}^u},{\mathbb {R}}^d)$ , $1\leq k \leq s$ , and a constant $\eta _{p_0}$ such that the corresponding family $T_{{\textbf {t}}}$ is $(n,\eta _{p_0})$ -generic on $U_{p_0}$ .

Proof of Proposition 7.4

Consider integers $ \nu (n), n_0$ and a constant $\epsilon (n)$ such that

(72) $$ \begin{align} ( 1 - 4\, du N^n \epsilon(n))^{N^n ud}> \frac{1}{2}, \end{align} $$

(73) $$ \begin{align} \displaystyle n+\nu(n)+2 < \frac{n^2}{3} < \bigg\lfloor \frac{n^3}{n+1} \bigg\rfloor - \bigg\lfloor \frac{n^3}{2n} \bigg\rfloor < \bigg\lfloor \frac{D}{n+1} \bigg\rfloor - \bigg\lfloor \frac{D}{2n} \bigg\rfloor \end{align} $$

for every $ n\geq n_0$ and every $D\geq n^3$ . We also suppose that $\overline {\mu }^{n_0}>6$ and that

(74) $$ \begin{align} K_4(n) \sum_{i>n+\nu(n)} (\overline{\unicode{x3bb}}^i + \underline{\mu}^{-i}) \leq \epsilon(n) \end{align} $$

for $K_4(n){\kern-1pt}={\kern-1pt}\underline {\unicode{x3bb} }^{-n+1}{\kern-2pt} \max \{ 4(1{\kern-1.5pt}-{\kern-1pt}\overline {\unicode{x3bb} })^{-1}{\kern-1pt}\| C\| _{C^2} (\| D_xC\| {\kern-1pt}+{\kern-1pt} 2N^nud \overline {\mu }^n ), 4(1{\kern-2pt}-{\kern-1pt}\overline {\unicode{x3bb} }^{-1}{\kern-1pt}\| C\|_{C^2}{\kern-1pt}+{\kern-1pt}2\overline {\mu }^n )\}.$

Given a point $x\in {\mathbb {T}^u}$ , and integer $n\in {\mathbb {N}}$ and a word ${\textbf {b}}\in I^n(x)$ , define

(75) $$ \begin{align} \mathcal{E}({\textbf{b}},x)=\{ {\textbf{a}} \in I^n(x), E^{i}({\textbf{b}}(x))={\textbf{a}}(x) \text{ for some } i\geq 0\}. \end{align} $$

For $\nu =\nu (n)$ as above, we consider $\epsilon _0=\epsilon _0(n)>0$ small such that $\epsilon _0 < \gamma $ and

(76) $$ \begin{align} E^{i}(B({\textbf{b}}(x), \epsilon_{0}))\cap B({\textbf{a}}(x), \overline{\mu}^{n+\nu}\epsilon_{0})\neq \emptyset \quad\text{only if } E^{i}({\textbf{b}}(x))={\textbf{a}}(x) \end{align} $$

for every $0\leq i \leq n+\nu $ and ${\textbf {a}}, {\textbf {b}}\in I^{\infty }(x)$ .

Notice that if ${\textbf {a}}(x)\neq {\textbf {b}}(x)$ for ${\textbf {a}},{\textbf {b}}\in I^{n}(x)$ , then, in particular, $B({\textbf {b}}(x), \epsilon _{0})\cap B({\textbf {a}}(x), \| E\| ^{n+\nu }\epsilon _{0}) = \emptyset .$ So, by the choice of $\epsilon _0$ , the distance between $B({\textbf {b}}(x), \epsilon _{0})$ and $B({\textbf {a}}(x), \epsilon _{0})$ is at least $(\overline {\mu }^{n+\nu }-2)\epsilon _0>4\epsilon _0$ .

In the following, denote by $E_{i',j'}$ the elementary matrix that has entry $1$ in the intersection of the $i'$ th line row and the $j'$ th column, and has all the other entries equal to $0$ .

For each ${\textbf {a}}\in I^{n}(x_0)$ and $p_0 = (x_0,y_0) \in T^n(D) $ , we consider the unique $y_n=y_n^{\textbf {a}}(x_0,y_0) \in {\mathbb {R}}^d$ such that $T^n({\textbf {a}}(x_0),y_n) = (x_0,y_0)$ . For $1\leq i' \leq d$ , $1 \leq j' \leq u$ , we consider a $C^\infty $ function $\phi ^{{\textbf {a}}}_{i',j'}:{\mathbb {T}^u}\rightarrow {\mathbb {R}}^d$ such that:

• • $\phi ^{{\textbf {a}}}_{i',j'}$ is supported in $B( {\textbf {a}}(x_0), \overline {\mu }^{-n} \epsilon _0)$ ;

• • $D \phi ^{{\textbf {a}}}_{i',j'} ({\textbf {a}}(x_0)) = (\prod _{j=1}^{n-1} D_yC([{\textbf {a}}]_j(x_0), y_j^{\textbf {a}}(x_0,y_0)))^{-1} E_{i',j'} DE^{n}({\textbf {a}}(x_0))$ ;

• • $\| D \phi ^{{\textbf {a}}}_{i',j'} (x)\| < 2 \underline {\unicode{x3bb} }^{-n+1} \overline {\mu }^{n} $ for every $x\in B( {\textbf {a}}(x_0), \overline {\mu }^{-n} \epsilon _0)$ ;

• • $\| \phi ^{{\textbf {a}}}_{i',j'} \| \leq 4 \underline {\unicode{x3bb} }^{-n+1}$ ,

where $y_j^{\textbf {a}}(x_0,y_0) = C_{[{\textbf {a}}]_{j+1}(x_0)}\circ \cdots \circ C_{{\textbf {a}}(x_0)}(y_0)$ .

Define $U_{x_0}:= B(x_0,(\underline {\mu }^{-1}\bar {\mu })^{-n}\epsilon _0/3)$ . For every $x\in U_{x_0}$ , there exists a bijection $\Phi _{x_0,x}:I^\infty (x_0)\to I^\infty (x)$ given by $\Phi _{x_0,x}({\textbf {a}})=\hat {{\textbf {a}}}=(\hat {a}_j)_{j=1}^\infty $ such that $\hat {a}_j = \pi ( h_{j,x_0}^{{\textbf {a}}}(x))$ , where $h_{j,x_0}^{{\textbf {a}}}$ is the inverse branch of $E^j$ that sends $x_0$ into $[a]_j(x_0)$ .

An important consequence of the construction of the $\phi ^{{\textbf {a}},y}_{i',j'}$ is the following lemma.

Lemma 7.5. Given a sequence $\sigma =({\textbf {a}}_{0},{\textbf {a}}_{1},\ldots ,{\textbf {a}}_{D})$ in $ I^{q}(x_0)$ with ${[{\textbf {a}}_{0}]_{n}, \ldots , [{\textbf {a}}_D]_n}$ distinct, $q \leq +\infty $ , and $\kappa =\lfloor ({D}/{2n})\rfloor $ , there exists a subsequence $\hat {\sigma }=({\textbf {b}}_0,{\textbf {b}}_1,\ldots ,{\textbf {b}}_\kappa )$ in $I^q(x_0)$ , with ${\textbf {b}}_0={\textbf {a}}_0$ , such that

(77) $$ \begin{align} \phi^{[{\textbf{b}}_{l'}]_n}_{i',j'}([\Phi_{x_0,x}({\textbf{b}}_l)]_i(x)) = 0 \end{align} $$

for every $x\in B(x_0,\epsilon _0)$ , $1\leq l' \leq \kappa $ , $1\leq i' \leq u$ , $1 \leq j' \leq d$ , $0 \leq l \leq \kappa $ , $l\neq l'$ , and $i=0,1,\ldots ,n+\nu $ . Moreover, for $l=l'$ , equation (77) holds if $i\neq n$ .

Proof. The proof is the very same of [12, Lemma 4.5] and follows as consequence of equation (76) and of the supports of $\phi ^{\textbf {a}}_{i',j'}$ .

Given any sequence $({\textbf {a}}_0,{\textbf {a}}_1,\ldots ,{\textbf {a}}_D)$ in $I^\infty (x)$ with $[{\textbf {a}}_i]_n$ distinct, we consider ${\hat {{\textbf {a}}}_i:=\Phi _{x_0,x}^{-1}({\textbf {a}}_i)}$ and the sequence $\sigma _0=(\hat {{\textbf {a}}}_0,\hat {{\textbf {a}}}_1,\ldots ,\hat {{\textbf {a}}}_D)$ in $I^\infty (x_0)$ , which also has $[\hat {{\textbf {a}}}_i]_n$ distinct, and consider $\hat {\sigma }_0=(\hat {{\textbf {b}}}_0,\hat {{\textbf {b}}}_1,\ldots ,\hat {{\textbf {b}}}_\kappa )$ the subsequence of $\sigma _0$ given by Lemma 7.5. Denote ${\textbf {b}}_l = \Phi _{x,z}(\hat {{\textbf {b}}}_l) \in I^\infty (x)$ for $l=0,1,\ldots ,\kappa $ and consider $\sigma =({\textbf {b}}_0, {\textbf {b}}_1,\ldots ,{\textbf {b}}_\kappa )$ the subsequence of $({\textbf {a}}_0,{\textbf {a}}_1,\ldots ,{\textbf {a}}_D)$ .

Given also $(\tilde y_0, \tilde y_1, \ldots , \tilde y_D)$ , we denote $\gamma _0 = (y_0,y_1, \ldots , y_\kappa )$ the corresponding subsequence. We will prove in the following that $\operatorname {Jac}(\psi _{x, \sigma , \gamma })({\textbf {t}})> \tfrac 12$ for every $(x, \gamma )$ in a neighborhood of $(x_0, \gamma _0)$ and every ${\textbf {t}}$ in a neighborhood of $\textbf {0}$ .

Remember that for ${\textbf {a}} \in I^n(x)$ and $y \in {\mathbb {R}}^d$ :

$$ \begin{align*} DS(x,({\textbf{a}},y);{\textbf{t}}) &= \sum_{i=1}^{n} \bigg(\prod_{j=1}^{i-1} D_yC_{\textbf{t}}([{\textbf{a}}]_j(x),y_{j,{\textbf{t}}}^{{\textbf{a}}}(x,y))\bigg)\\ &\quad \times D_xC_{\textbf{t}}([{\textbf{a}}]_i(x), y_{i;{\textbf{t}}}^{{\textbf{a}}}(x,y) )DE^{i}([{\textbf{a}}]_i(x))^{-1}, \end{align*} $$

where $\prod _{j=1}^{0} D_yC_{\textbf {t}}$ is the identity, $y_{i;{\textbf {t}}}^{{\textbf {a}}}(x,y)=(C_{\textbf {t}})_{[{\textbf {a}}]_{i+1}(x)}\circ \cdots \circ (C_{\textbf {t}})_{{\textbf {a}}(x)}(y)$ , and $y_{n,{\textbf {t}}}^{{\textbf {a}}}(x,y)=y$ . So $y_{0,{\textbf {t}}}^{{\textbf {a}}}(x,y)= S(x,({\textbf {a}},y);{\textbf {t}})$ .

Identifying a point ${\textbf {t}}\in {\mathbb {R}}^s={\mathbb {R}}^{ud\#{I^n(x)}}$ with $(T^{{\textbf {a}}})_{{\textbf {a}}\in {I^{n}(x)}}$ , where $T^{{\textbf {a}}}=[t^{{\textbf {a}}}_{i',j'}]$ is a $d\times u$ matrix, we consider

$$ \begin{align*} C_{\textbf{t}}(x,y) = C(x,y) + \sum_{{\textbf{a}}, i',j'} t^{({\textbf{a}})}_{i',j'} \phi^{\hat{{\textbf{a}}}}_{i',j'}(x)\end{align*} $$

for ${\textbf {a}}\in {I^n(x)}$ , $1\leq i'\leq d$ , $1\leq j'\leq u$ , where $\hat {{\textbf {a}}}=[\Phi _{x_0,x}^{-1}(\tilde {{\textbf {a}}})]_n\in I^n(x_0)$ , for some ${\tilde {{\textbf {a}}}\in I^{\infty }(x)}$ such that $[\tilde {{\textbf {a}}}]_n={\textbf {a}}$ .

A standard calculation gives the following expression for $D_{\textbf {t}} DS(x,({\textbf {a}},y);{\textbf {t}})$ .

Claim 7.6. For ${\textbf {a}} \in I^q(x)$ , denoting $x_j=[{\textbf {a}}]_j(x)$ and $y_{j,{\textbf {t}}}^{\textbf {t}} = y_{j,{\textbf {t}}}^{\textbf {t}}(x,y)$ , we have

(78) $$ \begin{align} D_{\textbf{t}} (DS(x,({\textbf{a}},y);{\textbf{t}})\cdot u)\cdot w = A_1(x,({\textbf{a}},y);{\textbf{t}})(u,w) + A_2(x,({\textbf{a}},y);{\textbf{t}})(u,w), \end{align} $$

where

(79) $$ \begin{align} A_1(x,({\textbf{a}},y);{\textbf{t}})(u,w)=\sum_{i=1}^{n} \bigg(\!D_{\textbf{t}} \bigg(\prod_{j=1}^{i-1} D_yC_{\textbf{t}}(x_j,y_{j,{\textbf{t}}}^{\textbf{a}})\bigg)\cdot w \!\bigg)D_xC_{\textbf{t}}(x_{i},y_{i;{\textbf{t}}}^{\textbf{a}})DE^{i}(x_{i})^{-1}\cdot u \end{align} $$

and

(80) $$ \begin{align} A_2(x,({\textbf{a}},y);{\textbf{t}})(u,w)=\sum_{i=1}^{n} \bigg(\prod_{j=1}^{i-1} D_yC_{\textbf{t}}(x_j,y_{j,{\textbf{t}}}^{\textbf{a}})\bigg) D_{\textbf{t}}[D_xC_{\textbf{t}}(x_{i},y_{i;{\textbf{t}}}^{\textbf{a}}) DE^{i}(x_{i})^{-1}\cdot u] \cdot w, \end{align} $$

and $A_1$ , $A_2$ are uniformly bounded (by a constant independent of ${\textbf {a}}$ ).

For ${\textbf {a}}\in I^{m}(x)$ , $ m < +\infty $ , we define $DS(x,({\textbf {a}},y);{\textbf {t}})$ as

$$ \begin{align*} \sum_{i=1}^{m} \bigg(\prod_{j=1}^{i-1} D_yC_{\textbf{t}}(x_j,y_{j,{\textbf{t}}}^{{\textbf{a}}})\bigg)D_xC_{\textbf{t}}(x_{i},y_{i;{\textbf{t}}}^{{\textbf{a}}})(DE^{i}(x_{i}))^{-1}. \end{align*} $$

For ${\textbf {a}}\in I^{\infty }(x)$ , we define it as the limit of $DS(x,([{\textbf {a}}]_m,y);{\textbf {t}})$ when m goes to infinity.

Fixing $v\in {\mathbb {R}}^{u}$ , the lth coordinate of $D_{\textbf {t}}(\psi _{x,\sigma ,\gamma }(x)\cdot v)$ applied in some vector $w\in {\mathbb {R}}^{s}$ , denoted by $L_{x,({\textbf {a}}_l,y_j);{\textbf {t}}}(v,w)$ , is given by

$$ \begin{align*} A_1(x,({\textbf{a}}_l,y_l);{\textbf{t}})(v,w) &- A_1(x,({\textbf{a}}_0,y_0);{\textbf{t}})(v,w) + A_2(x,({\textbf{a}}_l,y_l);{\textbf{t}})(v,w) \\ & - A_2(x,({\textbf{a}}_0,y_0);{\textbf{t}})(v,w). \end{align*} $$

Following equations (79) and (80), each term is a series summing from $1$ to m, let us write

(81) $$ \begin{align} L_{x,({\textbf{b}}_l,y_l);{\textbf{t}}}(v,w)=L^1_{x,({\textbf{b}}_l,y_l);{\textbf{t}}}(v,w)+L^2_{x,({\textbf{b}}_l,y_l);{\textbf{t}}}(v,w) \end{align} $$

with $L^1_{x,({\textbf {b}}_l,y);{\textbf {t}}}(v,w)$ being the sum of the first $n+\nu $ terms.

Consider $W_{0}= \{ (T^{{\textbf {a}}})_{{\textbf {a}}\in {I^n(y)}} | T^{{\textbf {a}}}=0 \text { if } {\textbf {a}}\neq [{\textbf {b}}_{l}]_n \text { for every } 1\leq l \leq \kappa \}$ a $\kappa u d$ -dimensional subspace of ${\mathbb {R}}^{s}$ . We identify $W_0$ with $(M(d\times u))^\kappa $ and we take the canonical base of $(M(d\times u))^\kappa $ formed by the vectors $V^{{\textbf {b}}_l}_{i,j}$ defined by

(82) $$ \begin{align} V^{{\textbf{b}}_l}_{i,j}=(M_1,M_2,\ldots,M_\kappa) = (0, \ldots, E_{i,j}, \ldots , 0), \end{align} $$

where the non-zero matrix $E_{i,j}$ is in the position corresponding to ${\textbf {a}}=[{\textbf {b}}_l]_n$ and $E_{i,j}$ is the elementary matrix whose only non-null entry is the $(i,j)$ -entry, which is 1 and $M_j=0$ if $j\neq l$ .

From Lemma 7.5, for every $0\leq l \leq \kappa $ , $1\leq l'\leq \kappa $ , and $i=0,1,\ldots ,n+\nu $ , the value of ${\phi ^{[\hat {{\textbf {b}}}_{l'}]_n}_{i',j'}([{\textbf {b}}_l]_i(x))}$ is non-zero only if $l=l'$ and $i=n$ .

Claim 7.7. We have $L^1_{x,([b_{l'}],y);{\textbf {t}}}(u,V^{{\textbf {b}}_l}_{i',j'})=0$ if $l'\neq l$ .

Proof. For $h=1,2,\ldots ,n+\nu $ , we have that

$$ \begin{align*} D_{\textbf{t}}(y_{h;{\textbf{t}}}^{[{\textbf{b}}_{l'}]_{n+\nu}})\cdot V^{{\textbf{b}}_l}_{i,j} =\sum_{k=1}^{n+\nu-h}\bigg(\prod_{j=1}^{k-1}(D_yC)_{[{\textbf{b}}_{l'}]_{h+j}(x)} (y_{h+j;{\textbf{t}}}^{[{\textbf{b}}_{l'}]_{n+\nu}})\bigg)\cdot (\phi^{{\textbf{b}}_l}_{i,j}([{\textbf{b}}_{l'}]_{h+k}(x))). \end{align*} $$

Then we conclude that for $l\neq l'$ ,

(83) $$ \begin{align} D_{\textbf{t}}(y_{h;{\textbf{t}}}^{[{\textbf{b}}_{l'}]_{n+\nu}})\cdot V^{{\textbf{b}}_l}_{i,j}=0. \end{align} $$

Notice that in equation (79), we have that

(84) $$ \begin{align} \!\!\!\!\!D_{\textbf{t}} \bigg(\prod_{j=1}^{i-1} D_yC_{\textbf{t}}(x_j,y_{j,{\textbf{t}}}^{\textbf{a}})\bigg)\cdot w=\sum_{\hat j=1}^{i-1}B(1,\hat{j})(D^2_yC(x_{\hat j},y_{\hat j,{\textbf{t}}}^{\textbf{a}})D_{\textbf{t}}(y_{i;{\textbf{t}}}^{\textbf{a}})\cdot w)B(\hat{j}+1,i) \end{align} $$

for $ B(m,k)=\prod _{j=m}^{k-1}D_yC_{\textbf {t}}(x_j,y_{j,{\textbf {t}}}^{\textbf {a}})$ , then $A_1(x,([{\textbf {b}}_{l'}]_{n+\nu },y);{\textbf {t}}) (u,V^{{\textbf {b}}_l}_{i',j'})=0$ if $l\neq l'$ .

For $A_2(x,([{\textbf {b}}_{l'}]_{n+\nu },y);{\textbf {t}}) (u,V^{{\textbf {b}}_l}_{i',j'})=0$ , notice that

$$ \begin{align*} D_{\textbf{t}}[D_xC_{\textbf{t}}(x_{i},y_{i;{\textbf{t}}}^{[{\textbf{b}}_{l'}]_{n+\nu}})&DE^{i}(x_{i})^{-1} \cdot u] \cdot V^{{\textbf{b}}_l}_{i',j'}\! =\! D_{\textbf{t}}[D_xC_{\textbf{t}}(x_{i},y_{i;{\textbf{t}}}^{[{\textbf{b}}_{l'}]_{n+\nu}}) \! \cdot\! V^{{\textbf{b}}_l}_{i',j'}]DE^{i}(x_{i})^{-1} \cdot u \end{align*} $$

and that $D_{\textbf {t}} D_xC_{\textbf {t}}(x_{i},y_{i;{\textbf {t}}}^{[{\textbf {b}}_{l'}]_{n+\nu }})$ is constant in the direction of $ V^{{\textbf {b}}_l}_{i',j'}$ since $y_{i;{\textbf {t}}}^{[{\textbf {b}}_l]_{n+\nu }}$ is not in the support of $\phi _{i',j'}^{[{\textbf {b}}_l]_n}$ , so this derivative is zero.

Claim 7.8. We have

$$ \begin{align*}L^1_{x_0,([b_{l}],y_l);{\textbf{t}}}(u,V^{{\textbf{b}}_l}_{i',j'})= V_{i',j'}^{{\textbf{b}}_l}(u)\quad\text{if } S(x_0,({\textbf{b}}_l,y_l))=z_0 \end{align*} $$

and

$$ \begin{align*} \| L^1_{x_0,([b_{l}],y_l);{\textbf{t}}}(u,V^{{\textbf{b}}_l}_{i',j'}) - V_{i',j'}^{{\textbf{b}}_l}(u) \| \to 0\quad \text{when } (x,S(x,({\textbf{b}}_l,y_l))) \to (x_0,z_0). \end{align*} $$

Proof. As before, from equation (77), we have that $\phi ^{[{\textbf {b}}_{l}]_n}_{i',j'}([\Phi _{x,y}({\textbf {b}}_l)]_j(x)) = 0$ except if $j=n$ . So the value of $L^1_{x,([b_{l}],y);{\textbf {t}}}(u,V^{{\textbf {b}}_l}_{i',j'})$ will be the terms of $A_1$ and $A_2$ corresponding to $i=n$ , that is,

$$ \begin{align*} \bigg(D_{\textbf{t}} &\bigg(\prod_{j=1}^{n-1} D_yC_{\textbf{t}}(x_j,y_{j,{\textbf{t}}}^{{\textbf{b}}_l})\bigg)\cdot w \bigg)D_xC_{\textbf{t}}(x_{n},y_{n;{\textbf{t}}}^{{\textbf{b}}_l})(DE^{n}(x_{n}))^{-1}\cdot u \\ & + \bigg(\prod_{j=1}^{n-1} D_yC_{\textbf{t}}(x_j,y_{j,{\textbf{t}}}^{{\textbf{b}}_l})\bigg) (D_{\textbf{t}}[D_xC_{\textbf{t}}(x_{n},y_{n;{\textbf{t}}}^{{\textbf{b}}_l})\cdot (DE^{n}(x_{n}))^{-1}\cdot u])\cdot V_{i',j'}^{{\textbf{b}}_l}. \end{align*} $$

The product $\prod _{j=1}^{n-1} D_yC_{\textbf {t}}(x_j,y_{j,{\textbf {t}}}^{{\textbf {b}}_l})$ is equal to $\prod _{j=1}^{n-1} D_yC(x_j,y_{j}^{{\textbf {b}}_l})$ , since the terms $(x_j)$ are out of the support for $j=1,\ldots , n-1$ ; so its derivative with respect to ${\textbf {t}}$ is zero. Then $D_{\textbf {t}}(y_{h;{\textbf {t}}}^{[{\textbf {b}}_{l'}]_{n+\nu }})\cdot V^{{\textbf {b}}_l}_{i,j}=0$ and the first term is zero.

The second term is equal to

(85) $$ \begin{align} \prod_{j=1}^{n-1} D_yC(x_j,y_{j,{\textbf{t}}}^{{\textbf{b}}_l}(x,y)) (D_{\textbf{t}}[D_xC_{\textbf{t}}(x_{n},y_{n;{\textbf{t}}}^{{\textbf{b}}_l})DE^{n}(x_{n})^{-1}\cdot u])\cdot V_{i',j'}^{{\textbf{b}}_l}. \end{align} $$

Writing $D_xC_{\textbf {t}}(x_{n},y_{n;{\textbf {t}}}^{{\textbf {b}}_l}) = D_xC(x_{n},y_{n;{\textbf {t}}}^{{\textbf {b}}_l}) + \sum t_{i',j',{{\textbf {b}}_l}} D_x\phi _{i',j'}^{{\textbf {b}}_l}(x_{n},y_{n;{\textbf {t}}}^{{\textbf {b}}_l})$ , we notice that

$$ \begin{align*} D_{\textbf{t}} D_xC_{\textbf{t}}(x_{n},y_{n;{\textbf{t}}}^{{\textbf{b}}_l}) = D_xC(x_{n},y_{n;{\textbf{t}}}^{{\textbf{b}}_l}) D_{\textbf{t}}(y_{h;{\textbf{t}}}^{[{\textbf{b}}_{l'}]_{n+\nu}}) + D_x\phi_{i',j'}^{{\textbf{b}}_l}(x_{n} ).\end{align*} $$

By construction, we have that

$$ \begin{align*} D \phi^{{{\textbf{b}}_l}}_{i',j'} ({{\textbf{b}}_l}(x_0)) = \bigg(\prod_{j=1}^{n-1} D_yC({{\textbf{b}}_l}(x_0), y_j^{{\textbf{b}}_l}(x_0,y_0({\textbf{b}}_l,x_0,z_0)))\bigg)^{-1} E_{i',j'} DE^{n}({{\textbf{b}}_l}(x_0)), \end{align*} $$

where $y_0({\textbf {b}}_l,x_0,z_0)$ satisfies $T^n({\textbf {b}}_l(x_0),y_0({\textbf {b}}_l,x_0,z_0))=(x_0,z_0)$ . Since $D_{\textbf {t}}(y_{h;{\textbf {t}}}^{[{\textbf {b}}_{l'}]_{n+\nu }})\cdot V^{{\textbf {b}}_l}_{i,j}=0$ , we have that equation (85) is equal to

$$ \begin{align*} &\prod_{j=1}^{n-1} D_yC(x_j,y_{j,{\textbf{t}}}^{{\textbf{b}}_l}(x,y)) \bigg(\prod_{j=1}^{n-1} D_yC({{\textbf{b}}_l}(x_0), y_j^{{\textbf{b}}_l}(x_0, y_0({\textbf{b}}_l,x_0,z_0) ))\bigg)^{-1} \cdot E_{i',j'} \\&\quad \cdot DE^{n}({{\textbf{b}}_l}(x_0)) DE^{n}({{\textbf{b}}_l}(x))^{-1}\cdot u \cdot V_{i',j'}^{{\textbf{b}}_l}. \end{align*} $$

So it is equal to $E_{i',j'}\cdot u \cdot V_{i',j'}^{{\textbf {b}}_l}$ when ${\textbf {t}}=\textbf {0}$ , $x=x_0$ , and $S(x,({\textbf {a}}_l,y_l))=z_0$ , which proves the first part of the statement. The second part follows noticing that $y_{j,{\textbf {t}}}^{{\textbf {b}}_l}(x,y) \to y_0({\textbf {b}}_l,x_0,z_0)$ and $x_j = {\textbf {b}}_l(x) \to {\textbf {b}}_l(x_0)$ when $(x,S(x,({\textbf {a}}_l,y))) \to (x_0,z_0) $ , so this term converges to $E_{i',j'}$ .

Therefore, if we denote $G_{x,\sigma ,\gamma } = D \psi _{x,\sigma ,\gamma }|_{W_0}(\textbf {0})$ , we have

$$ \begin{align*} G_{x_0,\sigma,\gamma_0}(V^{{\textbf{b}}_l}_{i,j})=L_{x_0,({\textbf{b}}_l,y_l)}(V^{{\textbf{b}}_l})=V^{{\textbf{b}}_l}_{i,j}+L^2_{x_0,({\textbf{b}}_l,y_l)}(V^{{\textbf{b}}_l}_{i,j}). \end{align*} $$

Claim 7.9. The norm $ \| L^2_{x,({\textbf {a}},y)}\| $ is uniformly bounded by $ K_4(n) {\sum _{r> n+\nu } (\overline {\unicode{x3bb} }^{r} + \underline {\mu }^{-r}} )$ , which is smaller than $\epsilon ({n}) $ .

Proof. Notice that $L^2_{x,({\textbf {a}},y)}$ is the tail beginning at $n+\nu +1$ (to q) of the series $A_1(x,{\textbf {a}};{\textbf {t}})$ and $A_2(x,{\textbf {a}};{\textbf {t}})$ . We can bound the terms in the obvious manner and obtain this inequality.

We can now complete the proof of Proposition 7.4. Indeed, $G_{x_0,\sigma ,\gamma _0}$ is represented in the canonical base by a $\kappa ud \times \kappa ud$ matrix $[G_{x_0,\sigma ,\gamma _0}]=I+R$ , where I is the identity matrix and R has all entries bounded by $\epsilon (n)$ . Since $\kappa \le N^n$ , the determinant of $G_{x_0,\sigma ,\gamma _0}$ is bounded from below by

(86) $$ \begin{align} (1-\kappa du\,\epsilon({n}))^{\kappa ud}\geq ( 1 - 4\, du N^n {\epsilon(n)} )^{N^n ud}> \tfrac{1}{2}. \end{align} $$

Following that $\operatorname {Jac}(\psi _{x_0,\sigma ,\gamma _0} )(\textbf {0}) \geq \operatorname {Jac}(\psi _{x_0,\sigma ,\gamma _0} |_{W_0})(\textbf {0})> \tfrac 12$ .

By continuity, there exists a constant $\eta = \eta _{(x_0,\gamma _0)}$ such that for every $(x,\gamma )$ in a $\eta $ -neighborhood $U_{x_0,\gamma _0}$ of $(x_0,\gamma _0)$ , $L^1_{x,([b_{l}],y_l);{\textbf {t}}}(u,V^{{\textbf {b}}_l}_{i',j'})$ is close to $L^1_{x_0,([b_{l}],y_0);{\textbf {t}}} (u,V^{{\textbf {b}}_l}_{i',j'})=E_{i',j'}$ , so $\operatorname {Jac}(\psi _{x,\sigma ,\gamma })(\textbf {t})>1/2 $ for any ${\textbf {t}}$ in $B(\textbf {0},\eta )$ .

7.2 Transversality is generic in the generic family

For s as before, we consider . We also consider constants $M, M_0, \tilde B, \delta $ that satisfy:

We can suppose that $\delta $ is rational and consider $K_5$ such that $[-K_0,K_0]^d$ decomposes into $K_5 \delta ^{-qd}$ d-cubes of side $\delta ^{q}$ , for every $q \geq 2$ .

Denote $p=p(q):= Bq$ for $B>\tilde B$ large so that any u-cube of width $\delta ^q$ contains at least $K_5 \delta ^{-qd}$ rectangles $\mathcal {R}({\textbf {c}})$ , ${\textbf {c}} \in I^{p(q)}$ .

Denoting $\delta (p)= \delta ^p$ , we have $\delta ^{p(q)} < d_\beta (q)$ .

For each ${\textbf {c}} \in I^{p(q)}$ , we consider one point $(x_{\textbf {c}},z_{\textbf {c}})$ in $\mathcal {R}({\textbf {c}}) \times [-K_0,K_0]^d$ with the property that $\{(x_{\textbf {c}}, z_{\textbf {c}})\}$ is a $\delta (q)$ -dense set in ${\mathbb {T}^u} \times [-K_0,K_0]^d$ .

Fix integers $n_0, D_0, \kappa _{0}\geq 2$ such that

(87) $$ \begin{align} (D_{0}+1)\beta^{-({n_{0}}/{2})} &<\frac{1}{2}, \end{align} $$

(88) $$ \begin{align} N^{\kappa_0 + B+1} \theta_\beta^{(u-d+1)\kappa_0} &< 1 ,\quad\kern1pt \end{align} $$

(89) $$ \begin{align} \quad\qquad\ \,\qquad\kappa_{0}+1 &< \frac{D_{0}}{2n_{0}}, \end{align} $$

(90) $$ \begin{align}\!\qquad\quad\qquad\qquad n_{0}^3 &< D_0. \end{align} $$

There exist such integers because $N \theta _\beta ^{u-d+1} < 1$ , since C is in $C^r(d;E;s)$ and .

Lemma 7.10. If $C\in \mathcal {NT}_\beta ^{M}$ , then for every $q_0 \geq 1$ , there exists $q>q_0$ such that there exist a word ${\textbf {c}} \in I^{p(q)}$ , $1+D_0$ words ${\textbf {a}}_{i}\in I^q({\textbf {c}})$ , and points $y_i \in [-K_0,K_0]^d$ with $[{\textbf {a}}_i]_{n_0}$ distinct such that for any $1\leq i \leq D_0$ ,

(91) $$ \begin{align} \mathfrak{m}( DS(x_{\textbf{c}},({\textbf{a}}_{i},y_i)) - DS(x_{\textbf{c}},({\textbf{a}}_{0},y_0)) ) &\leq K_6 \theta_\beta^{q}, \end{align} $$

(92) $$ \begin{align} \qquad\ \ \,\| S(x_{\textbf{c}},({\textbf{a}}_{i},y_i)) - S(x_{\textbf{c}},({\textbf{a}}_{0},y_0)) \| &\leq 4d_\beta(q), \end{align} $$

(93) $$ \begin{align}\qquad\qquad\qquad\quad \| S(x_{\textbf{c}},({\textbf{a}}_i,y_i)) - z_{\textbf{c}}\| &\leq 6 d_\beta(q) \end{align} $$

for some constant $K_6$ .

Proof. Given $q_0$ , we consider $\tilde {q}_0$ such that $\tilde {q}_0 ({ \log \beta }/{ 2u\log N})>q_0$ . Since $C\in \mathcal {NT}^M_\beta $ , we can take $\tilde {q}>\tilde {q}_0$ large such that there exist a word $\tilde {{\textbf {c}}}\in I^{p(\tilde {q})}$ , a subset $L\subset I^{\tilde {q}} ({\tilde {{\textbf {c}}}})$ , and some $\tilde {{\textbf {u}}}_0\in L$ such that $\# L \geq \beta ^{\tilde {q}}$ and for every $\tilde {{\textbf {u}}} \in L$ , there exist points $(x^{1}_{\tilde {{\textbf {u}}}},y^1_{\tilde {{\textbf {u}}}})$ and $(x^2_{\tilde {{\textbf {u}}}},y^2_{\tilde {{\textbf {u}}}})$ in $\mathcal {R}(\tilde {{\textbf {c}}}) \times [-K_0,K_0]^d $ satisfying

$$ \begin{align*} \mathfrak{m}( DS(x^1_{\tilde{{\textbf{u}}}},(\tilde{{\textbf{u}}},y^1_{\tilde{{\textbf{u}}}})) - DS(x^1_{\tilde{{\textbf{u}}}_0},(\tilde{{\textbf{u}}}_0,y^1_{\tilde{{\textbf{u}}}_0}) ) \leq 3\theta^{\tilde q} \alpha_0, \end{align*} $$

$$ \begin{align*} S(x^2_{\tilde{{\textbf{u}}}},(\tilde{{\textbf{u}}},y^2_{\tilde{{\textbf{u}}}})) - S(x^2_{\tilde{{\textbf{u}}}_0},(\tilde{{\textbf{u}}}_0,y^2_{\tilde{{\textbf{u}}}_0}) ) \leq d({\tilde q}). \end{align*} $$

Notice that $DS_{\textbf {c}}(\cdot ,({\textbf {a}},y))$ , $S_{\textbf {c}}(x,({\textbf {a}},\cdot ))$ and $DS_{\textbf {c}}(x,({\textbf {a}},\cdot ))$ are Lipschitz with some Lipschitz constant $L\geq \alpha _0$ independent of $x,{\textbf {a}},y$ .

For the smallest singular value, the following triangle inequality holds: $ \mathfrak {m}(A)\leq \mathfrak {m} (B) + \| A-B\|. $ Using it and noticing that $\underline {\mu }^{-p(\tilde q)} < d(\tilde q) < \theta ^{\tilde q}$ , we have that for some fixed $x^1\in \mathcal {R}({\tilde {{\textbf {c}}}})$ ,

(94) $$ \begin{align} \mathfrak{m}( DS(x^1,(\tilde{{\textbf{u}}},y^1_{\tilde{{\textbf{u}}}})) - DS(x^1,(\tilde{{\textbf{u}}}_0,y^1_{\tilde{{\textbf{u}}}_0})) ) \leq 2L\sqrt{d} \underline{\mu}^{-p(\tilde{q})} + 3\theta^{\tilde{q}} \alpha_0 \leq 5 \theta^{\tilde{q}} L \end{align} $$

and

(95) $$ \begin{align} \| S(x,(\tilde {\textbf{u}} , y^2_{\tilde {\textbf{u}}})) - S(x,(\tilde {\textbf{u}}_0 , y^2_{\tilde {\textbf{u}}_0}) )) \| \leq d(\tilde{q} ) + 2\sqrt{d} \alpha_0 \underline{\mu}^{-p(\tilde q)} <3d(\tilde q). \end{align} $$

We may have equal $[\tilde {\textbf {u}}]_{n_0}$ for distinct $\tilde {{\textbf {u}}}$ . So, to obtain words ${\textbf {a}}_i$ with distinct truncation $[{\textbf {a}}_i]_{n_0}$ , for each $0\leq j \leq \lfloor \tilde {q}/n_{0}\rfloor $ and ${\textbf {a}} \in L$ , we define

$$ \begin{align*}L(j,{\textbf{a}}) = \{ {\textbf{b}}\in L, [{\textbf{a}}]_{jn_0}=[{\textbf{b}}]_{jn_0} \}\end{align*} $$

if $j\geq 1$ and $L(0,{\textbf {a}})=L$ . Notice that $L(j_1,{\textbf {a}}) \supset L(j_2,{\textbf {a}})$ if $j_1\leq j_2$ and that $L(j,{\textbf {a}}_1) \cap L(j,{\textbf {a}}_2) = \emptyset $ if $[{\textbf {a}}_1]_{jn_0} \neq [{\textbf {a}}_2]_{jn_0}$ . We also define

$$ \begin{align*}H(j,{\textbf{a}}):= \{{\textbf{b}}\in L | {\textbf{b}} \in L(j,{\textbf{a}}) \cap L(j-1,{\textbf{u}}_0)\}\quad \text{and}\quad h_{j}:=\underset{{{\textbf{a}}}\in L}{\max} \#H(j,{\textbf{a}}) \end{align*} $$

for $j\geq 1$ and $h_{0}=\# L \geq \beta ^{\tilde {q}}$ .

Since $L(j,{\textbf {a}})$ has the same cardinality of $I^{\tilde {q}-jn_0}([{\textbf {a}}]_{jn_0})$ , we have that $h_{j}\leq N^{u(\tilde {q}-j n_0)}$ , so there exists $j\leq \lfloor \tilde {q}/n_0\rfloor $ such that $h_{j+1}< \beta ^{- n_0/ 2} h_{j}$ . Let $j_{*}$ be the minimum of such integers j and put $q=\tilde {q} - n_0 j_{*}$ . By the minimality of $j_{*}$ , we have that $h_{j_{*}}\geq \beta ^q $ . We also have that $q\geq \tilde {q} ({\log \beta }/{2u\log N})> q_0 $ .

Considering ${\textbf {v}}_0$ such that $h_{j_{*}} = \# H(j_{*},{\textbf {v}}_0)$ , the set $H(j_{*},{\textbf {v}}_0)$ contains at least $1+D_0$ sets $H(j_{*}+1,\tilde {{\textbf {u}}}_i)$ , because

(96) $$ \begin{align} h_{j_{*}} - (D_0 +1) h_{j_{*}+1}> h_{j_{*}}-(D_0 +1)\beta^{- n_0/2} h_{j_{*}}>0 \end{align} $$

due to equation (87).

We consider the disjoint sets $H(j_{*}+1,\tilde {{\textbf {u}}}_0)$ , $H(j_{*}+1,\tilde {{\textbf {u}}}_1), \ldots $ , $H(j_{*}+1,\tilde {{\textbf {u}}}_{D_0})$ . In particular, $[\tilde {{\textbf {u}}}_{i'}]_{(j_{*}+1)n_0}$ are distinct for $i'=0,1,\ldots ,D_0$ . So, there exist ${\textbf {b}}\in I^{\tilde {q}-q}$ and ${\textbf {a}}_{i}\in I^{q}$ , $0\leq i \leq D_0 $ such that ${\textbf {b}}{\textbf {a}}_{i}=\tilde {{\textbf {u}}}_i \in H(j_{*},{\textbf {v}}_0)$ for $0\leq i \leq D_0 $ and that $[{\textbf {a}}_{i}]_{n_0}\neq [{\textbf {a}}_{j}]_{n_0}$ if $i\neq j$ .

We rewrite equations (94) and (95) as

(97) $$ \begin{align} \| S(x,({\textbf{b}}{\textbf{a}}_{i},y^1_{{\textbf{b}}{\textbf{a}}_{i}})) - S(x,({\textbf{b}}{\textbf{a}}_{0},y^1_{{\textbf{b}}{\textbf{a}}_{0}})) \| \leq 3 d( \tilde{q}) \end{align} $$

and

(98) $$ \begin{align} \mathfrak{m}( DS(x,({\textbf{b}}{\textbf{a}}_{i},y^2_{{\textbf{b}}{\textbf{a}}_{i}})) - DS(x,({\textbf{b}}{\textbf{a}}_{0},y^2_{{\textbf{b}}{\textbf{a}}_{0}})) )\leq 5 \theta^{\tilde{q}} \alpha_0. \end{align} $$

Then we have the following lemma.

Lemma 7.11. There exists $K>0$ (independent of $q, \tilde q, {\textbf {b}}, {\textbf {a}}_1, {\textbf {a}}_2$ ) such that

(99)

(100)

Proof. First, notice the following relations for any ${\textbf {a}} $ and ${\textbf {b}} $ :

(101) $$ \begin{align} S(x,({\textbf{b}} {\textbf{a}}, y )) = S(x,({\textbf{b}}, y_0^{\textbf{a}}({\textbf{b}}(x),y))) \end{align} $$

and

(102) $$ \begin{align}DS(x,({\textbf{b}} {\textbf{a}}, y )) &= DS(x,({\textbf{b}}, y_0^{\textbf{a}}({\textbf{b}}(x),y)))\nonumber\\&\quad + \prod_{j=1}^{\tilde{q}-q} D_yC([{\textbf{b}}]_j(x), y_j^{{\textbf{b}}}(x,y_0^{{\textbf{a}}}({\textbf{b}}(x),y))) DS({\textbf{b}}(x),({\textbf{a}}, y )) DE^{-\tilde{q}+q}( {\textbf{b}}(x) ). \end{align} $$

To prove equation (99), we use that $H(y)=S(x,({\textbf {b}},y))=C^{\tilde q -q}(x,y)$ is a bi-Lipschitz function with and that $\tilde q - q \geq q ( ({2u\log N}/{\log \beta }) - 1 ) $ . So,

To prove equation (100), notice that

$$ \begin{align*} DS({\textbf{b}}(x),({\textbf{a}}, y )) &= \bigg( \prod_{j=1}^{\tilde{q}-q} D_yC([{\textbf{b}}]_j(x), y_j^{{\textbf{b}}}(x,y_0^{{\textbf{a}}}({\textbf{b}}(x),y))) \bigg)^{-1}\\&\quad \cdot \bigg[ DS(x,({\textbf{b}} {\textbf{a}}, y )) - DS(x,({\textbf{b}}, y_0^{\textbf{a}}({\textbf{b}}(x),y))) \bigg] DE^{\tilde{q}-q}( x ). \end{align*} $$

Then we can write $DS({\textbf {b}}(x),({\textbf {a}}_1, y_1 )) - DS({\textbf {b}}(x),({\textbf {a}}_2, y_2 ))$ as

$$ \begin{align*} \bigg[ \prod_{j=1}^{\tilde{q}-q} A^1_j(y_1) [ b_1(y_1) - c_1(y_1) ] - \prod_{j=1}^{\tilde{q}-q} A^2_j(y_2) [ b_2(y_2) - c_2(y_2) ] \bigg] DE^{\tilde{q}-q}( x ) \end{align*} $$

for $A^i_j(y) = D_yC([{\textbf {b}}]_j(x), y_j^{{\textbf {b}}}(x,y_0^{{\textbf {a}}_i}({\textbf {b}}(x),y)))^{-1}$ , $ b_i(y) = DS(x,({\textbf {b}} {\textbf {a}}_i, y)) $ , and $ c_i(y) = DS(x,({\textbf {b}}, y_0^{{\textbf {a}}_i}({\textbf {b}}(x),y))).$ Notice that and

Then

Using that , it follows that this smallest singular value is smaller or equal than

for some $K>0$ .

So we have that

$$ \begin{align*} \| S({\textbf{b}}(x),({\textbf{a}}_{i},y_i)) - S({\textbf{b}}(x),({\textbf{a}}_{0},y_0)) \| \leq 3 d_\beta(q),\end{align*} $$

$$ \begin{align*} \mathfrak{m}( DS({\textbf{b}}(x),({\textbf{a}}_{i},y_i)) - DS({\textbf{b}}(x),({\textbf{a}}_{0},y_0)) ) \leq K \theta_\beta^{q}.\end{align*} $$

Taking ${\textbf {c}}\in I^{p(q)}$ such that $\| {\textbf {b}}(x)-x_{\textbf {c}} \| < \delta ^{p(q)}$ and $\| S({\textbf {b}}(x),({\textbf {a}}_i,y_i)) - z_{\textbf {c}} \| < \delta ^{p(q)}$ , we have the conclusion of the lemma.

To finish the proof of Proposition 7.3, we will use the following two lemmas.

Lemma 7.12. Given integers s, k, and $\eta>0$ , there exists a constant $K_7>0$ such that if $G:{\mathbb {R}}^s \to {\mathbb {R}}^k$ is $C^1$ with $\operatorname {Jac}(G)({\textbf {t}})>\delta $ for every $\| {\textbf {t}}\| \leq \eta $ , then

(103) $$ \begin{align} m_s (G^{-1}(Y)\cap [-\eta,\eta]^s) \leq K_7 \frac{m_k(Y)}{\delta} \end{align} $$

for every measurable set $Y\subset {\mathbb {R}}^k$ .

Lemma 7.13. [12, Lemma 4.9]

For every $u\geq d$ , there exists a constant $K_8>0$ such that the set

(104) $$ \begin{align} \mathcal{X}(r):=\{ M \in M(d \times u ) , \| M \| \leq 2\alpha_0 , \mathfrak{m}(M) <r \} \end{align} $$

has $du$ -volume bounded by $K_8 r^{u-d+1}$ for every $r>0$ .

Proof of Proposition 7.3

We consider $\{ \phi _{i}\}_{i=1}^{s}$ the functions given by Proposition 7.2 for E, C, and $n=n_{0}$ .

Let us consider $\mathcal {NT}_0 := \{ {\textbf {t}} \in B( {\textbf {0}} , \eta ) \subset {\mathbb {R}}^s | f_{\textbf {t}} \in \mathcal {NT}_\beta ^M \}$ . If ${\textbf {t}}\in \mathcal {NT}_0$ , Lemma 7.10 implies that for every integer $q_0$ , there exist an integer $q\geq q_0$ , a word ${\textbf {c}} \in I^{p(q)}$ , and $1+D_0$ words ${\textbf {a}}_{i}\in I^q({\textbf {c}})$ with $[{\textbf {a}}_i]_{n_0}$ distinct and points $y_i \in [-K_0,K_0]^d$ such that

$$ \begin{align*}\mathfrak{m}( DS(x_{\textbf{c}},({\textbf{a}}_{i},y_i)) - DS(x_{\textbf{c}},({\textbf{a}}_{0},y_0)) ) \leq K_6 \theta^{q}_\beta, \end{align*} $$

$$ \begin{align*}\| S(x_{\textbf{c}},({\textbf{a}}_{i},y_i)) - S(x_{\textbf{c}},({\textbf{a}}_{0},y_0)) ) \leq 3 d_\beta (q), \end{align*} $$

$$ \begin{align*}\| S(x_{\textbf{c}},({\textbf{a}}_i,y_i))-z_{\textbf{c}}\| < 6 d_\beta (q) \end{align*} $$

for any $i =1,\ldots , D_0$ .

Given $x \in {\mathbb {T}^u} $ and $\sigma = ({\textbf {a}}_0,{\textbf {a}}_!, \ldots , {\textbf {a}}_D)$ , we say that $\gamma =(y_0,y_1,\ldots , y_D)$ is $\epsilon $ -close to z if $\| S(x,({\textbf {a}}_i,y_i)) - z\| <\epsilon $ for every $i=1,\ldots ,D$ . Consider the sets

$$ \begin{align*} \mathcal{B}^{q} = \{ (\sigma, {\textbf{c}}) \in (I^{q})^{1+\kappa_0} \times I^{p(q)} | \operatorname{Jac}(\psi_{x_{c},\sigma, \gamma })>\tfrac{1}{2} \text{ for some } \gamma \text{ } 6d_\beta(q)\text{-close to } z_{\textbf{c}} \}.\end{align*} $$

For $(\sigma ,{\textbf {c}})$ given, we have a unique $\gamma =\gamma (\sigma ,{\textbf {c}})=\{y_0,y_1,\ldots , y_D\}$ such that $S(x,({\textbf {a}}_i,y_i))=z_{\textbf {c}}$ .

Notice that if $\operatorname {Jac}(\psi _{x_{c},\sigma , \gamma })>\tfrac 12$ for some $\gamma $ $6d_\beta (q)$ -close to $z_{\textbf {c}}$ , then $\| \psi _{x_{c},\sigma , \gamma } - \psi _{x_{c},\sigma , \gamma (\sigma ,{\textbf {c}}) } \| \leq 2D_0 C (6d_\beta (q)). $ This implies that $\operatorname {Jac}(\psi _{x_{c},\sigma , \gamma (\sigma ,{\textbf {c}}) })>\tfrac 14$ for q large enough.

Define

(105) $$ \begin{align} \mathcal{NT}(q):=\underset{(\sigma,{\textbf{c}})\in\mathcal{B}^q}{\bigcup} \psi_{x_{\textbf{c}}, \hat{\sigma}, \gamma(\hat{\sigma},{\textbf{c}}) }^{-1}( \mathcal{X}(K_6 \theta_\beta^q )^{\kappa_0}). \end{align} $$

Consider also q large so that $6d_\beta (q) < \eta $ . For $(x_{\textbf {c}},z_{\textbf {c}})$ , the sequence $(\hat {{\textbf {a}}}_{0},\hat {{\textbf {a}}}_{1},\ldots , \hat {{\textbf {a}}}_{D_0})$ and points $(\tilde y_0,\tilde y_1,\ldots , \tilde y_D)$ , and the facts that the family $T_{{\textbf {t}}}^{n_0}$ is $(n_0,\eta )$ -generic and that $({D_0}/{2n_0})>\kappa _0 $ and $D_0> n_0^3$ , imply that there exists a subsequence $\sigma =({\textbf {b}}_0,{\textbf {b}}_1,\ldots ,{\textbf {b}}_{{\kappa _0}}) \in (I^q)^{1+\kappa _0}$ such that each entry of $\psi _{x_{\textbf {c}}, \sigma , \gamma }({\textbf {t}})$ , for the corresponding $\gamma =(y_0,y_1,\ldots ,y_\kappa )$ , is in the set

$$ \begin{align*}\mathcal{X}(K_6\theta_\beta^q )= \{ M\in M(d\times u), \| M \| \leq 2 \alpha_0\quad \text{and}\quad \mathfrak{m}({M}) < K_6 \theta_\beta^q \}.\end{align*} $$

This means that

(106) $$ \begin{align} \mathcal{NT}_0 \subset {\limsup}_{q\to\infty} \mathcal{NT}(q). \end{align} $$

Since $\# I^q = r N^{q-1}$ , we have that

(107) $$ \begin{align} \#\mathcal{B}^q \leq (r N^{(q-1)})^{(\kappa_0 +1)} r N^{p(q)-1}\,. \end{align} $$

Putting together Lemmas 7.12, 7.13, and equation (107), we get that the estimate

(108) $$ \begin{align} m_s(\mathcal{NT}(q) ) \leq r^{{2}+\kappa_0} N^{q+q\kappa_0 + p(q)-2 -\kappa_0} ({4 K_7} K_8(K_6 \theta_\beta^q )^{u-d+1})^{\kappa_0} \end{align} $$

is valid for every q.

So there is a constant $K_9>0$ such that equation (108) is bounded from above by

(109) $$ \begin{align} K_9 ( N^{\kappa_0 + B+1} \theta_\beta^{(u-d+1)\kappa_0} )^q \end{align} $$

for every q. By the choice of $\kappa _0$ , this value converges to zero exponentially fast when $q \to +\infty $ , implying, together with equation (106) and the Borel–Cantelli lemma, that $m_s(\mathcal {NT}_0 )=0$ . This concludes the proof of Proposition 7.3.

Proof of Theorem F

Since $C \in \mathcal {C}^r(s,d;E)$ , we can apply Proposition 7.3 for . So there exists a non-decreasing function d, a finite parameter family that defines a finite dimensional subspace of $C^r({\mathbb {T}^u} \times {\mathbb {R}}^d, {\mathbb {R}}^d)$ , and there exists a subset $\mathcal {R} \in C^r({\mathbb {T}^u} \times {\mathbb {R}}^d, {\mathbb {R}}^d)$ with full measure in a ball of radius $\eta $ centered in $\textbf {0}$ such that $\underset {q\to +\infty }{\limsup } ({1}/{q}) \log \tau _d(q) < \log \beta $ for $(E,C+H)$ for every $H \in \mathcal {R}$ .

Finally, it is immediate to see that putting together Theorem F with Theorems A $^{\prime }$ , C $^{\prime }$ , D $^{\prime }$ , and E $^{\prime }$ , Theorems A, C, D, and E (respectively) follow.