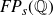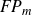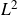1. Introduction
The class of right-angled Artin groups (RAAGs) generalises the class of finitely generated free groups, by allowing relations saying that some of the generators commute. In recent years, RAAGs have been extensively studied due to their rich structure, in particular, due to the variety of their subgroups. For example, it follows from works of I. Agol ([ Reference Agol2 ]) and D. Wise ([ Reference Wise28 ]) that fundamental groups of closed, irreducible, hyperbolic 3-manifolds are virtually subgroups of RAAGs.
In general, not all subgroups of RAAGs are again RAAGs, and Droms RAAGs are precisely those RAAGs with the property that all of their finitely generated subgroups are again RAAGs. In particular, finitely generated free groups are Droms RAAGs. Droms RAAGs can also be described as the ones where the defining graph does not contain induced squares or straight line paths with 3 edges (see [
Reference Droms18
]). Alternatively, the class of Droms RAAGs can be described as the
![]() $Z \ast$
-closure of
$Z \ast$
-closure of
![]() $\mathbb{Z}$
(see Section 2 for the definition).
$\mathbb{Z}$
(see Section 2 for the definition).
The class of limit groups over Droms RAAGs extends the class of limit groups over free groups. The theory of limit groups over free groups was developed by O. Kharlampovich, A. Miasnikov, under the name of fully residually free groups, and by Z. Sela, as a method for obtaining information on solutions of systems of equations over free groups. The class of limit groups over free groups contains all finitely generated free abelian groups and surface groups of Euler characteristic at most
![]() $-2$
. Limit groups over free groups are commutative transitive and, as shown by F. Dahmani ([
Reference Dahmani15
]), they satisfy the Howson property.
$-2$
. Limit groups over free groups are commutative transitive and, as shown by F. Dahmani ([
Reference Dahmani15
]), they satisfy the Howson property.
The study of limit groups over Droms RAAGs was initiated by M. Casals–Ruiz, A. Duncan and I. Kazachkov, in [
Reference Casals–Ruiz, Duncan and Kazachkov11
,
Reference Casals–Ruiz and Kazachkov12
], with the aim of studying systems of equations over RAAGs. A group
![]() $\Gamma$
is a limit group over a Droms RAAG if it is precisely a finitely generated group that is fully residually a Droms RAAG, that is, for every finite subset S of
$\Gamma$
is a limit group over a Droms RAAG if it is precisely a finitely generated group that is fully residually a Droms RAAG, that is, for every finite subset S of
![]() $\Gamma$
there is a Droms RAAG G together with a homomorphism of groups
$\Gamma$
there is a Droms RAAG G together with a homomorphism of groups
![]() $\varphi \,:\, \Gamma \mapsto G$
whose restriction to S is injective.
$\varphi \,:\, \Gamma \mapsto G$
whose restriction to S is injective.
Limit groups over Droms RAAGs share many properties with limit groups over free groups, including homological and homotopical finiteness properties. For example, Casals–Ruiz, Duncan and Kazachkov showed in [
Reference Casals–Ruiz, Duncan and Kazachkov11
] that limit groups over coherent RAAGs are finitely presented and they are subgroups of ICE groups over coherent RAAGs (see Definition 3·8). In particular, this holds for limit groups over Droms RAAGs and implies that limit groups over Droms RAAGs are of type
![]() $FP_{\infty}$
, and that their finitely generated subgroups are again limit groups over Droms RAAGs. In [
Reference Bridson and Wilton10
] M. Bridson and H. Wilton proved that finitely presentable subgroups of finitely generated residually free groups are separable and that the subgroups of type
$FP_{\infty}$
, and that their finitely generated subgroups are again limit groups over Droms RAAGs. In [
Reference Bridson and Wilton10
] M. Bridson and H. Wilton proved that finitely presentable subgroups of finitely generated residually free groups are separable and that the subgroups of type
![]() $FP_{\infty}$
are virtual retracts. Though limit groups over Droms RAAGs share many properties with limit groups over free groups, there are properties like commutative transitivity and the Howson property that do not hold for a general Droms RAAG. For example, by [
Reference Delgado16
], the RAAGs that satisfy the Howson property are precisely the free products of abelian groups, so in particular, are limit groups over free groups.
$FP_{\infty}$
are virtual retracts. Though limit groups over Droms RAAGs share many properties with limit groups over free groups, there are properties like commutative transitivity and the Howson property that do not hold for a general Droms RAAG. For example, by [
Reference Delgado16
], the RAAGs that satisfy the Howson property are precisely the free products of abelian groups, so in particular, are limit groups over free groups.
In [ Reference Kochloukova21 ] D. Kochloukova showed that limit groups over free groups are free-by-(torsion-free nilpotent). Our first result is a generalisation of this fact for limit groups over Droms RAAGs. The rest of the results in this paper will be heavily dependent on this fact.
Proposition 3·16. Every limit group over a Droms RAAG is free-by-(torsion-free nilpotent).
Let us recall some definitions. Let S be a subgroup of a direct product
![]() $G_1\times \cdots \times G_n$
. We say that S is full if
$G_1\times \cdots \times G_n$
. We say that S is full if
![]() $S \cap G_i \neq 1$
for all
$S \cap G_i \neq 1$
for all
![]() $i\in \{1,\dots,n\}$
and S is a subdirect product if
$i\in \{1,\dots,n\}$
and S is a subdirect product if
![]() $p_i(S)= G_i$
for all
$p_i(S)= G_i$
for all
![]() $i\in \{1,\dots,n\}$
, where
$i\in \{1,\dots,n\}$
, where
![]() $p_i$
is the projection map
$p_i$
is the projection map
![]() $G_1\times \cdots \times G_n \mapsto G_i$
.
$G_1\times \cdots \times G_n \mapsto G_i$
.
G. Baumslag, A. Miasnikov, V. Remeslennikov proved in [
Reference Baumslag, Miasnikov and Remeslennikov4
] that every finitely generated residually Droms RAAG is a subgroup of a direct product of finitely many limit groups over Droms RAAGs. The study of subdirect products of free groups was initiated by Baumslag and J. Roseblade in [
Reference Baumslag and Roseblade5
]. In a sequence of papers that culminated in [
Reference Bridson, Howie, Miller and Short7
,
Reference Bridson, Howie, Miller and Short8
], Bridson, J. Howie, C. Miller and H. Short studied subgroups of the direct product of limit groups over free groups. One of the results is that if
![]() $\Gamma_1,\dots, \Gamma_n$
are non-abelian limit groups over free groups and S is a full subdirect product of
$\Gamma_1,\dots, \Gamma_n$
are non-abelian limit groups over free groups and S is a full subdirect product of
![]() $\Gamma_1\times \cdots \times \Gamma_n$
, then S is of type
$\Gamma_1\times \cdots \times \Gamma_n$
, then S is of type
![]() $FP_2(\mathbb{Q})$
if and only if
$FP_2(\mathbb{Q})$
if and only if
![]() $p_{i,j}(S)$
is of finite index in
$p_{i,j}(S)$
is of finite index in
![]() $\Gamma_i \times \Gamma_j$
for all
$\Gamma_i \times \Gamma_j$
for all
![]() $1\leq i< j \leq n$
, where
$1\leq i< j \leq n$
, where
![]() $p_{i,j}$
denotes the projection map
$p_{i,j}$
denotes the projection map
![]() $S\mapsto \Gamma_i \times \Gamma_j$
. These results were generalised by J. Lopez de Gamiz Zearra in [
Reference Lopez de Gamiz Zearra23
] to the class of limit groups over Droms RAAGs (see Section 2·2). In addition, in [
Reference Kochloukova21
] Kochloukova generalised the previous result concerning limit groups over free groups by showing that if S is of type
$S\mapsto \Gamma_i \times \Gamma_j$
. These results were generalised by J. Lopez de Gamiz Zearra in [
Reference Lopez de Gamiz Zearra23
] to the class of limit groups over Droms RAAGs (see Section 2·2). In addition, in [
Reference Kochloukova21
] Kochloukova generalised the previous result concerning limit groups over free groups by showing that if S is of type
![]() $FP_s$
, then it virtually surjects onto s coordinates. However, the converse is still an open problem.
$FP_s$
, then it virtually surjects onto s coordinates. However, the converse is still an open problem.
We recall that a group S is of homological type
![]() $FP_s(R)$
(or it is
$FP_s(R)$
(or it is
![]() $FP_s$
over R) for a commutative, associative ring R with identity element if the trivial R G-module R has a projective resolution with all modules finitely generated in dimensions up to s. A group is of type
$FP_s$
over R) for a commutative, associative ring R with identity element if the trivial R G-module R has a projective resolution with all modules finitely generated in dimensions up to s. A group is of type
![]() $FP_s$
if it is
$FP_s$
if it is
![]() $FP_s$
over
$FP_s$
over
![]() $\mathbb{Z}$
. The aim of Section 4 is to extend the above results to the class of limit groups over Droms RAAGs.
$\mathbb{Z}$
. The aim of Section 4 is to extend the above results to the class of limit groups over Droms RAAGs.
Theorem 1·1.
Let
![]() $G_1, \dots, G_m$
be limit groups over Droms RAAGs such that each
$G_1, \dots, G_m$
be limit groups over Droms RAAGs such that each
![]() $G_i$
has trivial center and let
$G_i$
has trivial center and let
be a finitely generated full subdirect product. Suppose further that, for some fixed number
![]() $s \in \{ 2, \dots, m \}$
, for every subgroup
$s \in \{ 2, \dots, m \}$
, for every subgroup
![]() $S_0$
of finite index in S the homology group
$S_0$
of finite index in S the homology group
![]() $H_i (S_0 , \mathbb{Q})$
is finite dimensional (over
$H_i (S_0 , \mathbb{Q})$
is finite dimensional (over
![]() $\mathbb{Q}$
) for all
$\mathbb{Q}$
) for all
![]() $ i \leq s.$
Then for every canonical projection
$ i \leq s.$
Then for every canonical projection
the index of
![]() $p_{j_1, \dots, j_s} (S)$
in
$p_{j_1, \dots, j_s} (S)$
in
![]() $G_{j_1} \times \ldots \times G_{ j_s}$
is finite.
$G_{j_1} \times \ldots \times G_{ j_s}$
is finite.
In particular, if S is of type
![]() $FP_s$
over
$FP_s$
over
![]() $\mathbb{Q}$
, then for every canonical projection
$\mathbb{Q}$
, then for every canonical projection
![]() $p_{j_1, \dots, j_s}$
the index of
$p_{j_1, \dots, j_s}$
the index of
![]() $p_{j_1, \dots, j_s} (S)$
in
$p_{j_1, \dots, j_s} (S)$
in
![]() $G_{j_1} \times \cdots \times G_{ j_s}$
is finite.
$G_{j_1} \times \cdots \times G_{ j_s}$
is finite.
In Section 5 we discuss the growth of homology groups and the volume gradients of limit groups over Droms RAAGs and of finitely presented residually Droms RAAGs. The growth of homology groups is measured by the limit
whenever this limit exits. Here K is a field and
![]() $(B_{n})$
is an exhausting normal chain of G, that is, a chain
$(B_{n})$
is an exhausting normal chain of G, that is, a chain
![]() $(B_{n})$
of normal subgroups of finite index such that
$(B_{n})$
of normal subgroups of finite index such that
![]() $B_{n+1} \subseteq B_{n}$
and
$B_{n+1} \subseteq B_{n}$
and
![]() $\bigcap_{n} B_{n}=1$
. As every residually finite group has an exhausting normal chain, the same holds for limit groups over coherent RAAGs. Thanks to the approximation theorem of W. Lück we know that if K has characteristic 0, G is residually finite, finitely presented and of type
$\bigcap_{n} B_{n}=1$
. As every residually finite group has an exhausting normal chain, the same holds for limit groups over coherent RAAGs. Thanks to the approximation theorem of W. Lück we know that if K has characteristic 0, G is residually finite, finitely presented and of type
![]() $FP_{m}$
, then the limit exists for
$FP_{m}$
, then the limit exists for
![]() $i<m$
and equals the
$i<m$
and equals the
![]() $L^{2}$
-Betti number
$L^{2}$
-Betti number
![]() $\beta_{i}(G)$
. In particular, in this case the limit is independent of the exhausting normal chain.
$\beta_{i}(G)$
. In particular, in this case the limit is independent of the exhausting normal chain.
Given a group G of homotopical type
![]() $F_{m}$
,
$F_{m}$
,
![]() $\text{vol}_{m}(G)$
was defined in [
Reference Bridson and Kochloukova9
] as the least number of m-cells among all classifying spaces K(G,1) with finite m-skeleton. For instance,
$\text{vol}_{m}(G)$
was defined in [
Reference Bridson and Kochloukova9
] as the least number of m-cells among all classifying spaces K(G,1) with finite m-skeleton. For instance,
![]() $\text{vol}_{1}(G)$
equals d(G), where d(G) is the minimal number of generators of G. The most studied volume gradient is the 1-dimensional one. That is, the rank gradient of G with respect to
$\text{vol}_{1}(G)$
equals d(G), where d(G) is the minimal number of generators of G. The most studied volume gradient is the 1-dimensional one. That is, the rank gradient of G with respect to
![]() $(B_{n})$
, which is defined to be
$(B_{n})$
, which is defined to be
![]() $\lim_{n } d(B_{n}) / [G \,:\, B_{n}]$
and it is denoted by
$\lim_{n } d(B_{n}) / [G \,:\, B_{n}]$
and it is denoted by
![]() $RG(G,(B_{n}))$
. Its study was initiated by M. Lackenby in [
Reference Lackenby22
] and a combinatorial approach to the rank gradient was developed by M. Abert, N. Nikolov and A. Jaikin–Zapirain in [
Reference Abert, Nikolov and Jaikin–Zapirain1
]. In general, the m-dimensional volume gradient of G with respect to
$RG(G,(B_{n}))$
. Its study was initiated by M. Lackenby in [
Reference Lackenby22
] and a combinatorial approach to the rank gradient was developed by M. Abert, N. Nikolov and A. Jaikin–Zapirain in [
Reference Abert, Nikolov and Jaikin–Zapirain1
]. In general, the m-dimensional volume gradient of G with respect to
![]() $(B_{n})$
is
$(B_{n})$
is
In [ Reference Bridson and Kochloukova9 ] Bridson and Kochloukova calculated the above volume and homology type gradients for limit groups over free groups and in the case of residually free groups they found particular filtrations where the homology growth and the rank gradient can be calculated. The results about homology growth in [ Reference Bridson and Kochloukova9 ] and in this paper are independent of the characteristic of the field K.
In Section 5 we compute the homology growth and the volume gradients for a more general setting, namely, for limit groups over coherent RAAGs. Note that this class of groups is more general than the class of limit groups over Droms RAAGs. We use the approach from [ Reference Bridson and Kochloukova9 ] and we show that limit groups over coherent RAAGs are slow above dimension 1, hence are K-slow above dimension 1. This implies the following results.
Theorem 1·2.
Let G be a limit group over a coherent RAAG and let
![]() $(B_{n})$
be an exhausting normal chain in G. Then:
$(B_{n})$
be an exhausting normal chain in G. Then:
-
(i) the rank gradient
 $RG(G, (B_n)) = \lim_{n\to \infty} \frac{d(B_{n})}{[G \,:\, B_{n}]}= -\chi(G).$
;
$RG(G, (B_n)) = \lim_{n\to \infty} \frac{d(B_{n})}{[G \,:\, B_{n}]}= -\chi(G).$
; -
(ii) the deficiency gradient
 $DG(G, (B_n)) = \lim_{n\to \infty} \frac{\text{def}(B_{n})}{[G \,:\, B_{n}]}= \chi(G)$
;
$DG(G, (B_n)) = \lim_{n\to \infty} \frac{\text{def}(B_{n})}{[G \,:\, B_{n}]}= \chi(G)$
; -
(iii) the k-dimensional volume gradient
 $\lim_{n \to \infty} \frac{\text{vol}_{k}(B_{n})}{[G \,:\, B_{n}]} =0$
for
$\lim_{n \to \infty} \frac{\text{vol}_{k}(B_{n})}{[G \,:\, B_{n}]} =0$
for
 $k\geq 2$
.
$k\geq 2$
.
Theorem 1·3.
Let K be a field, G a limit group over a coherent RAAG and
![]() $(B_{n})$
an exhausting normal chain in G. Then:
$(B_{n})$
an exhausting normal chain in G. Then:
-
(i)
 $\lim_{n\to \infty} \frac{\dim_{K}H_{1}(B_{n},K)}{[G \,:\, B_{n}]}=-\chi(G)$
;
$\lim_{n\to \infty} \frac{\dim_{K}H_{1}(B_{n},K)}{[G \,:\, B_{n}]}=-\chi(G)$
; -
(ii)
 $\lim_{n\to \infty} \frac{\dim_{K} H_{j}(B_{n} , K)}{[G \,:\, B_{n}]}=0$
for all
$\lim_{n\to \infty} \frac{\dim_{K} H_{j}(B_{n} , K)}{[G \,:\, B_{n}]}=0$
for all
 $j\geq 2$
.
$j\geq 2$
.
Using results from [
Reference Bridson and Kochloukova9
] we also compute the homology growth up to dimension m and the volume gradients in low dimensions of residually Droms RAAGs of type
![]() $FP_m$
for
$FP_m$
for
![]() $m \geq 2$
. We cannot apply the same method to the class of residually coherent RAAGs since Theorem 1·1 is a key result in this method and in [
Reference Casals–Ruiz and Lopez de Gamiz Zearra14
] it is proved that this no longer holds for coherent RAAGs.
$m \geq 2$
. We cannot apply the same method to the class of residually coherent RAAGs since Theorem 1·1 is a key result in this method and in [
Reference Casals–Ruiz and Lopez de Gamiz Zearra14
] it is proved that this no longer holds for coherent RAAGs.
Theorem 1·4.
Let
![]() $m\geq 2$
be an integer, let G be a residually Droms RAAG of type
$m\geq 2$
be an integer, let G be a residually Droms RAAG of type
![]() $FP_m$
, and let
$FP_m$
, and let
![]() $\rho$
be the largest integer such that G contains a direct product of
$\rho$
be the largest integer such that G contains a direct product of
![]() $\rho$
non-abelian free groups. Then, there exists an exhausting sequence
$\rho$
non-abelian free groups. Then, there exists an exhausting sequence
![]() $(B_n)$
in G so that for all fields K:
$(B_n)$
in G so that for all fields K:
-
(i) if G is not of type
 $FP_{\infty}$
, then
$FP_{\infty}$
, then  \[\lim_{n \to \infty } \frac{\dim H_i(B_n, K)}{[G \,:\, B_n]}=0 \hbox{ for all }0\leq i \leq m;\]
\[\lim_{n \to \infty } \frac{\dim H_i(B_n, K)}{[G \,:\, B_n]}=0 \hbox{ for all }0\leq i \leq m;\]
-
(ii) if G is of type
 $FP_{\infty}$
then for all
$FP_{\infty}$
then for all
 $j\geq 1$
,
$j\geq 1$
,  \[ \lim_{n \to \infty } \frac{\dim H_{\rho} (B_n, K)}{[G \,:\, B_n]}= (-1)^{\rho} \chi(G), \quad \lim_{n \to \infty } \frac{\dim H_{j} (B_n, K)}{[G \,:\, B_n]}=0 \quad \text{for all} \quad j\neq \rho.\]
\[ \lim_{n \to \infty } \frac{\dim H_{\rho} (B_n, K)}{[G \,:\, B_n]}= (-1)^{\rho} \chi(G), \quad \lim_{n \to \infty } \frac{\dim H_{j} (B_n, K)}{[G \,:\, B_n]}=0 \quad \text{for all} \quad j\neq \rho.\]
Remark 1·5. The exhausting sequence
![]() $(B_n)$
will be constructed to be an exhausting normal chain in a subgroup of finite index in G.
$(B_n)$
will be constructed to be an exhausting normal chain in a subgroup of finite index in G.
The following result is a low dimensional homotopical version of Theorem 1·4.
Theorem 1·6.
Every group G that is a finitely presented residually Droms RAAG but is not a limit group over a Droms RAAG admits an exhausting normal chain
![]() $(B_n)$
in G with respect to which the rank gradient
$(B_n)$
in G with respect to which the rank gradient
Furthermore, if G is of type
![]() $FP_3$
but it is not commensurable with a product of two limit groups over Droms RAAGs,
$FP_3$
but it is not commensurable with a product of two limit groups over Droms RAAGs,
![]() $(B_n)$
can be chosen so that the deficiency gradient
$(B_n)$
can be chosen so that the deficiency gradient
![]() $DG(G,(B_n))=0.$
$DG(G,(B_n))=0.$
2. Preliminaries
2·1. Right-angled Artin groups
Let us recall the definition of a right-angled Artin group. Given a finite simplicial graph X with vertex set V(X), the corresponding right-angled Artin group (RAAG), denoted by GX, is given by the following presentation:
Subgroups of RAAGs can be wild, in particular, not all subgroups of RAAGs are themselves RAAGs. RAAGs that have all their finitely generated subgroups again of this type are known as Droms RAAGs. Droms RAAGs can also be described as the ones where the defining graph does not contain induced squares or straight line paths with 3 edges (see [ Reference Droms18 ]).
A group is coherent if all its finitely generated subgroups are also finitely presented. Droms proved that a RAAG is coherent if and only if its underlying graph contains no full subgraph isomorphic to an n-cycle, for
![]() $n \geq 4$
, see [
Reference Droms17
]. In particular, Droms RAAGs are coherent RAAGs.
$n \geq 4$
, see [
Reference Droms17
]. In particular, Droms RAAGs are coherent RAAGs.
Definition 2·1. Let
![]() $\mathcal{G}$
be a class of groups. The
$\mathcal{G}$
be a class of groups. The
![]() $Z \ast$
-closure of
$Z \ast$
-closure of
![]() $\mathcal{G}$
, denoted by
$\mathcal{G}$
, denoted by
![]() $Z \ast (\mathcal{G})$
, is the union of classes
$Z \ast (\mathcal{G})$
, is the union of classes
![]() $(Z \ast (\mathcal{G}))_{k}$
defined as follows. At level 0, the class
$(Z \ast (\mathcal{G}))_{k}$
defined as follows. At level 0, the class
![]() $(Z \ast (\mathcal{G}))_{0}$
equals
$(Z \ast (\mathcal{G}))_{0}$
equals
![]() $\mathcal{G}$
. A group G lies in
$\mathcal{G}$
. A group G lies in
![]() $(Z \ast (\mathcal{G}))_{k}$
if and only if
$(Z \ast (\mathcal{G}))_{k}$
if and only if
where
![]() $m\in \mathbb{N}\cup \{0\}$
and the group
$m\in \mathbb{N}\cup \{0\}$
and the group
![]() $G_{i}$
lies in
$G_{i}$
lies in
![]() $(Z \ast (\mathcal{G}))_{k-1}$
for all
$(Z \ast (\mathcal{G}))_{k-1}$
for all
![]() $i\in \{1,\dots,n\}$
.
$i\in \{1,\dots,n\}$
.
The level of G, denoted by l(G), is the smallest k for which G belongs to
![]() $(Z \ast (\mathcal{G}))_{k}$
.
$(Z \ast (\mathcal{G}))_{k}$
.
In this terminology, Droms showed in [
Reference Droms18
] that the class of Droms RAAGs is the
![]() $Z\ast-$
closure of
$Z\ast-$
closure of
![]() $\mathbb{Z}$
. Analogously, it is the
$\mathbb{Z}$
. Analogously, it is the
![]() $Z\ast-$
closure of the class of finitely generated free groups. We use the latter when we fix the level of a Droms RAAG.
$Z\ast-$
closure of the class of finitely generated free groups. We use the latter when we fix the level of a Droms RAAG.
Example 2·2. If G is a Droms RAAG such that
![]() $l(G)=0$
, then G is a finite rank free group. If
$l(G)=0$
, then G is a finite rank free group. If
![]() $l(G)=1$
, then
$l(G)=1$
, then
for some
![]() $m \geq 1$
, F free of finite rank and G is not
$m \geq 1$
, F free of finite rank and G is not
![]() $\mathbb{Z}$
. If
$\mathbb{Z}$
. If
![]() $l(G)=2$
, then
$l(G)=2$
, then
for some
![]() $m,n_{i}, k_{i} \in \mathbb{N} \cup \{0\}$
,
$m,n_{i}, k_{i} \in \mathbb{N} \cup \{0\}$
,
![]() $\sum_i n_i \geq 1$
,
$\sum_i n_i \geq 1$
,
![]() $l\geq 2$
and for
$l\geq 2$
and for
![]() $i\in \{1,\dots,l\}$
,
$i\in \{1,\dots,l\}$
,
![]() $F_{k_i}$
free of finite rank
$F_{k_i}$
free of finite rank
![]() $k_i$
.
$k_i$
.
2·2. Limit groups over Droms RAAGs
Definition 2·3. A group
![]() $\Gamma$
is a limit group over a Droms RAAG if it is precisely a finitely generated group that is fully residually a Droms RAAG, that is, for every finite subset S of
$\Gamma$
is a limit group over a Droms RAAG if it is precisely a finitely generated group that is fully residually a Droms RAAG, that is, for every finite subset S of
![]() $\Gamma$
there is a Droms RAAG G together with a homomorphism of groups
$\Gamma$
there is a Droms RAAG G together with a homomorphism of groups
![]() $\varphi \,:\, \Gamma \mapsto G$
whose restriction to S is injective.
$\varphi \,:\, \Gamma \mapsto G$
whose restriction to S is injective.
Definition 2·4. If G is a group, a limit group over G is a group H that is finitely generated and fully residually G, that is, for any finite set of non-trivial elements
![]() $S \subseteq H$
there is a homomorphism
$S \subseteq H$
there is a homomorphism
![]() $\varphi \,:\, H \mapsto G$
which is injective on S.
$\varphi \,:\, H \mapsto G$
which is injective on S.
Note that in Remark 2·4 G is a fixed group but in Remark 2·3 G actually depends on S.
Lemma 2·5.
A group
![]() $\Gamma$
is a limit group over a Droms RAAG if and only if there is a Droms RAAG G such that
$\Gamma$
is a limit group over a Droms RAAG if and only if there is a Droms RAAG G such that
![]() $\Gamma$
is a limit group over G.
$\Gamma$
is a limit group over G.
Proof. It suffices to show that every group
![]() $\Gamma$
that satisfies Remark 2·3 is a limit group over G for some appropriate Droms RAAG G. By definition, for any finite set of non-trivial elements
$\Gamma$
that satisfies Remark 2·3 is a limit group over G for some appropriate Droms RAAG G. By definition, for any finite set of non-trivial elements
![]() $S \subseteq \Gamma$
there is a homomorphism
$S \subseteq \Gamma$
there is a homomorphism
![]() $\varphi_S \,:\, \Gamma \mapsto G_S$
which is injective on S, where
$\varphi_S \,:\, \Gamma \mapsto G_S$
which is injective on S, where
![]() $G_S$
is a Droms RAAG. Then by substituting
$G_S$
is a Droms RAAG. Then by substituting
![]() $G_S$
if necessary with
$G_S$
if necessary with
![]() $\text{im}(\varphi_S)$
(since
$\text{im}(\varphi_S)$
(since
![]() $\text{im}(\varphi_S)$
is a Droms RAAG) we can assume that
$\text{im}(\varphi_S)$
is a Droms RAAG) we can assume that
![]() $d(G_S) \leq d(\Gamma)$
. But since there are only finitely many Droms RAAGs with at most
$d(G_S) \leq d(\Gamma)$
. But since there are only finitely many Droms RAAGs with at most
![]() $d(\Gamma)$
generators, say
$d(\Gamma)$
generators, say
![]() $D_1, \dots, D_t$
, we conclude that
$D_1, \dots, D_t$
, we conclude that
![]() $G_S \in \{ D_1, \ldots, D_t \}$
and
$G_S \in \{ D_1, \ldots, D_t \}$
and
![]() $G_S$
is a subgroup of the fixed Droms RAAG
$G_S$
is a subgroup of the fixed Droms RAAG
![]() $G \,:\!=\, D_1 \ast \cdots \ast D_t$
.
$G \,:\!=\, D_1 \ast \cdots \ast D_t$
.
By [ Reference Baumslag, Miasnikov and Remeslennikov4 , theorem F1], groups that are residually Droms RAAGs are precisely finitely generated subgroups of a finite direct product of limit groups over Droms RAAGs. In this section we state the basic properties of residually Droms RAAGs and limit groups over Droms RAAGs that we need in later sections.
Classical limit groups, i.e. limit groups over free groups, admit a hierarchical structure. Limit groups over free groups are the finitely generated subgroups of
![]() $\omega$
- residually free tower groups, known as
$\omega$
- residually free tower groups, known as
![]() $\omega$
-rft groups (see [
Reference Kharlampovich and Myasnikov20
,
Reference Sela25
]). An
$\omega$
-rft groups (see [
Reference Kharlampovich and Myasnikov20
,
Reference Sela25
]). An
![]() $\omega$
-rft space of height h is defined by induction on h and an
$\omega$
-rft space of height h is defined by induction on h and an
![]() $\omega$
-rft group is the fundamental group of an
$\omega$
-rft group is the fundamental group of an
![]() $\omega$
-rft space. A height 0 space is the wedge of a finite collection of circles, closed hyperbolic surfaces and tori of arbitrary dimension, excluding the closed surface of Euler characteristic
$\omega$
-rft space. A height 0 space is the wedge of a finite collection of circles, closed hyperbolic surfaces and tori of arbitrary dimension, excluding the closed surface of Euler characteristic
![]() $-1$
. An
$-1$
. An
![]() $\omega$
-rft space
$\omega$
-rft space
![]() $Y_h$
of height h is obtained from an
$Y_h$
of height h is obtained from an
![]() $\omega$
-rft space
$\omega$
-rft space
![]() $Y_{h-1}$
of height
$Y_{h-1}$
of height
![]() $h-1$
by attaching a block of abelian or quadratic type (for details see [
Reference Bridson and Howie6
,
Reference Sela25
]). The classical height of a limit group (over a free group) S is the minimal height of an
$h-1$
by attaching a block of abelian or quadratic type (for details see [
Reference Bridson and Howie6
,
Reference Sela25
]). The classical height of a limit group (over a free group) S is the minimal height of an
![]() $\omega$
-rft group that has a subgroup isomorphic to S.
$\omega$
-rft group that has a subgroup isomorphic to S.
Limit groups over Droms RAAGs admit a hierarchical structure that comes from the fact that Droms RAAGs are the direct product of a free abelian group (possibly trivial) and a free product, so we can use the work of Casals–Ruiz and Kazachkov on limit groups over free products (see [ Reference Casals–Ruiz and Kazachkov13 ]) to obtain that hierarchy.
Proposition 2·6 ([
Reference Bridson, Howie, Miller and Short8
, proposition 2·1]). Let G be a Droms RAAG such that
![]() $l(G)=0$
(that is, a finitely generated free group) and let
$l(G)=0$
(that is, a finitely generated free group) and let
![]() $\Gamma$
be a limit group over G of height
$\Gamma$
be a limit group over G of height
![]() $h(\Gamma)$
.
$h(\Gamma)$
.
If
![]() $h(\Gamma)=0$
, then
$h(\Gamma)=0$
, then
![]() $\Gamma$
equals
$\Gamma$
equals
![]() $M_{1}\ast \cdots \ast M_{j}$
and
$M_{1}\ast \cdots \ast M_{j}$
and
![]() $M_{1},\dots,M_{j}$
are free abelian groups or surface groups with Euler characteristic at most
$M_{1},\dots,M_{j}$
are free abelian groups or surface groups with Euler characteristic at most
![]() $-2$
.
$-2$
.
If
![]() $h(\Gamma)\geq 1$
, then
$h(\Gamma)\geq 1$
, then
![]() $\Gamma$
acts cocompactly on a tree T where the edge stabilisers are trivial or infinite cyclic and the vertex groups are limit groups over G of height at most
$\Gamma$
acts cocompactly on a tree T where the edge stabilisers are trivial or infinite cyclic and the vertex groups are limit groups over G of height at most
![]() $h(\Gamma)-1$
. Moreover, at least one of the vertex groups is nonabelian.
$h(\Gamma)-1$
. Moreover, at least one of the vertex groups is nonabelian.
Proposition 2·7 ([
Reference Casals–Ruiz and Kazachkov13
, theorem 8·2]). Let G be a Droms RAAG with
![]() $l(G) \geq 1$
so that G is of the form
$l(G) \geq 1$
so that G is of the form
![]() $\mathbb{Z}^m \times (G_{1}\ast \cdots \ast G_{n})$
and
$\mathbb{Z}^m \times (G_{1}\ast \cdots \ast G_{n})$
and
![]() $l(G_{i}) \leq l(G)-1$
for
$l(G_{i}) \leq l(G)-1$
for
![]() $i\in \{1,\dots,n\}$
and let
$i\in \{1,\dots,n\}$
and let
![]() $\Gamma$
be a limit group over G. Then,
$\Gamma$
be a limit group over G. Then,
![]() $\Gamma$
is
$\Gamma$
is
![]() $\mathbb{Z}^l \times \Lambda$
where
$\mathbb{Z}^l \times \Lambda$
where
![]() $\Lambda$
is a limit group over
$\Lambda$
is a limit group over
![]() $G_{1}\ast \cdots \ast G_{n}$
and if
$G_{1}\ast \cdots \ast G_{n}$
and if
![]() $m=0$
, then
$m=0$
, then
![]() $l=0$
. If
$l=0$
. If
![]() $h(\Lambda)=0$
, then
$h(\Lambda)=0$
, then
where for each
![]() $t\in \{1,\dots,j\}$
,
$t\in \{1,\dots,j\}$
,
![]() $A_{t}$
is a limit group over
$A_{t}$
is a limit group over
![]() $G_{i}$
for some
$G_{i}$
for some
![]() $i\in \{1,\dots,n\}$
.
$i\in \{1,\dots,n\}$
.
If
![]() $h(\Lambda) \geq 1$
, then
$h(\Lambda) \geq 1$
, then
![]() $\Lambda$
acts cocompactly on a tree T where the edge stabilisers are trivial or infinite cyclic and the vertex groups are limit groups over
$\Lambda$
acts cocompactly on a tree T where the edge stabilisers are trivial or infinite cyclic and the vertex groups are limit groups over
![]() $G_{1}\ast \cdots \ast G_{n}$
of height at most
$G_{1}\ast \cdots \ast G_{n}$
of height at most
![]() $h(\Lambda)-1$
. Moreover, at least one of the vertex groups has trivial center.
$h(\Lambda)-1$
. Moreover, at least one of the vertex groups has trivial center.
We observe that the notion of height in limit groups over Droms RAAGs given in Proposition 2·7 is a natural generalisation of the notion of height in limit groups over free groups given in Proposition 2·6 except that, for historical reasons, the definition of limit groups over free groups of height 0 includes more than free products of free abelian groups and allows the free factors to be surface groups with Euler characteristic at most
![]() $-2$
.
$-2$
.
In [ Reference Lopez de Gamiz Zearra23 ], following the paper [ Reference Bridson, Howie, Miller and Short8 ], the results concerning subgroups of direct products of limit groups over free groups were generalised to the case of limit groups over Droms RAAGs.
Theorem 2·8 ([
Reference Lopez de Gamiz Zearra23
, theorem 3·1]). If
![]() $\Gamma_{1},\dots, \Gamma_{n}$
are limit groups over Droms RAAGs and S is a subgroup of
$\Gamma_{1},\dots, \Gamma_{n}$
are limit groups over Droms RAAGs and S is a subgroup of
![]() $\Gamma_{1}\times \cdots \times \Gamma_{n}$
of type
$\Gamma_{1}\times \cdots \times \Gamma_{n}$
of type
![]() $FP_{n}(\mathbb{Q})$
, then S is virtually a direct product of limit groups over Droms RAAGs.
$FP_{n}(\mathbb{Q})$
, then S is virtually a direct product of limit groups over Droms RAAGs.
Theorem 2·9 ([
Reference Lopez de Gamiz Zearra23
, theorem 8·1]). Let
![]() $\Gamma_{1},\dots,\Gamma_{n}$
be limit groups over Droms RAAGs such that each
$\Gamma_{1},\dots,\Gamma_{n}$
be limit groups over Droms RAAGs such that each
![]() $\Gamma_i$
has trivial center and let
$\Gamma_i$
has trivial center and let
![]() $S< \Gamma_{1}\times \cdots \times \Gamma_{n}$
be a finitely generated full subdirect product. Then either:
$S< \Gamma_{1}\times \cdots \times \Gamma_{n}$
be a finitely generated full subdirect product. Then either:
-
(i) S is of finite index; or
-
(ii) S is of infinite index and has a finite index subgroup
 $S_{0}<S$
such that
$S_{0}<S$
such that
 $H_{j}(S_{0}, \mathbb{Q})$
has infinite dimension for some
$H_{j}(S_{0}, \mathbb{Q})$
has infinite dimension for some
 $j\leq n$
.
$j\leq n$
.
Another result that will be used later is associated to finitely presented residually Droms RAAGs. In order to state the result, we introduce the following definition: an embedding
![]() $S \hookrightarrow \Gamma_{0}\times \cdots \times \Gamma_{n}$
of a finitely generated group S that is residually a Droms RAAG as a full subdirect product of limit groups over Droms RAAGs is neat if
$S \hookrightarrow \Gamma_{0}\times \cdots \times \Gamma_{n}$
of a finitely generated group S that is residually a Droms RAAG as a full subdirect product of limit groups over Droms RAAGs is neat if
![]() $\Gamma_{0}$
is abelian (possibly trivial),
$\Gamma_{0}$
is abelian (possibly trivial),
![]() $S \cap \Gamma_{0}$
is of finite index in
$S \cap \Gamma_{0}$
is of finite index in
![]() $\Gamma_{0}$
and
$\Gamma_{0}$
and
![]() $\Gamma_{i}$
has trivial center for
$\Gamma_{i}$
has trivial center for
![]() $i\in \{1,\dots,n\}$
.
$i\in \{1,\dots,n\}$
.
Theorem 2·10 ([ Reference Lopez de Gamiz Zearra23 , theorem 10·1]). Let S be a finitely generated group that is residually a Droms RAAG. The following are equivalent:
-
(i) S is finitely presentable;
-
(ii) S is of type
 $FP_{2}(\mathbb{Q})$
;
$FP_{2}(\mathbb{Q})$
; -
(iii)
 $\dim H_{2}(S_{0},\mathbb{Q})$
is finite for all subgroups
$\dim H_{2}(S_{0},\mathbb{Q})$
is finite for all subgroups
 $S_{0}<S$
of finite index;
$S_{0}<S$
of finite index; -
(iv) there exists a neat embedding
 $S \hookrightarrow \Gamma_{0}\times \cdots \times \Gamma_{n}$
into a product of limit groups over Droms RAAGs such that the image of S under the projection to
$S \hookrightarrow \Gamma_{0}\times \cdots \times \Gamma_{n}$
into a product of limit groups over Droms RAAGs such that the image of S under the projection to
 $\Gamma_{i}\times \Gamma_{j}$
has finite index for
$\Gamma_{i}\times \Gamma_{j}$
has finite index for
 $0\leq i<j \leq n$
;
$0\leq i<j \leq n$
; -
(v) for every neat embedding
 $S \hookrightarrow \Gamma_{0}\times \cdots \times \Gamma_{n}$
into a product of limit groups over Droms RAAGs the image of S under the projection to
$S \hookrightarrow \Gamma_{0}\times \cdots \times \Gamma_{n}$
into a product of limit groups over Droms RAAGs the image of S under the projection to
 $\Gamma_{i}\times \Gamma_{j}$
has finite index for
$\Gamma_{i}\times \Gamma_{j}$
has finite index for
 $0\leq i<j \leq n$
.
$0\leq i<j \leq n$
.
3. Limit groups over Droms RAAGs are free-by-(torsion-free nilpotent)
Definition 3·1. A graph is called triangulated if it contains no induced copy of
![]() $C_{n}$
, for
$C_{n}$
, for
![]() $n\geq 4$
, where
$n\geq 4$
, where
![]() $C_n$
is the circle with n vertices.
$C_n$
is the circle with n vertices.
Recall that a RAAG is coherent precisely when its corresponding graph is triangulated, see [ Reference Droms17 ].
Theorem 3·2 ([
Reference Droms, Servatius and Servatius19
, theorem 2]). If G is the RAAG corresponding to the graph X, the commutator subgroup
![]() $G^\prime$
is free if and only if X is triangulated.
$G^\prime$
is free if and only if X is triangulated.
Lemma 3·3 Coherent RAAGs are free-by-(free abelian).
Proof. Let G be a coherent RAAG corresponding to the graph X. Then,
![]() $G^\prime$
is free, the abelianization is
$G^\prime$
is free, the abelianization is
![]() $\mathbb{Z}^n$
where n is the number of vertices in the graph X and there is a short exact sequence
$\mathbb{Z}^n$
where n is the number of vertices in the graph X and there is a short exact sequence
A filtration
![]() $\{G_{i}\}_{i\geq 1}$
of normal subgroups of a group G has property (i) if
$\{G_{i}\}_{i\geq 1}$
of normal subgroups of a group G has property (i) if
![]() $G / G_{i}$
is torsion-free and
$G / G_{i}$
is torsion-free and
![]() $\bigcap_{i\geq 1} G_{i}=1$
, and it has property (ii) if
$\bigcap_{i\geq 1} G_{i}=1$
, and it has property (ii) if
![]() $\bigcap_{i\geq 1} G_{i}=1$
and for each finitely generated abelian subgroup M of G there is
$\bigcap_{i\geq 1} G_{i}=1$
and for each finitely generated abelian subgroup M of G there is
![]() $i=i(M)$
such that
$i=i(M)$
such that
![]() $G_{i} \cap M=1$
.
$G_{i} \cap M=1$
.
Lemma 3·4.
Let G be a group and
![]() $\{G_{i}\}_{i\geq 1}$
be a filtration of normal subgroups of G. If
$\{G_{i}\}_{i\geq 1}$
be a filtration of normal subgroups of G. If
![]() $\{G_{i}\}_{i\geq 1}$
has property (i), it also has property (ii).
$\{G_{i}\}_{i\geq 1}$
has property (i), it also has property (ii).
Proof. Let M be a finitely generated abelian subgroup of G. Since
![]() $\bigcap_{i\geq 1} G_{i}=1$
, there is i such that
$\bigcap_{i\geq 1} G_{i}=1$
, there is i such that
![]() $G_{i} \cap M$
is not M. The group
$G_{i} \cap M$
is not M. The group
![]() $M / (M \cap G_{i})$
embeds in
$M / (M \cap G_{i})$
embeds in
![]() $G / G_{i}$
, so it is non-trivial and torsion-free, that is, a finite rank free abelian group. As M has finite Hirsch length, we deduce that
$G / G_{i}$
, so it is non-trivial and torsion-free, that is, a finite rank free abelian group. As M has finite Hirsch length, we deduce that
![]() $M \cap G_{j}$
is trivial for sufficiently large j.
$M \cap G_{j}$
is trivial for sufficiently large j.
Lemma 3·5.
Let H be a group, let G be
![]() $\mathbb{Z}^m \times H$
for some
$\mathbb{Z}^m \times H$
for some
![]() $m\in \mathbb{N}$
and let us denote the projection map
$m\in \mathbb{N}$
and let us denote the projection map
![]() $G \mapsto H$
by p. Suppose that
$G \mapsto H$
by p. Suppose that
![]() $\{ G_{i} \}_{i\geq 1}$
is a filtration of normal subgroups of G with property (ii). Then,
$\{ G_{i} \}_{i\geq 1}$
is a filtration of normal subgroups of G with property (ii). Then,
![]() $\{ p(G_{i}) \}_{i\geq 1}$
is a filtration of normal subgroups of H with property (ii).
$\{ p(G_{i}) \}_{i\geq 1}$
is a filtration of normal subgroups of H with property (ii).
Proof. Let us denote
![]() $\mathbb{Z}^m $
by A and let us define
$\mathbb{Z}^m $
by A and let us define
![]() $H_{i}$
to be
$H_{i}$
to be
![]() $p(G_i)$
. Thus,
$p(G_i)$
. Thus,
![]() $AG_{i}= AH_{i}$
. Let C be a finitely generated abelian subgroup of H. Note that the group
$AG_{i}= AH_{i}$
. Let C be a finitely generated abelian subgroup of H. Note that the group
![]() $A(H_{i}\cap C)$
is contained in
$A(H_{i}\cap C)$
is contained in
But since the filtration
![]() $\{G_{i}\}$
has Property (2), there is
$\{G_{i}\}$
has Property (2), there is
![]() $i_{1}= i(AC)$
such that
$i_{1}= i(AC)$
such that
![]() $G_{i_{1}} \cap AC=1$
. To sum up, since
$G_{i_{1}} \cap AC=1$
. To sum up, since
![]() $A \cap C \subseteq A \cap H=1$
,
$A \cap C \subseteq A \cap H=1$
,
![]() $A(H_{i}\cap C)$
being equal to A implies that
$A(H_{i}\cap C)$
being equal to A implies that
![]() $H_{i} \cap C=1$
for
$H_{i} \cap C=1$
for
![]() $i\geq i_{1}$
.
$i\geq i_{1}$
.
Proposition 3·6.
Let G be a Droms RAAG and
![]() $\{G_{i}\}_{i\geq 1}$
be a filtration of normal subgroups of G with property (ii). Then, for sufficiently large
$\{G_{i}\}_{i\geq 1}$
be a filtration of normal subgroups of G with property (ii). Then, for sufficiently large
![]() $i_{0}$
the group
$i_{0}$
the group
![]() $G_{i_{0}}$
is free.
$G_{i_{0}}$
is free.
Proof. Let G be a Droms RAAG of level l(G). If
![]() $l(G)=0$
, then G is a free group, so the statement clearly holds. If
$l(G)=0$
, then G is a free group, so the statement clearly holds. If
![]() $l(G)\geq 1$
, then G equals
$l(G)\geq 1$
, then G equals
![]() $\mathbb{Z}^m \times (K_{1}\ast \cdots \ast K_{k})$
for some
$\mathbb{Z}^m \times (K_{1}\ast \cdots \ast K_{k})$
for some
![]() $m\in \mathbb{N} \cup \{0\}$
and
$m\in \mathbb{N} \cup \{0\}$
and
![]() $K_{1},\dots,K_{k}$
Droms RAAGs of level less than l(G).
$K_{1},\dots,K_{k}$
Droms RAAGs of level less than l(G).
Let us denote
![]() $\mathbb{Z}^m$
and
$\mathbb{Z}^m$
and
![]() $K_{1}\ast \cdots \ast K_{k}$
by A and H, respectively, and the projection map
$K_{1}\ast \cdots \ast K_{k}$
by A and H, respectively, and the projection map
![]() $G \mapsto H$
by p. By hypothesis, there is
$G \mapsto H$
by p. By hypothesis, there is
![]() $i_{1}=i(A)$
such that
$i_{1}=i(A)$
such that
![]() $A \cap G_{i_{1}}=1$
.
$A \cap G_{i_{1}}=1$
.
Let us define
![]() $H_{i}$
to be
$H_{i}$
to be
![]() $p(G_i)$
. From Lemma 3·5 we get that there is
$p(G_i)$
. From Lemma 3·5 we get that there is
![]() $i_{2}\geq 1$
such that
$i_{2}\geq 1$
such that
![]() $\{H_{i}\}_{i\geq i_{2}}$
is a filtration of H with property (ii), so for
$\{H_{i}\}_{i\geq i_{2}}$
is a filtration of H with property (ii), so for
![]() $i_{3} = \max \{i_{1},i_{2}\}$
the filtration
$i_{3} = \max \{i_{1},i_{2}\}$
the filtration
![]() $\{H_{i}\}_{i\geq i_{3}}$
of normal subgroups of H has property (ii) and
$\{H_{i}\}_{i\geq i_{3}}$
of normal subgroups of H has property (ii) and
![]() $G_{i} \simeq H_{i}$
.
$G_{i} \simeq H_{i}$
.
The group
![]() $H_{i}$
is a free product of conjugates of
$H_{i}$
is a free product of conjugates of
![]() $H_{i} \cap K_{j}$
for
$H_{i} \cap K_{j}$
for
![]() $j\in \{1,\dots,k\}$
and a free group. For
$j\in \{1,\dots,k\}$
and a free group. For
![]() $j\in \{1,\dots, k\}$
,
$j\in \{1,\dots, k\}$
,
![]() $\{ H_{i} \cap K_{j}\}_{i\geq i_{3}}$
is a filtration of normal subgroups of
$\{ H_{i} \cap K_{j}\}_{i\geq i_{3}}$
is a filtration of normal subgroups of
![]() $K_{j}$
with property (ii), so by inductive hypothesis, there is
$K_{j}$
with property (ii), so by inductive hypothesis, there is
![]() $s_{j}$
such that
$s_{j}$
such that
![]() $H_{s_{j}} \cap K_{j}$
is free. In conclusion, by taking
$H_{s_{j}} \cap K_{j}$
is free. In conclusion, by taking
![]() $s_{0}$
to be
$s_{0}$
to be
![]() $\max \{s_{1},\dots,s_{k}\}$
,
$\max \{s_{1},\dots,s_{k}\}$
,
![]() $H_{s_{0}}$
is a free group.
$H_{s_{0}}$
is a free group.
Theorem 3·7.
Let G be a Droms RAAG with filtration
![]() $\{G_{i}\}_{i \geq 1}$
of normal subgroups such that
$\{G_{i}\}_{i \geq 1}$
of normal subgroups such that
![]() $G / G_{i}$
is torsion-free and
$G / G_{i}$
is torsion-free and
![]() $\bigcap_{i\geq 1} G_{i}=1$
. Then, for sufficiently large
$\bigcap_{i\geq 1} G_{i}=1$
. Then, for sufficiently large
![]() $i_{0}$
the group
$i_{0}$
the group
![]() $G_{i_{0}}$
is free.
$G_{i_{0}}$
is free.
In order to show that limit groups over Droms RAAGs are free-by-(torsion-free nilpotent), we will show that ICE groups over Droms RAAGs are free-by-(torsion-free nilpotent). A limit group over a Droms RAAG is a finitely generated subgroup of an ICE group over a Droms RAAG, so it will also be free-by-(torsion-free nilpotent).
Let us start recalling the definition of ICE groups over Droms RAAGs given in [ Reference Casals–Ruiz, Duncan and Kazachkov11 ].
Definition 3·8. Let H be a group and
![]() $Z \subseteq H$
the centraliser of an element. Then, the group
$Z \subseteq H$
the centraliser of an element. Then, the group
![]() $G= H \ast_{Z} (Z \times \mathbb{Z}^n)$
is said to be obtained from H by an extension of a centraliser. An ICE group over H is a group obtained from H by applying finitely many times the extension of a centraliser construction. In the classic limit groups, the standard condition that is asked is that the abelian subgroup Z is maximal in one of the vertex groups and indeed this assures 2-acylindricity of the action. However, if one asks Z to be not just abelian but a centraliser of an element, this maximality condition is satisfied.
$G= H \ast_{Z} (Z \times \mathbb{Z}^n)$
is said to be obtained from H by an extension of a centraliser. An ICE group over H is a group obtained from H by applying finitely many times the extension of a centraliser construction. In the classic limit groups, the standard condition that is asked is that the abelian subgroup Z is maximal in one of the vertex groups and indeed this assures 2-acylindricity of the action. However, if one asks Z to be not just abelian but a centraliser of an element, this maximality condition is satisfied.
Theorem 3·9 ([ Reference Casals–Ruiz, Duncan and Kazachkov11 ]). All ICE groups over Droms RAAGs are limit groups over Droms RAAGs. Moreover, a group is a limit group over a Droms RAAG if and only if it is a finitely generated subgroup of an ICE group over a Droms RAAG.
Remark 3·10. In [ Reference Casals–Ruiz, Duncan and Kazachkov11 , lemma 7·5] it is proved that any ICE over a Droms RAAG can be obtained by first extending centralisers of central elements, then extending centralisers of elliptic elements and finally considering extensions of centralisers of hyperbolic elements.
If G is a Droms RAAG such that
![]() $l(G)=0$
, then the centraliser of any non-trivial element
$l(G)=0$
, then the centraliser of any non-trivial element
![]() $t \in G$
is the infinite cyclic group
$t \in G$
is the infinite cyclic group
![]() $\langle t_1 \rangle$
, where
$\langle t_1 \rangle$
, where
![]() $\langle t \rangle \subseteq \langle t_1 \rangle$
and
$\langle t \rangle \subseteq \langle t_1 \rangle$
and
![]() $[\langle t_1 \rangle : \langle t \rangle] $
is maximal possible.
$[\langle t_1 \rangle : \langle t \rangle] $
is maximal possible.
Now let G be a Droms RAAG of the form
![]() $\mathbb{Z}^t \times (G_{1}\ast \cdots \ast G_{f})$
for
$\mathbb{Z}^t \times (G_{1}\ast \cdots \ast G_{f})$
for
![]() $t,f\in \mathbb{N} \cup \{0\}$
such that
$t,f\in \mathbb{N} \cup \{0\}$
such that
![]() $l(G_{i}) \leq l(G)-1$
for
$l(G_{i}) \leq l(G)-1$
for
![]() $i\in \{1,\dots,f\}$
, let
$i\in \{1,\dots,f\}$
, let
![]() $g\in G$
and let us denote the centraliser of g in G by
$g\in G$
and let us denote the centraliser of g in G by
![]() $C_{G}(g)$
.
$C_{G}(g)$
.
Firstly, by the result [
Reference Casals–Ruiz, Duncan and Kazachkov11
, lemma 7·5] mentioned above, we shall start extending centralisers of central elements. If
![]() $g\in \mathbb{Z}^t$
, then
$g\in \mathbb{Z}^t$
, then
![]() $C_{G}(g)= G$
, so the extension of a centraliser construction gives
$C_{G}(g)= G$
, so the extension of a centraliser construction gives
and we again get a Droms RAAG. That is, extending centralisers of central elements in Droms RAAGs leads to another Droms RAAG. Suppose that after extending centralisers of central elements, we have constructed the group
![]() $\mathbb{Z}^m \times (G_1 \ast \cdots \ast G_n)$
.
$\mathbb{Z}^m \times (G_1 \ast \cdots \ast G_n)$
.
Secondly, we extend centralisers of elliptic elements, so we assume that
![]() $g \in \mathbb{Z}^m g_0$
,
$g \in \mathbb{Z}^m g_0$
,
![]() $g_0 \neq 1$
and
$g_0 \neq 1$
and
![]() $g_0$
is an elliptic element in
$g_0$
is an elliptic element in
![]() $G_{1}\ast \cdots \ast G_{n}$
. Then,
$G_{1}\ast \cdots \ast G_{n}$
. Then,
![]() $g_0 \in \bigcup_{1 \leq i \leq n} G_i^G$
,
$g_0 \in \bigcup_{1 \leq i \leq n} G_i^G$
,
![]() $C_G(g) = C_G( g_0)$
and we can assume without loss of generality that
$C_G(g) = C_G( g_0)$
and we can assume without loss of generality that
![]() $g = g_0$
. Since extensions of centralizers are conjugate invariant, we can assume that
$g = g_0$
. Since extensions of centralizers are conjugate invariant, we can assume that
![]() $g \in G_{i}$
for some
$g \in G_{i}$
for some
![]() $i\in \{1,\dots,n\}$
. Thus,
$i\in \{1,\dots,n\}$
. Thus,
Therefore,
 \begin{align*} & G \ast_{C_{G}(g)} \left(C_{G}(g) \times \mathbb{Z}^k\right)\\& \quad \simeq\mathbb{Z}^m \times \Big{(}G_{1} \ast \cdots \ast G_{i-1} \ast \big{(}G_{i} \ast_{C_{G_{i}}(g)} (\mathbb{Z}^k \times C_{G_{i}}(g))\big{)} \ast G_{i+1} \ast \cdots \ast G_{n} \Big{)},\end{align*}
\begin{align*} & G \ast_{C_{G}(g)} \left(C_{G}(g) \times \mathbb{Z}^k\right)\\& \quad \simeq\mathbb{Z}^m \times \Big{(}G_{1} \ast \cdots \ast G_{i-1} \ast \big{(}G_{i} \ast_{C_{G_{i}}(g)} (\mathbb{Z}^k \times C_{G_{i}}(g))\big{)} \ast G_{i+1} \ast \cdots \ast G_{n} \Big{)},\end{align*}
so we get a group of the form
![]() $H\,:\!=\, \mathbb{Z}^{m} \times (H_1 \ast \cdots \ast H_n)$
. Elliptic elements of H lie again in
$H\,:\!=\, \mathbb{Z}^{m} \times (H_1 \ast \cdots \ast H_n)$
. Elliptic elements of H lie again in
![]() $ \mathbb{Z}^{m} g_0$
with
$ \mathbb{Z}^{m} g_0$
with
![]() $g_0 \neq 1$
and
$g_0 \neq 1$
and
![]() $g_0$
elliptic in
$g_0$
elliptic in
![]() $H_1 \ast \cdots \ast H_n$
. Extending centralisers of elliptic elements in groups of this form thus ends up giving again a group of the form
$H_1 \ast \cdots \ast H_n$
. Extending centralisers of elliptic elements in groups of this form thus ends up giving again a group of the form
![]() $\mathbb{Z}^l \times (K_1 \ast \cdots \ast K_v)$
.
$\mathbb{Z}^l \times (K_1 \ast \cdots \ast K_v)$
.
Thirdly, we shall extend the centraliser of a hyperbolic element in a group of the form
![]() $K \,:\!=\, \mathbb{Z}^l \times (K_1 \ast \cdots \ast K_v)$
. Hence, assume that
$K \,:\!=\, \mathbb{Z}^l \times (K_1 \ast \cdots \ast K_v)$
. Hence, assume that
![]() $g \in \mathbb{Z}^l g_0$
,
$g \in \mathbb{Z}^l g_0$
,
![]() $g_0 \neq 1$
and
$g_0 \neq 1$
and
![]() $g_0$
is a hyperbolic element in
$g_0$
is a hyperbolic element in
![]() $K_{1}\ast \cdots \ast K_{v}$
. Then,
$K_{1}\ast \cdots \ast K_{v}$
. Then,
![]() $g_0 \in (K_{1}\ast \cdots \ast K_{v}) \setminus \left(\bigcup_{1 \leq i \leq v} K_i^K\right)$
,
$g_0 \in (K_{1}\ast \cdots \ast K_{v}) \setminus \left(\bigcup_{1 \leq i \leq v} K_i^K\right)$
,
![]() $C_K(g) = C_K( g_0)$
and we can assume without loss of generality that
$C_K(g) = C_K( g_0)$
and we can assume without loss of generality that
![]() $g = g_0$
. Hence,
$g = g_0$
. Hence,
![]() $C_{K}(g)= \mathbb{Z}^l \times {\langle g_1 \rangle} \simeq \mathbb{Z}^{l+1}$
, where
$C_{K}(g)= \mathbb{Z}^l \times {\langle g_1 \rangle} \simeq \mathbb{Z}^{l+1}$
, where
![]() $\langle g \rangle \subseteq \langle g_1 \rangle$
and
$\langle g \rangle \subseteq \langle g_1 \rangle$
and
![]() $[\langle g_1 \rangle : \langle g \rangle] $
is maximal possible, and
$[\langle g_1 \rangle : \langle g \rangle] $
is maximal possible, and
 \begin{align*} K \ast_{C_{K}(g)} (C_{K}(g) \times \mathbb{Z}^k)& \simeq \Big{(}\mathbb{Z}^l \times (K_{1}\ast \cdots \ast K_{v})\Big{)} \ast_{\mathbb{Z}^l \times \langle g_1 \rangle} \left(\mathbb{Z}^l \times \langle g_1 \rangle \times \mathbb{Z}^k\right)\\ & \simeq \mathbb{Z}^l \times\Big{(} (K_{1}\ast \cdots \ast K_{v}) \ast_{\mathbb{Z}} \mathbb{Z}^{k+1} \Big{)}. \end{align*}
\begin{align*} K \ast_{C_{K}(g)} (C_{K}(g) \times \mathbb{Z}^k)& \simeq \Big{(}\mathbb{Z}^l \times (K_{1}\ast \cdots \ast K_{v})\Big{)} \ast_{\mathbb{Z}^l \times \langle g_1 \rangle} \left(\mathbb{Z}^l \times \langle g_1 \rangle \times \mathbb{Z}^k\right)\\ & \simeq \mathbb{Z}^l \times\Big{(} (K_{1}\ast \cdots \ast K_{v}) \ast_{\mathbb{Z}} \mathbb{Z}^{k+1} \Big{)}. \end{align*}
In this case, we obtain a group of the form
![]() $H \,:\!=\, \mathbb{Z}^{l} \times (A \ast_{B} C)$
. Hyperbolic elements of this group are elements
$H \,:\!=\, \mathbb{Z}^{l} \times (A \ast_{B} C)$
. Hyperbolic elements of this group are elements
![]() $g\in \mathbb{Z}^{l}g_0$
with
$g\in \mathbb{Z}^{l}g_0$
with
![]() $g_0$
hyperbolic in
$g_0$
hyperbolic in
![]() $A\ast_{B} C$
, that is,
$A\ast_{B} C$
, that is,
![]() $g_0 \in (A\ast_B C) \setminus \left(A^H \cup C^H\right)$
and extending centralizers of hyperbolic elements in groups of this form yields a group with the same structure.
$g_0 \in (A\ast_B C) \setminus \left(A^H \cup C^H\right)$
and extending centralizers of hyperbolic elements in groups of this form yields a group with the same structure.
Thus, the class of ICE groups over Droms RAAGs can be given the following hierarchical structure.
Definition 3·11. Assume that G is a Droms RAAG of level 0, that is, G is a free group. An ICE group over G of altitude 0 is precisely G. An ICE group over G of altitude
![]() $k\geq 1$
is an amalgamated free product over
$k\geq 1$
is an amalgamated free product over
![]() $\mathbb{Z}^{n_0}$
of an ICE group over G of altitude
$\mathbb{Z}^{n_0}$
of an ICE group over G of altitude
![]() $\leq k-1$
and a free abelian group
$\leq k-1$
and a free abelian group
![]() $\mathbb{Z}^{n_0} \times \mathbb{Z}^{m_0 }$
, where
$\mathbb{Z}^{n_0} \times \mathbb{Z}^{m_0 }$
, where
![]() $\mathbb{Z}^{n_0}$
embeds in
$\mathbb{Z}^{n_0}$
embeds in
![]() $\mathbb{Z}^{n_0} \times \mathbb{Z}^{m_0}$
naturally.
$\mathbb{Z}^{n_0} \times \mathbb{Z}^{m_0}$
naturally.
Assume that G is a Droms RAAG of level
![]() $l\geq 1$
, that is,
$l\geq 1$
, that is,
![]() $G= \mathbb Z^m \times (G_1 \ast \cdots \ast G_n)$
where each
$G= \mathbb Z^m \times (G_1 \ast \cdots \ast G_n)$
where each
![]() $G_i$
is a Droms RAAG of level less than l. An ICE group over G of altitude 0 is of the form
$G_i$
is a Droms RAAG of level less than l. An ICE group over G of altitude 0 is of the form
![]() $\mathbb Z^{m^\prime} \times (H_1 \ast \cdots \ast H_n)$
where
$\mathbb Z^{m^\prime} \times (H_1 \ast \cdots \ast H_n)$
where
![]() $m^\prime \geq m$
and
$m^\prime \geq m$
and
![]() $H_i$
is an ICE group over
$H_i$
is an ICE group over
![]() $G_i$
for
$G_i$
for
![]() $i\in \{1,\dots, n\}$
.
$i\in \{1,\dots, n\}$
.
An ICE group over G of altitude
![]() $k\geq 1$
is an amalgamated free product over
$k\geq 1$
is an amalgamated free product over
![]() $\mathbb{Z}^{n_0}$
of an ICE group over G of altitude
$\mathbb{Z}^{n_0}$
of an ICE group over G of altitude
![]() $\leq k-1$
and a free abelian group
$\leq k-1$
and a free abelian group
![]() $\mathbb{Z}^{n_0} \times \mathbb{Z}^{m_0}$
, where
$\mathbb{Z}^{n_0} \times \mathbb{Z}^{m_0}$
, where
![]() $\mathbb{Z}^{n_0}$
embeds in
$\mathbb{Z}^{n_0}$
embeds in
![]() $\mathbb{Z}^{n_0} \times \mathbb{Z}^{m_0}$
naturally.
$\mathbb{Z}^{n_0} \times \mathbb{Z}^{m_0}$
naturally.
Remark 3·12. The term used in the literature for the altitude of ICE groups over free groups is level. However, since level has been used when defining Droms RAAGs hierarchically, we have decided to use altitude for ICE groups over Droms RAAGs.
Theorem 3·13.
Let G be a Droms RAAG and let K be an ICE group over G. Let
![]() $\{{K }_{i}\}_{i \geq 1}$
be a filtration of normal subgroups of K with property (ii). Then, for sufficiently large
$\{{K }_{i}\}_{i \geq 1}$
be a filtration of normal subgroups of K with property (ii). Then, for sufficiently large
![]() $i_{0}$
the group
$i_{0}$
the group
![]() ${K }_{i_{0}}$
is free.
${K }_{i_{0}}$
is free.
Proof. We prove it by induction on the level l(G) of G as a Droms RAAG. Suppose that
![]() $l(G)=0$
. Then, if K has altitude 0, K is precisely G which is a free group, and the result is obvious. If K has altitude
$l(G)=0$
. Then, if K has altitude 0, K is precisely G which is a free group, and the result is obvious. If K has altitude
![]() $\geq 1$
, then K is of the form
$\geq 1$
, then K is of the form
and H is an ICE group over G of smaller altitude than K. Since
![]() $K_{i}$
is a normal subgroup of K,
$K_{i}$
is a normal subgroup of K,
![]() $K_{i}$
inherits a graph of groups decomposition where the vertex groups are of the form
$K_{i}$
inherits a graph of groups decomposition where the vertex groups are of the form
and the edge groups are of the form
Note that
![]() $\{K_{i} \cap H \}_{i\geq 1}$
is a filtration of H with property (ii), so by inductive hypothesis, there is
$\{K_{i} \cap H \}_{i\geq 1}$
is a filtration of H with property (ii), so by inductive hypothesis, there is
![]() $i_{1}$
such that
$i_{1}$
such that
![]() $K_{i_{1}} \cap H$
is free. In addition, the filtration
$K_{i_{1}} \cap H$
is free. In addition, the filtration
![]() $\{K_{i}\}_{i\geq 1}$
has property (ii), so there is
$\{K_{i}\}_{i\geq 1}$
has property (ii), so there is
![]() $i_{2}= i(\mathbb{Z}^{m_{0}} \times \mathbb{Z}^{n_0})$
such that
$i_{2}= i(\mathbb{Z}^{m_{0}} \times \mathbb{Z}^{n_0})$
such that
![]() $K_{i_{2}} \cap (\mathbb{Z}^{m_0} \times \mathbb{Z}^{ n_0})$
is trivial. In particular,
$K_{i_{2}} \cap (\mathbb{Z}^{m_0} \times \mathbb{Z}^{ n_0})$
is trivial. In particular,
![]() $K_{i_{2}} \cap \mathbb{Z}^{n_0}$
is also trivial. Therefore, taking
$K_{i_{2}} \cap \mathbb{Z}^{n_0}$
is also trivial. Therefore, taking
![]() $i_{0}$
to be
$i_{0}$
to be
![]() $\max \{i_{1}, i_{2}\}$
,
$\max \{i_{1}, i_{2}\}$
,
![]() $K_{i_{0}}$
is free.
$K_{i_{0}}$
is free.
Now suppose that
![]() $l(G) \geq 1$
. Then, G is of the form
$l(G) \geq 1$
. Then, G is of the form
for some
![]() $m\in \mathbb{N} \cup \{0\}$
and
$m\in \mathbb{N} \cup \{0\}$
and
![]() $G_{i}$
is a Droms RAAG with
$G_{i}$
is a Droms RAAG with
![]() $l(G_{i}) \leq l(G)-1$
for each
$l(G_{i}) \leq l(G)-1$
for each
![]() $i\in \{1,\dots,n\}$
. If K has altitude 0 as an ICE group over G, then
$i\in \{1,\dots,n\}$
. If K has altitude 0 as an ICE group over G, then
where
![]() $m^\prime \geq m$
and
$m^\prime \geq m$
and
![]() $H_{i}$
is an ICE group over
$H_{i}$
is an ICE group over
![]() $G_{i}$
for
$G_{i}$
for
![]() $i\in \{1,\dots,n\}$
. Let us denote the projection map
$i\in \{1,\dots,n\}$
. Let us denote the projection map
![]() $K \mapsto H_{1}\ast \cdots \ast H_{n}$
by p.
$K \mapsto H_{1}\ast \cdots \ast H_{n}$
by p.
By hypothesis, there is
![]() $i_{1}= i(\mathbb{Z}^{m^\prime})$
such that
$i_{1}= i(\mathbb{Z}^{m^\prime})$
such that
![]() $\mathbb{Z}^{m^\prime} \cap K_{i_{1}}=1$
. In addition, by Lemma 3·5,
$\mathbb{Z}^{m^\prime} \cap K_{i_{1}}=1$
. In addition, by Lemma 3·5,
![]() $\{ N_{i}\}_{i\geq 1}$
is a filtration of normal subgroups of
$\{ N_{i}\}_{i\geq 1}$
is a filtration of normal subgroups of
![]() $H_{1}\ast \cdots \ast H_{n}$
with property (ii), where
$H_{1}\ast \cdots \ast H_{n}$
with property (ii), where
![]() $N_{i}= p(K_{i})$
. As a consequence,
$N_{i}= p(K_{i})$
. As a consequence,
![]() $N_{i} \simeq K_{i}$
for
$N_{i} \simeq K_{i}$
for
![]() $i \geq i_1$
.
$i \geq i_1$
.
Note that the group
![]() $N_{i}$
is a free product of conjugates of
$N_{i}$
is a free product of conjugates of
![]() $N_{i} \cap H_{j}$
for
$N_{i} \cap H_{j}$
for
![]() $j\in \{1,\dots,n\}$
and a free group. For
$j\in \{1,\dots,n\}$
and a free group. For
![]() $j\in \{1,\dots,n\}$
,
$j\in \{1,\dots,n\}$
,
![]() $\{N_{i} \cap H_{j}\}_{i\geq 1}$
is a filtration of normal subgroups of
$\{N_{i} \cap H_{j}\}_{i\geq 1}$
is a filtration of normal subgroups of
![]() $H_{j}$
with property (ii), so by inductive hypothesis, there is
$H_{j}$
with property (ii), so by inductive hypothesis, there is
![]() $r_{j}$
such that
$r_{j}$
such that
![]() $N_{r_{j}} \cap H_{j}$
is free. In conclusion, taking
$N_{r_{j}} \cap H_{j}$
is free. In conclusion, taking
![]() $i_{0}$
to be
$i_{0}$
to be
![]() $\max \{i_1, r_{1},\dots,r_{n} \}$
,
$\max \{i_1, r_{1},\dots,r_{n} \}$
,
![]() $N_{i_{0}}$
is a free group.
$N_{i_{0}}$
is a free group.
Finally, suppose that K is an ICE group over G of altitude
![]() $k \geq 1$
. Then, K is an amalgamated free product over
$k \geq 1$
. Then, K is an amalgamated free product over
![]() $\mathbb{Z}^{n_0}$
of an ICE group over G of altitude
$\mathbb{Z}^{n_0}$
of an ICE group over G of altitude
![]() $\leq k-1$
and a free abelian group
$\leq k-1$
and a free abelian group
![]() $\mathbb{Z}^{ n_0} \times \mathbb{Z}^{ m_0}$
. This case may be treated as the case when K is an ICE group of altitude greater than 0 over a free group.
$\mathbb{Z}^{ n_0} \times \mathbb{Z}^{ m_0}$
. This case may be treated as the case when K is an ICE group of altitude greater than 0 over a free group.
Recall that
![]() $\gamma_i(G)$
denotes the lower central series of a group G. That is,
$\gamma_i(G)$
denotes the lower central series of a group G. That is,
We denote by tor(G) the set of torsion elements of G. In the case when G is finitely generated nilpotent, then
![]() $\langle tor(G) \rangle$
is the maximal finite subgroup of G.
$\langle tor(G) \rangle$
is the maximal finite subgroup of G.
Theorem 3·14.
Let G be a Droms RAAG, let K be an ICE group over G and define
![]() $K_{i}$
to be
$K_{i}$
to be
![]() $K_{i} / \gamma_{i}(K)= \langle \text{tor}(K / \gamma_{i}(K)) \rangle$
. Then,
$K_{i} / \gamma_{i}(K)= \langle \text{tor}(K / \gamma_{i}(K)) \rangle$
. Then,
![]() $K_{i+1} < K_{i}$
,
$K_{i+1} < K_{i}$
,
![]() $K_{i}$
is normal in K,
$K_{i}$
is normal in K,
![]() $K / K_{i}$
is torsion-free nilpotent and
$K / K_{i}$
is torsion-free nilpotent and
![]() $\bigcap_{i\geq 1} K_{i}=1$
.
$\bigcap_{i\geq 1} K_{i}=1$
.
Proof. By construction,
![]() $K_i / \gamma_i(K)$
is a characteristic subgroup of
$K_i / \gamma_i(K)$
is a characteristic subgroup of
![]() $K / \gamma_i(K)$
, so
$K / \gamma_i(K)$
, so
![]() $K_i$
is normal in K and
$K_i$
is normal in K and
![]() $K_{i+1} < K_i$
. It remains to show that
$K_{i+1} < K_i$
. It remains to show that
![]() $\bigcap_{i} K_i = 1$
. Suppose that
$\bigcap_{i} K_i = 1$
. Suppose that
![]() $k \in (\bigcap_{i} K_i) \setminus \{ 1 \}$
. Since K is a limit group over G, there is a homomorphism
$k \in (\bigcap_{i} K_i) \setminus \{ 1 \}$
. Since K is a limit group over G, there is a homomorphism
![]() $\varphi \,:\, K \mapsto G$
such that
$\varphi \,:\, K \mapsto G$
such that
![]() $\varphi(k) \not= 1$
. Let
$\varphi(k) \not= 1$
. Let
![]() $G_0 = \text{im}(\varphi)$
, so
$G_0 = \text{im}(\varphi)$
, so
![]() $G_0$
is a Droms RAAG. By [
Reference Wade26
, theorem 6·4], we have that
$G_0$
is a Droms RAAG. By [
Reference Wade26
, theorem 6·4], we have that
![]() $G_0 / \gamma_{i}(G_0)$
is torsion-free, hence
$G_0 / \gamma_{i}(G_0)$
is torsion-free, hence
![]() $\varphi(K_i) = \varphi(\gamma_i(K)) $
. Then
$\varphi(K_i) = \varphi(\gamma_i(K)) $
. Then
![]() $\varphi(k) \in \bigcap_i \varphi(K_i) = \bigcap_i \varphi(\gamma_i(K)) \subseteq \bigcap_i \gamma_i(G) = 1$
, a contradiction.
$\varphi(k) \in \bigcap_i \varphi(K_i) = \bigcap_i \varphi(\gamma_i(K)) \subseteq \bigcap_i \gamma_i(G) = 1$
, a contradiction.
Corollary 3·15 Every ICE group over a Droms RAAG is free-by-(torsion-free nilpotent).
Proposition 3·16. Every limit group over a Droms RAAG is free-by-(torsion-free nilpotent).
4. Corollaries on subdirect products of limit groups over Droms RAAGs
In this section we aim to prove Theorem 1·1. Theorem 1·1 is a generalisation of [ Reference Kochloukova21 , theorem 11].
Theorem 4·1 ([
Reference Kochloukova21
, theorem 11]). Let
![]() $G_1, \dots, G_m$
be non-abelian limit groups over free groups and let
$G_1, \dots, G_m$
be non-abelian limit groups over free groups and let
be a finitely generated subdirect product intersecting each factor
![]() $G_i$
non-trivially. Suppose further that, for some fixed natural number
$G_i$
non-trivially. Suppose further that, for some fixed natural number
![]() $s \in \{ 2, \ldots, m \}$
, for every subgroup
$s \in \{ 2, \ldots, m \}$
, for every subgroup
![]() $S_0$
of finite index in S the homology group
$S_0$
of finite index in S the homology group
![]() $H_i (S_0 , \mathbb{Q})$
is finite dimensional (over
$H_i (S_0 , \mathbb{Q})$
is finite dimensional (over
![]() $\mathbb{Q}$
) for all
$\mathbb{Q}$
) for all
![]() $i \leq s$
. Then for every canonical projection
$i \leq s$
. Then for every canonical projection
the index of
![]() $p_{j_1, \dots, j_s} (S)$
in
$p_{j_1, \dots, j_s} (S)$
in
![]() $G_{j_1} \times \cdots \times G_{ j_s}$
is finite.
$G_{j_1} \times \cdots \times G_{ j_s}$
is finite.
We observe that in [
Reference Kochloukova21
] the domain of
![]() $p_{j_1, \dots, j_s}$
is defined to be G and not as we stated it above, but in [
Reference Bridson, Howie, Miller and Short7
,
Reference Bridson, Howie, Miller and Short8
] it is S. It looks more convenient to stick to the latter.
$p_{j_1, \dots, j_s}$
is defined to be G and not as we stated it above, but in [
Reference Bridson, Howie, Miller and Short7
,
Reference Bridson, Howie, Miller and Short8
] it is S. It looks more convenient to stick to the latter.
The starting point in the proof of Theorem 1·1 is that the proof of Theorem 4·1 applies in bigger generality. We explain this in the following result.
Theorem 4·2.
Let
![]() $2 \leq s \leq m$
be integers and
$2 \leq s \leq m$
be integers and
![]() $S < G_1 \times \dots \times G_m$
be a finitely generated subdirect product such that:
$S < G_1 \times \dots \times G_m$
be a finitely generated subdirect product such that:
-
(i) there exist normal free subgroups
 $L_i$
in
$L_i$
in
 $G_i$
with
$G_i$
with
 $Q_i \,:\!=\, G_i / L_i$
nilpotent;
$Q_i \,:\!=\, G_i / L_i$
nilpotent; -
(ii) each
 $G_i$
is finitely presented;
$G_i$
is finitely presented; -
(iii) for every
 $1 \leq j_1 < \dots < j_s \leq m$
if
$1 \leq j_1 < \dots < j_s \leq m$
if
 $M_{j_1, \dots, j_s} $
is a subgroup of infinite index in the group
$M_{j_1, \dots, j_s} $
is a subgroup of infinite index in the group
 $G_{j_1} \times \cdots \times G_{j_s}$
, then there exists
$G_{j_1} \times \cdots \times G_{j_s}$
, then there exists
 $i \leq s$
and a subgroup
$i \leq s$
and a subgroup
 $M_{j_1, \ldots, j_s}^0$
of finite index in
$M_{j_1, \ldots, j_s}^0$
of finite index in
 $M_{j_1, \ldots, j_s}$
such that
$M_{j_1, \ldots, j_s}$
such that
 $H_i(M_{j_1, \ldots, j_s}^0, \mathbb{Q})$
is infinite dimensional over
$H_i(M_{j_1, \ldots, j_s}^0, \mathbb{Q})$
is infinite dimensional over
 $\mathbb{Q}$
;
$\mathbb{Q}$
; -
(iv) for every
 $1 \leq j_1 < \dots < j_s \leq m$
and every subgroup
$1 \leq j_1 < \dots < j_s \leq m$
and every subgroup
 $H_{j_i}$
of finite index in
$H_{j_i}$
of finite index in
 $G_{j_i}$
we have that if a subdirect product
$G_{j_i}$
we have that if a subdirect product
 $M_{j_1, \dots, j_s} \subseteq H_{j_1} \times \cdots \times H_{j_s}$
is finitely presented, then there is a subgroup
$M_{j_1, \dots, j_s} \subseteq H_{j_1} \times \cdots \times H_{j_s}$
is finitely presented, then there is a subgroup
 $K_{j_i}$
of finite index in
$K_{j_i}$
of finite index in
 $H_{j_i}$
and
$H_{j_i}$
and
 $N_{j_i}$
a normal subgroup of
$N_{j_i}$
a normal subgroup of
 $H_{j_i}$
such that
$H_{j_i}$
such that
 $K_{j_i} / N_{j_i}$
is nilpotent and
$K_{j_i} / N_{j_i}$
is nilpotent and
 $N_{j_1} \times \cdots \times N_{j_s} \subseteq M_{j_1, \ldots, j_s }$
;
$N_{j_1} \times \cdots \times N_{j_s} \subseteq M_{j_1, \ldots, j_s }$
; -
(v) S virtually surjects on pairs;
-
(vi)
 $L \,:\!=\, L_1 \times \cdots \times L_m \subseteq S$
;
$L \,:\!=\, L_1 \times \cdots \times L_m \subseteq S$
; -
(vii) for every subgroup
 $S_0$
of finite index in S, the homology group
$S_0$
of finite index in S, the homology group
 $H_i (S_0 , \mathbb{Q})$
is finite dimensional (over
$H_i (S_0 , \mathbb{Q})$
is finite dimensional (over
 $\mathbb{Q}$
) for all
$\mathbb{Q}$
) for all
 $ i \leq s$
.
$ i \leq s$
.
Then for every canonical projection
the index of
![]() $p_{j_1, \ldots, j_s} (S)$
in
$p_{j_1, \ldots, j_s} (S)$
in
![]() $G_{j_1} \times \cdots \times G_{ j_s}$
is finite.
$G_{j_1} \times \cdots \times G_{ j_s}$
is finite.
Proof. We will prove the result by induction on s. For
![]() $s = 2$
, this is condition (v).
$s = 2$
, this is condition (v).
Suppose that
![]() $s \geq 3$
. We divide the proof in several steps.
$s \geq 3$
. We divide the proof in several steps.
(a) Set
![]() $Q \,:\!=\, S / L < Q_1 \times \cdots \times Q_m$
. Consider the Lyndon–Hochschild–Serre spectral sequence
$Q \,:\!=\, S / L < Q_1 \times \cdots \times Q_m$
. Consider the Lyndon–Hochschild–Serre spectral sequence
that converges to
![]() $H_{i+j}(S,\mathbb{Q})$
.
$H_{i+j}(S,\mathbb{Q})$
.
Note that since each
![]() $L_i$
is a free group, for every
$L_i$
is a free group, for every
![]() $t \leq m$
we have that
$t \leq m$
we have that
where each summand is Q-invariant, where the Q-action is induced by conjugation. Thus,
By inductive hypothesis, S virtually surjects onto
![]() $s-1$
factors. This implies that
$s-1$
factors. This implies that
![]() $ H_j(L, \mathbb{Q})$
is a finitely generated
$ H_j(L, \mathbb{Q})$
is a finitely generated
![]() $\mathbb{Z}Q$
-module for
$\mathbb{Z}Q$
-module for
![]() $j \leq s-1$
, and hence,
$j \leq s-1$
, and hence,
For
![]() $ i \geq 2$
, we have that
$ i \geq 2$
, we have that
![]() $s+1 - i \leq s-1$
, so by (2),
$s+1 - i \leq s-1$
, so by (2),
![]() $E_{i,s+1 - i}^i $
is finite dimensional over
$E_{i,s+1 - i}^i $
is finite dimensional over
![]() $\mathbb{Q}$
. Hence, for all differential maps
$\mathbb{Q}$
. Hence, for all differential maps
![]() $d_{i, s+1-i }^i \,:\, E_{i,s+1 - i}^i \mapsto E_{0,s}^i$
, the subgroup
$d_{i, s+1-i }^i \,:\, E_{i,s+1 - i}^i \mapsto E_{0,s}^i$
, the subgroup
![]() $\text{im}\left(d_{i, s+ 1 - i }^i\right)$
is finite dimensional over
$\text{im}\left(d_{i, s+ 1 - i }^i\right)$
is finite dimensional over
![]() $\mathbb{Q}$
. Thus,
$\mathbb{Q}$
. Thus,
is finite dimensional over
![]() $\mathbb{Q}$
if and only if
$\mathbb{Q}$
if and only if
![]() $ E_{0,s}^i$
is finite dimensional over
$ E_{0,s}^i$
is finite dimensional over
![]() $\mathbb{Q}$
. This implies that
$\mathbb{Q}$
. This implies that
![]() $E^2_{0,s}$
is finite dimensional over
$E^2_{0,s}$
is finite dimensional over
![]() $\mathbb{Q}$
if and only if
$\mathbb{Q}$
if and only if
![]() $E^{ \infty}_{0,s}$
is finite dimensional over
$E^{ \infty}_{0,s}$
is finite dimensional over
![]() $\mathbb{Q}$
. Combining this with the convergence of the spectral sequence and (2) we deduce that
$\mathbb{Q}$
. Combining this with the convergence of the spectral sequence and (2) we deduce that
The condition that
![]() $H_s(S,\mathbb{Q})$
is finite dimensional over
$H_s(S,\mathbb{Q})$
is finite dimensional over
![]() $\mathbb{Q}$
implies that for each
$\mathbb{Q}$
implies that for each
![]() $1 \leq j_1 < j_2 < \cdots < j_s \leq m$
,
$1 \leq j_1 < j_2 < \cdots < j_s \leq m$
,
 \begin{align} & \dim_{\mathbb{Q}} \left( H_1\left(L_{j_1}, \mathbb{Q}\right) \otimes \dots \otimes H_1\left(L_{j_s}, \mathbb{Q}\right) \otimes_{\mathbb{Q}Q} \mathbb{Q}\right)\\[5pt]& \quad = \dim_{\mathbb{Q}} \left(H_1\left(L_{j_1}, \mathbb{Q}\right) \otimes \dots \otimes H_1\left(L_{j_s}, \mathbb{Q}\right) \otimes_{\mathbb{Q} h_{j_1, \ldots, j_s}(Q)} \mathbb{Q} \right)< \infty,\nonumber \end{align}
\begin{align} & \dim_{\mathbb{Q}} \left( H_1\left(L_{j_1}, \mathbb{Q}\right) \otimes \dots \otimes H_1\left(L_{j_s}, \mathbb{Q}\right) \otimes_{\mathbb{Q}Q} \mathbb{Q}\right)\\[5pt]& \quad = \dim_{\mathbb{Q}} \left(H_1\left(L_{j_1}, \mathbb{Q}\right) \otimes \dots \otimes H_1\left(L_{j_s}, \mathbb{Q}\right) \otimes_{\mathbb{Q} h_{j_1, \ldots, j_s}(Q)} \mathbb{Q} \right)< \infty,\nonumber \end{align}
where
![]() $h_{j_1, \dots, j_s} \,:\, Q \mapsto Q_{j_1} \times \cdots \times Q_{j_s}$
is the canonical projection.
$h_{j_1, \dots, j_s} \,:\, Q \mapsto Q_{j_1} \times \cdots \times Q_{j_s}$
is the canonical projection.
(b) We consider
![]() $\widetilde{S}$
a subgroup of finite index in
$\widetilde{S}$
a subgroup of finite index in
![]() $p_{j_1, \dots, j_s}(S)$
that contains
$p_{j_1, \dots, j_s}(S)$
that contains
![]() $\widetilde{L} \,:\!=\, L_{j_1} \times \cdots \times L_{j_s}$
and we set
$\widetilde{L} \,:\!=\, L_{j_1} \times \cdots \times L_{j_s}$
and we set
![]() $\widetilde{Q} \,:\!=\, \widetilde{S} / \widetilde{L}$
. Then, the Lyndon–Hochschild–Serre spectral sequence
$\widetilde{Q} \,:\!=\, \widetilde{S} / \widetilde{L}$
. Then, the Lyndon–Hochschild–Serre spectral sequence
converges to
![]() $H_{i+ j}(\widetilde{S}, \mathbb{Q})$
. By (1) and (3) we deduce that
$H_{i+ j}(\widetilde{S}, \mathbb{Q})$
. By (1) and (3) we deduce that
![]() $\dim_{\mathbb{Q}} \widetilde{E}^2_{i,j} < \infty$
for
$\dim_{\mathbb{Q}} \widetilde{E}^2_{i,j} < \infty$
for
![]() $j \leq s-1$
and
$j \leq s-1$
and
![]() $\dim_{\mathbb{Q}} \widetilde{E}^2_{0,s}< \infty$
. Then, by the convergence of the spectral sequence, we deduce that
$\dim_{\mathbb{Q}} \widetilde{E}^2_{0,s}< \infty$
. Then, by the convergence of the spectral sequence, we deduce that
![]() $\dim_{\mathbb{Q}} H_i(\widetilde{S},\mathbb{Q}) < \infty$
for
$\dim_{\mathbb{Q}} H_i(\widetilde{S},\mathbb{Q}) < \infty$
for
![]() $i \leq s$
.
$i \leq s$
.
(c) Now we consider
![]() $\widetilde{S}_0$
an arbitrary subgroup of finite index in
$\widetilde{S}_0$
an arbitrary subgroup of finite index in
![]() $p_{j_1, \dots, j_s}(S)$
. We view
$p_{j_1, \dots, j_s}(S)$
. We view
![]() $p_{j_1, \dots, j_s}(S)$
as a subdirect product of
$p_{j_1, \dots, j_s}(S)$
as a subdirect product of
![]() $G_{j_1} \times \cdots \times G_{j_s}$
. As S virtually surjects on pairs we have that
$G_{j_1} \times \cdots \times G_{j_s}$
. As S virtually surjects on pairs we have that
![]() $p_{j_1, \dots, j_s}(S)$
virtually surjects on pairs, so by [
Reference Bridson, Howie, Miller and Short7
, theorem A],
$p_{j_1, \dots, j_s}(S)$
virtually surjects on pairs, so by [
Reference Bridson, Howie, Miller and Short7
, theorem A],
![]() $p_{j_1, \dots, j_s}(S)$
is finitely presented. Hence
$p_{j_1, \dots, j_s}(S)$
is finitely presented. Hence
![]() $\widetilde{S}_0$
is finitely presented. Then, by condition (iv) applied to
$\widetilde{S}_0$
is finitely presented. Then, by condition (iv) applied to
![]() $\widetilde{S}_0$
considered as a subdirect product of
$\widetilde{S}_0$
considered as a subdirect product of
![]() $p_{j_1}(\widetilde{S}_0) \times \cdots \times p_{j_s}(\widetilde{S}_0)$
, there is a subgroup of finite index
$p_{j_1}(\widetilde{S}_0) \times \cdots \times p_{j_s}(\widetilde{S}_0)$
, there is a subgroup of finite index
![]() $K_{j_i}$
in
$K_{j_i}$
in
![]() $p_{j_i}(\widetilde{S}_0)$
such that for sufficiently big t we have that
$p_{j_i}(\widetilde{S}_0)$
such that for sufficiently big t we have that
![]() $ \gamma_t(K_{j_i}) \subseteq \widetilde{S}_0$
. By condition (i), we can choose t sufficiently big so that
$ \gamma_t(K_{j_i}) \subseteq \widetilde{S}_0$
. By condition (i), we can choose t sufficiently big so that
![]() $\gamma_t(G_k) \subseteq L_k$
is free for every
$\gamma_t(G_k) \subseteq L_k$
is free for every
![]() $ 1 \leq k \leq m$
. In particular,
$ 1 \leq k \leq m$
. In particular,
![]() $\gamma_t(K_{j_i}) $
is free.
$\gamma_t(K_{j_i}) $
is free.
Note that each
![]() $K_{j_i}$
can be chosen normal in
$K_{j_i}$
can be chosen normal in
![]() $p_{j_i}(\widetilde{S}_0)$
(by substituting if necessary
$p_{j_i}(\widetilde{S}_0)$
(by substituting if necessary
![]() $K_{j_i}$
with its core in
$K_{j_i}$
with its core in
![]() $p_{j_i}(\widetilde{S}_0)$
) and that
$p_{j_i}(\widetilde{S}_0)$
) and that
![]() $p_{j_i}(\widetilde{S}_0)$
has finite index in
$p_{j_i}(\widetilde{S}_0)$
has finite index in
![]() $G_{j_i} = p_{j_i}(S)$
, hence
$G_{j_i} = p_{j_i}(S)$
, hence
![]() $K_{j_i}$
has finite index in
$K_{j_i}$
has finite index in
![]() $G_{j_i}$
for
$G_{j_i}$
for
![]() $ 1 \leq i \leq s$
. Thus
$ 1 \leq i \leq s$
. Thus
![]() $\widetilde{S}_0 \cap ( K_{j_1} \times \ldots \times K_{j_s} )$
has finite index in
$\widetilde{S}_0 \cap ( K_{j_1} \times \ldots \times K_{j_s} )$
has finite index in
![]() $\widetilde{S}_0$
. By construction
$\widetilde{S}_0$
. By construction
![]() $\widetilde{S}_0$
is a subgroup of finite index in
$\widetilde{S}_0$
is a subgroup of finite index in
![]() $p_{j_1, \dots, j_s}(S)$
and so
$p_{j_1, \dots, j_s}(S)$
and so
![]() $\widetilde{S}_0 \cap ( K_{j_1} \times \ldots \times K_{j_s} )$
has finite index in
$\widetilde{S}_0 \cap ( K_{j_1} \times \ldots \times K_{j_s} )$
has finite index in
![]() $p_{j_1, \dots, j_s}(S)$
. We set
$p_{j_1, \dots, j_s}(S)$
. We set
![]() $S_0 = p_{j_1, \ldots, j_s}^{-1} \left(\widetilde{S}_0 \cap \left( K_{j_1} \times \ldots \times K_{j_s} \right)\right)$
and note it is a subgroup of finite index in S. Note that
$S_0 = p_{j_1, \ldots, j_s}^{-1} \left(\widetilde{S}_0 \cap \left( K_{j_1} \times \ldots \times K_{j_s} \right)\right)$
and note it is a subgroup of finite index in S. Note that
![]() $p_{j_i} (S_0) \subseteq K_{j_i}$
for
$p_{j_i} (S_0) \subseteq K_{j_i}$
for
![]() $ 1 \leq i \leq s$
.
$ 1 \leq i \leq s$
.
By condition (vii),
![]() $H_i (S_0 , \mathbb{Q})$
is finite dimensional (over
$H_i (S_0 , \mathbb{Q})$
is finite dimensional (over
![]() $\mathbb{Q}$
) for all
$\mathbb{Q}$
) for all
![]() $ i \leq s.$
Applying Step 2 for S substituted with
$ i \leq s.$
Applying Step 2 for S substituted with
![]() $S_0$
,
$S_0$
,
![]() $G_j$
substituted with
$G_j$
substituted with
![]() $p_j(S_0)$
and
$p_j(S_0)$
and
![]() $L_j$
substituted with
$L_j$
substituted with
![]() $\gamma_t(p_j(S_0))$
, we deduce that for every subgroup B of finite index in
$\gamma_t(p_j(S_0))$
, we deduce that for every subgroup B of finite index in
![]() $p_{j_1, \dots, j_s}(S_0) = \widetilde{S}_0 \cap \left( K_{j_1} \times \cdots \times K_{j_s} \right)$
such that B contains
$p_{j_1, \dots, j_s}(S_0) = \widetilde{S}_0 \cap \left( K_{j_1} \times \cdots \times K_{j_s} \right)$
such that B contains
![]() $\gamma_t(p_{j_1}(S_0)) \times \ldots \times \gamma_t(p_{j_s}(S_0))$
we have that
$\gamma_t(p_{j_1}(S_0)) \times \ldots \times \gamma_t(p_{j_s}(S_0))$
we have that
We apply this for
![]() $B = p_{j_1, \dots, j_s}(S_0) = \widetilde{S}_0 \cap ( K_{j_1} \times \ldots \times K_{j_s} )$
and note that B is a normal subgroup of finite index in
$B = p_{j_1, \dots, j_s}(S_0) = \widetilde{S}_0 \cap ( K_{j_1} \times \ldots \times K_{j_s} )$
and note that B is a normal subgroup of finite index in
![]() $\widetilde{S}_0$
. Hence the Lyndon–Hoschild–Serre spectral sequence
$\widetilde{S}_0$
. Hence the Lyndon–Hoschild–Serre spectral sequence
![]() $H_i(\widetilde{S}_0/B, H_j (B, \mathbb{Q}))$
that converges to
$H_i(\widetilde{S}_0/B, H_j (B, \mathbb{Q}))$
that converges to
![]() $H_{i+j}(\widetilde{S}_0, \mathbb{Q})$
implies that
$H_{i+j}(\widetilde{S}_0, \mathbb{Q})$
implies that
But this combined with condition (iii) and the fact that
![]() $\widetilde{S}_0$
is an arbitrary subgroup of finite index in
$\widetilde{S}_0$
is an arbitrary subgroup of finite index in
![]() $p_{j_1, \dots, j_s}(S)$
implies that
$p_{j_1, \dots, j_s}(S)$
implies that
![]() $p_{j_1, \dots, j_s} (S)$
has finite index in
$p_{j_1, \dots, j_s} (S)$
has finite index in
![]() $G_{j_1} \times \cdots \times G_{j_s}$
.
$G_{j_1} \times \cdots \times G_{j_s}$
.
Let
![]() $n \geq 0$
, R be an associative ring with identity and let M be a (right) R-module. Then M is of (homological) type
$n \geq 0$
, R be an associative ring with identity and let M be a (right) R-module. Then M is of (homological) type
![]() $FP_n$
if there is a projective resolution
$FP_n$
if there is a projective resolution
such that each projective R-module
![]() $P_i$
is finitely generated for
$P_i$
is finitely generated for
![]() $0 \leq i \leq n$
. A group G is of type
$0 \leq i \leq n$
. A group G is of type
![]() $FP_n$
over a commutative ring S if the trivial S G-module S is of type
$FP_n$
over a commutative ring S if the trivial S G-module S is of type
![]() $FP_n$
over the group algebra S G.
$FP_n$
over the group algebra S G.
Lemma 4·3 ([
Reference Kochloukova21
, lemma 6]). Let
![]() $Q_1, \ldots, Q_i$
be finitely generated nilpotent groups and
$Q_1, \ldots, Q_i$
be finitely generated nilpotent groups and
![]() $V_j$
be a finitely generated
$V_j$
be a finitely generated
![]() $\mathbb{Q} Q_j$
-module such that
$\mathbb{Q} Q_j$
-module such that
![]() $V_j$
contains a cyclic non-zero free
$V_j$
contains a cyclic non-zero free
![]() $\mathbb{Q} Q_j$
-submodule
$\mathbb{Q} Q_j$
-submodule
![]() $W_j$
for
$W_j$
for
![]() $ 1 \leq j \leq i$
. Suppose that
$ 1 \leq j \leq i$
. Suppose that
![]() $\widetilde{Q}$
is a subgroup of
$\widetilde{Q}$
is a subgroup of
![]() $Q \,:\!=\, Q_1 \times \cdots \times Q_i$
such that
$Q \,:\!=\, Q_1 \times \cdots \times Q_i$
such that
![]() $V_1 \otimes_{\mathbb{Q} } \cdots \otimes_{\mathbb{Q} } V_i$
is finitely generated as a
$V_1 \otimes_{\mathbb{Q} } \cdots \otimes_{\mathbb{Q} } V_i$
is finitely generated as a
![]() $\mathbb{Q} \widetilde{Q}$
-module. Then,
$\mathbb{Q} \widetilde{Q}$
-module. Then,
![]() $\widetilde{Q}$
has finite index in Q.
$\widetilde{Q}$
has finite index in Q.
Proposition 4·4 ([
Reference Kochloukova21
, proposition 7]). Let G be a group of negative Euler characteristic
![]() $\chi(G)$
such that the trivial
$\chi(G)$
such that the trivial
![]() $\mathbb{Q} G$
-module
$\mathbb{Q} G$
-module
![]() $\mathbb{Q}$
has a free resolution with finitely generated modules and finite length. Then, for any normal subgroup M of G such that
$\mathbb{Q}$
has a free resolution with finitely generated modules and finite length. Then, for any normal subgroup M of G such that
![]() $Q \,:\!=\, G / M$
is torsion-free nilpotent and M is free, the
$Q \,:\!=\, G / M$
is torsion-free nilpotent and M is free, the
![]() $\mathbb{Q} Q$
-module
$\mathbb{Q} Q$
-module
![]() $V = M / [M,M] \otimes_{\mathbb{Z}} \mathbb{Q}$
has a non-zero free
$V = M / [M,M] \otimes_{\mathbb{Z}} \mathbb{Q}$
has a non-zero free
![]() $\mathbb{Q} Q$
-submodule, where Q acts on
$\mathbb{Q} Q$
-submodule, where Q acts on
![]() $M=M / [M, M]$
via conjugation.
$M=M / [M, M]$
via conjugation.
Theorem 4·5.
Let
![]() $S < G_1 \times \cdots \times G_m$
be a finitely generated subdirect product such that:
$S < G_1 \times \cdots \times G_m$
be a finitely generated subdirect product such that:
-
(i) for each
 $ 1 \leq i \leq m$
the trivial
$ 1 \leq i \leq m$
the trivial
 $\mathbb{Q} G_i$
-module
$\mathbb{Q} G_i$
-module
 $\mathbb{Q}$
has a free resolution of finite length with finitely generated modules;
$\mathbb{Q}$
has a free resolution of finite length with finitely generated modules; -
(ii) for each
 $ 1 \leq i \leq m$
there is a normal free subgroup
$ 1 \leq i \leq m$
there is a normal free subgroup
 $L_i$
of
$L_i$
of
 $G_i$
such that
$G_i$
such that
 $G_i / L_i$
is torsion-free nilpotent;
$G_i / L_i$
is torsion-free nilpotent; -
(iii)
 $L_1 \times \cdots \times L_m \subseteq S$
;
$L_1 \times \cdots \times L_m \subseteq S$
; -
(iv) S is of type
 $FP_s$
over
$FP_s$
over
 $\mathbb{Q}$
;
$\mathbb{Q}$
; -
(v)
 $\chi(G_{i})<0$
.
$\chi(G_{i})<0$
.
Then, for every canonical projection
![]() $p_{j_1, \ldots, j_s} \,:\, S \mapsto G_{j_1} \times \cdots \times G_{ j_ s}$
the index of
$p_{j_1, \ldots, j_s} \,:\, S \mapsto G_{j_1} \times \cdots \times G_{ j_ s}$
the index of
![]() $p_{j_1, \ldots, j_s} (S)$
in
$p_{j_1, \ldots, j_s} (S)$
in
![]() $G_{j_1} \times \cdots \times G_{ j_s}$
is finite.
$G_{j_1} \times \cdots \times G_{ j_s}$
is finite.
Proof. Note that since
![]() $G_i$
is of type
$G_i$
is of type
![]() $FP_{\infty}$
over
$FP_{\infty}$
over
![]() $\mathbb{Q}$
, it is
$\mathbb{Q}$
, it is
![]() $FP_1$
over
$FP_1$
over
![]() $\mathbb{Q}$
and so
$\mathbb{Q}$
and so
![]() $G_i$
is finitely generated. By Proposition 4·4,
$G_i$
is finitely generated. By Proposition 4·4,
![]() $V_i \,:\!=\, (L_i/[L_i, L_i]) \otimes_{\mathbb{Z}} \mathbb{Q}$
has a non-zero free
$V_i \,:\!=\, (L_i/[L_i, L_i]) \otimes_{\mathbb{Z}} \mathbb{Q}$
has a non-zero free
![]() $\mathbb{Q} Q_i$
-submodule, where
$\mathbb{Q} Q_i$
-submodule, where
![]() $Q_i \,:\!=\, G_i/ L_i$
acts via conjugation.
$Q_i \,:\!=\, G_i/ L_i$
acts via conjugation.
Let
be a free resolution of the trivial
![]() $\mathbb{Q} S$
-module
$\mathbb{Q} S$
-module
![]() $\mathbb{Q}$
with
$\mathbb{Q}$
with
![]() $F_i$
finitely generated for
$F_i$
finitely generated for
![]() $i \leq s$
. We define L to be
$i \leq s$
. We define L to be
![]() $L_1 \times \cdots \times L_m$
and since each
$L_1 \times \cdots \times L_m$
and since each
![]() $L_i$
is free, by the K
$L_i$
is free, by the K
![]() $\ddot{\textrm{u}}$
nneth formula,
$\ddot{\textrm{u}}$
nneth formula,
 \begin{align*} H_s(L, \mathbb{Q}) & = \bigoplus_{1 \leq j_1 < \dots < j_s \leq m} L_{j_1} / \left[L_{j_1}, L_{j_1}\right] \otimes_{\mathbb{Z}} \dots \otimes_{\mathbb{Z}} L_{j_s} / \left[L_{j_s}, L_{j_s}\right] \otimes_{\mathbb{Z}} \mathbb{Q} \simeq\\& \bigoplus_{1 \leq j_1 < \dots < j_s \leq m} V_{j_1} \otimes_{\mathbb{Q}} \cdots \otimes_{\mathbb{Q}} V_{j_s}. \end{align*}
\begin{align*} H_s(L, \mathbb{Q}) & = \bigoplus_{1 \leq j_1 < \dots < j_s \leq m} L_{j_1} / \left[L_{j_1}, L_{j_1}\right] \otimes_{\mathbb{Z}} \dots \otimes_{\mathbb{Z}} L_{j_s} / \left[L_{j_s}, L_{j_s}\right] \otimes_{\mathbb{Z}} \mathbb{Q} \simeq\\& \bigoplus_{1 \leq j_1 < \dots < j_s \leq m} V_{j_1} \otimes_{\mathbb{Q}} \cdots \otimes_{\mathbb{Q}} V_{j_s}. \end{align*}
Note that
where
![]() $d_j \,:\, F_j \otimes_{\mathbb{Q}L} \mathbb{Q} \mapsto F_{j-1} \otimes_{\mathbb{Q}L} \mathbb{Q}$
is the differential of
$d_j \,:\, F_j \otimes_{\mathbb{Q}L} \mathbb{Q} \mapsto F_{j-1} \otimes_{\mathbb{Q}L} \mathbb{Q}$
is the differential of
![]() $\mathcal{F} \otimes_{\mathbb{Q}L} \mathbb{Q}$
. Since
$\mathcal{F} \otimes_{\mathbb{Q}L} \mathbb{Q}$
. Since
![]() $F_s \otimes_{\mathbb{Q}L} \mathbb{Q} $
is a finitely generated
$F_s \otimes_{\mathbb{Q}L} \mathbb{Q} $
is a finitely generated
![]() $\mathbb{Q}\widehat{Q}$
-module, where
$\mathbb{Q}\widehat{Q}$
-module, where
![]() $\widehat{Q} \,:\!=\, S/ L$
is a finitely generated nilpotent group and
$\widehat{Q} \,:\!=\, S/ L$
is a finitely generated nilpotent group and
![]() $\mathbb{Q}\widehat{Q}$
is a Noetherian ring, we deduce that
$\mathbb{Q}\widehat{Q}$
is a Noetherian ring, we deduce that
![]() $\ker(d_s)$
is a finitely generated
$\ker(d_s)$
is a finitely generated
![]() $\mathbb{Q}\widehat{Q}$
-module. In particular,
$\mathbb{Q}\widehat{Q}$
-module. In particular,
![]() $H_s(L, \mathbb{Q})$
and
$H_s(L, \mathbb{Q})$
and
![]() $V_{j_1} \otimes_{\mathbb{Q}} \cdots \otimes_{\mathbb{Q}} V_{j_s}$
are finitely generated
$V_{j_1} \otimes_{\mathbb{Q}} \cdots \otimes_{\mathbb{Q}} V_{j_s}$
are finitely generated
![]() $\mathbb{Q} \widehat{Q}$
-modules. Note that the action of
$\mathbb{Q} \widehat{Q}$
-modules. Note that the action of
![]() $\widehat{Q}$
on
$\widehat{Q}$
on
![]() $V_{j_1} \otimes_{\mathbb{Q}} \cdots \otimes_{\mathbb{Q}} V_{j_s}$
factors through
$V_{j_1} \otimes_{\mathbb{Q}} \cdots \otimes_{\mathbb{Q}} V_{j_s}$
factors through
![]() $\widetilde{Q} \,:\!=\, p_{j_1, \ldots, j_s} (S) / L_{j_1} \times \cdots \times L_{j_s}$
. Then, by Lemma 4·3,
$\widetilde{Q} \,:\!=\, p_{j_1, \ldots, j_s} (S) / L_{j_1} \times \cdots \times L_{j_s}$
. Then, by Lemma 4·3,
![]() $\widetilde{Q}$
has finite index in
$\widetilde{Q}$
has finite index in
![]() $Q_{j_1} \times \cdots \times Q_{j_s}$
. This is equivalent to
$Q_{j_1} \times \cdots \times Q_{j_s}$
. This is equivalent to
![]() $p_{j_1, \ldots, j_s} (S)$
having finite index in
$p_{j_1, \ldots, j_s} (S)$
having finite index in
![]() $G_{j_1} \times \cdots \times G_{ j_s}$
.
$G_{j_1} \times \cdots \times G_{ j_s}$
.
The next step is to prove that limit groups over Droms RAAGs satisfy the conditions of Theorem 4·5.
Lemma 4·6.
Let G be a Droms RAAG and
![]() $\Gamma$
a limit group over G. Then,
$\Gamma$
a limit group over G. Then,
![]() $\chi(\Gamma)\leq 0$
. Furthermore,
$\chi(\Gamma)\leq 0$
. Furthermore,
![]() $\chi(\Gamma)=0$
if and only if
$\chi(\Gamma)=0$
if and only if
![]() $\Gamma$
has non-trivial center. The latter happens precisely when
$\Gamma$
has non-trivial center. The latter happens precisely when
![]() $\Gamma = \mathbb{Z}^{l_0} \times \Lambda_0$
for some
$\Gamma = \mathbb{Z}^{l_0} \times \Lambda_0$
for some
![]() $l_0 \geq 1$
and with
$l_0 \geq 1$
and with
![]() $\Lambda_0$
a centerless subgroup of
$\Lambda_0$
a centerless subgroup of
![]() $\Gamma$
.
$\Gamma$
.
Proof. Let us prove it by induction on the level l(G) of G. If
![]() $l(G)=0$
, then G is a free group, so the result follows from [
Reference Kochloukova21
, lemma 5].
$l(G)=0$
, then G is a free group, so the result follows from [
Reference Kochloukova21
, lemma 5].
Now assume that
![]() $l(G)\geq 1$
. Then, G equals
$l(G)\geq 1$
. Then, G equals
where
![]() $m\in \mathbb{N} \cup \{0\}$
and
$m\in \mathbb{N} \cup \{0\}$
and
![]() $G_{i}$
is a Droms RAAG such that
$G_{i}$
is a Droms RAAG such that
![]() $l(G_{i}) \leq l(G)-1$
for
$l(G_{i}) \leq l(G)-1$
for
![]() $i\in \{1,\dots,n\}$
. From Proposition 2·7 we get that
$i\in \{1,\dots,n\}$
. From Proposition 2·7 we get that
![]() $\Gamma$
is of the form
$\Gamma$
is of the form
![]() $\mathbb{Z}^l \times \Lambda$
where
$\mathbb{Z}^l \times \Lambda$
where
![]() $\Lambda$
is a limit group over
$\Lambda$
is a limit group over
![]() $G_{1}\ast \cdots \ast G_{n}$
and if
$G_{1}\ast \cdots \ast G_{n}$
and if
![]() $m=0$
, then
$m=0$
, then
![]() $l=0$
. Therefore,
$l=0$
. Therefore,
so if
![]() $l\geq 1$
, then
$l\geq 1$
, then
![]() $\chi(\Gamma)=0$
. Let us compute
$\chi(\Gamma)=0$
. Let us compute
![]() $\chi(\Lambda)$
. If the height of
$\chi(\Lambda)$
. If the height of
![]() $\Lambda$
is 0, i.e.
$\Lambda$
is 0, i.e.
![]() $h(\Lambda)=0$
, then
$h(\Lambda)=0$
, then
where for each
![]() $t\in \{1,\dots,j\}$
$t\in \{1,\dots,j\}$
![]() $A_{t}$
is a limit group over
$A_{t}$
is a limit group over
![]() $G_{i}$
for some
$G_{i}$
for some
![]() $i\in \{1,\dots,n\}$
. Hence,
$i\in \{1,\dots,n\}$
. Hence,
so applying the inductive hypothesis, we get that
![]() $\chi(\Lambda) \leq 1-j$
. If
$\chi(\Lambda) \leq 1-j$
. If
![]() $j\geq 2$
, then
$j\geq 2$
, then
![]() $\chi(\Lambda)< 0$
. If
$\chi(\Lambda)< 0$
. If
![]() $j=1$
,
$j=1$
,
![]() $\chi(\Lambda)=\chi(A_{1})$
and
$\chi(\Lambda)=\chi(A_{1})$
and
![]() $A_{1}$
is a limit group over
$A_{1}$
is a limit group over
![]() $G_{i}$
. Thus, by induction,
$G_{i}$
. Thus, by induction,
![]() $\chi(A_{1})\leq 0$
and
$\chi(A_{1})\leq 0$
and
![]() $\chi(A_{1})=0$
if and only if
$\chi(A_{1})=0$
if and only if
![]() $A_{1}$
has non-trivial center. In this case the center
$A_{1}$
has non-trivial center. In this case the center
![]() $Z(A_1)$
is a direct factor of
$Z(A_1)$
is a direct factor of
![]() $A_1$
.
$A_1$
.
If
![]() $h(\Lambda)\geq 1$
, then
$h(\Lambda)\geq 1$
, then
![]() $\Lambda$
acts cocompactly on a tree T where the edge stabilisers are cyclic and the vertex groups are limit groups over
$\Lambda$
acts cocompactly on a tree T where the edge stabilisers are cyclic and the vertex groups are limit groups over
![]() $G_1\ast \cdots \ast G_n$
of height at most
$G_1\ast \cdots \ast G_n$
of height at most
![]() $h(\Lambda)-1$
. Moreover, at least one vertex group
$h(\Lambda)-1$
. Moreover, at least one vertex group
![]() $H_{v_{0}}$
has trivial center and so by inductive hypothesis,
$H_{v_{0}}$
has trivial center and so by inductive hypothesis,
![]() $\chi(H_{v_{0}}) < 0$
. If X is the quotient graph
$\chi(H_{v_{0}}) < 0$
. If X is the quotient graph
![]() $T / \Lambda$
,
$T / \Lambda$
,
Lemma 4·7.
Let
![]() $\Gamma$
be a limit group over a Droms RAAG. Then, the trivial
$\Gamma$
be a limit group over a Droms RAAG. Then, the trivial
![]() $\mathbb{Q}\Gamma$
-module
$\mathbb{Q}\Gamma$
-module
![]() $\mathbb{Q}$
has a free resolution with finitely generated modules and of finite length.
$\mathbb{Q}$
has a free resolution with finitely generated modules and of finite length.
Proof. Limit groups over Droms RAAGs are of type
![]() $FP_{\infty}$
over
$FP_{\infty}$
over
![]() $\mathbb{Z}$
(and so over
$\mathbb{Z}$
(and so over
![]() $\mathbb{Q}$
) and of finite cohomological dimension.
$\mathbb{Q}$
) and of finite cohomological dimension.
Proof of Theorem 1·1. By [
Reference Lopez de Gamiz Zearra23
, theorem 6·2],
![]() $G_i / (S \cap G_i)$
is virtually nilpotent for every
$G_i / (S \cap G_i)$
is virtually nilpotent for every
![]() $i\in \{1,\dots,m\}$
. By substituting
$i\in \{1,\dots,m\}$
. By substituting
![]() $G_i$
and S with subgroups of finite index if necessary we can assume that
$G_i$
and S with subgroups of finite index if necessary we can assume that
![]() $G_i / (S \cap G_i)$
is torsion-free nilpotent. By Proposition 3·16, there is a normal free subgroup
$G_i / (S \cap G_i)$
is torsion-free nilpotent. By Proposition 3·16, there is a normal free subgroup
![]() $M_i$
de
$M_i$
de
![]() $G_i$
such that
$G_i$
such that
![]() $G_i / M_i$
is torsion-free nilpotent, hence for
$G_i / M_i$
is torsion-free nilpotent, hence for
![]() $L_i = S \cap M_i$
we have that
$L_i = S \cap M_i$
we have that
![]() $L_i$
is a normal subgroup of
$L_i$
is a normal subgroup of
![]() $G_i$
such that
$G_i$
such that
![]() $L_i$
is free,
$L_i$
is free,
![]() $G_i / L_i$
is torsion-free nilpotent and
$G_i / L_i$
is torsion-free nilpotent and
![]() $L_1 \times \cdots \times L_{m} \subseteq S$
. Note that conditions 1 and 6 from Theorem 4·2 hold. The other conditions from Theorem 4·2 hold when each
$L_1 \times \cdots \times L_{m} \subseteq S$
. Note that conditions 1 and 6 from Theorem 4·2 hold. The other conditions from Theorem 4·2 hold when each
![]() $G_i$
is a limit group over a Droms RAAG with trivial center: condition (ii) is [
Reference Casals–Ruiz, Duncan and Kazachkov11
, Corollary 7·8], condition (iii) is Theorem 2·9, condition (v) is Theorem 2·10.
$G_i$
is a limit group over a Droms RAAG with trivial center: condition (ii) is [
Reference Casals–Ruiz, Duncan and Kazachkov11
, Corollary 7·8], condition (iii) is Theorem 2·9, condition (v) is Theorem 2·10.
Observe that a finite index subgroup of a limit group over a Droms RAAG is a limit group over a Droms RAAG. Hence condition (iv) follows from [ Reference Lopez de Gamiz Zearra23 , theorem 6·2]. Finally, condition (vii) is assumed in the statement.
5. On the
 $L^2$
-Betti numbers and volume gradients of limit groups over Droms RAAGs and their subdirect products
$L^2$
-Betti numbers and volume gradients of limit groups over Droms RAAGs and their subdirect products
The aim of this section is to study the growth of homology groups and the volume gradients for limit groups over Droms RAAGs and for finitely presented residually Droms RAAGs, following the paper [ Reference Bridson and Kochloukova9 ]. Some of the results concerning limit groups over Droms RAAGs hold in a more general setting, more precisely, they also hold for limit groups over coherent RAAGs. Thus, these results (see Theorem 1·2 and Theorem 1·3) will be stated for limit groups over coherent RAAGs. However, the results for finitely presented residually Droms RAAGs make use of Theorem 2·10 and in [ Reference Casals–Ruiz and Lopez de Gamiz Zearra14 ] it was shown that this no longer holds for coherent RAAGs. Thus, Theorem 1·4 and Theorem 1·6 are stated just for residually Droms RAAGs.
In order to study the homology growth and volume gradients, we work with exhausting normal chains: a chain
![]() $(B_{n})$
of normal subgroups of finite index such that
$(B_{n})$
of normal subgroups of finite index such that
![]() $B_{n+1} \subseteq B_{n}$
and
$B_{n+1} \subseteq B_{n}$
and
![]() $\bigcap_{n} B_{n}=1$
. Note that if a group is residually finite, then it has an exhausting normal chain. In particular, limit groups over coherent RAAGs have exhausting normal chains.
$\bigcap_{n} B_{n}=1$
. Note that if a group is residually finite, then it has an exhausting normal chain. In particular, limit groups over coherent RAAGs have exhausting normal chains.
A group G is of homotopical type
![]() $F_m$
if there is a classifying space K(G,1) with finite m-skeleton. Given a group G of homotopical type
$F_m$
if there is a classifying space K(G,1) with finite m-skeleton. Given a group G of homotopical type
![]() $F_{m}$
,
$F_{m}$
,
![]() $\text{vol}_{m}(G)$
is defined to be the least number of m-cells among all classifying spaces K(G,1) with finite m-skeleton. For instance,
$\text{vol}_{m}(G)$
is defined to be the least number of m-cells among all classifying spaces K(G,1) with finite m-skeleton. For instance,
![]() $\text{vol}_{1}(G)$
equals d(G), where d(G) is the minimal number of generators of G.
$\text{vol}_{1}(G)$
equals d(G), where d(G) is the minimal number of generators of G.
One of the aims of this section is to prove Theorem 1·2 and Theorem 1·3. These two results are proved in [ Reference Bridson and Kochloukova9 ] for limit groups over free groups via more technical results that make use of slowness of limit groups over free groups (see Section 5·1 for the definition). In [ Reference Bridson and Kochloukova9 ] it is shown that limit groups over free groups are slow above dimension 1 and hence are K-slow above dimension 1 for any field K. Thus, the key point is to show that limit groups over coherent RAAGs are also slow above dimension 1 (see Section 5·2).
Theorem 5·1 ([
Reference Bridson and Kochloukova9
, theorem D]). If a residually finite group G of type F is slow above dimension 1, then with respect to every exhausting normal chain
![]() $(B_{n})$
:
$(B_{n})$
:
-
(i) Rank gradient:
 \[ RG(G, (B_{n}))= \lim_{n\to \infty} \frac{d(B_{n})}{[G \,:\, B_{n}]}= -\chi(G);\]
\[ RG(G, (B_{n}))= \lim_{n\to \infty} \frac{d(B_{n})}{[G \,:\, B_{n}]}= -\chi(G);\]
-
(ii) deficiency gradient:
 \[ DG(G, (B_{n}))= \lim_{n\to \infty} \frac{\text{def}(B_{n})}{[G \,:\, B_{n}]} = \chi(G).\]
\[ DG(G, (B_{n}))= \lim_{n\to \infty} \frac{\text{def}(B_{n})}{[G \,:\, B_{n}]} = \chi(G).\]
Lemma 5·2 ([
Reference Bridson and Kochloukova9
, lemma 5·2]). Let K be a field and let G be a residually finite group of type F with an exhausting normal chain
![]() $(B_n)$
. If G is K-slow above dimension 1, then
$(B_n)$
. If G is K-slow above dimension 1, then
We state other results from [
Reference Bridson and Kochloukova9
] that will be important for us, as we will show that residually Droms RAAGs that are of type
![]() $FP_m$
for some
$FP_m$
for some
![]() $m \geq 2$
satisfy virtually the assumptions of Theorem 5·3.
$m \geq 2$
satisfy virtually the assumptions of Theorem 5·3.
Theorem 5·3 ([
Reference Bridson and Kochloukova9
, theorem F]). Let
![]() $G \subseteq G_{1}\times \cdots \times G_{k}$
be a subdirect product of residually finite groups of type F, each of which contains a normal free subgroup
$G \subseteq G_{1}\times \cdots \times G_{k}$
be a subdirect product of residually finite groups of type F, each of which contains a normal free subgroup
![]() $F_{i} < G_{i}$
such that
$F_{i} < G_{i}$
such that
![]() $G_{i} / F_{i}$
is torsion-free and nilpotent. Assume
$G_{i} / F_{i}$
is torsion-free and nilpotent. Assume
![]() $F_{i} \subseteq G \cap G_i$
. Let
$F_{i} \subseteq G \cap G_i$
. Let
![]() $m<k$
be an integer, let K be a field, and suppose that each
$m<k$
be an integer, let K be a field, and suppose that each
![]() $G_{i}$
is K-slow above dimension 1.
$G_{i}$
is K-slow above dimension 1.
If the projection of G to each m-tuple of factors
![]() $G_{j_{1}} \times \cdots \times G_{j_{m}}$
is of finite index, then there exists an exhausting normal chain
$G_{j_{1}} \times \cdots \times G_{j_{m}}$
is of finite index, then there exists an exhausting normal chain
![]() $(B_n)$
in G so that for
$(B_n)$
in G so that for
![]() $0\leq j \leq m$
,
$0\leq j \leq m$
,
Theorem 5·4 ([
Reference Bridson and Kochloukova9
, theorem G]). Every finitely presented residually free group G that is not a limit group over a free group admits an exhausting normal chain
![]() $(B_n)$
with respect to which the rank gradient
$(B_n)$
with respect to which the rank gradient
Furthermore, if G is of type
![]() $FP_3$
but it is not commesurable with a product of two limit groups over free groups,
$FP_3$
but it is not commesurable with a product of two limit groups over free groups,
![]() $(B_n)$
can be chosen so that the deficiency gradient
$(B_n)$
can be chosen so that the deficiency gradient
![]() $DG(G,(B_n))=0.$
$DG(G,(B_n))=0.$
5·1. Preliminaries on groups that are K-slow and slow above dimension 1’
Let us start recalling the definitions from [ Reference Bridson and Kochloukova9 ] about slowness and K-slowness.
Definition 5·5. Let G be a group. A sequence of non-negative integers
![]() $(r_{j})_{j\geq 0 }$
is a volume vector for G if there is a classifying space K(G,1) that, for all
$(r_{j})_{j\geq 0 }$
is a volume vector for G if there is a classifying space K(G,1) that, for all
![]() $j\in \mathbb{N}$
, has exactly
$j\in \mathbb{N}$
, has exactly
![]() $r_{j}$
j-cells.
$r_{j}$
j-cells.
Definition 5·6. A group G of homotopical type F is slow above dimension 1 if it is residually finite and for every exhausting normal chain
![]() $(B_n)$
, there exist volume vectors
$(B_n)$
, there exist volume vectors
![]() $(r_{j}(B_{n}))_{j}$
for
$(r_{j}(B_{n}))_{j}$
for
![]() $B_n$
with finitely many non-zero entries, so that
$B_n$
with finitely many non-zero entries, so that
for all
![]() $j\geq 2$
. G is slow if it satisfies the additional requirement that the limit exists and is zero for
$j\geq 2$
. G is slow if it satisfies the additional requirement that the limit exists and is zero for
![]() $j=1$
as well.
$j=1$
as well.
Example 5·7 ([ Reference Bridson and Kochloukova9 , examples 4·4]). Finitely generated torsion-free nilpotent groups are slow. The trivial group is slow. Free groups are slow above dimension 1. Surface groups are slow above dimension 1.
Proposition 5·8 ([ Reference Bridson and Kochloukova9 , proposition 4·5]). If a residually finite group G is the fundamental group of a finite graph of groups where all of the edge groups are slow and all of the vertex groups are slow above dimension 1, then G is slow above dimension 1.
Definition 5·9. Let K be a field and let G be a residually finite group. G is K-slow above dimension 1 if for every exhausting normal chain
![]() $(B_n)$
, we have
$(B_n)$
, we have
for all
![]() $j\geq 2$
.
$j\geq 2$
.
G is K-slow if it satisfies the additional requirement that the limit exists and is zero for
![]() $j=1$
as well.
$j=1$
as well.
It follows directly by the definitions that if a group G is slow above dimension 1 (respectively, slow), then it is K-slow above dimension 1 (respectively, K-slow).
Proposition 5·10 ([ Reference Bridson and Kochloukova9 , proposition 5·3]). Let K be a field. If a residually finite group G is the fundamental group of a finite graph of groups where all of the edge groups are K-slow and all of the vertex groups are K-slow above dimension 1, then G is K-slow above dimension 1.
5·2. Limit groups over coherent RAAGs are slow above dimension 1
Lemma 5·11 ([ Reference Casals–Ruiz, Duncan and Kazachkov11 , corollary 9·7]). Limit groups over coherent RAAGs are CAT(0).
In particular, since limit groups over coherent RAAGs are torsion-free, they are of type F.
Lemma 5·12. Coherent RAAGs are slow above dimension 1. In particular, Droms RAAGs are slow above dimension 1.
Proof. In [ Reference Droms17 ] Droms proved that if GX is a coherent RAAG, then GX splits as a finite graph of groups where all the vertex groups are free abelian. Thus, by Proposition 5·8, coherents RAAGs are slow above dimension 1.
The aim of this section is to show that limit groups over coherent RAAGs are slow above dimension 1. For that, we will use the work on [ Reference Casals–Ruiz, Duncan and Kazachkov11 , Reference Casals–Ruiz and Kazachkov12 ] about limit groups over coherent RAAGs.
Let us recall some definitions that are needed to understand the results below. If GX is a RAAG, the elements of X are called the canonical generators of GX. A non-exceptional surface is a surface which is not a non-orientable surface of genus 1, 2 or 3. We can use the following proposition to define graph towers over coherent RAAGs.
Proposition 5·13 ([ Reference Casals–Ruiz, Duncan and Kazachkov11 , lemma 7·3]). Let G be a coherent right-angled Artin group. A graph tower over G of height 0 is a coherent RAAG H which is obtained from G by extending centralizers of canonical generators of G.
A graph tower over G of height
![]() $\geq 1$
can be obtained as a free product with amalgamation, where the edge group is a free abelian group, one of the vertex groups is a graph tower over G of lower height and the other vertex group is either free abelian, or the direct product of a free abelian group and the fundamental group of a non-exceptional surface.
$\geq 1$
can be obtained as a free product with amalgamation, where the edge group is a free abelian group, one of the vertex groups is a graph tower over G of lower height and the other vertex group is either free abelian, or the direct product of a free abelian group and the fundamental group of a non-exceptional surface.
Theorem 5·14 ([
Reference Casals–Ruiz and Kazachkov12
, theorem 8·1]). Let
![]() $\Gamma$
be a limit group over a RAAG G. Then,
$\Gamma$
be a limit group over a RAAG G. Then,
![]() $\Gamma$
is a subgroup of a graph tower over G.
$\Gamma$
is a subgroup of a graph tower over G.
Lemma 5·15 [
Reference Wall27
]. Let
![]() $1\rightarrow C \rightarrow D \rightarrow E \rightarrow 1$
be a short exact sequence of groups of type F. Suppose that there are classifying spaces K(C,1) and K(E,1) with
$1\rightarrow C \rightarrow D \rightarrow E \rightarrow 1$
be a short exact sequence of groups of type F. Suppose that there are classifying spaces K(C,1) and K(E,1) with
![]() $\alpha_{t}(C)$
and
$\alpha_{t}(C)$
and
![]() $\alpha_{t}(E)$
t-cells, respectively. Then, there is a K(D,1) complex with
$\alpha_{t}(E)$
t-cells, respectively. Then, there is a K(D,1) complex with
![]() $\alpha_{i}(D)$
i-cells such that
$\alpha_{i}(D)$
i-cells such that
We now prove some results that will be used in order to show that limit groups over coherent RAAGs are slow above dimension 1.
Lemma 5·16.
Suppose that G is a group of homotopical type F, H is a normal subgroup of finite index in G and
![]() $(r_{j}(G))_{j}$
is a volume vector for G. Then,
$(r_{j}(G))_{j}$
is a volume vector for G. Then,
![]() $([G \,:\, H]r_{j}(G))_{j}$
is a volume vector for H.
$([G \,:\, H]r_{j}(G))_{j}$
is a volume vector for H.
Proof. Let Y be a classifying space K(G,1) that, for all
![]() $j\in \mathbb{N} \cup \{ 0 \} $
, has exactly
$j\in \mathbb{N} \cup \{ 0 \} $
, has exactly
![]() $r_{j}(G)$
j-cells. Then, if we denote by
$r_{j}(G)$
j-cells. Then, if we denote by
![]() $\widetilde{Y}$
the universal cover of Y,
$\widetilde{Y}$
the universal cover of Y,
![]() $\widetilde{Y}$
is contractible and
$\widetilde{Y}$
is contractible and
![]() $Y= \widetilde{Y} / G$
. Therefore,
$Y= \widetilde{Y} / G$
. Therefore,
![]() $\widetilde{Y} / H$
is a classifying space for H with exactly
$\widetilde{Y} / H$
is a classifying space for H with exactly
![]() $[G \,:\, H]r_{j}(G)$
j-cells.
$[G \,:\, H]r_{j}(G)$
j-cells.
Lemma 5·17. Let G be a group of homotopical type F and H a residually finite group where there is a short exact sequence
(a) If
![]() $n \geq 1$
, then H is slow.
$n \geq 1$
, then H is slow.
(b) If
![]() $n \geq 0$
and G is slow above dimension 1, then H is slow above dimension 1.
$n \geq 0$
and G is slow above dimension 1, then H is slow above dimension 1.
Proof. Let us denote
![]() $\mathbb{Z}^n$
by A.
$\mathbb{Z}^n$
by A.
(a) Let
![]() $(B_i)$
be a chain of finite index normal subgroups in H with
$(B_i)$
be a chain of finite index normal subgroups in H with
![]() $\bigcap B_i=1$
. We need to show that for each i there is a
$\bigcap B_i=1$
. We need to show that for each i there is a
![]() $K(B_i,1)$
complex with
$K(B_i,1)$
complex with
![]() $r_j(B_i)$
j-cells such that for each
$r_j(B_i)$
j-cells such that for each
![]() $j\geq 0$
,
$j\geq 0$
,
For each i, the short exact sequence from the statement induces a short exact sequence
Let us show that
Indeed, note that
![]() $[H \,:\, B_i]= [H \,:\, AB_i][AB_i \,:\, B_i]$
. Firstly,
$[H \,:\, B_i]= [H \,:\, AB_i][AB_i \,:\, B_i]$
. Firstly,
![]() $[AB_i \,:\, B_i]$
equals
$[AB_i \,:\, B_i]$
equals
![]() $[A \,:\, A \cap B_i]$
. Secondly,
$[A \,:\, A \cap B_i]$
. Secondly,
![]() $[H \,:\, A B_i]$
equals
$[H \,:\, A B_i]$
equals
![]() $[H / A \,:\, AB_i / A]$
, and
$[H / A \,:\, AB_i / A]$
, and
![]() $H / A \simeq G $
and
$H / A \simeq G $
and
![]() $ AB_i / A \simeq p(B_i).$
Therefore,
$ AB_i / A \simeq p(B_i).$
Therefore,
![]() $[H \,:\, AB_i] =[G \,:\, p(B_i)].$
$[H \,:\, AB_i] =[G \,:\, p(B_i)].$
Let
![]() $\alpha_{j}(G)$
be the number of j-cells in a fixed K(G,1) complex. By Lemma 5·16, there is a
$\alpha_{j}(G)$
be the number of j-cells in a fixed K(G,1) complex. By Lemma 5·16, there is a
![]() $K(p(B_{i}),1)$
complex with
$K(p(B_{i}),1)$
complex with
![]() $\alpha_{j}(p(B_{i}))$
j-cells such that
$\alpha_{j}(p(B_{i}))$
j-cells such that
Since
![]() $A\cap B_{i}$
has finite index in A, there is a
$A\cap B_{i}$
has finite index in A, there is a
![]() $K(A\cap B_{i},1)$
complex with
$K(A\cap B_{i},1)$
complex with
![]() $\left(\begin{array}{c}n\\j\end{array}\right)$
j-cells. By Lemma 5·15, there is a
$\left(\begin{array}{c}n\\j\end{array}\right)$
j-cells. By Lemma 5·15, there is a
![]() $K(B_{i},1)$
complex with
$K(B_{i},1)$
complex with
![]() $\alpha_{j}(B_{i})$
j-cells such that
$\alpha_{j}(B_{i})$
j-cells such that
and we set
![]() $r_j(B_i) = \alpha_j(B_i)$
. Then,
$r_j(B_i) = \alpha_j(B_i)$
. Then,
 \begin{align*} \lim_{i\to \infty} \frac{ r_{j}(B_{i})}{[ H \,:\, B_{i}]} & = \lim_{i\to \infty} \frac{ [ G \,:\, p(B_{i})]{{\sum}}_{0\leq a \leq j} {\left(\begin{array}{c}n\\j-a\end{array}\right)}\alpha_{a}(G)} {[G \,:\, p(B_{i})][A \,:\, B_{i} \cap A]}\\ & = {{\sum}}_{0\leq a \leq j} {\left(\begin{array}{c}n\\j-a\end{array}\right)}\alpha_{a}(G) \lim_{i\to \infty} \frac{1}{[A \,:\, B_{i} \cap A]} = 0. \end{align*}
\begin{align*} \lim_{i\to \infty} \frac{ r_{j}(B_{i})}{[ H \,:\, B_{i}]} & = \lim_{i\to \infty} \frac{ [ G \,:\, p(B_{i})]{{\sum}}_{0\leq a \leq j} {\left(\begin{array}{c}n\\j-a\end{array}\right)}\alpha_{a}(G)} {[G \,:\, p(B_{i})][A \,:\, B_{i} \cap A]}\\ & = {{\sum}}_{0\leq a \leq j} {\left(\begin{array}{c}n\\j-a\end{array}\right)}\alpha_{a}(G) \lim_{i\to \infty} \frac{1}{[A \,:\, B_{i} \cap A]} = 0. \end{align*}
(b) If
![]() $n\geq 1$
, then we apply a). If
$n\geq 1$
, then we apply a). If
![]() $n=0$
, by assumption G is slow above dimension 1.
$n=0$
, by assumption G is slow above dimension 1.
Theorem 5·18. Limit groups over coherent RAAGs are slow above dimension 1.
Proof. Let G be a coherent RAAG and let
![]() $\Gamma$
be a limit group over G. Then, by Theorem 5·14,
$\Gamma$
be a limit group over G. Then, by Theorem 5·14,
![]() $\Gamma$
is a subgroup of a graph tower over G, say L. Let us prove by induction on the height of L that
$\Gamma$
is a subgroup of a graph tower over G, say L. Let us prove by induction on the height of L that
![]() $\Gamma$
is slow above dimension 1 (see Proposition 5·13).
$\Gamma$
is slow above dimension 1 (see Proposition 5·13).
If L has height 0, L is a coherent RAAG. Therefore, L is the fundamental group of a graph of groups where the vertex groups are free abelian. Thus,
![]() $\Gamma$
also admits a decomposition as a graph of groups where the vertex groups are free abelian, so by Proposition 5·8 we get that
$\Gamma$
also admits a decomposition as a graph of groups where the vertex groups are free abelian, so by Proposition 5·8 we get that
![]() $\Gamma$
is slow above dimension 1.
$\Gamma$
is slow above dimension 1.
Now suppose that the height of L is greater than 0. Then, L is a free product with amalgamation, where the edge group is a free abelian group, one of the vertex groups is a graph tower over G of lower height and the other vertex group is either free abelian, or the direct product of a free abelian group and the fundamental group of a non-exceptional surface. Then,
![]() $\Gamma$
admits a decomposition as a graph of groups where the edge groups are free abelian (including the possibility that some are trivial), and the vertex groups are either subgroups of graph towers over G of lower height (and by induction, those vertex groups are slow above dimension 1) or free abelian groups or subgroups of the direct product of a free abelian group and the fundamental group of a non-exceptional surface. It suffices to show that finitely generated subgroups of the direct product of a free abelian group and the fundamental group of a non-exceptional surface are slow above dimension 1. Then, by Proposition 5·8 we obtain that
$\Gamma$
admits a decomposition as a graph of groups where the edge groups are free abelian (including the possibility that some are trivial), and the vertex groups are either subgroups of graph towers over G of lower height (and by induction, those vertex groups are slow above dimension 1) or free abelian groups or subgroups of the direct product of a free abelian group and the fundamental group of a non-exceptional surface. It suffices to show that finitely generated subgroups of the direct product of a free abelian group and the fundamental group of a non-exceptional surface are slow above dimension 1. Then, by Proposition 5·8 we obtain that
![]() $\Gamma$
is slow above dimension 1.
$\Gamma$
is slow above dimension 1.
If H is a finitely generated subgroup of
![]() $\mathbb{Z}^m \times G_0$
where
$\mathbb{Z}^m \times G_0$
where
![]() $m\in \mathbb{N} \cup \{0\}$
and
$m\in \mathbb{N} \cup \{0\}$
and
![]() $G_0$
is the fundamental group of a non-exceptional surface, then there is a short exact sequence
$G_0$
is the fundamental group of a non-exceptional surface, then there is a short exact sequence
where A is a free abelian group and N is a finitely generated subgroup of
![]() $G_0$
. In particular, N is either a surface group or a free group, so N is slow above dimension 1. Then, by Lemma 5·17, H is slow above dimension 1.
$G_0$
. In particular, N is either a surface group or a free group, so N is slow above dimension 1. Then, by Lemma 5·17, H is slow above dimension 1.
Remark 5·19. Observe that by Theorem 5·18 coherent RAAGs are slow above dimension 1. It is not true that every RAAG is slow above dimension 1, as this would imply that it is K-slow above dimension 1 for every field K. Indeed, by [
Reference Avramidi, Okun and Schreve3
, theorem 1], if G is a right-angled Artin group with underlying flag complex L, for any exhausting normal chain
![]() $(B_{n})$
in G,
$(B_{n})$
in G,
where
![]() $\bar{b}_{j-1}(L,K)$
denotes the reduced Betti number of L with coefficients in K.
$\bar{b}_{j-1}(L,K)$
denotes the reduced Betti number of L with coefficients in K.
Proof of Theorem 1·2. Parts (i) and (ii) follow from Theorem 5·1 and Theorem 5·18. Part (iii) follows from Theorem 5·18.
Proof of Theorem 1·3. It follows from Lemma 5·2 and the fact that Theorem 5·18 implies that every limit group over a coherent RAAG is K-slow above dimension 1.
Proof of Theorem 1·4. The proof is an adaptation of the proof from [ Reference Bridson and Kochloukova9 ] to the setting of residually Droms RAAGs. Thus, we just give a sketch of the proof.
From Theorem 2·10 we get that G is a full subdirect product of limit groups over Droms RAAGs
![]() $G_0 \times G_{1}\times \cdots \times G_{r}$
such that
$G_0 \times G_{1}\times \cdots \times G_{r}$
such that
![]() $G_0$
is abelian (possibly trivial),
$G_0$
is abelian (possibly trivial),
![]() $G \cap G_0$
has finite index in
$G \cap G_0$
has finite index in
![]() $G_0$
and
$G_0$
and
![]() $G_i$
has trivial center for
$G_i$
has trivial center for
![]() $i\in \{1, 2,\dots,r\}$
. By Proposition 3·16,
$i\in \{1, 2,\dots,r\}$
. By Proposition 3·16,
![]() $G_{i}$
is free-by-(torsion-free nilpotent).
$G_{i}$
is free-by-(torsion-free nilpotent).
Suppose that
![]() $G_0$
is trivial. Then, part (i) from Theorem 1·4 follows from Theorem 5·3 and Theorem 1·1. Indeed, by Proposition 3·16, each
$G_0$
is trivial. Then, part (i) from Theorem 1·4 follows from Theorem 5·3 and Theorem 1·1. Indeed, by Proposition 3·16, each
![]() $G_i$
has a free normal subgroup
$G_i$
has a free normal subgroup
![]() $N_i$
such that
$N_i$
such that
![]() $G_i / N_i$
is torsion-free nilpotent. By [
Reference Lopez de Gamiz Zearra23
, theorem 6·2],
$G_i / N_i$
is torsion-free nilpotent. By [
Reference Lopez de Gamiz Zearra23
, theorem 6·2],
![]() $G_i / (G \cap G_i)$
is virtually nilpotent, hence
$G_i / (G \cap G_i)$
is virtually nilpotent, hence
![]() $F_i = G \cap N_i$
is a free normal subgroup of
$F_i = G \cap N_i$
is a free normal subgroup of
![]() $G_i$
such that
$G_i$
such that
![]() $G_i/ F_i$
is virtually nilpotent. Hence there is a subgroup of finite index
$G_i/ F_i$
is virtually nilpotent. Hence there is a subgroup of finite index
![]() $\widetilde{G}_i$
in
$\widetilde{G}_i$
in
![]() $G_i$
that contains
$G_i$
that contains
![]() $F_i$
such that
$F_i$
such that
![]() $\widetilde{G}_i / F_i$
is torsion-free nilpotent. Then we can apply Theorem 5·3 for
$\widetilde{G}_i / F_i$
is torsion-free nilpotent. Then we can apply Theorem 5·3 for
![]() $\widetilde{G} \,:\!=\, G \cap ( \widetilde{G}_1 \times \cdots \times \widetilde{G}_r) < \widetilde{G}_1 \times \cdots \times \widetilde{G}_r$
. This guarantees an exhausting normal chain
$\widetilde{G} \,:\!=\, G \cap ( \widetilde{G}_1 \times \cdots \times \widetilde{G}_r) < \widetilde{G}_1 \times \cdots \times \widetilde{G}_r$
. This guarantees an exhausting normal chain
![]() $(B_n)$
of
$(B_n)$
of
![]() $\widetilde{G}$
that in general might not be a normal chain in G but it is still an exhausting chain in G such that for
$\widetilde{G}$
that in general might not be a normal chain in G but it is still an exhausting chain in G such that for
![]() $0\leq j \leq m$
,
$0\leq j \leq m$
,
![]() $ \lim_{n\to \infty} (\dim H_{j}(B_n,K))/([G \,:\, B_n])=0$
.
$ \lim_{n\to \infty} (\dim H_{j}(B_n,K))/([G \,:\, B_n])=0$
.
If
![]() $G_0$
is non-trivial,
$G_0$
is non-trivial,
![]() $G \cap G_0$
is non-trivial, free abelian and central, so part (i) from Theorem 1·4 follows from [
Reference Bridson and Kochloukova9
, lemma 7·2].
$G \cap G_0$
is non-trivial, free abelian and central, so part (i) from Theorem 1·4 follows from [
Reference Bridson and Kochloukova9
, lemma 7·2].
It remains to consider part (ii) from Theorem 1·4. From Theorem 2·8, G has a subgroup of finite index
![]() $H= H_1 \times \cdots \times H_{ r_0}$
where each
$H= H_1 \times \cdots \times H_{ r_0}$
where each
![]() $H_i$
is a limit group over Droms RAAGs. Following the proof of [
Reference Bridson and Kochloukova9
, theorem E], we can choose
$H_i$
is a limit group over Droms RAAGs. Following the proof of [
Reference Bridson and Kochloukova9
, theorem E], we can choose
![]() $ ( B_i)$
an exhausting normal chain in H and such that
$ ( B_i)$
an exhausting normal chain in H and such that
![]() $B_i = ( B_i \cap H_1 ) \times \cdots \times (B_i \cap H_{ r_0})$
. Then, as in [
Reference Bridson and Kochloukova9
], we can deduce that for
$B_i = ( B_i \cap H_1 ) \times \cdots \times (B_i \cap H_{ r_0})$
. Then, as in [
Reference Bridson and Kochloukova9
], we can deduce that for
![]() $j \geq 1$
,
$j \geq 1$
,
where
![]() $\delta_{j,{ r_0}}$
is the Kronecker symbol.
$\delta_{j,{ r_0}}$
is the Kronecker symbol.
A limit group over a Droms RAAG does not contain a direct product of two or more non-abelian free groups, since limit groups over Droms RAAGs are coherent (see [
Reference Casals–Ruiz, Duncan and Kazachkov11
, corollary 7·8]) and the direct product of two non-abelian free groups is not coherent. In addition, every limit group over a Droms RAAG that has trivial center contains a non-abelian free group (see, for instance, [
Reference Lopez de Gamiz Zearra23
, property 2·10]), so
![]() ${ r_0}= \rho$
unless one or more
${ r_0}= \rho$
unless one or more
![]() $H_i$
has non-trivial center. If some
$H_i$
has non-trivial center. If some
![]() $H_i$
has non-trivial center,
$H_i$
has non-trivial center,
![]() $\chi(H_i)= 0$
and so
$\chi(H_i)= 0$
and so
![]() $\chi(H) = 0$
and
$\chi(H) = 0$
and
![]() $ \chi(G)=0$
.
$ \chi(G)=0$
.
Proof of Theorem 1·6. In Theorem 5·4 Bridson and Kochloukova proved a low dimensional homotopical version of Theorem 1·4 for limit groups over free groups. The proof of Theorem 5·4 relies on some general results about residually finite groups, see [ Reference Bridson and Kochloukova9 , lemma 8·1, lemma 8·2], and some specific results for limit groups over free groups. The properties of limit groups over free groups that are used in the proof of Theorem 5·4 still hold for the class of limit groups over Droms RAAGs and correspond to Theorem 1·1 and Theorem 2·10, so the same proof can be used in order to show Theorem 1·6.
Acknowledgements
We are thankful to Montserrat Casals–Ruiz for helpful talks during the preparation of this manuscript and the referee for the suggestions that improved the paper. D. Kochloukova was partially supported by the CNPq grant 301779/2017-1 and by the FAPESP grant 2018/23690-6. J. Lopez de Gamiz Zearra was supported by the Basque Government grant IT974-16 and the Spanish Government grant MTM2017-86802-P.