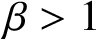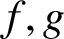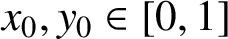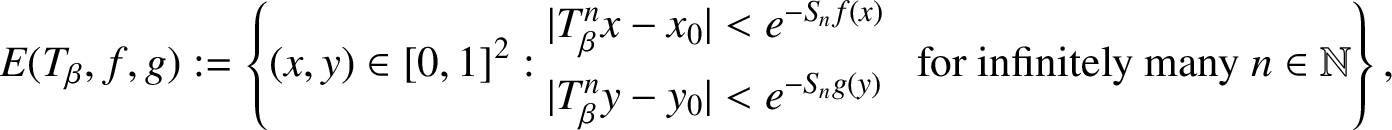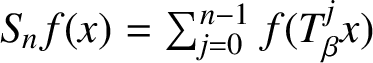1 Introduction
The study of the Diophantine properties of the distribution of orbits for a measure-preserving dynamical system has recently received much attention. Let
![]() $T:X\to X$
be a measure-preserving transformation of the system
$T:X\to X$
be a measure-preserving transformation of the system
![]() $(X,\mathcal {B},\mu )$
with a consistent metric d. If the transformation T is ergodic with respect to the measure
$(X,\mathcal {B},\mu )$
with a consistent metric d. If the transformation T is ergodic with respect to the measure
![]() $\mu $
, Poincaré’s recurrence theorem implies that, for almost every
$\mu $
, Poincaré’s recurrence theorem implies that, for almost every
![]() $x\in X$
, the orbit
$x\in X$
, the orbit
![]() $\{T^nx\}_{n=0}^\infty $
returns to an arbitrary but fixed neighbourhood of x infinitely often. That is, for any
$\{T^nx\}_{n=0}^\infty $
returns to an arbitrary but fixed neighbourhood of x infinitely often. That is, for any
![]() $x_0\in X$
, for
$x_0\in X$
, for
![]() $\mu $
-almost all
$\mu $
-almost all
![]() $x\in X,$
$x\in X,$
 $$ \begin{align*}\liminf\limits_{n\rightarrow\infty} d(T^nx,x_0)=0.\end{align*} $$
$$ \begin{align*}\liminf\limits_{n\rightarrow\infty} d(T^nx,x_0)=0.\end{align*} $$
Poincaré’s recurrence theorem is qualitative in nature but it does motivate the study of the distribution of T-orbits of points in X quantitatively. In other words, a natural motivation is to investigate how fast the above limit infimum tends to zero. To this end, the spotlight is on the size of the set
where
![]() $\varphi :\mathbb N\rightarrow \mathbb R_{\geq 0}$
is a positive function such that
$\varphi :\mathbb N\rightarrow \mathbb R_{\geq 0}$
is a positive function such that
![]() $\varphi (n)\rightarrow 0$
as
$\varphi (n)\rightarrow 0$
as
![]() $n\rightarrow \infty .$
Here and throughout, ‘i.m.’ is used for ‘infinitely many’. The set
$n\rightarrow \infty .$
Here and throughout, ‘i.m.’ is used for ‘infinitely many’. The set
![]() $D(T,\varphi )$
can be viewed as the collection of points in X whose T-orbit hits a shrinking target infinitely many times. The set
$D(T,\varphi )$
can be viewed as the collection of points in X whose T-orbit hits a shrinking target infinitely many times. The set
![]() $D(T,\varphi )$
is the dynamical analogue of the classical inhomogeneous well-approximable set
$D(T,\varphi )$
is the dynamical analogue of the classical inhomogeneous well-approximable set
As one would expect, the ‘size’ of both of these sets depends upon the nature of the function
![]() $\varphi $
, that is, how fast it approaches zero. The size of the set
$\varphi $
, that is, how fast it approaches zero. The size of the set
![]() $W(\varphi )$
in terms of Lebesgue measure or Hausdorff measure and dimension has been established even in the higher-dimensional (linear form) settings; see [Reference Beresnevich, Ramírez and Velani1, Reference Hussain and Simmons8, Reference Wang, Wu and Xu19] for further details. In contrast, not much is known for the higher-dimensional version of the set
$W(\varphi )$
in terms of Lebesgue measure or Hausdorff measure and dimension has been established even in the higher-dimensional (linear form) settings; see [Reference Beresnevich, Ramírez and Velani1, Reference Hussain and Simmons8, Reference Wang, Wu and Xu19] for further details. In contrast, not much is known for the higher-dimensional version of the set
![]() $D(T, \varphi )$
for general T.
$D(T, \varphi )$
for general T.
Following the work of Hill and Velani [Reference Hill and Velani6], the Hausdorff dimension of the set
![]() $D(T, \varphi )$
has been determined for many dynamical systems, from the system of rational expanding maps on their Julia sets to conformal iterated function systems [Reference Urbański15]. We refer the reader to [Reference Coons, Hussain and Wang3] for a comprehensive discussion regarding the Hausdorff dimension of various dynamical systems. In this paper, we confine ourselves to the two-dimensional shrinking target problem in beta dynamical systems with general errors of approximation.
$D(T, \varphi )$
has been determined for many dynamical systems, from the system of rational expanding maps on their Julia sets to conformal iterated function systems [Reference Urbański15]. We refer the reader to [Reference Coons, Hussain and Wang3] for a comprehensive discussion regarding the Hausdorff dimension of various dynamical systems. In this paper, we confine ourselves to the two-dimensional shrinking target problem in beta dynamical systems with general errors of approximation.
For a real number
![]() $\beta>1$
, define the transformation
$\beta>1$
, define the transformation
![]() $T_\beta :[0,1]\to [0,1]$
by
$T_\beta :[0,1]\to [0,1]$
by
This map generates the
![]() $\beta $
-dynamical system
$\beta $
-dynamical system
![]() $([0,1], T_\beta )$
. It is well known that
$([0,1], T_\beta )$
. It is well known that
![]() $\beta $
-expansion is a typical example of an expanding nonfinite Markov system whose properties are reflected by the orbit of some critical point; in other words, it is not a subshift of finite type with mixing properties. This causes difficulties in studying metrical questions related to
$\beta $
-expansion is a typical example of an expanding nonfinite Markov system whose properties are reflected by the orbit of some critical point; in other words, it is not a subshift of finite type with mixing properties. This causes difficulties in studying metrical questions related to
![]() $\beta $
-expansions. General
$\beta $
-expansions. General
![]() $\beta $
-expansions have been widely studied in the literature; see for instance [Reference Hussain, Li, Simmons and Wang7, Reference Hussain and Wang9, Reference Seuret and Wang12–Reference Tan and Wang14] and references therein. In particular, the Hausdorff dimension, denoted throughout by
$\beta $
-expansions have been widely studied in the literature; see for instance [Reference Hussain, Li, Simmons and Wang7, Reference Hussain and Wang9, Reference Seuret and Wang12–Reference Tan and Wang14] and references therein. In particular, the Hausdorff dimension, denoted throughout by
![]() $\dim _H$
, of
$\dim _H$
, of
![]() $D(T_\beta , \varphi )$
was obtained in [Reference Shen and Wang13] and the Lebesgue measure and Hausdorff dimension of the set
$D(T_\beta , \varphi )$
was obtained in [Reference Shen and Wang13] and the Lebesgue measure and Hausdorff dimension of the set
 $$ \begin{align*}D(T_{\beta}, \varphi_1,\varphi_2):=\left\{(x,y)\in [0,1]^2: \begin{array}{@{}ll@{}} \lvert T_{\beta}^{n}x-x_{0}\rvert <\varphi_1(n)\\[1ex] \lvert T_{\beta}^{n}y-y_{0}\rvert < \varphi_2(n) \end{array} {\text{ for i.m. }} n\in \mathbb N \right\} \end{align*} $$
$$ \begin{align*}D(T_{\beta}, \varphi_1,\varphi_2):=\left\{(x,y)\in [0,1]^2: \begin{array}{@{}ll@{}} \lvert T_{\beta}^{n}x-x_{0}\rvert <\varphi_1(n)\\[1ex] \lvert T_{\beta}^{n}y-y_{0}\rvert < \varphi_2(n) \end{array} {\text{ for i.m. }} n\in \mathbb N \right\} \end{align*} $$
was calculated in [Reference Hussain and Wang9]. Here
![]() $x_0, y_0\in [0, 1]$
are fixed and the approximating functions
$x_0, y_0\in [0, 1]$
are fixed and the approximating functions
![]() $\varphi _1, \varphi _2$
are positive functions of n.
$\varphi _1, \varphi _2$
are positive functions of n.
In 2014, Bugeaud and Wang [Reference Bugeaud and Wang2] calculated the Hausdorff dimension of the set with the error of approximation given by the ergodic sum, that is,
 $$ \begin{align*}E(T_\beta, h):=\{x\in [0,1]: \begin{array}{@{}ll@{}} \lvert T_{\beta}^{n}x-x_{0}\rvert <e^{-S_nh(x)}\end{array}{\text{for i.m. }} n\in \mathbb N \}, \end{align*} $$
$$ \begin{align*}E(T_\beta, h):=\{x\in [0,1]: \begin{array}{@{}ll@{}} \lvert T_{\beta}^{n}x-x_{0}\rvert <e^{-S_nh(x)}\end{array}{\text{for i.m. }} n\in \mathbb N \}, \end{align*} $$
where h is a positive continuous function on
![]() $[0,1]$
and
$[0,1]$
and
 $S_nh(x)=h(x)+\cdots +h(T_{\beta }^{n-1}x).$
Clearly the error of approximation is exponential depending upon the orbits
$S_nh(x)=h(x)+\cdots +h(T_{\beta }^{n-1}x).$
Clearly the error of approximation is exponential depending upon the orbits
![]() $T_\beta x$
. Note that it is still an open problem whether
$T_\beta x$
. Note that it is still an open problem whether
![]() $e^{-S_nh(x)}$
implies the arbitrary function
$e^{-S_nh(x)}$
implies the arbitrary function
![]() $\varphi (n)$
or not. However,
$\varphi (n)$
or not. However,
![]() $e^{-S_nf(x)}$
reduces to
$e^{-S_nf(x)}$
reduces to
![]() $\beta ^{-n\tau }$
by considering
$\beta ^{-n\tau }$
by considering
![]() $h(x)=\tau \log \lvert T'(x)\rvert $
for some
$h(x)=\tau \log \lvert T'(x)\rvert $
for some
![]() $\tau>0$
. Thus, the result of [Reference Bugeaud and Wang2] implies the Jarník–Besicovitch type result for the set under consideration.
$\tau>0$
. Thus, the result of [Reference Bugeaud and Wang2] implies the Jarník–Besicovitch type result for the set under consideration.
In this paper, we extend Bugeaud and Wang’s set
![]() $E(T_\beta , h)$
to the two-dimensional setting and calculate its Hausdorff dimension. Let
$E(T_\beta , h)$
to the two-dimensional setting and calculate its Hausdorff dimension. Let
![]() $f,g$
be two positive continuous function on
$f,g$
be two positive continuous function on
![]() $[0,1]$
and let
$[0,1]$
and let
![]() $x_0, y_0\in [0, 1]$
be fixed. Define
$x_0, y_0\in [0, 1]$
be fixed. Define
 $$ \begin{align*}E(T_\beta, f,g):=\left\{(x,y)\in [0,1]^2: \begin{array}{@{}ll@{}} \lvert T_{\beta}^{n}x-x_{0}\rvert <e^{-S_nf(x)}\\[1ex] \lvert T_{\beta}^{n}y-y_{0}\rvert < e^{-S_ng(y)} \end{array} \ {\text{for i.m. }} \ n\in \mathbb N \right\}. \end{align*} $$
$$ \begin{align*}E(T_\beta, f,g):=\left\{(x,y)\in [0,1]^2: \begin{array}{@{}ll@{}} \lvert T_{\beta}^{n}x-x_{0}\rvert <e^{-S_nf(x)}\\[1ex] \lvert T_{\beta}^{n}y-y_{0}\rvert < e^{-S_ng(y)} \end{array} \ {\text{for i.m. }} \ n\in \mathbb N \right\}. \end{align*} $$
The set
![]() $E(T_\beta , f,g)$
is the set of all points
$E(T_\beta , f,g)$
is the set of all points
![]() $(x, y)$
in the unit square such that the pair
$(x, y)$
in the unit square such that the pair
![]() $\{(T^{n}x, T^{n} y)\}$
is in the shrinking rectangle
$\{(T^{n}x, T^{n} y)\}$
is in the shrinking rectangle
![]() $B( x_0,e^{-S_nf(x)} )\times B( y_0,e^{-S_ng(y)} )$
for infinitely many n. The rectangle shrinks to zero at exponential rates given by
$B( x_0,e^{-S_nf(x)} )\times B( y_0,e^{-S_ng(y)} )$
for infinitely many n. The rectangle shrinks to zero at exponential rates given by
![]() $e^{-S_nf(x)}$
and
$e^{-S_nf(x)}$
and
![]() $e^{-S_ng(y)}$
. We shall prove the following result.
$e^{-S_ng(y)}$
. We shall prove the following result.
Theorem 1.1. Let
![]() $f,g$
be two continuous functions on
$f,g$
be two continuous functions on
![]() $[0,1]$
with
$[0,1]$
with
![]() $f(x)\geq g(y)$
for all
$f(x)\geq g(y)$
for all
![]() $x,y\in [0,1]$
. Then
$x,y\in [0,1]$
. Then
where
 $$ \begin{align*}s_1&=\inf\{s\geq 0: P(f-s(\log\beta+f))+P(-g)\leq 0\}, \\ s_2&=\inf\{s\geq 0: P(-s(\log\beta+g))+\log\beta\leq 0\}.\end{align*} $$
$$ \begin{align*}s_1&=\inf\{s\geq 0: P(f-s(\log\beta+f))+P(-g)\leq 0\}, \\ s_2&=\inf\{s\geq 0: P(-s(\log\beta+g))+\log\beta\leq 0\}.\end{align*} $$
Here
![]() $P(\cdot )$
stands for the pressure function for the
$P(\cdot )$
stands for the pressure function for the
![]() $\beta $
-dynamical system associated to continuous potentials f and g. To keep the introductory section short, we formally give the definition of the pressure function in Section 2. The reason why the Hausdorff dimension is in terms of the pressure function is because of the dynamical nature of the set
$\beta $
-dynamical system associated to continuous potentials f and g. To keep the introductory section short, we formally give the definition of the pressure function in Section 2. The reason why the Hausdorff dimension is in terms of the pressure function is because of the dynamical nature of the set
![]() $E(T_\beta , f, g)$
. For the detailed analysis of the properties of the pressure function and ergodic sums for general dynamical systems we refer the reader to [Reference Walters17, Ch. 9].
$E(T_\beta , f, g)$
. For the detailed analysis of the properties of the pressure function and ergodic sums for general dynamical systems we refer the reader to [Reference Walters17, Ch. 9].
The proof of this theorem splits into two parts: establishing the upper bound and then the lower bound. The upper bound is relatively easier to prove by using the definition of Hausdorff dimension on the natural cover of the set. However, establishing the lower bound is challenging and the main substance of this paper. Actually, the main obstacle in determining the metrical properties of general
![]() $\beta $
-expansions lies in the difficulty of estimating the length of a general cylinder and, since we are dealing with two-dimensional settings, the area of the cross-product of general cylinders. As far as the Hausdorff dimension is concerned, one does not need to take all points into consideration; instead, one may choose a subset of points with regular properties to approximate the set in question. This argument in turn requires some continuity of the dimensional number, when the system is approximated by its subsystem.
$\beta $
-expansions lies in the difficulty of estimating the length of a general cylinder and, since we are dealing with two-dimensional settings, the area of the cross-product of general cylinders. As far as the Hausdorff dimension is concerned, one does not need to take all points into consideration; instead, one may choose a subset of points with regular properties to approximate the set in question. This argument in turn requires some continuity of the dimensional number, when the system is approximated by its subsystem.
The paper is organised as follows. Section 2 is devoted to recalling some elementary properties of
![]() $\beta $
-expansions. Short proofs are also given when we could not find any reference. Definitions and some properties of the pressure function are stated in this section as well. In Section 3 we prove the upper bound of Theorem 1.1. In Section 4 we prove the lower bound of Theorem 1.1, and since this takes up a large proportion of the paper we subdivide this section into several subsections.
$\beta $
-expansions. Short proofs are also given when we could not find any reference. Definitions and some properties of the pressure function are stated in this section as well. In Section 3 we prove the upper bound of Theorem 1.1. In Section 4 we prove the lower bound of Theorem 1.1, and since this takes up a large proportion of the paper we subdivide this section into several subsections.
2 Preliminaries
We begin with a brief account of some basic properties of
![]() $\beta $
-expansions and we fix some notation. We then state and prove two propositions which give the covering and packing properties.
$\beta $
-expansions and we fix some notation. We then state and prove two propositions which give the covering and packing properties.
The
![]() $\beta $
-expansion of real numbers was first introduced by Rényi [Reference Rényi11], and is given by the following algorithm. For any
$\beta $
-expansion of real numbers was first introduced by Rényi [Reference Rényi11], and is given by the following algorithm. For any
![]() $\beta>1$
, let
$\beta>1$
, let
where
![]() $\lfloor \xi \rfloor $
is the integer part of
$\lfloor \xi \rfloor $
is the integer part of
![]() $\xi \in \mathbb {R}$
. By taking
$\xi \in \mathbb {R}$
. By taking
 $$ \begin{align*}\epsilon_{n}(x,\beta)=\lfloor\,\beta T_{\beta}^{n-1}x\rfloor\in \mathbb{N}\end{align*} $$
$$ \begin{align*}\epsilon_{n}(x,\beta)=\lfloor\,\beta T_{\beta}^{n-1}x\rfloor\in \mathbb{N}\end{align*} $$
recursively for each
![]() $n\geq 1,$
every
$n\geq 1,$
every
![]() $x\in [0,1)$
can be uniquely expanded into a finite or an infinite sequence
$x\in [0,1)$
can be uniquely expanded into a finite or an infinite sequence
 $$ \begin{align*} x=\frac{\epsilon_{1}(x,\beta)}{\beta}+\frac{\epsilon_{2}(x,\beta)}{\beta^2}+\cdots+\frac{\epsilon_{n}(x,\beta)}{\beta^n}+ \frac{T_{\beta}^n x}{\beta^n}, \end{align*} $$
$$ \begin{align*} x=\frac{\epsilon_{1}(x,\beta)}{\beta}+\frac{\epsilon_{2}(x,\beta)}{\beta^2}+\cdots+\frac{\epsilon_{n}(x,\beta)}{\beta^n}+ \frac{T_{\beta}^n x}{\beta^n}, \end{align*} $$
which is called the
![]() $\beta $
-expansion of x, and the sequence
$\beta $
-expansion of x, and the sequence
![]() $\{\epsilon _{n}(x,\beta )\}_{n\geq 1}$
is called the digit sequence of
$\{\epsilon _{n}(x,\beta )\}_{n\geq 1}$
is called the digit sequence of
![]() $x.$
We also write the
$x.$
We also write the
![]() $\beta $
-expansion of x as
$\beta $
-expansion of x as
The system
![]() $([0,1],T_{\beta })$
is called a
$([0,1],T_{\beta })$
is called a
![]() $\beta $
-dynamical system or just a
$\beta $
-dynamical system or just a
![]() $\beta $
-system.
$\beta $
-system.
Definition 2.1. A finite or an infinite sequence
![]() $(w_{1},w_{2},\ldots )$
is said to be admissible (with respect to the base
$(w_{1},w_{2},\ldots )$
is said to be admissible (with respect to the base
![]() $\beta $
), if there exists an
$\beta $
), if there exists an
![]() $x\in [0,1)$
such that the digit sequence of x equals
$x\in [0,1)$
such that the digit sequence of x equals
![]() $(w_{1},w_{2},\ldots ).$
$(w_{1},w_{2},\ldots ).$
Denote by
![]() $\Sigma _{\beta }^n$
the collection of all admissible sequences of length n and by
$\Sigma _{\beta }^n$
the collection of all admissible sequences of length n and by
![]() $\Sigma _{\beta }$
that of all infinite admissible sequences.
$\Sigma _{\beta }$
that of all infinite admissible sequences.
Let us now turn to the infinite
![]() $\beta $
-expansion of
$\beta $
-expansion of
![]() $1$
, which plays an important role in the study of
$1$
, which plays an important role in the study of
![]() $\beta $
-expansions. Applying algorithm (2-1) to the number
$\beta $
-expansions. Applying algorithm (2-1) to the number
![]() $x=1$
, then the number
$x=1$
, then the number
![]() $1$
can be expanded into a series, denoted by
$1$
can be expanded into a series, denoted by
 $$ \begin{align*}1=\frac{\epsilon_{1}(1,\beta)}{\beta}+\frac{\epsilon_{2}(1,\beta)}{\beta^2}+\cdots+\frac{\epsilon_{n}(1,\beta)}{\beta^n}+ \cdots.\end{align*} $$
$$ \begin{align*}1=\frac{\epsilon_{1}(1,\beta)}{\beta}+\frac{\epsilon_{2}(1,\beta)}{\beta^2}+\cdots+\frac{\epsilon_{n}(1,\beta)}{\beta^n}+ \cdots.\end{align*} $$
If the above series is finite, that is, there exists
![]() $m\geq 1$
such that
$m\geq 1$
such that
![]() $\epsilon _{m}(1,\beta )\neq 0$
but
$\epsilon _{m}(1,\beta )\neq 0$
but
![]() $\epsilon _{n}(1,\beta )=0$
for
$\epsilon _{n}(1,\beta )=0$
for
![]() $n>m$
, then
$n>m$
, then
![]() $\beta $
is called a simple Parry number. In this case, we write
$\beta $
is called a simple Parry number. In this case, we write
where
![]() $(w)^\infty $
denotes the periodic sequence
$(w)^\infty $
denotes the periodic sequence
![]() $(w,w,w,\ldots ).$
If
$(w,w,w,\ldots ).$
If
![]() $\beta $
is not a simple Parry number, we write
$\beta $
is not a simple Parry number, we write
In both cases, the sequence
![]() $(\epsilon _{1}^{*}(\,\beta ),\epsilon _{2}^{*}(\,\beta ),\ldots )$
is called the infinite
$(\epsilon _{1}^{*}(\,\beta ),\epsilon _{2}^{*}(\,\beta ),\ldots )$
is called the infinite
![]() $\beta $
-expansion of
$\beta $
-expansion of
![]() $1$
and we always have that
$1$
and we always have that
 $$ \begin{align*} 1=\frac{\epsilon_{1}^*(\,\beta)}{\beta}+\frac{\epsilon_{2}^*(\,\beta)}{\beta^2}+\cdots+\frac{\epsilon_{n}^*(\,\beta)}{\beta^n}+ \cdots. \end{align*} $$
$$ \begin{align*} 1=\frac{\epsilon_{1}^*(\,\beta)}{\beta}+\frac{\epsilon_{2}^*(\,\beta)}{\beta^2}+\cdots+\frac{\epsilon_{n}^*(\,\beta)}{\beta^n}+ \cdots. \end{align*} $$
The lexicographical order
![]() $\prec $
between infinite sequences is defined as
$\prec $
between infinite sequences is defined as
if there exists
![]() $k\geq 1$
such that
$k\geq 1$
such that
 $w_{j}=w_{j}'$
for
$w_{j}=w_{j}'$
for
![]() $1\leq j<k$
, while
$1\leq j<k$
, while
![]() $w_{k}<w_{k}'.$
The notation
$w_{k}<w_{k}'.$
The notation
![]() $w\preceq w'$
means that
$w\preceq w'$
means that
![]() $w\prec w'$
or
$w\prec w'$
or
![]() $w=w'.$
This ordering can be extended to finite blocks by identifying the finite block
$w=w'.$
This ordering can be extended to finite blocks by identifying the finite block
![]() $(w_{1},w_2,\ldots ,w_n)$
with the sequence
$(w_{1},w_2,\ldots ,w_n)$
with the sequence
![]() $(w_{1},w_2,\ldots ,w_n,0,0,\ldots )$
.
$(w_{1},w_2,\ldots ,w_n,0,0,\ldots )$
.
The following result due to Parry [Reference Parry10] is a criterion for the admissibility of a sequence.
Lemma 2.2 (Parry [Reference Parry10])
Let
![]() $\beta>1$
be a real number. Then a nonnegative integer sequence
$\beta>1$
be a real number. Then a nonnegative integer sequence
![]() $\epsilon =(\epsilon _1,\epsilon _2,\ldots )$
is admissible if and only if, for any
$\epsilon =(\epsilon _1,\epsilon _2,\ldots )$
is admissible if and only if, for any
![]() $k\geq 1$
,
$k\geq 1$
,
The following result of Rényi implies that the dynamical system
![]() $([0,1],T_\beta )$
admits
$([0,1],T_\beta )$
admits
![]() $\log \beta $
as its topological entropy.
$\log \beta $
as its topological entropy.
Lemma 2.3 (Rényi [Reference Rényi11])
Let
![]() $\beta>1.$
For any
$\beta>1.$
For any
![]() $n\geq 1,$
$n\geq 1,$
 $$ \begin{align*}\beta^{n}\leq\#\Sigma_{\beta}^n\leq\frac{\beta^{n+1}}{\beta-1},\end{align*} $$
$$ \begin{align*}\beta^{n}\leq\#\Sigma_{\beta}^n\leq\frac{\beta^{n+1}}{\beta-1},\end{align*} $$
where
![]() $\#$
denotes the cardinality of a finite set.
$\#$
denotes the cardinality of a finite set.
It is clear from this lemma that
 $$ \begin{align*}\lim_{n\to\infty}\frac{\log(\#\Sigma_{\beta}^n)}{n}=\log\beta.\end{align*} $$
$$ \begin{align*}\lim_{n\to\infty}\frac{\log(\#\Sigma_{\beta}^n)}{n}=\log\beta.\end{align*} $$
For any
 $\boldsymbol \epsilon _{n}:=(\epsilon _1,\ldots ,\epsilon _n)\in \Sigma _{\beta }^n,$
call
$\boldsymbol \epsilon _{n}:=(\epsilon _1,\ldots ,\epsilon _n)\in \Sigma _{\beta }^n,$
call
an n th-order cylinder
![]() $(\text {with respect to the base}~\beta )$
. It is a left-closed and right-open interval with the left endpoint
$(\text {with respect to the base}~\beta )$
. It is a left-closed and right-open interval with the left endpoint
 $$ \begin{align*}\frac{\epsilon_1}{\beta}+\frac{\epsilon_2}{\beta^2}+\cdots+\frac{\epsilon_n}{\beta^n} \end{align*} $$
$$ \begin{align*}\frac{\epsilon_1}{\beta}+\frac{\epsilon_2}{\beta^2}+\cdots+\frac{\epsilon_n}{\beta^n} \end{align*} $$
and length
 $$ \begin{align*}\lvert I_n(\boldsymbol\epsilon_n)\rvert \leq\frac{1}{\beta^n}.\end{align*} $$
$$ \begin{align*}\lvert I_n(\boldsymbol\epsilon_n)\rvert \leq\frac{1}{\beta^n}.\end{align*} $$
Here and throughout the paper, we use
![]() $\lvert \cdot \rvert $
to denote the length of an interval. Note that the unit interval can be naturally partitioned into a disjoint union of cylinders; that is, for any
$\lvert \cdot \rvert $
to denote the length of an interval. Note that the unit interval can be naturally partitioned into a disjoint union of cylinders; that is, for any
![]() $n\geq 1$
,
$n\geq 1$
,
 $$ \begin{align*} [0,1]=\bigcup\limits_{\boldsymbol\epsilon_n \in\Sigma_{\beta}^n} I_{n}(\boldsymbol\epsilon_n). \end{align*} $$
$$ \begin{align*} [0,1]=\bigcup\limits_{\boldsymbol\epsilon_n \in\Sigma_{\beta}^n} I_{n}(\boldsymbol\epsilon_n). \end{align*} $$
One difficulty in studying the metric properties of
![]() $\beta $
-expansions is that the length of a cylinder is not regular. It may happen that
$\beta $
-expansions is that the length of a cylinder is not regular. It may happen that
![]() $\lvert I_n(\epsilon _1,\ldots , \epsilon _n)\rvert \ll ~\beta ^{-n}$
. Here
$\lvert I_n(\epsilon _1,\ldots , \epsilon _n)\rvert \ll ~\beta ^{-n}$
. Here
![]() $a\ll b$
is used to indicate that there exists a constant
$a\ll b$
is used to indicate that there exists a constant
![]() $c>0$
such that
$c>0$
such that
![]() $a\leq cb$
. We write
$a\leq cb$
. We write
![]() $a\asymp b$
if
$a\asymp b$
if
![]() $a\ll b\ll a$
. The following notation plays an important role in bypassing this difficulty.
$a\ll b\ll a$
. The following notation plays an important role in bypassing this difficulty.
Definition 2.4 (Full cylinder)
A cylinder
![]() $I_{n}(\boldsymbol \epsilon _n)$
is called full if it has maximal length, that is, if
$I_{n}(\boldsymbol \epsilon _n)$
is called full if it has maximal length, that is, if
 $$ \begin{align*}\lvert I_{n}(\boldsymbol\epsilon_n)\rvert =\frac{1}{\beta^n}.\end{align*} $$
$$ \begin{align*}\lvert I_{n}(\boldsymbol\epsilon_n)\rvert =\frac{1}{\beta^n}.\end{align*} $$
Correspondingly, we also call the word
![]() $(\epsilon _1,\ldots ,\epsilon _n)$
, defining the full cylinder
$(\epsilon _1,\ldots ,\epsilon _n)$
, defining the full cylinder
![]() $I_{n}(\boldsymbol \epsilon _n)$
, a full word.
$I_{n}(\boldsymbol \epsilon _n)$
, a full word.
Next, we collect some properties about the distribution of full cylinders.
Proposition 2.5 (Fan and Wang [Reference Fan and Wang5])
An n th-order cylinder
![]() $I_{n}(\boldsymbol \epsilon _n)$
is full if and only if, for any admissible sequence
$I_{n}(\boldsymbol \epsilon _n)$
is full if and only if, for any admissible sequence
 $\boldsymbol \epsilon _m':=(\epsilon _{1}',\epsilon _{2}',\ldots ,\epsilon _{m}')\in \Sigma _{\beta }^m$
with
$\boldsymbol \epsilon _m':=(\epsilon _{1}',\epsilon _{2}',\ldots ,\epsilon _{m}')\in \Sigma _{\beta }^m$
with
![]() $m\geq 1$
,
$m\geq 1$
,
 $$ \begin{align*}(\boldsymbol\epsilon_n, \boldsymbol\epsilon_m')\in\Sigma_{\beta}^{n+m}.\end{align*} $$
$$ \begin{align*}(\boldsymbol\epsilon_n, \boldsymbol\epsilon_m')\in\Sigma_{\beta}^{n+m}.\end{align*} $$
Moreover.
So, for any two full cylinders
![]() $I_{n}(\boldsymbol \epsilon _{n}),~ I_{m}(\boldsymbol \epsilon _{m}')$
, the cylinder
$I_{n}(\boldsymbol \epsilon _{n}),~ I_{m}(\boldsymbol \epsilon _{m}')$
, the cylinder
![]() $I_{n+m}(\boldsymbol \epsilon _{n}, \boldsymbol \epsilon _{m}')$
is also full.
$I_{n+m}(\boldsymbol \epsilon _{n}, \boldsymbol \epsilon _{m}')$
is also full.
Lemma 2.6 (Bugeaud and Wang [Reference Bugeaud and Wang2])
For
![]() $n\geq 1$
, among every
$n\geq 1$
, among every
![]() $n+1$
consecutive cylinders of order n, there exists at least one full cylinder.
$n+1$
consecutive cylinders of order n, there exists at least one full cylinder.
As a consequence, one has the following relationship between balls and cylinders.
Proposition 2.7 (Covering property)
Let J be an interval of length
![]() ${\beta }^{-l}$
with
${\beta }^{-l}$
with
![]() $l\geq 1$
. Then it can be covered by at most
$l\geq 1$
. Then it can be covered by at most
![]() $2(l+1)$
cylinders of order l.
$2(l+1)$
cylinders of order l.
Proof. By Lemma 2.6, among any
![]() $2(l+1)$
consecutive cylinders of order l, there are at least two full cylinders. So the total length of these intervals is larger than
$2(l+1)$
consecutive cylinders of order l, there are at least two full cylinders. So the total length of these intervals is larger than
![]() $2{\beta }^{-l}$
. Thus J can be covered by at most
$2{\beta }^{-l}$
. Thus J can be covered by at most
![]() $2(l+1)$
cylinders of order l.
$2(l+1)$
cylinders of order l.
The following result may be of independent interest.
Proposition 2.8 (Packing property)
Fix
![]() $0<\epsilon <1$
. Let
$0<\epsilon <1$
. Let
![]() $~n_0$
be an integer such that
$~n_0$
be an integer such that
![]() $2n^2\beta <{\beta }^{(n-1)\epsilon }$
for all
$2n^2\beta <{\beta }^{(n-1)\epsilon }$
for all
![]() $n\ge n_0$
. Let
$n\ge n_0$
. Let
![]() $J\subset [0,1]$
be an interval of length r with
$J\subset [0,1]$
be an interval of length r with
![]() $0<r<2n_{0}\beta ^{-n_0}$
. Then inside J there exists a full cylinder
$0<r<2n_{0}\beta ^{-n_0}$
. Then inside J there exists a full cylinder
![]() $I_n$
satisfying
$I_n$
satisfying
Proof. Let
![]() $n>n_0$
be the integer such that
$n>n_0$
be the integer such that
Since every cylinder of order n is of length at most
![]() $\beta ^{-n}$
, the interval J contains at least
$\beta ^{-n}$
, the interval J contains at least
![]() $2n-2\geq n+1$
consecutive cylinders of order n. Thus, by Lemma 2.6, it contains a full cylinder of order n and we denote such a cylinder by
$2n-2\geq n+1$
consecutive cylinders of order n. Thus, by Lemma 2.6, it contains a full cylinder of order n and we denote such a cylinder by
![]() $I_n$
. By the choice of
$I_n$
. By the choice of
![]() $n_0$
, we have
$n_0$
, we have
This completes the proof.
We now define a sequence of numbers
![]() $\beta _N$
approximating
$\beta _N$
approximating
![]() $\beta $
from below. For any N with
$\beta $
from below. For any N with
![]() $\epsilon _N^*(\,\beta )\geq 1,$
define
$\epsilon _N^*(\,\beta )\geq 1,$
define
![]() $\beta _N$
to be the unique real solution to the algebraic equation
$\beta _N$
to be the unique real solution to the algebraic equation
 $$ \begin{align*} 1=\frac{\epsilon_{1}^*(\,\beta)}{\beta_N}+\frac{\epsilon_{2}^*(\,\beta)}{\beta_N^2}+\cdots+\frac{\epsilon_{N}^*(\,\beta)}{\beta_N^N}. \end{align*} $$
$$ \begin{align*} 1=\frac{\epsilon_{1}^*(\,\beta)}{\beta_N}+\frac{\epsilon_{2}^*(\,\beta)}{\beta_N^2}+\cdots+\frac{\epsilon_{N}^*(\,\beta)}{\beta_N^N}. \end{align*} $$
Then
![]() $\beta _N$
approximates
$\beta _N$
approximates
![]() $\beta $
from below and the
$\beta $
from below and the
![]() $\beta _N$
-expansion of unity is
$\beta _N$
-expansion of unity is
More importantly, by the admissible sequence criterion, we have, for any
 $\boldsymbol \epsilon _n \in \Sigma _{\beta _N}^n$
and
$\boldsymbol \epsilon _n \in \Sigma _{\beta _N}^n$
and
 $\boldsymbol \epsilon _m'\in \Sigma _{\beta _N}^m$
, that
$\boldsymbol \epsilon _m'\in \Sigma _{\beta _N}^m$
, that
 $$ \begin{align} (\boldsymbol\epsilon_n,0^N,\boldsymbol\epsilon_m')\in\Sigma_{\beta_N}^{n+N+m}, \end{align} $$
$$ \begin{align} (\boldsymbol\epsilon_n,0^N,\boldsymbol\epsilon_m')\in\Sigma_{\beta_N}^{n+N+m}, \end{align} $$
where
![]() $0^N$
means a zero word of length N.
$0^N$
means a zero word of length N.
From assertion (2-2), we get the following proposition.
Proposition 2.9. For any
 $\boldsymbol \epsilon _n\in \Sigma _{\beta _N}^n$
,
$\boldsymbol \epsilon _n\in \Sigma _{\beta _N}^n$
,
![]() $I_{n+N}(\boldsymbol \epsilon _n,0^N)$
is a full cylinder. So,
$I_{n+N}(\boldsymbol \epsilon _n,0^N)$
is a full cylinder. So,
 $$ \begin{align*}\frac{1}{\beta^{n+N}}\leq\lvert I_{n}(\boldsymbol\epsilon_n)\rvert\leq\frac{1}{\beta^{n}}.\end{align*} $$
$$ \begin{align*}\frac{1}{\beta^{n+N}}\leq\lvert I_{n}(\boldsymbol\epsilon_n)\rvert\leq\frac{1}{\beta^{n}}.\end{align*} $$
We end this section with a definition of the pressure function for a
![]() $\beta $
-dynamical system associated to some continuous potential g:
$\beta $
-dynamical system associated to some continuous potential g:
 $$ \begin{align} P(g, T_\beta):=\lim\limits_{n\rightarrow \infty}\frac{1}{n}\log\sum\limits_{\boldsymbol\epsilon_n \in\Sigma_\beta^n} \sup\limits_{y\in I_{n}(\boldsymbol\epsilon_n)}e^{S_ng(y)}, \end{align} $$
$$ \begin{align} P(g, T_\beta):=\lim\limits_{n\rightarrow \infty}\frac{1}{n}\log\sum\limits_{\boldsymbol\epsilon_n \in\Sigma_\beta^n} \sup\limits_{y\in I_{n}(\boldsymbol\epsilon_n)}e^{S_ng(y)}, \end{align} $$
where
![]() $S_ng(y)$
denotes the ergodic sum
$S_ng(y)$
denotes the ergodic sum
 $\sum _{j=0}^{n-1}g(T^j_\beta y)$
. Since g is continuous, the limit does not depend upon the choice of y. The existence of the limit (2-3) follows from subadditivity:
$\sum _{j=0}^{n-1}g(T^j_\beta y)$
. Since g is continuous, the limit does not depend upon the choice of y. The existence of the limit (2-3) follows from subadditivity:
 $$ \begin{align*}\log\sum\limits_{(\boldsymbol\epsilon_n, \boldsymbol\epsilon_m^\prime)\in\Sigma_\beta^{n+m}} e^{S_{n+m}g(y)}\leq \log\sum\limits_{\boldsymbol\epsilon_n \in\Sigma_\beta^{n}} e^{S_{n}g(y)}+\log\sum\limits_{\boldsymbol\epsilon_m^\prime\in\Sigma_\beta^{m}} e^{S_{m}g(y)}.\end{align*} $$
$$ \begin{align*}\log\sum\limits_{(\boldsymbol\epsilon_n, \boldsymbol\epsilon_m^\prime)\in\Sigma_\beta^{n+m}} e^{S_{n+m}g(y)}\leq \log\sum\limits_{\boldsymbol\epsilon_n \in\Sigma_\beta^{n}} e^{S_{n}g(y)}+\log\sum\limits_{\boldsymbol\epsilon_m^\prime\in\Sigma_\beta^{m}} e^{S_{m}g(y)}.\end{align*} $$
The reader is referred to [Reference Walters16] for more details.
3 Proof of Theorem 1.1: the upper bound
As is typical in determining the Hausdorff dimension of a set, we split the proof of Theorem 1.1 into two parts: the upper bound and the lower bound.
For any
 $\boldsymbol \epsilon _n=(\epsilon _1,\ldots ,\epsilon _n)\in \Sigma _\beta ^n$
and
$\boldsymbol \epsilon _n=(\epsilon _1,\ldots ,\epsilon _n)\in \Sigma _\beta ^n$
and
 $\boldsymbol \omega _n=(\omega _1,\ldots ,\omega _n)\in \Sigma _\beta ^n,$
we always take
$\boldsymbol \omega _n=(\omega _1,\ldots ,\omega _n)\in \Sigma _\beta ^n,$
we always take
 $$ \begin{align*}x^*=\frac{\epsilon_{1}}{\beta}+\frac{\epsilon_{2}}{\beta^{2}}+\cdots+\frac{\epsilon_{n}}{\beta^{n}}\end{align*} $$
$$ \begin{align*}x^*=\frac{\epsilon_{1}}{\beta}+\frac{\epsilon_{2}}{\beta^{2}}+\cdots+\frac{\epsilon_{n}}{\beta^{n}}\end{align*} $$
to be the left endpoint of
![]() $I_n(\boldsymbol \epsilon _n)$
and
$I_n(\boldsymbol \epsilon _n)$
and
 $$ \begin{align*}y^*=\frac{\omega_{1}}{\beta}+\frac{\omega_{2}}{\beta^{2}}+\cdots+\frac{\omega_{n}}{\beta^{n}}\end{align*} $$
$$ \begin{align*}y^*=\frac{\omega_{1}}{\beta}+\frac{\omega_{2}}{\beta^{2}}+\cdots+\frac{\omega_{n}}{\beta^{n}}\end{align*} $$
to be the left endpoint of
![]() $I_n(\boldsymbol \omega _n)$
.
$I_n(\boldsymbol \omega _n)$
.
Instead of directly considering the set
![]() $E(T_\beta ,f,g)$
, we consider a closely related limit supremum set
$E(T_\beta ,f,g)$
, we consider a closely related limit supremum set
 $$ \begin{align*}\overline{E}(T_\beta,f,g)=\bigcap_{N=1}^{\infty}\bigcup_{n=N}^{\infty}\bigcup_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^{n}}J_n(\boldsymbol\epsilon_n)\times J_n(\boldsymbol\omega_n),\end{align*} $$
$$ \begin{align*}\overline{E}(T_\beta,f,g)=\bigcap_{N=1}^{\infty}\bigcup_{n=N}^{\infty}\bigcup_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^{n}}J_n(\boldsymbol\epsilon_n)\times J_n(\boldsymbol\omega_n),\end{align*} $$
where
 $$ \begin{align*} J_n(\boldsymbol\epsilon_n)&=\{x\in[0,1]:\lvert T_\beta^nx-x_0\rvert <e^{-S_nf(x^*)}\},\\ J_n(\boldsymbol\omega_n)&=\{y\in[0,1]:\lvert T_\beta^ny-y_0\rvert <e^{-S_ng(y^*)}\}. \end{align*} $$
$$ \begin{align*} J_n(\boldsymbol\epsilon_n)&=\{x\in[0,1]:\lvert T_\beta^nx-x_0\rvert <e^{-S_nf(x^*)}\},\\ J_n(\boldsymbol\omega_n)&=\{y\in[0,1]:\lvert T_\beta^ny-y_0\rvert <e^{-S_ng(y^*)}\}. \end{align*} $$
In the sequel it is clear that the set
 $\overline {E}(T_\beta ,f,g)$
is easier to handle. Since f and g are continuous functions, for any
$\overline {E}(T_\beta ,f,g)$
is easier to handle. Since f and g are continuous functions, for any
![]() $\delta>0$
and n large enough, we have
$\delta>0$
and n large enough, we have
Thus we have
 $$ \begin{align*}\overline{E}(T_\beta, f+\delta,g+\delta)\subset E(T_\beta,f,g)\subset \overline{E}(T_\beta, f-\delta,g-\delta).\end{align*} $$
$$ \begin{align*}\overline{E}(T_\beta, f+\delta,g+\delta)\subset E(T_\beta,f,g)\subset \overline{E}(T_\beta, f-\delta,g-\delta).\end{align*} $$
Therefore, to calculate the Hausdorff dimension of the set
![]() $E(T_\beta ,f,g)$
, it is sufficient to determine the Hausdorff dimension of
$E(T_\beta ,f,g)$
, it is sufficient to determine the Hausdorff dimension of
 $\overline {E}(T_\beta ,f,g)$
.
$\overline {E}(T_\beta ,f,g)$
.
The length of
![]() $J_n(\boldsymbol \epsilon _n)$
satisfies
$J_n(\boldsymbol \epsilon _n)$
satisfies
since, for every
![]() $x\in J_n(\boldsymbol \epsilon _n)$
, we have
$x\in J_n(\boldsymbol \epsilon _n)$
, we have
 $$ \begin{align*}\bigg\lvert x-\bigg(\frac{\epsilon_1}{\beta}+\cdots+\frac{\epsilon_n+x_0}{\beta^n}\bigg)\bigg\rvert=\frac{\lvert T_\beta^nx-x_0\rvert}{\beta^n}<\beta^{-n}e^{-S_nf(x^*)}.\end{align*} $$
$$ \begin{align*}\bigg\lvert x-\bigg(\frac{\epsilon_1}{\beta}+\cdots+\frac{\epsilon_n+x_0}{\beta^n}\bigg)\bigg\rvert=\frac{\lvert T_\beta^nx-x_0\rvert}{\beta^n}<\beta^{-n}e^{-S_nf(x^*)}.\end{align*} $$
Similarly,
So,
 $\overline {E}(T_\beta ,f,g)$
is a limit supremum set defined by a collection of rectangles. There are two ways to cover a single rectangle
$\overline {E}(T_\beta ,f,g)$
is a limit supremum set defined by a collection of rectangles. There are two ways to cover a single rectangle
![]() $J_n(\boldsymbol \epsilon _n)\times J_n(\boldsymbol \omega _n)$
, as follows.
$J_n(\boldsymbol \epsilon _n)\times J_n(\boldsymbol \omega _n)$
, as follows.
3.1 Covering by shorter side length
Recall that
![]() $f(x)\geq g(y)$
for all
$f(x)\geq g(y)$
for all
![]() $x, y\in [0, 1]$
. This implies that
$x, y\in [0, 1]$
. This implies that
![]() $J_n(\boldsymbol \epsilon _n)$
is shorter in length than
$J_n(\boldsymbol \epsilon _n)$
is shorter in length than
![]() $J_n(\boldsymbol \omega _n)$
. Then the rectangle
$J_n(\boldsymbol \omega _n)$
. Then the rectangle
![]() $J_n(\boldsymbol \epsilon _n)\times J_n(\boldsymbol \omega _n)$
can be covered by
$J_n(\boldsymbol \epsilon _n)\times J_n(\boldsymbol \omega _n)$
can be covered by
 $$ \begin{align*}\frac{\beta^{-n}e^{-S_ng(y^*)}}{\beta^{-n}e^{-S_nf(x^*)}}=\frac{e^{S_nf(x^*)}}{e^{S_ng(y^*)}}\end{align*} $$
$$ \begin{align*}\frac{\beta^{-n}e^{-S_ng(y^*)}}{\beta^{-n}e^{-S_nf(x^*)}}=\frac{e^{S_nf(x^*)}}{e^{S_ng(y^*)}}\end{align*} $$
balls of side length
![]() $\beta ^{-n}e^{-S_nf(x^*)}.$
$\beta ^{-n}e^{-S_nf(x^*)}.$
Since, for each N,
 $$ \begin{align*}\overline{E}(T_\beta,f,g)\subseteq\bigcup_{n=N}^{\infty}\bigcup_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^{n}}J_n(\boldsymbol\epsilon_n)\times J_n(\boldsymbol\omega_n),\end{align*} $$
$$ \begin{align*}\overline{E}(T_\beta,f,g)\subseteq\bigcup_{n=N}^{\infty}\bigcup_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^{n}}J_n(\boldsymbol\epsilon_n)\times J_n(\boldsymbol\omega_n),\end{align*} $$
the s-dimensional Hausdorff measure
![]() $\mathcal H^s$
of
$\mathcal H^s$
of
 $\overline {E}(T_\beta ,f,g)$
can be estimated as
$\overline {E}(T_\beta ,f,g)$
can be estimated as
 $$ \begin{align*}\mathcal H^s(\overline{E}(T_\beta,f,g))\le \liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^n} \frac{e^{S_nf(x^*)}}{e^{S_ng(y^*)}}\bigg(\frac{1}{\beta^ne^{S_nf(x^*)}}\bigg)^s. \end{align*} $$
$$ \begin{align*}\mathcal H^s(\overline{E}(T_\beta,f,g))\le \liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^n} \frac{e^{S_nf(x^*)}}{e^{S_ng(y^*)}}\bigg(\frac{1}{\beta^ne^{S_nf(x^*)}}\bigg)^s. \end{align*} $$
Define
Then from the definition of the pressure function (2-3), it is clear that
 $$ \begin{align*}P(f-s(\log\beta+f))+P(-g)\leq 0 \ \iff \ \sum_{n=1}^{\infty} \sum_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^n} \frac{e^{S_nf(x^*)}}{e^{S_ng(y^*)}}\bigg(\frac{1}{\beta^ne^{S_nf(x^*)}}\bigg)^s<\infty.\end{align*} $$
$$ \begin{align*}P(f-s(\log\beta+f))+P(-g)\leq 0 \ \iff \ \sum_{n=1}^{\infty} \sum_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^n} \frac{e^{S_nf(x^*)}}{e^{S_ng(y^*)}}\bigg(\frac{1}{\beta^ne^{S_nf(x^*)}}\bigg)^s<\infty.\end{align*} $$
Hence, for any
![]() $s>s_1$
,
$s>s_1$
,
 $$ \begin{align*}\mathcal H^s(\overline{E}(T_\beta,f,g))= 0.\end{align*} $$
$$ \begin{align*}\mathcal H^s(\overline{E}(T_\beta,f,g))= 0.\end{align*} $$
Hence, it follows that
 $\dim _{\mathrm H} (\overline {E}(T_\beta ,f,g))\leq s_1.$
$\dim _{\mathrm H} (\overline {E}(T_\beta ,f,g))\leq s_1.$
3.2 Covering by longer side length
From the previous subsection (Section 3.1), it is clear that only one ball of side length
![]() $\beta ^{-n}e^{-S_ng(y^*)}$
is needed to cover the rectangle
$\beta ^{-n}e^{-S_ng(y^*)}$
is needed to cover the rectangle
![]() $J_n(\boldsymbol \epsilon _n)\times J_n(\boldsymbol \omega _n)$
. Hence, in this case, the s-dimensional Hausdorff measure
$J_n(\boldsymbol \epsilon _n)\times J_n(\boldsymbol \omega _n)$
. Hence, in this case, the s-dimensional Hausdorff measure
![]() $\mathcal H^s$
of
$\mathcal H^s$
of
 $\overline {E}(T_\beta ,f,g)$
can be estimated as
$\overline {E}(T_\beta ,f,g)$
can be estimated as
 $$ \begin{align*}\mathcal{H}^s(\overline{E}(T_\beta,f,g))\leq\liminf\limits_{N\rightarrow\infty}\sum_{n=N}^{\infty}\sum_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^n}\bigg(\frac{1}{\beta^{n}e^{S_ng(y^*)}}\bigg)^s. \end{align*} $$
$$ \begin{align*}\mathcal{H}^s(\overline{E}(T_\beta,f,g))\leq\liminf\limits_{N\rightarrow\infty}\sum_{n=N}^{\infty}\sum_{\boldsymbol\epsilon_n,\boldsymbol\omega_n\in \Sigma_{\beta}^n}\bigg(\frac{1}{\beta^{n}e^{S_ng(y^*)}}\bigg)^s. \end{align*} $$
Define
Then, from the definitions of the pressure function and Hausdorff measure, it follows that, for any
![]() $s>s_2$
,
$s>s_2$
,
 $\mathcal H^s(\overline {E}(T_\beta ,f,g))= 0.$
Hence,
$\mathcal H^s(\overline {E}(T_\beta ,f,g))= 0.$
Hence,
 $$ \begin{align*}\dim_{\mathrm H} (\overline{E}(T_\beta,f,g))\leq s_2.\end{align*} $$
$$ \begin{align*}\dim_{\mathrm H} (\overline{E}(T_\beta,f,g))\leq s_2.\end{align*} $$
4 Theorem 1.1: the lower bound
It should be clear from the previous section that proving the upper bound requires only a suitable covering of the set
 $\overline {E}(T_\beta ,f,g)$
. In contrast, proving the lower bound is a challenging task, requiring all possible coverings to be considered; it therefore represents the main problem in metric Diophantine approximation (in various settings). The following principle, commonly known as the mass distribution principle [Reference Falconer4], is used frequently for this purpose.
$\overline {E}(T_\beta ,f,g)$
. In contrast, proving the lower bound is a challenging task, requiring all possible coverings to be considered; it therefore represents the main problem in metric Diophantine approximation (in various settings). The following principle, commonly known as the mass distribution principle [Reference Falconer4], is used frequently for this purpose.
Proposition 4.1 (Falconer [Reference Falconer4])
Let E be a Borel measurable set in
![]() $\mathbb {R}^d$
and
$\mathbb {R}^d$
and
![]() $\mu $
be a Borel measure with
$\mu $
be a Borel measure with
![]() $\mu (E)>0$
. Assume that there exist two positive constants
$\mu (E)>0$
. Assume that there exist two positive constants
![]() $c,\delta $
such that, for any set U with diameter
$c,\delta $
such that, for any set U with diameter
![]() $\lvert U\rvert $
less than
$\lvert U\rvert $
less than
![]() $\delta $
,
$\delta $
,
![]() $\mu (U)\leq c \lvert U\rvert ^s$
. Then
$\mu (U)\leq c \lvert U\rvert ^s$
. Then
![]() $\dim _{\mathrm H} E\geq s$
.
$\dim _{\mathrm H} E\geq s$
.
Specifically, the mass distribution principle replaces the consideration of all coverings by the construction of a particular measure
![]() $\mu $
and it is typically deployed in two steps:
$\mu $
and it is typically deployed in two steps:
-
• construct a suitable Cantor subset
 $\mathcal F_\infty $
of
$\mathcal F_\infty $
of
 $\overline {E}(T_\beta ,f,g)$
and a probability measure
$\overline {E}(T_\beta ,f,g)$
and a probability measure
 $\mu $
supported on
$\mu $
supported on
 $\mathcal F_\infty $
;
$\mathcal F_\infty $
; -
• show that, for any fixed
 $c>0$
,
$c>0$
,
 $\mu $
satisfies the condition that, for any measurable set U of sufficiently small diameter,
$\mu $
satisfies the condition that, for any measurable set U of sufficiently small diameter,
 $\mu (U)\leq c \lvert U\rvert ^s$
.
$\mu (U)\leq c \lvert U\rvert ^s$
.
If this can be done, then by the mass distribution principle, it follows that
 $$ \begin{align*}\dim_{\mathrm H}(\overline{E}(T_\beta,f,g))\geq \dim_{\mathrm H}(\mathcal F_\infty)\geq s.\end{align*} $$
$$ \begin{align*}\dim_{\mathrm H}(\overline{E}(T_\beta,f,g))\geq \dim_{\mathrm H}(\mathcal F_\infty)\geq s.\end{align*} $$
The substantive, intricate part of this entire process is the construction of a suitable Cantor type subset
![]() $\mathcal F_\infty $
which supports a probability measure
$\mathcal F_\infty $
which supports a probability measure
![]() $\mu $
. In the remainder of this paper, we construct a suitable Cantor type subset of the set
$\mu $
. In the remainder of this paper, we construct a suitable Cantor type subset of the set
 $\overline {E}(T_\beta ,f,g)$
and demonstrate that it satisfies the mass distribution principle.
$\overline {E}(T_\beta ,f,g)$
and demonstrate that it satisfies the mass distribution principle.
4.1 Construction of the Cantor subset
We construct the Cantor subset
![]() $\mathcal F_\infty $
iteratively. Start by fixing an
$\mathcal F_\infty $
iteratively. Start by fixing an
![]() $\epsilon>0$
and assume that
$\epsilon>0$
and assume that
![]() $f(x)\geq (1+\epsilon )g(y)\geq g(y)$
for all
$f(x)\geq (1+\epsilon )g(y)\geq g(y)$
for all
![]() $x,y\in [0,1].$
We construct a Cantor subset level by level and note that each level depends on its predecessor. Choose a rapidly increasing subsequence
$x,y\in [0,1].$
We construct a Cantor subset level by level and note that each level depends on its predecessor. Choose a rapidly increasing subsequence
![]() $\{m_k\}_{k\geq 1}$
of positive integers with
$\{m_k\}_{k\geq 1}$
of positive integers with
![]() $m_1$
large enough.
$m_1$
large enough.
4.1.1 Level 1 of the Cantor set
Let
![]() $n_1=m_1$
. For any
$n_1=m_1$
. For any
 $U_1,W_1\in \Sigma _{\beta _N}^{n_1}$
ending with the zero word of order N (that is,
$U_1,W_1\in \Sigma _{\beta _N}^{n_1}$
ending with the zero word of order N (that is,
![]() $0^N$
), let
$0^N$
), let
![]() $x_1^*\in I_{n_1}(U_1), ~y_1^*\in I_{n_1}(W_1)$
. From Proposition 2.8, it follows that there are two full cylinders
$x_1^*\in I_{n_1}(U_1), ~y_1^*\in I_{n_1}(W_1)$
. From Proposition 2.8, it follows that there are two full cylinders
![]() $I_{k_1}(K_1), I_{l_1}(L_1)$
such that
$I_{k_1}(K_1), I_{l_1}(L_1)$
such that
 $$ \begin{align*} I_{k_1}(K_1)&\subset B(x_0,e^{-S_{n_1}f(x_1^*)}),\\ I_{l_1}(L_1) &\subset B(y_0,e^{-S_{n_1}g(y_1^*)}), \end{align*} $$
$$ \begin{align*} I_{k_1}(K_1)&\subset B(x_0,e^{-S_{n_1}f(x_1^*)}),\\ I_{l_1}(L_1) &\subset B(y_0,e^{-S_{n_1}g(y_1^*)}), \end{align*} $$
and
So, we get a subset
![]() $I_{n_1+k_1}(U_1,K_1)\times I_{n_1+l_1}(W_1,L_1)$
of
$I_{n_1+k_1}(U_1,K_1)\times I_{n_1+l_1}(W_1,L_1)$
of
![]() $J_{n_1}(U_1)\times J_{n_1}(W_1)$
. Since
$J_{n_1}(U_1)\times J_{n_1}(W_1)$
. Since
![]() $f(x)\geq (1+\epsilon )g(y)$
for all
$f(x)\geq (1+\epsilon )g(y)$
for all
![]() $x,y\in [0,1]$
, it follows that
$x,y\in [0,1]$
, it follows that
![]() $k_1\geq l_1.$
It should be noted that
$k_1\geq l_1.$
It should be noted that
![]() $K_1$
and
$K_1$
and
![]() $L_1$
depend on
$L_1$
depend on
![]() $U_1$
and
$U_1$
and
![]() $W_1$
, respectively. Consequently, for different
$W_1$
, respectively. Consequently, for different
![]() $U_1$
and
$U_1$
and
![]() $W_1,$
the choice of
$W_1,$
the choice of
![]() $K_1$
and
$K_1$
and
![]() $L_1$
may be different.
$L_1$
may be different.
The first level of the Cantor set is defined as
 $$ \begin{align*}\mathcal{F}_1=\{I_{n_1+k_1}(U_1,K_1)\times I_{n_1+l_1}(W_1,L_1):U_1,W_1\in \Sigma_{\beta_N}^{n_1} \text{ ending with } 0^N\},\end{align*} $$
$$ \begin{align*}\mathcal{F}_1=\{I_{n_1+k_1}(U_1,K_1)\times I_{n_1+l_1}(W_1,L_1):U_1,W_1\in \Sigma_{\beta_N}^{n_1} \text{ ending with } 0^N\},\end{align*} $$
which is composed of a collection of rectangles. Next, we cut each rectangle into balls with the radius as the shorter side length of the rectangle:
 $$ \begin{align*} I_{n_1+k_1}(U_1,K_1)&\times I_{n_1+l_1}(W_1,L_1)\\ &\quad\rightarrow\{I_{n_1+k_1} (U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1):H_1\in \Sigma_{\beta_N}^{k_1-l_1}\}. \end{align*} $$
$$ \begin{align*} I_{n_1+k_1}(U_1,K_1)&\times I_{n_1+l_1}(W_1,L_1)\\ &\quad\rightarrow\{I_{n_1+k_1} (U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1):H_1\in \Sigma_{\beta_N}^{k_1-l_1}\}. \end{align*} $$
Then we get a collection of balls
 $$ \begin{align*} \mathcal{G}_1=\{I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1) :U_1,W_1\in \Sigma_{\beta_N}^{n_1} \text{ ending with } 0^N, H_1\in \Sigma_{\beta_N}^{k_1-l_1}\}. \end{align*} $$
$$ \begin{align*} \mathcal{G}_1=\{I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1) :U_1,W_1\in \Sigma_{\beta_N}^{n_1} \text{ ending with } 0^N, H_1\in \Sigma_{\beta_N}^{k_1-l_1}\}. \end{align*} $$
4.1.2 Level 2 of the Cantor set
Fix a
![]() $J_1=I_{n_1+k_1}(\Gamma _1)\times I_{n_1+k_1}(\Upsilon _1)$
in
$J_1=I_{n_1+k_1}(\Gamma _1)\times I_{n_1+k_1}(\Upsilon _1)$
in
![]() $\mathcal {G}_1$
. We define the local sublevel
$\mathcal {G}_1$
. We define the local sublevel
![]() $\mathcal {F}_2(J_1)$
as follows.
$\mathcal {F}_2(J_1)$
as follows.
Choose a large integer
![]() $m_2$
such that
$m_2$
such that
 $$ \begin{align*}\frac{\epsilon}{1+\epsilon}\cdot m_2\log\beta\geq(n_1+\sup\{k_1:I_{n_1+k_1}(\Gamma_1)\})\|f\|,\end{align*} $$
$$ \begin{align*}\frac{\epsilon}{1+\epsilon}\cdot m_2\log\beta\geq(n_1+\sup\{k_1:I_{n_1+k_1}(\Gamma_1)\})\|f\|,\end{align*} $$
where
![]() $\|f\|=\sup \{\lvert f(x)\rvert :x\in [0,1]\}.$
$\|f\|=\sup \{\lvert f(x)\rvert :x\in [0,1]\}.$
Write
![]() $n_2=n_1+k_1+m_2.$
Just like the first level of the Cantor set, for any
$n_2=n_1+k_1+m_2.$
Just like the first level of the Cantor set, for any
 $U_2,W_2\in \Sigma _{\beta _N}^{m_2}$
ending with
$U_2,W_2\in \Sigma _{\beta _N}^{m_2}$
ending with
![]() $0^N$
, applying Proposition 2.8 to
$0^N$
, applying Proposition 2.8 to
![]() $J_{n_2}(\Gamma _1,U_2)\times J_{n_2}(\Upsilon _1,W_2)$
, we can get two full cylinders
$J_{n_2}(\Gamma _1,U_2)\times J_{n_2}(\Upsilon _1,W_2)$
, we can get two full cylinders
![]() $I_{k_2}(K_2)$
,
$I_{k_2}(K_2)$
,
![]() $I_{l_2}(L_2)$
such that
$I_{l_2}(L_2)$
such that
 $$ \begin{align*}I_{k_2}(K_2)\subset B(x_0,e^{-S_{n_2}f(x_2^*)}), \quad I_{l_2}(L_2)\subset B(y_0,e^{-S_{n_2}g(y_2^*)})\end{align*} $$
$$ \begin{align*}I_{k_2}(K_2)\subset B(x_0,e^{-S_{n_2}f(x_2^*)}), \quad I_{l_2}(L_2)\subset B(y_0,e^{-S_{n_2}g(y_2^*)})\end{align*} $$
and
where
![]() $x_2^*\in I_{n_2}(\Gamma _1,U_2),~y_2^*\in I_{n_2}(\Upsilon _1,W_2).$
$x_2^*\in I_{n_2}(\Gamma _1,U_2),~y_2^*\in I_{n_2}(\Upsilon _1,W_2).$
Obviously, we get a subset
![]() $I_{n_2+k_2}(\Gamma _1,U_2,K_2)\times I_{n_2+l_2}(\Upsilon _1,W_2,L_2)$
of
$I_{n_2+k_2}(\Gamma _1,U_2,K_2)\times I_{n_2+l_2}(\Upsilon _1,W_2,L_2)$
of
![]() $J_{n_2}(\Gamma _1,U_2)\times J_{n_2}(\Upsilon _1,W_2)$
and
$J_{n_2}(\Gamma _1,U_2)\times J_{n_2}(\Upsilon _1,W_2)$
and
![]() $k_2\geq l_2$
. Then, the second level of the Cantor set is defined as
$k_2\geq l_2$
. Then, the second level of the Cantor set is defined as
 $$ \begin{align*} \mathcal{F}_2(J_1)=\{I_{n_2+k_2}(\Gamma_1,U_2,K_2)\times &I_{n_2+l_2}(\Upsilon_1,W_2,L_2):U_2,W_2\in \Sigma_{\beta_N}^{m_2} \text{ ending with } 0^N\}, \end{align*} $$
$$ \begin{align*} \mathcal{F}_2(J_1)=\{I_{n_2+k_2}(\Gamma_1,U_2,K_2)\times &I_{n_2+l_2}(\Upsilon_1,W_2,L_2):U_2,W_2\in \Sigma_{\beta_N}^{m_2} \text{ ending with } 0^N\}, \end{align*} $$
which is composed of a collection of rectangles.
Next, we cut each rectangle into balls with the radius as the shorter side length of the rectangle:
 $$ \begin{align*} I_{n_2+k_2}(\Gamma_1,U_2,K_2)&\times I_{n_2+l_2}(\Upsilon_1,W_2,L_2)\rightarrow\{I_{n_2+k_2}(\Gamma_1,U_2,K_2)\\ &\quad\times I_{n_2+k_2}(\Upsilon_1,W_2,L_2,H_2):H_2\in \Sigma_{\beta_N}^{k_2-l_2}\}:=\mathcal{G}_2(J_1). \end{align*} $$
$$ \begin{align*} I_{n_2+k_2}(\Gamma_1,U_2,K_2)&\times I_{n_2+l_2}(\Upsilon_1,W_2,L_2)\rightarrow\{I_{n_2+k_2}(\Gamma_1,U_2,K_2)\\ &\quad\times I_{n_2+k_2}(\Upsilon_1,W_2,L_2,H_2):H_2\in \Sigma_{\beta_N}^{k_2-l_2}\}:=\mathcal{G}_2(J_1). \end{align*} $$
Therefore, the second level is defined as
 $$ \begin{align*}\mathcal{F}_2=\bigcup \limits_{J\in \mathcal{G}_1}\mathcal{F}_2(J),\quad\mathcal{G}_2=\bigcup\limits_{J\in \mathcal{G}_1}\mathcal{G}_2(J).\end{align*} $$
$$ \begin{align*}\mathcal{F}_2=\bigcup \limits_{J\in \mathcal{G}_1}\mathcal{F}_2(J),\quad\mathcal{G}_2=\bigcup\limits_{J\in \mathcal{G}_1}\mathcal{G}_2(J).\end{align*} $$
4.1.3 From level
 $i-1$
to level i
$i-1$
to level i
Assume that the
![]() $(i-1)$
th level of the Cantor set
$(i-1)$
th level of the Cantor set
![]() $\mathcal {G}_{i-1}$
has been defined. Let
$\mathcal {G}_{i-1}$
has been defined. Let
![]() $J_{i-1}=I_{n_{i-1}+k_{i-1}}(\Gamma _{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon _{i-1})$
be a generic element in
$J_{i-1}=I_{n_{i-1}+k_{i-1}}(\Gamma _{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon _{i-1})$
be a generic element in
![]() $\mathcal {G}_{i-1}.$
We define the local sublevel
$\mathcal {G}_{i-1}.$
We define the local sublevel
![]() $\mathcal {F}_i(J_{i-1})$
as follows.
$\mathcal {F}_i(J_{i-1})$
as follows.
Choose a large integer
![]() $m_{i}$
such that
$m_{i}$
such that
 $$ \begin{align} \frac{\epsilon}{1+\epsilon}\cdot m_i\log\beta\geq(n_{i-1}+\sup\{k_{i-1}:I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\})\|f\|. \end{align} $$
$$ \begin{align} \frac{\epsilon}{1+\epsilon}\cdot m_i\log\beta\geq(n_{i-1}+\sup\{k_{i-1}:I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\})\|f\|. \end{align} $$
Write
![]() $n_i=n_{i-1}+k_{i-1}+m_i.$
For each
$n_i=n_{i-1}+k_{i-1}+m_i.$
For each
 $U_i,W_i\in \Sigma _{\beta _N}^{m_i}$
ending with
$U_i,W_i\in \Sigma _{\beta _N}^{m_i}$
ending with
![]() $0^N$
, apply Proposition 2.8 to
$0^N$
, apply Proposition 2.8 to
We can get two full cylinders
![]() $I_{k_i}(K_i)$
,
$I_{k_i}(K_i)$
,
![]() $I_{l_i}(L_i)$
such that
$I_{l_i}(L_i)$
such that
 $$ \begin{align*}I_{k_i}(K_i)\subset B(x_0,e^{-S_{n_i}f(x_i^*)}), I_{l_i}(L_i)\subset B(y_0,e^{-S_{n_i}g(y_i^*)})\end{align*} $$
$$ \begin{align*}I_{k_i}(K_i)\subset B(x_0,e^{-S_{n_i}f(x_i^*)}), I_{l_i}(L_i)\subset B(y_0,e^{-S_{n_i}g(y_i^*)})\end{align*} $$
and
where
![]() $x_i^*\in I_{n_i}(\Gamma _{i-1},U_{i}), ~y_i^*\in I_{n_i}(\Upsilon _{i-1},W_{i}).$
$x_i^*\in I_{n_i}(\Gamma _{i-1},U_{i}), ~y_i^*\in I_{n_i}(\Upsilon _{i-1},W_{i}).$
Obviously, we get a subset
![]() $I_{n_i+k_i}(\Gamma _{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon _{i-1},W_i,L_i)$
of
$I_{n_i+k_i}(\Gamma _{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon _{i-1},W_i,L_i)$
of
![]() $J_{n_i}(\Gamma _{i-1},U_i)\times J_{n_i}(\Upsilon _{i-1},W_i)$
and
$J_{n_i}(\Gamma _{i-1},U_i)\times J_{n_i}(\Upsilon _{i-1},W_i)$
and
![]() $k_i\geq l_i$
. Then, the i th level of the Cantor set is defined as
$k_i\geq l_i$
. Then, the i th level of the Cantor set is defined as
 $$ \begin{align*} \mathcal{F}_i(J_{i-1})=\{I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon_{i-1},W_i,L_i) :U_i,W_i\in \Sigma_{\beta_N}^{m_i} \text{ ending with } 0^N\}, \end{align*} $$
$$ \begin{align*} \mathcal{F}_i(J_{i-1})=\{I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon_{i-1},W_i,L_i) :U_i,W_i\in \Sigma_{\beta_N}^{m_i} \text{ ending with } 0^N\}, \end{align*} $$
which is composed of a collection of rectangles. As before, we cut each rectangle into balls with the radius as the shorter side length of the rectangle:
 $$ \begin{align*} I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+l_i}&(\Upsilon_{i-1},W_i,L_i)\rightarrow\{I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\\ &\times I_{n_i+k_i}(\Upsilon_{i-1},W_i,L_i,H_i):H_i\in \Sigma_{\beta_N}^{k_i-l_i}\}:=\mathcal{G}_i(J_{i-1}). \end{align*} $$
$$ \begin{align*} I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+l_i}&(\Upsilon_{i-1},W_i,L_i)\rightarrow\{I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\\ &\times I_{n_i+k_i}(\Upsilon_{i-1},W_i,L_i,H_i):H_i\in \Sigma_{\beta_N}^{k_i-l_i}\}:=\mathcal{G}_i(J_{i-1}). \end{align*} $$
Therefore, the i th level is defined as
 $$ \begin{align*}\mathcal{F}_i=\bigcup \limits_{J\in \mathcal{G}_{i-1}}\mathcal{F}_i(J),~\mathcal{G}_i=\bigcup\limits_{J\in \mathcal{G}_{i-1}}\mathcal{G}_i(J).\end{align*} $$
$$ \begin{align*}\mathcal{F}_i=\bigcup \limits_{J\in \mathcal{G}_{i-1}}\mathcal{F}_i(J),~\mathcal{G}_i=\bigcup\limits_{J\in \mathcal{G}_{i-1}}\mathcal{G}_i(J).\end{align*} $$
Finally, the Cantor set is defined as
 $$ \begin{align*}\mathcal{F}_\infty=\bigcap\limits_{i=1}^\infty\bigcup\limits_{J\in \mathcal{F}_i}J=\bigcap\limits_{i=1}^\infty\bigcup\limits_{I\in \mathcal{G}_i}I.\end{align*} $$
$$ \begin{align*}\mathcal{F}_\infty=\bigcap\limits_{i=1}^\infty\bigcup\limits_{J\in \mathcal{F}_i}J=\bigcap\limits_{i=1}^\infty\bigcup\limits_{I\in \mathcal{G}_i}I.\end{align*} $$
It is straightforward to see that
 $\mathcal {F}_\infty \subset \overline {E}(T_\beta ,f,g)$
.
$\mathcal {F}_\infty \subset \overline {E}(T_\beta ,f,g)$
.
Remark 4.2. It should be noted that the integer
![]() $k_i$
depends upon
$k_i$
depends upon
![]() $\Gamma _{i-1}$
and
$\Gamma _{i-1}$
and
![]() $U_i$
. Assume that f is strictly positive, otherwise replace f by
$U_i$
. Assume that f is strictly positive, otherwise replace f by
![]() $f+\epsilon $
. Since
$f+\epsilon $
. Since
![]() $m_i$
can be chosen as
$m_i$
can be chosen as
![]() $m_i\gg n_{i-1}$
for all
$m_i\gg n_{i-1}$
for all
![]() $n_{i-1}$
, we have
$n_{i-1}$
, we have
 $$ \begin{align*}\beta^{-k_i}\asymp e^{-S_{n_i}f(x_i^*)}=(e^{-S_{m_i}f(T_\beta^{n_{i-1}+k_{i-1}}x_i^*)})^{1+\epsilon},\end{align*} $$
$$ \begin{align*}\beta^{-k_i}\asymp e^{-S_{n_i}f(x_i^*)}=(e^{-S_{m_i}f(T_\beta^{n_{i-1}+k_{i-1}}x_i^*)})^{1+\epsilon},\end{align*} $$
where
![]() $x_i^*\in I_{n_{i-1}+k_{i-1}+m_i}(\Gamma _{i-1},U_i)$
. In other words,
$x_i^*\in I_{n_{i-1}+k_{i-1}+m_i}(\Gamma _{i-1},U_i)$
. In other words,
![]() $k_i$
is almost dependent only on
$k_i$
is almost dependent only on
![]() $U_i$
and
$U_i$
and
 $$ \begin{align} \beta^{-k_i}\asymp e^{-S_{m_i}f(x_i')}, {x_i'}\in I_{m_i}(U_i). \end{align} $$
$$ \begin{align} \beta^{-k_i}\asymp e^{-S_{m_i}f(x_i')}, {x_i'}\in I_{m_i}(U_i). \end{align} $$
The same is true for
![]() $l_i$
:
$l_i$
:
 $$ \begin{align} \beta^{-l_i}\asymp e^{-S_{m_i}f(y_i')}, {y_i'}\in I_{m_i}(W_i). \end{align} $$
$$ \begin{align} \beta^{-l_i}\asymp e^{-S_{m_i}f(y_i')}, {y_i'}\in I_{m_i}(W_i). \end{align} $$
4.2 Supporting measure
We now construct a probability measure
![]() $\mu $
supported on
$\mu $
supported on
![]() $\mathcal {F}_\infty $
, which is defined by distributing masses among the cylinders with nonempty intersection with
$\mathcal {F}_\infty $
, which is defined by distributing masses among the cylinders with nonempty intersection with
![]() $\mathcal {F}_\infty $
. The process splits into two cases: when
$\mathcal {F}_\infty $
. The process splits into two cases: when
![]() $s_0>1$
and
$s_0>1$
and
![]() $ 0\leq s_0\leq 1$
.
$ 0\leq s_0\leq 1$
.
4.2.1 Case I:
 $s_0>1$
$s_0>1$
In this case, for any
![]() $1<s<s_0,$
notice that
$1<s<s_0,$
notice that
 $$ \begin{align*}\frac{e^{S_nf(x')}}{e^{S_ng(y')}}\bigg(\frac{1}{\beta^ne^{S_nf(x')}}\bigg)^s\leq\bigg(\frac{1}{\beta^ne^{S_ng(y')}}\bigg)^s.\end{align*} $$
$$ \begin{align*}\frac{e^{S_nf(x')}}{e^{S_ng(y')}}\bigg(\frac{1}{\beta^ne^{S_nf(x')}}\bigg)^s\leq\bigg(\frac{1}{\beta^ne^{S_ng(y')}}\bigg)^s.\end{align*} $$
This means that the covering of the rectangle
![]() $J_n(U)\times J_n(W)$
by balls of shorter side length is preferable and therefore, it reasonable to define the probability measure on smaller balls. To this end, let
$J_n(U)\times J_n(W)$
by balls of shorter side length is preferable and therefore, it reasonable to define the probability measure on smaller balls. To this end, let
![]() $s_i$
be the solution to the equation
$s_i$
be the solution to the equation
 $$ \begin{align*}\sum\limits_{U,W\in \Sigma_{\beta_N}^{m_i}} \frac{e^{S_{m_i}f(x_i')}}{e^{S_{m_i}g(y_i')}}\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}f(x_i')}}\bigg)^s=1,\end{align*} $$
$$ \begin{align*}\sum\limits_{U,W\in \Sigma_{\beta_N}^{m_i}} \frac{e^{S_{m_i}f(x_i')}}{e^{S_{m_i}g(y_i')}}\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}f(x_i')}}\bigg)^s=1,\end{align*} $$
where
![]() $x_i'\in I_{m_i}(U_i),~ y_i'\in I_{m_i}(W_i).$
$x_i'\in I_{m_i}(U_i),~ y_i'\in I_{m_i}(W_i).$
By the continuity of the pressure function
![]() $P(T_\beta ,f)$
with respect to
$P(T_\beta ,f)$
with respect to
![]() $\beta $
[Reference Tan and Wang14, Theorem 4.1], it can be shown that
$\beta $
[Reference Tan and Wang14, Theorem 4.1], it can be shown that
![]() $s_i\rightarrow s_0$
when
$s_i\rightarrow s_0$
when
![]() $m_i\rightarrow \infty $
. Thus, without loss of generality, we choose all
$m_i\rightarrow \infty $
. Thus, without loss of generality, we choose all
![]() $m_i$
large enough such that
$m_i$
large enough such that
![]() $s_i>1$
for all i and
$s_i>1$
for all i and
![]() $\lvert s_i-s_0\rvert =o(1).$
$\lvert s_i-s_0\rvert =o(1).$
We systematically define the measure
![]() $\mu $
on the Cantor set by defining it on the basic cylinders first. Recall that for level 1 of the Cantor set construction, we assumed that
$\mu $
on the Cantor set by defining it on the basic cylinders first. Recall that for level 1 of the Cantor set construction, we assumed that
![]() $n_1=m_1.$
For sublevels of the Cantor set, say
$n_1=m_1.$
For sublevels of the Cantor set, say
![]() $\mathcal F_k$
, the role of
$\mathcal F_k$
, the role of
![]() $m_k$
is to denote the number of positions where the digits can be chosen (almost) freely, while
$m_k$
is to denote the number of positions where the digits can be chosen (almost) freely, while
![]() $n_k$
denotes the length of a word in
$n_k$
denotes the length of a word in
![]() $\mathcal F_k$
before shrinking.
$\mathcal F_k$
before shrinking.
Let
![]() $I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1)$
be a generic cylinder in
$I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1)$
be a generic cylinder in
![]() $\mathcal {G}_1.$
Then define
$\mathcal {G}_1.$
Then define
 $$ \begin{align*}\mu(I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1))=\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}f(x_1')}}\bigg)^{s_1},\end{align*} $$
$$ \begin{align*}\mu(I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1))=\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}f(x_1')}}\bigg)^{s_1},\end{align*} $$
where
![]() $ x_1'\in I_{m_1}(U_1)$
. Assume that the measure on the cylinders of order
$ x_1'\in I_{m_1}(U_1)$
. Assume that the measure on the cylinders of order
![]() $i-1$
has been well defined. To define a measure on the i th cylinder, let
$i-1$
has been well defined. To define a measure on the i th cylinder, let
![]() $I_{n_i+k_i}(\Gamma _{i-1},U_i,K_i)\times I_{n_i+k_i}(\Upsilon _{i-1},W_i,L_i,H_i)$
be a generic i th cylinder in
$I_{n_i+k_i}(\Gamma _{i-1},U_i,K_i)\times I_{n_i+k_i}(\Upsilon _{i-1},W_i,L_i,H_i)$
be a generic i th cylinder in
![]() $\mathcal {G}_i$
. Define the probability measure
$\mathcal {G}_i$
. Define the probability measure
![]() $\mu $
as
$\mu $
as
 $$ \begin{align*} &\mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+k_i}(\Upsilon_{i-1},W_i,L_i,H_i)) \\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}f(x_i')}}\bigg)^{s_i}, \end{align*} $$
$$ \begin{align*} &\mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+k_i}(\Upsilon_{i-1},W_i,L_i,H_i)) \\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}f(x_i')}}\bigg)^{s_i}, \end{align*} $$
where
![]() $ x_i'\in I_{m_i}(U_i)$
. The measure of a rectangle in
$ x_i'\in I_{m_i}(U_i)$
. The measure of a rectangle in
![]() $\mathcal {F}_i$
is then given as
$\mathcal {F}_i$
is then given as
 $$ \begin{align*} &\mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon_{i-1},W_i,L_i))\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times{\#\Sigma_\beta^{k_i-l_i}}\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}f(x_i')}}\bigg)^{s_i}\\ &\quad\asymp \mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\frac{e^{S_{m_i}f(x_i')}}{e^{S_{m_i}g(y_i')}}\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}f(x_i')}}\bigg)^{s_i}, \end{align*} $$
$$ \begin{align*} &\mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon_{i-1},W_i,L_i))\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times{\#\Sigma_\beta^{k_i-l_i}}\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}f(x_i')}}\bigg)^{s_i}\\ &\quad\asymp \mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\frac{e^{S_{m_i}f(x_i')}}{e^{S_{m_i}g(y_i')}}\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}f(x_i')}}\bigg)^{s_i}, \end{align*} $$
where the last inequality follows from estimates (4-2) and (4-3).
4.2.2 Estimation of the
 $\mu $
-measure of cylinders
$\mu $
-measure of cylinders
For any
![]() $i\geq 1$
consider the generic cylinder,
$i\geq 1$
consider the generic cylinder,
We would like to show by induction that, for any
![]() $1<s< s_0$
,
$1<s< s_0$
,
When
![]() $i=1$
, the length of I is given as
$i=1$
, the length of I is given as
But, by the definition of the measure
![]() $\mu $
, it is clear that
$\mu $
, it is clear that
Now we consider the inductive process. Assume that
 $$ \begin{align*} \mu(I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times &I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})) \leq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert^{s/(1+\epsilon)}. \end{align*} $$
$$ \begin{align*} \mu(I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times &I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})) \leq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert^{s/(1+\epsilon)}. \end{align*} $$
Let
be a generic cylinder in
![]() $\mathcal {G}_i$
. One one hand, its length satisfies
$\mathcal {G}_i$
. One one hand, its length satisfies
 $$ \begin{align*} \lvert I\rvert&=\beta^{-n_i-k_i}=\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert \times\beta^{-m_i}\times\beta^{-k_i}\nonumber\\ &\geq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert \times\beta^{-m_i}(e^{-S_{n_i}f(x_i^*)})^{1+\epsilon}, \end{align*} $$
$$ \begin{align*} \lvert I\rvert&=\beta^{-n_i-k_i}=\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert \times\beta^{-m_i}\times\beta^{-k_i}\nonumber\\ &\geq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert \times\beta^{-m_i}(e^{-S_{n_i}f(x_i^*)})^{1+\epsilon}, \end{align*} $$
where
![]() $x_i^*\in I_{n_i}(\Gamma _i,U_i).$
$x_i^*\in I_{n_i}(\Gamma _i,U_i).$
We compare
![]() $S_{n_i}f(x_i^*)$
and
$S_{n_i}f(x_i^*)$
and
![]() $S_{m_i}f(x_i')$
. By (4-1) we have
$S_{m_i}f(x_i')$
. By (4-1) we have
 $$ \begin{align*}\lvert S_{n_i}f(x_i^*)-S_{m_i}f(x_i')\rvert &=\lvert S_{n_{i-1}+k_{i-1}}f(x_i^*)\rvert \\ &\leq({n_{i-1}+k_{i-1}})\|f\| \\ &\leq \frac{\epsilon}{1+\epsilon}m_i\log\beta, \end{align*} $$
$$ \begin{align*}\lvert S_{n_i}f(x_i^*)-S_{m_i}f(x_i')\rvert &=\lvert S_{n_{i-1}+k_{i-1}}f(x_i^*)\rvert \\ &\leq({n_{i-1}+k_{i-1}})\|f\| \\ &\leq \frac{\epsilon}{1+\epsilon}m_i\log\beta, \end{align*} $$
where
![]() $x_i'\in I_{m_i}(U_i).$
So we get
$x_i'\in I_{m_i}(U_i).$
So we get
 $$ \begin{align} \lvert I\rvert \geq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert \times(\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{1+\epsilon}. \end{align} $$
$$ \begin{align} \lvert I\rvert \geq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert \times(\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{1+\epsilon}. \end{align} $$
On the other hand, by the definition of the measure
![]() $\mu $
and induction, we have that
$\mu $
and induction, we have that
 $$ \begin{align*} \mu(I)&=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times(\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{s_i}\\ &\leq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert^{s/(1+\epsilon)} ((\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{1+\epsilon})^{s/(1+\epsilon)}\\ &\leq \lvert I\rvert^{s/(1+\epsilon)}. \end{align*} $$
$$ \begin{align*} \mu(I)&=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times(\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{s_i}\\ &\leq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert^{s/(1+\epsilon)} ((\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{1+\epsilon})^{s/(1+\epsilon)}\\ &\leq \lvert I\rvert^{s/(1+\epsilon)}. \end{align*} $$
In the following steps, for any
![]() $(x,y)\in \mathcal {F}_\infty ,$
we estimate the measure of
$(x,y)\in \mathcal {F}_\infty ,$
we estimate the measure of
![]() $I_n(x)\times I_n(y)$
compared with its length
$I_n(x)\times I_n(y)$
compared with its length
![]() $\beta ^{-n}.$
By the construction of
$\beta ^{-n}.$
By the construction of
![]() $\mathcal {F}_\infty ,$
there exists
$\mathcal {F}_\infty ,$
there exists
![]() $\{k_i,l_i\}_{i\geq 1}$
such that for all
$\{k_i,l_i\}_{i\geq 1}$
such that for all
![]() $i\geq 1,$
$i\geq 1,$
For any
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $i\geq 1$
be the integer such that
$i\geq 1$
be the integer such that
Step 1:
![]() $n_{i-1}+k_{i-1}+m_i+l_i\leq n \leq n_{i}+k_{i}=n_{i-1}+k_{i-1}+m_i+k_i.$
$n_{i-1}+k_{i-1}+m_i+l_i\leq n \leq n_{i}+k_{i}=n_{i-1}+k_{i-1}+m_i+k_i.$
The cylinder
![]() $I_n(x)\times I_n(y)$
contains
$I_n(x)\times I_n(y)$
contains
![]() $\beta ^{n_{i}+k_{i}-n}$
cylinders in
$\beta ^{n_{i}+k_{i}-n}$
cylinders in
![]() $\mathcal {G}_i$
with order
$\mathcal {G}_i$
with order
![]() $n_{i}+k_{i}$
. Note that by the definition of
$n_{i}+k_{i}$
. Note that by the definition of
![]() $\{k_j,l_j\}_{1\leq j\leq i}$
, the first i pairs
$\{k_j,l_j\}_{1\leq j\leq i}$
, the first i pairs
![]() $\{k_j,l_j\}_{1\leq j\leq i}$
depend only on the first
$\{k_j,l_j\}_{1\leq j\leq i}$
depend only on the first
![]() $n_i$
digits of
$n_i$
digits of
![]() $(x,y)$
. So the measures of the subcylinders of order
$(x,y)$
. So the measures of the subcylinders of order
![]() $n_{i}+k_{i}$
are the same. So, the measure of
$n_{i}+k_{i}$
are the same. So, the measure of
![]() $I_n(x)\times I_n(y)$
can be estimated as
$I_n(x)\times I_n(y)$
can be estimated as
 $$ \begin{align*} \mu(I_n(x)\times I_n(y)) &=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n{}_{i-1}+k{}_{i-1}}}(\Upsilon_{i-1})) \\ &\quad\times (\,\beta^{-m_i}e^{-S_{m{}_i}f(x{}_i')})^{s_i}\times \beta^{n_{i}+k_{i}-n}. \end{align*} $$
$$ \begin{align*} \mu(I_n(x)\times I_n(y)) &=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n{}_{i-1}+k{}_{i-1}}}(\Upsilon_{i-1})) \\ &\quad\times (\,\beta^{-m_i}e^{-S_{m{}_i}f(x{}_i')})^{s_i}\times \beta^{n_{i}+k_{i}-n}. \end{align*} $$
Thus by the measure estimation of cylinders of order
![]() $n_{i-1}+k_{i-1}$
and the choice of
$n_{i-1}+k_{i-1}$
and the choice of
![]() $k_i$
, one has that
$k_i$
, one has that
 $$ \begin{align*} \mu(I_n(x)\times I_n(y))&\leq (\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}(\,\beta^{-m_{i}-k_{i}})^{s/(1+\epsilon)}\times\beta^{n_{i}+k_{i}-n}\\ &=(\,\beta^{-n_{i}-k_{i}})^{s/(1+\epsilon)}\times\beta^{n_{i}+k_{i}-n} \\ &\leq (\,\beta^{-n})^{s/(1+\epsilon)}, \end{align*} $$
$$ \begin{align*} \mu(I_n(x)\times I_n(y))&\leq (\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}(\,\beta^{-m_{i}-k_{i}})^{s/(1+\epsilon)}\times\beta^{n_{i}+k_{i}-n}\\ &=(\,\beta^{-n_{i}-k_{i}})^{s/(1+\epsilon)}\times\beta^{n_{i}+k_{i}-n} \\ &\leq (\,\beta^{-n})^{s/(1+\epsilon)}, \end{align*} $$
by noting that
![]() $n \leq n_{i}+k_{i}$
and
$n \leq n_{i}+k_{i}$
and
![]() ${s/(1+\epsilon )}>1.$
${s/(1+\epsilon )}>1.$
Step 2:
![]() $n_{i-1}+k_{i-1}+m_i\leq n \leq n_{i}+l_{i}=n_{i-1}+k_{i-1}+m_i+l_i.$
$n_{i-1}+k_{i-1}+m_i\leq n \leq n_{i}+l_{i}=n_{i-1}+k_{i-1}+m_i+l_i.$
Recalling the definition of
![]() $n_{i}+k_{i}$
, the first i pairs
$n_{i}+k_{i}$
, the first i pairs
![]() $\{k_j,l_j\}_{1\leq j\leq i}$
depend only on the first
$\{k_j,l_j\}_{1\leq j\leq i}$
depend only on the first
![]() $n_i$
digits of
$n_i$
digits of
![]() $(x,y)$
. So the measures of the subcylinders in
$(x,y)$
. So the measures of the subcylinders in
![]() $\mathcal {G}_i$
with order
$\mathcal {G}_i$
with order
![]() $n_{i}+k_{i}$
are the same. It is clear that the cylinder
$n_{i}+k_{i}$
are the same. It is clear that the cylinder
![]() $I_n(x)\times I_n(y)$
contains
$I_n(x)\times I_n(y)$
contains
![]() $\beta ^{k_{i}-l_i}$
cylinders of order
$\beta ^{k_{i}-l_i}$
cylinders of order
![]() $n_{i}+k_{i}$
. So, the measure of
$n_{i}+k_{i}$
. So, the measure of
![]() $I_n(x)\times I_n(y)$
can be estimated as
$I_n(x)\times I_n(y)$
can be estimated as
 $$ \begin{align*} \mu(I_n(x)\times I_n(y)) &=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1})) \\ &\quad\times (\,\beta^{-m_i}e^{-S_{m_i}f(x_i^{\prime*})})^{s_i}\times \beta^{k_{i}-l_i}. \end{align*} $$
$$ \begin{align*} \mu(I_n(x)\times I_n(y)) &=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1})) \\ &\quad\times (\,\beta^{-m_i}e^{-S_{m_i}f(x_i^{\prime*})})^{s_i}\times \beta^{k_{i}-l_i}. \end{align*} $$
Thus by the measure estimation of cylinders of order
![]() $n_{i-1}+k_{i-1}$
and the choice of
$n_{i-1}+k_{i-1}$
and the choice of
![]() $k_i$
, one has that
$k_i$
, one has that
 $$ \begin{align*} \mu(I_n(x)\times I_n(y))&\leq (\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}(\,\beta^{-m_{i}-k_{i}})^{s/(1+\epsilon)}\times\beta^{k_{i}-l_i}\\ &=(\,\beta^{-n_{i}-k_{i}})^{s/(1+\epsilon)}\times\beta^{k_{i}-l_i}\\ &\leq(\,\beta^{-n_i-l_i})^{s/(1+\epsilon)} \\ &\leq (\,\beta^{-n})^{s/(1+\epsilon)}, \end{align*} $$
$$ \begin{align*} \mu(I_n(x)\times I_n(y))&\leq (\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}(\,\beta^{-m_{i}-k_{i}})^{s/(1+\epsilon)}\times\beta^{k_{i}-l_i}\\ &=(\,\beta^{-n_{i}-k_{i}})^{s/(1+\epsilon)}\times\beta^{k_{i}-l_i}\\ &\leq(\,\beta^{-n_i-l_i})^{s/(1+\epsilon)} \\ &\leq (\,\beta^{-n})^{s/(1+\epsilon)}, \end{align*} $$
by noting that
![]() $n \leq n_{i}+l_{i}$
and
$n \leq n_{i}+l_{i}$
and
![]() ${s/(1+\epsilon )}>1.$
${s/(1+\epsilon )}>1.$
Step 3:
![]() $n_{i-1}+k_{i-1}\leq n \leq n_{i-1}+k_{i-1}+m_i.$
$n_{i-1}+k_{i-1}\leq n \leq n_{i-1}+k_{i-1}+m_i.$
Assume that
![]() $U_i=(\epsilon _1,\epsilon _2,\ldots ,\epsilon _{m_i}), W_i=(\omega _1,\omega _2,\ldots ,\omega _{m_i}).$
We start off by denoting
$U_i=(\epsilon _1,\epsilon _2,\ldots ,\epsilon _{m_i}), W_i=(\omega _1,\omega _2,\ldots ,\omega _{m_i}).$
We start off by denoting
![]() $l=n-(n_{i-1}+k_{i-1})$
and
$l=n-(n_{i-1}+k_{i-1})$
and
![]() $h=m_i-l$
. Then
$h=m_i-l$
. Then
 $$ \begin{align*} &\mu(I_n(x)\times I_n(y))\\ &\quad=\sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}} \mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i) \times I_{n_i+k_i}(\Upsilon_{i-1},W_i,L_i,H_i))\times\beta^{k_{i}-l_i}\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l \\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}}(\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{s_i} \times\beta^{k_{i}-l_i}\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}}\frac{e^{S_{m_i}f(x_i')}}{e^{S_{m_i}g(y_i')}} (\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{s_i}. \end{align*} $$
$$ \begin{align*} &\mu(I_n(x)\times I_n(y))\\ &\quad=\sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}} \mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i) \times I_{n_i+k_i}(\Upsilon_{i-1},W_i,L_i,H_i))\times\beta^{k_{i}-l_i}\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l \\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}}(\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{s_i} \times\beta^{k_{i}-l_i}\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}}\frac{e^{S_{m_i}f(x_i')}}{e^{S_{m_i}g(y_i')}} (\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{s_i}. \end{align*} $$
Then by the estimation of the measure of cylinders of order
![]() $n_{i-1}+k_{i-1}$
and letting
$n_{i-1}+k_{i-1}$
and letting
 $(\widetilde {x_i'},\widetilde {y_i'})=(T_\beta ^lx_i',T_\beta ^ly_i')$
, we get
$(\widetilde {x_i'},\widetilde {y_i'})=(T_\beta ^lx_i',T_\beta ^ly_i')$
, we get
 $$ \begin{align*} \mu(I_n(x)\times I_n(y))&\leq(\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}\cdot\frac{e^{S_{l}f(x_i')}}{e^{S_{l}g(y_i')}}\cdot (\,\beta^{-l}e^{-S_{l}f(x_i')})^{s_i}\\ &\quad\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}}\frac{e^{S_{h}f(\widetilde{x_i'})}}{e^{S_{h}g(\widetilde{y_i'})}} \cdot(\,\beta^{-h}e^{-S_{h}f(\widetilde{x_i'})})^{s_i}. \end{align*} $$
$$ \begin{align*} \mu(I_n(x)\times I_n(y))&\leq(\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}\cdot\frac{e^{S_{l}f(x_i')}}{e^{S_{l}g(y_i')}}\cdot (\,\beta^{-l}e^{-S_{l}f(x_i')})^{s_i}\\ &\quad\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}}\frac{e^{S_{h}f(\widetilde{x_i'})}}{e^{S_{h}g(\widetilde{y_i'})}} \cdot(\,\beta^{-h}e^{-S_{h}f(\widetilde{x_i'})})^{s_i}. \end{align*} $$
The first part can be estimated as
 $$ \begin{align*} (\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}\cdot\frac{e^{S_{l}f(x_i')}}{e^{S_{l}g(y_i')}}\cdot (\,\beta^{-l}e^{-S_{l}f(x_i')})^{s_i}&\leq(\,\beta^{-(n_{i-1}+k_{i-1}+l)})^{s/(1+\epsilon)}\\ &=(\,\beta^{-n})^{ s/(1+\epsilon)}, \end{align*} $$
$$ \begin{align*} (\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}\cdot\frac{e^{S_{l}f(x_i')}}{e^{S_{l}g(y_i')}}\cdot (\,\beta^{-l}e^{-S_{l}f(x_i')})^{s_i}&\leq(\,\beta^{-(n_{i-1}+k_{i-1}+l)})^{s/(1+\epsilon)}\\ &=(\,\beta^{-n})^{ s/(1+\epsilon)}, \end{align*} $$
since
 $$ \begin{align*}\frac{e^{S_{l}f(x_i')}}{e^{S_{l}g(y_i')}}\cdot(e^{-S_{l}f(x_i')})^{s_i}\leq 1,\quad \text{for } s_i\geq1.\end{align*} $$
$$ \begin{align*}\frac{e^{S_{l}f(x_i')}}{e^{S_{l}g(y_i')}}\cdot(e^{-S_{l}f(x_i')})^{s_i}\leq 1,\quad \text{for } s_i\geq1.\end{align*} $$
To estimate the second part, we first recall that we defined
![]() $s_i$
to be the solution of the equation
$s_i$
to be the solution of the equation
 $$ \begin{align*}\sum\limits_{U,W\in \Sigma_{\beta_N}^{m_i}} \frac{e^{S_nf(x_i')}}{e^{S_ng(y_i')}}\bigg(\frac{1}{\beta^ne^{S_nf(x_i')}}\bigg)^s=1.\end{align*} $$
$$ \begin{align*}\sum\limits_{U,W\in \Sigma_{\beta_N}^{m_i}} \frac{e^{S_nf(x_i')}}{e^{S_ng(y_i')}}\bigg(\frac{1}{\beta^ne^{S_nf(x_i')}}\bigg)^s=1.\end{align*} $$
Therefore,
 $$ \begin{align*} 1=\sum\limits_{U_1,W_1\in \Sigma_{\beta_N}^{l}} \frac{e^{S_lf(x_i')}}{e^{S_lg(y_i')}}&\bigg(\frac{1}{\beta^le^{S_lf(x_i')}}\bigg)^{s_i}\times \sum\limits_{U_2,W_2\in \Sigma_{\beta_N}^{h}} \frac{e^{S_hf(\widetilde{x_i'})}}{e^{S_hg(\widetilde{y_i'})}}\bigg(\frac{1}{\beta^le^{S_hf(\widetilde{x_i'})}}\bigg)^{s_i}. \end{align*} $$
$$ \begin{align*} 1=\sum\limits_{U_1,W_1\in \Sigma_{\beta_N}^{l}} \frac{e^{S_lf(x_i')}}{e^{S_lg(y_i')}}&\bigg(\frac{1}{\beta^le^{S_lf(x_i')}}\bigg)^{s_i}\times \sum\limits_{U_2,W_2\in \Sigma_{\beta_N}^{h}} \frac{e^{S_hf(\widetilde{x_i'})}}{e^{S_hg(\widetilde{y_i'})}}\bigg(\frac{1}{\beta^le^{S_hf(\widetilde{x_i'})}}\bigg)^{s_i}. \end{align*} $$
So, by arguments similar to [Reference Tan and Wang14, pages 2095–2097] and [Reference Wang and Wu18, pages 1331–1332], we derive that
 $$ \begin{align*}\sum\limits_{U_2,W_2\in \Sigma_{\beta_N}^{h}} \frac{e^{S_hf(\widetilde{x_i'})}}{e^{S_hg(\widetilde{y_i'})}} \bigg(\frac{1}{\beta^le^{S_hf(\widetilde{x_i'})}}\bigg)^{s_i}\leq\beta^{l\epsilon}.\end{align*} $$
$$ \begin{align*}\sum\limits_{U_2,W_2\in \Sigma_{\beta_N}^{h}} \frac{e^{S_hf(\widetilde{x_i'})}}{e^{S_hg(\widetilde{y_i'})}} \bigg(\frac{1}{\beta^le^{S_hf(\widetilde{x_i'})}}\bigg)^{s_i}\leq\beta^{l\epsilon}.\end{align*} $$
Therefore,
As far as the measure of a general ball
![]() $B(x,r)$
with
$B(x,r)$
with
![]() $\beta ^{-n-1}\leq r<\beta ^{-n}$
is concerned, we notice that it can intersect at most three cylinders of order n. Thus,
$\beta ^{-n-1}\leq r<\beta ^{-n}$
is concerned, we notice that it can intersect at most three cylinders of order n. Thus,
So, finally, an application of the mass distribution principle (Proposition 4.1) yields that
 $$ \begin{align*}\dim_{\mathrm H} \overline{E}(T_\beta, f,g)\geq s_0.\end{align*} $$
$$ \begin{align*}\dim_{\mathrm H} \overline{E}(T_\beta, f,g)\geq s_0.\end{align*} $$
4.2.3 Case II:
 $0\leq s_0\leq 1$
$0\leq s_0\leq 1$
The arguments are similar to Case I but the calculations are different. In this case, for any
![]() $s<s_0\leq 1,$
it is trivial that
$s<s_0\leq 1,$
it is trivial that
 $$ \begin{align*}\frac{e^{S_nf(x')}}{e^{S_ng(y')}}\bigg(\frac{1}{\beta^ne^{S_nf(x')}}\bigg)^s\geq\bigg(\frac{1}{\beta^ne^{S_ng(y')}}\bigg)^s.\end{align*} $$
$$ \begin{align*}\frac{e^{S_nf(x')}}{e^{S_ng(y')}}\bigg(\frac{1}{\beta^ne^{S_nf(x')}}\bigg)^s\geq\bigg(\frac{1}{\beta^ne^{S_ng(y')}}\bigg)^s.\end{align*} $$
This means that the covering of the rectangle
![]() $J_n(U)\times J_n(W)$
by balls of larger side length is more preferable and therefore, it reasonable to define the probability measure of the rectangle to be the same measure as for the cylinder of order
$J_n(U)\times J_n(W)$
by balls of larger side length is more preferable and therefore, it reasonable to define the probability measure of the rectangle to be the same measure as for the cylinder of order
![]() $n_i+l_i$
.
$n_i+l_i$
.
Just as in Case I, let
![]() $s_i$
be the solution to the equation
$s_i$
be the solution to the equation
 $$ \begin{align*}\sum\limits_{U,W\in \Sigma_{\beta_N}^{m_i} \text{ ending with } 0^N} \bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^s=1,\end{align*} $$
$$ \begin{align*}\sum\limits_{U,W\in \Sigma_{\beta_N}^{m_i} \text{ ending with } 0^N} \bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^s=1,\end{align*} $$
where
![]() $y_i'\in I_{m_i}(W_i).$
By the continuity of the pressure function
$y_i'\in I_{m_i}(W_i).$
By the continuity of the pressure function
![]() $P(T_\beta ,f)$
with respect to
$P(T_\beta ,f)$
with respect to
![]() $\beta $
we can assume that for all
$\beta $
we can assume that for all
![]() $m_i$
large enough we have that
$m_i$
large enough we have that
![]() $s_i<1$
for all i and
$s_i<1$
for all i and
![]() $\lvert s_i-s_0\rvert =o(1).$
$\lvert s_i-s_0\rvert =o(1).$
We first define the measure
![]() $\mu $
on the basic cylinders. Let
$\mu $
on the basic cylinders. Let
![]() $I_{n_1+k_1}(U_1,K_1)\times I_{n_1+l_1}(W_1,L_1)$
be a generic cylinder in
$I_{n_1+k_1}(U_1,K_1)\times I_{n_1+l_1}(W_1,L_1)$
be a generic cylinder in
![]() $\mathcal {F}_1.$
Then define
$\mathcal {F}_1.$
Then define
 $$ \begin{align*}\mu(I_{n_1+k_1}(U_1,K_1)\times I_{n_1+l_1}(W_1,L_1))=\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}g(y_1')}}\bigg)^{s_1},\end{align*} $$
$$ \begin{align*}\mu(I_{n_1+k_1}(U_1,K_1)\times I_{n_1+l_1}(W_1,L_1))=\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}g(y_1')}}\bigg)^{s_1},\end{align*} $$
where
![]() $ y_1'\in I_{m_1}(W_1)$
. Then the measure is evenly distributed on its subcylinders in
$ y_1'\in I_{m_1}(W_1)$
. Then the measure is evenly distributed on its subcylinders in
![]() $\mathcal {G}_1$
. So, for a generic cylinder
$\mathcal {G}_1$
. So, for a generic cylinder
![]() $I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1)$
in
$I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1)$
in
![]() $\mathcal {G}_1$
, define
$\mathcal {G}_1$
, define
 $$ \begin{align*} \mu(I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1))&=\frac{1}{\#\Sigma_\beta^{k_1-l_1}}\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}g(y_1')}}\bigg)^{s_1}\\ &\asymp\frac{1}{\beta^{k_1-l_1}}\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}g(y_1')}}\bigg)^{s_1}. \end{align*} $$
$$ \begin{align*} \mu(I_{n_1+k_1}(U_1,K_1)\times I_{n_1+k_1}(W_1,L_1,H_1))&=\frac{1}{\#\Sigma_\beta^{k_1-l_1}}\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}g(y_1')}}\bigg)^{s_1}\\ &\asymp\frac{1}{\beta^{k_1-l_1}}\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}g(y_1')}}\bigg)^{s_1}. \end{align*} $$
Assume that the measure on the cylinders of order
![]() $(i-1)$
has been well defined. Then to define the measure on the i th cylinder we proceed as follows. Let
$(i-1)$
has been well defined. Then to define the measure on the i th cylinder we proceed as follows. Let
![]() $I_{n_i+k_i}(\Gamma _{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon _{i-1},W_i,L_i)$
be a generic cylinder in
$I_{n_i+k_i}(\Gamma _{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon _{i-1},W_i,L_i)$
be a generic cylinder in
![]() $\mathcal {F}_i$
. Then define
$\mathcal {F}_i$
. Then define
 $$ \begin{align*} &\mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon_{i-1},W_i,L_i)) \\&\quad= \mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}, \end{align*} $$
$$ \begin{align*} &\mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+l_i}(\Upsilon_{i-1},W_i,L_i)) \\&\quad= \mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}, \end{align*} $$
where
![]() $ y_i'\in I_{m_i}(W_i)$
. By the definition of
$ y_i'\in I_{m_i}(W_i)$
. By the definition of
![]() $k_i,l_i$
, the measure of a cylinder in
$k_i,l_i$
, the measure of a cylinder in
![]() $\mathcal {G}_i$
is then given as
$\mathcal {G}_i$
is then given as
 $$ \begin{align*} &\mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+k_i}(\Upsilon_{i-1},W_i,L_i,H_i))\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\frac{1}{\#\Sigma_\beta^{k_i-l_i}}\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}\\ &\quad\asymp \mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\frac{e^{S_{m_i}g(y_i')}}{e^{S_{m_i}f(x_i')}}\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}. \end{align*} $$
$$ \begin{align*} &\mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i)\times I_{n_i+k_i}(\Upsilon_{i-1},W_i,L_i,H_i))\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\frac{1}{\#\Sigma_\beta^{k_i-l_i}}\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}\\ &\quad\asymp \mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\frac{e^{S_{m_i}g(y_i')}}{e^{S_{m_i}f(x_i')}}\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}. \end{align*} $$
4.2.4 Estimation of the
 $\mu $
-measure of cylinders
$\mu $
-measure of cylinders
We first show by induction that, for any
![]() $i\geq 1$
and a generic cylinder
$i\geq 1$
and a generic cylinder
we have
When
![]() $i=1$
, on the one hand, the length of I is given as
$i=1$
, on the one hand, the length of I is given as
But on the other hand, by the definition of the measure
![]() $\mu $
, it is clear that
$\mu $
, it is clear that
 $$ \begin{align*} \mu(I)&\leq\frac{e^{S_{m_1}g(y_1')}}{e^{S_{m_1}f(x_1')}}\cdot\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}g(y_1')}}\bigg)^{s_1}\\ &\leq(\,\beta^{-m_1}e^{-S_{m_1}f(x_1')})^{s_1}\\ &\leq\lvert I\rvert^{s/(1+\epsilon)}, \end{align*} $$
$$ \begin{align*} \mu(I)&\leq\frac{e^{S_{m_1}g(y_1')}}{e^{S_{m_1}f(x_1')}}\cdot\bigg(\frac{1}{\beta^{m_1}e^{S_{m_1}g(y_1')}}\bigg)^{s_1}\\ &\leq(\,\beta^{-m_1}e^{-S_{m_1}f(x_1')})^{s_1}\\ &\leq\lvert I\rvert^{s/(1+\epsilon)}, \end{align*} $$
by noting that
![]() $s_1<1.$
$s_1<1.$
Just as in Case I, we consider the inductive process. Assume that
 $$ \begin{align*} \mu(I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times &I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1}))\leq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert^{s/(1+\epsilon)}. \end{align*} $$
$$ \begin{align*} \mu(I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times &I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1}))\leq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert^{s/(1+\epsilon)}. \end{align*} $$
Let
be a generic cylinder in
![]() $\mathcal {G}_i$
. By (4-4) we get
$\mathcal {G}_i$
. By (4-4) we get
 $$ \begin{align*}\lvert I\rvert\geq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert \times(\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{1+\epsilon}.\end{align*} $$
$$ \begin{align*}\lvert I\rvert\geq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert \times(\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{1+\epsilon}.\end{align*} $$
From the definition of the measure
![]() $\mu $
, induction and the fact that
$\mu $
, induction and the fact that
![]() $s_i<1$
, it follows that
$s_i<1$
, it follows that
 $$ \begin{align*} \mu(I)&=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\frac{e^{S_{m_i}g(y_i')}}{e^{S_{m_i}f(x_i')}} \times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}\\ &\leq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert^{s/(1+\epsilon)} ((\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{1+\epsilon})^{s/(1+\epsilon)}\\ &\leq \lvert I\rvert^{s/(1+\epsilon)}\\ &=(\,\beta^{-n_i-k_i})^{s/(1+\epsilon)}\\ &\asymp(\,\beta^{-m_i-k_i})^{s/(1+\epsilon)}. \end{align*} $$
$$ \begin{align*} \mu(I)&=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\frac{e^{S_{m_i}g(y_i')}}{e^{S_{m_i}f(x_i')}} \times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}\\ &\leq\lvert I_{n_{i-1}+k_{i-1}}(\Gamma_{i-1})\times I_{n_{i-1}+k_{i-1}}(\Upsilon_{i-1})\rvert^{s/(1+\epsilon)} ((\,\beta^{-m_i}e^{-S_{m_i}f(x_i')})^{1+\epsilon})^{s/(1+\epsilon)}\\ &\leq \lvert I\rvert^{s/(1+\epsilon)}\\ &=(\,\beta^{-n_i-k_i})^{s/(1+\epsilon)}\\ &\asymp(\,\beta^{-m_i-k_i})^{s/(1+\epsilon)}. \end{align*} $$
So, for a rectangle
in
![]() $\mathcal {F}_i,$
we have that
$\mathcal {F}_i,$
we have that
 $$ \begin{align*} \mu(J)&=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}\\ &\leq (\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}(\,\beta^{-m_i}\beta^{-l_i})^{s_i}\\ &\leq(\,\beta^{-n_{i}-l_{i}})^{s/(1+\epsilon)}. \end{align*} $$
$$ \begin{align*} \mu(J)&=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times\bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^{s_i}\\ &\leq (\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}(\,\beta^{-m_i}\beta^{-l_i})^{s_i}\\ &\leq(\,\beta^{-n_{i}-l_{i}})^{s/(1+\epsilon)}. \end{align*} $$
For any
![]() $(x,y)\in \mathcal {F}_\infty ,$
we estimate the measure of
$(x,y)\in \mathcal {F}_\infty ,$
we estimate the measure of
![]() $I_n(x)\times I_n(y)$
compared with its length
$I_n(x)\times I_n(y)$
compared with its length
![]() $\beta ^{-n}.$
By the construction of
$\beta ^{-n}.$
By the construction of
![]() $\mathcal {F}_\infty ,$
there exists
$\mathcal {F}_\infty ,$
there exists
![]() $\{k_i,l_i\}_{i\geq 1}$
such that for all
$\{k_i,l_i\}_{i\geq 1}$
such that for all
![]() $i\geq 1,$
$i\geq 1,$
For any
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $i\geq 1$
be the integer such that
$i\geq 1$
be the integer such that
Step I:
![]() $n_{i-1}+k_{i-1}+m_i+l_i\leq n \leq n_{i}+k_{i}=n_{i-1}+k_{i-1}+m_i+k_i.$
$n_{i-1}+k_{i-1}+m_i+l_i\leq n \leq n_{i}+k_{i}=n_{i-1}+k_{i-1}+m_i+k_i.$
In this case, the cylinder can intersect only one rectangle in
![]() $\mathcal {F}_i,$
so
$\mathcal {F}_i,$
so
 $$ \begin{align*} \mu(I_n(x)\times I_n(y)) &=\mu(I_{{n_{i}+k_{i}}}(\Gamma_{i-1},U_i,K_i)\times I_{{n_{i}+k_{i}}}(\Upsilon_{i-1},W_i,L_i))\\ &\leq(\,\beta^{-n_{i}-l_{i}})^{s/(1+\epsilon)} \\ &\leq (\,\beta^{-n})^{s/(1+\epsilon)}. \end{align*} $$
$$ \begin{align*} \mu(I_n(x)\times I_n(y)) &=\mu(I_{{n_{i}+k_{i}}}(\Gamma_{i-1},U_i,K_i)\times I_{{n_{i}+k_{i}}}(\Upsilon_{i-1},W_i,L_i))\\ &\leq(\,\beta^{-n_{i}-l_{i}})^{s/(1+\epsilon)} \\ &\leq (\,\beta^{-n})^{s/(1+\epsilon)}. \end{align*} $$
Step II:
![]() $n_{i-1}+k_{i-1}+m_i\leq n \leq n_{i}+l_{i}=n_{i-1}+k_{i-1}+m_i+l_i.$
$n_{i-1}+k_{i-1}+m_i\leq n \leq n_{i}+l_{i}=n_{i-1}+k_{i-1}+m_i+l_i.$
Now the cylinder
![]() $I_n(x)\times I_n(y)$
contains
$I_n(x)\times I_n(y)$
contains
![]() $\beta ^{n_{i}+l_{i}-n}$
cylinders in
$\beta ^{n_{i}+l_{i}-n}$
cylinders in
![]() $\mathcal {F}_i$
with order
$\mathcal {F}_i$
with order
![]() $n_{i}+l_{i}$
. Note that by the definition of
$n_{i}+l_{i}$
. Note that by the definition of
![]() $\{k_j,l_j\}_{1\leq j\leq i}$
, the first i pairs
$\{k_j,l_j\}_{1\leq j\leq i}$
, the first i pairs
![]() $\{k_j,l_j\}_{1\leq j\leq i}$
depend only on the first
$\{k_j,l_j\}_{1\leq j\leq i}$
depend only on the first
![]() $n_i$
digits of
$n_i$
digits of
![]() $(x,y)$
. So the measures of the subcylinders of order
$(x,y)$
. So the measures of the subcylinders of order
![]() $n_{i}+k_{i}$
are the same. So, the measure of
$n_{i}+k_{i}$
are the same. So, the measure of
![]() $I_n(x)\times I_n(y)$
can be estimated as
$I_n(x)\times I_n(y)$
can be estimated as
 $$ \begin{align*} \mu(I_n(x)\times I_n(y)) &=\mu(I_{{n_{i}+k_{i}}}(\Gamma_{i-1},U_i,K_i)\times I_{{n_{i}+k_{i}}}(\Upsilon_{i-1},W_i,L_i))\times \frac{1}{\beta^{n-n_{i}-l_{i}}}\\[-2pt] &\leq (\,\beta^{-n_{i}-l_{i}})^{s/(1+\epsilon)}\times \frac{1}{\beta^{n-n_{i}-l_{i}}} \\[-3pt] &\leq(\,\beta^{-n})^{s/(1+\epsilon)}. \end{align*} $$
$$ \begin{align*} \mu(I_n(x)\times I_n(y)) &=\mu(I_{{n_{i}+k_{i}}}(\Gamma_{i-1},U_i,K_i)\times I_{{n_{i}+k_{i}}}(\Upsilon_{i-1},W_i,L_i))\times \frac{1}{\beta^{n-n_{i}-l_{i}}}\\[-2pt] &\leq (\,\beta^{-n_{i}-l_{i}})^{s/(1+\epsilon)}\times \frac{1}{\beta^{n-n_{i}-l_{i}}} \\[-3pt] &\leq(\,\beta^{-n})^{s/(1+\epsilon)}. \end{align*} $$
Step III:
![]() $n_{i-1}+k_{i-1}\leq n \leq n_{i-1}+k_{i-1}+m_i.$
$n_{i-1}+k_{i-1}\leq n \leq n_{i-1}+k_{i-1}+m_i.$
Assume
![]() $U_i=(\epsilon _1,\epsilon _2,\ldots ,\epsilon _{m_i}), W_i=(\omega _1,\omega _2,\ldots ,\omega _{m_i}).$
Write
$U_i=(\epsilon _1,\epsilon _2,\ldots ,\epsilon _{m_i}), W_i=(\omega _1,\omega _2,\ldots ,\omega _{m_i}).$
Write
![]() $l=n-(n_{i-1}+k_{i-1})$
and
$l=n-(n_{i-1}+k_{i-1})$
and
![]() $h=m_i-l$
. Then
$h=m_i-l$
. Then
 $$ \begin{align*} &\mu(I_n(x)\times I_n(y))\\[-1pt] &\quad=\sum\limits_{\substack{ (\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\[-1pt] (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}} \mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i) \times I_{n_i+l_i}(\Upsilon_{i-1},W_i,L_i))\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}} (\,\beta^{-m_i}e^{-S_{m_i}g(y_i')})^{s_i}. \end{align*} $$
$$ \begin{align*} &\mu(I_n(x)\times I_n(y))\\[-1pt] &\quad=\sum\limits_{\substack{ (\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\[-1pt] (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}} \mu(I_{n_i+k_i}(\Gamma_{i-1},U_i,K_i) \times I_{n_i+l_i}(\Upsilon_{i-1},W_i,L_i))\\ &\quad=\mu(I_{{n_{i-1}+k_{i-1}}}(\Gamma_{i-1})\times I_{{n_{i-1}+k_{i-1}}}(\Upsilon_{i-1}))\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}} (\,\beta^{-m_i}e^{-S_{m_i}g(y_i')})^{s_i}. \end{align*} $$
Then by the estimate of the measure of cylinders of order
![]() $n_{i-1}+k_{i-1}$
and letting
$n_{i-1}+k_{i-1}$
and letting
 $\widetilde {y_i'}=T_\beta ^ly_i'$
, we get
$\widetilde {y_i'}=T_\beta ^ly_i'$
, we get
 $$ \begin{align*} &\mu(I_n(x)\times I_n(y))\\[-1pt] &\quad\leq(\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}\cdot(\,\beta^{-l}e^{-S_{l}g(y_i')})^{s_i}\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\[-1pt] (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}}(\,\beta^{-h}e^{-S_{h}g(\widetilde{y_i'})})^{s_i}\\ &\quad\leq(\,\beta^{-n})^{s/(1+\epsilon)}\cdot\sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}} (\,\beta^{-h}e^{-S_{h}g(\widetilde{y_i'})})^{s_i}. \end{align*} $$
$$ \begin{align*} &\mu(I_n(x)\times I_n(y))\\[-1pt] &\quad\leq(\,\beta^{-n_{i-1}-k_{i-1}})^{s/(1+\epsilon)}\cdot(\,\beta^{-l}e^{-S_{l}g(y_i')})^{s_i}\times \sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\[-1pt] (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}}(\,\beta^{-h}e^{-S_{h}g(\widetilde{y_i'})})^{s_i}\\ &\quad\leq(\,\beta^{-n})^{s/(1+\epsilon)}\cdot\sum\limits_{\substack{(\epsilon_{l+1},\ldots,\epsilon_{m_i})\in \Sigma_\beta^l\\ (\omega_{l+1},\ldots,\omega_{m_i})\in \Sigma_\beta^h}} (\,\beta^{-h}e^{-S_{h}g(\widetilde{y_i'})})^{s_i}. \end{align*} $$
Recall the definition of
![]() $s_i$
:
$s_i$
:
 $$ \begin{align*}\sum\limits_{U,W\in \Sigma_{\beta_N}^{m_i}} \bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^s=1.\end{align*} $$
$$ \begin{align*}\sum\limits_{U,W\in \Sigma_{\beta_N}^{m_i}} \bigg(\frac{1}{\beta^{m_i}e^{S_{m_i}g(y_i')}}\bigg)^s=1.\end{align*} $$
Then
 $$ \begin{align*} 1=\sum\limits_{U_1,W_1\in \Sigma_{\beta_N}^{l}} \bigg(\frac{1}{\beta^le^{S_lg(y_1')}}\bigg)^{s_i}\cdot \sum\limits_{U_2,W_2\in \Sigma_{\beta_N}^{h}} \bigg(\frac{1}{\beta^le^{S_hg(\widetilde{y_1'})}}\bigg)^{s_i}, \end{align*} $$
$$ \begin{align*} 1=\sum\limits_{U_1,W_1\in \Sigma_{\beta_N}^{l}} \bigg(\frac{1}{\beta^le^{S_lg(y_1')}}\bigg)^{s_i}\cdot \sum\limits_{U_2,W_2\in \Sigma_{\beta_N}^{h}} \bigg(\frac{1}{\beta^le^{S_hg(\widetilde{y_1'})}}\bigg)^{s_i}, \end{align*} $$
where
 $y_1^{\prime *}\in I_{l}(U_1),\widetilde {y_1'}\in I_{h}(W_2).$
$y_1^{\prime *}\in I_{l}(U_1),\widetilde {y_1'}\in I_{h}(W_2).$
So, with a similar argument to the previous section, we have that
 $$ \begin{align*}\sum\limits_{U_2,W_2\in \Sigma_{\beta_N}^{l} } \bigg(\frac{1}{\beta^he^{S_hg(\widetilde{y_h'})}}\bigg)^{s_i}\leq\beta^{l\epsilon}.\end{align*} $$
$$ \begin{align*}\sum\limits_{U_2,W_2\in \Sigma_{\beta_N}^{l} } \bigg(\frac{1}{\beta^he^{S_hg(\widetilde{y_h'})}}\bigg)^{s_i}\leq\beta^{l\epsilon}.\end{align*} $$
Therefore,
Notice that a general ball
![]() $B(x,r)$
with
$B(x,r)$
with
![]() $\beta ^{-n-1}\leq r<\beta ^{-n}$
can intersect at most three cylinders of order n. Therefore, the measure of the general ball can be estimated as
$\beta ^{-n-1}\leq r<\beta ^{-n}$
can intersect at most three cylinders of order n. Therefore, the measure of the general ball can be estimated as
So, finally, by using the mass distribution principle we have the lower bound of the Hausdorff dimension of this case,
 $$ \begin{align*}\dim_{\mathrm H} \overline{E}(T_\beta, f,g)\geq s_0.\end{align*} $$
$$ \begin{align*}\dim_{\mathrm H} \overline{E}(T_\beta, f,g)\geq s_0.\end{align*} $$
Hence, combining both cases, we have the desired conclusion.
Acknowledgments
We thank Professor Baowei Wang for useful discussions on this project. Special thanks are due to the referee and the associate editor for raising some pertinent questions, and for their suggestions that have improved the clarity and exposition of this article.