1. Introduction
A decrease followed by an increase in the age of marriage was observed in the twentieth century in all advanced economies. This stylized fact is intriguing because of the non-monotonic relationship between age of marriage and economic growth. Today, a high level of economic development is associated with late marriage, but for most of the twentieth century the opposite was true: economic growth was associated with early marriage. Studies published around the middle of the century document the trend toward an earlier marriage. For example, Newcomb (Reference Newcomb1937) writes with respect to the United States that
“Today the prospect of marriage and children is popular again; 60 percent of the girls and 50 percent of the men would like to marry within a year or two of graduation… boys and girls tend to take it for granted that they will be married, as they did not a decade ago.”
Almost 35 years later, Dixon (Reference Dixon1971) writes that
“The trend away from the ‘European’ pattern is most obvious in the wealthier nations of the West, especially in the English-speaking nations overseas and in England, France, Belgium and parts of Scandinavia. These are also countries with increasingly assertive and independent youth who are taking advantage of the opportunities to marry young that the wealthy and secure economies provide.”
The decades that followed have shown that the downward trend in the age of marriage was temporary. The age at first marriage has climbed sharply since the 1960s in the United States and advanced parts of Europe and since the 1970s and 1980s also in Southern Europe and Ireland. This upward trend reached the former Communist Eastern European countries in the 1990s.
This paper contributes by compilation of data on age at first marriage from 160 countries, which is a broad extension to the data from 16 countries, presented in Moro et al. (Reference Moro, Moslehi and Tanaka2017). The second contribution is to the literature on the relationship between age of marriage and economic development. Few economists have addressed the U-shaped dynamics so far. Moro et al. (Reference Moro, Moslehi and Tanaka2017) relate the marriage age U-shape in 16 developed countries to economic structure, and Iyigun and Lafortune (Reference Iyigun and Lafortune2016) relate the American dynamics to the spousal education gap.Footnote 1 In the present paper, I compare Western and non-Western countries and find that Western countries have experienced a much sharper U-shape (in both decreasing and increasing portions) than the non-Western ones. Moreover, in some non-Western regions, in particular in Eastern Europe, no decreasing portion is observed and the increase only starts in the 1990s. In addition, in post-World War II (WWII) West, age of marriage follows the same dynamics for men as for women and is correlated across countries. Earlier, the cross-country correlation was not the same strong. For example, age of marriage in the nineteenth century in the United States, England, and France plot three dissimilar time series. To summarize the link between age of marriage and postwar economy, I show that age of marriage has a U-shaped relationship with GDP per capita, clean of year and country fixed effects.
I propose a simple partial equilibrium model of the U-shaped dynamics.Footnote 2 The model's intuition is related to the literature that spans Galor and Well (Reference Galor and Weil1996) to Rendall (Reference Rendall2017) and is an expanded version of the Becker hypothesis of the return to marriage. It relies on search frictions to explain the increasing male marriageability following a male labor-biased industrial boom. The improved male marriageability leads to a decrease in age of marriage of both genders. In the long run, this effect is gradually overtaken by the opposite effect of increased married women's labor force participation when the economy shifts from brawn-based to gender-neutral technology. The idea is that the marriage strategy of women who plan to work after marriage is different from that of future housewives. The skills of a woman who plans to work after marriage matter and she is more likely to remain single until she is matched with a man of a similar level of skills. Essentially, the model posits that men experience an increase in productivity before women, and that the resulting rise in incomes leads to earlier marriage, but that eventually women's productivity sufficiently rises to the extent that assortative mating (on potential output) increases, thereby raising the incentive to delay marriage and reversing the trend in marriage age.
I provide empirical evidence from the United States in support of the model's prediction. For identification, I weight the labor productivity in each industry by each state's initial economic structure. I assume that the productivity growth, common to all of the United States, is exogenous to state-specific initial conditions. I apply the weighted productivity in the “male” sector to the Current Population Survey (CPS) data, and show the robust negative effect of male productivity on propensity of singlehood at young age of men and women. CPS data have been collected since 1962, during decades when age of marriage has been increased in the United States. Nevertheless, I document a negative effect of male productivity on age of marriage.
The difference between the Western European marriage pattern (EMP) and that of the rest of the world can be traced back to the Black Death [Hajnal (Reference Hajnal2017)]. To explain this difference, the literature has increasingly focused on the link between the EMP and female labor markets [De Moor and Van Zanden (Reference De Moor and Van Zanden2010); Díez Minguela (Reference Díez Minguela2011); Voigtländer and Voth (Reference Voigtländer and Voth2013)]. The EMP depicts a pattern of late marriage (25 years and older in pre-industrial Europe), a small spousal age gap, and a high proportion of never-married women.
Early urbanization decreased age of marriage as marriage markets became larger and the dependence of marriage on land ownership diminished [Dixon (Reference Dixon1971, Reference Dixon1978); Oppenheimer (Reference Oppenheimer1988)]. The strongest factor contributing to the independence between marriage and fertility was improving birth control technology and especially the introduction of the Pill in the 1960s. Although in the EMP, lack of efficient birth control technology was a reason for late marriage, in the late twentieth century improved birth control technology allowed late marriage. The Pill explains some 30% of the increase in the singlehood rates of young American women [Goldin and Katz (Reference Goldin and Katz2002)]. The reason that women preferred postponing marriage was increasing opportunities for female education and careers [Goldin (Reference Goldin1990, Reference Goldin2006)].
Economic shocks affect marriage rates, and Wilson (Reference Wilson2012) raises the issue of marriageability of low-income American men. Correspondingly, Autor et al. (Reference Autor, Dorn and Hanson2019) analyze the impact of negative shocks to American low-income males as a result of increasing competition with Chinese imports. They testify to the positive effect of these shocks to the share of single-parent households among the low-educated because of the lower marriageability of the low-educated men affected by the shocks. Moro et al. (Reference Moro, Moslehi and Tanaka2017) show that the fraction of married individuals is positively correlated with the share of manufacturing in the GDP. Schaller (Reference Schaller2016) finds that improvements in male labor market conditions are associated with increased fertility, while improvements in female labor market conditions have smaller negative effects. Blau et al. (Reference Blau, Kahn and Waldfogel2000) find an opposite-sign relationship between male and female labor market conditions and the share of married young women. Finally, Iyigun and Lafortune (Reference Iyigun and Lafortune2016) study the American marriage age U-shape in a model where age of marriage is endogenously associated with a spousal educational gap. To obtain this result, they assume that spouses cannot study simultaneously. In the empirical part of the paper, they show that the spousal educational gap is negatively related to exogenous variation in the marriage timing instrumented by minimum marriage age laws. My simple model differs from Iyigun and Lafortune (Reference Iyigun and Lafortune2016) in relying on a single force to explain both the decreasing and increasing age at first marriage. This simplicity could be achieved due to a realistic incorporation of search frictions in the marriage market model.Footnote 3
The remaining of the paper proceeds as follows. Section 2 discusses the marriage age dynamics in 160 countries and addresses the differences between Western and other countries. Section 3 shows the strict relationship between the U-shaped dynamics and GDP per capita. Section 4 frames the U-shaped dynamics in a broad context of 200 years of nuptiality history in Western countries to show that the twentieth century is different from the earlier period in terms of correlation between countries and genders. In section 5, I propose a simple model that may explain the U-shaped dynamics in a context of industrialization that affects men first and women later. Section 6 uses CPS data to provide supportive evidence for the model. Section 7 concludes.
2. Stylized facts
Tables 1 and 2 report the mean age at first marriage, averaged over countries within the same region, for the years 1950 to 2004. The raw data appear in Appendix A and the details of its compilation are provided in Appendix B. Averaging over groups of countries allows to summarize the data but also solves the problem of gaps in data at a country level. The average is unweighted, and, thus, is not dominated by large countries. The number of countries in each group is reported in parentheses.
Table 1. Mean age at first marriage, 1950–2004, men

Note: The table reports unweighted average age at first marriage of men. The raw data are found in Appendix A. The number of countries is reported in parentheses.
Table 2. Mean age at first marriage, 1950–2004, women

Note: The table reports unweighted average age at first marriage of women. The raw data are found in Appendix A. The number of countries is reported in parentheses.
Summarizing the table, the mean age of marriage decreased in Northern and Central Europe and in Western OffshootsFootnote 4 by half a year every decade between 1950 and 1970 and has increased by 1 year every decade since then. The decrease in Southern Europe, Ireland, and Latin America started in the late 1950s and early 1960s and lasted until the late 1970s and early 1980s. In Eastern Europe there was almost no decrease at all and the sharp increase is observed only since the 1990s. It is difficult to draw any conclusions on the trend in Asia and Africa in the first years of the sample because of the small number of countries. For the later years, the sample of Asian and African countries is larger and the trend in age of marriage is upward but the slope is not as sharp as in Europe and the Americas.Footnote 5
Figure 1 summarizes the findings by classifying all countries into two groups: Western countries, which include Central and Northern Europe and Western Offshoots, and other countries. The figure leads to three insights. First, the mean age of marriage changes faster in the West than in other parts of the world. This is true for both the decreasing and increasing portions of the U-shape. Second, in the West, age of marriage of men and women is much more strongly correlated than in the rest of the regions. Third, age of marriage of Western women has always been above that of non-Western women, except for the bottom point in the 1960s. For men, the picture is different. Men married older in non-Western countries than in Western ones until the 1970s, but the opposite has been true ever since then.

Figure 1. Mean age at first marriage.
Note: The figure presents the mean age at first marriage, averaged over countries. Data correspond to Tables 1 and 2. See Appendix A for raw data and Appendix B for details of its compilation. Western countries include Central and Northern Europe and Western Offshoots (United States, Canada, Australia, and New Zealand).
The post-WWII U-shape can be summarized by the following statistics. The unweighted cross-country mean age of marriage of Western women decreased from 23.8 to 22.5 between 1950 and 1965 while that of men decreased from 25.9 to 24.7. Age of marriage increased between 1965 and 2000 to 28.3 for women and 30.1 for men. In non-Western countries age of marriage of women decreased between 1950 and 1965 from 23.3 to 22.6, and increased between 1970 and 2000 to 25.6. For non-Western men, the decrease lasted until 1970 and constituted a drop from 26.3 to 25.3. It was followed by a rise to 27.8 until 2000.
Figure 2 shows the post-WWII mean age at first marriage in Western countries, divided into groups of related or similar countries: Northern Europe, Central Europe, Southern Europe and Ireland, and Western Offshoots. The figure plots different levels of age of marriage and different timing of the U-shape across the West. Western Offshoots had the earliest U-shape, and the turn from the decreasing to the increasing trend took place in the 1960s. By contrast, Southern Europe and Ireland only started to experience the decrease around that time. Western Offshoots had the lowest age of marriage until the 1980s, while age of marriage in Southern Europe and Ireland was the highest. However, after the sharp increase in Western Offshoots between 1960s and 1980s, age of marriage in this group of countries has been higher than in Southern Europe. Northern and Central Europe are close to each other. Similarly to Western Offshoots, Northern and Central Europe turned in the 1960s from decreasing to increasing age of marriage, but they have always had a higher level of age of marriage than Western Offshoots.
3. Relation to economic development
In this section, I provide evidence that the post-WWII marriage age U-shape in Western countries mirrors the post-war converging path of these economies. Figures 3 and 4 show the relationship between age at first marriage and GDP per capita for women and men, respectively.Footnote 6 The figures distinguish between Western and other countries, similarly to how it is done in Figure 1. The marriage age U-shape as a function of GDP is much clearer in Western than in other countries. The insight is that the U-shape is a reflection of the development path specific to the post-WWII West. Age of marriage sharply decreases with the industrial boom, and the turnaround from decrease to increase is associated with the later stage of economic development. Western countries vary in the timing of the development path. Correspondingly, they vary in the timing of the marriage age U-shape. For example, at the time that age of marriage in Southern Europe and Ireland started to decrease and the economy to boom, age of marriage in other parts of the Western world already started to increase. This makes the post-WWII decades a special event in economic and demographic history, where one observes a common growth pattern associated with common U-shaped dynamics of age of marriage.

Figure 3. Age at first marriage and GDP per capita, women.
Note: The figure presents the age at first marriage and log of real GDP per capita. GDP is taken from Maddison (Reference Maddison, van Ark and Crafts1996). Age of marriage corresponds to Tables 1 and 2. The lines are predicted values from a nonparametric kernel regression. See Appendix A for raw data and Appendix B for details of its compilation.

Figure 4. Age at first marriage and GDP per capita, men.
Note: The figure presents the age at first marriage and log of real GDP per capita. GDP is taken from Maddison (Reference Maddison, van Ark and Crafts1996). Age of marriage corresponds to Tables 1 and 2. The lines are predicted values from a nonparametric kernel regression. See Appendix A for raw data and Appendix B for details of its compilation.
Another perspective on the relationship between age of marriage in the West and post-WWII economic development is illustrated in Figures 5 and 6. These figures show the relationship between overall economic growth and overall change in the age of marriage during the 1960s–1990s period for men and women, respectively. The horizontal axis is the economic growth during the 30 years between 1960–1964 and 1990–1994, and the vertical axis is the corresponding change in the age of marriage (the difference is between the average of the 1990–1994 period and the average of the 1960–1964 period). The figures distinguish between the 15 original European Union countries, other Western countries, and non-Western countries. Across the old European Union, the correlation between overall change in the mean age at first marriage and overall change in the logged per capita GDP during this period is $-0.9$![]() for both genders. Other Western countries are also located on the same decreasing slope. Nordic countries and the United States are located at the top-left corner of the graph: between the 1960s and the 1990s, age of marriage in these countries rose sharply, but the economic growth was more moderate than in Southern Europe, located at the bottom-left corner.
for both genders. Other Western countries are also located on the same decreasing slope. Nordic countries and the United States are located at the top-left corner of the graph: between the 1960s and the 1990s, age of marriage in these countries rose sharply, but the economic growth was more moderate than in Southern Europe, located at the bottom-left corner.

Figure 5. Change in the age of marriage and economic growth between early 1960s and early 1990s, women.
Note: The figure presents the change in the age at first marriage, averaged over regions (each country in a region is one observation). The change is between the average over 1960–1964 period and the average over 1990–1994 period. GDP is taken from Maddison (Reference Maddison, van Ark and Crafts1996), and logged after averaging. Age of marriage corresponds to Tables 1 and 2. See Appendix A for raw data and Appendix B for details of its compilation.
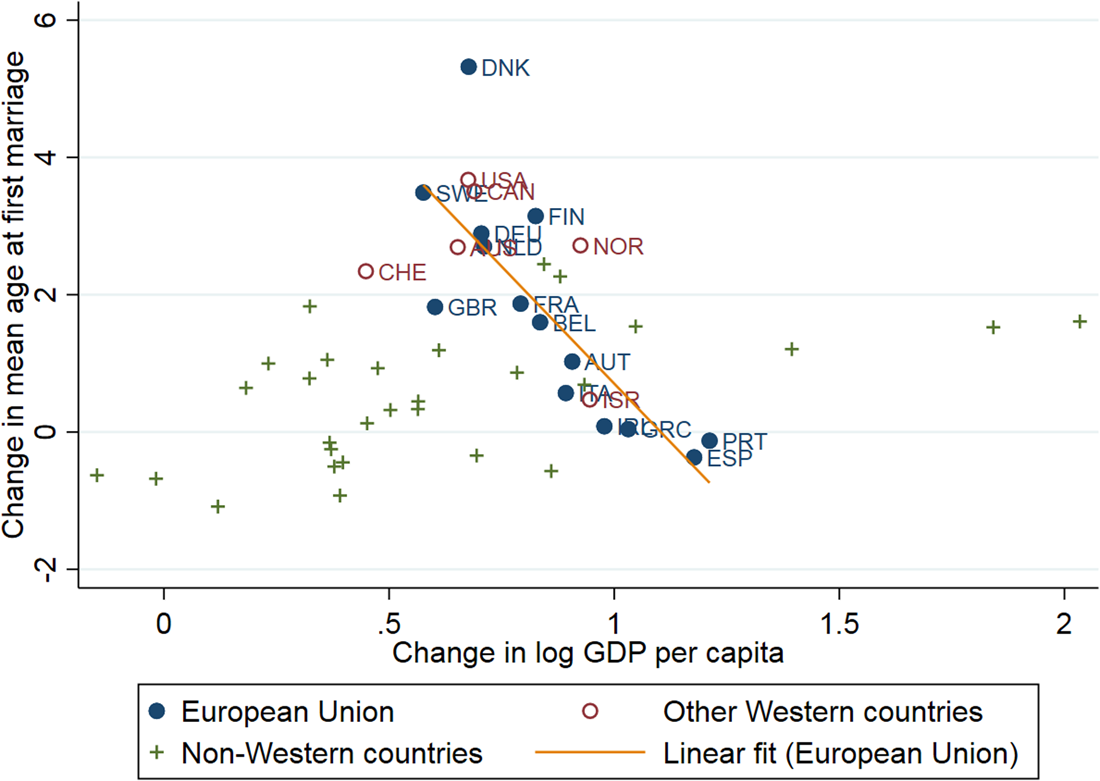
Figure 6. Change in the age of marriage and economic growth between early 1960s and early 1990s, men.
Note: The figure presents the change in the age at first marriage, averaged over regions (each country in a region is one observation). The change is between the average over 1960–1964 period and the average over 1990–1994 period. GDP is taken from Maddison (Reference Maddison, van Ark and Crafts1996), and logged after averaging. Age of marriage corresponds to Tables 1 and 2. See Appendix A for raw data and Appendix B for details of its compilation.
This almost-perfect negative correlation among Western but not other countries shows that the marriage age U-shape is a mirror reflection of the economic convergence path across Western countries. In other words, the fast economic growth during the industrial boom is associated with declining age of marriage, but as growth slows down age of marriage starts to rise. Although the former fast stage is related to the rising productivity in male labor-dominated sectors, the latter slow stage is related to tertiarization of the economy, associated with rising female labor force participation. In the United States, Northern and Central Europe the U-shape started either between the world wars or with the implementation of the Marshall Plan, and in Southern Europe and Ireland it started with the modernization of the economies in the 1960s. For example, in Spain, age of marriage started to decrease in 1962, at precisely the time the Stabilization Plan started to be implemented. Around the same time, the age of marriage in Nordic countries and the United States already turned from the decreasing to the increasing trend.
Some countries are missing from Figures 5 and 6, because of gaps in the marriage age data for the specific years considered in the figures. For a more complete cross-country picture of the relationship between the change in age of marriage and economic growth, I include in Appendix C the corresponding Figures C1 and C2, where countries are grouped into regions. The figures show a clear negative correlation between economic growth over the 1960s–1990s period and the change in age of marriage. Again, some non-Western regions are not located on the negative slope.
Evidence in Figures 5, 6, C1, and C2 is about the timing of the U-shape. It comes first in Northern Europe and Western Offshoots and later in Southern Europe and Ireland. As a result, comparison between 1960s and 1990s shows a strong negative correlation between change in age of marriage and change in GDP per capita: countries that grew the most during this period of time (Southern Europe and Ireland) have the smallest overall change in the age of marriage because of the U-shape phenomenon.
To make sure that the U-shaped relationship between age of marriage and GDP, observed in Figures 3 and 4, is not driven by country or year confounders, I estimate a two-way fixed effect model, where I regress the mean age at first marriage on the log of GDP per capita and its squared term:
where $MA^{g}_{it}$![]() is the mean age at first marriage of gender $g$
is the mean age at first marriage of gender $g$![]() in country $i$
in country $i$![]() in year $t$
in year $t$![]() . GDP is in real per capita terms and adopted from the Penn World Table [Feenstra et al. (Reference Feenstra, Inklaar and Timmer2015)], which reports GDP from 1950 on. Country and year fixed effects are, respectively, $\mu _i$
. GDP is in real per capita terms and adopted from the Penn World Table [Feenstra et al. (Reference Feenstra, Inklaar and Timmer2015)], which reports GDP from 1950 on. Country and year fixed effects are, respectively, $\mu _i$![]() and $\gamma _t$
and $\gamma _t$![]() . Standard errors are clustered by country.
. Standard errors are clustered by country.
The results are presented in Table 3. Columns 1 and 2 show the estimation results of equation (1), for men and women, respectively. The quadratic form is statistically significant and follows the U-shaped form. All predicted values are located within the positive quadrant: the predicted age at first marriage is between 24.6 and 30.4 for men and between 21.9 and 27.7 for women. The coefficients of the quadratic equation are different for men and for women. In particular, men experience a sharper change in age of marriage as a function of GDP. However, the GDP level when the U-shape is at its bottom point is similar for both genders: 9.1 log points for men and 9.2 log points for women. These findings explain the heterogeneity in the timing of the U-shape across different Western countries but also similarity across genders. In particular, they provide an economic interpretation of the differences between Western Offshoots, Northern, Central, and Southern Europe, observed in Figure 2.
Table 3. Age at first marriage and GDP per capita

Note: The table presents results of fixed-effects regressions of equation (1). Standard errors are clustered by country. $^{\ast }p< 0.1$![]() , $^{\ast \ast }p< 0.05$
, $^{\ast \ast }p< 0.05$![]() , $^{\ast \ast \ast }p< 0.01$
, $^{\ast \ast \ast }p< 0.01$![]() .
.
4. The U-shape as a special event
A zoom out to a broader historical perspective reveals that the post-WWII marriage age U-shape is a special event in the post-Malthusian history. The uniqueness of the post-WWII marriage age U-shape consists in the strong correlation between Western countries, the correlation between genders, and the strong correlation between the U-shape and the economic development path. By contrast, before WWII the trends in the marriage age in different Western countries were not synchronized. For instance, due to Wrigley et al. (Reference Wrigley, Davies, Schofield and Oeppen1997) and other sources, we can follow the mean age of marriage in England since 1600. Age of marriage decreased for men starting in the late seventeenth century and for women starting in 1700. It started to increase in the early nineteenth century and continued to increase slowly (with a short disturbance) until World War I (WWI). However, it decreased by about 2 years between WWI and 1970 and from then to the turn of the twenty-first century it steeply rose by about 5 years.
Wrigley et al. (Reference Wrigley, Davies, Schofield and Oeppen1997) find that the source of the long-term decrease in age of marriage was driven by the manufacturing-biased parishes of England as early as in the eighteenth century. Furthermore, Grebenik et al. (Reference Grebenik, Rowntree, Carrier, Colombo, Martin and Roberts1963) compare British data from the 1880s to data collected around 1960. They find that in the 1880s, male miners married at age 24, artisans and laborers at 25.5, farmers at 29, and professional men at 31. Age of marriage of men and women in England decreased after WWI and continued to decrease after WWII. However, for couples where the groom was a high-skilled worker (either manual or non-manual) age of marriage decreased by 1 year more than for couples where the groom was a low-skilled worker. This comparison between the 1880s and 1960 reveals the effect of improvement in the skills of English men on age of marriage.
The trend in other Western countries was not always similar to the one in England. Figure 7 presents time series for Western countries with data available since 1800. In Belgium, Denmark, and to a lesser degree France, age of marriage decreased during the nineteenth century. Belgium is a salient case of a steep fall in age of marriage from the extreme level of 30 in 1800. However, the same is not true for the United States, where age of marriage increased during almost all of the nineteenth century. In Germany age of marriage of women decreased starting in the 1930s but that of men decreased only after WWII. In Italy, age of marriage decreased only in the 1960s and 1970s. In contrast to age of marriage in France, England, and Belgium, age of marriage in Sweden increased from the middle of the eighteenth century until the 1930s when it started to decrease. Similarly, the age at first marriage in Switzerland decreased from the 1930s [Schoen and Baj (Reference Schoen and Baj1984)].

Figure 7. Mean age at first marriage since 1800 in Western countries.
Note: See Appendix B for details of data compilation
Three insights can be taken from these observations. First, before WWII different Western countries followed different trends in age of marriage. In particular, as discussed in Haines (Reference Haines1996), the relatively low age of marriage in the United States during colonial times is associated with the better economic capacity in the American colonies than in Europe. Second, age of marriage in some countries followed a long decreasing trend. This was the case in England in the eighteenth century and in France, Belgium, and Denmark in the nineteenth century. Finally, the starting point of the twentieth century U-shape varies across countries. In the United States the decrease starts around the Second Industrial Revolution. In Sweden, Switzerland, and England it starts after WWI. In Germany, Italy, and (not shown in the figure) Spain, Portugal, and Ireland it starts as late as the 1960s.
5. A model of the post-WWII U-shape
5.1. Outline
The proposed framework is a partial-equilibrium model, where economy has a single good but two technologies. One technology is male-only, while the other is gender-neutral. The main variables are labor force participation of married women and male income. The framework assumes search frictions. The key to the marriage age decrease is the reservation value in the marriage market. The idea is that women who plan to be housewives are homogeneous in terms of their productivity and offer the same home product. They participate in random search and hold a reservation value in terms of the mate's income. The reservation value decreases when male income rises, leading to a lower age of marriage. Women who work after marriage are different. Their market skills are heterogenous, and in the reasonable equilibrium they marry men of a similar level of skills. Their positive assortative matching takes longer than in random search. This reduced-form model skips mediating variables, such as educational attainment, demographic transition, and structural change, but is in line with stylized facts related to these variables.
5.2. Setup
5.2.1. Production
Consider an economy that uses labor to produce a single-market good. I assume existence of two technologies. Technology $A$![]() requires male physical ability, while technology $B$
requires male physical ability, while technology $B$![]() not.Footnote 7 Thus, women use technology $B$
not.Footnote 7 Thus, women use technology $B$![]() , while men use $max\{ A,\; B\}$
, while men use $max\{ A,\; B\}$![]() . For simplicity of notation, I assume that $A> B$
. For simplicity of notation, I assume that $A> B$![]() , so men use $A$
, so men use $A$![]() . Each individual is endowed with observed ability $\phi$
. Each individual is endowed with observed ability $\phi$![]() , distributed in the population with a cumulative distribution function $F( \phi )$
, distributed in the population with a cumulative distribution function $F( \phi )$![]() . Wages are $A\phi$
. Wages are $A\phi$![]() and $B \, \phi$
and $B \, \phi$![]() , for workers who use technologies $A$
, for workers who use technologies $A$![]() and $B$
and $B$![]() , respectively.
, respectively.
Women can produce home product instead of labor force participation.Footnote 8 The value of home product does not depend on ability and is worth one unit of the market product. The assumption that home product is constant does not contradict home productivity growth. Introduction of appliances makes housework faster and easier and gives housewives more time for leisure [Aguiar and Hurst (Reference Aguiar and Hurst2007)],Footnote 9 but the volume of meals to be cooked, space to be cleaned, and clothes to be washed remains unchanged.
5.2.2. Preferences
“It is not good that the man should be alone” (Genesis 2:18), and the utility of singles is zero. Married couples consume their income as a public good. The expected life-time consumption of a just-married couple, where the man has ability $x$![]() and the woman has ability $y$
and the woman has ability $y$![]() , is
, is
where $I\in \{ 0,\; 1\}$![]() indicates the wife's labor force participation extensive margin. The term $1-I$
indicates the wife's labor force participation extensive margin. The term $1-I$![]() indicates that if she does not work in the market, she produces one unit of home product. The age of marriage does not affect lifetime consumption. Individual preferences are given by a concave function $u( c)$
indicates that if she does not work in the market, she produces one unit of home product. The age of marriage does not affect lifetime consumption. Individual preferences are given by a concave function $u( c)$![]() . Let us denote
. Let us denote
5.2.3. Labor force participation
Similarly to Greenwood et al. (Reference Greenwood, Seshadri and Yorukoglu2005), all men and single women work in the market. A married woman chooses to work only if her market product is above home product, i.e., if $By> 1$![]() . Let $z = F( {1}/{B})$
. Let $z = F( {1}/{B})$![]() indicates the rank of the lowest-ability woman who participates in the labor force after marriage. Let us call “above-$z$
indicates the rank of the lowest-ability woman who participates in the labor force after marriage. Let us call “above-$z$![]() ” and “below-$z$
” and “below-$z$![]() ” individuals ranked above or below $z$
” individuals ranked above or below $z$![]() in the ability distribution, respectively. That is, below-$z$
in the ability distribution, respectively. That is, below-$z$![]() women have ability $y< {1}/{B}$
women have ability $y< {1}/{B}$![]() . They do not work after marriage, and they are identical in the sense that they all offer their mates one unit of home production. The above-$z$
. They do not work after marriage, and they are identical in the sense that they all offer their mates one unit of home production. The above-$z$![]() women work after marriage, and their market ability is distributed $F( y\vert y> {1}/{B})$
women work after marriage, and their market ability is distributed $F( y\vert y> {1}/{B})$![]() .
.
5.2.4. Marriage market
Finite equal numbers of men and women enter the economy each period and participate in the marriage market for up to two periods.
5.2.4.1. First period
The first period can be intuitively titled “high school” period, when all men and women are single and gather together at school or in the neighborhood of residence. All men and women sort into random couples. The man can choose to propose marriage and the woman can accept or reject the offer.
5.2.4.2. Second period
The second period can be intuitively titled “college” or “work” period. In this period, individuals are exogenously sorted according to ability, because college and industry design interactions between individuals with similar level of skills. Therefore, with probability one, men meet women of the same level of ability, means $x = y$![]() , whenever the corresponding woman is single or above-$z$
, whenever the corresponding woman is single or above-$z$![]() married. A man can propose marriage if he and his female mate are single, and the woman can accept or reject the offer.
married. A man can propose marriage if he and his female mate are single, and the woman can accept or reject the offer.
5.3. Segregating equilibrium
There exists an economically intuitive marriage market equilibrium that segregates housewives and women who work after marriage. This equilibrium is characterized by the following strategies in the first period:
(a) Above-$z$
 men do not propose and above-$z$
men do not propose and above-$z$ women do not accept marriage, unless they are randomly matched such that $x = y$
women do not accept marriage, unless they are randomly matched such that $x = y$ .
.(b) Below-$z$
 men propose marriage.
men propose marriage.(c) Below-$z$
 women accept a marriage proposal if and only if they receive it from a man with $x$
women accept a marriage proposal if and only if they receive it from a man with $x$ above the reservation value. The reservation value $x^\ast ( y)$
above the reservation value. The reservation value $x^\ast ( y)$ of a woman with ability $y$
of a woman with ability $y$ satisfies the indifference condition:(4)$$u( x^{\ast }( y) ,\; y) = p( y) u( y,\; y) $$where $p( y)$
satisfies the indifference condition:(4)$$u( x^{\ast }( y) ,\; y) = p( y) u( y,\; y) $$where $p( y)$
 is the probability that the man of her ability, whom she meets in the second period, is still single.
is the probability that the man of her ability, whom she meets in the second period, is still single.
Proposition 1. Segregating equilibrium exists.
Proof. (a) Given that in the second period, above-$z$![]() men are matched with single women of the same ability, an above-$z$
men are matched with single women of the same ability, an above-$z$![]() man with ability $x$
man with ability $x$![]() would not propose in the first period to a woman with $y< x$
would not propose in the first period to a woman with $y< x$![]() . Similarly, an above-$z$
. Similarly, an above-$z$![]() woman with ability $y$
woman with ability $y$![]() would not accept an offer from a man with $x< y$
would not accept an offer from a man with $x< y$![]() . (b) All below-$z$
. (b) All below-$z$![]() women offer the same housework as wives and men are indifferent between them. Below-$z$
women offer the same housework as wives and men are indifferent between them. Below-$z$![]() men do not meet above-$z$
men do not meet above-$z$![]() women in the second period, and, thus, propose in the first period. (c) Condition (4) indicates indifference between acceptance and rejection of a proposal. For proposals from men with $x> x^\ast ( y)$
women in the second period, and, thus, propose in the first period. (c) Condition (4) indicates indifference between acceptance and rejection of a proposal. For proposals from men with $x> x^\ast ( y)$![]() , acceptance generates higher utility than the expected utility from rejection. □
, acceptance generates higher utility than the expected utility from rejection. □
5.4. Comparative statics
5.4.1. Decreasing portion of the U-shape
Let technology $A$![]() advance. In the segregating equilibrium, the reservation value decreases and more individuals marry in the first period:
advance. In the segregating equilibrium, the reservation value decreases and more individuals marry in the first period:
Proposition 2. In the segregating equilibrium, ${\delta x^\ast ( y) }/{\delta A}< 0$![]() for below-$z$
for below-$z$![]() women.
women.
Proof. Consider (4), where $x^\ast ( y)$![]() is the initial reservation value. Note that $y< x^\ast ( y)$
is the initial reservation value. Note that $y< x^\ast ( y)$![]() because $p( y) < 1$
because $p( y) < 1$![]() . Thus, because of concavity of $u( c)$
. Thus, because of concavity of $u( c)$![]() , when $A$
, when $A$![]() grows, $u( x^\ast ( y) ,\; y)$
grows, $u( x^\ast ( y) ,\; y)$![]() increases more than $u( y,\; y)$
increases more than $u( y,\; y)$![]() . Moreover, the reservation value of other women decreases in equilibrium, leading to a weakly lower $p( y)$
. Moreover, the reservation value of other women decreases in equilibrium, leading to a weakly lower $p( y)$![]() . In order (4) to hold, reservation value $x^\ast ( y)$
. In order (4) to hold, reservation value $x^\ast ( y)$![]() decreases. □
decreases. □
This equilibrium path is stable in the sense that deviation of any number of women does not change the result that the reservation value decreases for the remaining women, because the proof of Proposition 2 still holds for them. Any equilibrium in which the reservation value does not decrease would not satisfy this stability property, because such an equilibrium would contradict the economic forces implied by concavity of $u( c)$![]() . For instance, there exists another Nash equilibrium, where all women reject marriage in the first period only because other women do the same. However, this equilibrium does not have economic intuition and is not stable: if some women deviate and marry in the first period, women who otherwise expect to marry the deviants’ husbands in the second period would also deviate, marrying other men and leading to deviation of more women, and so forth. By contrast, the stability of the segregating equilibrium path, in which the reservation value decreases as $A$
. For instance, there exists another Nash equilibrium, where all women reject marriage in the first period only because other women do the same. However, this equilibrium does not have economic intuition and is not stable: if some women deviate and marry in the first period, women who otherwise expect to marry the deviants’ husbands in the second period would also deviate, marrying other men and leading to deviation of more women, and so forth. By contrast, the stability of the segregating equilibrium path, in which the reservation value decreases as $A$![]() grows, makes it a good fit to describe dynamics in the marriage market. Even if only some women decrease their reservation value, it would push other women to do the same and marry in the first period, because less men remain available for the second period. This process continues until the whole marriage market converges to a lower marriage age.
grows, makes it a good fit to describe dynamics in the marriage market. Even if only some women decrease their reservation value, it would push other women to do the same and marry in the first period, because less men remain available for the second period. This process continues until the whole marriage market converges to a lower marriage age.
5.4.2. Increasing portion of the U-shape
The eventual increase of the marriage age follows from the increased market productivity of women. When $B$![]() grows, the threshold ability level $z$
grows, the threshold ability level $z$![]() , which determines the married female labor force participation, decreases.
, which determines the married female labor force participation, decreases.
Therefore, when the above-$z$![]() marriage market segment grows as the economy experiences an increase in female market productivity, at some point the effect of its growth on the age of marriage dominates the effect of the decreasing reservation value in the below-$z$
marriage market segment grows as the economy experiences an increase in female market productivity, at some point the effect of its growth on the age of marriage dominates the effect of the decreasing reservation value in the below-$z$![]() segment. The resulting dynamics plot a marriage age U-shape over time if female labor force participation first grows slowly and later expands rapidly.Footnote 10 In other words, in order for the decreasing portion of the marriage age U-shape to exist, there must be a period of time when the effect of an increase in the productivity of low-ability men exceeds the effect of increasing female labor force participation.
segment. The resulting dynamics plot a marriage age U-shape over time if female labor force participation first grows slowly and later expands rapidly.Footnote 10 In other words, in order for the decreasing portion of the marriage age U-shape to exist, there must be a period of time when the effect of an increase in the productivity of low-ability men exceeds the effect of increasing female labor force participation.
In summary, the two forces that push age of marriage in opposite directions are the decreasing first-period below-$z$![]() women reservation value, as male technology advances, and increasing married female labor force participation as gender-neutral technology advances. Note that these two forces are independent of each other, because the reservation values depend on the utility function, while married female labor force participation depends on the $B$
women reservation value, as male technology advances, and increasing married female labor force participation as gender-neutral technology advances. Note that these two forces are independent of each other, because the reservation values depend on the utility function, while married female labor force participation depends on the $B$![]() -technology.
-technology.
5.5. Discussion
The segregating equilibrium is consistent with a bunch of stylized facts, first of which is the marriage age U-shape over the post-WWII decades. The second stylized fact is the rise of labor force participation among educated young married women. In 1950 around 80% of American young married women did not participate in the labor force regardless of education, but in 1980 educated young married women participated in much larger proportions than their uneducated counterparts.Footnote 11 The positive correlation between education and labor force participation is observed also in other countries [Bridgman et al. (Reference Bridgman, Duernecker and Herrendorf2018)]. Although the reduced-form model is not explicit about education, the rise of female education appears implicitly: once a woman projects to participate in the labor force after marriage, the returns to exogenous ability may be enhanced by schooling. High-ability married women who participate in the labor force are more likely to be educated than their low-skilled counterparts who do not. The dynamics imply increasing high-ability married women's labor force participation and, therefore, a decreasing share of low-skilled single women in the female labor force. This change is consistent with documented shift from negative to positive self-selection into female labor force [Mulligan and Rubinstein (Reference Mulligan and Rubinstein2008)] and increasing female college attendance [Goldin (Reference Goldin2006)].
The third stylized fact is that marriage is positive assortative by education. In the United States, about 60% marry within the same educational group [Schwartz and Mare (Reference Schwartz and Mare2005)]. Moreover, the model recalls the empirical finding of Zhang (Reference Zhang1995) that a man's age of marriage and his wage are positively correlated if the wife is working but they are negatively correlated if the wife is not working. An additional important note is that age of marriage in the model is not necessarily correlated with the gender wage gap, because the gender gap depends not only on productivity, but also on selection into the female labor force.
6. Supportive evidence
In this section, I use the Current Population Survey [CPS, Flood et al. (Reference Flood, King, Rodgers, Ruggles and Warren2020)] data from the United States to test the main model's prediction, captured in Proposition 2, i.e., that “male” sectors productivity is negatively affecting age of marriage. I estimate the following model:
where $S( a,\; g) _{ist}$![]() is a dummy for being never-married at age $a$
is a dummy for being never-married at age $a$![]() . The unit of observation is individual $i$
. The unit of observation is individual $i$![]() of gender $g$
of gender $g$![]() , who lives in state $s$
, who lives in state $s$![]() and was 18 years old in year $t$
and was 18 years old in year $t$![]() .
.
The main explanatory variable $M$![]() is the labor productivity in the “male” sector. Below I explain in detail the construction of this variable and the identification assumption. The state and year fixed effects are $\gamma _{s}$
is the labor productivity in the “male” sector. Below I explain in detail the construction of this variable and the identification assumption. The state and year fixed effects are $\gamma _{s}$![]() and $\eta _{t}$
and $\eta _{t}$![]() , respectively. $X$
, respectively. $X$![]() is a set of controls. It includes a dummy for whites and the following state-level variables: four variables for the minimal legal age of marriage (minimal for men and for women, with and without parental consent), a dummy for early legal access, i.e., availability of oral contraception for single childless women below age 21 [from Bailey et al. (Reference Bailey, Guldi, Davido and Buzuvis2012)], a dummy for the possibility of no-fault divorce [from Vlosky and Monroe (Reference Vlosky and Monroe2002)], and a dummy for legal abortion [from Levine et al. (Reference Levine, Staiger, Kane and Zimmerman1999)]. Standard errors are clustered by state.
is a set of controls. It includes a dummy for whites and the following state-level variables: four variables for the minimal legal age of marriage (minimal for men and for women, with and without parental consent), a dummy for early legal access, i.e., availability of oral contraception for single childless women below age 21 [from Bailey et al. (Reference Bailey, Guldi, Davido and Buzuvis2012)], a dummy for the possibility of no-fault divorce [from Vlosky and Monroe (Reference Vlosky and Monroe2002)], and a dummy for legal abortion [from Levine et al. (Reference Levine, Staiger, Kane and Zimmerman1999)]. Standard errors are clustered by state.
6.1. Identification strategy
I seek an explanatory variable that accounts for productivity in the “male” sector with respect to the weight of this sector in each state's economy. The problem is that the dynamics of each state's economic structure is endogenous. In order to identify the effect of “male” sector labor productivity, I propose to fix the initial conditions in each state and use them as weights of the industries in the state's economy. The change over time comes from country-level productivity growth, but the variation across states comes from different initial conditions.
Identification assumption: The country-level labor productivity is exogenous to each state's initial economic structure.
In other words, I assume that states are small relatively to the whole country, so each state's initial conditions do not determine country-level productivity growth. Therefore, only the differences between the states’ initial conditions allow identification: had all the states the same initial conditions, year fixed effects would absorb any variation over time.
I use this identification assumption to define the main explanatory variable $M_{st}$![]() :
:

where $k$![]() is the index of an industry out of the total of $K$
is the index of an industry out of the total of $K$![]() industries. First, $w_{sk}$
industries. First, $w_{sk}$![]() generates across-state variation by accounting for the state's initial economic structure. Specifically, it is the initial $k$
generates across-state variation by accounting for the state's initial economic structure. Specifically, it is the initial $k$![]() 's weight in the state $s$
's weight in the state $s$![]() output. I use Renshaw et al. (Reference Renshaw, Trott and Friedenberg1988), who provide state-level decomposition of output by industry from 1963 on. I use the first years of these data, i.e., 1963–1965, to calculate the weights $w_{sk}$
output. I use Renshaw et al. (Reference Renshaw, Trott and Friedenberg1988), who provide state-level decomposition of output by industry from 1963 on. I use the first years of these data, i.e., 1963–1965, to calculate the weights $w_{sk}$![]() . Second, $y_{tk}$
. Second, $y_{tk}$![]() generates over-time variation by accounting for country-level per-worker output in industry $k$
generates over-time variation by accounting for country-level per-worker output in industry $k$![]() in year $t$
in year $t$![]() :
:
where $Y_{tk}$![]() is industry $k$
is industry $k$![]() country-level output and $L_{tk}$
country-level output and $L_{tk}$![]() is the industry's number of workers in year $t$
is the industry's number of workers in year $t$![]() . These data come from Dale Jorgenson's KLEMS project.Footnote 12 I convert the data into thousands of inflation-adjusted 1980 dollars.
. These data come from Dale Jorgenson's KLEMS project.Footnote 12 I convert the data into thousands of inflation-adjusted 1980 dollars.
Finally, $I_{k}^{m}$![]() is a binary indicator for being the industry “male.”Footnote 13 “Male” industry is composed of more than 70% male workers among 25–34 year old workers according to the American Census of 1990 [Steven et al. (Reference Steven, Katie, Ronald, Josiah and Matthew2017)]. By this definition, the male sectors are agriculture, mining, construction, and durable goods manufacturing. This retrospective definition with respect to the gender shares in 1990 is aimed at identification of sectors that remained dominated by male workers despite the increased female labor force participation.Footnote 14
is a binary indicator for being the industry “male.”Footnote 13 “Male” industry is composed of more than 70% male workers among 25–34 year old workers according to the American Census of 1990 [Steven et al. (Reference Steven, Katie, Ronald, Josiah and Matthew2017)]. By this definition, the male sectors are agriculture, mining, construction, and durable goods manufacturing. This retrospective definition with respect to the gender shares in 1990 is aimed at identification of sectors that remained dominated by male workers despite the increased female labor force participation.Footnote 14
6.2. Results
Panel A of Table 4 presents the results of estimation of equation (5). I estimate the model eight times: for men and women, separately for samples of individuals who are at least 21, 23, 25, and 27 years old. The results plot a robust statistically significant negative coefficient of the male sector in line with the model's predictions: a negative effect of the male sector on probability of singlehood.
Table 4. Male sector effect on singlehood and heterogeneity of the effect

Note: The table presents the results of OLS regressions of equation (5). All regressions control for minimal legal age of marriage, include year and state fixed effects, and control for whites, legalization of divorce, abortion, and early access to oral contraception. Standard errors are clustered by state. $^{\ast }p< 0.1$![]() , $^{\ast \ast }p< 0.05$
, $^{\ast \ast }p< 0.05$![]() , $^{\ast \ast \ast }p< 0.01$
, $^{\ast \ast \ast }p< 0.01$![]() .
.
CPS data have been collected since 1962, during the period of increasing age of marriage. Nevertheless, I document the negative effect of the male sector on age of marriage in CPS data. Furthermore, in order to test whether the male sector affected age of marriage even by the end of the twentieth century, I estimate the model separately for the years 1962–1989 and 1990–1999. The results of these two estimations appear in panels B and C of Table 4, respectively. The negative coefficient of the male sector is of a higher magnitude in the 1962–1989 period, especially for women. However, it is negative and statistically significant also in the 1990–1999 period. Overall, given that the mean value of the explanatory variable $M$![]() increased from 14 to 22 in the 1962–1989 period and from 22 to 27 in the 1990–1999 period, the estimation results suggest that the age of marriage in 1999 was 1 year lower than it should be if the male sector productivity had not increased since the 1960s.
increased from 14 to 22 in the 1962–1989 period and from 22 to 27 in the 1990–1999 period, the estimation results suggest that the age of marriage in 1999 was 1 year lower than it should be if the male sector productivity had not increased since the 1960s.
7. Conclusions
This paper addresses the twentieth century dynamics in the age of marriage across the globe with a focus on U-shaped dynamics, more prominent in Western than in other countries, and taking place mostly after WWII. The U-shape is special in its strong correlation across Western countries, in its relationship with the economic development path, and in correlation between the genders. The proposed explanation of the U-shape is that a shock on the male-biased sectors of industry triggers a decrease in the young women's reservation value and to an earlier marriage, as long as women do not work after marriage. However, the rise of gender-neutral technology pushes women to work after marriage, and the marriage market to sort according to ability. Individuals marry at a higher age, when sorting is imposed by meetings between men and women with similar levels of market skills.
Acknowledgments
I thank Joel Mokyr, James J. Heckman, Oded Galor, Yoram Weiss, Matthias Doepke, Analia Schlosser, Moshe Hazan, Hans-Joachim Voth, and Hosny Zoabi for their helpful suggestions at different stages of work on this research. I also thank the participants of seminars at Chicago University, Tel-Aviv University, Leibniz University Hannover, Bar-Ilan University, Ben-Gurion University, Haifa University, and the Summer School in Economic Growth at the University of Warwick for insightful comments.
Conflict of interest
The author declares that he has no conflict of interest.
Appendix A. Mean age at first marriage


Appendix B. Data compilation details
I compiled the data in Appendix A using the following sources:
1. United Nations Demographic Yearbook for 1948–2010 [UN (1948–2010)]
2. Council of Europe: mean female age at first marriage since 1960
3. National Statistics Bureaus of France, Norway, Sweden, Iceland, Canada, and Denmark
4. NBER collection of Marriage and Divorce Data of the National Vital Statistics System of the National Center for Health Statistics (U.S.A.)
5. U.S. Bureau of Census
6. Schoen and Baj (Reference Schoen and Baj1984) for Switzerland
The United Nations Demographic Yearbook [UN (1948–2010)] collects, compiles, and disseminates official statistics on a wide range of topics. Data have been collected from national statistical authorities since 1948 through a set of questionnaires dispatched annually by the United Nations Statistics Division to over 230 national statistical offices. The UN Demographic Yearbook marriage data are the total number of marriages between brides and grooms, whose ages are grouped by 5 years (e.g., 25–29 year old grooms with 20–24 year old brides). The marriages are not divided into first and subsequent marriages. Thus, I use only marriages until age of 40 as an approximation to first marriages. The mean age of marriage in the UN data, conditional on marriage before age of 40, strongly correlates with a series of age at first marriage from the Council of Europe and National Statistics Bureaus.
Since the ages in the UN Demographic Yearbook are totals grouped by 5-year intervals, I consider the calculated means as less accurate than from other sources, where the data are by definition the mean age at first marriage. Thus, I give preference to the data from the Council of Europe and national statistics bureaus whenever it is available. For countries that have data in both the Council of Europe and the UN Demographic Yearbook, but for more years in the latter than in the former, I attempt to improve the quality of the UN data by extrapolating the better-quality Council of Europe data. To this end, I regress the Council of Europe data on the UN data. Whenever $R^{2}$![]() is above 0.85, I extrapolate the Council of Europe data using the values predicted by the regression for the years appearing in the UN but not in the Council of Europe data.
is above 0.85, I extrapolate the Council of Europe data using the values predicted by the regression for the years appearing in the UN but not in the Council of Europe data.
For the United States, I use this extrapolation methodology to adjust the median age at first marriage as reported by the Bureau of Census for the post-1850 period to the mean age at first marriage calculated from the Marriage and Divorce Data of the National Vital Statistics System of the National Center for Health Statistics for the 1968–1995 period.
B.1 Construction of long time series
The data used in Figure 7 were constructed from the following sources: Haines (Reference Haines1996) who cites different sources, Wrigley et al. (Reference Wrigley, Davies, Schofield and Oeppen1997); Hajnal (Reference Hajnal1953), European Fertility Project of the Office of Population Research at Princeton University, and raw data used for tabulation in Appendix A (see details above). In cases of large disagreement, the later published source is considered as more credible. The time series are constructed in the following way.
Time series for 1800–2005:
United States: Females: 1800–1929: Haines (Reference Haines1996); 1930–2005: raw data for Appendix A. Males: 1800–1939: Haines (Reference Haines1996); 1940–2005: raw data for Appendix A.
Sweden: Females and males: 1870, 1901–1915: Swedish Statistical Bureau; 1954–2005: raw data for Appendix A.
Germany: Females: 1800–1950: Haines (Reference Haines1996); 1960–2005: raw data for Appendix A. Males: 1870–1970: Haines (Reference Haines1996); 1992–2005: raw data for Appendix A.
Italy: Females and males: 1900–1950: Haines (Reference Haines1996), 1954–2005: raw data for Appendix A.
Belgium: Females and males: 1850–1930: Haines (Reference Haines1996); 1954–2005: raw data for Appendix A.
Switzerland: Females: 1860–1940: European Fertility Project; 1950–2005: raw data for Appendix A. Males: 1950–2005: raw data for Appendix A.
Denmark: Females: 1852–1940: European Fertility Project; 1911–1949: Denmark Bureau of Statistics; 1950–2005: raw data for Appendix A. Males: 1911-1949: Denmark Bureau of Statistics; 1950–2005: raw data for Appendix A. France: Females: 1800–1820: Henry and Houdaille (Reference Henry and Houdaille1979); 1870–1950: Haines (Reference Haines1996); 1954–2005: raw data for Appendix A. Males: 1800–1900: Henry and Houdaille (Reference Henry and Houdaille1979); 1954–2005: raw data for Appendix A.
England: Females and males: 1800–1830: Wrigley et al. (Reference Wrigley, Davies, Schofield and Oeppen1997); 1850–1950: Haines (Reference Haines1996); 1960–2005: raw data for Appendix A.
Appendix C. Additional figures
See Figures C1 and C2.

Figure C1. Change in the age of marriage and economic growth between early 1960s and early 1990s, men.
Note: The figure presents the change in the age at first marriage, averaged over regions (each country in a region is one observation). The change is between the average over 1960–1964 period and the average over 1990–1994 period. GDP is taken from Maddison (Reference Maddison, van Ark and Crafts1996), and logged after averaging. Age of marriage corresponds to Tables 1 and 2. See Appendix A for raw data and Appendix B for details of its compilation. Western Offshoots include United States, Canada, Australia, and New Zealand.

Figure C2. Change in the age of marriage and economic growth between early 1960s and early 1990s, women.
Note: The figure presents the change in the age at first marriage, averaged over regions (each country in a region is one observation). The change is between the average over 1960—1964 period and the average over 1990—1994 period. GDP is taken from Maddison (Reference Maddison, van Ark and Crafts1996), and logged after averaging. Age of marriage corresponds to Tables 1 and 2. See Appendix A for raw data and Appendix B for details of its compilation. Western Offshoots include United States, Canada, Australia, and New Zealand.
















