The machine learning revolution in materials?

Abstract

Machine learning (ML) and artificial intelligence (AI) are quickly becoming commonplace in materials research. In addition to the standard workflow of fitting a model to a large set of data in order to make predictions, the materials community is finding novel and meaningful ways to integrate AI within their work. This has led to an acceleration not only of materials design and discovery, but also of other aspects of materials research as well, including faster computational models, the development of autonomous and intelligent “robot researchers,” and the automatic discovery of physical models. In this issue, we highlight a few of these applications and argue that AI/ML is delivering real-world, practical solutions to materials problems. It is also clear that we need AI/ML methods and models, “dialects” that are better adapted to materials research.

Introduction

Over a span of a decade, efforts such as the Materials Genome Initiative¹ (MGI) and the Integrated Computational Materials Engineering² (ICME) programs have seen large successes in the creation of a materials data and computational infrastructure. Large-scale systems have been developed and populated to allow for easy access to volumes of experimental and simulation data. These data and the associated infrastructure that have been built to ingest, store, and manipulate it are not ends in and of themselves, however. Instead, they are the means to the ambitious goal of accelerated materials design and discovery. A key question, therefore, is how to best use such data to achieve this goal.

In addition to the data and infrastructure, we must also consider the various techniques and methods used to analyze, interact with, or otherwise draw conclusions from that data. Indeed, with such a data infrastructure in place, data-driven techniques and analysis have already become commonplace within the materials science community. In the past few years, these data analytic techniques have enjoyed an evolution in accuracy, robustness, and utility comparable to the development of the materials data infrastructure itself.

The data analytic techniques employed by the materials community are broad and diverse. Exploratory data analysis and visualization techniques allow us to “look” at our data (a requisite first step in any analysis) to identify qualitative trends or outliers. Statistical regression techniques learn the mappings from material descriptors to properties or device performance. Unsupervised methods such as clustering or dimensionality reduction algorithms allow us to find hidden connections between and within families of materials by examining high dimensional representations of them and discovering structure within these representations. Combined, these techniques can help accelerate the design of materials with new or optimal properties by making predictions or discovering insights latent in the data.

One workflow, which we will broadly call virtual screening,³ involves collecting a large amount of numeric data specifying several descriptors for a set of materials, fitting a model to predict structure or properties of materials from these descriptors, and using this model to identify those materials that produce optimal structure or properties. Virtual screening can suggest material designs predicted to be optimal with respect to certain properties or structures. These designs are then tested in the laboratory, by synthesizing the materials and characterizing their properties. Given sufficient amounts of data, virtual screening can accelerate the design of optimal materials and is perhaps one of the most popular data analytic workflows used in the materials community. Examples of its success include the design of organic light-emitting diodes,⁴ metal–organic frameworks,⁵ and drugs.⁶

Virtual screening, however, is not the only way we can analyze or interact with data. Recently, the materials community has started to embrace state-of-the-art methods from machine learning (ML) and artificial intelligence (AI) in novel ways. A small sample of such methods includes autonomous research to power “robot” material researchers, techniques such as “deep learning” (DL)*— described next—and image processing to identify structure from microscope images, natural language processing to extract knowledge from the materials literature, and symbolic methods to learn physics models directly from data.

With this issue of MRS Bulletin, our goal is to highlight a small, but diverse, sample of cutting-edge ML/AI and discuss how it is being used to accelerate contemporary materials research, beyond more classical data-analysis workflows. Cognizant of the fact that the field of AI for materials is still in its adolescence, we also want to call attention to some potential avenues for a more meaningful integration of the two fields. The articles in this issue span a breadth of topics being researched throughout industry, national labs, and academia around the world. They offer concrete illustrations of how ML and AI are not simply academic pursuits undertaken for the sake of sophistication, but instead provide practical solutions to problems we face throughout the materials community.

A materials dialect for AI

As the materials community continues to employ even more sophisticated data analytics, it is perhaps healthy for us to collectively step back and take stock of the promises that such techniques engender, and whether they are actually bearing fruit. The Gartner hype cycle⁷ is an illustration of the expectation of a technology’s success or value over time (Figure 1). It divides the lifetime of a technology over five phases with names such as the “Peak of Inflated Expectations” and the “Trough of Disillusionment.”

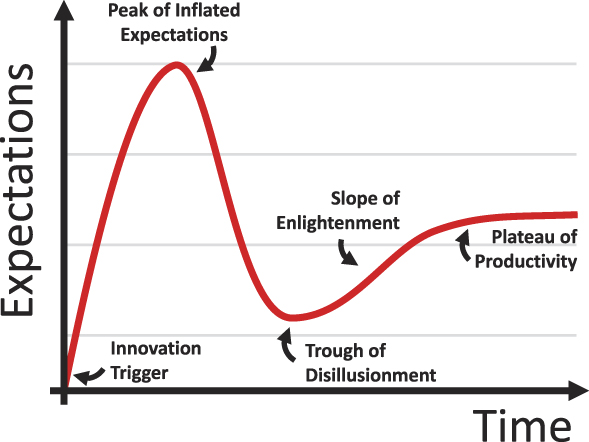
Figure 1. The Gartner hype cycle, which describes levels of expectations for new and developing technologies, breaking the lifetime into four distinct phases. The Innovation Trigger: the initial breakthrough and early proof of concept demonstrations. Peak of Inflated Expectations: Proof-of-concept demonstrations leads to a few well-published success stories. Trough of Disillusionment: Decreased interest due to the inability to quickly transition from proof-of-concept to practical solutions for early adopters. Slope of Enlightenment: A better understanding of the technology as it matures, resulting in improvements and more realistic adoption. Plateau of Productivity: Sustainable development in the technology leads to increased and long-term relevance and growth.

Where then does the application of ML and AI to materials stand in this hype cycle? To give this some context, in 2018, Gartner—the firm that publishes the annual Gartner hype cycle—placed the concept of “deep learning” at the top of the Peak of Inflated Expectations. For further context “Silicone Anode Batteries” was placed after Deep Learning on this peak. Both, having cleared this peak, seem well on their way to the Trough of Disillusionment, according to Gartner, which is a period after the initial, highly public proof-of-concept successes give way to waning interest and delays or failure of the technology to deliver. The hope is that technologies spend little time inside this trough and instead go on to the next stage, the “Slope of Enlightenment” in which the true, fundamental, and long-lasting benefits of the technology crystalize and become better understood.

AI technologies seem to be particularly susceptible to repeated periods of inflated expectations only to be followed by disillusionment. Another phrase has been coined to describe this—an AI winter.⁸ This describes periods of times in which AI research as a whole suffered major funding droughts. Many believe that we are in the advent of another AI winter.^9,10 With this rather pessimistic outlook, we should attempt to place the notion of “AI for materials” in an objective light so that we can define realistic expectations for the technology and what it can achieve within the near future.

In their article in this issue, Gomes et al.¹¹ provide a high-level perspective and critically examine the role of AI/ML in the materials community. The authors provide a brief primer on the most popular methods in AI/ML. They then argue that the state of the art in AI technology constitutes System-1 level capabilities, which entail efficient data processing, and statistical inference and reasoning. The application of AI/ML specifically to materials, however, offers a real testbed for the development of a System-2 type of intelligence that requires careful reasoning and planning, and a complex representation of knowledge. Over the past few hundred years, we humans have developed an advanced method of reasoning about the physical world—science itself. Therefore, the main challenge for AI in materials is to build similar (or even superior) capabilities within an artificial agent to assist in our materials research. The authors provide an overview of specific examples of how this has been or can be achieved to some degree within the materials community.

The idea of developing a System-2 level of intelligence for materials suggests a two-way street between AI and materials research. The materials community has indeed used data analytics, ML, and AI to achieve a certain level of success. Conversely, we could think of how specific features of the materials problems we encounter necessitate the development of AI/ML techniques and models that are cognizant of such features. That is, could we develop a dialect of AI specific to materials?

It may not be immediately obvious that we would need to develop such a dialect. Indeed, many techniques in AI are relatively abstract and agnostic to their ultimate applications. These purely “data-driven” methods simply require a data set to train their models in order to make predictions or perform other ML-related tasks. The same models that predict whether a person, described by a large number of factors such as age, geographic location, and browsing history, will click on a web advertisement can in theory be used to predict whether a material, itself described by a large number of descriptors such as composition, atomic radii, and lattice constants, will form a stable perovskite crystal structure. To these generic classification models, data is data regardless of the underlying application.

Given enough training data, such models are capable of making accurate predictions. For example, one online competition to predict advertisement click-through rates offered a training data set of approximately 40 million records.¹² This, however, points to one of the motivations for a materials-cognizant AI dialect. In most cases, we do not have 40 million data points to train our models. In our field, data ultimately come from experiments or simulations, and in many settings, obtaining such data is expensive and noisy, making the data itself limited, sparse, and uncertain in many scenarios. It may simply be (1) too difficult to obtain enough data to train larger, more sophisticated models, at least not without; (2) any proper quantification of uncertainty; or (3) the ability to draw on other sources of related information or knowledge. These three “features” common in many materials problems (specific instantiations are detailed in the following sections) illustrate how our field’s demands on AI deviate somewhat from the context in which many generic AI technologies are currently being developed. This, we believe, motivates a real need for AI with a materials perspective if we are to see a substantive and sustainable impact of that technology on our field and to avoid “AI-in-materials winter.”

Herein, too, lies an important value proposition for the AI community. These materials problems offer a new and unique platform to develop and test novel AI methodologies. Experiments and simulations offer a more direct (albeit noisy) observation of ground truth, which is more quantifiable than, for example, consumer preferences. This results in a fruitful testbed and an opportunity for the AI community to collaborate with materials researchers and advance both fields.

Guided and autonomous materials design and discovery

One way to address issues of data scarcity and uncertainty previously described is to use AI/ML to select which data to obtain. Key to this is the assumption that not all data points are equally useful, especially in the face of a specific materials task. Consider, for example, the materials design task of synthesizing nanoparticles with optimal properties. Suppose we wish to reduce polydispersity among a batch of nanoparticles being synthesized. These nanoparticles are grown in solution, with specific growth conditions, including chemical species of precursor materials, concentrations of these precursors, and synthesis temperature. Given enough training data describing synthesis conditions (inputs) and the width of the resulting nanoparticle size distribution (output), we could train a ML model to predict this size distribution as a function of synthesis conditions and subsequently use that model to identify which conditions minimize this distribution width.

The data requirements to train a model capable of making such a prediction with reasonable accuracy expand with respect to the number of input variables (i.e., synthesis conditions). The space of potential experiments—the space over which we would require a ML model to make accurate predictions—grows combinatorially as this number increases. This requirement is magnified by the expense (money and time) to run each experiment, as well as the noise or variability associated with the experimental responses. In many cases, specifically those experiments with a large number of growth parameters, it may not be feasible to obtain a sufficient number of data points, each requiring one or more experiments to account for experimental variability, in order to fit a globally accurate ML model.

In the face of such a scenario, we often must concede that any ML model fitted on a relatively small amount of noisy data will have uncertainties associated with it. We must further concede that the data we use to train such a model (i.e., the experiments we ultimately choose to run) cannot simply be uniformly selected among the combinatorially large space of potential experiments to consider, given a relatively small experimental budget. The result of such a naïve sampling strategy would be a ML model whose predictions would be uniformly uncertain throughout the domain. Ideally, we would instead obtain data in a focused way so that the ML model’s predictions would be more accurate in regions of interest, as defined by the experimental objectives. For example, in the nanoparticle synthesis case, if the initial data seem to suggest that high temperatures result in a broadening of the nanoparticle size distribution, then perhaps we ought to only consider experiments with low growth temperatures, given our objective to decrease the width of the size distribution. Of course, we would not have discovered this phenomenon if we never ran those high-temperature experiments to begin with. In other words, those experiments, while producing results not in line with our specific experimental objectives, did yield some useful information.

This example points to some important concepts. First, the decisions we make as to what experiments we wish to perform should be based on experiments we have run so far. We should select experiments in a sequential or iterative fashion. Second, the decision on which experiments we run will be based on the data obtained from previous experiments, which will be used, as we had conceded previously, to fit an imperfect, uncertain ML model. Finally, the experiments we carry out should be focused on our ultimate experimental objectives, but allow for some degree of exploration if such exploration could potentially yield important information—this is the so-called exploration versus exploitation¹³ dilemma.

The problem of selecting which experiment to perform is one considered in statistical decision theory. The goal is to select experiments using a decision policy so that we can obtain specific experimental objectives in as few experiments as possible. To assist this, many techniques often rely on the imperfect knowledge of the system obtained throughout the campaign, which is sometimes encoded using Bayesian statistical methods. These methods capture our state of “belief” about the response as a function of inputs and come equipped with both a prediction of this response in addition to a quantification of uncertainty for these predictions. That is, the Bayesian beliefs often employed for these types of decision-making problems measure what we know about a system, and how well we know it, given the limited data obtained throughout the course of the experimental campaign. These beliefs are used inside a decision-making policy to select experiments.¹⁴ The selected experiments are then run, and the results are fed back to update the Bayesian beliefs using Bayes’ Law, which dictates how our estimates change in the face of new data. The updated beliefs are then used to select subsequent experiments. This results in a decision–experiment–update iterative feedback loop (Figure 2) that is at the heart of a ML-guided search for optimal materials through design parameter space.

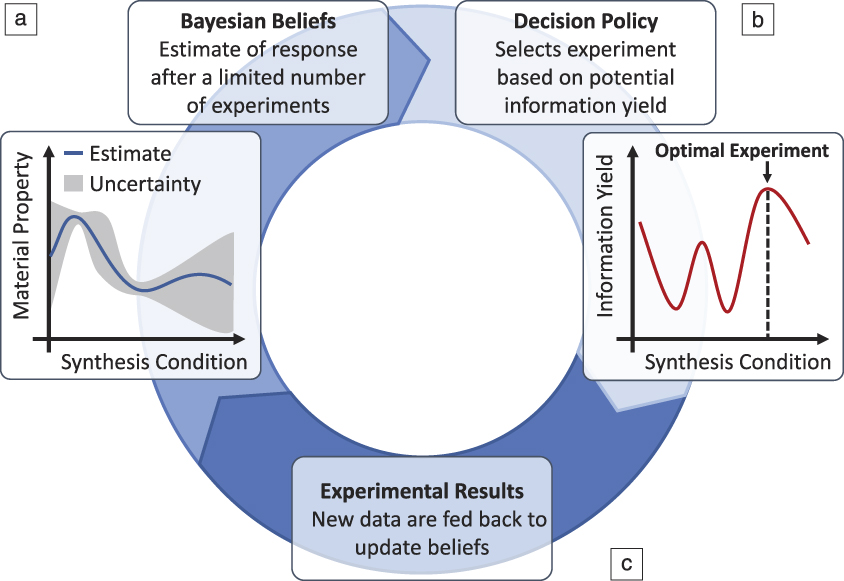
Figure 2. The closed-loop planning, execution, and learning from experiments for guided and autonomous research. (a) Beliefs about the system that are captured using Bayesian statistics, estimating a material property of interest; (b) a decision policy that balances exploration versus exploitation when selecting an experiment to run; (c) closing the loop by using the Bayesian update.

One interesting application of this type of ML-guided experimentation is its use within autonomous research systems. Examples of such autonomous research systems include ADAM¹⁵ and EVE,¹⁶ which were used for drug design and discovery, and ARES,¹⁷ which was used to learn controlled synthesis of carbon nanotubes (CNTs). Such autonomous “robot researchers” are not only capable of executing experiments and varying experimental parameters with no human intervention, but they can also automatically characterize the experimental responses. By implementing the belief modeling and decision-making algorithms previously described as the AI “brains” for a robot researcher, these systems are also able to select experiments to run.

Combined, the capabilities of an autonomous research system result in its ability to autonomously run entire experimental campaigns. There are many apparent advantages for using such systems for autonomous materials design, including the consistency afforded by robotic experimentations free from human errors, as well as the ability to run experiments continuously. Through the use of the previously discussed ML techniques, these systems can be intelligent in how they traverse through a combinatorially large parameter space. This results in the promise of autonomous research systems to deliver an efficient, tireless, and robust search for optimal materials.

ML for computational materials and vice versa

Prior to the advent of AI/ML methods, the materials community was already well versed in computational methods such as density functional theory (DFT) and molecular dynamics (MD) simulations. These classical computational materials methods offered insights into the thermodynamics and kinetics of materials at an atomistic (or finer) resolution and have proven invaluable to materials research. Given the insights promised by AI/ML, the coupling of the two computational disciplines within a materials context was inevitable. An interesting synergy arises when this coupling occurs. In one direction, researchers have found great success in using ML models to augment, and in some cases replace, traditionally expensive calculations. For example, ML models have been used to calculate potential energy surfaces for use in MD,¹⁸ approximate Kohn–Sham DFT,¹⁹ and replace quantum mechanical calculations.²⁰

In the other direction, it is interesting to ask whether data obtained by simulations can be used as labeled data for training ML models, with the expectation that such trained ML models will be applied to analyze real-world (i.e., nonsimulated) data. This is an important question to ask because of the data scarcity issue previously described—it is often difficult to obtain a sufficient amount of labeled training data needed to train large-scale ML models. By using simulated data in lieu of experimental results, classical computational materials could help bridge this divide.

At first glance, the ability to do this correctly seems to rest entirely on the fidelity of the simulation method. If the simulation is able to properly model and simulate the relevant features of a material system that contribute to a specific property, then simulated data should be useable as training data. However, some onus does rest upon the ML model itself, and specifically, its ability to generalize past any artificial features that are present solely by virtue of using simulated data. For example, we could consider the case of training a classifier to identify defects from images of a crystalline material. In reality, such images are noisy, have limited resolution, and depict complex configurations that include grains of different orientations and amorphous regions. Any simulation method designed to simulate several atomistic configurations with specific defects in order to train a classifier to detect such defects may not necessarily model such a rich and complex type of noise. If the simulations produce overly pristine crystalline training data, naïve classification models may be able to generalize to noisy, real-world data.

While the question of how to properly integrate simulated data in training models for specific materials applications remains open, we may ask more generally—what are the best practices when it comes to simulated data, and how does it interact with models, the real-world, and our ML or experimental objectives? This question has been addressed in a variety of fields within statistics and ML. One example of this is in the calibration of ML models using simulated and real data to produce surrogate models,²¹ which once trained, serve as a proxy for the true experimental response. Such models are used for predictions of these responses without the need for running further physical or computational experiments.

A more robust perspective is that taken in multifidelity modeling,²² which acknowledges computational simulations as but one source of ground truth, in addition to others, including reduced-order models, experimental data, and domain experts. In such models, each source of ground truth is accompanied with a measure of fidelity—how much trust to place on this source, as well as evaluation cost and how much time does it take to obtain a data point? This information can be used to provide a prediction with properly quantified uncertainties. It can also be used within an experimental design context, in which a decision-making policy not only selects the design parameters (inputs) to obtain an experimental response, but also decides which source to query for this response.²³ In this way, computational simulations can be used in tandem with experiments in an ML-guided manner to accelerate the materials design and discovery loop.

Symbolic learning for physics-based models

One common issue in the training of ML models is the extrapolation problem. ML models are trained on data, and based on these examples, the models are often tasked to provide predictions for new data. For example, based on several input–output pairs describing synthesis conditions (inputs) and mean CNT length (output), we may wish to train a model that predicts CNT length for synthesis conditions not yet considered. Provided there is a sufficient amount of such training data, it is simple enough to perform some interpolation to make predictions at data points similar to what the model was trained on. For example, if we know CNT lengths for CNTs grown at 700°C and at 720°C, barring any significant phase transitions, it may be reasonable to predict CNT length at 710°C by taking the averages of the known values. While this may seem overly simplistic, many models in nonparametric statistics (such as Gaussian processes²⁴) take such a perspective.

The extrapolation problem occurs when we are asked to make predictions for inputs that are quite dissimilar to those considered inside the training data set. For example, we may have CNT lengths for those grown between 500°C and 700°C. Can a ML model trained on this data predict CNT lengths for those grown at 1200°C? That is, can we extrapolate predictions beyond the examples contained in our training set? For purely data-driven, statistical models such as Gaussian processes, the common wisdom is that unqualified extrapolation is generally a bad idea and should be avoided. If performed, we must be careful and confident that the general trends would continue beyond our data set, and that predictions come with some qualification, or quantification of uncertainty if possible. Yet in a data-limited setting in which we often find ourselves in our field, some degree of extrapolation is sometimes necessary.

To be reasonably successful in our extrapolation attempts, or even to know whether extrapolation to some degree is appropriate, we must be able to supplement our limited data with other types of prior information. While the field of materials science may suffer from the inability to collect millions of data points—a luxury found in other applications of AI/ML—we instead enjoy access to a special type of prior knowledge to fill this gap, namely physics-based knowledge. For example, in the case of predicting CNT growth, a domain expert may acknowledge that at higher temperatures, other kinetic processes such as pyrolysis, significantly impact CNT growth, which would mean at first glance that predictions made by a ML model trained at lower temperatures may not be suitable for predictions at higher ones.

This incorporation of physics-based knowledge can be developed further. Instead of using this knowledge to indicate whether extrapolation is appropriate, we could instead try to build in the appropriate physics into the ML models in a way that would allow for extrapolation. Synthesizing physics-based knowledge with ML models is a topic that has received considerable interest, and one particularly ambitious direction is in the learning of physics models directly from the data. One prominent example of this is learning Newton’s laws of motion from the dynamical data of a double pendulum.²⁵

A key technology in this area is symbolic regression (SR), discussed by Sun et al. in this issue.²⁶ The authors give an overview of SR, which seeks to learn mathematical expressions that map inputs to output. This is in contrast to numerical regression techniques such as linear regression, which assume a particular mathematical form up to some unspecified values of parameters. Training this kind of model means optimizing these parameter values with respect to some error function based on training data. In SR, it is the mathematical form itself that must be learned. Analogously, these forms are obtained through an optimization procedure on mathematical expressions, usually some form of genetic algorithm optimization. The authors illustrate how this procedure can be augmented with physics-based expert knowledge in order to derive mathematical expressions that are physically realistic. The authors provide examples of SR in practice, including the prediction of cyclic voltammetry curves.

The promise of such a technique is that if the relevant physics were properly learned, then some degree of extrapolation would be possible, given a sufficient amount of data. If we learn the underlying generative mechanisms of the data, then rather than smoothing and performing interpolation in an empirical way, predictions would be based on first principles, or at least closer to first principles than purely statistical models. It remains to be seen whether SR can deliver on this promise consistently and at large scales. It is our opinion that any successful form of this technology would have to do more than the symbolic manipulations of basic SR. Rather, similar to the other examples described in earlier sections, prior knowledge must be properly taken into account, and uncertainties must be quantified for models generated using a SR, at least in the data-limited context.

Intelligent manufacturing

Finally, the Aggour et al. article in this issue²⁷ is a convergent illustration of how many of these or similar ML technologies previously discussed provide industry with real-world, practical solutions to challenging materials and manufacturing problems. The authors present a variety of vignettes of how AI, ML, and other computational techniques have assisted General Electric (GE) in the development of their various products and business units, including examples in additive and subtractive design and processing, modeling of machine lifetimes, and automated inspection and characterization of manufactured parts.

In addition to many of the previously mentioned examples, this article highlights further opportunities to incorporate AI and ML in materials work. For example, the authors describe the development and use of domain-specific formal semantic languages to describe design and manufacturing concepts. The use of such languages allows us to specify high-level ideas and concepts in a format that allows AI agents to perform reasoning and inference about such ideas. Using this language, the authors show how this reasoning can be used to infer manufacturability of parts and the parameterization of design rules. As previously mentioned, such an example of domain knowledge representation is quite important as we move to more problem-aware AI technologies.

Another topic discussed by the authors is the use of DL models to perform autonomous characterization and microstructural inspection of ceramic matrix composite (CMC) materials. Such models were used to perform image segmentation—identifying interesting features within an image, in this case, identifying fibers, material coating, matrix, and silicone components of CMC samples. In a similar vein, the authors demonstrate the use of DL models to process in situ signals obtained during electrical discharge machining drilling of cooling holes in aircraft engines to detect whether a drilled hole was defective in some way. The authors show how this approach leads to significant improvements in manufacturing efficiency, as such an analysis can be done on-site.

Generalizing from these examples, the analysis and detection of interesting features from microscopy or other types of spatially or temporally resolved characterization data stands to be one of the most promising applications of AI/ML to manufacturing and materials science. These methods can be used to identify and segment microstructure, detect various types of defects, identify crystal structure, or extract a variety of descriptors based solely on images of material samples. An enhanced ability to extract such descriptors from images or spectra results in the capability of automatically calculating accurate statistics on such images, which are often calculated manually with much effort. For example, by automatically detecting grain boundaries in an image, grain-size distributions become easy to compute.

As illustrated by the article, a key ML technology to perform such analysis on image, spectra or temporal data is DL.²⁸ In other regression models, such as linear regressions, experts often have to specify which features of the input data are important in a process called feature engineering. In DL, these features are learned automatically. Surprisingly, in many applications of DL, the features learned by the deep learner are better (have better predictive power) than those engineered by experts. This is especially true in high-dimensional image data, in which features learned are robust against rotation, scaling, and translation of images. As such, DL has seen recent success in image processing and computer vision.²⁹ As a field heavily dependent on microscopy images, it should come as no surprise that DL is immediately relevant to materials science and manufacturing, as this article illustrates.

The article offers many other applications in line with the topics discussed in previous sections. One vignette describes the use of convolutional neural networks to predict the calculations of finite element simulations with a high degree of accuracy at a fraction of computational cost. Yet another vignette describes manufacturing a cold-spray robot that incorporates closed-loop, real-time autonomous decision making based on in situ analysis of the manufacturing process.

Further advances and challenges

It is the authors’ opinion that it is myopic to think of the application of AI/ML to materials science as purely “data driven.” Knowledge in materials science is multifaceted. Our understanding of materials comes from experimental data, rich information from microscopy images or spectra, computer simulations, our knowledge of physics and chemistry, and years of practical experience and know-how contained in the brains of highly trained experts, or in the literature. (We would like to point out here that one major and exciting topic we did not have space to discuss is the work in Natural Language Processing to extract knowledge from the materials literature.)^30,31 Our dialect of AI should strive to incorporate these myriad forms of knowledge and information. As part of the ML revolution, we ought to think about how to do this properly, to limit biases and rigorously quantify uncertainties.

Consider the case of training an autonomous robot researcher to identify optimal synthesis and processing conditions that maximize some property of interest for the material it is tasked to synthesize. Experts in materials synthesis have, through years of trial and error, collected a library of specialized recipes, techniques, and tricks they use to fabricate good materials. It would be wasteful to not teach such knowledge to the robot to help in its search. To some, the idea of teaching this knowledge to the robot, rather than having it acquire or discover it on its own through the examination of a large set of training data is tantamount to cheating. To this, we would counter that such knowledge is training data. It is simply not represented as rows of numbers in some data file. But it is knowledge and it should be utilized. Therefore, a problem that we must address is how to represent such knowledge in a way amenable to training an AI/ML model and how to develop models that are capable of reasoning using this knowledge.

To those aware of the history of AI, this idea may seem similar to that of “expert systems,”³² which proliferated in the 1970s and 1980s. These systems were centered around the development of knowledge bases, descriptive languages for such knowledge, and inference or reasoning engines. The use of these systems fell out of favor around the 1990s, and many cited the difficulty in properly or concisely representing knowledge and populating the knowledge base as contributing heavily to their failure. It was too much effort to get domain experts to codify their knowledge for use in these systems.³³

While the authors do not claim that a revival of expert systems is the proper solution to this multifaceted knowledge problem, we feel that many of the ideas of the field deserve a fresh reexamination, especially under the light of our modern computational prowess and the advent of DL and autonomous feature engineering. As a cautionary tale against immediately discounting out-of-style techniques, we point out that neural networks suffered its own time as technologie démodé for about two decades between the 1970s and 1990s as well (signaling the first AI winter). Their revival occurred later on due to new training algorithms in addition to a general increase in computational power. Modern-day DL owes its existence to this revival. Could a similar revival of knowledge-based techniques, coupled with the power of DL and ideas from uncertainty quantification, nucleate a new phase for AI in materials? We can only speculate. Whatever form the next steps take, we hope that the technologies will become better at utilizing the breadth of rich and varied information available throughout all of materials science.