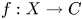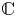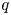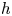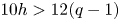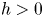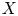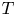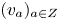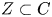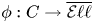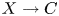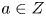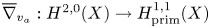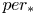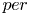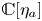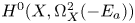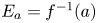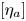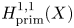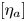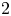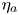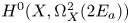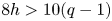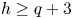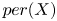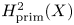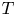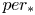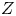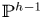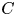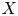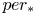1. Introduction
Suppose that ![]() $\mathcal {M}$ is a moduli stack of smooth projective varieties over
$\mathcal {M}$ is a moduli stack of smooth projective varieties over ![]() ${\mathbb {C}}$ and that
${\mathbb {C}}$ and that ![]() $per:\mathcal {M}\to \mathcal {P}=D/\Gamma$ is a corresponding period map. The derivative of
$per:\mathcal {M}\to \mathcal {P}=D/\Gamma$ is a corresponding period map. The derivative of ![]() $per$ is a homomorphism
$per$ is a homomorphism
The local Torelli problem is that of describing the kernel of this homomorphism and the local Schottky problem is the problem of describing its image. We say that the local Torelli theorem holds at a point ![]() $x$ of
$x$ of ![]() $\mathcal {M}$ if the derivative
$\mathcal {M}$ if the derivative ![]() $per_*$ of
$per_*$ of ![]() $per$ is injective at
$per$ is injective at ![]() $x$ and that the generic local Torelli theorem holds if it holds at every generic point of
$x$ and that the generic local Torelli theorem holds if it holds at every generic point of ![]() $\mathcal {M}$. We also say that the generic Torelli theorem holds if
$\mathcal {M}$. We also say that the generic Torelli theorem holds if ![]() $per$ has degree
$per$ has degree ![]() $1$ onto its image. The Schottky problem asks for a description of the image of the period map.
$1$ onto its image. The Schottky problem asks for a description of the image of the period map.
As explained on p. 228 of [Reference GriffithsGri84], if the generic local Torelli theorem holds and if it can be proved that a variety ![]() $X$ can be recovered from knowledge of the period point
$X$ can be recovered from knowledge of the period point ![]() $per(X)$ and the subspace
$per(X)$ and the subspace ![]() $per_*(T_\mathcal {M}(X))$ of the tangent space
$per_*(T_\mathcal {M}(X))$ of the tangent space ![]() $T_\mathcal {P}(X)$, then the generic Torelli theorem also holds.
$T_\mathcal {P}(X)$, then the generic Torelli theorem also holds.
In this paper we consider the problem for elliptic surfaces ![]() $f:X\to C$ with no multiple fibres (such surfaces we shall call simple) and show that the situation is closely parallel to that for curves, as follows.
$f:X\to C$ with no multiple fibres (such surfaces we shall call simple) and show that the situation is closely parallel to that for curves, as follows.
Suppose that the geometric genus of ![]() $X$ is
$X$ is ![]() $h$ and its irregularity
$h$ and its irregularity ![]() $q$, that
$q$, that ![]() $b_1(X)$ is even (so that, by a result of Miyaoka [Reference MiyaokaMiy74],
$b_1(X)$ is even (so that, by a result of Miyaoka [Reference MiyaokaMiy74], ![]() $X$ is Kähler), that
$X$ is Kähler), that ![]() $10 h>12(q-1)$ and that
$10 h>12(q-1)$ and that ![]() $h\ge q+3$. Assume also that
$h\ge q+3$. Assume also that ![]() $X$ is general, in a sense to be made precise later. Then we prove the following results, the first two of which are well-known tautologies.
$X$ is general, in a sense to be made precise later. Then we prove the following results, the first two of which are well-known tautologies.
For ![]() $a\in C$ we let
$a\in C$ we let ![]() $E_a$ denote the fibre
$E_a$ denote the fibre ![]() $f^{-1}(a)$ and
$f^{-1}(a)$ and ![]() $\omega _a^\vee$ the line in
$\omega _a^\vee$ the line in ![]() $H^{2,0}(X)^\vee$ whose kernel is
$H^{2,0}(X)^\vee$ whose kernel is ![]() $H^0(X,\Omega ^2_X(-E_a))$.
$H^0(X,\Omega ^2_X(-E_a))$.
Assume that ![]() $10 h>12(q-1)$.
$10 h>12(q-1)$.
(1) There is a classifying morphism
 $\phi =\phi _f:C\to \overline {\mathcal {M}}_1$, where
$\phi =\phi _f:C\to \overline {\mathcal {M}}_1$, where  $\overline {\mathcal {M}}_1$ is the stack of stable curves of genus
$\overline {\mathcal {M}}_1$ is the stack of stable curves of genus  $1$. Set
$1$. Set  $Z=\operatorname {Ram}_\phi \subset C$, the ramification
$Z=\operatorname {Ram}_\phi \subset C$, the ramification  $t$ divisor. (Up to noise which is removed by the language of stacks, this is the locus where the derivative of the
$t$ divisor. (Up to noise which is removed by the language of stacks, this is the locus where the derivative of the  $j$-invariant vanishes.)
$j$-invariant vanishes.)(2) If also
 $X$ is algebraic, then the tangent space at the point
$X$ is algebraic, then the tangent space at the point  $X$ to the stack of algebraic elliptic surfaces is naturally isomorphic to an invertible sheaf on
$X$ to the stack of algebraic elliptic surfaces is naturally isomorphic to an invertible sheaf on  $Z$.
$Z$.(3) Every choice of a point
 $a$ in
$a$ in  $Z$ and of a local coordinate on
$Z$ and of a local coordinate on  $C$ at
$C$ at  $a$ defines a
$a$ defines a  $1$-parameter variation of
$1$-parameter variation of  $X$. This is based on the construction of the version of Schiffer variations that is described on p. 443 of [Reference GarabedianGar49].
$X$. This is based on the construction of the version of Schiffer variations that is described on p. 443 of [Reference GarabedianGar49].(4) The derivative of the period map of this variation, which is a linear map
 $\overline {\nabla }_a:H^{2,0}(X)\to H^{1,1}_{\rm prim}(X),$ is of rank
$\overline {\nabla }_a:H^{2,0}(X)\to H^{1,1}_{\rm prim}(X),$ is of rank  $1$.
$1$.(5) There is a meromorphic
 $2$-form
$2$-form  $\eta _a\in H^0(X,\Omega ^2_X(2E_a))$ of the second kind (that is, the residue of
$\eta _a\in H^0(X,\Omega ^2_X(2E_a))$ of the second kind (that is, the residue of  $\eta _a$ along
$\eta _a$ along  $E_a$ vanishes) such that
$E_a$ vanishes) such that  $\overline {\nabla }_a=\omega _a^\vee \otimes [\eta _a]$.
$\overline {\nabla }_a=\omega _a^\vee \otimes [\eta _a]$.(6) Assume also that
 $h\ge q+3$. Then the canonical model of
$h\ge q+3$. Then the canonical model of  $X$ is a copy of
$X$ is a copy of  $C$ embedded as a curve of degree
$C$ embedded as a curve of degree  $h+q-1$ in a projective space
$h+q-1$ in a projective space  ${\mathbb {P}}(H^{2,0}(X)^\vee )={\mathbb {P}}^{h-1}$, and the set
${\mathbb {P}}(H^{2,0}(X)^\vee )={\mathbb {P}}^{h-1}$, and the set  $Z$ can be recovered, as a finite point set in
$Z$ can be recovered, as a finite point set in  ${\mathbb {P}}^{h-1}$, from the finite subset
${\mathbb {P}}^{h-1}$, from the finite subset  $\{\omega _a^\vee \otimes [\eta _a]\}_{a\in Z}$ of
$\{\omega _a^\vee \otimes [\eta _a]\}_{a\in Z}$ of  ${\mathbb {P}}((H^{2,0}(X)^\vee \otimes H^{1,1}_{\rm prim}(X))^\vee )$. Indeed, we exploit this set of
${\mathbb {P}}((H^{2,0}(X)^\vee \otimes H^{1,1}_{\rm prim}(X))^\vee )$. Indeed, we exploit this set of  $N$ points in projective space as an analogue of the theta divisor on the Jacobian of a curve.
$N$ points in projective space as an analogue of the theta divisor on the Jacobian of a curve.(7) Assume that
 $h\ge q+3$ and that
$h\ge q+3$ and that  $4h>5(q-1)$. Then the curve
$4h>5(q-1)$. Then the curve  $C$ can be recovered from
$C$ can be recovered from  $Z$ in
$Z$ in  ${\mathbb {P}}^{h-1}$ via quadratic interpolation.
${\mathbb {P}}^{h-1}$ via quadratic interpolation.(8) Given
 $C$ and
$C$ and  $Z$, we then prove a generic Torelli theorem for Jacobian elliptic surfaces.
$Z$, we then prove a generic Torelli theorem for Jacobian elliptic surfaces.
Remark It is clear that some of these constructions can be still be made when the phrase ‘elliptic curve’ is replaced by ‘Calabi–Yau variety whose compactified moduli stack is a smooth ![]() $1$-dimensional Deligne–Mumford stack whose first Chern class is positive’.
$1$-dimensional Deligne–Mumford stack whose first Chern class is positive’.
An essential difference between the case of curves and that of elliptic surfaces, however, is that for curves these variations arise for any point ![]() $a$ on
$a$ on ![]() $C$ while for surfaces they only arise for points of the ramification divisor
$C$ while for surfaces they only arise for points of the ramification divisor ![]() $Z$. Indeed, for other points
$Z$. Indeed, for other points ![]() $x$ of
$x$ of ![]() $C$ there is no meromorphic
$C$ there is no meromorphic ![]() $2$-form of the second kind with double poles along
$2$-form of the second kind with double poles along ![]() $E_x$. (I am grateful to Richard Thomas for explaining this to me.)
$E_x$. (I am grateful to Richard Thomas for explaining this to me.)
We now give some more details.
Definition 1.1 An elliptic surface is Jacobian if it has a specified section.
Jacobian implies simple, but not conversely.
In this paper the things of primary concern are the stacks ![]() $\mathcal {SE}$ and
$\mathcal {SE}$ and ![]() $\widetilde {\mathcal {JE}}$ of simple and Jacobian elliptic surfaces
$\widetilde {\mathcal {JE}}$ of simple and Jacobian elliptic surfaces ![]() $f:X\to C$ that are smooth and relatively minimal. We also consider the stack
$f:X\to C$ that are smooth and relatively minimal. We also consider the stack ![]() $\mathcal {JE}$ whose objects are the relative canonical models of surfaces in
$\mathcal {JE}$ whose objects are the relative canonical models of surfaces in ![]() $\widetilde {\mathcal {JE}}$; given
$\widetilde {\mathcal {JE}}$; given ![]() $f:X\to C$ in
$f:X\to C$ in ![]() $\widetilde {\mathcal {JE}}$ the relative canonical model is obtained by contracting all vertical
$\widetilde {\mathcal {JE}}$ the relative canonical model is obtained by contracting all vertical ![]() $(-2)$-curves in
$(-2)$-curves in ![]() ${\mathbb {X}}$ that are disjoint from the given section. There is an obvious morphism
${\mathbb {X}}$ that are disjoint from the given section. There is an obvious morphism ![]() $\widetilde {\mathcal {JE}}\to \mathcal {JE}$ that is a bijection on geometric points. At the level of miniversal deformation spaces, this morphism can be described by taking the geometric quotient by an action of the relevant Weyl group, as was shown by Artin and Brieskorn.
$\widetilde {\mathcal {JE}}\to \mathcal {JE}$ that is a bijection on geometric points. At the level of miniversal deformation spaces, this morphism can be described by taking the geometric quotient by an action of the relevant Weyl group, as was shown by Artin and Brieskorn.
We shall say that a surface ![]() $X$ in
$X$ in ![]() $\mathcal {SE}$ is general if its
$\mathcal {SE}$ is general if its ![]() $j$-invariant
$j$-invariant ![]() $C\to {\mathbb {P}}^1_j$ is non-constant and its singular fibres are all of type
$C\to {\mathbb {P}}^1_j$ is non-constant and its singular fibres are all of type ![]() $I_1$. We let
$I_1$. We let ![]() $\mathcal {SE}^{\rm gen}$ and
$\mathcal {SE}^{\rm gen}$ and ![]() $\mathcal {JE}^{\rm gen}$ denote the stacks of general simple surfaces and general Jacobian surfaces; these are open substacks of
$\mathcal {JE}^{\rm gen}$ denote the stacks of general simple surfaces and general Jacobian surfaces; these are open substacks of ![]() $\mathcal {SE}$ and
$\mathcal {SE}$ and ![]() $\widetilde {\mathcal {JE}}$. Note that
$\widetilde {\mathcal {JE}}$. Note that ![]() $\mathcal {JE}^{\rm gen}$ maps isomorphically to its image in
$\mathcal {JE}^{\rm gen}$ maps isomorphically to its image in ![]() $\mathcal {JE}$ so is also naturally an open substack of
$\mathcal {JE}$ so is also naturally an open substack of ![]() $\mathcal {JE}$. Then to give a point in
$\mathcal {JE}$. Then to give a point in ![]() $\mathcal {SE}^{\rm gen}$ is equivalent to giving a classifying morphism
$\mathcal {SE}^{\rm gen}$ is equivalent to giving a classifying morphism ![]() $F:C\to \overline {\mathcal {M}}_1$ that is non-constant and unramified over
$F:C\to \overline {\mathcal {M}}_1$ that is non-constant and unramified over ![]() $j=\infty$. The stack
$j=\infty$. The stack ![]() $\overline {\mathcal {M}}_1$ is not the same as the stack
$\overline {\mathcal {M}}_1$ is not the same as the stack ![]() $\overline {\mathcal {E}\ell \ell }$ of stable generalized elliptic curves; these stacks will be discussed in more detail in § 2. Giving a point in
$\overline {\mathcal {E}\ell \ell }$ of stable generalized elliptic curves; these stacks will be discussed in more detail in § 2. Giving a point in ![]() $\mathcal {JE}^{\rm gen}$ is equivalent to giving a morphism
$\mathcal {JE}^{\rm gen}$ is equivalent to giving a morphism ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$ that is non-constant over the
$\phi :C\to \overline {\mathcal {E}\ell \ell }$ that is non-constant over the ![]() $j$-line and unramified over
$j$-line and unramified over ![]() $j=\infty$.
$j=\infty$.
Assume that ![]() $f:X\to C$ is general in
$f:X\to C$ is general in ![]() $\mathcal {JE}$. Let
$\mathcal {JE}$. Let ![]() $Z$ denote the ramification divisor in
$Z$ denote the ramification divisor in ![]() $C$ of
$C$ of ![]() $\phi$. Say
$\phi$. Say ![]() $h=p_g(X)$ and
$h=p_g(X)$ and ![]() $q=h^1(\mathcal {O}_X)$, so that
$q=h^1(\mathcal {O}_X)$, so that ![]() $q$ is also the genus of
$q$ is also the genus of ![]() $C$. We shall assume throughout this paper that
$C$. We shall assume throughout this paper that
These assumptions ensure that ![]() $\deg \phi ^*T_{\overline {\mathcal {E}\ell \ell }}> 2q-2$, which in turn ensures the vanishing of certain obstruction spaces. From § 6 onwards we shall make the stronger assumptions that
$\deg \phi ^*T_{\overline {\mathcal {E}\ell \ell }}> 2q-2$, which in turn ensures the vanishing of certain obstruction spaces. From § 6 onwards we shall make the stronger assumptions that
These assumptions make it possible to apply theorems of Mumford and Saint-Donat about the defining equations of linearly normal projective curves.
Write ![]() $N=10h+8(1-q)$. Then, as is well known,
$N=10h+8(1-q)$. Then, as is well known, ![]() $\mathcal {SE}$ is smooth at the point corresponding to
$\mathcal {SE}$ is smooth at the point corresponding to ![]() $X$ and
$X$ and
Then we shall prove effective forms of both a generic local Torelli theorem and a generic Torelli theorem for the weight ![]() $2$ Hodge structure on
$2$ Hodge structure on ![]() $X$, in the following sense.
$X$, in the following sense.
If ![]() $X$ is a surface in
$X$ is a surface in ![]() $\mathcal {JE}$ with specified section
$\mathcal {JE}$ with specified section ![]() $\sigma$ and fibre
$\sigma$ and fibre ![]() $\xi$, then
$\xi$, then ![]() $H^2_{\rm prim}(X)$ and
$H^2_{\rm prim}(X)$ and ![]() $H^{1,1}_{\rm prim}(X)$ will denote the orthogonal complement
$H^{1,1}_{\rm prim}(X)$ will denote the orthogonal complement ![]() $\langle \sigma,\xi \rangle ^\perp$. If
$\langle \sigma,\xi \rangle ^\perp$. If ![]() $X$ is in
$X$ is in ![]() $\mathcal {SE}$ but is not necessarily algebraic, then
$\mathcal {SE}$ but is not necessarily algebraic, then ![]() $H^2_{\rm prim}(X)$ and
$H^2_{\rm prim}(X)$ and ![]() $H^{1,1}_{\rm prim}(X)$ will denote
$H^{1,1}_{\rm prim}(X)$ will denote ![]() $\xi ^\perp /{\mathbb {Z}}\xi$; these two definitions are equivalent for
$\xi ^\perp /{\mathbb {Z}}\xi$; these two definitions are equivalent for ![]() $X\in \mathcal {JE}$. Observe that
$X\in \mathcal {JE}$. Observe that ![]() $h^{1,1}_{\rm prim}(X)=N$. In fact
$h^{1,1}_{\rm prim}(X)=N$. In fact ![]() $\dim \mathcal {JE}=N$ also, so that
$\dim \mathcal {JE}=N$ also, so that ![]() $\dim \mathcal {JE} =h^{1,1}_{\rm prim}(X)$. We shall use this coincidence in § 5 to enhance the local structure of the derivative of the period map.
$\dim \mathcal {JE} =h^{1,1}_{\rm prim}(X)$. We shall use this coincidence in § 5 to enhance the local structure of the derivative of the period map.
From the description of ![]() $\mathcal {JE}^{\rm gen}$ as the stack that parametrizes those non-constant morphisms from curves to
$\mathcal {JE}^{\rm gen}$ as the stack that parametrizes those non-constant morphisms from curves to ![]() $\overline {\mathcal {E}\ell \ell }$ that are unramified over
$\overline {\mathcal {E}\ell \ell }$ that are unramified over ![]() $j=\infty$ we shall prove the following theorem, which appears as Theorem 4.10. It is the main result of the paper; everything else follows from it.
$j=\infty$ we shall prove the following theorem, which appears as Theorem 4.10. It is the main result of the paper; everything else follows from it.
Theorem 1.4 Fix a surface ![]() $f:X\to C$ that is a point
$f:X\to C$ that is a point ![]() $X$ of
$X$ of ![]() $\mathcal {JE}^{\rm gen}$ and corresponds to
$\mathcal {JE}^{\rm gen}$ and corresponds to ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$. For
$\phi :C\to \overline {\mathcal {E}\ell \ell }$. For ![]() $P\in C$ put
$P\in C$ put ![]() $E_P=f^{-1}(P)$ and let
$E_P=f^{-1}(P)$ and let ![]() $Z$ denote the ramification divisor
$Z$ denote the ramification divisor ![]() $\operatorname {Ram}_\phi$.
$\operatorname {Ram}_\phi$.
(1) Given a point
 $a$ of
$a$ of  $Z$ there is a tangent line
$Z$ there is a tangent line  ${\mathbb {C}} v_a$ to
${\mathbb {C}} v_a$ to  $\mathcal {JE}$ at the point
$\mathcal {JE}$ at the point  $X$.
$X$.(2) There is a meromorphic
 $2$-form
$2$-form  $\eta _a\in H^0(X,\Omega ^2_X(2E_a))$ of the second kind (that is, its residue
$\eta _a\in H^0(X,\Omega ^2_X(2E_a))$ of the second kind (that is, its residue  $\operatorname {Res}_{E_a}\eta _a$ vanishes).
$\operatorname {Res}_{E_a}\eta _a$ vanishes).(3) The corresponding map
is of rank \[ \overline{\nabla}_{v_a}:H^{2.0}(X)\to H^{1,1}_{\rm prim}(X) \]
\[ \overline{\nabla}_{v_a}:H^{2.0}(X)\to H^{1,1}_{\rm prim}(X) \]
 $1$. Its kernel is the space
$1$. Its kernel is the space  $H^0(X,\Omega ^2_X(-E_a))$ of
$H^0(X,\Omega ^2_X(-E_a))$ of  $2$-forms that vanish along
$2$-forms that vanish along  $E_a$ and its image is the line generated by the class
$E_a$ and its image is the line generated by the class  $[\eta _a]$ of
$[\eta _a]$ of  $\eta _a$, modulo
$\eta _a$, modulo  $\xi$.
$\xi$.
In order to prove this theorem we shall use Schiffer variations to construct, for each point ![]() $a\in \operatorname {Ram}_\phi$ where the ramification index of
$a\in \operatorname {Ram}_\phi$ where the ramification index of ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$ is
$\phi :C\to \overline {\mathcal {E}\ell \ell }$ is ![]() $m$ (so that
$m$ (so that ![]() $a$ is of multiplicity
$a$ is of multiplicity ![]() $m-1$ in
$m-1$ in ![]() $Z$) an
$Z$) an ![]() $(m-1)$-parameter deformation
$(m-1)$-parameter deformation ![]() $\mathcal {C}\to \Delta ^{m-1}$ of
$\mathcal {C}\to \Delta ^{m-1}$ of ![]() $C$ whose derivative can be calculated. Thus, when
$C$ whose derivative can be calculated. Thus, when ![]() $X$ is a point of
$X$ is a point of ![]() $\mathcal {JE}^{\rm gen}$, we have a detailed description of an
$\mathcal {JE}^{\rm gen}$, we have a detailed description of an ![]() $N$-dimensional subspace of the tangent space to moduli inside the tangent space to the period domain as the subspace spanned by certain explicit tensors of rank
$N$-dimensional subspace of the tangent space to moduli inside the tangent space to the period domain as the subspace spanned by certain explicit tensors of rank ![]() $1$. (Masa-Hiko Saito [Reference SaitoSai83] has proved the local Torelli theorem for simple elliptic surfaces with non-constant
$1$. (Masa-Hiko Saito [Reference SaitoSai83] has proved the local Torelli theorem for simple elliptic surfaces with non-constant ![]() $j$-invariant and for many surfaces with constant
$j$-invariant and for many surfaces with constant ![]() $j$-invariant. We shall extend his result slightly; see Theorem 2.10.)
$j$-invariant. We shall extend his result slightly; see Theorem 2.10.)
It is a matter of linear algebra to recover ![]() $Z$ as a subset of the projective space
$Z$ as a subset of the projective space ![]() ${\mathbb {P}}^{h-1}$ in which
${\mathbb {P}}^{h-1}$ in which ![]() $C$ is embedded as the canonical model of
$C$ is embedded as the canonical model of ![]() $X$, under the assumption that
$X$, under the assumption that ![]() $Z$ is reduced. We then use a theorem of Mumford [Reference MumfordMum70] and Saint-Donat [Reference Saint-DonatSai72], to the effect that linearly normal curves of genus
$Z$ is reduced. We then use a theorem of Mumford [Reference MumfordMum70] and Saint-Donat [Reference Saint-DonatSai72], to the effect that linearly normal curves of genus ![]() $q$ and degree at least
$q$ and degree at least ![]() $2q+2$ are intersections of quadrics, to show that
$2q+2$ are intersections of quadrics, to show that ![]() $C$ is determined by quadratic interpolation through
$C$ is determined by quadratic interpolation through ![]() $Z$. We go on to prove that from the pair
$Z$. We go on to prove that from the pair ![]() $(C,Z)$ we can recover the classifying morphism
$(C,Z)$ we can recover the classifying morphism ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$, modulo the automorphism group
$\phi :C\to \overline {\mathcal {E}\ell \ell }$, modulo the automorphism group ![]() ${\mathbb {G}}_m$ of
${\mathbb {G}}_m$ of ![]() $\overline {\mathcal {E}\ell \ell }$ provided that
$\overline {\mathcal {E}\ell \ell }$ provided that ![]() $\phi$ is generic. This recovery of
$\phi$ is generic. This recovery of ![]() $C$ and
$C$ and ![]() $\phi$ from the period data we regard as an effective theorem. It shows that any failure of generic Torelli for Jacobian surfaces can be detected in a pencil that is the closure of the
$\phi$ from the period data we regard as an effective theorem. It shows that any failure of generic Torelli for Jacobian surfaces can be detected in a pencil that is the closure of the ![]() ${\mathbb {G}}_m$-orbit thorough a generic point of
${\mathbb {G}}_m$-orbit thorough a generic point of ![]() $\mathcal {JE}^{\rm gen}$. (The fact that the automorphisms of
$\mathcal {JE}^{\rm gen}$. (The fact that the automorphisms of ![]() $\overline {\mathcal {E}\ell \ell }$ obstruct a direct deduction of generic Torelli from knowledge of
$\overline {\mathcal {E}\ell \ell }$ obstruct a direct deduction of generic Torelli from knowledge of ![]() $C$ and
$C$ and ![]() $Z$ was observed by Cox and Donagi [Reference Cox and DonagiCD86].)
$Z$ was observed by Cox and Donagi [Reference Cox and DonagiCD86].)
Once we know that the base curve ![]() $C$ is determined by Hodge-theoretical data of weight
$C$ is determined by Hodge-theoretical data of weight ![]() $2$ we go on to prove the generic Torelli theorem for Jacobian elliptic surfaces via ideas similar to those used by Chakiris [Reference ChakirisCha82, Reference ChakirisCha84] to prove generic Torelli when
$2$ we go on to prove the generic Torelli theorem for Jacobian elliptic surfaces via ideas similar to those used by Chakiris [Reference ChakirisCha82, Reference ChakirisCha84] to prove generic Torelli when ![]() $C={\mathbb {P}}^1$, but reinforced by the minimal model program.
$C={\mathbb {P}}^1$, but reinforced by the minimal model program.
There is also some further structure on the period map for ![]() $\mathcal {JE}^{\rm gen}$: the relevant vector bundles and homomorphisms between them can be described in terms of line bundles on the universal ramification divisor
$\mathcal {JE}^{\rm gen}$: the relevant vector bundles and homomorphisms between them can be described in terms of line bundles on the universal ramification divisor ![]() $\mathcal {Z}^{\rm gen}$ over
$\mathcal {Z}^{\rm gen}$ over ![]() $\mathcal {JE}^{\rm gen}$ of the universal classifying morphism to
$\mathcal {JE}^{\rm gen}$ of the universal classifying morphism to ![]() $\overline {\mathcal {E}\ell \ell }$. This can be seen as a local solution to the Schottky problem. The details are stated in Theorem 4.11.
$\overline {\mathcal {E}\ell \ell }$. This can be seen as a local solution to the Schottky problem. The details are stated in Theorem 4.11.
We also give a variational form of a partial solution to the global Schottky problem.
If ![]() $\mathcal {X}$ is a Deligne–Mumford stack, then
$\mathcal {X}$ is a Deligne–Mumford stack, then ![]() $[\mathcal {X}]$ will denote its geometric quotient.
$[\mathcal {X}]$ will denote its geometric quotient.
2. Preliminaries on stacks and tangent spaces
Everything in the next two sections is well known; if it is not due to either Kas [Reference KasKas66] or Kodaira [Reference KodairaKod63], then it is folklore.
The stack ![]() $\overline {\mathcal {E}\ell \ell }$ is the Deligne–Mumford stack over
$\overline {\mathcal {E}\ell \ell }$ is the Deligne–Mumford stack over ![]() ${\mathbb {C}}$ of stable generalized elliptic curves; that is, an
${\mathbb {C}}$ of stable generalized elliptic curves; that is, an ![]() $S$-point of
$S$-point of ![]() $\overline {\mathcal {E}\ell \ell }$ is a flat projective morphism
$\overline {\mathcal {E}\ell \ell }$ is a flat projective morphism ![]() $Y\to S$ with a section
$Y\to S$ with a section ![]() $S_0$ contained in the relatively smooth locus of
$S_0$ contained in the relatively smooth locus of ![]() $Y\to S$ and whose geometric fibres are reduced and irreducible nodal curves of arithmetic genus
$Y\to S$ and whose geometric fibres are reduced and irreducible nodal curves of arithmetic genus ![]() $1$. Such a curve is then, locally on
$1$. Such a curve is then, locally on ![]() $S$, a plane cubic with affine equation
$S$, a plane cubic with affine equation
where ![]() $g_4$ and
$g_4$ and ![]() $g_6$ are not both zero, so that
$g_6$ are not both zero, so that ![]() $\overline {\mathcal {E}\ell \ell }$ is the quotient stack
$\overline {\mathcal {E}\ell \ell }$ is the quotient stack ![]() ${\mathbb {P}}(4,6)=({\mathbb {A}}^2-\{0\})/{\mathbb {G}}_m$, where
${\mathbb {P}}(4,6)=({\mathbb {A}}^2-\{0\})/{\mathbb {G}}_m$, where ![]() ${\mathbb {G}}_m$ acts on
${\mathbb {G}}_m$ acts on ![]() ${\mathbb {A}}^2$ with weights
${\mathbb {A}}^2$ with weights ![]() $4,6$. Note that
$4,6$. Note that ![]() ${\mathbb {G}}_m$ acts on
${\mathbb {G}}_m$ acts on ![]() ${\mathbb {A}}^2$ via a homomorphism
${\mathbb {A}}^2$ via a homomorphism ![]() ${\mathbb {G}}_m\to {\mathbb {G}}_m^2$ (whose kernel is
${\mathbb {G}}_m\to {\mathbb {G}}_m^2$ (whose kernel is ![]() $\mu _2$) and the standard action of
$\mu _2$) and the standard action of ![]() ${\mathbb {G}}_m^2$ on
${\mathbb {G}}_m^2$ on ![]() ${\mathbb {A}}^2$, so that there is a residual action of
${\mathbb {A}}^2$, so that there is a residual action of ![]() ${\mathbb {G}}_m$ on
${\mathbb {G}}_m$ on ![]() $\overline {\mathcal {E}\ell \ell }$. This exhibits
$\overline {\mathcal {E}\ell \ell }$. This exhibits ![]() ${\mathbb {G}}_m$ as the full automorphism group of
${\mathbb {G}}_m$ as the full automorphism group of ![]() $\overline {\mathcal {E}\ell \ell }$; cf. Theorem 8.1 of [Reference Behrend and NoohiBN06] and the calculation there on p. 139.
$\overline {\mathcal {E}\ell \ell }$; cf. Theorem 8.1 of [Reference Behrend and NoohiBN06] and the calculation there on p. 139.
The geometric quotient ![]() $[\overline {\mathcal {E}\ell \ell }]$ of
$[\overline {\mathcal {E}\ell \ell }]$ of ![]() $\overline {\mathcal {E}\ell \ell }$ is the compactified
$\overline {\mathcal {E}\ell \ell }$ is the compactified ![]() $j$-line
$j$-line ![]() ${\mathbb {P}}^1_j$; if
${\mathbb {P}}^1_j$; if ![]() $\rho :\overline {\mathcal {E}\ell \ell }\to {\mathbb {P}}^1_j$ is the quotient morphism, then the automorphism group of each fibre of
$\rho :\overline {\mathcal {E}\ell \ell }\to {\mathbb {P}}^1_j$ is the quotient morphism, then the automorphism group of each fibre of ![]() $\rho$ is
$\rho$ is ![]() ${\mathbb {Z}}/2$, except over
${\mathbb {Z}}/2$, except over ![]() $j=j_6=0$, where it is
$j=j_6=0$, where it is ![]() ${\mathbb {Z}}/6$, and over
${\mathbb {Z}}/6$, and over ![]() $j=j_4=1728$, where it is
$j=j_4=1728$, where it is ![]() ${\mathbb {Z}}/4$. So
${\mathbb {Z}}/4$. So ![]() $\deg \rho =1/2$. As is well known, it is possible to write down a generalized elliptic curve over the open locus
$\deg \rho =1/2$. As is well known, it is possible to write down a generalized elliptic curve over the open locus ![]() $U$ of
$U$ of ![]() ${\mathbb {P}}^1_j$ defined by
${\mathbb {P}}^1_j$ defined by ![]() $j\ne 0,1728$, so that there is a section of
$j\ne 0,1728$, so that there is a section of ![]() $\rho$ over
$\rho$ over ![]() $U$. Moreover,
$U$. Moreover, ![]() $\rho ^{-1}(U)$ is isomorphic to
$\rho ^{-1}(U)$ is isomorphic to ![]() $U\times B({\mathbb {Z}}/2)$, but there is no global section of
$U\times B({\mathbb {Z}}/2)$, but there is no global section of ![]() $\rho$.
$\rho$.
There are two obvious line bundles on ![]() $\overline {\mathcal {E}\ell \ell }$: the bundle
$\overline {\mathcal {E}\ell \ell }$: the bundle ![]() $M$ of modular forms of weight
$M$ of modular forms of weight ![]() $1$, which is identified with the conormal bundle of the zero-section of the universal stable generalized elliptic curve, and the tangent bundle
$1$, which is identified with the conormal bundle of the zero-section of the universal stable generalized elliptic curve, and the tangent bundle ![]() $T_{\overline {\mathcal {E}\ell \ell }}$.
$T_{\overline {\mathcal {E}\ell \ell }}$.
Lemma 2.1 We have ![]() $T_{\overline {\mathcal {E}\ell \ell }}\cong M^{\otimes 10}$,
$T_{\overline {\mathcal {E}\ell \ell }}\cong M^{\otimes 10}$, ![]() $\deg M=1/24$ and
$\deg M=1/24$ and ![]() $\deg T_{\overline {\mathcal {E}\ell \ell }}=5/12$.
$\deg T_{\overline {\mathcal {E}\ell \ell }}=5/12$.
Proof. Quite generally the Picard group of ![]() ${\mathbb {P}}(a,b)$ is generated by
${\mathbb {P}}(a,b)$ is generated by ![]() $\mathcal {O}(1)$, which has degree
$\mathcal {O}(1)$, which has degree ![]() $1/ab$, and
$1/ab$, and ![]() $T_{{\mathbb {P}}(a,b)}$ is isomorphic to
$T_{{\mathbb {P}}(a,b)}$ is isomorphic to ![]() $\mathcal {O}(a+b)$, which then has degree
$\mathcal {O}(a+b)$, which then has degree ![]() $(a+b)/ab$.
$(a+b)/ab$.
The objects of the stack ![]() $\overline {\mathcal {M}}_1$ are stable curves of genus
$\overline {\mathcal {M}}_1$ are stable curves of genus ![]() $1$; the geometric fibres are isomorphic to stable generalized elliptic curves, but no section is given. This is an Artin stack, but not Deligne–Mumford. Indeed, the word ‘stable’ in this context is an abuse of language, but I am optimistic that it will cause no confusion.
$1$; the geometric fibres are isomorphic to stable generalized elliptic curves, but no section is given. This is an Artin stack, but not Deligne–Mumford. Indeed, the word ‘stable’ in this context is an abuse of language, but I am optimistic that it will cause no confusion.
Let ![]() $\mathcal {C}\to \overline {\mathcal {M}}_1$ and
$\mathcal {C}\to \overline {\mathcal {M}}_1$ and ![]() $\mathcal {E}\to \overline {\mathcal {E}\ell \ell }$ denote the universal objects and let
$\mathcal {E}\to \overline {\mathcal {E}\ell \ell }$ denote the universal objects and let ![]() $\mathcal {G}\to \overline {\mathcal {E}\ell \ell }$ denote the Néron model of
$\mathcal {G}\to \overline {\mathcal {E}\ell \ell }$ denote the Néron model of ![]() $\mathcal {E}\to \overline {\mathcal {E}\ell \ell }$, so that
$\mathcal {E}\to \overline {\mathcal {E}\ell \ell }$, so that ![]() $\mathcal {G}$ is the open substack of
$\mathcal {G}$ is the open substack of ![]() $\mathcal {E}$ obtained by deleting the singular point of the fibre over
$\mathcal {E}$ obtained by deleting the singular point of the fibre over ![]() $j=\infty$.
$j=\infty$.
The next result is due to Altman and Kleiman [Reference Altman and KleimanAK80], although reformulated here in the language of stacks. We have chosen to include a slightly different proof that emphasizes automorphism groups rather than Picard varieties so that the relevant classifying stacks enter more easily.
Theorem 2.2 There is a morphism ![]() $\pi :\overline {\mathcal {M}}_1\to \overline {\mathcal {E}\ell \ell }$ via which
$\pi :\overline {\mathcal {M}}_1\to \overline {\mathcal {E}\ell \ell }$ via which ![]() $\overline {\mathcal {M}}_1$ is isomorphic to the classifying stack
$\overline {\mathcal {M}}_1$ is isomorphic to the classifying stack ![]() $B\mathcal {G}$ over
$B\mathcal {G}$ over ![]() $\overline {\mathcal {E}\ell \ell }$.
$\overline {\mathcal {E}\ell \ell }$.
Proof. Let ![]() $G\to \overline {\mathcal {M}}_1$ denote the connected component of the relative automorphism group scheme of
$G\to \overline {\mathcal {M}}_1$ denote the connected component of the relative automorphism group scheme of ![]() $\mathcal {C}\to \overline {\mathcal {M}}_1$. Thus,
$\mathcal {C}\to \overline {\mathcal {M}}_1$. Thus, ![]() $G\to \overline {\mathcal {M}}_1$ is elliptic over the open substack
$G\to \overline {\mathcal {M}}_1$ is elliptic over the open substack ![]() $M_1$ of
$M_1$ of ![]() $\overline {\mathcal {M}}_1$ defined by
$\overline {\mathcal {M}}_1$ defined by ![]() $j\ne \infty$ and over
$j\ne \infty$ and over ![]() $j=\infty$ the fibre of
$j=\infty$ the fibre of ![]() $G$ is the multiplicative group
$G$ is the multiplicative group ![]() ${\mathbb {G}}_m$.
${\mathbb {G}}_m$.
Lemma 2.3 There is a unique open embedding ![]() $G\hookrightarrow \widetilde {G}$, over
$G\hookrightarrow \widetilde {G}$, over ![]() $\overline {\mathcal {M}}_1$, where
$\overline {\mathcal {M}}_1$, where ![]() $\widetilde {G}\to \overline {\mathcal {M}}_1$ is a stable generalized elliptic curve and
$\widetilde {G}\to \overline {\mathcal {M}}_1$ is a stable generalized elliptic curve and ![]() $G$ is its relative smooth locus.
$G$ is its relative smooth locus.
Proof. To construct ![]() $\widetilde {G}$ we need to patch the puncture of
$\widetilde {G}$ we need to patch the puncture of ![]() $G\to \overline {\mathcal {M}}_1$ that lies over
$G\to \overline {\mathcal {M}}_1$ that lies over ![]() $j=\infty$. In a suitable neighbourhood
$j=\infty$. In a suitable neighbourhood ![]() $S$ of the locus
$S$ of the locus ![]() $j=\infty$ in
$j=\infty$ in ![]() $\overline {\mathcal {M}}_1$ the process of patching the puncture is a matter of ‘reversing the process of deleting a closed point from a normal
$\overline {\mathcal {M}}_1$ the process of patching the puncture is a matter of ‘reversing the process of deleting a closed point from a normal ![]() $2$-dimensional analytic space (or scheme)’, so the patch is unique if it exists. Therefore, it is enough to exhibit the patch locally on
$2$-dimensional analytic space (or scheme)’, so the patch is unique if it exists. Therefore, it is enough to exhibit the patch locally on ![]() $\overline {\mathcal {M}}_1$, in the neighbourhood
$\overline {\mathcal {M}}_1$, in the neighbourhood ![]() $S$.
$S$.
Put ![]() $\mathcal {C}_S=\mathcal {C}\times _{\overline {\mathcal {M}}_1}S$. Since
$\mathcal {C}_S=\mathcal {C}\times _{\overline {\mathcal {M}}_1}S$. Since ![]() $S$ is local and
$S$ is local and ![]() $\mathcal {C}_S\to S$ is generically smooth, there is a section over
$\mathcal {C}_S\to S$ is generically smooth, there is a section over ![]() $S$ of
$S$ of ![]() $\mathcal {C}_S\to S$ that is contained in the relative smooth locus. Use this section to put the structure of a stable generalized elliptic curve on
$\mathcal {C}_S\to S$ that is contained in the relative smooth locus. Use this section to put the structure of a stable generalized elliptic curve on ![]() $\mathcal {C}_S\to S$. This structure on
$\mathcal {C}_S\to S$. This structure on ![]() $\mathcal {C}_S\to S$ provides the patch for
$\mathcal {C}_S\to S$ provides the patch for ![]() $G_S=G\times _{\overline {\mathcal {M}}_1}S\to S$ and yields
$G_S=G\times _{\overline {\mathcal {M}}_1}S\to S$ and yields ![]() $\widetilde {G}\to S$; the lemma is proved.
$\widetilde {G}\to S$; the lemma is proved.
Sending ![]() $\mathcal {C}\to \overline {\mathcal {M}}_1$ to
$\mathcal {C}\to \overline {\mathcal {M}}_1$ to ![]() $\widetilde {G}\to \overline {\mathcal {M}}_1$ defines a morphism
$\widetilde {G}\to \overline {\mathcal {M}}_1$ defines a morphism ![]() $\pi : \overline {\mathcal {M}}_1\to \overline {\mathcal {E}\ell \ell }$.
$\pi : \overline {\mathcal {M}}_1\to \overline {\mathcal {E}\ell \ell }$.
A gerbe is a morphism of stacks that is locally surjective on both objects and morphisms. A neutral gerbe is a gerbe with a section.
Lemma 2.4 The morphism ![]() $\pi$ is a neutral gerbe.
$\pi$ is a neutral gerbe.
Proof. It is enough to show that:
(1)
 $\pi$ has a section (then it is certainly locally surjective on objects); and
$\pi$ has a section (then it is certainly locally surjective on objects); and(2)
 $\pi$ is locally surjective on morphisms.
$\pi$ is locally surjective on morphisms.
For part (1), use the forgetful morphism ![]() $\overline {\mathcal {E}\ell \ell }\to \overline {\mathcal {M}}_1$ to get a section of
$\overline {\mathcal {E}\ell \ell }\to \overline {\mathcal {M}}_1$ to get a section of ![]() $\pi$.
$\pi$.
Part (2) is equally clear: a morphism of stable generalized elliptic curves is, in particular, a morphism of the underlying stable curves.
Finally, suppose that ![]() $\mathcal {X}\to \mathcal {Y}$ is a neutral gerbe with section
$\mathcal {X}\to \mathcal {Y}$ is a neutral gerbe with section ![]() $s:\mathcal {Y}\to \mathcal {X}$. The stabilizer group scheme is a group scheme
$s:\mathcal {Y}\to \mathcal {X}$. The stabilizer group scheme is a group scheme ![]() $\mathcal {H}'\to \mathcal {X}$; define
$\mathcal {H}'\to \mathcal {X}$; define ![]() $\mathcal {H}\to \mathcal {Y}$ to be the pull back of
$\mathcal {H}\to \mathcal {Y}$ to be the pull back of ![]() $\mathcal {H}'$ via
$\mathcal {H}'$ via ![]() $s$. If
$s$. If ![]() $\mathcal {H}\to \mathcal {Y}$ is flat, then [Reference Laumon and Moret-BaillyLM00] there is an isomorphism
$\mathcal {H}\to \mathcal {Y}$ is flat, then [Reference Laumon and Moret-BaillyLM00] there is an isomorphism ![]() $\mathcal {X}\to B\mathcal {H}$. Since the Néron model
$\mathcal {X}\to B\mathcal {H}$. Since the Néron model ![]() $\mathcal {G}\to \overline {\mathcal {E}\ell \ell }$ is flat, the theorem is proved.
$\mathcal {G}\to \overline {\mathcal {E}\ell \ell }$ is flat, the theorem is proved.
Note that ![]() $G\to \overline {\mathcal {M}}_1$ is isomorphic to the pull back under
$G\to \overline {\mathcal {M}}_1$ is isomorphic to the pull back under ![]() $\pi$ of the Néron model
$\pi$ of the Néron model ![]() $\mathcal {G}\to \overline {\mathcal {E}\ell \ell }$.
$\mathcal {G}\to \overline {\mathcal {E}\ell \ell }$.
As already remarked, a general simple surface ![]() $f:X\to C$ determines, and is determined by, a morphism
$f:X\to C$ determines, and is determined by, a morphism ![]() $F=F_f:C\to \overline {\mathcal {M}}_1$ that is unramified over
$F=F_f:C\to \overline {\mathcal {M}}_1$ that is unramified over ![]() $j=\infty$. Let
$j=\infty$. Let ![]() $\phi =\phi _f=\pi \circ F:C\to \overline {\mathcal {E}\ell \ell }$ denote the composite, so that the induced Jacobian elliptic surface is the compactified relative automorphism group scheme of
$\phi =\phi _f=\pi \circ F:C\to \overline {\mathcal {E}\ell \ell }$ denote the composite, so that the induced Jacobian elliptic surface is the compactified relative automorphism group scheme of ![]() $f:X\to C$.
$f:X\to C$.
For example, if ![]() $f:X\to {\mathbb {P}}^1$ is a primary Hopf surface, then
$f:X\to {\mathbb {P}}^1$ is a primary Hopf surface, then ![]() $\phi _f$ is constant: the relative automorphism group scheme is a constant relative group scheme
$\phi _f$ is constant: the relative automorphism group scheme is a constant relative group scheme ![]() $E\times {\mathbb {P}}^1\to {\mathbb {P}}^1$.
$E\times {\mathbb {P}}^1\to {\mathbb {P}}^1$.
Lemma 2.5 If ![]() $X\to C$ has non-constant
$X\to C$ has non-constant ![]() $j$-invariant, then the irregularity
$j$-invariant, then the irregularity ![]() $q$ of
$q$ of ![]() $X$ equals the geometric genus of
$X$ equals the geometric genus of ![]() $C$.
$C$.
Proof. This is well known, and easy.
Lemma 2.6 Suppose that ![]() $f:X\to C$ is a general simple surface. Then
$f:X\to C$ is a general simple surface. Then
(1)
 $\deg \phi = 2 c_2(X)=24\chi (X,\mathcal {O}_X)$;
$\deg \phi = 2 c_2(X)=24\chi (X,\mathcal {O}_X)$;(2)
 $\deg \phi ^*M=\chi (X,\mathcal {O}_X\!)$;
$\deg \phi ^*M=\chi (X,\mathcal {O}_X\!)$;(3)
 $\deg \phi ^*T_{\overline {\mathcal {E}\ell \ell }}=10\chi (X,\mathcal {O}_X)$.
$\deg \phi ^*T_{\overline {\mathcal {E}\ell \ell }}=10\chi (X,\mathcal {O}_X)$.
Proof. Since ![]() $c_2(X)$ equals the total number of nodes in the singular fibres of
$c_2(X)$ equals the total number of nodes in the singular fibres of ![]() $X\to C$, part (1) follows from consideration of the inverse image of the locus
$X\to C$, part (1) follows from consideration of the inverse image of the locus ![]() $j=\infty$, the fact that
$j=\infty$, the fact that ![]() $\deg \rho =1/2$ and Noether's formula. The rest follows immediately.
$\deg \rho =1/2$ and Noether's formula. The rest follows immediately.
We next consider various tangent spaces.
Regard ![]() $B\mathcal {G}$ as the quotient of
$B\mathcal {G}$ as the quotient of ![]() $\overline {\mathcal {E}\ell \ell }$ by
$\overline {\mathcal {E}\ell \ell }$ by ![]() $\mathcal {G}$. Since
$\mathcal {G}$. Since ![]() $\overline {\mathcal {M}}_1$ is isomorphic to
$\overline {\mathcal {M}}_1$ is isomorphic to ![]() $B\mathcal {G}$, locally on
$B\mathcal {G}$, locally on ![]() $\overline {\mathcal {E}\ell \ell }$, the tangent complex
$\overline {\mathcal {E}\ell \ell }$, the tangent complex ![]() $T^\bullet _{\overline {\mathcal {M}}_1}$ is a
$T^\bullet _{\overline {\mathcal {M}}_1}$ is a ![]() $2$-term complex, which is obtained by descending a
$2$-term complex, which is obtained by descending a ![]() $2$-term complex on
$2$-term complex on ![]() $\overline {\mathcal {E}\ell \ell }$. In degree
$\overline {\mathcal {E}\ell \ell }$. In degree ![]() $0$, this complex is
$0$, this complex is ![]() $T_{\overline {\mathcal {E}\ell \ell }}$, in degree
$T_{\overline {\mathcal {E}\ell \ell }}$, in degree ![]() $-1$ it is the adjoint bundle
$-1$ it is the adjoint bundle ![]() $\operatorname {Ad} \mathcal {G}$ and the differential is the derivative of the action of
$\operatorname {Ad} \mathcal {G}$ and the differential is the derivative of the action of ![]() $\mathcal {G}$ on
$\mathcal {G}$ on ![]() $\overline {\mathcal {E}\ell \ell }$.
$\overline {\mathcal {E}\ell \ell }$.
Since this action is trivial, the differential in ![]() $T^\bullet _{\overline {\mathcal {M}}_1}$ is zero. Moreover, since
$T^\bullet _{\overline {\mathcal {M}}_1}$ is zero. Moreover, since ![]() $\mathcal {G}$ has no characters (it is generically an elliptic curve) it follows that
$\mathcal {G}$ has no characters (it is generically an elliptic curve) it follows that ![]() $T^\bullet _{\overline {\mathcal {M}}_1}$ is quasi-isomorphic to the pull back of the complex
$T^\bullet _{\overline {\mathcal {M}}_1}$ is quasi-isomorphic to the pull back of the complex ![]() $\operatorname {Ad} \mathcal {G}[1]\oplus T_{\overline {\mathcal {E}\ell \ell }}[0]$ on
$\operatorname {Ad} \mathcal {G}[1]\oplus T_{\overline {\mathcal {E}\ell \ell }}[0]$ on ![]() $\overline {\mathcal {E}\ell \ell }$.
$\overline {\mathcal {E}\ell \ell }$.
Note that ![]() $(\operatorname {Ad}\mathcal {G})^\vee$ is exactly the line bundle
$(\operatorname {Ad}\mathcal {G})^\vee$ is exactly the line bundle ![]() $M$ of modular forms of weight
$M$ of modular forms of weight ![]() $1$.
$1$.
Now fix a point ![]() $X$ of
$X$ of ![]() $\mathcal {SE}$. That is, we fix a general simple elliptic surface
$\mathcal {SE}$. That is, we fix a general simple elliptic surface ![]() $f:X\to C$. This equals the datum of a morphism
$f:X\to C$. This equals the datum of a morphism ![]() $F:C\to \overline {\mathcal {M}}_1$. Set
$F:C\to \overline {\mathcal {M}}_1$. Set ![]() $\phi =\pi \circ F:C\to \overline {\mathcal {E}\ell \ell }$. Then
$\phi =\pi \circ F:C\to \overline {\mathcal {E}\ell \ell }$. Then ![]() $F^*T^\bullet _{\overline {\mathcal {M}}_1}$ is quasi-isomorphic to
$F^*T^\bullet _{\overline {\mathcal {M}}_1}$ is quasi-isomorphic to ![]() $\phi ^*\operatorname {Ad} \mathcal {G}[1]\oplus \phi ^*T_{\overline {\mathcal {E}\ell \ell }}$. There is a distinguished triangle
$\phi ^*\operatorname {Ad} \mathcal {G}[1]\oplus \phi ^*T_{\overline {\mathcal {E}\ell \ell }}$. There is a distinguished triangle
where ![]() $K^\bullet$ is a
$K^\bullet$ is a ![]() $2$-term complex of coherent sheaves on
$2$-term complex of coherent sheaves on ![]() $C$,
$C$, ![]() $K^{-1}=\phi ^*\operatorname {Ad} \mathcal {G}$,
$K^{-1}=\phi ^*\operatorname {Ad} \mathcal {G}$, ![]() $K^0$ is the skyscraper sheaf
$K^0$ is the skyscraper sheaf ![]() $\mathrm {coker} (T_C\to \phi ^*T_{\overline {\mathcal {E}\ell \ell }})$ and the differential in
$\mathrm {coker} (T_C\to \phi ^*T_{\overline {\mathcal {E}\ell \ell }})$ and the differential in ![]() $K^\bullet$ is zero.
$K^\bullet$ is zero.
Proposition 2.7 The tangent space ![]() $T_{\mathcal {SE}}(X)$ is naturally isomorphic to the hypercohomology group
$T_{\mathcal {SE}}(X)$ is naturally isomorphic to the hypercohomology group ![]() ${\mathbb {H}}^0(C,K^\bullet )$ and the obstructions to the smoothness of
${\mathbb {H}}^0(C,K^\bullet )$ and the obstructions to the smoothness of ![]() $\mathcal {SE}$ at
$\mathcal {SE}$ at ![]() $X$ lie in
$X$ lie in ![]() ${\mathbb {H}}^1(C,K^\bullet )$.
${\mathbb {H}}^1(C,K^\bullet )$.
Proof. This follows from the identification of the points of ![]() $\mathcal {SE}$ with morphisms from curves to
$\mathcal {SE}$ with morphisms from curves to ![]() $\overline {\mathcal {M}}_1$. In this latter context the result is well known.
$\overline {\mathcal {M}}_1$. In this latter context the result is well known.
Let ![]() $Z$ denote the ramification divisor
$Z$ denote the ramification divisor ![]() $Z=\operatorname {Ram}_\phi =\operatorname {Ram}_F$ on
$Z=\operatorname {Ram}_\phi =\operatorname {Ram}_F$ on ![]() $C$. Then
$C$. Then ![]() $K^0$ is an invertible sheaf on
$K^0$ is an invertible sheaf on ![]() $Z$, so that there is a non-canonical isomorphism
$Z$, so that there is a non-canonical isomorphism ![]() $K^0\mathop {\to }\limits ^{\cong }\mathcal {O}_Z$.
$K^0\mathop {\to }\limits ^{\cong }\mathcal {O}_Z$.
The distinguished triangle just mentioned gives an exact sequence
 \begin{align*} {0}&\to H^0(C,T_C) \to{\mathbb{H}}^0(C,F^*T^\bullet_{\overline{\mathcal{M}}_1})\to{\mathbb{H}}^0(C,K^\bullet)\\ &\to {H^1(C,T_C)} \to {\mathbb{H}}^1(C,F^*T^\bullet_{bsm_1})\to{\mathbb{H}}^1(C,K^\bullet)\to 0. \end{align*}
\begin{align*} {0}&\to H^0(C,T_C) \to{\mathbb{H}}^0(C,F^*T^\bullet_{\overline{\mathcal{M}}_1})\to{\mathbb{H}}^0(C,K^\bullet)\\ &\to {H^1(C,T_C)} \to {\mathbb{H}}^1(C,F^*T^\bullet_{bsm_1})\to{\mathbb{H}}^1(C,K^\bullet)\to 0. \end{align*}
Then ![]() $H^2(C,\phi ^*\operatorname {Ad} G)=0$ and
$H^2(C,\phi ^*\operatorname {Ad} G)=0$ and ![]() $H^1(C,\phi ^*T_{\overline {\mathcal {E}\ell \ell }})=0$, since
$H^1(C,\phi ^*T_{\overline {\mathcal {E}\ell \ell }})=0$, since
from the assumption (1.2), so that ![]() ${\mathbb {H}}^1(C,K^\bullet )={\mathbb {H}}^1(C,F^*T^\bullet _{\overline {\mathcal {M}}_1})=0$ and there is an exact commutative diagram
${\mathbb {H}}^1(C,K^\bullet )={\mathbb {H}}^1(C,F^*T^\bullet _{\overline {\mathcal {M}}_1})=0$ and there is an exact commutative diagram

in which the two middle rows are canonically split.
(1) The stack
 $\mathcal {SE}$ is smooth at the point
$\mathcal {SE}$ is smooth at the point  $X$.
$X$.(2) Its dimension there is
 $11h+8(1-q)$.
$11h+8(1-q)$.(3) The degree of the ramification divisor
 $\operatorname {Ram}_\phi =\operatorname {Ram}_F$ is
$\operatorname {Ram}_\phi =\operatorname {Ram}_F$ is  $N$.
$N$.(4) We have
 $\phi ^*M\cong f_*\omega _{X/C}\cong (R^1f_*\mathcal {O}_X)^\vee$ and
$\phi ^*M\cong f_*\omega _{X/C}\cong (R^1f_*\mathcal {O}_X)^\vee$ and  $\deg \phi ^*M=\chi (X,\mathcal {O}_X)=h+1-q$.
$\deg \phi ^*M=\chi (X,\mathcal {O}_X)=h+1-q$.
Proof. Except for part (4), which is well known, this follows from the preceding discussion.
Suppose that ![]() $f:X\to C$ is a point of
$f:X\to C$ is a point of ![]() $\mathcal {JE}^{\rm gen}$ and defines
$\mathcal {JE}^{\rm gen}$ and defines ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$. Set
$\phi :C\to \overline {\mathcal {E}\ell \ell }$. Set ![]() $Z=\operatorname {Ram}_\phi$.
$Z=\operatorname {Ram}_\phi$.
(1) There is a short exact sequence
 \[ 0\to H^0(C,\phi^*T_{\overline{\mathcal{E}\ell\ell}})\to T_{\mathcal{JE}}(X) \to H^1(C,T_C)\to 0. \]
\[ 0\to H^0(C,\phi^*T_{\overline{\mathcal{E}\ell\ell}})\to T_{\mathcal{JE}}(X) \to H^1(C,T_C)\to 0. \]
(2) The tangent space
 $T_{\mathcal {JE}}(X)$ is naturally isomorphic to
$T_{\mathcal {JE}}(X)$ is naturally isomorphic to  $H^0(Z,K^0)$.
$H^0(Z,K^0)$.(3) The moduli stack
 $\mathcal {JE}$ is smooth at the point
$\mathcal {JE}$ is smooth at the point  $X$ and its dimension there is
$X$ and its dimension there is  $N$.
$N$.
Since ![]() $Z$ is
$Z$ is ![]() $0$-dimensional and
$0$-dimensional and ![]() $K^0$ is an invertible sheaf on
$K^0$ is an invertible sheaf on ![]() $Z$,
$Z$, ![]() $H^0(Z,K^0)$ is non-canonically isomorphic to
$H^0(Z,K^0)$ is non-canonically isomorphic to ![]() $H^0(Z,\mathcal {O}_Z)$.
$H^0(Z,\mathcal {O}_Z)$.
We shall usually write ![]() $\phi ^*M=L=f_*\omega _{X/C}$. Then
$\phi ^*M=L=f_*\omega _{X/C}$. Then ![]() $\phi ^*T_{\overline {\mathcal {E}\ell \ell }}\cong L^{\otimes 10}$, so that
$\phi ^*T_{\overline {\mathcal {E}\ell \ell }}\cong L^{\otimes 10}$, so that
At this point we give a slight refinement of Saito's local Torelli theorem. The argument is essentially his.
Theorem 2.10 Suppose that ![]() $f:X\to C$ is a simple elliptic surface with
$f:X\to C$ is a simple elliptic surface with ![]() $r$ singular fibres. Put
$r$ singular fibres. Put ![]() $L=f_*\omega _{X/C}$. Assume that
$L=f_*\omega _{X/C}$. Assume that ![]() $r\ge \deg L+3$ and that
$r\ge \deg L+3$ and that ![]() $\deg L\ge 2$. Then the local Torelli theorem holds for
$\deg L\ge 2$. Then the local Torelli theorem holds for ![]() $X$.
$X$.
Proof. From the main result of [Reference SaitoSai83] it is enough to consider the situation where the ![]() $j$-invariant is constant. Following [Reference SaitoSai83] it is enough to show that the natural homomorphisms
$j$-invariant is constant. Following [Reference SaitoSai83] it is enough to show that the natural homomorphisms
and
are surjective. Recall that ![]() $K_X\sim f^*(K_C+L)$, so that
$K_X\sim f^*(K_C+L)$, so that ![]() $f_*(\Omega ^1_X\otimes \Omega ^2_X\!)\cong \mathcal {O}_C(K_C+L)\otimes f_*\Omega ^1_X$, and that
$f_*(\Omega ^1_X\otimes \Omega ^2_X\!)\cong \mathcal {O}_C(K_C+L)\otimes f_*\Omega ^1_X$, and that ![]() $\vert K_C+L\vert$ has no base points.
$\vert K_C+L\vert$ has no base points.
Lemma 2.11 If ![]() $\mathcal {F},\mathcal {G}$ are coherent sheaves on a
$\mathcal {F},\mathcal {G}$ are coherent sheaves on a ![]() $1$-dimensional projective scheme
$1$-dimensional projective scheme ![]() $C$ over a field
$C$ over a field ![]() $k$ and if
$k$ and if ![]() $\mathcal {F}$ is generated by
$\mathcal {F}$ is generated by ![]() $H^0(C,\mathcal {F})$, then the natural multiplication
$H^0(C,\mathcal {F})$, then the natural multiplication
is surjective.
Proof. There is an exact sequence
tensoring this with ![]() $\mathcal {G}$ gives an exact sequence
$\mathcal {G}$ gives an exact sequence
Taking ![]() $H^1$ of this sequence gives the result.
$H^1$ of this sequence gives the result.
In particular, taking ![]() $\mathcal {F}=\Omega ^1_C\otimes L=f_*\Omega ^2_X$ and
$\mathcal {F}=\Omega ^1_C\otimes L=f_*\Omega ^2_X$ and ![]() $\mathcal {G}=f_*\Omega ^1_X$ shows that
$\mathcal {G}=f_*\Omega ^1_X$ shows that ![]() $\mu _1$ is surjective.
$\mu _1$ is surjective.
Now consider ![]() $\mu _2$. Set
$\mu _2$. Set ![]() $A=\sum _1^r a_i$, the critical subset of
$A=\sum _1^r a_i$, the critical subset of ![]() $C$. The exact sequences (4.17) and (4.18) of [Reference SaitoSai83] are
$C$. The exact sequences (4.17) and (4.18) of [Reference SaitoSai83] are
and
where ![]() $\mathcal {T}^1$ is a skyscraper sheaf. The second sequence then gives
$\mathcal {T}^1$ is a skyscraper sheaf. The second sequence then gives
where ![]() $\delta \ge 0$, via the process of saturating a subsheaf. Since
$\delta \ge 0$, via the process of saturating a subsheaf. Since ![]() $\deg A>\deg L$, by assumption, this last sequence splits and
$\deg A>\deg L$, by assumption, this last sequence splits and
From its definition, ![]() $\mu _2$ is then the direct sum
$\mu _2$ is then the direct sum
of multiplication maps
and
The first of these is obviously surjective, while the surjectivity of the second follows from [Reference MumfordMum70, Theorem 6, p. 52] and the facts that ![]() $\deg (K_C+L)\ge 2q$ and
$\deg (K_C+L)\ge 2q$ and ![]() $\deg (K_C-L+A+\delta )\ge 2q+1$.
$\deg (K_C-L+A+\delta )\ge 2q+1$.
3. The comparison between  $\mathcal {SE}^{\rm gen}$ and
$\mathcal {SE}^{\rm gen}$ and  $\mathcal {JE}^{\rm gen}$
$\mathcal {JE}^{\rm gen}$
The morphism ![]() $\pi :\overline {\mathcal {M}}_1\to \overline {\mathcal {E}\ell \ell }$ defines a morphism
$\pi :\overline {\mathcal {M}}_1\to \overline {\mathcal {E}\ell \ell }$ defines a morphism ![]() $\Pi :\mathcal {SE}^{\rm gen}\to \mathcal {JE}^{\rm gen}$. If we fix a point
$\Pi :\mathcal {SE}^{\rm gen}\to \mathcal {JE}^{\rm gen}$. If we fix a point ![]() $f:X\to C$ of
$f:X\to C$ of ![]() $\mathcal {JE}^{\rm gen}$, then
$\mathcal {JE}^{\rm gen}$, then ![]() $\Pi ^{-1}(X)$ is identified with
$\Pi ^{-1}(X)$ is identified with ![]() $H^1(C,\mathcal {H})$, where
$H^1(C,\mathcal {H})$, where ![]() $\mathcal {H}\to C$ is the Néron model of
$\mathcal {H}\to C$ is the Néron model of ![]() $X\to C$.
$X\to C$.
The sheaves ![]() $L^\vee$ and
$L^\vee$ and ![]() $\mathcal {H}$ are group schemes over
$\mathcal {H}$ are group schemes over ![]() $C$. Define
$C$. Define ![]() $\mathcal {F}=R^1f_*{\mathbb {Z}}$; this is a constructible sheaf of
$\mathcal {F}=R^1f_*{\mathbb {Z}}$; this is a constructible sheaf of ![]() ${\mathbb {Z}}$-modules on
${\mathbb {Z}}$-modules on ![]() $C$ that is of generic rank
$C$ that is of generic rank ![]() $2$.
$2$.
The following results are due, in essence, to Kodaira. In particular, Proposition 3.2 is a variant of [Reference KodairaKod63, Theorem 11.7, p. 1341]; there he proves only that ![]() $H^2(C,\mathcal {F})$ is finite, but he does not assume that
$H^2(C,\mathcal {F})$ is finite, but he does not assume that ![]() $f:X\to C$ is general.
$f:X\to C$ is general.
Lemma 3.1 There is a short exact sequence
of sheaves of commutative groups on ![]() $C$.
$C$.
Proof. This follows from the exponential exact sequence on ![]() $X$ and the identification
$X$ and the identification ![]() $\mathcal {H}=\ker (R^1f_*\mathcal {O}_X^*\to R^2f_*{\mathbb {Z}})$.
$\mathcal {H}=\ker (R^1f_*\mathcal {O}_X^*\to R^2f_*{\mathbb {Z}})$.
Proposition 3.2 We have ![]() $H^2(C,\mathcal {F})=0$ and the homomorphism
$H^2(C,\mathcal {F})=0$ and the homomorphism ![]() $H^1(C,L^\vee )\to H^1(C,\mathcal {H})$ is surjective.
$H^1(C,L^\vee )\to H^1(C,\mathcal {H})$ is surjective.
Proof. It is enough to show that ![]() $H^2(C,\mathcal {F})=0$.
$H^2(C,\mathcal {F})=0$.
For any ring ![]() $A$, there is a Leray spectral sequence
$A$, there is a Leray spectral sequence
Since the fibres of ![]() $f$ are irreducible curves and
$f$ are irreducible curves and ![]() $X\to C$ has a section, the hypotheses of Théorème 1.1 of [Reference Deligne and KatzDK, XVIII] are satisfied, so that this degenerates at
$X\to C$ has a section, the hypotheses of Théorème 1.1 of [Reference Deligne and KatzDK, XVIII] are satisfied, so that this degenerates at ![]() $E_2$. Take
$E_2$. Take ![]() $A={\mathbb {Z}}$; then there is a short exact sequence
$A={\mathbb {Z}}$; then there is a short exact sequence
Thus, ![]() $H^2(C,\mathcal {F})$ is identified with the torsion subgroup
$H^2(C,\mathcal {F})$ is identified with the torsion subgroup ![]() $\operatorname {Tors} H^3(X,{\mathbb {Z}})$ of
$\operatorname {Tors} H^3(X,{\mathbb {Z}})$ of ![]() $H^3(X,{\mathbb {Z}})$.
$H^3(X,{\mathbb {Z}})$.
Suppose that ![]() $\ell$ is a prime dividing the order of
$\ell$ is a prime dividing the order of ![]() $\operatorname {Tors} H^3(X,{\mathbb {Z}})$. Since
$\operatorname {Tors} H^3(X,{\mathbb {Z}})$. Since ![]() $H^4(X,A)$ is isomorphic to
$H^4(X,A)$ is isomorphic to ![]() $A$, it follows from taking cohomology of the short exact sequence
$A$, it follows from taking cohomology of the short exact sequence
that ![]() $H^3(X,{\mathbb {Z}}/\ell )\cong H^3(X,{\mathbb {Z}})\otimes {\mathbb {Z}}/\ell$. In addition, Poincaré duality gives an isomorphism
$H^3(X,{\mathbb {Z}}/\ell )\cong H^3(X,{\mathbb {Z}})\otimes {\mathbb {Z}}/\ell$. In addition, Poincaré duality gives an isomorphism ![]() $H^3(X,{\mathbb {Z}}/\ell )\to H^1(X,{\mathbb {Z}}/\ell )^\vee,$ where
$H^3(X,{\mathbb {Z}}/\ell )\to H^1(X,{\mathbb {Z}}/\ell )^\vee,$ where ![]() ${}^\vee$ denotes the dual
${}^\vee$ denotes the dual ![]() ${\mathbb {Z}}/\ell$-vector space.
${\mathbb {Z}}/\ell$-vector space.
The spectral sequence ![]() $E^{pq}_{r,{\mathbb {Z}}/\ell }$ shows that
$E^{pq}_{r,{\mathbb {Z}}/\ell }$ shows that ![]() $\beta :H^1(C,{\mathbb {Z}}/\ell )\to H^1(X,{\mathbb {Z}}/\ell )$ is injective, so if it is not surjective, then the map
$\beta :H^1(C,{\mathbb {Z}}/\ell )\to H^1(X,{\mathbb {Z}}/\ell )$ is injective, so if it is not surjective, then the map ![]() $i^*: H^1(X,{\mathbb {Z}}/\ell )\to H^1(\sigma,{\mathbb {Z}}/\ell )$ induced by the inclusion
$i^*: H^1(X,{\mathbb {Z}}/\ell )\to H^1(\sigma,{\mathbb {Z}}/\ell )$ induced by the inclusion ![]() $i:\sigma \hookrightarrow X$ of the zero section is not injective. Then there is an étale
$i:\sigma \hookrightarrow X$ of the zero section is not injective. Then there is an étale ![]() ${\mathbb {Z}}/\ell$-cover
${\mathbb {Z}}/\ell$-cover ![]() $\alpha :\widetilde X\to X$ that is split over
$\alpha :\widetilde X\to X$ that is split over ![]() $\sigma$. Thus,
$\sigma$. Thus, ![]() $\widetilde X\to C$ is elliptic and has a section
$\widetilde X\to C$ is elliptic and has a section ![]() $\widetilde {\sigma }$ such that
$\widetilde {\sigma }$ such that ![]() $N_{\widetilde {\sigma },\widetilde X}\cong N_{\sigma /X}$. However,
$N_{\widetilde {\sigma },\widetilde X}\cong N_{\sigma /X}$. However,
Thus, ![]() $\beta$ is an isomorphism, so that
$\beta$ is an isomorphism, so that ![]() $H^3(X,{\mathbb {Z}}/\ell )\cong ({\mathbb {Z}}/\ell )^{2q}$ and, therefore,
$H^3(X,{\mathbb {Z}}/\ell )\cong ({\mathbb {Z}}/\ell )^{2q}$ and, therefore, ![]() $H^3(X,{\mathbb {Z}})$ is torsion-free.
$H^3(X,{\mathbb {Z}})$ is torsion-free.
Let ![]() $\mathcal {SE}_{h,q}$ denote the substack of
$\mathcal {SE}_{h,q}$ denote the substack of ![]() $\mathcal {SE}$ that consists of surfaces whose geometric genus is
$\mathcal {SE}$ that consists of surfaces whose geometric genus is ![]() $h$ and whose irregularity is
$h$ and whose irregularity is ![]() $q$. This is a union of connected components of
$q$. This is a union of connected components of ![]() $\mathcal {SE}$.
$\mathcal {SE}$.
The next result is an immediate corollary of Proposition 3.2.
Corollary 3.3
(1) The closed substack
 $\Pi ^{-1}(X)$ is irreducible.
$\Pi ^{-1}(X)$ is irreducible.(2) The substack
 $\mathcal {SE}_{h,q}$ is irreducible.
$\mathcal {SE}_{h,q}$ is irreducible.
Now suppose that ![]() $Y\in \Pi ^{-1}(X)$. According to [Reference KodairaKod63, Theorem 11.5, p. 1338],
$Y\in \Pi ^{-1}(X)$. According to [Reference KodairaKod63, Theorem 11.5, p. 1338], ![]() $Y$ is algebraic if and only if it defines a torsion element of
$Y$ is algebraic if and only if it defines a torsion element of ![]() $H^1(C,\mathcal {H})$.
$H^1(C,\mathcal {H})$.
Proposition 3.4 The algebraic surfaces are dense in ![]() $\Pi ^{-1}(X)$.
$\Pi ^{-1}(X)$.
Proof. We must show that the image of ![]() $H^1(C,R^1f_*{\mathbb {Z}})\otimes {\mathbb {Q}}$ in
$H^1(C,R^1f_*{\mathbb {Z}})\otimes {\mathbb {Q}}$ in ![]() $H^1(C,R^1f_*\mathcal {O}_X\!)$ is dense.
$H^1(C,R^1f_*\mathcal {O}_X\!)$ is dense.
Let ![]() $\xi ^\perp$ denote the orthogonal complement of
$\xi ^\perp$ denote the orthogonal complement of ![]() $\xi$ in
$\xi$ in ![]() $H^2(X,{\mathbb {Z}})$. Then, via the Leray spectral sequence, there is a commutative square
$H^2(X,{\mathbb {Z}})$. Then, via the Leray spectral sequence, there is a commutative square

where the vertical arrows are isomorphisms. Then ![]() $\beta$ has dense image, from the Kähler property of
$\beta$ has dense image, from the Kähler property of ![]() $X$, and the proposition is proved.
$X$, and the proposition is proved.
4. Schiffer variations for elliptic surfaces and the derivative of the period map
Fix a curve ![]() $C$, a point
$C$, a point ![]() $a\in C$, a local coordinate
$a\in C$, a local coordinate ![]() $z$ on
$z$ on ![]() $C$ at
$C$ at ![]() $a$, an integer
$a$, an integer ![]() $e\ge 2$ and a real number
$e\ge 2$ and a real number ![]() $\delta$ such that
$\delta$ such that ![]() $0<\delta \ll 1$ and the region
$0<\delta \ll 1$ and the region ![]() $\vert z\vert <\delta$ is an open disc
$\vert z\vert <\delta$ is an open disc ![]() $D=D_z$ in
$D=D_z$ in ![]() $C$. We begin by recalling, from [Reference GarabedianGar49, p. 443], the construction of certain variations that we shall call Schiffer variations: these are families
$C$. We begin by recalling, from [Reference GarabedianGar49, p. 443], the construction of certain variations that we shall call Schiffer variations: these are families ![]() $\pi :\mathcal {C}\to \Delta ^{e-1}=\Delta ^{e-1}_{\underline {t}}$ over
$\pi :\mathcal {C}\to \Delta ^{e-1}=\Delta ^{e-1}_{\underline {t}}$ over ![]() $(e-1)$-dimensional polydiscs with coordinates
$(e-1)$-dimensional polydiscs with coordinates ![]() $\underline {t}=(t_2,\ldots,t_{e})$ whose closed fibre
$\underline {t}=(t_2,\ldots,t_{e})$ whose closed fibre ![]() $\pi ^{-1}(\underline {0})$ is
$\pi ^{-1}(\underline {0})$ is ![]() $C$. They are constructed as follows.
$C$. They are constructed as follows.
In ![]() ${\mathbb {C}}^{e-1}_{\underline {t}}$ take the polydisc
${\mathbb {C}}^{e-1}_{\underline {t}}$ take the polydisc ![]() $\Delta ^{e-1}_{\underline {t}}$ defined by
$\Delta ^{e-1}_{\underline {t}}$ defined by ![]() $\vert t_j\vert <\delta ^{4e}$ for all
$\vert t_j\vert <\delta ^{4e}$ for all ![]() $j$. In
$j$. In ![]() $C\times \Delta ^{e-1}_{\underline {t}}$ take the complement
$C\times \Delta ^{e-1}_{\underline {t}}$ take the complement ![]() $U$ of the closed subset
$U$ of the closed subset ![]() $\bigcup _j(\vert z\vert ^{4e}\le \vert t_j\vert )$. Thus,
$\bigcup _j(\vert z\vert ^{4e}\le \vert t_j\vert )$. Thus, ![]() $U$ is a thickening of the punctured curve
$U$ is a thickening of the punctured curve ![]() $C-\{a\}$. Then put
$C-\{a\}$. Then put ![]() $G=U\cap (\vert z\vert <\delta )$.
$G=U\cap (\vert z\vert <\delta )$.
In ![]() ${\mathbb {C}}^2_{z,w}\times \Delta ^{e-1}_{\underline {t}}$ take the subset
${\mathbb {C}}^2_{z,w}\times \Delta ^{e-1}_{\underline {t}}$ take the subset ![]() $F$ defined by
$F$ defined by
 \[ \vert t_j\vert < \vert z\vert^{4e} \ \forall j,\ \vert z\vert <\delta,\ \vert w-z\vert < \vert z\vert ^{2e}\ \textrm{and}\ w^e+e\sum_0^{e-2} t_{e-j}w^{j}=z^e. \]
\[ \vert t_j\vert < \vert z\vert^{4e} \ \forall j,\ \vert z\vert <\delta,\ \vert w-z\vert < \vert z\vert ^{2e}\ \textrm{and}\ w^e+e\sum_0^{e-2} t_{e-j}w^{j}=z^e. \]
Then there are projections ![]() $p:F\to U$ and
$p:F\to U$ and ![]() $q:F\to {\mathbb {C}}_w\times \Delta ^{e-1}_{\underline {t}}$.
$q:F\to {\mathbb {C}}_w\times \Delta ^{e-1}_{\underline {t}}$.
Lemma 4.1 The projections ![]() $p$ and
$p$ and ![]() $q$ are open embeddings.
$q$ are open embeddings.
Proof. It is enough to show that they are unramified and separate points.
The ramification locus of ![]() $p$ is defined by
$p$ is defined by
Since ![]() $\vert t_{e-j}\vert <\vert z\vert ^{4e}$ this gives
$\vert t_{e-j}\vert <\vert z\vert ^{4e}$ this gives ![]() $\vert w\vert <\vert z\vert ^4$. Then
$\vert w\vert <\vert z\vert ^4$. Then ![]() $\vert z\vert -\vert z\vert ^{2e}<\vert z\vert ^4$, so that
$\vert z\vert -\vert z\vert ^{2e}<\vert z\vert ^4$, so that ![]() $z=0$ and
$z=0$ and ![]() $p$ is unramified.
$p$ is unramified.
To check the separation of points, suppose that
for ![]() $\alpha =1,2$ and
$\alpha =1,2$ and ![]() $w_1\ne w_2$. Then
$w_1\ne w_2$. Then
 \[ \prod_{r=1}^{e-1}(w_1-\zeta_e^r w_2)=e\sum_{j=1}^{e-2} t_{e-j}\prod_{s=1}^{j-1}(w_1-\zeta_j^sw_2), \]
\[ \prod_{r=1}^{e-1}(w_1-\zeta_e^r w_2)=e\sum_{j=1}^{e-2} t_{e-j}\prod_{s=1}^{j-1}(w_1-\zeta_j^sw_2), \]
where, for any integer ![]() $n$,
$n$, ![]() $\zeta _n$ is a primitive
$\zeta _n$ is a primitive ![]() $n$th root of unity. Since
$n$th root of unity. Since ![]() $\vert w_1-z\vert <\vert z\vert ^{2e}$ and
$\vert w_1-z\vert <\vert z\vert ^{2e}$ and ![]() $\vert \zeta _j^s w_2-\zeta _j^s z\vert <\vert z\vert ^{2e}$ it follows that
$\vert \zeta _j^s w_2-\zeta _j^s z\vert <\vert z\vert ^{2e}$ it follows that
Thus,
 \[ \biggl\vert e\sum_{j=1}^{e-2} t_{e-j}\prod_{s=1}^{j-1}(w_1-\zeta_j^sw_2)\biggr\vert \le 4e(e-2)\vert z\vert^{4e+1}. \]
\[ \biggl\vert e\sum_{j=1}^{e-2} t_{e-j}\prod_{s=1}^{j-1}(w_1-\zeta_j^sw_2)\biggr\vert \le 4e(e-2)\vert z\vert^{4e+1}. \]
On the other hand, ![]() $\vert w_1-z\vert <\vert z\vert ^{2e}$ and
$\vert w_1-z\vert <\vert z\vert ^{2e}$ and ![]() $\vert \zeta _e^r-\zeta _e^rz\vert <\vert z\vert ^{2e},$ so that
$\vert \zeta _e^r-\zeta _e^rz\vert <\vert z\vert ^{2e},$ so that
where ![]() $\lambda =\vert \sin (2\pi /e)\vert /2$. Thus,
$\lambda =\vert \sin (2\pi /e)\vert /2$. Thus,
 \[ \biggl\vert \prod_{r=1}^{e-1}(w_1-\zeta_e^rw_2)\biggr\vert \ge\lambda^{e-1}\vert z\vert^{e-1} \]
\[ \biggl\vert \prod_{r=1}^{e-1}(w_1-\zeta_e^rw_2)\biggr\vert \ge\lambda^{e-1}\vert z\vert^{e-1} \]
and, therefore,
This contradiction proves the result for ![]() $p$.
$p$.
The argument for ![]() $q$ is similar but easier, so we omit it.
$q$ is similar but easier, so we omit it.
Lemma 4.2 The image of ![]() $p$ is
$p$ is ![]() $G$.
$G$.
Proof. This is a matter of showing that, given ![]() $(z,\underline {t})\in G$, we can solve the equation
$(z,\underline {t})\in G$, we can solve the equation ![]() $w^e+e\sum t_{e-j}w^j-z^e=0$ with
$w^e+e\sum t_{e-j}w^j-z^e=0$ with ![]() $\vert w-z\vert <\vert z\vert ^{2e}$. Without the inequality there are
$\vert w-z\vert <\vert z\vert ^{2e}$. Without the inequality there are ![]() $e$ solutions; if
$e$ solutions; if ![]() $\vert w-z\vert \ge \vert z\vert ^{2e}$ for all of them, then we get a contradiction to
$\vert w-z\vert \ge \vert z\vert ^{2e}$ for all of them, then we get a contradiction to ![]() $z^e-w^e=e\sum t_{e-j}w^j$ and the inequalities satisfied by the
$z^e-w^e=e\sum t_{e-j}w^j$ and the inequalities satisfied by the ![]() $t_{e-j}$.
$t_{e-j}$.
For each ![]() $\underline {t}\in \Delta ^{e-1}_{\underline {t}}$ the intersection
$\underline {t}\in \Delta ^{e-1}_{\underline {t}}$ the intersection ![]() $q(F)\cap ({\mathbb {C}}_w\times \{\underline {t}\})$ is an annulus
$q(F)\cap ({\mathbb {C}}_w\times \{\underline {t}\})$ is an annulus ![]() $A_{\underline {t}}$ in
$A_{\underline {t}}$ in ![]() ${\mathbb {C}}_w\times \{\underline {t}\}$ that surrounds zero. Let
${\mathbb {C}}_w\times \{\underline {t}\}$ that surrounds zero. Let ![]() $R_{\underline {t}}$ denote the open simply connected region in
$R_{\underline {t}}$ denote the open simply connected region in ![]() ${\mathbb {C}}_w\times \{\underline {t}\}$ that contains
${\mathbb {C}}_w\times \{\underline {t}\}$ that contains ![]() $0$ and has the same outer boundary as
$0$ and has the same outer boundary as ![]() $A_{\underline {t}}$, and put
$A_{\underline {t}}$, and put ![]() $H=\bigsqcup _{\underline {t}}R_{\underline {t}}$. Thus,
$H=\bigsqcup _{\underline {t}}R_{\underline {t}}$. Thus, ![]() $H$ is a tubular neighbourhood of
$H$ is a tubular neighbourhood of ![]() $\{0\}\times \Delta ^{e-1}_{\underline {t}}$ in
$\{0\}\times \Delta ^{e-1}_{\underline {t}}$ in ![]() ${\mathbb {C}}_w\times \Delta ^{e-1}_{\underline {t}}$ and
${\mathbb {C}}_w\times \Delta ^{e-1}_{\underline {t}}$ and ![]() $q(F)\subseteq H$.
$q(F)\subseteq H$.
Define ![]() $\mathcal {C}$ to be the result of glueing
$\mathcal {C}$ to be the result of glueing ![]() $U$ and
$U$ and ![]() $H$ together along
$H$ together along ![]() $F$ via the maps
$F$ via the maps ![]() $p$ and
$p$ and ![]() $q$. This is Hausdorff and, after shrinking
$q$. This is Hausdorff and, after shrinking ![]() $\Delta ^{e-1}_{\underline {t}}$ if necessary, the morphism
$\Delta ^{e-1}_{\underline {t}}$ if necessary, the morphism ![]() $\pi :\mathcal {C}\to \Delta ^{e-1}_{\underline {t}}$ is proper and is the morphism that we sought. This is sometimes expressed by saying that
$\pi :\mathcal {C}\to \Delta ^{e-1}_{\underline {t}}$ is proper and is the morphism that we sought. This is sometimes expressed by saying that ![]() $\mathcal {C}_{\underline {t}}$ is constructed from
$\mathcal {C}_{\underline {t}}$ is constructed from ![]() $C$ by deleting a small
$C$ by deleting a small ![]() $z$-disc around
$z$-disc around ![]() $a$ and glueing in a
$a$ and glueing in a ![]() $w$-disc, where
$w$-disc, where ![]() $w$ is defined implicitly by
$w$ is defined implicitly by ![]() $w^e+e\sum _0^{e-2} t_{e-j}w^{j}=z^e.$
$w^e+e\sum _0^{e-2} t_{e-j}w^{j}=z^e.$
Until after Theorem 4.11 we fix a point ![]() $f:X\to C$ of
$f:X\to C$ of ![]() $\mathcal {JE}^{\rm gen}$ and a point
$\mathcal {JE}^{\rm gen}$ and a point ![]() $a$ in the ramification divisor
$a$ in the ramification divisor ![]() $Z=\operatorname {Ram}_\phi$ of the classifying morphism
$Z=\operatorname {Ram}_\phi$ of the classifying morphism ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$. In particular,
$\phi :C\to \overline {\mathcal {E}\ell \ell }$. In particular, ![]() $\phi$ is unramified over
$\phi$ is unramified over ![]() $j=\infty$. Put
$j=\infty$. Put ![]() $E_a=f^{-1}(a)$ and denote by
$E_a=f^{-1}(a)$ and denote by ![]() $e=e(a)$ the ramification index at
$e=e(a)$ the ramification index at ![]() $a$ of
$a$ of ![]() $\phi$, so that
$\phi$, so that ![]() $a$ has multiplicity
$a$ has multiplicity ![]() $e-1$ in
$e-1$ in ![]() $Z$. Assume that the disc
$Z$. Assume that the disc ![]() $D$ is sufficiently small, so that it contains no other points of
$D$ is sufficiently small, so that it contains no other points of ![]() $Z$. We use the Schiffer variations of
$Z$. We use the Schiffer variations of ![]() $C$ that we have just described to construct variations of
$C$ that we have just described to construct variations of ![]() $X$.
$X$.
Proposition 4.3 For some choice of local coordinate ![]() $z$ on
$z$ on ![]() $C$ at
$C$ at ![]() $a$ the morphism
$a$ the morphism ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$ lifts to a morphism
$\phi :C\to \overline {\mathcal {E}\ell \ell }$ lifts to a morphism ![]() $\Phi :\mathcal {C}\to \overline {\mathcal {E}\ell \ell }$ in such a way that the restriction of
$\Phi :\mathcal {C}\to \overline {\mathcal {E}\ell \ell }$ in such a way that the restriction of ![]() $\Phi$ to
$\Phi$ to ![]() $U$ factors through the projection
$U$ factors through the projection ![]() $U\to C-\{a\}$.
$U\to C-\{a\}$.
Proof. Given a local coordinate ![]() $s$ on
$s$ on ![]() $\overline {\mathcal {E}\ell \ell }$ we have
$\overline {\mathcal {E}\ell \ell }$ we have ![]() $\phi ^*s=z^e$ for some local coordinate
$\phi ^*s=z^e$ for some local coordinate ![]() $z$ on
$z$ on ![]() $C$. Then we define
$C$. Then we define ![]() $\Phi$ on
$\Phi$ on ![]() $H$ by
$H$ by
 \[ \Phi^*s=w^e+e\sum_{j=0}^{e-2}t_{e-j}w^{j} \]
\[ \Phi^*s=w^e+e\sum_{j=0}^{e-2}t_{e-j}w^{j} \]
and on ![]() $U$ we define
$U$ we define ![]() $\Phi$ by composing
$\Phi$ by composing ![]() $\phi$ with the projection
$\phi$ with the projection ![]() $U\to C-\{a\}$.
$U\to C-\{a\}$.
Any Jacobian deformation of the surface ![]() $X$ determines, for each point
$X$ determines, for each point ![]() $a\in Z$, a deformation of the finite scheme
$a\in Z$, a deformation of the finite scheme ![]() $V_{e(a)}=\textbf {Spec}{\mathbb {C}}[t]/(t^{e(a)})$, so that there is a morphism of local analytic deformation spaces
$V_{e(a)}=\textbf {Spec}{\mathbb {C}}[t]/(t^{e(a)})$, so that there is a morphism of local analytic deformation spaces ![]() $\Psi :\operatorname {Def}_X\to \prod _{a\in Z}\operatorname {Def}_{V_{e(a)}}.$ Recall that
$\Psi :\operatorname {Def}_X\to \prod _{a\in Z}\operatorname {Def}_{V_{e(a)}}.$ Recall that ![]() $\operatorname {Def}_{V_{e(a)}}$ is smooth of dimension
$\operatorname {Def}_{V_{e(a)}}$ is smooth of dimension ![]() $e(a)-1$.
$e(a)-1$.
Proposition 4.4
(1) The morphism
 $\Psi$ is a local analytic isomorphism.
$\Psi$ is a local analytic isomorphism.(2) The universal ramification divisor
 $\mathcal {Z}$ is smooth over
$\mathcal {Z}$ is smooth over  ${\mathbb {C}}$.
${\mathbb {C}}$.
Proof. Part (1) is a an immediate consequence of the formula used to define ![]() $\Phi ^*s$, and part (2) follows at once.
$\Phi ^*s$, and part (2) follows at once.
Thus, we have morphisms ![]() $\mathcal {X} \mathop {\to }\limits ^{F}\mathcal {C}\to \Delta ^{e-1}_{\underline {t}}$ and
$\mathcal {X} \mathop {\to }\limits ^{F}\mathcal {C}\to \Delta ^{e-1}_{\underline {t}}$ and ![]() $F:\mathcal {X}\to \mathcal {C}$ is a family, parametrized by
$F:\mathcal {X}\to \mathcal {C}$ is a family, parametrized by ![]() $\Delta ^{e-1}_{\underline {t}}$, of Jacobian elliptic surface whose fibre over
$\Delta ^{e-1}_{\underline {t}}$, of Jacobian elliptic surface whose fibre over ![]() $0\in \Delta _{\underline {t}}^{e-1}$ is
$0\in \Delta _{\underline {t}}^{e-1}$ is ![]() $f:X\to C$.
$f:X\to C$.
Fix a suitable basis of ![]() $H_2(X,{\mathbb {Z}})$, which we identify with
$H_2(X,{\mathbb {Z}})$, which we identify with ![]() $H_2(\mathcal {X}_{\underline {t}},{\mathbb {Z}})$. Then there are holomorphic
$H_2(\mathcal {X}_{\underline {t}},{\mathbb {Z}})$. Then there are holomorphic ![]() $(e+1)$-forms
$(e+1)$-forms ![]() $\Omega ^{(1)},\ldots,\Omega ^{(h)}$ on
$\Omega ^{(1)},\ldots,\Omega ^{(h)}$ on ![]() $\mathcal {X}$ such that the residues
$\mathcal {X}$ such that the residues
form a normalized basis of ![]() $H^0(\mathcal {X}_{\underline {t}},\Omega ^2_{\mathcal {X}_{\underline {t}}})$ for all
$H^0(\mathcal {X}_{\underline {t}},\Omega ^2_{\mathcal {X}_{\underline {t}}})$ for all ![]() $\underline {t}$. In particular, there are
$\underline {t}$. In particular, there are ![]() $2$-cycles
$2$-cycles ![]() $A_1,\ldots,A_h$ on
$A_1,\ldots,A_h$ on ![]() $\mathcal {X}_{\underline {t}}$ such that
$\mathcal {X}_{\underline {t}}$ such that ![]() $\int _{A_i}\omega ^{(j)}(\underline {t})=\delta _i^j$, the Kronecker delta.
$\int _{A_i}\omega ^{(j)}(\underline {t})=\delta _i^j$, the Kronecker delta.
Since the line bundle ![]() $\Omega ^{e+1}_{\mathcal {X}}$ pulls back from a line bundle on
$\Omega ^{e+1}_{\mathcal {X}}$ pulls back from a line bundle on ![]() $\mathcal {C}$, we can expand
$\mathcal {C}$, we can expand ![]() $\Omega ^{(j)}$ as
$\Omega ^{(j)}$ as
where ![]() $v$ is a fibre coordinate.
$v$ is a fibre coordinate.
Lemma 4.5
(1) We have
 $w=z(1-\sum _{i=0}^{e-2} t_{e-i}z^{i-e}) =z(1-\sum _{i=2}^et_iz^{-i})$ modulo
$w=z(1-\sum _{i=0}^{e-2} t_{e-i}z^{i-e}) =z(1-\sum _{i=2}^et_iz^{-i})$ modulo  $(\underline {t})^2$.
$(\underline {t})^2$.(2) We have
 $dw\wedge d{\underline {t}}\wedge dv= (1+{\sum }_{i=2}^e(i-1)t_{i}z^{-i})\, dz\wedge \,d{\underline {t}}\wedge \, dv$ modulo
$dw\wedge d{\underline {t}}\wedge dv= (1+{\sum }_{i=2}^e(i-1)t_{i}z^{-i})\, dz\wedge \,d{\underline {t}}\wedge \, dv$ modulo  $(\underline {t})^2$.
$(\underline {t})^2$.
Proof. Immediate from ![]() $w^e+e\sum t_{e-i}w^i=z^e$.
$w^e+e\sum t_{e-i}w^i=z^e$.
Remark Lemma 4.5(1) shows that, in terms of ![]() $H^1(C,T_C)$, the first-order deformation obtained from
$H^1(C,T_C)$, the first-order deformation obtained from ![]() $\mathcal {C}\to \Delta ^{e-1}_{\underline {t}}$ is the one that arises from integrating the space of Čech
$\mathcal {C}\to \Delta ^{e-1}_{\underline {t}}$ is the one that arises from integrating the space of Čech ![]() $1$-cocycles with values in
$1$-cocycles with values in ![]() $T_C$, with respect to the cover
$T_C$, with respect to the cover ![]() $\{D,\ C-\{a\}\}$ of
$\{D,\ C-\{a\}\}$ of ![]() $C$, that is generated by the vector fields
$C$, that is generated by the vector fields ![]() $z^{-1}\,d/dz,\ldots, z^{-(e-1)}\,d/dz$ on
$z^{-1}\,d/dz,\ldots, z^{-(e-1)}\,d/dz$ on ![]() $D-\{a\}$. However, there are different kinds of Schiffer variation that lead to the same space of cocycles; this feature is part of their strength.
$D-\{a\}$. However, there are different kinds of Schiffer variation that lead to the same space of cocycles; this feature is part of their strength.
We substitute this into the expansion of ![]() $\Omega ^{(j)}$. Since
$\Omega ^{(j)}$. Since
modulo ![]() $(\underline {t})^2$, we get
$(\underline {t})^2$, we get
modulo ![]() $(\underline {t})^2$.
$(\underline {t})^2$.
Next, write ![]() $\omega ^{(j)}(t)=\omega ^{(j)}+ \sum _{i=0}^{e-2} t_{e-i}\eta _{e-i}^{(j)}$ modulo
$\omega ^{(j)}(t)=\omega ^{(j)}+ \sum _{i=0}^{e-2} t_{e-i}\eta _{e-i}^{(j)}$ modulo ![]() $(\underline {t})^2$, where
$(\underline {t})^2$, where
Moreover, every ![]() $2$-cycle
$2$-cycle ![]() $\gamma$ on
$\gamma$ on ![]() $X$ that is disjoint from
$X$ that is disjoint from ![]() $E$ is identified, via a
$E$ is identified, via a ![]() $C^\infty$ collapsing map, with a
$C^\infty$ collapsing map, with a ![]() $2$-cycle on
$2$-cycle on ![]() $\mathcal {X}_{\underline {t}}$ and
$\mathcal {X}_{\underline {t}}$ and
Consider the class ![]() $[\omega ^{(j)}(t)]\in H^2(\mathcal {X}_{\underline {t}},{\mathbb {C}})$. Let
$[\omega ^{(j)}(t)]\in H^2(\mathcal {X}_{\underline {t}},{\mathbb {C}})$. Let ![]() $\mathcal {E}\subset \mathcal {X}_{\underline {t}}$ be a fibre. Then
$\mathcal {E}\subset \mathcal {X}_{\underline {t}}$ be a fibre. Then ![]() $[\omega ^{(j)}(t)]\in \mathcal {E}^\perp$. Moreover, from the exact sequence
$[\omega ^{(j)}(t)]\in \mathcal {E}^\perp$. Moreover, from the exact sequence
and the formula (4.7) it follows that ![]() $\eta _i^{(j)}$ defines a class
$\eta _i^{(j)}$ defines a class
such that
Griffiths transversality shows that, in fact, ![]() $[\eta _i^{(j)}]$ lies in
$[\eta _i^{(j)}]$ lies in ![]() ${\it Fil}^1={\it Fil}^1H^{2}_{\rm prim}(X)$. (We let
${\it Fil}^1={\it Fil}^1H^{2}_{\rm prim}(X)$. (We let ![]() ${\it Fil}^i$ refer to the
${\it Fil}^i$ refer to the ![]() $i$’th piece of the Hodge filtration of
$i$’th piece of the Hodge filtration of ![]() $H^{2}_{\rm prim}(X)$.)
$H^{2}_{\rm prim}(X)$.)
We have constructed, for each ![]() $a\in Z$ of ramification index
$a\in Z$ of ramification index ![]() $e(a)=e$, an
$e(a)=e$, an ![]() $(e-1)$-parameter variation
$(e-1)$-parameter variation ![]() $\mathcal {X} \to \Delta ^{e-1}$ of
$\mathcal {X} \to \Delta ^{e-1}$ of ![]() $X$ such that the tangent space
$X$ such that the tangent space ![]() $T_{\Delta ^{e-1}}(\underline {0})$ is identified with the cyclic skyscraper sheaf
$T_{\Delta ^{e-1}}(\underline {0})$ is identified with the cyclic skyscraper sheaf ![]() $L_a$ of length
$L_a$ of length ![]() $e-1$ on
$e-1$ on ![]() $C$ that is supported at
$C$ that is supported at ![]() $a$ and determined by
$a$ and determined by ![]() $Z$. For any
$Z$. For any ![]() $v\in L_a$ consider the derivative
$v\in L_a$ consider the derivative
Let
denote the composite of ![]() $\nabla _v$ with the projection
$\nabla _v$ with the projection ![]() ${\it Fil}^1\to H^{1,1}_{\rm prim}(X)$. If
${\it Fil}^1\to H^{1,1}_{\rm prim}(X)$. If ![]() $L_a$ is of length
$L_a$ is of length ![]() $1$, then we write
$1$, then we write ![]() $\nabla _a$ rather than
$\nabla _a$ rather than ![]() $\nabla _v$.
$\nabla _v$.
Assume that the geometric genus ![]() $h$ of
$h$ of ![]() $X$ is not zero. In addition, given
$X$ is not zero. In addition, given ![]() $\omega \in H^0(X,\Omega ^2_X)$ and
$\omega \in H^0(X,\Omega ^2_X)$ and ![]() $P\in C$, put
$P\in C$, put ![]() $\omega (P)=({\omega }/{dz\wedge dv})(Q)$ for an arbitrary point
$\omega (P)=({\omega }/{dz\wedge dv})(Q)$ for an arbitrary point ![]() $Q\in E_P$ and identify
$Q\in E_P$ and identify ![]() $\omega$ with the pullback of a tensor on
$\omega$ with the pullback of a tensor on ![]() $C$. Denote by
$C$. Denote by ![]() $\sigma \subset X$ the given zero-section of
$\sigma \subset X$ the given zero-section of ![]() $f:X\to C$.
$f:X\to C$.
Proposition 4.8 Suppose that ![]() $0\ne \omega \in H^0(X,\Omega ^2_X)$ and that
$0\ne \omega \in H^0(X,\Omega ^2_X)$ and that ![]() $(\omega )_0$ is disjoint from
$(\omega )_0$ is disjoint from ![]() $Z$. Then the cup product
$Z$. Then the cup product ![]() $\omega :H^1(X,\Theta _X(-\log \sigma ))\to H^{1,1}_{\rm prim}(X)$ is injective.
$\omega :H^1(X,\Theta _X(-\log \sigma ))\to H^{1,1}_{\rm prim}(X)$ is injective.
Proof. Up to now we have identified the tangent space ![]() $T_{\mathcal {JE}}(X)$ with a line bundle on
$T_{\mathcal {JE}}(X)$ with a line bundle on ![]() $Z$; we can also identify it with
$Z$; we can also identify it with ![]() $H^1(X,\Theta _X(-\log \sigma ))$. Since
$H^1(X,\Theta _X(-\log \sigma ))$. Since ![]() $\Theta _X(-\log \sigma )\otimes \Omega ^2_X$ is isomorphic to
$\Theta _X(-\log \sigma )\otimes \Omega ^2_X$ is isomorphic to ![]() $\Omega ^1_X(\log \sigma )(-\sigma )$ we get a short exact sequence
$\Omega ^1_X(\log \sigma )(-\sigma )$ we get a short exact sequence
where ![]() $\mathcal {F}_P$ is a rank 2 vector bundle on
$\mathcal {F}_P$ is a rank 2 vector bundle on ![]() $E_P$ that fits into a short exact sequence
$E_P$ that fits into a short exact sequence
The coboundary map ![]() $H^0(E_P,\mathcal {O}_{E_P})\to H^1(E_P,\mathcal {O}_{E_P}(-\sigma _P))$ is identified with the Kodaira–Spencer map, so is an isomorphism from our assumption about
$H^0(E_P,\mathcal {O}_{E_P})\to H^1(E_P,\mathcal {O}_{E_P}(-\sigma _P))$ is identified with the Kodaira–Spencer map, so is an isomorphism from our assumption about ![]() $(\omega )_0$. Thus,
$(\omega )_0$. Thus, ![]() $H^0(E_P,\mathcal {F}_P)=0$ and then the homomorphism
$H^0(E_P,\mathcal {F}_P)=0$ and then the homomorphism
is injective. This homomorphism factors through the cup product with which we are concerned, and the proposition is proved.
Write ![]() $b_{p,\underline {0}}^{(j)}=b_p$. Then
$b_{p,\underline {0}}^{(j)}=b_p$. Then ![]() $\omega ^{(j)}=\sum b^{(j)}_{p\ge 0}z^pdz\wedge dv$ and
$\omega ^{(j)}=\sum b^{(j)}_{p\ge 0}z^pdz\wedge dv$ and ![]() $b^{(j)}_{0}=\omega ^{(j)}(a)$.
$b^{(j)}_{0}=\omega ^{(j)}(a)$.
Theorem 4.9
(1) We have
 $\eta _i^{(j)}\in H^0(X,\Omega ^2_X(iE_a))_{\rm 2nd\ kind}$.
$\eta _i^{(j)}\in H^0(X,\Omega ^2_X(iE_a))_{\rm 2nd\ kind}$.(2) We have
 $\eta _i^{(j)}= \sum _{p\ge 0}(i-p-1) b^{(j)}_pz^{p-i}\, dz\wedge dv$ modulo
$\eta _i^{(j)}= \sum _{p\ge 0}(i-p-1) b^{(j)}_pz^{p-i}\, dz\wedge dv$ modulo  $H^0(X,\Omega ^2_X\!)$.
$H^0(X,\Omega ^2_X\!)$.(3) The classes
 $[\eta _2^{(1)}],\ldots,[\eta _2^{(h)}]$ span a line
$[\eta _2^{(1)}],\ldots,[\eta _2^{(h)}]$ span a line  ${\mathbb {C}}[\eta _{a,2}]$ in
${\mathbb {C}}[\eta _{a,2}]$ in  ${\it Fil}^1/{\it Fil}^2$ where
${\it Fil}^1/{\it Fil}^2$ where  $\eta _{a,2}\in H^0(X,\Omega ^2_X$
$\eta _{a,2}\in H^0(X,\Omega ^2_X$  $(2E_a)) _{\rm 2nd\ kind}$.
$(2E_a)) _{\rm 2nd\ kind}$.(4) More generally, for each
 $\ell$ with
$\ell$ with  $2\le \ell \le e(a)$, there exists a form
$2\le \ell \le e(a)$, there exists a form  $\eta _{a,\ell }\in H^0(X,\Omega ^2_X$
$\eta _{a,\ell }\in H^0(X,\Omega ^2_X$  $(\ell E_a)) _{\rm 2nd\ kind}$ such that the classes
$(\ell E_a)) _{\rm 2nd\ kind}$ such that the classes  $[\eta ^{(j)}_k]_{j\in [1,h],k\in [2,\ell ]}$ span an
$[\eta ^{(j)}_k]_{j\in [1,h],k\in [2,\ell ]}$ span an  $(\ell -1)$-dimensional subspace
$(\ell -1)$-dimensional subspace  ${\mathbb {C}}.\{[\eta _{a,2},\ldots,[\eta _{a,\ell }]\}$ of
${\mathbb {C}}.\{[\eta _{a,2},\ldots,[\eta _{a,\ell }]\}$ of  $H^{1,1}_{\rm prim}(X)$.
$H^{1,1}_{\rm prim}(X)$.
Proof. This follows from further consideration of the expansion (4.6). To begin, write ![]() $b^{(j)}_{p,\underline {0}}=b^{(j)}_0$. Then we get
$b^{(j)}_{p,\underline {0}}=b^{(j)}_0$. Then we get
 \[ \omega^{(j)}(\underline{t})= \sum_{p,\underline{q}}b^{(j)}_{p,\underline{q}}z^p \biggl(1+\sum_i(i-p-1)t_iz^{-i}\biggr)\,dz\wedge dv, \]
\[ \omega^{(j)}(\underline{t})= \sum_{p,\underline{q}}b^{(j)}_{p,\underline{q}}z^p \biggl(1+\sum_i(i-p-1)t_iz^{-i}\biggr)\,dz\wedge dv, \]
modulo ![]() $(\underline {t}).H^0(X,\Omega ^2_X)$, so that
$(\underline {t}).H^0(X,\Omega ^2_X)$, so that
where the second equality holds modulo ![]() $H^0(X,\Omega ^2_X)$. Observe that
$H^0(X,\Omega ^2_X)$. Observe that
so that ![]() $\dim H^0(X,\Omega ^2_X(iE_a))_{\rm 2nd\ kind}\le h+i-1.$ Then inspection of these coefficients and the linear independence provided by Proposition 4.8 are enough to prove the theorem.
$\dim H^0(X,\Omega ^2_X(iE_a))_{\rm 2nd\ kind}\le h+i-1.$ Then inspection of these coefficients and the linear independence provided by Proposition 4.8 are enough to prove the theorem.
We can restate all this in more intrinsic terms, as follows. Let ![]() $\underline {\omega }$ denote the vector
$\underline {\omega }$ denote the vector ![]() $[\omega ^{(1)},\ldots,\omega ^{(h)}]$ and
$[\omega ^{(1)},\ldots,\omega ^{(h)}]$ and ![]() $\underline {\omega }_{(i)}$ its
$\underline {\omega }_{(i)}$ its ![]() $i$th derivative with respect to
$i$th derivative with respect to ![]() $z$.
$z$.
Theorem 4.10 For each ![]() $a\in Z$ and each
$a\in Z$ and each ![]() $k=2,\ldots,e(a)$ there is an explicit meromorphic
$k=2,\ldots,e(a)$ there is an explicit meromorphic ![]() $2$-form
$2$-form
such that ![]() $[\eta _{a,k}]$ lies in
$[\eta _{a,k}]$ lies in ![]() ${\it Fil}^1$ and the image of
${\it Fil}^1$ and the image of ![]() $\overline {\nabla }_{\partial /\partial t_k}:{\it Fil}^2\to {\it Fil}^1$ is spanned by the classes
$\overline {\nabla }_{\partial /\partial t_k}:{\it Fil}^2\to {\it Fil}^1$ is spanned by the classes ![]() $[\eta _{a,2}],\ldots, [\eta _{a,k}]$. The kernel of
$[\eta _{a,2}],\ldots, [\eta _{a,k}]$. The kernel of ![]() $\overline {\nabla }_{\partial /\partial t_k}$ contains
$\overline {\nabla }_{\partial /\partial t_k}$ contains ![]() $H^0(X,\Omega ^2_X(-(k-1)E))$.
$H^0(X,\Omega ^2_X(-(k-1)E))$.
Moreover, given the identification ![]() $H^0(X,\Omega ^2_X)\cong H^0(X,\Omega ^2_X\!)^\vee$ provided by the basis
$H^0(X,\Omega ^2_X)\cong H^0(X,\Omega ^2_X\!)^\vee$ provided by the basis ![]() $\underline {\omega }$,
$\underline {\omega }$, ![]() $\overline {\nabla }_{\partial /\partial t_k}$ is, as an element of
$\overline {\nabla }_{\partial /\partial t_k}$ is, as an element of ![]() $H^0(X,\Omega ^2_X\!)\otimes {\it Fil}^1$, a linear combination of the tensors
$H^0(X,\Omega ^2_X\!)\otimes {\it Fil}^1$, a linear combination of the tensors ![]() $\underline {\omega }(a)\otimes [\eta _{a,k}],\ldots,\underline {\omega }_{(k-2)}(a)\otimes [\eta _{a,2}]$.
$\underline {\omega }(a)\otimes [\eta _{a,k}],\ldots,\underline {\omega }_{(k-2)}(a)\otimes [\eta _{a,2}]$.
Finally, if ![]() $h+q-1\ge e(a)$, then
$h+q-1\ge e(a)$, then ![]() $\overline {\nabla }_{\partial /\partial t_k}$ is of rank
$\overline {\nabla }_{\partial /\partial t_k}$ is of rank ![]() $k-1$.
$k-1$.
Proof. As remarked, this is, except for the final statement, nothing more than a restatement in intrinsic terms of what we have just proved. For the final part we need to know that the vectors ![]() $\underline {\omega }(a),\ldots, \underline {\omega }_{(e(a)-2)}$ are linearly independent. This follows from the cohomology of the exact sequence
$\underline {\omega }(a),\ldots, \underline {\omega }_{(e(a)-2)}$ are linearly independent. This follows from the cohomology of the exact sequence
and the assumption that ![]() $h+q-1\ge e(a)$.
$h+q-1\ge e(a)$.
Theorem 4.11
(1) If
 $a,b\in Z$ are distinct, then, for all
$a,b\in Z$ are distinct, then, for all  $v\in L_a$ and for all
$v\in L_a$ and for all  $\eta _{b,k}$ with
$\eta _{b,k}$ with  $k\in [2,e(b)]$,
$k\in [2,e(b)]$,  $\overline {\nabla }_v\eta _{b,k}$ is a linear combination of the classes
$\overline {\nabla }_v\eta _{b,k}$ is a linear combination of the classes  $\{[\eta _{a,i}]\}_{i\in [2, e(a)]}$ and
$\{[\eta _{a,i}]\}_{i\in [2, e(a)]}$ and  $\{[\eta _{b,j}]\}_{j\in [2,e(b)]}$. In particular,
$\{[\eta _{b,j}]\}_{j\in [2,e(b)]}$. In particular,  $\overline {\nabla }_v\eta _{b,k}$ lies in
$\overline {\nabla }_v\eta _{b,k}$ lies in  ${\it Fil}^1$.
${\it Fil}^1$.(2) If
 $a,b\in Z$ are distinct, then the classes
$a,b\in Z$ are distinct, then the classes  $[\eta _{a,i}]$ and
$[\eta _{a,i}]$ and  $[\eta _{b,k}]$ are orthogonal.
$[\eta _{b,k}]$ are orthogonal.(3) The classes
 $[\eta _{a,i}]$ form a basis of
$[\eta _{a,i}]$ form a basis of  $H^{1,1}_{\rm prim}(X)$ as
$H^{1,1}_{\rm prim}(X)$ as  $a$ runs over the points of
$a$ runs over the points of  $Z$ and
$Z$ and  $i$ runs from
$i$ runs from  $2$ to
$2$ to  $e(a)$.
$e(a)$.(4) If
 $Z$ is reduced, then the classes
$Z$ is reduced, then the classes  $[\eta _{a,2}]$ form an orthogonal basis of
$[\eta _{a,2}]$ form an orthogonal basis of  $H^{1,1}_{\rm prim}(X)$ as
$H^{1,1}_{\rm prim}(X)$ as  $a$ runs over the points of
$a$ runs over the points of  $Z$.
$Z$.
Proof. (1) We use the same family ![]() $\mathcal {X}\to \mathcal {C}\to \Delta ^{e(a)-1}$ corresponding to the point
$\mathcal {X}\to \mathcal {C}\to \Delta ^{e(a)-1}$ corresponding to the point ![]() $a$ as before. This variation is constant outside a small neighbourhood of
$a$ as before. This variation is constant outside a small neighbourhood of ![]() $a$ and the morphism to
$a$ and the morphism to ![]() $\overline {\mathcal {E}\ell \ell }$ is also constant outside this neighbourhood. Thus, the ramification locus
$\overline {\mathcal {E}\ell \ell }$ is also constant outside this neighbourhood. Thus, the ramification locus ![]() $Z$ is also constant there.
$Z$ is also constant there.
The point ![]() $b$ moves in a family of points
$b$ moves in a family of points ![]() $b(\underline {t})\in \mathcal {C}_{\underline {t}}$, each
$b(\underline {t})\in \mathcal {C}_{\underline {t}}$, each ![]() $b(\underline {t})$ being of constant multiplicity
$b(\underline {t})$ being of constant multiplicity ![]() $e(b)-1$ in the ramification divisor
$e(b)-1$ in the ramification divisor ![]() $Z_{\underline {t}}\subset \mathcal {C}_{\underline {t}}$. The fibre
$Z_{\underline {t}}\subset \mathcal {C}_{\underline {t}}$. The fibre ![]() $E_b$ in
$E_b$ in ![]() $X$ moves in a family
$X$ moves in a family ![]() $\mathcal {E}_{b(\underline {t})}$. Then, for each
$\mathcal {E}_{b(\underline {t})}$. Then, for each ![]() $k\in [2, e(b)]$,
$k\in [2, e(b)]$,
modulo ![]() $t^2$. Similarly to what we did before, we write
$t^2$. Similarly to what we did before, we write
for some meromorphic ![]() $(e(a)+1)$-form
$(e(a)+1)$-form
Then the same kind of calculation in terms of a power series expansion as before shows that ![]() $\nabla _{\partial /\partial t_i}\eta _{b(\underline {t}),k}$ is an element of
$\nabla _{\partial /\partial t_i}\eta _{b(\underline {t}),k}$ is an element of ![]() $H^0(X,\Omega ^2_X(iE_a + kE_b))$ whose residues along both
$H^0(X,\Omega ^2_X(iE_a + kE_b))$ whose residues along both ![]() $E_a$ and
$E_a$ and ![]() $E_b$ are zero. Therefore,
$E_b$ are zero. Therefore, ![]() $\nabla _a(\eta _{b,k})$ is, modulo
$\nabla _a(\eta _{b,k})$ is, modulo ![]() $H^{2,0}(X)$, a linear combination as described.
$H^{2,0}(X)$, a linear combination as described.
(2) Choose an element ![]() $\omega$ of
$\omega$ of ![]() $H^{2,0}(X)$ that does not vanish along
$H^{2,0}(X)$ that does not vanish along ![]() $E_a$. Thus,
$E_a$. Thus, ![]() $\nabla _{\partial /\partial t_i}\omega$ is a non-zero multiple of
$\nabla _{\partial /\partial t_i}\omega$ is a non-zero multiple of ![]() $\eta _{a,i}$. We can assume that
$\eta _{a,i}$. We can assume that ![]() $\nabla _{\partial /\partial t_i}\omega =\eta _{a,i}$. Now
$\nabla _{\partial /\partial t_i}\omega =\eta _{a,i}$. Now ![]() $\langle \omega, \eta _{b,k}\rangle =0$, since
$\langle \omega, \eta _{b,k}\rangle =0$, since ![]() $H^{2,0}(X)$ is orthogonal to
$H^{2,0}(X)$ is orthogonal to ![]() $H^{1,1}(X)$, so that
$H^{1,1}(X)$, so that
since, as we have just proved, ![]() $\nabla _{\partial /\partial t_i}\eta _{b,k}\in {\it Fil}^1$.
$\nabla _{\partial /\partial t_i}\eta _{b,k}\in {\it Fil}^1$.
Parts (3) and (4) follow from the linear independence of the ![]() $[\eta _{a,i}]$ and the fact that there are
$[\eta _{a,i}]$ and the fact that there are ![]() $N$ of them, where
$N$ of them, where ![]() $N=\dim H^{1,1}_{\rm prim}(X).$
$N=\dim H^{1,1}_{\rm prim}(X).$
Remark The fact that the ![]() $\eta _{a,i}$ form a basis of
$\eta _{a,i}$ form a basis of ![]() $H^{1,1}_{\rm prim}(X)$ follows from Theorem 3.24 and Remark 3.29 of [Reference Cox and ZuckerCZ79], or from Proposition 4.8. However, the orthogonality seems to be new.
$H^{1,1}_{\rm prim}(X)$ follows from Theorem 3.24 and Remark 3.29 of [Reference Cox and ZuckerCZ79], or from Proposition 4.8. However, the orthogonality seems to be new.
Until now ![]() $f:X\to C$ has been a point in
$f:X\to C$ has been a point in ![]() $\mathcal {JE}^{\rm gen}$. Now, however, allow
$\mathcal {JE}^{\rm gen}$. Now, however, allow ![]() $X$ to have
$X$ to have ![]() $A_1$-singularities, so that
$A_1$-singularities, so that ![]() $f:X\to C$ is defined by a classifying morphism
$f:X\to C$ is defined by a classifying morphism ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$ that is simply ramified over
$\phi :C\to \overline {\mathcal {E}\ell \ell }$ that is simply ramified over ![]() $j=\infty$. Let
$j=\infty$. Let ![]() $\widetilde X\to X$ be the minimal model, so that
$\widetilde X\to X$ be the minimal model, so that ![]() $\widetilde X$ has singular fibres of types
$\widetilde X$ has singular fibres of types ![]() $I_1$ and
$I_1$ and ![]() $I_2$ and
$I_2$ and ![]() $X\to C$ is the relative canonical model of
$X\to C$ is the relative canonical model of ![]() $\widetilde X\to C$. Suppose that
$\widetilde X\to C$. Suppose that ![]() $D_1,\ldots, D_r$ are the exceptional
$D_1,\ldots, D_r$ are the exceptional ![]() $(-2)$-curves on
$(-2)$-curves on ![]() $\widetilde X$. Suppose that
$\widetilde X$. Suppose that ![]() $a_1,\ldots, a_r$ are the points in
$a_1,\ldots, a_r$ are the points in ![]() $Z$ lying over
$Z$ lying over ![]() $j=\infty$ and that
$j=\infty$ and that ![]() $a_{r+1},\ldots, a_N$ are the other points of
$a_{r+1},\ldots, a_N$ are the other points of ![]() $Z$. For
$Z$. For ![]() $a=a_i$ with
$a=a_i$ with ![]() $i\le r$ define
$i\le r$ define ![]() $[\eta _a]=[D_i]$. The surface
$[\eta _a]=[D_i]$. The surface ![]() $\widetilde X$ is a point in the stack
$\widetilde X$ is a point in the stack ![]() $\widetilde {\mathcal {JE}}$ whose points are minimal models of points of
$\widetilde {\mathcal {JE}}$ whose points are minimal models of points of ![]() $\mathcal {JE}$. We can extend Theorem 4.11 to this context, as follows. For simplicity we state it with the assumption that
$\mathcal {JE}$. We can extend Theorem 4.11 to this context, as follows. For simplicity we state it with the assumption that ![]() $Z$ is reduced.
$Z$ is reduced.
Theorem 4.12 Suppose that ![]() $Z$ is reduced. Put
$Z$ is reduced. Put ![]() $\eta _{a,2}=\eta _a$ for each
$\eta _{a,2}=\eta _a$ for each ![]() $a\in Z$.
$a\in Z$.
(1) Each point
 $a$ in
$a$ in  $Z$ defines a line
$Z$ defines a line  $v_a$ in the tangent space
$v_a$ in the tangent space  $H^1(\widetilde X,T_{\widetilde X})=T_{\mathcal {JE}}\widetilde X$ such that the covariant derivative
is proportional to the rank one tensor
$H^1(\widetilde X,T_{\widetilde X})=T_{\mathcal {JE}}\widetilde X$ such that the covariant derivative
is proportional to the rank one tensor \[ \overline{\nabla}_a:H^2(\widetilde X,\Omega^2_{\widetilde X}) \to H^{1,1}_{\rm prim}(\widetilde X) \]
\[ \overline{\nabla}_a:H^2(\widetilde X,\Omega^2_{\widetilde X}) \to H^{1,1}_{\rm prim}(\widetilde X) \]
 $\omega _a^\vee \otimes \eta _a$.
$\omega _a^\vee \otimes \eta _a$.(2) The classes
 $[\eta _a]_{a\in Z}$ form an orthogonal basis of
$[\eta _a]_{a\in Z}$ form an orthogonal basis of  $H^{1,1}_{\rm prim}(\widetilde X)$.
$H^{1,1}_{\rm prim}(\widetilde X)$.
Proof. We only need to prove part (1) when ![]() $a=a_i$ for
$a=a_i$ for ![]() $i\le r$. Regard the surface
$i\le r$. Regard the surface ![]() $\widetilde X$ as the specialization of a surface in
$\widetilde X$ as the specialization of a surface in ![]() $\mathcal {JE}^{\rm gen}$. It follows by continuity that
$\mathcal {JE}^{\rm gen}$. It follows by continuity that ![]() $\overline {\nabla }_a=\omega _a^\vee \otimes \theta _a$ for some class
$\overline {\nabla }_a=\omega _a^\vee \otimes \theta _a$ for some class ![]() $\theta _a$. To see that
$\theta _a$. To see that ![]() $\theta _a$ is proportional to
$\theta _a$ is proportional to ![]() $[D_a]$ we argue as follows.
$[D_a]$ we argue as follows.
Suppose that ![]() $\Gamma =\sum \Gamma _j$ is a configuration of
$\Gamma =\sum \Gamma _j$ is a configuration of ![]() $(-2)$-curves on a smooth surface
$(-2)$-curves on a smooth surface ![]() $\widetilde X$ that contracts to a single du Val singularity
$\widetilde X$ that contracts to a single du Val singularity ![]() $P\in X$. Then we identify
$P\in X$. Then we identify ![]() $H^2(\widetilde X,\Omega ^2_{\widetilde X}) =H^0(X,\omega _X)$ and put
$H^2(\widetilde X,\Omega ^2_{\widetilde X}) =H^0(X,\omega _X)$ and put
There is a short exact sequence
which gives the following commutative diagram.

Taking ![]() $\Gamma =D_a$ leads to the fact that
$\Gamma =D_a$ leads to the fact that ![]() $\theta _a$ is proportional to
$\theta _a$ is proportional to ![]() $[D_a]$.
$[D_a]$.
Part (2) is proved as in Theorem 4.11.
5. A local Schottky theorem
In this section we use the coincidence that ![]() $\dim H^{1,1}_{\rm prim}=\dim \mathcal {JE}$ to put further structure on the derivative of the period map.
$\dim H^{1,1}_{\rm prim}=\dim \mathcal {JE}$ to put further structure on the derivative of the period map.
The vector spaces ![]() $H^{1,1}_{\rm prim}(X)$ fit together into a vector bundle
$H^{1,1}_{\rm prim}(X)$ fit together into a vector bundle ![]() $\mathcal {H}=\mathcal {H}^{1,1}_{\rm prim}$ on
$\mathcal {H}=\mathcal {H}^{1,1}_{\rm prim}$ on ![]() $\mathcal {JE}^{\rm gen}$. We shall restrict attention to the open substack
$\mathcal {JE}^{\rm gen}$. We shall restrict attention to the open substack ![]() $\mathcal {JE}^{ss}$ of
$\mathcal {JE}^{ss}$ of ![]() $\mathcal {JE}^{\rm gen}$ over which the universal ramification divisor
$\mathcal {JE}^{\rm gen}$ over which the universal ramification divisor ![]() $\mathcal {Z}$ is étale, so that, under the projection
$\mathcal {Z}$ is étale, so that, under the projection ![]() $\rho :\mathcal {Z}^{ss}\to \mathcal {JE}^{ss}$, the sheaf
$\rho :\mathcal {Z}^{ss}\to \mathcal {JE}^{ss}$, the sheaf ![]() $\rho _*\mathcal {O}_{\mathcal {Z}^{ss}}$ is a sheaf of semi-simple rings on
$\rho _*\mathcal {O}_{\mathcal {Z}^{ss}}$ is a sheaf of semi-simple rings on ![]() $\mathcal {JE}^{ss}$.
$\mathcal {JE}^{ss}$.
Proposition 5.1 On ![]() $\mathcal {JE}^{ss}$ the vector bundle
$\mathcal {JE}^{ss}$ the vector bundle ![]() $\mathcal {H}$ is naturally a line bundle
$\mathcal {H}$ is naturally a line bundle ![]() $\mathcal {B}$ on
$\mathcal {B}$ on ![]() $\mathcal {Z}^{ss}$.
$\mathcal {Z}^{ss}$.
Proof. Essentially, we do this componentwise, using the orthogonal basis of ![]() $H^{1,1}_{\rm prim}(X)$ that is provided by the classes
$H^{1,1}_{\rm prim}(X)$ that is provided by the classes ![]() $([\eta _a])_{a\in Z}$ described in the previous section.
$([\eta _a])_{a\in Z}$ described in the previous section.
Let ![]() $x\in \mathcal {JE}^{ss}$, and choose an analytic neighbourhood
$x\in \mathcal {JE}^{ss}$, and choose an analytic neighbourhood ![]() $U$ of
$U$ of ![]() $x$ such that
$x$ such that ![]() $\rho ^{-1}(U)$ is a disjoint union
$\rho ^{-1}(U)$ is a disjoint union
of copies of ![]() $U$.
$U$.
Suppose ![]() $h\in \rho _*\mathcal {O}_{\mathcal {Z}}$. So
$h\in \rho _*\mathcal {O}_{\mathcal {Z}}$. So ![]() $h\vert _{U_a}$ is identified with a holomorphic function
$h\vert _{U_a}$ is identified with a holomorphic function ![]() $h_a$ defined on
$h_a$ defined on ![]() $U$. If
$U$. If ![]() $s\in \Gamma (U,\mathcal {H})$, then we can write
$s\in \Gamma (U,\mathcal {H})$, then we can write ![]() $s=\sum f_a[\eta _a]$ where
$s=\sum f_a[\eta _a]$ where ![]() $f_a$ is a function on
$f_a$ is a function on ![]() $U$. Now define
$U$. Now define ![]() $hs$ by the formula
$hs$ by the formula
Proposition 5.2 There is a perfect ![]() $\mathcal {O}_{\mathcal {Z}^{ss}}$-bilinear pairing
$\mathcal {O}_{\mathcal {Z}^{ss}}$-bilinear pairing ![]() $\beta :\mathcal {B}\times \mathcal {B}\to \mathcal {O}_{\mathcal {Z}^{ss}}$ such that
$\beta :\mathcal {B}\times \mathcal {B}\to \mathcal {O}_{\mathcal {Z}^{ss}}$ such that ![]() $Tr(\rho _*\beta )$ is the intersection product on
$Tr(\rho _*\beta )$ is the intersection product on ![]() $\mathcal {H}$.
$\mathcal {H}$.
Proof. We define the pairing ![]() $\beta$ in terms of the notation used in the proof of Proposition 5.1, as follows:
$\beta$ in terms of the notation used in the proof of Proposition 5.1, as follows:
It is clear that ![]() $\beta$ is perfect.
$\beta$ is perfect.
Recall that, tautologically, the tangent bundle ![]() $T_{\mathcal {JE}^{\rm gen}}$ is naturally a line bundle
$T_{\mathcal {JE}^{\rm gen}}$ is naturally a line bundle ![]() $\mathcal {S}$ on
$\mathcal {S}$ on ![]() $\mathcal {Z}$. That is,
$\mathcal {Z}$. That is, ![]() $T_{\mathcal {JE}^{\rm gen}}=\rho _*\mathcal {S}$. The derivative
$T_{\mathcal {JE}^{\rm gen}}=\rho _*\mathcal {S}$. The derivative ![]() $per_*$ of the period map is an
$per_*$ of the period map is an ![]() $\mathcal {O}_{\mathcal {JE}^{\rm gen}}$-linear map
$\mathcal {O}_{\mathcal {JE}^{\rm gen}}$-linear map
Define
where ![]() $\mathcal {C}$ is the pull back of the universal curve over
$\mathcal {C}$ is the pull back of the universal curve over ![]() $\mathcal {M}_q$ to
$\mathcal {M}_q$ to ![]() $\mathcal {JE}^{\rm gen}$ and
$\mathcal {JE}^{\rm gen}$ and ![]() $\Phi :\mathcal {C}\to \overline {\mathcal {E}\ell \ell }$ is the classifying morphism. Then
$\Phi :\mathcal {C}\to \overline {\mathcal {E}\ell \ell }$ is the classifying morphism. Then
where ![]() $F:\mathcal {X}\to \mathcal {C}$ is the universal Jacobian surface. There is an evaluation map
$F:\mathcal {X}\to \mathcal {C}$ is the universal Jacobian surface. There is an evaluation map
and this map is surjective.
Proposition 5.3 On the locus ![]() $\mathcal {JE}^{ss}$ there is a factorization of
$\mathcal {JE}^{ss}$ there is a factorization of ![]() $per_*$ given by a commutative diagram
$per_*$ given by a commutative diagram

where ![]() $\widetilde {per_*}$ is
$\widetilde {per_*}$ is ![]() $\rho _*\mathcal {O}_{\mathcal {Z}^{ss}}$-linear.
$\rho _*\mathcal {O}_{\mathcal {Z}^{ss}}$-linear.
Proof. This is a consequence of part (3) of Theorem 4.10.
We have proved almost all of the next result. It is a local Schottky theorem in that it gives a precise description of the image of the tangent bundle to moduli under the period map.
Theorem 5.4 (Local Schottky)
There is an isomorphism
of line bundles on ![]() $\mathcal {Z}^{ss}$ such that
$\mathcal {Z}^{ss}$ such that
Proof. It is clear from the preceding discussion that there is a homomorphism ![]() ${\widetilde {\widetilde {per_*}}}$ of line bundles on
${\widetilde {\widetilde {per_*}}}$ of line bundles on ![]() $\mathcal {Z}^{ss}$ with the desired properties. Since
$\mathcal {Z}^{ss}$ with the desired properties. Since ![]() $per_*$ is injective on fibres, so is
$per_*$ is injective on fibres, so is ![]() ${\widetilde {\widetilde {per_*}}}$, and we are done.
${\widetilde {\widetilde {per_*}}}$, and we are done.
6. Recovering  $\operatorname {Ram}_\phi$ and
$\operatorname {Ram}_\phi$ and  $C$ from the infinitesimal period data
$C$ from the infinitesimal period data
For the rest of this paper we make the assumptions (1.3).
Suppose that ![]() $f_i:X_i\to C_i$ are two points of
$f_i:X_i\to C_i$ are two points of ![]() $\mathcal {JE}^{ss}$ that have equal geometric genus
$\mathcal {JE}^{ss}$ that have equal geometric genus ![]() $h$ and irregularity
$h$ and irregularity ![]() $q$, and that each classifying morphism
$q$, and that each classifying morphism ![]() $\phi _i:C_i\to \overline {\mathcal {E}\ell \ell }$ is simply ramified. Say
$\phi _i:C_i\to \overline {\mathcal {E}\ell \ell }$ is simply ramified. Say ![]() $\operatorname {Ram}_{\phi _i}=Z_i$ and
$\operatorname {Ram}_{\phi _i}=Z_i$ and ![]() $\deg Z_i=N$, so that
$\deg Z_i=N$, so that ![]() $N=10h+8(1-q)$. Recall that
$N=10h+8(1-q)$. Recall that ![]() $L_=\phi _i^*M$. Our assumptions ensure that
$L_=\phi _i^*M$. Our assumptions ensure that ![]() $Z_i$ is reduced and the linear system
$Z_i$ is reduced and the linear system ![]() $\vert K_{X_i}\vert = f_i^*\vert K_{C_i}+L_i\vert$ has no base points and embeds
$\vert K_{X_i}\vert = f_i^*\vert K_{C_i}+L_i\vert$ has no base points and embeds ![]() $C_i$ in
$C_i$ in ![]() ${\mathbb {P}}^{h-1}$ as the canonical model of
${\mathbb {P}}^{h-1}$ as the canonical model of ![]() $X_i$. Note that
$X_i$. Note that ![]() $\deg C_i = h+q-1$.
$\deg C_i = h+q-1$.
Theorem 6.1 Assume that both surfaces have the same infinitesimal variation of Hodge structure (IVHS). Then ![]() $C_1=C_2$ and
$C_1=C_2$ and ![]() $Z_1=Z_2$.
$Z_1=Z_2$.
Proof. Our assumptions mean that the two surfaces give the same point and the same tangent space under the period map after each cohomology group ![]() $H^2(X_i,{\mathbb {Z}})$ has been appropriately normalized. In particular, such a normalization gives a normalized basis
$H^2(X_i,{\mathbb {Z}})$ has been appropriately normalized. In particular, such a normalization gives a normalized basis ![]() $\underline {\omega }_i=[\omega ^{(1)}_i,\ldots,\omega ^{(h)}_i]$ of
$\underline {\omega }_i=[\omega ^{(1)}_i,\ldots,\omega ^{(h)}_i]$ of ![]() $H^0(X_i,\Omega ^2_{X_i})$ for each
$H^0(X_i,\Omega ^2_{X_i})$ for each ![]() $i$. We can therefore regard the curves
$i$. We can therefore regard the curves ![]() $C_i$ as embedded in the same projective space
$C_i$ as embedded in the same projective space ![]() ${\mathbb {P}}^{h-1}$. That is, any point
${\mathbb {P}}^{h-1}$. That is, any point ![]() $P$ of
$P$ of ![]() $C_i$ is identified with the point
$C_i$ is identified with the point ![]() $\underline {\omega }_i(\widetilde P)$ in
$\underline {\omega }_i(\widetilde P)$ in ![]() ${\mathbb {P}}^{h-1}$, where
${\mathbb {P}}^{h-1}$, where ![]() $\widetilde P\in X$ is any point of
$\widetilde P\in X$ is any point of ![]() $X$ that lies over
$X$ that lies over ![]() $P$. The basis
$P$. The basis ![]() $\underline {\omega }_i$ also gives an identification of
$\underline {\omega }_i$ also gives an identification of ![]() $H^0(X_i,\Omega ^2_{X_i})$ with its dual.
$H^0(X_i,\Omega ^2_{X_i})$ with its dual.
We show first that ![]() $Z_1=Z_2$. We then deduce, by quadratic interpolation, that
$Z_1=Z_2$. We then deduce, by quadratic interpolation, that ![]() $C_1=C_2$.
$C_1=C_2$.
By the results of § 4, especially Theorem 4.10, the tangent space ![]() $T_{\mathcal {JE}}X_1$ is of dimension
$T_{\mathcal {JE}}X_1$ is of dimension ![]() $N$ and its image in
$N$ and its image in ![]() $H^0(X_1,\Omega ^2_{X_1})^\vee \otimes H^{1,1}_{\rm prim}(X_1)$ is a direct sum
$H^0(X_1,\Omega ^2_{X_1})^\vee \otimes H^{1,1}_{\rm prim}(X_1)$ is a direct sum ![]() $\bigoplus _{a\in Z_1} L_{a}$ where
$\bigoplus _{a\in Z_1} L_{a}$ where ![]() $L_{a}$ is a line described by Theorem 4.10. We make the identifications
$L_{a}$ is a line described by Theorem 4.10. We make the identifications
and assume that the tangent spaces ![]() $T_{\mathcal {JE}}X_1$ and
$T_{\mathcal {JE}}X_1$ and ![]() $T_{\mathcal {JE}}X_2=\bigoplus _{b\in Z_2}M_{b}$ are equal as subspaces of
$T_{\mathcal {JE}}X_2=\bigoplus _{b\in Z_2}M_{b}$ are equal as subspaces of ![]() $U\otimes V$. We know that
$U\otimes V$. We know that ![]() $L_{a}$ is spanned by the rank
$L_{a}$ is spanned by the rank ![]() $1$ tensor
$1$ tensor ![]() $u^{(i)}_0\otimes v^{(i)}_0$ (the image of
$u^{(i)}_0\otimes v^{(i)}_0$ (the image of ![]() $\overline {\nabla }_{\partial /\partial t_2}$). Similarly,
$\overline {\nabla }_{\partial /\partial t_2}$). Similarly, ![]() $M_{b}$ is spanned by a rank 1 tensor
$M_{b}$ is spanned by a rank 1 tensor ![]() $p^{(j)}_0\otimes q^{(j)}_0$.
$p^{(j)}_0\otimes q^{(j)}_0$.
Lemma 6.2 Suppose that:
(1)
 $U$ and
$U$ and  $V$ are vector spaces such that
$V$ are vector spaces such that  $\dim U=h$ and
$\dim U=h$ and  $\dim V=N$;
$\dim V=N$;(2)
 $u_1,\ldots,u_N\in U$;
$u_1,\ldots,u_N\in U$;(3) no two of the
 $u_i$ are linearly dependent;
$u_i$ are linearly dependent;(4)
 $v_1,\ldots,v_N\in V$ and form a basis of
$v_1,\ldots,v_N\in V$ and form a basis of  $V$;
$V$;(5)
 $\xi \in U\otimes V$ and there is a linear relation
and, finally;
$\xi \in U\otimes V$ and there is a linear relation
and, finally; \[ \xi=\sum_1^N\lambda_k u_k\otimes v_k \]
\[ \xi=\sum_1^N\lambda_k u_k\otimes v_k \]
(6)
 $\xi =x\otimes y$, a tensor of rank
$\xi =x\otimes y$, a tensor of rank  $1$.
$1$.
Then there is a unique index ![]() $i$ such that
$i$ such that ![]() $\xi$ is proportional to
$\xi$ is proportional to ![]() $u_i\otimes v_i$.
$u_i\otimes v_i$.
Proof. Let ![]() $(v_i^\vee )$ be the dual basis of
$(v_i^\vee )$ be the dual basis of ![]() $V^\vee$. There is an index
$V^\vee$. There is an index ![]() $j$ such that
$j$ such that ![]() $\langle y, v_j^\vee \rangle \ne 0$. Then
$\langle y, v_j^\vee \rangle \ne 0$. Then
so ![]() $x$ is a multiple of
$x$ is a multiple of ![]() $u_j$. Since no two of the
$u_j$. Since no two of the ![]() $u_i$ are linearly dependent, this index
$u_i$ are linearly dependent, this index ![]() $j$ is unique, so
$j$ is unique, so ![]() $y=\mu _jv_j$ and then
$y=\mu _jv_j$ and then ![]() $x\otimes v_j=\sum \lambda '_ku_k\otimes v_k.$
$x\otimes v_j=\sum \lambda '_ku_k\otimes v_k.$
Say ![]() $Z_1=\{a_1,\ldots,a_N\}$ and
$Z_1=\{a_1,\ldots,a_N\}$ and ![]() $Z_2=\{a'_1,\ldots,a'_N\}$. Take
$Z_2=\{a'_1,\ldots,a'_N\}$. Take ![]() $U= H^{2,0}(X_1)$ and
$U= H^{2,0}(X_1)$ and ![]() $V=H^{1,1}_{\rm prim}(X_1)$ and write
$V=H^{1,1}_{\rm prim}(X_1)$ and write
From Theorem 4.10 and the assumption that the IVHS of the two surfaces ![]() $X_1$ and
$X_1$ and ![]() $X_2$ are isomorphic, the tensors
$X_2$ are isomorphic, the tensors ![]() $x'_l\otimes y'_l$ span the same
$x'_l\otimes y'_l$ span the same ![]() $N$-dimensional subspace of
$N$-dimensional subspace of ![]() $U\otimes V$ as do the tensors
$U\otimes V$ as do the tensors ![]() $x_k\otimes y_k$. In particular, each
$x_k\otimes y_k$. In particular, each ![]() $x'_l\otimes y'_l$ is a linear combination of the tensors
$x'_l\otimes y'_l$ is a linear combination of the tensors ![]() $x_k\otimes y_k$. Then, by Lemma 6.2, for each index
$x_k\otimes y_k$. Then, by Lemma 6.2, for each index ![]() $l$ there is a unique index
$l$ there is a unique index ![]() $m$ such that
$m$ such that ![]() $x_l$ is proportional to
$x_l$ is proportional to ![]() $x'_m$. That is,
$x'_m$. That is, ![]() $a_l=a'_m$, and therefore
$a_l=a'_m$, and therefore ![]() $Z_1= Z_2=Z$, say.
$Z_1= Z_2=Z$, say.
By the assumptions (1.3) each ![]() $C_i$ is non-degenerately embedded in
$C_i$ is non-degenerately embedded in ![]() ${\mathbb {P}}^{h-1}$ by a complete linear system, and
${\mathbb {P}}^{h-1}$ by a complete linear system, and ![]() $\deg C_i\ge 2q+2$, so that, by the results of [Reference MumfordMum70] and [Reference Saint-DonatSai72],
$\deg C_i\ge 2q+2$, so that, by the results of [Reference MumfordMum70] and [Reference Saint-DonatSai72], ![]() $C_i$ is an intersection of quadrics. Since
$C_i$ is an intersection of quadrics. Since
again by (1.3), each ![]() $C_i$ equals the intersection of the quadrics through
$C_i$ equals the intersection of the quadrics through ![]() $Z$, so that
$Z$, so that ![]() $C_1=C_2$.
$C_1=C_2$.
We can reformulate this as follows.
Theorem 6.4 If the ramification divisor ![]() $\operatorname {Ram}_\phi$ of the classifying morphism
$\operatorname {Ram}_\phi$ of the classifying morphism ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$ is reduced, then the IVHS of the surface
$\phi :C\to \overline {\mathcal {E}\ell \ell }$ is reduced, then the IVHS of the surface ![]() $X$ determines the base curve
$X$ determines the base curve ![]() $C$, the divisor
$C$, the divisor ![]() $\operatorname {Ram}_\phi$ and the line bundle
$\operatorname {Ram}_\phi$ and the line bundle ![]() $L=\phi ^*M$.
$L=\phi ^*M$.
Proof. What remains to be done is to show that we can recover the bundle ![]() $L$. For this, observe that our argument has shown that the IVHS of
$L$. For this, observe that our argument has shown that the IVHS of ![]() $X$ determines the embedding
$X$ determines the embedding ![]() $i:C \hookrightarrow {\mathbb {P}}^{h-1}$ as the canonical model of
$i:C \hookrightarrow {\mathbb {P}}^{h-1}$ as the canonical model of ![]() $X$ and that
$X$ and that ![]() $i^*\mathcal {O}(1)=\mathcal {O}_C(K_C+L).$
$i^*\mathcal {O}(1)=\mathcal {O}_C(K_C+L).$
Remark (1) Theorems 6.1 and 6.4 lead to the problem of trying to recover a morphism ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$ from knowledge of
$\phi :C\to \overline {\mathcal {E}\ell \ell }$ from knowledge of ![]() $C$, the divisor
$C$, the divisor ![]() $\operatorname {Ram}_\phi$ and the line bundle
$\operatorname {Ram}_\phi$ and the line bundle ![]() $L$. However, it is impossible to do more than recover
$L$. However, it is impossible to do more than recover ![]() $\phi$ modulo the action of the automorphism group
$\phi$ modulo the action of the automorphism group ![]() ${\mathbb {G}}_m$ of
${\mathbb {G}}_m$ of ![]() $\overline {\mathcal {E}\ell \ell }$. In this direction, we shall prove Proposition 8.7.
$\overline {\mathcal {E}\ell \ell }$. In this direction, we shall prove Proposition 8.7.
(2) If instead of ![]() $\operatorname {Ram}_\phi$ being reduced we assume only that
$\operatorname {Ram}_\phi$ being reduced we assume only that ![]() $h+q-1\ge e(a)+e(b)-1$ for all
$h+q-1\ge e(a)+e(b)-1$ for all ![]() $a,b\in \operatorname {Ram}_\phi$, then a refinement of the argument given here shows that Theorem 6.4 still holds.
$a,b\in \operatorname {Ram}_\phi$, then a refinement of the argument given here shows that Theorem 6.4 still holds.
7. The structure of the tangent bundle to  $\mathcal {SE}^{\rm gen}$
$\mathcal {SE}^{\rm gen}$
Recall from § 3 that we have a morphism ![]() $\pi :\overline {\mathcal {M}}_1\to \overline {\mathcal {E}\ell \ell }$ that gives, locally on
$\pi :\overline {\mathcal {M}}_1\to \overline {\mathcal {E}\ell \ell }$ that gives, locally on ![]() $\overline {\mathcal {E}\ell \ell }$, an isomorphism
$\overline {\mathcal {E}\ell \ell }$, an isomorphism ![]() $\overline {\mathcal {M}}_1\to B\mathcal {G}$, so that the tangent complex
$\overline {\mathcal {M}}_1\to B\mathcal {G}$, so that the tangent complex ![]() $T^\bullet _{\overline {\mathcal {M}}_1}$ is locally isomorphic to the
$T^\bullet _{\overline {\mathcal {M}}_1}$ is locally isomorphic to the ![]() $2$-term complex
$2$-term complex
whose differential is zero. The morphism ![]() $\pi$ determines a morphism
$\pi$ determines a morphism
Suppose that ![]() $f:X\to C$ corresponds to
$f:X\to C$ corresponds to ![]() $\psi :C\to \overline {\mathcal {M}}_1$ and maps under
$\psi :C\to \overline {\mathcal {M}}_1$ and maps under ![]() $\Pi$ to
$\Pi$ to ![]() $Y\to C$. Say
$Y\to C$. Say ![]() $\phi =\pi \circ \psi$. Observe that
$\phi =\pi \circ \psi$. Observe that ![]() $\operatorname {Ram}_\phi =\operatorname {Ram}_\psi =Z,$ say. The description just given of
$\operatorname {Ram}_\phi =\operatorname {Ram}_\psi =Z,$ say. The description just given of ![]() $T^\bullet _{\overline {\mathcal {M}}_1}$ leads to a short exact sequence
$T^\bullet _{\overline {\mathcal {M}}_1}$ leads to a short exact sequence
where ![]() $L=\phi ^*M$. The subobject
$L=\phi ^*M$. The subobject ![]() $H^1(C,-L)$ in this sequence is identified with the tangent space
$H^1(C,-L)$ in this sequence is identified with the tangent space ![]() $T_{\Pi ^{-1}(Y)}X$ to the fibre of
$T_{\Pi ^{-1}(Y)}X$ to the fibre of ![]() $\Pi$ though
$\Pi$ though ![]() $X$. Thus,
$X$. Thus,
which is, in turn, naturally isomorphic to both ![]() $H^{2,0}(X)^\vee$ and to
$H^{2,0}(X)^\vee$ and to ![]() $H^{2,0}(Y)^\vee$. Let
$H^{2,0}(Y)^\vee$. Let ![]() $\xi$ denote the class of a fibre of
$\xi$ denote the class of a fibre of ![]() $X\to C$; then the period map gives the following commutative diagram with exact rows.
$X\to C$; then the period map gives the following commutative diagram with exact rows.

Theorem 7.1 If ![]() $Z$ is reduced and disjoint from the locus
$Z$ is reduced and disjoint from the locus ![]() $j=\infty$, then the IVHS of the surface
$j=\infty$, then the IVHS of the surface ![]() $X$ determines the ramification locus
$X$ determines the ramification locus ![]() $Z$, the base curve
$Z$, the base curve ![]() $C$ and the line bundle
$C$ and the line bundle ![]() $\phi ^*M$.
$\phi ^*M$.
Proof. Put ![]() $H^{2,0}(X)^\vee =H^{2,0}(Y)^\vee =U$ and
$H^{2,0}(X)^\vee =H^{2,0}(Y)^\vee =U$ and ![]() $\xi ^\perp =V$, so that
$\xi ^\perp =V$, so that ![]() $\dim U=h$ and
$\dim U=h$ and ![]() $\dim V=N+1$. The image of
$\dim V=N+1$. The image of ![]() $T_{\mathcal {SE}}(X)$ under
$T_{\mathcal {SE}}(X)$ under ![]() $per_{X,*}$ is an
$per_{X,*}$ is an ![]() $(N+h)$-dimensional subspace
$(N+h)$-dimensional subspace ![]() $W$ of
$W$ of ![]() $U\otimes V$ such that
$U\otimes V$ such that ![]() $W$ contains a subspace
$W$ contains a subspace ![]() $U\otimes \xi$ and
$U\otimes \xi$ and ![]() $W/U\otimes \xi$, which is the image of
$W/U\otimes \xi$, which is the image of ![]() $T_{\mathcal {JE}}(Y)$ under
$T_{\mathcal {JE}}(Y)$ under ![]() $per_{Y,*}$, is spanned by rank 1 tensors
$per_{Y,*}$, is spanned by rank 1 tensors
where the vectors ![]() $y_1,\ldots,y_N$ form a basis of
$y_1,\ldots,y_N$ form a basis of ![]() $V/\xi =H^{1,1}_{\rm prim}(Y)$. Let
$V/\xi =H^{1,1}_{\rm prim}(Y)$. Let ![]() $\pi :V\to V/\xi$ denote the projection.
$\pi :V\to V/\xi$ denote the projection.
Suppose that the same IVHS arises also from another surface ![]() $X'$. Then there is a vector
$X'$. Then there is a vector ![]() $\xi '\in V$ that arises from
$\xi '\in V$ that arises from ![]() $X$ such that
$X$ such that ![]() $(1_U\otimes \pi )(U\otimes \xi ')$ is a subspace of
$(1_U\otimes \pi )(U\otimes \xi ')$ is a subspace of ![]() $U\otimes V/\xi$ and lies in the subspace of
$U\otimes V/\xi$ and lies in the subspace of ![]() $U\otimes V/\xi$ that is spanned by the
$U\otimes V/\xi$ that is spanned by the ![]() $x_i\otimes y_i$. However, by Lemma 6.2, the
$x_i\otimes y_i$. However, by Lemma 6.2, the ![]() $x_i\otimes y_i$ are the only rank 1 tensors in
$x_i\otimes y_i$ are the only rank 1 tensors in ![]() $U\otimes V/\xi$, so that
$U\otimes V/\xi$, so that ![]() $(1_U\otimes \pi )(U\otimes \xi ')=0$ and, therefore,
$(1_U\otimes \pi )(U\otimes \xi ')=0$ and, therefore, ![]() $\xi '$ is proportional to
$\xi '$ is proportional to ![]() $\xi$. Consider the vectors
$\xi$. Consider the vectors ![]() $x_i',y_i'$ that arise from
$x_i',y_i'$ that arise from ![]() $X'$; then the tensors
$X'$; then the tensors ![]() $x_i\otimes y_i$ and
$x_i\otimes y_i$ and ![]() $x_i'\otimes y_i'$ lie in the same vector space
$x_i'\otimes y_i'$ lie in the same vector space ![]() $U\otimes V/\xi$, and then we can use Lemma 6.2 again to conclude the proof.
$U\otimes V/\xi$, and then we can use Lemma 6.2 again to conclude the proof.
Compare the case of ![]() $\mathcal {M}_q$: over the non-hyperelliptic locus Schiffer variations give a cone structure in the tangent bundle, where at each point
$\mathcal {M}_q$: over the non-hyperelliptic locus Schiffer variations give a cone structure in the tangent bundle, where at each point ![]() $C$ of
$C$ of ![]() $\mathcal {M}_q$ the corresponding cone is the cone over the bicanonical model of
$\mathcal {M}_q$ the corresponding cone is the cone over the bicanonical model of ![]() $C$, the generators of the cone map, under the period map, to tensors (quadratic forms) of rank
$C$, the generators of the cone map, under the period map, to tensors (quadratic forms) of rank ![]() $1$ and, again, these account for all the rank
$1$ and, again, these account for all the rank ![]() $1$ tensors in the image.
$1$ tensors in the image.
8. Recovering information from  $C$ and
$C$ and  $Z$
$Z$
We shall show (Proposition 8.7) that ![]() $\phi _1:C\to \overline {\mathcal {E}\ell \ell }$ is generic and if
$\phi _1:C\to \overline {\mathcal {E}\ell \ell }$ is generic and if ![]() $\phi _2:C\to \overline {\mathcal {E}\ell \ell }$ is another morphism such that
$\phi _2:C\to \overline {\mathcal {E}\ell \ell }$ is another morphism such that ![]() $\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}$ and
$\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}$ and ![]() $\phi _1^*M\cong \phi _2^*M$, then
$\phi _1^*M\cong \phi _2^*M$, then ![]() $\phi _1$ and
$\phi _1$ and ![]() $\phi _2$ are equivalent modulo the action of
$\phi _2$ are equivalent modulo the action of ![]() $\operatorname {Aut}_{\overline {\mathcal {E}\ell \ell }}={\mathbb {G}}_m$ provided that also there are sufficiently many points
$\operatorname {Aut}_{\overline {\mathcal {E}\ell \ell }}={\mathbb {G}}_m$ provided that also there are sufficiently many points ![]() $a_i\in Z$ such that
$a_i\in Z$ such that ![]() $\phi _1(a_i)$ is isomorphic to
$\phi _1(a_i)$ is isomorphic to ![]() $\phi _2(a_i)$. Therefore an effective form of generic Torelli holds for Jacobian elliptic surfaces modulo this action of
$\phi _2(a_i)$. Therefore an effective form of generic Torelli holds for Jacobian elliptic surfaces modulo this action of ![]() ${\mathbb {G}}_m$.
${\mathbb {G}}_m$.
To begin, we rewrite some results of Tannenbaum [Reference TannenbaumTan84] in the context of Deligne–Mumford stacks. Assume that ![]() $\mathcal {S}$ is a smooth
$\mathcal {S}$ is a smooth ![]() $2$-dimensional Deligne–Mumford stack (the relevant example will be
$2$-dimensional Deligne–Mumford stack (the relevant example will be ![]() $\mathcal {S}=\overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }$), that
$\mathcal {S}=\overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }$), that ![]() $C$ is a smooth projective curve and that
$C$ is a smooth projective curve and that ![]() $\pi :C\to \mathcal {S}$ is a morphism that factors as
$\pi :C\to \mathcal {S}$ is a morphism that factors as

where ![]() $D$ is a projective curve with only cusps,
$D$ is a projective curve with only cusps, ![]() $\pi '$ is birational and
$\pi '$ is birational and ![]() $i$ induces surjections of henselian local rings at all points. (We shall say that ‘
$i$ induces surjections of henselian local rings at all points. (We shall say that ‘![]() $\pi$ is birational onto its image’.) Then there is a conormal sheaf
$\pi$ is birational onto its image’.) Then there is a conormal sheaf ![]() $\mathcal {N}^\vee _D$, a line bundle on
$\mathcal {N}^\vee _D$, a line bundle on ![]() $D$, which is generated by the pull back under
$D$, which is generated by the pull back under ![]() $i$ of the kernel
$i$ of the kernel ![]() $\mathcal {I}_D$ of
$\mathcal {I}_D$ of ![]() $\mathcal {O}_{\mathcal {S}}\to i_*\mathcal {O}_D$. It fits into a short exact sequence
$\mathcal {O}_{\mathcal {S}}\to i_*\mathcal {O}_D$. It fits into a short exact sequence
Thus, the adjunction formula (or duality for the morphism ![]() $i:D\to \mathcal {S}$) gives an isomorphism
$i:D\to \mathcal {S}$) gives an isomorphism
There is also a homomorphism ![]() $\mathcal {N}_D\to T^1(D,\mathcal {O}_D)$; let
$\mathcal {N}_D\to T^1(D,\mathcal {O}_D)$; let ![]() $\mathcal {N}'_D$ denote its kernel. The space
$\mathcal {N}'_D$ denote its kernel. The space ![]() $H^0(D,\mathcal {N}'_D)$ is the tangent space to the functor that classifies deformations of the morphism
$H^0(D,\mathcal {N}'_D)$ is the tangent space to the functor that classifies deformations of the morphism ![]() $i:D\to \mathcal {S}$ that are locally trivial in the étale (or analytic) topology.
$i:D\to \mathcal {S}$ that are locally trivial in the étale (or analytic) topology.
These conditions imply that there is a reduced effective divisor ![]() $R$ on
$R$ on ![]() $C$ such that
$C$ such that ![]() $T_C(R)=T_{C}\otimes \mathcal {O}_C(R)$ is the saturation of
$T_C(R)=T_{C}\otimes \mathcal {O}_C(R)$ is the saturation of ![]() $T_{C}$ in
$T_{C}$ in ![]() $\pi ^*T_{\mathcal {S}}$. Define
$\pi ^*T_{\mathcal {S}}$. Define ![]() $\mathcal {N}'_\pi$ by
$\mathcal {N}'_\pi$ by
this is a line bundle on ![]() $C$.
$C$.
Define ![]() $\mathcal {J}\subset \mathcal {O}_{\mathcal {S}}$ to be the Jacobian ideal of the ideal
$\mathcal {J}\subset \mathcal {O}_{\mathcal {S}}$ to be the Jacobian ideal of the ideal ![]() $\mathcal {I}_D$. The next result is a slight variant of Lemma 1.5 of [Reference TannenbaumTan84].
$\mathcal {I}_D$. The next result is a slight variant of Lemma 1.5 of [Reference TannenbaumTan84].
Lemma 8.1 We have ![]() $\pi '_*\mathcal {N}'_\pi =\mathcal {N}_D'$.
$\pi '_*\mathcal {N}'_\pi =\mathcal {N}_D'$.
Proof. We have ![]() $\Omega ^1_D=\mathcal {J}.\omega _D$, by direct calculation, and, from the definition of
$\Omega ^1_D=\mathcal {J}.\omega _D$, by direct calculation, and, from the definition of ![]() $\mathcal {N}'_D$, we have
$\mathcal {N}'_D$, we have ![]() $\mathcal {N}'_D=\mathcal {J}.\mathcal {N}_D$.
$\mathcal {N}'_D=\mathcal {J}.\mathcal {N}_D$.
From the definition, ![]() $\omega ^\vee _{C}(R)\otimes \mathcal {N}'_\pi \cong \pi ^*\omega _{\mathcal {S}}^\vee$. Let
$\omega ^\vee _{C}(R)\otimes \mathcal {N}'_\pi \cong \pi ^*\omega _{\mathcal {S}}^\vee$. Let ![]() $\mathcal {C}$ denote the conductor ideal. Then
$\mathcal {C}$ denote the conductor ideal. Then ![]() $\omega _{C}\cong \mathcal {C}\otimes \pi '^*\omega _D$, so that
$\omega _{C}\cong \mathcal {C}\otimes \pi '^*\omega _D$, so that
Now ![]() $\mathcal {C}=\mathcal {O}_{C}(-R)$, by the nature of a cusp, and
$\mathcal {C}=\mathcal {O}_{C}(-R)$, by the nature of a cusp, and ![]() $\mathcal {J}.\mathcal {O}_{C}=\mathcal {O}_{C}(-2R)$ for the same reason. Thus,
$\mathcal {J}.\mathcal {O}_{C}=\mathcal {O}_{C}(-2R)$ for the same reason. Thus,
and, therefore,
Corollary 8.2 The tangent space ![]() $H^0(C,\mathcal {N}'_\pi )$ is isomorphic to the tangent space of the deformation functor that classifies those deformations of the morphism
$H^0(C,\mathcal {N}'_\pi )$ is isomorphic to the tangent space of the deformation functor that classifies those deformations of the morphism ![]() $\pi :C\to \mathcal {S}$ where the length of the
$\pi :C\to \mathcal {S}$ where the length of the ![]() $\mathcal {O}_{C}$-module
$\mathcal {O}_{C}$-module ![]() $\mathrm {coker}(\pi ^*\Omega ^1_{\mathcal {S}}\to \Omega ^1_{C})$ is preserved.
$\mathrm {coker}(\pi ^*\Omega ^1_{\mathcal {S}}\to \Omega ^1_{C})$ is preserved.
Proof. By the lemma, ![]() $H^0(C,\mathcal {N}'_\pi )$ is the tangent space to locally trivial deformations of the morphism
$H^0(C,\mathcal {N}'_\pi )$ is the tangent space to locally trivial deformations of the morphism ![]() $i:D\to \mathcal {S}$. Since
$i:D\to \mathcal {S}$. Since ![]() $D$ has only cusps, a deformation of
$D$ has only cusps, a deformation of ![]() $i$ is locally trivial if and only if it preserves the length of
$i$ is locally trivial if and only if it preserves the length of ![]() $\mathrm {coker}(\pi ^*\Omega ^1_{\mathcal {S}}\to \Omega ^1_{C})$.
$\mathrm {coker}(\pi ^*\Omega ^1_{\mathcal {S}}\to \Omega ^1_{C})$.
Proposition 8.3 Fix a generic morphism ![]() $\phi _1:C\to \overline {\mathcal {E}\ell \ell }$ and consider the morphisms
$\phi _1:C\to \overline {\mathcal {E}\ell \ell }$ and consider the morphisms ![]() $\phi _2:C\to \overline {\mathcal {E}\ell \ell }$ such that
$\phi _2:C\to \overline {\mathcal {E}\ell \ell }$ such that ![]() $(\phi _1,\phi _2):C\to \overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }$ is birational onto its image.
$(\phi _1,\phi _2):C\to \overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }$ is birational onto its image.
(1) If
 $q\ge 2$, there are no such morphisms
$q\ge 2$, there are no such morphisms  $\phi _2$.
$\phi _2$.(2) If
 $q=1$, there are only finitely many such
$q=1$, there are only finitely many such  $\phi _2$.
$\phi _2$.(3) If
 $q=0$, then these morphisms
$q=0$, then these morphisms  $\phi _2$ form a family of dimension at most
$\phi _2$ form a family of dimension at most  $3$.
$3$.
Proof. Assume that ![]() $\phi _2$ exists. Take
$\phi _2$ exists. Take ![]() $\overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }=\mathcal {S}$ and
$\overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }=\mathcal {S}$ and ![]() $(\phi _1,\phi _2)=\pi$. Then there is a factorization
$(\phi _1,\phi _2)=\pi$. Then there is a factorization

as before, and the divisor ![]() $R$ is
$R$ is ![]() $R=\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}$. We get
$R=\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}$. We get
 \begin{align*} \deg \mathcal{N}'_\pi&=2\deg\phi_1^*T_{\overline{\mathcal{E}\ell\ell}}+2q-2-N\\ &= 2.24(h+1-q).\frac{5}{12}+2q-2-N\\ &=10h+10(1-q), \end{align*}
\begin{align*} \deg \mathcal{N}'_\pi&=2\deg\phi_1^*T_{\overline{\mathcal{E}\ell\ell}}+2q-2-N\\ &= 2.24(h+1-q).\frac{5}{12}+2q-2-N\\ &=10h+10(1-q), \end{align*}
so that
However, ![]() $\dim \mathcal {JE}=N,$ and the proposition is proved.
$\dim \mathcal {JE}=N,$ and the proposition is proved.
Corollary 8.4 Fix ![]() $r\ge 0$ and suppose that
$r\ge 0$ and suppose that ![]() $\phi _1:C\to \overline {\mathcal {E}\ell \ell }$ is generic. Consider the morphisms
$\phi _1:C\to \overline {\mathcal {E}\ell \ell }$ is generic. Consider the morphisms ![]() $\phi _2:C\to \overline {\mathcal {E}\ell \ell }$ such that
$\phi _2:C\to \overline {\mathcal {E}\ell \ell }$ such that ![]() $\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}=Z$, say, and there exist distinct points
$\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}=Z$, say, and there exist distinct points ![]() $a_1,\ldots,a_r\in Z$ such that
$a_1,\ldots,a_r\in Z$ such that ![]() $\phi _1(a_i)$ is isomorphic to
$\phi _1(a_i)$ is isomorphic to ![]() $\phi _2(a_i)$ for all
$\phi _2(a_i)$ for all ![]() $i=1,\ldots, r$ and, moreover,
$i=1,\ldots, r$ and, moreover, ![]() $(\phi _1,\phi _2):C\to \overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }$ is birational onto its image.
$(\phi _1,\phi _2):C\to \overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }$ is birational onto its image.
Then no such ![]() $\phi _2$ exist provided that one of the following is true:
$\phi _2$ exist provided that one of the following is true: ![]() $q\ge 2$;
$q\ge 2$; ![]() $q=1$ and
$q=1$ and ![]() $r\ge 1$; or
$r\ge 1$; or ![]() $q=0$ and
$q=0$ and ![]() $r\ge 4$.
$r\ge 4$.
Proof. The further constraints on ![]() $\phi _2$ imply that, in the notation of the proof of Proposition 8.3, the curve
$\phi _2$ imply that, in the notation of the proof of Proposition 8.3, the curve ![]() $D$ has
$D$ has ![]() $r$ cusps that lie on the diagonal of
$r$ cusps that lie on the diagonal of ![]() $\mathcal {S}$. Therefore, there are
$\mathcal {S}$. Therefore, there are ![]() $r$ further constraints on
$r$ further constraints on ![]() $\phi _2$ and the corollary follows.
$\phi _2$ and the corollary follows.
Lemma 8.5 If ![]() $\phi :C\to \overline {\mathcal {E}\ell \ell }$ is generic, then there is no non-trivial factorization through a curve of the composite morphism
$\phi :C\to \overline {\mathcal {E}\ell \ell }$ is generic, then there is no non-trivial factorization through a curve of the composite morphism ![]() $\gamma :C\to {\mathbb {P}}^1_j$.
$\gamma :C\to {\mathbb {P}}^1_j$.
Proof. Suppose that
is a non-trivial factorization of ![]() $\gamma =\pi \circ \phi$. Say
$\gamma =\pi \circ \phi$. Say ![]() $\deg \alpha =a$ and
$\deg \alpha =a$ and ![]() $\deg \beta = b$. By the assumption of genericity, the divisor
$\deg \beta = b$. By the assumption of genericity, the divisor ![]() $Z=\operatorname {Ram}_\phi$ is reduced and its image
$Z=\operatorname {Ram}_\phi$ is reduced and its image ![]() $B=\gamma _*Z$ in
$B=\gamma _*Z$ in ![]() ${\mathbb {P}}^1_j$ consists of distinct points, none of which equals
${\mathbb {P}}^1_j$ consists of distinct points, none of which equals ![]() $j_4$ or
$j_4$ or ![]() $j_6$.
$j_6$.
Suppose ![]() $\alpha$ is branched over
$\alpha$ is branched over ![]() $y\in {\mathbb {P}}^1_j$ and
$y\in {\mathbb {P}}^1_j$ and ![]() $y\ne j_4,j_6$. Then
$y\ne j_4,j_6$. Then ![]() $\gamma ^{-1}(y)\subset Z$, so that
$\gamma ^{-1}(y)\subset Z$, so that ![]() $Z\to B$ is not one-to-one. Thus,
$Z\to B$ is not one-to-one. Thus, ![]() $\alpha$ is branched only over
$\alpha$ is branched only over ![]() $j_4,j_6$, and so is the cyclic cover of
$j_4,j_6$, and so is the cyclic cover of ![]() ${\mathbb {P}}^1_j$ that is branched at these two points and is of degree
${\mathbb {P}}^1_j$ that is branched at these two points and is of degree ![]() $a$. Since
$a$. Since ![]() $\phi$ is étale over
$\phi$ is étale over ![]() $j_4,$ and over
$j_4,$ and over ![]() $j_6$ it follows that
$j_6$ it follows that ![]() $a\vert 2$ and
$a\vert 2$ and ![]() $a\vert 3$, a contradiction.
$a\vert 3$, a contradiction.
Suppose that ![]() $\Delta$ is any irreducible curve of bidegree
$\Delta$ is any irreducible curve of bidegree ![]() $(1,1)$ in
$(1,1)$ in ![]() ${\mathbb {P}}^1_j\times {\mathbb {P}}^1_j,$ let
${\mathbb {P}}^1_j\times {\mathbb {P}}^1_j,$ let ![]() $\widetilde {\Delta }'$ denote the fibre product
$\widetilde {\Delta }'$ denote the fibre product
and let ![]() $\widetilde {\Delta }$ be the normalization of
$\widetilde {\Delta }$ be the normalization of ![]() $\widetilde {\Delta }'$. Note that, generically,
$\widetilde {\Delta }'$. Note that, generically, ![]() $\widetilde {\Delta }$ is isomorphic to
$\widetilde {\Delta }$ is isomorphic to ![]() $\Delta \times B({\mathbb {Z}}/2\times {\mathbb {Z}}/2)$, so that
$\Delta \times B({\mathbb {Z}}/2\times {\mathbb {Z}}/2)$, so that ![]() $\deg (\widetilde {\Delta }\to \Delta )=\tfrac {1}{4}$.
$\deg (\widetilde {\Delta }\to \Delta )=\tfrac {1}{4}$.
Lemma 8.6 We have ![]() $\deg T_{\widetilde {\Delta }}=5/24$ if
$\deg T_{\widetilde {\Delta }}=5/24$ if ![]() $\Delta$ contains the points
$\Delta$ contains the points ![]() $(j_4,j_4)$ and
$(j_4,j_4)$ and ![]() $(j_6,j_6)$ and
$(j_6,j_6)$ and ![]() $\deg T_{\widetilde {\Delta }}\le 1/12$ otherwise.
$\deg T_{\widetilde {\Delta }}\le 1/12$ otherwise.
Proof. We consider separately the cases according to which of the special points ![]() $(j_4,j_4)$,
$(j_4,j_4)$, ![]() $(j_4,j_6)$,
$(j_4,j_6)$, ![]() $(j_6,j_4)$ and
$(j_6,j_4)$ and ![]() $(j_6,j_6)$ lie on
$(j_6,j_6)$ lie on ![]() $\Delta$ and summarize the results in Table 1. Each case depends on local calculation. For example, suppose that
$\Delta$ and summarize the results in Table 1. Each case depends on local calculation. For example, suppose that ![]() $(j_4,j_4)$ and
$(j_4,j_4)$ and ![]() $(j_6,j_6)\in \Delta$. Then
$(j_6,j_6)\in \Delta$. Then ![]() $\widetilde {\Delta }'$ has a double point with an action of
$\widetilde {\Delta }'$ has a double point with an action of ![]() $({\mathbb {Z}}/4)^2$ lying over
$({\mathbb {Z}}/4)^2$ lying over ![]() $(j_4,j_4)$ and a triple point with an action of
$(j_4,j_4)$ and a triple point with an action of ![]() $({\mathbb {Z}}/6)^2$ over
$({\mathbb {Z}}/6)^2$ over ![]() $(j_6,j_6)$. In each case the branches are permuted transitively by the group, so that
$(j_6,j_6)$. In each case the branches are permuted transitively by the group, so that ![]() $\widetilde {\Delta }$ has one point with an action of
$\widetilde {\Delta }$ has one point with an action of ![]() ${\mathbb {Z}}/4\times {\mathbb {Z}}/2$ and another with an action of
${\mathbb {Z}}/4\times {\mathbb {Z}}/2$ and another with an action of ![]() ${\mathbb {Z}}/6\times {\mathbb {Z}}/2$. Thus,
${\mathbb {Z}}/6\times {\mathbb {Z}}/2$. Thus,
 \begin{align*} \deg T_{\widetilde{\Delta}}&=\deg T_{\Delta}.\deg B(({\mathbb{Z}}/2)^2)+ (-\deg B(({\mathbb{Z}}/2)^2)+\deg B({\mathbb{Z}}/4\times{\mathbb{Z}}/2))\\ &\quad + (-\deg B(({\mathbb{Z}}/2)^2)+\deg B({\mathbb{Z}}/6\times{\mathbb{Z}}/2))=1/8+1/12=5/24. \end{align*}
\begin{align*} \deg T_{\widetilde{\Delta}}&=\deg T_{\Delta}.\deg B(({\mathbb{Z}}/2)^2)+ (-\deg B(({\mathbb{Z}}/2)^2)+\deg B({\mathbb{Z}}/4\times{\mathbb{Z}}/2))\\ &\quad + (-\deg B(({\mathbb{Z}}/2)^2)+\deg B({\mathbb{Z}}/6\times{\mathbb{Z}}/2))=1/8+1/12=5/24. \end{align*}

Proposition 8.7 Suppose that ![]() $\phi _1:C\to \overline {\mathcal {E}\ell \ell }$ is generic and that
$\phi _1:C\to \overline {\mathcal {E}\ell \ell }$ is generic and that ![]() $\phi _2:C\to \overline {\mathcal {E}\ell \ell }$ is another morphism such that
$\phi _2:C\to \overline {\mathcal {E}\ell \ell }$ is another morphism such that ![]() $\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}=Z$ and there are
$\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}=Z$ and there are ![]() $r$ points
$r$ points ![]() $a_i\in Z$ such that
$a_i\in Z$ such that ![]() $\phi _1(a_i)$ is isomorphic to
$\phi _1(a_i)$ is isomorphic to ![]() $\phi _2(a_i)$ for all
$\phi _2(a_i)$ for all ![]() $i$. Assume also that one of the following is true:
$i$. Assume also that one of the following is true: ![]() $q\ge 2$;
$q\ge 2$; ![]() $q=1$ and
$q=1$ and ![]() $r\ge 1$; or
$r\ge 1$; or ![]() $q=0$ and
$q=0$ and ![]() $r\ge 4$.
$r\ge 4$.
(1) The image of the composite morphism
 $C\to {\mathbb {P}}^1_j\times {\mathbb {P}}^1_j$ is a curve
$C\to {\mathbb {P}}^1_j\times {\mathbb {P}}^1_j$ is a curve  $\Delta$ of bidegree
$\Delta$ of bidegree  $(1,1)$.
$(1,1)$.(2) The curve
 $\Delta$ passes through the points
$\Delta$ passes through the points  $(j_4,j_4)$ and
$(j_4,j_4)$ and  $(j_6,j_6)$.
$(j_6,j_6)$.Suppose also that
 $\phi _1^*M\cong \phi _2^*M$.
$\phi _1^*M\cong \phi _2^*M$.(3) The morphism
 $(\phi _1,\phi _2): C\to \overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }$ factors through the graph of an automorphism of
$(\phi _1,\phi _2): C\to \overline {\mathcal {E}\ell \ell }\times \overline {\mathcal {E}\ell \ell }$ factors through the graph of an automorphism of  $\overline {\mathcal {E}\ell \ell }$.
$\overline {\mathcal {E}\ell \ell }$.(4) We have that
 $\phi _1$ and
$\phi _1$ and  $\phi _2$ are equivalent under the action of
$\phi _2$ are equivalent under the action of  $\operatorname {Aut}_{\overline {\mathcal {E}\ell \ell }}$.
$\operatorname {Aut}_{\overline {\mathcal {E}\ell \ell }}$.
Proof. Part (1) follows from Proposition 8.3 and Lemma 8.5.
(2) Suppose this is false. Then, by Lemma 8.6,
However, ![]() $\dim _{(\phi _1,\phi _2)}\operatorname {Mor}(C,\widetilde {\Delta }) \ge \dim _{\phi _1}\operatorname {Mor}(C,\overline {\mathcal {E}\ell \ell })$, a contradiction.
$\dim _{(\phi _1,\phi _2)}\operatorname {Mor}(C,\widetilde {\Delta }) \ge \dim _{\phi _1}\operatorname {Mor}(C,\overline {\mathcal {E}\ell \ell })$, a contradiction.
For parts (3) and (4) we can now use the ![]() ${\mathbb {G}}_m$-action to ensure that
${\mathbb {G}}_m$-action to ensure that ![]() $\Delta$ is the diagonal. Then the two surfaces
$\Delta$ is the diagonal. Then the two surfaces ![]() $X_i\to C$ have the same
$X_i\to C$ have the same ![]() $j$-invariant, so that one is a quadratic twist of the other via a quadratic cover
$j$-invariant, so that one is a quadratic twist of the other via a quadratic cover ![]() $\widetilde C\to C$. Since both surfaces are semistable, this quadratic cover is étale. Suppose it corresponds to the
$\widetilde C\to C$. Since both surfaces are semistable, this quadratic cover is étale. Suppose it corresponds to the ![]() $2$-torsion class
$2$-torsion class ![]() $P$ on
$P$ on ![]() $C$. From the identification of
$C$. From the identification of ![]() $\phi _i^*M$ with the conormal bundle of the zero section, it follows that
$\phi _i^*M$ with the conormal bundle of the zero section, it follows that ![]() $\phi _2^*M= \phi _1^*M + P$, so that
$\phi _2^*M= \phi _1^*M + P$, so that ![]() $P=0$, and the result is proved.
$P=0$, and the result is proved.
9. Generic Torelli for Jacobian surfaces
Define ![]() $r(q)= 2$ if
$r(q)= 2$ if ![]() $q\ge 1$ and
$q\ge 1$ and ![]() $r(0)=4$. Let
$r(0)=4$. Let ![]() $\widetilde {\mathcal {JE}}_{C,L}$ (or
$\widetilde {\mathcal {JE}}_{C,L}$ (or ![]() $\mathcal {JE}_{C,L}$) denote the closed substack of
$\mathcal {JE}_{C,L}$) denote the closed substack of ![]() $\widetilde {\mathcal {JE}}$ (or
$\widetilde {\mathcal {JE}}$ (or ![]() $\mathcal {JE}$) defined by the properties that the base of the elliptic fibration is
$\mathcal {JE}$) defined by the properties that the base of the elliptic fibration is ![]() $C$ and
$C$ and ![]() $\phi ^*M$ is isomorphic to
$\phi ^*M$ is isomorphic to ![]() $L$. Let
$L$. Let ![]() $\widetilde {\mathcal {JE}}_r$ denote the substack of
$\widetilde {\mathcal {JE}}_r$ denote the substack of ![]() $\widetilde {\mathcal {JE}}$ with
$\widetilde {\mathcal {JE}}$ with ![]() $r$ fibres of type
$r$ fibres of type ![]() $I_2$ and put
$I_2$ and put ![]() $\widetilde {\mathcal {JE}}_{C,L,r}=\widetilde {\mathcal {JE}}_{C,L}\cap \mathcal {JE}_r$.
$\widetilde {\mathcal {JE}}_{C,L,r}=\widetilde {\mathcal {JE}}_{C,L}\cap \mathcal {JE}_r$.
Let ![]() $\mathcal {Z}'\to \mathcal {JE}_r$ be the restriction of the universal ramification divisor
$\mathcal {Z}'\to \mathcal {JE}_r$ be the restriction of the universal ramification divisor ![]() $\rho :\mathcal {Z}\to \mathcal {JE}$. Then
$\rho :\mathcal {Z}\to \mathcal {JE}$. Then ![]() $\mathcal {Z}'$ has a closed substack
$\mathcal {Z}'$ has a closed substack ![]() $\mathcal {Z}_r$ obtained by discarding the part of
$\mathcal {Z}_r$ obtained by discarding the part of ![]() $\mathcal {Z}$ that lies over
$\mathcal {Z}$ that lies over ![]() $j=\infty$.
$j=\infty$.
Lemma 9.1 The substacks ![]() $\widetilde {\mathcal {JE}}_r$,
$\widetilde {\mathcal {JE}}_r$, ![]() $\mathcal {JE}_r$,
$\mathcal {JE}_r$, ![]() $\widetilde {\mathcal {JE}}_{C,L,r}$,
$\widetilde {\mathcal {JE}}_{C,L,r}$, ![]() $\mathcal {JE}_{C,L,r}$ and
$\mathcal {JE}_{C,L,r}$ and ![]() $\mathcal {Z}_r$ are irreducible when
$\mathcal {Z}_r$ are irreducible when ![]() $r=r(q)$.
$r=r(q)$.
Proof. We show first that ![]() $\mathcal {JE}_{C,L,r}$ is irreducible. For this, refer to the Weierstrass equation
$\mathcal {JE}_{C,L,r}$ is irreducible. For this, refer to the Weierstrass equation
of a Jacobian surface ![]() $X$ over
$X$ over ![]() $C$. Fix distinct points
$C$. Fix distinct points ![]() $P_1,\ldots, P_r\in C$. Then
$P_1,\ldots, P_r\in C$. Then ![]() $X$ has fibres of type
$X$ has fibres of type ![]() $I_2$ (or worse) over each
$I_2$ (or worse) over each ![]() $P_i$ if and only if
$P_i$ if and only if
where the prime denotes the derivative with respect to a local coordinate ![]() $z$ at
$z$ at ![]() $P_i$. (For this, we use the description of
$P_i$. (For this, we use the description of ![]() $\mathcal {Z}$ in terms of transvectants that is given in § 10.) Expand
$\mathcal {Z}$ in terms of transvectants that is given in § 10.) Expand ![]() $g_n$ in terms of
$g_n$ in terms of ![]() $z$ to get
$z$ to get
then the condition on the fibres of ![]() $X$ is expressed by a pair of equations (one pair for each
$X$ is expressed by a pair of equations (one pair for each ![]() $P_i$)
$P_i$)
Since ![]() $r\le 4$ these equations define an irreducible subvariety
$r\le 4$ these equations define an irreducible subvariety ![]() $V_r$ of
$V_r$ of ![]() $H^0(C,4L)\times H^0(C,6L)$ and the irreducibility of
$H^0(C,4L)\times H^0(C,6L)$ and the irreducibility of ![]() $\mathcal {JE}_{C,L,r}$ is proved. The irreducibility of
$\mathcal {JE}_{C,L,r}$ is proved. The irreducibility of ![]() $\mathcal {JE}_r$ follows at once, and then so too does the irreducibility of
$\mathcal {JE}_r$ follows at once, and then so too does the irreducibility of ![]() $\widetilde {\mathcal {JE}}_{C,L,r}$ and
$\widetilde {\mathcal {JE}}_{C,L,r}$ and ![]() $\widetilde {\mathcal {JE}}_r$.
$\widetilde {\mathcal {JE}}_r$.
Since ![]() $\mathcal {Z}_r\cap \mathcal {JE}_{C,L,r}$ is dominated by
$\mathcal {Z}_r\cap \mathcal {JE}_{C,L,r}$ is dominated by ![]() $V_r$, the irreducibility of
$V_r$, the irreducibility of ![]() $\mathcal {Z}_r$ is also proved.
$\mathcal {Z}_r$ is also proved.
Theorem 9.2
(1) Suppose that
 $\phi _i:C\to \overline {\mathcal {E}\ell \ell }$ is a morphism corresponding to the Jacobian surface
$\phi _i:C\to \overline {\mathcal {E}\ell \ell }$ is a morphism corresponding to the Jacobian surface  $f_i:X_i\to C$, for
$f_i:X_i\to C$, for  $i=1,2$. Assume that
$i=1,2$. Assume that  $\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}=Z$, say, that
$\operatorname {Ram}_{\phi _1}=\operatorname {Ram}_{\phi _2}=Z$, say, that  $Z$ is reduced and that
$Z$ is reduced and that  $\phi _1^*M=\phi _2^*M$. Suppose that there are
$\phi _1^*M=\phi _2^*M$. Suppose that there are  $r=r(q)$ points
$r=r(q)$ points  $a_1,\ldots, a_r\in Z$ such that
$a_1,\ldots, a_r\in Z$ such that  $\phi _i(a_k)$ lies over
$\phi _i(a_k)$ lies over  $j=\infty$ for
$j=\infty$ for  $i=1,2$ and
$i=1,2$ and  $k=1,\ldots, r$. Then
$k=1,\ldots, r$. Then  $X_1$ is isomorphic to
$X_1$ is isomorphic to  $X_2$.
$X_2$.(2) A generic Jacobian elliptic surface with
 $r(q)$ singular fibres of type
$r(q)$ singular fibres of type  $I_2$ is determined by its IVHS.
$I_2$ is determined by its IVHS.(3) Generic Torelli holds for Jacobian surfaces with
 $r(q)$ singular fibres of type
$r(q)$ singular fibres of type  $I_2$.
$I_2$.
Proof. Part (1) is a consequence of Proposition 8.7. Part (2) is merely a restatement of part (1), and then part (3) follows in the usual way.
Next, we use the minimal model program to prove a version of the good reduction result from [Reference ChakirisCha82] and [Reference ChakirisCha84].
Theorem 9.3 Suppose that ![]() $\mathcal {X}\to \Delta$ is a semistable
$\mathcal {X}\to \Delta$ is a semistable ![]() $1$-parameter degeneration of Jacobian elliptic surfaces over a fixed curve
$1$-parameter degeneration of Jacobian elliptic surfaces over a fixed curve ![]() $C$ of genus
$C$ of genus ![]() $q$ and that there is no monodromy on the second Betti cohomology of
$q$ and that there is no monodromy on the second Betti cohomology of ![]() $\mathcal {X}_{\bar \eta }$. Assume also that, under the period map, the image of
$\mathcal {X}_{\bar \eta }$. Assume also that, under the period map, the image of ![]() $0\in \Delta$ is the primitive weight 2 Hodge structure of a Jacobian elliptic surface
$0\in \Delta$ is the primitive weight 2 Hodge structure of a Jacobian elliptic surface ![]() $g:V\to C$ such that
$g:V\to C$ such that ![]() $p_g(V)=p_g(\mathcal {X}_{\bar \eta })$ and this Hodge structure is irreducible.
$p_g(V)=p_g(\mathcal {X}_{\bar \eta })$ and this Hodge structure is irreducible.
Then ![]() $\mathcal {X}\to \Delta$ has good reduction.
$\mathcal {X}\to \Delta$ has good reduction.
Proof. We can follow the proof of Theorem 9.1 of [Reference Shepherd-BarronShe21] as far as the end of Lemma 9.9 of [Reference Shepherd-BarronShe21]. This leads to a model ![]() $\mathcal {X}\to \Delta$ such that:
$\mathcal {X}\to \Delta$ such that:
(1)
 $\mathcal {X}$ has
$\mathcal {X}$ has  ${\mathbb {Q}}$-factorial canonical singularities and
${\mathbb {Q}}$-factorial canonical singularities and  $\mathcal {X}_0$ has semi log canonical (slc) singularities;
$\mathcal {X}_0$ has semi log canonical (slc) singularities;(2) there is a surface
 $S$ with a proper semi–stable morphism
$S$ with a proper semi–stable morphism  $g:S\to \Delta$ and a projective morphism
$g:S\to \Delta$ and a projective morphism  $f:\mathcal {X}\to S$ with only
$f:\mathcal {X}\to S$ with only  $1$-dimensional fibres such that
$1$-dimensional fibres such that  $K_{\mathcal {X}/\Delta }$ is the pullback under
$K_{\mathcal {X}/\Delta }$ is the pullback under  $f$ of a
$f$ of a  $g$-ample
$g$-ample  ${\mathbb {Q}}$-line bundle
${\mathbb {Q}}$-line bundle  $L$ on
$L$ on  $S$.
$S$.
Then ![]() $S_0$ is a tree, and
$S_0$ is a tree, and ![]() $S_0=\sum C_i$ where
$S_0=\sum C_i$ where ![]() $C_0\cong C$ and
$C_0\cong C$ and ![]() $C_j\cong {\mathbb {P}}^1$ for all
$C_j\cong {\mathbb {P}}^1$ for all ![]() $j>0$. Since
$j>0$. Since ![]() $S$ has only singularities of type
$S$ has only singularities of type ![]() $A$, each curve
$A$, each curve ![]() $C_i$ is a
$C_i$ is a ![]() ${\mathbb {Q}}$-Cartier divisor on
${\mathbb {Q}}$-Cartier divisor on ![]() $S$. Let
$S$. Let ![]() $f_i:X_i=f^{-1}(C_i)\to C_i$ be the morphism induced by
$f_i:X_i=f^{-1}(C_i)\to C_i$ be the morphism induced by ![]() $f$. Thus,
$f$. Thus, ![]() $X_i$ is
$X_i$ is ![]() ${\mathbb {Q}}$-Cartier on
${\mathbb {Q}}$-Cartier on ![]() $\mathcal {X}$ and
$\mathcal {X}$ and ![]() $K_{\mathcal {X}/\Delta }\vert _{X_i}\sim f_i^*L_i$ for some
$K_{\mathcal {X}/\Delta }\vert _{X_i}\sim f_i^*L_i$ for some ![]() ${\mathbb {Q}}$-line bundle
${\mathbb {Q}}$-line bundle ![]() $L_i$ on
$L_i$ on ![]() $C_i$ of degree
$C_i$ of degree ![]() $\alpha _i>0$, where
$\alpha _i>0$, where ![]() $\sum \alpha _i=h+q-1$.
$\sum \alpha _i=h+q-1$.
Since the Hodge structure on ![]() $H_{\rm prim}^2(V)$ is irreducible and, from the absence of monodromy,
$H_{\rm prim}^2(V)$ is irreducible and, from the absence of monodromy, ![]() $\sum p_g(X_i)\le p_g(V)$, there is a unique index
$\sum p_g(X_i)\le p_g(V)$, there is a unique index ![]() $i_0$ such that the Hodge structure on
$i_0$ such that the Hodge structure on ![]() $H^2(X_{i_0},{\mathbb {Q}})$ maps onto that on
$H^2(X_{i_0},{\mathbb {Q}})$ maps onto that on ![]() $H^2(V,{\mathbb {Q}})$. It follows that
$H^2(V,{\mathbb {Q}})$. It follows that ![]() $i_0=0$.
$i_0=0$.
Suppose that ![]() $X_0$ meets
$X_0$ meets ![]() $X_1,\ldots, X_s$. Since
$X_1,\ldots, X_s$. Since ![]() $X_0$ is
$X_0$ is ![]() ${\mathbb {Q}}$-Gorenstein, and even Gorenstein in codimension one, the adjunction formula shows that there exist
${\mathbb {Q}}$-Gorenstein, and even Gorenstein in codimension one, the adjunction formula shows that there exist ![]() $\delta _1,\ldots, \delta _s\in {\mathbb {Q}}_{>0}$ such that
$\delta _1,\ldots, \delta _s\in {\mathbb {Q}}_{>0}$ such that ![]() $K_{X_0}\sim _{\mathbb {Q}} f_0^*(\alpha _0-\sum \delta _i)$.
$K_{X_0}\sim _{\mathbb {Q}} f_0^*(\alpha _0-\sum \delta _i)$.
Let ![]() $\gamma :\widetilde X\to X_0$ denote the minimal resolution. Then there is an effective
$\gamma :\widetilde X\to X_0$ denote the minimal resolution. Then there is an effective ![]() ${\mathbb {Q}}$-divisor
${\mathbb {Q}}$-divisor ![]() $D$ on
$D$ on ![]() $\widetilde X$ such that
$\widetilde X$ such that
Thus,
On the other hand,
Therefore, ![]() $s=0$, so that
$s=0$, so that ![]() $\mathcal {X}_0=X_0$, and
$\mathcal {X}_0=X_0$, and ![]() $D=0$. Therefore,
$D=0$. Therefore, ![]() $X_0$ has only du Val singularities and the result is reduced to the existence of a simultaneous resolution for such singularities.
$X_0$ has only du Val singularities and the result is reduced to the existence of a simultaneous resolution for such singularities.
Remark There are degenerating families of elliptic surfaces ![]() $\mathcal {X}\to \mathcal {C}\to \Delta$ with no monodromy on
$\mathcal {X}\to \mathcal {C}\to \Delta$ with no monodromy on ![]() $H^2$ but where
$H^2$ but where ![]() $\mathcal {C}$ has bad reduction. For example, take an elliptic K3 surface
$\mathcal {C}$ has bad reduction. For example, take an elliptic K3 surface ![]() $X\to {\mathbb {P}}^1$ with two isomorphic fibres of type
$X\to {\mathbb {P}}^1$ with two isomorphic fibres of type ![]() $\overline {D}_4$. Then this can be plumbed to itself to give such a family: the generic fibre has
$\overline {D}_4$. Then this can be plumbed to itself to give such a family: the generic fibre has ![]() $p_g=q=1$ and
$p_g=q=1$ and ![]() $\mathcal {C}\to \Delta$ is the Tate curve.
$\mathcal {C}\to \Delta$ is the Tate curve.
Corollary 9.4 The period map ![]() $[per]:[\mathcal {JE}]\to [D/\Gamma ]$ of geometric quotients is proper and one-to-one over the image of the generic point of the locus of surfaces with
$[per]:[\mathcal {JE}]\to [D/\Gamma ]$ of geometric quotients is proper and one-to-one over the image of the generic point of the locus of surfaces with ![]() $r(q)$ fibres of type
$r(q)$ fibres of type ![]() $I_2$.
$I_2$.
Lemma 9.5 Suppose that ![]() $V\hookrightarrow Y$ is a closed embedding of normal analytic spaces. Suppose also that
$V\hookrightarrow Y$ is a closed embedding of normal analytic spaces. Suppose also that ![]() $H$ is a finite group and
$H$ is a finite group and ![]() $G$ a subgroup of
$G$ a subgroup of ![]() $H$ such that
$H$ such that ![]() $H$ acts on
$H$ acts on ![]() $Y$, that
$Y$, that ![]() $G$ preserves
$G$ preserves ![]() $V$ and that, moreover,
$V$ and that, moreover, ![]() $G=\{g\in H : g(V)=V\}$.
$G=\{g\in H : g(V)=V\}$.
Then the morphism ![]() $[V/G]\to [Y/H]$ of geometric quotients is bimeromorphic onto its image.
$[V/G]\to [Y/H]$ of geometric quotients is bimeromorphic onto its image.
Proof. We can replace ![]() $Y$ by the largest open subspace
$Y$ by the largest open subspace ![]() $Y^0$ of
$Y^0$ of ![]() $Y$ such that
$Y$ such that ![]() $Y^0$ is preserved by
$Y^0$ is preserved by ![]() $H$ and
$H$ and ![]() $Y^0\to [Y^0/H]$ is étale. Then the result is clear.
$Y^0\to [Y^0/H]$ is étale. Then the result is clear.
Lemma 9.6 A generic pair ![]() $(C,Z)$ has no automorphisms.
$(C,Z)$ has no automorphisms.
Proof. We consider the various values of ![]() $q$ separately:
$q$ separately:
(1)
 $q\ge 3$; a generic curve has no automorphisms;
$q\ge 3$; a generic curve has no automorphisms;(2)
 $q=2$; then
$q=2$; then  $Z$ is invariant under the hyperelliptic involution of
$Z$ is invariant under the hyperelliptic involution of  $C$; in this case the dimension of the set
$C$; in this case the dimension of the set  $\Sigma$ of pairs
$\Sigma$ of pairs  $(C,Z)$ is at most
$(C,Z)$ is at most  $\dim \mathcal {M}_2+N/2$, which is less than
$\dim \mathcal {M}_2+N/2$, which is less than  $\dim \mathcal {JE}$;
$\dim \mathcal {JE}$;(3)
 $q=1$; either
$q=1$; either  $Z$ is invariant under an involution, and then we argue as in the case where
$Z$ is invariant under an involution, and then we argue as in the case where  $q=2$, or
$q=2$, or  $Z$ is invariant under a translation; in this case
$Z$ is invariant under a translation; in this case  $Z$ is determined by any one of its points and
$Z$ is determined by any one of its points and  $\dim \Sigma \le 2$;
$\dim \Sigma \le 2$;(4)
 $q=0$; suppose
$q=0$; suppose  $1\ne g\in PGL_2({\mathbb {C}})$; if
$1\ne g\in PGL_2({\mathbb {C}})$; if  $g$ fixes one point, then
$g$ fixes one point, then  $\dim \Sigma \le 2$, and if
$\dim \Sigma \le 2$, and if  $g$ fixes
$g$ fixes  $2$ points, then
$2$ points, then  $\dim \Sigma \le 3$.
$\dim \Sigma \le 3$.
We now take ![]() $V$ to be a miniversal deformation space of a surface
$V$ to be a miniversal deformation space of a surface ![]() $\widetilde X$ with
$\widetilde X$ with ![]() $r=r(q)$ fibres of type
$r=r(q)$ fibres of type ![]() $I_2$ and
$I_2$ and ![]() $Y$ a germ of the domain
$Y$ a germ of the domain ![]() $D$ at the period point of
$D$ at the period point of ![]() $\widetilde X$.
$\widetilde X$.
Suppose that ![]() $H\subset O(H^2_{\rm prim}(\widetilde X,{\mathbb {Z}}))$ is the automorphism group of the polarized Hodge structure of the
$H\subset O(H^2_{\rm prim}(\widetilde X,{\mathbb {Z}}))$ is the automorphism group of the polarized Hodge structure of the ![]() $\widetilde X$ and that
$\widetilde X$ and that ![]() $G\subset H$ is the subgroup consisting of those elements of
$G\subset H$ is the subgroup consisting of those elements of ![]() $H$ that preserve the image of
$H$ that preserve the image of ![]() $V$ in
$V$ in ![]() $Y$. Since
$Y$. Since ![]() $H$ is finite, we can identify the germs
$H$ is finite, we can identify the germs ![]() $Y$ and
$Y$ and ![]() $V$, which are smooth, with their tangent spaces. In turn,
$V$, which are smooth, with their tangent spaces. In turn, ![]() $V=H^{2,0}(\widetilde X)^\vee \otimes H^{1,1}_{\rm prim}(\widetilde X)$ and
$V=H^{2,0}(\widetilde X)^\vee \otimes H^{1,1}_{\rm prim}(\widetilde X)$ and ![]() $H$ acts on both components of this tensor product. Let
$H$ acts on both components of this tensor product. Let ![]() $W=W(A_1^r)$ denote the Weyl group generated by reflexions
$W=W(A_1^r)$ denote the Weyl group generated by reflexions ![]() $\sigma _{[\eta _a]}$ in the classes
$\sigma _{[\eta _a]}$ in the classes ![]() $[\eta _a]$ where
$[\eta _a]$ where ![]() $a$ lies over
$a$ lies over ![]() $j=\infty$; then
$j=\infty$; then ![]() $\sigma _{[\eta _a]}$ lies in
$\sigma _{[\eta _a]}$ lies in ![]() $H$, so that
$H$, so that ![]() $W\subset H$. Also
$W\subset H$. Also ![]() $(\pm 1)$ is a subgroup of
$(\pm 1)$ is a subgroup of ![]() $H$ and acts trivially on
$H$ and acts trivially on ![]() $D$.
$D$.
Proposition 9.7 We have ![]() $G= (\pm 1)\times W$.
$G= (\pm 1)\times W$.
Proof. Let ![]() $g\in G$. We know that the subspace
$g\in G$. We know that the subspace ![]() $V$ of
$V$ of ![]() $Y$ is based by the rank
$Y$ is based by the rank ![]() $1$ tensors
$1$ tensors ![]() $\omega _a^\vee \otimes [\eta _a]$ and that these are the only rank
$\omega _a^\vee \otimes [\eta _a]$ and that these are the only rank ![]() $1$ tensors in
$1$ tensors in ![]() $V$. Therefore,
$V$. Therefore, ![]() $g$ permutes the lines
$g$ permutes the lines ![]() ${\mathbb {C}}\omega _a^\vee$ and so acts on the pair
${\mathbb {C}}\omega _a^\vee$ and so acts on the pair ![]() $(C,Z)$, where
$(C,Z)$, where ![]() $C$ is embedded in
$C$ is embedded in ![]() ${\mathbb {P}}^{h-1}$ via
${\mathbb {P}}^{h-1}$ via ![]() $\vert K_C+L\vert$. This action is trivial, by the previous lemma, and so
$\vert K_C+L\vert$. This action is trivial, by the previous lemma, and so ![]() $g$ acts as a scalar on
$g$ acts as a scalar on ![]() $H^{2,0}(\widetilde X)$. We can then take this scalar to be
$H^{2,0}(\widetilde X)$. We can then take this scalar to be ![]() $1$. Then
$1$. Then ![]() $g$ fixes each line
$g$ fixes each line ![]() ${\mathbb {C}}[\eta _a]$. The classes
${\mathbb {C}}[\eta _a]$. The classes ![]() $[\eta _a]$ are orthogonal and can be normalized by imposing the condition that
$[\eta _a]$ are orthogonal and can be normalized by imposing the condition that ![]() $[\eta _a]^2=-2$ for all
$[\eta _a]^2=-2$ for all ![]() $a\in Z$. This normalization is unique up to a choice of sign for each
$a\in Z$. This normalization is unique up to a choice of sign for each ![]() $a$. Since
$a$. Since ![]() $\mathcal {Z}_r$ is irreducible, one choice of sign, for a point in
$\mathcal {Z}_r$ is irreducible, one choice of sign, for a point in ![]() $Z_r$, determines all the other signs, except when
$Z_r$, determines all the other signs, except when ![]() $a$ lies over
$a$ lies over ![]() $j=\infty$. This last ambiguity is exactly taken care of by the Weyl group and so
$j=\infty$. This last ambiguity is exactly taken care of by the Weyl group and so ![]() $G\subset (\pm 1)\times W$.
$G\subset (\pm 1)\times W$.
It is clear that ![]() $(\pm 1)\times W\subset G$.
$(\pm 1)\times W\subset G$.
Theorem 9.8 (Generic Torelli)
The period map ![]() $[per]:[\mathcal {JE}]\to [D/\Gamma ]$ is birational onto its image.
$[per]:[\mathcal {JE}]\to [D/\Gamma ]$ is birational onto its image.
10. The variational Schottky problem for Jacobian surfaces
The Schottky problem is that of determining the image of a moduli space under a period map. As explained by Donagi [Reference DonagiDon84], there is a variational approach to this. For curves of genus ![]() $q$ that are neither hyperelliptic, trigonal nor plane quintics, his approach leads (see p. 257 of [Reference DonagiDon84]) to the statement that the image of the variational period map lies in the Grassmannian that parametrizes
$q$ that are neither hyperelliptic, trigonal nor plane quintics, his approach leads (see p. 257 of [Reference DonagiDon84]) to the statement that the image of the variational period map lies in the Grassmannian that parametrizes ![]() $3q-3$-dimensional quotient spaces
$3q-3$-dimensional quotient spaces ![]() $W$ of
$W$ of ![]() $\operatorname {Sym}^2V$, where
$\operatorname {Sym}^2V$, where ![]() $V$ is a fixed
$V$ is a fixed ![]() $q$-dimensional vector space, and the kernel of
$q$-dimensional vector space, and the kernel of ![]() $\operatorname {Sym}^2V\to W$ defines a smooth linearly normal curve
$\operatorname {Sym}^2V\to W$ defines a smooth linearly normal curve ![]() $C$ of genus
$C$ of genus ![]() $q$ in
$q$ in ![]() ${\mathbb {P}}(V)$. (It follows from this that the embedding
${\mathbb {P}}(V)$. (It follows from this that the embedding ![]() $C\hookrightarrow {\mathbb {P}}(V)$ can be identified with the canonical embedding of
$C\hookrightarrow {\mathbb {P}}(V)$ can be identified with the canonical embedding of ![]() $C$.)
$C$.)
For Jacobian elliptic surfaces of geometric genus ![]() $h$ and irregularity
$h$ and irregularity ![]() $q$ we get something equally concrete.
$q$ we get something equally concrete.
Let ![]() $\mathcal {Z}\to \mathcal {JE}^{\rm gen}$ be the universal ramification locus, of degree
$\mathcal {Z}\to \mathcal {JE}^{\rm gen}$ be the universal ramification locus, of degree ![]() $10+8(1-q)$ over
$10+8(1-q)$ over ![]() $\mathcal {JE}^{\rm gen}$. The image of
$\mathcal {JE}^{\rm gen}$. The image of ![]() $\mathcal {Z}$ lies in a tensor product
$\mathcal {Z}$ lies in a tensor product ![]() $U\otimes V$ where
$U\otimes V$ where ![]() $\dim U=h$ and
$\dim U=h$ and ![]() $\dim V=10h+8(1-q)$. Projecting to
$\dim V=10h+8(1-q)$. Projecting to ![]() ${\mathbb {P}}(U)={\mathbb {P}}^{h-1}$ leads to the following variational partial solution to the Schottky problem. The solution is only partial because this projection factors through the quotient stack
${\mathbb {P}}(U)={\mathbb {P}}^{h-1}$ leads to the following variational partial solution to the Schottky problem. The solution is only partial because this projection factors through the quotient stack ![]() $\mathcal {JE}^{\rm gen}/{\mathbb {G}}_m$.
$\mathcal {JE}^{\rm gen}/{\mathbb {G}}_m$.
Recall that ![]() $\mathcal {JE}^{\rm gen}$ can be described as follows.
$\mathcal {JE}^{\rm gen}$ can be described as follows.
Suppose that ![]() $\mathcal {P}=\mathcal {P}^{h+1-q}\to \mathcal {M}_q$ is the universal Picard variety of degree
$\mathcal {P}=\mathcal {P}^{h+1-q}\to \mathcal {M}_q$ is the universal Picard variety of degree ![]() $h+1-q$ line bundles
$h+1-q$ line bundles ![]() $L$ on a curve
$L$ on a curve ![]() $C$ of genus
$C$ of genus ![]() $q$. Then writing the equation of
$q$. Then writing the equation of ![]() $X$ in affine Weierstrass form, namely as
$X$ in affine Weierstrass form, namely as
shows that ![]() $g_n\in H^0(C,nL)$ and
$g_n\in H^0(C,nL)$ and ![]() $\mathcal {JE}^{\rm gen}$ is birationally equivalent to a
$\mathcal {JE}^{\rm gen}$ is birationally equivalent to a ![]() $B({\mathbb {Z}}/2)$-gerbe over a bundle over
$B({\mathbb {Z}}/2)$-gerbe over a bundle over ![]() $\mathcal {P}$ whose fibre is the quotient stack
$\mathcal {P}$ whose fibre is the quotient stack
The action of ![]() ${\mathbb {G}}_m$ on
${\mathbb {G}}_m$ on ![]() $\overline {\mathcal {E}\ell \ell }$ leads to an action of
$\overline {\mathcal {E}\ell \ell }$ leads to an action of ![]() ${\mathbb {G}}_m$ on
${\mathbb {G}}_m$ on ![]() $\mathcal {JE}^{\rm gen}$ and the quotient
$\mathcal {JE}^{\rm gen}$ and the quotient ![]() $\mathcal {JE}^{\rm gen}/{\mathbb {G}}_m$ is birationally equivalent to a
$\mathcal {JE}^{\rm gen}/{\mathbb {G}}_m$ is birationally equivalent to a ![]() $B({\mathbb {Z}}/2)$-gerbe over the universal
$B({\mathbb {Z}}/2)$-gerbe over the universal ![]() $\vert 4L\vert \times \vert 6L\vert$-bundle over
$\vert 4L\vert \times \vert 6L\vert$-bundle over ![]() $\mathcal {P}$.
$\mathcal {P}$.
Theorem 10.1 The image of the variational period map for Jacobian elliptic surfaces lies in the locus ![]() $\mathcal {V}=\mathcal {V}_{h,q}$ of zero-cycles
$\mathcal {V}=\mathcal {V}_{h,q}$ of zero-cycles ![]() $Z$ in
$Z$ in ![]() ${\mathbb {P}}^{h-1}$ such that:
${\mathbb {P}}^{h-1}$ such that:
(1)
 $\deg Z=10h+8(1-q)$;
$\deg Z=10h+8(1-q)$;(2) the intersection of the quadrics through
 $Z$ is a curve
$Z$ is a curve  $C$ of genus
$C$ of genus  $q$ and degree
$q$ and degree  $h+q-1$;
$h+q-1$;(3) the divisor
 $Z$ on
$Z$ on  $C$ is linearly equivalent to
$C$ is linearly equivalent to  $10L+K_C$ and the hyperplane class
$10L+K_C$ and the hyperplane class  $H$ on
$H$ on  $C$ is
$C$ is  $H= L+K_C$; thus,
$H= L+K_C$; thus,  $Z\sim 10H-9K_C$.
$Z\sim 10H-9K_C$.
Proof. This follows at once from the results of the previous section.
We can make this more precise. First, recall the idea of transvectants: if ![]() $N$ is a line bundle on a variety
$N$ is a line bundle on a variety ![]() $V$ over a field
$V$ over a field ![]() $k$ and
$k$ and ![]() $m,n\in {\mathbb {Z}}$, then there is a homomorphism
$m,n\in {\mathbb {Z}}$, then there is a homomorphism
of sheaves on ![]() $V$ defined, in terms of a local generator
$V$ defined, in terms of a local generator ![]() $s$ of
$s$ of ![]() $N$, by
$N$, by
Suppose that ![]() $V$ is projective; then at the level of global sections this defines a
$V$ is projective; then at the level of global sections this defines a ![]() $k$-linear homomorphism
$k$-linear homomorphism
of finite-dimensional vector spaces. This morphism has several names, depending on the context; for example, the first transvectant, the first Ueberschiebung, the Jacobian determinant, the Gauss map, the Wahl map and the first Rankin–Cohen bracket. Its relevance for us lies in the case where ![]() $V=C$,
$V=C$, ![]() $N=L$,
$N=L$, ![]() $m=4$ and
$m=4$ and ![]() $n=6$.
$n=6$.
Lemma 10.2 The ramification divisor ![]() $Z$, which is a point in
$Z$, which is a point in ![]() $\vert 10L+K_C\vert$, lies in the image of the projectivized first transvectant, which is a rational bilinear map
$\vert 10L+K_C\vert$, lies in the image of the projectivized first transvectant, which is a rational bilinear map
Proof. Consider the elliptic surface given, in affine terms, by the equation ![]() $y^2=4x^3-g_4x-g_6,$ where
$y^2=4x^3-g_4x-g_6,$ where ![]() $g_n$ is a section of
$g_n$ is a section of ![]() $L^{\otimes n}$. Then the
$L^{\otimes n}$. Then the ![]() $j$-invariant is a fractional linear function of the quantity
$j$-invariant is a fractional linear function of the quantity ![]() $j_1=g_4^3/g_6^2$, and the lemma follows from calculating the zero locus of
$j_1=g_4^3/g_6^2$, and the lemma follows from calculating the zero locus of ![]() $d j_1/dz$ when
$d j_1/dz$ when ![]() $z$ is a local coordinate on
$z$ is a local coordinate on ![]() $C$.
$C$.
Corollary 10.3 The universal ramification divisor ![]() $\mathcal {Z}$ is irreducible.
$\mathcal {Z}$ is irreducible.
Proof. The universal ramification divisor ![]() $\mathcal {Z}$ is dominated by
$\mathcal {Z}$ is dominated by ![]() $\vert 6L\vert \times \vert 4L\vert$.
$\vert 6L\vert \times \vert 4L\vert$.
Let ![]() $V(L)$ denote the image of the projectivized first transvectant.
$V(L)$ denote the image of the projectivized first transvectant.
Theorem 10.4 The image of the variational period map for Jacobian elliptic surfaces equals the locus ![]() $\mathcal {T}$ of triples
$\mathcal {T}$ of triples ![]() $(C,L,Z)$ where:
$(C,L,Z)$ where:
(1)
 $C\in \mathcal {M}_q$;
$C\in \mathcal {M}_q$;(2)
 $L\in \operatorname {Pic}^{h+1-q}_C;$
$L\in \operatorname {Pic}^{h+1-q}_C;$(3)
 $Z\in V(L)$.
$Z\in V(L)$.
This locus is irreducible.
Proof. The only thing left to do is to observe that ![]() $\mathcal {T}$ is irreducible. However,
$\mathcal {T}$ is irreducible. However, ![]() $\mathcal {T}$ is dominated by
$\mathcal {T}$ is dominated by ![]() $\mathcal {Z}$.
$\mathcal {Z}$.
11. Multiple surfaces
An elliptic surface ![]() $f:X\to C$ is multiple if it is not simple; that is, if it has multiple fibres. As far as the period map is concerned there is not much to be said about these. Kodaira proved that, given
$f:X\to C$ is multiple if it is not simple; that is, if it has multiple fibres. As far as the period map is concerned there is not much to be said about these. Kodaira proved that, given ![]() $f:X\to C$, there is a simple elliptic surface
$f:X\to C$, there is a simple elliptic surface ![]() $g:Y\to C$ such that
$g:Y\to C$ such that ![]() $X$ is obtained from
$X$ is obtained from ![]() $Y$ by logarithmic transformations; in particular, there is a finite subset
$Y$ by logarithmic transformations; in particular, there is a finite subset ![]() $S$ of
$S$ of ![]() $C$ such that, if
$C$ such that, if ![]() $C_0=C-S$,
$C_0=C-S$, ![]() $X_0=f^{-1}(C_0)$ and
$X_0=f^{-1}(C_0)$ and ![]() $Y_0=g^{-1}(C_0)$, then
$Y_0=g^{-1}(C_0)$, then ![]() $X_0$ and
$X_0$ and ![]() $Y_0$ are isomorphic relative to
$Y_0$ are isomorphic relative to ![]() $C_0$, but are not usually bimeromorphic. In this situation the sheaves
$C_0$, but are not usually bimeromorphic. In this situation the sheaves ![]() $f_*\omega _{X/C}$ and
$f_*\omega _{X/C}$ and ![]() $g_*\omega _{Y/C}$ are isomorphic [Reference SchmidSch73, p. 234]. It follows that
$g_*\omega _{Y/C}$ are isomorphic [Reference SchmidSch73, p. 234]. It follows that ![]() $f_*\Omega ^2_X$ and
$f_*\Omega ^2_X$ and ![]() $g_*\Omega ^2_Y$ are isomorphic and then that the weight 2 Hodge structures on
$g_*\Omega ^2_Y$ are isomorphic and then that the weight 2 Hodge structures on ![]() $X$ and
$X$ and ![]() $Y$ are isomorphic.
$Y$ are isomorphic.
We deduce that the period map can detect neither the presence nor the location of multiple fibres on an elliptic surface.
Acknowledgements
I am very grateful to P. Griffiths, I. Grojnowski, R. Thomas and T. Scholl for some valuable discussions.
Conflicts of Interest
None.