Hostname: page-component-784d4fb959-nxbs6 Total loading time: 0 Render date: 2025-07-16T08:37:48.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Hilbert type operators acting from the Bloch space into Bergman spaces

Part of: Spaces and algebras of analytic functions Special classes of linear operators

Published online by Cambridge University Press:  26 November 2024

Pengcheng Tang
Pengcheng Tang*
Affiliation:
School of Mathematics and Statistics, Hunan University of Science and Technology, Xiangtan, Hunan, China
*
Email: www.tangtpc.com@foxmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let µ be a finite positive Borelmeasure on 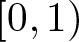$[0,1)$ and 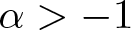$\alpha \gt -1$. The generalized integral operator of Hilbert type 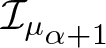$\mathcal {I}_{\mu_{\alpha+1}}$ is defined on the spaces 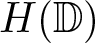$H(\mathbb{D})$ of analytic functions in the unit disc 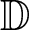$\mathbb{D}$ as follows:

\begin{equation*}\mathcal {I}_{\mu_{\alpha+1}}(f)(z)=\int_{0}^{1} \frac{f(t)}{(1-tz)^{\alpha+1}}d\mu(t),\ \ f\in H(\mathbb{D}),\ \ z\in \mathbb{D} .\end{equation*}

In this paper, we give a unified characterization of the measures µ for which the operator 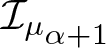$\mathcal {I}_{\mu_{\alpha+1}}$ is bounded from the Bloch space to a Bergman space for all 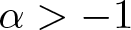$\alpha \gt -1$. Additionally, we also investigate the action of 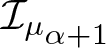$\mathcal {I}_{\mu_{\alpha+1}}$ from the Bloch space to the Hardy spaces and the Besov spaces.

Keywords

Hilbert operatorBloch spaceBergman space

MSC classification

Primary: 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators
Secondary: 30H30: Bloch spaces 30H20: Bergman spaces, Fock spaces

Information

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 68 , Issue 1 , February 2025 , pp. 205 - 225
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Avetisyan, K., A note on mixed norm spaces of analytic functions, Aust. J. Math. Anal. Appl. 9(1) (2012), 1–6.Google Scholar
Bao, G., and Wulan, H., Hankel matrices acting on Dirichlet spaces, J. Math. Anal. Appl. 409 (1) (2014), 228–235.CrossRefGoogle Scholar
Buckley, S., Koskela, P. and Vukotić, D., Fractional integration, differentiation, and weighted Bergman spaces, Math. Proc. Cambridge Philos. Soc. 126(2) (1999), 369–385.CrossRefGoogle Scholar
Chatzifountas, C., Girela, D., and Peláez, J., A generalized Hilbert matrix acting on Hardy spaces, J. Math. Anal. Appl. 413 (1) (2014), 154–168.CrossRefGoogle Scholar
Diamantopoulos, E., Hilbert matrix on Bergman spaces, Illinois J. Math. 48(3) (2004), 1067–1078.CrossRefGoogle Scholar
Diamantopoulos, E., and Siskakis, A., Composition operators and the Hilbert matrix, Studia Math. 140 (2) (2000), 191–198.CrossRefGoogle Scholar
Dostanić, M., Jevtić, M., and Vukotić, D., Norm of the Hilbert matrix on Bergman and Hardy spaces and a theorem of Nehari type, J. Funct. Anal. 254 (11) (2008), 2800–2815.CrossRefGoogle Scholar
Duren, P., Theory of Hp Spaces (Academic Press, New York, 1970).Google Scholar
Galanopoulos, P., Girela, D., and Merchán, N., Cesàro-like operators acting on spaces of analytic functions, Anal. Math. Phys. 12 (2) (2022), .CrossRefGoogle Scholar
Galanopoulos, P. and Peláez, J., A Hankel matrix acting on Hardy and Bergman spaces, Studia Math. 200(3) (2010), 201–220.CrossRefGoogle Scholar
Girela, D. and Merchán, N., A Hankel matrix acting on spaces of analytic functions, Integral Equ. Oper. Theory 89(4) (2017), 581–594.CrossRefGoogle Scholar
Girela, D., and Merchán, N., A generalized Hilbert operator acting on conformally invariant spaces, Banach J. Math. Anal. Appl. 12 (2) (2018), 374–398.CrossRefGoogle Scholar
Girela, D., and Merchán, N., Hankel matrices acting on the Hardy space ${H}^1$ and on Dirichlet spaces, Rev. Mat. Comput. 32 (3) (2019), 799–822.CrossRefGoogle Scholar
Jevtić, M., and Karapetrović, B., Generalized Hilbert matrices acting on spaces that are close to the Hardy space ${H}^1$ and to the space BMOA, Complex Anal. Oper. Theory 13 (3) (2019), 2357–2370.CrossRefGoogle Scholar
Lanucha, B., Nowak, M., and Pavlović, M., Hilbert matrix operator on spaces of analytic functions, Ann. Acad. Sci. Fenn. Math. 37 (1) (2012), 161–174.CrossRefGoogle Scholar
Li. Zhao, Z. W. and Su, Z., A Derivative-Hilbert operator acting from Besov spaces into Bloch space, J. Math. Inequal. 16(3) (2022), 1229–1242.CrossRefGoogle Scholar
Mateljević, M., and Pavlović, M., ${L}^{p}$ behaviour of the integral means of analytic functions, Studia Math. 77 (3) (1984), 219–237.CrossRefGoogle Scholar
Merchán, N., Mean Lipschitz spaces and a generalized Hilbert operator, Collect. Math. 70 (1) (2019), 59–69.CrossRefGoogle Scholar
Pavlović, M. and Mateljević, M., L p-behavior of power series with positive coefficients and Hardy spaces, Proc. Amer. Math. Soc. 87(2) (1983), 309–316.Google Scholar
Pavlović, M., Analytic functions with decreasing coefficients and Hardy and Bloch spaces, Proc. Edinb. Math. Soc. 56 (2) (2013), 623–635.CrossRefGoogle Scholar
Rudin, W., Function Theory in the Unit Ball of ${C}^{n}$ (Springer, New York, 1980).CrossRefGoogle Scholar
Tang, P., and Zhang, X., Generalized integral type Hilbert operator acting between weighted Bloch spaces, Math. Meth. Appl. Sci. 46 (3) (2023), 18458–18472.CrossRefGoogle Scholar
Ye, S. and Zhou, Z., A Derivative-Hilbert operator acting on the Bloch space, Complex Anal. Oper. Theory 15(5) (2021), .CrossRefGoogle Scholar
Ye, S. and Zhou, Z., A Derivative-Hilbert operator acting on Bergman spaces, J. Math. Anal. Appl. 506(1) (2022), .CrossRefGoogle Scholar
Zhu, K., Operator Theory in Function Spaces (Marcel Dekker, New York, 1990) Reprint: Math. Surveys and Monographs, Vol. 138, American Mathematical Society, Providence, Rhode Island (2007).Google Scholar
Zygmund, A., Trigonometric Series, VolumeI,II (Cambridge University Press, London, 1959).Google Scholar