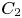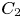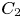Introduction
Reflexive homology is the homology theory associated to the reflexive crossed simplicial group. It is the most general way to extend Hochschild homology to detect an order-reversing involution.
The study of involutive structures in algebraic topology has been very fruitful in recent years with the development of real topological Hochschild homology [Reference Angelini-Knoll, Gerhardt and Hill1, Reference Dotto18, Reference Dotto, Moi and Patchkoria20, Reference Dotto, Moi, Patchkoria and Reeh21, Reference Dotto, Patchkoria and Moi23, Reference Høgenhaven44, Reference Høgenhaven45], real algebraic $K$![]() -theory [Reference Dotto19, Reference Dotto and Ogle22, Reference Hesselholt and Madsen43] and a renaissance in the study of Hermitian $K$
-theory [Reference Dotto19, Reference Dotto and Ogle22, Reference Hesselholt and Madsen43] and a renaissance in the study of Hermitian $K$![]() -theory [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle8–Reference Calmés, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10].
-theory [Reference Calmès, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle8–Reference Calmés, Dotto, Harpaz, Hebestreit, Land, Moi, Nardin, Nikolaus and Steimle10].
In this paper we study the relationship between reflexive homology and the $C_2$![]() -equivariant homology of free loop spaces. The study of free loop spaces occurs widely in topology and geometry. In topology they play an important role in string topology [Reference Chas and Sullivan12] and topological Hochschild and cyclic homology [Reference Blumberg, Cohen and Schlichtkrull3, Reference Nikolaus and Scholze60]. See also [Reference Cohen, Hess and Voronov13] for more on both of these topics. In geometry, the free loop space is intimately connected with the study of closed geodesics on manifolds [Reference Lyusternik and Fet54], [Reference Gromoll and Meyer41]. See also [Reference Oancea61] for a survey of results in this area.
-equivariant homology of free loop spaces. The study of free loop spaces occurs widely in topology and geometry. In topology they play an important role in string topology [Reference Chas and Sullivan12] and topological Hochschild and cyclic homology [Reference Blumberg, Cohen and Schlichtkrull3, Reference Nikolaus and Scholze60]. See also [Reference Cohen, Hess and Voronov13] for more on both of these topics. In geometry, the free loop space is intimately connected with the study of closed geodesics on manifolds [Reference Lyusternik and Fet54], [Reference Gromoll and Meyer41]. See also [Reference Oancea61] for a survey of results in this area.
Crossed simplicial groups were introduced independently by Fiedorowicz and Loday [Reference Fiedorowicz and Loday31] and Krasauskas [Reference Krasauskas47] in order to study equivariant homology. One way of thinking about a crossed simplicial group is as the structure required to build group actions into Hochschild homology in the same fashion as the cyclic homology theory due to Connes [Reference Connes14] (see also [Reference Loday51]). Since their introduction, crossed simplicial groups have been well-studied and have found applications in other areas such as the categorification of monoids in symmetric and braided monoidal categories [Reference Graves36–Reference Graves38, Reference Lack49, Reference Pirashvili63] and combinatorial models for marked surfaces with a $G$![]() -structure [Reference Dyckerhoff and Kapranov25].
-structure [Reference Dyckerhoff and Kapranov25].
A classification result [Reference Fiedorowicz and Loday31, 3.6], [Reference Krasauskas47, 1.5] tells us that any crossed simplicial group occurs as an extension of a fundamental crossed simplicial group. These fundamental crossed simplicial groups are subobjects of the hyperoctahedral crossed simplicial group [Reference Fiedorowicz and Loday31, Section 3]: trivial; reflexive; cyclic; dihedral; symmetric; and hyperoctahedral. Most of these crossed simplicial groups have been well-studied. Whilst the associated homology theories have a range of interesting applications, for the purposes of this introduction we will restrict ourselves to results about loop spaces.
The homology theories associated to the trivial crossed simplicial group and the cyclic crossed simplicial group are Hochschild homology and cyclic homology respectively. These homology theories, when applied to the group algebra of a discrete group, calculate the homology and the $S^1$![]() -equivariant homology of the free loop space on the classifying space of the group respectively [Reference Loday51, 7.3.13]. Indeed, the connections between the cyclic homology theory and free loop spaces is well-established [Reference Burghelea and Fiedorowicz6, Reference Burghelea7, Reference Carlsson and Cohen11, Reference Goodwillie35, Reference Jones46, Reference Vigué-Poirrier and Burghelea69]. The dihedral homology theory [Reference Krasauskas, Lapin and Solov'ev48, Reference Loday50] is used to calculate the $O(2)$
-equivariant homology of the free loop space on the classifying space of the group respectively [Reference Loday51, 7.3.13]. Indeed, the connections between the cyclic homology theory and free loop spaces is well-established [Reference Burghelea and Fiedorowicz6, Reference Burghelea7, Reference Carlsson and Cohen11, Reference Goodwillie35, Reference Jones46, Reference Vigué-Poirrier and Burghelea69]. The dihedral homology theory [Reference Krasauskas, Lapin and Solov'ev48, Reference Loday50] is used to calculate the $O(2)$![]() -equivariant homology of free loop spaces [Reference Dunn24, Reference Lodder53, Reference Ungheretti68].
-equivariant homology of free loop spaces [Reference Dunn24, Reference Lodder53, Reference Ungheretti68].
In spite of the fact that crossed simplicial groups and their associated homology theories are well-studied, the reflexive crossed simplicial group appears only ephemerally in the literature; usually only being considered insofar as it relates to the dihedral crossed simplicial group. For example, Krasauskas, Lapin and Solov'ev [Reference Krasauskas, Lapin and Solov'ev48, Section 3] give a definition of reflexive homology in terms of hyperhomology in order to obtain a dihedral version of Connes’ periodicity long exact sequence. Spaliński [Reference Spaliński66, Section 3] shows that the category of reflexive sets admits a model structure that is Quillen equivalent to the category of $C_2$![]() -spaces with the fixed-point model structure and uses this as a tool for giving a discrete model of $O(2)$
-spaces with the fixed-point model structure and uses this as a tool for giving a discrete model of $O(2)$![]() -equivariant homotopy theory, which also arises from the dihedral crossed simplicial group.
-equivariant homotopy theory, which also arises from the dihedral crossed simplicial group.
In this paper we study the reflexive homology theory in its own right. The term ‘reflexive’ for this crossed simplicial group was first used in [Reference Krasauskas47, Proposition 1.5]. As the homology theory associated to a crossed simplicial group, reflexive homology is defined as functor homology over a small category which we will denote $\Delta R^{op}$![]() . The structure of the indexing category $\Delta R^{op}$
. The structure of the indexing category $\Delta R^{op}$![]() can be thought of as encoding an order-reversing involution compatible with a unital, associative multiplication. In this sense, the reflexive homology theory offers the most general framework for extending Hochschild homology to detect the action of an involution.
can be thought of as encoding an order-reversing involution compatible with a unital, associative multiplication. In this sense, the reflexive homology theory offers the most general framework for extending Hochschild homology to detect the action of an involution.
The paper is structured as follows.
In § 1 we define reflexive homology in terms of functor homology and use this to define the reflexive homology of an involutive algebra over a commutative ring. We provide the necessary background material on functor homology and Hochschild homology and survey the results that currently exist in the literature.
In § 2 we define a bicomplex that can be used to calculate reflexive homology. We use this to show that our functor homology definition coincides with the hyperhomology definition of [Reference Krasauskas, Lapin and Solov'ev48]. We also show that when working over a field of characteristic zero, reflexive homology can be calculated using the quotient of the Hochschild complex by the involution action.
In § 3 we define reflexive hyperhomology for chain complexes of left $\Delta R^{op}$![]() -modules in terms of hyper-derived functors and recall some important examples.
-modules in terms of hyper-derived functors and recall some important examples.
In § 4 we prove that reflexive homology satisfies Morita invariance. Explicitly, we show that for an involutive algebra $A$![]() , the reflexive homology of the involutive algebra of $(m\times m)$
, the reflexive homology of the involutive algebra of $(m\times m)$![]() -matrices with entries in $A$
-matrices with entries in $A$![]() is isomorphic to the reflexive homology of $A$
is isomorphic to the reflexive homology of $A$![]() .
.
In § 5 we provide some computations. We calculate the reflexive homology of the ground ring and describe degree zero reflexive homology for commutative algebras with involution.
In § 6 we calculate the reflexive homology of a tensor algebra. We show that this can be described in terms of the group homology of $C_2$![]() with coefficients in the Hochschild homology of the tensor algebra, as calculated by Loday and Quillen [Reference Loday and Quillen52]. As a consequence, we show that the reflexive homology of a tensor algebra has a grading.
with coefficients in the Hochschild homology of the tensor algebra, as calculated by Loday and Quillen [Reference Loday and Quillen52]. As a consequence, we show that the reflexive homology of a tensor algebra has a grading.
In § 7 we calculate the reflexive homology of a group algebra. We prove that this is isomorphic to the homology of the $C_2$![]() -equivariant Borel construction on the free loop space of the classifying space of the group. By combining this with the cyclic homology of a group algebra [Reference Loday51, 7.3.13], we show that the dihedral homology of a group algebra is isomorphic to the homology of the $O(2)$
-equivariant Borel construction on the free loop space of the classifying space of the group. By combining this with the cyclic homology of a group algebra [Reference Loday51, 7.3.13], we show that the dihedral homology of a group algebra is isomorphic to the homology of the $O(2)$![]() -equivariant Borel construction on the free loop space of the classifying space of the group. Furthermore, we give a direct sum decomposition of the reflexive homology of a group algebra, indexed over the conjugacy classes of the group, where the summands are given in terms of a reflexive analogue of group homology.
-equivariant Borel construction on the free loop space of the classifying space of the group. Furthermore, we give a direct sum decomposition of the reflexive homology of a group algebra, indexed over the conjugacy classes of the group, where the summands are given in terms of a reflexive analogue of group homology.
In § 8 we use our reflexive hyperhomology to prove that we can calculate the $C_2$![]() -equivariant homology of certain free loop spaces and free loop-suspension spaces in terms of the singular chain complex on certain Moore loop spaces.
-equivariant homology of certain free loop spaces and free loop-suspension spaces in terms of the singular chain complex on certain Moore loop spaces.
Other constructions that build an involution into Hochschild homology exist in the literature. Braun [Reference Braun4] introduced involutive Hochschild homology in order to study involutive algebras and involutive $A_{\infty }$![]() -algebras. The homological algebra of this theory was developed by Fernàndez-València and Giansiracusa [Reference Fernàndez-València and Giansiracusa29]. In particular, they show that under nice conditions involutive Hochschild homology can be described as Tor over an involutive analogue of the enveloping algebra. In § 9 we show that under these conditions there is an isomorphism between involutive Hochschild homology and reflexive homology.
-algebras. The homological algebra of this theory was developed by Fernàndez-València and Giansiracusa [Reference Fernàndez-València and Giansiracusa29]. In particular, they show that under nice conditions involutive Hochschild homology can be described as Tor over an involutive analogue of the enveloping algebra. In § 9 we show that under these conditions there is an isomorphism between involutive Hochschild homology and reflexive homology.
In § 10, we provide some exposition on how the structure of the reflexive crossed simplicial group appears in the study of real topological Hochschild homology. In particular, we observe that real simplicial objects in a category are precisely the same as reflexive objects in a category. An important example of this is the dihedral nerve construction, which plays an important role in defining real topological Hochschild homology.
Conventions
Throughout the paper we will let $k$![]() be a commutative ring. An unadorned tensor product symbol, $\otimes$
be a commutative ring. An unadorned tensor product symbol, $\otimes$![]() , will denote the tensor product of $k$
, will denote the tensor product of $k$![]() -modules. The category of $k$
-modules. The category of $k$![]() -modules will be denoted by $\mathbf {Mod}_k$
-modules will be denoted by $\mathbf {Mod}_k$![]() . We will denote by $\mathbf {Top}$
. We will denote by $\mathbf {Top}$![]() the category of compactly generated weak Hausdorff topological spaces. Let $\mathbf {Top}_{\star }$
the category of compactly generated weak Hausdorff topological spaces. Let $\mathbf {Top}_{\star }$![]() denote the category of based compactly generated weak Hausdorff topological spaces. We will usually refer to a ‘topological space’ or a ‘based topological space’. When referring to a weak equivalence of topological spaces we mean a $\pi _{\star }$
denote the category of based compactly generated weak Hausdorff topological spaces. We will usually refer to a ‘topological space’ or a ‘based topological space’. When referring to a weak equivalence of topological spaces we mean a $\pi _{\star }$![]() -isomorphism. Several of our results relate to free loop spaces so we will introduce notation for this here. Let $\mathcal {L}$
-isomorphism. Several of our results relate to free loop spaces so we will introduce notation for this here. Let $\mathcal {L}$![]() denote the functor $\mathrm {Maps}(S^1,\, -)$
denote the functor $\mathrm {Maps}(S^1,\, -)$![]() , which sends a based topological space $X$
, which sends a based topological space $X$![]() to the space of unbased continuous maps $S^1\rightarrow X$
to the space of unbased continuous maps $S^1\rightarrow X$![]() .
.
1. Reflexive homology
In this section we recall the definition of the reflexive crossed simplicial group and define its associated homology theory.
1.1 Functor homology and Hochschild homology
We start by recalling some constructions from functor homology, using Hochschild homology as an example.
For a small category $\mathbf {C}$![]() there are abelian categories $\mathbf {CMod}=\mathrm {Fun}(\mathbf {C},\, \mathbf {Mod}_k)$
there are abelian categories $\mathbf {CMod}=\mathrm {Fun}(\mathbf {C},\, \mathbf {Mod}_k)$![]() and $\mathbf {ModC}=\mathrm {Fun}(\mathbf {C}^{op},\, \mathbf {Mod}_k)$
and $\mathbf {ModC}=\mathrm {Fun}(\mathbf {C}^{op},\, \mathbf {Mod}_k)$![]() . There is a tensor product
. There is a tensor product
defined as the coend
as in [Reference Lane55, Section 3]. It is well-known that this tensor product is right exact with respect to both variables and preserves direct sums [Reference Pirashvili and Richter62, Section 1.6]. The left derived functors of this tensor product are denoted by $\mathrm {Tor}_{\star }^{\mathbf {C}}(-,\,-)$![]() . When $G=k^{\ast }$
. When $G=k^{\ast }$![]() , the constant functor at $k$
, the constant functor at $k$![]() , we write $H_{\star }(\mathbf {C},\,F)= \mathrm {Tor}_{\star }^{\mathbf {C}}(k^{\ast },\, F)$
, we write $H_{\star }(\mathbf {C},\,F)= \mathrm {Tor}_{\star }^{\mathbf {C}}(k^{\ast },\, F)$![]() .
.
As an example, we can recover Hochschild homology of a simplicial $k$![]() -module. Recall the category $\Delta$
-module. Recall the category $\Delta$![]() , whose objects are the sets $[n]=\left \lbrace 0,\,\dotsc,\, n\right \rbrace$
, whose objects are the sets $[n]=\left \lbrace 0,\,\dotsc,\, n\right \rbrace$![]() for $n\geqslant 0$
for $n\geqslant 0$![]() and whose morphisms are order-preserving maps [Reference Loday51, B.1]. If we take $\mathbf {C}=\Delta ^{op}$
and whose morphisms are order-preserving maps [Reference Loday51, B.1]. If we take $\mathbf {C}=\Delta ^{op}$![]() and a simplicial $k$
and a simplicial $k$![]() -module $F\colon \Delta ^{op}\rightarrow \mathbf {Mod}_k$
-module $F\colon \Delta ^{op}\rightarrow \mathbf {Mod}_k$![]() we recover Hochschild homology. One example that we will be particularly interested in is studying $k$
we recover Hochschild homology. One example that we will be particularly interested in is studying $k$![]() -algebras so we recall the Loday functor.
-algebras so we recall the Loday functor.
Let $A$![]() be an associative $k$
be an associative $k$![]() -algebra and let $M$
-algebra and let $M$![]() be an $A$
be an $A$![]() -bimodule. There is a functor
-bimodule. There is a functor
given on objects by $[n]\mapsto M\otimes A^{\otimes n}$![]() and determined on morphisms by
and determined on morphisms by

and

The chain complex associated to this simplicial $k$![]() -module is the Hochschild complex $C_{\star }(A,\,M)$
-module is the Hochschild complex $C_{\star }(A,\,M)$![]() and its homology is Hochschild homology, $HH_{\star }(A,\,M)$
and its homology is Hochschild homology, $HH_{\star }(A,\,M)$![]() . In particular we have
. In particular we have
1.2 Reflexive homology
An important source of functor homology theories come from crossed simplicial groups, introduced independently by Fiedorowicz and Loday [Reference Fiedorowicz and Loday31] and Krasauskas [Reference Krasauskas47].
In this paper we will study the homology theory associated to the reflexive crossed simplicial group.
Definition 1.1 Let $R_n=\left \langle r_n\mid r_n^2=1\right \rangle \cong C_2$![]() for $n\geqslant 0$
for $n\geqslant 0$![]() .
.
The family of groups $\left \lbrace R_{\star }\right \rbrace$![]() forms a crossed simplicial group [Reference Fiedorowicz and Loday31, Example 2], whose geometric realization is $C_2$
forms a crossed simplicial group [Reference Fiedorowicz and Loday31, Example 2], whose geometric realization is $C_2$![]() .
.
Definition 1.2 The category $\Delta R$![]() has the sets $[n]=\left \lbrace 0,\,\dotsc,\, n\right \rbrace$
has the sets $[n]=\left \lbrace 0,\,\dotsc,\, n\right \rbrace$![]() for $n\geqslant 0$
for $n\geqslant 0$![]() as objects. An element of $\mathrm {Hom}_{\Delta R}([n],\,[m])$
as objects. An element of $\mathrm {Hom}_{\Delta R}([n],\,[m])$![]() is a pair $(\varphi,\, g)$
is a pair $(\varphi,\, g)$![]() where $g\in R_n$
where $g\in R_n$![]() and $\varphi \in \mathrm {Hom}_{\Delta }([n],\,[m])$
and $\varphi \in \mathrm {Hom}_{\Delta }([n],\,[m])$![]() . The composition is determined as follows. For a face map $\delta _i\in \mathrm {Hom}_{\Delta }([n],\,[n+1])$
. The composition is determined as follows. For a face map $\delta _i\in \mathrm {Hom}_{\Delta }([n],\,[n+1])$![]() we define $r_{n+1}\circ \delta _i=\delta _{n-i}\circ r_n$
we define $r_{n+1}\circ \delta _i=\delta _{n-i}\circ r_n$![]() and for a degeneracy map $\sigma _j\in \mathrm {Hom}_{\Delta }([n],\,[n-1])$
and for a degeneracy map $\sigma _j\in \mathrm {Hom}_{\Delta }([n],\,[n-1])$![]() we define $r_{n}\circ \sigma _j=\sigma _{n-j}\circ r_{n-1}$
we define $r_{n}\circ \sigma _j=\sigma _{n-j}\circ r_{n-1}$![]() .
.
Remark 1.3 The category $\Delta R$![]() also appears in [Reference Krasauskas, Lapin and Solov'ev48, Section 1] with the notation $\Delta \ltimes \mathbb {Z}/2$
also appears in [Reference Krasauskas, Lapin and Solov'ev48, Section 1] with the notation $\Delta \ltimes \mathbb {Z}/2$![]() .
.
Definition 1.4 Let $F\in \mathrm {Fun}(\Delta R^{op},\,\mathbf {Mod}_k)$![]() . We define the reflexive homology of $F$
. We define the reflexive homology of $F$![]() to be $HR_{\star }(F)=\mathrm {Tor}_{\star }^{\Delta R^{op}}(k^{\ast },\, F)$
to be $HR_{\star }(F)=\mathrm {Tor}_{\star }^{\Delta R^{op}}(k^{\ast },\, F)$![]() , where $k^{\ast }\in \mathrm {Fun}(\Delta R,\, \mathbf {Mod}_k)$
, where $k^{\ast }\in \mathrm {Fun}(\Delta R,\, \mathbf {Mod}_k)$![]() is the constant functor at $k$
is the constant functor at $k$![]() .
.
We can extend the Loday functor to a functor $\mathcal {L}(A,\,M)\colon \Delta R^{op}\rightarrow \mathbf {Mod}_k$![]() in two different ways but first we require some definitions.
in two different ways but first we require some definitions.
Definition 1.5 A $k$![]() -algebra is said to be involutive if it is equipped with an anti-homomorphism of algebras $A\rightarrow A$
-algebra is said to be involutive if it is equipped with an anti-homomorphism of algebras $A\rightarrow A$![]() of order two, which we will denote by $a\mapsto \overline {a}$
of order two, which we will denote by $a\mapsto \overline {a}$![]() . In other words, we equip $A$
. In other words, we equip $A$![]() with a $k$
with a $k$![]() -linear endomorphism which reverses the order of multiplication and squares to the identity.
-linear endomorphism which reverses the order of multiplication and squares to the identity.
Following Loday [Reference Loday51, 5.2.1] we recall the notion of an involutive $A$![]() -bimodule.
-bimodule.
Definition 1.6 Let $A$![]() be an involutive $k$
be an involutive $k$![]() -algebra. An involutive $A$
-algebra. An involutive $A$![]() -bimodule is an $A$
-bimodule is an $A$![]() -bimodule $M$
-bimodule $M$![]() equipped with a map $m\mapsto \overline {m}$
equipped with a map $m\mapsto \overline {m}$![]() such that $\overline {a_1ma_2}= \overline {a_2}\, \overline {m}\, \overline {a_1}$
such that $\overline {a_1ma_2}= \overline {a_2}\, \overline {m}\, \overline {a_1}$![]() for $a_1$
for $a_1$![]() , $a_2\in A$
, $a_2\in A$![]() .
.
Example 1.7 Taking $M=A$![]() gives one example of an involutive $A$
gives one example of an involutive $A$![]() -bimodule. If $A$
-bimodule. If $A$![]() is equipped with an augmentation $\varepsilon \colon A\rightarrow k$
is equipped with an augmentation $\varepsilon \colon A\rightarrow k$![]() we can also take $M=k$
we can also take $M=k$![]() with the trivial involution.
with the trivial involution.
With these definitions we can extend the Loday functor to $\Delta R^{op}$![]() in two ways.
in two ways.
Definition 1.8 Let $A$![]() be an involutive $k$
be an involutive $k$![]() -algebra and let $M$
-algebra and let $M$![]() be an involutive $A$
be an involutive $A$![]() -bimodule. We extend the Loday functor $\mathcal {L}(A,\,M)$
-bimodule. We extend the Loday functor $\mathcal {L}(A,\,M)$![]() to a functor
to a functor
by defining
Definition 1.9 Let $A$![]() be an involutive $k$
be an involutive $k$![]() -algebra and let $M$
-algebra and let $M$![]() be an involutive $A$
be an involutive $A$![]() -bimodule. We define
-bimodule. We define
Definition 1.10 Let $A$![]() be an involutive $k$
be an involutive $k$![]() -algebra and let $M$
-algebra and let $M$![]() be an involutive $A$
be an involutive $A$![]() -bimodule. We extend the Loday functor $\mathcal {L}(A,\,M)$
-bimodule. We extend the Loday functor $\mathcal {L}(A,\,M)$![]() to a functor
to a functor
by defining
Definition 1.11 Let $A$![]() be an involutive $k$
be an involutive $k$![]() -algebra and let $M$
-algebra and let $M$![]() be an involutive $A$
be an involutive $A$![]() -bimodule. We define
-bimodule. We define
Remark 1.12 When we take $M=A$![]() we will omit the coefficients from the notation and write $\mathcal {L}^{\pm }(A)$
we will omit the coefficients from the notation and write $\mathcal {L}^{\pm }(A)$![]() and $HR_{\star }^{\pm }(A)$
and $HR_{\star }^{\pm }(A)$![]() .
.
Remark 1.13 These reflexive homology groups fit into long exact sequences with the dihedral homology groups by [Reference Krasauskas, Lapin and Solov'ev48, Proposition 3.1]. There exist long exact sequences
and
where the dihedral homology groups $HD_{\star }^+(A)$![]() and $HD_{\star }^{-}(A)$
and $HD_{\star }^{-}(A)$![]() are defined in [Reference Krasauskas, Lapin and Solov'ev48, Section 1]. Furthermore, as discussed in [Reference Loday51, 5.2], if the ground ring $k$
are defined in [Reference Krasauskas, Lapin and Solov'ev48, Section 1]. Furthermore, as discussed in [Reference Loday51, 5.2], if the ground ring $k$![]() contains $\mathbb {Q}$
contains $\mathbb {Q}$![]() then the direct sum of these long exact sequences is Connes’ long exact sequence connecting Hochschild homology and cyclic homology [Reference Loday51, Theorem 2.2.1].
then the direct sum of these long exact sequences is Connes’ long exact sequence connecting Hochschild homology and cyclic homology [Reference Loday51, Theorem 2.2.1].
Remark 1.14 For an involutive $k$![]() -algebra $A$
-algebra $A$![]() , there is natural map $HR_{\star }^+(A) \rightarrow HO_{\star }(A)$
, there is natural map $HR_{\star }^+(A) \rightarrow HO_{\star }(A)$![]() , where $HO_{\star }$
, where $HO_{\star }$![]() denotes the hyperoctahedral homology theory of [Reference Graves39] and [Reference Fiedorowicz30, Section 2]. One can obtain this map by composing the map $HR_{\star }^+(A) \rightarrow HD_{\star }^+(A)$
denotes the hyperoctahedral homology theory of [Reference Graves39] and [Reference Fiedorowicz30, Section 2]. One can obtain this map by composing the map $HR_{\star }^+(A) \rightarrow HD_{\star }^+(A)$![]() from the previous remark with the map $HD_{\star }(A) \rightarrow HO_{\star }(A)$
from the previous remark with the map $HD_{\star }(A) \rightarrow HO_{\star }(A)$![]() of [Reference Graves39, Subsection 3.3].
of [Reference Graves39, Subsection 3.3].
2. Biresolution
We begin this section by defining a biresolution of the $k$![]() -constant right $\Delta R^{op}$
-constant right $\Delta R^{op}$![]() -module $k^{\ast }$
-module $k^{\ast }$![]() . Fiedorowicz and Loday [Reference Fiedorowicz and Loday31, 6.7] give a general construction for such a biresolution using the homogeneous bar resolution for a group [Reference Lane56, VII.6]. The bicomplex defined here is smaller, making use of the periodic resolution of the group $C_2$
. Fiedorowicz and Loday [Reference Fiedorowicz and Loday31, 6.7] give a general construction for such a biresolution using the homogeneous bar resolution for a group [Reference Lane56, VII.6]. The bicomplex defined here is smaller, making use of the periodic resolution of the group $C_2$![]() . It is also worth noting that our bicomplex includes into the tricomplex of Krasauskas, Lapin and Solov'ev [Reference Krasauskas, Lapin and Solov'ev48, Section 2] for computing dihedral homology.
. It is also worth noting that our bicomplex includes into the tricomplex of Krasauskas, Lapin and Solov'ev [Reference Krasauskas, Lapin and Solov'ev48, Section 2] for computing dihedral homology.
Definition 2.1 We define a bicomplex $C_{\star,\star }$![]() of right $\Delta R^{op}$
of right $\Delta R^{op}$![]() -modules as follows. Firstly we set
-modules as follows. Firstly we set
for all $p,\,q\geqslant 0$![]() .
.
The horizontal differential $d\colon C_{p,q}\rightarrow C_{p-1,q}$![]() for $q\geqslant 0$
for $q\geqslant 0$![]() and $p\geqslant 1$
and $p\geqslant 1$![]() is given by
is given by

where the map $r_q$![]() is defined by pre-composition.
is defined by pre-composition.
The vertical differential $b\colon C_{p,q}\rightarrow C_{p,q-1}$![]() for $p\geqslant 0$
for $p\geqslant 0$![]() and $q\geqslant 1$
and $q\geqslant 1$![]() is given by
is given by

where the maps $\delta _i$![]() are defined by pre-composition.
are defined by pre-composition.
Proposition 2.2 The bicomplex $C_{\star,\star }$![]() of definition 2.1 is a biresolution of the $k$
of definition 2.1 is a biresolution of the $k$![]() -constant right $\Delta R^{op}$
-constant right $\Delta R^{op}$![]() -module $k^{\ast }$
-module $k^{\ast }$![]() .
.
Proof. It suffices to show that the bicomplex of $k$![]() -modules obtained by evaluating $C_{\star,\star }$
-modules obtained by evaluating $C_{\star,\star }$![]() on each object $[n]$
on each object $[n]$![]() of $\Delta R^{op}$
of $\Delta R^{op}$![]() is a resolution of $k$
is a resolution of $k$![]() .
.
We fix an object $[n]$![]() . We observe that $C_{p,q}([n])$
. We observe that $C_{p,q}([n])$![]() is a free $k[C_2]$
is a free $k[C_2]$![]() -module on the set of generators $\mathrm {Hom}_{\Delta }([q],\,[n])$
-module on the set of generators $\mathrm {Hom}_{\Delta }([q],\,[n])$![]() for each $p\geqslant 0$
for each $p\geqslant 0$![]() .
.
Consider the $E^1$![]() -page of the spectral sequence obtained by taking the horizontal homology of the bicomplex $C_{\star,\star }([n])$
-page of the spectral sequence obtained by taking the horizontal homology of the bicomplex $C_{\star,\star }([n])$![]() . The rows are exact complexes of finitely generated $k[C_2]$
. The rows are exact complexes of finitely generated $k[C_2]$![]() -modules. Therefore, the $E^1$
-modules. Therefore, the $E^1$![]() -page is isomorphic to the complex
-page is isomorphic to the complex
with differential $b$![]() concentrated in the column $p=0$
concentrated in the column $p=0$![]() . This is the complex associated to the standard simplicial model of the $n$
. This is the complex associated to the standard simplicial model of the $n$![]() -simplex, which is acyclic. We deduce that the $E^2$
-simplex, which is acyclic. We deduce that the $E^2$![]() -page of the spectral sequence is isomorphic to a copy of $k$
-page of the spectral sequence is isomorphic to a copy of $k$![]() concentrated in bidegree $(0,\,0)$
concentrated in bidegree $(0,\,0)$![]() as required.
as required.
In the introduction we said that Krasauskas, Lapin and Solov'ev [Reference Krasauskas, Lapin and Solov'ev48, Section 3] had given a definition of reflexive homology in terms of hyperhomology. We now demonstrate that the functor homology definition coincides with that definition.
Proposition 2.3 Let $F\in \mathrm {Fun}(\Delta R^{op},\,\mathrm {Mod}_k)$![]() . The reflexive homology $HR_{\star }(F)$
. The reflexive homology $HR_{\star }(F)$![]() is naturally isomorphic to the hyperhomology of the group $C_2$
is naturally isomorphic to the hyperhomology of the group $C_2$![]() with coefficients in the Hochschild complex $C_{\star }(F)$
with coefficients in the Hochschild complex $C_{\star }(F)$![]() .
.
Proof. We observe that for $F\in \mathrm {Fun}(\Delta R^{op},\,\mathrm {Mod}_k)$![]() , the Hochschild complex $C_{\star }(F)$
, the Hochschild complex $C_{\star }(F)$![]() is a complex of $k[C_2]$
is a complex of $k[C_2]$![]() -modules. Consider the bicomplex $C_{\star,\star }\otimes _{\Delta R^{op}} F$
-modules. Consider the bicomplex $C_{\star,\star }\otimes _{\Delta R^{op}} F$![]() . On the one hand, by definition, the homology of this bicomplex is $HR_{\star }(F)$
. On the one hand, by definition, the homology of this bicomplex is $HR_{\star }(F)$![]() . On the other hand, it is a bicomplex of $k$
. On the other hand, it is a bicomplex of $k$![]() -modules with the Hochschild complex $C_{\star }(F)$
-modules with the Hochschild complex $C_{\star }(F)$![]() in the column $p=0$
in the column $p=0$![]() such that the homology of row $n$
such that the homology of row $n$![]() for $n\geqslant 0$
for $n\geqslant 0$![]() is the group homology of $C_2$
is the group homology of $C_2$![]() with coefficients in $F([n])$
with coefficients in $F([n])$![]() . In other words, it is a bicomplex of $k$
. In other words, it is a bicomplex of $k$![]() -modules which computes the hyperhomology of $C_2$
-modules which computes the hyperhomology of $C_2$![]() with coefficients in the complex $C_{\star }(F)$
with coefficients in the complex $C_{\star }(F)$![]() .
.
Proposition 2.4 Suppose that $2$![]() is invertible in the ground ring. Let $A$
is invertible in the ground ring. Let $A$![]() be an involutive $k$
be an involutive $k$![]() -algebra and let $M$
-algebra and let $M$![]() be an involutive $A$
be an involutive $A$![]() -bimodule. There exist isomorphisms of graded $k$
-bimodule. There exist isomorphisms of graded $k$![]() -modules
-modules
Proof. Consider the horizontal homology spectral sequences of the bicomplexes of $k$![]() -modules $C_{\star,\star }\otimes _{\Delta R^{op}}\mathcal {L}^+(A,\,M)$
-modules $C_{\star,\star }\otimes _{\Delta R^{op}}\mathcal {L}^+(A,\,M)$![]() and $C_{\star, \star }\otimes _{\Delta R^{op}} \mathcal {L}^{-}(A,\,M)$
and $C_{\star, \star }\otimes _{\Delta R^{op}} \mathcal {L}^{-}(A,\,M)$![]() . In each case, the homology of the rows of the bicomplex is $H_{\star }(C_2,\, M\otimes A^{\otimes n})$
. In each case, the homology of the rows of the bicomplex is $H_{\star }(C_2,\, M\otimes A^{\otimes n})$![]() , for the given actions of $C_2$
, for the given actions of $C_2$![]() on $M\otimes A^{\otimes n}$
on $M\otimes A^{\otimes n}$![]() . Since $2$
. Since $2$![]() is invertible in $k$
is invertible in $k$![]() and $C_2$
and $C_2$![]() is finite, $H_{n}(C_2,\, M \otimes A^{\otimes n})=0$
is finite, $H_{n}(C_2,\, M \otimes A^{\otimes n})=0$![]() for $n\geqslant 1$
for $n\geqslant 1$![]() . Therefore, in each case, the $E^1$
. Therefore, in each case, the $E^1$![]() -page consists of the Hochschild complex with the $C_2$
-page consists of the Hochschild complex with the $C_2$![]() action factored out, concentrated in the column $p=0$
action factored out, concentrated in the column $p=0$![]() .
.
3. Reflexive hyperhomology
We can extend the definition of reflexive homology to chain complexes of left $\Delta R^{op}$![]() -modules by defining reflexive hyperhomology. This is a property common to all crossed simplicial groups, as described in [Reference Dunn24, Section 3] for example. We define reflexive hyperhomology in terms of hypertor functors (see [Reference Weibel70, 5.7.8] for instance) over the category $\Delta R^{op}$
-modules by defining reflexive hyperhomology. This is a property common to all crossed simplicial groups, as described in [Reference Dunn24, Section 3] for example. We define reflexive hyperhomology in terms of hypertor functors (see [Reference Weibel70, 5.7.8] for instance) over the category $\Delta R^{op}$![]() . In our case, these can be described explicitly as the hyper-derived functors of the tensor product $k^{\ast } \otimes _{\Delta R^{op}}-$
. In our case, these can be described explicitly as the hyper-derived functors of the tensor product $k^{\ast } \otimes _{\Delta R^{op}}-$![]() where $k^{\ast }$
where $k^{\ast }$![]() is the $k$
is the $k$![]() -constant right $\Delta R^{op}$
-constant right $\Delta R^{op}$![]() -module.
-module.
Definition 3.1 A non-negatively graded reflexive chain complex is a functor $F\colon \Delta R^{op}\rightarrow \mathbf {ChCpx}$![]() , where $\mathbf {ChCpx}$
, where $\mathbf {ChCpx}$![]() , is the category of non-negatively graded chain complexes of $k$
, is the category of non-negatively graded chain complexes of $k$![]() -modules. Equivalently, a reflexive chain complex is a non-negatively graded chain complex of left $\Delta R^{op}$
-modules. Equivalently, a reflexive chain complex is a non-negatively graded chain complex of left $\Delta R^{op}$![]() -modules.
-modules.
Example 3.2 One example of a reflexive chain complex arises by composing a reflexive topological space $X\colon \Delta R^{op} \rightarrow \mathbf {Top}$![]() with the singular chain complex functor $S_{\star }(-,\,k)$
with the singular chain complex functor $S_{\star }(-,\,k)$![]() .
.
Example 3.3 Another important example of a reflexive chain complex arises from involutive DGAs. Recall that a DGA (differential graded algebra, or sometimes chain algebra), $(A,\,d)$![]() , is a graded $k$
, is a graded $k$![]() -algebra, $A$
-algebra, $A$![]() , equipped with a $k$
, equipped with a $k$![]() -linear map $d\colon A \rightarrow A$
-linear map $d\colon A \rightarrow A$![]() satisfying the following properties. The map $d$
satisfying the following properties. The map $d$![]() has degree $-1$
has degree $-1$![]() , it squares to zero and it satisfies the graded Leibniz rule: $d(ab)=(da)b+(-1)^{\left \lvert a \right \rvert }a(db)$
, it squares to zero and it satisfies the graded Leibniz rule: $d(ab)=(da)b+(-1)^{\left \lvert a \right \rvert }a(db)$![]() , where $\left \lvert a \right \rvert$
, where $\left \lvert a \right \rvert$![]() denotes the degree of a homogeneous element $a$
denotes the degree of a homogeneous element $a$![]() .
.
An involutive DGA, $(A,\,d,\,i)$![]() , is a DGA, $(A,\,d)$
, is a DGA, $(A,\,d)$![]() , equipped with a chain map
, equipped with a chain map
written $i(a)=\overline {a}$![]() . The map $i$
. The map $i$![]() must square to the identity and satisfy $\overline {ab}= (-1)^{\left \lvert a \right \rvert \cdot \left \lvert b \right \rvert } \overline {b}\overline {a}$
must square to the identity and satisfy $\overline {ab}= (-1)^{\left \lvert a \right \rvert \cdot \left \lvert b \right \rvert } \overline {b}\overline {a}$![]() .
.
Given an involutive DGA $(A,\,d,\,i)$![]() , we can form its reflexive bar construction, $\Gamma (A,\,d,\,i)$
, we can form its reflexive bar construction, $\Gamma (A,\,d,\,i)$![]() , using the simplicial and reflexive structure described in [Reference Dunn24, Section 3]. The $n$
, using the simplicial and reflexive structure described in [Reference Dunn24, Section 3]. The $n$![]() -simplices are given by $(A,\,d)^{\otimes (n+1)}$
-simplices are given by $(A,\,d)^{\otimes (n+1)}$![]() . Let $a=a_0\otimes \cdots \otimes a_n$
. Let $a=a_0\otimes \cdots \otimes a_n$![]() . The face maps are given by
. The face maps are given by

The degeneracy maps are given by
for $0\leqslant j\leqslant n$![]() .
.
The reflexive operators are defined by
where $\lvert \lvert a \rvert \rvert = \sum _{i=1}^{n-1} \sum _{j=i+1}^n \left \lvert a_i\right \rvert \cdot \left \lvert a_j\right \rvert$![]() .
.
This is another example of a reflexive chain complex.
One example that will be of particular interest in § 8.2 is the following. If $M$![]() is an involutive topological monoid, the singular chain complex $S_{\star }(M,\,k)$
is an involutive topological monoid, the singular chain complex $S_{\star }(M,\,k)$![]() is an involutive DGA with the involution induced from the one on $M$
is an involutive DGA with the involution induced from the one on $M$![]() .
.
We now define reflexive homology of a chain complex of left $\Delta R^{op}$![]() -modules
-modules
Definition 3.4 Let $k_0^{\ast }$![]() denote the right $\Delta R^{op}$
denote the right $\Delta R^{op}$![]() -module $k^{\ast }$
-module $k^{\ast }$![]() thought of as a chain complex concentrated in degree zero. Let $F_{\star }$
thought of as a chain complex concentrated in degree zero. Let $F_{\star }$![]() be a non-negatively graded chain complex of left $\Delta R^{op}$
be a non-negatively graded chain complex of left $\Delta R^{op}$![]() -modules. For each $n\geqslant 0$
-modules. For each $n\geqslant 0$![]() , we define the $n^{th}$
, we define the $n^{th}$![]() reflexive homology of $F_{\star }$
reflexive homology of $F_{\star }$![]() by
by
Remark 3.5 We can use the biresolution of definition 2.1 to construct a chain complex for computing the reflexive homology of a reflexive chain complex. Since the chain complex $k_0^{\ast }$![]() is concentrated in degree zero, the tensor product of chain complexes $k_0^{\ast }\otimes _{\Delta R^{op}} F_{\star }$
is concentrated in degree zero, the tensor product of chain complexes $k_0^{\ast }\otimes _{\Delta R^{op}} F_{\star }$![]() is equivalent to applying the functor $k^{\ast }\otimes _{\Delta R^{op}}-$
is equivalent to applying the functor $k^{\ast }\otimes _{\Delta R^{op}}-$![]() to the chain complex $F_{\star }$
to the chain complex $F_{\star }$![]() degree-wise. Replacing $k^{\ast }$
degree-wise. Replacing $k^{\ast }$![]() by the biresolution of definition 2.1 we obtain a chain complex of bicomplexes, that is, a tricomplex. Applying the total complex functor for tricomplexes we obtain a chain complex which calculates $\mathbf {Tor}_{n}^{\Delta R^{op}}(k_0^{\ast } ,\, F_{\star })$
by the biresolution of definition 2.1 we obtain a chain complex of bicomplexes, that is, a tricomplex. Applying the total complex functor for tricomplexes we obtain a chain complex which calculates $\mathbf {Tor}_{n}^{\Delta R^{op}}(k_0^{\ast } ,\, F_{\star })$![]() .
.
4. Morita invariance
In this section we prove Morita invariance results for reflexive homology. It is a remarkable property of Hochschild homology [Reference Dennis and Igusa17, Theorem 3.7] (see also [Reference Loday51, Section 1.2]), cyclic homology [Reference Loday and Quillen52, Corollary 1.7] and dihedral homology [Reference Krasauskas, Lapin and Solov'ev48, Theorem 3.4] that the given homology theory applied to the algebra of $(m\times m)$![]() -matrices with entries in a $k$
-matrices with entries in a $k$![]() -algebra $A$
-algebra $A$![]() , involutive in the case of dihedral homology, is isomorphic to the homology of $A$
, involutive in the case of dihedral homology, is isomorphic to the homology of $A$![]() . We prove that reflexive homology shares this property. We also prove a more general result. We show that if two algebras are Hermitian Morita equivalent and satisfy a compatibility condition, then they have the same reflexive homology. It is worth remarking that Morita invariance is not a property shared by every homology theory associated to a crossed simplicial group. For example, it is shown in [Reference Ault2, Remark 88] and [Reference Graves40, Corollary 5.11] that neither symmetric homology nor hyperoctahedral homology satisfy Morita invariance.
. We prove that reflexive homology shares this property. We also prove a more general result. We show that if two algebras are Hermitian Morita equivalent and satisfy a compatibility condition, then they have the same reflexive homology. It is worth remarking that Morita invariance is not a property shared by every homology theory associated to a crossed simplicial group. For example, it is shown in [Reference Ault2, Remark 88] and [Reference Graves40, Corollary 5.11] that neither symmetric homology nor hyperoctahedral homology satisfy Morita invariance.
4.1 Morita equivalence and Hermitian Morita equivalence
We begin by recalling the definition of Morita equivalence for two (not necessarily involutive) $k$![]() -algebras.
-algebras.
Definition 4.1 Two unital $k$![]() -algebras, $A$
-algebras, $A$![]() and $B$
and $B$![]() , are said to be Morita equivalent if there is an $A$
, are said to be Morita equivalent if there is an $A$![]() -$B$
-$B$![]() -bimodule $P$
-bimodule $P$![]() and a $B$
and a $B$![]() -$A$
-$A$![]() -bimodule $Q$
-bimodule $Q$![]() together with an isomorphism of $A$
together with an isomorphism of $A$![]() -bimodules, $u\colon P\otimes _B Q \rightarrow A$
-bimodules, $u\colon P\otimes _B Q \rightarrow A$![]() , and an isomorphism of $B$
, and an isomorphism of $B$![]() -bimodules, ${v\colon Q\otimes _{A} P\rightarrow B}$
-bimodules, ${v\colon Q\otimes _{A} P\rightarrow B}$![]() .
.
The concept of Morita equivalence can be extended to involutive $k$![]() -algebras. This notion is known as Hermitian Morita equivalence. This was introduced by Frölich and McEvett [Reference Fröhlich and McEvett33, Section 8] (see also [Reference Hahn42] and [Reference Farinati and Solotar27, Section 2]).
-algebras. This notion is known as Hermitian Morita equivalence. This was introduced by Frölich and McEvett [Reference Fröhlich and McEvett33, Section 8] (see also [Reference Hahn42] and [Reference Farinati and Solotar27, Section 2]).
Definition 4.2 Let $A$![]() and $B$
and $B$![]() be two unital, involutive $k$
be two unital, involutive $k$![]() -algebras. We say that $A$
-algebras. We say that $A$![]() and $B$
and $B$![]() are Hermitian Morita equivalent if:
are Hermitian Morita equivalent if:
• $A$
 and $B$
and $B$ are Morita equivalent in the sense of definition 4.1;
are Morita equivalent in the sense of definition 4.1;• the isomorphisms $u$
 and $v$
and $v$ satisfy
satisfy
– $u(p\otimes q)p^{\prime }= pv(q\otimes p^{\prime })$
 and
and– $v(q\otimes p)q^{\prime }=qu(p\otimes q^{\prime })$

for all $p,\,p^{\prime }\in P$
 and $q,\,q^{\prime }\in Q$
and $q,\,q^{\prime }\in Q$ ;
;• there exists an additive bijection $\theta \colon P\rightarrow Q$
 satisfying
satisfying
– $\theta (apb)= \overline {b} \,\theta (p) \,\overline {a}$
 for all $a \in A$
for all $a \in A$ , $b\in B$
, $b\in B$ and $p\in P$
and $p\in P$ ,
,– $u(p\otimes \theta (p^{\prime })) = \overline {u(p^{\prime }\otimes \theta (p))}$
 and
and– $v(\theta (p)\otimes p^{\prime }) = \overline {v(\theta (p^{\prime })\otimes p)}$
 .
.
Remark 4.3 It follows from the fact that $u$![]() and $v$
and $v$![]() are isomorphisms that there exist sets of elements in $P$
are isomorphisms that there exist sets of elements in $P$![]() , say $\left \lbrace p_1,\,\dotsc,\, p_l\right \rbrace$
, say $\left \lbrace p_1,\,\dotsc,\, p_l\right \rbrace$![]() and $\left \lbrace p_1^{\prime } ,\, \dotsc,\, p_m^{\prime }\right \rbrace$
and $\left \lbrace p_1^{\prime } ,\, \dotsc,\, p_m^{\prime }\right \rbrace$![]() , and sets of elements in $Q$
, and sets of elements in $Q$![]() , say $\left \lbrace q_1,\,\dotsc,\, q_l\right \rbrace$
, say $\left \lbrace q_1,\,\dotsc,\, q_l\right \rbrace$![]() and $\left \lbrace q_1^{\prime } ,\, \dotsc,\, q_m^{\prime }\right \rbrace$
and $\left \lbrace q_1^{\prime } ,\, \dotsc,\, q_m^{\prime }\right \rbrace$![]() , such that
, such that

Definition 4.4 Let $A$![]() and $B$
and $B$![]() be two unital, involutive $k$
be two unital, involutive $k$![]() -algebras. Suppose that $A$
-algebras. Suppose that $A$![]() and $B$
and $B$![]() are Hermitian Morita equivalent. Suppose that the additive bijection $\theta$
are Hermitian Morita equivalent. Suppose that the additive bijection $\theta$![]() sends the set $\left \lbrace p_1,\,\dotsc,\, p_l\right \rbrace$
sends the set $\left \lbrace p_1,\,\dotsc,\, p_l\right \rbrace$![]() to the set $\left \lbrace q_1,\,\dotsc,\, q_l\right \rbrace$
to the set $\left \lbrace q_1,\,\dotsc,\, q_l\right \rbrace$![]() . In this case we say that $A$
. In this case we say that $A$![]() and $B$
and $B$![]() are compatible.
are compatible.
4.2 The case of involutive matrix algebras
In this subsection we prove that reflexive homology satisfies Morita invariance for matrix algebras.
Let $A$![]() be an involutive $k$
be an involutive $k$![]() -algebra. The algebra of $(m\times m)$
-algebra. The algebra of $(m\times m)$![]() -matrices with entries in $A$
-matrices with entries in $A$![]() , $\mathcal {M}_m(A)$
, $\mathcal {M}_m(A)$![]() , is an involutive $k$
, is an involutive $k$![]() -algebra with involution defined by $\overline {(x_{ij})}=(\overline {x_{ji}})$
-algebra with involution defined by $\overline {(x_{ij})}=(\overline {x_{ji}})$![]() . In other words, we take the transpose and apply the involution of $A$
. In other words, we take the transpose and apply the involution of $A$![]() entry-wise.
entry-wise.
For $n\geqslant 0$![]() , we define a $k$
, we define a $k$![]() -module morphism
-module morphism
by
where $x_{ij}^{(k)}$![]() is the element in the $i^{th}$
is the element in the $i^{th}$![]() row of the $j^{th}$
row of the $j^{th}$![]() column of the matrix $X^{(k)}$
column of the matrix $X^{(k)}$![]() . As noted in [Reference Krasauskas, Lapin and Solov'ev48, Section 3] this map is compatible with simplicial structure and the involution operators $r_n$
. As noted in [Reference Krasauskas, Lapin and Solov'ev48, Section 3] this map is compatible with simplicial structure and the involution operators $r_n$![]() for $n\geqslant 0$
for $n\geqslant 0$![]() . It follows that there are induced maps
. It follows that there are induced maps
on reflexive homology for all $m\geqslant 1$![]() and $n\geqslant 0$
and $n\geqslant 0$![]() .
.
Theorem 4.5 The morphism
on reflexive homology induced from the trace map is an isomorphism for all $m\geqslant 1$![]() and $n\geqslant 0$
and $n\geqslant 0$![]() .
.
Proof. By proposition 2.3 we can consider $\mathrm {Tr}_{\star }$![]() as a morphism on hyperhomology. By the Morita invariance for Hochschild homology the trace maps induce isomorphisms $HH_{\star }(\mathcal {M}_m(A)) \rightarrow HH_{\star }(A)$
as a morphism on hyperhomology. By the Morita invariance for Hochschild homology the trace maps induce isomorphisms $HH_{\star }(\mathcal {M}_m(A)) \rightarrow HH_{\star }(A)$![]() .
.
Consider the bicomplexes $C_{\star,\star }\otimes _{\Delta R^{op}} \mathcal {L}^{\pm }(\mathcal {M}_m(A))$![]() and $C_{\star,\star }\otimes _{\Delta R^{op}} \mathcal {L}^{\pm }(A)$
and $C_{\star,\star }\otimes _{\Delta R^{op}} \mathcal {L}^{\pm }(A)$![]() . The isomorphisms $HH_{\star }(\mathcal {M}_m(A)) \rightarrow HH_{\star }(A)$
. The isomorphisms $HH_{\star }(\mathcal {M}_m(A)) \rightarrow HH_{\star }(A)$![]() ensure that the vertical homology spectral sequences for these bicomplexes have isomorphic $E^1$
ensure that the vertical homology spectral sequences for these bicomplexes have isomorphic $E^1$![]() -pages. The result now follows from the comparison theorem [Reference Weibel70, 5.2.12].
-pages. The result now follows from the comparison theorem [Reference Weibel70, 5.2.12].
4.3 A more general result
In this section we prove a more general Morita invariance statement for reflexive homology. We show that if two algebras are Hermitian Morita equivalent and are compatible in the sense of definition 4.4, then they have the same reflexive homology.
Definition 4.6 Let $A$![]() and $B$
and $B$![]() be two unital, involutive $k$
be two unital, involutive $k$![]() -algebras. Suppose that $A$
-algebras. Suppose that $A$![]() and $B$
and $B$![]() are Hermitian Morita equivalent, so there exist bimodules $P$
are Hermitian Morita equivalent, so there exist bimodules $P$![]() and $Q$
and $Q$![]() and an additive bijection $\theta \colon P\rightarrow Q$
and an additive bijection $\theta \colon P\rightarrow Q$![]() as in definitions 4.1 and 4.2. Let $M$
as in definitions 4.1 and 4.2. Let $M$![]() be an involutive $A$
be an involutive $A$![]() -bimodule. We define an involution the the $B$
-bimodule. We define an involution the the $B$![]() -bimodule $Q\otimes _A M\otimes _A P$
-bimodule $Q\otimes _A M\otimes _A P$![]() by
by
Theorem 4.7 Let $A$![]() and $B$
and $B$![]() be two unital, involutive $k$
be two unital, involutive $k$![]() -algebras. Suppose that they are Hermitian Morita equivalent and that they are compatible in the sense of definition 4.4. Let $M$
-algebras. Suppose that they are Hermitian Morita equivalent and that they are compatible in the sense of definition 4.4. Let $M$![]() be an involutive $A$
be an involutive $A$![]() -bimodule. There exist natural isomorphisms of graded $k$
-bimodule. There exist natural isomorphisms of graded $k$![]() -modules
-modules
where $Q\otimes _A M \otimes _A P$![]() is equipped with the involution of definition 4.6.
is equipped with the involution of definition 4.6.
Proof. In [Reference Loday51, 1.2.7], Loday defines a chain homotopy equivalence
between the Hochschild complexes. One can check that this is compatible with the involutions on both complexes, yielding a $C_2$![]() -equivariant chain homotopy equivalence, from which the result follows.
-equivariant chain homotopy equivalence, from which the result follows.
5. Calculations
In this section we provide some computations of reflexive homology. We can calculate the reflexive homology of the ground ring in two different ways; using the theory of crossed simplicial groups and direct computation from our bicomplex in the previous section. We demonstrate that our calculations agree with what is already known when working over a field of characteristic zero. We also give explicit descriptions of reflexive homology in degree zero for a commutative algebra.
Proposition 5.1 There is an isomorphism of graded $k$![]() -modules $HR_{\star }^+(k) \cong H_{\star }(BC_2 ,\, k)$
-modules $HR_{\star }^+(k) \cong H_{\star }(BC_2 ,\, k)$![]() .
.
Proof. Let $T\colon \Delta R^{op}\rightarrow \mathbf {Set}$![]() denote the trivial reflexive set. Explicitly, $T$
denote the trivial reflexive set. Explicitly, $T$![]() sends every object in $\Delta R^{op}$
sends every object in $\Delta R^{op}$![]() to the one point set $\left \lbrace \ast \right \rbrace$
to the one point set $\left \lbrace \ast \right \rbrace$![]() with trivial involution. Using [Reference Fiedorowicz and Loday31, Corollary 6.13] we have
with trivial involution. Using [Reference Fiedorowicz and Loday31, Corollary 6.13] we have
as required.
We can also obtain this calculation directly from the bicomplex defined in the previous section.
Proposition 5.2 Let $k$![]() be a commutative ring with trivial involution. Then
be a commutative ring with trivial involution. Then

where ${}_2k$![]() denotes the $2$
denotes the $2$![]() -torsion of $k$
-torsion of $k$![]() .
.
Proof. We will prove the result for $HR_n^+(k)$![]() . The result for $HR_n^{-}(k)$
. The result for $HR_n^{-}(k)$![]() is similar.
is similar.
Consider the bicomplex $C_{\star, \star }\otimes _{\Delta R^{op}} \mathcal {L}^+(k)$![]() . Since the Hochschild homology of $k$
. Since the Hochschild homology of $k$![]() is isomorphic to $k$
is isomorphic to $k$![]() concentrated in degree zero [Reference Loday51, 1.1.6], taking the vertical homology yields the complex
concentrated in degree zero [Reference Loday51, 1.1.6], taking the vertical homology yields the complex
in row zero. The result now follows by taking homology of this complex.
Corollary 5.3 If $2$![]() is invertible in the ground ring then $HR_{\star }^+(k)$
is invertible in the ground ring then $HR_{\star }^+(k)$![]() is isomorphic to $k$
is isomorphic to $k$![]() concentrated in degree zero and $HR_{\star }^{-}(k)$
concentrated in degree zero and $HR_{\star }^{-}(k)$![]() is zero in all degrees.
is zero in all degrees.
Proof. If $2$![]() is invertible in $k$
is invertible in $k$![]() then the quotient module $k/2k$
then the quotient module $k/2k$![]() and the $2$
and the $2$![]() -torsion ${}_2k$
-torsion ${}_2k$![]() are both zero and the result follows from proposition 5.2.
are both zero and the result follows from proposition 5.2.
Remark 5.4 Recall from remark 1.13 that when we work over a field of characteristic zero, the direct sum of $HR_{\star }^+$![]() and $HR_{\star }^{-}$
and $HR_{\star }^{-}$![]() is isomorphic to Hochschild homology, $HH_{\star }$
is isomorphic to Hochschild homology, $HH_{\star }$![]() . We note that our calculations for the ground ring $k$
. We note that our calculations for the ground ring $k$![]() agree with this. When $k$
agree with this. When $k$![]() is a field of characteristic zero we see that $HR_{\star }^+(k)\oplus HR_{\star }^{-}(k)$
is a field of characteristic zero we see that $HR_{\star }^+(k)\oplus HR_{\star }^{-}(k)$![]() is isomorphic to $k$
is isomorphic to $k$![]() concentrated in degree zero, which is isomorphic to $HH_{\star }(k)$
concentrated in degree zero, which is isomorphic to $HH_{\star }(k)$![]() [Reference Loday51, 1.1.6].
[Reference Loday51, 1.1.6].
Theorem 5.5 Let $A$![]() be a commutative $k$
be a commutative $k$![]() -algebra.
-algebra.
• If $A$
 has the trivial involution then $HR_0^+(A)\cong A$
has the trivial involution then $HR_0^+(A)\cong A$ and $HR_0^{-}(A)\cong A/2A$
and $HR_0^{-}(A)\cong A/2A$ .
.• If $A$
 has a non-trivial involution then $HR_0^+(A)$
has a non-trivial involution then $HR_0^+(A)$ is isomorphic to the coinvariants of $A$
is isomorphic to the coinvariants of $A$ under the involution.
under the involution.
Proof. One can deduce these results directly from the bicomplex that computes reflexive homology.
6. Reflexive homology of a tensor algebra
In this section we calculate the reflexive homology of a tensor algebra. Let $M$![]() be a $k$
be a $k$![]() -module and consider a module automorphism $m\mapsto \overline {m}$
-module and consider a module automorphism $m\mapsto \overline {m}$![]() which squares to the identity. The identity automorphism is an example of such.
which squares to the identity. The identity automorphism is an example of such.
Consider the tensor algebra

where $M^{\otimes 0}=k$![]() . The product is given by concatenation, see [Reference Loday51, A.1] for instance. The tensor algebra has an involution determined on the $n^{th}$
. The product is given by concatenation, see [Reference Loday51, A.1] for instance. The tensor algebra has an involution determined on the $n^{th}$![]() summand by
summand by
Note that the involution on $k$![]() is trivial.
is trivial.
Taking $A=TM$![]() in the definition of the Loday functor $\mathcal {L}^+(A)$
in the definition of the Loday functor $\mathcal {L}^+(A)$![]() , we obtain an induced involution on $\mathcal {L}^+(A)([n])=(TM)^{\otimes {n+1}}$
, we obtain an induced involution on $\mathcal {L}^+(A)([n])=(TM)^{\otimes {n+1}}$![]() given by
given by
where each $A_i \in TM$![]() .
.
Theorem 6.1 Let $M$![]() be a $k$
be a $k$![]() -module with a module automorphism $m\mapsto \overline {m}$
-module with a module automorphism $m\mapsto \overline {m}$![]() which squares to the identity. There is a natural isomorphism of $k$
which squares to the identity. There is a natural isomorphism of $k$![]() -modules
-modules

Proof. Consider the reflexive bicomplex for $TM$![]() . By taking the vertical homology we obtain the $E^1$
. By taking the vertical homology we obtain the $E^1$![]() -page of a spectral sequence whose entries are the Hochschild homology groups of $TM$
-page of a spectral sequence whose entries are the Hochschild homology groups of $TM$![]() with horizontal differentials induced from $1\pm r$
with horizontal differentials induced from $1\pm r$![]() .
.
Loday and Quillen [Reference Loday and Quillen52, Lemma 5.2] have calculated the Hochschild homology of a tensor algebra as follows:

where $(M^{\otimes q})^t$![]() are the invariants of the action of the cyclic group $C_q$
are the invariants of the action of the cyclic group $C_q$![]() on $M^{\otimes q}$
on $M^{\otimes q}$![]() and $M^{\otimes q}/\left \langle 1-t\right \rangle$
and $M^{\otimes q}/\left \langle 1-t\right \rangle$![]() are the coinvariants.
are the coinvariants.
Therefore the $E^1$![]() -page of our spectral sequence is concentrated in rows zero and one as follows:
-page of our spectral sequence is concentrated in rows zero and one as follows:

An argument similar to [Reference Lodder53, Lemma 2.2.1] tells us that in row zero we have
and in row one we have
Furthermore, an argument similar to [Reference Lodder53, Lemma 2.3.2] tells us that the differentials on the $E^2$![]() -page are zero and so the spectral sequence collapses.
-page are zero and so the spectral sequence collapses.
Taking homology on the $E^1$![]() -page yields
-page yields
with all other $E_{p,q}^2=0$![]() , from which we can read off the result.
, from which we can read off the result.
Remark 6.2 We deduce from the theorem that the reflexive homology of a tensor algebra has a grading induced from the grading on the Hochschild homology. In homological degree zero, for $q\geqslant 0$![]() , we have
, we have
Note that when $q=0$![]() we have
we have
and when $q=1$![]() we have
we have
In homological degree $p$![]() we have
we have
and
for $q\geqslant 1$![]() .
.
We note that, as mentioned above, our grading on the reflexive homology of a tensor algebra is induced from the grading on the Hochschild homology of a tensor algebra. For cyclic homology [Reference Loday and Quillen52, Proposition 5.4] and dihedral homology [Reference Lodder53, Theorem 2.1.1] there is a grading induced directly from the grading on a tensor algebra. In both of these cases this follows from analysis of the norm map $N$![]() (see [Reference Loday51, 2.1.0] for instance) which we do not have in the reflexive case.
(see [Reference Loday51, 2.1.0] for instance) which we do not have in the reflexive case.
7. Reflexive homology of a group algebra
In this section we will study the reflexive homology of the group algebra of a discrete group. We will recall simplicial models for the bar construction and for the classifying space on a group. We will show that these extend to reflexive sets. We will show that the reflexive homology of a group algebra is isomorphic to the $C_2$![]() -equivariant homology of the free loop space on $BG$
-equivariant homology of the free loop space on $BG$![]() . As a consequence we will deduce the analogous result for dihedral homology, namely that the dihedral homology of a group algebra is isomorphic to the $O(2)$
. As a consequence we will deduce the analogous result for dihedral homology, namely that the dihedral homology of a group algebra is isomorphic to the $O(2)$![]() -equivariant homology of the free loop space on $BG$
-equivariant homology of the free loop space on $BG$![]() . We will then show that we can decompose the reflexive homology of a group algebra in terms of the conjugacy classes of the group.
. We will then show that we can decompose the reflexive homology of a group algebra in terms of the conjugacy classes of the group.
These results fit into a broader story of using the homology theories associated to crossed simplicial groups to calculate interesting information about loop spaces. Hochschild homology and cyclic homology of $k[G]$![]() are known to coincide with the homologies of $\mathcal {L}BG$
are known to coincide with the homologies of $\mathcal {L}BG$![]() and the $S^1$
and the $S^1$![]() -equivariant Borel construction on $\mathcal {L}BG$
-equivariant Borel construction on $\mathcal {L}BG$![]() respectively [Reference Loday51, 7.3.13]. The symmetric and hyperoctahedral theories are known to compute the homology and $C_2$
respectively [Reference Loday51, 7.3.13]. The symmetric and hyperoctahedral theories are known to compute the homology and $C_2$![]() -equivariant homology of certain infinite loop spaces on $BG$
-equivariant homology of certain infinite loop spaces on $BG$![]() , see [Reference Ault2, Corollary 40] and [Reference Graves39, Theorem 8.8].
, see [Reference Ault2, Corollary 40] and [Reference Graves39, Theorem 8.8].
The decomposition we provide fits into a bigger picture of decomposing homology theories associated to crossed simplicial groups in the case of a group algebra. Results of this form were proved by Burghelea [Reference Burghelea7, Theorem 1] for Hochschild and cyclic homology (see also [Reference Loday51, Theorem 7.4.6]) and by Loday [Reference Loday50, Proposition 4.9] for dihedral homology.
7.1 Bar construction and classifying spaces
We recall some simplicial models for the bar construction [Reference Loday51, 7.3.10] and classifying space [Reference Loday51, B.12] of a group and extend them to reflexive sets.
Definition 7.1 Let $G$![]() be a discrete group. For $n\geqslant 0$
be a discrete group. For $n\geqslant 0$![]() , let $\Gamma _nG=G^{n+1}$
, let $\Gamma _nG=G^{n+1}$![]() , the $(n+1)$
, the $(n+1)$![]() -fold Cartesian product. The face maps are defined by
-fold Cartesian product. The face maps are defined by

The degeneracy maps insert the identity element of $G$![]() into the tuple. We extend this to a reflexive set by defining
into the tuple. We extend this to a reflexive set by defining
Remark 7.2 Loday has already shown that $\Gamma _{\star }G$![]() is a cyclic set, by defining
is a cyclic set, by defining
One can easily check that the reflexive structure and the cyclic structure are compatible, giving $\Gamma _{\star }G$![]() the structure of a dihedral set. The fact that the reflexive structure that we have defined is compatible with the cyclic structure of $\Gamma _{\star }G$
the structure of a dihedral set. The fact that the reflexive structure that we have defined is compatible with the cyclic structure of $\Gamma _{\star }G$![]() is key to proving Theorem 7.7.
is key to proving Theorem 7.7.
Definition 7.3 Let $B_nG=G^{n}$![]() for $n\geqslant 0$
for $n\geqslant 0$![]() . The face maps are given by
. The face maps are given by

The degeneracy maps insert the identity element into the tuple. We can extend this to a reflexive set by defining
Definition 7.4 Let $G$![]() be a discrete group. We define the reflexive homology of $G$
be a discrete group. We define the reflexive homology of $G$![]() to be
to be
Remark 7.5 Note that we have a projection map, which is a map of reflexive sets,
determined in degree $n$![]() by $(g_0,\,\dotsc,\, g_n) \mapsto (g_1,\,\dotsc,\, g_n)$
by $(g_0,\,\dotsc,\, g_n) \mapsto (g_1,\,\dotsc,\, g_n)$![]() .
.
Remark 7.6 As for $\Gamma _{\star }G$![]() , $B_{\star }G$
, $B_{\star }G$![]() has a cyclic structure. This is given by
has a cyclic structure. This is given by
as described in [Reference Loday51, 7.3.3] (with $z=1$![]() ) for example. This is compatible with the reflexive structure on $B_{\star }G$
) for example. This is compatible with the reflexive structure on $B_{\star }G$![]() , as described in [Reference Dunn24, 2.3], giving $B_{\star }G$
, as described in [Reference Dunn24, 2.3], giving $B_{\star }G$![]() the structure of a dihedral set.
the structure of a dihedral set.
7.2 Reflexive homology of a group algebra
Let $G$![]() be a discrete group. In this subsection we prove that the reflexive homology of a group algebra $k[G]$
be a discrete group. In this subsection we prove that the reflexive homology of a group algebra $k[G]$![]() is isomorphic to the homology of the $C_2$
is isomorphic to the homology of the $C_2$![]() -equivariant Borel construction on the free loop space of $BG$
-equivariant Borel construction on the free loop space of $BG$![]() .
.
Theorem 7.7 Let $G$![]() be a discrete group. Let $k[G]$
be a discrete group. Let $k[G]$![]() denote its group algebra and let $BG$
denote its group algebra and let $BG$![]() be its classifying space. Let $\mathcal {L}BG$
be its classifying space. Let $\mathcal {L}BG$![]() denote the free loop space on $BG$
denote the free loop space on $BG$![]() . There is an isomorphism of graded $k$
. There is an isomorphism of graded $k$![]() -modules
-modules
where the $C_2$![]() -action on $\mathcal {L}BG$
-action on $\mathcal {L}BG$![]() is induced from the reflexive structure of $B_{\star }G$
is induced from the reflexive structure of $B_{\star }G$![]() and reversing the direction of loops.
and reversing the direction of loops.
Proof. In [Reference Loday51, 7.3.11], Loday shows that there is a homotopy equivalence $\gamma \colon \left \lvert \Gamma _{\star }G\right \rvert \rightarrow \mathcal {L}BG$![]() . This is done by considering the adjoint functors $S^1\times -$
. This is done by considering the adjoint functors $S^1\times -$![]() and $\mathcal {L}(-)$
and $\mathcal {L}(-)$![]() . In particular, there is a map
. In particular, there is a map
where the first map is induced from the cyclic structure of $\Gamma _{\star }G$![]() , as described in [Reference Fiedorowicz and Loday31, Section 5], and the second is induced from the projection map $p\colon \Gamma _{\star }G \rightarrow B_{\star }G$
, as described in [Reference Fiedorowicz and Loday31, Section 5], and the second is induced from the projection map $p\colon \Gamma _{\star }G \rightarrow B_{\star }G$![]() described in remark 7.5. The adjoint map is $\gamma$
described in remark 7.5. The adjoint map is $\gamma$![]() , the necessary homotopy equivalence.
, the necessary homotopy equivalence.
We extend this to a $C_2$![]() -equivariant homotopy equivalence. As noted in remark 7.2, the reflexive structure of $\Gamma _{\star }G$
-equivariant homotopy equivalence. As noted in remark 7.2, the reflexive structure of $\Gamma _{\star }G$![]() is compatible with the cyclic structure. Explicitly, the circle $S^1$
is compatible with the cyclic structure. Explicitly, the circle $S^1$![]() is the geometric realization of the cyclic crossed simplicial group, $\left \lbrace C_n \right \rbrace$
is the geometric realization of the cyclic crossed simplicial group, $\left \lbrace C_n \right \rbrace$![]() , by [Reference Loday51, 6.3.6]. The level-wise involution determined by sending the generator of the cyclic group to its inverse induces a $C_2$
, by [Reference Loday51, 6.3.6]. The level-wise involution determined by sending the generator of the cyclic group to its inverse induces a $C_2$![]() -action on the geometric realization. Similarly, the reflexive structures on $\Gamma _{\star }G$
-action on the geometric realization. Similarly, the reflexive structures on $\Gamma _{\star }G$![]() and $B_{\star }G$
and $B_{\star }G$![]() induce $C_2$
induce $C_2$![]() -actions on the realizations. Note that the involution on geometric realizations also flips the simplex. One easily checks that with these definitions the map
-actions on the realizations. Note that the involution on geometric realizations also flips the simplex. One easily checks that with these definitions the map
is $C_2$![]() -equivariant. Under the adjunction between $S^1 \times -$
-equivariant. Under the adjunction between $S^1 \times -$![]() and $\mathcal {L}(-)$
and $\mathcal {L}(-)$![]() this yields that
this yields that
is a $C_2$![]() -equivariant map, with the involution on $\mathcal {L}BG$
-equivariant map, with the involution on $\mathcal {L}BG$![]() given by applying the involution on $BG$
given by applying the involution on $BG$![]() and reversing the direction of loops. Combining this with [Reference Loday51, 7.3.11], we see that $\gamma$
and reversing the direction of loops. Combining this with [Reference Loday51, 7.3.11], we see that $\gamma$![]() is a $C_2$
is a $C_2$![]() -equivariant homotopy equivalence.
-equivariant homotopy equivalence.
Using [Reference Loday51, 7.3.13] and [Reference Fiedorowicz and Loday31, 6.13], we have
as required.
Using the fact that the reflexive structure that we have described is compatible with the cyclic structure of [Reference Loday51, 7.3.11] we can deduce the analogous result for dihedral homology.
Theorem 7.8 Let $G$![]() be a discrete group. Let $k[G]$
be a discrete group. Let $k[G]$![]() denote its group algebra and let $BG$
denote its group algebra and let $BG$![]() be its classifying space. Let $\mathcal {L}BG$
be its classifying space. Let $\mathcal {L}BG$![]() denote the free loop space on $BG$
denote the free loop space on $BG$![]() . There is an isomorphism of graded $k$
. There is an isomorphism of graded $k$![]() -modules
-modules
where the $O(2)$![]() -action on $\mathcal {L}BG$
-action on $\mathcal {L}BG$![]() is induced from the dihedral structure of $B_{\star }G$
is induced from the dihedral structure of $B_{\star }G$![]() and the action of $O(2)$
and the action of $O(2)$![]() on loops.
on loops.
Proof. Since the reflexive structure of $\Gamma _{\star }G$![]() and $B_{\star }G$
and $B_{\star }G$![]() used in Theorem 7.7 is compatible with the cyclic structures used in [Reference Loday51, 7.3.11], we can deduce that $\gamma$
used in Theorem 7.7 is compatible with the cyclic structures used in [Reference Loday51, 7.3.11], we can deduce that $\gamma$![]() is an $O(2)$
is an $O(2)$![]() -equivariant map, from which the result follows.
-equivariant map, from which the result follows.
7.3 Decomposition by conjugacy classes
In this subsection we prove that the reflexive homology of the group algebra of a discrete group can be decomposed into a direct sum indexed by the conjugacy classes of the group, where the summands are defined in terms of a reflexive analogue of group homology. We prove that under nice conditions, for example when the group is abelian, we can give a simple description of the summands.
Definition 7.9 Let $G$![]() be a discrete group.
be a discrete group.
• Let $\overline {k[G]}$
 denote $k[G]$
denote $k[G]$ considered as a right $k[G]$
considered as a right $k[G]$ -module with the action $h\ast g = g^{-1}hg$
-module with the action $h\ast g = g^{-1}hg$ .
.• Let $\left \langle G\right \rangle$
 denote the set of conjugacy classes of $G$
denote the set of conjugacy classes of $G$ . We will choose a representative $z$
. We will choose a representative $z$ in each class and denote the class by $\left \langle z \right \rangle$
in each class and denote the class by $\left \langle z \right \rangle$ .
.• For $z\in G$
 we denote by $G_z$
we denote by $G_z$ the centralizer of $z$
the centralizer of $z$ in $G$
in $G$ , that is, $G_z=\left \lbrace g\in G : gz=zg\right \rbrace$
, that is, $G_z=\left \lbrace g\in G : gz=zg\right \rbrace$ .
.
Definition 7.10 For a group $G$![]() and a right $k[G]$
and a right $k[G]$![]() -module $M$
-module $M$![]() we denote by $C_{\star }(G,\,M)$
we denote by $C_{\star }(G,\,M)$![]() the Eilenberg-Mac Lane complex [Reference Loday51, C.2, C.3]. We will denote an element in degree $n$
the Eilenberg-Mac Lane complex [Reference Loday51, C.2, C.3]. We will denote an element in degree $n$![]() by $h\otimes [g_1,\, \dotsc,\,g_n]$
by $h\otimes [g_1,\, \dotsc,\,g_n]$![]() .
.
In order to prove our decomposition of the reflexive homology of a group algebra we need to recall certain reflexive sets. The involutions defined here can be found in the proof of [Reference Loday50, Proposition 4.9].
Definition 7.11 Let $G$![]() be a discrete group.
be a discrete group.
• We define the action of $r_{n}$
 on $k[G]^{\otimes n+1}$
on $k[G]^{\otimes n+1}$ to be determined by
\[ r_{n}\left(g_0,\dotsc , g_n\right) = ({-}1)^{n(n+1)/2} \left(g_0^{{-}1}, g_n^{{-}1}, \dotsc , g_1^{{-}1}\right). \]
to be determined by
\[ r_{n}\left(g_0,\dotsc , g_n\right) = ({-}1)^{n(n+1)/2} \left(g_0^{{-}1}, g_n^{{-}1}, \dotsc , g_1^{{-}1}\right). \]
• Let $M=\overline {k[G]}$
 . The action of $r_n$
. The action of $r_n$ on $C_{n}(G,\,M)$
on $C_{n}(G,\,M)$ is given by
\[ r_{n} \left(h \otimes \left[g_1,\dotsc , g_n\right]\right) = ({-}1)^{n(n+1)/2}\left( g^{{-}1} h^{{-}1} g \otimes \left[g_n^{{-}1}, \dotsc , g_1^{{-}1}\right]\right) \]where $g=g_1\cdots g_n$
is given by
\[ r_{n} \left(h \otimes \left[g_1,\dotsc , g_n\right]\right) = ({-}1)^{n(n+1)/2}\left( g^{{-}1} h^{{-}1} g \otimes \left[g_n^{{-}1}, \dotsc , g_1^{{-}1}\right]\right) \]where $g=g_1\cdots g_n$
 .
.• We define the action of $r_n$
 on
\[ \bigoplus_{\left\langle z \right\rangle \in \left\langle G\right\rangle} C_n\left(G, k\left[ G/G_z\right]\right) \]by
on
\[ \bigoplus_{\left\langle z \right\rangle \in \left\langle G\right\rangle} C_n\left(G, k\left[ G/G_z\right]\right) \]by \[ r_{n} \left(h \otimes \left[g_1,\dotsc , g_n\right]\right) = ({-}1)^{n(n+1)/2}\left( g^{{-}1} h^{{-}1} g \otimes \left[g_n^{{-}1}, \dotsc , g_1^{{-}1}\right]\right) \]where $g=g_1\cdots g_n$
\[ r_{n} \left(h \otimes \left[g_1,\dotsc , g_n\right]\right) = ({-}1)^{n(n+1)/2}\left( g^{{-}1} h^{{-}1} g \otimes \left[g_n^{{-}1}, \dotsc , g_1^{{-}1}\right]\right) \]where $g=g_1\cdots g_n$
 .
.
Theorem 7.12 Let $G$![]() be a discrete group. For each $n\geqslant 0$
be a discrete group. For each $n\geqslant 0$![]() there is an isomorphism of $k$
there is an isomorphism of $k$![]() -modules
-modules
Proof. Let $M=\overline {k[G]}$![]() . Recall the Mac Lane isomorphism
. Recall the Mac Lane isomorphism
from [Reference Loday51, Section 7.4] for example. The Mac Lane isomorphism is compatible with the actions described in definition 7.11. Recall from the proof of [Reference Loday50, Proposition 4.7] that there is an isomorphism of right $k[G]$![]() -modules
-modules
This isomorphism is also compatible with the actions described in definition 7.11
We therefore have isomorphisms
compatible with the reflexive $k$![]() -module structures and the result follows upon taking reflexive homology.
-module structures and the result follows upon taking reflexive homology.
Corollary 7.13 If $G$![]() is an abelian group then
is an abelian group then
Proof. If $G$![]() is abelian, then each element $z\in G$
is abelian, then each element $z\in G$![]() has its own conjugacy class and the centralizer $G_z$
has its own conjugacy class and the centralizer $G_z$![]() is isomorphic to $G$
is isomorphic to $G$![]() .
.
For non-abelian groups we can also identify some of the summands in the decomposition.
Proposition 7.14 Let $G$![]() be a discrete group. The $\left \langle 1\right \rangle$
be a discrete group. The $\left \langle 1\right \rangle$![]() -component of $HR_{\star }^+(k[G])$
-component of $HR_{\star }^+(k[G])$![]() is isomorphic to $HR_{\star }^+(G,\,k)$
is isomorphic to $HR_{\star }^+(G,\,k)$![]() .
.
Proof. The centralizer $G_1$![]() is equal to $G$
is equal to $G$![]() so the reflexive homology of $C_{\star }(G ,\, k[G/G_1])$
so the reflexive homology of $C_{\star }(G ,\, k[G/G_1])$![]() is the reflexive homology of $C_{\star }(G,\,k)$
is the reflexive homology of $C_{\star }(G,\,k)$![]() .
.
Proposition 7.15 Let $G$![]() be a discrete group. Let $z \in G$
be a discrete group. Let $z \in G$![]() be a central element of order two. The $\left \langle z\right \rangle$
be a central element of order two. The $\left \langle z\right \rangle$![]() -component of $HR_{\star }^+(k[G])$
-component of $HR_{\star }^+(k[G])$![]() is isomorphic to $HR_{\star }^+(G,\,k)$
is isomorphic to $HR_{\star }^+(G,\,k)$![]() .
.
Proof. Recall from the proof of [Reference Loday50, Proposition 4.7] that there is a quasi-isomorphism
for any $z\in G$![]() . When $z$
. When $z$![]() is a central element of order two this quasi-isomorphism is compatible with the reflexive structure described in definition 7.11, whence the result.
is a central element of order two this quasi-isomorphism is compatible with the reflexive structure described in definition 7.11, whence the result.
8. Reflexive homology of singular chains on a Moore loop space
Goodwillie [Reference Goodwillie35, Section V] proved that for a sufficiently nice space $X$![]() , the cyclic homology of the singular chain complex of the Moore loop space of $X$
, the cyclic homology of the singular chain complex of the Moore loop space of $X$![]() is isomorphic to the $S^1$
is isomorphic to the $S^1$![]() -equivariant homology of the free loop space on $X$
-equivariant homology of the free loop space on $X$![]() . Dunn [Reference Dunn24, 3.6] proved that this result can be extended to a result for the dihedral homology theory and $O(2)$
. Dunn [Reference Dunn24, 3.6] proved that this result can be extended to a result for the dihedral homology theory and $O(2)$![]() -equivariant homology. In this section we will prove the analogous theorem for the reflexive homology theory and $C_2$
-equivariant homology. In this section we will prove the analogous theorem for the reflexive homology theory and $C_2$![]() -equivariant homology. We will also provide a $C_2$
-equivariant homology. We will also provide a $C_2$![]() -equivariant analogue of Lodder's result for free-loop suspension spaces [Reference Lodder53, 3.3.3].
-equivariant analogue of Lodder's result for free-loop suspension spaces [Reference Lodder53, 3.3.3].
8.1 Locally equiconnected spaces
In this brief subsection we recall what it means for a space to be locally equiconnected, commonly abbreviated to LEC. Our results rely on the work of Dunn [Reference Dunn24], which requires this assumption in relation to Milnor's simplicial group model for loop-suspension spaces (see [Reference Lewis34, Reference Milnor59]). Local equiconnectivity was introduced by Fox [Reference Fox32] as a strengthened form of local contractibilty and a weakened form of the absolute neighbourhood retract property. There are several equivalent definitions but we will use the definition in terms of Hurewicz cofibrations. The reader is directed to [Reference Strøm67], where the definition originally occurred, and [Reference Bredon5, Chapter VII], for a textbook account of Hurewicz cofibrations.
Definition 8.1 A topological space is said to be locally equiconnected if the diagonal map $X\rightarrow X \times X$![]() is a Hurewicz cofibration.
is a Hurewicz cofibration.
Example 8.2 The notion of LEC space also appears in work of Serre, where it is called ULC [Reference Serre64, p. 490]. All CW-complexes are LEC spaces [Reference Dyer and Eilenberg26, Corollary III.2].
8.2 Moore loops and free loop spaces
We begin by recalling the definition of the Moore loop space.
Definition 8.3 Let $M\colon \mathbf {Top}_{\star }\rightarrow \mathbf {Top}_{\star }$![]() denote the Moore loop functor. For $X\in \mathbf {Top_{\star }}$
denote the Moore loop functor. For $X\in \mathbf {Top_{\star }}$![]() with basepoint $\star$
with basepoint $\star$![]() , the topological space $M(X)$
, the topological space $M(X)$![]() is the subset of
is the subset of
consisting of all pairs of the form $( f,\, r)$![]() such that $f(t)=\star$
such that $f(t)=\star$![]() for all $t\geqslant r$
for all $t\geqslant r$![]() . In general we will omit the $r$
. In general we will omit the $r$![]() and refer to a Moore loop $f$
and refer to a Moore loop $f$![]() .
.
Let $Y$![]() be a group-like LEC topological monoid with involution. As noted in example 3.3, the singular chain complex $S_{\star }(Y,\, k)$
be a group-like LEC topological monoid with involution. As noted in example 3.3, the singular chain complex $S_{\star }(Y,\, k)$![]() is an involutive DGA, with the involution induced from $Y$
is an involutive DGA, with the involution induced from $Y$![]() . Recall the reflexive bar construction, $\Gamma (S_{\star }(Y,\, k))$
. Recall the reflexive bar construction, $\Gamma (S_{\star }(Y,\, k))$![]() , on $S_{\star }(Y,\, k)$
, on $S_{\star }(Y,\, k)$![]() from example 3.3.
from example 3.3.
Theorem 8.4 Let $Y$![]() be a group-like LEC topological monoid with involution. There is an isomorphism of graded $k$
be a group-like LEC topological monoid with involution. There is an isomorphism of graded $k$![]() -modules
-modules
where the $C_2$![]() -action on $\mathcal {L}BY$
-action on $\mathcal {L}BY$![]() is induced from the involution on $Y$
is induced from the involution on $Y$![]() and reversing the direction of loops.
and reversing the direction of loops.
Proof. This follows directly from [Reference Dunn24, 3.6]. We note that the given theorem relies on Dunn's propositions 2.10, 3.2, 3.3 and 3.5. One can check that these results hold when we only consider the simplicial and reflexive structure from the dihedral objects considered in that paper.
Corollary 8.5 Let $X$![]() be a connected, LEC topological space. There is an isomorphism of graded $k$
be a connected, LEC topological space. There is an isomorphism of graded $k$![]() -modules
-modules
where $X$![]() is equipped with the trivial involution and $MX$
is equipped with the trivial involution and $MX$![]() is equipped with the involution which reverses the direction of loops.
is equipped with the involution which reverses the direction of loops.
Proof. May [Reference May58, 15.4] shows that there is a map $\xi \colon BMX\rightarrow X$![]() , which is a weak homotopy equivalence if $X$
, which is a weak homotopy equivalence if $X$![]() is connected. As noted in [Reference Dunn24, 2.9], with the given involutions the map $\xi$
is connected. As noted in [Reference Dunn24, 2.9], with the given involutions the map $\xi$![]() is $C_2$
is $C_2$![]() -equivariant. The corollary now follows from Theorem 8.4 by setting $Y=MX$
-equivariant. The corollary now follows from Theorem 8.4 by setting $Y=MX$![]() .
.
8.3 Moore loops and free loop-suspension spaces
In this section we prove a reflexive analogue of Lodder's result for free loop-suspension spaces [Reference Lodder53, 3.3.3]. We identify the $C_2$![]() -equivariant homology of a free loop-suspension space $\mathcal {L}\Sigma X$
-equivariant homology of a free loop-suspension space $\mathcal {L}\Sigma X$![]() as the reflexive homology of the singular chains on a reflexive space constructed from the Moore loop space of $X$
as the reflexive homology of the singular chains on a reflexive space constructed from the Moore loop space of $X$![]() . In this case we can use a smaller construction than the reflexive bar construction on a DGA since the suspension of a topological space is always path-connected.
. In this case we can use a smaller construction than the reflexive bar construction on a DGA since the suspension of a topological space is always path-connected.
We begin by recalling the definition of the suspension functor.
Definition 8.6 Let $\Sigma \colon \mathbf {Top}_{\star } \rightarrow \mathbf {Top}_{\star }$![]() denote the suspension functor $S^1 \wedge -$
denote the suspension functor $S^1 \wedge -$![]() .
.
Definition 8.7 Let $X$![]() be a based topological space. Let $\Sigma X=S^1 \wedge X$
be a based topological space. Let $\Sigma X=S^1 \wedge X$![]() be equipped with the involution $\overline {(t,\,x)}=(1-t,\,x)$
be equipped with the involution $\overline {(t,\,x)}=(1-t,\,x)$![]() , given by reversing the suspension co-ordinate. We define a reflexive topological space
, given by reversing the suspension co-ordinate. We define a reflexive topological space
as follows.
For each $n\geqslant 0$![]() , we have $M\Sigma X([n])=(M\Sigma X)^{n+1}$
, we have $M\Sigma X([n])=(M\Sigma X)^{n+1}$![]() , the $(n+1)$
, the $(n+1)$![]() -fold Cartesian product of the Moore loop space on $\Sigma X$
-fold Cartesian product of the Moore loop space on $\Sigma X$![]() .
.
The face maps $\partial _i\colon M\Sigma X([n])\rightarrow M\Sigma X([n-1])$![]() are given by concatenation of loops:
are given by concatenation of loops:

The degeneracy maps $s_j\colon M\Sigma X([n])\rightarrow M\Sigma X([n+1])$![]() are given by inserting the trivial loop:
are given by inserting the trivial loop:
for $0\leqslant j \leqslant n$![]() .
.
The reflexive operators $r_n\colon M\Sigma X([n]) \rightarrow M\Sigma X([n])$![]() for $n\geqslant 0$
for $n\geqslant 0$![]() are given by reversing the direction of loops and applying the involution on $\Sigma X$
are given by reversing the direction of loops and applying the involution on $\Sigma X$![]() :
:
Definition 8.8 Let $\mathcal {S}$![]() denote the reflexive chain complex obtained by taking the singular chain complex $S_{\star }(M\Sigma X(-),\, k)$
denote the reflexive chain complex obtained by taking the singular chain complex $S_{\star }(M\Sigma X(-),\, k)$![]() on the reflexive topological space $M\Sigma X(-)$
on the reflexive topological space $M\Sigma X(-)$![]() .
.
Theorem 8.9 Let $X$![]() be a based topological space. Let $\mathcal {S}$
be a based topological space. Let $\mathcal {S}$![]() denote the singular chain complex on the reflexive topological space $M\Sigma X(-)$
denote the singular chain complex on the reflexive topological space $M\Sigma X(-)$![]() . There is an isomorphism of graded $k$
. There is an isomorphism of graded $k$![]() -modules
-modules
Proof. By combining the constructions in [Reference Loday51, Appendix B] for singular homology with results on homotopy colimits for crossed simplicial groups [Reference Fiedorowicz and Loday31, Section 6] we see that given a reflexive space $Y_{\star }$![]() , there are isomorphisms
, there are isomorphisms
where the $C_2$![]() -action on $\left \lvert Y_{\star }\right \rvert$
-action on $\left \lvert Y_{\star }\right \rvert$![]() is induced from the reflexive structure.
is induced from the reflexive structure.
Goodwillie [Reference Goodwillie35, Section V] has constructed a weak equivalence $\left \lvert M\Sigma X(-)\right \rvert \rightarrow \mathcal {L}\Sigma X$![]() . By incorporating the reflexive action defined in [Reference Lodder53, Section 3.4] we extend this to a $C_2$
. By incorporating the reflexive action defined in [Reference Lodder53, Section 3.4] we extend this to a $C_2$![]() -equivariant weak equivalence. The proof of this fact follows by mimicking [Reference Lodder53, 3.4.1], replacing the dihedral crossed simplicial group with the reflexive crossed simplicial group.
-equivariant weak equivalence. The proof of this fact follows by mimicking [Reference Lodder53, 3.4.1], replacing the dihedral crossed simplicial group with the reflexive crossed simplicial group.
We therefore have a weak equivalence
which yields
as required.
9. Relationship to involutive Hochschild homology
Involutive Hochschild homology was introduced by Braun [Reference Braun4] to study involutive algebras and involutive $A_{\infty }$![]() -algebras. Fernàndez-València and Giansiracusa [Reference Fernàndez-València and Giansiracusa29] developed the homological algebra of involutive Hochschild homology. In particular, they showed that involutive Hochschild homology can be expressed as $\mathrm {Tor}$
-algebras. Fernàndez-València and Giansiracusa [Reference Fernàndez-València and Giansiracusa29] developed the homological algebra of involutive Hochschild homology. In particular, they showed that involutive Hochschild homology can be expressed as $\mathrm {Tor}$![]() over an involutive version of the enveloping algebra. The original motivation for constructing involutive Hochschild homology was to extend work of Costello [Reference Costello15] to study the connection between unoriented two-dimensional topological conformal field theories and involutive Calabi-Yau $A_{\infty }$
over an involutive version of the enveloping algebra. The original motivation for constructing involutive Hochschild homology was to extend work of Costello [Reference Costello15] to study the connection between unoriented two-dimensional topological conformal field theories and involutive Calabi-Yau $A_{\infty }$![]() -algebras [Reference Braun4], [Reference Fernàndez-València28]. Involutive Hochschild homology also arises in the study of the (co)homology of involutive dendriform algebras [Reference Das and Saha16]. We show that under certain conditions involutive Hochschild homology coincides with reflexive homology.
-algebras [Reference Braun4], [Reference Fernàndez-València28]. Involutive Hochschild homology also arises in the study of the (co)homology of involutive dendriform algebras [Reference Das and Saha16]. We show that under certain conditions involutive Hochschild homology coincides with reflexive homology.
Let $k$![]() be a field. Let $A$
be a field. Let $A$![]() be an involutive $k$
be an involutive $k$![]() -algebra and let $A^e=A\otimes A^{op}$
-algebra and let $A^e=A\otimes A^{op}$![]() denote the enveloping algebra. For this section only, let $C_2=\left \langle t\mid t^2=1\right \rangle$
denote the enveloping algebra. For this section only, let $C_2=\left \langle t\mid t^2=1\right \rangle$![]() . The group $C_2$
. The group $C_2$![]() acts on $A^e$
acts on $A^e$![]() by the rule $t(a_1\otimes a_2)=\overline {a_2} \otimes \overline {a_1}$
by the rule $t(a_1\otimes a_2)=\overline {a_2} \otimes \overline {a_1}$![]() . Fernàndez-València and Giansiracusa define the involutive enveloping algebra $A^{ie}$
. Fernàndez-València and Giansiracusa define the involutive enveloping algebra $A^{ie}$![]() to be $A^e\otimes k[C_2]$
to be $A^e\otimes k[C_2]$![]() with the product determined by
with the product determined by
The involutive Hochschild homology of $A$![]() with coefficients in an involutive $A$
with coefficients in an involutive $A$![]() -bimodule $M$
-bimodule $M$![]() , denoted by $iHH_{\star }(A,\,M)$
, denoted by $iHH_{\star }(A,\,M)$![]() , is defined to be $\mathrm {Tor}_{\star }^{A^{ie}}(A,\,M)$
, is defined to be $\mathrm {Tor}_{\star }^{A^{ie}}(A,\,M)$![]() [Reference Fernàndez-València and Giansiracusa29, 3.3.1]. Recall that an involutive vector space is projective if, when viewed as a $k[C_2]$
[Reference Fernàndez-València and Giansiracusa29, 3.3.1]. Recall that an involutive vector space is projective if, when viewed as a $k[C_2]$![]() -module, it is a direct summand of a free module.
-module, it is a direct summand of a free module.
Theorem 9.1 Let $k$![]() be a field of characteristic zero. Let $A$
be a field of characteristic zero. Let $A$![]() be a projective involutive $k$
be a projective involutive $k$![]() -algebra and let $M$
-algebra and let $M$![]() be an involutive $A$
be an involutive $A$![]() -bimodule. There exists an isomorphism of graded $k$
-bimodule. There exists an isomorphism of graded $k$![]() -modules
-modules
Proof. Proposition 2.4 and [Reference Fernàndez-València and Giansiracusa29, 3.3.2] tell us that, under these conditions, both $HR_{\star }^+(A,\,M)$![]() and $iHH_{\star }(A,\,M)$
and $iHH_{\star }(A,\,M)$![]() are isomorphic to the homology of the quotient of the Hochschild complex by the involution action, from which the result follows.
are isomorphic to the homology of the quotient of the Hochschild complex by the involution action, from which the result follows.
10. Reflexive structure in real topological Hochschild homology
The structure of the reflexive crossed simplicial group arises implicitly in the literature on real topological Hochschild homology, although the category $\Delta R$![]() very rarely explicitly arises. In this expository section we explain how certain constructions in real topological Hochschild homology can be stated in terms of the reflexive crossed simplicial group.
very rarely explicitly arises. In this expository section we explain how certain constructions in real topological Hochschild homology can be stated in terms of the reflexive crossed simplicial group.
We begin by recalling the definition of a real simplicial object from [Reference Dotto18, 1.4.1], [Reference Dotto, Moi, Patchkoria and Reeh21, 1.2], [Reference Høgenhaven45, 1.1], [Reference Angelini-Knoll, Gerhardt and Hill1, 2.3].
Definition 10.1 A real simplicial object $X$![]() in a category $\mathbf {C}$
in a category $\mathbf {C}$![]() is a functor $X\colon \Delta ^{op}\rightarrow \mathbf {C}$
is a functor $X\colon \Delta ^{op}\rightarrow \mathbf {C}$![]() together with maps $\omega _n\colon X([n])\rightarrow X([n])$
together with maps $\omega _n\colon X([n])\rightarrow X([n])$![]() such that $\omega _n^2=id_{X([n])}$
such that $\omega _n^2=id_{X([n])}$![]() and
and
• $d_i\circ \omega _n = \omega _{n-1}d_{n-i}$
 ,
,• $s_i\circ \omega _n = \omega _{n+1}s_{n-i}$
 .
.
Remark 10.2 By comparing with definition 1.2 we see that a real simplical object $X$![]() in a category $\mathbf {C}$
in a category $\mathbf {C}$![]() is precisely a functor $X\colon \Delta R^{op} \rightarrow \mathbf {C}$
is precisely a functor $X\colon \Delta R^{op} \rightarrow \mathbf {C}$![]() . In other words, it is the same thing as a reflexive object in $\mathbf {C}$
. In other words, it is the same thing as a reflexive object in $\mathbf {C}$![]() . We note that the category $\Delta R$
. We note that the category $\Delta R$![]() does appear in [Reference Dotto, Moi, Patchkoria and Reeh21, 1.2] with the notation $\Delta _R^{op}$
does appear in [Reference Dotto, Moi, Patchkoria and Reeh21, 1.2] with the notation $\Delta _R^{op}$![]() .
.
Example 10.3 If we take $\mathbf {C}=\mathbf {Set}$![]() , we obtain the category of reflexive sets or real simplicial sets. As noted in the introduction, Spaliński [Reference Spaliński66, Section 3] has shown that the category of reflexive sets admits a model structure that is Quillen equivalent to the category of $C_2$
, we obtain the category of reflexive sets or real simplicial sets. As noted in the introduction, Spaliński [Reference Spaliński66, Section 3] has shown that the category of reflexive sets admits a model structure that is Quillen equivalent to the category of $C_2$![]() -spaces with the fixed-point model structure. Furthermore, reflexive sets play an important role in the homotopy theory of dihedral sets (see [Reference Spaliński65] and [Reference Spaliński66]).
-spaces with the fixed-point model structure. Furthermore, reflexive sets play an important role in the homotopy theory of dihedral sets (see [Reference Spaliński65] and [Reference Spaliński66]).
It is worth remarking that, using the crossed simplical group structure, we can use a result of Fiedorowicz and Loday [Reference Fiedorowicz and Loday31, 6.13] to calculate the homology of $C_2$![]() -equivariant Borel constructions. Let $X$
-equivariant Borel constructions. Let $X$![]() be a reflexive set and let $k[X]$
be a reflexive set and let $k[X]$![]() be the composition with the free $k$
be the composition with the free $k$![]() -module functor. There is an isomorphism of graded $k$
-module functor. There is an isomorphism of graded $k$![]() -modules $HR_{\star }^+(k[X]) \cong H_{\star }(EC_2 \times _{C_2} \left \lvert X\right \rvert,\, k)$
-modules $HR_{\star }^+(k[X]) \cong H_{\star }(EC_2 \times _{C_2} \left \lvert X\right \rvert,\, k)$![]() .
.
Example 10.4 Let $\mathbf {C}=\mathbf {Sp}^{O}$![]() , the category of orthogonal ring spectra as introduced in [Reference Mandell, May, Schwede and Shipley57]. Let $(A,\,w)$
, the category of orthogonal ring spectra as introduced in [Reference Mandell, May, Schwede and Shipley57]. Let $(A,\,w)$![]() be an orthogonal ring spectrum with anti-involution in the sense of [Reference Dotto, Moi, Patchkoria and Reeh21, Definition 2.1] and let $(M,\,j)$
be an orthogonal ring spectrum with anti-involution in the sense of [Reference Dotto, Moi, Patchkoria and Reeh21, Definition 2.1] and let $(M,\,j)$![]() be an $A$
be an $A$![]() -bimodule in the sense of definition 2.5 of the same paper. The dihedral nerve $N_{\wedge }^{di}(A,\,M)$
-bimodule in the sense of definition 2.5 of the same paper. The dihedral nerve $N_{\wedge }^{di}(A,\,M)$![]() of [Reference Dotto, Moi, Patchkoria and Reeh21, Definition 2.9] is a functor $\Delta R^{op} \rightarrow \mathbf {Sp}^{O}$
of [Reference Dotto, Moi, Patchkoria and Reeh21, Definition 2.9] is a functor $\Delta R^{op} \rightarrow \mathbf {Sp}^{O}$![]() . In other words, it is a reflexive object in the category of orthogonal spectra or a real simplicial orthogonal spectrum. We note that this is called dihedral because, in the case where we take $M=A$
. In other words, it is a reflexive object in the category of orthogonal spectra or a real simplicial orthogonal spectrum. We note that this is called dihedral because, in the case where we take $M=A$![]() , there is also an action of the cyclic groups, giving the structure of a functor $\Delta D^{op}\rightarrow \mathbf {Sp}^{O}$
, there is also an action of the cyclic groups, giving the structure of a functor $\Delta D^{op}\rightarrow \mathbf {Sp}^{O}$![]() .
.
The dihedral nerve plays an important role in the construction of $\mathrm {THR}_{\bullet }(A;M)$![]() (see [Reference Dotto, Moi, Patchkoria and Reeh21, Definition 2.18]) whose geometric realization is the real topological Hochschild homology of $A$
(see [Reference Dotto, Moi, Patchkoria and Reeh21, Definition 2.18]) whose geometric realization is the real topological Hochschild homology of $A$![]() with coefficients in $M$
with coefficients in $M$![]() . We note that $\mathrm {THR}_{\bullet }(A;M)$
. We note that $\mathrm {THR}_{\bullet }(A;M)$![]() is itself a real simplicial orthogonal spectrum and therefore can be considered as a functor $\Delta R^{op}\rightarrow \mathbf {Sp}^{O}$
is itself a real simplicial orthogonal spectrum and therefore can be considered as a functor $\Delta R^{op}\rightarrow \mathbf {Sp}^{O}$![]() .
.
Remark 10.5 Our reflexive homology theory, as defined in § 1, takes as input a $k$![]() -algebra with involution and gives a graded $k$
-algebra with involution and gives a graded $k$![]() -module as output. In recent work, Angelini-Knoll, Gerhardt and Hill [Reference Angelini-Knoll, Gerhardt and Hill1] have introduced another theory for rings with involution, called real Hochschild homology. This theory takes as input the Mackey functor associated to a ring with involution (see [Reference Angelini-Knoll, Gerhardt and Hill1, 6.12]) and gives a graded equivariant Mackey functor as output (see [Reference Angelini-Knoll, Gerhardt and Hill1, 6.15]). They also prove that their theory is related to real topological Hochschild homology via a linearization map [Reference Angelini-Knoll, Gerhardt and Hill1, 6.20].
-module as output. In recent work, Angelini-Knoll, Gerhardt and Hill [Reference Angelini-Knoll, Gerhardt and Hill1] have introduced another theory for rings with involution, called real Hochschild homology. This theory takes as input the Mackey functor associated to a ring with involution (see [Reference Angelini-Knoll, Gerhardt and Hill1, 6.12]) and gives a graded equivariant Mackey functor as output (see [Reference Angelini-Knoll, Gerhardt and Hill1, 6.15]). They also prove that their theory is related to real topological Hochschild homology via a linearization map [Reference Angelini-Knoll, Gerhardt and Hill1, 6.20].
Acknowledgements
I would like to thank James Brotherston, James Cranch, Callum Reader and Sarah Whitehouse for interesting and helpful conversations at various stages of writing this paper. I would like to thank the referee for their helpful comments and suggestions.