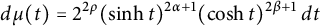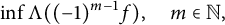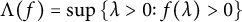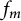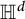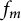Logan’s problem for Jacobi transforms

Abstract

We consider direct and inverse Jacobi transforms with measures

$$\begin{align*}d\mu(t)=2^{2\rho}(\operatorname{sinh} t)^{2\alpha+1}(\operatorname{cosh} t)^{2\beta+1}\,dt\end{align*}$$

and

$$\begin{align*}d\sigma(\lambda)=(2\pi)^{-1}\Bigl|\frac{2^{\rho-i\lambda}\Gamma(\alpha+1)\Gamma(i\lambda)} {\Gamma((\rho+i\lambda)/2)\Gamma((\rho+i\lambda)/2-\beta)}\Bigr|^{-2}\,d\lambda,\end{align*}$$

respectively. We solve the following generalized Logan problem: to find the infimum

$$\begin{align*}\inf\Lambda((-1)^{m-1}f), \quad m\in \mathbb{N}, \end{align*}$$

where $\Lambda (f)=\sup \,\{\lambda>0\colon f(\lambda )>0\}$ and the infimum is taken over all nontrivial even entire functions f of exponential type that are Jacobi transforms of positive measures with supports on an interval. Here, if $m\ge 2$, then we additionally assume that $\int _{0}^{\infty }\lambda ^{2k}f(\lambda )\,d\sigma (\lambda )=0$ for $k=0,\dots ,m-2$.

We prove that admissible functions for this problem are positive-definite with respect to the inverse Jacobi transform. The solution of Logan’s problem was known only when $\alpha =\beta =-1/2$. We find a unique (up to multiplication by a positive constant) extremizer $f_m$. The corresponding Logan problem for the Fourier transform on the hyperboloid $\mathbb {H}^{d}$ is also solved. Using the properties of the extremizer $f_m$ allows us to give an upper estimate of the length of a minimal interval containing not less than n zeros of positive definite functions. Finally, we show that the Jacobi functions form the Chebyshev systems.

1 Introduction

In this paper, we continue the discussion of the generalized Logan problem for entire functions of exponential type, that are, functions represented as compactly supported integral transforms. In [13], we investigated this problem for the Fourier, Hankel, and Dunkl transforms. Here, we consider the new case of the Jacobi transform, which is closely related to the harmonic analysis on the real hyperbolic spaces [25].

The one-dimensional Logan problem first appeared as a problem in the number theory [22]. Its multidimensional analogs (see, e.g., [26]) are also connected to the Fourier-analytical method used by Selberg to prove a sharp form of Linnik’s large sieve inequality. Considering various classes of admissible functions in the multivariate Logan’s problem gives rise to the so-called Delsarte extremal problems, which have numerous applications to discrete mathematics and metric geometry (see the discussion in [13]). At present, Logan’s and Delsarte’s problems can be considered as an important part of uncertainty type extremal problems, where conditions both on a function and its Fourier transform are imposed [6, 11, 12] (see also [3, 4, 17]).

Typically, the main object in such questions is the classical Fourier transform in Euclidean space. However, similar questions in other symmetric spaces, especially in hyperbolic spaces, are of great interest (see, e.g., [7, 16]). Harmonic analysis in these cases is built with the help of the Fourier–Jacobi transform (see [19, 25]). A particular case of the Jacobi transform is the well-known Mehler–Fock transform [27].

We would like to stress that since the classes of admissible functions and corresponding functionals in the multidimensional Logan’s problem (see Problem E for hyperboloid in Section 5) are invariant under the group of motions, the problem reduces to the case of radial functions. Thus, it is convenient to start with the one-dimensional case (Problem D) and then find a solution in the whole generality.

Positive definiteness of the extremizer in the generalized Logan problem for the Hankel transform (see Problem C) turns out to be crucial to obtain lower bounds for energy in the Gaussian core model [5]. We will see that the extremizer in the generalized Logan problem for the Jacobi transform is also positive definite (with respect to Jacobi transform).

1.1 Historical background

Logan stated and proved [22, 23] the following two extremal problems for real-valued positive definite bandlimited functions on $\mathbb {R}$ . Since such functions are even, we consider these problems for functions on $\mathbb {R}_{+}:=[0,\infty )$ .

Problem A Find the smallest $\lambda _1>0$ such that

$$\begin{align*}f(\lambda)\le 0,\quad \lambda>\lambda_1, \end{align*}$$

where f is entire function of exponential type at most $2\tau $ satisfying

(1.1) $$ \begin{align} f(\lambda)=\int_{0}^{2\tau}\cos\lambda t\,d\nu(t),\quad f(0)=1, \end{align} $$

where $\nu $ is a function of bounded variation, nondecreasing in some neighborhood of the origin.

Logan showed that admissible functions are integrable, $\lambda _1=\pi /2\tau $ , and the unique extremizer is the positive definite function

$$\begin{align*}f_1(\lambda)=\frac{\cos^2(\tau\lambda)}{1-\lambda^2/(\pi/2\tau)^2}, \end{align*}$$

satisfying $\int _{0}^{\infty }f_1(\lambda )\,d\lambda =0$ .

Recall that a function f defined on $\mathbb {R}$ is positive definite if for any integer N

$$\begin{align*}\sum_{i,j=1}^Nc_i\overline{c_j}\,f(x_i-x_j)\ge 0,\quad \forall\,c_1,\dots,c_N\in \mathbb{C},\quad \forall\,x_1,\dots,x_N\in \mathbb{R}. \end{align*}$$

Let $C_b(\mathbb {R}_{+})$ be the space of continuous bounded functions f on $\mathbb {R}_{+}$ with norm $\|f\|_{\infty }=\sup _{\mathbb {R}_{+}}|f|$ . For an even function $f\in C_b(\mathbb {R}_{+})$ , by Bochner’s theorem, f is positive definite if and only if

$$ \begin{align*} f(x)=\int_{0}^{\infty}\cos\lambda t\,d\nu(t), \end{align*} $$

where $\nu $ is a nondecreasing function of bounded variation (see, e.g., [8, 9.2.8]). In particular, if $f\in L^{1}(\mathbb {R}_{+})$ , then its cosine Fourier transform is nonnegative.

Problem B Find the smallest $\lambda _2>0$ such that

$$\begin{align*}f(\lambda)\ge 0,\quad \lambda>\lambda_2, \end{align*}$$

where f is an integrable function satisfying (1.1) and having mean value zero.

It turns out that admissible functions are integrable with respect to the weight $\lambda ^2$ , and $\lambda _2=3\pi /2\tau $ . Moreover, the unique extremizer is the positive definite function

$$\begin{align*}f_2(\lambda)=\frac{\cos^2(\tau\lambda)}{(1-\lambda^2/(\pi/2\tau)^2)(1-\lambda^2/(3\pi/2\tau)^2)}, \end{align*}$$

satisfying $ \int _{0}^{\infty }\lambda ^{2}f_2(\lambda )\,d\lambda =0$ .

Let $m\in \mathbb {N}$ . Problems A and B can be considered as special cases of the generalized m-Logan problem.

Problem C Find the smallest $\lambda _m>0$ such that

$$\begin{align*}(-1)^{m-1}f(\lambda)\le 0,\quad \lambda>\lambda_m, \end{align*}$$

where, for $m=1$ , f satisfies (1.1) and, for $m\ge 2$ , additionally

$$\begin{align*}f\in L^1(\mathbb{R}_{+}, \lambda^{2m-4}\,d\lambda),\quad \int_{0}^{\infty}\lambda^{2k} f(\lambda)\,d\lambda=0,\quad k=0,\dots,m-2. \end{align*}$$

If $m=1,2$ , we recover Problems A and B, respectively. We solved Problem C in [13]. It turns out that the unique extremizer is the positive definite function

$$\begin{align*}f_m(\lambda)=\frac{\cos^2(\tau\lambda)}{(1-\lambda^2/(\pi/2\tau)^2) (1-\lambda^2/(3\pi/2\tau)^2)\cdots(1-\lambda^2/((2m-1)\pi/2\tau)^2)}, \end{align*}$$

satisfying $f_m\in L^1(\mathbb {R}_{+}, \lambda ^{2m-2}\,d\lambda )$ and $\int _{0}^{\infty }\lambda ^{2m-2}f_m(\lambda )\,d\lambda =0$ .

Moreover, we have solved a more general version of the problem C when f is the Hankel transform of a measure, that is,

$$\begin{align*}f(\lambda)=\int_{0}^{2\tau}j_{\alpha}(\lambda t)\,d\nu(\lambda),\quad f(0)=1, \end{align*}$$

where $\nu $ is a function of bounded variation, nondecreasing in some neighborhood of the origin, and for $m\ge 2,$

$$\begin{align*}f\in L^1(\mathbb{R}_{+}, \lambda^{2m+2\alpha-3}\,d\lambda),\quad \int_{0}^{\infty} \lambda^{2k+2\alpha+1}f(\lambda)\,d\lambda=0,\quad k=0,\dots,m-2. \end{align*}$$

Here, $\alpha \ge -1/2$ and $j_{\alpha }(t)=(2/t)^{\alpha }\Gamma (\alpha +1)J_{\alpha }(t)$ is the normalized Bessel function. The representation (1.1) then follows for $\alpha =-1/2$ . Note that $ j_{\alpha }(\lambda t)$ is the eigenfunction of the following Sturm–Liouville problem:

$$\begin{align*}(t^{2\alpha+1}u_{\lambda}'(t))'+ \lambda^2 t^{2\alpha+1} u_{\lambda}(t)=0,\quad u_{\lambda}(0)=1,\quad u_{\lambda}'(0)=0,\quad t,\lambda\in \mathbb{R}_{+}. \end{align*}$$

1.2 m-Logan problem for the Jacobi transform

In this paper, we solve the analog of Problem C for the Jacobi transform with the kernel $\varphi _{\lambda }(t)$ being the eigenfunction of the Sturm–Liouville problem

(1.2) $$ \begin{align} \begin{gathered} (\Delta(t)\varphi_{\lambda}'(t))'+ (\lambda^2+\rho^2)\Delta(t)\varphi_{\lambda}(t)=0, \\ \varphi_{\lambda}(0)=1,\quad \varphi'_{\lambda}(0)=0, \end{gathered} \end{align} $$

with the weight function given by

$$ \begin{align*} \Delta(t)=\Delta^{(\alpha,\beta)}(t)=2^{2\rho}(\operatorname{sinh} t)^{2\alpha+1}(\operatorname{cosh} t)^{2\beta+1},\quad t\in \mathbb{R}_{+}, \end{align*} $$

where

$$\begin{align*}\alpha\geq\beta\geq-1/2,\quad \rho=\alpha+\beta+1. \end{align*}$$

The following representation for the Jacobi function is known

$$\begin{align*}\varphi_{\lambda}(t)=\varphi_{\lambda}^{(\alpha,\beta)}(t)= F\Bigl(\frac{\rho+i\lambda}{2},\frac{\rho-i\lambda}{2};\alpha+1;-(\operatorname{sinh} t)^{2}\Bigr), \end{align*}$$

where $F(a,b;c;z)$ is the Gauss hypergeometric function.

For the precise definitions of direct and inverse Jacobi transforms, see the next section. In the case $\alpha =\beta =-1/2$ , we have $\Delta (t)=1$ and the Jacobi transform is reduced to the cosine Fourier transform.

Set, for a real-valued continuous function f on $\mathbb {R}_{+}$ ,

$$\begin{align*}\Lambda(f)=\Lambda(f,\mathbb{R}_{+})=\sup\,\{\lambda>0\colon\, f(\lambda)>0\} \end{align*}$$

( $\Lambda (f)=0$ if $f\leq 0$ ) and

$$\begin{align*}\Lambda_{m}(f)=\Lambda((-1)^{m-1}f).\end{align*}$$

Consider the class $\mathcal {L}_{m}(\tau ,\mathbb {R}_{+})$ , $m\in \mathbb {N}$ , $\tau>0$ , of real-valued even functions $f\in C_b(\mathbb {R}_{+})$ such that:

(1) f is the Jacobi transform of a measure

(1.3) $$ \begin{align} f(\lambda)=\int_{0}^{2\tau}\varphi_{\lambda}(t)\,d\nu(t), \quad \lambda\in \mathbb{R}_{+}, \end{align} $$

where $\nu $ is a nontrivial function of bounded variation nondecreasing in some neighborhood of the origin.

(2) If $m\ge 2$ , then, additionally, $f\in L^1(\mathbb {R}_{+},\lambda ^{2m-4}\,d\sigma )$ and there holds

(1.4) $$ \begin{align} \int_{0}^{\infty}\lambda^{2k}f(\lambda)\,d\sigma(\lambda)=0,\quad k=0,1,\dots,m-2, \end{align} $$

where $\sigma $ is the spectral measure of the Sturm–Liouville problem (1.2), that is,

(1.5) $$ \begin{align} d\sigma(\lambda)=d\sigma^{(\alpha,\beta)}(\lambda)=s(\lambda)\,d\lambda, \end{align} $$

where the spectral weight

$$\begin{align*}s(\lambda)=s^{(\alpha,\beta)}(\lambda)=(2\pi)^{-1}\Bigl|\frac{2^{\rho-i\lambda}\Gamma(\alpha+1)\Gamma(i\lambda)} {\Gamma((\rho+i\lambda)/2)\Gamma((\rho+i\lambda)/2-\beta)}\Bigr|^{-2}. \end{align*}$$

This class $\mathcal {L}_{m}(\tau ,\mathbb {R}_{+})$ is not empty. In particular, we will show that it contains the function

(1.6) $$ \begin{align} f_m(\lambda)=\varphi_{\lambda}(\tau)F_m(\lambda), \end{align} $$

where

(1.7) $$ \begin{align} F_m(\lambda)=\frac{\varphi_{\lambda}(\tau)}{(1-\lambda^2/\lambda_1^2(\tau))\cdots(1-\lambda^2/\lambda_m^2(\tau))} \end{align} $$

and $0<\lambda _{1}(t)<\dots <\lambda _{k}(t)<\cdots $ are the positive zeros of $\varphi _{\lambda }(t)$ as a function in $\lambda $ .

The m-Logan problem for Jacobi transform on the half-line is formulated as follows.

Problem D Find

$$\begin{align*}L_m(\tau,\mathbb{R}_{+})=\inf\{\Lambda_{m}(f)\colon\, f\in \mathcal{L}_{m}(\tau,\mathbb{R}_{+})\}. \end{align*}$$

Remark 1.1 In the case $\alpha =\beta =-1/2$ , Problem D becomes Problem C. Even though the ideas to solve Problem D are similar to those we used in the solution of Problem C, the proof is far from being just a generalization. In more detail, considering the cosine Fourier transform or, more generally, the Hankel transform, we note that its kernel, i.e., the normalized Bessel function $j_{\alpha }(\lambda t)$ , is symmetric with respect to the arguments t and $\lambda $ . Moreover, in this case, the Sturm–Liouville weight $t^{2\alpha +1}$ coincides, up to constant, to the spectral weight $\lambda ^{2\alpha +1}$ , so the direct and inverse Hankel transforms also coincide (see [13]). In the case of the Jacobi transform, there is no such symmetry for the kernel $\varphi _{\lambda }(t)$ and weights $\Delta (t)$ and $s(\lambda )$ , which gives rise to new, both conceptual and technical difficulties. In particular, the crucial part of our technique to attack the main problem is to obtain growth estimates of $\varphi _{\lambda }(t)$ and $s(\lambda )$ showing that extremal functions belong to suitable function classes. To prove these facts, we rely on the properties of the general Sturm–Liouville problem, whereas for the normalized Bessel function, they were proved directly.

1.3 The main result

Theorem 1.2 Let $m\in \mathbb {N}$ , $\tau>0$ . Then

$$\begin{align*}L_m(\tau,\mathbb{R}_{+})=\lambda_m(\tau), \end{align*}$$

and the function $f_{m}$ is the unique extremizer up to multiplication by a positive constant. Moreover, $f_{m}$ is positive definite with respect to the inverse Jacobi transform and

(1.8) $$ \begin{align} \int_{0}^{\infty}\lambda^{2k}f_{m}(\lambda)\,d\sigma(\lambda)=0,\quad k=0,1,\dots,m-1. \end{align} $$

Remark 1.3 We note the inverse Jacobi transform $g_m(t)=\mathcal {J}^{-1}f_{m}(t)\ge 0$ . Furthermore, the function $F_m$ given by (1.7) is positive definite since $G_m(t)=\mathcal {J}^{-1}F_{m}(t)$ is nonnegative and decreases on $[0,\tau ]$ , and it has zero of multiplicity $2m-1$ at $t=\tau $ . The relationship between $g_m(t)$ and $G_m(t)$ is given by $g_m(t)=T^{\tau }G_m(t)$ , where $T^{\tau }$ is the generalized translation operator (see Section 2).

1.4 Structure of the paper

The presentation follows our paper [13]. Section 2 contains some facts on the Jacobi harmonic analysis as well as a Gauss quadrature formula with zeros of the Jacobi functions as nodes. In Section 3, we prove that the Jacobi functions form the Chebyshev systems, which is used in the proof of Theorem 1.2.

In Section 4, we give the solution of the generalized Logan problem for the Jacobi transform. Using Theorem 1.2, in Section 5, we solve the multidimensional Logan problem for the Fourier transform on the hyperboloid.

Finally, Section 6 is devoted to the problem on the minimal interval containing n zeros of functions represented by the Jacobi transform of a nonnegative bounded Stieltjes measure. Originally, such questions were investigated by Logan in [24] for the cosine transform. It is worth mentioning that extremizers in this problem and Problem D are closely related.

2 Elements of Jacobi harmonic analysis

Below we give some needed facts (see [9, 10, 14, 18, 19]).

Let $\mathcal {E}^{\tau }$ be the class of even entire functions $g(\lambda )$ of exponential type at most $\tau>0$ , satisfying the estimate $|g(\lambda )|\leq c_g\,e^{\tau |\mathrm {Im}\,\lambda |}$ , $\lambda \in \mathbb {C}$ .

The Jacobi function $\varphi _{\lambda }(t)$ is an even analytic function of t on $\mathbb {R}$ and it belongs to the class $\mathcal {E}^{|t|}$ with respect to $\lambda $ . Moreover, the following conditions hold:

(2.1) $$ \begin{align} |\varphi_{\lambda}(t)|\leq 1,\quad \varphi_{0}(t)>0, \quad \lambda,t\in \mathbb{R}. \end{align} $$

From the general properties of the eigenfunctions of the Sturm–Liouville problem (see, for example, [21]), one has that, for $t>0$ , $\lambda \in \mathbb {C}$ ,

(2.2) $$ \begin{align} \varphi_{\lambda}(t)=\varphi_{0}(t)\prod_{k=1}^{\infty}\left(1-\frac{\lambda^2}{\lambda_{k}^2(t)}\right), \end{align} $$

where $0<\lambda _{1}(t)<\dots <\lambda _{k}(t)<\cdots $ are the positive zeros of $\varphi _{\lambda }(t)$ as a function of $\lambda $ .

We also have that $\lambda _{k}(t)=t_{k}^{-1}(t)$ , where $t_{k}(\lambda )$ are the positive zeros of the function $\varphi _{\lambda }(t)$ as a function of t. The zeros $t_{k}(\lambda )$ , as well as the zeros $\lambda _{k}(t)$ , are continuous and strictly decreasing [21, Chapter I, Section 3].

2.1 Properties of some special functions

In what follows, we will need the asymptotic behavior of the Jacobi function and spectral weight (see [14]:

(2.3) $$ \begin{align} \varphi_{\lambda}(t)=\frac{(2/\pi)^{1/2}}{(\Delta(t)s(\lambda))^{1/2}} \left(\cos \left(\lambda t-\frac{\pi(\alpha+1/2)}{2}\right)+e^{t|\mathrm{Im}\,\lambda|}O(|\lambda|^{-1})\right),\nonumber\\ |\lambda|\to +\infty,\quad t>0, \end{align} $$

(2.4) $$ \begin{align} s(\lambda)=(2^{\rho+\alpha}\Gamma(\alpha+1))^{-2}\lambda^{2\alpha+1}(1+O(\lambda^{-1})),\quad \lambda\to +\infty. \end{align} $$

From (2.3) and (2.4), it follows that, for fixed $t>0$ and uniformly on $\lambda \in \mathbb {R}_{+}$ ,

(2.5) $$ \begin{align} |\varphi_{\lambda}(t)|\lesssim\frac{1}{(\lambda+1)^{\alpha+1/2}}, \end{align} $$

where as usual $F_{1}\lesssim F_{2}$ means $F_{1}\le CF_{2}$ . Also, we denote $F_1\asymp F_2$ if ${C}^{-1}F_1\le F_2\le C F_1$ with $C\ge 1$ .

In the Jacobi harmonic analysis, an important role is played by the function

(2.6) $$ \begin{align} \psi_{\lambda}(t)=\psi_{\lambda}^{(\alpha, \beta)}(t)=\frac{\varphi_{\lambda}^{(\alpha, \beta)}(t)}{\varphi_{0}^{(\alpha, \beta)}(t)}=\frac{\varphi_{\lambda}(t)}{\varphi_{0}(t)}, \end{align} $$

which is the solution of the Sturm–Liouville problem

(2.7) $$ \begin{align} (\Delta_{*}(t)\,\psi_{\lambda}'(t))'+ \lambda^2\Delta_{*}(t)\psi_{\lambda}(t)=0,\quad \psi_{\lambda}(0)=1,\quad \psi_{\lambda}'(0)=0, \end{align} $$

where $\Delta _{*}(t)=\varphi _{0}^2(t)\Delta (t)$ is the modified weight function.

The positive zeros $0<\lambda _{1}^*(t)<\dots <\lambda _{k}^{*}(t)<\cdots $ of the function $\psi _{\lambda }'(t)$ of $\lambda $ alternate with the zeros of the function $\varphi _{\lambda }(t)$ [14]:

(2.8) $$ \begin{align} 0<\lambda_{1}(t)<\lambda_{1}^{*}(t)<\lambda_{2}(t)<\dots<\lambda_{k}(t)<\lambda_{k}^{*}(t)<\lambda_{k+1}(t)<\cdots. \end{align} $$

For the derivative of the Jacobi function, one has

(2.9) $$ \begin{align} (\varphi_{\lambda}^{(\alpha,\beta)}(t))_t'=-\frac{(\rho^{2}+\lambda^{2})\operatorname{sinh} t\operatorname{cosh} t}{2(\alpha+1)}\,\varphi_{\lambda}^{(\alpha+1,\beta+1)}(t). \end{align} $$

Moreover, according to (1.2),

$$\begin{align*}\bigl\{\Delta(t)\bigl(\varphi_{\mu}(t)\varphi'_{\lambda}(t)-\varphi_{\mu}'(t)\varphi_{\lambda}(t)\bigr)\bigr\}_t'= (\mu^2-\lambda^2)\Delta(t)\varphi_{\mu}(t)\varphi_{\lambda}(t), \end{align*}$$

and therefore

(2.10) $$ \begin{align} \int_{0}^{\tau}\Delta(t)\varphi_{\mu}(t)\varphi_{\lambda}(t)\,dt= \frac{\Delta(\tau)\bigl(\varphi_{\mu}(t)\varphi'_{\lambda}(t)-\varphi_{\mu}'(\tau)\varphi_{\lambda}(\tau)\bigr)} {\mu^2-\lambda^2}.\\ \end{align} $$

Lemma 2.1 For the Jacobi functions, the following recurrence formula

(2.11) $$ \begin{align} &\frac{(\lambda^2+(\alpha+\beta+3)^2)(\operatorname{sinh} t\operatorname{cosh} t)^{2}}{4(\alpha+1)(\alpha+2)}\,\varphi_{\lambda}^{(\alpha+2,\beta+2)}(t)\nonumber\\& \quad =\frac{(\alpha+1)\operatorname{cosh}^2t+(\beta+1)\operatorname{sinh}^2t}{\alpha+1}\,\varphi_{\lambda}^{(\alpha+1,\beta+1)}(t)- \varphi_{\lambda}^{(\alpha,\beta)}(t) \end{align} $$

and the formula for derivatives

(2.12) $$ \begin{align} \bigl((\operatorname{sinh} t)^{2\alpha+3}(\operatorname{cosh} t)^{2\beta+3}\varphi_{\lambda}^{(\alpha+1,\beta+1)}(t)\bigr)_t'=2(\alpha+1)(\operatorname{sinh} t)^{2\alpha+1}(\operatorname{cosh} t)^{2\beta+1}\varphi_{\lambda}^{(\alpha,\beta)}(t) \end{align} $$

are valid.

Proof Indeed, (2.11) and (2.12) are easily derived from (1.2) and (2.9). To prove (2.11), we rewrite (1.2) as

$$\begin{align*}\Delta(t)\varphi_{\lambda}"(t)+\Delta'(t)\varphi_{\lambda}'(t)+(\lambda^2+\rho^2)\Delta(t)\varphi_{\lambda}(t)=0, \end{align*}$$

and then we replace the first and second derivatives by the Jacobi functions using (2.9). To show (2.12), we use (2.9) and (2.11).

Many properties (e.g., inequality (2.1)) of the Jacobi function follow from the Mehler representation

(2.13) $$ \begin{align} \varphi_{\lambda}(t)=\frac{c_{\alpha}}{\Delta(t)} \int_{0}^{t}A_{\alpha,\beta}(s,t)\cos{}(\lambda s)\,ds,\quad A_{\alpha,\beta}(s,t)\ge 0, \end{align} $$

where $c_{\alpha }=\frac {\Gamma (\alpha +1)}{\Gamma (1/2)\,\Gamma (\alpha +1/2)}$ and

$$ \begin{align*} A_{\alpha,\beta}(s,t)=2^{\alpha+2\beta+5/2}\operatorname{sinh}{}(2t)\operatorname{cosh}^{\beta-\alpha}t \bigl(\operatorname{cosh}{}(2t)-\operatorname{cosh}{}(2s)\bigr)^{\alpha-1/2} \\ {}\times F\Bigl(\alpha+\beta,\alpha-\beta;\alpha+\frac{1}{2};\frac{\operatorname{cosh} t-\operatorname{cosh} s}{2\operatorname{cosh} t}\Bigr). \end{align*} $$

We will need some properties of the following functions:

(2.14) $$ \begin{align} \begin{gathered} \eta_{\varepsilon}(\lambda)=\psi_{\lambda}(\varepsilon)=\frac{\varphi_{\lambda}(\varepsilon)}{\varphi_0(\varepsilon)},\quad \varepsilon>0,\quad \lambda\ge 0,\\ \eta_{m-1,\varepsilon}(\lambda)=(-1)^{m-1}\Bigl(\eta_{\varepsilon}(\lambda)-\sum_{k=0}^{m-2} \frac{\eta_{\varepsilon}^{(2k)}(0)}{(2k)!}\,\lambda^{2k}\Bigr),\quad m\ge 2,\\ \rho_{m-1,\varepsilon}(\lambda)=\frac{(2m-2)!\, \eta_{m-1,\varepsilon}(\lambda)}{(-1)^{m-1}\eta_{\varepsilon}^{(2m-2)}(0)}. \end{gathered} \end{align} $$

Lemma 2.2 For any $\varepsilon>0$ , $m\ge 2$ , $\lambda \in \mathbb {R}_{+}$ ,

$$\begin{align*}\eta_{m-1,\varepsilon}(\lambda)\ge 0,\quad (-1)^{m-1}\eta_{\varepsilon}^{(2m-2)}(0)>0, \end{align*}$$

$$\begin{align*}\rho_{m-1,\varepsilon}(\lambda)\ge 0, \quad \lim\limits_{\varepsilon\to 0}\rho_{m-1,\varepsilon}(\lambda)=\lambda^{2m-2}. \end{align*}$$

Proof Using the inequality

$$\begin{align*}(-1)^{m-1}\Bigl(\cos \lambda- \sum_{k=0}^{m-2}\frac{(-1)^{k} \lambda^{2k}}{(2k)!}\Bigr)\ge 0 \end{align*}$$

and (2.13), we get

$$\begin{align*}\eta_{m-1,\varepsilon}(\lambda)\ge 0,\quad (-1)^{m-1}\eta_{\varepsilon}^{(2m-2)}(0)=\frac{c_{\alpha}}{\Delta(\varepsilon)\varphi_{0}(\varepsilon)} \int_{0}^{\varepsilon}A_{\alpha,\beta}(s,\varepsilon)s^{2m-2}\,ds>0. \end{align*}$$

Hence, $\rho _{m-1,\varepsilon }(\lambda )\ge 0$ . For any $\lambda \in \mathbb {R}_{+}$ ,

$$\begin{align*}\eta_{\varepsilon}(\lambda) =\sum_{k=0}^{\infty}\frac{\eta_{\varepsilon}^{(2k)}(0)}{(2k)!}\,\lambda^{2k}. \end{align*}$$

By differentiating equality (2.2) in $\lambda $ and substituting $\lambda =0$ , we obtain

$$\begin{align*}(-1)^k\eta_{\varepsilon}^{(2k)}(0) =2^k\sum_{i_1=1}^{\infty}\frac{1}{\lambda_{i_1}^2(\varepsilon)} \sum_{i_2\neq i_1}^{\infty} \frac{1}{\lambda_{i_2}^2(\varepsilon)}\dots \sum_{i_k\neq i_1,\dots,i_{k-1}}^{\infty}\frac{1}{\lambda_{i_k}^2(\varepsilon)}. \end{align*}$$

Hence,

$$\begin{align*}|\eta_{\varepsilon}"(0)|=2\sum_{i=1}^{\infty}\frac{1}{\lambda_{i}^2(\varepsilon)}, \end{align*}$$

and for $k\ge m$ ,

$$\begin{align*}\Bigl|\frac{\eta_{\varepsilon}^{(2k)}(0)}{\eta_{\varepsilon}^{(2m-2)}(0)}\Bigr|\leq |\eta_{\varepsilon}"(0)|^{k-m+1}. \end{align*}$$

Therefore,

$$ \begin{align*} \frac{|\rho_{m-1,\varepsilon}(\lambda)-\lambda^{2m-2}|}{(2m-2)!}&= \Bigl|\frac{\eta_{m-1,\varepsilon}(\lambda)}{\eta_{\varepsilon}^{(2m-2)}(0)}-\frac{\lambda^{2m-2}}{(2m-2)!}\Bigr|= \Bigl|\frac{\eta_{m,\varepsilon}(\lambda)}{\eta_{\varepsilon}^{(2m-2)}(0)}\Bigr|\\&\le \sum_{k=m}^{\infty}\Bigl|\frac{\eta_{\varepsilon}^{(2k)}(0)}{\eta_{\varepsilon}^{(2m-2)}(0)} \Bigr|\frac{\lambda^{2k}}{(2k)!}\le |\eta_{\varepsilon}"(0)|\sum_{k=m}^\infty| \eta_{\varepsilon}"(0)|^{k-m}\frac{\lambda^{2k}}{(2k)!}. \end{align*} $$

It remains to show that

$$ \begin{align*} \lim\limits_{\varepsilon\to 0}|\eta_{\varepsilon}"(0))|=0. \end{align*} $$

Zeros $\lambda _{k}(\varepsilon )$ monotonically decrease on $\varepsilon $ and, for any k, $\lim \limits _{\varepsilon \to 0}\lambda _{k}(\varepsilon )=\infty $ . In view of (2.3), we have $\lambda _{k}(1)\asymp k$ as $k\to \infty $ . Finally, the result follows from

$$\begin{align*}|\eta_{\varepsilon}"(0))|\le \sum_{k=1}^N\frac{1}{\lambda_{k}^2(\varepsilon)}+ \sum_{k=N+1}^{\infty}\frac{1}{\lambda_{k}^2(1)}\lesssim \sum_{k=1}^N\frac{1}{\lambda_{k}^2(\varepsilon)}+\frac{1}{N}.\\[-41pt] \end{align*}$$

2.2 Jacobi transforms, translation, and positive definiteness

As usual, if X is a manifold with the positive measure $\rho $ , then by $L^{p}(X,d\rho )$ , $p\ge 1$ , we denote the Lebesgue space with the finite norm $\|f\|_{p,d\rho }=\bigl (\int _{X}|f|^p\,d\rho \bigr )^{1/p}$ . For $p=\infty $ , $C_b(X)$ is the space of continuous bounded functions with norm $\|f\|_{\infty }=\sup _{X}|f|$ . Let $\mathrm {supp}\,f$ be the support of a function f.

Let $t,\lambda \in \mathbb {R}_{+}$ , $d\mu (t)=\Delta (t)\,dt$ and $d\sigma (\lambda )$ be the spectral measure (1.5). Then $L^{2}(\mathbb {R}_{+}, d\mu )$ and $L^{2}(\mathbb {R}_{+}, d\sigma )$ are Hilbert spaces with the inner products

$$\begin{align*}(g, G)_{\mu}=\int_{0}^{\infty}g(t)\overline{G(t)}\,d\mu(t),\quad (f, F)_{\sigma}=\int_{0}^{\infty}f(\lambda)\overline{F(\lambda)}\,d\sigma(\lambda). \end{align*}$$

The main concepts of harmonic analysis in $L^{2}(\mathbb {R}_{+}, d\mu )$ and $L^{2}(\mathbb {R}_{+}, d\sigma )$ are the direct and inverse Jacobi transforms, namely,

$$\begin{align*}\mathcal{J}g(\lambda)=\mathcal{J}^{(\alpha,\beta)}g(\lambda)=\int_{0}^{\infty}g(t)\varphi_{\lambda}(t)\,d\mu(t) \end{align*}$$

and

$$\begin{align*}\mathcal{J}^{-1}f(t)=(\mathcal{J}^{(\alpha,\beta)})^{-1}f(t)=\int_{0}^{\infty}f(\lambda)\varphi_{\lambda}(t)\,d\sigma(\lambda). \end{align*}$$

We recall a few basic facts. If $g\in L^{2}(\mathbb {R}_{+}, d\mu )$ , $f\in L^{2}(\mathbb {R}_{+}, d\sigma )$ , then $\mathcal {J}g\in L^{2}(\mathbb {R}_{+}, d\sigma )$ , $\mathcal {J}^{-1}f\in L^{2}(\mathbb {R}_{+}, d\mu )$ and $g(t)=\mathcal {J}^{-1}(\mathcal {J}g)(t)$ , $f(\lambda )=\mathcal {J}(\mathcal {J}^{-1}f)(\lambda )$ in the mean square sense and, moreover, the Parseval relations hold.

In addition, if $g\in L^{1}(\mathbb {R}_{+}, d\mu )$ , then $\mathcal {J}g\in C_b(\mathbb {R}_{+})$ and $\|\mathcal {J}g\|_{\infty }\leq \|g\|_{1,d\mu }$ . If $f\in L^{1}(\mathbb {R}_{+}, d\sigma )$ , then $\mathcal {J}^{-1}f\in C_b(\mathbb {R}_{+})$ and $\|\mathcal {J}^{-1}f\|_{\infty }\leq \|f\|_{1,d\sigma }$ .

Furthermore, assuming $g\in L^{1}(\mathbb {R}_{+}, d\mu )\cap C_b(\mathbb {R}_{+})$ , $\mathcal {J}g\in L^{1}(\mathbb {R}_{+}, d\sigma )$ , one has, for any $t\in \mathbb {R}_{+}$ ,

$$\begin{align*}g(t)=\int_{0}^{\infty}\mathcal{J}g(\lambda)\varphi_{\lambda}(t)\,d\sigma(\lambda). \end{align*}$$

Similarly, assuming $f\in L^{1}(\mathbb {R}_{+}, d\sigma )\cap C_b(\mathbb {R}_{+})$ , $\mathcal {J}^{-1}f\in L^{1}(\mathbb {R}_{+}, d\mu )$ , one has, for any $\lambda \in \mathbb {R}_{+}$ ,

$$\begin{align*}f(\lambda)=\int_{0}^{\infty}\mathcal{J}^{-1}f(t)\varphi_{\lambda}(t)\,d\mu(t). \end{align*}$$

Let $\mathcal {B}_1^{\tau }, \tau>0$ , be the Bernstein class of even entire functions from $\mathcal {E}^{\tau }$ , whose restrictions to $\mathbb {R}_{+}$ belong to $L^{1}(\mathbb {R}_{+}, d\sigma )$ . For functions from the class $\mathcal {B}_1^{\tau }$ , the following Paley–Wiener theorem is valid.

Lemma 2.3 [15, 18]

A function f belongs to $\mathcal {B}_1^{\tau }$ if and only if

$$\begin{align*}f\in L^{1}(\mathbb{R}_{+}, d\sigma)\cap C_b(\mathbb{R}_{+})\quad \text{and}\quad \mathrm{supp}\,\mathcal{J}^{-1}f\subset[0,\tau]. \end{align*}$$

Moreover, there holds

$$\begin{align*}f(\lambda)=\int_{0}^{\tau}\mathcal{J}^{-1}f(t)\varphi_{\lambda}(t)\,d\mu(t),\quad \lambda\in \mathbb{R}_{+}. \end{align*}$$

Let us now discuss the generalized translation operator and convolution. In view of (2.1), the generalized translation operator in $L^{2}(\mathbb {R}_{+}, d\mu )$ is defined by [9, Section 4]

$$\begin{align*}T^tg(x)=\int_{0}^{\infty}\varphi_{\lambda}(t) \varphi_{\lambda}(x)\mathcal{J}g(\lambda)\,d\sigma(\lambda),\quad t,x\in \mathbb{R}_{+}. \end{align*}$$

If $\alpha \ge \beta \ge -1/2$ , $\alpha>-1/2$ , the following integral representation holds:

(2.15) $$ \begin{align} T^tg(x)=\int_{|t-x|}^{t+x}g(u)K(t,x,u)\,d\mu(u), \end{align} $$

where the kernel K is nonnegative and symmetric. Note that, for $\alpha =\beta =-1/2$ , we arrive at $T^tg(x)=(g(t+x)+g(|t-x|))/2$ .

Using representation (2.15), we can extend the generalized translation operator to the spaces $L^{p}(\mathbb {R}_{+}, d\mu )$ , $1\leq p\leq \infty $ , and, for any $t\in \mathbb {R}_{+}$ , we have $\|T^t\|_{p\to p}=1$ [9, Lemma 5.2].

The operator $T^t$ possesses the following properties:

(1) $\text {If}\ g(x)\geq 0,\ \text {then}\ T^tg(x)\geq 0$ .

(2) $T^t\varphi _{\lambda }(x)=\varphi _{\lambda }(t)\varphi _{\lambda }(x), \ \mathcal {J}(T^tg)(\lambda )=\varphi _{\lambda }(t)\mathcal {J}g(\lambda )$ .

(3) $T^tg(x)=T^xg(t), \ T^t1=1$ .

(4) $\text {If}\ g \in L^{1}(\mathbb {R}^d_{+}, d\mu ),\ \text {then}\ \int _{0}^{\infty }T^tg(x)\,d\mu (x)=\int _{0}^{\infty }g(x)\,d\mu (x)$ .

(5) $\text {If}\ \mathrm {supp}\,g\subset [0, \delta ],\ \text {then} \ \mathrm {supp}\,T^tg\subset [0, \delta +t]$ .

Using the generalized translation operator $T^t$ , we can define the convolution and positive-definite functions. Following [9], we set

$$\begin{align*}(g\ast G)_{\mu}(x)=\int_{0}^{\infty}T^tg(x)G(t)\,d\mu(t). \end{align*}$$

Lemma 2.4 [9, Section 5]

If $g, G\in L^{1}(\mathbb {R}_{+}, d\mu )$ , then $\mathcal {J}(g\ast G)_{\mu }=\mathcal {J}g\,\mathcal {J}G$ . Moreover, if $\mathrm {supp}\,g\subset [0, \delta ]$ , $\mathrm {supp}\,G\subset [0, \tau ]$ , then $\mathrm {supp}\,(g\ast G)_{\mu }\subset [0, \delta +\tau ]$ .

An even continuous function g is called positive-definite with respect to Jacobi transform $\mathcal {J}$ if for any N

$$\begin{align*}\sum_{i,j=1}^Nc_i\overline{c_j}\,T^{x_i}g(x_j)\ge 0,\quad \forall\,c_1,\dots,c_N\in\mathbb{C},\quad \forall\,x_1,\dots,x_N\in\mathbb{R}_{+}, \end{align*}$$

or, equivalently, the matrix $(T^{x_i}g(x_j))_{i,j=1}^{N}$ is positive semidefinite. If a continuous function g has the representation

$$\begin{align*}g(x)=\int_{0}^{\infty}\varphi_{\lambda}(x)\,d\nu(\lambda), \end{align*}$$

where $\nu $ is a nondecreasing function of bounded variation, then g is positive definite. Indeed, using the property (2) for the operator $T^{t}$ , we obtain

$$ \begin{align*} &\sum_{i,j=1}^Nc_i\overline{c_j}\,T^{x_i}g(x_j)=\int_{0}^{\infty}\sum_{i,j=1}^Nc_i\overline{c_j} \,T^{x_i}\varphi_{\lambda}(x_j)\,d\nu(\lambda) \\& \qquad =\int_{0}^{\infty}\sum_{i,j=1}^Nc_i\overline{c_j} \,\varphi_{\lambda}(x_i)\varphi_{\lambda}(x_j)\,d\nu(\lambda)=\int_{0}^{\infty} \Bigl|\sum_{i=1}^Nc_i \,\varphi_{\lambda}(x_i)\Bigr|^2\,d\nu(\lambda)\ge 0. \end{align*} $$

If $g\in L^{1}(\mathbb {R}_{+}, d\mu )$ , then a sufficient condition for positive definiteness of g is ${\mathcal {J}g(\lambda )\ge 0}$ .

We can also define the generalized translation operator in $L^{2}(\mathbb {R}_{+}, d\sigma )$ by

$$\begin{align*}S^{\eta}f(\lambda)=\int_{0}^{\infty}\varphi_{\eta}(t) \varphi_{\lambda}(t)\mathcal{J}^{-1}f(t)\,d\mu(t),\quad \eta,\lambda\in \mathbb{R}_{+}. \end{align*}$$

Then, for $\alpha \ge \beta \ge -1/2$ , $\alpha>-1/2$ , the following integral representation holds:

(2.16) $$ \begin{align} S^{\eta}f(\lambda)=\int_{0}^{\infty}f(\zeta)L(\eta,\lambda,\zeta)\,d\sigma(\zeta), \end{align} $$

where the kernel

$$\begin{align*}L(\eta,\lambda,\zeta)=\int_{0}^{\infty}\varphi_{\eta}(t) \varphi_{\lambda}(t)\varphi_{\zeta}(t)\,d\mu(t),\quad \int_{0}^{\infty}L(\eta,\lambda,\zeta)\,d\sigma(\zeta)=1, \end{align*}$$

is nonnegative continuous and symmetric [10]. Using (2.16), we can extend the generalized translation operator to the spaces $L^{p}(\mathbb {R}_{+}, d\sigma )$ , $1\leq p\leq \infty $ , and, for any $\eta \in \mathbb {R}_{+}$ , $\|S^\eta \|_{p\to p}=1$ [10].

One has:

(1) $\text {If}\ f(\lambda )\geq 0,\ \text {then}\ S^{\eta }f(\lambda )\geq 0$ .

(2) $S^{\eta }\varphi _{\lambda }(t)=\varphi _{\eta }(t)\varphi _{\lambda }(t), \ \mathcal {J}^{-1}( S^{\eta }f)(t)=\varphi _{\eta }(t)\mathcal {J}^{-1}f(t)$ .

(3) $S^{\eta }f(\lambda )=S^{\lambda }f(\eta ), \ S^{\eta }1=1$ .

(4) $\text {If}\ f \in L^{1}(\mathbb {R}^d_{+}, d\sigma ),\ \text {then}\ \int _{0}^{\infty }S^{\eta }f(\lambda )\,d\sigma (\lambda )=\int _{0}^{\infty }f(\lambda )\,d\sigma (\lambda )$ .

The function $\zeta \mapsto L(\eta ,\lambda ,\zeta )$ is analytic for $|\mathrm {Im}\,\zeta |<\rho $ . Hence, the restriction of this function to $\mathbb {R}_{+}$ has no compact support, in contrast with the function $x\mapsto K(t,s,x)$ in (2.15).

Similarly to above, we define

$$\begin{align*}(f\ast F)_{\sigma}(\lambda)=\int_{0}^{\infty}S^{\eta}f(\lambda)F(\eta)\,d\sigma(\eta). \end{align*}$$

If $f, F\in L^{1}(\mathbb {R}_{+}, d\sigma )$ , then $\mathcal {J}^{-1}(f\ast F)_{\sigma }=\mathcal {J}^{-1}f\,\mathcal {J}^{-1}F$ .

An even continues function is called positive definite with respect to the inverse Jacobi transform $\mathcal {J}^{-1}$ if

$$\begin{align*}\sum_{i,j=1}^Nc_i\overline{c_j}\,S^{\lambda_i}f(\lambda_j)\ge 0,\quad \forall\,c_1,\dots,c_N\in\mathbb{C},\quad \forall\,\lambda_1,\dots,\lambda_N\in\mathbb{R}_{+}, \end{align*}$$

or, equivalently, the matrix $(S^{\lambda _i}f(\lambda _j))_{i,j=1}^{N}$ is positive semidefinite. If a continuous function f has the representation

$$\begin{align*}f(\lambda)=\int_{0}^{\infty}\varphi_{\lambda}(t)\,d\nu(t), \end{align*}$$

where $\nu $ is a nondecreasing function of bounded variation, then f is positive definite. If $f\in L^{1}(\mathbb {R}_{+}, d\sigma )$ , then a sufficient condition for positive definiteness is $\mathcal {J}^{-1}f(t)\ge 0$ .

2.3 Gauss quadrature and lemmas on entire functions

In what follows, we will need the Gauss quadrature formula on the half-line for entire functions of exponential type.

Lemma 2.5 [14]

For an arbitrary function $f\in \mathcal {B}_1^{2\tau }$ , the Gauss quadrature formula with positive weights holds

(2.17) $$ \begin{align} \int_{0}^{\infty}f(\lambda)\,d\sigma(\lambda)= \sum_{k=0}^{\infty}\gamma_{k}(\tau)f(\lambda_{k}(\tau)). \end{align} $$

The series in (2.17) converges absolutely.

Lemma 2.6 [13]

Let $\alpha>-1/2$ . There exists an even entire function $\omega _{\alpha }(z)$ of exponential type $2$ , positive for $z>0$ , and such that

$$ \begin{align*} \omega_{\alpha}(x)&\asymp x^{2\alpha+1},\quad x\to +\infty,\\ |\omega_{\alpha}(iy)|&\asymp y^{2\alpha+1}e^{2y},\quad y\to +\infty. \end{align*} $$

The next lemma is an easy consequence of Akhiezer’s result [20, Appendix VII.10].

Lemma 2.7 Let F be an even entire function of exponential type $\tau>0$ bounded on $\mathbb {R}$ . Let $\Omega $ be an even entire function of finite exponential type, let all the zeros of $\Omega $ be zeros of F, and let, for some $m\in \mathbb {Z}_{+}$ ,

$$\begin{align*}\liminf_{y\to +\infty}e^{-\tau y}y^{2m}|\Omega(iy)|>0. \end{align*}$$

Then the function $F(z)/\Omega (z)$ is an even polynomial of degree at most $2m$ .

3 Chebyshev systems of Jacobi functions

Let I be an interval on $\mathbb {R}_{+}$ . By $N_{I}(g)$ , we denote the number of zeros of a continuous function g on interval I, counting multiplicity. A family of real-valued functions $\{\varphi _{k}(t)\}_{k=1}^{\infty }$ defined on an interval I is a Chebyshev system (T-system) if for any $n\in \mathbb {N}$ and any nontrivial linear combination

$$\begin{align*}p(t)=\sum_{k=1}^{n}A_{k}\varphi_{k}(t),\end{align*}$$

there holds $N_{I}(p)\le n-1$ (see, e.g., [1, Chapter II]).

Our goal is to prove that some systems, constructed with the help of Jacobi functions, are the Chebyshev systems. We will use the convenient for us version of Sturm’s theorem on zeros of linear combinations of eigenfunctions of the Sturm–Liouville problem (see [2]).

Theorem 3.1 [2]

Let $\{u_{k}\}_{k=1}^{\infty }$ be the system of eigenfunctions associated with eigenvalues $\xi _1<\xi _2<\dots $ of the following Sturm–Liouville problem on the interval $[0,\tau ]$ :

(3.1) $$ \begin{align} (wu')'+\xi wu=0,\quad u'(0)=0,\quad \cos \theta\,u(\tau)+\sin \theta\,u'(\tau)=0, \end{align} $$

where $\xi =\lambda ^{2}+\lambda _{0}^{2}$ , $\xi _{k}=\lambda _{k}^{2}+\lambda _{0}^{2}$ , $w\in C[0,\tau ]$ , $w\in C^{1}(0,\tau )$ , $w>0$ on $(0,\tau )$ , $\theta \in [0,\pi /2]$ .

Then for any nontrivial real polynomial of the form

$$\begin{align*}p=\sum_{k=m}^{n}a_{k}u_{k},\quad m,n\in \mathbb{N},\quad m\le n, \end{align*}$$

we have

$$\begin{align*}m-1\le N_{(0,\tau)}(p)\le n-1. \end{align*}$$

In particular, every kth eigenfunction $u_{k}$ has exactly $k-1$ simple zeros.

As above, we assume that $\tau>0$ , $\alpha \ge \beta \ge -1/2$ , $\alpha>-1/2$ , $\varphi _{\lambda }(t)=\varphi _{\lambda }^{(\alpha ,\beta )}(t)$ , $\psi _{\lambda }(t)=\psi _{\lambda }^{(\alpha ,\beta )}(t)$ , $\lambda _k(t)=\lambda _k^{(\alpha ,\beta )}(t)$ , and $\lambda _k^{*}(t)=\lambda _k^{*\,(\alpha ,\beta )}(t)$ for $k\in \mathbb {N}$ . Let $0<\mu _1(t)<\mu _2(t)<\dots $ be the positive zeros of the function $\varphi _{\lambda }'(t)$ of $\lambda $ .

Theorem 3.2 (i) The families of the Jacobi functions

(3.2) $$ \begin{align} \{\varphi_{\lambda_k(\tau)}(t)\}_{k=1}^{\infty},\quad \{\varphi_{\mu_k(\tau)}(t)\}_{k=1}^{\infty} \end{align} $$

form Chebyshev systems on $[0,\tau )$ and $(0,\tau )$ , respectively.

(ii) The families of the Jacobi functions

$$\begin{align*}\{\varphi_{\mu_k(\tau)}'(t)\}_{k=1}^{\infty},\quad \{\varphi_{\lambda_k(\tau)}'(t)\}_{k=1}^{\infty}, \quad\{\varphi_{\mu_k(\tau)}(t)-\varphi_{\mu_k(\tau)}(\tau)\}_{k=1}^{\infty} \end{align*}$$

form Chebyshev systems on $(0,\tau )$ .

Proof The families (3.2) are the systems of eigenvalues for the Sturm–Liouville problem (3.1) when $\lambda _{0}=\rho = \alpha +\beta +1 $ , $w(t)=\Delta (t)$ , and $\theta =0,\pi /2$ . Then, by Theorem 3.1, the statement of part (i) is valid for the interval $(0,\tau )$ . In order to include the endpoint $t=0$ for the family $\{\varphi _{\lambda _k(\tau )}(t)\}_{k=1}^{\infty }$ , we first take care of part (ii).

Since

$$\begin{align*}\varphi_{\lambda}'(t)=-\frac{(\lambda^2+\rho^2)\operatorname{sinh} t\operatorname{cosh} t}{2(\alpha+1)}\varphi_{\lambda}^{(\alpha+1,\beta+1)}(t),\quad \rho>0, \end{align*}$$

it is sufficiently to prove that the families $\{\varphi _{\mu _k(\tau )}^{(\alpha +1,\beta +1)}(t)\}_{k=1}^{\infty }$ and $\{\varphi _{\lambda _k(\tau )}^{(\alpha +1,\beta +1)}(t)\}_{k=1}^{\infty }$ are the Chebyshev systems on $(0,\tau )$ .

For the family $\{\varphi _{\mu _k(\tau )}^{(\alpha +1,\beta +1)}(t)\}_{k=1}^{\infty }$ , this again follows from Theorem 3.1 since it is the system of eigenvalues of the Sturm–Liouville problem (3.1) with $\lambda _{0}=\rho , $ $w(t)=\Delta ^{(\alpha +1,\beta +1)}(t)$ , and $\theta =0$ .

For the second family $\{\varphi _{\lambda _k(\tau )}^{(\alpha +1,\beta +1)}(t)\}_{k=1}^{\infty }$ , let us assume that the polynomial

$$\begin{align*}p(t)=\sum_{k=1}^{n}a_{k}\varphi_{\lambda_k(\tau)}^{(\alpha+1,\beta+1)}(t) \end{align*}$$

has n zeros on $(0,\tau )$ . We consider the function $g(t)=(\operatorname {sinh} t)^{2\alpha +2}(\operatorname {cosh} t)^{2\beta +2}p(t)$ . It has $n+1$ zeros including $t=0$ . By Rolle’s theorem, for a smooth real function g, one has $N_{(0,\tau )}(g')\ge N_{(0,\tau )}(g)-1\ge n$ (see [2]). In light of (2.13), we obtain

$$\begin{align*}g'(t)=2(\alpha+1)(\operatorname{sinh} t)^{2\alpha+2}(\operatorname{cosh} t)^{2\beta+2}\sum_{k=1}^{n}a_{k}\varphi_{\lambda_k(\tau)}(t). \end{align*}$$

This contradicts the fact that $\{\varphi _{\lambda _k(\tau )}(t)\}_{k=1}^{\infty }$ is the Chebyshev system on $(0,\tau )$ .

To show that $\{\varphi _{\mu _k(\tau )}(t)-\varphi _{\mu _k(\tau )}(\tau )\}_{k=1}^{\infty }$ is the Chebyshev system on $(0,\tau )$ , assume that $p(t)=\sum _{k=1}^{n}a_{k}(\varphi _{\mu _k(\tau )}(t)-\varphi _{\mu _k(\tau )}(\tau ))$ has n zeros on $(0,\tau )$ . Taking into account the zero $t=\tau $ , its derivative $p'(t)=\sum _{k=1}^{n}a_{k}\varphi _{\mu _k(\tau )}'(t)$ has at least n zeros on $(0,\tau )$ . This cannot be true because $\{\varphi _{\mu _k(\tau )}'(t)\}_{k=1}^{\infty }$ is the Chebyshev system on $(0,\tau )$ .

Now we are in a position to show that the first system in (3.2) is Chebyshev on $[0,\tau )$ . If $p(t)=\sum _{k=1}^{n}a_{k}\varphi _{\lambda _k(\tau )}(t)$ has n zeros on $[0,\tau )$ , then always $p(0)=0$ . Moreover, $p(\tau )=0$ . Therefore, $p'(t)$ has at least n zeros on $(0,\tau )$ , which is impossible since $p'(t)=\sum _{k=1}^{n}a_{k}\varphi _{\lambda _k(\tau )}'(t)$ and $\{\varphi _{\lambda _k(\tau )}'(t)\}_{k=1}^{\infty }$ is the Chebyshev system on $(0,\tau )$ .

Theorem 3.3 (i) The families of the Jacobi functions

(3.3) $$ \begin{align} \{\psi_{\lambda_k(\tau)}(t)\}_{k=1}^{\infty},\quad \{1\}\cup\{\psi_{\lambda_k^{*}(\tau)}(t)\}_{k=1}^{\infty} \end{align} $$

form Chebyshev systems on $(0,\tau )$ and $[0,\tau ]$ , respectively.

(ii) The families of the Jacobi functions

$$\begin{align*}\{\psi_{\lambda_k^{*}(\tau)}'(t)\}_{k=1}^{\infty},\quad \{\psi_{\lambda_k^{*}(\tau)}(t)-\psi_{\lambda_k^{*}(\tau)}(\tau)\}_{k=1}^{\infty} \end{align*}$$

form Chebyshev systems on $(0,\tau )$ .

Proof The families (3.3) are the systems of eigenvalues for the Sturm–Liouville problem (3.1) in the case $\lambda _{0}=0$ , $\Delta _{*}(t)=\varphi _0^2(t)\Delta (t)$ , and $\theta =0,\pi /2$ . Then the statement of part (i) is valid for the interval $(0,\tau )$ . In order to include the endpoints, we first prove part (ii).

Let $w(t)=\Delta _{*}(t)=\varphi _0^2(t)\Delta (t)$ , $W(t)=\int _{0}^tw(s)\,ds$ , $w_0(t)=W^2(t)w^{-1}(t)$ . It is known [14] that $v_{\lambda }(t)=-w(t)W^{-1}(t)\lambda ^{-2}\psi _{\lambda }'(t)$ is the eigenfunction of the Sturm–Liouville problem

$$\begin{align*}(w_0v')'+\lambda^2w_0v=0,\quad v'(0)=0. \end{align*}$$

Hence, the family $\{v_{\lambda _k^{*}(\tau )}'(t)\}_{k=1}^{\infty }$ is the system of eigenvalues for the Sturm–Liouville problem

$$\begin{align*}(w_0v')'+\lambda^2w_0v=0,\quad v'(0)=0,\quad v(\tau)=0. \end{align*}$$

By Theorem 3.1, the family $\{v_{\lambda _k^{*}(\tau )}'(t)\}_{k=1}^{\infty }$ and the family $\{\psi _{\lambda _k^{*}(\tau )}'(t)\}_{k=1}^{\infty }$ are the Chebyshev systems on $(0,\tau )$ .

To prove that $\{\psi _{\lambda _k^{*}(\tau )}(t)-\psi _{\lambda _k^{*}(\tau )}(\tau )\}_{k=1}^{\infty }$ forms the Chebyshev system on $(0,\tau )$ , we assume that $p(t)=\sum _{k=1}^{n}a_{k}(\psi _{\lambda _k^{*}(\tau )}(t)-\psi _{\lambda _k^{*}(\tau )}(\tau ))$ has n zeros on $(0,\tau )$ . Taking into account the zero $t=\tau $ , its derivative $p'(t)=\sum _{k=1}^{n}a_{k}\psi _{\lambda _k^{*}(\tau )}'(t)$ has at least n zeros on $(0,\tau )$ . This contradicts the fact that $\{\psi _{\lambda _k^{*}(\tau )}'(t)\}_{k=1}^{\infty }$ is the Chebyshev system on $(0,\tau )$ .

Now we are in a position to show that the second system in (3.3) is Chebyshev on $[0,\tau ]$ . If $p(t)=\sum _{k=0}^{n-1}a_{k}\psi _{\lambda _k^{*}(\tau )}(t)$ (we assume $\lambda _0^{*}(\tau )=0$ ) has n zeros on $[0,\tau ]$ , then one of the endpoints is zero. Then $p'(t)=\sum _{k=1}^{n-1}a_{k}\psi _{\lambda _k^{*}(\tau )}'(t)$ has at least $n-1$ zeros on $(0,\tau )$ , which is impossible for Chebyshev system $\{\psi _{\lambda _k^{*}(\tau )}'(t)\}_{k=1}^{\infty }$ .

4 Proof of Theorem 1.2

Below we give a solution of the generalized m-Logan problem for the Jacobi transform. As above, let $m\in \mathbb {N}$ and $\tau>0$ . For brevity, we denote

$$\begin{align*}\lambda_{k}=\lambda_k(\tau),\quad \gamma_k=\gamma_k(\tau). \end{align*}$$

We need the following lemma.

Lemma 4.1 Let $f(\lambda )$ be a nontrivial function from $\mathcal {L}_{m}(\tau ,\mathbb {R}_{+})$ such that $\Lambda _{m}(f)<\infty $ . Then

(4.1) $$ \begin{align} f\in L^1(\mathbb{R}_{+},\lambda^{2m-2}\,d\sigma),\quad (-1)^{m-1}\int_{0}^{\infty}\lambda^{2m-2}f(\lambda)\,d\sigma(\lambda)\ge 0, \end{align} $$

Proof Let $m=1$ . Let $\varepsilon>0$ , $\chi _{\varepsilon }(t)$ be the characteristic function of the interval $[0, \varepsilon ]$ ,

$$\begin{align*}\Psi_{\varepsilon}(t)=c_{\varepsilon}^{-2}(\chi_{\varepsilon}\ast \chi_{\varepsilon})_{\mu}(t),\quad c_{\varepsilon}=\int_{0}^{\varepsilon}\,d\mu. \end{align*}$$

By Lemma 2.4, $\mathrm {supp}\,\Psi _{\varepsilon }\subset [0,2\varepsilon ]$ . According to the properties (1)–(4) of the generalized translation operator $T^t$ and Lemma 2.4, we have

$$\begin{align*}\Psi_{\varepsilon}(t)\geq 0,\quad \mathcal{J}\Psi_{\varepsilon}(\lambda)=c_{\varepsilon}^{-2}(\mathcal{J}\chi_{\varepsilon}(\lambda))^2, \end{align*}$$

$$\begin{align*}\int_{0}^{\infty}\Psi_{\varepsilon}(t)\,d\mu(t)= c_{\varepsilon}^{-2}\int_{0}^{\infty}\chi_{\varepsilon}(x)\int_{0}^{\infty}T^x\chi_{\varepsilon}(t)\,d\mu(t)\,d\mu(x)=1. \end{align*}$$

Since $\chi _{\varepsilon }\in L^{1}(\mathbb {R}_{+}, d\mu )\cap L^{2}(\mathbb {R}_{+}, d\mu )$ , $\mathcal {J}\chi _{\varepsilon }\in L^{2}(\mathbb {R}_{+}, d\sigma )\cap C_b(\mathbb {R}_{+})$ , and

$$\begin{align*}|\mathcal{J}\chi_{\varepsilon}(\lambda)|\leq c_{\varepsilon},\quad\lim\limits_{\varepsilon\to 0}c_{\varepsilon}^{-1}\mathcal{J}\chi_{\varepsilon}(\lambda)=\lim\limits_{\varepsilon\to 0}c_{\varepsilon}^{-1}\int_{0}^{\varepsilon}\varphi_{\lambda}(t)\,d\mu(t)=1, \end{align*}$$

we obtain

$$\begin{align*}\mathcal{J}\Psi_{\varepsilon}\in L^{1}(\mathbb{R}_{+}, d\sigma)\cap C_b(\mathbb{R}_{+}), \quad 0\leq \mathcal{J}\Psi_{\varepsilon}(\lambda)\leq 1,\quad \lim\limits_{\varepsilon\to 0}\mathcal{J}\Psi_{\varepsilon}(\lambda)=1. \end{align*}$$

The fact that $\mathcal {L}_{1}(\tau ,\mathbb {R}_{+})\subset L^1(\mathbb {R}_{+},d\nu _{\alpha })$ can be verified with the help of Logan’s method from [23, Lemma]. Indeed, let $f\in \mathcal {L}_{1}(\tau ,\mathbb {R}_{+})$ be given by (1.5). Taking into account that $d\nu \ge 0$ in some neighborhood of the origin, we derive, for sufficiently small $\varepsilon>0$ , that

$$ \begin{align*} 0&\le \int_{0}^{2\varepsilon}\Psi_{\varepsilon}(t)\,d\nu(t)= \int_{0}^{\infty}\Psi_{\varepsilon}(t)\,d\nu(t)= \int_{0}^{\infty}f(\lambda)\mathcal{J}\Psi_{\varepsilon}(\lambda)\,d\sigma(\lambda)\\ &=\int_{0}^{\lambda_{1}(f)}f(\lambda)\mathcal{J}\Psi_{\varepsilon}(\lambda)(\lambda)\,d\sigma(\lambda)- \int_{\lambda_{1}(f)}^{\infty}|f(\lambda)|\mathcal{J}\Psi_{\varepsilon}(\lambda)\,d\sigma(\lambda). \end{align*} $$

This gives

$$\begin{align*}\int_{\lambda_{1}(f)}^{\infty}|f(\lambda)|\mathcal{J}\Psi_{\varepsilon}(\lambda)\,d\sigma(\lambda)\le \int_{0}^{\lambda_{1}(f)}f(\lambda)\mathcal{J}\Psi_{\varepsilon}(\lambda)\,d\sigma(\lambda)\le \int_{0}^{\lambda_{1}(f)}|f(\lambda)|\,d\sigma(\lambda). \end{align*}$$

Letting $\varepsilon \to 0$ , by Fatou’s lemma, we have

$$\begin{align*}\int_{\lambda_{1}(f)}^{\infty}|f(\lambda)|\,d\sigma(\lambda)\le \int_{0}^{\lambda_{1}(f)}|f(\lambda)|\,d\sigma(\lambda)<\infty. \end{align*}$$

Let $m\ge 2$ . In light of the definition of the class $\mathcal {L}_{m}(\tau ,\mathbb {R}_{+})$ , we have $f\in L^1(\mathbb {R}_{+},d\sigma )$ and $d\nu (t)\ge 0$ on segment $[0,\varepsilon ]$ , therefore $d\nu (t)=\mathcal {J}^{-1}f(t)d\mu (t)$ and $\mathcal {J}^{-1}f(\varepsilon )\ge 0$ for sufficiently small $\varepsilon $ .

Consider the function $\rho _{m-1,\varepsilon }(\lambda )$ defined by (2.14). Using Lemma 2.2, the orthogonality property (1.4), and the equality $(-1)^{m}f(\lambda )=|f(\lambda )|$ for $\lambda \ge \Lambda _{m}(f)$ , we arrive at

(4.2) $$ \begin{align} &(-1)^{m-1}\int_{0}^{\infty}\rho_{m-1,\varepsilon}(\lambda)f(\lambda)\,d\sigma(\lambda)\nonumber\\& \quad =\frac{(2m-2)!}{(-1)^{m-1}\varphi_0(\varepsilon)\psi_{\varepsilon}^{(2m-2)}(0)} \int_{0}^{\infty}f(\lambda)\varphi_{\lambda}(\varepsilon)\,d\sigma(\lambda)\nonumber\\& \quad =\frac{(2m-2)!}{(-1)^{m-1}\varphi_0(\varepsilon)\psi_{\varepsilon}^{(2m-2)}(0)}\,\mathcal{J}^{-1}f(\varepsilon)\ge 0. \end{align} $$

Thus,

$$\begin{align*}(-1)^{m}\int_{\Lambda_{m}(f)}^{\infty}\rho_{m-1,\varepsilon}(\lambda)f(\lambda)\,d\sigma(\lambda)\le (-1)^{m-1}\int_{0}^{\Lambda_{m}(f)}\rho_{m-1,\varepsilon}(\lambda)f(\lambda)\,d\sigma(\lambda). \end{align*}$$

Taking into account (4.2), Lemma 2.2, and Fatou’s lemma, we have

$$ \begin{align*} &(-1)^{m}\int_{\Lambda_{m}(f)}^{\infty}\lambda^{2m-2}f(\lambda)\,d\sigma(\lambda) =(-1)^{m}\int_{\Lambda_{m}(f)}^{\infty}\lim_{\varepsilon\to 0}\rho_{m-1,\varepsilon}(\lambda)f(\lambda)\,d\sigma(\lambda)\\ &\qquad \le\liminf_{\varepsilon\to 0}{}(-1)^{m}\int_{\Lambda_{m}(f)}^{\infty}\rho_{m-1,\varepsilon}(\lambda)f(\lambda)\,d\sigma(\lambda)\\ &\qquad \le\liminf_{\varepsilon\to 0}{}(-1)^{m-1}\int_0^{\Lambda_{m}(f)}\rho_{m-1,\varepsilon}(\lambda)f(\lambda)\,d\sigma(\lambda)\\ &\qquad =(-1)^{m-1}\int_0^{\Lambda_{m}(f)}\lim_{\varepsilon\to 0}\rho_{m-1,\varepsilon}(\lambda)f(\lambda)\,d\sigma(\lambda)\\ &\qquad =(-1)^{m-1}\int_0^{\Lambda_{m}(f)}\lambda^{2m-2}f(\lambda)\,d\sigma(\lambda)<\infty. \end{align*} $$

Therefore, we obtain that $f\in L^1(\mathbb {R}_{+},\lambda ^{2m-2}\,d\sigma )$ and, using (4.2), the condition $ (-1)^{m-1}\int _{0}^{\infty }\lambda ^{2m-2}f(\lambda )\,d\sigma (\lambda )\ge 0$ holds and (4.1) follows.

Proof of Theorem 1.2

The proof is divided into several steps.

4.1 Lower bound

First, we establish the inequality

$$ \begin{align*} L_m(\tau,\mathbb{R}_{+})\ge \lambda_m. \end{align*} $$

Consider a function $f\in \mathcal {L}_{m}(\tau ,\mathbb {R}_{+})$ . Let us show that $\lambda _m\le \Lambda _{m}(f)$ . Assume the converse, i.e., $\Lambda _{m}(f)<\lambda _{m}$ . Then $(-1)^{m-1}f(\lambda )\le 0$ for $\lambda \ge \Lambda _{m}(f)$ . Using (4.1) implies $\lambda ^{2m-2}f(\lambda )\in \mathcal {B}_{1}^{2\tau }$ . Therefore, by Gauss’ quadrature formula (2.17) and (1.4), we obtain

(4.3) $$ \begin{align} 0&\le(-1)^{m-1}\int_{0}^{\infty}\lambda^{2m-2}f(\lambda)\,d\sigma(\lambda) = (-1)^{m-1}\int_{0}^{\infty}\prod_{k=1}^{m-1}(\lambda^2-\lambda_{k}^2) f(\lambda)\,d\sigma(\lambda) \notag\\ &= (-1)^{m-1}\sum_{s=m}^{\infty} \gamma_{s}f(\lambda_{s})\prod_{k=1}^{m-1}(\lambda_{s}^2-\lambda_{k}^2)\le 0. \end{align} $$

Therefore, $\lambda _{s}$ for $s\ge m$ are zeros of multiplicity $2$ for f. Similarly, applying Gauss’ quadrature formula for f, we derive that

(4.4) $$ \begin{align} 0=\int_{0}^{\infty} \prod_{\substack{k=1\\ k\ne s}}^{m-1}(\lambda^2-\lambda_{k}^2)f(\lambda)\,d\sigma(\lambda) = \gamma_{s}\prod_{\substack{k=1\\ k\ne s}}^{m-1}(\lambda_{s}^2-\lambda_{k}^2)f(\lambda_{s}),\quad s=1,\dots,m-1. \end{align} $$

Therefore, $\lambda _{s}$ for $s=1,\dots ,m-1$ are zeros of f.

From $f\in L^1(\mathbb {R}_{+},\,d\sigma )$ and asymptotic behavior of $s(\lambda )$ given by (2.4) it follows that $f\in L^1(\mathbb {R}_{+},\lambda ^{2\alpha +1}\,d\lambda )$ . Consider the function $\omega _{\alpha }(\lambda )$ from Lemma 2.6 and set

$$\begin{align*}W(\lambda)=\omega_{\alpha}(\lambda)f(\lambda),\quad \Omega(\lambda)=\frac{\omega_{\alpha}(\lambda)\varphi_{\lambda}^2(\tau)} {\prod_{k=1}^{m-1}(1-\lambda^2/\lambda_{k}^2)}. \end{align*}$$

Then functions W and $\Omega $ are even and have exponential type $4$ . Since $\omega _{\alpha }(\lambda )\asymp \lambda ^{2\alpha +1}$ , $\lambda \to +\infty $ , then $W\in L^{1}(\mathbb {R})$ and W is bounded on $\mathbb {R}$ .

From (2.3) and Lemma 2.6, we have

$$\begin{align*}|\Omega(iy)|\asymp y^{-2m+2}e^{4y},\quad y\to +\infty. \end{align*}$$

Taking into account that all zeros of $\Omega (\lambda )$ are also zeros of $F(\lambda )$ and Lemma 2.7, we arrive at

$$\begin{align*}f(\lambda)=\frac{\varphi_{\lambda}^2(\tau)\sum_{k=0}^{m-1}c_k\lambda^{2k}} {\prod_{k=1}^{m-1}(1-\lambda^2/\lambda_{k}^2)}, \end{align*}$$

where $c_{k}\neq 0$ for some k. By (2.3), $\varphi _{\lambda }^2(\tau )=O(\lambda ^{-2\alpha -1})$ as $\lambda \to +\infty $ , and by (2.4) $\varphi _{\lambda }^2(\tau )\notin L^{1}(\mathbb {R}_{+},d\sigma )$ . This contradicts $f\in L^1(\mathbb {R}_{+},\lambda ^{2m-2}\,d\sigma )$ . Thus, $\Lambda _{m}(f)\ge \lambda _{m}$ and $L_m(\tau , \mathbb {R}_{+})\ge \lambda _{m}$ .

4.2 Extremality of $f_{m}$

Now we consider the function $f_{m}$ given by (1.6). Note that by (2.5) we have the estimate $f_{m}(\lambda )=O(\lambda ^{-2\alpha -1-2m})$ as $\lambda \to +\infty $ and hence $f_{m}\in L^1(\mathbb {R}_{+},\lambda ^{2m-2}\,d\sigma )$ . Moreover, $f_m$ is an entire function of exponential type $2\tau $ and $\Lambda _{m}(f_{m})=\lambda _{m}$ .

To verify facts that $f_{m}(\lambda )$ is positive definite with respect to the inverse Jacobi transform and the property (1.8) holds, we first note that Gauss’ quadrature formula implies (1.8). From the property (2) of the generalized translation operator $T^t$ , one has that $g_m(t)=T^{\tau }G_m(t)$ (see Remark 1.3). Since $T^t$ is a positive operator, to show the inequality $g_m(t)\ge 0$ , it is enough to prove $G_m(t)\ge 0$ . This will be shown in the next subsection.

Thus, we have shown that $f_{m}$ is the extremizer. The uniqueness of $f_m$ will be proved later.

4.3 Positive definiteness of $F_{m}$

Our goal here is to find the function $G_m(t)$ such that $F_m(\lambda )=\mathcal {J}G_m(\lambda )$ and show that it is nonnegative.

For fixed $\mu _1,\dots ,\mu _k\in \mathbb {R}$ , consider the polynomial

$$\begin{align*}\omega_k(\mu)=\omega(\mu,\mu_1,\dots,\mu_k)=\prod_{i=1}^k(\mu_i-\mu), \quad \mu\in \mathbb{R}. \end{align*}$$

Then

$$\begin{align*}\frac{1}{\omega_k(\mu)}=\sum_{i=1}^k\frac{1}{\omega_k'(\mu_i)(\mu_i-\mu)}. \end{align*}$$

Setting $k=m$ , $\mu =\lambda ^2$ , $\mu _i=\lambda _i^2$ , $i=1,\dots ,m$ , we have

(4.5) $$ \begin{align} \frac{1}{\prod_{i=1}^{m}(1-\lambda^2/\lambda_{i}^2)} = \prod_{i=1}^{m}\lambda_{i}^2 \frac{1}{\omega_{m}(\lambda^2)} = \prod_{i=1}^{m}\lambda_{i}^2\sum_{i=1}^{m}\frac{1}{\omega_{m}'(\lambda_{i}^2)(\lambda_{i}^2-\lambda^2)} = \sum_{i=1}^{m}\frac{A_i}{\lambda_{i}^2-\lambda^2}, \end{align} $$

where

(4.6) $$ \begin{align} \omega_{m}'(\lambda_i^2)=\prod_{\substack{j=1\\ j\ne i}}^{m}(\lambda_{j}^2-\lambda_{i}^2)\quad\mbox{and}\quad A_i= \frac{\prod_{{j=1}}^{m}\lambda_{j}^2} {\omega_m'(\lambda_{i}^2)}. \end{align} $$

Note that

(4.7) $$ \begin{align} \mathrm{sign}\,A_i=(-1)^{i-1}. \end{align} $$

For simplicity, we set

$$\begin{align*}\Phi_{i}(t):=\varphi_{\lambda_i}(t),\quad i=1,\dots,m, \end{align*}$$

and observe that $\Phi _{i}(t)$ are eigenfunctions and $\lambda _{i}^2+\rho ^2$ are eigenvalues of the following Sturm–Liouville problem on $[0,1]$ :

(4.8) $$ \begin{align} (\Delta(t) u'(t))'+(\lambda^2+\rho^2)\Delta(t)u(t)=0,\quad u'(0)=0,\quad u(\tau)=0. \end{align} $$

Let $\chi (t)$ be the characteristic function of $[0,\tau ]$ . In light of (2.10) and $\Phi _{i}(\tau )=0$ , we have

$$\begin{align*}\int_{0}^{\infty}\Phi_{i}(t)\varphi_{\lambda}(t)\chi(t)\Delta(t)\,dt= \int_0^{\tau}\Phi_{i}(t)\varphi_{\lambda}(t)\Delta(t)\,dt= -\frac{\Delta(\tau)\Phi_{i}'(\tau)\varphi_{\lambda}(\tau)} {\lambda_i^2-\lambda^2}, \end{align*}$$

or, equivalently,

(4.9) $$ \begin{align} \mathcal{J}\Bigl(-\frac{\Phi_{i}\chi}{\Delta(\tau)\Phi_{i}'(\tau)}\Bigr)(\lambda)= \frac{\varphi_{\lambda}(\tau)}{\lambda_{i}^2-\lambda^2}. \end{align} $$

It is important to note that

(4.10) $$ \begin{align} \mathrm{sign}\,\Phi_{i}'(\tau)=(-1)^i. \end{align} $$

Now we examine the following polynomial in eigenfunctions $\Phi _{i}(t)$ :

(4.11) $$ \begin{align} p_{m}(t)=-\frac{1}{\Delta(\tau)}\sum_{i=1}^{m}\frac{A_i}{\Phi_{i}'(\tau)}\,\Phi_{i}(t)=: \sum_{i=1}^{m}B_i\Phi_{i}(t). \end{align} $$

By virtue of (4.7) and (4.10), we derive that $B_i>0$ , $p_{m}(0)>0$ , and $p_{m}(\tau )=0$ . Furthermore, because of (4.5) and (4.9),

(4.12) $$ \begin{align} \mathcal{J}(p_{m}\chi)(\lambda)= \frac{\varphi_{\lambda}(\tau)}{\prod_{i=1}^{m}(1-\lambda^2/\lambda_{i}^2)}=: F_{m}(\lambda). \end{align} $$

Hence, it suffices to verify that $p_{m}(t)\ge 0$ on $[0,\tau ]$ . Define the Vandermonde determinant $ \Delta (\mu _1,\dots ,\mu _k)=\prod _{1\le j<i\le k}^{k}(\mu _i-\mu _j), $ then

$$\begin{align*}\frac{\Delta(\mu_1,\dots,\mu_k)}{\omega_k'(\mu_i)}= (-1)^{i-1}\Delta(\mu_1,\dots,\mu_{i-1},\mu_{i+1},\dots,\mu_k). \end{align*}$$

From (4.5) and (4.6), we have

(4.13)

Here and in what follows, if $m=1$ , we consider only the $(1,1)$ entries of the matrices.

We now show that

(4.14)

Using (4.8), we get

$$\begin{align*}\Phi_{i}"(t)+\Delta'(t)\Delta^{-1}(t)\Phi_{i}'(t)+(\lambda^2_i+\rho^2)\Phi_{i}(t)=0. \end{align*}$$

By Leibniz’s rule,

$$\begin{align*}\Phi_{i}^{(s+2)}(t)+\Delta'(t)\Delta^{-1}(t)\Phi_{i}^{(s+1)}(t)+(s(\Delta'(t)\Delta^{-1}(t))'+\lambda_i^2+\rho^2) \Phi_{i}^{(s)}(t) \end{align*}$$

$$\begin{align*}+\sum_{j=1}^{s-1}\binom{s}{j-1}(\Delta'(t)\Delta^{-1}(t))^{(s+1-j)}\Phi_{i}^{(j)}(t), \end{align*}$$

which implies for $t=\tau $ that

$$\begin{align*}\Phi_{i}^{(s+2)}(\tau)=-\Delta'(\tau)\Delta^{-1}(\tau)\Phi_{i}^{(s+1)}(\tau)-(s(\Delta'(\tau)\Delta^{-1}(\tau))'+\lambda_i^2+\rho^2) \Phi_{i}^{(s)}(\tau) \end{align*}$$

$$\begin{align*}-\sum_{j=1}^{s-1}\binom{s}{j-1}(\Delta'(\tau)\Delta^{-1}(\tau))^{(s+1-j)}\Phi_{i}^{(j)}(\tau),\quad \Phi_{i}^{(0)}(\tau)=\Phi_{i}(\tau)=0. \end{align*}$$

Assuming $s=0,1$ we obtain

$$\begin{align*}\Phi_{i}"(\tau)=-\Delta'(\tau)\Delta^{-1}(\tau)\Phi_{i}'(\tau), \end{align*}$$

$$\begin{align*}\Phi_{i}"'(\tau)=((\Delta'(\tau)\Delta^{-1}(\tau))^2-(\Delta'(\tau)\Delta^{-1}(\tau))'+\rho^2+\lambda_i^2)\Phi_{i}'(\tau). \end{align*}$$

By induction, we then derive, for $k=0,1,\dots ,$

$$\begin{align*}\Phi_{i}^{(2k+1)}(\tau)=\Phi_{i}'(\tau)\sum_{j=0}^{k}a_{kj}\lambda_{i}^{2j},\quad \Phi_{i}^{(2k+2)}(\tau)=\Phi_{i}'(\tau)\sum_{j=0}^{k}b_{kj}\lambda_{i}^{2j}, \end{align*}$$

where $a_{kj}$ , $b_{kj}$ depend on $\alpha ,\beta ,\tau $ and do not depend of $\lambda _i$ , and, moreover, $a_{kk}=(-1)^k$ . This yields, for $k=1,2,\dots ,$ that

(4.15) $$ \begin{align} \frac{\Phi_{i}^{(2k)}(\tau)}{\Phi_{i}'(\tau)}=\sum_{s=1}^{k}c_{0s}\, \frac{\Phi_{i}^{(2s-1)}(\tau)}{\Phi_{i}'(\tau)} \end{align} $$

and

(4.16) $$ \begin{align} \frac{\Phi_{i}^{(2k+1)}(\tau)}{\Phi_{i}'(\tau)}=\sum_{s=1}^{k}c_{1s}\, \frac{\Phi_{i}^{(2s-1)}(\tau)}{\Phi_{i}'(\tau)}+(-1)^k\lambda_i^{2k}, \end{align} $$

where $c_{0s},c_{1s}$ do not depend of $\lambda _i$ . The latter implies (4.14) since

Further, taking into account (4.13) and (4.14), we derive

(4.17) $$ \begin{align} p_{m}^{(1)}(\tau)=p_{m}^{(3)}(\tau)=\cdots=p_{m}^{(2m-1)}(\tau)=0. \end{align} $$

Therefore, by (4.11) and (4.15), we obtain for $j=1,\dots ,m-1$ that

$$ \begin{align*} p_{m}^{(2j)}(\tau)&=-\frac{1}{\Delta(\tau)}\sum_{i=1}^{m}A_i\,\frac{\Phi_{i}^{(2j)}(\tau)} {\Phi_{1}'(\tau)}=-\frac{1}{\Delta(\tau)}\sum_{i=1}^{m}A_i \sum_{s=1}^{j}c_{0s}\,\frac{\Phi_{i}^{(2s-1)}(\tau)} {\Phi_{1}'(\tau)}\\ &=-\frac{1}{\Delta(\tau)}\sum_{s=1}^{j}c_{0s} \sum_{i=1}^{m}A_i\,\frac{\Phi_{i}^{(2s-1)}(\tau)}{\Phi_{1}'(\tau)}= \sum_{s=1}^{j}c_{0s}p^{(2s-1)}(\tau)=0. \end{align*} $$

Together with (4.17) this implies that the zero $t=\tau $ of the polynomial $p_{m}(t)$ has multiplicity $2m-1$ . Then taking into account (4.12), the same also holds for $G_m(t)$ .

The next step is to prove that $p_{m}(t)$ does not have zeros on $[0,\tau )$ and hence $p_{m}(t)>0$ on $[0,\tau )$ , which implies that $G_{m}(t)\ge 0$ for $t\ge 0$ . We will use the facts that $\{\Phi _{i}(t)\}_{i=1}^{m}$ is the Chebyshev system on the interval $(0,\tau )$ (see Theorem 3.2) and any polynomial of degree m on $(0,\tau )$ has at most $m-1$ zeros, counting multiplicity.

We consider the polynomial

(4.18)

For any $0<\varepsilon <\tau /(m-1)$ , it has $m-1$ zeros at the points $t_j=\tau -j\varepsilon $ , $j=1,\dots , m-1$ . Letting $\varepsilon \to 0$ , we observe that the polynomial $\lim \limits _{\varepsilon \to 0}p(t,\varepsilon )$ does not have zeros on $(0,\tau )$ . If we demonstrate that

(4.19) $$ \begin{align} \lim\limits_{\varepsilon\to 0}p(t,\varepsilon)=c_2p_{m}(t), \end{align} $$

with some $c_2>0$ , then there holds that the polynomial $p_{m}(t)$ is strictly positive on $[0,\tau )$ .

To prove (4.19), we use Taylor’s formula, for $j=1,\dots ,m-1$ ,

$$\begin{align*}\frac{\Phi_{i}(\tau-j\varepsilon)}{(-j\varepsilon)^{2j-1}\Phi_{i}'(\tau)}= \sum_{s=1}^{2j-2}\frac{\Phi_{i}^{(s)}(\tau)}{s!\,(-j\varepsilon)^{2j-1-s}\Phi_{i}'(\tau)}+ \frac{\Phi_{i}^{(2j-1)}(\tau)+o(1)}{(2j-1)!\,\Phi_{i}'(\tau)}. \end{align*}$$

Using formulas (4.15) and (4.16) and progressively subtracting the row j from the row $j-1$ in the determinant (4.18), we have

Finally, in light of (4.13) and (4.14), we arrive at (4.19).

4.4 Monotonicity of $G_m$

The polynomial $p(t,\varepsilon )$ vanishes at m points: $t_{j}=\tau -j\varepsilon $ , $j=1,\dots ,m-1$ , and $t_{m}=\tau $ , thus its derivative $p'(t,\varepsilon )$ has $m-1$ zeros on the interval $(\tau -\varepsilon , \tau )$ .

In virtue of (2.7),

$$\begin{align*}\Phi_{i}'(t)=-\frac{(\rho^{2}+\lambda_i^{2})\operatorname{sinh} t\operatorname{cosh} t}{2(\alpha+1)}\,\varphi_{\lambda_i}^{(\alpha+1,\beta+1)}(t),\quad t\in [0,\tau]. \end{align*}$$

This and Theorem 3.2 imply that $\{\Phi _{i}'(t)\}_{i=1}^{m}$ is the Chebyshev system on $(0,\tau )$ . Therefore, $p'(t,\varepsilon )$ does not have zeros on $(0,\tau -\varepsilon ]$ . Then, for $\varepsilon \to 0$ , we derive that $p_{m}'(t)$ does not have zeros on $(0,\tau )$ . Since $p_{m}(0)>0$ and $p_{m}(\tau )=0$ , then $p_{m}'(t)<0$ on $(0,\tau )$ . Thus, $p_{m}(t)$ and $G_m(t)$ are decreasing on the interval $[0,\tau ]$ .

4.5 Uniqueness of the extremizer $f_{m}$

We will use Lemmas 2.6 and 2.7. Let $f(\lambda )$ be an extremizer and $\Lambda _{m}(f)=\lambda _m$ . Consider the functions

$$\begin{align*}F(\lambda)=\omega_{\alpha}(\lambda)f(\lambda),\quad \Omega(\lambda)=\omega_{\alpha}(\lambda)f_{m}(\lambda), \end{align*}$$

where $f_{m}$ is defined in (1.6) and $\omega _{\alpha }$ is given in Lemma 2.6.

Note that all zeros of $\Omega (\lambda )$ are also zeros of $F(\lambda )$ . Indeed, we have $(-1)^{m-1}f(\lambda )\le 0$ for $\lambda \ge \lambda _{m}$ and $f(\lambda _{m})=0$ (otherwise $\Lambda _{m}(f)<\lambda _{m}$ , which is a contradiction). This and (4.3) imply that the points $\lambda _{s}$ , $s\ge m+1$ , are double zeros of f. By (4.4), we also have that $f(\lambda _{s})=0$ for $s=1,\dots ,m-1$ and therefore the function f has zeros (at least, of order one) at the points $\lambda _{s}$ , $s=1,\dots ,m$ .

Using asymptotic relations given in Lemma 2.6, we derive that $F(\lambda )$ is the entire function of exponential type, integrable on real line and therefore bounded. Taking into account (2.3) and Lemma 2.6, we get

$$\begin{align*}|\Omega(iy)|\asymp y^{-2m}e^{4y},\quad y\to +\infty. \end{align*}$$

Now using Lemma 2.7, we arrive at $f(\lambda )=q(\lambda )f_{m}(\lambda )$ , where $q(\lambda )$ is an even polynomial of degree at most $2m$ . Note that the degree cannot be $2s$ , $s=1,\dots ,m$ , since in this case (2.3) implies that $f\notin L^1(\mathbb {R}_{+},\lambda ^{2m-2}\,d\sigma )$ . Thus, $f(\lambda )=cf_{m}(\lambda )$ , $c>0$ .

5 Generalized Logan problem for Fourier transform on hyperboloid

We will use some facts of harmonic analysis on hyperboloid $\mathbb {H}^{d}$ and Lobachevskii space from [27, Chapter X].

Let $d\in \mathbb {N}$ , $d\geq 2$ , and suppose that $\mathbb {R}^{d}$ is d-dimensional real Euclidean space with inner product $(x,y)=x_{1}y_{1}+\dots +x_{d}y_{d}$ , and norm $|x|=\sqrt {(x,x)}$ . As usual,

$$\begin{align*}\mathbb{S}^{d-1}=\{x\in\mathbb{R}^{d}\colon |x|=1\} \end{align*}$$

is the Euclidean sphere, $\mathbb {R}^{d,1}$ is $(d+1)$ -dimensional real pseudo-Euclidean space with bilinear form $[x,y]=-x_{1}y_{1}-\dots -x_{d}y_{d}+x_{d+1}y_{d+1}$ . The upper sheet of two sheets hyperboloid is defined by

$$\begin{align*}\mathbb{H}^{d}=\{x\in \mathbb{R}^{d,1}\colon [x,x]=1,\,x_{d+1}>0\} \end{align*}$$

and

$$\begin{align*}d(x,y)=\operatorname{arcosh}{}[x,y]=\ln{}([x,y]+\sqrt{[x,y]^2-1}) \end{align*}$$

is the distance between $x,y\in \mathbb {H}^{d}$ .

The pair $\bigl (\mathbb {H}^{d},d({\cdot },{\cdot })\bigr )$ is known as the Lobachevskii space. Let $o=(0,\dots ,0,1)\in \mathbb {H}^{d}$ , and let $B_{r}=\{x\in \mathbb {H}^{d}\colon d(o,x)\leq r\}$ be the ball.

In this section, we will use the Jacobi transform with parameters $(\alpha ,\beta )=(d/2-1,-1/2)$ . In particular,

$$\begin{align*}d\mu(t)=\Delta(t)\,dt=2^{d-1}\operatorname{sinh}^{d-1}t\,dt, \end{align*}$$

$$\begin{align*}d\sigma(\lambda)=s(\lambda)\,d\lambda=2^{3-2d} \Gamma^{-2}\left(\frac{d}{2}\right)\left|\frac{\Gamma\bigl(\frac{d-1}{2}+i\lambda\bigr)}{\Gamma(i\lambda)}\right|^2d\,\lambda. \end{align*}$$

For $t>0$ , $\zeta \in \mathbb {S}^{d-1}$ , $x=(\operatorname {sinh} t\, \zeta ,\operatorname {cosh} t)\in \mathbb {H}^{d}$ , we let

$$\begin{align*}d\omega(\zeta)=\frac{1}{|\mathbb{S}^{d-1}|}\,d\zeta, \quad d\eta(x)=d\mu(t)\,d\omega(\zeta) \end{align*}$$

be the Lebesgue measures on $\mathbb {S}^{d-1}$ and $\mathbb {H}^{d}$ , respectively. Note that $d\omega $ is the probability measure on the sphere, invariant under rotation group $SO(d)$ and the measure $d\eta $ is invariant under hyperbolic rotation group $SO_0(d,1)$ .

For $\lambda \in \mathbb {R}_{+}=[0, \infty )$ , $\xi \in \mathbb {S}^{d-1}$ , $y=(\lambda , \xi )\in \mathbb {R}_{+}\times \mathbb {S}^{d-1}=:\widehat {\mathbb {H}}^{d}$ , we let

$$\begin{align*}d\hat{\eta}(y)=d\sigma(\lambda)\,d\omega(\xi). \end{align*}$$

Harmonic analysis in $L^{2}(\mathbb {H}^{d}, d\eta )$ and $L^{2}(\widehat {\mathbb {H}}^{d}, d\hat {\eta })$ is based on the direct and inverse (hyperbolic) Fourier transforms

$$ \begin{align*} \mathcal{F}g(y)=\int_{\mathbb{H}^{d}}g(x)[x,\xi']^{-\frac{d-1}{2}-i\lambda}\,d\eta(x), \end{align*} $$

$$ \begin{align*} \mathcal{F}^{-1}f(x)=\int_{\widehat{\mathbb{H}}^{d}}f(y)[x,\xi']^{-\frac{d-1}{2}+i\lambda}\,d\hat{\eta}(y), \end{align*} $$

where $\xi '=(\xi , 1)$ , $\xi \in \mathbb {S}^{d-1}$ . We stress that the kernels of the Fourier transforms are unbounded, which cause additional difficulties.

If $f\in L^{2}(\mathbb {H}^{d}, d\eta )$ , $g\in L^{2}(\widehat {\mathbb {H}}^{d}, d\hat {\eta })$ , then

$$\begin{align*}\mathcal{F}g\in L^{2}(\widehat{\mathbb{H}}^{d}, d\hat{\eta}),\quad \mathcal{F}^{-1}(f)\in L^{2}(\mathbb{H}^{d}, d\eta), \end{align*}$$

and $g(x)=\mathcal {F}^{-1}(\mathcal {F}g)(x)$ , $f(y)=\mathcal {F}(\mathcal {F}^{-1}f)(y)$ in the mean-square sense. The Plancherel formulas are written as follows:

$$\begin{align*}\int_{\mathbb{H}^{d}}|g(x)|^2\,d\eta(x)=\int_{\widehat{\mathbb{H}}^{d}} |\mathcal{F}g(y)|^2\,d\hat{\eta}(y), \end{align*}$$

$$\begin{align*}\int_{\widehat{\mathbb{H}}^{d}}|f(y)|^2\,d\hat{\eta}(y)=\int_{\mathbb{H}^{d}} |\mathcal{F}^{-1}f(x)|^2\,d\eta(x). \end{align*}$$

The Jacobi function $\varphi _{\lambda }(t)=\varphi _{\lambda }^{(d/2-1,-1/2)}(t)$ is obtained by averaging over the sphere of Fourier transform kernels

$$\begin{align*}\varphi_{\lambda}(t)=\int_{\mathbb{S}^{d-1}}[x,\xi']^{-\frac{d-1}{2}\pm i\lambda}\,d\omega(\xi), \end{align*}$$

where $x=(\operatorname {sinh} t\,\zeta ,\operatorname {cosh} t)$ , $\zeta \in \mathbb {S}^{d-1}$ , $\xi '=(\xi ,1)$ . We note that spherical functions $g(x)=g_0(d(o,x))=g_0(t)$ and $f(y)=f_0(\lambda )$ satisfy

$$\begin{align*}\mathcal{F}g(y)=\mathcal{J}g_{0}(\lambda),\quad \mathcal{F}^{-1}f(x)=\mathcal{J}^{-1}f_{0}(t). \end{align*}$$

To pose m-Logan problem in the case of the hyperboloid, let $f(y)$ be a real-valued continuous function on $\widehat {\mathbb {H}}^{d}$ , $y=(\lambda , \xi )$ , and let

$$\begin{align*}\Lambda(f)= \Lambda(f,\widehat{\mathbb{H}}^{d})=\sup\,\{\lambda>0\colon f(y)=f(\lambda,\xi)>0,\ \xi\in\mathbb{S}^{d-1}\} \end{align*}$$

and, as above, $\Lambda _{m}(f)=\Lambda ((-1)^{m-1}f)$ , $m\in \mathbb {N}$ .

Consider the class $\mathcal {L}_{m}(\tau ,\widehat {\mathbb {H}}^{d})$ of real-valued functions f on $\widehat {\mathbb {H}}^{d}$ such that:

(1) $f\in L^1(\widehat {\mathbb {H}}^{d}, \lambda ^{2m-2}\,d\hat {\eta }(\lambda ))\cap C_b(\widehat {\mathbb {H}}^{d})$ , $f\ne 0$ , $\mathcal {F}^{-1}f\ge 0$ , $\mathrm {supp}\,\mathcal {F}^{-1}f\subset B_{2\tau }$ ;

(2) $\int _{\widehat {\mathbb {H}}^{d}}\lambda ^{2k}f(y)\,d\hat {\eta }(y)=0$ , $k=0,1,\dots ,m-1$ .

Problem E Find

$$\begin{align*}L_m(\tau, \widehat{\mathbb{H}}^{d})=\inf \{\Lambda_{m}(f)\colon f\in \mathcal{L}_{m}(\tau,\widehat{\mathbb{H}}^{d})\}. \end{align*}$$

Let us show that in the generalized Logan problem on hyperboloid, one can restrict oneself to only spherical functions depending on $\lambda $ .

If a function $f\in \mathcal {L}_{m}(\tau ,\widehat {\mathbb {H}}^{d})$ and $y=(\lambda , \xi )\in \widehat {\mathbb {H}}^{d}$ , then the function

$$\begin{align*}f_{0}(\lambda)=\int_{\mathbb{S}^{d-1}}f(y)\,d\omega(\xi) \end{align*}$$

satisfies the following properties:

(1) $f_0\in L^1(\mathbb {R}_{+}, \lambda ^{2m-2}d\sigma )\cap C_b(\mathbb {R}_{+}), \ f_0\ne 0, \ \mathcal {J}^{-1}f_{0}(t)\ge 0, \ \mathrm {supp}\,\mathcal {J}^{-1}f_0\subset [0,2\tau ]$ ;

(2) $\int _{0}^{\infty }\lambda ^{2k}f_{0}(\lambda )\,d\sigma (\lambda )=0$ , $k=0,1,\dots ,m-1$ ;

(3) $\Lambda _m(f_{0},\mathbb {R}_{+})=\Lambda _m(f,\widehat {\mathbb {H}}^{d})$ .

By Paley–Wiener theorem (see Lemma 2.3) $f_{0}\in \mathcal {B}_1^{2\tau }$ ,

$$\begin{align*}f_0(\lambda)=\int_{0}^{2\tau}\mathcal{J}^{-1}f_0(t)\varphi_{\lambda}(t)\,d\mu(t) \end{align*}$$

and $f_0\in \mathcal {L}_{m}(\tau ,\mathbb {R}_{+})$ . Hence, $L_m(\tau , \widehat {\mathbb {H}}^{d})=L_m(\tau , \mathbb {R}_{+})$ , and from Theorem 1.2, we derive the following result.

Theorem 5.1 If $d,m\in \mathbb {N}$ , $\tau>0$ , $\lambda _1(\tau )<\dots <\lambda _m(\tau )$ are the zeros of $\varphi _{\lambda }^{(d/2-1,-1/2)}(\tau )$ , then

$$\begin{align*}L_m(\tau, \widehat{\mathbb{H}}^{d})=\lambda_m(\tau). \end{align*}$$

The extremizer

$$\begin{align*}f_m(y)= \frac{(\varphi_{\lambda}^{(d/2-1,-1/2)}(\tau))^2}{(1-\lambda^2/\lambda_1^2(\tau))\cdots(1-\lambda^2/\lambda_m^2(\tau))}, \quad y=(\lambda, \xi)\in\widehat{\mathbb{H}}^{d}, \end{align*}$$

is unique in the class of spherical functions up to multiplication by a positive constant.

6 Number of zeros of positive definite function

In [24], it was proved that $[0,\pi n/4\tau ]$ is the minimal interval containing not less n zeros of functions from the class (1.1). Moreover, in this case,

$$\begin{align*}F_{n} (x)=\Bigl(\cos \frac{2\tau x}{n}\Bigr)^n \end{align*}$$

is the unique extremal function.

Note that $x=\pi n/4\tau $ is a unique zero of $F_{n}$ on $[0,\pi n/4\tau ]$ of multiplicity n. Moreover, the functions $F_{n}(\pi n(x-1/4\tau ))$ for $n=1$ and $3$ coincide, up to constants, with the cosine Fourier transform of $f_1$ and $f_2$ (see Introduction) on $[0,1]$ .

In this section, we study a similar problem for the Jacobi transform $\mathcal {J}$ with $\alpha \ge \beta \ge -1/2$ , $\alpha>-1/2$ . For the Bessel transform, this question was investigated in [13]. We will use the approach which was developed in Section 4. The key argument in the proof is based on the properties of the polynomial $p_{m}(t)$ defined in (4.11).

Recall that $N_{I}(g)$ stands from the number of zeros of g on interval $I\subset \mathbb {R}_{+}$ , counting multiplicity and $\lambda _m(t)$ , $\lambda _m^{*}(t)$ are the zeros of functions $\varphi _{\lambda }(t)$ (see (1.2)) and $\psi _{\lambda }'(t)$ (see (2.6)), respectively, and, moreover, $t_m(\lambda )$ , $t_m^{*}(\lambda )$ are inverse functions for $\lambda _m(t)$ and $\lambda _m^{*}(t)$ .

We say that $g\in \mathcal {L}^+_\gamma $ , $\gamma>0$ , if

(6.1) $$ \begin{align} g(t)=\int_{0}^{\gamma}\varphi_{\lambda}(t)\,d\nu(\lambda),\quad g(0)>0, \end{align} $$

with a nonnegative bounded Stieltjes measure $d\nu $ . Note that the function $g(t)$ is analytic on $\mathbb {R}$ but not entire.

We set, for $g\in \mathcal {L}^+_\gamma $ ,

$$\begin{align*}\mathrm{L}\,(g,n):=\inf{}\{L>0\colon N_{[0,L]}(g)\ge n\},\quad n\in \mathbb{N}. \end{align*}$$

Theorem 6.1 We have

(6.2) $$ \begin{align} \inf_{g\in\mathcal{L}^+_\gamma} \mathrm{L}\,(g,n)\le \theta_{n,\gamma}= \begin{cases} t_{m}(\gamma),& n=2m-1,\\ t_{m}^{*}(\gamma),& n=2m. \end{cases} \end{align} $$

Moreover, there exists a positive definite function $G_{n}\in \mathcal {L}^+_\gamma $ such that $\mathrm {L}\,(G_{n},n)= \theta _{n,\gamma }$ .

Proof Put $\tau :=t_m(\gamma )$ . First, let $n=2m-1$ . Consider the polynomial (see (4.11))

$$\begin{align*}G_{n}(t)= \sum_{i=1}^mB_i(\tau)\varphi_{\lambda_i(\tau)}(t),\quad t\in \mathbb{R}_{+}, \end{align*}$$

constructed in Theorem 1.2. It has positive coefficients $B_i(\tau )$ and the unique zero $t=\tau $ of multiplicity $2m-1$ on the interval $[0,\tau ]$ . Hence, $G_{n}$ is of the form (6.1), positive definite, and such that $t=\tau $ is a unique zero of multiplicity $2m-1$ on the interval $[0,\tau ]$ . Therefore,

$$\begin{align*}\mathrm{L}\,(G_n,2m-1)\le \tau. \end{align*}$$

Second, let $n=2m$ , $\lambda _{i}^{*}:=\lambda _{i}^{*}(\tau )$ . As in Theorem 1.2, we define numbers $A_i^{*}:=A_i^{*}(\tau )$ from the relation

(6.3) $$ \begin{align} \sum_{i=1}^{m}\frac{A_i^{*}}{\lambda_{i}^{*\,2}-\lambda^2}= \frac{1}{\prod_{i=1}^{m}(1-\lambda^2/\lambda_{i}^{*\,2})}. \end{align} $$

Recall that $\mathrm {sign}\,A_i^{*}=(-1)^{i-1}$ . Set

$$\begin{align*}\Psi_i(t):=\psi_{\lambda_{i}^{*}}(t)-\psi_{\lambda_{i}^{*}}(\tau),\quad i=1,\dots,m, \end{align*}$$

where $\psi _{\lambda }(t)$ is defined in (2.6). In view of (2.7), $\psi _{\lambda _{i}^{*}}(t)$ are eigenfunctions and $\lambda _{i}^{*\,2}$ are eigenvalues of the following Sturm–Liouville problem on $[0,\tau ]$ :

$$\begin{align*}(w(t)u'(t))'+\lambda^2w(t)u(t)=0,\quad u'(0)=0,\quad u'(\tau)=0, \end{align*}$$

where the weight $w(t)=\varphi _0^2(t)\Delta (t)$ . Since $\Psi _i'(\tau )=0$ , then from equation

(6.4) $$ \begin{align} (w(t)\Psi_i'(t)(t))'+\lambda^2w(t)\psi_{\lambda_{i}^{*}}(t)=0, \end{align} $$

it follows $\Psi _i"(\tau )=-\lambda _{i}^{*\,2}\psi _{\lambda _{i}^{*}}(\tau )$ .

Let us consider the polynomial

(6.5) $$ \begin{align} r_m(t)=\sum_{i=1}^{m}A_i^{*}\,\frac{\Psi_i(t)}{\Psi_i"(\tau)}=:\sum_{i=1}^{m}B_i^{*}\Psi_i(t). \end{align} $$

By (2.8), $\mathrm {sign}\,\psi _{\lambda _{i}^{*}}(\tau )=(-1)^i$ , hence, $B_i^{*}>0$ , $r_m(0)>0$ , $r_m(\tau )=0$ .

Let us show that at the point $t=\tau $ polynomial $r_m(t)$ has zero of order $2m$ . As in Theorem 1.2,

(6.6)

Show that

(6.7)

Differentiating (6.4) and substituting $t=\tau $ , we get, for $s\ge 1$ ,

$$ \begin{align*} \Psi_i^{(s+2)}(\tau)=-w'(\tau)w^{-1}(\tau)\Psi_i^{(s+1)}(\tau)-(s(w'(\tau)w^{-1}(\tau))'+\lambda_i^{{\prime}2}) \Psi_i^{(s)}(\tau) \\{} -\sum_{j=2}^{s-1}\binom{s}{j-1}(w'(\tau)w^{-1}(\tau))^{(s+1-j)}\Psi_i^{(j)}(\tau),\quad \Psi_i(\tau)=\Psi_i'(\tau)=0. \end{align*} $$

From this recurrence formula by induction, we deduce that, for $k=0,1,\dots ,$

(6.8) $$ \begin{align} \begin{gathered} \Psi_i^{(2k+2)}(\tau)=(r_0^k+r_1^k\lambda_i^{*\,2}+\cdots+r_k^k\lambda_i^{*\,2k})\Psi_i"(\tau),\\ \Psi_i^{(2k+3)}(\tau)=(p_0^k+p_1^k\lambda_i^{*\,2}+\cdots+p_k^k\lambda_i^{*\,2k})\Psi_i"(\tau), \end{gathered} \end{align} $$

where $r_0^k,\dots ,r_k^k$ , $p_0^k,\dots ,p_k^k$ depend from $\alpha $ , $\beta $ , $\tau $ and do not depend from $\lambda _i^{*}$ . Moreover, $r_k^k=(-1)^k$ .

From (6.8), it follows that, for $k=1,2,\dots ,$

(6.9) $$ \begin{align} \frac{\Psi_i^{(2k+1)}(\tau)}{\Psi_i"(\tau)}=\sum_{s=1}^{k}c_{s}^1\, \frac{\Psi_i^{(2s)}(\tau)}{\Psi_i"(\tau)}, \end{align} $$

(6.10) $$ \begin{align} \frac{\Psi_i^{(2k+2)}(\tau)}{\Psi_i"(\tau)}=\sum_{s=1}^{k}c_{s}^2\, \frac{\Psi_i^{(2s)}(\tau)}{\Psi_i"(\tau)}+(-1)^k\lambda_i^{{\prime}2k}, \end{align} $$

where $c_{s}^1$ , $c_{s}^2$ do not depend from $\lambda _i^{*}$ . Applying (6.10), we obtain (6.7)

The equalities (6.6) and (6.7) mean that

$$\begin{align*}r_m(\tau)=r_m"(\tau)=\cdots=r_m^{(2m-2)}(\tau)=0. \end{align*}$$

According to (6.9),

$$ \begin{align*} r_m^{(2j+1)}(\tau)&=\sum_{i=1}^{m}A_i^{*}\,\frac{\Psi_i^{(2j+1)}(\tau)} {\Psi_i"(\tau)}=\sum_{i=1}^{m}A_i^{*}\sum_{s=1}^{j}c_s^1(\alpha)\, \frac{\Psi_i^{(2s)}(\tau)} {\Psi_i'(\tau)}\\&=\sum_{s=1}^{j}c_s^1(\alpha)\sum_{i=1}^{m}A_i^{*}\,\frac{\Psi_i^{(2s)}(\tau)} {\Psi_i'(\tau)}=\sum_{s=1}^{j}c_s^1(\alpha)r^{(2s)}(\tau)=0,\quad j=1,\dots,m-1. \end{align*} $$

Since $r_m'(\tau )=0$ , then at the point $t=\tau $ the polynomial $r_m(t)$ has zero of multiplicity $2m$ .

We show that it has no other zeros on the interval $[0,\tau ]$ . We take into account that the system $\{\psi _{i}(t)\}_{i=1}^m$ is a Chebyshev system on the interval $(0,\tau )$ (see Theorem 3.3) and any polynomial of order m on the interval $(0,\tau )$ has at most $m-1$ zeros, counting multiplicity.

We consider the following polynomial in Chebyshev system $\{\Psi _i(t)\}_{i=1}^m$ :

(6.11)

For any $0<\varepsilon <\tau /(m-1)$ , it has $m-1$ zeros at the points $t_j=\tau -j\varepsilon $ , $j=1,\dots ,m-1$ , and has no other zeros on $(0,\tau )$ . The limit polynomial as $\varepsilon \to 0$ does not have zeros on $(0,\tau )$ .

In order to calculate it, we apply the expansions

$$\begin{align*}\frac{\Psi_i(\tau-j\varepsilon)}{(j\varepsilon)^{2j}\Psi_i"(\tau)}= \sum_{s=2}^{2j-1}\frac{\Psi_i^{(s)}(\tau)}{s!\,(-j\varepsilon)^{2j-s}\Psi_i"(\tau)}+ \frac{\Psi_i^{(2j)}(\tau)+o(1)}{(2j)!\,\Psi_i"(\tau)},\quad j=1,\dots,m-1, \end{align*}$$

formulas (6.9) and (6.10), and we subtract successively in the determinant (6.11) from the subsequent rows the previous ones to obtain

From here and (6.6) and (6.7), it follows that

$$\begin{align*}\lim\limits_{\varepsilon\to 0}r_m(t,\varepsilon)=c_2r_m(t),\quad c_2>0. \end{align*}$$

Hence, the polynomial $r_m(t)$ is positive on the interval $[0,\tau )$ .

The polynomial $r_m(t,\varepsilon )$ vanishes at m points, including $\tau $ , and therefore its derivative $r_m'(t,\varepsilon )$ has $m-1$ zeros between $\tau -(m-1)\varepsilon $ and $\tau $ . Since the system $\{\Psi _i'(t)\}_{i=1}^{m}$ is the Chebyshev system on $(0,\tau )$ (see Theorem 3.3), then $r_m'(t,\varepsilon )$ does not have zeros on $(0,\tau )$ . Hence, for $\varepsilon \to 0$ , we derive that $r_m'(t)$ does not have zeros on $(0,\tau )$ . Since $r_{m}(0)>0$ and $r_{m}(\tau )=0$ , then $r_{m}'(t)<0$ on $(0,\tau )$ . Thus, the polynomial $r_{m}(t)$ decreases on the interval $[0,\tau ]$ .

Since $\Psi _i"(\tau )=-\lambda _{i}^{*\,2}\psi _{\lambda _{i}^{*}}(\tau )$ , polynomial (6.5) can be written as

$$\begin{align*}r_m(t)=\sum_{i=1}^m\frac{A_i^{*}(\tau)}{\lambda_{i}^{*\,2}}+\sum_{i=1}^mB_i^{*}(\tau)\psi_{\lambda_i^{*}(\tau)}(t). \end{align*}$$

Setting $\lambda =0$ in (6.3), we obtain $ \sum _{i=1}^m\frac {A_i^{*}(\tau )}{\lambda _{i}^{*\,2}}=1, $ therefore

$$\begin{align*}r_m(t)=1+\sum_{i=1}^mB_i^{*}(\tau)\psi_{\lambda_i^{*}(\tau)}(t). \end{align*}$$

This polynomial has positive coefficients and the unique zero $t=\tau $ of multiplicity $2m$ on the interval $[0,\tau ]$ . Since $\psi _{\lambda }(t)=\varphi _{\lambda }(t)/\varphi _0(t)$ and $\varphi _0(t)>0$ , the function

$$\begin{align*}G_{n}(t)=\varphi_0(t)+\sum_{i=1}^mB_i^{*}(t_m^{*}(\gamma))\varphi_{\lambda_i^{*}(t_m^{*}(\gamma))}(t) \end{align*}$$

is of the form (6.1), positive definite, and such that $t=t_m^{*}(\gamma )$ is a unique zero of multiplicity $2m$ on the interval $[0,t_m(\gamma )]$ . Hence,

$$\begin{align*}\mathrm{L}\,(G_n,2m)\le t_m^{*}(\gamma).\\[-35pt] \end{align*}$$

Remark 6.2 From the proof of Theorem 6.1, it follows that inequality (6.2) is also valid for functions represented by

$$\begin{align*}g(t)=\int_{0}^{\gamma}\psi_{\lambda}(t)\,d\nu(\lambda),\quad g(0)>0, \end{align*}$$

with a nonnegative bounded Stieltjes measure $d\nu $ .