1 Introduction
The need to minimize mass and maximize the efficiency of design components is an important issue in nearly all engineering disciplines. In addition to the reduction of energy consumption, there are other factors such as material and manufacturing cost savings, increased dynamics and the reduction of vibrations that are driving the development.
The main advantage of trusses in comparison to monolithic structures is the high degree of utilization of the material, because of the division of the structure into individual struts, which are only subjected to compressive and tensile stresses due to their straightness, slenderness and flexible attaching principle. Struts are considerably stiffer when they are only subjected to axial loads in contrast to bending moments.
Lightweight design with wooden trusses was already used by the ancient Romans and Greeks to build roofs with so far unachieved spannings as stated by Marconi (Reference Marconi2014). Since then, applications of trusses of all scales have been developed. These vary from the support structures described by Meza et al. (Reference Meza, Zelhofer, Clarke, Mateos, Kochmann and Greer2015) in the micrometer range up to the
![]() $400~\text{m}$
spanning Ikitsuki truss bridge in Japan. In the interval between these limits, there are cranes, towers, roofs, light aircraft fuselages and high-performance vehicle frames available as trusses.
$400~\text{m}$
spanning Ikitsuki truss bridge in Japan. In the interval between these limits, there are cranes, towers, roofs, light aircraft fuselages and high-performance vehicle frames available as trusses.
Currently, there is a widespread application of trusses which are completely made of steel and can be manufactured very economically but have a very low specific stiffness. On the other hand, there are carbon-fiber-reinforced plastic (CFRP) trusses which have a high specific stiffness but which are characterized by very high development and manufacturing costs.
Hybrid lightweight design combines several different materials into one structure, as described by Zhu, Li & Childs (Reference Zhu, Li and Childs2018) for aviation, by Goede et al. (Reference Goede, Stehlin, Rafflenbeul, Kopp and Beeh2009) for automotive, by Zeng et al. (Reference Zeng, Chen, Zhao, Haifeng, Dongdong and Qilin2019) for civil engineering and by Klein (Reference Klein2013) in general. The material is used where properties such as stiffness and strength best meet the application-specific needs. This enables optimum use of the lightweight potential of the individual materials. Anisotropic CFRP have a very high specific stiffness and strength but only in fiber direction. Transverse to the fiber orientation, stiffness and strength are reduced by about one order of magnitude, which is why CFRP can exploit the lightweight potential especially in uniaxial stress conditions. In multi-axial stress conditions, the composite material is also subjected to stress transverse to the fiber, which means that the potential of the composite cannot be fully exploited.
In a multi-axial stress state, an isotropic material such as aluminum has the advantage that the strength and stiffness are direction-independent and thus the material can be fully utilized even in a multi-axial stress state. In general, uniaxial stress states occur as defined in the struts of trusses and multi-axial stress states occur in the nodes. This was shown as an example by Klein, Witzgall & Wartzack (Reference Klein, Witzgall and Wartzack2014) using a bicycle frame as a demonstrator. The hybrid design is therefore predestined for trusses since the uniaxially stressed struts can be made of CFRP and the multi-axially stressed nodes of aluminum. The lightweight design potential of the materials is thus fully exploited in the structure.
The expected benefits of reducing costs and mass and increasing stiffness can only be fully utilized if an efficient method of connecting the struts to the nodes is found and the reliability of the joint is ensured.
1.1 Problem statement
CFRP trusses currently have low market coverage because product development and manufacturing are not standardized, resulting in high design, engineering and manufacturing costs. The common production processes for CFRP are not suitable for the efficient production of complex spatial truss structures. Therefore, CFRP trusses are usually expensive custom-made products which cannot compete with conventional aluminum or steel trusses in the price–performance comparison, although an increase in specific stiffness of up to 20% has already been proven by Rathert, Witzgall & Wartzack (Reference Rathert, Witzgall, Wartzack, Ermanni, Meboldt, Wartzack, Krause and Zogg2018). The use of CFRP trusses is therefore widespread in aerospace applications that require particularly low masses, even though the production costs are high. The overall cost advantage results from lower energy usage during operation since CFRP structures have lower masses that have to be accelerated and moved.
The use of hybrid trusses makes it possible in many areas to increase stiffness and respectively reduce mass if the manufacturing costs are the main influence on the chosen design. As a result, the hybrid truss is the synthesis of expensive but lightweight pure CFRP trusses and cheap but heavy metal trusses. Possible applications, for example, include chassis for motor vehicles (see Figure 1), attachments in the agricultural sector and industrial walkways for plants.

Figure 1. Hybrid design motorcycle frame done by Rathert et al. (Reference Rathert, Witzgall, Wartzack, Ermanni, Meboldt, Wartzack, Krause and Zogg2018) as a demonstrator.
In addition to the production, the design and development of CFRP trusses is particularly time-consuming and cost-intensive. The design process has no fixed guidelines and is only partially supported by software products, which is why the designer has to perform the structural analysis and model generation manually. Software products that combine the entire design process in one tool are not available, unlike steel construction where such products are commonplace.
1.2 Solution approach
In order to facilitate the economic use of lightweight CFRP trusses even for small numbers of units and in further industrial sectors, a hybrid modular system is proposed, which is supported by a computer-aided engineering (CAE) tool based design methods from sketch to computer-aided design (CAD) model generation. The proposed design method supports the design of CFRP trusses from topology creation to CAD model data generation. The individual steps are shown in Figure 2.

Figure 2. Overview of the method. The steps are shown in their sequential order.
The first step is the generation and optimization of the topology, whereby the nodes and links are defined on the basis of a design space. Then the struts, nodes and joints are dimensioned for strength to obtain a basic structure. In a further step, struts, nodes and joints are optimized to meet additional boundary conditions such as overall stiffness. Subsequently, a strength verification of the structure is performed and a complete CAD model is generated based on the result.
The modular system supported by the method is extensible. Existing truss systems should also be supported by the method. The expected advantages are an increase in efficiency by standardized CFRP profiles as well as a standardized design process which also enables structures from batch size one.
2 State of the art
In the following sections, the state of the art in the area of already implemented fiber-reinforced plastics (FRP) trusses, modular FRP struts, joints, structural optimization, structural analysis and design software is presented.
2.1 FRP truss structures
FRP trusses can be subdivided according to their manufacturing method into trusses made in one piece on winding or braiding machines and trusses assembled from several individual parts. An overview of the trusses considered in this paper is shown in Figure 3.

Figure 3. Overview of trusses compared in this paper. The trusses are divided into two categories.
2.1.1 Truss made in one piece
Rackliffe, Jensen & Lucas (Reference Rackliffe, Jensen and Lucas2006) have introduced IsoTruss, a complicated CFRP truss which is produced on a braiding machine. The IsoTruss is manufactured as a whole and therefore has the advantage that it can be manufactured quasi-continuously and highly automated, without having to be assembled in several labor-intensive steps. It is oblong and consists of 8–12 nodes distributed around the circumference which are repeated periodically over the length, as shown in Figure 4(a). Between the nodes are straight solid struts of CFRP.

Figure 4. Schematic drawing of the trusses. (a) The truss according to Rackliffe and (b) after Woods. On the left is the side view and on the right is the top view of the trusses.
A system proposed by Woods, Hill & Friswell (Reference Woods, Hill and Friswell2016) avoids the high investment costs of a braiding machine by introducing a winding process for truss structures. The oblong truss consists of three larger parallel CFRP solid struts which are wound in triangles with smaller CFRP solid struts and remind of 3-point traverses as illustrated in Figure 4(b).
These manufacturing processes enable a high degree of automation and a reproducible production under constant conditions, thus allowing an economic production of the trusses. Due to the manufacturing process, only beam-shaped oblong structures can be produced in both cases. The dimensions are limited by the used machines. In addition, a specific mandrel is required for each truss to be produced.
2.1.2 Assembled hybrid trusses
A hybrid truss as a supporting structure of a pedestrian bridge was published by Yang, Bai & Ding (Reference Yang, Bai and Ding2015). Pultruded glass-fiber-reinforced plastic (GFRP) struts are bonded with steel tubes, which are screwed in triangular shape to welded gusset plates. The system uses simple components but is not suitable for the design of any kind of truss because the nodes do not allow any connection angles.
Zhang et al. (Reference Zhang, Zhao, Huang, Li, Chen and Miao2014) published a hybrid truss for bridges which consists of GFRP struts and aluminum nodes joint by a pre-tightened teeth connection. The shown truss allows a high utilization of the material potential; however, the system is only modular and universally usable to a limited extend due to the design of the joint and the high expense to be manufactured.
Luo et al. (Reference Luo, Huang, He, Qi and Bai2019) proposes a system for shell-shaped truss structures consisting of GFRP struts and steel plates which are screwed together. The system is modular for shell-shaped structures but cannot connect struts from any direction.
There are several systems for trusses which are offered by companies and are already in use. The systems listed below can be disassembled and are partly suitable for complicated trusses.
The companies Rock West Composites (2019) and DragonPlate (2019) offer modular and hybrid truss systems. The nodes are made of metal, plastic or CFRP, and the circular hollow profile struts are inserted and bonded directly into the nodes. Advantages are the high flexibility and simple assembly. A disadvantage is the limitation of the connection angle to a multiple of
![]() $90^{\circ }$
.
$90^{\circ }$
.

Figure 5. Drawing of the node of Imprimere AG. Example with two connected struts at right angles.
The hybrid trusses from Imprimere AG (2019) consist of CFRP struts and spherical aluminum nodes as is shown in Figure 5. The struts are equipped with bonded adapters at the ends which are screwed into the aluminum nodes. The system is very modular and can be used for almost any connection angle.
In summary, there are already many FRP hybrid trusses in use which are at least partly modular. The systems are, to some extent, suitable to be integrated into the modular system, whether in adapted form or directly, as with the Imprimere AG system.
The existing and exemplary presented trusses are well-designed structures but have the disadvantage that the design of a new truss based on these systems is not supported by a method which is integrated in a CAE tool. In order to achieve a broader use of hybrid lightweight trusses, it is necessary to methodically carry out and automate the designing process. The design of trusses without continuous CAE support is inefficient and thus prevents their use in many fields of application.
2.2 Struts
Truss struts are basically subjected to tensile and compressive loads. CFRP struts generally have metal adapters at both ends for force application. The CFRP middle section of the strut has a layered structure which is designed to maximize strength, stiffness and buckling resistance. According to investigations of Jegley et al. (Reference Jegley, Wu, Phelps, McKenney and Oremon2012) on struts for space applications, a ply layup of
![]() $[0_{8}/\pm 45/90]$
with a percentage of each ply of 80%, 10% and 10% is well suited for a wide range of diameters and enables minimal mass of struts. It is remarkable that the theoretically optimal strut with 100% fiber orientation of
$[0_{8}/\pm 45/90]$
with a percentage of each ply of 80%, 10% and 10% is well suited for a wide range of diameters and enables minimal mass of struts. It is remarkable that the theoretically optimal strut with 100% fiber orientation of
![]() $0^{\circ }$
is not optimal anymore considering initial imperfections and damage tolerance.
$0^{\circ }$
is not optimal anymore considering initial imperfections and damage tolerance.
The calculation of the bearable loads of the CFRP can be done with the quadratic failure criterion according to Tsai–Wu. The criterion is widely used because it is user-friendly as described by Hinton, Soden and Kaddour (Reference Hinton, Soden and Kaddour2004) and the failure can be predicted well. In comparison to other failure criteria such as Puck, only five material properties need to be determined, which saves a lot of effort. Although the failure criterion according to Puck has a higher accuracy, the associated effort to characterize the material is considered out of proportion in the context of this work, which is why the characterization of the struts should be done with Tsai–Wu. The criterion is used for each ply and indicates whether failure occurs or not.
If a high proportion of the fibers is aligned axially in the strut direction, tensile failure of the struts is not to be expected because the bonded connection fails much earlier for common designs. Buckling can occur due to compression forces, whereby the buckling load
![]() $F_{\text{E}}$
for an isotropic material can be calculated as follows:
$F_{\text{E}}$
for an isotropic material can be calculated as follows:
where
![]() $E$
is the modulus of elasticity,
$E$
is the modulus of elasticity,
![]() $I$
is the area moment of inertia,
$I$
is the area moment of inertia,
![]() $l$
is the free strut length and
$l$
is the free strut length and
![]() $\unicode[STIX]{x1D707}$
depends on the support of the strut ends. For fiber-reinforced composites, the equation of Euler is not sufficiently accurate and can be extended by the following formulation as described by Lee and Hewson (Reference Lee, Hewson and Richards1979) and confirmed by Zhu et al. (Reference Zhu, He, Lu, Ling, Zhu and Liu2015) for CFRP pipes with various stacking sequences and a length and inside diameter of 1.5 and 0.05 m, respectively. In addition, the shear deformation
$\unicode[STIX]{x1D707}$
depends on the support of the strut ends. For fiber-reinforced composites, the equation of Euler is not sufficiently accurate and can be extended by the following formulation as described by Lee and Hewson (Reference Lee, Hewson and Richards1979) and confirmed by Zhu et al. (Reference Zhu, He, Lu, Ling, Zhu and Liu2015) for CFRP pipes with various stacking sequences and a length and inside diameter of 1.5 and 0.05 m, respectively. In addition, the shear deformation
![]() $E_{L}/G_{LT}$
is taken into account to achieve sufficiently accurate results:
$E_{L}/G_{LT}$
is taken into account to achieve sufficiently accurate results:
The parameter
![]() $E_{L}$
is the longitudinal modulus of elasticity in the direction of the strut,
$E_{L}$
is the longitudinal modulus of elasticity in the direction of the strut,
![]() $G_{LT}$
the longitudinal transverse shear modulus of the strut and the empirical constants
$G_{LT}$
the longitudinal transverse shear modulus of the strut and the empirical constants
![]() $a=0.6723$
,
$a=0.6723$
,
![]() $b=0.3235$
,
$b=0.3235$
,
![]() $c=6.03$
and
$c=6.03$
and
![]() $d=0.091$
. Depending on the stacking sequence, Zhu et al. (Reference Zhu, He, Lu, Ling, Zhu and Liu2015) found in a case study that Equation (1) had an error of 2%–190% compared to finite element method (FEM) simulations. The extended formulation had an error of 1%–20% compared to the FEM results. Thus, the extended equation achieves considerably more accurate results.
$d=0.091$
. Depending on the stacking sequence, Zhu et al. (Reference Zhu, He, Lu, Ling, Zhu and Liu2015) found in a case study that Equation (1) had an error of 2%–190% compared to finite element method (FEM) simulations. The extended formulation had an error of 1%–20% compared to the FEM results. Thus, the extended equation achieves considerably more accurate results.
Hartwich, Oltmann & Krause (Reference Hartwich, Oltmann, Krause, Ermanni, Meboldt, Wartzack, Krause and Zogg2018) describe the demands for buckling experiments of cylindrical CRFP struts. In particular, the influence of radial and off-axis acting forces on the buckling is investigated.
2.3 Joining
Two systems for connecting CFRP pipes to nodes have been described by Schütze (Reference Schütze1997), a form fit and an adhesive joint. The form fit is realized by a metal cone, which can transmit high tensile forces. The adhesive joint is produced by a bonding between the adapters and the strut. The adapters bonded into the strut ends are connected to the nodes by a thread, as shown in Figure 6. The system described by Schütze achieves a high degree of utilization of the material and also has high manufacturing costs.

Figure 6. Different types of joints. (a) The adhesive joint of Schütze. (b) The form locking joint of Schütze.
According to a review done by Pramanik et al. (Reference Pramanik, Basak, Dong, Sarker, Uddin, Littlefair, Dixit and Chattopadhyaya2017), bonding is the most common method for joining CFRP and aluminum in aerospace, automotive and construction industries. In addition to the main purpose of force transmission, bonding seals the joint and simultaneously galvanically separates the materials from each other, preventing corrosion of the metallic part. Bonding is the most practical and economic method for joining thin-walled components.
The adhesive-appropriate design of the joints has a significant influence on the load-bearing capacity and durability of a bonding, as described by Habenicht (Reference Habenicht2009). A well-designed adhesive layer is only exposed to shear stress, and peel stresses are, in particular, avoided. In the case of overlapping pipe bonding, peel stresses are excluded by the component geometry, which is why bonding is excellently suited for forming the connection between struts and nodes in trusses.
The transferable axial load of a pipe bonding can be adapted for a particular diameter by the overlap length. The shear stress distribution in the adhesive layer, described by Volkerson (Reference Volkerson1953), results in the fact that the failure of a properly designed bonding always begins at the ends of the overlap. The shear stress peaks located at these ends can only be reduced to a certain limit even if the overlap length is increased. Therefore, the overlap length of the bond is to be limited to a practical interval, whereby it can be derived from investigations of Qiu et al. (Reference Qiu, Feng, Yang, Zhu and Bai2017) and Siebert (Reference Siebert2006) that the overlap length
![]() $L$
is reasonable in the range of
$L$
is reasonable in the range of
![]() $0.5\,D\leqslant L\leqslant 2\,D$
of diameter
$0.5\,D\leqslant L\leqslant 2\,D$
of diameter
![]() $D$
. In this range, the dimensioning of the bonding can be done using the equation
$D$
. In this range, the dimensioning of the bonding can be done using the equation
with
![]() $\unicode[STIX]{x1D70F}$
being the shear strength of the adhesive,
$\unicode[STIX]{x1D70F}$
being the shear strength of the adhesive,
![]() $F$
being the axial tensile force and
$F$
being the axial tensile force and
![]() $D$
and
$D$
and
![]() $l$
being the diameter and the length of the bonding, respectively.
$l$
being the diameter and the length of the bonding, respectively.
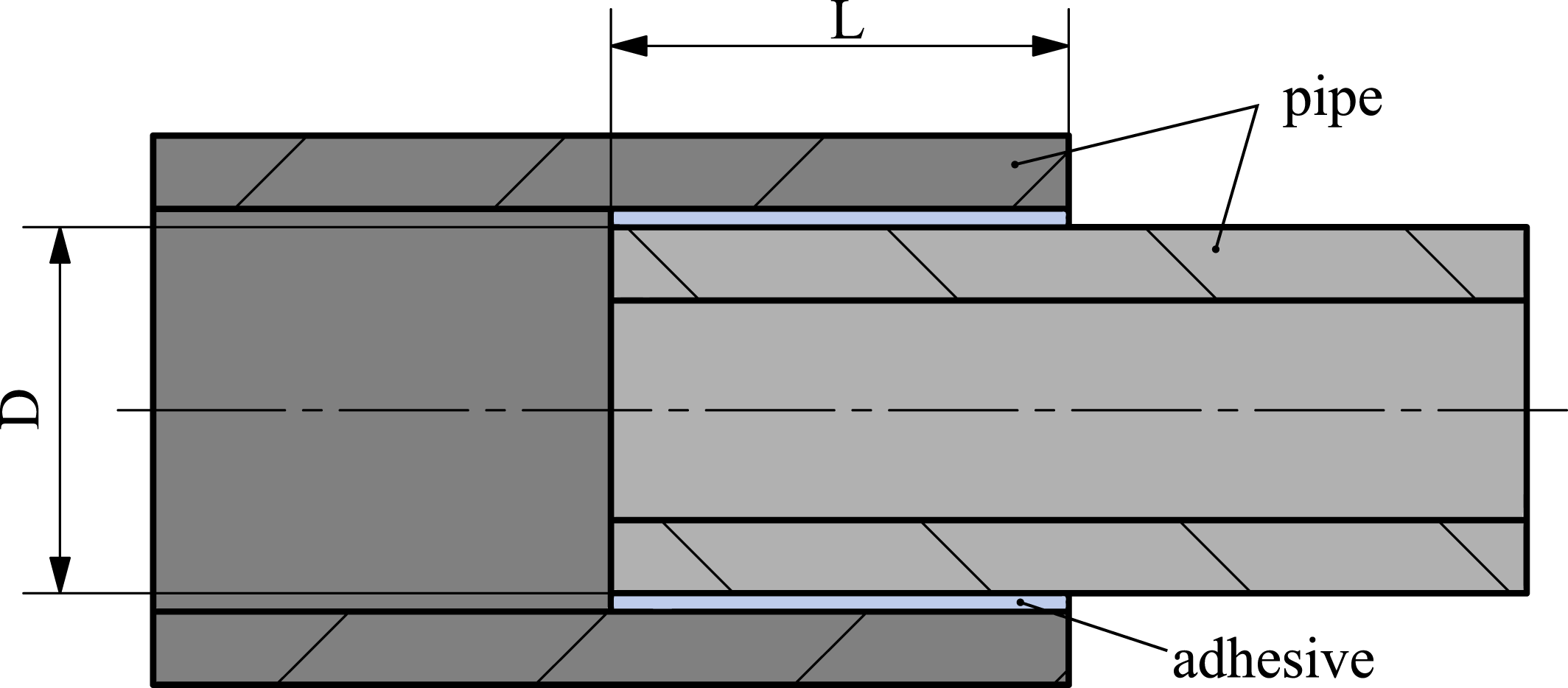
Figure 7. Overlapping pipe bonding. The bonding has the dimensions
![]() $L$
and
$L$
and
![]() $D$
and is between the inner and outer pipes.
$D$
and is between the inner and outer pipes.
The shear strength of the adhesive which is determined by tensile shear tests according to DIN EN 1465 can be only limitedly applied as stated by Rasche and Syperek (Reference Rasche and Syperek2015). The results of the tests are dependent on the sample geometry and its material properties and can only be partially transferred to other components. Therefore, it is preferable to determine the shear strength of the adhesive using specimens close to the conceived component.
The production method of bonding has a decisive influence on the strength that can be achieved by overlap pipe bonding. Measurements carried out by Siebert (Reference Siebert2006) have shown that by injecting the adhesive into the bonding gap, it is possible to achieve significantly increased strengths compared to applying the adhesive at the joint and subsequently pushing it together.
2.4 Structural optimization
Structural optimization, as described by Bendsøe & Sigmund (Reference Bendsøe and Sigmund2004), can be divided into the areas of topology, shape and parameter optimization. The aim is to find a geometry which is optimal for a certain function while satisfying additional constrains. In topology optimization, the basic layout of the structure is determined, commonly based on FEM. Shape optimization describes the optimization of the form, like finding the optimal diameter for a hole in a plate or for a truss by moving individual nodes. Parameter optimization determines, for example, the stacking sequence of a laminate or the cross-sectional area of a individual strut of a truss.

Figure 8. Progression of topology optimization. First, the design space is defined (a), then the design space is discretized and meshed (b). The optimal struts are found (c) and a final shape optimization is done (d) as described by LimitState.
According to Pfeiffer et al. (Reference Pfeiffer, Rammerstorfer, Guazzelli, Schrefler, Serafini, Rozvany and Lewiński2014), topology optimization can be divided into two basic methods: continuous and discrete topology optimization. The continuous topology optimization generates as a result of complicated solids which are formed with irregular surfaces and cross-sectional areas, as can be seen from the investigations of Völkl et al. (Reference Völkl, Klein, Franz and Wartzack2018) for a transversal isotropic and an isotropic material model. Therefore, it is not suitable for a modular system with discrete struts, cross-sections and nodes since the result must be in the form of a discrete skeleton structure. The discrete topology optimization generates structure out of beams and rods which can be adapted to a modular system of discrete struts and nodes.
Topology optimization can be applied as a numerical method to generate optimized truss structures following the steps as illustrated in Figure 14. The first step is the definition of the design space, load and boundary conditions. For the design space, any shape is possible but it needs to be finite. The boundary conditions need to allow a statically determined support. In the next step, the design space is meshed and all potential members are generated. Meshing has a significant influence on the resulting structure for discrete topology optimization since a finer mesh typically generates a result with more struts as a coarser mesh and vice versa. In the final step, the optimal structure is found by deleting struts from the model until the mass is minimized and all additional constrains, like buckling, are satisfied.
2.4.1 Topology and shape optimization
As shown by Fairclough et al. (Reference Fairclough, Gilbert, Thirion and Tyas2018), a general problem of topology optimization is that the structures found are complicated and impractical and cannot be realized in a real workpiece. Standard topology optimization, which finds the theoretical optimum (or close to), creates structures with too many nodes and struts and too small angles between the struts. Thus, the production of these structures is complex and costly and therefore has no general advantage in comparison to conventional design methods.
A topology optimization method was described by Mohr et al. (Reference Mohr, Stein, Matzies and Knapek2014) and implemented in the software TTRR (truss topology robust redundant). Robust design as described by Kellermeyer, Klein & Wartzack (Reference Kellermeyer, Klein and Wartzack2017) is implemented by TTRR, but the method generates trusses which have a high number of partly crossing struts. Furthermore, many struts connect in one node, which can be seen in a paper of Mohr et al. (Reference Mohr, Stein, Matzies and Knapek2014). The physical realization of such structures is hardly compatible with a modular system using standardized elements. An example done by Rathert et al. (Reference Rathert, Witzgall, Wartzack, Ermanni, Meboldt, Wartzack, Krause and Zogg2018) is shown in Figure 9, and as described by him, the result of TTRR topology optimization is not realizable without further simplification such as combining several nodes into one.

Figure 9. Topology optimization result of a motorcycle frame done with TTRR by Rathert. The structure is hardly manufacturable due to the number of nodes and the small angle between the struts.
Another approach in discrete topology and shape optimization according to Dorn, Gomory & Greenberg (Reference Dorn, Gomory and Greenberg1964), Gilbert and Tyas (Reference Gilbert and Tyas2003) and Pritchard, Gilbert & Tyas (Reference Pritchard, Gilbert and Tyas2005) is implemented in the software LimitState:Form. The structure volume is minimized as a target quantity, whereby the yield strength of the material is taken into account. The introduction of additional constraints into the optimization, which, for example, take into account the constraint of minimum angles, can eliminate the problem of non-producible structures as shown by He et al. (Reference He, Gilbert, Johnson and Pritchard2018). It was shown that structures can be obtained which have nearly the same mass as the theoretical optimum but, at the same time, are much easier to manufacture. A case study by Fairclough et al. (Reference Fairclough, Gilbert, Thirion and Tyas2018) showed for a three-dimensional demonstrator, see Figure 10, that a reduction of the number of nodes by 74% results in an increase of the mass by approximately 3%.

Figure 10. Topology optimization example done by Fairclough with LimitState:Form.
Therefore, it can be concluded that LimitState:Form is a suitable tool for topology and shape optimization of manufacturing-compatible trusses.
2.4.2 Parameter optimization of struts
The determination of strut profiles for the truss based on a modular system is a discrete optimization since a predefined selection of struts is available. There are a lot of optimization methods for composite structures available as shown in Nikbakt, Kamarian & Shakeri (Reference Nikbakt, Kamarian and Shakeri2018). Not all optimization methods can be applied to discrete systems since, for instance, the calculation of gradients in discrete systems is impossible or only possible to a limited extent. Therefore, the widely used gradient-based methods cannot be applied. Genetic algorithms can be used with discrete systems but require a very high number of function evaluations in order to reliably find an optimum. With a monotonously increasing target function, the bisection method is excellently suited to find a solution. With this method, the solution is reliable and unique.
The bisection method is very efficient to reduce a wide interval. With increasingly smaller intervals, the step size also becomes smaller, which reduces efficiency of the bisection algorithm. With discrete systems, the smallest possible interval is given, whereby the interval halving procedure is used only in its efficient range and thus represents a method which can be applied for the modular system.
2.5 Structural analysis and design software
Although the approach presented in this paper concerns mechanical engineering, it is worth taking a look at the civil engineering sector because in this field, the automated design and analysis of structures in steel construction is common and commercial software for structural design can be obtained from several vendors, e.g. Dlubal and SCIA. These programs implement the relevant European standards for steel construction such as DIN EN 1090 and DIN EN 1093 as well as further norms such as for timber construction. The optimization of the strut profiles, the static and dynamic strength verification and the stability analysis of steel structures are state of the art. The documentation of all calculation results and geometry data is included as well.
Software like LimitState:Form, whose capabilities are described by He et al. (Reference He, Gilbert, Johnson and Pritchard2018), was developed for mechanical engineering and supports topology optimization of trusses. However, it is not possible to use a modular system as a database, which means that a seamless dimensioning of hybrid trusses is not possible. Furthermore, it is not possible to design, optimize and calculate hybrid trusses from CFRP hollow sections and aluminum connectors. The calculation of bonded joints is also not included.
These programs mainly implement standards in the field of civil engineering and are primarily used for the planning of load-bearing steel structures which are not designed as FRP lightweight structures. The key elements for the design of hybrid frameworks, such as CFRP analysis, are not available, and, therefore, the design method developed in this research project cannot be based on these civil engineering programs.
Therefore, it is necessary to develop a new method which is CAE-based and supports the design of FRP trusses.
3 A novel CAE-based design method
This section describes the concept of a new CAE-based design method for hybrid trusses. The hybrid trusses are to be composed of an expandable modular system, which is described in its basic version. The design methods and the planned CAE tool supporting the methods are then described by their steps topology optimization, structure analysis, structure synthesis and model generation. The combination of different methods is the innovation and research goal.
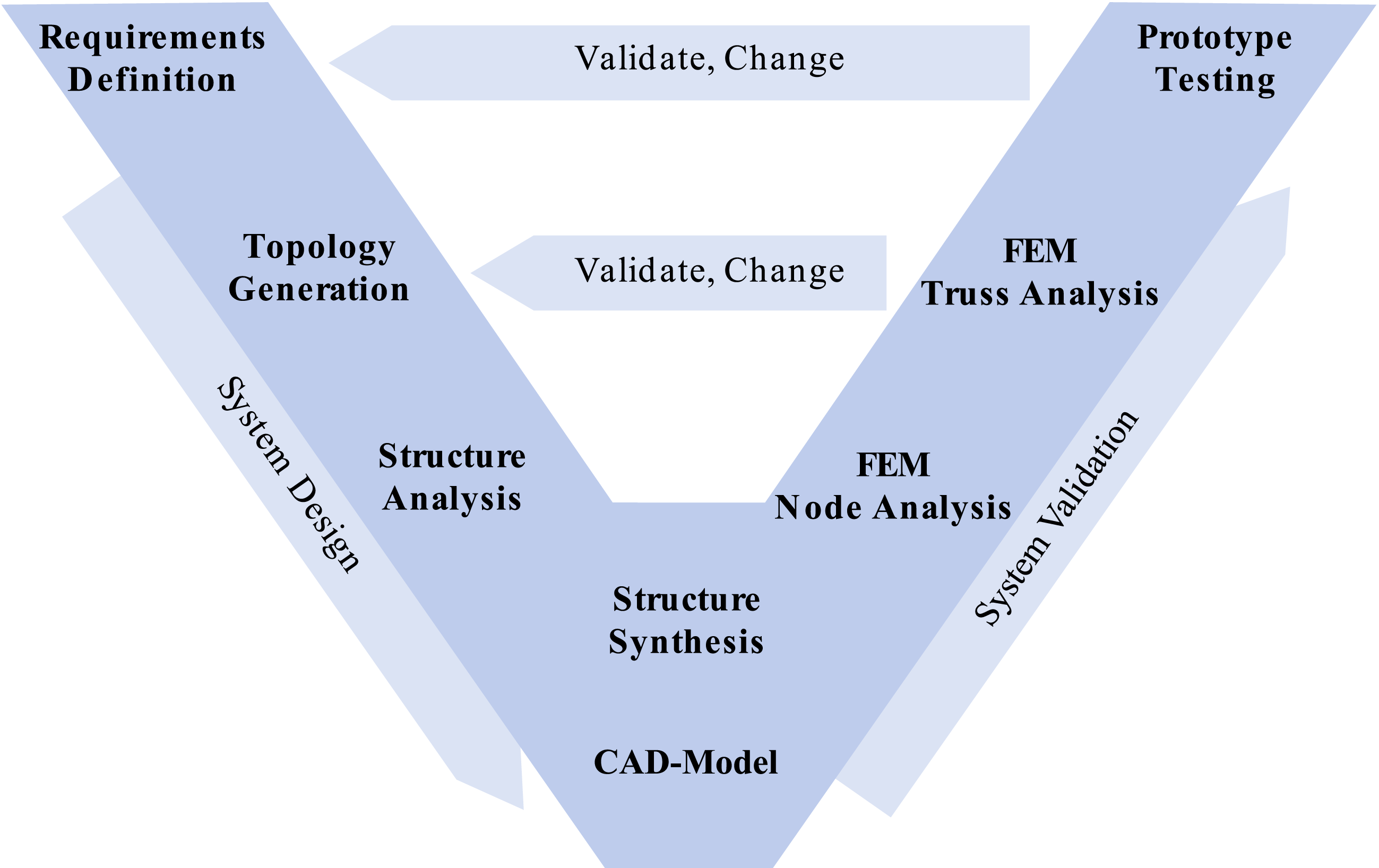
The method corresponds with the V-model procedure according to VDI 2206 and is shown in Figure 11. In the left descending branch, the requirements are specified and the system design is further detailed with each step, and on the right ascending branch, the model is validated. If one step of the validation determines that the requirements are not met, the system returns to the corresponding point in the descending branch.
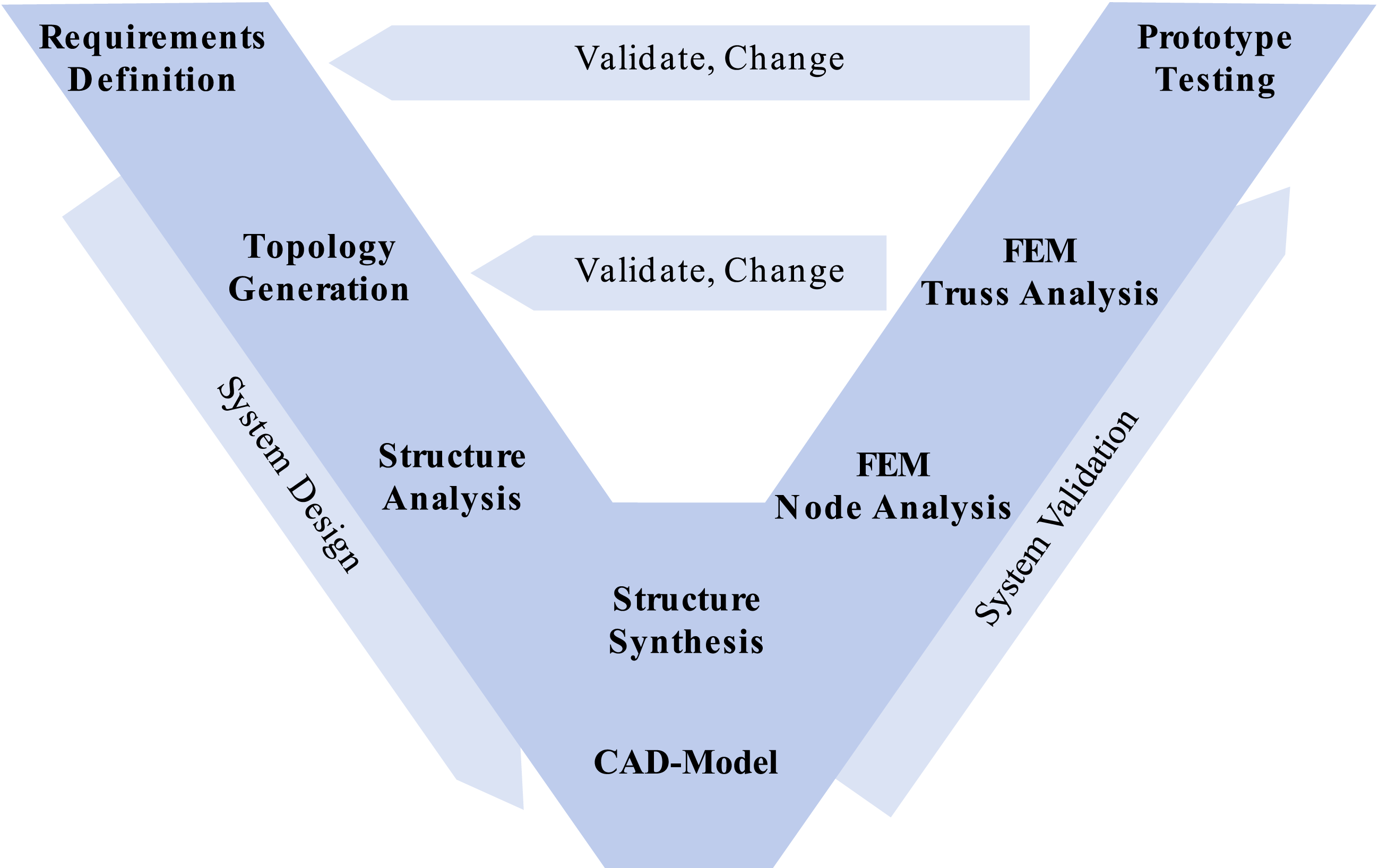
Figure 11. The method is based on the V-model. The steps are starting from the requirement definition and ending with the prototype test.
The definition of the requirements include all that are needed for the next step as well as the global requirements such as overall stiffness and strength. The steps from topology generation to FEM simulation are described in detail in the following sections.
3.1 Modular truss system components
In order to develop the method, basic components are required which serve as reference elements. The described components are not to be regarded as the only possible realization of the trusses but as the basis for the development of an extensible system.
The hardware components of the modular system in its simplest form are CFRP-pipe struts, welded nodes made of semi-finished aluminum products and sleeves, which guarantee the assembly of any spatial truss. CFRP pipes have been selected because of their higher specific stiffness and strength compared to GFRP or other commonly used FRPs and because the range of possible stiffness and strength is particularly large due to the various CFRP types. Aluminum as node material is corrosion resistant and has a low density, and the CFRP joining technique has been well researched. Furthermore, it is available in many different shapes, sizes and alloys as a semi-finished product.
The components of the modular system are available in discrete steps. The diameter range is
![]() $18~\text{mm}\leqslant D\leqslant 60~\text{mm}$
and in steps of
$18~\text{mm}\leqslant D\leqslant 60~\text{mm}$
and in steps of
![]() $\unicode[STIX]{x0394}D=2~\text{mm}$
. This allows to cover a wide range of applications and, at the same time, to achieve standardization. The CFRP hollow profile struts can be produced using the winding process. The winding process has the advantage that the ply layup of the laminate can be designed as freely as possible. This allows us to design struts for tension, compression, bending, torsion and combined loads. The wall thickness is in the range
$\unicode[STIX]{x0394}D=2~\text{mm}$
. This allows to cover a wide range of applications and, at the same time, to achieve standardization. The CFRP hollow profile struts can be produced using the winding process. The winding process has the advantage that the ply layup of the laminate can be designed as freely as possible. This allows us to design struts for tension, compression, bending, torsion and combined loads. The wall thickness is in the range
![]() $1~\text{mm}\leqslant s\leqslant 4~\text{mm}$
. The inner diameter of wound strut is precise and therefore needs no further cutting machining before bonding.
$1~\text{mm}\leqslant s\leqslant 4~\text{mm}$
. The inner diameter of wound strut is precise and therefore needs no further cutting machining before bonding.
The nodes are welded from round aluminum hollow sections. This allows struts to be connected to the nodes from almost any connection angle. The struts in trusses are usually arranged in triangles. As a result, the nodes and struts cannot be mounted directly in the case of overlapping bonding. This problem can be solved by additional sleeves which are pushed to their position between the strut and the node after the strut has been placed in the truss.

Figure 12. Demonstration of an example node with three connections. The node is made of aluminum, the struts of CFRP. The sleeve to be seen in the cut-out is the connection between the node and the strut.
The joint can be produced by adhesive injection. The adhesive is injected through a hole until it flows out through another hole on the opposite side. Adhesive injection makes it possible to fill the bonding gap completely with adhesive, containing virtually no cavities. Furthermore, the joint is protected from dirt until the adhesive is applied and all joints in the truss can be created in a single work step. A further reinforcement of the bond with blind rivets can increase the load-bearing capacity of the joint by up to 20% as mentioned by Pramanik et al. (Reference Pramanik, Basak, Dong, Sarker, Uddin, Littlefair, Dixit and Chattopadhyaya2017).
3.2 Topology generation
The start of the CAE-based design process is the generation of the topology. The creation of a manufacturable and efficient topology is an important step in the design of a truss. Manufacturable in this case means in particular as few nodes and struts as possible, large angles between the struts and not too short struts. Although, the structural mass must remain as low as possible. The specific stiffness and strength, i.e. the stiffness related to the mass, should be as high as possible. In order to achieve these targets, the use of software is essential. The software LimitState:Form as described earlier is therefore highly suitable for the topology generation and optimization. An example of topology optimization is shown in Figure 14 and depicts how starting from the installation space the discretization is performed and shows the resulting structure after optimization. The used tool for topology optimization, LimitState:Form, generates the skeleton of the truss after defining the design space, the boundary conditions and generation of one or more load cases. After the topology optimization, it is possible as an intermediate step of the optimization to neglect or combine struts or nodes as well as deleting struts whose load is less than a limit value in relation to the remaining members. The procedure makes it possible to generate the truss skeleton very efficiently with tool support.
For some development tasks, it is required that the structure can be defined manually without using a topology optimizer. For example, if an existing steel truss is to be redesigned into a hybrid truss or if the structure is defined by esthetic or ergonomic specifications. The design method, which is subject of this paper, also considers that the truss skeleton is generated directly by a user without using the topology optimizer. For the next step, only the coordinates of the nodes and the existing links are necessary.
3.3 Structure analysis
For the next steps, a MATLAB-based implementation is used. The truss skeleton is read and a corresponding object is created for each component. An overview of the class structure can be seen in Figure 13. A truss object consists of strut, node, joint and coordinate objects. To make the software modular and extensible, a separate subclass is defined for each component which is to be represented.
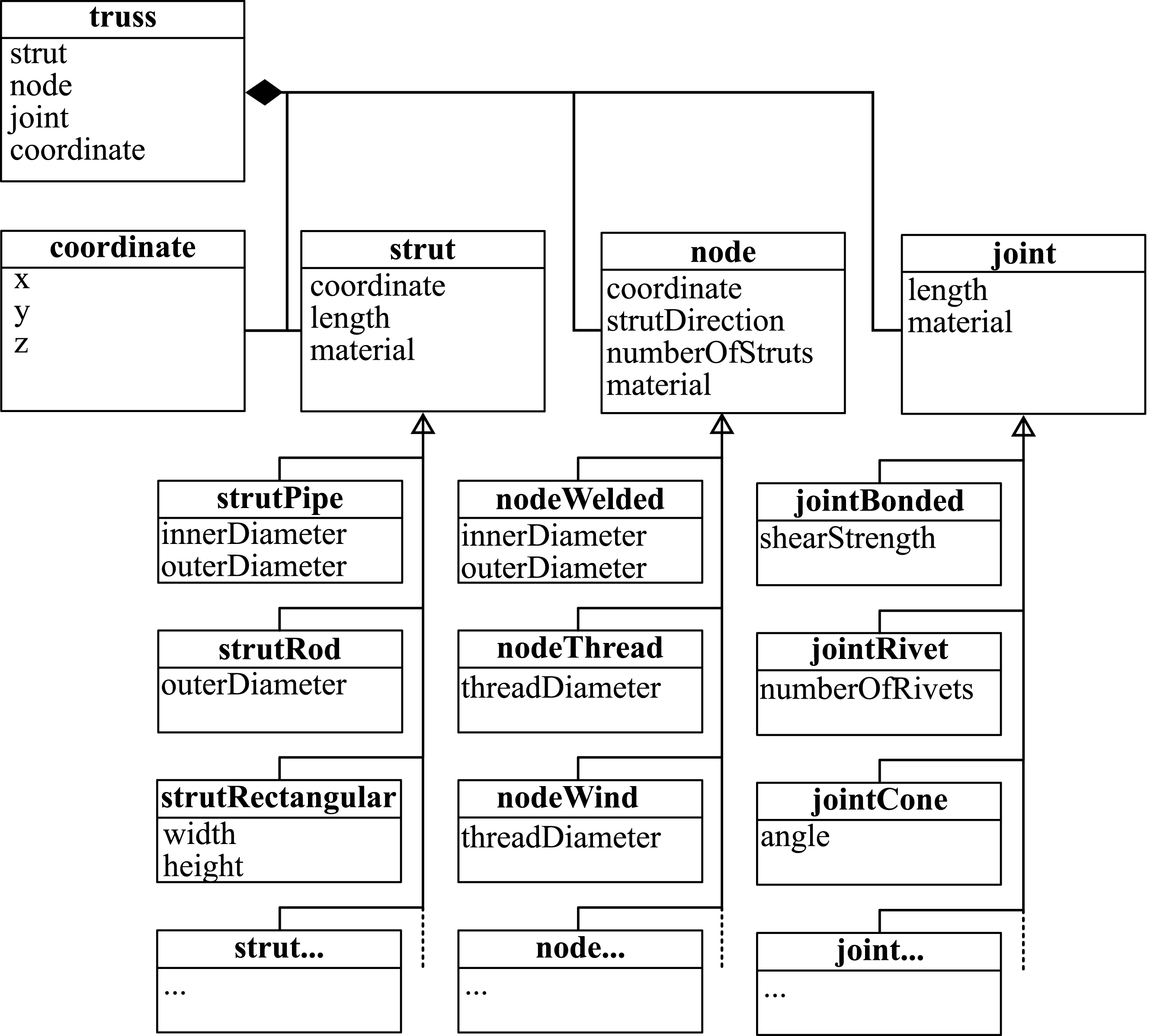
Figure 13. Diagram of the potential classes for the truss structure model. The class truss defines the main class and stores all data. The classes node*, strut* and joint* inherit from the respective superclasses in order to make the system modular and expandable. For example, to add another type of node, a corresponding subclass is defined.
The first step is to assign the smallest cross-section from the modular system to the struts and then generate an APDL (ANSYS parametric design language) script for Ansys Mechanical, which contains and solves an FEM beam model of the entire truss. The calculated stresses of the struts and displacements of the nodes are used for dimensioning the struts and nodes. For this purpose, the strength and structural stability of the struts as well as the strength of the joints and nodes are taken into account with analytical and empirical equations. The sustainable stresses of the struts of the modular system are determined in advance for each size. To the struts and nodes are assigned matching profiles from the modular system by comparing the existing load with the sustainable load. Since the stresses of the struts change as a result of the change of the profiles of the bending rigidly calculated truss, this step is repeated until no more changes to the strut profiles are required. The determined truss generally consists of several different profiles and is the lightest truss that can be realized with the modular system since a reduction of the cross-sections would lead to failure of a strut, joint or node.
3.4 Structure synthesis
The mass of the truss should be minimal, and, at the same time, further constraints must be fulfilled. The absolute stiffness of the truss should exceed a certain value, and a fixed upper limit of different profile dimensions of the struts is set as a second condition to reduce the complexity of the truss. The number of variables that can be optimized corresponds to the number of struts
![]() $N$
and can be very high. In order to find an optimum efficiently, a further constraint is introduced. The ratio of the axial struts stiffness to each other should correspond to the ratio of the axial struts load. This requirement can only be fulfilled approximately in a discrete system. By considering the additional condition, the struts have approximately the same stress level and the number of degrees of freedom is reduced from
$N$
and can be very high. In order to find an optimum efficiently, a further constraint is introduced. The ratio of the axial struts stiffness to each other should correspond to the ratio of the axial struts load. This requirement can only be fulfilled approximately in a discrete system. By considering the additional condition, the struts have approximately the same stress level and the number of degrees of freedom is reduced from
![]() $N$
to one. The stiffness of the most loaded strut makes sense as the remaining degree of freedom. The formulation used is as follows:
$N$
to one. The stiffness of the most loaded strut makes sense as the remaining degree of freedom. The formulation used is as follows:
with
![]() $m$
being the mass,
$m$
being the mass,
![]() $l$
being the vector of the strut lengths,
$l$
being the vector of the strut lengths,
![]() $A$
being the vector of the cross-sectional areas and
$A$
being the vector of the cross-sectional areas and
![]() $\unicode[STIX]{x1D70C}$
being the vector of the densities.
$\unicode[STIX]{x1D70C}$
being the vector of the densities.
![]() $\unicode[STIX]{x1D6FF}_{\text{i}}$
is the displacement,
$\unicode[STIX]{x1D6FF}_{\text{i}}$
is the displacement,
![]() $F_{\text{i}}$
is the load at node
$F_{\text{i}}$
is the load at node
![]() $i$
and
$i$
and
![]() $c$
is the specified stiffness.
$c$
is the specified stiffness.
![]() $E$
is the vector of the modulus of elasticity of the struts in the axial direction.
$E$
is the vector of the modulus of elasticity of the struts in the axial direction.
![]() $N_{\text{d}}$
is the number of different profiles and
$N_{\text{d}}$
is the number of different profiles and
![]() $N_{\text{d lim}}$
is the corresponding limit. As the stiffness of the struts increases, so does the overall stiffness and mass of the truss; therefore, Equation (6) is a monotonously increasing target function.
$N_{\text{d lim}}$
is the corresponding limit. As the stiffness of the struts increases, so does the overall stiffness and mass of the truss; therefore, Equation (6) is a monotonously increasing target function.
In order to find the solution with a high efficiency, the bisection method is used. The bisection method is very efficient for large intervals but gets more inefficient with each step because of the reduction of the interval. Especially with intervals smaller than one, an improvement of the solution requires many iteration steps. In the discrete modular system covered in this paper, the smallest possible interval is already specified by the modular system and is therefore within the efficient range of the bisection method. The usable interval of the strut profiles for optimization reaches from the minimum profile limited by the strength to the largest profile available in the modular system. Since the objective function is monotonously increasing, the constraints are used for each iteration step to determine which interval to use for the next step. The interval is reduced by half until all conditions are met and no further halving of the interval is possible. The number of required optimization steps
![]() $k$
is independent of the size of the truss to be optimized but depends on the number of existing profiles
$k$
is independent of the size of the truss to be optimized but depends on the number of existing profiles
![]() $N_{\text{p}}$
in the modular system. The number of optimization steps is proportional to the logarithm of the number of existing profiles
$N_{\text{p}}$
in the modular system. The number of optimization steps is proportional to the logarithm of the number of existing profiles
![]() $k\sim \log N_{\text{p}}$
and thus increases underproportionally. For example, a modular system consisting of 100 different struts requires only seven iteration steps.
$k\sim \log N_{\text{p}}$
and thus increases underproportionally. For example, a modular system consisting of 100 different struts requires only seven iteration steps.
With the formulation of the optimization problem by Equations (6)–(9), the bisection method reaches the global minimum.
The method described in this paper is implemented in MATLAB and uses Ansys Mechanical as a solver. The structure found from the optimization contains all parameters for the next step.
3.5 CAD model generation and design verification
Design tables in Catia V5 are to be used for the automized design of the identified structure. There are generic node models for each node type and the struts. The geometry parameters as well as the coordinates and orientation are specified in the design table. A model is created for each element of the truss and merged into an overall model.
For an additional FEM simulation, a surface model of the truss or a node can also be generated. The possibility to create a partial model of the truss is especially interesting because the highest loaded node is already known by the previous analysis and can be checked representative for the rest of the truss. The modeling of a submodel significantly reduces the computation time and at the same time enables a detailed investigation of the structure and a high-resolution result.
The FEM simulation and analysis of a partial model enables the efficient validation of the nodes. The node and a part of each strut are modeled as a surface model and meshed with shell elements. The struts are simulated with an anisotropic material model and the nodes with an isotropic material model. The verification of the stresses in the adhesive layers can also be done with the partial model.
A shell model of the entire truss can be used to validate the global requirements such as overall stiffness. In a final step, the determined structure can be finally verified by testing a prototype.
4 Case study: beam-shaped truss
In this chapter, a case study with a beam-shaped truss is done showing the steps from topology to parameter optimization. The area of application of this type of beam is, for example, a traverse for mobile stages. Lightweight components allow a quick and easy assembly and disassembly which is usually done by hand and thus spares the workers and also allows to build larger stages. Another possible application is the cantilever of manually movable mini cranes as used on construction sites to lift heavy bricks to their position or in workshops to place heavy workpieces to machines. The lightweight arm reduces the mass to be moved by the worker and thus unburdens him. The set boundary conditions of the topology optimization are shown in Figure 14 and define a design space of
![]() $5~\text{m}\times 0.5~\text{m}\times 0.5~\text{m}$
, a fixed constraint at the left edge and three different load cases. Each of the three load cases applies a force in one direction in space to the truss of
$5~\text{m}\times 0.5~\text{m}\times 0.5~\text{m}$
, a fixed constraint at the left edge and three different load cases. Each of the three load cases applies a force in one direction in space to the truss of
![]() $F_{x,y,z}=10\,000~\text{N}$
. After the discretization of the design space, the topology and shape optimization leads to the result shown in Figure 14 at the bottom, which is the basis for the subsequent discrete parameter optimization.
$F_{x,y,z}=10\,000~\text{N}$
. After the discretization of the design space, the topology and shape optimization leads to the result shown in Figure 14 at the bottom, which is the basis for the subsequent discrete parameter optimization.

Figure 14. Progression of topology optimization. First, the design space is defined, then the design space is discretized and meshed. The optimal structure is then found using an optimization method.
The truss resulting from the topology optimization consists of 64 struts and 30 nodes and is of symmetrical and regular shape. A maximum of eight struts are joined in one node and the smallest angle between the struts is around
![]() $42^{\circ }$
. Therefore, the manufacturability is so far ensured and the next step of the method can be done.
$42^{\circ }$
. Therefore, the manufacturability is so far ensured and the next step of the method can be done.
For the subsequent parameter optimization, a force of
![]() $F=10\,000~\text{N}$
acting only in the
$F=10\,000~\text{N}$
acting only in the
![]() $z$
-direction is used in order to simplify the presentation of the method. The truss and the boundary conditions are shown in Figure 15. As a further boundary condition, the total stiffness of the truss at the tip is set to
$z$
-direction is used in order to simplify the presentation of the method. The truss and the boundary conditions are shown in Figure 15. As a further boundary condition, the total stiffness of the truss at the tip is set to
![]() $c_{0}\geqslant 200~\text{N}~\text{mm}^{-1}$
. The size of the struts and the deformation of the truss can be taken from Figure 16. The deformation is scaled by a factor of 10.
$c_{0}\geqslant 200~\text{N}~\text{mm}^{-1}$
. The size of the struts and the deformation of the truss can be taken from Figure 16. The deformation is scaled by a factor of 10.
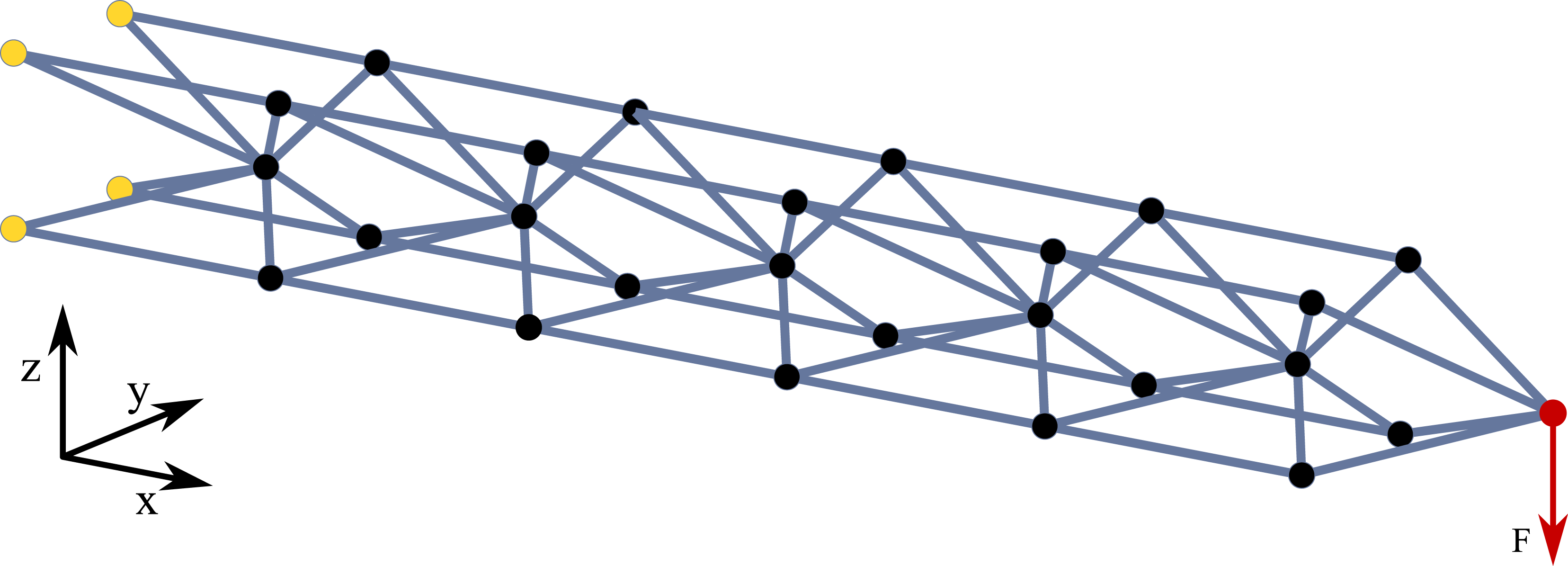
Figure 15. Illustration of the truss used for the case study. The beam-shaped beam consists of 64 struts and 30 nodes. The truss is constrained at the yellow marked nodes and all three translations are locked. The force
![]() $F$
is applied to the red node and acts in negative
$F$
is applied to the red node and acts in negative
![]() $z$
-direction.
$z$
-direction.

Figure 16. Illustration of the truss used under load and deformation. The resulting deformations are scaled by a factor of 10.
The dimensions of the struts in the modular system are as defined in the previous chapter and have a uniform ply buildup of
![]() $[0_{8}/\pm 45/90]$
with a percentage of individual plies of 80%, 10% and 10%. The used material parameters of the CFRP are listed in Table 1. The engineering constants modulus of elasticity and shear modulus of the laminate are determined by the classical laminate theory, taking into account the transverse contraction impediment. The modulus of elasticity in the direction of the pipe axis becomes
$[0_{8}/\pm 45/90]$
with a percentage of individual plies of 80%, 10% and 10%. The used material parameters of the CFRP are listed in Table 1. The engineering constants modulus of elasticity and shear modulus of the laminate are determined by the classical laminate theory, taking into account the transverse contraction impediment. The modulus of elasticity in the direction of the pipe axis becomes
![]() $E_{x}=152~\text{GPa}$
the shear modulus
$E_{x}=152~\text{GPa}$
the shear modulus
![]() $G_{xy}=11.1~\text{GPa}$
.
$G_{xy}=11.1~\text{GPa}$
.
Table 1. Material parameters of CFRP

The truss is modeled as an FEM beam model in Ansys APDL with BEAM188 elements. The quadratic two-node element BEAM188 is based on Timoshenko’s beam theory and takes shear deformation into account. With a number of 10 elements per strut, the displacements are converging for the model. The interval to be optimized is defined by the struts listed in the modular system, which are sorted according to the axial stiffness
![]() $E_{x}A$
and span the parameter space considering Equation (8).
$E_{x}A$
and span the parameter space considering Equation (8).

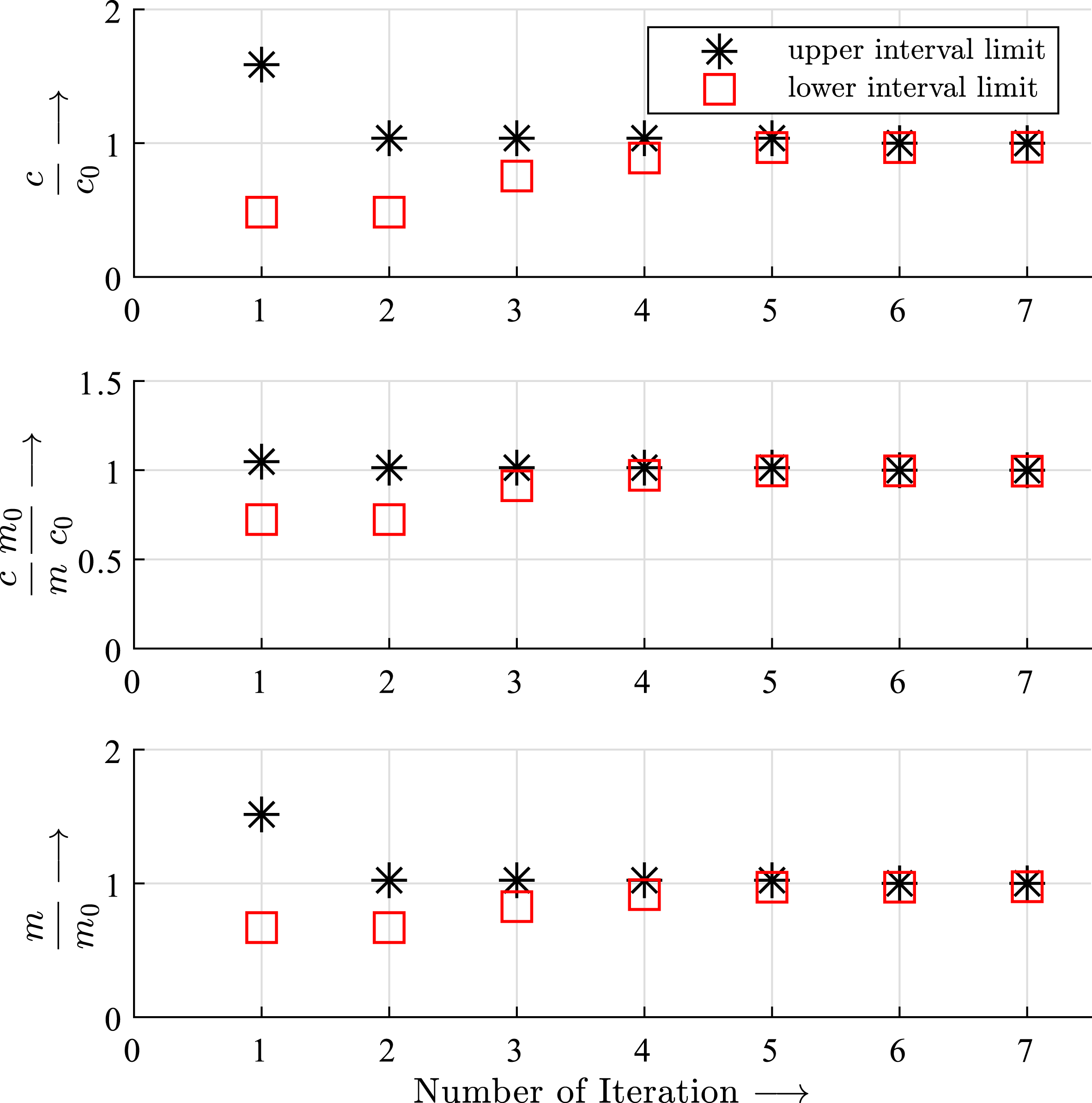
Figure 17. Progress of the optimization with the bisection method. The values are normalized with the resulting values of the mass
![]() $m_{0}$
and the stiffness
$m_{0}$
and the stiffness
![]() $c_{0}$
of the optimization. It turns out that the optimization converges and reaches the target value after seven steps. The specific stiffness
$c_{0}$
of the optimization. It turns out that the optimization converges and reaches the target value after seven steps. The specific stiffness
![]() $c/m$
is approximately constant.
$c/m$
is approximately constant.
The lower limit of the interval is additionally defined by Equations (5) and (4) and is the starting point of the optimization. For the upper limit of the interval, Equation (8) is ignored and all truss struts get the stiffest strut of the modular system. The truss with the highest overall stiffness is thus generated, which can be done with the modular system.
The optimization is finished as soon as Equations (6) and (7) are fulfilled and no more halving of the interval is possible. The progress of the optimization is shown in Figure 17 and demonstrates that after seven iterations, the optimum is found.
The normalized diagram clearly shows that with each iteration and halving of the interval, the stiffness interval of the truss
![]() $c$
is also approximately halved and finally reaches the target value
$c$
is also approximately halved and finally reaches the target value
![]() $c_{0}$
. The stiffness in relation to the mass serves as an indicator of the efficiency of the calculated solution and is approximately constant or increasing during the optimization. The mass of the truss is minimal by taking into account the constraint of Equation (7).
$c_{0}$
. The stiffness in relation to the mass serves as an indicator of the efficiency of the calculated solution and is approximately constant or increasing during the optimization. The mass of the truss is minimal by taking into account the constraint of Equation (7).
The simulated deflection of the tip of the truss is
![]() $\unicode[STIX]{x1D6FF}=49.9~\text{mm}$
which gives a stiffness of
$\unicode[STIX]{x1D6FF}=49.9~\text{mm}$
which gives a stiffness of
![]() $c=200.4~\text{N}~\text{mm}^{-1}$
. Thus, the required stiffness is achieved and very well met. The mass of the optimized truss is
$c=200.4~\text{N}~\text{mm}^{-1}$
. Thus, the required stiffness is achieved and very well met. The mass of the optimized truss is
![]() $m_{\text{tot}}=10.2~\text{kg}$
where the mass of the struts is
$m_{\text{tot}}=10.2~\text{kg}$
where the mass of the struts is
![]() $m_{\text{struts}}=8.3~\text{kg}$
. The smallest struts found have an inner diameter of
$m_{\text{struts}}=8.3~\text{kg}$
. The smallest struts found have an inner diameter of
![]() $D_{i}=18~\text{mm}$
with a wall thickness of
$D_{i}=18~\text{mm}$
with a wall thickness of
![]() $s=1~\text{mm}$
and the largest struts found have an inner diameter of
$s=1~\text{mm}$
and the largest struts found have an inner diameter of
![]() $D_{i}=34~\text{mm}$
with a wall thickness of
$D_{i}=34~\text{mm}$
with a wall thickness of
![]() $s=3~\text{mm}$
. It can be summarized as the case study shows that the presented method is capable of designing and optimizing hybrid trusses.
$s=3~\text{mm}$
. It can be summarized as the case study shows that the presented method is capable of designing and optimizing hybrid trusses.
5 Conclusion
Currently, there are no methods available for the entire design process of CFRP-hybrid trusses based on a modular system. By the development of such a design method, hybrid trusses can be applied in a wide range of applications and can significantly improve the properties such as mass and stiffness of structures. In order to enable a general usage of the method in practice, CAE-tool support must be implemented from topology optimization all the way to CAD model generation. This enables considerable savings in development time and costs and also reduces the risk of development-related errors compared to conventional design methods. The topology optimization must deliver manufacturable structures as a result, even if the theoretical optimum of the mass is not achieved. As a result, manufacturing and material costs are reduced because the components are designed more suitable for production.
The design process needs to consider additional constraints like overall stiffness of the truss. The optimization with bisection method can be used to efficiently select the appropriate struts from a modular system. The method continuously converges toward the result. The method is effective, highly efficient and enables the optimization with relatively low use of computing power.
The bisection method very efficiently finds the global minimum, but Equation (8) limits the solution space. Therefore, the bisection method is very useful as a global optimizer. To improve the solution further, it is possible to neglect Equation (8) and to do a second optimization with an additional optimization method like the genetic algorithm. The solution found by the bisection method can then be used as part of the initial population as a starting point to improve the convergence of the algorithm.
The method published in this paper for CAD-based design of hybrid lightweight trusses represents an important step to take the advantages of these structures to a broader area of application. The goal is to implement a CAE tool which enables an engineer without specific knowledge about fiber composites to design such trusses reliably and optimally. This makes it possible to design cost-effective lightweight trusses.
The methods and their single steps will be confirmed by experiments, and to enable the design of any hybrid truss structures made of CFRP and aluminum, the method will be further detailed. In conclusion, this work is the basis for further research and development and it is indeed possible to create an automated design methodology as an extension for CAD programs.
Acknowledgments
The authors thankfully acknowledge the funding by the Federal Ministry for Economic Affairs and Energy (BMWi) on the basis of a resolution of the German Bundestag under grant number ZF4222610PO8.