Three Patterns of Inheritance of Quantitative Dermatoglyphic Traits: Kosovo Albanian Twin Study

Abstract

Dermatoglyphs are epidermal ridge configurations on the fingers, palms and soles that are formed during fetal development, and therefore only the intrauterine environment can have any influence on their formation. This study aims at investigating the genetic and environmental contribution in determining quantitative dermatoglyphic traits in 32 monozygotic (MZ) and 35 dizygotic (DZ) same-sex twins from the Albanian population of Kosovo. All genetic analyses were run in the statistical program Mx. After assumptions testing, based on the pattern of MZ–DZ correlations, univariate models were fitted to the data in order to estimate additive genetic (A), common (C) and individual (E) environmental influences for all variables. The exception was the atd-angle for which a model with nonadditive genetic (D) influences was tested, since DZ correlations were less than half of MZ correlations. Goodness of fit of the full ACE or ADE model was compared to the saturated model. The fit of nested models (AE, CE, DE or E) was compared to the full models (ACE or ADE). Our results indicate that additive genetic component strongly contributes to individual differences in finger ridge counts (49−81%), and weakly (0−50%) on the formation of the palmar ridge counts between the palmar triradii a, b, c, and d. The specific pattern found for the atd-angle implies the impact of a nonadditive genetic component, possibly the effect of a major gene. Further, more powered studies are needed to confirm this pattern, especially for resolving the issue of the huge difference in MZ and DZ twin similarity for the atd-angle palmar trait.

Dermatoglyphs are the epidermal ridge configurations on the fingers, palms and soles that develop between the 7th and 21st weeks of gestation (Cummins & Midlo, 1961). Particularities of fingerprints have been noticed ever since ancient times. The use of friction ridge skin as a signature in China, Japan, India and possibly in other regions prior to European discovery is well documented (Maslarski, 2015). The Chinese, for example, used their fingerprints instead of a stamp when validating documents. The first European dermatoglyphic researches in people and primates were conducted by Galton (1875), Faulds (1905) and Herschel (1916). Finger and palm prints (dermatoglyphs) have been used in various disciplines: criminology, medical genetics, anthropology, and population and quantitative genetics.

It is interesting to note that Francis Galton (1822−1911) — the founding father of quantitative genetics methodology — was also the founder of dactyloscopy. He identified a common pattern in fingerprints and devised a classification system that has survived to this day. Galton estimated the probability of two persons having the same fingerprint and studied the heritability and racial differences in fingerprints. He also recognized the potential of studying twins — as a natural experimental situation to disentangle genetic and environmental influences — and envisaged testing whether twins who were similar at birth diverged in dissimilar environments, and whether twins dissimilar at birth converged when growing up in similar environments.

The classical twin design is built on the premise that differences in similarity between monozygotic (MZ) and dizygotic (DZ) twins can be used to parse phenotypic trait variance into genetic and environmental components. The decomposition relies on important assumptions: MZ twins share 100%, while DZ twins share on average 50% of their inherited genome; twins within MZ and DZ pairs share the raising environment to the same extent (equal environment assumption), and there is no correlation or interaction between genes and environment (Falconer & Mackay, 1998; Neale & Maes, 2004). The observed intrapair correlations among genetically identical MZ twins and fraternal DZ twins are contrasted in order to partition the phenotypic variance into additive genetic variance (A), dominance genetic variance (D), shared or common (C) and nonshared or individual environmental variance (E) (Falconer & Mackay, 1998; Neale & Maes, 2004). The additive (A) genetic variance is referred to as narrow-sense heritability (h²), while the sum of additive and dominance genetic proportions of variance is referred to as broad-sense heritability (H²).

Genetic influences are implied if the correlation between MZ twin pairs is higher than the correlation between DZ twin pairs. An influence of the common environment — that is, shared among family members — is implied when the DZ twin pair correlation is higher than half of the correlation between MZ twin pairs. Also, if MZ correlations are more than twice the DZ correlations, nonadditive genetic effects are expected. Namely, in the classical twin design, the nonadditive genetic influences (D) and common family environmental influences (C) are confounded and cannot be estimated simultaneously (Benito et al., 2016; Chen et al., 2015; Willems et al., 2019). On the other hand, the unique environmental factors are person-specific and are not shared between twins. Identical twin correlations’ deviation from 1 (100%) provides a direct estimate of the individual environmental influences, since identical twins share both their entire genetic make-up as well as part of the environment (the common environment; Falconer & Mackay, 1998; Willems et al., 2019).

As in any family-based modeling, classic twin studies rely on previously mentioned assumptions, the most debated being that MZ and DZ twins share their raising environment to the same extent (Chen et al., 2015). Since quantitative dermatoglyphic traits bear an important advantage of lifelong stability (from the very moment of a person’s birth), the possible violation of this potentially most problematic assumption is minimal, and consequently, the obtained values of estimated phenotypic components are more reliable than what could be expected for the majority of other investigated human traits.

Kosovo is located on the Balkan Peninsula between the mountain ranges of the Dinaric Alps of south-eastern Europe, and its majority inhabitants are Kosovar Albanians (92.9%). It occupies an area of 10,887 km², and according to the last census data (2011) has a population of 1.8 million. The Albanians are an autochthonous population of the south-western Balkan Peninsula who speak a language very distinct from those of the surrounding populations. The Albanian population perceives itself as direct descendants of an Illyrian tribe called Dardanet, who were the first known inhabitants of this region since classical antiquity (Mirdita, 1972, 1995; Stipcevic, 1980, 1996). The size and geographical characteristics of Kosovo is the scene supporting genetic isolation of its population and maintaining both the long-lasting ethnical homogeneity as well as the similarities of their living conditions. The high level of genetic and environmental homogeneity makes this population advantageous for performing twin studies (e.g., Temaj et al., 2012) aimed at decomposing the environmental and genetic sources of human variation.

In the present study, we used a set of quantitative dermatoglyphic traits of a sample of Albanian twins from Kosovo to estimate the heritability and other components of variance to disentangle the genetic and environmental influences acting on formation of these traits. Previous studies have indicated that the heritability of dermatoglyphic traits is high (Machado et al., 2010; Reed et al., 2006).

Materials and Methods

Dermatoglyphic prints were collected and analyzed using the Cummins and Midlo (1961) methods. Fingerprinting was done by covering the hand palmar surface with topographic ink, and by using a glass plate and a roller. A rotary tool was used to cover palms and fingers, always starting from the first finger on the right hand and finishing with the fifth finger on the left hand. Palmar surface was greased with topographic ink and the fingerprints were left on a white sheet of paper, placed on a convex cylindrical surface. This method provides an accurate print of the palmar surface, including the central part of the palm. After that, the establishment of dermatoglyphic patterns was done by means of a binocular magnifying glass.

The quantitative dermatoglyphic hand and palm originally measured properties included 18 measures: the number of papillary ridges on the apical pads of all 10 fingers, counting the ridges intercepted by a line joining the delta and the core (finger ridge count; FRC), the ridge counts between the palmar triradii a, b, c and d (a-b RC, b-c RC and c-d RC) on both hands, while the atd-angle was measured in degrees on the right and left palm (Figure 1; graphical presentation from: Cvjetičanin et al., 2021). In this study, we present the results for nine quantitative dermatoglyphic traits, since all analyses are performed on the ‘average hand’, where for each person their measures from the left and right hands are summed and divided by 2.

Fig. 1. The investigated dermatoglyphic traits. Left: the area where the number of papillary ridges on the apical pads of fingers are counted (finger ridge count; FRC). Middle: the area where the palmar triradii a, b, c and d are positioned and ridge counts between them are counted (a-b RC, b-c RC and c-d RC); the position of t-triradius and the presentation of the a-t-d relation (atd-angle, measured in degrees). Right: the position of the finger and palmar quantitative dermatoglyphic traits on the hand. Reprint used with permission of authors (Cvjetičanin et al., 2021).

The sample consisted of prints of 67 same-sex twin pairs: 17 MZ male pairs, 15 MZ female pairs, 26 DZ male pairs and 9 DZ female pairs, all originating from the Albanian population living in Kosovo. Since sex-specific twin samples were rather small (especially the DZ female sample), the components of variances were estimated on the combined male and female samples. Those two interventions — using average hand quantitative dermatoglyphic traits, as well as the calculation of the variance components using the sex combined MZ and DZ twin data sets — are both employed in order to obtain as reliable results as possible with these rather small sample sizes.

All genetic analyses were run in the statistical program Mx (Neale et al., 2006). First, a saturated model was run to test the assumptions and check for homogeneity of means and variances as well as to obtain MZ–DZ correlations for each variable. After assumptions testing, based on the pattern of MZ–DZ correlations, univariate models were fitted to the data in order to estimate additive genetic (A), common family (C) and individual (E) environmental influences for all variables except atd-angle for which a model with nonadditive genetic (D) influences was tested instead of common environmental influences, since DZ correlations were less than half of MZ correlations, indicating the presence of nonadditive genetic influences. Goodness of fit of the full ACE or ADE model was compared to the saturated model. After that, nested models were run (AE, CE, DE or E) and their fit was compared to the full models (ACE or ADE).

Results

Results of the genetic analyses are presented in Table 1. We report values of the saturated model and the full model due to our small sample size, since applying the principle of parsimony with large effects of sampling can lead to adoption of the false model (Sullivan & Eaves, 2002). As can be seen, all intraclass correlations for FRC measures indicate that there is a significant influence of genetic factors, since all MZ correlations are higher than DZ correlations. This is confirmed with univariate genetic analyses. Ridge counts on five fingers have high heritability estimates (from 49% to 81%), an important individual environment component (from 19% to 22%), and the lowest impact of a common family environment (from 0% to 29%). All confidence intervals for common family environment are very wide and include zero, as could be expected with the small sample size. This finding indicates that the ridge counts on the fingers are determined by genetics and influenced by some random stochastic events that are not related to the intrauterine environment shared by the other twin.

Table 1. Fit of the saturated and full models, intraclass correlations and parameter estimates for different dermatoglyphic traits

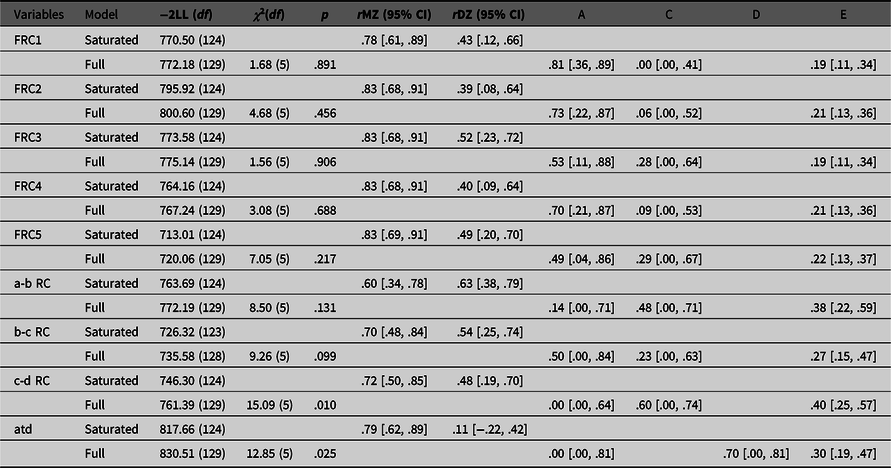
Note: FRC1, first finger ridge count; FRC2, second finger ridge count; FRC3, third finger ridge count; FRC4, fourth finger ridge count; FRC5, fifth finger ridge count; a-b RC, ridge count between palmar triradii a and b; b-c RC, ridge count between palmar triradii b and c; c-d RC, ridge count between palmar triradii c and d; atd, atd-angle in degrees; –2LL, minus twice the log-likelihood of the data; df, degrees of freedom; χ²(df), -2LL (and df) difference between saturated and full model; p, p value; rMZ, intraclass correlations for monozygotic twins; rDZ, intraclass correlations for dizygotic twins; A, additive genetic variance; D, nonadditive genetic variance; C, common family environmental variance; E, individual environmental variance; 95% confidence intervals shown in square brackets.

A more complicated pattern is seen in palmar quantitative dermatoglyphic traits. In contrast to the fingers, MZ–DZ intraclass correlations for the ridge counts between the palmar triradius a, b, c and d (a-b, b-c and c-d ridge counts) all indicate the importance of both genetic and common family environment on their formation. Both heritability and common family environment estimates have wide confidence intervals which include zero. Those estimates explain together around 60−70%, while the individual environment estimates explain from 27−40% of individual differences between a-b, b-c and c-d ridge counts. For c-d ridge count, the fit of the full model compared to the saturated model is low due to the fact that there is a significant difference in variances among the twins. When those variances are equated, the MZ correlation for c-d ridge count is .45, and the DZ correlation is .41, leading to a higher estimate of common family environment and a lower estimate of heritability than would be expected from the intraclass correlations presented in Table 1.

Finally, for the atd-angle, intraclass correlations indicated the importance of nonadditive genetic influences because of the extremely high difference in intraclass correlations of MZ (r = .79) and DZ (r = .11) same-sex twins. Therefore, for this trait, the ADE model was run. Both additive (A) and nonadditive (D) genetic estimates have wide confidence intervals that include zero. Although the model-fitting estimate was .00 for A and .70 for D, a DE model is an unrealistic model and our power to detect nonadditive genetic variance was low (see Posthuma & Boomsma, 2000). In addition, goodness of fit of the full model compared to the saturated model was poor. As with the c-d ridge count, the poor fit was due to the fact that there was a significant difference in variances among the twins. However, the pattern of intraclass correlations when variances are equated is similar to the pattern when they are not equated, suggesting an ADE model. Results of the univariate genetic analysis for the atd-angle indicate that 70% of individual differences are explained by genetic factors and 30% by the individual environmental component.

Discussion

The present study assessed the impact of genetic and environmental factors on the quantitative dermatoglyphic traits of same-sex MZ and DZ twins from Kosovo. In twins, since they share an intrauterine environment, it would be expected that the impact of a common environmental component on dermatoglyphic traits could be generally higher than the impact of the individual environment. However, noxious environmental factors could leave traces on dermatoglyphic patterns that could be recognized through increased dissimilarity of twins.

Our results generally showed that genetic factors play a pivotal role in dermatoglyphic traits formation, which is consistent with the findings of previous studies (Cantor et al., 1983; Holt, 1979; Martin et al., 1982; Reed et al., 2006; Sengupta & Karmakar, 2004). Our results also pointed to substantial differences in the heritability pattern that characterizes different types of dermatoglyphic traits, that is, a higher heritability of finger quantitative dermatoglyphic traits compared to palmar quantitative dermatoglyphic traits, and this pattern is in accordance with other studies (e.g., Karmakar et al., 2011). Chattopadhyay and Ganeson (1984) suggest that different sets of genes are responsible for the FRCs and palmar ridge counts, and we supplement this thesis with an idea that emerges from the results of our research — a set of genes responsible for finger traits has a stronger genetic impact than the set of genes responsible for palmar traits. Minor differences, like those found in heritability between the fingers, are expected as there is so much variation during the formation of dermatoglyphs that affects the proportion of genetic and environmental effects so that it is almost impossible to detect two very similar dermatoglyphs (Machado et al., 2010).

A remarkable finding of our study is a pattern obtained for the atd-angle, which indicates a substantial action of an as yet unknown major gene that manifests as a large MZ and minimal DZ similarity for this trait. In a complete partition of the observed phenotypic variance, for traits in which the familial aggregation is solely due to additive genetic effects, the MZ correlation is expected to be exactly twice as large as the DZ correlation (r _MZ = 2r _DZ). If there are additional influences from common environmental effects (C), the additive pattern becomes distorted by making DZ more similar to MZ twins (i.e., r _MZ < 2r _DZ). When the deviance goes in the other direction (r _MZ > 2r _DZ), dominance genetic effects (D) are usually assumed to cause the distortion from pure additivity (Chen et al., 2015), as is the case of the atd-angle in Kosovo Albanian twins. Our analysis indicates that both additive and nonadditive genetic effects contribute to individual differences in the atd-angle, but since large sample sizes are needed to detect nonadditive genetic influences our parameter estimates include zero and confidence intervals are wide. This finding should therefore be further examined in a larger twin sample.

Strengths and Weaknesses of the Study

The main weakness of this study is the small sample size of twin pairs (far below 100 pairs), which may provide inadequate power to significantly declare the contribution of variance components indicating a deviation from additivity (Chen et al., 2015; Hill et al., 2008; Willems et al., 2019). The envisioned stochastic deviation in the results derived from the small sample size is reduced here by performing the analyses on ‘average hand’ traits. This, in addition to sample enlargement by using the sex-combined MZ and DZ twin pairs, produced fairly reliable results that are seen as coherent in the variance component estimation values among dermatoglyphic traits of the same kind (i.e., FRCs, ridge counts between the palmar triradii and degrees of the atd-angle). The combined-sex sample, which enlarged the MZ and DZ samples, disabled the possibility to perform sex-specific twin analyses. This procedure helped to increase the validity of heritability and other components’ estimates and to overcome, at least partially, the distortions in estimates originating from the small sample sizes.

Heritability is by definition population-specific. Therefore, the strength of the present study is that all twins come from the same population living in a small region, as is the case with Albanians from Kosovo. This fact has substantially contributed to the exclusion of noise coming from genetic heterogeneity typical of studies when twin or family samples originate from large admixtured populations (Karmakar et al., 2011). This advantage additionally helped to overcome the negative effects of small sample sizes, which is visible in the consistency of the obtained variance components estimations.

The additional strength of the study comes from the very traits for which the components of variance were estimated. Namely, critics of twin models state that the assumption of equal environment is not valid, because MZ twins receive a more similar treatment, and that heritability estimates are therefore not trustworthy (e.g., Burt & Simons, 2014; Willems et al., 2019). Here, we want to emphasize that dermatoglyphs are the kind of traits that are formed during the fetal phase of development; at birth they are completely formed and remain stable throughout life. Therefore, the age of a person does not change it, and more importantly, the possible environmental differences after birth could not have an additional impact that could theoretically be gender-related. This further eliminates any obstacle to using a sex-combined sample.

Conclusion

Here presented results, obtained from a sample of same-sex twin pairs originating from the Albanian population living in Kosovo, indicate a strong genetic component (49−81%) acting on FRCs and a weak genetic component (0−50%) involved in the palmar ridge counts formation (it should also be remembered that our estimate of E is confounded with any measurement error and we did not estimate these for the different measure used in our study, although we expected it to be low). The specific pattern found for the atd-angle — a drastically higher correlation of MZ in comparison to DZ twins — implies the impact of the dominance genetic component; perhaps the impact of a gene of major effect. Further, more powered studies are needed to confirm this pattern, especially for resolving the issue of a huge difference in MZ and DZ twin similarity for the atd-angle palmar trait.