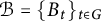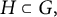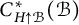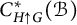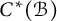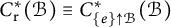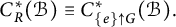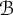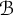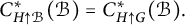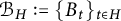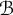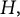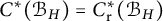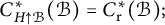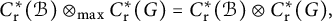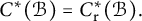1 Introduction
In the 1950s and early 1960s, Mackey and Blattner [Reference Blattner4, Reference Mackey13] described an induction process
![]() $V \rightsquigarrow {\mathop {\mathrm {Ind}}}_H^G(V)$
that creates a unitary representation
$V \rightsquigarrow {\mathop {\mathrm {Ind}}}_H^G(V)$
that creates a unitary representation
![]() ${\mathop {\mathrm {Ind}}}_H^G(V)$
of a locally compact group G out of a unitary representation V of a closed subgroup
${\mathop {\mathrm {Ind}}}_H^G(V)$
of a locally compact group G out of a unitary representation V of a closed subgroup
![]() $H\subset G$
(we write
$H\subset G$
(we write
![]() $H\leqslant G$
).
$H\leqslant G$
).
When translated into the language of C*-algebras,
![]() $V \rightsquigarrow {\mathop {\mathrm {Ind}}}_H^G(V)$
becomes an induction process
$V \rightsquigarrow {\mathop {\mathrm {Ind}}}_H^G(V)$
becomes an induction process
![]() $\pi \rightsquigarrow {\mathop {\mathrm {Ind}}}_{C^{*}(H)}^{C^{*}(G)}(\pi )$
for representations of (full) group C*-algebras. Rieffel noticed this in [Reference Rieffel17], where he presented an (abstract) induction process for representations of C*-algebras he used to describe
$\pi \rightsquigarrow {\mathop {\mathrm {Ind}}}_{C^{*}(H)}^{C^{*}(G)}(\pi )$
for representations of (full) group C*-algebras. Rieffel noticed this in [Reference Rieffel17], where he presented an (abstract) induction process for representations of C*-algebras he used to describe
![]() $\pi \rightsquigarrow {\mathop {\mathrm {Ind}}}_{C^{*}(H)}^{C^{*}(G)}(\pi ).$
Later, in [Reference Fell, Douady and Soglio-Hérault9], Fell presented two induction theories: one for Banach *-algebraic bundles and one for *-algebras; generalizing the works of Mackey–Blattner and Rieffel (respectively). Most of what we need is contained in Fell’s original notes, but we prefer to use the standard references [Reference Fell and Doran10, Reference Fell and Doran11].
$\pi \rightsquigarrow {\mathop {\mathrm {Ind}}}_{C^{*}(H)}^{C^{*}(G)}(\pi ).$
Later, in [Reference Fell, Douady and Soglio-Hérault9], Fell presented two induction theories: one for Banach *-algebraic bundles and one for *-algebras; generalizing the works of Mackey–Blattner and Rieffel (respectively). Most of what we need is contained in Fell’s original notes, but we prefer to use the standard references [Reference Fell and Doran10, Reference Fell and Doran11].
Fell had a problem the other authors did not: not all the representations can be induced. This led him to the concept of inducible representation of a *-algebra and a notion of positivity for representations of Banach *-algebraic bundles. The respective definitions themselves [Reference Fell and Doran11, Chapter XI Sections 4.9 and 8.6] reveal that Fell’s theories are related in the same way Mackey, Blattner, and Rieffel’s are. This is made explicit in [Reference Fell and Doran11, Chapter XI Section 9.26 and Chapter XI Section 10].
We make use of all definitions and results of [Reference Fell and Doran10, Reference Fell and Doran11] (e.g., integration, weak equivalence, and weak containment of *-representations). All the groups considered in this work are locally compact (this includes Hausdorff) and we abbreviate “*-representation” and “unitary representation” to representation. The integrated form of a representation S is indicated by adding
![]() $\tilde { }$
somewhere inside or over the expression
$\tilde { }$
somewhere inside or over the expression
![]() $S.$
Whenever
$S.$
Whenever
![]() $\mathcal {X}=\{X_t\}_{t\in P}$
is a Banach bundle, P stands for the base space and
$\mathcal {X}=\{X_t\}_{t\in P}$
is a Banach bundle, P stands for the base space and
![]() $X_t$
for the fiber over
$X_t$
for the fiber over
![]() $t\in P.$
The set of continuous cross-sections of
$t\in P.$
The set of continuous cross-sections of
![]() $\mathcal {X}$
with compact support will be denoted by
$\mathcal {X}$
with compact support will be denoted by
![]() $C_c(\mathcal {X}),$
and not by
$C_c(\mathcal {X}),$
and not by
![]() $\mathcal {L}(\mathcal {X})$
as in [Reference Fell and Doran11].
$\mathcal {L}(\mathcal {X})$
as in [Reference Fell and Doran11].
Fell’s absorption principle states that given a saturated Banach *-algebraic bundle
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
;
$\mathcal {B}=\{B_t\}_{t\in G}$
;
![]() $H\leqslant G;$
a nondegenerate representation S of
$H\leqslant G;$
a nondegenerate representation S of
![]() $\mathcal {B}$
and a unitary representation U of
$\mathcal {B}$
and a unitary representation U of
![]() $H,$
the representation
$H,$
the representation
![]() $S|_{\mathcal {B}_H}\otimes U $
of the reduction
$S|_{\mathcal {B}_H}\otimes U $
of the reduction
![]() $\mathcal {B}_H:=\{B_t\}_{t\in H}$
is
$\mathcal {B}_H:=\{B_t\}_{t\in H}$
is
![]() $\mathcal {B}$
-positive and the respective induced representation of
$\mathcal {B}$
-positive and the respective induced representation of
![]() $\mathcal {B}$
is unitary equivalent to
$\mathcal {B}$
is unitary equivalent to
![]() $S\otimes {\mathop {\mathrm {Ind}}}_H^G(U),$
which we write as
$S\otimes {\mathop {\mathrm {Ind}}}_H^G(U),$
which we write as
For
![]() $H=\{e\}$
(e being the unit of G) and
$H=\{e\}$
(e being the unit of G) and
![]() $U\colon H\to \mathbb {C}$
trivial,
$U\colon H\to \mathbb {C}$
trivial,
![]() ${\mathop {\mathrm {Ind}}}_H^G(U)$
is the left regular representation
${\mathop {\mathrm {Ind}}}_H^G(U)$
is the left regular representation
![]() $\lambda \colon G\to \mathbb {B}(L^2(G))$
and we get
$\lambda \colon G\to \mathbb {B}(L^2(G))$
and we get
![]() $S\otimes \lambda \cong {\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}}(S|_{B_e}).$
$S\otimes \lambda \cong {\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}}(S|_{B_e}).$
The representations of the form
![]() $S\otimes \lambda $
are explicitly considered by Exel and Ng in [Reference Exel and Ng8] and, as we shall see later, those of the form
$S\otimes \lambda $
are explicitly considered by Exel and Ng in [Reference Exel and Ng8] and, as we shall see later, those of the form
![]() ${\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}}(\phi )$
appear as
${\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}}(\phi )$
appear as
![]() $ \lambda _{\mathcal {B}}\otimes _\phi 1,$
with
$ \lambda _{\mathcal {B}}\otimes _\phi 1,$
with
![]() $\lambda _{\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_e(\mathcal {B}))$
being the reduced representation of [Reference Exel and Ng8, Definition 2.7]. Exel and Ng used those two families of representations to give natural definitions of the reduced cross-sectional C*-algebra of a Fell bundle,
$\lambda _{\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_e(\mathcal {B}))$
being the reduced representation of [Reference Exel and Ng8, Definition 2.7]. Exel and Ng used those two families of representations to give natural definitions of the reduced cross-sectional C*-algebra of a Fell bundle,
![]() $C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
and
$C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
and
![]() $C^{*}_R(\mathcal {B})$
, which turn out to be isomorphic [Reference Exel and Ng8, Theorem 2.14]. Exel–Ng’s ideas go back to Raeburn’s work on coactions [Reference Raeburn15], as pointed out in [Reference Exel and Ng8, p. 515].
$C^{*}_R(\mathcal {B})$
, which turn out to be isomorphic [Reference Exel and Ng8, Theorem 2.14]. Exel–Ng’s ideas go back to Raeburn’s work on coactions [Reference Raeburn15], as pointed out in [Reference Exel and Ng8, p. 515].
The construction of
![]() $C^{*}_R(\mathcal {B})$
can be extended considerably by using the ideas of [Reference Kaliszewski, Landstad and Quigg12] of producing exotic crossed products for C*-dynamical systems out of quotients Q of the full group C*-algebra
$C^{*}_R(\mathcal {B})$
can be extended considerably by using the ideas of [Reference Kaliszewski, Landstad and Quigg12] of producing exotic crossed products for C*-dynamical systems out of quotients Q of the full group C*-algebra
![]() $C^{*}(G).$
Say we have a locally compact group G and a quotient map
$C^{*}(G).$
Say we have a locally compact group G and a quotient map
![]() $q\colon C^{*}(G)\to Q.$
Let
$q\colon C^{*}(G)\to Q.$
Let
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle and take faithful nondegenerate representations
$\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle and take faithful nondegenerate representations
![]() $\pi \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
and
$\pi \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
and
![]() $\rho \colon Q\to \mathbb {B}(Y),$
so
$\rho \colon Q\to \mathbb {B}(Y),$
so
![]() $\pi \otimes \rho \colon C^{*}(\mathcal {B})\otimes Q\to \mathbb {B}(X\otimes Y)$
is faithful and nondegenerate (we are considering minimal tensor products). Both
$\pi \otimes \rho \colon C^{*}(\mathcal {B})\otimes Q\to \mathbb {B}(X\otimes Y)$
is faithful and nondegenerate (we are considering minimal tensor products). Both
![]() $\pi $
and
$\pi $
and
![]() $\rho \circ q$
are the integrated forms (or disintegrate to) representations
$\rho \circ q$
are the integrated forms (or disintegrate to) representations
![]() $S\colon \mathcal {B}\to \mathbb {B}(X)$
and
$S\colon \mathcal {B}\to \mathbb {B}(X)$
and
![]() $U\colon G\to \mathbb {B}(Y).$
For the canonical representation
$U\colon G\to \mathbb {B}(Y).$
For the canonical representation
![]() $\iota ^q\colon G\to M(Q)$
we have
$\iota ^q\colon G\to M(Q)$
we have
![]() $[S\otimes U]_b (\pi (f)\otimes \rho (z)) = \pi (bf)\otimes \rho (\iota ^q(t)z),$
for all
$[S\otimes U]_b (\pi (f)\otimes \rho (z)) = \pi (bf)\otimes \rho (\iota ^q(t)z),$
for all
![]() $b\in B_t$
,
$b\in B_t$
,
![]() $f\in C_c(\mathcal {B})$
and
$f\in C_c(\mathcal {B})$
and
![]() $z\in Q.$
Hence, the image of the integrated form
$z\in Q.$
Hence, the image of the integrated form
![]() $S\tilde { \otimes } U\colon C^{*}(\mathcal {B})\to \mathbb {B}(X\otimes Y)$
(of
$S\tilde { \otimes } U\colon C^{*}(\mathcal {B})\to \mathbb {B}(X\otimes Y)$
(of
![]() $S\otimes U$
) is contained in
$S\otimes U$
) is contained in
![]() $M(C^{*}(\mathcal {B})\otimes Q)$
and
$M(C^{*}(\mathcal {B})\otimes Q)$
and
![]() $\delta ^{\mathcal {B} q}:=S \tilde { \otimes } U\colon C^{*}(\mathcal {B})\to M(C^{*}(\mathcal {B})\otimes Q)$
is independent of
$\delta ^{\mathcal {B} q}:=S \tilde { \otimes } U\colon C^{*}(\mathcal {B})\to M(C^{*}(\mathcal {B})\otimes Q)$
is independent of
![]() $(\pi ,\rho ).$
We define the q-cross-sectional C*-algebra
$(\pi ,\rho ).$
We define the q-cross-sectional C*-algebra
![]() $C^{*}_q(\mathcal {B}):=\delta ^{\mathcal {B} q}(C^{*}(\mathcal {B})).$
If
$C^{*}_q(\mathcal {B}):=\delta ^{\mathcal {B} q}(C^{*}(\mathcal {B})).$
If
![]() $\mathcal {B}$
is the semidirect product bundle of a C*-dynamical system
$\mathcal {B}$
is the semidirect product bundle of a C*-dynamical system
![]() $(A,G,\alpha )$
,
$(A,G,\alpha )$
,
![]() $C^{*}_q(\mathcal {B})\equiv A\rtimes _{q\alpha }G$
is a quotient of the full crossed product
$C^{*}_q(\mathcal {B})\equiv A\rtimes _{q\alpha }G$
is a quotient of the full crossed product
![]() $C^{*}(\mathcal {B})=A\rtimes _\alpha G.$
$C^{*}(\mathcal {B})=A\rtimes _\alpha G.$
Take, for example, the integrated form
![]() $ \tilde { \lambda } \colon C^{*}(G)\to C^{*}_{\mathop {\mathrm {r}}}(G)$
of the left regular representation
$ \tilde { \lambda } \colon C^{*}(G)\to C^{*}_{\mathop {\mathrm {r}}}(G)$
of the left regular representation
![]() $\lambda \colon G\to \mathbb {B}(L^2(G)).$
By definition,
$\lambda \colon G\to \mathbb {B}(L^2(G)).$
By definition,
![]() $C^{*}_{\tilde { \lambda } }(\mathcal {B})=C^{*}_R(\mathcal {B}).$
Since
$C^{*}_{\tilde { \lambda } }(\mathcal {B})=C^{*}_R(\mathcal {B}).$
Since
![]() $\lambda $
is induced by the trivial representation of
$\lambda $
is induced by the trivial representation of
![]() $\{e\},$
it is natural to replace
$\{e\},$
it is natural to replace
![]() $\{e\}$
with any other subgroup
$\{e\}$
with any other subgroup
![]() $H\leqslant G$
and consider
$H\leqslant G$
and consider
![]() $q\colon C^{*}(G)\to C^{*}(G)/I,$
with I the intersection of the kernels of all integrated forms of representations induced from
$q\colon C^{*}(G)\to C^{*}(G)/I,$
with I the intersection of the kernels of all integrated forms of representations induced from
![]() $H.$
This associates an H-cross-sectional C*-algebra
$H.$
This associates an H-cross-sectional C*-algebra
![]() $C^{*}_{H\uparrow G}(\mathcal {B}):=C^{*}_q(\mathcal {B})$
to every Fell bundle
$C^{*}_{H\uparrow G}(\mathcal {B}):=C^{*}_q(\mathcal {B})$
to every Fell bundle
![]() $\mathcal {B}$
over
$\mathcal {B}$
over
![]() $G.$
$G.$
There is still another natural quotient
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}):=C^{*}(\mathcal {B})/J$
one may associate to
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}):=C^{*}(\mathcal {B})/J$
one may associate to
![]() $H.$
Take for J the intersection of all the kernels of integrated forms of representations of
$H.$
Take for J the intersection of all the kernels of integrated forms of representations of
![]() $\mathcal {B}$
induced from
$\mathcal {B}$
induced from
![]() $\mathcal {B}$
-positive representations of
$\mathcal {B}$
-positive representations of
![]() $\mathcal {B}_H.$
In case
$\mathcal {B}_H.$
In case
![]() $\mathcal {B}$
is saturated, all representations of
$\mathcal {B}$
is saturated, all representations of
![]() $\mathcal {B}_H$
count [Reference Fell and Doran11, p. 1159]. This is also the case if
$\mathcal {B}_H$
count [Reference Fell and Doran11, p. 1159]. This is also the case if
![]() $H=\{e\}.$
$H=\{e\}.$
We claim that
![]() $C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
Indeed, given a representation
$C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
Indeed, given a representation
![]() $\phi $
of
$\phi $
of
![]() $B_e\equiv \mathcal {B}_H,$
the abstractly induced representation
$B_e\equiv \mathcal {B}_H,$
the abstractly induced representation
![]() ${\mathop {\mathrm {Ind}}}_{B_e\uparrow C_c(\mathcal {B})}^p(\phi )$
of [Reference Fell and Doran11] is
${\mathop {\mathrm {Ind}}}_{B_e\uparrow C_c(\mathcal {B})}^p(\phi )$
of [Reference Fell and Doran11] is
![]() $(\lambda _{\mathcal {B}}\otimes _\phi 1)|_{C_c(\mathcal {B})}.$
By [Reference Fell and Doran11, Chapter XI Section 9.26],
$(\lambda _{\mathcal {B}}\otimes _\phi 1)|_{C_c(\mathcal {B})}.$
By [Reference Fell and Doran11, Chapter XI Section 9.26],
![]() $\lambda _{\mathcal {B}}\otimes _\phi 1$
is the integrated form
$\lambda _{\mathcal {B}}\otimes _\phi 1$
is the integrated form
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _{\{e\}}^{\mathcal {B}}(\phi ).$
Hence, for all
$\tilde { {\mathop {\mathrm {Ind}}} } _{\{e\}}^{\mathcal {B}}(\phi ).$
Hence, for all
![]() $f\in C^{*}(\mathcal {B}), $
we have
$f\in C^{*}(\mathcal {B}), $
we have
![]() $\|\lambda _{\mathcal {B}}(f)\|\geq \| \lambda _{\mathcal {B}}(f)\otimes _\phi 1 \|=\|\tilde { {\mathop {\mathrm {Ind}}} } _{\{e\}}^{\mathcal {B}}(\phi )_f\|$
with equality if
$\|\lambda _{\mathcal {B}}(f)\|\geq \| \lambda _{\mathcal {B}}(f)\otimes _\phi 1 \|=\|\tilde { {\mathop {\mathrm {Ind}}} } _{\{e\}}^{\mathcal {B}}(\phi )_f\|$
with equality if
![]() $\phi $
is faithful. It is then clear that
$\phi $
is faithful. It is then clear that
![]() $J=\ker (\lambda _{\mathcal {B}})$
and
$J=\ker (\lambda _{\mathcal {B}})$
and
![]() $C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})=\lambda _{\mathcal {B}}(C^{*}(\mathcal {B}))\equiv C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
$C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})=\lambda _{\mathcal {B}}(C^{*}(\mathcal {B}))\equiv C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
Fell’s absorption principle comes into play when we want to compare
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
and
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
and
![]() $C^{*}_{H\uparrow G}(\mathcal {B}),$
for a general
$C^{*}_{H\uparrow G}(\mathcal {B}),$
for a general
![]() $H\leqslant G.$
To start with, we have canonical quotient maps
$H\leqslant G.$
To start with, we have canonical quotient maps
Assume
![]() $\mathcal {B}$
is saturated and take faithful representations
$\mathcal {B}$
is saturated and take faithful representations
![]() $\tilde { S } $
and
$\tilde { S } $
and
![]() $\tilde { U } $
of
$\tilde { U } $
of
![]() $C^{*}(\mathcal {B})$
and
$C^{*}(\mathcal {B})$
and
![]() $C^{*}(H),$
respectively. By [Reference Fell and Doran11, Chapter XI Section 12.4],
$C^{*}(H),$
respectively. By [Reference Fell and Doran11, Chapter XI Section 12.4],
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _H^G(U)$
factors through a faithful representation of
$\tilde { {\mathop {\mathrm {Ind}}} } _H^G(U)$
factors through a faithful representation of
![]() $C^{*}(G)/I_H$
and our construction of
$C^{*}(G)/I_H$
and our construction of
![]() $C^{*}_{H\uparrow G}(\mathcal {B})$
implies
$C^{*}_{H\uparrow G}(\mathcal {B})$
implies
![]() $\| q^{H\uparrow G}_{\mathcal {B}}(f) \| = \|[S\tilde { \otimes } U]_f\|$
for all
$\| q^{H\uparrow G}_{\mathcal {B}}(f) \| = \|[S\tilde { \otimes } U]_f\|$
for all
![]() $f\in C^{*}(\mathcal {B}).$
By Fell’s absorption principle,
$f\in C^{*}(\mathcal {B}).$
By Fell’s absorption principle,
![]() $\|[S\tilde { \otimes } U]_f\| = \|\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(S|_{\mathcal {B}_H}\otimes U)_f\|\leq \| q^{H\uparrow \mathcal {B}}(f) \|.$
This implies
$\|[S\tilde { \otimes } U]_f\| = \|\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(S|_{\mathcal {B}_H}\otimes U)_f\|\leq \| q^{H\uparrow \mathcal {B}}(f) \|.$
This implies
![]() $\| q^{H\uparrow G}_{\mathcal {B}}(f) \|\leq \| q^{H\uparrow \mathcal {B}}(f) \|.$
In other words, there exists a unique quotient map
$\| q^{H\uparrow G}_{\mathcal {B}}(f) \|\leq \| q^{H\uparrow \mathcal {B}}(f) \|.$
In other words, there exists a unique quotient map
![]() $\pi _H^{\mathcal {B}}$
making of
$\pi _H^{\mathcal {B}}$
making of

a commutative diagram.
One of the main results of [Reference Exel and Ng8] is that
![]() $\pi _{\{e\}}^{\mathcal {B}}\colon C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\to C^{*}_R(\mathcal {B})$
is an isomorphism, even if
$\pi _{\{e\}}^{\mathcal {B}}\colon C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\to C^{*}_R(\mathcal {B})$
is an isomorphism, even if
![]() $\mathcal {B}$
is not saturated (in which case the mere existence of
$\mathcal {B}$
is not saturated (in which case the mere existence of
![]() $\pi _{\{e\}}^{\mathcal {B}}$
is in question). When
$\pi _{\{e\}}^{\mathcal {B}}$
is in question). When
![]() $\mathcal {B}$
is saturated and H is normal, we can get the same conclusion out of (1.1). Indeed, let T be a representation of
$\mathcal {B}$
is saturated and H is normal, we can get the same conclusion out of (1.1). Indeed, let T be a representation of
![]() $\mathcal {B}_H$
with faithful integrated form. By [Reference Fell and Doran11, Chapter XI Section 12.8],
$\mathcal {B}_H$
with faithful integrated form. By [Reference Fell and Doran11, Chapter XI Section 12.8],
![]() $T\preceq {\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T)|_{\mathcal {B}_H}\preceq S|_{\mathcal {B}_H}$
and this implies
$T\preceq {\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T)|_{\mathcal {B}_H}\preceq S|_{\mathcal {B}_H}$
and this implies
![]() $\tilde { S|_{\mathcal {B}_H} } $
is faithful. The continuity of the induction process with respect to the regional topology [Reference Fell and Doran11, Chapter XI Section 12.4] implies
$\tilde { S|_{\mathcal {B}_H} } $
is faithful. The continuity of the induction process with respect to the regional topology [Reference Fell and Doran11, Chapter XI Section 12.4] implies
![]() $\|q^{H\uparrow \mathcal {B}}(f)\|=\|{\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(S|_{\mathcal {B}_H})_f\|$
for all
$\|q^{H\uparrow \mathcal {B}}(f)\|=\|{\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(S|_{\mathcal {B}_H})_f\|$
for all
![]() $f\in C^{*}(\mathcal {B}).$
For the trivial representation
$f\in C^{*}(\mathcal {B}).$
For the trivial representation
![]() $\kappa \colon H\to \mathbb {C},$
Fell’s absorption principle gives
$\kappa \colon H\to \mathbb {C},$
Fell’s absorption principle gives
 $$ \begin{align} \|q^{H\uparrow \mathcal{B}}(f)\| & =\| {\mathop{\mathrm{Ind}}}_H^{\mathcal{B}}(S|_{B_H}) \|=\| [S \tilde{ \otimes } {\mathop{\mathrm{Ind}}}_H^G(\kappa)]_f \|\leq \| [S\tilde{ \otimes } {\mathop{\mathrm{Ind}}}_H^G(U)]_f \| \nonumber \\ & = \|q^{H\uparrow G}_{\mathcal{B}}(f)\|; \end{align} $$
$$ \begin{align} \|q^{H\uparrow \mathcal{B}}(f)\| & =\| {\mathop{\mathrm{Ind}}}_H^{\mathcal{B}}(S|_{B_H}) \|=\| [S \tilde{ \otimes } {\mathop{\mathrm{Ind}}}_H^G(\kappa)]_f \|\leq \| [S\tilde{ \otimes } {\mathop{\mathrm{Ind}}}_H^G(U)]_f \| \nonumber \\ & = \|q^{H\uparrow G}_{\mathcal{B}}(f)\|; \end{align} $$
which clearly implies
![]() $\pi _H^{\mathcal {B}}$
is isometric. These arguments can not be extended to non-normal subgroups. Consider, for example,
$\pi _H^{\mathcal {B}}$
is isometric. These arguments can not be extended to non-normal subgroups. Consider, for example,
![]() $\mathcal {B}$
as the trivial bundle over G with constant fiber
$\mathcal {B}$
as the trivial bundle over G with constant fiber
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $H\leqslant G$
such that the canonical *-homomorphism
$H\leqslant G$
such that the canonical *-homomorphism
![]() $C^{*}(H)\to M(C^{*}(G))$
is not faithful.
$C^{*}(H)\to M(C^{*}(G))$
is not faithful.
How was that Exel and Ng manage to define
![]() $\pi _{\{e\}}^{\mathcal {B}}$
and prove it is faithful even for non saturated
$\pi _{\{e\}}^{\mathcal {B}}$
and prove it is faithful even for non saturated
![]() $\mathcal {B}$
? The short answer is that they developed a version of (1.1) where
$\mathcal {B}$
? The short answer is that they developed a version of (1.1) where
![]() $\cong $
is replaced by a weak equivalence
$\cong $
is replaced by a weak equivalence
![]() $\approx $
of representations. Exel–Ng’s absorption principle states that for any given nondegenerate representation S of
$\approx $
of representations. Exel–Ng’s absorption principle states that for any given nondegenerate representation S of
![]() $\mathcal {B},$
$\mathcal {B},$
The statement and proof of this claim is implicit in that of [Reference Exel and Ng8, Theorem 2.14] when the authors show
![]() $\lambda _{\mathcal {B}}(a)\otimes _{S|_{B_e}} 1=0\Leftrightarrow [S \tilde { \otimes } \lambda ]_a=0.$
Notice (1.5) suffices to define
$\lambda _{\mathcal {B}}(a)\otimes _{S|_{B_e}} 1=0\Leftrightarrow [S \tilde { \otimes } \lambda ]_a=0.$
Notice (1.5) suffices to define
![]() $\pi _{\{e\}}^{\mathcal {B}}$
and make (1.4) work.
$\pi _{\{e\}}^{\mathcal {B}}$
and make (1.4) work.
All the facts presented before led us to the following questions concerning a general Fell bundle
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
(saturated or not) and
$\mathcal {B}=\{B_t\}_{t\in G}$
(saturated or not) and
![]() $H\leqslant G.$
$H\leqslant G.$
-
(1) Are all representations of
 $\mathcal {B}_H$
inducible to
$\mathcal {B}_H$
inducible to
 $\mathcal {B}$
(i.e.
$\mathcal {B}$
(i.e.
 $\mathcal {B}$
-positive)?
$\mathcal {B}$
-positive)? -
(2) Can one imitate Exel–Ng’s construction of
 $\lambda _{\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_e(\mathcal {B}))$
using H instead of
$\lambda _{\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_e(\mathcal {B}))$
using H instead of
 $\{e\}$
? More specifically, we ask for the possibility of constructing a right
$\{e\}$
? More specifically, we ask for the possibility of constructing a right
 $C^{*}(\mathcal {B}_H)$
-Hilbert module
$C^{*}(\mathcal {B}_H)$
-Hilbert module
 $L^2_H(\mathcal {B})$
and *-homomorphism such that, for every representation T of
$L^2_H(\mathcal {B})$
and *-homomorphism such that, for every representation T of $$ \begin{align*} \Lambda^{H\mathcal{B}}\colon C^{*}(\mathcal{B})\to \mathbb{B}(L^2_H(\mathcal{B})) \end{align*} $$
$$ \begin{align*} \Lambda^{H\mathcal{B}}\colon C^{*}(\mathcal{B})\to \mathbb{B}(L^2_H(\mathcal{B})) \end{align*} $$
 $\mathcal {B}_H,$
one has
$\mathcal {B}_H,$
one has
 $\Lambda ^{H\mathcal {B}}\otimes _{\tilde { T } }1 =\tilde { {\mathop {\mathrm {Ind}}} } _{H}^{\mathcal {B}}(T)$
. In case this can be done, it would follow immediately that
$\Lambda ^{H\mathcal {B}}\otimes _{\tilde { T } }1 =\tilde { {\mathop {\mathrm {Ind}}} } _{H}^{\mathcal {B}}(T)$
. In case this can be done, it would follow immediately that
 $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B})).$
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B})).$
-
(3) Is there any general weak form of (1.1)? We mean something similar to (1.5) which one may use to define
 $\pi _H^{\mathcal {B}}.$
$\pi _H^{\mathcal {B}}.$
-
(4) Assuming questions (2) and (3) admit affirmative answers, under which circumstances is
 $\pi _H^{\mathcal {B}}$
an isomorphism? In other words, when is
$\pi _H^{\mathcal {B}}$
an isomorphism? In other words, when is
 $\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))$
universal for the representations of
$\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))$
universal for the representations of
 $\mathcal {B}$
of the form
$\mathcal {B}$
of the form
 $S\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U)$
? We know this is true if H is normal and
$S\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U)$
? We know this is true if H is normal and
 $\mathcal {B}$
saturated, is saturation really necessary?
$\mathcal {B}$
saturated, is saturation really necessary?
The outline of this article is as follows. After this introduction, the first main Theorem gives an affirmative answer to question (1) and right after that we construct the *-homomorphism
![]() $\Lambda ^{H\mathcal {B}}$
of question (2). We then prove
$\Lambda ^{H\mathcal {B}}$
of question (2). We then prove
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
and
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
and
![]() $C^{*}_{H\uparrow G}(\mathcal {B})$
have certain universal properties for different families of representations of
$C^{*}_{H\uparrow G}(\mathcal {B})$
have certain universal properties for different families of representations of
![]() $\mathcal {B}.$
Those characterizations are used to compute
$\mathcal {B}.$
Those characterizations are used to compute
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
and
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
and
![]() $C^{*}_{H\uparrow G}(\mathcal {B})$
in a concrete example revealing that many of our theorems fail if some hypotheses are removed. As an application we construct certain “exotic coactions”
$C^{*}_{H\uparrow G}(\mathcal {B})$
in a concrete example revealing that many of our theorems fail if some hypotheses are removed. As an application we construct certain “exotic coactions”
![]() $\delta \colon C^{*}_{H\uparrow G}(\mathcal {B})\to M(C^{*}_{H\uparrow G}(\mathcal {B})\otimes Q^G_H)$
for specific quotients
$\delta \colon C^{*}_{H\uparrow G}(\mathcal {B})\to M(C^{*}_{H\uparrow G}(\mathcal {B})\otimes Q^G_H)$
for specific quotients
![]() $Q^G_H$
of
$Q^G_H$
of
![]() $C^{*}(G).$
In the last part of Section 3, we show that if G is inner amenable and
$C^{*}(G).$
In the last part of Section 3, we show that if G is inner amenable and
![]() $C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\otimes _{\max } C^{*}_{\mathop {\mathrm {r}}}(G)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\otimes C^{*}_{\mathop {\mathrm {r}}}(G),$
then
$C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\otimes _{\max } C^{*}_{\mathop {\mathrm {r}}}(G)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\otimes C^{*}_{\mathop {\mathrm {r}}}(G),$
then
![]() $C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B}).$
$C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B}).$
Our answer to question (3) occupies most of Section 4, which ends with a series of corollaries. In one of them we construct a *-homomorphism that, in some situations, happens to be the inverse of the
![]() $\pi ^{\mathcal {B}}_H$
of (1.3). Another of the corollaries is an extension of Exel–Ng’s absorption principles to normal subgroups other than
$\pi ^{\mathcal {B}}_H$
of (1.3). Another of the corollaries is an extension of Exel–Ng’s absorption principles to normal subgroups other than
![]() $\{e\}.$
$\{e\}.$
In the fifth and final section, we study the dependence of
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
and
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
and
![]() $C^{*}_{H\uparrow G}(\mathcal {B})$
with respect to
$C^{*}_{H\uparrow G}(\mathcal {B})$
with respect to
![]() $H.$
The main result states that if the normalizer of H is open in
$H.$
The main result states that if the normalizer of H is open in
![]() $G,$
then
$G,$
then
![]() $C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
if and only if
$C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
if and only if
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})= C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
As a corollary of this we get that
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})= C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
As a corollary of this we get that
![]() $C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
implies
$C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
implies
![]() $C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B}_H).$
$C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B}_H).$
2 Positivity and induction
We take from [Reference Fell and Doran10, Reference Fell and Doran11] all the definitions, constructions and results concerning representations, C*-algebras, Banach and C*-algebraic bundles (the latter are called Fell bundles). Any notation different from that of [Reference Fell and Doran10, Reference Fell and Doran11] will be introduced along with its corresponding explanation.
Given a (right or left) Hilbert module
![]() $X,$
we denote
$X,$
we denote
![]() $\mathbb {B}(X)$
the C*-algebra of adjointable maps from X to
$\mathbb {B}(X)$
the C*-algebra of adjointable maps from X to
![]() $X.$
Whenever A is a C*-algebra and
$X.$
Whenever A is a C*-algebra and
![]() $\pi \colon A\to \mathbb {B}(X)$
a nondegenerate *-homomorphism,
$\pi \colon A\to \mathbb {B}(X)$
a nondegenerate *-homomorphism,
![]() $\overline {\pi }\colon M(A)\to \mathbb {B}(X)$
stands for the unique extension of
$\overline {\pi }\colon M(A)\to \mathbb {B}(X)$
stands for the unique extension of
![]() $\pi .$
We use the symbol
$\pi .$
We use the symbol
![]() $\langle \ ,\ \rangle $
to denote inner products (except when we recall the definition of Banach *-algebraic bundle). The modular function of a locally compact group G will be denoted by
$\langle \ ,\ \rangle $
to denote inner products (except when we recall the definition of Banach *-algebraic bundle). The modular function of a locally compact group G will be denoted by
![]() $\Delta _G$
and integration with respect to a left invariant Haar measure will be indicated by
$\Delta _G$
and integration with respect to a left invariant Haar measure will be indicated by
![]() $dt.$
$dt.$
Whenever A and B are C*-algebras and there exists a canonical *-homomorphism
![]() $\pi \colon A\to B,$
the expression
$\pi \colon A\to B,$
the expression
![]() $A=B$
means
$A=B$
means
![]() $\pi $
is an isomorphism and we think
$\pi $
is an isomorphism and we think
![]() $a=\pi (a)$
for all
$a=\pi (a)$
for all
![]() $a\in A.$
This is the case when we write
$a\in A.$
This is the case when we write
![]() $C^{*}(G)=C^{*}_{\mathop {\mathrm {r}}}(G)$
(i.e. G is amenable) or
$C^{*}(G)=C^{*}_{\mathop {\mathrm {r}}}(G)$
(i.e. G is amenable) or
![]() $A\otimes B=A\otimes _{\max }B.$
$A\otimes B=A\otimes _{\max }B.$
When we say
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
is a Banach *-algebraic bundle we are implicitly assuming the existence of a structure
$\mathcal {B}=\{B_t\}_{t\in G}$
is a Banach *-algebraic bundle we are implicitly assuming the existence of a structure
![]() $\langle B,\pi ,\cdot \rangle $
making
$\langle B,\pi ,\cdot \rangle $
making
![]() $\mathcal {B}\equiv \langle B,\pi ,\cdot \rangle $
a Banach *-algebraic bundle in the sense of [Reference Fell and Doran11, Chapter VIII Section 3.1]. When we write
$\mathcal {B}\equiv \langle B,\pi ,\cdot \rangle $
a Banach *-algebraic bundle in the sense of [Reference Fell and Doran11, Chapter VIII Section 3.1]. When we write
![]() $b\in \mathcal {B}$
we mean
$b\in \mathcal {B}$
we mean
![]() $b\in B.$
Notice that the fibre
$b\in B.$
Notice that the fibre
![]() $B_e$
over the unit
$B_e$
over the unit
![]() $e\in G$
is a Banach *-algebra. By definition,
$e\in G$
is a Banach *-algebra. By definition,
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle (i.e. C*-algebraic bundle) if
$\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle (i.e. C*-algebraic bundle) if
![]() $\|b^{*}b\|=\|b\|^2$
and
$\|b^{*}b\|=\|b\|^2$
and
![]() $b^{*}b$
is positive in the C*-algebra
$b^{*}b$
is positive in the C*-algebra
![]() $B_e,$
for all
$B_e,$
for all
![]() $b\in B.$
Given a Banach *-algebraic (Fell) bundle
$b\in B.$
Given a Banach *-algebraic (Fell) bundle
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
and
$\mathcal {B}=\{B_t\}_{t\in G}$
and
![]() $H\leqslant G,$
the reduction
$H\leqslant G,$
the reduction
![]() $\mathcal {B}_H:=\{B_t\}_{t\in H}$
is a Banach *-algebraic (Fell, respectively) bundle with the structure inherited from
$\mathcal {B}_H:=\{B_t\}_{t\in H}$
is a Banach *-algebraic (Fell, respectively) bundle with the structure inherited from
![]() $\mathcal {B}.$
$\mathcal {B}.$
The concrete and abstract induction processes of [Reference Fell and Doran11] can be applied to any
![]() $\mathcal {B}$
-positive representation
$\mathcal {B}$
-positive representation
![]() $S\colon \mathcal {B}_H\to \mathbb {B}(X)$
and give two unitary equivalent representations of
$S\colon \mathcal {B}_H\to \mathbb {B}(X)$
and give two unitary equivalent representations of
![]() $\mathcal {B}$
[Reference Fell and Doran11, Chapter XI Section 9.26], any of which we denote by
$\mathcal {B}$
[Reference Fell and Doran11, Chapter XI Section 9.26], any of which we denote by
![]() ${\mathop {\mathrm {Ind}}}_{H}^{\mathcal {B}}(S)$
and call the representation of
${\mathop {\mathrm {Ind}}}_{H}^{\mathcal {B}}(S)$
and call the representation of
![]() $\mathcal {B}$
induced by S. The definition of
$\mathcal {B}$
induced by S. The definition of
![]() $\mathcal {B}$
-positivity we adopt is that of [Reference Fell and Doran11, Chapter XI Section 8.6]. By [Reference Fell and Doran11, Chapter XI Section 8.9], a representation
$\mathcal {B}$
-positivity we adopt is that of [Reference Fell and Doran11, Chapter XI Section 8.6]. By [Reference Fell and Doran11, Chapter XI Section 8.9], a representation
![]() $S\colon \mathcal {B}_H\to \mathbb {B}(X)$
is
$S\colon \mathcal {B}_H\to \mathbb {B}(X)$
is
![]() $\mathcal {B}$
-positive if for every coset
$\mathcal {B}$
-positive if for every coset
![]() $rH \in G/H\equiv \{tH\colon t\in G\},$
every integer
$rH \in G/H\equiv \{tH\colon t\in G\},$
every integer
![]() $n>0,$
all
$n>0,$
all
![]() $b_1,\ldots ,b_n\in \mathcal {B}_{rH},$
and all
$b_1,\ldots ,b_n\in \mathcal {B}_{rH},$
and all
![]() $\xi _1,\ldots ,\xi _n\in X,$
$\xi _1,\ldots ,\xi _n\in X,$
 $$ \begin{align} \sum_{i,j=1}^n \langle S_{b_j^{*}b_i}\xi_i,\xi_j\rangle \geq 0. \end{align} $$
$$ \begin{align} \sum_{i,j=1}^n \langle S_{b_j^{*}b_i}\xi_i,\xi_j\rangle \geq 0. \end{align} $$
We give an alternative formulation in Corollary 2.2.
In [Reference Fell and Doran11, pp. 1159] Fell proves the theorem below for saturated bundles and asks if saturation can be removed from the hypotheses. It indeed can and, as pointed out by Fell in the same page, this leads to a simpler formulation of positivity for representations of Banach *-algebraic bundles (Corollary 2.2).
Theorem 2.1 If
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle and
$\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle and
![]() $H\leqslant G,$
then all the representations of
$H\leqslant G,$
then all the representations of
![]() $\mathcal {B}_H$
are
$\mathcal {B}_H$
are
![]() $\mathcal {B}$
-positive.
$\mathcal {B}$
-positive.
Proof Let
![]() $T\colon \mathcal {B}_H\to \mathbb {B}(X)$
be a representation. Fix
$T\colon \mathcal {B}_H\to \mathbb {B}(X)$
be a representation. Fix
![]() $t\in G$
and elements
$t\in G$
and elements
![]() $b_1,\ldots ,b_n\in \mathcal {B}_{tH}.$
Take
$b_1,\ldots ,b_n\in \mathcal {B}_{tH}.$
Take
![]() $s_1,\ldots ,s_n\in H$
such that
$s_1,\ldots ,s_n\in H$
such that
![]() $b_j\in B_{ts_j}$
(
$b_j\in B_{ts_j}$
(
![]() $j=1,\ldots , n$
). Set
$j=1,\ldots , n$
). Set
![]() $\mathfrak {s}:=(s_1,\ldots , s_n)$
and
$\mathfrak {s}:=(s_1,\ldots , s_n)$
and
![]() $t\mathfrak {s}:=(ts_1,\ldots ,ts_n)$
and define the matrix space
$t\mathfrak {s}:=(ts_1,\ldots ,ts_n)$
and define the matrix space
It is of key importance to notice that
![]() $\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\equiv \mathbb {M}_{\mathfrak {s}}(\mathcal {B}_H).$
$\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\equiv \mathbb {M}_{\mathfrak {s}}(\mathcal {B}_H).$
By [Reference Abadie and Ferraro2, Lemma 2.8],
![]() $\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
is a C*-algebra with usual matrix multiplication as product and
$\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
is a C*-algebra with usual matrix multiplication as product and
![]() $*$
-transpose as involution. A quick way of proving this is by taking a representation
$*$
-transpose as involution. A quick way of proving this is by taking a representation
![]() $R\colon \mathcal {B}\to \mathbb {B}(Y)$
with all the restrictions
$R\colon \mathcal {B}\to \mathbb {B}(Y)$
with all the restrictions
![]() $R|_{B_t}$
being isometric (which exists by [Reference Fell and Doran11, Chapter VIII Section 16.10]) and to identify
$R|_{B_t}$
being isometric (which exists by [Reference Fell and Doran11, Chapter VIII Section 16.10]) and to identify
![]() $\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
with the concrete C*-algebra
$\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
with the concrete C*-algebra
The matrix
![]() $M:=(b_i^{*}b_j)_{i,j=1}^n$
belongs to
$M:=(b_i^{*}b_j)_{i,j=1}^n$
belongs to
![]() $\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
and, regarding
$\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
and, regarding
![]() $\mathcal {B}$
as a
$\mathcal {B}$
as a
![]() $\mathcal {B}-\mathcal {B}$
-equivalence bundle, we can easily adapt the proof of [Reference Abadie and Ferraro2, Lemma 2.8] to show that M is positive in
$\mathcal {B}-\mathcal {B}$
-equivalence bundle, we can easily adapt the proof of [Reference Abadie and Ferraro2, Lemma 2.8] to show that M is positive in
![]() $\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\equiv \mathbb {M}_{\mathfrak {s}}(\mathcal {B}_H).$
An alternative (direct) proof is as follows.
$\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\equiv \mathbb {M}_{\mathfrak {s}}(\mathcal {B}_H).$
An alternative (direct) proof is as follows.
Notice that for all
![]() $M=(M_{i,j})_{i,j=1}^n\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
and all
$M=(M_{i,j})_{i,j=1}^n\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
and all
![]() $i=1,\ldots ,n$
we have
$i=1,\ldots ,n$
we have
![]() $M_{i,i}\in B_e.$
So we may define a trace function
$M_{i,i}\in B_e.$
So we may define a trace function
![]() $\operatorname {tr}\colon \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\to B_e$
by
$\operatorname {tr}\colon \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\to B_e$
by
![]() $\operatorname {tr}(M):=\sum _{i=1}^n M_{i,i}.$
The operations
$\operatorname {tr}(M):=\sum _{i=1}^n M_{i,i}.$
The operations
 $$ \begin{align*} \mathbb{M}_{t\mathfrak{s}}(\mathcal{B})\times & B_e\to B_e & (M,b)&\mapsto (M_{i,j}b)_{i,j=1}^n\\ \langle\ ,\ \rangle_{B_e}\colon \mathbb{M}_{t\mathfrak{s}}(\mathcal{B})\times & \mathbb{M}_{t\mathfrak{s}}(\mathcal{B})\to B_e & (M,N)&\mapsto \langle M,N\rangle_{B_e}:=\operatorname{tr}(M^{*}N) \end{align*} $$
$$ \begin{align*} \mathbb{M}_{t\mathfrak{s}}(\mathcal{B})\times & B_e\to B_e & (M,b)&\mapsto (M_{i,j}b)_{i,j=1}^n\\ \langle\ ,\ \rangle_{B_e}\colon \mathbb{M}_{t\mathfrak{s}}(\mathcal{B})\times & \mathbb{M}_{t\mathfrak{s}}(\mathcal{B})\to B_e & (M,N)&\mapsto \langle M,N\rangle_{B_e}:=\operatorname{tr}(M^{*}N) \end{align*} $$
make of
![]() $\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
a full right
$\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})$
a full right
![]() $B_e$
-Hilbert module which we denote by
$B_e$
-Hilbert module which we denote by
![]() $\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e}.$
$\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e}.$
For every
![]() $M\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B}),$
the operator
$M\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B}),$
the operator
![]() $\phi _M\colon \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e}\to \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e}, N\mapsto MN,$
is adjointable because for all
$\phi _M\colon \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e}\to \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e}, N\mapsto MN,$
is adjointable because for all
![]() $N,P\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e},$
$N,P\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e},$
Moreover, the natural representation
![]() $\phi \colon \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\to \mathbb {B}(\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e})$
,
$\phi \colon \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\to \mathbb {B}(\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e})$
,
![]() $M\mapsto \phi _M,$
is a *-homomorphism.
$M\mapsto \phi _M,$
is a *-homomorphism.
To prove that
![]() $\phi $
is faithful, we take an approximate unit
$\phi $
is faithful, we take an approximate unit
![]() $\{e_i\}_{i\in I}$
of
$\{e_i\}_{i\in I}$
of
![]() $\mathbb {M}_{t\mathfrak {s}}(\mathcal {B}).$
For all
$\mathbb {M}_{t\mathfrak {s}}(\mathcal {B}).$
For all
![]() $M\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B}),$
we have
$M\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B}),$
we have
![]() $\sum _{i,j=1}^n (M_{i,j})^{*}M_{i,j} = \operatorname {tr}(M^{*}M)=\lim _i\operatorname {tr}((Me_i)^{*}M)=\lim _i \langle \phi _Me_i,M\rangle _{B_e}.$
Thus,
$\sum _{i,j=1}^n (M_{i,j})^{*}M_{i,j} = \operatorname {tr}(M^{*}M)=\lim _i\operatorname {tr}((Me_i)^{*}M)=\lim _i \langle \phi _Me_i,M\rangle _{B_e}.$
Thus,
![]() $\phi _M=0$
implies
$\phi _M=0$
implies
![]() $\sum _{i,j=1}^n (M_{i,j})^{*}M_{i,j}=0$
and this yields
$\sum _{i,j=1}^n (M_{i,j})^{*}M_{i,j}=0$
and this yields
![]() $M=0.$
$M=0.$
Now that we know
![]() $\phi $
is faithful, to prove that
$\phi $
is faithful, to prove that
![]() $M:=(b_i^{*}b_j)_{i,j=1}^n \geq 0 $
(in
$M:=(b_i^{*}b_j)_{i,j=1}^n \geq 0 $
(in
![]() $\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\equiv \mathbb {M}_{\mathfrak {s}}(\mathcal {B}_H)$
) it suffices to show that
$\mathbb {M}_{t\mathfrak {s}}(\mathcal {B})\equiv \mathbb {M}_{\mathfrak {s}}(\mathcal {B}_H)$
) it suffices to show that
![]() $\phi _M\geq 0.$
This is the case because for all
$\phi _M\geq 0.$
This is the case because for all
![]() $N\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e}$
we have
$N\in \mathbb {M}_{t\mathfrak {s}}(\mathcal {B})_{B_e}$
we have
 $$ \begin{align*} \langle \phi_M N,N\rangle_{B_e} = \operatorname{tr}((\phi_M N)^{*}N)=\operatorname{tr}(N^{*}M^{*}N)=\sum_{i=1}^n\left(\sum_{j=1}^n b_jN_{j,i}\right)^{*}\left(\sum_{k=1}^n b_kN_{k,i}\right)\geq 0; \end{align*} $$
$$ \begin{align*} \langle \phi_M N,N\rangle_{B_e} = \operatorname{tr}((\phi_M N)^{*}N)=\operatorname{tr}(N^{*}M^{*}N)=\sum_{i=1}^n\left(\sum_{j=1}^n b_jN_{j,i}\right)^{*}\left(\sum_{k=1}^n b_kN_{k,i}\right)\geq 0; \end{align*} $$
where the last inequality follows from the fact that the definition of Fell bundle requires
![]() $c^{*}c$
to be positive in
$c^{*}c$
to be positive in
![]() $B_e$
for all
$B_e$
for all
![]() $c\in B.$
$c\in B.$
If
![]() $N:= M^{1/2}\in \mathbb {M}_{\mathfrak {ts}}(\mathcal {B})\equiv \mathbb {M}_{\mathfrak {s}}(\mathcal {B}_H),$
then all the entries
$N:= M^{1/2}\in \mathbb {M}_{\mathfrak {ts}}(\mathcal {B})\equiv \mathbb {M}_{\mathfrak {s}}(\mathcal {B}_H),$
then all the entries
![]() $N_{i,j}$
of N belong to
$N_{i,j}$
of N belong to
![]() $\mathcal {B}_H$
and for all
$\mathcal {B}_H$
and for all
![]() $\xi _1,\ldots , \xi _n\in X$
we have
$\xi _1,\ldots , \xi _n\in X$
we have
 $$ \begin{align*} \sum_{i,j=1}^n\langle T_{b_j^{*}b_i}\xi_i,\xi_j\rangle = \sum_{i,j,k=1}^n \langle T_{{N_{k,j}}^{*}N_{k,i}} \xi_i,\xi_j\rangle = \sum_{k=1}^n \langle \sum_{i=1}^n T_{N_{k,i}}\xi_i,\sum_{j=1}^nT_{N_{k,j}}\xi_j\rangle\geq 0; \end{align*} $$
$$ \begin{align*} \sum_{i,j=1}^n\langle T_{b_j^{*}b_i}\xi_i,\xi_j\rangle = \sum_{i,j,k=1}^n \langle T_{{N_{k,j}}^{*}N_{k,i}} \xi_i,\xi_j\rangle = \sum_{k=1}^n \langle \sum_{i=1}^n T_{N_{k,i}}\xi_i,\sum_{j=1}^nT_{N_{k,j}}\xi_j\rangle\geq 0; \end{align*} $$
proving that T is
![]() $\mathcal {B}$
-positive.
$\mathcal {B}$
-positive.
Corollary 2.2 (c.f. [Reference Fell and Doran11, Chapter XI Section 11.11])
Let
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
be a Banach *-algebraic bundle and H a closed subgroup of
$\mathcal {B}=\{B_t\}_{t\in G}$
be a Banach *-algebraic bundle and H a closed subgroup of
![]() $G.$
For any representation
$G.$
For any representation
![]() $S\colon \mathcal {B}_H\to \mathbb {B}(X)$
the following conditions are equivalent:
$S\colon \mathcal {B}_H\to \mathbb {B}(X)$
the following conditions are equivalent:
-
(1) S is
 $\mathcal {B}$
-positive.
$\mathcal {B}$
-positive. -
(2)
 $\langle S_{b^{*}b}\xi ,\xi \rangle \geq 0$
for all
$\langle S_{b^{*}b}\xi ,\xi \rangle \geq 0$
for all
 $b\in \mathcal {B}$
and
$b\in \mathcal {B}$
and
 $\xi \in X.$
$\xi \in X.$
2.1 Fell’s abstract induction process for Fell fundles
Take a Fell bundle
![]() $\mathcal {B}=\{B_t\}_{t\in G}.$
The convolution product
$\mathcal {B}=\{B_t\}_{t\in G}.$
The convolution product
![]() $f*g,$
the adjoint
$f*g,$
the adjoint
![]() $f^{*}$
and norm
$f^{*}$
and norm
![]() $\|f\|_1$
of
$\|f\|_1$
of
![]() $f,g\in C_c(\mathcal {B})$
are given by
$f,g\in C_c(\mathcal {B})$
are given by
The
![]() $L^1$
-cross-sectional algebra
$L^1$
-cross-sectional algebra
![]() $L^1(\mathcal {B})$
of
$L^1(\mathcal {B})$
of
![]() $\mathcal {B}$
is the
$\mathcal {B}$
is the
![]() $\|\ \|_1$
-completion of
$\|\ \|_1$
-completion of
![]() $C_c(\mathcal {B}).$
$C_c(\mathcal {B}).$
The cross-sectional C*-algebra of
![]() $\mathcal {B}$
,
$\mathcal {B}$
,
![]() $C^{*}(\mathcal {B}),$
is the enveloping C*-algebra of
$C^{*}(\mathcal {B}),$
is the enveloping C*-algebra of
![]() $L^1(\mathcal {B})$
and we know from [Reference Fell and Doran11, Chapter VIII Section 16.4] that
$L^1(\mathcal {B})$
and we know from [Reference Fell and Doran11, Chapter VIII Section 16.4] that
![]() $L^1(\mathcal {B})$
is reduced, meaning that we may think of
$L^1(\mathcal {B})$
is reduced, meaning that we may think of
![]() $L^1(\mathcal {B})$
as a dense *-subalgebra of
$L^1(\mathcal {B})$
as a dense *-subalgebra of
![]() $C^{*}(\mathcal {B}).$
The integrated form of a representation
$C^{*}(\mathcal {B}).$
The integrated form of a representation
![]() $T\colon \mathcal {B}\to \mathbb {B}(X)$
is the unique representation
$T\colon \mathcal {B}\to \mathbb {B}(X)$
is the unique representation
![]() $\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
such that
$\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
such that
![]() $\tilde { T } _f \xi = \int _G T_{f(t)}\xi \, dt$
for all
$\tilde { T } _f \xi = \int _G T_{f(t)}\xi \, dt$
for all
![]() $f\in C_c(\mathcal {B})$
and
$f\in C_c(\mathcal {B})$
and
![]() $\xi \in X.$
All representations of
$\xi \in X.$
All representations of
![]() $C^{*}(\mathcal {B})$
arise this way (so they can be “disintegrated”) and
$C^{*}(\mathcal {B})$
arise this way (so they can be “disintegrated”) and
![]() $\tilde { T } $
determines
$\tilde { T } $
determines
![]() $T.$
$T.$
The definition of weak containment (and equivalence) of representations we adopt are those of [Reference Fell and Doran10, Chapter VII Section 1] and [Reference Fell and Doran11, Chapter VIII Section 21]. Given two sets of representations,
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $\mathcal {T},$
the expressions
$\mathcal {T},$
the expressions
![]() $\mathcal {S}\preceq \mathcal {T}$
and
$\mathcal {S}\preceq \mathcal {T}$
and
![]() $\mathcal {S}\approx \mathcal {T}$
mean that
$\mathcal {S}\approx \mathcal {T}$
mean that
![]() $\mathcal {S}$
is weakly contained in
$\mathcal {S}$
is weakly contained in
![]() $\mathcal {T}$
and that
$\mathcal {T}$
and that
![]() $\mathcal {S}$
is weakly equivalent to
$\mathcal {S}$
is weakly equivalent to
![]() $\mathcal {T},$
respectively.
$\mathcal {T},$
respectively.
The basic ingredients we need to perform Fell’s abstract induction process (see [Reference Fell and Doran11, Chapter XI Sections 8.7 and 9.25]) are a closed subgroup
![]() $H\subset G;$
a representation
$H\subset G;$
a representation
![]() $T\colon \mathcal {B}_H\to \mathbb {B}(X);$
the “normalized restriction”
$T\colon \mathcal {B}_H\to \mathbb {B}(X);$
the “normalized restriction”
 $$ \begin{align} p \colon & C_c(\mathcal{B})\to C_c(\mathcal{B}_H) & p(f)(t)&=\left(\frac{\Delta_G(t)}{\Delta_H(t)}\right)^{1/2}f(t) \end{align} $$
$$ \begin{align} p \colon & C_c(\mathcal{B})\to C_c(\mathcal{B}_H) & p(f)(t)&=\left(\frac{\Delta_G(t)}{\Delta_H(t)}\right)^{1/2}f(t) \end{align} $$
and the action
![]() $C_c(\mathcal {B})\times C_c(\mathcal {B}_H) \to C_c(\mathcal {B})$
,
$C_c(\mathcal {B})\times C_c(\mathcal {B}_H) \to C_c(\mathcal {B})$
,
![]() $(f,u)\mapsto fu,$
given by
$(f,u)\mapsto fu,$
given by
 $$ \begin{align} \qquad fu(t)= \int_H f(ts)u(s^{-1})\left(\frac{\Delta_G(s)}{\Delta_H(s)}\right)^{1/2}\, ds. \end{align} $$
$$ \begin{align} \qquad fu(t)= \int_H f(ts)u(s^{-1})\left(\frac{\Delta_G(s)}{\Delta_H(s)}\right)^{1/2}\, ds. \end{align} $$
It is shown in [Reference Fell and Doran11, Chapter XI Section 8.4] that for all
![]() $f,g\in C_c(\mathcal {B})$
and
$f,g\in C_c(\mathcal {B})$
and
![]() $u,v\in C_c(\mathcal {B}_H),$
$u,v\in C_c(\mathcal {B}_H),$
We abbreviate
![]() $\frac {\Delta _G(t)}{\Delta _H(t)}$
to
$\frac {\Delta _G(t)}{\Delta _H(t)}$
to
![]() $\Delta _H^G(t)$
and write
$\Delta _H^G(t)$
and write
![]() $p_H$
instead of p only when not doing so may cause any confusion.
$p_H$
instead of p only when not doing so may cause any confusion.
Any representation
![]() $T\colon \mathcal {B}_H\to \mathbb {B}(X)$
is
$T\colon \mathcal {B}_H\to \mathbb {B}(X)$
is
![]() $\mathcal {B}$
-positive and this implies that there is a unique pre-inner product
$\mathcal {B}$
-positive and this implies that there is a unique pre-inner product
![]() $[\ ,\ ]_T$
on the algebraic tensor product
$[\ ,\ ]_T$
on the algebraic tensor product
![]() $C_c(\mathcal {B})\odot X$
such that, for all
$C_c(\mathcal {B})\odot X$
such that, for all
![]() $f,g\in C_c(\mathcal {B})$
and
$f,g\in C_c(\mathcal {B})$
and
![]() $\xi ,\eta \in X$
,
$\xi ,\eta \in X$
,
![]() $[ f\odot \xi ,g\odot \eta ]_T = \langle \tilde { T } _{p(g^{*}*f)}\xi ,\eta \rangle .$
We denote by
$[ f\odot \xi ,g\odot \eta ]_T = \langle \tilde { T } _{p(g^{*}*f)}\xi ,\eta \rangle .$
We denote by
![]() $X^p_T$
the Hilbert space obtained as the completion of the quotient
$X^p_T$
the Hilbert space obtained as the completion of the quotient
with respect to the natural (quotient) inner product, which we denote by
![]() $\langle \ , \ \rangle .$
$\langle \ , \ \rangle .$
The image of an elementary tensor
![]() $f\odot \xi \in C_c(\mathcal {B})\odot X$
(via the quotient map and the inclusion into the completion) will be denoted
$f\odot \xi \in C_c(\mathcal {B})\odot X$
(via the quotient map and the inclusion into the completion) will be denoted
![]() $f\otimes _T \xi .$
By construction,
$f\otimes _T \xi .$
By construction,
By [Reference Fell and Doran11, Chapter XI Section 9.26] the (abstractly) induced representation
![]() ${\mathop {\mathrm {Ind}}}^{\mathcal {B}}_H(T)\colon \mathcal {B}\to \mathbb {B}(X^p_T),$
and its integrated form
${\mathop {\mathrm {Ind}}}^{\mathcal {B}}_H(T)\colon \mathcal {B}\to \mathbb {B}(X^p_T),$
and its integrated form
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T) \colon C^{*}(\mathcal {B})\to \mathbb {B}(X^p_T) $
can be characterized by saying that
$\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T) \colon C^{*}(\mathcal {B})\to \mathbb {B}(X^p_T) $
can be characterized by saying that
for all
![]() $b\in \mathcal {B}$
,
$b\in \mathcal {B}$
,
![]() $f,g\in C_c(\mathcal {B})$
and
$f,g\in C_c(\mathcal {B})$
and
![]() $\xi \in X,$
where the action of
$\xi \in X,$
where the action of
![]() $\mathcal {B}$
on
$\mathcal {B}$
on
![]() $C_c(\mathcal {B})$
used in the first identity is
$C_c(\mathcal {B})$
used in the first identity is
Remark 2.3 The trivial one-dimensional complex Banach bundle over G,
![]() $\mathcal {T}_G=\{\mathbb {C}\delta _t\}_{t\in G},$
is a saturated Fell bundle with the operations
$\mathcal {T}_G=\{\mathbb {C}\delta _t\}_{t\in G},$
is a saturated Fell bundle with the operations
![]() $(z\delta _r)(w\delta _s)=zw\delta _{rs}$
and
$(z\delta _r)(w\delta _s)=zw\delta _{rs}$
and
![]() $(z\delta _r)^{*} =\overline {z}\delta _r.$
We can easily identify
$(z\delta _r)^{*} =\overline {z}\delta _r.$
We can easily identify
![]() $C_c(\mathcal {T}_G)$
,
$C_c(\mathcal {T}_G)$
,
![]() $L^1(\mathcal {T}_G)$
and
$L^1(\mathcal {T}_G)$
and
![]() $C^{*}(\mathcal {T}_G)$
with
$C^{*}(\mathcal {T}_G)$
with
![]() $C_c(G),L^1(G)$
and
$C_c(G),L^1(G)$
and
![]() $C^{*}(G),$
respectively. The unitary representations of G are in one to one correspondence with the nondegenerate representations of
$C^{*}(G),$
respectively. The unitary representations of G are in one to one correspondence with the nondegenerate representations of
![]() $\mathcal {T}_G.$
Up to this identification, the induction process
$\mathcal {T}_G.$
Up to this identification, the induction process
![]() $U\mapsto {\mathop {\mathrm {Ind}}}_H^G(U)$
is the same as
$U\mapsto {\mathop {\mathrm {Ind}}}_H^G(U)$
is the same as
![]() $U\mapsto {\mathop {\mathrm { Ind}}}_{H}^{\mathcal {T}_G}(U).$
$U\mapsto {\mathop {\mathrm { Ind}}}_{H}^{\mathcal {T}_G}(U).$
2.1.1 The induction module
With
![]() $\langle \ ,\ \rangle _{H}^{\mathcal {B}}\colon C_c(\mathcal {B})\times C_c(\mathcal {B})\to C_c(\mathcal {B}_H)$
defined by
$\langle \ ,\ \rangle _{H}^{\mathcal {B}}\colon C_c(\mathcal {B})\times C_c(\mathcal {B})\to C_c(\mathcal {B}_H)$
defined by
![]() $\langle f,g\rangle _H^{\mathcal {B}}:=p(f^{*}*g)$
,
$\langle f,g\rangle _H^{\mathcal {B}}:=p(f^{*}*g)$
,
![]() $C_c(\mathcal {B})$
becomes a right
$C_c(\mathcal {B})$
becomes a right
![]() $C_c(\mathcal {B}_H)$
-rigged left
$C_c(\mathcal {B}_H)$
-rigged left
![]() $C_c(\mathcal {B})$
-module (in the sense of [Reference Fell and Doran11]) with the action (2.3) on the right and the natural action by convolution on the left. If we consider
$C_c(\mathcal {B})$
-module (in the sense of [Reference Fell and Doran11]) with the action (2.3) on the right and the natural action by convolution on the left. If we consider
![]() $C_c(\mathcal {B}_H)$
as a dense *-subalgebra of
$C_c(\mathcal {B}_H)$
as a dense *-subalgebra of
![]() $C^{*}(\mathcal {B}_H),$
then
$C^{*}(\mathcal {B}_H),$
then
![]() $\langle \ ,\ \rangle _{H}^{\mathcal {B}}$
is positive in the sense that
$\langle \ ,\ \rangle _{H}^{\mathcal {B}}$
is positive in the sense that
![]() $\langle f ,f \rangle _{H}^{\mathcal {B}}\geq 0$
for all
$\langle f ,f \rangle _{H}^{\mathcal {B}}\geq 0$
for all
![]() $f\in C_c(\mathcal {B}).$
Indeed, take a nondegenerate representation
$f\in C_c(\mathcal {B}).$
Indeed, take a nondegenerate representation
![]() $T\colon \mathcal {B}_H\to \mathbb {B}(X)$
with faithful integrated form. Then
$T\colon \mathcal {B}_H\to \mathbb {B}(X)$
with faithful integrated form. Then
![]() $\tilde { T } _{\langle f ,f \rangle _{H}^{\mathcal {B}}}\equiv \tilde { T } _{p(f^{*}*f)}\geq 0$
because T is
$\tilde { T } _{\langle f ,f \rangle _{H}^{\mathcal {B}}}\equiv \tilde { T } _{p(f^{*}*f)}\geq 0$
because T is
![]() $\mathcal {B}$
-positive [Reference Fell and Doran11, Chapter XI Sections 8.6–8.9].
$\mathcal {B}$
-positive [Reference Fell and Doran11, Chapter XI Sections 8.6–8.9].
We are now in the situation of [Reference Raeburn and Williams16, Lemma 2.16], so there exists a right
![]() $C^{*}(\mathcal {B}_H)$
-Hilbert module
$C^{*}(\mathcal {B}_H)$
-Hilbert module
![]() $L^2_H(\mathcal {B})$
(with inner product
$L^2_H(\mathcal {B})$
(with inner product
![]() $\langle \ ,\ \rangle _{C^{*}(\mathcal {B}_H)}$
) and a linear map
$\langle \ ,\ \rangle _{C^{*}(\mathcal {B}_H)}$
) and a linear map
![]() $q\colon C_c(\mathcal {B})\to L^2_H(\mathcal {B})$
with dense image and
$q\colon C_c(\mathcal {B})\to L^2_H(\mathcal {B})$
with dense image and
![]() $\langle q(f),q(g)\rangle _{C^{*}(\mathcal {B}_H)}=p(f^{*}*g)$
for all
$\langle q(f),q(g)\rangle _{C^{*}(\mathcal {B}_H)}=p(f^{*}*g)$
for all
![]() $f,g\in C_c(\mathcal {B}).$
To prove q is faithful, we start by noticing that
$f,g\in C_c(\mathcal {B}).$
To prove q is faithful, we start by noticing that
![]() $q(f)=0$
implies
$q(f)=0$
implies
![]() $p(f^{*}*f)(e)=0,$
which translates to
$p(f^{*}*f)(e)=0,$
which translates to
![]() $\int _G f(t)^{*}f(t)\, dt=0.$
This last condition implies
$\int _G f(t)^{*}f(t)\, dt=0.$
This last condition implies
![]() $f=0$
because
$f=0$
because
![]() $t\mapsto f(t)^{*}f(t)$
is a continuous function with compact support from G to the positive cone of
$t\mapsto f(t)^{*}f(t)$
is a continuous function with compact support from G to the positive cone of
![]() $B_e.$
$B_e.$
Now that we know that q is injective, we omit any reference to it and think of
![]() $C_c(\mathcal {B})$
as a dense subspace of
$C_c(\mathcal {B})$
as a dense subspace of
![]() $L^2_H(\mathcal {B}).$
For example, we make no distinction between
$L^2_H(\mathcal {B}).$
For example, we make no distinction between
![]() $\langle f,g\rangle _{C^{*}(\mathcal {B}_H)}$
,
$\langle f,g\rangle _{C^{*}(\mathcal {B}_H)}$
,
![]() $\langle f,g\rangle _H^{\mathcal {B}}$
, and
$\langle f,g\rangle _H^{\mathcal {B}}$
, and
![]() $p(f^{*}*g).$
$p(f^{*}*g).$
The following remark will be used repeatedly (and even without mention) in the rest of the article.
Remark 2.4 Given a non empty set
![]() $A,$
Hilbert spaces X and Y and functions
$A,$
Hilbert spaces X and Y and functions
![]() $x\colon A\to X$
and
$x\colon A\to X$
and
![]() $y\colon A\to Y$
such that
$y\colon A\to Y$
such that
![]() $\langle x(a),x(b)\rangle = \langle y(a),y(b)\rangle $
for all
$\langle x(a),x(b)\rangle = \langle y(a),y(b)\rangle $
for all
![]() $a,b\in A,$
there exists a unique linear isometry
$a,b\in A,$
there exists a unique linear isometry
![]() $I\colon \overline {\mathop {\mathrm {span}}}\{x(a)\colon a\in A\}\to \overline {\mathop {\mathrm {span}}}\{y(a)\colon a\in A\}$
such that
$I\colon \overline {\mathop {\mathrm {span}}}\{x(a)\colon a\in A\}\to \overline {\mathop {\mathrm {span}}}\{y(a)\colon a\in A\}$
such that
![]() $I\circ x=y.$
$I\circ x=y.$
The proposition we are about to state is a reinterpretation of [Reference Fell and Doran11, Chapter XI Section 9.26]. It reveals that when working with Fell bundles, the induction process can be carried out using Hilbert modules and not just left rigged modules.
Proposition 2.5 There exists a unique *-homomorphism
![]() $\Lambda ^{H\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_H(\mathcal {B})) $
such that
$\Lambda ^{H\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_H(\mathcal {B})) $
such that
![]() $\Lambda ^{H\mathcal {B}}_f g=f*g$
for all
$\Lambda ^{H\mathcal {B}}_f g=f*g$
for all
![]() $f,g\in C_c(\mathcal {B}).$
Moreover, for any representation
$f,g\in C_c(\mathcal {B}).$
Moreover, for any representation
![]() $T\colon \mathcal {B}_H\to \mathbb {B}(X)$
it follows that
$T\colon \mathcal {B}_H\to \mathbb {B}(X)$
it follows that
Proof Take any representation
![]() $T\colon \mathcal {B}_H\to \mathbb {B}(X).$
By [Reference Fell and Doran11, Chapter XI Section 9.26] the representation
$T\colon \mathcal {B}_H\to \mathbb {B}(X).$
By [Reference Fell and Doran11, Chapter XI Section 9.26] the representation
![]() $\tilde { T } |_{C_c(\mathcal {B})}$
is inducible to
$\tilde { T } |_{C_c(\mathcal {B})}$
is inducible to
![]() $C_c(\mathcal {B})$
via the conditional expectation p of (2.2) and the resulting induced representation is
$C_c(\mathcal {B})$
via the conditional expectation p of (2.2) and the resulting induced representation is
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)|_{C_c(\mathcal {B})}.$
Then, for all
$\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)|_{C_c(\mathcal {B})}.$
Then, for all
![]() $f,g\in C_c(\mathcal {B})$
and
$f,g\in C_c(\mathcal {B})$
and
![]() $\xi \in X$
we have
$\xi \in X$
we have
Since we can choose T so that
![]() $\tilde { T } $
is faithful, we have
$\tilde { T } $
is faithful, we have
![]() $\langle f*g,f*g\rangle _H^{\mathcal {B}}\leq \|f\|_1^2\langle g,g\rangle _H^{\mathcal {B}}$
and
$\langle f*g,f*g\rangle _H^{\mathcal {B}}\leq \|f\|_1^2\langle g,g\rangle _H^{\mathcal {B}}$
and
for all
![]() $f,g,h\in C_c(\mathcal {B}).$
This implies the existence of a map
$f,g,h\in C_c(\mathcal {B}).$
This implies the existence of a map
![]() $\Lambda ^{0}\colon C_c(\mathcal {B})\to \mathbb {B}(L^2_H(\mathcal {B}))$
such that
$\Lambda ^{0}\colon C_c(\mathcal {B})\to \mathbb {B}(L^2_H(\mathcal {B}))$
such that
![]() $\Lambda ^{0}_fg=f*g$
,
$\Lambda ^{0}_fg=f*g$
,
![]() $\|\Lambda ^{0}_f\|\leq \|f\|_1$
and
$\|\Lambda ^{0}_f\|\leq \|f\|_1$
and
![]() $(\Lambda ^{0}_f)^{*}=\Lambda ^{0}_{f^{*}}.$
$(\Lambda ^{0}_f)^{*}=\Lambda ^{0}_{f^{*}}.$
Note that
![]() $\Lambda ^{0}$
is a *-homomorphism which is contractive with respect to
$\Lambda ^{0}$
is a *-homomorphism which is contractive with respect to
![]() $\|\ \|_1,$
so it admits a unique extension to a *-homomorphism
$\|\ \|_1,$
so it admits a unique extension to a *-homomorphism
![]() $\Lambda ^{1}\colon L^1(\mathcal {B})\to \mathbb {B}(L^2_H(\mathcal {B}));$
which we can extend in a unique way to a *-homomorphism
$\Lambda ^{1}\colon L^1(\mathcal {B})\to \mathbb {B}(L^2_H(\mathcal {B}));$
which we can extend in a unique way to a *-homomorphism
![]() $\Lambda ^{H\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_H(\mathcal {B})).$
$\Lambda ^{H\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_H(\mathcal {B})).$
The tensor product
![]() $L^2_H(\mathcal {B})\otimes _{\tilde { T } }X$
is the closed linear span of elementary tensors
$L^2_H(\mathcal {B})\otimes _{\tilde { T } }X$
is the closed linear span of elementary tensors
![]() $f\otimes _{\tilde { T } }\xi $
(
$f\otimes _{\tilde { T } }\xi $
(
![]() $f\in C_c(\mathcal {B})$
and
$f\in C_c(\mathcal {B})$
and
![]() $\xi \in X$
) with
$\xi \in X$
) with
![]() $\langle f\otimes _{\tilde { T } }\xi ,g\otimes _{\tilde { T } }\eta \rangle =\langle \tilde { T } _{\langle g,f\rangle _H^{\mathcal {B}}}\xi ,\eta \rangle = \langle f\otimes _T\xi ,g\otimes _T\eta \rangle .$
So there exists a unique unitary
$\langle f\otimes _{\tilde { T } }\xi ,g\otimes _{\tilde { T } }\eta \rangle =\langle \tilde { T } _{\langle g,f\rangle _H^{\mathcal {B}}}\xi ,\eta \rangle = \langle f\otimes _T\xi ,g\otimes _T\eta \rangle .$
So there exists a unique unitary
![]() $U\colon L^2_H(\mathcal {B})\otimes _{\tilde { T } }X\to X^p_T$
sending
$U\colon L^2_H(\mathcal {B})\otimes _{\tilde { T } }X\to X^p_T$
sending
![]() $f\otimes _{\tilde { T } }\xi $
to
$f\otimes _{\tilde { T } }\xi $
to
![]() $f\otimes _T\xi .$
This operator intertwines
$f\otimes _T\xi .$
This operator intertwines
![]() $\Lambda ^{H\mathcal {B}}\otimes _{\tilde { T } }1$
and
$\Lambda ^{H\mathcal {B}}\otimes _{\tilde { T } }1$
and
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)$
because for all
$\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)$
because for all
![]() $f,g\in C_c(\mathcal {B})$
and
$f,g\in C_c(\mathcal {B})$
and
![]() $\xi \in X$
we have
$\xi \in X$
we have
 $$ \begin{align*} U^{*} \tilde{ {\mathop{\mathrm{Ind}}} } _H^{\mathcal{B}}(T)_fU (g\otimes_{\tilde{ T } }\eta) & =U^{*}((f*g)\otimes_T\eta)=(f*g)\otimes_{\tilde{ T } }\eta \\ & = [\Lambda^{H\mathcal{B}}\otimes_{\tilde{ T } }1]_f(g\otimes_{\tilde{ T } }\eta); \end{align*} $$
$$ \begin{align*} U^{*} \tilde{ {\mathop{\mathrm{Ind}}} } _H^{\mathcal{B}}(T)_fU (g\otimes_{\tilde{ T } }\eta) & =U^{*}((f*g)\otimes_T\eta)=(f*g)\otimes_{\tilde{ T } }\eta \\ & = [\Lambda^{H\mathcal{B}}\otimes_{\tilde{ T } }1]_f(g\otimes_{\tilde{ T } }\eta); \end{align*} $$
which implies
![]() $U^{*} \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)_fU=[\Lambda ^{H\mathcal {B}}\otimes _{\tilde { T } }1]_f$
for all
$U^{*} \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)_fU=[\Lambda ^{H\mathcal {B}}\otimes _{\tilde { T } }1]_f$
for all
![]() $f\in C^{*}(\mathcal {B}).$
$f\in C^{*}(\mathcal {B}).$
Remark 2.6 One may use [Reference Fell and Doran11, Chapter VIII Section 12.7] to disintegrate
![]() $\Lambda ^{H\mathcal {B}}$
into a Fréchet representation
$\Lambda ^{H\mathcal {B}}$
into a Fréchet representation
![]() ${\Lambda ^{H\mathcal {B}}}'$
which happens to be given by
${\Lambda ^{H\mathcal {B}}}'$
which happens to be given by
![]() ${\Lambda ^{H\mathcal {B}}}^{\prime }_b f = bf,$
for all
${\Lambda ^{H\mathcal {B}}}^{\prime }_b f = bf,$
for all
![]() $b\in \mathcal {B}$
and
$b\in \mathcal {B}$
and
![]() $f\in C_c(\mathcal {B})\subset L^2_H(\mathcal {B}).$
This ultimately follows from the fact that for all
$f\in C_c(\mathcal {B})\subset L^2_H(\mathcal {B}).$
This ultimately follows from the fact that for all
![]() $b\in \mathcal {B}$
and
$b\in \mathcal {B}$
and
![]() $f,g\in C_c(\mathcal {B})$
,
$f,g\in C_c(\mathcal {B})$
,
![]() ${\Lambda ^{H\mathcal {B}}}^{\prime }_b (f*g) ={\Lambda ^{H\mathcal {B}}}^{\prime }_b \Lambda ^{H\mathcal {B}}_f g = \Lambda ^{H\mathcal {B}}_{bf}g = (bf)*g = b(f*g).$
${\Lambda ^{H\mathcal {B}}}^{\prime }_b (f*g) ={\Lambda ^{H\mathcal {B}}}^{\prime }_b \Lambda ^{H\mathcal {B}}_f g = \Lambda ^{H\mathcal {B}}_{bf}g = (bf)*g = b(f*g).$
Remark 2.7 (Systems of Imprimitivity)
As pointed out in [Reference Fell and Doran11, Chapter XI Section 14.4], there is a natural action
![]() $C_0(G/H)\times C_c(\mathcal {B})\to C_c(\mathcal {B})$
,
$C_0(G/H)\times C_c(\mathcal {B})\to C_c(\mathcal {B})$
,
![]() $(f,g)\mapsto fg,$
where
$(f,g)\mapsto fg,$
where
![]() $fg (r) = f(rH)g(r).$
Moreover, Fell shows that given a representation
$fg (r) = f(rH)g(r).$
Moreover, Fell shows that given a representation
![]() $T\colon \mathcal {B}_H\to \mathbb {B}(X),$
the action of
$T\colon \mathcal {B}_H\to \mathbb {B}(X),$
the action of
![]() $C_0(G/H)$
induces a representation
$C_0(G/H)$
induces a representation
In particular,
![]() $\langle \xi ,\tilde { T } _{\langle fg,fg\rangle }\xi \rangle = \| \psi ^T_f(g\otimes _T\xi ) \|^2\leq \|f\|^2\|g\otimes _T\xi \|^2= \|f\|^2\langle \xi ,\langle g,g\rangle \xi \rangle $
and this yields
$\langle \xi ,\tilde { T } _{\langle fg,fg\rangle }\xi \rangle = \| \psi ^T_f(g\otimes _T\xi ) \|^2\leq \|f\|^2\|g\otimes _T\xi \|^2= \|f\|^2\langle \xi ,\langle g,g\rangle \xi \rangle $
and this yields
![]() $\langle fg,fg\rangle \leq \|f\|^2\langle g,g\rangle .$
This is the key fact one needs to prove the existence of a unique *-homomorphism
$\langle fg,fg\rangle \leq \|f\|^2\langle g,g\rangle .$
This is the key fact one needs to prove the existence of a unique *-homomorphism
![]() $\psi \colon C_0(G/H)\to \mathbb {B}(L^2_H(\mathcal {B}))$
such that
$\psi \colon C_0(G/H)\to \mathbb {B}(L^2_H(\mathcal {B}))$
such that
![]() $\psi _fg = fg$
for all
$\psi _fg = fg$
for all
![]() $(f,g)\in C_0(G/H)\times C_c(\mathcal {B}).$
It turns out that
$(f,g)\in C_0(G/H)\times C_c(\mathcal {B}).$
It turns out that
![]() $\psi $
is nondegenerate and
$\psi $
is nondegenerate and
![]() $\psi ^T_f = \psi _f\otimes _{\tilde { T } }1.$
The pair
$\psi ^T_f = \psi _f\otimes _{\tilde { T } }1.$
The pair
![]() $(\Lambda ^{H\mathcal {B}},\psi )$
is a kind of universal system of imprimitivity because, according to [Reference Fell and Doran11, Chapter XI 14.3–14.4], by disintegrating
$(\Lambda ^{H\mathcal {B}},\psi )$
is a kind of universal system of imprimitivity because, according to [Reference Fell and Doran11, Chapter XI 14.3–14.4], by disintegrating
![]() $\Lambda ^{H\mathcal {B}}\otimes _{\tilde { T } }1$
and
$\Lambda ^{H\mathcal {B}}\otimes _{\tilde { T } }1$
and
![]() $\psi \otimes _{\tilde { T } }1$
one gets
$\psi \otimes _{\tilde { T } }1$
one gets
![]() ${\mathop {\mathrm { Ind}}}_H^{\mathcal {B}}(T)$
and the projection-valued measure induced by
${\mathop {\mathrm { Ind}}}_H^{\mathcal {B}}(T)$
and the projection-valued measure induced by
![]() $T.$
It then should come as no surprise that, denoting
$T.$
It then should come as no surprise that, denoting
![]() $\tau $
the natural action of G on
$\tau $
the natural action of G on
![]() $C_0(G/H),$
one obtains
$C_0(G/H),$
one obtains
![]() ${\Lambda ^{H\mathcal {B}}}^{\prime }_b \psi _f = \psi _{\tau _t(f)} {\Lambda ^{H\mathcal {B}}}^{\prime }_b$
for all
${\Lambda ^{H\mathcal {B}}}^{\prime }_b \psi _f = \psi _{\tau _t(f)} {\Lambda ^{H\mathcal {B}}}^{\prime }_b$
for all
![]() $b\in B_t$
and
$b\in B_t$
and
![]() $f\in C_0(G/H).$
$f\in C_0(G/H).$
Remark 2.8 If
![]() $H=\{e\},$
then
$H=\{e\},$
then
![]() $L^2_H(\mathcal {B})=L^2_e(\mathcal {B})$
and
$L^2_H(\mathcal {B})=L^2_e(\mathcal {B})$
and
![]() $\Lambda ^{H\mathcal {B}}=\lambda _{\mathcal {B}}.$
Indeed, in this situation
$\Lambda ^{H\mathcal {B}}=\lambda _{\mathcal {B}}.$
Indeed, in this situation
![]() $B_e\equiv C_c(\mathcal {B}_H)$
and the inner product of
$B_e\equiv C_c(\mathcal {B}_H)$
and the inner product of
![]() $f,g\in C_c(\mathcal {B})$
in
$f,g\in C_c(\mathcal {B})$
in
![]() $L^2_e(\mathcal {B})$
is
$L^2_e(\mathcal {B})$
is
![]() $\int _Gf(t)^{*}g(t)\, dt=f^{*}*g(e)\equiv p(f^{*}*g)=\langle f,g\rangle _H^{\mathcal {B}}.$
The action of (2.3) reduces to
$\int _Gf(t)^{*}g(t)\, dt=f^{*}*g(e)\equiv p(f^{*}*g)=\langle f,g\rangle _H^{\mathcal {B}}.$
The action of (2.3) reduces to
![]() $(fb)(t) =f(t)b$
and this is the action used by Exel and Ng to construct
$(fb)(t) =f(t)b$
and this is the action used by Exel and Ng to construct
![]() $L^2_e(\mathcal {B}).$
Hence,
$L^2_e(\mathcal {B}).$
Hence,
![]() $L^2_H(\mathcal {B})=L^2_e(\mathcal {B}).$
The rest is an immediate consequence of the last proposition above and [Reference Exel and Ng8, Proposition 2.6].
$L^2_H(\mathcal {B})=L^2_e(\mathcal {B}).$
The rest is an immediate consequence of the last proposition above and [Reference Exel and Ng8, Proposition 2.6].
Remark 2.9 If
![]() $H=G$
then
$H=G$
then
![]() $L^2_H(\mathcal {B})$
is the C*-algebra
$L^2_H(\mathcal {B})$
is the C*-algebra
![]() $C^{*}(\mathcal {B})$
considered as a right
$C^{*}(\mathcal {B})$
considered as a right
![]() $C^{*}(\mathcal {B})$
-Hilbert module and
$C^{*}(\mathcal {B})$
-Hilbert module and
![]() $\Lambda ^{G\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(C^{*}(\mathcal {B}))$
is the natural inclusion. This is the case because
$\Lambda ^{G\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(C^{*}(\mathcal {B}))$
is the natural inclusion. This is the case because
![]() $\langle f,g\rangle _G^{\mathcal {B}} = p(f^{*}*g)=f^{*}*g$
and the action (2.3) is given by the convolution product.
$\langle f,g\rangle _G^{\mathcal {B}} = p(f^{*}*g)=f^{*}*g$
and the action (2.3) is given by the convolution product.
3 Universal properties of cross-sectional C*-algebras
Let
![]() $\mathcal {B}$
be a Fell bundle and
$\mathcal {B}$
be a Fell bundle and
![]() $\mathcal {F}$
a non empty family of representations of
$\mathcal {F}$
a non empty family of representations of
![]() $\mathcal {B}.$
We say that a C*-algebra A is universal for
$\mathcal {B}.$
We say that a C*-algebra A is universal for
![]() $\mathcal {F}$
if there exists a surjective *-homomorphism
$\mathcal {F}$
if there exists a surjective *-homomorphism
![]() $\pi \colon C^{*}(\mathcal {B})\to A$
such that (i) for every
$\pi \colon C^{*}(\mathcal {B})\to A$
such that (i) for every
![]() $(S\colon \mathcal {B}\to \mathbb {B}(X))\in \mathcal {F},$
there exists a representation
$(S\colon \mathcal {B}\to \mathbb {B}(X))\in \mathcal {F},$
there exists a representation
![]() $\rho ^S\colon A\to \mathbb {B}(X)$
with
$\rho ^S\colon A\to \mathbb {B}(X)$
with
![]() $\rho ^S\circ \pi =\tilde { S } $
and (ii) for some
$\rho ^S\circ \pi =\tilde { S } $
and (ii) for some
![]() $S\in \mathcal {F}$
,
$S\in \mathcal {F}$
,
![]() $\rho ^S$
is faithful. Notice
$\rho ^S$
is faithful. Notice
![]() $\rho ^S$
is unique because
$\rho ^S$
is unique because
![]() $\pi $
is surjective.
$\pi $
is surjective.
Say
![]() $S\in \mathcal {F}$
is such that
$S\in \mathcal {F}$
is such that
![]() $\rho ^S$
is faithful. Then
$\rho ^S$
is faithful. Then
![]() $\ker (\pi )=\ker (\tilde { S } )=\cap \{\ker (\tilde { T } )\colon T\in \mathcal {F}\}$
and this implies the existence of an isomorphism
$\ker (\pi )=\ker (\tilde { S } )=\cap \{\ker (\tilde { T } )\colon T\in \mathcal {F}\}$
and this implies the existence of an isomorphism
![]() $\hat {\pi }\colon A\to C^{*}(\mathcal {B})/\cap \{\ker (\tilde { T } )\colon T\in \mathcal {F}\}$
such that
$\hat {\pi }\colon A\to C^{*}(\mathcal {B})/\cap \{\ker (\tilde { T } )\colon T\in \mathcal {F}\}$
such that
![]() $\hat {\pi }\circ \pi $
is the natural quotient map. Given another surjective *-homomorphism
$\hat {\pi }\circ \pi $
is the natural quotient map. Given another surjective *-homomorphism
![]() $\kappa \colon C^{*}(\mathcal {B})\to C$
satisfying (i) and (ii),
$\kappa \colon C^{*}(\mathcal {B})\to C$
satisfying (i) and (ii),
![]() $\mu :=(\hat {\kappa })^{-1}\circ \hat {\pi }\colon A\to C$
is the unique isomorphism such that
$\mu :=(\hat {\kappa })^{-1}\circ \hat {\pi }\colon A\to C$
is the unique isomorphism such that
![]() $\mu \circ \pi = \kappa .$
$\mu \circ \pi = \kappa .$
The next propositions imply
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
is universal for the representations of
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
is universal for the representations of
![]() $\mathcal {B}$
induced from representations of
$\mathcal {B}$
induced from representations of
![]() $\mathcal {B}_H;$
while
$\mathcal {B}_H;$
while
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
is for those of the form
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
is for those of the form
![]() $T\otimes {\mathop {\mathrm {Ind}}}_H^G(U)$
, T being a representation of
$T\otimes {\mathop {\mathrm {Ind}}}_H^G(U)$
, T being a representation of
![]() $\mathcal {B}$
and U one of
$\mathcal {B}$
and U one of
![]() $H.$
$H.$
Proposition 3.1 Let
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle,
$\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle,
![]() $H\leqslant G$
and
$H\leqslant G$
and
![]() $T\colon \mathcal {B}_H\to \mathbb {B}(X)$
a representation. Then there exists a unique representation
$T\colon \mathcal {B}_H\to \mathbb {B}(X)$
a representation. Then there exists a unique representation
![]() $\rho \colon C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})\to \mathbb {B}(X^p_T)$
such that
$\rho \colon C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})\to \mathbb {B}(X^p_T)$
such that
![]() $\rho \circ q^{H\uparrow \mathcal {B}}=\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T).$
Moreover, if
$\rho \circ q^{H\uparrow \mathcal {B}}=\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T).$
Moreover, if
![]() $\tilde { T } $
is faithful then so is
$\tilde { T } $
is faithful then so is
![]() $\rho .$
$\rho .$
Proof Let
![]() $J\subset C^{*}(\mathcal {B})$
be the intersection of all the kernels of integrated forms of representations of
$J\subset C^{*}(\mathcal {B})$
be the intersection of all the kernels of integrated forms of representations of
![]() $\mathcal {B}$
induced from representations of
$\mathcal {B}$
induced from representations of
![]() $\mathcal {B}_H.$
We obviously have
$\mathcal {B}_H.$
We obviously have
![]() $J\subset \ker (\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)),$
so there exists a unique function
$J\subset \ker (\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)),$
so there exists a unique function
![]() $\rho \colon C^{*}(\mathcal {B})/J\to \mathbb {B}(X^p_T)$
such that
$\rho \colon C^{*}(\mathcal {B})/J\to \mathbb {B}(X^p_T)$
such that
![]() $\rho \circ q^{H\uparrow \mathcal {B}} = \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)$
(implying
$\rho \circ q^{H\uparrow \mathcal {B}} = \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T)$
(implying
![]() $\rho $
is a representation).
$\rho $
is a representation).
Assume
![]() $\tilde { T } $
is faithful and let S be any other representation of
$\tilde { T } $
is faithful and let S be any other representation of
![]() $\mathcal {B}_H.$
Both S and its nondegenerate part induce the same representation of
$\mathcal {B}_H.$
Both S and its nondegenerate part induce the same representation of
![]() $\mathcal {B},$
so we may assume both S and T are nondegenerate. We have
$\mathcal {B},$
so we may assume both S and T are nondegenerate. We have
![]() $\tilde { S } \preceq \tilde { T } $
because
$\tilde { S } \preceq \tilde { T } $
because
![]() $\tilde { T } $
is faithful. By the definition of weak containment for bundles,
$\tilde { T } $
is faithful. By the definition of weak containment for bundles,
![]() $S\preceq T$
and the continuity of the induction process with respect the regional topology [Reference Fell and Doran11, Chapter XI Section 12.4] implies
$S\preceq T$
and the continuity of the induction process with respect the regional topology [Reference Fell and Doran11, Chapter XI Section 12.4] implies
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(S)\preceq \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T).$
Hence,
$\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(S)\preceq \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T).$
Hence,
![]() $\ker (\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T))\subset \ker (\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(S))$
and it follows that
$\ker (\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T))\subset \ker (\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(S))$
and it follows that
![]() $J=\ker (\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T))$
or, in other words, that
$J=\ker (\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T))$
or, in other words, that
![]() $\rho $
is faithful.
$\rho $
is faithful.
Proposition 3.2 Let
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle and
$\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle and
![]() $H\leqslant G.$
Given nondegenerate representations
$H\leqslant G.$
Given nondegenerate representations
![]() $T\colon \mathcal {B}\to \mathbb {B}(X)$
and
$T\colon \mathcal {B}\to \mathbb {B}(X)$
and
![]() $U\colon H\to \mathbb {B}(Y)$
there exists a (unique) representation
$U\colon H\to \mathbb {B}(Y)$
there exists a (unique) representation
![]() $\rho \colon C^{*}_{H\uparrow G}(\mathcal {B})\to \mathbb {B}(X\otimes Y)$
such that
$\rho \colon C^{*}_{H\uparrow G}(\mathcal {B})\to \mathbb {B}(X\otimes Y)$
such that
![]() $\rho \circ q^{H\uparrow G}_{\mathcal {B}} =T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U).$
Moreover,
$\rho \circ q^{H\uparrow G}_{\mathcal {B}} =T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U).$
Moreover,
![]() $\rho $
is faithful if
$\rho $
is faithful if
![]() $\tilde { T } $
and
$\tilde { T } $
and
![]() $\tilde { U } $
are.
$\tilde { U } $
are.
Proof By definition, we may think of
![]() $C^{*}_{H\uparrow G}(\mathcal {B})$
as the image of the *-homomorphism
$C^{*}_{H\uparrow G}(\mathcal {B})$
as the image of the *-homomorphism
![]() $\delta \colon C^{*}(\mathcal {B})\to M(C^{*}(\mathcal {B})\otimes Q)$
associated with the quotient map
$\delta \colon C^{*}(\mathcal {B})\to M(C^{*}(\mathcal {B})\otimes Q)$
associated with the quotient map
![]() $q\colon C^{*}(G)\to Q:=C^{*}(G)/I;$
with
$q\colon C^{*}(G)\to Q:=C^{*}(G)/I;$
with
![]() $I\subset C^{*}(G)$
the intersection of all the kernels of integrated form of *-representations induced from
$I\subset C^{*}(G)$
the intersection of all the kernels of integrated form of *-representations induced from
![]() $H.$
Hence,
$H.$
Hence,
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _H^G(U)$
factors through a representation
$\tilde { {\mathop {\mathrm {Ind}}} } _H^G(U)$
factors through a representation
![]() $\pi \colon Q\to \mathbb {B}(Y)$
and we get a representation
$\pi \colon Q\to \mathbb {B}(Y)$
and we get a representation
![]() $\tilde { T } \otimes \pi \colon C^{*}(\mathcal {B})\otimes Q\to \mathbb {B}(X\otimes Y)$
we may extend to the multiplier algebra to get a representation
$\tilde { T } \otimes \pi \colon C^{*}(\mathcal {B})\otimes Q\to \mathbb {B}(X\otimes Y)$
we may extend to the multiplier algebra to get a representation
![]() $\overline {\tilde { T } \otimes \pi }.$
$\overline {\tilde { T } \otimes \pi }.$
When we described
![]() $\delta \colon C^{*}(\mathcal {B})\to M(C^{*}(\mathcal {B})\otimes Q)$
in the introduction we made use of canonical unitary representation
$\delta \colon C^{*}(\mathcal {B})\to M(C^{*}(\mathcal {B})\otimes Q)$
in the introduction we made use of canonical unitary representation
![]() $\iota \colon G\to M(Q)$
and the action of
$\iota \colon G\to M(Q)$
and the action of
![]() $\mathcal {B}$
on
$\mathcal {B}$
on
![]() $C_c(\mathcal {B})\subset C^{*}(\mathcal {B}).$
In fact,
$C_c(\mathcal {B})\subset C^{*}(\mathcal {B}).$
In fact,
![]() $\delta _f (g\otimes z) =\int _G f(t)g\otimes \iota (t)z\, dt$
for all
$\delta _f (g\otimes z) =\int _G f(t)g\otimes \iota (t)z\, dt$
for all
![]() $f,g\in C_c(\mathcal {B})$
and
$f,g\in C_c(\mathcal {B})$
and
![]() $z\in Q.$
This yields
$z\in Q.$
This yields
![]() $ \overline {\tilde { T } \otimes \pi }\circ \delta = T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U).$
Since we are identifying
$ \overline {\tilde { T } \otimes \pi }\circ \delta = T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U).$
Since we are identifying
![]() $C^{*}_{H\uparrow G}(\mathcal {B})=\delta (C^{*}(\mathcal {B})),$
the quotient
$C^{*}_{H\uparrow G}(\mathcal {B})=\delta (C^{*}(\mathcal {B})),$
the quotient
![]() $q^{H\uparrow G}_{\mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{H\uparrow G}(\mathcal {B})$
becomes
$q^{H\uparrow G}_{\mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{H\uparrow G}(\mathcal {B})$
becomes
![]() $f\mapsto \delta _f$
and we may therefore define
$f\mapsto \delta _f$
and we may therefore define
![]() $\rho $
as the restriction of
$\rho $
as the restriction of
![]() $\overline {\tilde { T } \otimes \pi }$
to
$\overline {\tilde { T } \otimes \pi }$
to
![]() $C^{*}_{H\uparrow G}(\mathcal {B}).$
Say we have some other representation
$C^{*}_{H\uparrow G}(\mathcal {B}).$
Say we have some other representation
![]() $\rho '\colon C^{*}_{H\uparrow G}(\mathcal {B})\to \mathbb {B}(X\otimes Y)$
such that
$\rho '\colon C^{*}_{H\uparrow G}(\mathcal {B})\to \mathbb {B}(X\otimes Y)$
such that
![]() $\rho '\circ q^{H\uparrow G}_{\mathcal {B}}=T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U).$
Then
$\rho '\circ q^{H\uparrow G}_{\mathcal {B}}=T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U).$
Then
![]() $\rho '\circ q^{H\uparrow G}_{\mathcal {B}} =\rho \circ q^{H\uparrow G}_{\mathcal {B}}$
and this yields
$\rho '\circ q^{H\uparrow G}_{\mathcal {B}} =\rho \circ q^{H\uparrow G}_{\mathcal {B}}$
and this yields
![]() $\rho =\rho '$
because
$\rho =\rho '$
because
![]() $q^{H\uparrow G}_{\mathcal {B}}$
is surjective.
$q^{H\uparrow G}_{\mathcal {B}}$
is surjective.
Assume the integrated forms of T and U are faithful. Then,
![]() $\pi $
is faithful because given any other representation V of H we have
$\pi $
is faithful because given any other representation V of H we have
![]() $\tilde { V } \preceq \tilde { U } \Rightarrow V\preceq U\Rightarrow {\mathop {\mathrm {Ind}}}_H^G(V)\preceq {\mathop {\mathrm {Ind}}}_H^G(U)\Rightarrow \tilde { {\mathop {\mathrm {Ind}}} } _H^G(V)\preceq \tilde { {\mathop {\mathrm {Ind}}} } _H^G(U)$
and this implies I is the kernel of
$\tilde { V } \preceq \tilde { U } \Rightarrow V\preceq U\Rightarrow {\mathop {\mathrm {Ind}}}_H^G(V)\preceq {\mathop {\mathrm {Ind}}}_H^G(U)\Rightarrow \tilde { {\mathop {\mathrm {Ind}}} } _H^G(V)\preceq \tilde { {\mathop {\mathrm {Ind}}} } _H^G(U)$
and this implies I is the kernel of
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _H^G(U)$
or, in other words,
$\tilde { {\mathop {\mathrm {Ind}}} } _H^G(U)$
or, in other words,
![]() $\pi $
is faithful and so must be
$\pi $
is faithful and so must be
![]() $\overline {\tilde { T } \otimes \pi };$
which clearly implies
$\overline {\tilde { T } \otimes \pi };$
which clearly implies
![]() $\rho $
is faithful.
$\rho $
is faithful.
Remark 3.3 Say
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle and we have conjugated subgroups
$\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle and we have conjugated subgroups
![]() $H\leqslant G$
and
$H\leqslant G$
and
![]() $K=rH{r^{-1}}.$
By [Reference Fell and Doran11, Chapter XI Section 12.21], up to unitary equivalences, the classes of representations of G induced from H and K agree. Then there exists an isomorphism
$K=rH{r^{-1}}.$
By [Reference Fell and Doran11, Chapter XI Section 12.21], up to unitary equivalences, the classes of representations of G induced from H and K agree. Then there exists an isomorphism
![]() $\chi \colon C^{*}_{H\uparrow G}(\mathcal {B})\to C^{*}_{K\uparrow G}(\mathcal {B})$
such that
$\chi \colon C^{*}_{H\uparrow G}(\mathcal {B})\to C^{*}_{K\uparrow G}(\mathcal {B})$
such that
![]() $\chi \circ q^{H\uparrow G}_{\mathcal {B}}=q^{K\uparrow G}_{\mathcal {B}}.$
$\chi \circ q^{H\uparrow G}_{\mathcal {B}}=q^{K\uparrow G}_{\mathcal {B}}.$
In the introduction, we showed
![]() $C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})=\lambda _{\mathcal {B}}(C^{*}(\mathcal {B}))$
and we know from Remark 2.8 that
$C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})=\lambda _{\mathcal {B}}(C^{*}(\mathcal {B}))$
and we know from Remark 2.8 that
![]() $\lambda _{\mathcal {B}}=\Lambda ^{\{e\}\mathcal {B}}.$
Thus
$\lambda _{\mathcal {B}}=\Lambda ^{\{e\}\mathcal {B}}.$
Thus
![]() $C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})= \Lambda ^{\{e\}\mathcal {B}}(C^{*}(\mathcal {B})).$
This is a particular case of a more general fact.
$C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})= \Lambda ^{\{e\}\mathcal {B}}(C^{*}(\mathcal {B})).$
This is a particular case of a more general fact.
Corollary 3.4 For every Fell bundle
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
and
$\mathcal {B}=\{B_t\}_{t\in G}$
and
![]() $H\leqslant G,$
the quotient map
$H\leqslant G,$
the quotient map
![]() $C^{*}(\mathcal {B})\to \Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))$
,
$C^{*}(\mathcal {B})\to \Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))$
,
![]() $f\mapsto \Lambda ^{H\mathcal {B}}(f),$
makes of
$f\mapsto \Lambda ^{H\mathcal {B}}(f),$
makes of
![]() $\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))$
a universal C*-algebra for the representations of
$\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))$
a universal C*-algebra for the representations of
![]() $\mathcal {B}$
induced from
$\mathcal {B}$
induced from
![]() $\mathcal {B}_H.$
$\mathcal {B}_H.$
Proof Let
![]() $T\colon \mathcal {B}_H\to \mathbb {B}(X)$
be a representation. By Proposition 2.5, there exists a *-homomorphism
$T\colon \mathcal {B}_H\to \mathbb {B}(X)$
be a representation. By Proposition 2.5, there exists a *-homomorphism
![]() $\theta \colon \mathbb {B}(L^2_H(\mathcal {B}))\to \mathbb {B}(L^2_H(\mathcal {B})\otimes _{\tilde { T } }X)$
such that
$\theta \colon \mathbb {B}(L^2_H(\mathcal {B}))\to \mathbb {B}(L^2_H(\mathcal {B})\otimes _{\tilde { T } }X)$
such that
![]() $\theta (M)=M\otimes _{\tilde { T } }1$
and
$\theta (M)=M\otimes _{\tilde { T } }1$
and
![]() $\theta \circ \Lambda ^{H\mathcal {B}} = \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T).$
The restriction
$\theta \circ \Lambda ^{H\mathcal {B}} = \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T).$
The restriction
![]() $\theta |_{\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))}\colon \Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))\to \mathbb {B}(X^p_T)$
is then the unique representation
$\theta |_{\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))}\colon \Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))\to \mathbb {B}(X^p_T)$
is then the unique representation
![]() $\rho $
of
$\rho $
of
![]() $\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))$
such that
$\Lambda ^{H\mathcal {B}}(C^{*}(\mathcal {B}))$
such that
![]() $\rho \circ \Lambda ^{H\mathcal {B}}= \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T).$
If
$\rho \circ \Lambda ^{H\mathcal {B}}= \tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(T).$
If
![]() $\tilde { T } $
is faithful then
$\tilde { T } $
is faithful then
![]() $\theta $
is also, which clearly implies
$\theta $
is also, which clearly implies
![]() $\rho $
is faithful.
$\rho $
is faithful.
3.1 An example
Here, we present an explicit example of a Fell bundle
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
and
$\mathcal {B}=\{B_t\}_{t\in G}$
and
![]() $H\leqslant G$
such that:
$H\leqslant G$
such that:
-
• The normalizer of H is open (because G is discrete).
-
•
 $\lambda _{\mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
is not an isomorphism.
$\lambda _{\mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
is not an isomorphism. -
• For all
 $r\in H$
,
$r\in H$
,
 $C^{*}_{rH{r^{-1}} \uparrow G}(\mathcal {B})=C^{*}(\mathcal {B})$
(see Remark 3.3).
$C^{*}_{rH{r^{-1}} \uparrow G}(\mathcal {B})=C^{*}(\mathcal {B})$
(see Remark 3.3). -
•
 $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}(\mathcal {B})$
and if
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}(\mathcal {B})$
and if
 $r\in G\setminus H,$
then
$r\in G\setminus H,$
then
 $C^{*}_{rH{r^{-1}} \uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
$C^{*}_{rH{r^{-1}} \uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
The lemma below is of key importance in the rest of the article, in particular in the example presented right after its proof. We state it in full generality and not only for discrete groups. By considering trivial Fell bundles over groups with constant fiber
![]() $\mathbb {C},$
it is easy to use the Lemma to prove the analogous statement for unitary representations of groups.
$\mathbb {C},$
it is easy to use the Lemma to prove the analogous statement for unitary representations of groups.
Lemma 3.5 If
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle and the normalizer of
$\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle and the normalizer of
![]() $H\leqslant G$
is open, then
$H\leqslant G$
is open, then
-
(1) For every nondegenerate representation T of
 $\mathcal {B}_H$
we have
$\mathcal {B}_H$
we have
 $T\preceq {\mathop {\mathrm { Ind}}}_H^{\mathcal {B}}(T)|_{\mathcal {B}_H}.$
$T\preceq {\mathop {\mathrm { Ind}}}_H^{\mathcal {B}}(T)|_{\mathcal {B}_H}.$
-
(2) Given a nondegenerate representation
 $T\colon \mathcal {B}\to \mathbb {B}(Y)$
,
$T\colon \mathcal {B}\to \mathbb {B}(Y)$
,
 $\tilde { T|_{\mathcal {B}_H} } $
is faithful if
$\tilde { T|_{\mathcal {B}_H} } $
is faithful if
 $\tilde { T } $
is.
$\tilde { T } $
is.
Proof By [Reference Fell and Doran11, Chapter XI Section 12.8] and [Reference Fell and Doran11, Chapter XI Section 14.21], the first claim holds if H is either open or closed in
![]() $H.$
To deal with the general case, we let N be the normalizer of H in
$H.$
To deal with the general case, we let N be the normalizer of H in
![]() $G.$
Using induction in stages [Reference Fell and Doran11, Chapter XI Section 12.15], the continuity of the induction and restriction processes with respect to the regional topology [Reference Fell and Doran11, Chapter XI Section 12.4 and Chapter VIII Section 21.20] we get
$G.$
Using induction in stages [Reference Fell and Doran11, Chapter XI Section 12.15], the continuity of the induction and restriction processes with respect to the regional topology [Reference Fell and Doran11, Chapter XI Section 12.4 and Chapter VIII Section 21.20] we get
and
![]() ${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T)|_{\mathcal {B}_H}\succeq T$
by transitivity.
${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T)|_{\mathcal {B}_H}\succeq T$
by transitivity.
To prove the second claim, we take nondegenerate representations S and T of
![]() $\mathcal {B}_H$
and
$\mathcal {B}_H$
and
![]() $\mathcal {B},$
respectively, with faithful integrated forms. We have
$\mathcal {B},$
respectively, with faithful integrated forms. We have
![]() ${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(S)\preceq T,$
so
${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(S)\preceq T,$
so
![]() $S\preceq {\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(S)|_{\mathcal {B}_H}\preceq T|_{\mathcal {B}_H}$
and
$S\preceq {\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(S)|_{\mathcal {B}_H}\preceq T|_{\mathcal {B}_H}$
and
![]() $\tilde { T|_{\mathcal {B}_H} } $
must be faithful because
$\tilde { T|_{\mathcal {B}_H} } $
must be faithful because
![]() $\tilde { S } $
is.
$\tilde { S } $
is.
Take for G the free group in three generators,
![]() $\mathbb {F}_3=<a,b,c>,$
and think of
$\mathbb {F}_3=<a,b,c>,$
and think of
![]() $\mathbb {F}_2=<a,b>$
as a subgroup of
$\mathbb {F}_2=<a,b>$
as a subgroup of
![]() $\mathbb {F}_3.$
Let
$\mathbb {F}_3.$
Let
![]() $\mathcal {T}=\{\mathbb {C}\delta _t\}_{t\in \mathbb {F}_3}$
be the trivial Fell bundle and define
$\mathcal {T}=\{\mathbb {C}\delta _t\}_{t\in \mathbb {F}_3}$
be the trivial Fell bundle and define
Then,
![]() $\mathcal {B}$
is a Fell bundle with the structure inherited from
$\mathcal {B}$
is a Fell bundle with the structure inherited from
![]() $\mathcal {T}.$
$\mathcal {T}.$
Nondegenerate representations of
![]() $\mathcal {B}$
and unitary representations of
$\mathcal {B}$
and unitary representations of
![]() $\mathbb {F}_2$
are in one to one correspondence via an association
$\mathbb {F}_2$
are in one to one correspondence via an association
where
![]() $U^T_t:= T_{ 1 \delta _t }.$
This identification preserves direct sums, weak containment, and unitary equivalence.
$U^T_t:= T_{ 1 \delta _t }.$
This identification preserves direct sums, weak containment, and unitary equivalence.
Given a nondegenerate representation
![]() $T\colon \mathcal {B}\to \mathbb {B}(X)$
and
$T\colon \mathcal {B}\to \mathbb {B}(X)$
and
![]() $f\in C_c(\mathcal {B}),$
let
$f\in C_c(\mathcal {B}),$
let
![]() $f'\in C_c(\mathbb {F}_2)$
be such that
$f'\in C_c(\mathbb {F}_2)$
be such that
![]() $f(t)=f'(t)\delta _s$
for all
$f(t)=f'(t)\delta _s$
for all
![]() $t\in \mathbb {F}_2.$
It is easy so show
$t\in \mathbb {F}_2.$
It is easy so show
![]() $\tilde { T } _f = \tilde { U } ^T_{f'}$
and this implies the existence of a unique isomorphism
$\tilde { T } _f = \tilde { U } ^T_{f'}$
and this implies the existence of a unique isomorphism
![]() $\pi \colon C^{*}(\mathcal {B})\to C^{*}(\mathbb {F}_2)$
extending
$\pi \colon C^{*}(\mathcal {B})\to C^{*}(\mathbb {F}_2)$
extending
![]() $C_c(\mathcal {B})\to C_c(\mathbb {F}_2)$
,
$C_c(\mathcal {B})\to C_c(\mathbb {F}_2)$
,
![]() $f\mapsto f'.$
Hence,
$f\mapsto f'.$
Hence,
![]() $C^{*}(\mathcal {B})=C^{*}(\mathbb {F}_2).$
$C^{*}(\mathcal {B})=C^{*}(\mathbb {F}_2).$
Fix
![]() $t\in \mathbb {F}_3$
and set
$t\in \mathbb {F}_3$
and set
![]() $H:=t\mathbb {F}_2{t^{-1}}.$
We want to identify
$H:=t\mathbb {F}_2{t^{-1}}.$
We want to identify
![]() $C^{*}_{H\uparrow \mathbb {F}_3}(\mathcal {B})$
and
$C^{*}_{H\uparrow \mathbb {F}_3}(\mathcal {B})$
and
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}).$
According to Remark 3.3,
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}).$
According to Remark 3.3,
![]() $C^{*}_{H\uparrow \mathbb {F}_3}(\mathcal {B})=C^{*}_{\mathbb {F}_2\uparrow \mathbb {F}_3}(\mathcal {B})$
and to compute this last algebra we take nondegenerate faithful representations
$C^{*}_{H\uparrow \mathbb {F}_3}(\mathcal {B})=C^{*}_{\mathbb {F}_2\uparrow \mathbb {F}_3}(\mathcal {B})$
and to compute this last algebra we take nondegenerate faithful representations
![]() $\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
and
$\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
and
![]() $\tilde { V } \colon C^{*}(\mathbb {F}_2)\to \mathbb {B}(Y).$
We have
$\tilde { V } \colon C^{*}(\mathbb {F}_2)\to \mathbb {B}(Y).$
We have
Since V weakly contains the trivial representation of
![]() $\mathbb {F}_2$
and
$\mathbb {F}_2$
and
![]() $V\preceq {\mathop {\mathrm {Ind}}}_{\mathbb {F}_2}^{\mathbb {F}_3}(V)|_{\mathbb {F}_2}$
(Lemma 3.5), we have
$V\preceq {\mathop {\mathrm {Ind}}}_{\mathbb {F}_2}^{\mathbb {F}_3}(V)|_{\mathbb {F}_2}$
(Lemma 3.5), we have
![]() $U^T\preceq U^T\otimes V\preceq U^T\otimes {\mathop {\mathrm {Ind}}}_{\mathbb {F}_2}^{\mathbb {F}_3}(V)|_{\mathbb {F}_2}.$
Thus the integrated form of
$U^T\preceq U^T\otimes V\preceq U^T\otimes {\mathop {\mathrm {Ind}}}_{\mathbb {F}_2}^{\mathbb {F}_3}(V)|_{\mathbb {F}_2}.$
Thus the integrated form of
![]() $U^{T\otimes {\mathop {\mathrm {Ind}}}_{\mathbb {F}_2}^{\mathbb {F}_3}(V)}$
is faithful and, consequently,
$U^{T\otimes {\mathop {\mathrm {Ind}}}_{\mathbb {F}_2}^{\mathbb {F}_3}(V)}$
is faithful and, consequently,
![]() $ T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_{\mathbb {F}_2}^{\mathbb {F}_3}(V) $
is a faithful representation of
$ T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_{\mathbb {F}_2}^{\mathbb {F}_3}(V) $
is a faithful representation of
![]() $C^{*}(\mathcal {B})$
that factors through a representation of
$C^{*}(\mathcal {B})$
that factors through a representation of
![]() $C^{*}_{\mathbb {F}_2\uparrow \mathbb {F}_3}(\mathcal {B})$
via
$C^{*}_{\mathbb {F}_2\uparrow \mathbb {F}_3}(\mathcal {B})$
via
![]() $q^{\mathbb {F}_2\uparrow \mathbb {F}_3}_{\mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{\mathbb {F}_2\uparrow \mathbb {F}_3}(\mathcal {B}).$
It is then clear that
$q^{\mathbb {F}_2\uparrow \mathbb {F}_3}_{\mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{\mathbb {F}_2\uparrow \mathbb {F}_3}(\mathcal {B}).$
It is then clear that
![]() $q^{\mathbb {F}_2\uparrow \mathbb {F}_3}_{\mathcal {B}}$
is faithful and we may think
$q^{\mathbb {F}_2\uparrow \mathbb {F}_3}_{\mathcal {B}}$
is faithful and we may think
![]() $C^{*}_{\mathbb {F}_2\uparrow \mathbb {F}_3}(\mathcal {B}) =C^{*}(\mathbb {F}_2).$
$C^{*}_{\mathbb {F}_2\uparrow \mathbb {F}_3}(\mathcal {B}) =C^{*}(\mathbb {F}_2).$
To compute
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}),$
we must consider the representations of
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}),$
we must consider the representations of
![]() $\mathcal {B}_H.$
The only non zero fibers of
$\mathcal {B}_H.$
The only non zero fibers of
![]() $\mathcal {B}_H$
are those over
$\mathcal {B}_H$
are those over
![]() $H\cap \mathbb {F}_2.$
We divide the discussion in two cases:
$H\cap \mathbb {F}_2.$
We divide the discussion in two cases:
![]() $t\in \mathbb {F}_2$
and
$t\in \mathbb {F}_2$
and
![]() $t\notin \mathbb {F}_2.$
In the first case,
$t\notin \mathbb {F}_2.$
In the first case,
![]() $\mathcal {B}_H$
is the trivial bundle over the group
$\mathcal {B}_H$
is the trivial bundle over the group
![]() $H=\mathbb {F}_2$
and representations of
$H=\mathbb {F}_2$
and representations of
![]() $\mathcal {B}$
,
$\mathcal {B}$
,
![]() $\mathcal {B}_H$
and
$\mathcal {B}_H$
and
![]() $\mathbb {F}_2$
are in one to one correspondence
$\mathbb {F}_2$
are in one to one correspondence
![]() $T\leftrightsquigarrow T|_{\mathcal {B}_H}\leftrightsquigarrow U^T.$
Moreover, this association preserves weak containment and direct sums. By Lemma 3.5, for every representation S of
$T\leftrightsquigarrow T|_{\mathcal {B}_H}\leftrightsquigarrow U^T.$
Moreover, this association preserves weak containment and direct sums. By Lemma 3.5, for every representation S of
![]() $\mathcal {B}_H$
we have
$\mathcal {B}_H$
we have
![]() $S\preceq {\mathop {\mathrm { Ind}}}_H^{\mathcal {B}}(S)|_{\mathcal {B}_H}$
so
$S\preceq {\mathop {\mathrm { Ind}}}_H^{\mathcal {B}}(S)|_{\mathcal {B}_H}$
so
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(S)$
is faithful if
$\tilde { {\mathop {\mathrm {Ind}}} } _H^{\mathcal {B}}(S)$
is faithful if
![]() $\tilde { S } $
is. By Proposition 3.1,
$\tilde { S } $
is. By Proposition 3.1,
![]() $q^{H\uparrow \mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
is an isomorphism and thus we get
$q^{H\uparrow \mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
is an isomorphism and thus we get
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}) = C^{*}(\mathbb {F}_2).$
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}) = C^{*}(\mathbb {F}_2).$
Now assume
![]() $t\notin \mathbb {F}_2,$
in which case the word t contains a letter c or
$t\notin \mathbb {F}_2,$
in which case the word t contains a letter c or
![]() $c^{-1}$
and this implies
$c^{-1}$
and this implies
![]() $H\cap \mathbb {F}_2=\{e\}.$
The only non zero fiber of
$H\cap \mathbb {F}_2=\{e\}.$
The only non zero fiber of
![]() $\mathcal {B}_H$
is then
$\mathcal {B}_H$
is then
![]() $B_e=\mathbb {C}\delta _e$
and for every representation T of
$B_e=\mathbb {C}\delta _e$
and for every representation T of
![]() $\mathcal {B}_H$
we have
$\mathcal {B}_H$
we have
![]() $T\cong {\mathop {\mathrm { Ind}}}_{\{e\}}^{\mathcal {B}_H}(T|_{B_e}).$
By induction in stages [Reference Fell and Doran11, Chapter XI Section 12.15] and Proposition 3.1,
$T\cong {\mathop {\mathrm { Ind}}}_{\{e\}}^{\mathcal {B}_H}(T|_{B_e}).$
By induction in stages [Reference Fell and Doran11, Chapter XI Section 12.15] and Proposition 3.1,
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
For the identity
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
For the identity
![]() $\phi \colon B_e\to \mathbb {C}$
,
$\phi \colon B_e\to \mathbb {C}$
,
![]() $U^{{\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}}(\phi )}$
is the regular representation of
$U^{{\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}}(\phi )}$
is the regular representation of
![]() $\mathbb {F}_2$
and thus we may think of
$\mathbb {F}_2$
and thus we may think of
![]() $q^{H\uparrow \mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
as the regular representation
$q^{H\uparrow \mathcal {B}}\colon C^{*}(\mathcal {B})\to C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
as the regular representation
![]() $\Lambda ^{\mathbb {F}_2}\colon C^{*}(\mathbb {F}_2)\to C^{*}_{\mathop {\mathrm {r}}}(\mathbb {F}_2).$
$\Lambda ^{\mathbb {F}_2}\colon C^{*}(\mathbb {F}_2)\to C^{*}_{\mathop {\mathrm {r}}}(\mathbb {F}_2).$
3.2 Exotic coactions
Let G be a locally compact group and fix
![]() $H\leqslant G.$
For the trivial Fell bundle
$H\leqslant G.$
For the trivial Fell bundle
![]() $\mathcal {T}_G=\{\mathbb {C}\delta _t\}_{t\in G,}$
we have
$\mathcal {T}_G=\{\mathbb {C}\delta _t\}_{t\in G,}$
we have
![]() $C^{*}(G)=C^{*}(\mathcal {T}_G).$
Since
$C^{*}(G)=C^{*}(\mathcal {T}_G).$
Since
![]() $\mathcal {T}_G$
is saturated, we have a *-homomorphism
$\mathcal {T}_G$
is saturated, we have a *-homomorphism
![]() $\pi ^{\mathcal {T}_G}_H$
as in (1.3). We know
$\pi ^{\mathcal {T}_G}_H$
as in (1.3). We know
![]() $\pi ^{\mathcal {T}_G}_H$
is an isomorphism if H is normal. The reason for this is, basically, that the trivial representation
$\pi ^{\mathcal {T}_G}_H$
is an isomorphism if H is normal. The reason for this is, basically, that the trivial representation
![]() $\tau _H\colon H\to \mathbb {C}$
is weakly contained in
$\tau _H\colon H\to \mathbb {C}$
is weakly contained in
![]() ${\mathop {\mathrm { Ind}}}_H^G(\tau _H)|_H,$
which also happens if the normalizer of H is open in G (Lemma 3.5). In [Reference Derighetti6] Derighetti gives a number of conditions implying
${\mathop {\mathrm { Ind}}}_H^G(\tau _H)|_H,$
which also happens if the normalizer of H is open in G (Lemma 3.5). In [Reference Derighetti6] Derighetti gives a number of conditions implying
![]() $\tau _H\preceq {\mathop {\mathrm {Ind}}}_H^G(\tau _H)|_H.$
$\tau _H\preceq {\mathop {\mathrm {Ind}}}_H^G(\tau _H)|_H.$
Remark 3.6 If there exists a representation V of G such that
![]() $\tau _H\preceq V|_H,$
then
$\tau _H\preceq V|_H,$
then
![]() $\pi ^{\mathcal {T}_G}_H$
is an isomorphism. Indeed, for every representation U of H with faithful integrated form,
$\pi ^{\mathcal {T}_G}_H$
is an isomorphism. Indeed, for every representation U of H with faithful integrated form,
![]() ${\mathop {\mathrm {Ind}}}_H^G(U)\preceq {\mathop {\mathrm {Ind}}}_H^G( V|_H\otimes U )\cong V\otimes {\mathop {\mathrm {Ind}}}_H^G(U).$
Hence, the fact that
${\mathop {\mathrm {Ind}}}_H^G(U)\preceq {\mathop {\mathrm {Ind}}}_H^G( V|_H\otimes U )\cong V\otimes {\mathop {\mathrm {Ind}}}_H^G(U).$
Hence, the fact that
![]() $\|q^{H\uparrow \mathcal {T}_G}(f)\|\leq \| [V\otimes {\mathop {\mathrm {Ind}}}_H^G(U)]_f \|\leq \|q^{H\uparrow G}_{\mathcal {T}_G}(f)\|=\|\pi ^{\mathcal {T}_G}_H(q^{H\uparrow \mathcal {T}_G}(f))\|$
for all
$\|q^{H\uparrow \mathcal {T}_G}(f)\|\leq \| [V\otimes {\mathop {\mathrm {Ind}}}_H^G(U)]_f \|\leq \|q^{H\uparrow G}_{\mathcal {T}_G}(f)\|=\|\pi ^{\mathcal {T}_G}_H(q^{H\uparrow \mathcal {T}_G}(f))\|$
for all
![]() $f\in C^{*}(G),$
implies the desired result.
$f\in C^{*}(G),$
implies the desired result.
Definition 3.1 We say, G satisfies Derighetti’s weak condition with respect to
![]() $H\leqslant G$
if for some representation U of H it follows that
$H\leqslant G$
if for some representation U of H it follows that
![]() $\tau _H\preceq {\mathop {\mathrm {Ind}}}_H^G(U)|_H.$
$\tau _H\preceq {\mathop {\mathrm {Ind}}}_H^G(U)|_H.$
We now focus our attention on the quotients
![]() $Q^G_H:=C^{*}_{H\uparrow G}(\mathcal {T}_G)$
of
$Q^G_H:=C^{*}_{H\uparrow G}(\mathcal {T}_G)$
of
![]() $C^{*}(G)$
and the natural quotient maps
$C^{*}(G)$
and the natural quotient maps
![]() $q^G_H\equiv q^{H\uparrow G}_{\mathcal {T}_G}\colon C^{*}(G)\to Q^H_G.$
$q^G_H\equiv q^{H\uparrow G}_{\mathcal {T}_G}\colon C^{*}(G)\to Q^H_G.$
Theorem 3.7 If
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle and
$\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle and
![]() $\delta \colon C^{*}(\mathcal {B})\to M(C^{*}(\mathcal {B})\otimes Q^G_H)$
the *-homomorphism corresponding to
$\delta \colon C^{*}(\mathcal {B})\to M(C^{*}(\mathcal {B})\otimes Q^G_H)$
the *-homomorphism corresponding to
![]() $q^G_H$
(see the introduction), then there exists a unique *-homomorphism
$q^G_H$
(see the introduction), then there exists a unique *-homomorphism
![]() $\rho \colon C^{*}_{H\uparrow G}(\mathcal {B})\to M(C^{*}_{H\uparrow G}(\mathcal {B})\otimes Q^G_H)$
making
$\rho \colon C^{*}_{H\uparrow G}(\mathcal {B})\to M(C^{*}_{H\uparrow G}(\mathcal {B})\otimes Q^G_H)$
making

a commutative diagram. Moreover,
![]() $\rho $
is faithful if G satisfies Derighetti’s weak condition with respect to
$\rho $
is faithful if G satisfies Derighetti’s weak condition with respect to
![]() $H.$
$H.$
Proof Let
![]() $\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
,
$\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
,
![]() $\tilde { U } \colon C^{*}(H)\to \mathbb {B}(Y),$
and
$\tilde { U } \colon C^{*}(H)\to \mathbb {B}(Y),$
and
![]() $\tilde { V } \colon C^{*}(G)\to \mathbb {B}(Z)$
be nondegenerate faithful representations. By Proposition 3.2, there are unique faithful representations
$\tilde { V } \colon C^{*}(G)\to \mathbb {B}(Z)$
be nondegenerate faithful representations. By Proposition 3.2, there are unique faithful representations
![]() $\mu \colon C^{*}_{H\uparrow G}(\mathcal {B})\to \mathbb {B}( X\otimes Y )$
and
$\mu \colon C^{*}_{H\uparrow G}(\mathcal {B})\to \mathbb {B}( X\otimes Y )$
and
![]() $\nu \colon Q^G_H\to \mathbb {B}(Z\otimes Y)$
such that
$\nu \colon Q^G_H\to \mathbb {B}(Z\otimes Y)$
such that
![]() $\mu \circ q^{H\uparrow G}_{\mathcal {B}} = T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U)$
and
$\mu \circ q^{H\uparrow G}_{\mathcal {B}} = T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U)$
and
![]() $\nu \circ q^G_H = V\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U).$
We make extensive use of the faithful nondegenerate representation
$\nu \circ q^G_H = V\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U).$
We make extensive use of the faithful nondegenerate representation
![]() $\mu \otimes \nu \colon C^{*}_{H\uparrow G}(\mathcal {B})\otimes Q^G_H\to \mathbb {B}(X\otimes Y\otimes Z\otimes Y)$
and of its extension
$\mu \otimes \nu \colon C^{*}_{H\uparrow G}(\mathcal {B})\otimes Q^G_H\to \mathbb {B}(X\otimes Y\otimes Z\otimes Y)$
and of its extension
![]() $\overline {\mu \otimes \nu }$
to the multiplier algebra.
$\overline {\mu \otimes \nu }$
to the multiplier algebra.
We have
![]() $(\mu \otimes \nu )\circ (q^{H\uparrow G}_{\mathcal {B}}\otimes 1)= (T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U))\otimes \mu $
and this implies
$(\mu \otimes \nu )\circ (q^{H\uparrow G}_{\mathcal {B}}\otimes 1)= (T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U))\otimes \mu $
and this implies
![]() $\overline {(\mu \otimes \nu )}\circ \overline {(q^{H\uparrow G}_{\mathcal {B}}\otimes 1)}\circ \delta $
is the integrated form of
$\overline {(\mu \otimes \nu )}\circ \overline {(q^{H\uparrow G}_{\mathcal {B}}\otimes 1)}\circ \delta $
is the integrated form of
 $$ \begin{align*} (T\otimes {\mathop{\mathrm{Ind}}}_H^G(U))\otimes (V\otimes {\mathop{\mathrm{Ind}}}_H^G(U)) & \cong T\otimes V \otimes {\mathop{\mathrm{ Ind}}}_H^G({\mathop{\mathrm{Ind}}}_H^G(U)|_H\otimes U)\\ & \cong T\otimes {\mathop{\mathrm{Ind}}}_H^G(V|_H\otimes {\mathop{\mathrm{Ind}}}_H^G(U)|_H\otimes U). \end{align*} $$
$$ \begin{align*} (T\otimes {\mathop{\mathrm{Ind}}}_H^G(U))\otimes (V\otimes {\mathop{\mathrm{Ind}}}_H^G(U)) & \cong T\otimes V \otimes {\mathop{\mathrm{ Ind}}}_H^G({\mathop{\mathrm{Ind}}}_H^G(U)|_H\otimes U)\\ & \cong T\otimes {\mathop{\mathrm{Ind}}}_H^G(V|_H\otimes {\mathop{\mathrm{Ind}}}_H^G(U)|_H\otimes U). \end{align*} $$
It then follows from Proposition 3.2 that for all
![]() $f\in C^{*}(\mathcal {B}),$
we have
$f\in C^{*}(\mathcal {B}),$
we have
and the existence of
![]() $\rho $
follows (uniqueness being immediate).
$\rho $
follows (uniqueness being immediate).
Assume G satisfies Derighetti’s weak condition with respect to H and let W be a representation of H such that
![]() $\tau _H\preceq {\mathop {\mathrm { Ind}}}_H^G(W)|_H.$
Then,
$\tau _H\preceq {\mathop {\mathrm { Ind}}}_H^G(W)|_H.$
Then,
 $W\preceq U\Rightarrow {\mathop {\mathrm {Ind}}}_H^G(W)\preceq {\mathop {\mathrm {Ind}}}_H^G(U)\Rightarrow \tau _H\preceq {\mathop {\mathrm { Ind}}}_H^G(W)|_H\preceq {\mathop {\mathrm {Ind}}}_H^G(U)|_H\Rightarrow \tau _H\preceq {\mathop {\mathrm {Ind}}}_H^G(U)|_H.$
In addition,
$W\preceq U\Rightarrow {\mathop {\mathrm {Ind}}}_H^G(W)\preceq {\mathop {\mathrm {Ind}}}_H^G(U)\Rightarrow \tau _H\preceq {\mathop {\mathrm { Ind}}}_H^G(W)|_H\preceq {\mathop {\mathrm {Ind}}}_H^G(U)|_H\Rightarrow \tau _H\preceq {\mathop {\mathrm {Ind}}}_H^G(U)|_H.$
In addition,
![]() $\tau _H\preceq V|_H$
because
$\tau _H\preceq V|_H$
because
![]() ${\mathop {\mathrm {Ind}}}_H^G(U)\preceq V.$
Hence,
${\mathop {\mathrm {Ind}}}_H^G(U)\preceq V.$
Hence,
![]() $U\cong \tau _H\otimes \tau _H\otimes U\preceq V|_H\otimes {\mathop {\mathrm {Ind}}}_H^G(U)|_H\otimes U$
and the inequality of (3.1) becomes an equality (implying
$U\cong \tau _H\otimes \tau _H\otimes U\preceq V|_H\otimes {\mathop {\mathrm {Ind}}}_H^G(U)|_H\otimes U$
and the inequality of (3.1) becomes an equality (implying
![]() $\rho $
is isometric).
$\rho $
is isometric).
Let
![]() $\rho ^{\mathcal {B}}\colon C^{*}_{H\uparrow G}(\mathcal {B})\to M(C^{*}_{H\uparrow G}\otimes Q^G_H) $
and
$\rho ^{\mathcal {B}}\colon C^{*}_{H\uparrow G}(\mathcal {B})\to M(C^{*}_{H\uparrow G}\otimes Q^G_H) $
and
![]() $\rho ^{HG}\colon Q^G_H\to M(Q^H_H\otimes Q^G_H)$
be the *-homomorphisms given by the theorem above. To prove the coaction identity
$\rho ^{HG}\colon Q^G_H\to M(Q^H_H\otimes Q^G_H)$
be the *-homomorphisms given by the theorem above. To prove the coaction identity
![]() $\overline {(\rho ^{\mathcal {B}} \otimes \iota )}\circ \rho ^{\mathcal {B}} = \overline {(\iota \otimes \rho ^{HG} ) }\circ \rho ^{\mathcal {B}} $
, one may take faithful nondegenerate representations
$\overline {(\rho ^{\mathcal {B}} \otimes \iota )}\circ \rho ^{\mathcal {B}} = \overline {(\iota \otimes \rho ^{HG} ) }\circ \rho ^{\mathcal {B}} $
, one may take faithful nondegenerate representations
![]() $\tilde { T } $
,
$\tilde { T } $
,
![]() $\tilde { U } $
and
$\tilde { U } $
and
![]() $\tilde { V } $
of
$\tilde { V } $
of
![]() $C^{*}(\mathcal {B})$
,
$C^{*}(\mathcal {B})$
,
![]() $C^{*}(H)$
and
$C^{*}(H)$
and
![]() $C^{*}(G),$
respectively, and consider the (faithful) representations
$C^{*}(G),$
respectively, and consider the (faithful) representations
![]() $\mu $
and
$\mu $
and
![]() $\nu $
of
$\nu $
of
![]() $C^{*}_{H\uparrow G}(\mathcal {B})$
and
$C^{*}_{H\uparrow G}(\mathcal {B})$
and
![]() $Q^G_H,$
respectively, such that
$Q^G_H,$
respectively, such that
![]() $\mu \circ q^{H\uparrow G}_{\mathcal {B}}=T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U)$
and
$\mu \circ q^{H\uparrow G}_{\mathcal {B}}=T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_H^G(U)$
and
![]() $\nu \circ q^G_H = V\tilde { \otimes } {\mathop {\mathrm { Ind}}}_H^G(U).$
The extension
$\nu \circ q^G_H = V\tilde { \otimes } {\mathop {\mathrm { Ind}}}_H^G(U).$
The extension
![]() $\overline {(\mu \otimes \nu \otimes \nu )}$
is a faithful representation of
$\overline {(\mu \otimes \nu \otimes \nu )}$
is a faithful representation of
![]() $M(C^{*}_{H\uparrow G}(\mathcal {B})\otimes Q^G_H\otimes Q^G_H)$
and
$M(C^{*}_{H\uparrow G}(\mathcal {B})\otimes Q^G_H\otimes Q^G_H)$
and
![]() $\overline {(\mu \otimes \nu \otimes \nu )} \circ \overline {(\rho ^{\mathcal {B}} \otimes \iota )}\circ \rho ^{\mathcal {B}}\circ q^{H\uparrow G}_{\mathcal {B}}$
is the integrated form of
$\overline {(\mu \otimes \nu \otimes \nu )} \circ \overline {(\rho ^{\mathcal {B}} \otimes \iota )}\circ \rho ^{\mathcal {B}}\circ q^{H\uparrow G}_{\mathcal {B}}$
is the integrated form of
as that of
![]() $\overline {(\mu \otimes \nu \otimes \nu )}\circ \overline {(\iota \otimes \rho ^{HG} ) }\circ \rho ^{\mathcal {B}}\circ q^{H\uparrow G}_{\mathcal {B}}$
is, implying
$\overline {(\mu \otimes \nu \otimes \nu )}\circ \overline {(\iota \otimes \rho ^{HG} ) }\circ \rho ^{\mathcal {B}}\circ q^{H\uparrow G}_{\mathcal {B}}$
is, implying
The identity above implies
![]() $\overline {(\rho ^{\mathcal {B}} \otimes \iota )}\circ \rho ^{\mathcal {B}} = \overline {(\iota \otimes \rho ^{HG} ) }\circ \rho ^{\mathcal {B}} $
because
$\overline {(\rho ^{\mathcal {B}} \otimes \iota )}\circ \rho ^{\mathcal {B}} = \overline {(\iota \otimes \rho ^{HG} ) }\circ \rho ^{\mathcal {B}} $
because
![]() $\overline {(\mu \otimes \nu \otimes \nu )}$
is faithful and
$\overline {(\mu \otimes \nu \otimes \nu )}$
is faithful and
![]() $q^{H\uparrow G}_{\mathcal {B}}$
surjective.
$q^{H\uparrow G}_{\mathcal {B}}$
surjective.
3.3 Inner amenable groups
Buss, Echterhoff, and Willett have asked [Reference Buss, Echterhoff and Willett5, Question 8.8] for a class
![]() $\mathcal {C}$
of groups for which the nuclearity of
$\mathcal {C}$
of groups for which the nuclearity of
![]() $A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G$
implies the amenability of the action
$A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G$
implies the amenability of the action
![]() $\alpha .$
McKee and Pourshashami [Reference McKee and Pourshahami14] showed
$\alpha .$
McKee and Pourshashami [Reference McKee and Pourshahami14] showed
![]() $\mathcal {C}$
contains all inner amenable groups.
$\mathcal {C}$
contains all inner amenable groups.
We are not dealing with amenability here, but with weak containment. So, it is natural to replace nuclearity of
![]() $A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G$
with something weaker. We propose
$A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G$
with something weaker. We propose
![]() $(A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G)\otimes _{\max } C^{*}_{\mathop {\mathrm {r}}}(G) =(A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G)\otimes C^{*}_{\mathop {\mathrm {r}}}(G) $
and ask for which class
$(A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G)\otimes _{\max } C^{*}_{\mathop {\mathrm {r}}}(G) =(A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G)\otimes C^{*}_{\mathop {\mathrm {r}}}(G) $
and ask for which class
![]() $\mathcal {C}$
of groups this condition implies
$\mathcal {C}$
of groups this condition implies
![]() $A\rtimes _\alpha G=A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G.$
In Corollary 3.9, we show
$A\rtimes _\alpha G=A\rtimes _{{\mathop {\mathrm {r}}} \alpha }G.$
In Corollary 3.9, we show
![]() $\mathcal {C}$
contains all inner amenable groups.
$\mathcal {C}$
contains all inner amenable groups.
Following the ideas presented in the introduction, given a Fell bundle
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
one can construct a *-homomorphism
$\mathcal {B}=\{B_t\}_{t\in G}$
one can construct a *-homomorphism
such that given a nondegenerate representations
![]() $\pi \colon C^{*}(\mathcal {B})\otimes _{\max } C^{*}(G)\to \mathbb {B}(X)$
,
$\pi \colon C^{*}(\mathcal {B})\otimes _{\max } C^{*}(G)\to \mathbb {B}(X)$
,
![]() $\overline {\pi }\circ \Phi $
is the integrated form of
$\overline {\pi }\circ \Phi $
is the integrated form of
![]() $TU\colon \mathcal {B}\to \mathbb {B}(X)$
,
$TU\colon \mathcal {B}\to \mathbb {B}(X)$
,
![]() $(b\in B_t)\mapsto T_bU_t,$
with the integrated forms of
$(b\in B_t)\mapsto T_bU_t,$
with the integrated forms of
![]() $T\colon \mathcal {B}\to \mathbb {B}(X)$
and
$T\colon \mathcal {B}\to \mathbb {B}(X)$
and
![]() $U\colon G\to \mathbb {B}(X)$
being
$U\colon G\to \mathbb {B}(X)$
being
![]() $f\mapsto \overline {\pi }(f\otimes _{\max } 1)$
and
$f\mapsto \overline {\pi }(f\otimes _{\max } 1)$
and
![]() $g\mapsto \overline {\pi }(1\otimes _{\max } g),$
respectively. One may arrange
$g\mapsto \overline {\pi }(1\otimes _{\max } g),$
respectively. One may arrange
![]() $\pi $
so that
$\pi $
so that
![]() $U\colon G\to \mathbb {B}(X)$
is trivial (
$U\colon G\to \mathbb {B}(X)$
is trivial (
![]() $t\mapsto 1$
) and
$t\mapsto 1$
) and
![]() $\tilde { T } $
is faithful, so
$\tilde { T } $
is faithful, so
![]() $\overline {\pi }\circ \Phi =\tilde { T } $
and it follows that
$\overline {\pi }\circ \Phi =\tilde { T } $
and it follows that
![]() $\Phi $
is faithful.
$\Phi $
is faithful.
It is shown in [Reference Exel7] that if G is discrete, then the diagonal arrow of the commutative diagram

is faithful. This is not an exclusive property of discrete groups.
Proposition 3.8 If G is inner amenable, then
![]() $\Phi ^{\mathop {\mathrm {r}}}$
is faithful.
$\Phi ^{\mathop {\mathrm {r}}}$
is faithful.
Proof Let
![]() $\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
a nondegenerate faithful representation. The left and right regular representations
$\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
a nondegenerate faithful representation. The left and right regular representations
![]() $\lambda ,\rho \colon G\to \mathbb {B}(L^2(G))$
commute and are unitary equivalent, so the ranges of
$\lambda ,\rho \colon G\to \mathbb {B}(L^2(G))$
commute and are unitary equivalent, so the ranges of
![]() $T\otimes \rho $
and
$T\otimes \rho $
and
![]() $1\otimes \lambda $
commute and their integrated forms combine to produce a representation
$1\otimes \lambda $
commute and their integrated forms combine to produce a representation
The composition
![]() $\overline {\pi }\circ \overline {\lambda _{\mathcal {B}} \otimes _{\max } \tilde { \lambda } }\circ \Phi = \overline {\pi }\circ \Phi ^{\mathop {\mathrm {r}}}$
is the integrated form of
$\overline {\pi }\circ \overline {\lambda _{\mathcal {B}} \otimes _{\max } \tilde { \lambda } }\circ \Phi = \overline {\pi }\circ \Phi ^{\mathop {\mathrm {r}}}$
is the integrated form of
![]() $T\otimes \omega $
with
$T\otimes \omega $
with
![]() $\omega \colon G\to \mathbb {B}(L^2(G))$
given by
$\omega \colon G\to \mathbb {B}(L^2(G))$
given by
![]() $\omega _t =\lambda _t\rho _t.$
To say G is inner amenable is equivalent to say
$\omega _t =\lambda _t\rho _t.$
To say G is inner amenable is equivalent to say
![]() $\omega $
weakly contains the trivial representation of
$\omega $
weakly contains the trivial representation of
![]() $G,$
so
$G,$
so
![]() $T\preceq T\otimes \omega $
and it follows that
$T\preceq T\otimes \omega $
and it follows that
![]() $\overline {\pi }\circ \Phi ^{\mathop {\mathrm {r}}} =T\tilde { \otimes } \omega $
is faithful. Hence,
$\overline {\pi }\circ \Phi ^{\mathop {\mathrm {r}}} =T\tilde { \otimes } \omega $
is faithful. Hence,
![]() $\Phi ^r$
is faithful.
$\Phi ^r$
is faithful.
Corollary 3.9 If G is inner amenable and
![]() $C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\otimes _{\max } C^{*}_{\mathop {\mathrm {r}}}(G)=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B})\otimes C^{*}_{\mathop {\mathrm {r}}}(G),$
then
$C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\otimes _{\max } C^{*}_{\mathop {\mathrm {r}}}(G)=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B})\otimes C^{*}_{\mathop {\mathrm {r}}}(G),$
then
![]() $C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
$C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
Proof For
![]() $H=\{e\}$
the *-homomorphism
$H=\{e\}$
the *-homomorphism
![]() $\delta \colon C^{*}(\mathcal {B})\to \mathbb {B}( C^{*}(\mathcal {B})\otimes Q^G_H)$
we use to define
$\delta \colon C^{*}(\mathcal {B})\to \mathbb {B}( C^{*}(\mathcal {B})\otimes Q^G_H)$
we use to define
![]() $C^{*}_{H\uparrow G}(\mathcal {B})=\delta (C^{*}(\mathcal {B}))$
is
$C^{*}_{H\uparrow G}(\mathcal {B})=\delta (C^{*}(\mathcal {B}))$
is
![]() $\Phi ^{\mathop {\mathrm {r}}}$
and
$\Phi ^{\mathop {\mathrm {r}}}$
and
![]() $C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
But
$C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
But
![]() $\Phi ^{\mathop {\mathrm {r}}}$
is faithful, so
$\Phi ^{\mathop {\mathrm {r}}}$
is faithful, so
![]() $C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
$C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
4 An absorption principle
Fell’s absorption principle does not hold for non saturated Fell bundles. Indeed, the example of Section 3.1 reveals
![]() $ T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_{r\mathbb {F}_2 {r^{-1}}}^{\mathcal {B}}(V)$
may be a faithful representation of
$ T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_{r\mathbb {F}_2 {r^{-1}}}^{\mathcal {B}}(V)$
may be a faithful representation of
![]() $C^{*}(\mathcal {B})$
while
$C^{*}(\mathcal {B})$
while
![]() ${\mathop {\mathrm { Ind}}}_{r\mathbb {F}_2{r^{-1}}}^{\mathcal {B}}(T|_{\mathcal {B}_{r\mathbb {F}_2{r^{-1}}}}\otimes V)$
factors through a faithful representation of
${\mathop {\mathrm { Ind}}}_{r\mathbb {F}_2{r^{-1}}}^{\mathcal {B}}(T|_{\mathcal {B}_{r\mathbb {F}_2{r^{-1}}}}\otimes V)$
factors through a faithful representation of
![]() $C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\neq C^{*}(\mathcal {B}).$
Therefore,
$C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})\neq C^{*}(\mathcal {B}).$
Therefore,
![]() ${\mathop {\mathrm {Ind}}}_{r\mathbb {F}_2{r^{-1}}}^{\mathcal {B}}(T|_{\mathcal {B}_{r\mathbb {F}_2{r^{-1}}}}\otimes V)$
can not be unitary equivalent to
${\mathop {\mathrm {Ind}}}_{r\mathbb {F}_2{r^{-1}}}^{\mathcal {B}}(T|_{\mathcal {B}_{r\mathbb {F}_2{r^{-1}}}}\otimes V)$
can not be unitary equivalent to
![]() $T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_{r\mathbb {F}_2{r^{-1}}}^{\mathcal {B}}(V)$
(not even weakly equivalent).
$T\tilde { \otimes } {\mathop {\mathrm {Ind}}}_{r\mathbb {F}_2{r^{-1}}}^{\mathcal {B}}(V)$
(not even weakly equivalent).
The theorem we present below is our best answer to question (3) of the Introduction on Fell’s principle. It emerged during our attempt to generalize Fell’s and Exel–Ng’s absorption principles. The computations revealed that the “moving around” technique of [Reference Exel and Ng8, pp. 515] is appropriate when the inducing subgroup H is stable by conjugation (normal). In the general case, conjugation “moves H around” and this is the reason why the conjugated subgroups
![]() $tH{t^{-1}}$
appear bellow. The proof is quite technical, we suggest to skip it on a first read.
$tH{t^{-1}}$
appear bellow. The proof is quite technical, we suggest to skip it on a first read.
Theorem 4.1 Let
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle,
$\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle,
![]() $H\leqslant G$
,
$H\leqslant G$
,
![]() $T\colon \mathcal {B}\to \mathbb {B}(X)$
a nondegenerate representation and
$T\colon \mathcal {B}\to \mathbb {B}(X)$
a nondegenerate representation and
![]() $U\colon H\to \mathbb {B}(Y)$
a unitary representation. If for each
$U\colon H\to \mathbb {B}(Y)$
a unitary representation. If for each
![]() $t\in G$
we denote by
$t\in G$
we denote by
![]() ${}_tU$
the conjugated representation
${}_tU$
the conjugated representation
![]() $tH{t^{-1}} \to \mathbb {B}(Y), \ r\mapsto U_{{t^{-1}} r t},$
then
$tH{t^{-1}} \to \mathbb {B}(Y), \ r\mapsto U_{{t^{-1}} r t},$
then
Proof For convenience, we introduce the following notation:
The Hilbert space induced by U is
![]() $Y^p_U$
and we regard
$Y^p_U$
and we regard
![]() $X\otimes ^G Y^p_U:=\ell ^2(G)\otimes X\otimes Y^p_U$
as an
$X\otimes ^G Y^p_U:=\ell ^2(G)\otimes X\otimes Y^p_U$
as an
![]() $\ell ^2$
-direct sum of
$\ell ^2$
-direct sum of
![]() $\# G$
copies of
$\# G$
copies of
![]() $X\otimes Y^p_U$
. Similarly, the direct sum of
$X\otimes Y^p_U$
. Similarly, the direct sum of
![]() $\#G$
copies of
$\#G$
copies of
![]() $T\otimes V$
is
$T\otimes V$
is
which is the composition of
![]() $T\otimes V$
with the faithful *-homomorphism
$T\otimes V$
with the faithful *-homomorphism
If we denote by
![]() $T\tilde { \otimes } V$
and
$T\tilde { \otimes } V$
and
![]() $T\tilde { \otimes } ^G V$
the integrated forms of
$T\tilde { \otimes } ^G V$
the integrated forms of
![]() $T\otimes V$
and
$T\otimes V$
and
![]() $T\otimes ^G V,$
respectively, then
$T\otimes ^G V,$
respectively, then
![]() $\Theta \circ (T\tilde { \otimes } V)=T\tilde { \otimes } ^GV.$
Indeed, for all
$\Theta \circ (T\tilde { \otimes } V)=T\tilde { \otimes } ^GV.$
Indeed, for all
![]() $f\in C_c(\mathcal {B})$
and every elementary tensor
$f\in C_c(\mathcal {B})$
and every elementary tensor
![]() $g\otimes \xi \otimes \eta \in \ell ^2(G)\otimes X\otimes Y^p_U,$
we have
$g\otimes \xi \otimes \eta \in \ell ^2(G)\otimes X\otimes Y^p_U,$
we have
 $$ \begin{align*} [T\tilde{ \otimes } ^GV]_f(g\otimes \xi\otimes \eta) & = \int_G g\otimes [T\otimes V]_{f(t)}(\xi\otimes \eta)\, dt =g\otimes \left([T\tilde{ \otimes } V]_f (\xi\otimes\eta)\right)\\ & = \Theta\circ [T\tilde{ \otimes } V]_f(g\otimes \xi\otimes \eta). \end{align*} $$
$$ \begin{align*} [T\tilde{ \otimes } ^GV]_f(g\otimes \xi\otimes \eta) & = \int_G g\otimes [T\otimes V]_{f(t)}(\xi\otimes \eta)\, dt =g\otimes \left([T\tilde{ \otimes } V]_f (\xi\otimes\eta)\right)\\ & = \Theta\circ [T\tilde{ \otimes } V]_f(g\otimes \xi\otimes \eta). \end{align*} $$
Since
![]() $\Theta $
is an isometry and both
$\Theta $
is an isometry and both
![]() $T\otimes V$
and all the members of
$T\otimes V$
and all the members of
![]() $\{{\mathop {\mathrm {Ind}}}_{{}_t H}^{\mathcal {B}}({}_{t|}T\otimes {}_tU)\}_{t\in G}$
are nondegenerate, we can use [Reference Fell and Doran11, Chapter XI Section 8.20] to the deduce it suffices to show that
$\{{\mathop {\mathrm {Ind}}}_{{}_t H}^{\mathcal {B}}({}_{t|}T\otimes {}_tU)\}_{t\in G}$
are nondegenerate, we can use [Reference Fell and Doran11, Chapter XI Section 8.20] to the deduce it suffices to show that
The
![]() $\ell ^2$
-direct sum
$\ell ^2$
-direct sum
is a nondegenerate representation whose integrated form is
![]() $\tilde { S } = \oplus _{t\in G} \tilde { {\mathop {\mathrm {Ind}}} } _{{}_tH}^{\mathcal {B}}({}_{t|}T\otimes {}_tU)$
and
$\tilde { S } = \oplus _{t\in G} \tilde { {\mathop {\mathrm {Ind}}} } _{{}_tH}^{\mathcal {B}}({}_{t|}T\otimes {}_tU)$
and
![]() $\|\tilde { S } _f\|=\sup \{ \|\tilde { {\mathop {\mathrm {Ind}}} } _{{}_t H}^{\mathcal {B}}({}_{t|}T\otimes {}_tU)_f\|\colon t\in G \}.$
Thus, S is weakly equivalent to
$\|\tilde { S } _f\|=\sup \{ \|\tilde { {\mathop {\mathrm {Ind}}} } _{{}_t H}^{\mathcal {B}}({}_{t|}T\otimes {}_tU)_f\|\colon t\in G \}.$
Thus, S is weakly equivalent to
![]() $T\otimes ^G V$
if and only if (4.1) holds.
$T\otimes ^G V$
if and only if (4.1) holds.
To compare
![]() $T\otimes ^G V$
and
$T\otimes ^G V$
and
![]() $S,$
we will construct a linear isometry between their domains,
$S,$
we will construct a linear isometry between their domains,
that intertwines S and
![]() $T\otimes ^GV.$
To state the properties defining
$T\otimes ^GV.$
To state the properties defining
![]() $I,$
we need to prove the existence of a (unique) linear function
$I,$
we need to prove the existence of a (unique) linear function
which is continuous in the inductive limit topology and satisfies
for all
![]() $f\in C_c(G)$
,
$f\in C_c(G)$
,
![]() $\xi \in X$
,
$\xi \in X$
,
![]() $\eta \in Y$
and
$\eta \in Y$
and
![]() $t\in G,$
where we regard the algebraic tensor product
$t\in G,$
where we regard the algebraic tensor product
![]() $C_c(G)\odot (X\otimes ^G Y)$
as a subspace of
$C_c(G)\odot (X\otimes ^G Y)$
as a subspace of
![]() $C_c(G,X\otimes ^G Y)$
in the usual way (
$C_c(G,X\otimes ^G Y)$
in the usual way (
![]() $f\odot u$
is the function
$f\odot u$
is the function
![]() $t\mapsto f(t)u$
).
$t\mapsto f(t)u$
).
Uniqueness of L follows from the fact that the functions of the form
![]() $f\odot (\delta _t\otimes \xi \otimes \eta )$
span a subset of
$f\odot (\delta _t\otimes \xi \otimes \eta )$
span a subset of
![]() $C_c(G,X\otimes ^G Y)$
which is dense in the inductive limit topology [Reference Fell and Doran10, Chapter II Section 14.6]. To prove the existence of
$C_c(G,X\otimes ^G Y)$
which is dense in the inductive limit topology [Reference Fell and Doran10, Chapter II Section 14.6]. To prove the existence of
![]() $L,$
we take
$L,$
we take
![]() $u,v\in C_c(G,X\otimes ^G Y)$
such that
$u,v\in C_c(G,X\otimes ^G Y)$
such that
![]() $u = f\odot (\delta _r\otimes \xi \otimes \eta )$
and
$u = f\odot (\delta _r\otimes \xi \otimes \eta )$
and
![]() $v=g\odot (\delta _s\otimes \zeta \otimes \kappa )$
for some
$v=g\odot (\delta _s\otimes \zeta \otimes \kappa )$
for some
![]() $f,g\in C_c(G)$
,
$f,g\in C_c(G)$
,
![]() $r,s\in G$
,
$r,s\in G$
,
![]() $\xi ,\zeta \in X$
and
$\xi ,\zeta \in X$
and
![]() $\eta ,\kappa \in Y.$
The inner product of the candidates for
$\eta ,\kappa \in Y.$
The inner product of the candidates for
![]() $L(u)$
and
$L(u)$
and
![]() $L(v)$
is
$L(v)$
is
 $$ \begin{align} \langle & \delta_r\otimes \xi \otimes [f\otimes_{U} \eta],\delta_s\otimes \zeta \otimes [g \otimes_{U} \kappa]\rangle \nonumber\\ & = \langle \delta_r,\delta_s\rangle\langle \xi,\zeta\rangle \langle f\otimes_{U} \eta,g \otimes_{U} \kappa\rangle \nonumber \\ & = \langle \delta_r,\delta_s\rangle \langle \xi,\zeta\rangle \int_{H} \int_G \Delta_H^G(t)^{1/2} \overline{f(z)} g(zt) \langle \eta, U_t \kappa\rangle \,dzdt \nonumber \\ & = \int_{H} \int_G \Delta_H^G(t)^{1/2} \overline{f(z)} g(zt) \langle \delta_r \otimes \xi\otimes\eta, (1\otimes 1\otimes U_t)(\delta_s\otimes \zeta\otimes \kappa )\rangle \,dzdt\nonumber \\ &= \int_{H} \int_G \Delta_H^G(t)^{1/2} \langle u(z), (1\otimes 1\otimes U_t)v(zt)\rangle \,dzdt. \end{align} $$
$$ \begin{align} \langle & \delta_r\otimes \xi \otimes [f\otimes_{U} \eta],\delta_s\otimes \zeta \otimes [g \otimes_{U} \kappa]\rangle \nonumber\\ & = \langle \delta_r,\delta_s\rangle\langle \xi,\zeta\rangle \langle f\otimes_{U} \eta,g \otimes_{U} \kappa\rangle \nonumber \\ & = \langle \delta_r,\delta_s\rangle \langle \xi,\zeta\rangle \int_{H} \int_G \Delta_H^G(t)^{1/2} \overline{f(z)} g(zt) \langle \eta, U_t \kappa\rangle \,dzdt \nonumber \\ & = \int_{H} \int_G \Delta_H^G(t)^{1/2} \overline{f(z)} g(zt) \langle \delta_r \otimes \xi\otimes\eta, (1\otimes 1\otimes U_t)(\delta_s\otimes \zeta\otimes \kappa )\rangle \,dzdt\nonumber \\ &= \int_{H} \int_G \Delta_H^G(t)^{1/2} \langle u(z), (1\otimes 1\otimes U_t)v(zt)\rangle \,dzdt. \end{align} $$
Fix a compact
![]() $D\subset G$
and denote by
$D\subset G$
and denote by
![]() $C_D(G,X\otimes ^G Y)$
the set formed by those
$C_D(G,X\otimes ^G Y)$
the set formed by those
![]() $f\in C_c(G,X\otimes ^G Y)$
with
$f\in C_c(G,X\otimes ^G Y)$
with
![]() ${\mathop {\mathrm { supp}}}(f)\subset D.$
This vector space is a Banach space with the norm
${\mathop {\mathrm { supp}}}(f)\subset D.$
This vector space is a Banach space with the norm
![]() $\|\ \|_\infty .$
Let
$\|\ \|_\infty .$
Let
![]() $C_D^\odot $
be the subspace of
$C_D^\odot $
be the subspace of
![]() $C_D(G,X\otimes ^G Y)$
spanned by the functions of the form
$C_D(G,X\otimes ^G Y)$
spanned by the functions of the form
![]() $f\odot (\delta _t\otimes \xi \otimes \eta )$
with
$f\odot (\delta _t\otimes \xi \otimes \eta )$
with
![]() $f\in C_D(G)$
,
$f\in C_D(G)$
,
![]() $t\in G$
,
$t\in G$
,
![]() $\xi \in X$
and
$\xi \in X$
and
![]() $\eta \in Y.$
We clearly have
$\eta \in Y.$
We clearly have
![]() $C_c(G)C_D^\odot \subset C_D^\odot .$
If for each
$C_c(G)C_D^\odot \subset C_D^\odot .$
If for each
![]() $t\in G,$
we define
$t\in G,$
we define
![]() $C_D^\odot (t)$
as the closure of
$C_D^\odot (t)$
as the closure of
![]() $\{u(t)\colon u\in C_D^\odot \},$
then
$\{u(t)\colon u\in C_D^\odot \},$
then
![]() $C_D^\odot (t)=X\otimes ^G Y$
for every t in the interior of D and
$C_D^\odot (t)=X\otimes ^G Y$
for every t in the interior of D and
![]() $\{0\}$
otherwise. By [Reference Abadie1, Lemma 5.1], the closure of
$\{0\}$
otherwise. By [Reference Abadie1, Lemma 5.1], the closure of
![]() $C_D^\odot $
in
$C_D^\odot $
in
![]() $C_c(G,X\otimes ^G Y)$
with respect to the inductive limit topology is
$C_c(G,X\otimes ^G Y)$
with respect to the inductive limit topology is
![]() $\{f\in C_c(G,X\otimes ^G Y)\colon f(t)\in C_D^\odot (t)\, \forall \, t\in G \}=C_D(G,X\otimes ^G Y).$
$\{f\in C_c(G,X\otimes ^G Y)\colon f(t)\in C_D^\odot (t)\, \forall \, t\in G \}=C_D(G,X\otimes ^G Y).$
Take any
![]() $u,v\in C_D(G,X\otimes ^G Y).$
By the preceding paragraph, there are sequences
$u,v\in C_D(G,X\otimes ^G Y).$
By the preceding paragraph, there are sequences
![]() $\{u_n\}_{n\in \mathbb {N}}$
and
$\{u_n\}_{n\in \mathbb {N}}$
and
![]() $\{v_n\}_{n\in \mathbb {N}}$
in
$\{v_n\}_{n\in \mathbb {N}}$
in
![]() $C_D^\odot $
converging uniformly to u and
$C_D^\odot $
converging uniformly to u and
![]() $v,$
respectively. Then for all
$v,$
respectively. Then for all
![]() $n\in \mathbb {N}$
there exists, a positive integer
$n\in \mathbb {N}$
there exists, a positive integer
![]() $m_n$
and (for each
$m_n$
and (for each
![]() $j=1,\ldots ,m_n$
) elements
$j=1,\ldots ,m_n$
) elements
![]() $f_{n,j},g_{n,j}\in C_D(G)$
,
$f_{n,j},g_{n,j}\in C_D(G)$
,
![]() $r_{n,j},s_{n,j}\in G$
,
$r_{n,j},s_{n,j}\in G$
,
![]() $\xi _{n,j},\zeta _{n,j}\in X$
and
$\xi _{n,j},\zeta _{n,j}\in X$
and
![]() $\zeta _{n,j},\kappa _{n,j}\in Y$
such that
$\zeta _{n,j},\kappa _{n,j}\in Y$
such that
 $$ \begin{align*} u_n &=\sum_{j=1}^{m_n} f_{n,j}\odot (\delta_{r_{n,j}}\otimes \xi_{n,j}\otimes \eta_{n,j} ) & v_n&=\sum_{j=1}^{m_n}g_{n,j}\odot (\delta_{s_{n,j}}\otimes \zeta_{n,j}\otimes \kappa_{n,j}). \end{align*} $$
$$ \begin{align*} u_n &=\sum_{j=1}^{m_n} f_{n,j}\odot (\delta_{r_{n,j}}\otimes \xi_{n,j}\otimes \eta_{n,j} ) & v_n&=\sum_{j=1}^{m_n}g_{n,j}\odot (\delta_{s_{n,j}}\otimes \zeta_{n,j}\otimes \kappa_{n,j}). \end{align*} $$
By (4.6), for all
![]() $a,b\in \mathbb {N}$
we have
$a,b\in \mathbb {N}$
we have
 $$ \begin{align*} &\left\|\sum_{j=1}^{m_a} \delta_{r_{a,j}} \otimes (\xi_{a,j}\otimes [f_{a,j}\otimes_{U} \eta_{a,j}] )-\sum_{k=1}^{m_b}\delta_{s_{b,k}}\otimes ( \zeta_{b,k}\otimes [g_{b,k}\otimes_{U} \kappa_{b,k}] )\right\|^2 \\ &\quad = \left| \int_{H} \int_G \Delta_H^G(t)^{1/2} \langle (u_a-v_b)(z), (1\otimes 1\otimes U_t)(u_a-v_b)(zt)\rangle \,dzdt \right|. \end{align*} $$
$$ \begin{align*} &\left\|\sum_{j=1}^{m_a} \delta_{r_{a,j}} \otimes (\xi_{a,j}\otimes [f_{a,j}\otimes_{U} \eta_{a,j}] )-\sum_{k=1}^{m_b}\delta_{s_{b,k}}\otimes ( \zeta_{b,k}\otimes [g_{b,k}\otimes_{U} \kappa_{b,k}] )\right\|^2 \\ &\quad = \left| \int_{H} \int_G \Delta_H^G(t)^{1/2} \langle (u_a-v_b)(z), (1\otimes 1\otimes U_t)(u_a-v_b)(zt)\rangle \,dzdt \right|. \end{align*} $$
For the inner product inside the integral above to be non zero, we must have
![]() $z,tz\in D,$
which implies
$z,tz\in D,$
which implies
![]() $t= tz z^{-1}\in H\cap (DD^{-1}).$
If
$t= tz z^{-1}\in H\cap (DD^{-1}).$
If
![]() $\alpha _D$
and
$\alpha _D$
and
![]() $\beta _D$
are the measures of D and
$\beta _D$
are the measures of D and
![]() $H\cap (D^{-1}D)$
with respect to the Haar measures of G and
$H\cap (D^{-1}D)$
with respect to the Haar measures of G and
![]() $H,$
respectively, and
$H,$
respectively, and
![]() $\gamma _D:=\sup \{ \Delta _H^G(t)^{1/2} \colon t\in H\cap (D^{-1}D)\},$
then
$\gamma _D:=\sup \{ \Delta _H^G(t)^{1/2} \colon t\in H\cap (D^{-1}D)\},$
then
 $$ \begin{align*} \left\|\sum_{j=1}^{m_a} \delta_{r_{a,j}} \otimes (\xi_{a,j}\otimes [f_{a,j}\otimes_{U} \eta_{a,j}] )-\sum_{k=1}^{m_b}\delta_{s_{b,k}}\otimes ( \zeta_{b,k}\otimes [g_{b,k}\otimes_{U} \kappa_{b,k}] )\right\|^2 \end{align*} $$
$$ \begin{align*} \left\|\sum_{j=1}^{m_a} \delta_{r_{a,j}} \otimes (\xi_{a,j}\otimes [f_{a,j}\otimes_{U} \eta_{a,j}] )-\sum_{k=1}^{m_b}\delta_{s_{b,k}}\otimes ( \zeta_{b,k}\otimes [g_{b,k}\otimes_{U} \kappa_{b,k}] )\right\|^2 \end{align*} $$
is not greater than
![]() $\|u_a-v_b\|_\infty ^2 \alpha _D\beta _D\gamma _D.$
$\|u_a-v_b\|_\infty ^2 \alpha _D\beta _D\gamma _D.$
Several conclusion arise from that bound:
-
(1) If we take
 $u=v$
and
$u=v$
and
 $v_b=u_b,$
it follows that
$v_b=u_b,$
it follows that
 $\{\sum _{j=1}^{m_a} \delta _{r_{a,j}} \otimes (\xi _{a,j}\otimes [f_{a,j}\otimes _{U} \eta _{a,j}]) \}_{a\in \mathbb {N}}$
is a Cauchy sequence in
$\{\sum _{j=1}^{m_a} \delta _{r_{a,j}} \otimes (\xi _{a,j}\otimes [f_{a,j}\otimes _{U} \eta _{a,j}]) \}_{a\in \mathbb {N}}$
is a Cauchy sequence in
 $X\otimes ^G Y^p_U;$
the limit of which we denote by
$X\otimes ^G Y^p_U;$
the limit of which we denote by
 $L_D(\{u_n\}_{n\in \mathbb {N}}).$
$L_D(\{u_n\}_{n\in \mathbb {N}}).$
-
(2) If
 $u=v$
and we take limit in a and
$u=v$
and we take limit in a and
 $b,$
we get
$b,$
we get
 $L_D(\{u_n\}_{n\in \mathbb {N}})= L_D(\{v_n\}_{n\in \mathbb {N}}).$
Thus, we may define a function
$L_D(\{u_n\}_{n\in \mathbb {N}})= L_D(\{v_n\}_{n\in \mathbb {N}}).$
Thus, we may define a function
 $L_D\colon C_D(G,X\otimes ^G Y)\to X\otimes ^G Y^p_U,\ u\mapsto L_D(u):=L_D(\{u_n\}_{n\in \mathbb {N}}).$
$L_D\colon C_D(G,X\otimes ^G Y)\to X\otimes ^G Y^p_U,\ u\mapsto L_D(u):=L_D(\{u_n\}_{n\in \mathbb {N}}).$
-
(3) Taking limit in a and b we obtain
 $\| L_D(u)-L_D(v) \|\leq \|u-v\|_{\infty } \sqrt {\alpha _D\beta _D\gamma _D},$
so
$\| L_D(u)-L_D(v) \|\leq \|u-v\|_{\infty } \sqrt {\alpha _D\beta _D\gamma _D},$
so
 $L_D$
is continuous.
$L_D$
is continuous. -
(4)
 $L_D(f\odot (\delta _t\otimes \xi \otimes \eta ))=\delta _t\otimes \xi \otimes (f\otimes _U\eta )$
and
$L_D(f\odot (\delta _t\otimes \xi \otimes \eta ))=\delta _t\otimes \xi \otimes (f\otimes _U\eta )$
and
 $L_D$
is linear when restricted to
$L_D$
is linear when restricted to
 $C_D^\odot .$
Thus
$C_D^\odot .$
Thus
 $L_D$
is linear.
$L_D$
is linear. -
(5) By (4.6) and the continuity of
 $L_D,$
(4.7)
$L_D,$
(4.7) $$ \begin{align} \langle L_D(u),L_D(v)\rangle = \int_G \int_H \Delta_H^G(t)^{1/2}\langle u(s), (1\otimes 1 \otimes U_t)v(st)\rangle \,dt ds. \end{align} $$
$$ \begin{align} \langle L_D(u),L_D(v)\rangle = \int_G \int_H \Delta_H^G(t)^{1/2}\langle u(s), (1\otimes 1 \otimes U_t)v(st)\rangle \,dt ds. \end{align} $$
It follows immediately that
![]() $L_E$
is an extension of
$L_E$
is an extension of
![]() $L_D$
whenever
$L_D$
whenever
![]() $E\subset G$
is a compact set containing
$E\subset G$
is a compact set containing
![]() $D.$
Then, there exists a unique function
$D.$
Then, there exists a unique function
![]() $L\colon C_c(G,X\otimes ^G Y)\to X\otimes ^G Y^p_U$
extending all the
$L\colon C_c(G,X\otimes ^G Y)\to X\otimes ^G Y^p_U$
extending all the
![]() $L_D$
’s. This extension is linear and continuous in the inductive limit topology by [Reference Fell and Doran10, Chapter II Section 14.3]. Note also that L satisfies (4.5) and, consequently, it has dense range.
$L_D$
’s. This extension is linear and continuous in the inductive limit topology by [Reference Fell and Doran10, Chapter II Section 14.3]. Note also that L satisfies (4.5) and, consequently, it has dense range.
Now that we know L exists, we are one step closer of being able to specify the properties defining the map I of (4.3). Given
![]() $r\in G$
,
$r\in G$
,
![]() $f\in C_c(\mathcal {B})$
,
$f\in C_c(\mathcal {B})$
,
![]() $\xi \in X$
and
$\xi \in X$
and
![]() $\eta \in Y$
we define
$\eta \in Y$
we define
![]() $[r,f,\xi ,\eta ]\in C_c(G,X\otimes ^G Y)$
by
$[r,f,\xi ,\eta ]\in C_c(G,X\otimes ^G Y)$
by
We claim there exists a unique linear and continuous map I with the domains and ranges specified in (4.3) and such that for all
![]() $t\in G$
,
$t\in G$
,
![]() $f\in C_c(\mathcal {B})$
,
$f\in C_c(\mathcal {B})$
,
![]() $\xi \in X$
and
$\xi \in X$
and
![]() $\eta \in Y,$
$\eta \in Y,$
To prove this claim, we start by taking elementary tensors
![]() $f\otimes _{{}_{r|}T\otimes {}_r U}(\xi \otimes \eta )$
and
$f\otimes _{{}_{r|}T\otimes {}_r U}(\xi \otimes \eta )$
and
![]() $g\otimes _{{}_{t|}T\otimes {}_tU}(\zeta \otimes \kappa )$
on (possibly equal) direct summands of
$g\otimes _{{}_{t|}T\otimes {}_tU}(\zeta \otimes \kappa )$
on (possibly equal) direct summands of
![]() $\bigoplus _{s\in G} (X\otimes Y)^{p_s}_{{}_{s|}T\otimes {}_sU}.$
Notice the r and the t in the subindexes indicate the direct summands the tensors belongs to. By (4.7), we have
$\bigoplus _{s\in G} (X\otimes Y)^{p_s}_{{}_{s|}T\otimes {}_sU}.$
Notice the r and the t in the subindexes indicate the direct summands the tensors belongs to. By (4.7), we have
 $$ \begin{align*} \langle & L([r,f,\xi,\eta]),L([t,g,\zeta,\kappa])\rangle= \\ & = \int_G\int_H \Delta_H^G(w)^{1/2}\Delta_G(rt)^{-1/2} \langle \delta_r\otimes T_{f(z{r^{-1}} )}\xi \otimes \eta ,\delta_t\otimes T_{g(zw{t^{-1}})}\zeta\otimes U_w\kappa\rangle \,dwdz \\ & = \int_H\int_G \Delta_H^G(w)^{1/2} \underbrace{\Delta_G(rt)^{-1/2}\langle \delta_r,\delta_t\rangle}_{=\Delta_G({r^{-1}})\langle \delta_r,\delta_t\rangle} \langle T_{f(z{r^{-1}} )}\xi \otimes \eta ,T_{g(zw{r^{-1}})}\zeta\otimes U_w\kappa\rangle \,dzdw \\ & = \int_H\int_G \Delta_H^G(w)^{1/2} \langle \delta_r,\delta_t\rangle \langle T_{f(z)}\xi \otimes \eta ,T_{g(zr w{r^{-1}})}\zeta\otimes U_w\kappa\rangle \,dzdw\\ &= \int_H\int_G \Delta_{{}_rH}^G(rw{r^{-1}})^{1/2} \langle \delta_r,\delta_t\rangle \langle \xi \otimes \eta ,T_{f(z)^{*}g(zr w{r^{-1}} )}\zeta\otimes {}_r U_{rw{r^{-1}}}\kappa\rangle \,dzdw \\ &= \int_{{}_rH}\int_G \Delta_{{}_rH}^G(w)^{1/2} \langle \delta_r,\delta_t\rangle \langle \xi \otimes \eta ,T_{f(z)^{*}g(zw)}\zeta\otimes {}_r U_{w}\kappa\rangle \,dzdw \\ &= \langle \delta_r,\delta_t\rangle \langle \xi \otimes \eta ,[{}_{r|}T\tilde{ \otimes } {}_r U]_{p_r(f^{*}*g)}(\zeta\otimes \kappa)\rangle \\ &= \langle f\otimes_{{}_{r|}T\otimes {}_r U}(\xi\otimes \eta),g\otimes_{{}_{t|}T\otimes {}_tU}(\zeta\otimes\kappa)\rangle. \end{align*} $$
$$ \begin{align*} \langle & L([r,f,\xi,\eta]),L([t,g,\zeta,\kappa])\rangle= \\ & = \int_G\int_H \Delta_H^G(w)^{1/2}\Delta_G(rt)^{-1/2} \langle \delta_r\otimes T_{f(z{r^{-1}} )}\xi \otimes \eta ,\delta_t\otimes T_{g(zw{t^{-1}})}\zeta\otimes U_w\kappa\rangle \,dwdz \\ & = \int_H\int_G \Delta_H^G(w)^{1/2} \underbrace{\Delta_G(rt)^{-1/2}\langle \delta_r,\delta_t\rangle}_{=\Delta_G({r^{-1}})\langle \delta_r,\delta_t\rangle} \langle T_{f(z{r^{-1}} )}\xi \otimes \eta ,T_{g(zw{r^{-1}})}\zeta\otimes U_w\kappa\rangle \,dzdw \\ & = \int_H\int_G \Delta_H^G(w)^{1/2} \langle \delta_r,\delta_t\rangle \langle T_{f(z)}\xi \otimes \eta ,T_{g(zr w{r^{-1}})}\zeta\otimes U_w\kappa\rangle \,dzdw\\ &= \int_H\int_G \Delta_{{}_rH}^G(rw{r^{-1}})^{1/2} \langle \delta_r,\delta_t\rangle \langle \xi \otimes \eta ,T_{f(z)^{*}g(zr w{r^{-1}} )}\zeta\otimes {}_r U_{rw{r^{-1}}}\kappa\rangle \,dzdw \\ &= \int_{{}_rH}\int_G \Delta_{{}_rH}^G(w)^{1/2} \langle \delta_r,\delta_t\rangle \langle \xi \otimes \eta ,T_{f(z)^{*}g(zw)}\zeta\otimes {}_r U_{w}\kappa\rangle \,dzdw \\ &= \langle \delta_r,\delta_t\rangle \langle \xi \otimes \eta ,[{}_{r|}T\tilde{ \otimes } {}_r U]_{p_r(f^{*}*g)}(\zeta\otimes \kappa)\rangle \\ &= \langle f\otimes_{{}_{r|}T\otimes {}_r U}(\xi\otimes \eta),g\otimes_{{}_{t|}T\otimes {}_tU}(\zeta\otimes\kappa)\rangle. \end{align*} $$
The existence of I then follows immediately from Remark 4.1 if one considers the functions
 $$ \begin{align*} b&\colon G\times C_c(\mathcal{B})\times X\times Y\to \bigoplus_{t\in G}(X\otimes Y)^{p_t}_{{}_{t|}T\otimes{}_tU} & b(r,f,\xi,\eta)&=f\otimes_{{}_{r|}T\otimes {}_r U}(\xi\otimes \eta)\\ c& \colon G\times C_c(\mathcal{B})\times X\times Y\to X\otimes^G Y^p_U & c(r,f,\xi,\eta)&=L([r,f,\xi,\eta]). \end{align*} $$
$$ \begin{align*} b&\colon G\times C_c(\mathcal{B})\times X\times Y\to \bigoplus_{t\in G}(X\otimes Y)^{p_t}_{{}_{t|}T\otimes{}_tU} & b(r,f,\xi,\eta)&=f\otimes_{{}_{r|}T\otimes {}_r U}(\xi\otimes \eta)\\ c& \colon G\times C_c(\mathcal{B})\times X\times Y\to X\otimes^G Y^p_U & c(r,f,\xi,\eta)&=L([r,f,\xi,\eta]). \end{align*} $$
We are not sure if I is surjective, but we can use the ideas of [Reference Exel and Ng8] to “move” the image of I to “fill”
![]() $X\otimes ^G Y.$
The movement is via the map
$X\otimes ^G Y.$
The movement is via the map
where
![]() $\mathtt {lt}\colon G\to \mathbb {B}(\ell ^2(G))$
is the left regular representation of the discrete version of G (
$\mathtt {lt}\colon G\to \mathbb {B}(\ell ^2(G))$
is the left regular representation of the discrete version of G (
![]() $\mathtt {lt}_t(\delta _s)=\delta _{ts}$
). Note
$\mathtt {lt}_t(\delta _s)=\delta _{ts}$
). Note
![]() $\rho $
and
$\rho $
and
![]() $\Theta $
have commuting ranges, so the range of
$\Theta $
have commuting ranges, so the range of
![]() $\rho $
commutes with that of
$\rho $
commutes with that of
![]() $T\tilde { \otimes } ^GV=\Theta \circ (T\tilde { \otimes } G).$
We remark that the continuity of
$T\tilde { \otimes } ^GV=\Theta \circ (T\tilde { \otimes } G).$
We remark that the continuity of
![]() $\rho $
(which may fail) plays no rôle in the proof.
$\rho $
(which may fail) plays no rôle in the proof.
Let K be the image of
![]() $I.$
We claim that
$I.$
We claim that
![]() $ G\cdot K:= {\mathop {\mathrm {span}}}\{\rho _t K\colon t\in G\}$
is dense in
$ G\cdot K:= {\mathop {\mathrm {span}}}\{\rho _t K\colon t\in G\}$
is dense in
![]() $X\otimes ^G Y^p_U.$
To prove this we define, for each
$X\otimes ^G Y^p_U.$
To prove this we define, for each
![]() $t\in G,$
the function
$t\in G,$
the function
In particular,
![]() $\mu _t (f\odot (\delta _r\otimes \xi \otimes \eta ))=f\odot (\delta _{tr}\otimes \xi \otimes \eta ).$
Hence,
$\mu _t (f\odot (\delta _r\otimes \xi \otimes \eta ))=f\odot (\delta _{tr}\otimes \xi \otimes \eta ).$
Hence,
 $$ \begin{align*} L\circ \mu_t (f\odot (\delta_r\otimes \xi\otimes \eta)) & = L(f \odot (\delta_{tr}\otimes \xi\otimes \eta)) =\delta_{tr}\otimes \xi \otimes [f\otimes_{U} \eta] \\ & =\rho_t (\delta_{r}\otimes \xi \otimes [f\otimes_{U} \eta]) =\rho_t L(f\odot( \delta_r\otimes \xi\otimes \eta )) \end{align*} $$
$$ \begin{align*} L\circ \mu_t (f\odot (\delta_r\otimes \xi\otimes \eta)) & = L(f \odot (\delta_{tr}\otimes \xi\otimes \eta)) =\delta_{tr}\otimes \xi \otimes [f\otimes_{U} \eta] \\ & =\rho_t (\delta_{r}\otimes \xi \otimes [f\otimes_{U} \eta]) =\rho_t L(f\odot( \delta_r\otimes \xi\otimes \eta )) \end{align*} $$
and we get
![]() $L\circ \mu _t =\rho _t \circ L$
because both
$L\circ \mu _t =\rho _t \circ L$
because both
![]() $L\circ \mu _t $
and
$L\circ \mu _t $
and
![]() $\rho _t \circ L$
are linear and continuous in the inductive limit topology and agree on a dense set. Thus
$\rho _t \circ L$
are linear and continuous in the inductive limit topology and agree on a dense set. Thus
![]() $\overline {G\cdot K}$
contains the image through L of
$\overline {G\cdot K}$
contains the image through L of
Note
![]() $C(G)K_0\subset K_0.$
Besides,
$C(G)K_0\subset K_0.$
Besides,
Fixing
![]() $z\in G$
and varying
$z\in G$
and varying
![]() $r,t\in G$
,
$r,t\in G$
,
![]() $\xi \in X$
,
$\xi \in X$
,
![]() $\eta \in Y$
and
$\eta \in Y$
and
![]() $f\in C_c(\mathcal {B}),$
the elements we obtain on the right-hand side of (4.10) are all those of the form
$f\in C_c(\mathcal {B}),$
the elements we obtain on the right-hand side of (4.10) are all those of the form
![]() $\delta _{s}\otimes T_b \xi \otimes \eta ,$
for arbitrary
$\delta _{s}\otimes T_b \xi \otimes \eta ,$
for arbitrary
![]() $s\in G$
,
$s\in G$
,
![]() $b\in \mathcal {B}$
,
$b\in \mathcal {B}$
,
![]() $\xi \in X$
and
$\xi \in X$
and
![]() $\eta \in Y.$
The closed linear span of this vectors is
$\eta \in Y.$
The closed linear span of this vectors is
![]() $X\otimes ^G Y$
because T is nondegenerate, and we conclude (using [Reference Fell and Doran10, Chapter II Section 14.3]) that
$X\otimes ^G Y$
because T is nondegenerate, and we conclude (using [Reference Fell and Doran10, Chapter II Section 14.3]) that
![]() $K_0$
is dense in
$K_0$
is dense in
![]() $C_c(G,X\otimes ^G Y)$
in the inductive limit topology. Hence,
$C_c(G,X\otimes ^G Y)$
in the inductive limit topology. Hence,
![]() $\overline {G\cdot K}$
contains the dense set
$\overline {G\cdot K}$
contains the dense set
![]() $L(K_0)$
and it follows that
$L(K_0)$
and it follows that
![]() $\overline {G\cdot K}=X\otimes ^G Y^p_U.$
$\overline {G\cdot K}=X\otimes ^G Y^p_U.$
Our next goal is to show that I intertwines the S of (4.2) and
![]() $T\otimes ^G V.$
To prove this claim, we fix
$T\otimes ^G V.$
To prove this claim, we fix
![]() $r,s,t\in G$
,
$r,s,t\in G$
,
![]() $b\in B_r$
,
$b\in B_r$
,
![]() $f\in C_c(\mathcal {B})$
,
$f\in C_c(\mathcal {B})$
,
![]() $g\in C_c(G)$
,
$g\in C_c(G)$
,
![]() $\xi ,\zeta \in X$
and
$\xi ,\zeta \in X$
and
![]() $\eta , \kappa \in Y.$
For convenience, we denote by u and v the tensors
$\eta , \kappa \in Y.$
For convenience, we denote by u and v the tensors
![]() $f\otimes _{{}_{s|}T\otimes {}_{s}U} (\xi \otimes \eta ) $
and
$f\otimes _{{}_{s|}T\otimes {}_{s}U} (\xi \otimes \eta ) $
and
![]() $g\odot (\delta _t\otimes \zeta \otimes \kappa ),$
respectively. Recalling (4.7) we get
$g\odot (\delta _t\otimes \zeta \otimes \kappa ),$
respectively. Recalling (4.7) we get
 $$ \begin{align*} \langle & [T\otimes^G V]_b \circ I (u ),L(v ) \rangle = \langle L([s,f,\xi,\eta]),[T\otimes^G V]_{b^{*}}(\delta_t\otimes \zeta\otimes (g\otimes_{U}\kappa)) \rangle \nonumber\\ &= \langle L([s,f,\xi,\eta]),\delta_t\otimes T_{b^{*}}\zeta\otimes ( {r^{-1}} g\otimes_{U}\kappa ) \rangle \nonumber\\ &= \langle L([s,f,\xi,\eta]),L({r^{-1}} g\odot( \delta_t \otimes T_{b^{*}}\zeta\otimes \kappa))\rangle\\ & =\int_H\int_G \Delta_H^G(w)^{1/2} \langle [s,f,\xi,\eta](z),\delta_t \otimes T_{b^{*}}\zeta\otimes U_w\kappa \rangle g(r zw)\,dzdw\\ & =\int_H\int_G \Delta_H^G(w)^{1/2} \Delta_G(s)^{-1/2} \langle \delta_s\otimes T_{f(zs^{-1})}\xi\otimes \eta,\delta_t \otimes T_{b^{*}}\zeta\otimes U_w\kappa \rangle g(r zw)\,dzdw\\ & =\int_H\int_G \Delta_H^G(w)^{1/2} \Delta_G(s)^{-1/2}\langle \delta_s,\delta_t\rangle \langle T_{bf({r^{-1}} zs^{-1})}\xi\otimes \eta,\zeta\otimes U_w\kappa \rangle g(zw)\,dzdw\\ & =\int_H\int_G \Delta_H^G(w)^{1/2} \Delta_G(s)^{-1/2}\langle \delta_s,\delta_t\rangle \langle T_{(bf)(zs^{-1})}\xi\otimes \eta,\zeta\otimes U_w\kappa \rangle g(zw)\,dzdw\\ & =\langle L([s,bf,\xi,\eta]),L(g\odot (\delta_t\otimes \zeta\otimes \kappa))\rangle =\langle I(bf\otimes_{{}_{|s}T\otimes {}_s U}(\xi\otimes \eta)),L(v)\rangle\\ &= \langle I\circ S_b(u),L(v)\rangle. \end{align*} $$
$$ \begin{align*} \langle & [T\otimes^G V]_b \circ I (u ),L(v ) \rangle = \langle L([s,f,\xi,\eta]),[T\otimes^G V]_{b^{*}}(\delta_t\otimes \zeta\otimes (g\otimes_{U}\kappa)) \rangle \nonumber\\ &= \langle L([s,f,\xi,\eta]),\delta_t\otimes T_{b^{*}}\zeta\otimes ( {r^{-1}} g\otimes_{U}\kappa ) \rangle \nonumber\\ &= \langle L([s,f,\xi,\eta]),L({r^{-1}} g\odot( \delta_t \otimes T_{b^{*}}\zeta\otimes \kappa))\rangle\\ & =\int_H\int_G \Delta_H^G(w)^{1/2} \langle [s,f,\xi,\eta](z),\delta_t \otimes T_{b^{*}}\zeta\otimes U_w\kappa \rangle g(r zw)\,dzdw\\ & =\int_H\int_G \Delta_H^G(w)^{1/2} \Delta_G(s)^{-1/2} \langle \delta_s\otimes T_{f(zs^{-1})}\xi\otimes \eta,\delta_t \otimes T_{b^{*}}\zeta\otimes U_w\kappa \rangle g(r zw)\,dzdw\\ & =\int_H\int_G \Delta_H^G(w)^{1/2} \Delta_G(s)^{-1/2}\langle \delta_s,\delta_t\rangle \langle T_{bf({r^{-1}} zs^{-1})}\xi\otimes \eta,\zeta\otimes U_w\kappa \rangle g(zw)\,dzdw\\ & =\int_H\int_G \Delta_H^G(w)^{1/2} \Delta_G(s)^{-1/2}\langle \delta_s,\delta_t\rangle \langle T_{(bf)(zs^{-1})}\xi\otimes \eta,\zeta\otimes U_w\kappa \rangle g(zw)\,dzdw\\ & =\langle L([s,bf,\xi,\eta]),L(g\odot (\delta_t\otimes \zeta\otimes \kappa))\rangle =\langle I(bf\otimes_{{}_{|s}T\otimes {}_s U}(\xi\otimes \eta)),L(v)\rangle\\ &= \langle I\circ S_b(u),L(v)\rangle. \end{align*} $$
Since u and v are arbitrary basic tensors and L has dense range, by linearity and continuity we get that
![]() $[T\otimes ^G V]_b \circ I = I\circ S_b;$
which implies that for all
$[T\otimes ^G V]_b \circ I = I\circ S_b;$
which implies that for all
![]() $f\in C_c(\mathcal {B})$
$f\in C_c(\mathcal {B})$
The same identity holds for all
![]() $f\in C^{*}(\mathcal {B})$
because
$f\in C^{*}(\mathcal {B})$
because
![]() $C_c(\mathcal {B})$
is dense in
$C_c(\mathcal {B})$
is dense in
![]() $C^{*}(\mathcal {B}).$
$C^{*}(\mathcal {B}).$
Recall that
![]() $G\cdot K$
spans a dense subset of
$G\cdot K$
spans a dense subset of
![]() $\ell ^2(G)\otimes X\otimes Y^p_U, $
thus for all
$\ell ^2(G)\otimes X\otimes Y^p_U, $
thus for all
![]() $g\in C^{*}(\mathcal {B}), $
we have
$g\in C^{*}(\mathcal {B}), $
we have
 $$ \begin{align*} [T\tilde{ \otimes } ^G V]_g=0 & \Leftrightarrow \ [T\tilde{ \otimes } ^G V]_g\rho_t \circ I=0\ \forall \ t\in G \Leftrightarrow \ \rho_t [T\tilde{ \otimes } ^G V]_g\circ I=0\ \forall \ t\in G\\ & \Leftrightarrow \ [T\tilde{ \otimes } ^G V]_g\circ I=0 \Leftrightarrow \ I\circ \tilde{ S } _g = 0 \Leftrightarrow \tilde{ S } _g = 0, \end{align*} $$
$$ \begin{align*} [T\tilde{ \otimes } ^G V]_g=0 & \Leftrightarrow \ [T\tilde{ \otimes } ^G V]_g\rho_t \circ I=0\ \forall \ t\in G \Leftrightarrow \ \rho_t [T\tilde{ \otimes } ^G V]_g\circ I=0\ \forall \ t\in G\\ & \Leftrightarrow \ [T\tilde{ \otimes } ^G V]_g\circ I=0 \Leftrightarrow \ I\circ \tilde{ S } _g = 0 \Leftrightarrow \tilde{ S } _g = 0, \end{align*} $$
where the last equivalence follows from the fact that I is an isometry. We may then define a *-homomorphism
![]() $\Omega \colon (T\tilde { \otimes } ^G V)(C^{*}(\mathcal {B}))\to \tilde { S } (C^{*}(\mathcal {B}))$
by
$\Omega \colon (T\tilde { \otimes } ^G V)(C^{*}(\mathcal {B}))\to \tilde { S } (C^{*}(\mathcal {B}))$
by
![]() $\Omega \left ([T\tilde { \otimes } ^G V]_g\right )=\tilde { S } _g.$
$\Omega \left ([T\tilde { \otimes } ^G V]_g\right )=\tilde { S } _g.$
The thesis of the theorem was shown to be the equivalent to (4.1) which, in turn, is equivalent to say
![]() $\Omega $
is an isometry. But
$\Omega $
is an isometry. But
![]() $\Omega $
is indeed an isometry because it is an injective *-homomorphism between two C*-algebras.
$\Omega $
is indeed an isometry because it is an injective *-homomorphism between two C*-algebras.
The first application of Theorem 4.1 is the comparison of the C*-algebras
![]() $C^{*}_{H\uparrow G}(\mathcal {B})$
and
$C^{*}_{H\uparrow G}(\mathcal {B})$
and
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
when the normalizer of H is open in
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
when the normalizer of H is open in
![]() $G.$
This covers the cases examined in the example of Section 3.1, where there is always a quotient map
$G.$
This covers the cases examined in the example of Section 3.1, where there is always a quotient map
![]() $\Theta ^H_{\mathcal {B}}\colon C^{*}_{H\uparrow G}(\mathcal {B})\to C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
that it is not always injective.
$\Theta ^H_{\mathcal {B}}\colon C^{*}_{H\uparrow G}(\mathcal {B})\to C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
that it is not always injective.
Corollary 4.2 Given a Fell bundle
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
and
$\mathcal {B}=\{B_t\}_{t\in G}$
and
![]() $H\leqslant G$
with open normalizer, there exists a *-homomorphism
$H\leqslant G$
with open normalizer, there exists a *-homomorphism
![]() $\Theta ^H_{\mathcal {B}}\colon C^{*}_{H\uparrow G}(\mathcal {B})\to C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
such that
$\Theta ^H_{\mathcal {B}}\colon C^{*}_{H\uparrow G}(\mathcal {B})\to C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})$
such that
![]() $\Theta ^{\mathcal {B}}_H\circ q^{H\uparrow G}_{\mathcal {B}}=q^{H\uparrow \mathcal {B}}.$
If for all
$\Theta ^{\mathcal {B}}_H\circ q^{H\uparrow G}_{\mathcal {B}}=q^{H\uparrow \mathcal {B}}.$
If for all
![]() $r\in G$
we identify
$r\in G$
we identify
![]() $C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{rH{r^{-1}}\uparrow G}(\mathcal {B})$
as indicated in Remark 3.3, then
$C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{rH{r^{-1}}\uparrow G}(\mathcal {B})$
as indicated in Remark 3.3, then
![]() $\cap _{r\in G} \ker (\Theta ^{rH{r^{-1}}}_{\mathcal {B}})=\{0\}.$
Moreover,
$\cap _{r\in G} \ker (\Theta ^{rH{r^{-1}}}_{\mathcal {B}})=\{0\}.$
Moreover,
![]() $\Theta ^H_{\mathcal {B}}$
is an isomorphism if either
$\Theta ^H_{\mathcal {B}}$
is an isomorphism if either
![]() $\mathcal {B}$
is saturated or H normal.
$\mathcal {B}$
is saturated or H normal.
Proof Let
![]() $\tilde { T } \colon \mathcal {B}\to \mathbb {B}(X)$
be a faithful nondegenerate representation and
$\tilde { T } \colon \mathcal {B}\to \mathbb {B}(X)$
be a faithful nondegenerate representation and
![]() $\kappa \colon H\to \mathbb {C}$
the trivial representation. By Propositions 3.1 and 3.2, Lemma 3.5, and Theorem 4.1, for all
$\kappa \colon H\to \mathbb {C}$
the trivial representation. By Propositions 3.1 and 3.2, Lemma 3.5, and Theorem 4.1, for all
![]() $f\in C^{*}(\mathcal {B}),$
we have
$f\in C^{*}(\mathcal {B}),$
we have
which implies the existence of
![]() $\Theta ^H_{\mathcal {B}}.$
Uniqueness is a consequence of the fact that
$\Theta ^H_{\mathcal {B}}.$
Uniqueness is a consequence of the fact that
![]() $q^{H\uparrow G}_{\mathcal {B}}$
is surjective. In case
$q^{H\uparrow G}_{\mathcal {B}}$
is surjective. In case
![]() $\mathcal {B}$
is saturated,
$\mathcal {B}$
is saturated,
![]() $\Theta ^H_{\mathcal {B}}$
is the inverse of the
$\Theta ^H_{\mathcal {B}}$
is the inverse of the
![]() $\pi ^H_{\mathcal {B}}$
of (1.3).
$\pi ^H_{\mathcal {B}}$
of (1.3).
To prove the claim about the intersection of the kernels, we take a faithful nondegenerate representation
![]() $\tilde { U } $
of
$\tilde { U } $
of
![]() $H.$
The integrated form of all the restrictions
$H.$
The integrated form of all the restrictions
![]() $T|_{\mathcal {B}_{rH{r^{-1}}}}$
and conjugations
$T|_{\mathcal {B}_{rH{r^{-1}}}}$
and conjugations
![]() ${}_r U$
have faithful integrated forms, so for all
${}_r U$
have faithful integrated forms, so for all
![]() $f\in C^{*}(\mathcal {B}),$
we have
$f\in C^{*}(\mathcal {B}),$
we have
 $$ \begin{align*} q^{H\uparrow G}_{\mathcal{B}}(f)\in \bigcap_{r\in G} \ker(\Theta^{rH{r^{-1}}}_{\mathcal{B}}) & \Leftrightarrow q^{rH{r^{-1}} \uparrow \mathcal{B}}_{\mathcal{B}}(f)\ \forall\ r\in G \nonumber \\ &\Leftrightarrow \| {\mathop{\mathrm{Ind}}}_{rH{r^{-1}}}^{\mathcal{B}}(T|_{\mathcal{B}_{rH{r^{-1}}}}\otimes {}_r U)_f \|=0\ \forall\ r\in G\nonumber \\ & \Leftrightarrow \|[T\otimes {\mathop{\mathrm{Ind}}}_H^G(U)]_f\|=0 \nonumber\\ & \Leftrightarrow q^{H\uparrow G}_{\mathcal{B}}(f)=0, \end{align*} $$
$$ \begin{align*} q^{H\uparrow G}_{\mathcal{B}}(f)\in \bigcap_{r\in G} \ker(\Theta^{rH{r^{-1}}}_{\mathcal{B}}) & \Leftrightarrow q^{rH{r^{-1}} \uparrow \mathcal{B}}_{\mathcal{B}}(f)\ \forall\ r\in G \nonumber \\ &\Leftrightarrow \| {\mathop{\mathrm{Ind}}}_{rH{r^{-1}}}^{\mathcal{B}}(T|_{\mathcal{B}_{rH{r^{-1}}}}\otimes {}_r U)_f \|=0\ \forall\ r\in G\nonumber \\ & \Leftrightarrow \|[T\otimes {\mathop{\mathrm{Ind}}}_H^G(U)]_f\|=0 \nonumber\\ & \Leftrightarrow q^{H\uparrow G}_{\mathcal{B}}(f)=0, \end{align*} $$
which completes the proof.
In many parts of [Reference Fell and Doran11] Fell gets a result for representations of Banach *-algebraic bundles out of the corresponding result for Fell bundles. Such techniques yield the following.
Corollary 4.3 Let
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
be a Banach *-algebraic bundle over a locally compact group,
$\mathcal {B}=\{B_t\}_{t\in G}$
be a Banach *-algebraic bundle over a locally compact group,
![]() $H\leqslant G$
,
$H\leqslant G$
,
![]() $T\colon \mathcal {B}\to \mathbb {B}(X)$
a nondegenerate representation and
$T\colon \mathcal {B}\to \mathbb {B}(X)$
a nondegenerate representation and
![]() $U\colon H\to \mathbb {B}(Y)$
a unitary representation. If for each
$U\colon H\to \mathbb {B}(Y)$
a unitary representation. If for each
![]() $t\in G$
we denote by
$t\in G$
we denote by
![]() ${}_tU$
the conjugated representation
${}_tU$
the conjugated representation
![]() $tH{t^{-1}} \to \mathbb {B}(Y), \ r\mapsto U_{{t^{-1}} r t},$
then
$tH{t^{-1}} \to \mathbb {B}(Y), \ r\mapsto U_{{t^{-1}} r t},$
then
![]() $\{T|_{\mathcal {B}_{tH{t^{-1}}}}\otimes {}_tU\}_{t\in G}$
is a set of
$\{T|_{\mathcal {B}_{tH{t^{-1}}}}\otimes {}_tU\}_{t\in G}$
is a set of
![]() $\mathcal {B}$
-positive representations and
$\mathcal {B}$
-positive representations and
Proof Let
![]() $\mathcal {C}$
be the bundle C*-completion of
$\mathcal {C}$
be the bundle C*-completion of
![]() $\mathcal {B}$
and let
$\mathcal {B}$
and let
![]() $\rho \colon \mathcal {B}\to \mathcal {C}$
be the canonical quotient map of [Reference Fell and Doran11, Chapter VIII Section 16.7]. The construction of
$\rho \colon \mathcal {B}\to \mathcal {C}$
be the canonical quotient map of [Reference Fell and Doran11, Chapter VIII Section 16.7]. The construction of
![]() $\mathcal {C}$
implies the existence of a unique representation
$\mathcal {C}$
implies the existence of a unique representation
![]() $S\colon \mathcal {C}\to \mathbb {B}(X)$
such that
$S\colon \mathcal {C}\to \mathbb {B}(X)$
such that
![]() $S\circ \rho = T.$
$S\circ \rho = T.$
Theorem 2.1 implies
![]() $S|_{\mathcal {C}_{tH{t^{-1}}}}\otimes {}_t U $
is
$S|_{\mathcal {C}_{tH{t^{-1}}}}\otimes {}_t U $
is
![]() $\mathcal {C}$
-positive for every
$\mathcal {C}$
-positive for every
![]() $t\in G.$
Hence, by [Reference Fell and Doran11, Chapter XI Section 12.6], the composition
$t\in G.$
Hence, by [Reference Fell and Doran11, Chapter XI Section 12.6], the composition
![]() $(S|_{\mathcal {C}_{tH{t^{-1}}}}\otimes {}_t U)\circ (\rho |_{\mathcal {B}_{tH{t^{-1}}}})\equiv T|_{\mathcal {B}_{tH{t^{-1}}}}\otimes {}_tU$
is
$(S|_{\mathcal {C}_{tH{t^{-1}}}}\otimes {}_t U)\circ (\rho |_{\mathcal {B}_{tH{t^{-1}}}})\equiv T|_{\mathcal {B}_{tH{t^{-1}}}}\otimes {}_tU$
is
![]() $\mathcal {B}$
-positive for all
$\mathcal {B}$
-positive for all
![]() $t\in G.$
$t\in G.$
We know that
![]() $S\otimes {\mathop {\mathrm {Ind}}}_H^G(U)\approx \{{\mathop {\mathrm {Ind}}}_{tH{t^{-1}} }^{\mathcal {C}}(S|_{\mathcal {C}_{tH{t^{-1}}}}\otimes {}_tU) \}_{t\in G},$
which implies
$S\otimes {\mathop {\mathrm {Ind}}}_H^G(U)\approx \{{\mathop {\mathrm {Ind}}}_{tH{t^{-1}} }^{\mathcal {C}}(S|_{\mathcal {C}_{tH{t^{-1}}}}\otimes {}_tU) \}_{t\in G},$
which implies
It is clear that
![]() $(S\otimes {\mathop {\mathrm {Ind}}}_H^G(U))\circ \rho = (S\circ \rho )\otimes {\mathop {\mathrm {Ind}}}_H^G(U) = T\otimes {\mathop {\mathrm { Ind}}}_H^G(U).$
On the other hand, by [Reference Fell and Doran11, Chapter XI Section 12.6], for all
$(S\otimes {\mathop {\mathrm {Ind}}}_H^G(U))\circ \rho = (S\circ \rho )\otimes {\mathop {\mathrm {Ind}}}_H^G(U) = T\otimes {\mathop {\mathrm { Ind}}}_H^G(U).$
On the other hand, by [Reference Fell and Doran11, Chapter XI Section 12.6], for all
![]() $t\in G$
we have
$t\in G$
we have
 $$ \begin{align*} {\mathop{\mathrm{Ind}}}_{tH{t^{-1}} }^{\mathcal{C}}(S|_{\mathcal{C}_{tH{t^{-1}}}}\otimes {}_tU)\circ \rho & = {\mathop{\mathrm{Ind}}}_{tH{t^{-1}} }^{\mathcal{B}}\left( (S|_{\mathcal{C}_{tH{t^{-1}}}}\otimes {}_tU)\circ (\rho|_{\mathcal{B}_{tH{t^{-1}}}})\right) \\ & ={\mathop{\mathrm{Ind}}}_{tH{t^{-1}} }^{\mathcal{B}}( T|_{\mathcal{B}_{tH{t^{-1}}}}\otimes {}_tU). \end{align*} $$
$$ \begin{align*} {\mathop{\mathrm{Ind}}}_{tH{t^{-1}} }^{\mathcal{C}}(S|_{\mathcal{C}_{tH{t^{-1}}}}\otimes {}_tU)\circ \rho & = {\mathop{\mathrm{Ind}}}_{tH{t^{-1}} }^{\mathcal{B}}\left( (S|_{\mathcal{C}_{tH{t^{-1}}}}\otimes {}_tU)\circ (\rho|_{\mathcal{B}_{tH{t^{-1}}}})\right) \\ & ={\mathop{\mathrm{Ind}}}_{tH{t^{-1}} }^{\mathcal{B}}( T|_{\mathcal{B}_{tH{t^{-1}}}}\otimes {}_tU). \end{align*} $$
4.1 Exel–Ng’s absorption principle
If the subgroup H of Theorem 2.3 is normal in
![]() $G,$
then all the restrictions
$G,$
then all the restrictions
![]() $T|_{\mathcal {B}_{tH{t^{-1}}}}$
become
$T|_{\mathcal {B}_{tH{t^{-1}}}}$
become
![]() $T|_{\mathcal {B}_H}$
and
$T|_{\mathcal {B}_H}$
and
![]() $T\otimes {\mathop {\mathrm {Ind}}}_H^G(U)\approx \{{\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T|_{\mathcal {B}_H}\otimes {}_tU)\}_{t\in G}.$
One can arrange U to have
$T\otimes {\mathop {\mathrm {Ind}}}_H^G(U)\approx \{{\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T|_{\mathcal {B}_H}\otimes {}_tU)\}_{t\in G}.$
One can arrange U to have
![]() ${}_tU\approx U$
for all
${}_tU\approx U$
for all
![]() $t\in G$
. Indeed, this is the case if
$t\in G$
. Indeed, this is the case if
![]() $\tilde { U } $
is faithful or
$\tilde { U } $
is faithful or
![]() $U:=\bigoplus _{s\in G} {}_s V$
for some other representation V of
$U:=\bigoplus _{s\in G} {}_s V$
for some other representation V of
![]() $H.$
$H.$
Corollary 4.4 If, in addition to the hypotheses of Theorem 2.3, we assume that H is normal in G and
![]() ${}_tU\approx U$
for all
${}_tU\approx U$
for all
![]() $t\in G,$
then
$t\in G,$
then
![]() $T\otimes {\mathop {\mathrm {Ind}}}_H^G(U)\approx {\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T|_{\mathcal {B}_H}\otimes U).$
$T\otimes {\mathop {\mathrm {Ind}}}_H^G(U)\approx {\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T|_{\mathcal {B}_H}\otimes U).$
Proof It is clear that
![]() ${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T|_{\mathcal {B}_H}\otimes U)\preceq \{{\mathop {\mathrm {Ind}}}_{tH{t^{-1}} }^{\mathcal {B}}(T|_{\mathcal {B}_{tH{t^{-1}}}}\otimes {}_tU) \}_{t\in G}.$
Besides, for any
${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T|_{\mathcal {B}_H}\otimes U)\preceq \{{\mathop {\mathrm {Ind}}}_{tH{t^{-1}} }^{\mathcal {B}}(T|_{\mathcal {B}_{tH{t^{-1}}}}\otimes {}_tU) \}_{t\in G}.$
Besides, for any
![]() $t\in G$
we have
$t\in G$
we have
![]() $T|_{\mathcal {B}_H}\otimes {}_t U\preceq T|_{\mathcal {B}_H}\otimes U$
and, since induction preserves weak containment,
$T|_{\mathcal {B}_H}\otimes {}_t U\preceq T|_{\mathcal {B}_H}\otimes U$
and, since induction preserves weak containment,
Then,
![]() ${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T|_{\mathcal {B}_H}\otimes U)\approx \{{\mathop {\mathrm {Ind}}}_{tH{t^{-1}} }^{\mathcal {B}}(T|_{\mathcal {B}_{tH{t^{-1}}}}\otimes {}_tU) \}_{t\in G}$
and the thesis follows from Theorem 2.3 (and the transitivity of weak equivalence).
${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}}(T|_{\mathcal {B}_H}\otimes U)\approx \{{\mathop {\mathrm {Ind}}}_{tH{t^{-1}} }^{\mathcal {B}}(T|_{\mathcal {B}_{tH{t^{-1}}}}\otimes {}_tU) \}_{t\in G}$
and the thesis follows from Theorem 2.3 (and the transitivity of weak equivalence).
The hypotheses of the Corollary above are fulfilled if
![]() $T\colon \mathcal {B}\to \mathbb {B}(X)$
is any representation,
$T\colon \mathcal {B}\to \mathbb {B}(X)$
is any representation,
![]() $H=\{e\}$
and
$H=\{e\}$
and
![]() $U\colon H\to \mathbb {C},\ s\mapsto 1.$
In this case, Corollary 4.4 becomes Exel–Ng’s absorption principle.
$U\colon H\to \mathbb {C},\ s\mapsto 1.$
In this case, Corollary 4.4 becomes Exel–Ng’s absorption principle.
5 Weak containment and subgroups
In [Reference Exel and Ng8] a Fell bundle
![]() $\mathcal {B}$
is called amenable if
$\mathcal {B}$
is called amenable if
![]() $C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
(i.e.
$C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
(i.e.
![]() $\lambda _{\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_e(\mathcal {B}))$
is faithful). This is equivalent to say any representation T of
$\lambda _{\mathcal {B}}\colon C^{*}(\mathcal {B})\to \mathbb {B}(L^2_e(\mathcal {B}))$
is faithful). This is equivalent to say any representation T of
![]() $\mathcal {B}$
is weakly contained in some other of the form
$\mathcal {B}$
is weakly contained in some other of the form
![]() $S\otimes \lambda $
(this is the so called weak containment property, WCP).
$S\otimes \lambda $
(this is the so called weak containment property, WCP).
The recent developments on amenable actions (á la Anantharaman–Delaroche) suggest Exel and Ng should have named amenable those bundles having the approximation property they introduced in [Reference Exel and Ng8]. We follow this stream, so amenability implies the WCP.
The reduced representation
![]() $\lambda _{\mathcal {B}},$
considered as a map from
$\lambda _{\mathcal {B}},$
considered as a map from
![]() $C^{*}_{G\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{G\uparrow G}(\mathcal {B})=C^{*}(\mathcal {B})$
to
$C^{*}_{G\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{G\uparrow G}(\mathcal {B})=C^{*}(\mathcal {B})$
to
![]() $C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\{e\}\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}),$
is a particular case of the maps
$C^{*}_{\{e\}\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\{e\}\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}),$
is a particular case of the maps
![]() $\mu $
and
$\mu $
and
![]() $\nu $
of
$\nu $
of
Proposition 5.1 Let
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle. Given subgroups
$\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle. Given subgroups
![]() $K \leqslant H\leqslant G,$
there exist unique *-homomorphisms
$K \leqslant H\leqslant G,$
there exist unique *-homomorphisms
![]() $\mu ^{HK}_{\mathcal {B}}\colon C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})\to C^{*}_{K\uparrow \mathcal {B}}(\mathcal {B})$
and
$\mu ^{HK}_{\mathcal {B}}\colon C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})\to C^{*}_{K\uparrow \mathcal {B}}(\mathcal {B})$
and
![]() $\nu ^{HK}_{\mathcal {B}}\colon C^{*}_{H\uparrow G}(\mathcal {B})\to C^{*}_{K\uparrow G}(\mathcal {B})$
such that
$\nu ^{HK}_{\mathcal {B}}\colon C^{*}_{H\uparrow G}(\mathcal {B})\to C^{*}_{K\uparrow G}(\mathcal {B})$
such that
![]() $\mu ^{HK}_{\mathcal {B}}\circ q^{H\uparrow \mathcal {B}}=q^{K\uparrow \mathcal {B}}$
and
$\mu ^{HK}_{\mathcal {B}}\circ q^{H\uparrow \mathcal {B}}=q^{K\uparrow \mathcal {B}}$
and
![]() $\nu ^{HK}_{\mathcal {B}}\circ q^{H\uparrow G}_{\mathcal {B}}=q^{K\uparrow G}_{\mathcal {B}}.$
$\nu ^{HK}_{\mathcal {B}}\circ q^{H\uparrow G}_{\mathcal {B}}=q^{K\uparrow G}_{\mathcal {B}}.$
Proof The existence of
![]() $\mu ^{HK}_{\mathcal {B}}$
is equivalent to the validity of
$\mu ^{HK}_{\mathcal {B}}$
is equivalent to the validity of
![]() $\| q^{K\uparrow \mathcal {B}}(f) \|\leq \| q^{H\uparrow \mathcal {B}}(f) \|$
for all
$\| q^{K\uparrow \mathcal {B}}(f) \|\leq \| q^{H\uparrow \mathcal {B}}(f) \|$
for all
![]() $f\in C^{*}(\mathcal {B}).$
To prove this, we take a faithful nondegenerate representation
$f\in C^{*}(\mathcal {B}).$
To prove this, we take a faithful nondegenerate representation
![]() $\tilde { T } \colon C^{*}(\mathcal {B}_K)\to \mathbb {B}(X).$
By Proposition 3.1 and induction in stages [Reference Fell and Doran11, Chapter XI Section 12.15],
$\tilde { T } \colon C^{*}(\mathcal {B}_K)\to \mathbb {B}(X).$
By Proposition 3.1 and induction in stages [Reference Fell and Doran11, Chapter XI Section 12.15],
The proof of the existence of
![]() $\nu ^{HK}_{\mathcal {B}}$
is similar. It combines induction in stages with Proposition 3.2, the details are left to the reader with the suggestion to consult (5.2).
$\nu ^{HK}_{\mathcal {B}}$
is similar. It combines induction in stages with Proposition 3.2, the details are left to the reader with the suggestion to consult (5.2).
Corollary 5.2 The restrictions of both
![]() $q^{H\uparrow \mathcal {B}}$
and
$q^{H\uparrow \mathcal {B}}$
and
![]() $q^{H\uparrow G}_{\mathcal {B}}$
to
$q^{H\uparrow G}_{\mathcal {B}}$
to
![]() $L^1(\mathcal {B})$
are faithful.
$L^1(\mathcal {B})$
are faithful.
Proof We have
![]() $ \mu ^{H\{e\}}_{\mathcal {B}} \circ q^{H\uparrow \mathcal {B}} = q^{\{e\}\uparrow \mathcal {B}} = \lambda _{\mathcal {B}}=q^{\{e\}\uparrow G}_{\mathcal {B}} = \nu ^{H\{e\}}_{\mathcal {B}} \circ q^{H\uparrow G}_{\mathcal {B}},$
so it suffices to consider the case
$ \mu ^{H\{e\}}_{\mathcal {B}} \circ q^{H\uparrow \mathcal {B}} = q^{\{e\}\uparrow \mathcal {B}} = \lambda _{\mathcal {B}}=q^{\{e\}\uparrow G}_{\mathcal {B}} = \nu ^{H\{e\}}_{\mathcal {B}} \circ q^{H\uparrow G}_{\mathcal {B}},$
so it suffices to consider the case
![]() $H=\{e\}.$
In [Reference Fell and Doran11, Chapter VIII Section 16.4] Fell proves that the direct sum of the integrated forms of the generalized regular representations of
$H=\{e\}.$
In [Reference Fell and Doran11, Chapter VIII Section 16.4] Fell proves that the direct sum of the integrated forms of the generalized regular representations of
![]() $\mathcal {B}$
is faithful. This is equivalent to say that
$\mathcal {B}$
is faithful. This is equivalent to say that
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _{\{e\}}^{\mathcal {B}}(\pi )|_{L^1(\mathcal {B})}=\lambda _{\mathcal {B}}\otimes _\pi 1|_{L^1(\mathcal {B})}$
is faithful, with
$\tilde { {\mathop {\mathrm {Ind}}} } _{\{e\}}^{\mathcal {B}}(\pi )|_{L^1(\mathcal {B})}=\lambda _{\mathcal {B}}\otimes _\pi 1|_{L^1(\mathcal {B})}$
is faithful, with
![]() $\pi $
the universal representation of
$\pi $
the universal representation of
![]() $B_e.$
Thus,
$B_e.$
Thus,
![]() $\lambda _{\mathcal {B}}|_{L^1(\mathcal {B})}$
is faithful.
$\lambda _{\mathcal {B}}|_{L^1(\mathcal {B})}$
is faithful.
Corollary 5.3 In the situation of Proposition 5.1, the following claims hold:
-
(1)
 $C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
$C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
 $\Leftrightarrow $
$\Leftrightarrow $
 $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
for all
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
for all
 $ H\leqslant G$
$ H\leqslant G$
 $\Leftrightarrow $
$\Leftrightarrow $
 $C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
for all
$C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
for all
 $H\leqslant G.$
$H\leqslant G.$
-
(2) If
 $C^{*}(\mathcal {B}_H)=C^{*}_{K\uparrow \mathcal {B}_H}(\mathcal {B}_H),$
then
$C^{*}(\mathcal {B}_H)=C^{*}_{K\uparrow \mathcal {B}_H}(\mathcal {B}_H),$
then
 $C^{*}_{K\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}).$
$C^{*}_{K\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B}).$
-
(3) If
 $C^{*}(H)=Q^H_K,$
then
$C^{*}(H)=Q^H_K,$
then
 $C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{K\uparrow G}(\mathcal {B}).$
$C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{K\uparrow G}(\mathcal {B}).$
-
(4) If H is amenable, then
 $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})=C^{*}_{H\uparrow G}(\mathcal {B}).$
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})=C^{*}_{H\uparrow G}(\mathcal {B}).$
Proof The first claim follows easily after one notices
![]() $\mu ^{G\{e\}}_{\mathcal {B}} =\mu ^{H\{e\}}_{\mathcal {B}} \circ \mu ^{GH}_{\mathcal {B}}$
;
$\mu ^{G\{e\}}_{\mathcal {B}} =\mu ^{H\{e\}}_{\mathcal {B}} \circ \mu ^{GH}_{\mathcal {B}}$
;
![]() $\nu ^{G\{e\}}_{\mathcal {B}} =\nu ^{H\{e\}}_{\mathcal {B}} \circ \nu ^{GH}_{\mathcal {B}}$
and identifies
$\nu ^{G\{e\}}_{\mathcal {B}} =\nu ^{H\{e\}}_{\mathcal {B}} \circ \nu ^{GH}_{\mathcal {B}}$
and identifies
![]() $\mu ^{G\{e\}}_{\mathcal {B}}=\lambda _{\mathcal {B}}=\nu ^{G\{e\}}_{\mathcal {B}}.$
For the second claim, we go back to (5.1). The hypothesis implies the integrated form of
$\mu ^{G\{e\}}_{\mathcal {B}}=\lambda _{\mathcal {B}}=\nu ^{G\{e\}}_{\mathcal {B}}.$
For the second claim, we go back to (5.1). The hypothesis implies the integrated form of
![]() ${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}_K}(T)$
is faithful, so the inequality of (5.1) becomes an equality.
${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}_K}(T)$
is faithful, so the inequality of (5.1) becomes an equality.
The proof of the third claim is similar. Take faithful nondegenerate representations
![]() $\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
and
$\tilde { T } \colon C^{*}(\mathcal {B})\to \mathbb {B}(X)$
and
![]() $\tilde { U } \colon C^{*}(K)\to \mathbb {B}(Y).$
Then,
$\tilde { U } \colon C^{*}(K)\to \mathbb {B}(Y).$
Then,
![]() $\tilde { {\mathop {\mathrm {Ind}}} } _K^H(U)$
is faithful and Proposition 3.2 (together with induction in stages) implies that for all
$\tilde { {\mathop {\mathrm {Ind}}} } _K^H(U)$
is faithful and Proposition 3.2 (together with induction in stages) implies that for all
![]() $f\in C^{*}(\mathcal {B})$
$f\in C^{*}(\mathcal {B})$
which clearly implies
![]() $\nu ^{HK}_{\mathcal {B}}$
is isometric.
$\nu ^{HK}_{\mathcal {B}}$
is isometric.
If H is amenable and we set
![]() $K=\{e\},$
then
$K=\{e\},$
then
![]() $C^{*}_{K\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{K\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B})$
;
$C^{*}_{K\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{K\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B})$
;
![]() $C^{*}(H)=C^{*}_{\mathop {\mathrm {r}}}(H)=Q^H_K$
and
$C^{*}(H)=C^{*}_{\mathop {\mathrm {r}}}(H)=Q^H_K$
and
![]() $C^{*}(\mathcal {B}_H)= C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
(see [Reference Exel and Ng8]). Thus the last claim is a consequence of the preceding ones.
$C^{*}(\mathcal {B}_H)= C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
(see [Reference Exel and Ng8]). Thus the last claim is a consequence of the preceding ones.
The converse of claim (2) of the Corollary above is intimately related to question (4) of the Introduction. If we put
![]() $K=\{e\}$
in the claim, then we get that
$K=\{e\}$
in the claim, then we get that
![]() $C^{*}(\mathcal {B}_H)= C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
implies
$C^{*}(\mathcal {B}_H)= C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
implies
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
Whenever the converse holds, one can use claim (1) of Corollary 5.3 to deduce the WCP passes from
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
Whenever the converse holds, one can use claim (1) of Corollary 5.3 to deduce the WCP passes from
![]() $\mathcal {B}$
to
$\mathcal {B}$
to
![]() $\mathcal {B}_H.$
This is false in general because
$\mathcal {B}_H.$
This is false in general because
![]() $\mathcal {B}$
may be the semidirect product bundle of a C*-dynamical system
$\mathcal {B}$
may be the semidirect product bundle of a C*-dynamical system
![]() $(A,G,\alpha ),$
in which case
$(A,G,\alpha ),$
in which case
![]() $\mathcal {B}_H$
is that of the restricted system
$\mathcal {B}_H$
is that of the restricted system
![]() $(A,H,\alpha |_H).$
By [Reference Buss, Echterhoff and Willett5, Section 5.3], it is not true that
$(A,H,\alpha |_H).$
By [Reference Buss, Echterhoff and Willett5, Section 5.3], it is not true that
![]() $A\rtimes _\alpha G = A\rtimes _{{\mathop {\mathrm {r}}}\alpha } G$
(i.e.
$A\rtimes _\alpha G = A\rtimes _{{\mathop {\mathrm {r}}}\alpha } G$
(i.e.
![]() $C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
) implies
$C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
) implies
![]() $A\rtimes _{\alpha |_H} H = A\rtimes _{{\mathop {\mathrm {r}}}\alpha |_H} H$
(
$A\rtimes _{\alpha |_H} H = A\rtimes _{{\mathop {\mathrm {r}}}\alpha |_H} H$
(
![]() $C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
).
$C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
).
In Theorem 5.5, we show that whenever the normalizer of H is open in G,
![]() $\mathcal {B}_H$
has the WCP if and only if
$\mathcal {B}_H$
has the WCP if and only if
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
When applied to semidirect product bundles, this gives a condition on H for the WCP to pass from
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
When applied to semidirect product bundles, this gives a condition on H for the WCP to pass from
![]() $(A,G,\alpha )$
to
$(A,G,\alpha )$
to
![]() $(A,H,\alpha |_H)$
(see Corollary 5.6); giving a partial affirmative answer to Question (b) of [Reference Anantharaman-Delaroche3, Section 9].
$(A,H,\alpha |_H)$
(see Corollary 5.6); giving a partial affirmative answer to Question (b) of [Reference Anantharaman-Delaroche3, Section 9].
We need a (probably well known) fact about the regular representations of subgroups.
Proposition 5.4 Let G be a locally compact group and H a closed subgroup of G with open normalizer. If we denote by
![]() $\lambda ^G$
the left regular representation of
$\lambda ^G$
the left regular representation of
![]() $G,$
then
$G,$
then
![]() $\lambda ^G|_H\approx \lambda ^H.$
$\lambda ^G|_H\approx \lambda ^H.$
Proof Assume H is open in G and decompose
![]() $L^2(G)$
into a direct sum with respect to the right cosets
$L^2(G)$
into a direct sum with respect to the right cosets
![]() $H\setminus G=\{Ht\colon t\in G\},$
that is
$H\setminus G=\{Ht\colon t\in G\},$
that is
![]() $L^2(G)=\bigoplus _{Z\in H\setminus G} L^2(Z).$
With this decomposition
$L^2(G)=\bigoplus _{Z\in H\setminus G} L^2(Z).$
With this decomposition
![]() $\lambda ^G|_H$
becomes a direct sum of representations unitary equivalent to
$\lambda ^G|_H$
becomes a direct sum of representations unitary equivalent to
![]() $\lambda ^H,$
so
$\lambda ^H,$
so
![]() $\lambda ^G|_H\approx \lambda ^H.$
$\lambda ^G|_H\approx \lambda ^H.$
We now assume that H is normal in G and that the left invariant Haar measures of
![]() $G,H$
and
$G,H$
and
![]() $G/H$
have been normalized so that
$G/H$
have been normalized so that
![]() $ \int _G f(t)\, dt = \int _{G/H} \int _H f(ts)\, dsd(tH)$
for all
$ \int _G f(t)\, dt = \int _{G/H} \int _H f(ts)\, dsd(tH)$
for all
![]() $f\in C_c(G)$
(exactly as in [Reference Fell and Doran10, Chapter III Section 13.17]). Besides, we let
$f\in C_c(G)$
(exactly as in [Reference Fell and Doran10, Chapter III Section 13.17]). Besides, we let
![]() $\Gamma \colon G\to \mathbb {R}^+$
be the continuous homomorphism of [Reference Fell and Doran10, Chapter III Section 13.20], i.e., the unique function such that
$\Gamma \colon G\to \mathbb {R}^+$
be the continuous homomorphism of [Reference Fell and Doran10, Chapter III Section 13.20], i.e., the unique function such that
![]() $\int _H f(sts^{-1})\, dt =\Gamma (s)\int _H f(t)\, dt $
for all
$\int _H f(sts^{-1})\, dt =\Gamma (s)\int _H f(t)\, dt $
for all
![]() $f\in C_c(H)$
and
$f\in C_c(H)$
and
![]() $s\in G.$
$s\in G.$
For any
![]() $f\in C_c(H)$
and
$f\in C_c(H)$
and
![]() $\xi \in C_c(G)\subset L^2(G),$
we have
$\xi \in C_c(G)\subset L^2(G),$
we have
 $$ \begin{align} \| \tilde{ (\lambda^G|_H) } _f \xi \|^2 & =\int_G\int_H f^{*}*f(t)\xi({t^{-1}} s)\overline{\xi(s)}dtds\nonumber \\ & = \int_{G/H} \int_H\int_H f^{*}*f(t)\xi({t^{-1}} sr)\overline{\xi(sr)}\, dtdrd(sH) \nonumber \\ & = \int_{G/H} \Gamma(s)\int_H\int_H f^{*}*f(t)\xi({t^{-1}} rs)\overline{\xi(rs)}dtdrd(sH). \end{align} $$
$$ \begin{align} \| \tilde{ (\lambda^G|_H) } _f \xi \|^2 & =\int_G\int_H f^{*}*f(t)\xi({t^{-1}} s)\overline{\xi(s)}dtds\nonumber \\ & = \int_{G/H} \int_H\int_H f^{*}*f(t)\xi({t^{-1}} sr)\overline{\xi(sr)}\, dtdrd(sH) \nonumber \\ & = \int_{G/H} \Gamma(s)\int_H\int_H f^{*}*f(t)\xi({t^{-1}} rs)\overline{\xi(rs)}dtdrd(sH). \end{align} $$
To bound the inner double integral in the last term above we define, for each
![]() $s\in G$
,
$s\in G$
,
![]() $\xi _s\in C_c(H)\subset L^2(H)$
by
$\xi _s\in C_c(H)\subset L^2(H)$
by
![]() $\xi _s(z)=\xi (zs).$
Then
$\xi _s(z)=\xi (zs).$
Then
and we can continue (5.3) to get
Thus
![]() $\| \tilde { (\lambda ^G|_H) } _f\|\leq \|\tilde { \lambda ^H } _f\|$
for all
$\| \tilde { (\lambda ^G|_H) } _f\|\leq \|\tilde { \lambda ^H } _f\|$
for all
![]() $f\in C_c(H)$
and this implies
$f\in C_c(H)$
and this implies
![]() $\lambda ^G|_H\preceq \lambda ^H.$
Lemma 3.5 gives
$\lambda ^G|_H\preceq \lambda ^H.$
Lemma 3.5 gives
![]() $\lambda ^H\preceq \lambda ^G|_H,$
so
$\lambda ^H\preceq \lambda ^G|_H,$
so
![]() $\lambda ^H\approx \lambda ^G|_H.$
$\lambda ^H\approx \lambda ^G|_H.$
For the general case, we define N as the normalizer of H in G and use the arguments of the proof of Lemma 3.5 to get
![]() $ \lambda ^G|_H =\lambda ^G|_N|_H\approx \lambda ^N|_H\approx \lambda ^H,$
which implies
$ \lambda ^G|_H =\lambda ^G|_N|_H\approx \lambda ^N|_H\approx \lambda ^H,$
which implies
![]() $\lambda ^G|_H\approx \lambda ^H.$
$\lambda ^G|_H\approx \lambda ^H.$
Theorem 5.5 Let
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle and
$\mathcal {B}=\{B_t\}_{t\in G}$
be a Fell bundle and
![]() $H\leqslant G.$
If the normalizer of H is open, then
$H\leqslant G.$
If the normalizer of H is open, then
![]() $C^{*}_{H\uparrow \mathcal {B} }(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
if and only if
$C^{*}_{H\uparrow \mathcal {B} }(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
if and only if
![]() $C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
and these conditions hold if
$C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
and these conditions hold if
![]() $C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B}).$
$C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm { r}}}(\mathcal {B}).$
Proof We have
![]() $\mu ^{H\{e\}}_{\mathcal {B}}\circ \Theta ^H_{\mathcal {B}}=\nu ^{H\{e\}}_{\mathcal {B}}.$
Hence,
$\mu ^{H\{e\}}_{\mathcal {B}}\circ \Theta ^H_{\mathcal {B}}=\nu ^{H\{e\}}_{\mathcal {B}}.$
Hence,
![]() $C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
(i.e.,
$C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
(i.e.,
![]() $\nu ^{H\{e\}}_{\mathcal {B}}$
an isomorphism) if and only if
$\nu ^{H\{e\}}_{\mathcal {B}}$
an isomorphism) if and only if
![]() $C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
(both
$C^{*}_{H\uparrow G}(\mathcal {B})=C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
(both
![]() $\mu ^{H\{e\}}_{\mathcal {B}}$
and
$\mu ^{H\{e\}}_{\mathcal {B}}$
and
![]() $\Theta ^H_{\mathcal {B}}$
are isomorphisms). By Corollary 5.3,
$\Theta ^H_{\mathcal {B}}$
are isomorphisms). By Corollary 5.3,
![]() $C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
implies
$C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H)$
implies
![]() $C^{*}_{H\uparrow \mathcal {B} }(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
$C^{*}_{H\uparrow \mathcal {B} }(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}).$
Suppose
![]() $C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
and take a faithful nondegenerate representation
$C^{*}_{H\uparrow \mathcal {B}}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
and take a faithful nondegenerate representation
![]() $\tilde { T } $
of
$\tilde { T } $
of
![]() $\mathcal {B}.$
By Proposition 3.1,
$\mathcal {B}.$
By Proposition 3.1,
![]() ${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}} (T|_{\mathcal {B}_H})\approx {\mathop {\mathrm { Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})$
and this, together with Lemma 3.5, yields
${\mathop {\mathrm {Ind}}}_H^{\mathcal {B}} (T|_{\mathcal {B}_H})\approx {\mathop {\mathrm { Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})$
and this, together with Lemma 3.5, yields
![]() $T|_{\mathcal {B}_H}\preceq {\mathop {\mathrm {Ind}}}_H^{\mathcal {B}} (T|_{\mathcal {B}_H})|_{\mathcal {B}_H}\approx {\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})|_{\mathcal {B}_H}$
$T|_{\mathcal {B}_H}\preceq {\mathop {\mathrm {Ind}}}_H^{\mathcal {B}} (T|_{\mathcal {B}_H})|_{\mathcal {B}_H}\approx {\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})|_{\mathcal {B}_H}$
![]() $\Rightarrow $
$\Rightarrow $
![]() $T|_{\mathcal {B}_H}\preceq {\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})|_{\mathcal {B}_H}.$
By Exel–Ng’s absorption principle,
$T|_{\mathcal {B}_H}\preceq {\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})|_{\mathcal {B}_H}.$
By Exel–Ng’s absorption principle,
![]() ${\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})|_{\mathcal {B}_H}\approx T|_{\mathcal {B}_H}\otimes \lambda ^G|_H$
and from Lemma 5.4 we get
${\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})|_{\mathcal {B}_H}\approx T|_{\mathcal {B}_H}\otimes \lambda ^G|_H$
and from Lemma 5.4 we get
![]() ${\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})|_{\mathcal {B}_H}\approx T|_{\mathcal {B}_H}\otimes \lambda ^H$
and we conclude
${\mathop {\mathrm {Ind}}}_{\{e\}}^{\mathcal {B}} (T|_{B_e})|_{\mathcal {B}_H}\approx T|_{\mathcal {B}_H}\otimes \lambda ^H$
and we conclude
![]() $T|_{\mathcal {B}_H}\preceq T|_{\mathcal {B}_H}\otimes \lambda ^H.$
Lemma 3.5 implies the integrated for of
$T|_{\mathcal {B}_H}\preceq T|_{\mathcal {B}_H}\otimes \lambda ^H.$
Lemma 3.5 implies the integrated for of
![]() $T|_{\mathcal {B}_H}$
is faithful, thus
$T|_{\mathcal {B}_H}$
is faithful, thus
![]() $\mathcal {B}_H$
has the WCP.
$\mathcal {B}_H$
has the WCP.
Corollary 5.6 If
![]() $\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle,
$\mathcal {B}=\{B_t\}_{t\in G}$
is a Fell bundle,
![]() $C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
and the normalizer of
$C^{*}(\mathcal {B})=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B})$
and the normalizer of
![]() $H\leqslant G$
is open, then
$H\leqslant G$
is open, then
![]() $C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H).$
$C^{*}(\mathcal {B}_H)=C^{*}_{\mathop {\mathrm {r}}}(\mathcal {B}_H).$