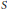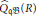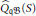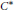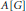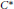We investigate the behavior of the quasi-Baer and the right FI-extending right ring hulls under various ring extensions including group ring extensions, full and triangular matrix ring extensions, and infinite matrix ring extensions. As a consequence, we show that for semiprime rings  $R$ and
$R$ and 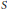 $S$, if
$S$, if  $R$ and
$R$ and 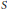 $S$ are Morita equivalent, then so are the quasi-Baer right ring hulls
$S$ are Morita equivalent, then so are the quasi-Baer right ring hulls 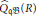 ${{\widehat{\text{Q}}}_{\mathfrak{q}}}\mathfrak{B}(R)$ and
${{\widehat{\text{Q}}}_{\mathfrak{q}}}\mathfrak{B}(R)$ and 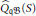 ${{\widehat{\text{Q}}}_{\mathfrak{q}}}\mathfrak{B}(S)$ of
${{\widehat{\text{Q}}}_{\mathfrak{q}}}\mathfrak{B}(S)$ of  $R$ and
$R$ and 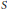 $S$, respectively. As an application, we prove that if unital
$S$, respectively. As an application, we prove that if unital 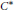 ${{C}^{*}}$-algebras
${{C}^{*}}$-algebras  $A$ and
$A$ and  $B$ are Morita equivalent as rings, then the bounded central closure of
$B$ are Morita equivalent as rings, then the bounded central closure of  $A$ and that of B are strongly Morita equivalent as
$A$ and that of B are strongly Morita equivalent as 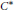 ${{C}^{*}}$-algebras. Our results show that the quasi-Baer property is always preserved by infinite matrix rings, unlike the Baer property. Moreover, we give an affirmative answer to an open question of Goel and Jain for the commutative group ring
${{C}^{*}}$-algebras. Our results show that the quasi-Baer property is always preserved by infinite matrix rings, unlike the Baer property. Moreover, we give an affirmative answer to an open question of Goel and Jain for the commutative group ring 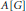 $A[G]$ of a torsion-free Abelian group
$A[G]$ of a torsion-free Abelian group  $G$ over a commutative semiprime quasi-continuous ring
$G$ over a commutative semiprime quasi-continuous ring  $A$. Examples that illustrate and delimit the results of this paper are provided.
$A$. Examples that illustrate and delimit the results of this paper are provided.