Let E be a totally real set on a Stein open set Ω on a complete noncompact Kähler manifold (M,g) with nonnegative holomorphic bisectional curvature such that (Ω,g) has bounded geometry at E. Then every function f in a Cp class with compact support on Ω and 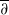 -flat on E up to order p−1,p≥2 (respectively, in a Gevrey class of order s>1, with compact support on Ω and
-flat on E up to order p−1,p≥2 (respectively, in a Gevrey class of order s>1, with compact support on Ω and 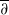 -flat on E up to infinite order) can be approximated on compacts subsets of E by holomorphic functions fk on Ω with degree of approximation equal k−p/2 (respectively, exp (−c(s)k1/2(s−1)) ).
-flat on E up to infinite order) can be approximated on compacts subsets of E by holomorphic functions fk on Ω with degree of approximation equal k−p/2 (respectively, exp (−c(s)k1/2(s−1)) ).