It is known that every torsion-free soluble group G of finite Hirsch number hG is countable, and its homological and cohomological dimensions over the integers and rationals satisfy the inequalities
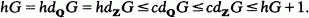
We prove that G must be finitely generated if the equality hG = cdQG holds. Moreover, we show that if G is a countable soluble group of finite Hirsch number, but not necessarily torsion-free, and if hG = cdQG, then hḠ = cdQḠ for every homomorphic image Ḡ of G.