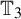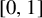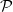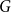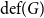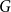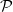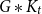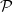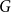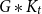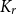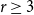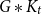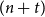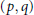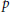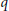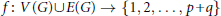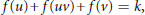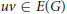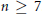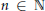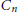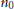We give an example of an FIID vertex-labeling of ${\mathbb T}_3$ whose marginals are uniform on $[0,1]$, and if we delete the edges between those vertices whose labels are different, then some of the remaining clusters are infinite. We also show that no such process can be finitary.

Motivated by analogous questions in the setting of Steiner triple systems and Latin squares, Nenadov, Sudakov and Wagner [Completion and deficiency problems, Journal of Combinatorial Theory Series B, 2020] recently introduced the notion of graph deficiency. Given a global spanning property $\mathcal P$ and a graph $G$ , the deficiency $\text{def}(G)$ of the graph $G$ with respect to the property $\mathcal P$ is the smallest non-negative integer t such that the join $G*K_t$ has property $\mathcal P$ . In particular, Nenadov, Sudakov and Wagner raised the question of determining how many edges an n-vertex graph $G$ needs to ensure $G*K_t$ contains a $K_r$ -factor (for any fixed $r\geq 3$ ). In this paper, we resolve their problem fully. We also give an analogous result that forces $G*K_t$ to contain any fixed bipartite $(n+t)$ -vertex graph of bounded degree and small bandwidth.

A subgraph of an edge-coloured graph is called rainbow if all its edges have different colours. We prove a rainbow version of the blow-up lemma of Komlós, Sárközy, and Szemerédi that applies to almost optimally bounded colourings. A corollary of this is that there exists a rainbow copy of any bounded-degree spanning subgraph H in a quasirandom host graph G, assuming that the edge-colouring of G fulfills a boundedness condition that is asymptotically best possible.

This has many applications beyond rainbow colourings: for example, to graph decompositions, orthogonal double covers, and graph labellings.

In 1970, Kotzig and Rosa defined the concept of edge-magic labelings as follows. Let $G$ be a simple 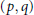$\left( p,\,q \right)$-graph (that is, a graph of order 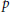$p$ and size 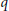$q$ without loops or multiple edges). A bijective function 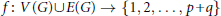$f:\,V\left( G \right)\cup E\left( G \right)\,\to \,\left\{ 1,\,2,\,.\,.\,.\,,\,p\,+\,q \right\}$ is an edge-magic labeling of $G$ if 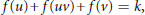$f\left( u \right)\,+\,f\left( uv \right)\,+f\left( v \right)\,=\,k$, for all 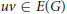$uv\,\in \,E\left( G \right)$. A graph that admits an edge-magic labeling is called an edge-magic graph, and 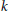$k$ is called the magic sum of the labeling. An old conjecture of Godbold and Slater states that all possible theoretical magic sums are attained for each cycle of order 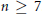$n\,\ge \,7$. Motivated by this conjecture, we prove that for all ${{n}_{0}}\,\in \,\mathbb{N}$, there exists 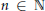$n\,\in \,\mathbb{N}$ such that the cycle 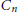${{C}_{n}}$ admits at least 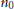${{n}_{0}}$ edge-magic labelings with at least 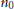${{n}_{0}}$ mutually distinct magic sums. We do this by providing a lower bound for the number of magic sums of the cycle 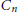${{C}_{n}}$, depending on the sum of the exponents of the odd primes appearing in the prime factorization of $n$.

Böttcher, Schacht and Taraz (Math. Ann., 2009) gave a condition on the minimum degree of a graph G on n vertices that ensures G contains every r-chromatic graph H on n vertices of bounded degree and of bandwidth o(n), thereby proving a conjecture of Bollobás and Komlós (Combin. Probab. Comput., 1999). We strengthen this result in the case when H is bipartite. Indeed, we give an essentially best-possible condition on the degree sequence of a graph G on n vertices that forces G to contain every bipartite graph H on n vertices of bounded degree and of bandwidth o(n). This also implies an Ore-type result. In fact, we prove a much stronger result where the condition on G is relaxed to a certain robust expansion property. Our result also confirms the bipartite case of a conjecture of Balogh, Kostochka and Treglown concerning the degree sequence of a graph which forces a perfect H-packing.