We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
It is shown that a system of congruences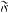 
1(x) ≡ . . . ≡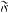
(x) = 0 (mod m)
where each 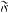i(x) = 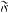i,(x1, .. . ,x2,) is a form of degree at most k has a nontrivial solution x satisfying |xi|≦cm(½)+∊ (i=1,...,S)
with c = c(k,r,∊), provided that ∊ > 0 and that S > S1(k,r,∊).
