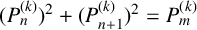 $(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
$(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
 $\boldsymbol {p}$-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES
$\boldsymbol {p}$-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES
 $S$-PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
$S$-PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES