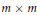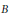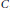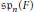10 results
Finite subgroups of automorphisms of K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE BOREL CHARACTER
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 26 July 2021, pp. 747-797
- Print publication:
- March 2023
-
- Article
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
Nonsingular bilinear maps revisited
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 17 March 2020, pp. 377-390
- Print publication:
- February 2021
-
- Article
- Export citation
APPLICATIONS OF SYSTEMS OF QUADRATIC FORMS TO GENERALISED QUADRATIC FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 374-386
- Print publication:
- December 2020
-
- Article
- Export citation
SYMMETRIC SQUARE-CENTRAL ELEMENTS IN PRODUCTS OF ORTHOGONAL INVOLUTIONS IN CHARACTERISTIC TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 17 August 2017, pp. 412-425
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Bilinear and Quadratic Forms on Rational Modules of Split Reductive Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 2 / 01 April 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 395-421
- Print publication:
- 01 April 2016
-
- Article
-
- You have access
- Export citation
EFFECTIVE ISOMETRIC EMBEDDINGS FOR CERTAIN HERMITIAN HOLOMORPHIC LINE BUNDLES
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 16 June 2006, pp. 607-624
- Print publication:
- June 2006
-
- Article
- Export citation
Diagonal Plus Tridiagonal Representatives for Symplectic Congruence Classes of Symmetric Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 3 / 01 September 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 394-404
- Print publication:
- 01 September 2005
-
- Article
-
- You have access
- Export citation
Singular invariant hyperfunctions on the square matrix space and the alternating matrix space
-
- Journal:
- Nagoya Mathematical Journal / Volume 169 / 2003
- Published online by Cambridge University Press:
- 22 January 2016, pp. 19-75
- Print publication:
- 2003
-
- Article
-
- You have access
- Export citation