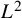 $L^2$-Bound of the Eisenstein series
$L^2$-Bound of the Eisenstein series
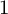 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 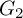 $G_2$
$G_2$
 $\mathrm {GL}(n)\times \mathrm {GL}(n)$
Rankin–Selberg L-functions
$\mathrm {GL}(n)\times \mathrm {GL}(n)$
Rankin–Selberg L-functions
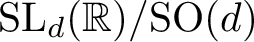 $\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
$\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$ IN THE BENJAMINI–SCHRAMM LIMIT
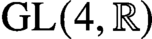 $\mathrm {GL}(4, \mathbb R) $ (with an appendix by Bingrong Huang)
$\mathrm {GL}(4, \mathbb R) $ (with an appendix by Bingrong Huang)
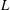 $L$-FUNCTIONS
$L$-FUNCTIONS