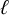 $\ell $
-adic cohomology
$\ell $
-adic cohomology
 $\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
$\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
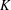 $K$-RATIONAL CUBOIDS
$K$-RATIONAL CUBOIDS