Every field $K$ admits proper projective extensions, that is, Galois extensions where the Galois group is a non-trivial projective group, unless $K$ is separably closed or $K$ is a pythagorean formally real field without cyclic extensions of odd degree. As a consequence, it turns out that almost all absolute Galois groups decompose as proper semidirect products.
We show that each local field has a unique maximal projective extension, and that the same holds for each global field of positive characteristic. In characteristic 0, we prove that Leopoldt's conjecture for all totally real number fields is equivalent to the statement that, for all totally real number fields, all projective extensions are cyclotomic. So the realizability of any non-procyclic projective group as Galois group over ${\mathbb Q}$ produces counterexamples to the Leopoldt conjecture.
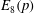 ${E}_{8}(p)$
${E}_{8}(p)$
