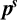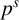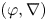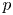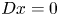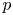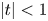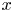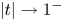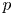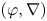7 results
GHOSTS AND CONGRUENCES FOR
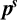 $\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
$\boldsymbol {p}^{\boldsymbol {s}}$-APPROXIMATIONS OF HYPERGEOMETRIC PERIODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 02 August 2023, pp. 96-127
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Logarithmic growth filtrations for
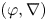 $(\varphi ,\nabla )$-modules over the bounded Robba ring
$(\varphi ,\nabla )$-modules over the bounded Robba ring
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 1265-1301
- Print publication:
- June 2021
-
- Article
- Export citation
Corrigendum: Local and global structure of connections on nonarchimedean curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2658-2665
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
Local and global structure of connections on nonarchimedean curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 6 / June 2015
- Published online by Cambridge University Press:
- 07 January 2015, pp. 1096-1156
- Print publication:
- June 2015
-
- Article
- Export citation
Dwork’s conjecture on the logarithmic growth of solutions of p-adic differential equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 484-494
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Limites de représentations cristallines
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 6 / November 2004
- Published online by Cambridge University Press:
- 15 October 2004, pp. 1473-1498
- Print publication:
- November 2004
-
- Article
-
- You have access
- Export citation
On the Quadratic Residues (Mod p) in the Interval (0, p/4)
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 1 / 01 March 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 123-124
- Print publication:
- 01 March 1983
-
- Article
-
- You have access
- Export citation