Let $(A,\mathfrak{m})$ be a Cohen–Macaulay local ring, and then the notion of a $T$-split sequence was introduced in the part-1 of this paper for the $\mathfrak{m}$-adic filtration with the help of the numerical function $e^T_A$. In this article, we explore the relation between Auslander–Reiten (AR)-sequences and $T$-split sequences. For a Gorenstein ring $(A,\mathfrak{m})$, we define a Hom-finite Krull–Remak–Schmidt category $\mathcal{D}_A$ as a quotient of the stable category $\underline{\mathrm{CM}}(A)$. This category preserves isomorphism, that is, $M\cong N$ in $\mathcal{D}_A$ if and only if $M\cong N$ in $\underline{\mathrm{CM}}(A)$.This article has two objectives: first objective is to extend the notion of $T$-split sequences, and second objective is to explore the function $e^T_A$ and $T$-split sequences. When $(A,\mathfrak{m})$ is an analytically unramified Cohen–Macaulay local ring and $I$ is an $\mathfrak{m}$-primary ideal, then we extend the techniques in part-1 of this paper to the integral closure filtration with respect to $I$ and prove a version of Brauer–Thrall-II for a class of such rings.

Let $(A,\mathfrak{m})$ be a regular local ring of dimension $d \geq 1$, I an $\mathfrak{m}$-primary ideal. Let N be a nonzero finitely generated A-module. Consider the functions

\begin{equation*}t^I(N, n) = \sum_{i = 0}^{d}\ell(\text{Tor}^A_i(N, A/I^n)) \ \text{and}\ e^I(N, n) = \sum_{i = 0}^{d}\ell(\text{Ext}_A^i(N, A/I^n))\end{equation*}

of polynomial type and let their degrees be $t^I(N) $ and $e^I(N)$. We prove that $t^I(N) = e^I(N) = \max\{\dim N, d -1 \}$. A crucial ingredient in the proof is that $D^b(A)_f$, the bounded derived category of A with finite length cohomology, has no proper thick subcategories.

We invoke the Bernstein–Gel$'$fand–Gel$'$fand (BGG) correspondence to study subcomplexes of free resolutions given by two well-known complexes, the Koszul and the Eagon–Northcott. This approach provides a complete characterization of the ranks of free modules in a subcomplex in the Koszul case and imposes numerical restrictions in the Eagon–Northcott case.

We conduct a systematic study of the Ehrhart theory of certain slices of rectangular prisms. Our polytopes are generalizations of the hypersimplex and are contained in the larger class of polypositroids introduced by Lam and Postnikov; moreover, they coincide with polymatroids satisfying the strong exchange property up to an affinity. We give a combinatorial formula for all the Ehrhart coefficients in terms of the number of weighted permutations satisfying certain compatibility properties. This result proves that all these polytopes are Ehrhart positive. Additionally, via an extension of a result by Early and Kim, we give a combinatorial interpretation for all the coefficients of the $h^*$-polynomial. All of our results provide a combinatorial understanding of the Hilbert functions and the h-vectors of all algebras of Veronese type, a problem that had remained elusive up to this point. A variety of applications are discussed, including expressions for the volumes of these slices of prisms as weighted combinations of Eulerian numbers; some extensions of Laplace’s result on the combinatorial interpretation of the volume of the hypersimplex; a multivariate generalization of the flag Eulerian numbers and refinements; and a short proof of the Ehrhart positivity of the independence polytope of all uniform matroids.

Hilbert–Kunz multiplicity and F-signature are numerical invariants of commutative rings in positive characteristic that measure severity of singularities: for a regular ring both invariants are equal to one and the converse holds under mild assumptions. A natural question is for what singular rings these invariants are closest to one. For Hilbert–Kunz multiplicity this question was first considered by the last two authors and attracted significant attention. In this paper, we study this question, i.e., an upper bound, for F-signature and revisit lower bounds on Hilbert–Kunz multiplicity.

Unfortunately, there is a mistake in [PS, Lemma 3.10] which invalidates [PS, Theorem 3.12]. We show that the theorem still holds if the ring is assumed to be Gorenstein.

We prove that the integral closure of a strongly Golod ideal in a polynomial ring over a field of characteristic zero is strongly Golod, positively answering a question of Huneke. More generally, the rational power $I_{\unicode[STIX]{x1D6FC}}$ of an arbitrary homogeneous ideal is strongly Golod for $\unicode[STIX]{x1D6FC}\geqslant 2$ and, if $I$ is strongly Golod, then $I_{\unicode[STIX]{x1D6FC}}$ is strongly Golod for $\unicode[STIX]{x1D6FC}\geqslant 1$. We also show that all the coefficient ideals of a strongly Golod ideal are strongly Golod.

Let (R, ) be an analytically unramified local ring of positive prime characteristic p. For an ideal I, let I* denote its tight closure. We introduce the tight Hilbert function $$H_I^*\left( n \right) = \Im \left( {R/\left( {{I^n}} \right)*} \right)$$ and the corresponding tight Hilbert polynomial $$P_I^*\left( n \right)$$, where I is an m-primary ideal. It is proved that F-rationality can be detected by the vanishing of the first coefficient of $$P_I^*\left( n \right)$$. We find the tight Hilbert polynomial of certain parameter ideals in hypersurface rings and Stanley-Reisner rings of simplicial complexes.

We prove results concerning the multiplicity as well as the Cohen–Macaulay and Gorenstein properties of the special fiber ring $\mathscr{F}(E)$ of a finitely generated $R$-module $E\subsetneq R^{e}$ over a Noetherian local ring $R$ with infinite residue field. Assuming that $R$ is Cohen–Macaulay of dimension 1 and that $E$ has finite colength in $R^{e}$, our main result establishes an asymptotic length formula for the multiplicity of $\mathscr{F}(E)$, which, in addition to being of independent interest, allows us to derive a Cohen–Macaulayness criterion and to detect a curious relation to the Buchsbaum–Rim multiplicity of $E$ in this setting. Further, we provide a Gorensteinness characterization for $\mathscr{F}(E)$ in the more general situation where $R$ is Cohen–Macaulay of arbitrary dimension and $E$ is not necessarily of finite colength, and we notice a constraint in terms of the second analytic deviation of the module $E$ if its reduction number is at least three.

We establish the continuity of Hilbert–Kunz multiplicity and F-signature as functions from a Cohen–Macaulay local ring $(R,\mathfrak{m},k)$ of prime characteristic to the real numbers at reduced parameter elements with respect to the $\mathfrak{m}$-adic topology.

For a pair 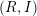$(R,I)$, where 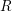$R$ is a standard graded domain of dimension 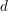$d$ over an algebraically closed field of characteristic 0, and 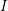$I$ is a graded ideal of finite colength, we prove that the existence of 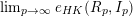$\lim _{p\rightarrow \infty }e_{HK}(R_{p},I_{p})$ is equivalent, for any fixed 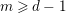$m\geqslant d-1$, to the existence of 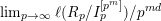$\lim _{p\rightarrow \infty }\ell (R_{p}/I_{p}^{[p^{m}]})/p^{md}$. This we get as a consequence of Theorem 1.1: as 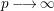$p\longrightarrow \infty$, the convergence of the Hilbert–Kunz (HK) density function 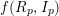$f(R_{p},I_{p})$ is equivalent to the convergence of the truncated HK density functions 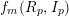$f_{m}(R_{p},I_{p})$ (in 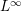$L^{\infty }$ norm) of the mod 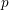$p$reductions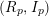$(R_{p},I_{p})$, for any fixed 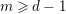$m\geqslant d-1$. In particular, to define the HK density function 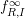$f_{R,I}^{\infty }$ in char 0, it is enough to prove the existence of 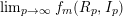$\lim _{p\rightarrow \infty }f_{m}(R_{p},I_{p})$, for any fixed 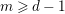$m\geqslant d-1$. This allows us to prove the existence of 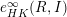$e_{HK}^{\infty }(R,I)$ in many new cases, for example, when Proj R is a Segre product of curves.

We prove that the generalized Hilbert–Kunz function of a graded module $M$ over a two-dimensional standard graded normal $K$-domain over an algebraically closed field $K$ of prime characteristic $p$ has the form $gHK(M,q)=e_{gHK}(M)q^{2}+\unicode[STIX]{x1D6FE}(q)$, with rational generalized Hilbert–Kunz multiplicity $e_{gHK}(M)$ and a bounded function $\unicode[STIX]{x1D6FE}(q)$. Moreover, we prove that if $R$ is a $\mathbb{Z}$-algebra, the limit for $p\rightarrow +\infty$ of the generalized Hilbert–Kunz multiplicity $e_{gHK}^{R_{p}}(M_{p})$ over the fibers $R_{p}$ exists, and it is a rational number.

Let be a Noetherian local ring and let M be a finitely generated R-module of dimension d. Let be a system of parameters of M and let be a d-tuple of positive integers. In this paper we study the length of generalized fractions M(1/(x1, … , xd, 1)), which was introduced by Sharp and Hamieh. First, we study the growth of the function

Then we give an explicit calculation for the function in the case in which M admits a certain Macaulay extension. Most previous results on this topic are improved in a clearly understandable way.

We study the relationship between the reduction number of a primary ideal of a local ring relative to one of its minimal reductions and the multiplicity of the corresponding Sally module. This paper is focused on three goals: (i) to develop a change of rings technique for the Sally module of an ideal to allow extension of results from Cohen–Macaulay rings to more general rings; (ii) to use the fiber of the Sally modules of almost complete intersection ideals to connect its structure to the Cohen–Macaulayness of the special fiber ring; (iii) to extend some of the results of (i) to two-dimensional Buchsbaum rings. Along the way, we provide an explicit realization of the $S_{2}$-fication of arbitrary Buchsbaum rings.

We prove that the Hilbert–Kunz multiplicity is upper semi-continuous in F-finite rings and algebras of essentially finite type over an excellent local ring.

We give explicit formulas for the Hilbert series of residual intersections of a scheme in terms of the Hilbert series of its conormal modules. In a previous paper, we proved that such formulas should exist. We give applications to the number of equations defining projective varieties and to the dimension of secant varieties of surfaces and three-folds.

We study the interplay between the cohomology of the Koszul complex of the partial derivatives of a homogeneous polynomial f and the pole order filtration P on the cohomology of the open set U = ℙn \ D, with D the hypersurface defined by f = 0. The relation is expressed by some spectral sequences. These sequences may, on the one hand, in many cases be used to determine the filtration P for curves and surfaces and, on the other hand, to obtain information about the syzygies involving the partial derivatives of the polynomial f. The case of a nodal hypersurface D is treated in terms of the defects of linear systems of hypersurfaces of various degrees passing through the nodes of D. When D is a nodal surface in ℙ3, we show that F2H3(U) ≠ P2H3(U) as soon as the degree of D is at least 4.

Let A be a Noetherian local ring with the maximal ideal m, and let I be an m-primary ideal in A. This paper examines the equality on Hilbert coefficients of I first presented by Elias and Valla, but without assuming that A is a Cohen–Macaulay local ring. That equality is related to the Buchsbaumness of the associated graded ring of I.

Let (R,m) be a local ring, and let M and N be finite R-modules. In this paper we give a formula for the degree of the polynomial giving the lengths of the modules ExtiR(M,N/mnN). A number of corollaries are given, and more general filtrations are also considered.

Let $(A,\mathfrak{m})$ be a Noetherian local ring with infinite residue field and let $I$ be an ideal in $A$ and let $F(I)={{\oplus }_{n\ge 0}}{{I}^{n}}/\mathfrak{m}{{I}^{n}}$ be the fiber cone of $I$. We prove certain relations among the Hilbert coefficients ${{f}_{0\,}}(I),\,{{f}_{1}}(I),\,{{f}_{2}}(I)$ of $F(I)$ when the $a$-invariant of the associated graded ring $G(I)$ is negative.