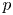 $p$-adic monodromy theorem for de Rham local systems
$p$-adic monodromy theorem for de Rham local systems
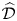 $\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
$\widehat {\mathcal {D}}$-modules on rigid analytic spaces III: weak holonomicity and operations
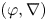 $(\varphi ,\nabla )$-modules over the bounded Robba ring
$(\varphi ,\nabla )$-modules over the bounded Robba ring