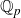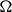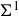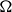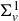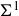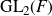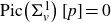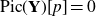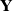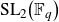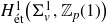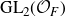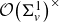1. Introduction
Let p be a prime, F a finite extension of
![]() ${\mathbb Q}_p$
, and K the completion of the maximal unramified extension of F. Let
${\mathbb Q}_p$
, and K the completion of the maximal unramified extension of F. Let
![]() ${\mathcal M}_0$
be the disjoint union of
${\mathcal M}_0$
be the disjoint union of
![]() $\mathbb{Z}$
copies of
$\mathbb{Z}$
copies of
![]() $\Omega$
, where
$\Omega$
, where
![]() $\Omega$
is the Drinfeld upper half plane: the rigid analytic space over K defined by removing all F-rational points from
$\Omega$
is the Drinfeld upper half plane: the rigid analytic space over K defined by removing all F-rational points from
![]() ${\mathbb P}^{1,\text{an}}_K$
. The work of Drinfeld [
Reference Drinfeld14
] implies the existence of a tower of finite étale coverings
${\mathbb P}^{1,\text{an}}_K$
. The work of Drinfeld [
Reference Drinfeld14
] implies the existence of a tower of finite étale coverings
![]() $({\mathcal M}_{n})_{n \geq 0}$
of
$({\mathcal M}_{n})_{n \geq 0}$
of
![]() ${\mathcal M}_0$
equipped with compatible actions of
${\mathcal M}_0$
equipped with compatible actions of
![]() $\text{GL}_2(F)$
, which has been shown to realise both the local Langlands and Jacquet–Langlands correspondence in its étale cohomology [
Reference Boyer4
,
Reference Carayol5
,
Reference Harris18
,
Reference Harris and Taylor19
]. On the other hand, there is at present no formulated p-adic local Langlands correspondence for
$\text{GL}_2(F)$
, which has been shown to realise both the local Langlands and Jacquet–Langlands correspondence in its étale cohomology [
Reference Boyer4
,
Reference Carayol5
,
Reference Harris18
,
Reference Harris and Taylor19
]. On the other hand, there is at present no formulated p-adic local Langlands correspondence for
![]() $\text{GL}_2(F)$
for general finite extensions F. The Drinfeld tower is expected to be of importance in yielding natural representations of
$\text{GL}_2(F)$
for general finite extensions F. The Drinfeld tower is expected to be of importance in yielding natural representations of
![]() $\text{GL}_2(F)$
that should appear in any such correspondence. For example, the geometric p-adic étale cohomology of the Drinfeld tower has been shown to encode the p-adic local Langlands correspondence for
$\text{GL}_2(F)$
that should appear in any such correspondence. For example, the geometric p-adic étale cohomology of the Drinfeld tower has been shown to encode the p-adic local Langlands correspondence for
![]() $F = {\mathbb Q}_p$
[
Reference Colmez, Dospinescu and Nizioł7
].
$F = {\mathbb Q}_p$
[
Reference Colmez, Dospinescu and Nizioł7
].
The preimage of the index zero piece
![]() $\Omega \hookrightarrow {\mathcal M}_0$
in the tower
$\Omega \hookrightarrow {\mathcal M}_0$
in the tower
![]() $({\mathcal M}_n)_{n \geq 0}$
defines a tower
$({\mathcal M}_n)_{n \geq 0}$
defines a tower
![]() $(\Sigma^n)_{n \geq 0}$
of finite étale coverings of
$(\Sigma^n)_{n \geq 0}$
of finite étale coverings of
![]() $\Sigma^0 = \Omega$
. The transition morphisms are equivariant for the action of the stabilising subgroup
$\Sigma^0 = \Omega$
. The transition morphisms are equivariant for the action of the stabilising subgroup
![]() $\text{GL}_2(F)^{+} = \left\{g \in \text{GL}_2(F) \mid \det(g) \in \mathcal{O}^\times\right\}$
. Let
$\text{GL}_2(F)^{+} = \left\{g \in \text{GL}_2(F) \mid \det(g) \in \mathcal{O}^\times\right\}$
. Let
![]() ${\mathcal T}$
be the Bruhat–Tits tree for
${\mathcal T}$
be the Bruhat–Tits tree for
![]() $\text{GL}_2(F)$
, v the central vertex of
$\text{GL}_2(F)$
, v the central vertex of
![]() ${\mathcal T}$
, and
${\mathcal T}$
, and
![]() $r \,:\, \Sigma^1 \rightarrow \Omega \rightarrow {\mathcal T}$
the retraction map. In this paper we study the open affinoid subset
$r \,:\, \Sigma^1 \rightarrow \Omega \rightarrow {\mathcal T}$
the retraction map. In this paper we study the open affinoid subset
![]() $\Sigma^1_{v} \,{:}\,{\raise-1.5pt{=}}\, r^{-1}(v)$
of
$\Sigma^1_{v} \,{:}\,{\raise-1.5pt{=}}\, r^{-1}(v)$
of
![]() $\Sigma^1$
. This is stable under the action of
$\Sigma^1$
. This is stable under the action of
![]() $\text{GL}_2(\mathcal{O}_F)$
and after a finite extension of K,
$\text{GL}_2(\mathcal{O}_F)$
and after a finite extension of K,
![]() $\Sigma^1_{v}$
splits up into
$\Sigma^1_{v}$
splits up into
![]() $q-1$
geometrically connected components, each isomorphic to
$q-1$
geometrically connected components, each isomorphic to
![]() $\text{Sp}(B)$
, where,
$\text{Sp}(B)$
, where,
The group
![]() $\text{GL}_2(F)^+$
acts with two orbits on the set of vertices of
$\text{GL}_2(F)^+$
acts with two orbits on the set of vertices of
![]() ${\mathcal T}$
, and one can show that for any vertex w adjacent to v,
${\mathcal T}$
, and one can show that for any vertex w adjacent to v,
![]() $\Sigma^1_w \cong \Sigma^1_{v}$
. As any such w will be in the other orbit from v,
$\Sigma^1_w \cong \Sigma^1_{v}$
. As any such w will be in the other orbit from v,
![]() $\Sigma^1_w \cong \Sigma^1_{v}$
for all vertices
$\Sigma^1_w \cong \Sigma^1_{v}$
for all vertices
![]() $w \in {\mathcal T}$
, and consequently this open subset often determines global properties of
$w \in {\mathcal T}$
, and consequently this open subset often determines global properties of
![]() $\Sigma^1$
. For example, the first de-Rham cohomology
$\Sigma^1$
. For example, the first de-Rham cohomology
![]() $H^1_{\text{dR}}\!\left(\Sigma^1\right)$
as a representation of
$H^1_{\text{dR}}\!\left(\Sigma^1\right)$
as a representation of
![]() $\text{GL}_2(F)$
is determined by
$\text{GL}_2(F)$
is determined by
![]() $H^1_{\text{dR}}\!\left(\Sigma^1_v\right)$
[
Reference Junger21
, theorem 6·1].
$H^1_{\text{dR}}\!\left(\Sigma^1_v\right)$
[
Reference Junger21
, theorem 6·1].
Our main result is that
![]() $\text{Pic}\!\left(\Sigma^1_{v}\right)[p] = 0$
(Theorem 3·2). The p-adic étale cohomology groups of Drinfeld spaces are of considerable interest [
Reference Bosco3
,
Reference Colmez, Dospinescu, Hauseux and Nizioł6
–
Reference Colmez, Dospinescu and Nizioł9
,
Reference Orlik24
], and one immediate consequence of Theorem 3·2 is a description of the
$\text{Pic}\!\left(\Sigma^1_{v}\right)[p] = 0$
(Theorem 3·2). The p-adic étale cohomology groups of Drinfeld spaces are of considerable interest [
Reference Bosco3
,
Reference Colmez, Dospinescu, Hauseux and Nizioł6
–
Reference Colmez, Dospinescu and Nizioł9
,
Reference Orlik24
], and one immediate consequence of Theorem 3·2 is a description of the
![]() $\text{GL}_2(\mathcal{O}_F)$
-representation
$\text{GL}_2(\mathcal{O}_F)$
-representation
![]() $H^1_{\acute{\text{e}}\text{t}}\!\left(\Sigma^1_v, {\mathbb Z}_p(1)\right)$
, as the p-adic completion of
$H^1_{\acute{\text{e}}\text{t}}\!\left(\Sigma^1_v, {\mathbb Z}_p(1)\right)$
, as the p-adic completion of
![]() $\mathcal{O}\!\left(\Sigma^1_v\right)^\times$
(Theorem 3·4). This description is very explicit, as the unit group
$\mathcal{O}\!\left(\Sigma^1_v\right)^\times$
(Theorem 3·4). This description is very explicit, as the unit group
![]() $\mathcal{O}\!\left(\Sigma^1_v\right)^\times$
has been described by Junger [
Reference Junger22
, theorem 5·1].
$\mathcal{O}\!\left(\Sigma^1_v\right)^\times$
has been described by Junger [
Reference Junger22
, theorem 5·1].
Our main interest in Theorem 3·2 is the following. A precise statement of the p-adic local Langlands correspondence is formulated when
![]() $F = {\mathbb Q}_p$
[
Reference Colmez, Dospinescu and Paškūnas10
], and Dospinescu and Le Bras [
Reference Dospinescu and Le Bras13
] have used this to show that for
$F = {\mathbb Q}_p$
[
Reference Colmez, Dospinescu and Paškūnas10
], and Dospinescu and Le Bras [
Reference Dospinescu and Le Bras13
] have used this to show that for
![]() $F = {\mathbb Q}_p$
and all
$F = {\mathbb Q}_p$
and all
![]() $n \geq 1$
, the representation
$n \geq 1$
, the representation
![]() $\mathcal{O}(\Sigma^{n})$
is naturally a coadmissible module over D(G, K), the distribution algebra of G.
$\mathcal{O}(\Sigma^{n})$
is naturally a coadmissible module over D(G, K), the distribution algebra of G.
In an effort to remove the restriction on F, Ardakov and Wadsley show in their forthcoming work [
Reference Ardakov and Wadsley1
] using p-adic
![]() ${\mathcal D}$
-modules that the representation
${\mathcal D}$
-modules that the representation
![]() $\mathcal{O}\!\left(\Sigma^1\right)$
splits up naturally into a direct sum of coadmissible D(G, K)-modules. This decomposition contains
$\mathcal{O}\!\left(\Sigma^1\right)$
splits up naturally into a direct sum of coadmissible D(G, K)-modules. This decomposition contains
![]() $\mathcal{O}(\Omega)$
, and all other components are shown to be topologically irreducible D(G, K)-modules. The benefits of this approach over that of [
Reference Dospinescu and Le Bras13
], are that it holds for general field extensions F, is purely local, and establishes topological irreducibility. The obvious disadvantage is that it describes
$\mathcal{O}(\Omega)$
, and all other components are shown to be topologically irreducible D(G, K)-modules. The benefits of this approach over that of [
Reference Dospinescu and Le Bras13
], are that it holds for general field extensions F, is purely local, and establishes topological irreducibility. The obvious disadvantage is that it describes
![]() $\mathcal{O}(\Sigma^n)$
only for
$\mathcal{O}(\Sigma^n)$
only for
![]() $n = 1$
. One would like to establish similar results for
$n = 1$
. One would like to establish similar results for
![]() $\mathcal{O}(\Sigma^n)$
for
$\mathcal{O}(\Sigma^n)$
for
![]() $n \geq 2$
, where the situation is significantly more complicated. This is partially due to the fact that
$n \geq 2$
, where the situation is significantly more complicated. This is partially due to the fact that
![]() $\Sigma^n \rightarrow \Sigma^{n-1}$
has degree a power of p, whearas the degree of
$\Sigma^n \rightarrow \Sigma^{n-1}$
has degree a power of p, whearas the degree of
![]() $\Sigma^1 \rightarrow \Omega$
is coprime to p. The methods of [
Reference Ardakov and Wadsley1
] use the standard result that
$\Sigma^1 \rightarrow \Omega$
is coprime to p. The methods of [
Reference Ardakov and Wadsley1
] use the standard result that
![]() $\text{Pic}(\Omega) = 0$
, and in attempting to transfer these methods to
$\text{Pic}(\Omega) = 0$
, and in attempting to transfer these methods to
![]() $\mathcal{O}(\Sigma^2)$
, one considers the group
$\mathcal{O}(\Sigma^2)$
, one considers the group
![]() $\text{Pic}\!\left(\Sigma^1\right)[p]$
instead. Almost nothing is known about
$\text{Pic}\!\left(\Sigma^1\right)[p]$
instead. Almost nothing is known about
![]() $\text{Pic}\!\left(\Sigma^1\right)[p]$
, which is strongly expected to be non-zero. Our result that
$\text{Pic}\!\left(\Sigma^1\right)[p]$
, which is strongly expected to be non-zero. Our result that
![]() $\text{Pic}\!\left(\Sigma^1_v\right)[p] = 0$
is therefore slightly suprising. It also provides the first steps towards computing
$\text{Pic}\!\left(\Sigma^1_v\right)[p] = 0$
is therefore slightly suprising. It also provides the first steps towards computing
![]() $\text{Pic}\!\left(\Sigma^1\right)[p]$
(by choosing an appropriate Čech cover), and allows one the possibility of using similar methods to [
Reference Ardakov and Wadsley1
] locally.
$\text{Pic}\!\left(\Sigma^1\right)[p]$
(by choosing an appropriate Čech cover), and allows one the possibility of using similar methods to [
Reference Ardakov and Wadsley1
] locally.
In order to prove Theorem 3·2, we consider the affine curve
![]() ${\mathbf Y}$
defined by,
${\mathbf Y}$
defined by,
over the residue field of K, where
![]() ${\mathbb F}_q$
is the residue field of F. This curve was first considered by Drinfeld, who showed that all the discrete series representations of
${\mathbb F}_q$
is the residue field of F. This curve was first considered by Drinfeld, who showed that all the discrete series representations of
![]() $\text{SL}_2\left({\mathbb F}_q\right)$
can be realised in the cohomology of
$\text{SL}_2\left({\mathbb F}_q\right)$
can be realised in the cohomology of
![]() ${\mathbf Y}$
[
Reference Bonnafé2
, preface]. Inspired by this, these ideas were generalised to all reductive groups
${\mathbf Y}$
[
Reference Bonnafé2
, preface]. Inspired by this, these ideas were generalised to all reductive groups
![]() ${\mathbb G}$
by Deligne and Lusztig in their landmark paper [
Reference Deligne and Lusztig12
]. They introduce what are now called Deligne–Lusztig varieties, which assign to
${\mathbb G}$
by Deligne and Lusztig in their landmark paper [
Reference Deligne and Lusztig12
]. They introduce what are now called Deligne–Lusztig varieties, which assign to
![]() ${\mathbb G}\!\left({\mathbb F}_q\right)$
and
${\mathbb G}\!\left({\mathbb F}_q\right)$
and
![]() $w \in W$
, the Weyl group, a base space X(w) and a finite covering Y(w), and it is in the étale cohomology of Y(w) that the cuspidal representations are realised. These are spaces of considerable interest, and the Picard groups of the base spaces X(w) have been considered in [
Reference Hansen17
]. Here we consider
$w \in W$
, the Weyl group, a base space X(w) and a finite covering Y(w), and it is in the étale cohomology of Y(w) that the cuspidal representations are realised. These are spaces of considerable interest, and the Picard groups of the base spaces X(w) have been considered in [
Reference Hansen17
]. Here we consider
![]() ${\mathbf Y} = Y(w)$
in the special case of
${\mathbf Y} = Y(w)$
in the special case of
![]() $\mathbb{G} = \text{SL}_2$
, and
$\mathbb{G} = \text{SL}_2$
, and
![]() $w \neq 1$
. It would be interesting to study the Picard groups of Y(w) more generally.
$w \neq 1$
. It would be interesting to study the Picard groups of Y(w) more generally.
2. Deligne–Lusztig curves
Throughout this section, let
![]() ${\mathbb F}$
be an algebraic field extension of
${\mathbb F}$
be an algebraic field extension of
![]() ${\mathbb F}_q$
. We consider the affine curve,
${\mathbb F}_q$
. We consider the affine curve,
and its projective closure,
We also consider the projective curve,
We would first like to show that
![]() $\text{Pic}({\mathbf Z})[p] = 0$
.
$\text{Pic}({\mathbf Z})[p] = 0$
.
Lemma 2·1.
![]() ${\mathbf Z}$
is a smooth integral projective curve over
${\mathbf Z}$
is a smooth integral projective curve over
![]() ${\mathbb F}$
. Furthermore, if
${\mathbb F}$
. Furthermore, if
![]() ${\mathbb F}_{q^4} \subset {\mathbb F}$
, then
${\mathbb F}_{q^4} \subset {\mathbb F}$
, then
![]() ${\mathbf W} \cong {\mathbf Z}$
.
${\mathbf W} \cong {\mathbf Z}$
.
Proof. The polynomial
![]() $P(X,Y,Z) = Z^{q+1} - (XY^q - YX^q) \in {\mathbb F}[X,Y,Z]$
is prime, which follows from Eisenstein’s criterion for
$P(X,Y,Z) = Z^{q+1} - (XY^q - YX^q) \in {\mathbb F}[X,Y,Z]$
is prime, which follows from Eisenstein’s criterion for
![]() $P \in {\mathbb F}[X,Y][Z]$
, at the prime ideal (X). Therefore
$P \in {\mathbb F}[X,Y][Z]$
, at the prime ideal (X). Therefore
![]() ${\mathbf Z}$
is integral. Furthermore,
${\mathbf Z}$
is integral. Furthermore,
![]() ${\mathbf Z}$
is smooth, because the system
${\mathbf Z}$
is smooth, because the system
![]() $\partial_X P = \partial_Y P = \partial_Z P = 0$
has no solutions over
$\partial_X P = \partial_Y P = \partial_Z P = 0$
has no solutions over
![]() ${\mathbf Z}(\overline{{\mathbb F}})$
. For the isomorphism, let
${\mathbf Z}(\overline{{\mathbb F}})$
. For the isomorphism, let
![]() $\lambda \in {\mathbb F}_{q^2}$
with
$\lambda \in {\mathbb F}_{q^2}$
with
![]() $\lambda^{q-1} = -1$
, and let
$\lambda^{q-1} = -1$
, and let
![]() $\mu \in \overline{{\mathbb F}}$
with
$\mu \in \overline{{\mathbb F}}$
with
![]() $\mu^{q+1} = \lambda^q$
. The element
$\mu^{q+1} = \lambda^q$
. The element
![]() $\mu$
lies in
$\mu$
lies in
![]() ${\mathbb F}_{q^4}$
, as,
${\mathbb F}_{q^4}$
, as,
so,
Then the claimed isomorphism is given by,
Indeed,
and similarly
![]() $U(\lambda^{-1}V)^q - (\lambda^{-1} V) U^q = (\mu^{-1} W)^{q+1}$
.
$U(\lambda^{-1}V)^q - (\lambda^{-1} V) U^q = (\mu^{-1} W)^{q+1}$
.
Proposition 2·2.
![]() $\text{Pic}({\mathbf Z})[p] = 0$
.
$\text{Pic}({\mathbf Z})[p] = 0$
.
Proof. By Lemma 2·1,
![]() ${\mathbf Z}_{\overline{{\mathbb F}}} \cong {\mathbf W}_{\overline{{\mathbb F}}}$
, and thus the group
${\mathbf Z}_{\overline{{\mathbb F}}} \cong {\mathbf W}_{\overline{{\mathbb F}}}$
, and thus the group
![]() $\text{Pic}\!\left({\mathbf Z}_{\overline{{\mathbb F}}}\right)[p] \cong \text{Pic}\!\left({\mathbf W}_{\overline{{\mathbb F}}}\right)[p] \cong J(\overline{{\mathbb F}})[p]$
, where J is the Jacobian of
$\text{Pic}\!\left({\mathbf Z}_{\overline{{\mathbb F}}}\right)[p] \cong \text{Pic}\!\left({\mathbf W}_{\overline{{\mathbb F}}}\right)[p] \cong J(\overline{{\mathbb F}})[p]$
, where J is the Jacobian of
![]() ${\mathbf W}$
.
${\mathbf W}$
.
![]() ${\mathbf W}$
is known as the Hermitian curve, defined by affine equation
${\mathbf W}$
is known as the Hermitian curve, defined by affine equation
![]() $w^{q+1} = v^q + v$
, and is maximal over
$w^{q+1} = v^q + v$
, and is maximal over
![]() ${\mathbb F}_{q^2}$
[
Reference Stichtenoth26
, lemma 6·4·4], hence
${\mathbb F}_{q^2}$
[
Reference Stichtenoth26
, lemma 6·4·4], hence
![]() $J(\overline{{\mathbb F}})[p] = 0$
by [
Reference Garcia and Tafazolian15
, corollary 2·5]. Then, because pullback induces an exact sequence
$J(\overline{{\mathbb F}})[p] = 0$
by [
Reference Garcia and Tafazolian15
, corollary 2·5]. Then, because pullback induces an exact sequence
![]() $0 \rightarrow \text{Pic}({\mathbf Z}) \rightarrow \text{Pic}\!\left({\mathbf Z}_{\overline{{\mathbb F}}}\right)$
[
25
, Tag 0CC5], and p-torsion is left exact,
$0 \rightarrow \text{Pic}({\mathbf Z}) \rightarrow \text{Pic}\!\left({\mathbf Z}_{\overline{{\mathbb F}}}\right)$
[
25
, Tag 0CC5], and p-torsion is left exact,
![]() $\text{Pic}({\mathbf Z})[p] = 0$
.
$\text{Pic}({\mathbf Z})[p] = 0$
.
Our next goal is to establish that
![]() $\text{Pic}({\mathbf Y})[p] = 0$
.
$\text{Pic}({\mathbf Y})[p] = 0$
.
Lemma 2·3.
![]() ${\mathbf Z}(\overline{{\mathbb F}}) \setminus {\mathbf Y}(\overline{{\mathbb F}})$
consists of the
${\mathbf Z}(\overline{{\mathbb F}}) \setminus {\mathbf Y}(\overline{{\mathbb F}})$
consists of the
![]() $q+1$
points,
$q+1$
points,
Furthermore,
![]() ${\mathcal P} = {\mathbf Z}\!\left({\mathbb F}_q\right)$
.
${\mathcal P} = {\mathbf Z}\!\left({\mathbb F}_q\right)$
.
Proof. If
![]() $(a\,:\,b\,:\,c) \in {\mathbf Z}(\overline{{\mathbb F}})$
with
$(a\,:\,b\,:\,c) \in {\mathbf Z}(\overline{{\mathbb F}})$
with
![]() $c =0$
, then
$c =0$
, then
![]() $b^q a - a^q b = 0$
, so
$b^q a - a^q b = 0$
, so
![]() $b^q a = a^q b$
. If
$b^q a = a^q b$
. If
![]() $a \neq 0$
, then
$a \neq 0$
, then
![]() $\left( {b}/{a}\right)^q = {b}/{a}$
, so
$\left( {b}/{a}\right)^q = {b}/{a}$
, so
![]() ${b}/{a} \in {\mathbb F}_q$
, and
${b}/{a} \in {\mathbb F}_q$
, and
![]() $(a\,:\,b) \in {\mathbb P}^1\left({\mathbb F}_q\right)$
. Similarly, if
$(a\,:\,b) \in {\mathbb P}^1\left({\mathbb F}_q\right)$
. Similarly, if
![]() $b \neq 0$
,
$b \neq 0$
,
![]() $(a\,:\,b) \in {\mathbb P}^1\left({\mathbb F}_q\right)$
. Thus
$(a\,:\,b) \in {\mathbb P}^1\left({\mathbb F}_q\right)$
. Thus
![]() ${\mathbf Z}(\overline{{\mathbb F}}) \setminus {\mathbf Y}(\overline{{\mathbb F}})= {\mathcal P}$
. To see
${\mathbf Z}(\overline{{\mathbb F}}) \setminus {\mathbf Y}(\overline{{\mathbb F}})= {\mathcal P}$
. To see
![]() ${\mathbf Z}(\overline{{\mathbb F}}) \setminus {\mathbf Y}(\overline{{\mathbb F}}) = {\mathbf Z}\!\left({\mathbb F}_q\right)$
, there are no points
${\mathbf Z}(\overline{{\mathbb F}}) \setminus {\mathbf Y}(\overline{{\mathbb F}}) = {\mathbf Z}\!\left({\mathbb F}_q\right)$
, there are no points
![]() $(a\,:\,b\,:\,c) \in {\mathbf Z}\!\left({\mathbb F}_q\right)$
with
$(a\,:\,b\,:\,c) \in {\mathbf Z}\!\left({\mathbb F}_q\right)$
with
![]() $c = 1$
, because if so then
$c = 1$
, because if so then
![]() $1 = ab^q - ba^q = ab - ba = 0$
, as
$1 = ab^q - ba^q = ab - ba = 0$
, as
![]() $a,b \in {\mathbb F}_q$
.
$a,b \in {\mathbb F}_q$
.
Therefore the closed points of
![]() ${\mathbf Z} \setminus {\mathbf Y}$
are
${\mathbf Z} \setminus {\mathbf Y}$
are
![]() ${\mathcal P}$
[
Reference Görtz and Wedhorn16
, proposition 5·4], which we enumerate by
${\mathcal P}$
[
Reference Görtz and Wedhorn16
, proposition 5·4], which we enumerate by
![]() ${\mathcal P} = \{P_0,\, ... \, ,P_q\}$
. From [
Reference Weibel27
, exercise 5·12 (a)] we have an exact sequence,
${\mathcal P} = \{P_0,\, ... \, ,P_q\}$
. From [
Reference Weibel27
, exercise 5·12 (a)] we have an exact sequence,
where the first map sends,
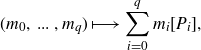 \begin{align}(m_0,\, ... \, ,m_q) \longmapsto \sum_{i = 0}^q m_i [P_i],\end{align}
\begin{align}(m_0,\, ... \, ,m_q) \longmapsto \sum_{i = 0}^q m_i [P_i],\end{align}
and the second sends, for I a finite set of closed points of
![]() ${\mathbf Z}$
,
${\mathbf Z}$
,
Let
![]() $\Gamma = \langle [P_0] ,\, ... \, ,[P_{q}] \rangle \subset \text{Cl}({\mathbf Z})$
be the image of
$\Gamma = \langle [P_0] ,\, ... \, ,[P_{q}] \rangle \subset \text{Cl}({\mathbf Z})$
be the image of
![]() ${\mathbb Z}^{q+1}$
in
${\mathbb Z}^{q+1}$
in
![]() $\text{Cl}({\mathbf Z})$
. The resulting exact sequence,
$\text{Cl}({\mathbf Z})$
. The resulting exact sequence,
yields the long exact sequence,
from the right derived functors of
![]() $\textrm{Hom}_{{\mathbb Z}}({\mathbb Z} / p{\mathbb Z}, -)$
. Then from Proposition 2·2 and the above discussion we have the following.
$\textrm{Hom}_{{\mathbb Z}}({\mathbb Z} / p{\mathbb Z}, -)$
. Then from Proposition 2·2 and the above discussion we have the following.
Proposition 2·4. There is an exact sequence
where the map
![]() $\Gamma / p\Gamma \rightarrow \text{Cl}({\mathbf Z}) / p \text{Cl}({\mathbf Z})$
is that induced by the inclusion
$\Gamma / p\Gamma \rightarrow \text{Cl}({\mathbf Z}) / p \text{Cl}({\mathbf Z})$
is that induced by the inclusion
![]() $\Gamma \hookrightarrow \text{Cl}({\mathbf Z})$
.
$\Gamma \hookrightarrow \text{Cl}({\mathbf Z})$
.
Remark. We note that if
![]() ${\mathbf Z} \setminus {\mathbf Y}$
contained exactly one degree 1 closed point Q, then we could establish that
${\mathbf Z} \setminus {\mathbf Y}$
contained exactly one degree 1 closed point Q, then we could establish that
![]() $\text{Pic}({\mathbf Y})[p] = 0$
almost immediately in the following way. In the exact sequence,
$\text{Pic}({\mathbf Y})[p] = 0$
almost immediately in the following way. In the exact sequence,
the map
![]() ${\mathbb Z} \rightarrow \text{Cl}({\mathbf Z})$
is actually injective and split by the degree homomorphism, hence
${\mathbb Z} \rightarrow \text{Cl}({\mathbf Z})$
is actually injective and split by the degree homomorphism, hence
![]() $\text{Cl}({\mathbf Z}) \cong {\mathbb Z} \times \text{Cl}({\mathbf Y})$
so,
$\text{Cl}({\mathbf Z}) \cong {\mathbb Z} \times \text{Cl}({\mathbf Y})$
so,
In particular, this can be applied to show that the class groups of affine dehomogenisations of
![]() ${\mathbf Z}$
with respect to both X and Y both have no p-torsion.
${\mathbf Z}$
with respect to both X and Y both have no p-torsion.
We want to show that
![]() $\text{Cl}({\mathbf Y})[p] = 0$
, and so in light of Proposition 2·4, we want to show that,
$\text{Cl}({\mathbf Y})[p] = 0$
, and so in light of Proposition 2·4, we want to show that,
is injective. In order to do so, we now examine the structure of
![]() $\Gamma$
. First we compute the principal divisors of some rational functions on
$\Gamma$
. First we compute the principal divisors of some rational functions on
![]() ${\mathbf Z}$
.
${\mathbf Z}$
.
Definition 2·5. For
![]() $(a\,:\,b) \in {\mathbb P}^1\left({\mathbb F}_q\right)$
, we let
$(a\,:\,b) \in {\mathbb P}^1\left({\mathbb F}_q\right)$
, we let
![]() $P_{(a\,:\,b)}$
be the closed point of
$P_{(a\,:\,b)}$
be the closed point of
![]() ${\mathbf Z}$
defined by
${\mathbf Z}$
defined by
![]() $(a\,:\,b\,:\,0) \in {\mathbb P}^1(\overline{{\mathbb F}})$
.
$(a\,:\,b\,:\,0) \in {\mathbb P}^1(\overline{{\mathbb F}})$
.
Lemma 2·6.
Let
![]() $(a\,:\,b), (c\,:\,d) \in {\mathbb P}^1\left({\mathbb F}_q\right)$
with
$(a\,:\,b), (c\,:\,d) \in {\mathbb P}^1\left({\mathbb F}_q\right)$
with
![]() $(a\,:\,b) \neq (c\,:\,d)$
. Then the rational function,
$(a\,:\,b) \neq (c\,:\,d)$
. Then the rational function,
has associated principal divisor,
Proof. Consider the morphism
![]() $\zeta \,:\, {\mathbf Z} \rightarrow {\mathbb P}^1$
corresponding to the extension of function fields
$\zeta \,:\, {\mathbf Z} \rightarrow {\mathbb P}^1$
corresponding to the extension of function fields
![]() ${\mathbb F}({\mathbb P}^1) \rightarrow {\mathbb F}({\mathbf Z})$
, which sends,
${\mathbb F}({\mathbb P}^1) \rightarrow {\mathbb F}({\mathbf Z})$
, which sends,
where
![]() ${\mathbb P}^1 = \textrm{Proj}({\mathbb F}[S,T])$
, and
${\mathbb P}^1 = \textrm{Proj}({\mathbb F}[S,T])$
, and
![]() ${\mathbb F}({\mathbb P}^1) = {\mathbb F}(S/T)$
. On
${\mathbb F}({\mathbb P}^1) = {\mathbb F}(S/T)$
. On
![]() $\overline{{\mathbb F}}$
-points,
$\overline{{\mathbb F}}$
-points,
![]() $\zeta \,:\, {\mathbf Z} \rightarrow {\mathbb P}^1$
is given by,
$\zeta \,:\, {\mathbf Z} \rightarrow {\mathbb P}^1$
is given by,
This extension
![]() ${\mathbb F}({\mathbb P}^1) \rightarrow {\mathbb F}({\mathbf Z})$
has degree
${\mathbb F}({\mathbb P}^1) \rightarrow {\mathbb F}({\mathbf Z})$
has degree
![]() $q+1$
because it differs by an automorphism of
$q+1$
because it differs by an automorphism of
![]() ${\mathbb P}^1$
from the extension
${\mathbb P}^1$
from the extension
![]() ${\mathbb F}({\mathbb P}^1) \rightarrow {\mathbb F}({\mathbf Z})$
, defined by,
${\mathbb F}({\mathbb P}^1) \rightarrow {\mathbb F}({\mathbf Z})$
, defined by,
which clearly has degree
![]() $q+1$
. Let
$q+1$
. Let
![]() $Q_0, Q_{\infty}$
be the closed points of
$Q_0, Q_{\infty}$
be the closed points of
![]() ${\mathbb P}^1$
defined by
${\mathbb P}^1$
defined by
![]() $(0\,:\,1), (1\,:\,0) \in {\mathbb P}^1(\overline{{\mathbb F}})$
respectively. By [
Reference Liu23
, corollary 3·9], we have that,
$(0\,:\,1), (1\,:\,0) \in {\mathbb P}^1(\overline{{\mathbb F}})$
respectively. By [
Reference Liu23
, corollary 3·9], we have that,
and
![]() $\deg(\zeta^*([Q_0])) = \deg(\zeta^*([Q_{\infty}])) = [{\mathbb F}({\mathbb P}^1)\,:\,{\mathbb F}({\mathbf Z})] = q+1$
. But
$\deg(\zeta^*([Q_0])) = \deg(\zeta^*([Q_{\infty}])) = [{\mathbb F}({\mathbb P}^1)\,:\,{\mathbb F}({\mathbf Z})] = q+1$
. But
![]() $\zeta^*([Q_0])$
is some integer multiple of
$\zeta^*([Q_0])$
is some integer multiple of
![]() $\left[P_{(a\,:\,b)}\right]$
and
$\left[P_{(a\,:\,b)}\right]$
and
![]() $\zeta^*([Q_{\infty}])$
some integer multiple of
$\zeta^*([Q_{\infty}])$
some integer multiple of
![]() $\left[P_{(c\,:\,d)}\right]$
, hence,
$\left[P_{(c\,:\,d)}\right]$
, hence,
Let
![]() $\Gamma^0 \subset \Gamma$
be the degree 0 subgroup of
$\Gamma^0 \subset \Gamma$
be the degree 0 subgroup of
![]() $\Gamma$
, and
$\Gamma$
, and
![]() $\text{Cl}^0({\mathbf Z}) \subset \text{Cl}({\mathbf Z})$
the degree 0 subgroup of
$\text{Cl}^0({\mathbf Z}) \subset \text{Cl}({\mathbf Z})$
the degree 0 subgroup of
![]() $\text{Cl}({\mathbf Z})$
.
$\text{Cl}({\mathbf Z})$
.
Lemma 2·7.
The function
![]() $\phi \,:\, {\mathbb Z} \times ({\mathbb Z} / (q+1) {\mathbb Z})^q \rightarrow \Gamma$
,
$\phi \,:\, {\mathbb Z} \times ({\mathbb Z} / (q+1) {\mathbb Z})^q \rightarrow \Gamma$
,
is a surjective homomorphism. In particular,
![]() $\Gamma^0$
is a quotient of
$\Gamma^0$
is a quotient of
![]() $({\mathbb Z} / (q+1) {\mathbb Z})^q$
.
$({\mathbb Z} / (q+1) {\mathbb Z})^q$
.
Proof. For each
![]() $P_k \in {\mathcal P}$
, we can write
$P_k \in {\mathcal P}$
, we can write
![]() $P_k = P_{(a_k\,:\,b_k)}$
for some
$P_k = P_{(a_k\,:\,b_k)}$
for some
![]() $a_k, b_k \in {\mathbb F}_q$
. For each
$a_k, b_k \in {\mathbb F}_q$
. For each
![]() $0 \leq i \neq j \leq q$
, consider the rational function,
$0 \leq i \neq j \leq q$
, consider the rational function,
Taking the divisor of f,
in
![]() $\Gamma$
, by Lemma 2·6. Therefore,
$\Gamma$
, by Lemma 2·6. Therefore,
![]() $\phi$
is a well-defined homomorphism, which is surjective because
$\phi$
is a well-defined homomorphism, which is surjective because
![]() $\{[P_0],\, ...\, ,[P_q]\}$
generate
$\{[P_0],\, ...\, ,[P_q]\}$
generate
![]() $\Gamma$
. Finally, as
$\Gamma$
. Finally, as
![]() $\Gamma^0=\langle [P_1] - [P_0] ,\, ...\, ,[P_q] - [P_0] \rangle$
, then
$\Gamma^0=\langle [P_1] - [P_0] ,\, ...\, ,[P_q] - [P_0] \rangle$
, then
![]() $\Gamma^0$
is a quotient of
$\Gamma^0$
is a quotient of
![]() $({\mathbb Z} / (q+1) {\mathbb Z})^q$
.
$({\mathbb Z} / (q+1) {\mathbb Z})^q$
.
We are finally in a position to prove the main result of this section.
Theorem 2·8.
![]() $\text{Pic}({\mathbf Y})[p] = 0$
.
$\text{Pic}({\mathbf Y})[p] = 0$
.
Proof. We can split the degree homomorphism with
![]() $[P_0]$
, as
$[P_0]$
, as
![]() $[P_0]$
has degree 1 and
$[P_0]$
has degree 1 and
![]() $\langle [P_0] \rangle$
is free [
Reference Weibel27
, exercise 5·12 (b)]. Then,
$\langle [P_0] \rangle$
is free [
Reference Weibel27
, exercise 5·12 (b)]. Then,
is an isomorphism, which restricts to,
We then obtain the following commutative diagram,

Here, the vertical maps are induced from the inclusions of
![]() $\Gamma$
into
$\Gamma$
into
![]() $\text{Cl}({\mathbf Z})$
and of
$\text{Cl}({\mathbf Z})$
and of
![]() $\Gamma^0$
into
$\Gamma^0$
into
![]() $\text{Cl}^0({\mathbf Z})$
, the left horizontal maps are induced by
$\text{Cl}^0({\mathbf Z})$
, the left horizontal maps are induced by
![]() $\psi$
, and the right horizontal maps are the standard identifications.
$\psi$
, and the right horizontal maps are the standard identifications.
Now, by Lemma 2·7,
![]() $\Gamma^0$
is a quotient of
$\Gamma^0$
is a quotient of
![]() $({\mathbb Z} / (q+1){\mathbb Z})^{q}$
, thus
$({\mathbb Z} / (q+1){\mathbb Z})^{q}$
, thus
![]() $\Gamma^0 / p \Gamma^0 = 0$
. Consequently,
$\Gamma^0 / p \Gamma^0 = 0$
. Consequently,
![]() $\Gamma / p\Gamma \rightarrow \text{Cl}({\mathbf Z}) / p \text{Cl}({\mathbf Z})$
is an injection. Therefore,
$\Gamma / p\Gamma \rightarrow \text{Cl}({\mathbf Z}) / p \text{Cl}({\mathbf Z})$
is an injection. Therefore,
![]() $\text{Cl}({\mathbf Y})[p] = 0$
, by the exact sequence of Proposition 2·4.
$\text{Cl}({\mathbf Y})[p] = 0$
, by the exact sequence of Proposition 2·4.
3. Rigid curves
Let F be a finite extension of
![]() ${\mathbb Q}_p$
with uniformiser
${\mathbb Q}_p$
with uniformiser
![]() $\pi$
and residue field
$\pi$
and residue field
![]() ${\mathbb F}_q$
. Let K be a complete field extension of F with residue field
${\mathbb F}_q$
. Let K be a complete field extension of F with residue field
![]() ${\mathbb F}$
, such that
${\mathbb F}$
, such that
![]() ${\mathbb F}$
is an algebraic extension of
${\mathbb F}$
is an algebraic extension of
![]() ${\mathbb F}_q$
. Let R be the ring of integers of K and
${\mathbb F}_q$
. Let R be the ring of integers of K and
![]() $\varpi \in K$
an element with
$\varpi \in K$
an element with
![]() $0 < |\varpi| < 1$
.
$0 < |\varpi| < 1$
.
Let A be the affinoid algebra,
for which the associated rigid space
![]() $\text{Sp}(A)$
has admissible formal model
$\text{Sp}(A)$
has admissible formal model
![]() $\text{Spf}(A_0)$
, where,
$\text{Spf}(A_0)$
, where,
Let
![]() $u \,{:}\,{\raise-1.5pt{=}}\, x^q - x \in A_0^\times \subset A^\times$
, and let B be the affinoid algebra,
$u \,{:}\,{\raise-1.5pt{=}}\, x^q - x \in A_0^\times \subset A^\times$
, and let B be the affinoid algebra,
Consider the ring extension,
![]() $B_0$
is
$B_0$
is
![]() $\varpi$
-torsion free, and the natural map,
$\varpi$
-torsion free, and the natural map,
is an isomorphism (because
![]() $u \in A_0^\times$
is a unit), hence
$u \in A_0^\times$
is a unit), hence
![]() $B_0$
is an admissible R-algebra. The special fibre of
$B_0$
is an admissible R-algebra. The special fibre of
![]() $\text{Spf}(B_0)$
is,
$\text{Spf}(B_0)$
is,
where
![]() $v = y^q - y$
, and the generic fibre of
$v = y^q - y$
, and the generic fibre of
![]() $\text{Spf}(B_0)$
is
$\text{Spf}(B_0)$
is
![]() $\text{Sp}(B_0 \otimes_R K) = \text{Sp}(B)$
.
$\text{Sp}(B_0 \otimes_R K) = \text{Sp}(B)$
.
Lemma 3·1.
![]() $\text{Pic}(\text{Sp}(B)) \cong \text{Pic}({\mathbf Y})$
.
$\text{Pic}(\text{Sp}(B)) \cong \text{Pic}({\mathbf Y})$
.
Proof. First note that there is an isomorphism of
![]() ${\mathbb F}$
-algebras,
${\mathbb F}$
-algebras,
given by
![]() $r \mapsto 1/t$
,
$r \mapsto 1/t$
,
![]() $s \mapsto y / t$
, with inverse
$s \mapsto y / t$
, with inverse
![]() $y \mapsto s/r$
,
$y \mapsto s/r$
,
![]() $t \mapsto 1/r$
. Thus
$t \mapsto 1/r$
. Thus
![]() $\textrm{Spec}(B_0 \otimes_R {\mathbb F}) \cong {\mathbf Y}$
, and
$\textrm{Spec}(B_0 \otimes_R {\mathbb F}) \cong {\mathbf Y}$
, and
![]() $\text{Spf}(B_0)$
is a smooth admissible formal model of
$\text{Spf}(B_0)$
is a smooth admissible formal model of
![]() $\text{Sp}(B)$
. Therefore by [
Reference Heuer20
, lemma 3·6], the natural maps,
$\text{Sp}(B)$
. Therefore by [
Reference Heuer20
, lemma 3·6], the natural maps,
are isomorphisms and we’re done.
We can now state our main results. If K contains
![]() $\breve{F}$
the completion of the maximal unramified extension of F, then we can consider the rigid analytic space
$\breve{F}$
the completion of the maximal unramified extension of F, then we can consider the rigid analytic space
![]() $\Sigma^1$
defined over any such K. For an overview of the construction and properties of
$\Sigma^1$
defined over any such K. For an overview of the construction and properties of
![]() $\Sigma^1$
see [
Reference Junger22
, section 2]. If
$\Sigma^1$
see [
Reference Junger22
, section 2]. If
![]() $v \in {\mathcal T}$
is the central vertex of the Bruhat-Tits tree, then the open affinoid subset
$v \in {\mathcal T}$
is the central vertex of the Bruhat-Tits tree, then the open affinoid subset
![]() $\Sigma^1_{v} \,{:}\,{\raise-1.5pt{=}}\, r^{-1}(v) \subset \Sigma^1$
has coordinate ring isomorphic to,
$\Sigma^1_{v} \,{:}\,{\raise-1.5pt{=}}\, r^{-1}(v) \subset \Sigma^1$
has coordinate ring isomorphic to,
by [ Reference Junger22 , theorem 2·7].
Let
![]() $\omega$
be a primitive
$\omega$
be a primitive
![]() $(q^2 - 1)$
st root of
$(q^2 - 1)$
st root of
![]() $\pi$
in
$\pi$
in
![]() $\overline{F}$
. From now on we strengthen our assumption on the complete field extension K of F and assume that,
$\overline{F}$
. From now on we strengthen our assumption on the complete field extension K of F and assume that,
We note that this forces
![]() ${\mathbb F}$
to be an algebraic closure of
${\mathbb F}$
to be an algebraic closure of
![]() ${\mathbb F}_q$
, and that this assumption holds for any complete field extension K of
${\mathbb F}_q$
, and that this assumption holds for any complete field extension K of
![]() $\breve{F}(\omega)$
which is contained in
$\breve{F}(\omega)$
which is contained in
![]() ${\mathbb C}_p$
.
${\mathbb C}_p$
.
Theorem 3·2.
![]() $\text{Pic}\!\left(\Sigma^1_v\right)[p] = 0$
.
$\text{Pic}\!\left(\Sigma^1_v\right)[p] = 0$
.
Proof. Because K contains
![]() $\omega$
,
$\omega$
,
and therefore,
by Lemma 3·1. But then
![]() $\text{Pic}\!\left(\Sigma^1_v\right)[p] \cong \text{Pic}({\mathbf Y})[p]^{q-1}$
, which is zero by Theorem 2·8.
$\text{Pic}\!\left(\Sigma^1_v\right)[p] \cong \text{Pic}({\mathbf Y})[p]^{q-1}$
, which is zero by Theorem 2·8.
Recall that
![]() $\Sigma^1_v = r^{-1}(v)$
is the pre-image of v, the central vertex of the Bruhat–Tits tree. The vertex v is fixed by
$\Sigma^1_v = r^{-1}(v)$
is the pre-image of v, the central vertex of the Bruhat–Tits tree. The vertex v is fixed by
![]() $\text{GL}_2(\mathcal{O}_F)$
, and because r is equivariant,
$\text{GL}_2(\mathcal{O}_F)$
, and because r is equivariant,
![]() $\text{GL}_2(\mathcal{O}_F)$
acts on
$\text{GL}_2(\mathcal{O}_F)$
acts on
![]() $\Sigma^1_v$
.
$\Sigma^1_v$
.
Corollary 3·3. The natural map,
arising from the Kummer exact sequence is an isomorphism of
![]() $\text{GL}_2(\mathcal{O}_F)$
-modules.
$\text{GL}_2(\mathcal{O}_F)$
-modules.
Proof. Because K has characteristic 0, we can consider the Kummer exact sequence for rigid analytic spaces [
Reference de Jong and van der Put11
, section 3·2]. Then the result follows from Theorem 3·2 after taking the long exact sequence in étale cohomology, using that
![]() $\text{Pic}\!\left(\Sigma^1_v\right) \cong H^1_{\acute{\text{e}}\text{t}}\!\left(\Sigma^1_v, {\mathbb G}_m\right)$
[
Reference de Jong and van der Put11
, proposition 3·2·4].
$\text{Pic}\!\left(\Sigma^1_v\right) \cong H^1_{\acute{\text{e}}\text{t}}\!\left(\Sigma^1_v, {\mathbb G}_m\right)$
[
Reference de Jong and van der Put11
, proposition 3·2·4].
As a consequence, we may now compute
![]() $H^1_{\acute{\text{e}}\text{t}}\!\left(\Sigma^1_v, {\mathbb Z}_p(1)\right)$
as the p-adic completion of
$H^1_{\acute{\text{e}}\text{t}}\!\left(\Sigma^1_v, {\mathbb Z}_p(1)\right)$
as the p-adic completion of
![]() $\mathcal{O}\!\left(\Sigma^1_v\right)^\times$
. This is completely explicit, as the group
$\mathcal{O}\!\left(\Sigma^1_v\right)^\times$
. This is completely explicit, as the group
![]() $\mathcal{O}\!\left(\Sigma^1_v\right)^{\times}$
has been computed by Junger [
Reference Junger22
, theorem 5·1].
$\mathcal{O}\!\left(\Sigma^1_v\right)^{\times}$
has been computed by Junger [
Reference Junger22
, theorem 5·1].
Theorem 3·4.
There is an isomorphism of
![]() ${\mathbb Z}_p$
-linear representations of
${\mathbb Z}_p$
-linear representations of
![]() $\text{GL}_2(\mathcal{O}_F)$
,
$\text{GL}_2(\mathcal{O}_F)$
,
Proof. For all
![]() $n \geq 1$
the diagram,
$n \geq 1$
the diagram,
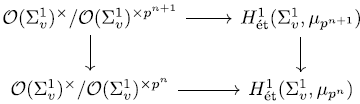
commutes. Then by the definition of
![]() $H^1_{\acute{\text{e}}\text{t}}\!\left(\Sigma^1_v, {\mathbb Z}_p(1)\right)$
and Corollary 3·3,
$H^1_{\acute{\text{e}}\text{t}}\!\left(\Sigma^1_v, {\mathbb Z}_p(1)\right)$
and Corollary 3·3,
Acknowledgements
The author would like to thank Konstantin Ardakov, Damien Junger and the referee for their comments on this paper. This research was financially supported by the EPSRC.