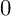 $0$
STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
$0$
STRATUM OF THE MODULI SPACE OF CYCLIC COVERS OF THE PROJECTIVE LINE
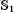 ) and the group of automorphisms of the algebra
) and the group of automorphisms of the algebra 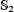 of one-sided inverses of a polynomial algebra in two variables
of one-sided inverses of a polynomial algebra in two variables