Research Article
The Essential Dimension of Stacks of Parabolic Vector Bundles over Curves
-
- Published online by Cambridge University Press:
- 01 November 2012, pp. 455-488
-
- Article
- Export citation
Orderings and signatures of higher level on multirings and hyperfields
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2012, pp. 489-518
-
- Article
- Export citation
On the conjectural Leibniz cohomology for groups
-
- Published online by Cambridge University Press:
- 30 November 2012, pp. 519-563
-
- Article
- Export citation
Invariants birationnels dans la suite spectrale de Bloch-Ogus
-
- Published online by Cambridge University Press:
- 07 June 2012, pp. 565-582
-
- Article
- Export citation
K1(
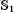 ) and the group of automorphisms of the algebra
) and the group of automorphisms of the algebra 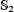 of one-sided inverses of a polynomial algebra in two variables
of one-sided inverses of a polynomial algebra in two variables
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2012, pp. 583-601
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
KAG volume 10 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 25 January 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
KAG volume 10 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 25 January 2013, pp. b1-b2
-
- Article
-
- You have access
- Export citation


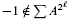 to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined.
to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined. , (
, ( . We relate one of these invariants with the cokernel of the l-adic cycle class map
. We relate one of these invariants with the cokernel of the l-adic cycle class map  , which gives an analogue of a result of Colliot-Thélène and Voisin [5] 3.11 over ℂ for varieties over a finite field.
, which gives an analogue of a result of Colliot-Thélène and Voisin [5] 3.11 over ℂ for varieties over a finite field.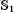 ) and the group of automorphisms of the algebra
) and the group of automorphisms of the algebra 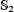 of one-sided inverses of a polynomial algebra in two variables
of one-sided inverses of a polynomial algebra in two variables
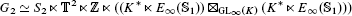
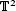 is the 2-dimensional algebraic torus,
is the 2-dimensional algebraic torus, 