2 results
Effective characterization of quasi-abelian surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 February 2023, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Auslander-Reiten quiver of an infinitesimal group
-
- Journal:
- Nagoya Mathematical Journal / Volume 160 / 2000
- Published online by Cambridge University Press:
- 22 January 2016, pp. 103-121
- Print publication:
- 2000
-
- Article
-
- You have access
- Export citation

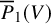
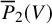
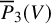
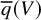
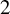
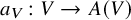
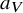
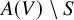
 be an infinitesimal group scheme, defined over an algebraically closed field of characteristic p. We employ rank varieties of
be an infinitesimal group scheme, defined over an algebraically closed field of characteristic p. We employ rank varieties of 