In 1989 Happel asked the question whether, for a finite-dimensional algebra $A$ over an algebraically closed field $k,\ \text{\rm gl.dim\,} A< \infty$ if and only if $\text{\rm hch.dim\,} A < \infty$. Here, the Hochschild cohomology dimension of $A$ is given by $\text{\rm hch.dim\,} A := \inf \{ n \in \mathbb{N}_0 \mid \dim \textit{HH}^i(A)=0 \text{ for }i > n \}$. Recently Buchweitz, Green, Madsen and Solberg gave a negative answer to Happel's question. They found a family of pathological algebras $A_q$ for which $\text{\rm gl.dim\,} A_q = \infty$ but $\text{\rm hch.dim\,} A_q=2$. These algebras are pathological in many aspects. However, their Hochschild homology behaviors are not pathological any more; indeed one has $\text{\rm hh.dim\,} A_q = \infty=\text{\rm gl.dim\,} A_q$. Here, the Hochschild homology dimension of $A$ is given by $\text{\rm hh.dim\,} A := \inf \{ n \in \mathbb{N}_0 \mid \dim \textit{HH}_i(A)=0 \text{ for } i > n\}$. This suggests posing a seemingly more reasonable conjecture by replacing the Hochschild cohomology dimension in Happel's question with the Hochschild homology dimension: $\text{\rm gl.dim\,} A < \infty$ if and only if $\text{\rm hh.dim\,} A < \infty$ if and only if $\text{\rm hh.dim\,} A = 0$. The conjecture holds for commutative algebras and monomial algebras. In the case where $A$ is a truncated quiver algebra, these conditions are equivalent to the condition that the quiver of $A$ has no oriented cycles. Moreover, an algorithm for computing the Hochschild homology of any monomial algebra is provided. Thus the cyclic homology of any monomial algebra can be read off when the underlying field is characteristic 0.
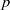 $\lowercase p$ Iwahori–Hecke algebras are Gorenstein
$\lowercase p$ Iwahori–Hecke algebras are Gorenstein