14 results
Unitary representations of type B rational Cherednik algebras and crystal combinatorics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 29 September 2021, pp. 140-169
- Print publication:
- February 2023
-
- Article
- Export citation
A GENERALIZATION OF THE THEORY OF STANDARDLY STRATIFIED ALGEBRAS I: STANDARDLY STRATIFIED RINGOIDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 07 October 2020, pp. 1-36
- Print publication:
- January 2022
-
- Article
- Export citation
LOCALIZATIONS OF THE HEARTS OF COTORSION PAIRS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 03 July 2019, pp. 564-583
- Print publication:
- September 2020
-
- Article
- Export citation
ANALOGUES OF CENTRALIZER SUBALGEBRAS FOR FIAT 2-CATEGORIES AND THEIR 2-REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1793-1829
- Print publication:
- November 2020
-
- Article
- Export citation
ROUQUIER’S CONJECTURE AND DIAGRAMMATIC ALGEBRA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 16 November 2017, e27
-
- Article
-
- You have access
- Open access
- Export citation
Homomorphisms between standard modules over finite-type KLR algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 621-646
- Print publication:
- March 2017
-
- Article
- Export citation
Classification of finite-dimensional irreducible modules over
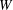 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}W$-algebras
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}W$-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 6 / June 2014
- Published online by Cambridge University Press:
- 07 April 2014, pp. 1024-1076
- Print publication:
- June 2014
-
- Article
- Export citation
ON THE SMOOTHNESS OF CENTRES OF RATIONAL CHEREDNIK ALGEBRAS IN POSITIVE CHARACTERISTIC
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue A / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 27-54
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
On the abelianization of derived categories and a negative solution to Rosický’s problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 06 November 2012, pp. 125-147
- Print publication:
- January 2013
-
- Article
- Export citation
The Calogero-Moser partition for G(m, d, n)
-
- Journal:
- Nagoya Mathematical Journal / Volume 207 / September 2012
- Published online by Cambridge University Press:
- 11 January 2016, pp. 47-77
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Towards a combinatorial representation theory for the rational Cherednik algebra of type G(r, p, n)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 419-445
-
- Article
-
- You have access
- Export citation
Commuting Families in Hecke and Temperley-Lieb Algebras
-
- Journal:
- Nagoya Mathematical Journal / Volume 195 / 2009
- Published online by Cambridge University Press:
- 11 January 2016, pp. 125-152
- Print publication:
- 2009
-
- Article
-
- You have access
- Export citation
Cyclotomic Nazarov-Wenzl Algebras
-
- Journal:
- Nagoya Mathematical Journal / Volume 182 / June 2006
- Published online by Cambridge University Press:
- 11 January 2016, pp. 47-134
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
SOME IRREDUCIBLE REPRESENTATIONS OF BRAUER'S CENTRALIZER ALGEBRAS
-
- Journal:
- Glasgow Mathematical Journal / Volume 46 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 11 October 2004, pp. 499-513
- Print publication:
- September 2004
-
- Article
-
- You have access
- Export citation

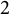
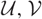
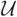
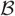
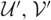
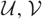
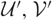
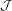
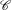
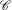
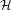

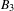
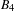
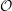
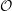
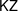
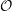
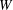
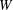
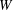
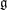

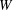
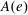
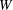
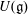

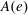
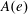
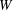
 for the rational Cherednik algebra of type
for the rational Cherednik algebra of type 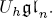 . We also give the explicit specializations of these results to the finite Temperley-Lieb algebra.
. We also give the explicit specializations of these results to the finite Temperley-Lieb algebra.