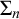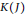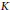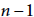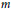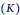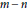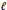4 results
THE WEAK VOPĚNKA PRINCIPLE FOR DEFINABLE CLASSES OF STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 June 2022, pp. 145-168
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CATEGORICAL COMPLEXITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e34
-
- Article
-
- You have access
- Open access
- Export citation
Wedge Operations and Torus Symmetries II
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 4 / 01 August 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 767-789
- Print publication:
- 01 August 2017
-
- Article
-
- You have access
- Export citation
On the Limitations of Sketches
-
- Journal:
- Canadian Mathematical Bulletin / Volume 35 / Issue 3 / 01 September 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 287-294
- Print publication:
- 01 September 1992
-
- Article
-
- You have access
- Export citation