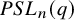 $PSL_n(q)$
and
$PSL_n(q)$
and
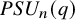 $PSU_n(q)$
by their
$PSU_n(q)$
by their
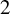 $2$
-fusion systems, q odd
$2$
-fusion systems, q odd
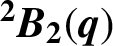 $^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
$^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
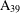 $\text{A}_{39}$
$\text{A}_{39}$