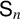COMMON ZEROS OF IRREDUCIBLE CHARACTERS

Abstract

We study the zero-sharing behavior among irreducible characters of a finite group. For symmetric groups $\mathsf {S}_n$, it is proved that, with one exception, any two irreducible characters have at least one common zero. To further explore this phenomenon, we introduce the common-zero graph of a finite group G, with nonlinear irreducible characters of G as vertices, and edges connecting characters that vanish on some common group element. We show that for solvable and simple groups, the number of connected components of this graph is bounded above by three. Lastly, the result for $\mathsf {S}_n$ is applied to prove the nonequivalence of the metrics on permutations induced from faithful irreducible characters of the group.

1 Introduction

Studying zeros of characters (and character values in general) is a fundamental problem in the representation theory of finite groups. While values of linear characters are never zero, it is a classical result of Burnside that every nonlinear irreducible character always vanishes at some element. This was improved by Malle et al. [22] who showed that the element can be chosen to be of prime-power order.

More recently, Miller [28] proved that almost all values of irreducible characters of the symmetric group $\mathsf {S}_n$ are zero as n increases. Specifically, if $P_n$ is the probability that $\chi (\sigma )=0$ where $\chi $ is uniformly chosen at random from the set ${{\operatorname {Irr}}}(\mathsf {S}_n)$ of irreducible characters of $\mathsf {S}_n$ and $\sigma $ is chosen at random from $\mathsf {S}_n$ , then $P_n\rightarrow 1$ as $n\rightarrow \infty $ . This remarkable observation has inspired several subsequent results on the abundance of zeros of character values; see [7, 16, 27, 35].

Here we investigate the many-zero phenomenon from a different perspective: when do two distinct irreducible characters of a finite group have a common zero? For symmetric groups, our answer is complete.

Theorem A. Let $n\in {\mathbb {Z}}^{\geq 8}$ and $\chi ,\psi \in {{\operatorname {Irr}}}(\mathsf {S}_n)$ both have degree larger than $1$ . Then $\chi $ and $\psi $ have a common zero if and only if $\{\chi (1),\psi (1)\}\neq \{n(n-3)/2,(n-1)(n-2)/2\}$ .

Remark 1. It is well known that irreducible characters of $\mathsf {S}_n$ are parameterized by partitions of n, and so we use $\chi ^\lambda $ to denote the character corresponding to a partition $\lambda $ . The characters of degrees $n(n-3)/2$ and $(n-1)(n-2)/2$ are corresponding to the partitions $(n-2,2)$ , $(n-2,1^2)$ , and their conjugates. Since $\chi ^{(n-2,2)}\equiv \chi ^{(n-2,1^2)}+1\text { }(\mathrm {mod}\ 2)\,$ (see [15, page 93]), $\chi ^{(n-2,2)}$ and $\chi ^{(n-2,1^2)}$ indeed do not share common zeros.

In Section 6, we discuss an application of Theorem A to a problem concerning the partition equivalence of character-induced metrics on permutations. A metric on a finite group G is a binary function $d:G\times G\rightarrow {\mathbb {R}}^{\geq 0}$ that assigns a nonnegative real number to each pair of group elements, satisfying the properties of a metric, such as positivity, symmetry, and the triangle inequality. If $\chi $ is a faithful character of G, then the induced function $\mathbf {d}_\chi $ defined by $\mathbf {d}_\chi (a,b):=(\chi (1)- Re (\chi (ab^{-1})))^{1/2}$ is a G-invariant metric on G (see [4, Section 6D]). (Here $Re(z)$ is the real part of a complex number z.) Let $\mathcal {P}(\mathbf {d}_\chi )$ be the partition of G determined by the equivalence relation: $a\thicksim b$ if and only if $\mathbf {d}_\chi (1,a)=\mathbf {d}_\chi (1,b)$ . Two metrics $\mathbf {d}_\chi $ and $\mathbf {d}_\psi $ are called partition equivalent (or $\mathcal {P}$ -equivalent for short) if $\mathcal {P}(\mathbf {d}_\chi )=\mathcal {P}(\mathbf {d}_\psi )$ (see [36]). Using Theorem A, we prove that the metrics $\mathbf {d}_{\chi }$ on permutations induced from the faithful irreducible characters $\chi $ of the group are pairwise non- $\mathcal {P}$ -equivalent.

Zero-sharing behavior for arbitrary groups is harder to understand. To explore it further, we introduce the common-zero graph of G, denoted by $\Gamma _v(G)$ : the vertices are the nonlinear irreducible characters of G and two characters are joined by an edge if they vanish on some common element. Theorem A shows that $\Gamma _v(\mathsf {S}_n)$ with $n\geq 8$ is almost complete and, in particular, connected. This is not true in general. For solvable groups, we prove the following theorem.

Theorem B. Let G be a finite solvable group. Then the number of connected components of $\Gamma _v(G)$ is at most $2$ .

We have observed that two irreducible characters tend to have a common zero if their degrees are not coprime. Although exceptions exist, they are rare and difficult to find. This suggests that the well-studied common-divisor graph $\Gamma (G)$ , whose vertices are the same nonlinear irreducible characters of G and two vertices are joined if their degrees are not coprime, is somewhat close to a subgraph of $\Gamma _v(G)$ . Manz et al. [25] proved that $\Gamma (G)$ in fact has at most three connected components for all groups. This observation together with Theorems A and B suggest the following conjecture.

Conjecture C. The number of connected components in $\Gamma _v(G)$ for any finite group G is at most $3$ .

The next result provides further evidence for the conjecture.

Theorem D. Let G be a finite simple group. Then the number of connected components of $\Gamma _v(G)$ is at most $3$ .

The bounds in both Theorems B and D are the best possible, as shown by $\mathsf {S}_4, \operatorname {GL}_2(3)$ and $\operatorname {PSL}_2(q)$ for several choices of q.

The paper is organized as follows. In Section 2, we present some preliminary results on the dual graph of $\Gamma _v(G)$ for vanishing conjugacy classes. Section 3 contains the proofs of Theorem A and the alternating-group case of Theorem D. Theorem B on solvable groups is proved in Section 4. We then handle simple groups of Lie type and complete the proof of Theorem D in Section 5. The topic of character-induced metrics on permutations is presented in Section 6. In the final Section 7, we discuss some relationships between common zeros and character degrees.

2 The dual graph for vanishing classes

For studying the common-zero graph $\Gamma _v(G)$ , it is sometimes convenient to consider the dual one for vanishing conjugacy classes.

As usual, let ${{\operatorname {Irr}}}(G)$ denote the set of all (ordinary) irreducible characters of a finite group G and ${{\operatorname {cl}}}(G)$ the set of all conjugacy classes. An element $x\in G$ is called vanishing if there exists $\chi \in {{\operatorname {Irr}}}(G)$ such that $\chi (x)=0$ . Accordingly, a conjugacy class $K\in {{\operatorname {cl}}}(G)$ is called vanishing if it contains a vanishing element. These concepts were introduced by Isaacs et al. in [13] and since then, they have been studied in great depth. See the survey paper [6] of Dolfi, Pacifici, and Sanus for more information.

The dual graph we referred to, which we denote by $\Delta _v(G)$ , has vertices being the vanishing conjugacy classes of G and two classes are joined if there exists an irreducible character in ${{\operatorname {Irr}}}(G)$ that vanishes simultaneously on both classes. The common-zero graph $\Gamma _v(G)$ and this $\Delta _v(G)$ have the same number of connected components, among other things.

Lemma 2.1. Let G be a finite group. Then:

1. (i) if $\mathcal {C}$ is the set of conjugacy classes in one connected component of $\Delta _v(G)$ , then $\{\chi \in {{\operatorname {Irr}}}(G)\mid \chi\ \text{vanishes at some class in}\ \mathcal {C}\}$ is a connected component in $\Gamma _v(G)$ ;

2. (ii) if $\mathcal {A}$ is the set of characters in a connected component in $\Gamma _v(G)$ , then the set $\{K\in {{\operatorname {cl}}}(G)\mid \chi (K)=0\ \text {for some}\ \chi \in \mathcal {D}\}$ is a connected component in $\Delta _v(G)$ ;

3. (iii) if f is the map from the set of connected components of $\Delta _v(G)$ to the set of connected components of $\Gamma _v(G)$ defined in item (i) and h is the map from the set of connected components of $\Gamma _v(G)$ to the set of connected components of $\Delta _v(G)$ defined in item (ii), then f and h are bijections and one is the inverse of the other. In particular, $\Gamma _v(G)$ and $\Delta _v(G)$ have the same number of connected components;

4. (iv) the difference between the diameter of a connected component $\mathcal {C}$ of $\Delta _v(G)$ and that of $f(\mathcal {C})$ is at most one.

Proof. Let $\mathcal {A}=\{\chi \in {{\operatorname {Irr}}}(G)\mid \chi \ \text {vanishes at some class in}\ \mathcal {C}\}$ . We want to see that if $\alpha ,\beta \in \mathcal {A}$ , then there exists a path in $\Gamma _v(G)$ joining $\alpha $ and $\beta $ . Let $C,D\in \mathcal {C}$ such that $\alpha (C)=\beta (D)=0$ . Since $\mathcal {C}$ is a connected component in $\Delta _v(G)$ , there exists a path

$$ \begin{align*} C=C_0\leftrightarrow C_1\leftrightarrow\cdots\leftrightarrow C_{d-1}\leftrightarrow C_d=D \end{align*} $$

joining C and D. By the definition of the graph $\Delta _v(G)$ , this means that there exist $\chi _i\in {{\operatorname {Irr}}}(G)$ such that $\chi _i(C_{i-1})=\chi _i(C_i)=0$ for $i=1,\ldots ,d$ . Therefore,

$$ \begin{align*} \alpha\leftrightarrow\chi_1\leftrightarrow\cdots\leftrightarrow\chi_d\leftrightarrow\beta \end{align*} $$

is a path in $\Gamma _v(G)$ joining $\alpha $ and $\beta $ . This proves that $\mathcal {A}$ is contained in a connected component of $\Gamma _v(G)$ .

Similarly, we can prove that if $\mathcal {A}$ is the set of characters in a connected component in $\Gamma _v(G)$ , then $\mathcal {D}=\{K\in {{\operatorname {cl}}}(G)\mid \,\chi (K)=0\ \text {for some}\ \chi \in \mathcal {A}\}$ is contained in a connected component in $\Delta _v(G)$ .

Now, suppose that $\mathcal {A}\subsetneq \mathcal {B}$ , where $\mathcal {B}$ is a connected component of $\Gamma _v(G)$ . Let $\gamma \in \mathcal {B}-\mathcal {A}$ . Therefore, $\gamma (K)\neq 0$ for every $K\in \mathcal {C}$ . Since $\alpha ,\gamma \in \mathcal {A}$ , there exists a path in $\Gamma _v(G)$ joining $\alpha $ and $\gamma $ . This means that there exist $\eta ,\mu $ in this path that are linked; one of them belongs to $\mathcal {A}$ and the other does not. Suppose that $\eta \in \mathcal {A}$ and $\mu \not \in \mathcal {A}$ . Then, there exists $D\not \in \mathcal {C}$ such that $\eta (D)=\mu (D)=0$ . Since $\eta \in \mathcal {A}$ , there exists $C\in \mathcal {C}$ such that $\eta (C)=0$ . By the definition of $\Delta _v(G)$ , C and D are linked by means of $\eta $ . This is a contradiction.

We omit the proofs of the remaining parts, which are similar.

The next result is essential in studying the number of connected components of our graphs. We write ${{\operatorname {Van}}}(\chi )$ for the set of zeros (or roots) of a character $\chi $ . Clearly two characters $\chi $ and $\psi $ have common zeros if and only if ${{\operatorname {Van}}}(\chi )\cap {{\operatorname {Van}}}(\psi ) \neq \emptyset $ . This explains the relevance of ${{\operatorname {Van}}}(\chi )$ in the current context.

Lemma 2.2. Let G be a group, $N\trianglelefteq \, G$ , and $\chi \in {{\operatorname {Irr}}}(G)$ . If ${{\operatorname {Van}}}(\chi )\subseteq N$ , then $\chi _N\in {{\operatorname {Irr}}}(N)$ .

Proof. Let $\theta \in {{\operatorname {Irr}}}(N)$ lie under $\chi $ and let $T=I_G(\theta )$ . By Clifford’s correspondence, there exists $\psi \in {{\operatorname {Irr}}}(T)$ such that $\psi ^G=\chi $ . By the formula for the induced character, $\chi $ vanishes on $G-\bigcup _{g\in G}T^g$ . Since a group is never the union of the conjugates of a proper subgroup, this implies that $\theta $ is G-invariant. Thus, $\chi _N=e\theta $ for some positive integer e and we want to see that $e=1$ . Arguing by contradiction, assume that $e>1$ .

Let $(G^*,N^*,\theta ^*)$ be a character triple isomorphic to $(G,N,\theta )$ with $N^*\leq {\mathbf Z}(G^*)$ and $\theta ^*$ linear and faithful. (We refer the reader to Section 5.4 and in particular Corollary 5.9 of [33] for background on character triples.) Let $\chi ^\ast \in {{\operatorname {Irr}}}(G^\ast \mid \theta ^\ast )$ correspond to $\chi $ under the isomorphism. Note that $\chi ^*$ is not linear and $\chi ^*_{N^*}=e\theta ^*$ . Since $\theta ^*$ is linear, ${{\operatorname {Van}}}(\chi ^*)\cap N^*=\emptyset $ . Therefore, there exists $x^*\in G^*-N^*$ such that $\chi ^*(x^*)=0$ . Let $x\in G$ such that

$$ \begin{align*}(Nx)^\ast=N^\ast x^\ast,\end{align*}$$

where $^\ast :G/N\longrightarrow G^\ast /N^\ast $ is the associated group isomorphism. Note that $x\not \in N$ . By [33, Lemma 5.17(a)], there exists an algebraic integer $\alpha $ such that

$$ \begin{align*}\chi(x)=\alpha\chi^\ast(x^\ast)=0,\end{align*} $$

contradicting the hypothesis that ${{\operatorname {Van}}}(\chi )\subseteq N$ .

Let ${{\operatorname {Van}}}(G)$ denote the set of vanishing elements of G, so ${{\operatorname {Van}}}(G)=\bigcup _{\chi \in {{\operatorname {Irr}}}(G)}{{\operatorname {Van}}}(\chi )$ . Although ${{\operatorname {Van}}}(G)$ has been extensively studied in the literature, it is not fully understood yet. For instance, for solvable groups, it is an open conjecture [13] that ${{\operatorname {Van}}}(G)$ always contains $G-{\mathbf F}(G)$ . The case of nilpotent groups is known though.

Lemma 2.3. Let G be a nilpotent group. Then ${{\operatorname {Van}}}(G)=G-{\mathbf Z}(G)$ .

Proof. This is [13, Theorem B].

As we see throughout, and in particular in Section 7, there is a somewhat mysterious relationship between the set of zeros of an irreducible character and its degree. There are two graphs associated to character degrees that have been well studied in the literature. The first is the already mentioned common-divisor graph $\Gamma (G)$ . (We note that in the definition of $\Gamma (G)$ , one could take the character degrees of G instead to be the vertices. The resulting graph and $\Gamma (G)$ are fundamentally the same.) The second is the prime graph $\Delta (G)$ with vertices being the primes that divide some character degree of G and two vertices joined if the product of the primes divides the degree of some irreducible character of G. The survey paper [18] of Lewis is a good place for an overview of the known results on these and other character-degree related graphs, up until 2008. Many more have been obtained since then.

We already mentioned that two irreducible characters tend to have a common zero if their degrees are not coprime. Therefore, $\Gamma (G)$ is often close to a subgraph of $\Gamma _v(G)$ , but not always a subgraph. There are counterexamples among groups of Lie type, like $\operatorname {PSL}_2(11)$ , and among sporadic groups, like $M_{12}$ . There are also solvable counterexamples, the smallest one being $\texttt {SmallGroup}(324, 160)$ in the notation of GAP [8]. It would be interesting to understand when $\Gamma (G)$ is a subgraph of $\Gamma _v(G)$ . If $\Gamma (G)$ is a subgraph of $\Gamma _v(G)$ , then the number of connected components of $\Gamma _v(G)$ is at most 3, by the main result of [25].

3 Alternating and symmetric groups

In this section, we prove Theorem A and the alternating group case of Theorem D. We start by comparing zeros of irreducible characters of symmetric groups and components of their restrictions to alternating groups.

Lemma 3.1. Let $\chi \in {{\operatorname {Irr}}}(\mathsf {S}_n)$ and $\psi \in {{\operatorname {Irr}}}(\mathsf {A}_n)$ be such that $\psi $ appears in $\chi _{\mathsf {A}_n}$ , and let $\sigma \in \mathsf {A}_n$ . Then $\chi (\sigma )=0$ if and only if $\psi (\sigma )=0$ .

Proof. If $\psi (\sigma )\not \in \{\chi (\sigma ),\chi (\sigma )/2\}$ , $\chi $ is labeled by the partition $\lambda $ , and $\mu $ is the cycle partition of $\sigma $ , then by [14, Theorems 2.5.7 and 2.5.13] $\lambda $ is self-conjugated and $\mu $ is the partition consisting of the diagonal hook-lengths of $\lambda $ . However, in this case, $\chi (\sigma )\not =0$ by [14, Corollary 2.4.8] and $\psi (\sigma )\not =0$ by [14, Theorem 2.5.13].

In the next theorem, we show that irreducible characters of $\mathsf {S}_n$ almost always have a common zero in $\mathsf {A}_n$ . It can be checked that the following result is false for small n.

Theorem 3.2. Let $n\geq 8$ and $\chi ,\psi \in {{\operatorname {Irr}}}(\mathsf {S}_n)$ both have degree larger than $1$ . Then $\chi $ and $\psi $ have no common zero if and only if, up to multiplying $\chi $ or $\psi $ with $\mathrm {sgn}$ , $\{\chi ,\psi \}=\{\chi ^{(n-2,2)},\chi ^{(n-2,1^2)}\}$ . If $n\geq 9$ , and $\chi $ and $\psi $ have a common zero, then they also have a common zero in $\mathsf {A}_n$ .

Proof. If $\chi =\chi ^{(n-2,2)}$ and $\psi =\chi ^{(n-2,1^2)}$ (up to exchange or multiplying with $\mathrm {sgn}$ ), then by [15, page 93], we have that $\psi \equiv \chi +1\text { }(\mathrm {mod}\ 2)\,$ . So in this case, $\chi $ and $\psi $ cannot have common zeros. So we may now assume that this is not the case.

The cases $n=8$ and $9$ can be checked by looking at character tables. So assume now that $n\geq 10$ .

Let $\lambda $ and $\mu $ be the partitions labeling $\chi $ and $\psi $ , respectively, so that $\chi =\chi ^\lambda $ and $\psi =\chi ^\mu $ . Note that $\lambda ,\mu \not \in \{(n),(1^n)\}$ since $\chi $ and $\psi $ have degree larger than 1. Further, for any partition $\gamma \vdash n$ , let $\tau _\gamma \in \mathsf {S}_n$ have cycle partition $\gamma $ .

Case 1: n is even. We have that $\tau _{(n-k,k)}\in \mathsf {A}_n$ for any $1\leq k\leq n/2$ . For $1\leq k\leq 4$ , let $N_{n,k}:=\{\gamma \vdash n\mid \chi ^\gamma (\tau _{(n-k,k)})=0\}$ be the set of partitions labeling characters that do not vanish on $\tau _{(n-k,k)}$ . We then have that $N_{n,k}=B_{n,k}\cup C_{n,k}\cup D_{n,k}$ with

$$ \begin{align*} B_{n,1}&=\{(n),(1^n)\},\\C_{n,1}&=\emptyset,\\D_{n,1}&=\{(n-h,2,1^{h-2})\mid 2\leq h\leq n-2\},\\B_{n,2}&=\{(n),(n-1,1),(2,1^{n-2}),(1^n)\},\\C_{n,2}&=\{(n-2,2),(2^2,1^{n-4})\},\\D_{n,2}&=\{(n-h,3,1^{h-3})\mid 3\leq h\leq n-3\}\cup\{(n-h,2^2,1^{h-4})\mid 4\leq h\leq n-2\},\\B_{n,3}&=\{(n),(n-1,1),(n-2,1^2),(3,1^{n-3}),(2,1^{n-2}),(1^n)\},\\C_{n,3}&=\{(n-3,3),(n-3,2,1),(n-4,2^2),(3^2,1^{n-6}),(3,2,1^{n-5}),(2^3,1^{n-6})\},\\D_{n,3}&=\{(n-h,4,1^{h-4})\mid 4\leq h\leq n-4\}\cup\{(n-h,3,2,1^{h-5})\mid 5\leq h\leq n-3\}\\&\quad\cup\{(n-h,2^3,1^{h-6})\mid 6\leq h\leq n-2\},\\B_{n,4}&=\{(n),(n-1,1),(n-2,1^2),(n-3,1^3),(4,1^{n-4}),(3,1^{n-3}),(2,1^{n-2}),(1^n)\},\\C_{n,4}&=\{(n-4,4),(n-4,3,1),(n-4,2,1^2),(n-5,3,2),(n-5,2^2,1),(n-6,2^3),\\&\quad(4^2,1^{n-8}),(4,3,1^{n-7}),(4,2,1^{n-6}),(3^2,2,1^{n-8}),(3,2^2,1^{n-7}),(2^4,1^{n-8})\},\\D_{n,4}&=\{(n-h,5,1^{h-5})\mid 5\leq h\leq n-5\}\cup\{(n-h,4,2,1^{h-6})\mid 6\leq h\leq n-4\}\\&\quad\cup\{(n-h,3,2^2,1^{h-7})\mid 7\leq h\leq n-3\}\cup\{(n-h,2^4,1^{h-8})\mid 8\leq h\leq n-2\}. \end{align*} $$

To see this, note that in view of the Murnaghan–Nakayama formula (see [14, Section 2.4.7]), if $\gamma \in N_{n,k}$ , then $\gamma $ is obtained by adding a $(n-k)$ -hook to a hook-partition of k and that this condition is also sufficient for $\gamma \in N_{n,k}$ since $k\leq 4<n/2$ (so that there is at most one way in which hooks of the given length can be recursively removed from any given partition of n).

So if $\chi $ and $\psi $ have no common zero in $\mathsf {A}_n$ , then $\{\lambda ,\mu \}\cap N_{n,k}\not =\emptyset $ for any $1\leq k\leq 4$ . Note that the sets $D_{n,k}$ are pairwise disjoint. The same is true for the sets $C_{n,k}$ since $n\geq 10$ . Assume first that neither $\lambda $ nor $\mu $ is in

$$ \begin{align*}\cup B_{n,k}\setminus\{(n),(1^n)\}=\{(n-1,1),(n-2,1^2),(n-3,1^3),(4,1^{n-4}),(3,1^{n-3}),(2,1^{n-2})\}.\end{align*} $$

Then $\lambda \in C_{n,k_1}\cap D_{n,k_2}$ and $\mu \in C_{n,k_3}\cap D_{n,k_4}$ for some pairwise different $1\leq k_i\leq 4$ . In particular, $\lambda ,\mu \in \bigcup _{k=1}^4 C_{n,k}$ . In each of these cases, it can be checked that $\chi ^\lambda (\tau _{(n-5,5)})=\chi ^\mu (\tau _{(n-5,5)})=0$ .

Next assume that $\lambda\hspace{-0.5pt} \in\hspace{-0.5pt} \{(n-3,1^3),(4,1^{n-4})\}$ . Then $\mu\hspace{-0.5pt} \in\hspace{-0.5pt} N_{n,1}\hspace{-0.5pt}\cap\hspace{-0.5pt} N_{n,2}\hspace{-0.5pt}\cap\hspace{-0.5pt} N_{n,3}\hspace{-0.5pt}=\hspace{-0.5pt}\{(n), (1^n)\}$ , leading to a contradiction.

If $\lambda \in \{(n-2,1^2),(3,1^{n-3})\}$ , then

$$ \begin{align*}\mu\in N_{n,1}\cap N_{n,2}=\{(n),(n-2,2),(2^2,1^{n-4}),(1^n)\},\end{align*} $$

so that $\mu \in \{(n-2,2),(2^2,1^{n-4})\}$ , which had been excluded at the beginning of the proof.

If $\lambda \in \{(n-1,1),(2,1^{n-2})\}$ , then $\mu \in N_{n,1}\setminus \{(n),(1^n)\}$ and so $\mu =(n-h,2,1^{h-2})$ for some $2\leq h\leq n-2$ . In this case, we have that $\chi ^\lambda (\tau _\gamma )=\chi ^\mu (\tau _\gamma )=0$ for some $\gamma \in \{(n-5,2^2,1), (n-6,3,2,1)\}$ .

Case 2: n is odd. In this case, $\tau _{(n)},\tau _{(n-k,k-1,1)}\in \mathsf {A}_n$ for $2\leq k\leq (n+1)/2$ . Let $N_{n,0}:=\{\gamma \vdash n\mid \chi ^\gamma (\tau _{(n)})=0\}$ and for $2\leq k\leq 4$ , let $N_{n,k}:=\{\gamma \vdash n\mid \chi ^\gamma (\tau _{(n-k,k-1,1)})=0\}$ . We can write $N_{n,k}=B_{n,k}\cup C_{n,k}\cup D_{n,k}$ with

$$ \begin{align*} B_{n,0}&=\emptyset,\\C_{n,0}&=\emptyset,\\D_{n,0}&=\{(n-h,1^h)\mid 0\leq h\leq n-1\},\\B_{n,2}&=\{(n),(n-2,2),(2^2,1^{n-4}),(1^n)\},\\C_{n,2}&=\{(n-1,1),(2,1^{n-2})\},\\D_{n,2}&=\{(n-h,3,1^{h-3})\mid 3\leq h\leq n-3\}\cup\{(n-h,2^2,1^{h-4})\mid 4\leq h\leq n-2\},\\B_{n,3}&=\{(n),(n-3,2,1),(3,2,1^{n-5}),(1^n)\},\\C_{n,3}&=\{(n-2,1^2),(n-4,2^2),(3^2,1^{n-6}),(3,1^{n-3})\},\\D_{n,3}&=\{(n-h,4,1^{h-4})\mid 4\leq h\leq n-4\}\cup\{(n-h,2^3,1^{h-6})\mid 6\leq h\leq n-2\},\\B_{n,4}&=\{(n),(n-2,2),(n-3,3),(2^3,1^{n-6}),(2^2,1^{n-4}),(1^n)\},\\C_{n,4}&=\{(n-3,1^3),(n-4,2,1^2),(n-5,2^2,1),(n-6,2^3),(4^2,1^{n-8}),(4,3,1^{n-7}),\\&\ \quad(4,2,1^{n-6}),(4,1^{n-4})\},\\D_{n,4}&=\{(n-h,5,1^{h-5})\mid 5\leq h\leq n-5\}\cup\{(n-h,3^2,1^{h-6})\mid 6\leq h\leq n-3\}\\&\quad\cup\{(n-h,2^4,1^{h-8})\mid 8\leq h\leq n-2\}. \end{align*} $$

This can be seen again by noting that if $\gamma \in N_{n,k}$ , then $\gamma $ can be obtained by adding an $(n-k)$ -hook to a partition $\overline {\gamma }\vdash k$ . Further, if $2\leq k\leq 4$ , then $\chi ^{\overline {\gamma }}(\tau _{(k-1,1)})\not =0$ . These conditions are again sufficient for $\gamma \in N_{n,k}$ since $k<n/2$ .

Again the sets $D_{n,k}$ are pairwise disjoint; the same holds for the sets $C_{n,k}$ since $n\geq 11$ and we may assume that $\{\lambda ,\mu \}\cap N_{n,k}\not =\emptyset $ for $k\in \{0,2,3,4\}$ . Assume first that neither $\lambda $ nor $\mu $ is contained in $\cup B_{n,k}$ . Then, similarly to Case 1, $\lambda ,\mu \in \cup C_{n,k}$ . In particular, $\chi (\tau _{(n-5,4,1)})=0$ and $\psi (\tau _{(n-5,4,1)})=0$ . So we may now assume that $\lambda \in (\cup B_{n,k})\setminus \{(n),(1^n)\}$ .

If $\lambda \in \{(n-2,2),(2^2,1^{n-2})\}$ , then $\mu \in N_{n,0}\cap N_{n,3}$ and then $\mu \in \{(n-2,1^2),(3,1^{n-3})\}$ , which had been excluded at the beginning of the proof.

If $\lambda \in \{(n-3,3),(2^3,1^{n-6})\}$ , then again $\mu \in N_{n,0}\cap N_{n,3}$ , so $\mu \in \{(n-2,1^2),(3,1^{n-3})\}$ and then $\chi ^\lambda (\tau _{(n-5,4,1)})=\chi ^\mu (\tau _{(n-5,4,1)})=0$ .

If $\lambda \in \{(n-3,2,1),(3,2,1^{n-5})\}$ , then $\mu \in N_{n,0}\cap N_{n,2}\cap N_{n,4}=\{(n),(1^n)\}$ , leading to a contradiction.

We now prove Theorem A.

Proof of Theorem A

We check that $\chi (1)=n(n-3)/2$ if and only if $\chi \in \{\chi ^{(n-2,2)},\chi ^{(2^2,1^{n-4})}\}$ and that $\chi (1)=(n-1)(n-2)/2$ if and only if $\chi \in \{\chi ^{(n-2,1^2)},\chi ^{(3,1^{n-3})}\}$ . The theorem then follows by Theorem 3.2.

The ‘if’ parts are easily checked using the hook formula. The ‘only if’ parts for $n=8$ are also easily checked. So assume now that $n\geq 9$ . Note that $\chi ^{(n)}(1),\chi ^{(1^n)}(1)=1$ and $\chi ^{(n-1,1)}(1),\chi ^{(2,1^n)}(1)=n-1$ . We show that $\chi ^\lambda (1)>(n-1)(n-2)/2$ for any $\lambda \vdash n$ with $\lambda _1,\lambda _1'\leq n-3$ (with $\lambda '$ the partition that is conjugated to $\lambda $ ), which concludes the proof of the ‘only if’ parts.

For $n{\kern-1pt}={\kern-1pt}9$ and $10$ , this can easily be checked by looking at character tables. So assume that $n\geq 11$ and that the claim holds for $n-1$ and $n-2$ . Then by induction, $\chi ^\mu (1)\geq (n-1)(n-4)/2$ for any $\mu \vdash n-1$ with $\mu _1,\mu _1'\leq n-3$ and $\chi ^\nu (1)>(n-3)(n-4)/2$ for any $\nu \vdash n-2$ with $\nu _1,\nu _1'\leq n-5$ . If $\lambda $ has at least two removable nodes A and B, then, by the branching rule,

$$ \begin{align*}\chi^\lambda(1)\geq\chi^{\lambda\setminus\{A\}}(1)+\chi^{\lambda\setminus\{B\}}(1)\geq (n-1)(n-4)>(n-1)(n-2)/2.\end{align*} $$

If $\lambda $ has only one removable node, then $\lambda =(a^b)$ for some $a,b$ with $ab=n$ . Further, $2\leq a,b\leq n/2<n-5$ . So

$$ \begin{align*}\chi^\lambda(1)= \chi^{(a^{b-2},(a-1)^2)}(1)+\chi^{(a^{b-1},a-2)}(1)>(n-3)(n-4)>(n-1)(n-2)/2,\end{align*} $$

which concludes the proof.

We next prove the following result, which implies Theorem D for alternating groups (if $n=5$ or $6$ , it can be checked that $\Gamma _v(\mathsf {A}_n)$ has $3$ , respectively 2, connected components by looking at character tables).

Theorem 3.3. Let $n\geq 7$ . Then each of $\Gamma _v(\mathsf {S}_n)$ , $\Gamma _v(\mathsf {A}_n)$ , $\Delta _v(\mathsf {S}_n)$ , and $\Delta _v(\mathsf {A}_n)$ is connected. Further, $\Gamma _v(\mathsf {S}_n)$ and $\Gamma _v(\mathsf {A}_n)$ have diameter $2$ , and $\Delta _v(\mathsf {S}_n)$ and $\Delta _v(\mathsf {A}_n)$ diameter at most $2$ .

Note that by the above theorem (and checking small cases), we have that $\Gamma (\mathsf {S}_n)\subseteq \Gamma _v(\mathsf {S}_n)$ and $\Gamma (\mathsf {A}_n)\subseteq \Gamma _v(\mathsf {A}_n)$ . To prove the theorem, we need the following lemma.

Lemma 3.4. Let $n\geq 7$ and $\sigma \in \mathsf {S}_n$ be a vanishing element. Then there exists $\chi \in {{\operatorname {Irr}}}(\mathsf {S}_n)\setminus \{\chi ^{(n-2,2)},\chi ^{(2^2,1^{n-4})}\}$ with $\chi (\sigma )\not =0$ .

Proof. For $n\leq 9$ , the result can be proved looking at character tables. So assume from now on that $n\geq 10$ .

Let $\tau $ be the cycle partition of $\sigma $ . If $\tau _1\geq 4$ , then there exists a $\tau _1$ -core $\lambda $ of n by [9, Theorem 1]. In particular, $\chi ^\lambda (\sigma )=0$ in view of the Murnaghan–Nakayama formula. If $\tau _1\leq n-4$ , then neither $(n-2,2)$ nor $(2^2,1^{n-4})$ is a $\tau _1$ -core. If $\tau _1\geq n-3$ , then we can take $\lambda =(n-5,5)$ as a $\tau _1$ -core.

So we may now assume that $\tau =(3^a,2^b,1^c)$ for some $a,b,c\geq 0$ with $3a+2b+c=n$ . Taking $\lambda =(n-4,2,1^2)$ , $(n-1,1)$ , or $(n-3,1^2)$ depending on whether n is congruent to 0, 1, or 2 modulo 3, respectively, we may assume that $n-3a\geq 4$ (since for this choice of $\lambda $ , we have that $|\lambda _{(3)}|\geq 4$ , so that $\chi ^\lambda (\sigma )=0$ if $n-3a\leq 3$ ).

If b is odd, then $\chi ^\lambda (\tau )=0$ for any $\lambda =\lambda '$ , in particular for $\lambda =(n/2,2,1^{n/2-2})$ or $((n+1)/2,1^{(n-1)/2})$ depending on the parity of n, since then $\chi ^\lambda =\chi ^\lambda \cdot \mathrm {sgn}$ . So we may assume that b is even.

Using the determinantal formula, we have that

$$ \begin{align*}\chi^{(n-2,2)}=1{\uparrow}_{\mathsf{S}_{n-2,2}}^{\mathsf{S}_n}-1{\uparrow}_{\mathsf{S}_{n-1}}^{\mathsf{S}_n},\end{align*} $$

where $\mathsf {S}_{n-2,2}\cong \mathsf {S}_{n-2}\times \mathsf {S}_2$ is a maximal Young subgroup. We now show that $\chi ^{(n-2,2)}(\sigma )\not =0$ . Multiplying with $\mathrm {sgn}$ , this also gives $\chi ^{(2^2,1^{n-4})}(\sigma )\not =0$ , so that the lemma follows.

By the above formulas, we have that

$$ \begin{align*}\chi^{(n-2,2)}(\sigma)=b+\binom{c}{2}-c=b+\frac{c(c-3)}{2}.\end{align*} $$

So $\chi ^{(n-2,2)}(\sigma )\not =0$ unless $(b,c)\in \{(0,0),(0,3),(1,1),(1,2)\}$ . Each of these choices contradicts $2b+c=n-3a\geq 4$ or b even.

Proof of Theorem 3.3

For $n=7$ or $8$ , the theorem can be easily checked. So assume that $n\geq 9$ . By Theorem 3.2, we have that $\Gamma _v(\mathsf {S}_n)$ is connected with diameter 2. Further if $g,h\in \mathsf {S}_n$ are vanishing elements, then by Lemma 3.4, there are $\chi ,\psi \in {{\operatorname {Irr}}}(\mathsf {S}_n)\setminus \{\chi ^{(n-2,2)},\chi ^{(2^2,1^{n-4})}\}$ with $\chi (g)=0$ and $\psi (h)=0$ . Since $\chi $ and $\psi $ have a common zero, it follows that $\Delta _v(\mathsf {S}_n)$ is connected and that it has diameter at most 2.

Let now $\chi ,\psi \in {{\operatorname {Irr}}}(\mathsf {A}_n)$ have degrees larger than 1. Then $\chi $ and $\psi $ have a common zero by Lemma 3.1 and Theorem 3.2 if and only if $\{\chi ,\psi \}\not =\{(\chi ^{(n-2,2)})_{\mathsf {A}_n},(\chi ^{(n-2,1^2)})_{\mathsf {A}_n}\}$ (note that $(\chi ^{(n-2,2)})_{\mathsf {A}_n}$ and $(\chi ^{(n-2,1^2)})_{\mathsf {A}_n}$ are both irreducible by [14, Theorem 2.5.7]). Further, any vanishing element $g\in \mathsf {A}_n$ is a zero of some irreducible character $\not =(\chi ^{(n-2,2)})_{\mathsf {A}_n}$ by Lemmas 3.1 and 3.4. We can then conclude as in the $\mathsf {S}_n$ case.

4 Solvable groups

Here we prove Theorem B. We begin with the easy case of nilpotent groups.

Theorem 4.1. Let G be a nilpotent group. Then any two nonlinear irreducible characters of G share a common zero. Equivalently, $\Gamma _v(G)$ is complete.

Proof. Let $\chi ,\psi \in {{\operatorname {Irr}}}(G)$ be nonlinear. Since nilpotent groups are monomial and maximal subgroups of nilpotent groups are normal, we have that there exist normal maximal subgroups M and N of G such that $\chi $ is induced from M and $\psi $ is induced from N. By the character-induction formula, both characters vanish outside $M\cup N$ . Since $G\neq M\cup N$ by comparing orders, the result follows.

Theorem 4.1 fails when the group is not nilpotent. The group $\operatorname {SL}_2(3)$ is already a counterexample. In fact, $\Gamma _v(\operatorname {SL}_2(3))$ is disconnected. We also note that the graph $\Delta _v(G)$ (defined in Section 2) for G nilpotent does not need to be complete, as the dihedral group $\mathsf {D}_{16}$ shows.

Next, we consider nilpotent-by-abelian groups. As usual, ${\mathbf F}(G)$ denotes the Fitting subgroup of G.

Lemma 4.2. Let G be a finite group such that $G/{\mathbf F}(G)$ is abelian. Then there exists $\lambda \in {{\operatorname {Irr}}}({\mathbf F}(G))$ such that $\chi =\lambda ^G\in {{\operatorname {Irr}}}(G)$ . In particular, $\chi $ vanishes on $G-{\mathbf F}(G)$ and all the G-classes in $G-{\mathbf F}(G)$ are linked in $\Delta _v(G)$ .

Proof. This follows from the proof of [26, Lemma 18.1].

With a slight abuse of language, sometimes we say that $x,y\in G$ are linked in $\Delta _v(G)$ to mean that the conjugacy classes of x and y are linked in $\Delta _v(G)$ , or that x belongs to a connected component of $\Delta _v(G)$ to mean that the class of x belongs to that connected component.

Lemma 4.3. Let G be a finite group such that $G/{\mathbf F}(G)$ is abelian. Then $\Delta _v(G)$ has at most two connected components, one of which contains all the classes in $G-{\mathbf F}(G)$ . If there are two connected components, then the second one contains all the vanishing classes in ${\mathbf F}(G)-{\mathbf Z}({\mathbf F}(G))$ .

Proof. By Lemma 4.2, all the classes in $G-{\mathbf F}(G)$ are linked. Let $\Delta _1$ be the connected component containing these classes. Suppose first that ${\mathbf F}(G)$ is abelian. Then Lemma 2.2 implies that for any $\chi \in {{\operatorname {Irr}}}(G)$ nonlinear, ${{\operatorname {Van}}}(\chi )\not \subseteq {\mathbf F}(G)$ . Therefore, all the vanishing classes are linked to some class in $G-{\mathbf F}(G)$ , which implies that $\Delta _v(G)$ is connected.

Suppose now that ${\mathbf F}(G)$ is not abelian and that $\Delta _v(G)$ is not connected. Let $\Delta _1,\ldots ,\Delta _t$ be the connected components of the graph, where $\Delta _1$ contains all classes in $G-{\mathbf F}(G)$ . So all the classes in $\Delta _2,\ldots ,\Delta _t$ are contained in ${\mathbf F}(G)$ . Let y be a representative of a class in one of these components. Then, y is a vanishing element and for every $\chi \in {{\operatorname {Irr}}}(G)$ satisfying $\chi (y)=0$ ,

$$ \begin{align*}\chi_{{\mathbf F}(G)}\in{{\operatorname{Irr}}}({\mathbf F}(G)),\end{align*} $$

by Lemma 2.2. In particular, y is a vanishing element of ${\mathbf F}(G)$ , that is, all the classes in $\Delta _2,\ldots ,\Delta _t$ are contained in ${\mathbf F}(G)-{\mathbf Z}({\mathbf F}(G))$ . Suppose that $y_1,y_2\in {\mathbf F}(G)-{\mathbf Z}({\mathbf F}(G))$ lie in vanishing classes. Let $\chi _i\in {{\operatorname {Irr}}}(G)$ such that $\chi _i(y_i)=0$ . Then,

$$ \begin{align*}\varphi_i:=(\chi_i)_{{\mathbf F}(G)}\in{{\operatorname{Irr}}}({\mathbf F}(G)).\end{align*} $$

By Theorem 4.1, there exists $t\in {\mathbf F}(G)$ such that $\varphi _i(t)=0$ for $i=1,2$ . However, then $y_1$ and t are linked by means of $\chi _1$ , and t and $y_2$ are linked by means of $\chi _2$ . Thus, $y_1$ and $y_2$ belong to the same connected component. It follows that all the vanishing classes in ${\mathbf F}(G)$ belong to the same connected component. The result follows.

Recall that the Fitting series of a finite group G is the sequence of characteristic subgroups ${\mathbf F}_i(G)$ defined by ${\mathbf F}_0(G)=1$ , ${\mathbf F}_1(G)={\mathbf F}(G)$ , and ${\mathbf F}_{i+1}(G)/{\mathbf F}_i(G)={\mathbf F}(G/{\mathbf F}_i(G))$ for $i\geq 1$ . If G is solvable, there exists an integer n such that ${\mathbf F}_n(G)=G$ . The smallest such integer is called the Fitting height of G. As usual, given $N\trianglelefteq G$ and $\theta \in {{\operatorname {Irr}}}(N)$ , we write ${{\operatorname {Irr}}}(G|\theta )$ to denote the set of irreducible characters of G lying over $\theta $ .

Lemma 4.4. Let G be a solvable group of Fitting height n. If $G/{\mathbf F}_{n-1}(G)$ is not abelian, then $\Delta _v(G)$ has at most two connected components.

Proof. We may assume that $n>1$ . Set $F:={\mathbf F}_{n-1}(G)$ and let $Z/{\mathbf F}_{n-1}(G)={\mathbf Z}(G/{\mathbf F}_{n-1}(G))$ . By Lemma 2.3 and Theorem 4.1, we know that all the classes in $G-Z$ belong to the same connected component $\Delta _1$ . Since $Z/F$ is abelian, Lemma 4.2 applied to $Z/{\mathbf F}_{n-2}(G)$ implies that there exists $\varphi \in {{\operatorname {Irr}}}(Z)$ that vanishes on all the classes in $Z-F$ . Therefore, the same holds for any $\chi \in {{\operatorname {Irr}}}(G|\varphi )$ . In particular, all the classes in $Z-F$ belong to the same connected component $\Delta _2$ (possibly $\Delta _1=\Delta _2$ ). We claim that any vanishing element $x\in F$ belongs to either $\Delta _1$ or $\Delta _2$ . Let $\chi \in {{\operatorname {Irr}}}(G)$ such that $\chi (x)=0$ . We may assume that ${{\operatorname {Van}}}(\chi )\subseteq F$ . By Lemma 2.2, $\chi _F\in {{\operatorname {Irr}}}(F)$ . Let $\psi \in {{\operatorname {Irr}}}(G/F)$ be nonlinear. By Gallagher’s theorem [12, Corollary 6.17], $\chi \psi \in {{\operatorname {Irr}}}(G)$ vanishes at both x and some element in $G-F$ . This proves the claim. Thus, $\Delta _1$ and $\Delta _2$ are all the connected components.

We can now complete the proof of Theorem B.

Theorem 4.5. Let G be a solvable group. Then $\Gamma _v(G)$ has at most two connected components.

Proof. By Lemma 2.1, it suffices to show that $\Delta _v(G)$ has at most two connected components. Let n be the Fitting height of G. By Theorem 4.1, we may assume that $n>1$ . By Lemma 4.4, we may assume that $G/{\mathbf F}_{n-1}(G)$ is abelian. By Lemma 4.2, all the classes in $G-{\mathbf F}_{n-1}(G)$ belong to the same connected component, say $\Delta _1$ . By Lemma 4.3, we may assume that $n\geq 3$ .

Suppose first that ${\mathbf F}_{n-1}(G)/{\mathbf F}_{n-2}(G)$ is abelian. Using Lemma 4.2 again, the classes in ${\mathbf F}_{n-1}(G)-{\mathbf F}_{n-2}(G)$ belong to the same connected component, say $\Delta _2$ (possibly $\Delta _2=\Delta _1$ ). Suppose that $x\in {\mathbf F}_{n-2}(G)$ is a vanishing element. We want to see that the class of x belongs to $\Delta _1$ or $\Delta _2$ . Suppose not. Then, if $\chi \in {{\operatorname {Irr}}}(G)$ is such that $\chi (x)=0$ , we have that $\chi $ does not have any zeros in $G-{\mathbf F}_{n-2}(G)$ . By Lemma 2.2, it follows that $\chi _{{\mathbf F}_{n-2}(G)}\in {{\operatorname {Irr}}}({\mathbf F}_{n-2}(G))$ . Using Gallagher’s theorem, we deduce that $\chi \psi \in {{\operatorname {Irr}}}(G)$ for every $\psi \in {{\operatorname {Irr}}}(G/{\mathbf F}_{n-2}(G))$ . We can assume that $\psi $ is nonlinear. Since this character has zeros on $G-{\mathbf F}_{n-2}(G)$ , we have a contradiction.

Finally, we may assume that ${\mathbf F}_{n-1}(G)/{\mathbf F}_{n-2}(G)$ is not abelian. In this case, we prove that $\Gamma _v(G)$ has at most two connected components. Let $\Phi $ be the (normal) subgroup of G such that

$$ \begin{align*}\Phi/{\mathbf F}_{n-2}(G)=\Phi(G/{\mathbf F}_{n-2}(G)).\end{align*} $$

By Lemma 4.2 applied to $G/\Phi $ , there exists $\lambda \in {{\operatorname {Irr}}}({\mathbf F}_{n-1}(G)/\Phi )$ such that

$$ \begin{align*}\psi:=\lambda^G\in{{\operatorname{Irr}}}(G).\end{align*} $$

Clearly, by Lemma 2.2, all the irreducible characters of G whose restriction to ${\mathbf F}_{n-1}(G)$ is not irreducible belong to the connected component of $\psi $ . Now we claim that all the characters in

$$ \begin{align*}\mathcal{A}= \{\chi\in{{\operatorname{Irr}}}(G)\mid\chi_{\Phi}\in{{\operatorname{Irr}}}(\Phi),\chi(1)>1\}\end{align*} $$

belong to the connected component of $\psi $ and that all the characters in

$$ \begin{align*}\mathcal{B}=\{\chi\in{{\operatorname{Irr}}}(G)\mid\chi_{{\mathbf F}_{n-1}}(G)\in{{\operatorname{Irr}}}({\mathbf F}_{n-1}(G)), \chi_{\Phi}\not\in{{\operatorname{Irr}}}(\Phi)\}\end{align*} $$

belong to the same connected component. The result follows.

Let $\chi \in \mathcal {A}$ . By the definition of $\mathcal {A}$ , $\chi _{\Phi }\in {{\operatorname {Irr}}}(\Phi )$ . By Gallagher again, $\chi \psi \in {{\operatorname {Irr}}}(G)$ , which implies that $\chi $ and $\chi \psi $ are linked in $\Gamma _v(G)$ . Since $\chi \psi $ vanishes on $G-{\mathbf F}_{n-1}(G)$ , we deduce that $\chi \psi $ is linked to $\psi $ . Therefore, there is a path of length $2$ joining $\chi $ and $\psi $ . We have thus seen that the characters in $\mathcal {A}$ and $\psi $ are in the same connected component.

It remains to prove that the characters in $\mathcal {B}$ belong to the same connected component. First, we see that for any $\chi \in \mathcal {B}$ , there exists $U_{\chi }\trianglelefteq G$ such that $\Phi \leq U_{\chi }<{\mathbf F}_{n-1}(G)$ and $\chi $ vanishes on ${\mathbf F}_{n-1}(G)-U_{\chi }$ . Let $\varphi \in {{\operatorname {Irr}}}(\Phi )$ lie under $\chi $ . Suppose that $\varphi $ is ${\mathbf F}_{n-1}(G)$ -invariant, so that $({\mathbf F}_{n-1}(G),\Phi ,\varphi )$ is a character triple with ${\mathbf F}_{n-1}(G)/\Phi ={\mathbf F}(G/\Phi )$ abelian by Gaschütz’s theorem [26, Theorem 1.12]. The existence of $U_{\chi }$ follows from [37, Lemma 2.2]. Now, we assume that $\varphi $ is not ${\mathbf F}_{n-1}(G)$ -invariant. Let $T:=I_G(\varphi )$ and note that $G=T{\mathbf F}_{n-1}(G)$ (because $\chi $ restricts irreducibly to ${\mathbf F}_{n-1}(G)$ ). In particular, $T\cap {\mathbf F}_{n-1}(G)\trianglelefteq G$ (because $T\cap {\mathbf F}_{n-1}(G)\trianglelefteq T$ , ${\mathbf F}_{n-1}(G)/\Phi $ is abelian and T contains $\Phi $ , so $T\cap {\mathbf F}_{n-1}(G)$ is also normal in ${\mathbf F}_{n-1}(G)$ ). Set $U_{\chi }=T\cap {\mathbf F}_{n-1}(G)$ and note that it satisfies the properties that we want.

Therefore, if $\chi ,\psi \in \mathcal {B}$ , then both characters vanish on ${\mathbf F}_{n-1}(G)-(U_{\chi }\cup U_{\psi })$ . Since

$$ \begin{align*}U_{\chi}\cup U_{\psi}\subsetneq{\mathbf F}_{n-1}(G),\end{align*} $$

we conclude that all the characters in $\mathcal {B}$ are linked. This completes the proof.

As mentioned at the end of Section 2, there are examples of solvable groups with $\Delta _v(G)$ disconnected. The Fitting height of the group appears to be a relevant factor to decide the connectedness of $\Delta _v(G)$ . The solvable examples mentioned there have Fitting height $3$ . There are also similar examples of Fitting height $3$ among odd order groups. Let $H\leq \operatorname {GL}_3(3)$ be a Frobenius group of order $39$ and let $G=HV$ be the semidirect product of H acting on V, where V is the natural module for $\operatorname {GL}_3(3)$ . It is easy to check that this group has Fitting height $3$ and $\Delta _v(G)$ is disconnected. We conclude this section with the following theorem.

Theorem 4.6. Let G be a solvable group. Suppose that either the Fitting height of G exceeds $9$ or that G has odd order and Fitting height at least $5$ . Then $\Delta _v(G)$ is connected and has diameter at most $2$ .

Proof. By [38, Theorem 5.2], there exists $\mu \in {{\operatorname {Irr}}}({\mathbf F}_8(G))$ such that $\chi =\mu ^G\in {{\operatorname {Irr}}}(G)$ . In particular, $\chi $ vanishes on $G-{\mathbf F}_8(G)$ . Thus, all classes in $G-{\mathbf F}_8(G)$ belong to the same connected component $\Delta _1$ . Furthermore, they are linked. Let $x\in {{\operatorname {Van}}}(G)$ and assume that x is not linked to any class in $G-{\mathbf F}_8(G)$ . Let $\psi \in {{\operatorname {Irr}}}(G)$ such that $\psi (x)=0$ . Therefore, ${{\operatorname {Van}}}(\psi )\subseteq {\mathbf F}_8(G)$ . Lemma 2.2 implies that $\psi _{{\mathbf F}_8(G)}\in {{\operatorname {Irr}}}({\mathbf F}_8(G))$ . Thus, $\psi \gamma \in {{\operatorname {Irr}}}(G)$ for every nonlinear $\gamma \in {{\operatorname {Irr}}}(G/{\mathbf F}_8(G))$ . This character vanishes both at x and at some element in $G-{\mathbf F}_8(G)$ . This is a contradiction.

Suppose now that $|G|$ is odd. By [30, Theorem D], there exists $\chi \in {{\operatorname {Irr}}}(G)$ such that $\chi $ vanishes on $G-{\mathbf F}_3(G)$ . The result follows by similar arguments as above.

We conjecture that if G is solvable and $\Delta _v(G)$ is disconnected, then the Fitting height of G is at most $3$ .

5 Groups of Lie type

In this section, we complete the proof of Theorem D.

In [22, Theorem 5.1], Malle et al. proved that, for every finite simple group G of Lie type, there exist four conjugacy classes (of elements of prime order) in G such that every nontrivial irreducible character of G vanishes on at least one of them. This instantly shows that the common-zero graph $\Gamma _v(G)$ of G has at most four connected components. With some more work, this bound can be lowered to 3. Note that 3 is the best possible bound, as shown by $\operatorname {PSL}_2(q)$ for several choices of q.

In fact, it is known that, with the possible exception of $G=\mathrm {P}\Omega _{2n}^+(q)$ , every simple group of Lie type has a pair of conjugacy classes, say $(C,D)$ , called a strongly orthogonal pair, such that

$$ \begin{align*}\chi(C)\chi(D)=0\end{align*} $$

for every $\chi \in {{\operatorname {Irr}}}(G)$ but only two characters. One of them, of course, is the trivial character $\mathbf {1}_G$ and the other is usually the Steinberg one ${\mathsf {St}}_G$ . This was done in the proofs of [23, Theorems 2.1–2.6] for classical groups and in [20, Section 10] for groups of exceptional types. In this case, $\Gamma _v(G)$ clearly has at most three connected components.

We are left with only one family $G=\mathrm {P}\Omega _{2n}^+(q)$ . It is worth noting that the common-zero graph of several simple groups of Lie type is indeed connected, although we have not made an effort to make this precise in previous cases. We take the opportunity of this remaining case to prove the connectedness of the graph.

Recall that, for p a prime, a p-defect zero character of G is a character with degree divisible by $|G|_p$ . We use a well-known fact that p-defect zero irreducible characters vanish on every p-singular element. It follows that if p divides $|G|$ , then all the p-defect zero characters of G share a common zero. To see that a character is of p-defect zero, we frequently use a case of Zsigmondy’s theorem stating that, for every $n\in {\mathbb {Z}}^{\geq 2}$ and $q\in {\mathbb {Z}}^{\geq 2}$ with $(n,q)\neq (6,2)$ and $q+1$ not a $2$ -power when $n=2$ , there is a prime (called a primitive prime divisor) that divides $q^n-1$ and does not divide $q^k-1$ for any positive integer $k<n$ . Following [22], we denote such a prime by $\ell (n)$ .

Orders and character degrees of G are conveniently expressed as products of a power of q and cyclotomic polynomials $\Phi _i$ evaluated at q, up to a constant. Note that $\ell (n)$ can be defined as a prime dividing $\Phi _n$ but not $\Phi _k$ for any $k<n$ .

Theorem 5.1. Let G be a finite simple group of Lie type. Then $\Gamma _v(G)$ has at most three connected components.

Proof. As mentioned above, we may assume that $G=\mathrm {P}\Omega _{2n}^+(q)$ with $n\geq 4$ , and we aim to prove that $\Gamma _v(G)$ is connected. Let $G_{sc}$ be the corresponding finite reductive group of simply connected type, so that $G_{sc}=\mathrm {Spin}_{2n}(q)$ is the full covering group of G and $G=G_{sc}/{\mathbf Z}(G_{sc})$ .

Maximal tori and their orders of finite reductive groups are well known, see for example [21, Section 3A]. Here a maximal torus of $G_{sc}$ is defined to be the F-fixed points of a maximal torus of the ambient algebraic group $\mathbf G$ under a suitable Frobenius map $F:\mathbf G\rightarrow \mathbf G$ such that $G_{sc}=\mathbf G^F$ . Specifically, the $G_{sc}$ -conjugacy classes of F-stable maximal tori of $\mathbf G$ are parameterized by pairs of partitions $(\lambda ,\mu )$ of n (that is, $\lambda =(\lambda _1,\lambda _2,\ldots )$ and $\mu =(\mu _1,\mu _2,\ldots )$ with $\sum _i \lambda _i+\sum _j \mu _j=n$ ) such that the number of parts of $\mu $ is even. The order of the corresponding (conjugate) maximal tori of $G_{sc}$ is

$$ \begin{align*} \prod_{\lambda_i}(q^{\lambda_i}-1)\prod_{\mu_j}(q^{\mu_j}+1). \end{align*} $$

Consider three tori $\mathcal {T}_i$ ( $1\leq i\leq 3$ ) of $G_{sc}$ of orders

$$ \begin{align*} |\mathcal{T}_1|=(q^{n-1}+1)(q+1), |\mathcal{T}_2|=(q^{n-2}+1)(q^2+1),\end{align*} $$

and

$$ \begin{align*} |\mathcal{T}_3| = \begin{cases} q^{n}-1 &\text{if } n \text{ is odd},\\ (q^{n-1}-1)(q-1) &\text{if } n \text{ is even}. \end{cases} \end{align*} $$

Assume for a moment that $n\geq 5$ and $(n,q)\neq (5,2)$ . In particular, primitive prime divisors

$$ \begin{align*}\ell_1:=\ell(2n-2), \ell_2:=\ell(2n-4),\end{align*} $$

and

$$ \begin{align*} \ell_3:= \begin{cases} \ell(n) &\text{if } n \text{ is odd},\\ \ell(n-1) &\text{if } n \text{ is even}, \end{cases} \end{align*} $$

exist. Furthermore, $\ell _i$ divides $|\mathcal {T}_i|$ and the $\ell _i$ -Sylow subgroups of $G_{sc}$ are cyclic (see [24, Theorem 25.14]). Let $g_i\in \mathcal {T}_i$ be of order $\ell _i$ . We use the same notation $g_i$ and $\mathcal {T}_i$ for their images under the natural projection from $G_{sc}$ to G.

We first argue that all the nonunipotent characters of G (as well as of $G_{sc}$ ) are contained in one connected component. (Here, a character of G is called nonunipotent if its lift to $G_{sc}$ is nonunipotent. See [5, Definition 13.19] for the definition of unipotent characters of finite reductive groups.) For this, it is sufficient to show that any such character of $G_{sc}$ vanishes on at least two $g_i$ . This can be argued similarly as in [21, Section 3B]. Assume otherwise. Then there is $\chi $ belonging to the Lusztig series $\mathcal E(G_{sc},s)$ for some nontrivial semisimple element

$$ \begin{align*}s\in G_{ad}:=\mathrm{P}(\mathrm{CO}_{2n}(q)^0)\end{align*} $$

such that $\chi $ is nonzero on at least two $g_i$ .

Suppose that $\chi (g_1)\neq 0$ . Then $\ell _1$ does not divide $\chi (1)$ (otherwise, since every character degree is a product of a power of q and some $\Phi _k$ up to a constant, we have that $\Phi _{2n-2}$ appears in the product for $\chi (1)$ ; which would imply that $\chi $ is of $\ell _1$ -defect zero, and hence vanishes at $g_1$ , which is a contradiction). It follows from the character-degree formula in Lusztig’s parameterization [5, Remark 13.24] that $|{\mathbf C}_{G_{ad}}(s)|$ is divisible by $\ell _1$ and moreover ${\mathbf C}_{G_{ad}}(s)$ contains a conjugate of $\mathcal {T}_1^\ast $ , where $\mathcal {T}_i^\ast $ is the torus of $G_{ad}$ dual to $\mathcal {T}_i$ . What we have shown also applies to the cases $\chi (g_2)\neq 0$ and $\chi (g_3)\neq 0$ . Since $\chi $ is nonzero on at least two $g_i$ , we deduce that ${\mathbf C}_{G_{ad}}(s)$ contains certain conjugates of at least two $\mathcal {T}_i^\ast $ . Using the known structure of centralizers of semisimple elements in finite reductive groups (see [34, Lemmas 2.3 and 2.5], for instance, for the case of split orthogonal groups), we see that s must be trivial, violating the nonunipotent assumption on $\chi $ .

Lusztig’s classification of ordinary irreducible characters of finite reductive groups, together with the aforementioned character-degree formula and the known centralizers of semisimple elements also show that, for each i, G possesses a nonunipotent character of $\ell _i$ -defect $0$ , which thus vanishes on $g_i$ . For instance, for $i=1$ , we choose a semisimple element $s\in G =[G_{ad},G_{ad}]$ so that $\Phi _{2n-2}$ , a polynomial in q, is not a factor of $|\mathbf {C}_{G_{ad}}(s)|$ . Every character in the Lusztig series $\mathcal E(G_{sc},s)$ then has degree divisible by $\Phi _{2n-2}$ and $\ell _1$ -defect $0$ . Moreover, these characters (of $G_{sc}$ ) restrict trivially to ${\mathbf Z}(G_{sc})$ (see [11, Lemma 5.8], for instance), and therefore they are lifts of characters of G.

We now turn to (nontrivial) unipotent characters. First assume that n is odd. As mentioned in [21, Section 3G], all these characters except the Steinberg one have degrees divisible by either $\ell _1$ or $\ell _3$ , and therefore have either $\ell _1$ -defect or $\ell _3$ -defect zero, and thus vanish on either $g_1$ or $g_3$ . We now know that all members of ${{\operatorname {Irr}}}(G)\backslash \{\mathbf {1}_G,{\mathsf {St}}_G\}$ are contained in just one connected component of $\Gamma _v(G)$ . Thus, we would be done if ${\mathsf {St}}_G$ has a common zero with any other irreducible character of the group. This is not difficult to see. Let r be the defining characteristic of the group. Consider $g\in G$ that is an r-singular element but not an r-element and $p\neq r$ that is a prime divisor of $|g|$ . Then g is a vanishing element for both ${\mathsf {St}}_G$ and any p-defect zero characters.

Now assume that n is even. According to [21, Section 3G], if a nontrivial unipotent character of G has degree not divisible by either $\ell _1$ or $\ell _3$ , it must be either the Steinberg character or one of the two others labeled by the symbols

$$ \begin{align*}{n-1 \choose 1} \quad\text{and}\quad {0\hspace{6pt}\cdots \hspace{6pt} n-3\hspace{6pt}n-1 \choose 1\hspace{6pt}\cdots\hspace{6pt}n-2\hspace{6pt} n-1}.\end{align*} $$

(We refer the reader to [2, Section 13.8] for the labeling and degree formulas of unipotent characters of classical groups.) The degrees of these two characters, however, are divisible by $\Phi _{2n-4}$ . They are therefore of $\ell _2$ -defect zero, and thus vanish at $g_2$ , proving that they are in the same connected component with nonunipotent characters. As with the case of odd n, $\Gamma _v(G)$ is therefore connected.

Consider $G=\mathrm {P}\Omega ^+_8(q)$ . As the case $(n,q)=(4,2)$ can be checked using [8], we assume that $q>2$ , so that the primitive prime divisors $\ell _1,\ell _2,\ell _3$ still exist. (Note that $|G|$ is now divisible by $\Phi _4^2$ and the condition $\chi (g_2)\neq 0$ does not imply that ${\mathbf C}_{G_{ad}}(s)$ contains a conjugate of $\mathcal {T}_2^\ast $ , as we had earlier.) We still have that every nonunipotent character of G vanishes at either $g_1$ or $g_3$ . However, the (two) unipotent characters of G labeled by the symbol ${2 \choose 2}$ have degree $q^2\Phi _3\Phi _6$ , and hence are of both $\ell _1$ - and $\ell _3$ -defect zero. They therefore vanish on both $g_1$ and $g_3$ , and it follows that all the nonunipotent characters of G are contained in one connected component of $\Gamma _v(G)$ . As mentioned above, this connected component also contains all (nontrivial) unipotent characters except possibly the Steinberg one or the two characters labeled by ${3 \choose 1}$ and ${0\hspace {6pt}1 \hspace {6pt} 3 \choose 1\hspace {6pt}2\hspace {6pt}3}$ , which are of degrees $q\Phi _4^2$ and $q^7\Phi _4^2$ , respectively. These characters are of $\ell _2$ -defect zero and vanish on every $\ell _2$ -singular element. However, G has another $\ell _2$ -defect zero unipotent character, namely the one labeled by ${1\hspace {6pt}2 \choose 0\hspace {6pt}3}$ , of degree $q^3\Phi _3\Phi _4^2/2$ , and thus the two exceptional characters are in the same connected component with the nonunipotent characters. Finally, the Steinberg character is handled as above, and $\Gamma _v(G)$ is connected.

When $(n,q)=(5,2)$ , the above arguments still go through with $\mathcal {T}_2$ replaced by a maximal torus of order $(q^3-1)(q^2-1)$ and $\ell _2$ being $\ell (3)$ (and keep $\mathcal {T}_1$ and $\mathcal {T}_3$ ). This concludes the proof.

Theorem 5.2. If G is a sporadic simple group, then $\Gamma _v(G)$ is connected.

Proof. This can be checked using GAP [8].

Theorem D readily follows from Theorems 3.3, 5.1, 5.2, and the classification of finite simple groups (the cases $\mathsf {A}_5$ and $\mathsf {A}_6$ can be easily checked and the case of cyclic groups of prime order is a triviality).

6 Equivalence of character-induced metrics

In this section, we discuss an application of Theorem A to a problem on character-induced metrics on permutations.

A metric $\mathbf {d}$ on a set X is a binary function $\mathbf {d}:X\times X\rightarrow {\mathbb {R}}^{\geq 0}$ such that, for every $a,b,c\in X$ :

• • $\mathbf {d}(a,b)=0$ if and only if $a=b$ ;

• • $\mathbf {d}(a,b)=\mathbf {d}(b,a)$ ; and

• • $\mathbf {d}(a,b)\leq \mathbf {d}(a,c)+\mathbf {d}(c,b)$ .

When $X=G$ is a finite group, a metric $\mathbf {d}$ is of particular interest when it is bi-invariant (also called G-invariant); that is,

$$ \begin{align*}\mathbf{d}(a,b)=\mathbf{d}(ac,bc)=\mathbf{d}(ca,cb)\end{align*} $$

for every $a,b,c\in G$ . See [3, Ch. 10] for more background on the theory of metrics on groups.

In his book [4, Section 6D], Diaconis introduces the matrix norm approach as a method for constructing (bi-invariant) metrics on finite groups. Through this construction, many well-known metrics on permutations, including the Hamming distance, can be obtained. This approach relies on faithful unitary representations

$$ \begin{align*}\rho:G\rightarrow GL(V)\end{align*} $$

and the Frobenius norm on matrices

$$ \begin{align*}\|M\|:=\bigg(\sum_{i,j} M_{ij}\overline{M}_{ij}\bigg)^{1/2}=Tr(MM^\ast)^{1/2}.\end{align*} $$

(Recall that $M^\ast $ is the conjugate transpose of a matrix M and $\overline {z}$ is the conjugate of a complex number z. Also, $\rho $ is unitary if $\rho (g)\rho (g)^\ast =\rho (g)^\ast \rho (g)=I$ for every $g\in G$ .) If $\rho $ is such a representation, then

$$ \begin{align*}\mathbf{d}_\rho(a,b):=\|\rho(a)-\rho(b)\|\end{align*} $$

is a metric on G. Letting $\chi $ be the character afforded by $\rho $ (and in fact, every character can be afforded by a unitary representation),

$$ \begin{align*} \mathbf{d}_\chi(a,b):=\mathbf{d}_\rho(a,b)=\! \sqrt{2}(\chi(1)- Re (\chi(ab^{-1})))^{1/2}, \end{align*} $$

where $Re(z)$ denotes the real part of a complex number z.

Clearly the distances $\mathbf {d}(1,a)$ between the identity element and other elements of the group completely determine a bi-invariant metric $\mathbf {d}$ . Let $\mathcal {P}(\mathbf {d})$ be the partition of G determined by the equivalence relation:

$$ \begin{align*}a\thicksim b \quad\text{if and only if } \mathbf{d}(1,a)=\mathbf{d}(1,b).\end{align*} $$

Two metrics $\mathbf {d}_1$ and $\mathbf {d}_2$ are called $\mathcal {P}$ -equivalent if $\mathcal {P}(\mathbf {d}_1)=\mathcal {P}(\mathbf {d}_2)$ (see for example [36]).

It is well known that every character of the symmetric group $\mathsf {S}_n$ is rational-valued. Therefore, if $\chi \in {{\operatorname {Irr}}}(\mathsf {S}_n)$ , then $\mathcal {P}(\mathbf {d}_\chi )$ is determined by the relation:

$$ \begin{align*}\pi\thicksim \sigma \quad\text{if and only if }\chi(\pi)=\chi(\sigma).\end{align*} $$

Here, using Theorem A, we prove the nonequivalence of the metrics on permutations induced from irreducible characters.

Theorem 6.1. Let $n\in {\mathbb {Z}}^{\geq 3}$ . The metrics $\mathbf {d}_{\chi }$ on the permutations in $\mathsf {S}_n$ induced from the faithful irreducible characters $\chi $ of the group are pairwise non- $\mathcal {P}$ -equivalent.

Before proving the above theorem, we need a few preliminary lemmas. As it can be proved that for $n\neq 4$ , all irreducible nonlinear characters of $\mathsf {S}_n$ are faithful and there are only two linear characters, so that the restriction to faithful irreducible characters is not a big restriction.

Lemma 6.2. Let $\{\lambda ,\mu \}$ be one of the pairs $\{(n-2,2),(n-2,1^2)\}$ , $\{(2,2,1^{n-4}), (n-2,1^2)\}$ , $\{(n-2,2),(3,1^{n-3})\}$ , and $\{(2,2,1^{n-4}),(3,1^{n-3})\}$ . Then $\chi ^\lambda $ and $\chi ^\mu $ induce non- $\mathcal {P}$ -equivalent metrics.

Proof. We provide arguments only for $\lambda =(n-2,2)$ and $\mu =(n-2,1^2)$ with $n\geq 4$ . The other cases are similar. Let $\sigma _1:=(1\, \cdots \,n-3)$ and $\sigma _2:=\sigma _1(n-2 \,\,n-1)$ . It is easy to see that $\chi ^\lambda $ vanishes on both $\sigma _1$ and $\sigma _2$ , while $\chi ^\mu $ takes values 1 on $\sigma _1$ and $-1$ on $\sigma _2$ . This shows that the partitions determined by $\chi ^\lambda $ and $\chi ^\mu $ are different, as desired.

Lemma 6.3. Let $\chi \in {{\operatorname {Irr}}}(\mathsf {S}_n)$ such that $\chi \neq \mathrm {sgn}\cdot \chi $ . There exist $\pi ,\sigma \in \mathsf {S}_n$ of different signature such that $\chi (\pi )=\pm \chi (\sigma )\neq 0$ .

Proof. Suppose that $\lambda $ is the partition of n corresponding to $\chi $ . The assumption on $\chi $ implies that $\lambda $ is not self-conjugate, or equivalently, the Young diagram $[\lambda ]$ of $\lambda $ is not symmetric. Following [14], we use $R_{ij}$ for the part of the rim of $[\lambda ]$ corresponding to the hook at $(i,j)$ . The length of the hook at $(i,j)$ is denoted by $h_{ij}$ .

If $\lambda \in \{(n),(1^n)\}$ , then $\chi $ is the trivial or sign character, so the result is clear ( $n\geq 2$ as $\lambda $ is not self-conjugate). So we may now assume that $(1,2)$ and $(2,1)$ are both nodes of $\lambda $ .

First we consider the case where $[\lambda ]\backslash R_{11}$ is not symmetric (in particular, $[\lambda ]\backslash R_{11}$ is nonempty). Let $\overline {\lambda }$ be the partition with Young diagram $[\lambda ]\backslash R_{11}$ . By induction, there exist $\overline {\pi }$ and $\overline {\sigma }$ in $\mathsf {S}_{n-h_{11}}$ of different signature such that

$$ \begin{align*} \chi^{\overline{\lambda}}(\overline{\pi})=\pm \chi^{\overline{\lambda}}(\overline{\sigma})\neq 0. \end{align*} $$

Let $\tau $ be a cycle of length $n-h_{11}$ in $\mathsf {S}_{n-h_{11}}$ , and set

$$ \begin{align*} \pi:=\tau\overline{\pi} \quad\text{and}\quad \sigma:=\tau\overline{\sigma}. \end{align*} $$

By the Murnaghan–Nakayama formula, we have

$$ \begin{align*} \chi^\lambda(\pi)=\pm \chi^{\overline{\lambda}}(\overline{\pi}) \quad\text{and}\quad \chi^\lambda(\sigma)=\pm \chi^{\overline{\lambda}}(\overline{\sigma}), \end{align*} $$

which implies what we wanted.

It remains to consider the case where $[\lambda ]\backslash R_{11}$ is symmetric. Since $[\lambda ]$ itself is not symmetric but $[\lambda ]\backslash R_{11}$ is, it follows that $h_{12}\neq h_{21}$ . Without loss of generality, assume that $h_{12}>h_{21}$ , so that $h_{12}$ is the second largest hook length in $[\lambda ]$ and it occurs with multiplicity 1. Note that $[\lambda ]\backslash R_{12}$ can be obtained from $[\lambda ]\backslash R_{11}$ by adding some nodes to the first column and that $[\lambda ]\backslash R_{12}$ has at least two nodes in the first column. It follows that $[\lambda ]\backslash R_{12}$ is not symmetric. Repeating the above arguments, we arrive at the same conclusion.

Lemma 6.4. Let $\chi ,\psi \in {{\operatorname {Irr}}}(\mathsf {S}_n)$ . If ${{\operatorname {Van}}}(\chi )={{\operatorname {Van}}}(\psi )$ , then $\chi =\psi $ up to multiplying with $\mathrm {sgn}$ .

Proof. Let $\lambda ,\mu $ be the partitions of n with $\chi =\chi ^\lambda $ and $\psi =\chi ^\mu $ . We may assume that $\mu \not \in \{\lambda ,\lambda '\}$ (with $\lambda $ and $\lambda '$ being conjugated partitions).

Then by [31, Theorem 2], $H(\lambda )\not = H(\mu )$ or $H([\lambda ]\backslash R_{11})\not =H([\mu ]\backslash R_{11})$ . The lemma then follows by the proofs of [32, Propositions 3.3.8 and 3.3.9].

Proof of Theorem 6.1

The result can be checked for $n\leq 7$ from the known character tables, so we suppose that $n\geq 8$ . Assume that $\chi ,\psi \in {{\operatorname {Irr}}}(\mathsf {S}_n)\backslash \{\textbf {1}_{\mathsf {S}_n},\mathrm {sgn}\}$ such that $\mathcal {P}(\mathbf {d}_\chi )=\mathcal {P}(\mathbf {d}_\psi )$ , and let $\lambda $ and $\mu $ be the partitions of n corresponding to $\chi $ and $\mu $ , respectively.

We know that $\{\lambda ,\mu \}$ is not one of the pairs considered in Lemma 6.2. It follows that, by Theorem A, $\chi $ and $\psi $ have a common zero. As $\mathcal {P}(\mathbf {d}_\chi )=\mathcal {P}(\mathbf {d}_\psi )$ , we deduce that ${{\operatorname {Van}}}(\chi )={{\operatorname {Van}}}(\psi )$ , and thus, by Lemma 6.4,

$$ \begin{align*} \psi\in\{\chi, \mathrm{sgn}\cdot\chi\}. \end{align*} $$

We therefore would be done if $\chi $ and $\mathrm {sgn}\cdot \chi $ produce different partitions on $\mathsf {S}_n$ ; that is, $\mathcal {P}(\chi )\neq \mathcal {P}(\mathrm {sgn}\cdot \chi )$ . For this, it is sufficient to show that there exist permutations $\pi $ and $\sigma $ of different signature such that

$$ \begin{align*}\chi(\pi)=\pm\chi(\sigma)\neq 0.\end{align*} $$

This is done in Lemma 6.3, and the proof is complete.

7 Relation with character degrees

The results we have observed suggest that the common-zero graph $\Gamma _v(G)$ and the common-divisor graph $\Gamma (G)$ share many similar properties. However, studying $\Gamma _v(G)$ seems to be more challenging. Both solvable and nonsolvable groups with disconnected $\Gamma (G)$ have been classified [17, 19]. To achieve a similar classification for $\Gamma _v$ and, in particular, to show that $\Gamma _v(G)$ has at most three connected components for all G, we believe that the following question is crucial.

Question 7.1. Let G be a finite group. Is it true that if $\Gamma (G)$ is connected, then $\Gamma _v(G)$ is connected?

As presented in Section 2, there are examples of groups with irreducible characters that are linked in $\Gamma (G)$ but not in $\Gamma _v(G)$ . In other words, there exist irreducible characters that have noncoprime degrees and no common zeros. There are also examples of irreducible characters that have common zeros and coprime degrees, for instance, the irreducible characters of degree $3$ and $8$ in the semidirect product of $\operatorname {GL}_2(3)$ acting on its natural module. Following up Lemma 6.4, we wonder what would happen if two irreducible characters have exactly the same vanishing set.

Proposition 7.2. Let G be a finite group and let $\chi ,\psi \in {{\operatorname {Irr}}}(G)$ be such that $(\chi (1), \psi (1))=1$ . Then ${{\operatorname {Van}}}(\chi )\not \subseteq {{\operatorname {Van}}}(\psi )$ and ${{\operatorname {Van}}}(\psi )\not \subseteq {{\operatorname {Van}}}(\chi )$ . In particular, if ${{\operatorname {Van}}}(\chi )={{\operatorname {Van}}}(\psi )$ , then $(\chi (1),\psi (1))\neq 1$ .

Proof. By symmetry, it suffices to prove that ${{\operatorname {Van}}}(\chi )\not \subseteq {{\operatorname {Van}}}(\psi )$ . Let $\chi (1)$ be a $\pi $ -number for some set of primes $\pi $ , so that $\psi (1)$ is a $\pi '$ -number. By way of contradiction, suppose that ${{\operatorname {Van}}}(\chi )\subseteq {{\operatorname {Van}}}(\psi )$ . By [22], there exists $p\in \pi $ and $x\in G$ of p-power order such that $\chi (x)=0$ . It follows that $\psi (x)=0$ . Note that $\psi $ has degree not divisible by p. Therefore, [33, Corollary 4.20] implies that $\psi (x)\neq 0$ , which is a contradiction.

In symmetric groups, more is true: two irreducible characters must have the same degree if they have the same vanishing set, by Lemma 6.4. However, this is not the case in general, as shown by $\operatorname {SL}_2(5)$ or $\operatorname {PSL}_2(11)$ . One can find more counterexamples using [8], including solvable groups. Moreover, there exist irreducible characters having the same vanishing set but where neither of the degrees divides the other. Before showing one example, we need the following lemma.

Lemma 7.3. Let q, s, and p be such that q and p are primes, and s is odd with $(q,s)= (q-1,s)=1$ and $p=(q^s-1)/(q-1)$ . Let $Q:=\{(a_1,\ldots ,a_{s-1})\mid a_i\in {\mathbb {F}}_{q^s}\}$ with the following operation:

$$ \begin{align*}(a_i)\cdot(b_i)=\bigg(a_i+b_i+\sum_{j=1}^{i-1}a_{i-j}^{q^j}b_j\bigg).\end{align*} $$

Further, fix $x\in {\mathbb {F}}_{q^s}^*$ of order p and let $C:=\langle x\rangle $ and $G:=Q\rtimes C$ through the action $(a_i)^{x^j}=(x^{j(q^i-1)/(q-1)}a_i)$ of C on Q.

Then Q and G are groups. Further, if $\chi \not =1$ is any nontrivial irreducible character of Q, then $\chi ^G$ is an irreducible character of G with ${{\operatorname {Van}}}(\chi ^G)=G\setminus Q$ .

Proof. This is stated in [1, Example 1, Section 5], but there is an error in the proof appearing after [1, Proposition 5.1] of why $\chi ^G$ does not vanish on Q, so we give a new proof of this fact here. Further, it is not stated there that $\chi ^G$ vanishes outside Q, but this follows from Q being normal.

Let $H=\{(a_i)\in Q\mid a_i\in {\mathbb {F}}_q\}$ and $H_k:=\{(a_i)\in H\mid a_i=0\text { for }i<k\}$ for $1\leq k\leq s$ .

Though it is not stated in [1, Proposition 5.1], the characters $\chi _\alpha ^c$ appearing there are pairwise distinct, see the proof of [10, Theorem 4.8], so that indeed, for some $\alpha \not =1$ , $\chi ^G=\chi _\alpha ^G$ is irreducible. By [10, Theorem 4.1], any element in Q is G-conjugate to some element in H. So it is enough to prove that $\chi _\alpha ^G$ does not vanish on H.

Fix any $1\not =\alpha \in {{\operatorname {Irr}}}(H)$ and any $h\in H$ . We may assume that $h\not =1$ . Let $1\leq k,j<~s$ with $\alpha \in {{\operatorname {Irr}}}(H/H_{k+1})\setminus {{\operatorname {Irr}}}(H/H_k)$ and $h\in H_j\setminus H_{j+1}$ . For any $g\in G$ , we have that if $h^g=(a_i)$ , then $a_i=0$ for $i<j$ and $a_j\not =0$ . If further $g\in Q$ and $c\in C$ , then the j th components of $h^c$ and $(h^c)^g$ coincide.

If $j>k$ , then $h^c\in Q_{k+1}$ for every $c\in C$ , so in this case, the argument from [1, Section 5] works.

Assume next that $j<k$ . Since $C=\langle x\rangle $ with $x\in {\mathbb {F}}_{q^s}^*$ of order $p=(q^s-1)/(q-1)$ , then the j th component of $h^c$ is not in ${\mathbb {F}}_q$ and so by the above paragraph, it follows that $h^c$ is not Q-conjugate to any element of $HQ_k$ for $1\not =c\in C$ . So in this case, $\chi _\alpha ^G(h)\not =0$ by the argument in [1, Section 5].

Consider now $j=k$ . Then $h^c\in Q_k\subseteq HQ_k$ for every $c\in C$ . By [10, Lemma 3.3, Proposition 4.7], we have that $\{(a_i)\in Q_k\mid \text {Tr}(a_k)=0\}\subseteq \operatorname {Ker}(\chi _\alpha )$ (apply [10, Lemma 3.3] with $m=k$ to $Q/Q_{k+1}$ ). In particular, if $h_c=(0^{k-1},\text {Tr}((h^c)_k),0^{s-k-1})$ , then $h^c=h_ck$ for some $k\in \operatorname {Ker}(\chi _\alpha )$ . In view of [10, Proposition 4.7], we then have that

$$ \begin{align*}\chi_\alpha^G(h)=q^{(s-1)(k-1)/2}(\alpha(h_1)+\cdots+\alpha(h_p))\end{align*} $$

with $h_1,\ldots ,h_p\in H_k$ . Note that H is abelian (see [1, Example 1, Section 5]). As H is a q-group with q a prime and $\alpha $ is a irreducible character of H, $\alpha (h_1)+\cdots +\alpha (h_p)$ is a sum of p not necessarily primitive $q^a$  th roots of unity for some $a\geq 1$ . As p is also prime and by definition, $p\not =q$ , it follows that also in this case, $\chi _\alpha ^G(h)\not =0$ (this is similar to the proof of [33, Lemma 4.19]).

Example 7.4. Let $q_1$ , $s_1$ , $q_2$ , $s_2$ , p with p and $q_1\not =q_2$ primes, $s_1,s_2$ odd, $(q_i,s_i)=(q_i-1,s_i)=1$ , and $p=(q_i^{s_i}-1)/(q_i-1)$ for $1\leq i\leq 2$ . These relations are satisfied by $q_1=2$ , $s_1=5$ , $q_2=5$ , $s_2=3$ , and $p=31$ .

Let $G:=(Q_1\times Q_2)\rtimes C$ with subgroups $G_i=Q_1\rtimes C$ as in Lemma 7.3. As $G_i\cong G/Q_{3-i}$ , any irreducible representation of $G_i$ can also be viewed as an irreducible representation of G. Take any irreducible nonlinear characters $\overline {\chi }$ and $\overline {\psi }$ of $Q_1$ and $Q_2$ , and let $\chi :=\overline {\chi }^{G_1}$ and $\psi :=\overline {\psi }^{G_2}$ . Then $\chi $ and $\psi $ are irreducible and ${{\operatorname {Van}}}_{G_1}(\chi )=G_1\setminus Q_1$ and ${{\operatorname {Van}}}_{G_2}(\psi )=G_2\setminus Q_2$ by Lemma 7.3. When viewing them as G characters as above, it then follows that ${{\operatorname {Van}}}_G(\chi )=G\setminus (Q_1\times Q_2)={{\operatorname {Van}}}_G(\psi )$ . Further, since $Q_i$ are $q_i$ -groups and $|C|=p$ , by definition, $\chi (1)=q_1^ap$ and $\psi (1)=q_2^bp$ for some $a,b\geq 1$ . In particular, neither $\chi (1)$ nor $\psi (1)$ divides the other.

Note that in this example, neither character is faithful or primitive. It is still open whether more can be said if at least one of the two characters is of one of these types.

There is one important family of groups among which we have found no counterexamples to irreducible characters having the same degree if they have the same vanishing set.

Question 7.5. Let G be a finite p-group. Suppose that $\chi ,\psi \in {{\operatorname {Irr}}}(G)$ and ${{\operatorname {Van}}}(\chi )={{\operatorname {Van}}}(\psi )$ . Is it true that $\chi (1)=\psi (1)$ ?

This was communicated to one of us by J. Sangroniz years ago. We can now show that Question 7.5 has an affirmative answer when one of the two characters has degree p. We begin with a general lemma.

Lemma 7.6. Let G be a finite group and let $N\trianglelefteq G$ . Suppose that $|G:N|=p$ is prime. Then $\chi (x)=0$ for every $x\in G-N$ if and only if $\chi $ is induced from N.

Proof. The result is clear if $\chi $ is induced from N. Now, assume that $\chi (x)=0$ for every $x\in G-N$ . We want to see that $\chi $ is induced from N. Assume not. Then $\chi _N\in {{\operatorname {Irr}}}(N)$ by [12, Corollary 6.19]. Hence,

$$ \begin{align*} 1&=[\chi,\chi]=\frac{1}{|G|}\sum_{g\in G}|\chi(g)|^2= \frac{1}{|G|}\sum_{g\in N}|\chi(g)|^2\\ &=(1/p)\frac{1}{|N|}\sum_{g\in N}|\chi(g)|^2=(1/p)[\chi_N,\chi_N]=1/p, \end{align*} $$

which is a contradiction.

As usual, if G is a group, ${\mathbf Z}_2(G)$ is the subgroup of G such that ${\mathbf Z}(G/{\mathbf Z}(G))={\mathbf Z}_2(G)/{\mathbf Z}(G)$ .

Lemma 7.7. Let G be a finite p-group and N be a proper normal subgroup of G. Suppose that there exists $\delta \in {{\operatorname {Irr}}}(N)$ such that $\chi =\delta ^G\in {{\operatorname {Irr}}}(G)$ . Then ${{\operatorname {Van}}}(\chi )\cap N\neq \emptyset $ .

Proof. Without loss of generality, we may assume that $\chi $ is faithful. Note that ${\mathbf Z}(G)<N$ . Therefore, $N/{\mathbf Z}(G)\cap {\mathbf Z}_2(G)/{\mathbf Z}(G)>1$ . Thus, there exists a noncentral element $x\in N\cap {\mathbf Z}_2(G)$ . Now, a similar argument as at the end of the proof of [29, Theorem C] shows that $\chi (x)=0$ .

Now we are ready to prove the promised result.

Proposition 7.8. Let G be a finite p-group. Suppose that $\chi ,\psi \in {{\operatorname {Irr}}}(G)$ and ${{\operatorname {Van}}}(\chi )={{\operatorname {Van}}}(\psi )$ . If $\chi (1)=p$ , then $\psi (1)=p$ .

Proof. We argue by induction on $|G|$ . Suppose first that there exists M maximal in G such that $\chi _M,\psi _M\in {{\operatorname {Irr}}}(M)$ . Then the result follows from the inductive hypothesis.

Now let M be a maximal subgroup of G. The hypothesis ${{\operatorname {Van}}}(\chi )={{\operatorname {Van}}}(\psi )$ and Lemma 7.6 imply that one of the characters is induced from M if and only if the other character is also induced from M. Therefore, we may assume that for any M maximal in G, both $\chi $ and $\psi $ are induced from M.

Let ${\mathbf Z}(G)\leq N\trianglelefteq G$ such that $G/N$ is elementary abelian of order $p^2$ . Let $\nu \in {{\operatorname {Irr}}}(N)$ lie under $\chi $ . Let $T:=I_G(\nu )$ . Since $\chi (1)=p$ , Clifford’s correspondence implies that $N<T$ . Therefore, if $T<G$ , then T is a maximal subgroup of G. Write $G/N=T/N\times U/N$ for some U maximal in G. Since $I_U(\nu )=N$ , $\nu $ induces irreducibly to $\mu \in {{\operatorname {Irr}}}(U)$ . Note that $\nu $ lies under $\chi $ , so by comparing degrees, we have $\chi _U=\mu $ , and this is a contradiction. It follows that $\nu $ is G-invariant. The previous paragraph also implies that $G-N\subseteq {{\operatorname {Van}}}(\chi )={{\operatorname {Van}}}(\psi )$ . Now, by [12, Problem 6.3], $\chi $ is fully ramified with respect to $G/N$ . In particular, since $\nu $ is linear, we conclude that $\chi $ has no zeros in N, whence

$$ \begin{align*}G-N={{\operatorname{Van}}}(\chi)={{\operatorname{Van}}}(\psi).\end{align*} $$

Now let $\delta \in {{\operatorname {Irr}}}(N)$ lie under $\psi $ . Suppose first that $L:=I_G(\delta )$ is maximal in G. It follows from the Clifford theory that $\psi (1)/\delta (1)=p$ . Write $G/N=L/N\times V/N$ for some V maximal in G, so that $\eta =\delta ^V\in {{\operatorname {Irr}}}(V)$ lies under $\psi $ . We conclude that $\chi _V=\eta $ . By Lemma 7.6, $G-V\not \subseteq {{\operatorname {Van}}}(\psi )$ , which is a contradiction.

Now assume that $L=G$ . Using [12, Problem 6.3] again, we see that $\psi $ is fully ramified with respect to $G/N$ . Therefore, $\psi _N=p\delta $ . Since ${{\operatorname {Van}}}(\psi )\cap N=\emptyset $ , it follows that $\delta $ is linear, by Burnside’s theorem. The result follows in this case too.

Finally, assume that $L=N$ , so that $\psi =\delta ^G$ . By Lemma 7.7, $\psi $ has some zero in N. This is the final contradiction.

As a concluding remark, we do not consider in this paper the number of conjugacy classes on which two certain irreducible characters vanish simultaneously, or the number of irreducible characters sharing a certain common zero. We do think that this topic deserves further attention.